Abstract
Purpose
The study presents an averaged anterior eye geometry model combined with a localised material model that is straightforward, appropriate and amenable for implementation in finite element (FE) modelling.
Methods
Both right and left eye profile data of 118 subjects (63 females and 55 males) aged 22–67 years (38.5 ± 7.6) were used to build an averaged geometry model. Parametric representation of the averaged geometry model was achieved through two polynomials dividing the eye into three smoothly connected volumes. This study utilised the collagen microstructure x-ray data of 6 ex-vivo healthy human eyes, 3 right eyes and 3 left eyes in pairs from 3 donors, 1 male and 2 females aged between 60 and 80 years, to build a localised element-specific material model for the eye.
Results
Fitting the cornea and the posterior sclera sections to a 5th-order Zernike polynomial resulted in 21 coefficients. The averaged anterior eye geometry model recorded a limbus tangent angle of 37° at a radius of 6.6 mm from the corneal apex. In terms of material models, the difference between the stresses generated in the inflation simulation up to 15 mmHg in the ring-segmented material model and localised element-specific material model were significantly different (p < 0.001) with the ring-segmented material model recording average Von-Mises stress 0.0168 ± 0.0046 MPa and the localised element-specific material model recording average Von-Mises stress 0.0144 ± 0.0025 MPa.
Conclusions
The study illustrates an averaged geometry model of the anterior human eye that is easy to generate through two parametric equations. This model is combined with a localised material model that can be used either parametrically through a Zernike fitted polynomial or non-parametrically as a function of the azimuth angle and the elevation angle of the eye globe. Both averaged geometry and localised material models were built in a way that makes them easy to implement in FE analysis without additional computation cost compared to the limbal discontinuity so-called idealised eye geometry model or ring-segmented material model.
Keywords: Eye model, Localised eye, Ideal eye, Average eye, Mathematical model
1. Introduction
Finite element (FE) modelling of the human ocular globe can provide a powerful tool for the diagnosis and treatment of ocular disorders and diseases [1]. By simulating geometries and material properties of the human eye in conjunction with relevant physiological loads, it is possible to gain important but otherwise elusive insights into progressive ocular diseases [2] as well as estimate prognostic outcomes of clinical treatments [3,4]. In order to describe the human ocular globe mathematically, it is first necessary to model the associated geometry. At present, the approach to modelling the eye will either use a limbal discontinuity (so-called idealised) model [5], models that use simplified spherical non-physiological geometries in conjunction with scattered physiological dimensions measurements at the key points, or, patient-specific models which seek to achieve a high level of individualised anatomical and biomechanical accuracy [6].
On one hand, idealised limbal discontinuity geometry models are quite simple and relatively easy to construct, and as such, are very practical for running wide-ranged parametric studies that investigate the effects of certain geometrical and biomechanical aspects, such as the effect of central corneal thickness (CCT) on the eye's response to load [7]. Typically, corneal idealised limbal discontinuity models are appropriate when used for parametric studies to isolate the effects of specific parameters. In these models, either conic [[8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27]] or biconic [25,[28], [29], [30], [31], [32], [33], [34]] equations are used to model the cornea [35], however, the idealisation of the scleral geometry can be often seen in the literature through the modelling of the sclera as a perfect sphere [[36], [37], [38]]. On the other hand, oversimplification of the model geometry can cause significant misrepresentations of the peripheral cornea and limbus [35] and, therefore, render the models unsuitable for applications such as predicting interactions between soft contact lenses and the front surface of the eye where transitions in anterior geometry are largely relevant [[39], [40], [41]].
In contrast, patient-specific models are more reliable in predicting the response of the eye to load or light and even the outcome of surgical procedures through predicting the accurate geometry of the eye's surfaces and proportions that allows light raytracing [42], but their suitability comes into question with a wide range of parametric investigations as their geometric adaptability is very limited, having been constructed with explicit dimensions of specific eyes belonging to individual patients [[43], [44], [45], [46], [47], [48]]. As a result, researchers who investigate new objectives in eye simulation and treatments must either implement limbal discontinuity models that are idealised and do not precisely represent eye geometry or generate a very large number of patient-specific models often presenting a challenge due to the increased need for clinical measurements, mathematical modelling, and computational power. Many measurements of eye component dimensions have been reported in the literature, Table 1; however, building a full eye geometrical model needs a good assembly of corneal and scleral dimensions in a 3D space. Currently, there is a lack of an averaged 3D eye model that can represent the geometry of the human eye better than the limbal discontinuity idealised geometrical eye model and does not require the computing cost of modelling a lot of patient-specific models.
Table 1.
Measurement of the human eye components as reported in the literature.
| No | Year | Citation | Device | Sample size | Ethnicity | Findings |
|---|---|---|---|---|---|---|
| 1 | 2020 | [49] | Digital Vernier calliper, Ultrasound pachymeter |
5 human donor sclerae, age range 36–72 years | Caucasian | Sclera equatorial diameter: 24.26 ± 0.38 mm Sclera thickness: Anterior foramen 0.757 ± 0.059 mm Equator 0.630 ± 0.076 mm Posterior pole: 1.076 ± 0.023 mm |
| 2 | 2020 | [50] | Visual field analyser | 37 controls amongst 156 glaucomatous and hypertensive eyes | CCT: 0.553 ± 0.033 mm |
|
| 3 | 2020 | [51] | Pascal dynamic contour tonometer | One hundred subjects (100 eyes) aged between 17 and 30 years | CCT: 0.545 ± 0.033 mm Central corneal radius: 7.75 ± 0.26 mm |
|
| 4 | 2019 | [52] | Optical biometer, Ultrasound pachymeter |
2346, grade 7 students participated with an average age of 13.8 years 1133 girls 1213 boys |
Chinese | Axial length: 23.59 ± 0.90 mm CCT: 0.535 mm |
| 5 | 2019 | [53] | Ultrasound pachymeter, Optical coherence tomography, Corrected specular microscopy, Corneal topography with a combined Scheimpflug–Placido system, Optical biometry, Specular microscopy |
CCT: 0.545 ± 0.031 mm CCT: 0.545 ± 0.033 mm CCT: 0.538 ± 0.032 mm CCT: 0.536 ± 0.032 mm CCT 0.528 ± 0.03 mm CCT: 0.525 ± 0.032 mm |
||
| 6 | 2019 | [54] | Fourier transform profilometer | This is a prospective case series including 88 healthy eyes of 88 patients with an age ranging from 21 to 73 years | Central corneal radius: 8.54 ± 0.38 mm Sclera radius: 13.35 ± 1.29 mm |
|
| 7 | 2019 | [55] | Optical biometer | 43 subjects (55 eyes) with a mean age of 71 years | Horizontal visible iris diameter: 12.16 ± 0.447 mm CCT: 0.562 ± 0.032 mm |
|
| 8 | 2018 | [56] | Ultrasound pachymeter | 72 subjects, 40 females & 32 males |
Malays | Average corneal thickness (CCT) was 0.598 ± 0.035 mm |
| 9 | 2017 | [57] | Tonometer | 158 healthy adults (158 eyes) | Chinese | CCT: 0.539 ± 0.033 mm |
| 10 | 2017 | [58] | Optical coherence tomography | 30 healthy subjects, age 23.8 ± 2 years, 11 males & 19 females |
Central corneal radius: 7.74 ± 0.26 mm Corneal eccentricity: 0.49 ± 0.12 mm |
|
| 11 | 2015 | [59] | Light microscopy | 281 eyes of 281 subjects mean age of 24.8 6 23.1 years (range, 1–83 years) | Chinese | Axial length: 24.3 6 3.9 mm Scleral thickness: 0.467 ± 0.091 mm (Limbus) 0.357 ± 0.094 mm (Equator) 0.711 ± 0.170 mm (Posterior pole) |
| 12 | 2015 | [60] | Scheimplflug topography | Right eye | CCT: 0.585 mm |
|
| 13 | 2014 | [61] | Computed tomography scan | 250 | Transverse length: 24.2 mm Sagittal length: 23.7 mm Axial length: 22.0–24.8 mm Diameter: 21–27 mm |
|
| 14 | 2013 | [33] | Scheimpflug topography | 342 Human Central and minimum corneal thicknesses |
CCT: 0.541 ± 0.028 mm (OD) 0.541 ± 0.029 mm (OS) |
|
| 15 | 2013 | [32] | Scheimpflug topography | The corneal shape of 407 normal eyes of 211 subjects with ages ranging from 4 to 79 years old | CCT: 0.55 ± 0.034 mm PCT: 0.729 ± 0.048 mm |
|
| 16 | 2012 | [62] | Light microscopy | 238 human eyes (mean age of 62.0 ± 13.1 years) | Scleral thickness: 0.536 ± 0.14 mm (Limbus) 0.396 ± 0.17 mm (Equator) 0.9–1.0 mm (Posterior pole) |
|
| 17 | 2012 | [62] | Light microscopy | 238 human globes of 238 subjects. Ages between 24 and 89 years. Mean age is 62 ± 13.1 Population was subdivided into 162 eyes enucleated due to malignant choroidal melanoma, and 76 eyes enucleated because of secondary angle-closure glaucoma |
Scleral thickness: 0.50 ± 0.11 mm (Limbus) 0.42 ± 0.15 mm (Equator) 0.946 ± 0.18 mm (Posterior pole) |
|
| 18 | 2011 | [63] | Scheimpflug topography, Ultrasound pachymeter |
67 eyes of 40 patients 24 males and 16 females Mean age was 38.65 ± 14.58 years Ages between 19 and 76 years |
CCT: 0.550 ± 0.034 mm CCT:0.548 ± 0.034 mm |
|
| 19 | 2011 | [64] | Ultrasound pachymeter | central corneal thickness (CCT) measurements were taken in 99 subjects (age, 21 ± 2 years) who were free of ocular and systemic disease. |
CCT: 0.546 ± 0.03 mm |
|
| 20 | 2011 | [65] | Optical coherence tomography | Ocular surface topography was analysed in 50 subjects aged 22.8 years (SD ± 5.0) | The mean horizontal corneal diameter was 13.39 ± 0.44 mm | |
| 21 | 2010 | [66] | Electronic Vernier calliper | 36 human donor sclerae. The average and standard deviation of the donors' age were 62.3 ± 19.4 years (range 52–96 years). |
Scleral thickness: 0.767 ± 0.035 mm (Limbus) 0.701 ± 0.096 mm (Equator) 1.062 ± 0.006 mm (Posterior pole) |
|
| 22 | 2009 | [67] | Scheimpflug topography, Noncontact specular microscope, Ultrasound pachymeter |
2 groups of patients. Group 1: normal subject: 47 normal volunteers (94 eyes) with an average age of 33 years (range 21–46 years). |
CCT: 0.553 ± 0.037 mm CCT: 0.512 ± 0.039 mm, CCT: 0.533 ± 0.038 mm |
|
| 23 | 2009 | [68] | MRI scanner | 11 enucleated human globes 7 normal, 4 with a reported history of glaucoma |
Limbus: 0.588 ± 0.063 mm Equator: 0.491 ± 0.091 mm Posterior Pole: 0.996 ± 0.181 mm |
|
| 24 | 2006 | [69] | Ultrasound biomicroscopy | 140 eyes of 140 subjects with no previous history of intraocular surgery were enrolled. Age 57.0 ± 15.7 years |
Refractive error −1.3 ± 5.0 dioptres. | |
| 25 | 2005 | [70] | Slit-scanning topography | 370 right eyes and 373 left eyes 148 females & 242 males, age 10–80 years |
Corneal diameter: 11.71 ± 0.42 mm CCT: 11.77 ± 0.37 mm in males,11.64 ± 0.47 mm in females. |
|
| 26 | 2005 | [20] | Scheimpflug imaging system | 114 right eyes from 114 patients. 57 males and 57 females, age 18–65 years |
Central corneal radius (anterior): 7.79 ± 0.27 mm Central corneal radius (posterior): 6.53 ± 0.25 mm. |
|
| 27 | 2004 | [71] | Light microscopy | 111 Human globes, age 60.2 ± 15.0 years | CCT: 0.617 ± 0.108 mm Central lamina cribrosa thickness: 0.378 ± 0.118 mm |
|
| 28 | 2004 | [72] | Ultrasound pachymetry | 90 eyes,age 55.04 ± 15.11 years | CCT: 565.0 ± 42.5 μm | |
| 29 | 2003 | [13] | Scheimpflug imaging system | 83 subjects,40 females & 43 males, age 37.7 ± 12.2 (range 16–62) years | Central corneal radius (anterior): 7.87 ± 0.27 mm Central corneal radius (posterior): 6.40 ± 0.28 |
|
| 30 | 1997 | [73] | Millimeter scale ruler | 55 eyes (ex vivo) | Scleral thickness: Limbus 0.53 ± 0.14 mm Equator 0.39 ± 0.17 mm Posterior (near optic nerve): 0.9–1.0 mm |
In terms of ocular material modelling, the eye exhibits age-dependent, anisotropic, hyperelastic and viscoelastic behaviour [[74], [75], [76], [77], [78]]. As the eye's material stiffness varies with location on the eyewall, more complicated models reflecting regional variations were needed [[79], [80], [81], [82]]. Ocular material models range from linear elastic homogenous models [[83], [84], [85], [86]] to ring-segmented nonlinear anisotropic models [[87], [88], [89], [90], [91], [92], [93], [94], [95]] and, more recently, constitutive models based on the eye's microstructure as captured via x-ray [81,96]. However, considering x-ray scattering data resulted in good detail of how collagen fibril density and arrangement varied throughout the thickness of the cornea [89,94,96,97], the need for writing customised user-subroutines for the eye's constitutive FE models made these models less attractive as the computational cost is considerably higher, and more importantly, replicating these customised constitutive models is always quite a complicated challenge. Currently, there is a lack of local element-specific FE material models of the eye that do not rely on user-subroutines and hence, there is no simple way of considering the local variation of human eye material characteristics in FE analysis and a local element-specific material model could offer an accurate simple applicable model.
This study represents an averaged geometry model combined with a localised element-specific material model for the anterior human eye, that is suitable for FE modelling purposes. The model is not oversimplified or complicated; however, it represents geometrical and biomechanical variations of the human eye for the acquisition of localised deformations. Through a limited set of equations, both eye geometry and material FE model can be generated and used for different anterior eye biomedical applications. The model has precise material properties that were quantified by x-ray scans over the whole eye globe, averaged measured topography in the cornea and anterior sclera and interpolated geometry in the equatorial and posterior sclera using clinically measured axial lengths, hence the emphasis on using the presented model for anterior eye related applications. The model is designed in a way that ensures its replicability in terms of both geometry and material characteristics.
2. Materials and methods
2.1. Data record review
In order to determine the geometrical model, the study used a collection of fully anonymised clinical data which cannot be linked to individuals and has been utilised in various previously published studies in the ocular geometry research field [[98], [99], [100]]. Only healthy eyes were selected from the record to be processed in solely secondary analyses; therefore, no participants were recruited for this study. Both right and left anonymised eye profile data were extracted from the recorded data of 118 Caucasian subjects (63 females and 55 males) aged 22–67 years (Mean ± SD = 38.5 ± 7.6 years). Recorded data for individuals who were myopic, astigmatic, had a history of trauma or suffering from ocular diseases or had ocular surgeries were excluded.
In order to determine the material model, this study utilised the microstructure data of 6 ex-vivo healthy human eyes used in a previous study, three right eyes and three left eyes in pairs from 3 donors, one male and two females aged between 60 and 80 years [82]. The limited number of eyes used for the material characterisation process was due to the profound complexity of carrying out high-intensity synchrotron x-rays scans and the consequent microstructure analyses associated with this process. Like the clinical data, tissues analysed for this study were obtained and handled following the local ethical regulations and tenets of the Declaration of Helsinki were obeyed throughout. The Cardiff University's Human Science Ethical Committee of the School of Optometry and Vision Sciences (Cardiff University, UK), in addition to the Southeast Wales Research Ethics Committee (Cardiff, UK) approved the use of the human tissue utilised for this study in x-ray scattering research. Resulted data of the x-ray-based analyses were used to construct a localised element-specific material model in the current study.
The eye surface profile scan process was carried out using a contact-less corneo-scleral Eye Surface Profiler (ESP), (Eaglet Eye BV, AP Houten, The Netherlands). The ESP is an eye height profilometer that uses the profilometry capture technique and has the potential to measure the corneo-scleral profile beyond the limbus [101]. Participants were instructed to open up their eyes wide before the ESP measurements to obtain surface reading coverage up to a few millimetres beyond the limbus. After three measurements triggered per eye, the reading with the largest scleral surface coverage was included in the analysis.
Exported data from the ESP software characterised topographical information of eyes and was imported into MATLAB in binary data container format (*.mat). Custom built MATLAB codes independent from this software were then used to extract and process the ESP data. A mesh grid covering −10 to 10 mm in 700 increments in the nasal-temporal direction and −8 to 8 mm in 800 increments in the superior-inferior direction. A scalar representation NaN (not a number) was used to denote missing elevation values at the edges where the ESP was unable to collect a reading. Measurements in which the corneo-scleral area was covered by eyelids were excluded [102]. Participants’ axial length was extracted from an optical biometer (Lenstar 900, Haag-Streit, US) which acquired and averaged several measurements during each acquisition. This measurement was essential in constructing the posterior portion of the presented eye model.
2.2. Statistical analysis
The null hypothesis, at a pre-selected 95% confidence, from MATLAB's Statistics and Machine Learning Toolbox, was used to investigate the inferences of findings based on statistical evidence. Statistical analysis of the dataset was completed with Kolmogorov-Smirnov test (Eq. (1)) via MATLAB [103], confirming the normal distribution of the samples.
| Eq.1 |
Where and correspond to empirical distribution functions of sample one and sample two correspondingly, and is the supremum function [104].
This provided a comparison between the cumulative distributions of both data sets. Applying a two-sample t-test allowed the investigation of significance between pairs of data sets. The probability value (p) lies within the closed period [0.0 1.0], where values of P > 0.05 indicate that the null hypothesis is valid and probability P < 0.05 confirms that the assessed findings represent an independent record [105]. The “ttest2” function was selected in MATLAB for returning p-values and binary test decisions for the null hypothesis.
2.3. Mathematical modelling
The mathematical modelling of the eye in this study was carried out in two main blocks: geometrical modelling and material modelling. First, an averaged geometry eye model was generated and further compared to the conventional limbal discontinuity idealised geometry eye model. The second stage was to develop a local element-specific material model and compare it with a conventional ring-segmented material model, Fig. 1.
Fig. 1.

Mathematical modelling plan layout. Green items are the main elements of this study; however, red items are presented to allow comparison of the new models with conventional models.
2.4. Geometrical modelling
Three main data pre-processing steps were followed for each measurement: (a) alignment, (b) removal of edge artefacts, and (c) averaging, followed by two stages of analysis (d) averaged eye 3D surfaces modelling (e) parametric representation of averaged eye model and finally describing the conventional (f) limbal discontinuity idealised eye model to compare it with the new averaged eye model presented in this study.
2.4.1. Alignment
The ESP implements visual axis alignment internally; however, it is necessary for extra analyses to be performed to ensure that all eyes' topography data share the same alignment [99,106]. An adequate alignment relies on the ESP red-cross system focusing is not always possible. The offset of the foveal centre, the light-receptive part of the retina responsible for sharp vision, lies 3.4 mm temporal to the optic disk boundary [107], combined with 2.5 mm offset in the temporal direction to the eye's optical axis [108] results in a rotation of the eye to a tilted orientation to allow refracted light to fall on the fovea. A 3D non-parametric method, previously presented [106], was used to locate the limbus profile of each eye individually so that a best-fit plane could be imposed on each eye's topography data set directly though the located limbus. A 3D rotation matrix [109] then rotated the topography data around the X-axis and Y-axis by the tilt angles αy and αx in turn to complete the limbus alignment process in the XY-Plane.
2.4.2. Removal of edge artefacts
After applying the alignment procedure to ensure that all eyes are equally orientated, artificial edges from each eye's profile were identified and removed. Abrupt changes in the surface data pertain to the effects of tear film meniscus, eyelid edges or lashes encroaching on the imaged region and do not conform with the eye's natural shape [102]. A moving median of the eye height data was calculated along the eye meridians, and, considering the robust principles of shape that cannot be affected by outliers, this allowed edge effects to be detected and discarded [102].
2.4.3. Averaging
As the corneal, limbal and scleral portions of each eye were identified while the removal of edge artefacts process took place [102], a best-fit sphere was fitted to each sclera using the least-squares error method while the posterior hemispherical part was stretched linearly to meet the axial length geometrical measurement requirements. As the ESP provides a measurement of a portion of the anterior sclera, this measured portion was not replaced by the best-fitted sphere surface, the fitted sphere was only used for representing the unmeasured parts of the sclera before stretching the posterior hemispherical. At this stage, the origin for each eye's 3D cartesian dataset was shifted to the sclera centre (best-fitted sphere centre) before being translated to spherical coordinates where the azimuth angle varied between 0° and 359°, the elevation angle (E) varied between 90° at the corneal apex and −90° at the posterior pole and finally, the radius represented the distance between every point on the eye's surface and the sclera centre. The limbus position of the averaged model was determined based on the average elevation angle of the limbus of individual eyes, however, the limbus position of individual eyes was located using the non-parametric method presented in Abass et al. [106], which detects the remarkable change in the corneal surface tangent angle between the corneal surface and the scleral surface. The corneal posterior surface was built based on the averaged measurements reported in Table 1, with a central thickness CCT of 0.55 mm [[67], [110], [111]] and limbal thickness of 0.7 mm (CCT+0.15 mm [[110], [111], [112]]) and the scleral internal wall was built with an equatorial thickness of 0.56 mm [62,113] and posterior pole thickness of 0.84 mm (1.2 of the limbal thickness [66]) linearly changing with the elevation angle E from participant to participant. Once the data for all eyes was represented in the spherical coordinate system, and average values of the radii at each azimuth and elevation angle were calculated. To avoid any bias in the results because of the natural correlation between fellow eyes, previous processes were initially performed on right and left eyes independently. Once the averaging process was achieved for right and left eye sets, the left eye averaged geometry was flipped around the superior-inferior plan and then averaged once again with the right eye's averaged geometry and the pre-processing stage was completed.
2.4.4. Averaged eye 3D surfaces modelling
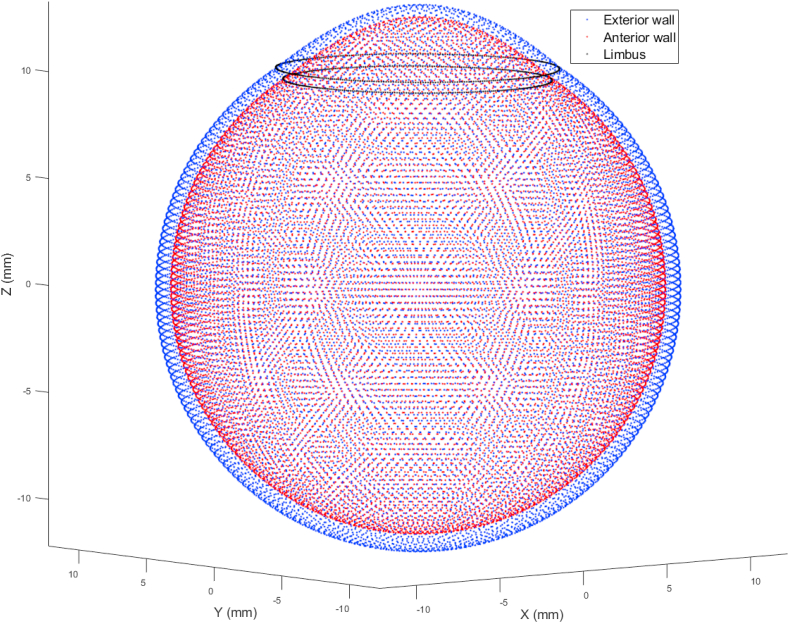
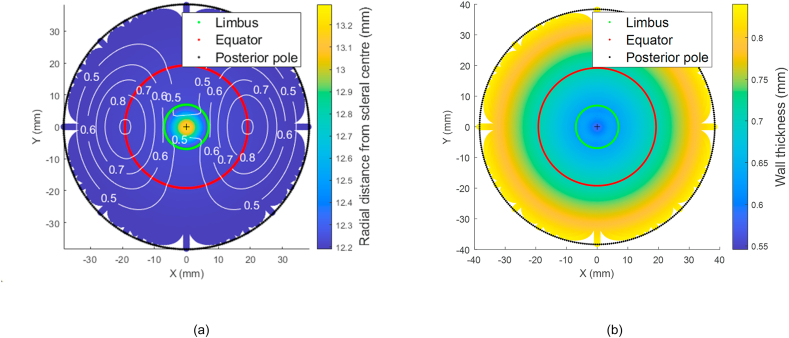
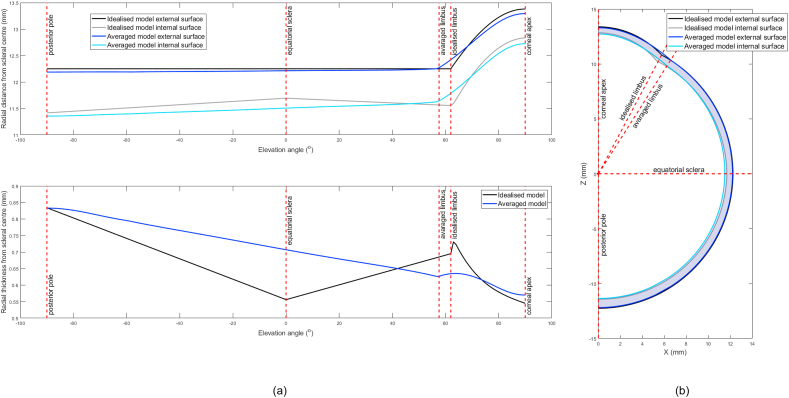
Completion of the averaging process allows the averaged eye model to be represented in a 3D point cloud plot as shown in Fig. 2. For display purposes, the averaged eye 3D surfaces model globe was flattened with the corneal apex located at the centre, Fig. 3(a,b). Distances on the surface of the eye globe were calculated by multiplying the elevation angle, measured from the corneal apex, at each point by the radial distance at this point as measured from the scleral centre. The position of the limbus on the averaged eye globe was located by averaging the limbal elevation position of all studied eyes and hence used as a landmark for the edge of the cornea (Ec), Fig. 4(a and b).
Fig. 2.
Mean eye globe model resulting from averaging 118 eyes.
Fig. 3.
(a) Mean radial distances of the averaged eye 3D surfaces model flattened to two-dimensional view. The white contour line represents the standard deviation (b) Average eye globe thickness map flattened to two-dimensional view.
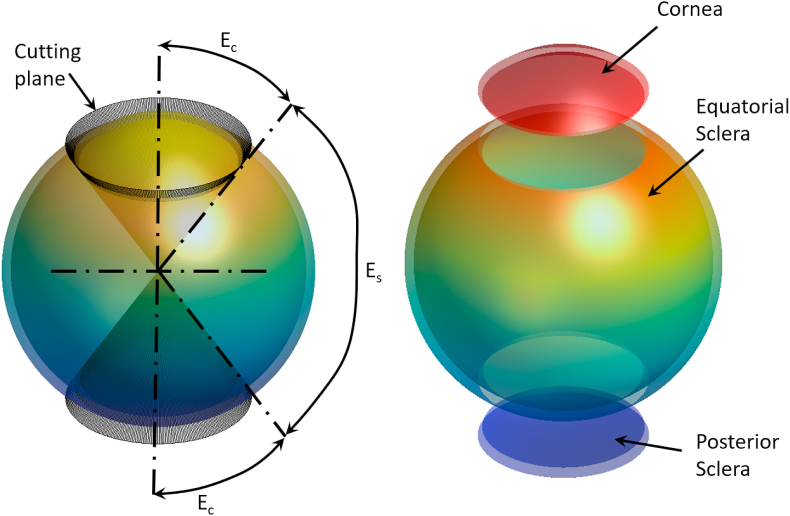
Fig. 4.
The eye globe is divided into three sections based on the corneal edge elevation angle Ec and equatorial scleral elevation angle Es, (a) The deviation process, (b) Eye globe volumes separated for display purposes.
2.4.5. Parametric representation of the averaged eye geometry model
The averaged eye globe model was then divided into three sections: the cornea, the equatorial sclera, and the posterior sclera. The division process was carried out in 3D using the corneal edge elevation angle Ec to split the cornea portion and the same angle to split the posterior sclera portion while the equatorial scleral angle was set to Es = 180°-2Ec, Fig. 4(a and b). The rationale behind this deviation is to allow using Zernike polynomials in the corneal and posterior scleral sections as Zernike polynomials are ideal for spherical surfaces and give a good representation of the surface geometry by controlling 21 parameters, however, the equatorial scleral section is not that complicated so it can be represented using a 5th-degree polynomial and controlled by 6 parameters only. Therefore, both cornea and posterior sclera sections were fitted to 5th-order Zernike polynomials, with normalised radius r∈[0,1] (Eq. (2)). Polynomial coefficients a1 to a21 were calculated using the minimum least-squares method.
| Eq.2 |
Relevant cartesian coordinates of the cornea can be expressed as:
| Eq.3 |
where is the limbus anterior radius and is the azimuth angle that varies between 0° and 359° [114]. Similarly, the posterior surface of the corneal surface was fit to Eq. (2) and the relevant cartesian coordinates of the cornea can be expressed as:
| Eq.4 |
where is the limbus internal radius. Subindices “c”, “i” and “o” stand for the cornea, inner surface, outer surface, and “l” for the limbus, respectively.
The sclera equatorial section was fitted to a 5th order polynomial as a radius (Rs) estimated as a function of the sclera elevation angle (Es = 90° to −90° in 1° steps), Eq. (5) where coefficients a1 to a6 were determined for every individual external and internal surface independently using least-square error method.
| Eq.5 |
While using Eq. (6) to Eq. (11), Rs = Rso represents the radius of the external surface and Rs = Rsi represents the radius of the internal surface of the sclera in the spherical coordinate system and subindex “s” stands for the sclera. Relevant cartesian coordinates of the sclera can be expressed as in Eq. (6), Eq. (7) & Eq. (8)
| Eq.6 |
| Eq.7 |
| Eq.8 |
for the external surface, and Eq. (9), Eq. (10) & Eq. (11)
| Eq.9 |
| Eq.10 |
| Eq.11 |
for the internal surface.
Finally, the posterior scleral section was fitted to a 5th order Zernike polynomial, with normalised radius r∈[0,1] (Eq. (2)). Polynomial coefficients a1 to a21 were calculated using the minimum least-squares method. Relevant cartesian coordinates of the cornea can be expressed as in Eq. (12)
| Eq.12 |
Similarly, the posterior surface of the corneal surface was fit to Eq. (3) and the relevant cartesian coordinates of the cornea can be expressed as in Eq. (13)
| Eq.13 |
where is the limbus internal radius.
2.4.6. Limbal discontinuity idealised geometrical eye model
For comparison purposes, a limbal discontinuity geometrical eye model was also built. The eye geometrical model described in this section is a conventional so-called idealised model that has been used extensively in ophthalmology-related parametric studies [37,115]. The purpose of presenting its characteristics here is to allow the comparison between the limbal discontinuity eye model and the averaged eye model presented in the current study. The rotationally symmetric limbal discontinuity model was constructed with an anterior corneal radius 7.8 mm, conical shape factor 0.8 [35], central thickness CCT 0.545 mm, scleral radius 12.25 mm (Table 1), limbal thickness 0.695 mm, equatorial thickness 0.556 mm, posterior pole thickness 0.834, and limbus diameter 11.5 mm. The anterior sclera surface was taken as a perfect sphere centred at the origin (0,0,0) with no consideration for the axial length as a separate variable that might alter the posterior geometry of the model. The axial length in the ideal model configuration comes as a result of combining the dimensions of the other eye components.
2.4.7. Finite element modelling
FE models built in this study consisted of 28,800 three-dimensional 8-node solid hybrid elements (C3D8H) with 43,206 nodes in 2 layers based on a mesh convergence study. The equator nodes were restricted in the axial direction as a boundary condition for the simulation. Analyses were carried out in ABAQUS (Dassault Systèmes, Vélizy-Villacoublay, France) FE computer software that has been licenced to the University of Liverpool, UK. The internal surface of the eye was defined as an element-based surface, and the internal pressure was applied statically in equal increments of 0.1 from 0.0 to 1.0 in a normalised time scale. Static loading time increment is a fraction of the total extent of the ABAQUS simulation step, not a physical time. In this case, it was selected to obtain a well-distributed stress-strain curve over 10 frames. To achieve the eyes’ stress-free geometry (at intraocular pressure IOP = 0 mmHg), eye globe models were initially constructed with the pressured dimensions, and then a stress-free adaptation of each model was calculated by following the iterative method presented in [116]. In each case, the stress-free model was calculated by considering a typical IOP of 15 mmHg [117] and a maximal node position error under 10−4 mm. When the stress-free models were established, they were pressurised to 15 mmHg to mimic the aqueous and vitreous effects simulate physiological IOP. Analyses were carried out using the implicit integration scheme while the nonlinear geometry option “NLGEOM” of ABAQUS was set to “ON” during the simulation process.
2.5. Material modelling
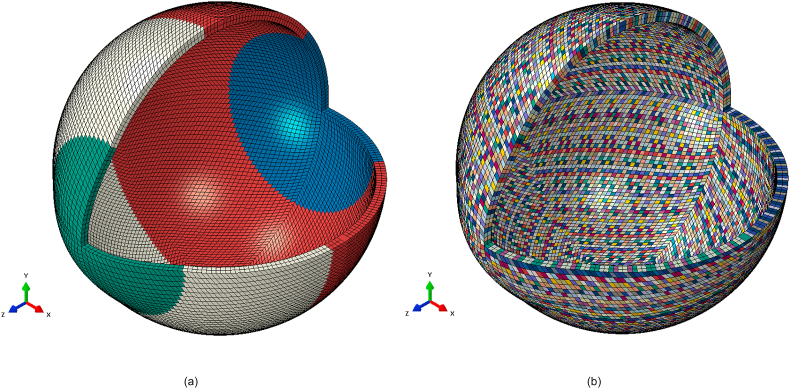
Following the geometrical modelling, two material models were compared in this study, the newly created localised element-specific material model and the conventional ring-segmented material model, Fig. 5(a and b).
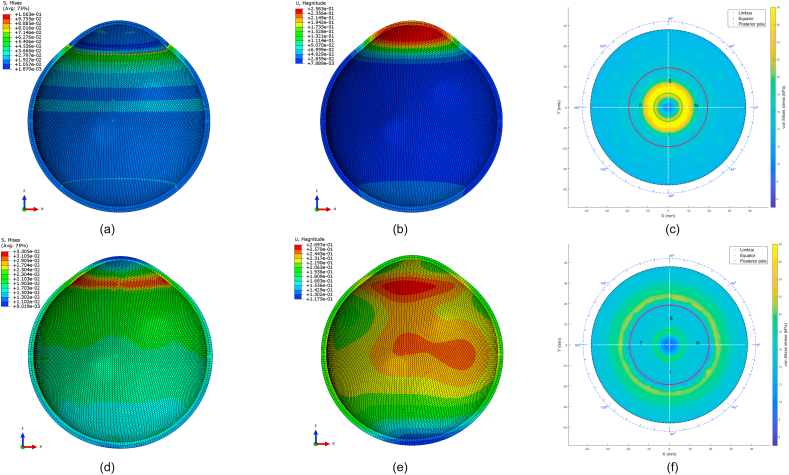
Fig. 5.
Averaged geometry eye model with different colours corresponding to different materials (a) Ring-segmented material model, (b) Localised element-specific material model.
2.5.1. Localised element-specific material model
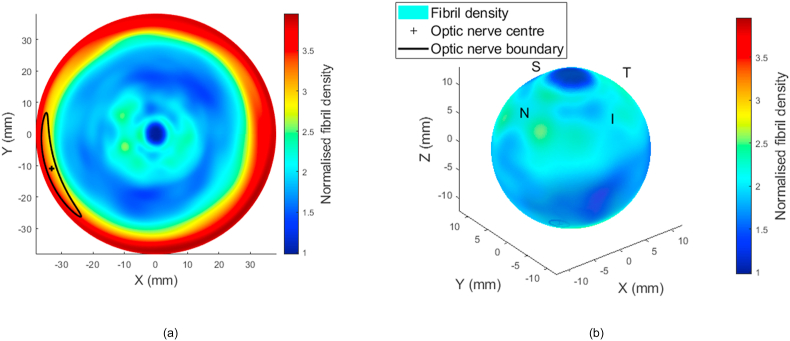
Eyes’ x-ray scattering data was used to build the localised element-specific material numerical model of the eye. Left eyes data were flipped around the superior-inferior plane and matched with right eyes [118,119] before being averaged with them; therefore, the model represented in this study is for an average right eye; however, a left eye model could be obtained by flipping the average right eye model around the superior-inferior plane. The process of calculating the collagen content is described in Ref. [82], where wide-angle x-ray scattering was applied to healthy ex-vivo eyes. Each eye was dissected into anterior and posterior cups, and a method was developed to use the microstructure data obtained for the dissected tissue to build 3D maps of fibril density. During this process, gaps that result from cutting the eyes to allow scanning them in 2D were filled by linearly distributing the data in the neighbouring scanned tissues. Ex-vivo thickness measurements were taken using an ±5 μm accuracy ultrasound pachymeter (Pachmate 55; DGH Technologies, Exton, PA). Thickness measurements were obtained at the centre of each cornea and along eight meridians marked axially at increments of 2.5 mm. The final values of a combined single map were the average of 6 maps that had been flattened into a common 2D grid; these values represented a mean of three measurements taken at each point possessing a standard deviation of less than 10 μm for all pachymetry thickness measurements. In order to estimate corneal tissue thickness throughout the entire corneal surface, cubic interpolation was applied to the thickness maps. By dividing the total x-ray scattering intensity by the local tissue thickness, the fibril density could then be calculated. A digital electronic Vernier calliper (D00352, Duratool, Taiwan) with a 10 μm accuracy was used to measure the position of the optic nerve head relative to eight drawn meridians, as well as the overall diameter for each eye. The flattened 2D mapped collagen map presented in Fig. 6(a) is plotted against peripheral lengths of the eye globe with the centre at the corneal apex for displaying purposes, Fig. 6(b).
Fig. 6.
(a) Fibril density map of the eye flattened in 2D with the corneal apex at the centre and the posterior pole at the periphery. The map is normalised against the fibril density at the corneal apex at the centre of the map. (b) Fibril density map of the eye mapped to the 3D eye shape.
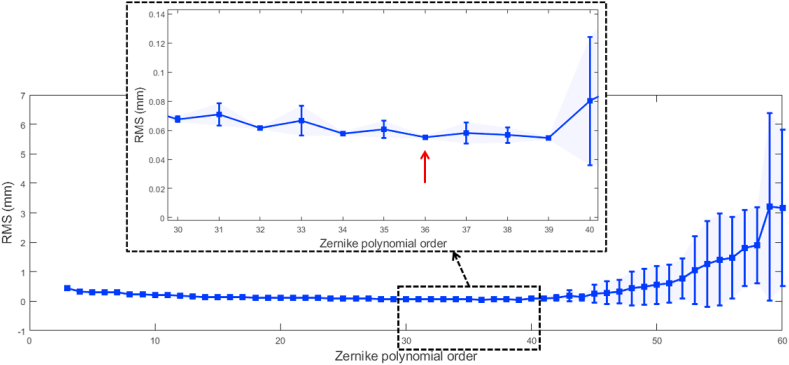
A Zernike polynomial was chosen for fitting the normalised collagen map in Fig. 6, where the order of the polynomial was selected based on the K-fold cross-validation method, Fig. 7. Collagen map data were shuffled randomly and split into K = 5 groups. The cross-validation process was carried out in 5 loops for each Zernike polynomial order where each group was taken as a test set while the other 4 groups were taken together as a training set. The polynomial was fitted to the training set and evaluated against the test set. The model evaluation score was evaluated by the average root-mean-square (RMS) of the error among the 5 groups, along with its standard deviation. Our investigation showed that an order of 36 is the best for fitting the Zernike polynomial that represents the collagen contents, hence the material stiffness map (see the supplementary material S1, S2). Such high order was needed to ensure an accurate representation of the material stiffness in certain areas like the limbus and the optic nerve zones as an undesirable smoothing effect was noticed at these areas when a lower order is considered. This high order could be viewed as a disadvantage of the parametric material model, but it only needs to be calculated once in each FE model. Running this parametric material model took 0.0323 s in an Intel(R) 4 Core (TM) i7-4790 CPU operating at 3.60 GHz in an MS Windows 10 system. In addition, as the parametric material model has a relatively high order, a non-parametric model was also provided as a matrix corresponding to eye azimuth angles from 0° to 359° and elevation angles from 90° to −90° (see the supplementary material S3). Running this parametric material model took 1.435 s in the same mentioned computing unit.
Fig. 7.
K-fold cross-validation RMS error with standard deviation plotted as error bars.
In this study, incompressible, hyperelastic nonlinear stress-strain material behaviour was considered [120,121], and a first-order Ogden material model was used in the FE modelling in the form of strain energy density function (Eq. (14)):
| Eq.14 |
where is the strain energy, are the deviatoric principal stretches (ratios of final lengths to initial lengths), the rigidity modulus (MPa) and the exponent of material stress-strain behaviour curve. The variation of collagen fibril density from region to region in the eye globe wall was considered to be proportional to the alteration of rigidity modulus in the Ogden model. This approach was derived from the Ogden material model and based on the stress-strain relation that in simple tension mode and Eulerian description [122], Eq. (15):
| Eq.15 |
where is the Cauchy stress (MPa) and is the tension stretch ratio. The rigidity modulus linearly alters the Cauchy stress tensor, and therefore, it was chosen to act as a link between total collagen fibrils contents resulting from x-ray refraction analyses and the modelled eye material stiffness. In order to vary the stiffness accordingly, the variation of collagen fibril density was reflected in the rigidity modulus .
Considering the age-related effect on ocular tissue material requires adjusting material parameters accordingly. Hence, rearranging Eq. (15) results in Eq. (16)
and for age 70 years as
| Eq.16 |
with the exponent fixed to a scaler and eyes being strained to equal starch , then Eq. (17)
| Eq.17 |
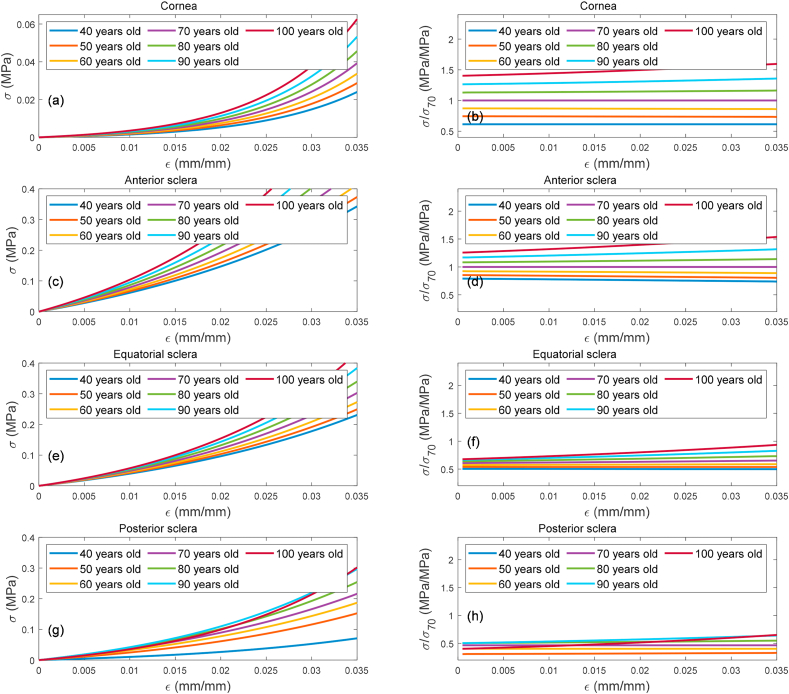
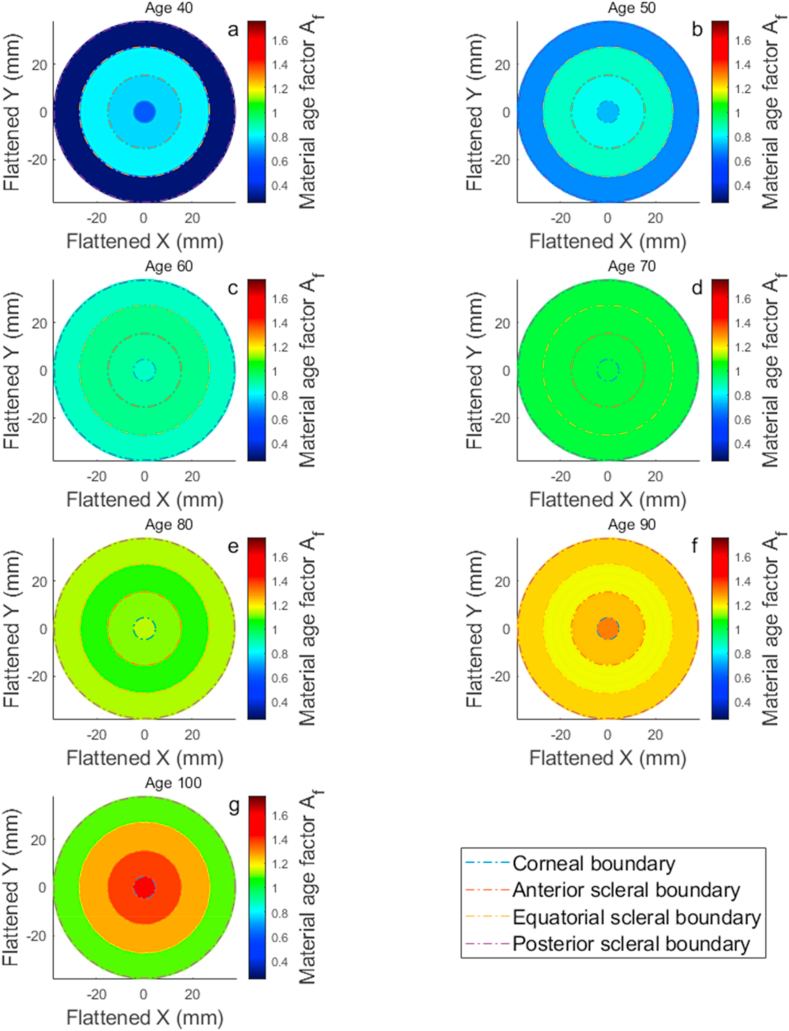
where is an age factor determined by normalising the averaged stress-strain behaviour of both cornea and sclera following [75,123] against the median noted age of 70 years, Fig. 8(a,b,c,d,e,f,g,h). The can be broken down into 4 main parameters covering the cornea , anterior sclera , equatorial sclera , and posterior sclera , Table 2. Ages under 40 years were excluded in these material age related analyses to avoid inaccuracies resulting from using a limited number of human donors used to estimate eye material stiffness at such an early age range [75,123]. To facilitate the material model and allow covering the eye matter stiffness variation with age, the material age factor was represented as a map for each age, Fig. 9(a,b,c,d,e,f,g), where the discretised spline robust smoothing was applied to ensure a smooth transition between eye globe boundaries [124].
Fig. 8.
Age related effect in corneal stiffness represented by stress-strain behaviour as concluded in [75,123], a, c, e & g. Stresses in the second column subfigures b, d, f & h) were normalised against the stress behaviour of age 70 years ocular tissues.
Table 2.
The material age factor .
| Elevation angles | Age factor |
Age range in years old |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||
| Cornea | Ec = 55.0°: 90.0° | 0.61 | 0.74 | 0.87 | 1.00 | 1.14 | 1.31 | 1.49 | |
| Sclera | Es = 7.5°:55.0° | 0.77 | 0.83 | 0.91 | 1.00 | 1.11 | 1.24 | 1.38 | |
| Es = −47.5°: 7.5° | 0.80 | 0.86 | 0.92 | 1.00 | 1.08 | 1.17 | 1.26 | ||
| Es = −90.0°: −47.5° | 0.29 | 0.68 | 0.87 | 1.00 | 1.13 | 1.22 | 1.09 | ||
Fig. 9.
Age related effect in corneal material stiffness age factor maps flatten to two-dimensional views and cover the age range 40(a) to 100(g) years. Subplots b, c, d, e & f represent ages 50, 60, 70, 80 and 90 years, respectively.
2.5.2. Ring-segmented material model
For comparison purposes, the ring-segmented eye was modelled as a hyperelastic material with a density of 1000 kg/m3 and split into four regions; the cornea (μc = 0.07, αc = 110.8), and the sclera in three elevation angles at 55°, 7.5°, −47.5° measured from scleral geometric centre, segmented the equatorial and posterior sclera, the latter allowed the characterisation of mechanical properties within circumferential regions containing isotropic elements that replicated macroscale scleral displacements. Shear modulus parameters were imposed as μs1 = 0.441, αs1 = 124.5, μs2 = 0.349, αs2 = 138.5, μs3 = 0.308 and αs3 = 162.2. To represent the mechanical response of the eye's tissue under loading conditions, first-order Ogden material models [122] from earlier experimental studies were used [120,123,125].
3. Results
When eyes were averaged based on their surfaces' radial distances from the scleral centre in the spherical coordinate system, variation in the form of higher standard deviation was noticed in the nasal-temporal direction ±0.9 mm, while it was a limited variation in the superior-inferior direction <±0.01 mm, Fig. 3(a). On the other hand, the thickness profile followed the reported values in the literature with a minimum thickness of 0.558 mm at the corneal apex, 0.624 mm at the limbus and 0.833 mm at the posterior pole, Fig. 3(b).
Fitting the cornea and the posterior sclera sections to a 5th-order Zernike polynomial resulted in 21 coefficients for each surface, as shown in Table 3. Fitting the equatorial sclera to a 5th order polynomial resulted in 6 coefficients for each of the interior and posterior scleral walls.
Table 3.
Eye globe model polynomial fitting coefficients.
| Exterior wall |
Interior wall |
|||||
|---|---|---|---|---|---|---|
| Cornea (Eq. (1)) | Equatorial Sclera (Eq. (6)) | Posterior Sclera (Eq. (1)) | Cornea (Eq. (1)) | Equatorial Sclera (Eq. (6)) | Posterior Sclera (Eq. (1)) | |
| a1 | 11.788 | 12.213 | −11.254 | 11.218 | 11.506 | −10.478 |
| a2 | 0.040 | 0.027 | 0.000 | 0.039 | 0.110 | 0.001 |
| a3 | 0.008 | −0.011 | 0.000 | 0.008 | −0.018 | 0.000 |
| a4 | −0.003 | −0.030 | 0.000 | −0.004 | −0.040 | 0.000 |
| a5 | −1.478 | 0.019 | 0.961 | −1.456 | 0.025 | 0.908 |
| a6 | 0.022 | 0.034 | 0.000 | 0.016 | 0.044 | 0.000 |
| a7 | −0.002 | – | −0.003 | 0.000 | – | 0.000 |
| a8 | −0.030 | – | −0.032 | 0.000 | – | 0.000 |
| a9 | −0.007 | – | −0.007 | 0.000 | – | 0.000 |
| a10 | −0.002 | – | −0.002 | 0.000 | – | 0.000 |
| a11 | −0.001 | – | −0.001 | 0.000 | – | 0.000 |
| a12 | 0.001 | – | 0.001 | 0.000 | – | 0.000 |
| a13 | 0.027 | – | 0.049 | 0.027 | – | 0.031 |
| a14 | −0.007 | – | −0.010 | 0.000 | – | 0.000 |
| a15 | 0.002 | – | 0.006 | 0.000 | – | 0.000 |
| a16 | 0.003 | – | 0.004 | 0.000 | – | 0.000 |
| a17 | 0.001 | – | 0.001 | 0.000 | – | 0.000 |
| a18 | −0.008 | – | −0.005 | 0.000 | – | 0.000 |
| a19 | 0.000 | – | 0.001 | 0.000 | – | 0.000 |
| a20 | 0.001 | – | 0.002 | 0.000 | – | 0.000 |
| a21 | 0.000 | – | 0.000 | 0.000 | – | 0.000 |
For the purpose of comparison, the geometry of the nasal side of both the limbal discontinuity model and the average eye model were plotted in Fig. 10(a and b). The comparison showed that the averaged model was significantly different from the ideal eye model in the posterior limbal area, anterior and posterior sclera, and the inner wall of the whole eye, Table 4. Measurements of the optic nerve head diameter recorded 3.1 ± 0.3 mm with its centre virtually located 1.0 mm and 3.0 mm from the nasal and inferior meridians, respectively, at an average acute angle of 15° with the corneal axis considering the scleral centre as an origin. Lastly, the limbal discontinuity geometry model recorded a limbus tangent angle of 46° at a radius of 5.8 mm; however, the averaged eye geometry model recorded a limbus tangent angle of 37° at a radius of 6.6 mm.
Fig. 10.
Limbal discontinuity (idealised) eye model versus averaged eye model geometries (a) against elevation angle, (b) in Cartesian coordinates.
Table 4.
Statistical significance (p) of the difference between the ideal eye model and the average eye model geometries, as reported in Fig. 10.
| Cornea | Limbus | Sclera | Full eye | |
|---|---|---|---|---|
| Elevation angle | 60°: 90° | 55°: 65° | −90°: 55° | −90°: 90° |
| Outer wall | 0.760 | 0.067 | <0.001a | 0.221 |
| Inner wall | 0.888 | <0.001a | <0.001a | <0.014a |
| Wall thickness | 0.244 | <0.001a | <0.001a | <0.001a |
Statistically significant.
In terms of material models, the difference between the stresses built in the inflation simulation up to 15 mmHg in the ring-segmented material model and localised element-specific material model were significantly different (p < 0.001) with the ring-segmented material model recording average von-Mises stress 0.0168 ± 0.0046 MPa (range 0.0100–0.0291 MPa) and the localised element-specific material model recording average von-Mises stress 0.0144 ± 0.0025 MPa (range 0.0091–0.0222 MPa), Fig. 11.
Fig. 11.
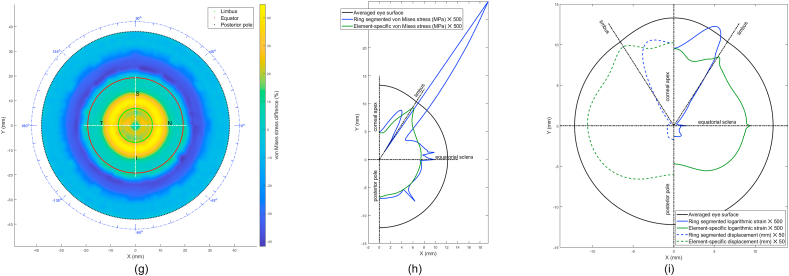
Finite element model of the averaged human eye; (a, b, c) without considering localised material model (Ogden model parameters are μc = 0.07, αc = 110.8, μs1 = 0.441, αs1 = 124.5, μs2 = 0.349, αs2 = 138.5, μs3 = 0.308 and αs3 = 162.2); (d, e, f) considering localised material model. Von Mises stresses distribution is shown in (a, d), and displacements distribution (b, e) is plotted at 15 mmHg IOP. The difference between von mises stress in the ring-segmented model (c), and regional element-specific model (f) is shown in (g) as a map and in (h) as a polar plot. Finally, maximum logarithmic strains resulted in the stress-free analysis and their relevant displacements are presented in (i). The Z-axis is aligned with the axial direction of the eye in all subplots.
Ring-segmented and localised element-specific material models recorded marked differences in their average strains in the stress-free analysis. As can be seen in Fig. 11(i), the ring-segmented model recorded its highest logarithmic strain (0.0267) at the peripheral cornea; however, the element-specific model's highest logarithmic strain was at the corneal apex (0.0203). In the sclera, the logarithmic strain distribution of the element-specific model was more regular than the ring-segmented model and recorded around 10 times the value of the logarithmic strain of the ring-segmented model. When 3D displacements were compared (at IOP = 15 mmHg) relative to the stress-free geometry (at IOP = 0 mmHg), the ring-segmented model recorded a peak (0.2181 mm) at the mid cornea (r ~ 3 mm) and low displacements around the sclera while the element-specific model displacements were regular around the eyewall with a peak displacement of 0.2314 mm at the limbus.
4. Discussion
With a focus on anterior eye geometry, the current study built an eye model that suits anterior eye applications like contact and non-contact IOP measurement and contact lenses fitting as examples. This study presents a novel averaged anterior eye model that is more representative of the anterior eye geometry and material behaviour than the limbal discontinuity eye model with ring-segmented material properties. Therefore, it can be used in a wide range of anterior eye parametric studies with the same computational cost as the ideal model but with more accurate geometry and material characterisation. The study also presents a localised element-specific material model for the ocular globe that is suitable for FE analysis and works better than a ring-segmented model in terms of stress distribution, Fig. 11, with no need for a custom coded user-subroutine.
The findings are discussed in two subsections, Geometry and Material. In the first subsection, the presented averaged eye model is compared to the limbal discontinuity eye model in terms of geometry. In the second subsection, the averaged eye geometry was used with two material models, the ring-segmented model, and the presented localised element-specific model. Using the same geometry in the second section aims to neutralise the effect of geometry while material models are being compared. The results showed that the presented averaged eye geometry model has two clear advantages over the limbal discontinuity geometry model, which consists of a conical cornea and spherical sclera axisymmetric eye globe. The advantages are in both the geometrical and material representations.
4.1. Geometry
In terms of geometry, the averaged eye geometry model resolved the disadvantage of limbus misrepresentation in parametric eye models [126], as no sharp angle resulted in the limbus-sclera connection. The limbal discontinuity geometry model recorded a limbus tangent angle of 9° more than the average eye geometry model with a limbal radius 0.8 mm smaller than the average eye geometry model. This is in-line with our previous finding that through the use of conic modelling as in the limbal discontinuity geometry model, the eye's limbus is being mislocated [35]. In contrast, the averaged eye geometry model has the limbus in place with its true tangent angle with the corneal surface, Fig. 11. However, the presented eye model does not include a comprehensive, detailed geometrical representation of the optic nerve head and its scleral canal; it marks their position and allocates the relevant material characteristics of the posterior eye in this area for ex-vivo inflated eyes measurements, which were aligned with the literature [127,128]. The presented model has a mathematical form able to be reused and assessed compared to Razaghi et al. [86], where the eye geometry was built via a stereolithography (STL) exported model with no parametric representation of the eye geometry. STL files are hard to edit outside of the model scaling since they contain an approximation of the original 3D surface and not the surface itself. It approximates the surface of a 3D model using a series of interlocking triangles; therefore, it is simpler to reconstruct an STL model from scratch than to modify an existing one. Furthermore, to enhance the resolution of an STL file, the user needs to increase the number of triangular planes that approximate a surface. This increases the file size of the 3D model, but even with the highest possible resolution, the STL format still has lower fidelity compared to parametric surface models.
4.2. Material
In terms of material behaviour, dividing the eye model to ring segments with varying material parameters for each segment, as in the ring-segmented model, Fig. 5(a), did not reflect the regional variation in the eye stiffness as detected by determination of fibril density via x-ray scattering techniques, Fig. 6. When compared with the localised element-specific model, ring-segmented material models [[87], [88], [89], [90], [91], [92], [93], [94], [95]] showed 40% higher stresses around the limbus when the eye inflated under the IOP. Although the limbal area is a stress concentration area in both models, it is not markedly concentrated in the localised element-specific model as it always appeared in the ring-segmented model. Instead, stresses are more disseminated with two regions that recorded a slightly higher concentration of stresses, the limbus and the posterior sclera. These findings are in line with Moore et al. who reported a stress concentration effect around the limbus in a parametric conic ring-segmented model [126]. In terms of logarithmic strain recorded in the stress-free analysis, the element-specific material model recorded a more logical strain peak at the corneal apex; however, the ring-segmented model recorded a maximum strain around the peripheral cornea. The distributions of the logarithmic strain and its related displacement were more regular in the element-specific material model than in the ring-segmented model, which displays a displacement peak at the peripheral cornea, unlike the element-specific material model, which displayed another peak at the limbus and no steeply sharp peaks at all. Both models displayed small peaks around the eye equator, however, these peaks are believed to be artefacts due to the models’ boundary conditions [35,102]. Additionally, both models showed that the central cornea retains most of its shape while the limbal region deforms under internal pressure in agreement with Boyce et al. [129]. Compared to Razaghi et al. [86], only linear elastic material models were used across the whole eye globe in clear oversimplification. Technically, the current study could not be compared to Karimi et al. [85] as their study was limited to an indentation test used to validate a finite element model. With no inflation or tensile tests, it is difficult to evaluate their results against other common eye models [130]. In terms of allocating different material properties in different directions, anisotropic fibre distribution throughout the ocular globe can be seen within some models reported in the literature. This was modelled within the cornea [88,95,96] and the sclera [46] and allows for representation of heterogeneity and anisotropy in complex collagenous tissues, but with quite complicated material modelling methods.
The current study has a few limitations. The lack of 3D in-vivo geometry measurements of the posterior segment of the eye led to the use of the axial length to stretch the posterior hemispherical representation of the posterior eye in the presented averaged geometry model. Ideally, in-vivo measurements of the posterior eye could improve the geometrical representation of the posterior portion of the model; however, the model presented in this study is designed for anterior eye applications only. Therefore, the presented model is not ideal for applications that require a detailed geometrical description of the optic nerve head and scleral canal in comparison to other methods that focus on these posterior eye structures [46,47]. Also, the number of eyes used for determining the localised element-specific material model was limited to 6 because of the complications associated with obtaining human eyes for research and the limited available access to high-powered synchrotron facilities, which is necessary for obtaining large, low-noise x-ray datasets from biological tissues.
5. Conclusions
The current study presents an averaged geometry model of the anterior human eye that is easy to generate through two parametric equations (Eq. (1) & Eq. (4)). This model is combined with a material model that can be used either parametrically through a Zernike fitted polynomial or non-parametrically as a function of the azimuth angle and the elevation angle of the eye globe. Both models were built in a sense that makes them easy to implement in FE analysis without additional computational cost compared to the limbal discontinuity so-called idealised eye geometry or ring-segmented material models.
Financial disclosure
J. Towler's PhD project is funded by the Samuel Crossley-Barnes Endowment. The grant recipient is B. Geraghty, who recruited J. Towler as a PhD student at the University of Liverpool. The funder undertook no involvement in study design, data collection, analysis, the decision to publish, or the preparation of the manuscript. Other authors have no funding to declare relating to this work.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e13944.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
Zernike polynomial expression for normalised total collagen contents.
Zernike polynomial coefficients (to be used with S1).
Non-parametric representation for normalised total collagen contents.
References
- 1.Pinero D.P., Alcon N. Corneal biomechanics: a review. Clin. Exp. Optom. 2015;98(2):107–116. doi: 10.1111/cxo.12230. [DOI] [PubMed] [Google Scholar]
- 2.Dupps W.J., Jr. Biomechanical modeling of corneal ectasia. J. Refract. Surg. 2005;21(2):186–190. doi: 10.3928/1081-597X-20050301-15. [DOI] [PubMed] [Google Scholar]
- 3.Alastrué V. Biomechanical modeling of refractive corneal surgery. J. Biomech. Eng. 2005;128(1):150. doi: 10.1115/1.2132368. [DOI] [PubMed] [Google Scholar]
- 4.Schwiegerling J., Snyder R.W. Custom photorefractive keratectomy ablations for the correction of spherical and cylindrical refractive error and higher-order aberration. J. Opt. Soci. Am. A: Opt. Image Sci. Vis. 1998;15(9):2572–2579. doi: 10.1364/josaa.15.002572. [DOI] [PubMed] [Google Scholar]
- 5.Elsheikh A., et al. Numerical study of the effect of corneal layered structure on ocular biomechanics. Curr. Eye Res. 2009;34(1):26–35. doi: 10.1080/02713680802535263. [DOI] [PubMed] [Google Scholar]
- 6.Roy A.S., Dupps W.J., Jr. Patient-specific computational modeling of keratoconus progression and differential responses to collagen cross-linking. Invest. Ophthalmol. Vis. Sci. 2011;52(12):9174–9187. doi: 10.1167/iovs.11-7395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eliasy A., et al. Determination of corneal biomechanical behavior in-vivo for healthy eyes using CorVis ST tonometry: stress-strain index. Front. Bioeng. Biotechnol. 2019;7(105) doi: 10.3389/fbioe.2019.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mainstone J.C., et al. Corneal shape in hyperopia. Clin. Exp. Optom. 1998;81(3):131–137. doi: 10.1111/j.1444-0938.1998.tb06731.x. [DOI] [PubMed] [Google Scholar]
- 9.Holladay J.T., Dudeja D.R., Chang J. Functional vision and corneal changes after laser in situ keratomileusis determined by contrast sensitivity, glare testing, and corneal topography11None of the authors has a financial interest in any device described. J. Cataract Refract. Surg. 1999;25(5):663–669. doi: 10.1016/s0886-3350(99)00011-5. [DOI] [PubMed] [Google Scholar]
- 10.Douthwaite W.A., et al. The EyeSys videokeratoscopic assessment of apical radius and p-value in the normal human cornea. Ophthalmic Physiol. Opt. 1999;19(6):467–474. doi: 10.1046/j.1475-1313.1999.00462.x. [DOI] [PubMed] [Google Scholar]
- 11.Holmes-Higgin D.K., et al. SLACK INCORPORATED; United States: 1999. Characterization of the Aspheric Corneal Surface with Intrastromal Corneal Ring Segments; p. 520. [DOI] [PubMed] [Google Scholar]
- 12.Budak K., et al. Evaluation of relationships among refractive and topographic parameters11Myrna Kahn, Baylor College of Medicine, Houston, Texas, provided statistical consultation. J. Cataract Refract. Surg. 1999;25(6):814–820. doi: 10.1016/s0886-3350(99)00036-x. [DOI] [PubMed] [Google Scholar]
- 13.Dubbelman M., et al. Radius and asphericity of the posterior corneal surface determined by corrected Scheimpflug photography. Acta Ophthalmol. Scand. 2002;80(4):379–383. doi: 10.1034/j.1600-0420.2002.800406.x. [DOI] [PubMed] [Google Scholar]
- 14.Bottos K.M., et al. Corneal asphericity and spherical aberration after refractive surgery. J. Cataract Refract. Surg. 2011;37(6):1109–1115. doi: 10.1016/j.jcrs.2010.12.058. [DOI] [PubMed] [Google Scholar]
- 15.Cuesta J.R.J., et al. Impact of interocular differences in corneal asphericity on binocular summation. Am. J. Ophthalmol. 2003;135(3):279–284. doi: 10.1016/s0002-9394(02)01968-2. [DOI] [PubMed] [Google Scholar]
- 16.Manns F., et al. Radius of curvature and asphericity of the anterior and posterior surface of human cadaver crystalline lenses. Exp. Eye Res. 2004;78(1):39–51. doi: 10.1016/j.exer.2003.09.025. [DOI] [PubMed] [Google Scholar]
- 17.Somani S., Tuan K.A., Chernyak D. Corneal asphericity and retinal image quality: a case study and simulations. J. Refract. Surg. 2004;20(5):S581–S585. doi: 10.3928/1081-597X-20040901-32. [DOI] [PubMed] [Google Scholar]
- 18.Llorente L., et al. Myopic versus hyperopic eyes: axial length, corneal shape and optical aberrations. J. Vis. 2004;4(4):5. doi: 10.1167/4.4.5. [DOI] [PubMed] [Google Scholar]
- 19.Davis W.R., et al. Corneal asphericity and apical curvature in children: a cross-sectional and longitudinal evaluation. Invest. Ophthalmol. Vis. Sci. 2005;46(6):1899–1906. doi: 10.1167/iovs.04-0558. [DOI] [PubMed] [Google Scholar]
- 20.Dubbelman M., Sicam V.A.D.P., Van der Heijde G.L. The shape of the anterior and posterior surface of the aging human cornea. Vis. Res. 2006;46(6):993–1001. doi: 10.1016/j.visres.2005.09.021. [DOI] [PubMed] [Google Scholar]
- 21.Gonzalez-Meijome J.M., et al. Asphericity of the anterior human cornea with different corneal diameters. J. Cataract Refract. Surg. 2007;33(3):465–473. doi: 10.1016/j.jcrs.2006.11.004. [DOI] [PubMed] [Google Scholar]
- 22.Nieto-Bona A., Lorente-Velazquez A., Montes-Mico R. Relationship between anterior corneal asphericity and refractive variables. Graefe’s Arch. Clin. Exp. Ophthalmol. 2009;247(6):815–820. doi: 10.1007/s00417-008-1013-2. [DOI] [PubMed] [Google Scholar]
- 23.Pinero D.P., et al. Corneal volume, pachymetry, and correlation of anterior and posterior corneal shape in subclinical and different stages of clinical keratoconus. J. Cataract Refract. Surg. 2010;36(5):814–825. doi: 10.1016/j.jcrs.2009.11.012. [DOI] [PubMed] [Google Scholar]
- 24.Zhang Z., et al. Corneal asphericity and its related factors in 1052 Chinese subjects. Optom. Vis. Sci. 2011;88(10):1232–1239. doi: 10.1097/OPX.0b013e31822717ca. [DOI] [PubMed] [Google Scholar]
- 25.Priest A.D. University of Waterloo; 2005. The Development of an Average, Anatomically Based, Young Adult, GRIN Eye Model. [Google Scholar]
- 26.Shukla V.V., Sawalakhe P.V., Shende P. FEA of contact between scleral buckle and human eye tissues. Asia-Pacif. J. Sci. Techn. 2022;27(1):14–Jan. [Google Scholar]
- 27.de la Caridad Núñez-Chongo O., et al. Lecture Notes in Mechanical Engineering. 2022. Studying the fluid-structure interaction in a computational model of the human eye during non contact tonometry tests; pp. 217–228. [Google Scholar]
- 28.Langenbucher A., Viestenz A., Seitz B. SLACK INCORPORATED; United States: 2002. Conoidal Fitting of Corneal Topography Height Data after Excimer Laser Penetrating Keratoplasty; p. 63. [DOI] [PubMed] [Google Scholar]
- 29.Mastropasqua L., et al. Photorefractive keratectomy with aspheric profile of ablation versus conventional photorefractive keratectomy for myopia correction: six-month controlled clinical trial. J. Cataract Refract. Surg. 2006;32(1):109–116. doi: 10.1016/j.jcrs.2005.11.026. [DOI] [PubMed] [Google Scholar]
- 30.Navarro R., Gonzalez L., Hernandez J.L. Optics of the average normal cornea from general and canonical representations of its surface topography. J. Opt. Soci. Am. A. 2006;23(2):219–232. doi: 10.1364/josaa.23.000219. [DOI] [PubMed] [Google Scholar]
- 31.Ortiz S., et al. In vivo human crystalline lens topography. Biomed. Opt Express. 2012;3(10):2471–2488. doi: 10.1364/BOE.3.002471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Navarro R., Rozema J.J., Tassignon M.J. Optical changes of the human cornea as a function of age. Optom. Vis. Sci. 2013;90(6):587–598. doi: 10.1097/OPX.0b013e3182928bc6. [DOI] [PubMed] [Google Scholar]
- 33.Bao F., et al. Evaluation of the shape symmetry of bilateral normal corneas in a Chinese population. PLoS One. 2013;8(8) doi: 10.1371/journal.pone.0073412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ballesta A., et al. Lecture Notes in Mechanical Engineering. 2022. Variable complexity corneal surfaces characterization by modal geometrical reconstruction methods: comparative study; pp. 237–247. [Google Scholar]
- 35.Moore J. Limbus misrepresentation in parametric eye models. PLoS One. 2020;15(9) doi: 10.1371/journal.pone.0236096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jesus D.A., Kedzia R., Iskander D.R. Precise measurement of scleral radius using anterior eye profilometry. Contact Lens Anterior Eye. 2017;40(1):47–52. doi: 10.1016/j.clae.2016.11.003. [DOI] [PubMed] [Google Scholar]
- 37.Chen K.J., et al. Development and validation of a new intraocular pressure estimate for patients with soft corneas. J. Cataract Refract. Surg. 2019;45(9):1316–1323. doi: 10.1016/j.jcrs.2019.04.004. [DOI] [PubMed] [Google Scholar]
- 38.Bao F., et al. Development and clinical verification of numerical simulation for laser in situ keratomileusis. J. Mech. Behav. Biomed. Mater. 2018;83:126–134. doi: 10.1016/j.jmbbm.2018.04.016. [DOI] [PubMed] [Google Scholar]
- 39.Abass A., et al. Simulated optical performance of soft contact lenses on the eye. PLoS One. 2019;14(5):e0216484. doi: 10.1371/journal.pone.0216484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Moore J., et al. Simulation of the effect of material properties on soft contact lens on-eye power. Bioengineering. 2019;6(4) doi: 10.3390/bioengineering6040094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Doll T., et al. Which feature influences on-eye power change of soft toric contact lenses: design or corneal shape? PLoS One. 2020;15(11):e0242243. doi: 10.1371/journal.pone.0242243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lopes B.T., et al. Determination of optic axes by corneal topography among Italian, Brazilian, and Chinese populations. Photonics. 2021;8(2):61. [Google Scholar]
- 43.Studer H.P., et al. Patient-specific finite-element simulation of the human cornea: a clinical validation study on cataract surgery. J. Biomech. 2013;46(4):751–758. doi: 10.1016/j.jbiomech.2012.11.018. [DOI] [PubMed] [Google Scholar]
- 44.Simonini I., Pandolfi A. Customized finite element modelling of the human cornea. PLoS One. 2015;10(6):e0130426. doi: 10.1371/journal.pone.0130426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Grytz R., et al. Material properties of the posterior human sclera. J. Mech. Behav. Biomed. Mater. 2014;29:602–617. doi: 10.1016/j.jmbbm.2013.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Karimi A., et al. Finite element modeling of the complex anisotropic mechanical behavior of the human sclera and pia mater. Comput. Methods Progr. Biomed. 2022;215 doi: 10.1016/j.cmpb.2022.106618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Karimi A., et al. Analysis of the effects of finite element type within a 3D biomechanical model of a human optic nerve head and posterior pole. Comput. Methods Progr. Biomed. 2021:198. doi: 10.1016/j.cmpb.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Karimi A., et al. Ocular biomechanics during improvised explosive device blast: a computational study using eye-specific models. Injury. 2022;53(4):1401–1415. doi: 10.1016/j.injury.2022.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Geraghty B., et al. Inflation experiments and inverse finite element modelling of posterior human sclera. Journal of Biomechanics. 2020;98 doi: 10.1016/j.jbiomech.2019.109438. [DOI] [PubMed] [Google Scholar]
- 50.Vinciguerra R., et al. Corneal biomechanics and biomechanically corrected intraocular pressure in primary open-angle glaucoma, ocular hypertension and controls. British Journal of Ophthalmology. 2020;104(1):121–126. doi: 10.1136/bjophthalmol-2018-313493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Pye D.C. A clinical method for estimating the modulus of elasticity of the human cornea in vivo. PLoS ONE. 2020;15(1) doi: 10.1371/journal.pone.0224824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pan C.W., et al. Central corneal thickness and its association with birth parameters in Chinese adolescents. Ophthalmic Epidemiology. 2019;26(5):360–366. doi: 10.1080/09286586.2019.1632903. [DOI] [PubMed] [Google Scholar]
- 53.Gokcinar N.B., et al. Agreement and repeatability of central corneal thickness measurements by four different optical devices and an ultrasound pachymeter. International Ophthalmology. 2019;39(7):1589–1598. doi: 10.1007/s10792-018-0983-2. [DOI] [PubMed] [Google Scholar]
- 54.Pinero D.P., et al. Characterization of corneoscleral geometry using fourier transform profilometry in the healthy eye. Eye & contact lens. 2019;45(3):201–207. doi: 10.1097/ICL.0000000000000560. [DOI] [PubMed] [Google Scholar]
- 55.Zhang W., et al. Influence of corneal diameter on surgically induced astigmatism in small-incision cataract surgery. Canadian Journal of Ophthalmology. 2019;54(5):556–559. doi: 10.1016/j.jcjo.2018.12.013. [DOI] [PubMed] [Google Scholar]
- 56.Mohidin N., Ling L.C. Central and peripheral corneal thickness in Malays and its variation with age. Bangladesh Journal of Medical Science. 2018;17(4):600–605. [Google Scholar]
- 57.Wang W., et al. Corneal biomechanical metrics of healthy Chinese adults using Corvis ST. Contact Lens and Anterior Eye. 2017;40(2):97–103. doi: 10.1016/j.clae.2016.12.003. [DOI] [PubMed] [Google Scholar]
- 58.Bandlitz S., et al. Scleral topography analysed by optical coherence tomography. Contact Lens and Anterior Eye. 2017;40(4):242–247. doi: 10.1016/j.clae.2017.04.006. [DOI] [PubMed] [Google Scholar]
- 59.Shen L., et al. Scleral thickness in Chinese eyes. Investigative Ophthalmology and Visual Science. 2015;56(4):2720–2727. doi: 10.1167/iovs.14-15631. [DOI] [PubMed] [Google Scholar]
- 60.Ariza-Gracia M.A., et al. Coupled biomechanical response of the cornea assessed by non-contact tonometry. A simulation study. PLoS ONE. 2015;10(3) doi: 10.1371/journal.pone.0121486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bekerman I., Gottlieb P., Vaiman M. Variations in eyeball diameters of the healthy adults. Journal of Ophthalmology. 2014;2014:5. doi: 10.1155/2014/503645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Vurgese S., Panda-Jonas S., Jonas J.B. Scleral thickness in human eyes. PLoS One. 2012;7(1) doi: 10.1371/journal.pone.0029692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fares U., et al. Correlation of central and peripheral corneal thickness in healthy corneas. Cont Lens Anterior Eye. 2012;35(1):39–45. doi: 10.1016/j.clae.2011.07.004. [DOI] [PubMed] [Google Scholar]
- 64.Lau W., Pye D. A clinical description of ocular response analyzer measurements. Investigative Ophthalmology and Visual Science. 2011;52(6):2911–2916. doi: 10.1167/iovs.10-6763. [DOI] [PubMed] [Google Scholar]
- 65.Hall L.A., et al. The influence of corneoscleral topography on soft contact lens fit. Investigative Ophthalmology and Visual Science. 2011;52(9):6801–6806. doi: 10.1167/iovs.11-7177. [DOI] [PubMed] [Google Scholar]
- 66.Elsheikh A., et al. Regional variation in the biomechanical properties of the human sclera. Experimental Eye Research. 2010;90:624–633. doi: 10.1016/j.exer.2010.02.010. [DOI] [PubMed] [Google Scholar]
- 67.Al-Ageel S., Al-Muammar A.M. Comparison of central corneal thickness measurements by Pentacam, noncontact specular microscope, and ultrasound pachymetry in normal and post-LASIK eyes. Saudi J Ophthalmol. 2009;23(3–4):181–187. doi: 10.1016/j.sjopt.2009.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Norman R.E., et al. Dimensions of the human sclera: thickness measurement and regional changes with axial length. Exp Eye Res. 2010;90(2):277–284. doi: 10.1016/j.exer.2009.11.001. [DOI] [PubMed] [Google Scholar]
- 69.Oliveira C., et al. Central corneal thickness is not related to anterior scleral thickness or axial length. Journal of Glaucoma. 2006;15(3):190–194. doi: 10.1097/01.ijg.0000212220.42675.c5. [DOI] [PubMed] [Google Scholar]
- 70.Rufer F., Schroder A., Erb C. White-to-white corneal diameter: normal values in healthy humans obtained with the Orbscan II topography system. Cornea. 2005;24(3):259–261. doi: 10.1097/01.ico.0000148312.01805.53. [DOI] [PubMed] [Google Scholar]
- 71.Jonas J.B., Holbach L. Central corneal thickness and thickness of the lamina cribrosa in human eyes. Invest Ophthalmol Vis Sci. 2005;46(4):1275–1279. doi: 10.1167/iovs.04-0851. [DOI] [PubMed] [Google Scholar]
- 72.Oliveira C., et al. Correlation between central corneal thickness, scleral thickness and refractive error. Investigative Ophthalmology & Visual Science. 2004;45(13):963. [Google Scholar]
- 73.Olsen T.W., et al. Human sclera: thickness and surface area. Am J Ophthalmol. 1998;125(2):237–241. doi: 10.1016/s0002-9394(99)80096-8. [DOI] [PubMed] [Google Scholar]
- 74.Elsheikh A., et al. Journal of the Royal Society Interface; 2010. Characterization of Age-Related Variation in Corneal Biomechanical Properties. rsif20100108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Geraghty B., et al. Age-related variations in the biomechanical properties of human sclera. J. Mech. Behav. Biomed. Mater. 2012;16:181–191. doi: 10.1016/j.jmbbm.2012.10.011. [DOI] [PubMed] [Google Scholar]
- 76.Kling S., Hafezi F. Corneal biomechanics–a review. Ophthalmic Physiol. Opt. 2017;37(3):240–252. doi: 10.1111/opo.12345. [DOI] [PubMed] [Google Scholar]
- 77.Wolffsohn J.S., et al. Changes of corneal biomechanics with keratoconus. Cornea. 2012;31(8):849–854. doi: 10.1097/ICO.0b013e318243e42d. [DOI] [PubMed] [Google Scholar]
- 78.Elsheikh A., Alhasso D., Rama P. Biomechanical properties of human and porcine corneas. Exp. Eye Res. 2008;86(5):783–790. doi: 10.1016/j.exer.2008.02.006. [DOI] [PubMed] [Google Scholar]
- 79.Aghamohammadzadeh H., Newton R.H., Meek K.M. X-ray scattering used to map the preferred collagen orientation in the human cornea and limbus. Structure. 2004;12(2):249–256. doi: 10.1016/j.str.2004.01.002. [DOI] [PubMed] [Google Scholar]
- 80.Meek K.M., Boote C. The use of X-ray scattering techniques to quantify the orientation and distribution of collagen in the corneal stroma. Prog. Retin. Eye Res. 2009;28(5):369–392. doi: 10.1016/j.preteyeres.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 81.Zhou D., et al. Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue. J. R. Soc. Interface. 2019;16(154) doi: 10.1098/rsif.2018.0685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zhou D., et al. Analysis of X-ray scattering microstructure data for implementation in numerical simulations of ocular biomechanical behaviour. PLoS One. 2019;14(4):e0214770. doi: 10.1371/journal.pone.0214770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Vito R.P., Shin T.J., McCarey B.E. A mechanical model of the cornea: the effects of physiological and surgical factors on radial keratotomy surgery. J. Refract. Surg. 1989;5(2):82–88. [PubMed] [Google Scholar]
- 84.Hanna K.D., et al. Computer simulation of lamellar keratectomy and laser myopic keratomileusis. J. Refract. Surg. 1988;4(6):222–231. [Google Scholar]
- 85.Karimi A., et al. A combination of the finite element analysis and experimental indentation via the cornea. J. Mech. Behav. Biomed. Mater. 2019;90:146–154. doi: 10.1016/j.jmbbm.2018.10.017. [DOI] [PubMed] [Google Scholar]
- 86.Razaghi R., Biglari H., Karimi A. Finite element modeling of the eyeglass-related traumatic ocular injuries due to high explosive detonation. Eng. Fail. Anal. 2020;117 [Google Scholar]
- 87.Pandolfi A., Holzapfel G.A. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J. Biomech. Eng. 2008;130(6) doi: 10.1115/1.2982251. [DOI] [PubMed] [Google Scholar]
- 88.Pandolfi A., Manganiello F. A model for the human cornea: constitutive formulation and numerical analysis. Biomech. Model. Mechanobiol. 2006;5(4):237–246. doi: 10.1007/s10237-005-0014-x. [DOI] [PubMed] [Google Scholar]
- 89.Whitford C., et al. Biomechanical model of the human cornea: considering shear stiffness and regional variation of collagen anisotropy and density. J. Mech. Behav. Biomed. Mater. 2015;42:76–87. doi: 10.1016/j.jmbbm.2014.11.006. [DOI] [PubMed] [Google Scholar]
- 90.Grytz R., Meschke G. Constitutive modeling of crimped collagen fibrils in soft tissues. J. Mech. Behav. Biomed. Mater. 2009;2(5):522–533. doi: 10.1016/j.jmbbm.2008.12.009. [DOI] [PubMed] [Google Scholar]
- 91.McDonnell P.J. Constitutive laws for biomechanical IVIodeling of refractive surgery. J. Biomech. Eng. 1996;118:473. doi: 10.1115/1.2796033. [DOI] [PubMed] [Google Scholar]
- 92.Girard M.J.A., et al. Peripapillary and posterior scleral mechanics—Part I: development of an anisotropic hyperelastic constitutive model. J. Biomech. Eng. 2009;131(5):51011–51019. doi: 10.1115/1.3113682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Coudrillier B., et al. Collagen structure and mechanical properties of the human sclera: analysis for the effects of age. J. Biomech. Eng. 2015;137(4) doi: 10.1115/1.4029430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Studer H., et al. Biomechanical model of human cornea based on stromal microstructure. J. Biomech. 2010;43(5):836–842. doi: 10.1016/j.jbiomech.2009.11.021. [DOI] [PubMed] [Google Scholar]
- 95.Rahmati S.M., Razaghi R., Karimi A. Biomechanics of the keratoconic cornea: theory, segmentation, pressure distribution, and coupled FE-optimization algorithm. J. Mech. Behav. Biomed. Mater. 2021;113 doi: 10.1016/j.jmbbm.2020.104155. [DOI] [PubMed] [Google Scholar]
- 96.Whitford C., et al. A viscoelastic anisotropic hyperelastic constitutive model of the human cornea. Biomech. Model. Mechanobiol. 2018;17(1):19–29. doi: 10.1007/s10237-017-0942-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Pinsky P.M., van der Heide D., Chernyak D. Computational modeling of mechanical anisotropy in the cornea and sclera. Journal of Cataract \& Refractive Surgery. 2005;31(1):136–145. doi: 10.1016/j.jcrs.2004.10.048. [DOI] [PubMed] [Google Scholar]
- 98.Consejo A., et al. Mean shape of the human limbus. J Cataract Refract Surg. 2017;43(5):667–672. doi: 10.1016/j.jcrs.2017.02.027. [DOI] [PubMed] [Google Scholar]
- 99.Consejo A., Radhakrishnan H., Iskander D.R. Scleral changes with accommodation. Ophthalmic Physiol Opt. 2017;37(3):263–274. doi: 10.1111/opo.12377. [DOI] [PubMed] [Google Scholar]
- 100.Consejo A., et al. Rotation asymmetry of the human sclera. Acta Ophthalmol. 2018;97(2):e266–e270. doi: 10.1111/aos.13901. [DOI] [PubMed] [Google Scholar]
- 101.Iskander D.R., et al. Principles of operation, accuracy and precision of an eye surface profiler. Ophthalmic Physiol Opt. 2016;36(3):266–278. doi: 10.1111/opo.12292. [DOI] [PubMed] [Google Scholar]
- 102.Abass A., et al. Artefact-free topography based scleral-asymmetry. PLOS ONE. 2019;14(7):e0219789. doi: 10.1371/journal.pone.0219789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Marsaglia G., Tsang W.W., Wang J. Evaluating Kolmogorov's distribution. Journal of Statistical Software. 2003;8(i18) [Google Scholar]
- 104.Knuth D.E. ume 2. Addison Wesley Longman; US: 2014. Art of Computer Programming. (Seminumerical Algorithms). [Google Scholar]
- 105.Everitt B.S., Skrondal A. 4 ed. Cambridge University Press; Cambridge, UK: 2010. The Cambridge Dictionary of Statistics. [Google Scholar]
- 106.Abass A., et al. Three-dimensional non-parametric method for limbus detection. PLOS ONE. 2018;13(11):e0207710. doi: 10.1371/journal.pone.0207710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Kolb H.F.E., Nelson R. Facts and Figures Concerning the Human Retina. University of Utah Health Sciences Center; Salt Lake City (UT): 1995. W.T.O.o.t.R.a.V. System. [PubMed] [Google Scholar]
- 108.Gross H. Wiley-VCH; Weinheim: 2005. Handbook of Optical Systems. [Google Scholar]
- 109.Arvo J. In: Graphics Gems III. David K., editor. Academic Press Professional, Inc.; USA: 1992. Fast random rotation matrices; pp. 117–120. [Google Scholar]
- 110.Feizi S., et al. Central and peripheral corneal thickness measurement in normal and keratoconic eyes using three corneal pachymeters. J Ophthalmic Vis Res. 2014;9(3):296–304. doi: 10.4103/2008-322X.143356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Chaudhry I.A. Measurement of central corneal thickness in health and disease. Saudi journal of ophthalmology. 2009;23(3–4):179–180. doi: 10.1016/j.sjopt.2009.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Avitabile T., et al. Evaluation of central and peripheral corneal thickness with ultrasound biomicroscopy in normal and keratoconic eyes. Cornea. 1997;16(6):639–644. [PubMed] [Google Scholar]
- 113.Shen L., et al. Scleral thickness in Chinese eyes. Invest Ophthalmol Vis Sci. 2015;56(4):2720–2727. doi: 10.1167/iovs.14-15631. [DOI] [PubMed] [Google Scholar]
- 114.Wei Y., et al. Performance of Zernike polynomials in reconstructing raw-elevation data captured by pentacam HR, medmont E300 and eye surface profiler. Heliyon. 2021;7(12) doi: 10.1016/j.heliyon.2021.e08623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Maklad O., et al. Simulation of air puff tonometry test using arbitrary Lagrangian–eulerian (ALE) deforming mesh for corneal material characterisation. International Journal of Environmental Research and Public Health. 2020;17(1):54. doi: 10.3390/ijerph17010054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Elsheikh A., et al. Stress free configuration of the human eye. Med Eng Phys. 2013;35(2):211–216. doi: 10.1016/j.medengphy.2012.09.006. [DOI] [PubMed] [Google Scholar]
- 117.Wang Y.X., et al. Intraocular pressure and its normal range adjusted for ocular and systemic parameters. The Beijing eye study 2011. PLoS One. 2018;13(5):e0196926. doi: 10.1371/journal.pone.0196926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Consejo A., et al. Effect of corneal tilt on the determination of asphericity. Sensors. 2021;21(22):7636. doi: 10.3390/s21227636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Fathy A., et al. The efficiency of using mirror imaged topography in fellow eyes analyses of pentacam HR data. Symmetry. 2021;13(11):2132. [Google Scholar]
- 120.Elsheikh A., et al. Assessment of corneal biomechanical properties and their variation with age. Current Eye Research. 2007;32(1):11–19. doi: 10.1080/02713680601077145. [DOI] [PubMed] [Google Scholar]
- 121.Whitford C., et al. Ex vivo testing of intact eye globes under inflation conditions to determine regional variation of mechanical stiffness. Eye Vis (Lond) 2016;3:21. doi: 10.1186/s40662-016-0052-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Ogden R.W., Hill R. Large deformation isotropic elasticity - on the correlation of theory and experiment for incompressible rubberlike solids. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 1972;326(1567):565–584. [Google Scholar]
- 123.Elsheikh A., et al. Characterization of age-related variation in corneal biomechanical properties. Journal of the Royal Society Interface. 2010;7(51):1475–1485. doi: 10.1098/rsif.2010.0108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Garcia D. Robust smoothing of gridded data in one and higher dimensions with missing values. Computational Statistics & Data Analysis. 2010;54(4):1167–1178. doi: 10.1016/j.csda.2009.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Geraghty B., et al. Inflation experiments and inverse finite element modelling of posterior human sclera. J Biomech. 2020;98 doi: 10.1016/j.jbiomech.2019.109438. [DOI] [PubMed] [Google Scholar]
- 126.Moore J., et al. Limbus misrepresentation in parametric eye models. PLOS ONE. 2020;15(9):e0236096. doi: 10.1371/journal.pone.0236096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Hogan M.J., Alvarado J.A., Weddell J.E. WB Saunders; Phildelphia, London, Toronto: 1971. Histology of the Human Eye. [Google Scholar]
- 128.Tasman W., Jaeger E.A., Ovid Technologies I. Lippincott Williams & Wilkins; 2013. Duane's Ophthalmology. [Google Scholar]
- 129.Boyce B.L., et al. Full-field deformation of bovine cornea under constrained inflation conditions. Biomaterials. 2008;29(28):3896–3904. doi: 10.1016/j.biomaterials.2008.06.011. [DOI] [PubMed] [Google Scholar]
- 130.Elsheikh A., Anderson K. Comparative study of corneal strip extensometry and inflation tests. Journal of the Royal Society Interface. 2005;2(3):177–185. doi: 10.1098/rsif.2005.0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Zernike polynomial expression for normalised total collagen contents.
Zernike polynomial coefficients (to be used with S1).
Non-parametric representation for normalised total collagen contents.