Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors

Abstract

We can determine the effects of many possible sequence variations in transcription factor binding sites using microarray binding experiments. Analysis of wild-type and mutant Zif268 (Egr1) zinc fingers bound to microarrays containing all possible central 3 bp triplet binding sites indicates that the nucleotides of transcription factor binding sites cannot be treated independently. This indicates that the current practice of characterizing transcription factor binding sites by mutating individual positions of binding sites one base pair at a time does not provide a true picture of the sequence specificity. Similarly, current bioinformatic practices using either just a consensus sequence, or even mononucleotide frequency weight matrices to provide more complete descriptions of transcription factor binding sites, are not accurate in depicting the true binding site specificities, since these methods rely upon the assumption that the nucleotides of binding sites exert independent effects on binding affinity. Our results stress the importance of complete reference tables of all possible binding sites for comparing protein binding preferences for various DNA sequences. We also show results suggesting that microarray binding data using particular subsets of all possible binding sites can be used to extrapolate the relative binding affinities of all possible full-length binding sites, given a known binding site for use as a starting sequence for site preference refinement.

INTRODUCTION

The DNA binding site preference of transcription factors is commonly described using a consensus sequence, even though one sequence cannot accurately depict the binding site preferences. More recently, mononucleotide frequency weight matrices have been introduced as a more accurate way of describing the DNA sequence specificities of transcription factors (1). A few researchers have even applied oligonucleotide weight matrices in an attempt to capture neighbor-dependent information (2–4). Such weight matrices, and even consensus sequences, are often used to search genomes for potential binding sites for transcription factors and thus to identify the genes regulated by these factors (5,6).

However, the use of binding site weight matrices to identify potential new target sites for binding by the transcription factor makes the assumption that the nucleotides of the DNA binding site can be treated independently in evaluating potential new matches to the matrix (1). Therefore, we performed analyses to determine whether this independence assumption is valid. In addition, we probed the practical question of whether one can predict new sites on the basis of a few known sites. For this analysis, we generated a probability distribution over all potential sequences using a hidden Markov model (HMM) (7) derived from a weight matrix created from a few sites. Since the statistical properties of HMMs are quite well understood (8), they provide us with a solid statistical foundation from which to draw conclusions about nucleotide interdependence. However, even when contained within the structure of a HMM, this use of binding site weight matrices makes the assumption that individual nucleotides, or groups of nucleotides, within the DNA binding site can be treated independently (1).

Prior analysis of DNA binding site selections using optimized zinc finger proteins provided evidence for context-dependent effects in zinc finger recognition (9). More recently, analysis of the binding of Salmonella bacteriophage repressor Mnt to DNA sequences carrying all possible dinucleotide combinations at positions 16 and 17 of the 21 bp binding site indicated that interactions of Mnt with nucleotides at these positions are not independent (10).

We present compelling evidence that the assumption that nucleotides of DNA binding sites can be treated independently is problematical in describing the true binding preferences of transcription factors. Therefore, the use of a completely specified reference table is desirable for depicting these binding preferences accurately. Furthermore, binding site weight matrices are often based upon only a few known binding sites (5,6), many of which may be identical, making the resulting weight matrix not much better than a consensus sequence.

Microarrays containing all possible 3 bp binding sites for the variable zinc finger were used to quantitate the binding site preferences of a collection of mouse Zif268 mutants selected from a phage display library of the second finger (11). A phage display library, prepared by randomizing critical amino acid residues in the second of three fingers of the mouse Zif268 domain (Fig. 1), provided a rich source of zinc finger proteins with variant DNA binding specificities (12). Analysis of the microarray binding data led to the discovery that the nucleotides of a transcription factor binding site exert significant interdependent effects on the DNA binding affinity of the transcription factor. Furthermore, we provide evidence that extrapolating particular subsets of binding sites can determine not only the preferential full-length binding site, but also the approximate rank ordering of those sequences bound with the highest affinities.

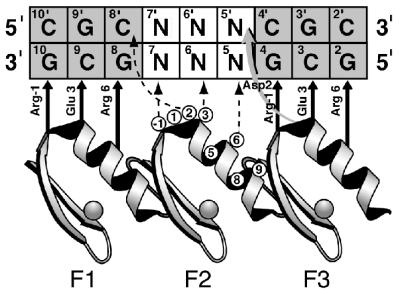
Figure 1.

Model depicting interactions between the Zif268 phage display library and the DNA used in microarray binding experiments. The three zinc fingers of Zif268 (F1, F2 and F3) are aligned to show contacts to the nucleotides of the DNA binding site as inferred from the crystal structure of Zif268 and biochemical experiments. The zinc finger amino acid positions are numbered relative to the first helical residue (position 1). The randomized positions in the α-helix of the second finger are circled. DNA base pairs marked N were fixed as particular sequences (11). © Copyright (2001) National Academy of Sciences of the USA.

MATERIALS AND METHODS

Calculation of K_a^app values

For each Zif variant being examined, each of the DNA concentration-normalized fluorescence intensities was expressed as a fraction of the total fluorescence intensity of the 64 different DNA sequences per replicate on the microarrays. These signal intensities correlated well with a hyperbolic function of the K_d^app values, based on fractional occupancy. Therefore, for each variant Zif phage a calibration curve was constructed by determining the K_d^app values of a few representative sequences that spanned the range of relative fluorescence intensities on the microarrays spotted with all different triplet binding sites for finger 2. These calibration curves were used to interpolate the K_d^app values for the remaining sequences on the microarrays (11).

The calibration curves were calculated using the average fluorescence intensities from all nine replicates spotted on the microarrays. The average calibration curve for each variant was then used to calculate the individual K_d^app values for each of the individual spots on the microarrays. The K_a^app of each spot was determined from 1/K_d^app. The individual K_a^app data for each of the nine replicates for each of the five Zif268 variants are available at http://arep.med.harvard.edu/Bulyk/NAR2002supplementary/.

Significance testing

The significance of the various interdependence metrics, as well as the significance of differences between the observed K_a^app values and K_a^app values extrapolated from subsets of binding sites, was calculated using the two-tailed non-pooled t-test (13), where

t = (x₁ – x₂)/√[(s₁²/n₁) + (s₂²/n₂)]

with degrees of freedom

Δ = [(s₁²/n₁) + (s₂²/n₂)]²/[(s₁²/n₁)²/(n₁ – 1) + (s₂²/n₂)²/(n₂ – 1)]

Because multiple hypotheses were tested to determine the statistical significance of the difference between the observed and calculated K_a^app values of a number of triplet sequences for each Zif268 variant, measures were taken to ensure that individual tests were not counted as statistically significant simply because of the probability of achieving a false positive at a particular significance cut-off. For example, if 20 individual comparisons are evaluated using α = 0.05, the expected number of Type I errors (i.e. false positives) is 1. The Bonferroni correction is a method developed to deal with problems arising from multiple tests (14).

We used the modified Bonferroni method to correct for multiple hypothesis testing (15). Briefly, the individual comparisons were rank ordered from most to least significant. For the most significant difference, a significance cut-off α′ was used, such that α′ = α/k, where k is the number of cases tested. If the most significant difference was found to be statistically significant using α′, then we proceeded to the second most significant difference and used

α′ = α/(k – 1)

If this test was found to be statistically significant, then we proceeded to the third most significant difference and used

α′ = α/(k – 2)

We proceeded in this manner until the test case was found not to be statistically significant. All lower ranking tests were then also not statistically significant.

For our significance testing we used an initial α = 0.05, which corresponded to α′ = 0.000781 for the highest ranking test case if 64 individual comparisons are being evaluated.

Hidden Markov model design and decoding

HMMs can be thought of as models that generate sequences of symbols, such as nucleotides, with a certain probability distribution. Since the total probability of all sequences in the distribution must sum to one, the probability of one cannot increase without causing a corresponding decrease in another (16). HMMs have an extensive history of use in computer science dating to the 1960s (17) and have recently been applied to a variety of biological linear sequence analysis problems (16,18–23).

Our HMM was designed to model a sequence of DNA containing both DNA binding sites and background DNA. As input, it takes a set of known binding sites, hereafter referred to as the training set, and their corresponding K_a^app values; the model outputs the posterior probability of a particular nucleotide being in a binding site. Each position in the binding site is assigned a state, referred to as a ‘match’ state, with emission probabilities equal to the weight table entry corresponding to that position. The match states transition linearly to each other with transition probabilities of one. An ‘insert’ state is created that emits the nucleotides at background probability, with transitions to itself and the first match state. The last match state transitions with probability one to the insert state. A silent (non-emitting) start state transitions to both the first match state and the insert state, allowing for the possibility of the sequence starting with a binding site. While our analysis employed only zero and first order models, the design can be generalized to higher orders, up to two less than the length of the binding site in question.

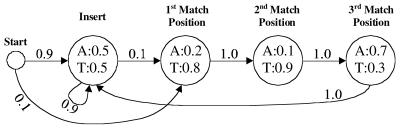
For the zero order model, a mononucleotide position weight matrix is created from the training set, with weights equal to the respective binding affinities of the sites. For example, the ‘A’ entry in the first position is calculated by summing all sites of the form ‘ANN’ found in the training set. Next, a pseudo-count is added to each entry, in proportion to the corresponding background frequency of the nucleotide, for a total addition of one; this allows for the possibility that a test site contains a mononucleotide not found in any of the training sequences. Once all of the weights are calculated, they are normalized such that the weights for each position sum to one. A diagram of a zero order model is shown in Figure 2.

Figure 2.

Zero order HMM using an alphabet of two nucleotides (A,T) for clarity. Circles represent states; arrows represent transitions. The numbers alongside the arrows specify transition probabilities. The emission distribution for each state (except for the silent start state) is contained within each circle. If this were a real zero order model, the four emitting states would contain distributions over all four nucleotides. Adapted from Durbin et al. (8).

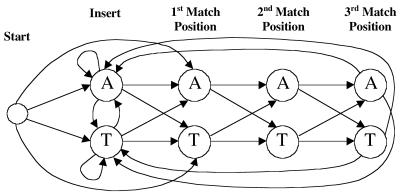
In the first order (dinucleotide) model, each state depends on the previous state, as shown in Figure 3. Every position in the binding site corresponds to four states in the model; one for each nucleotide in each position. Instead of having an emission distribution over all nucleotides, each match state emits only one nucleotide. Again, the match states transition in a strictly linear fashion. For example, the four states corresponding to the first position of the binding site transition only to the four states corresponding to the second position of the binding site. Transition probabilities between the states are specified by normalizing the dinucleotide frequencies plus a pseudo-count. For example, if the dinucleotide CA were found across positions one and two of a binding site, it would affect the transition probability between the first position ‘C’ match state and the second position ‘A’ match state. In addition to the match states, four insert states are constructed in a similar fashion, with transitions among themselves corresponding to the background frequency and transitions to the first position match states. The four match states in the last position transition to the insert state. Again, a silent start state is created that transitions to both the insert states and the first position match states.

Figure 3.

First order HMM using an alphabet of two nucleotides (A,T) for clarity. Circles represent states; arrows represent transitions. The letter inside each circle is the only nucleotide emitted by that state (at 100% probability). To represent the full first order model, there would be four states for each position. Adapted from Durbin et al. (8).

Posterior probability P of the nucleotide at position i being in match state k given a specific sequence x can be calculated by means of a dynamic programming algorithm:

P = [f_k(i)b_k(i)]/P(x)

where

f_k(i) = e_k(x_i)∑_l[a_lkf_l(i – 1)]

b_k(i) = ∑_l[a_kle_l(x_i)b_l(i + 1)]

P(x) = ∑_l f_l(L)

k and l can be any state, f_k(i) is the probability of the sequence x from the beginning (position 1) up to position i with the restriction that the ith state is k, e_l(x_i) is the emission probability of the nucleotide at position i from state l, a_kl is the transition probability from state k to state l, L is the last position in the sequence x, b_k(i) is the probability of the sequence x from position i to the end (L) with the restriction that the ith state is k and P(x) is the probability of the sequence x being generated by the model (8). The posterior probability of a given nucleotide x_i being in a binding site is simply the summation of the posterior probability of the given position i over all match states k.

RESULTS

Mononucleotide weight matrices

We evaluated the possibility of using the microarray binding data to calculate an accurate binding site weight matrix by comparing the observed K_a^app for each of the 64 triplets on the microarray with the K_a^app values calculated from mononucleotide K_a^app values. The observed K_a^app values were determined from microarray fluorescence intensity data (see Materials and Methods). In order to do this comparison, the mononucleotide K_a^app at each of the three positions of the central triplet was calculated by summing all the individual K_a^app values for sequences containing that nucleotide. For example, for comparing the observed versus calculated K_a^app for the triplet ACG, the K_a^app of A at position 1 was determined from the sum of the K_a^app values of all 16 ANN triplets. Similarly, the K_a^app of C at position 2 was determined from the sum of the K_a^app values of all 16 NCN triplets and the K_a^app of G at position 3 was determined from the sum of the K_a^app values of all 16 NNG triplets. We then determined whether the K_a^app values calculated by multiplying the mononucleotide K_a^app values for the three positions of the triplets (1NN × N2N × NN3) were essentially the same as the observed K_a^app values.

Using a non-pooled t-test adjusted for multiple hypothesis testing using the modified Bonferroni method to evaluate the statistical significance of the 64 observed versus calculated K_a^app values, we determined that there is a statistically significant interdependence between the three mononucleotide positions of the triplet binding site for finger 2. The correlation coefficients between the individual observed K_a^app values and the K_a^app values calculated according to a mononucleotide weight matrix derived from the same protein binding microarray data are shown in Table 1. The correlation coefficients between the ranks determined from the individual observed K_a^app values and the ranks determined from the K_a^app values calculated according to a mononucleotide weight matrix derived from the same protein binding microarray data are shown in Table 2. Although the overall correlation coefficients between the sets of observed K_a^app values and the sets of calculated K_a^app values were quite high (between 0.69 and 1.0), the rank correlation coefficients were only between 0.5 and 0.8.

Table 1. Correlation coefficients between observed K_a^app values and those calculated by a microarray data-based weight matrix 1NN × N2N × NN3 assuming complete positional independence (1*2*3), between observed K_a^app values and those calculated by a microarray data-based weight matrix 12N × NN3 assuming interdependence between nucleotide positions 1 and 2 (12*3) and between observed K_a^app values and those calculated by a microarray data-based weight matrix 1NN × N23 assuming interdependence between nucleotide positions 2 and 3 (1*23).

Zif268 variant	Observed Kaapp versus 1*2*3	Observed Kaapp versus 12*3	Observed Kaapp versus 1*23
Wild-type	0.975	0.986	0.988
LRHN	0.790	1.000	1.000
RGPD	0.896	0.947	0.946
REDV	1.000	1.000	1.000
KASN	0.691	1.000	1.000

Table 2. Correlation coefficients between ranks calculated from the observed K_a^app values and those calculated by a microarray data-based weight matrix 1NN × N2N × NN3 (1*2*3), between ranks calculated from the observed K_a^app values and those calculated by a microarray data-based weight matrix 12N × NN3 (12*3) and between ranks calculated from the observed K_a^app values and those calculated by a microarray data-based weight matrix 1NN × N23 (1*23).

Zif268 variant	Observed versus 1*2*3 rank	Observed versus 12*3 rank	Observed versus 1*23 rank
Wild-type	0.793	0.792	0.714
LRHN	0.773	0.760	0.830
RGPD	0.730	0.700	0.761
REDV	0.698	0.666	0.758
KASN	0.532	0.599	0.573

Only those triplets with observed signal intensities above background were used in determining the correlation coefficients of the calculated versus observed ranks: for wild-type Zif268 and the mutant REDV these were the top 15 triplets, for LRHN the top 13 triplets, for RGPD the top 17 triplets and for KASN all 64 triplets.

These analyses indicate that the mononucleotides of transcription factor binding sites do not exert independent effects on binding. There are a number of possible hypotheses for this observation. For example, a substitution of one particular base pair in a transcription factor DNA binding site might alter the packing of a DNA binding domain into the major and/or minor grooves of the DNA. Moreover, a single base pair substitution might also affect the local DNA structure and thus the geometry of various functional groups of the DNA binding site available for interaction with a transcription factor DNA binding domain.

Dinucleotide weight matrices

We evaluated two additional variations for calculating weight matrices using the K_a^app data. These additional variations (12N × NN3 and 1NN × N23) grouped together two of the three nucleotides of the triplet binding site and treated only the remaining nucleotide as independent. For example, for comparing the observed versus calculated K_a^app for the triplet ACG using 12N × NN3, the K_a^app of the dinucleotide AC at positions 1 and 2 was determined from the sum of the K_a^app values of all four ACN triplets and the K_a^app of G at position 3 was determined from the sum of the K_a^app values of all 16 NNG triplets. Likewise, for comparing the observed versus calculated K_a^app for the triplet ACG using 1NN × N23, the K_a^app of A at position 1 was determined from the sum of the K_a^app values of all 16 ANN triplets and the K_a^app of the dinucleotide CG at positions 2 and 3 was determined from the sum of the K_a^app values of all four NCG triplets.

As for the mononucleotide weight matrices, using a non-pooled t-test adjusted for multiple hypothesis testing to evaluate the statistical significance of the 64 observed versus calculated K_a^app values, we determined that there is a statistically significant interdependence between the positions of the triplet binding site for finger 2. The correlation coefficients between the individual observed K_a^app values and the K_a^app values calculated using 12N × NN3 and 1NN × N23 data derived from the same protein binding microarray data are shown in Table 1. The correlation coefficients between the ranks determined from the individual observed K_a^app values and the ranks determined from the K_a^app values calculated according to a mononucleotide weight matrix derived from the same protein binding microarray data are shown in Table 2. For four out of five Zif268 variants, one of these dinucleotide frequency calculations gave higher rank correlation coefficients than considering mononucleotide frequencies alone. Only for wild-type Zif268 did considering dinucleotide frequencies yield essentially the same correlation coefficient as did mononucleotide frequencies. However, for the four variants for which considering dinucleotide frequencies gave better approximations of K_a^app values, which dinucleotide yielded higher correlation coefficients varied. For LRHN, RGPD and REDV consideration of the first dinucleotide (12N) frequencies yielded higher rank correlation coefficients, while for KASN consideration of the second dinucleotide (N23) frequencies yielded a higher rank correlation coefficient.

This suggests that for these three Zif variants the mononucleotides of the first dinucleotide as well as the second dinucleotide exert cooperative effects on binding. However, it appears that the extent of cooperativity of various dinucleotides of a binding site is not a constant rule, even for variants of a single transcription factor that differ in just a portion of the DNA binding domain (for the Zif268 variants, only finger 2 of a three finger Cys₂His₂ zinc finger DNA binding domain was mutated). Consideration of dinucleotide frequencies improved the rank correlation coefficients for most of the Zif268 variants as compared to consideration of mononucleotide frequencies alone and provided fairly good approximations of the rank ordering of the binding sites. Nevertheless, the rank correlation coefficients after consideration of dinucleotide frequencies were still less than 0.8 for four out of five of the Zif268 variants. This indicates that there is some higher order level of nucleotide interdependence in DNA binding sites and further stresses the importance of complete reference tables of all possible binding sites for comparing protein binding preferences for various DNA sequences.

Positive and negative controls

In order to verify that our analyses were capable of detecting mononucleotide, dinucleotide or trinucleotide interdependence, we created four types of positive and negative controls that exhibited these different types of nucleotide interdependence. Mean correlation coefficients resulting from the six types of analyses on the five types of controls, as averaged over 1000 independent sets of each control, are displayed in Web table 1 at http://arep.med.harvard.edu/Bulyk/NAR2001supplementary/. As expected, the different types of analyses resulted in high correlation coefficients when used to analyze the controls designed with the corresponding types of nucleotide interdependence and lower correlation coefficients when used to analyze controls designed with other types of interdependence.

Predictive value of the hidden Markov models

Very rarely have experimental K_a^app data been available for a large number of possible DNA binding sites for a given DNA binding protein. Therefore, we decided to restrict the training set of binding site sequences and test the predictive ability of the zero order and first order HMMs. Our first test used 60% of the sites to construct the model and analyzed the remaining 40%; the second test used 80% of the sites to construct the model and analyzed the remaining 20%. The remaining sites (i.e. either 40% or 20% of the sites, respectively) were strung together to form one contiguous sequence, with 50 random nucleotides inserted between each site. For example, a sequence containing the sites ACG, GGG and TAC would be of the form ACG(N₅₀)GGG(N₅₀)TAC. For each of the five variants, only those sites with observed K_a^app values above background level were used (for wild-type Zif268 and REDV, the top 15; for LRHN, the top 13; for RGPD, the top 17; for KASN, all 64). Eliminating background sites avoided the situation that would occur if the 20% of sites being tested all had background K_a^app values and thus were all identical, making a correlation impossible. The correlation coefficients between the observed K_a^app values and posterior probabilities calculated from zero order and first order HMMs are shown in Table 3. These analyses indicate that binding site data for even a majority of binding sites with K_a^app values above background can provide a rough approximation of the K_a^app values, but even with data for 80% of the above background sites, the rank correlation coefficients are still somewhat low (no higher than 0.62 for these five Zif268 variants).

Table 3. Correlation coefficients between observed K_a^app values and posterior probabilities calculated from zero order (complete position independence, based upon mononucleotide weight matrix data) and first order (strict immediate neighbor dependence, based upon dinucleotide weight matrix data) HMMs, as constructed from 60% of sites and tested on the remaining 40%, and constructed from 80% of sites and tested on the remaining 20%.

Zif268 variant	Observed Kaapp versus 60%/40% zero order	Observed Kaapp versus 60%/40% first order	Observed Kaapp versus 80%/20% zero order	Observed Kaapp versus 80%/20% first order
Wild-type	0.511	0.241	0.620	0.372
LRHN	0.420	0.526	0.526	0.405
RGPD	0.432	0.556	0.465	0.529
REDV	0.475	0.103	0.551	0.144
KASN	0.164	–0.052	0.206	–0.080

For each of these two construct/test groupings, 500 random sets of triplets were analyzed and the means of their correlation coefficients were calculated.

Extrapolation of full-length binding sites from subsets of binding sites

We considered whether 1NN and NN3 microarray data could be combined to accurately calculate the individual 123 microarray data. If this could be done, then only 32 sequences would be required to determine the preferences for 64 different triplet sites: 4² + 4². More significantly, only 144 sequences would be required to determine the preference for 1 048 576 different 10 bp long sites. In general, the number of sequences required would scale linearly with the binding site length according to 16(n – 1), where n is the length of the site in base pairs.

Combining 1NN and NN3 microarray data to infer the individual 123 K_a^app values can be performed using the joint probability function Pr(123) = Pr(12│3) Pr(3). Pr(12│3) can be determined from NN3 microarray data and Pr(3) can be determined from 1NN microarray data. Therefore, we are using one-quarter of the dataset to calculate mononucleotide frequencies for NN3 and a partially overlapping set of that data, also comprising one-quarter of the total dataset, to calculate dinucleotide frequencies for 12N.

In order to test this approximation, we derived 1NN and NN3 data from the available NNN microarray data. In order to calculate Pr(12│3), we divided each of the individual observed K_a^app values of type 123 by the sum of the K_a^app values of type NN3. For example, in order to calculate Pr(AC│G) for wild-type Zif268, the observed K_a^app values for ACG were divided by the sum of the K_a^app values of type NNG for each of the replicates on the microarray. In order to calculate Pr(3), the probabilities of each of the 16 sequences of type 1NN were calculated by dividing the individual observed K_a^app values by the sum of the K_a^app values of all 16 sequences of type 1NN. Pr(3) was then calculated as the sum of the K_a^app values of the four 1N3 sequences. Sixteen triplets for each of the five Zif268 variants were used as test cases for this approximation. For example, Pr(G) for wild-type Zif268 was calculated by first dividing the individual observed K_a^app values of each of the 16 sequences of type TNN by the sum of these K_a^app values and then calculating the sum of the K_a^app values of the four TNG sequences.

These 16 triplets were chosen so as to use 1NN and NN3 data that would most accurately reflect the triplet with the highest average K_a^app for the given variant. For example, TNN and NNT data were derived from the LRHN microarray binding data, so that the probability of T at the third position would be derived from the set of TNN sequences and the probability of TA at the first and second positions of the triplet would be derived from NNT data. We chose to use this methodology, since these triplets will probably include the most data-rich sequences in terms of specific binding by the variant.

The extrapolated K_a^app values for the 16 triplets calculated in this manner for each of the five Zif268 variants correlated extremely well with the observed K_a^app values. The rank correlation coefficients between observed K_a^app values and K_a^app values for all five variants were all over 0.97 (see Table 4). REDV had the lowest rank correlation coefficient of the five variants; it differed only in the ordering of the three binding sites ranked 6, 7 and 8 in the observed versus extrapolated rankings. Thus, if for a particular transcription factor a binding site has already been identified that can be used as a starting sequence from which to vary each dinucleotide, then the optimal full-length binding site for that transcription factor can be extrapolated from its binding preferences for only a small subset of all possible full-length binding sites. In practice, one would perform microarray binding experiments starting at one set of dinucleotides and then, given the results of the extrapolation of those binding experiments, vary the adjacent dinucleotides accordingly. Analysis of Zif268 binding experiments using microarrays spotted with the 16 GCN NAG GCG sequences, in addition to the data we have already gathered using GCG NNN GCG microarrays, would allow one to verify that 12NN and NN34 K_a^app values can be combined to calculate the K_a^app values of 1234. If so, this would mean that one could determine the binding site preferences of transcription factors by a series of protein binding microarrays, stepping out 1 nt at a time to determine the optimal full-length binding site. Finally, the K_d^app of the extrapolated 10 bp site for Zif268 could be compared with the K_d^app of the 10 bp site used in the co-crystal structure (24) to determine whether the extrapolated site has a higher binding affinity.

Table 4. Correlation coefficients between ranks calculated from the observed K_a^app values and K_a^app values calculated by extrapolating from partial microarray data 1NN and NN3.

Zif268 variant	Observed versus extrapolated rank
Wild-type	1
LRHN	1
RGPD	1
REDV	0.976
KASN	0.994

Correlation coefficients were based on a comparison of the ranks for 16 sequences for each of the five Zif268 variants.

DISCUSSION

These results provide compelling evidence that the use of binding site mononucleotide frequency weight matrices, currently the state-of-the-art bioinformatic technology for describing the binding site preferences of transcription factors, does not accurately depict the true binding site preferences. Analysis of microarray binding data led to the discovery that there is significant interdependence between the nucleotides of a transcription factor binding site. Taking into account the interactions between adjacent nucleotides provides a more accurate rank ordering of binding sites than does consideration of mononucleotide frequencies alone (see Table 2), but still does not completely describe all the interactions between the nucleotides of the binding site.

Much discussion has taken place regarding the possibility of a DNA recognition code that would describe sequence-specific DNA binding accurately (9,25–28). If a DNA recognition code does exist, it is likely to have different rules for each of the different structural classes of transcription factors (27), and it is likely that transcription factors of different structural classes will exhibit varying degrees of nucleotide position interdependence in their DNA binding sites. We have shown evidence that there is a significant degree of nucleotide position interdependence in a set of related Cys₂His₂ zinc fingers. Further analyses of DNA–protein interactions, including high throughput analyses capable of providing quantitative binding data for a great number of DNA variants (10,11), of members of other structural classes of DNA binding proteins will provide the necessary data to determine the extent of nucleotide position interdependence in binding sites for these various types of transcription factors.

In addition, our analyses indicate that microarray binding data using particular subsets of binding sites can be extrapolated to calculate the relative binding affinities of the preferential full-length binding sites, given that some binding site is already known that can be used as a starting sequence for which to vary each dinucleotide. Such extrapolation would be useful in the analysis of microarray binding experiments in order to derive the binding site preferences of transcription factors such as those with a series of zinc fingers in tandem, while keeping cost and labor to a minimum by using only a small fraction of all possible binding sites on the microarrays.

Supplementary Material is available at the World Wide Web site http://arep.med.harvard.edu/Bulyk/NAR2002supplementary/.