Geometric transformation of cognitive maps for generalization across hippocampal-prefrontal circuits

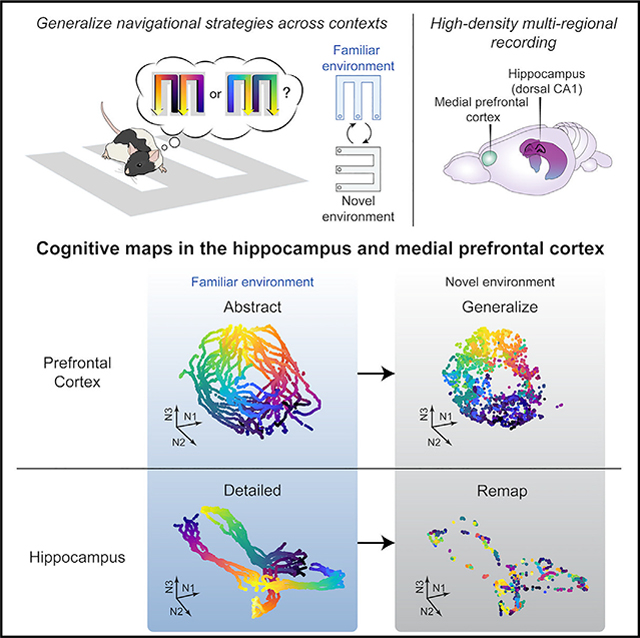
SUMMARY

The ability to abstract information to guide decisions during navigation across changing environments is essential for adaptation and requires the integrity of the hippocampal-prefrontal circuitry. The hippocampus encodes navigational information in a cognitive map, but it remains unclear how cognitive maps are transformed across hippocampal-prefrontal circuits to support abstraction and generalization. Here, we simultaneously record hippocampal-prefrontal ensembles as rats generalize navigational rules across distinct environments. We find that, whereas hippocampal representational maps maintain specificity of separate environments, prefrontal maps generalize across environments. Furthermore, while both maps are structured within a neural manifold of population activity, they have distinct representational geometries. Prefrontal geometry enables abstraction of rule-informative variables, a representational format that generalizes to novel conditions of existing variable classes. Hippocampal geometry lacks such abstraction. Together, these findings elucidate how cognitive maps are structured into distinct geometric representations to support abstraction and generalization while maintaining memory specificity.

In brief

Tang et al. show that, as rats generalize rules across environments, cognitive maps are constructed on neural manifolds in the hippocampus and prefrontal cortex with distinct geometries for complementary functions. Prefrontal geometry enables abstraction of task knowledge generalizable across contexts, whereas hippocampal manifolds remap to maintain memory specificity.

Graphical Abstract

INTRODUCTION

Memory generalization, the ability to abstract knowledge from prior experiences, is critical for adaptive behavior in novel situations. In the spatial memory domain, generalization manifests in the application of learned navigational rules across environments with distinct sensory cues. Animals can thus rapidly adapt in new contexts without having to learn de novo. Considerable research in humans and animals has established that the hippocampus is essential for memory of contextual details^1,2 and that generalization across contexts requires the medial prefrontal cortex (PFC).^3–7 Memory generalization thus depends on distributed circuits in the hippocampus and PFC; however, little is known about the underlying neural representations.

Memory generalization can be facilitated by a systematic organization of past episodes into a map-like representation, a “cognitive map,”⁸ and a promising neural substrate for spatial cognitive maps is provided by hippocampal place cells.⁹ Place cells form context-specific spatial maps by responding to particular locations in an environment and remapping to distinct place codes in a new environment.^9–12 How these spatial cognitive maps are transformed across hippocampal-prefrontal representations to enable abstraction and generalization remains largely unknown. Recently, several studies have reported spatially tuned neurons in rodent PFC that strikingly resemble hippocampal place cells.^13–23 Furthermore, similar to the hippocampus,^24–26 spatial locations are conjunctively encoded with other task-relevant variables in the PFC,^17,27–30 termed “mixed selectivity.”^31–33 These parallel representations with shared task information raise a fundamental question about how these representations can also subserve the distinct functions in memory generalization ascribed to the hippocampus and PFC.

An emerging theoretical framework suggests that circuit function is determined not only by representational content but also by representational geometry, the structural arrangement of task-relevant variables in a space of neural population states, called a manifold.^26,34–36 A recent study demonstrated the existence of a geometric neural manifold in the hippocampus that represents task knowledge in the current environment during navigation.²⁶ However, it is unclear whether the PFC preserves or reorganizes the hippocampal manifold structure and whether and how these representational geometries contribute to generalization across environments. To address these questions, we simultaneously recorded hippocampal-PFC neural ensembles as rats generalized memory-guided decision-making in a hippocampal-PFC-dependent navigation task across two distinct environments. This approach allows for a quantitative comparison of the intrinsic structures of hippocampal-PFC representations, as well as their dynamics, during generalization of navigational behavior.

RESULTS

Rats generalize learned rules across contexts

We trained five rats to perform a spatial memory task known to require hippocampal-prefrontal interactions^37–39 and to switch between familiar and novel environments. In this continuous alternation W-maze task (Figure 1A, left), rats had to return to the center (C) from either the right (R) or left (L) side of a W-track (inbound trajectory left or right [IN_L or IN_R]) and then correctly choose the opposite side (outbound trajectory right or left [OUT_R or OUT_L]) to be rewarded at the end of each trajectory. Therefore, the critical memory demand of this task is to learn and remember the correct IN-OUT sequences (IN_R-OUT_L and IN_L-OUT_R), termed “task sequences.”

Figure 1. Prior knowledge facilitates learning in novel environment.

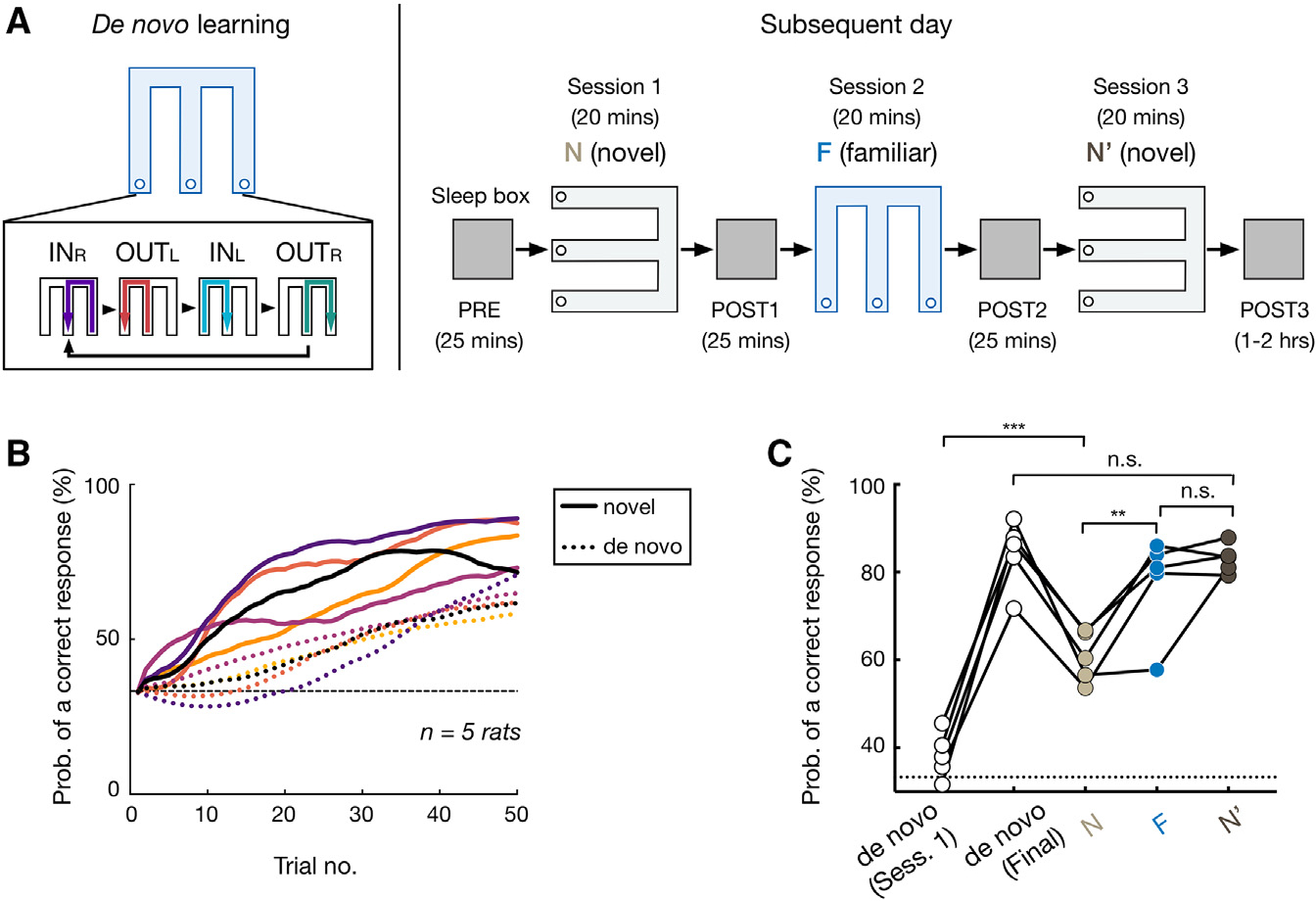
(A) Experimental design.

(B and C) After de novo learning, rats $(\mathrm{n}=5)$ acquired the task more rapidly in the novel environment (novel learning).

(B) Proportion correct for the first 50 trials during de novo vs. novel learning. Each pair of dashed (de novo learning) and solid (novel learning) lines represents an animal (color coded).

(C) Proportion correct against session number (data points for individual animals; repeated-measures ANOVA with Tukey’s post hoc, $F=40.48$, n.s., $\text{p}>0.75$, ***p = 0.0002, **p = 0.0045). De novo (session 1), the first W-track session of de novo learning; de novo (final), final performance of de novo learning before N-F-N′ sessions. Horizontal dashed line: chance level.

See also Figure S1.

Animals initially had no prior W-track experience and first learned the task in one environment with at least eight 20-min W-track sessions interleaved with rest sessions in a sleep box (de novo learning; final performance, 84.3% ± 7.7%, mean ± SD; STAR Methods). On a subsequent day, they were introduced to a novel W-track in a visually distinct room for one session (denoted as N; Figure S1A), then returned to the familiar environment (F) where they had learned the task de novo on previous days, and finally reexposed to the novel environment (N′; Figure 1A, right). Compared with de novo learning, all animals acquired the inbound and outbound task rules faster in the novel environment (Figures 1B, 1C, and S1B). To determine whether rats had indeed generalized learned rules, instead of confusing the novel environment with the familiar one, we examined the performance of another set of well-learned rats $(\mathrm{n}=3)$, which were exposed to the familiar environment first and then switched to the novel environment within a day, for an opposite order of exposures as F-N-F′-N′ (STAR Methods). We found that for both animal groups, the performance in the familiar environment was significantly higher than that in the novel one regardless of the order of experience (Figures 1C and S1C), suggesting that animals were able to remember and distinguish the two environments. Together, these data suggest that rats learned to generalize spatial rules across environments.

PFC spatial map generalizes, while CA1 completely remaps, across contexts

Since rats demonstrated transfer of learned knowledge from one environment to another, we leveraged this behavior to assess neural representations that support memory generalization. We recorded simultaneously from the PFC and the dorsal CA1 region of the hippocampus using high-density arrays with 32–64 tetrodes (Figure S2; STAR Methods). Cells were stably tracked across environments (mean ± SD = 30.5 ± 9.8 CA1 and 37.4 ± 19.3 PFC cells per session per animal; Figure S2). In agreement with previous hippocampal findings,^9–12 CA1 place cells exhibited extensive remapping in response to environment switches (Figures 2A–2C and S3). Notably, the distributions of CA1 spatial-representation similarity between two environments were not different from distributions obtained by shuffling cell identities in the same environment (Figure S3A), suggesting that CA1 place cells provide statistically independent ensemble activity in separate environments (i.e., global remapping).^11,12 Furthermore, the previous CA1 representation was reinstated upon reexposure to the same environment (Figures 2A–2C and S3). Therefore, the hippocampus maintains unique maps of individual environments, even when the animals perform the same spatial memory task.

Figure 2. Hippocampus shows global remapping, whereas prefrontal spatial representations generalize across environments.

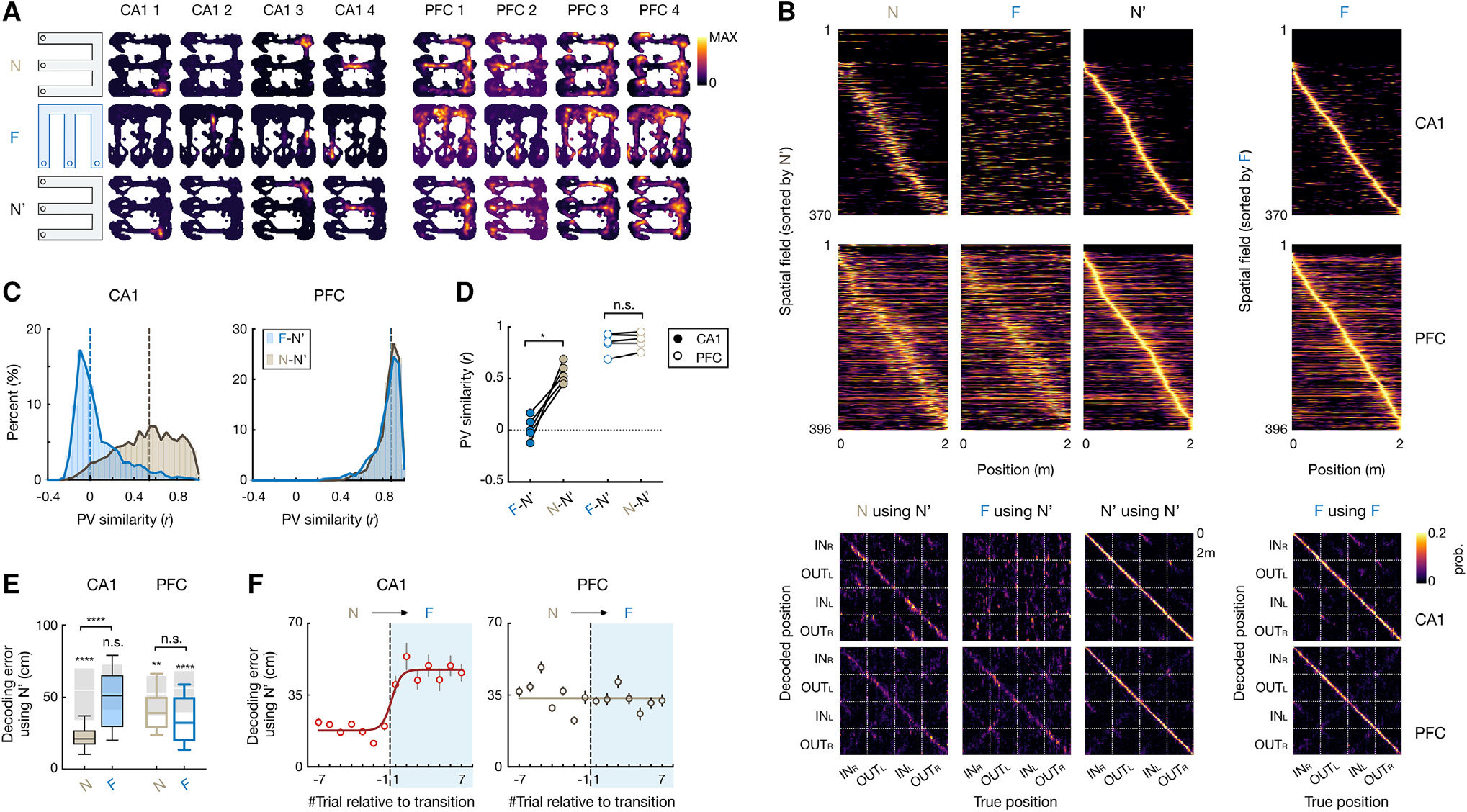
(A) 2D rate maps of 4 CA1 and 4 PFC cells simultaneously recorded across environments (N, F, and N′).

(B) Top two rows: normalized rate maps on 2-m-long linearized trajectories of all spatial-tuned neurons tracked over environments, sorted by peak activity in N′ (left 3 columns) and in F (right). Bottom two rows: corresponding confusion matrices between true and decoded positions (with leave-one-out cross-validation; STAR Methods), where diagonal elements represent decoding accuracy.

(C and D) Population vector (PV) similarity across novel (N-N′; light gray) and familiar-novel (F-N′; blue) environments. Dashed vertical line on histogram: median. Each circle in (D) is for an animal (repeated-measures ANOVA with Tukey’s post hoc, $F=83.24$, n.s., $\mathrm{p}=0.41$, *p = 0.01).

(E) Decoding error using spatial maps from N′. Kruskal-Wallis test with Dunn’s post hoc comparing N and F, n.s., $\mathrm{p}>0.99$, ****p < 0.0001. $\text{p}$ values above each box were computed by comparing with its cell-ID shuffles (shaded boxes; n.s., $\mathrm{p}=0.14$, **p = 0.0023, ****p < 0.0001, Wilcoxon paired test). Box plots show median, 75^th (box), and 90^th (whiskers) percentile.

(F) Trial-by-trial decoding error during environment switch (N to F; median ± SEMs; line, sigmoid fit). Trial −1 vs. 1: p(CA1) = 0.038, and p(PFC) > 0.99, Kruskal-Wallis test with Dunn’s post hoc.

See also Figures S2–S4.

In striking contrast with hippocampal global remapping, we found that the PFC spatial representation was stable across environments (Figures 2A and 2B). While there was representational drift of PFC cells even within the same environment¹⁶ (Figure 2B), the PFC spatial-representation similarity between two different environments was just as large as with repeated testing in the same environment (Figures 2C–2E, S3A, and S3B), suggesting that novel and familiar environments shared the same prefrontal map. Furthermore, there was greater assimilation of PFC representations across environments with experience, while CA1 place cells maintained their independent representations (Figures S3C and S3D). Of note, the persistence of environment-specific representations in the hippocampus suggests that the animals did not ignore environmental cues when generalizing task knowledge, as it has been shown that inattentiveness to environmental cues changes spatial coding and reduces hippocampal place-field stability.^40,41

Since the environments shared both the same rules (i.e., remembering correct task sequences) and the same reward configuration, we examined the degree of generalization attributed to coding of reward expectation and task sequences. Previous studies have shown that firing rates of some hippocampal^42–44 and prefrontal^45,46 neurons ramp up as the animal moves toward the reward, representing relative proximity of goals and thus reflecting reward expectation.^47–49 Consistent with previous reports, we identified ramping neurons in both CA1 and PFC (Figures S4A and S4B; STAR Methods). We found that PFC ramping cells generalized reward representations, but the CA1 representation remapped across environments (Figures S4A and S4B). In addition, the generalization for reward ramping cells was seen to a similar degree to other cells within regions (Figure S4C). Finally, in both regions, the similarity of population activity across different environments at reward wells was the same as other locations (Figure S4D). Therefore, the generalization of PFC maps was not simply attributed to reward expectation.

To determine how fast ensemble codes shift upon environment switch, we next examined trial-to-trial dynamics of CA1 and PFC representations. We used Bayesian decoding to apply spatial representations of CA1 and PFC cells from the novel environment to reconstruct locations in the familiar and novel environments (STAR Methods). Confirming the remapping results, the error between actual and reconstructed positions in the familiar environment was significantly higher than that in the novel environment and no better than chance for CA1, whereas PFC decoding was well above chance and similar across environments (Figures 2B and 2E). Interestingly, the decoding error rapidly increased during the first trial after environment switching for CA1 but remained stable for PFC (Figure 2F; trial −1 vs. 1: $\text{p}=0.038\text{and}>0.99$ for CA1 and PFC, respectively, Kruskal-Wallis test with Dunn’s post hoc). Together, these data suggest that when animals performed the same memory task in different environments, unique CA1 representations appeared immediately after introduction to a novel environment, contributing to separation of spatial contexts in memory, whereas PFC representations carried over from one environment to the other, allowing generalization.

Distinct geometries of CA1 and PFC representations

To further investigate how CA1 and PFC neurons encode task knowledge, we examined their single-cell responses to different task variables. We found that PFC and CA1 single-cell codes had distinct generalization properties for multiple task variables beyond spatial locations. First, many PFC cells exhibited similar activity profiles at the same trajectory phase (defined by the distance from the starting point) across different trajectory types (Figure S5), termed “path equivalence.”^50,51 Such path equivalence is relatively rare in CA1^52,53 (Figure S5). Furthermore, beyond simple “path equivalence” comprising one generalized representation of all trajectories as previously suggested,^50,52,53 we found that the firing patterns of PFC neurons specifically distinguished the two IN-OUT task sequences critical for task performance (IN_R-OUT_L vs. IN_L-OUT_R in Figure 1A; “task-sequence selectivity”) and thus generalized the responses across the two IN and OUT trajectories covering distinct spatial locations within a task sequence (Figures 3B, 3C, and S5F). In contrast, most CA1 cells showed consistent firing for trajectories with similar spatial coverage (IN_R-OUT_R or IN_L-OUT_L; Figures 3A and 3C). As a result, the selectivity indices of IN (IN_L vs. IN_R) and OUT (OUT_L vs. OUT_R) trajectories exhibited a positive correlation for CA1 and an opposite, negative correlation for PFC (Figure 3D; STAR Methods). We noted, however, that while the two trajectories within a task sequence shared similar motor patterns (e.g., performing an L/R turn), the response of PFC cells was not a pure encoding of actions because spatial positions associated with similar actions can still be accurately decoded from PFC activity^17,22 (Figures 2B and 2E). Therefore, the PFC representation did not strictly encode spatial or motor information, per se,²⁹ but variable conjunctions relevant to the task rule. Finally, consistent with spatial remapping results, these properties were stable across environments for PFC neurons but not CA1 (Figures 3E and S5E).

Figure 3. Distinct geometric representations of task space in CA1 and PFC.

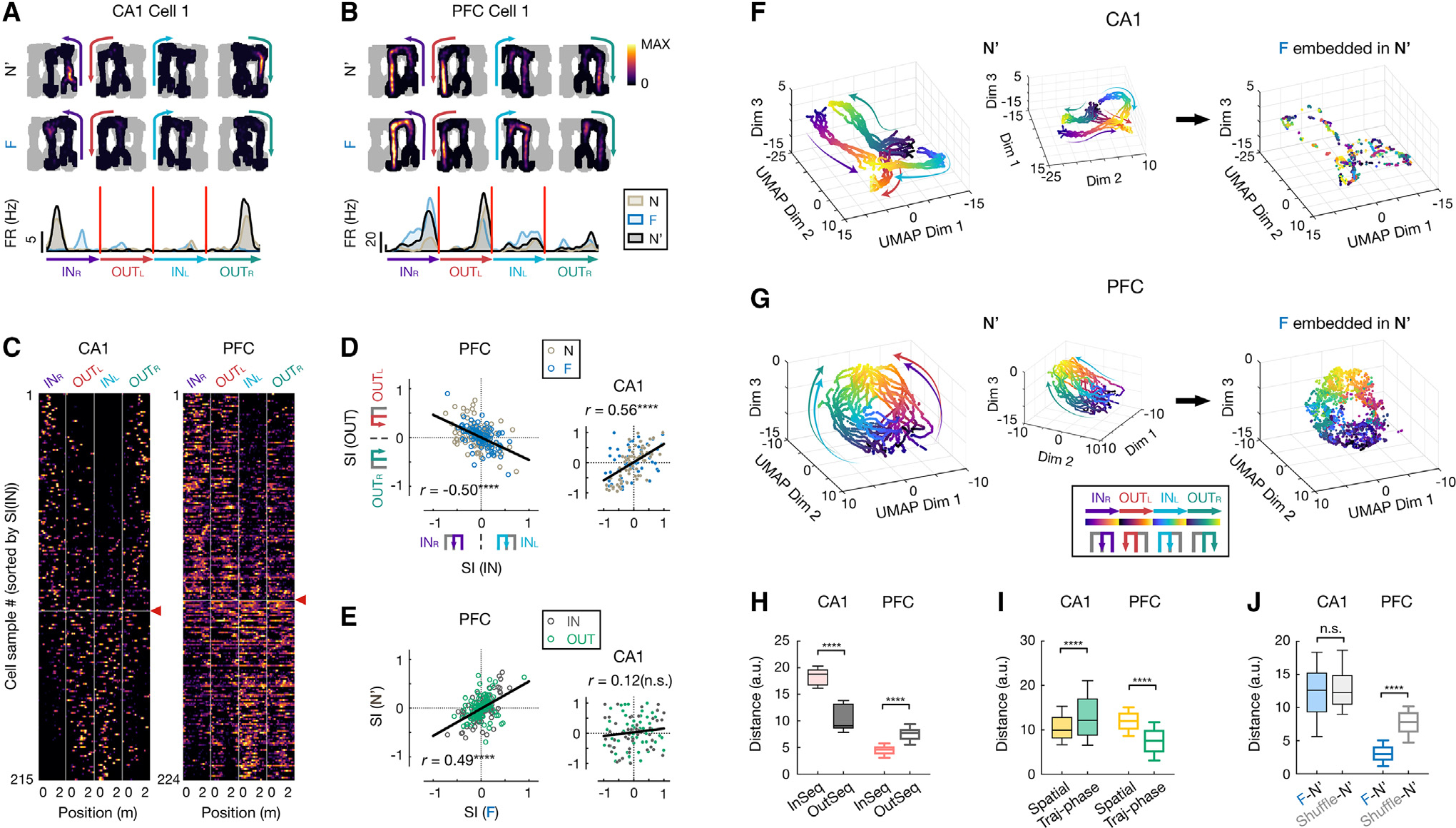
(A–E) CA1 and PFC neurons show distinct task-sequence selectivity.

(A and B) Firing fields on different trajectories of example (A) CA1 and (B) PFC cells. Top: 2D rate maps on each of 4 trajectories in the rewarded order (IN_R, OUT_L, IN_L, OUT_R, color coded) in N′ and F (all locations visited in a given session in gray). Bottom: corresponding rate maps on linearized trajectories (color-coded arrowheads indicate trajectory start and end).

(C) Linearized rate maps on the 4 trajectories of all spatially tuned neurons, sorted by selectivity index of inbound trajectories (i.e., SI(IN); IN_L vs. IN_R). The vertical lines separate each trajectory type. Horizontal line with a red arrowhead: division between cell samples with SI(IN) < 0 (above; selective to IN_R) vs.> 0 (below; selective to IN_L).

(D) Selectivity index of inbound against outbound trajectories (SI(IN) vs. SI(OUT); PFC, $r=-0.5$, ****p = 1.35e16; CA1, $\mathrm{r}=0.56$, ****p = 1.39e11; Pearson correlation).

(E) Selectivity index in familiar against novel environment (PFC, $r=0.49$, ****p = 2.77e–14; CA1, $r=0.12$, n.s., $\text{p}=0.22$; Pearson correlation). Dark gray: SI(IN); green: SI(OUT). Each dot is a cell sample, and lines show least-squares linear fits in (D) and (E).

(F and G) 3D unsupervised embeddings of neural manifolds using UMAP in (F) CA1 and (G) PFC. Each dot represents the populational neural state (same 98 and 171 cells for CA1 and PFC, respectively) at one spatial position of a single trajectory pass (color coded by trajectory types and phases). Arrow-headed lines on manifolds schematically illustrate direction of motion along trajectory phases (from start to end). Left and middle: two different views of the manifold from the N′ session. Right: embeddings of population activity from F, guided by its template from N′ (STAR Methods).

(H) Distance between pair of trajectories in manifold. InSeq, pair of trajectories in a correct task sequence (IN_R and OUT_L or IN_L and OUT_R); OutSeq, pair of trajectories out of the sequence (IN_R and OUT_R or IN_L and OUT_L).

(I) Distance between pair of neural states at same physical spatial locations or trajectory phases (traj-phases) in manifold.

(J) Distance between F and N′ neural manifolds. Shuffle: cell IDs of N′ activity randomly shuffled.

Box plots in (H)–(J) show median, 75^th (box), and 90^th (whiskers) percentile (rank-sum tests, n.s., $\text{p}=0.16$, ****p < 0.0001).

See also Figures S5 and S6.

The examination of single-cell encoding profiles revealed extensive heterogeneity, with a gradient in selectivity and generalization properties in each region (Figures 2 and 3). To further gain insights into how CA1 and PFC circuits engaged individual neurons into functional ensembles to encode task knowledge, we characterized the structure of population activity by extracting neural manifolds using uniform manifold approximation and projection (UMAP; STAR Methods). This unsupervised algorithm revealed that the population activity of PFC cells resides on a ring-shaped manifold, making it distinct from the CA1 neural manifold with a double “V” shape that topologically resembles the physical spatial structure of the W-maze (Figures 3F and 3G, left).

To validate the manifold approach, we examined if the extracted geometric structure accurately reflected the diverse tuning properties of individual cells. If so, four key predictions should be true. First, locations along different trajectories should have distinct population neural states in the manifolds to support episodic encoding of locations in both CA1 and PFC, with the location-selective firing of individual neurons differentiating the context of specific trajectories (Figures 2B and 3E).^{17,22,27,28,52,54} Figures 3F and 3G demonstrate that neural states of single passes of the same trajectory exhibited similar dynamics, yet maintained separation between those belonging to different trajectories, enabling trajectory-specific representations of locations. Second, the task-sequence selectivity of PFC cells (Figure 3D) predicts that the trajectories in a correct task sequence (InSeq; IN_R-OUT_L or IN_L-OUT_R) should reside in closer proximity than those out of the sequence (OutSeq; IN_R-OUT_R or IN_L-OUT_L). Indeed, the two InSeq trajectory pairs lie close together on opposite sides of the ring of the PFC manifold (Figure 3G). When measuring the distance between neural trajectories (STAR Methods), we found that the distance between two InSeq trajectories was significantly smaller than two OutSeq ones in the PFC manifold, whereas OutSeq pairs with same spatial coverages had smaller distances than InSeq pairs in the CA1 manifold (Figure 3H). Third, the same trajectory phase across the four different trajectory types should be geometrically aligned in the PFC manifold to encode “path equivalence.” Indeed, for PFC, the same phases of different trajectories (e.g., the start points) were aligned, regardless of their physical distances (Figure 3G, left). As a result, the distances between PFC neural states for the same trajectory phases were significantly smaller than those for the same spatial locations, while the opposite is true for CA1 (Figure 3I). Fourth, the generalization of PFC spatial representations (Figure 2) predicts that the manifold structure should be preserved across environments. To test this, we embedded the population activity from the familiar environment into the manifold extracted from the activity in the novel environment (Figures 3F and 3G, right; STAR Methods). We found that the geometric structure of the PFC manifold was largely preserved across environments, whereas the distortion of the CA1 manifold was similar to that from random shuffles (Figure 3J). In all the cases above, the distance relationship of neural states, which determines the representational geometry, was preserved between the low-dimensional manifold space and the original high-dimensional neural space (Figure S6). Together, our data reveal that neural ensembles in CA1 and PFC simultaneously represent multiple task variables with distinct geometries that are consistent with single-neuron selectivity. More importantly, the demonstration of population-level neural manifolds uncovers an internal structure that is not readily apparent from individual neuronal responses, elucidating how two seemingly opposing functions of the single-neuron codes, i.e., maintenance of episodic detail (e.g., location and trajectory specificity) and generalization across experiences, can operate in tandem at the level of neural populations.

Distinct abstraction in CA1 and PFC

Generalization is posited to arise from abstraction of commonalities across experiences.^3,32,35 Previous studies have operationally defined abstraction using the generalization performance of neural decoders across task conditions not used for training (cross-condition generalization performance [CCGP]), which requires a specific representational geometry.^35,55 Unlike traditional cross-validation decoders, trained on a subset of samples from all conditions and tested on held-out samples from the same conditions, CCGP evaluates a decoder’s ability to reuse its existing trained structure to separate similar but novel inputs, allowing generalization.³⁵

To assess if CA1 and PFC manifolds emerged as an abstraction of task variables, we further characterized their representational geometries using CCGP. To simplify decoding, we considered an early and a late phase for each trajectory in the neural manifolds (Figures 3F and 3G, left), resulting in 8 different clusters for each region (Figures 4A and 4B; STAR Methods). We then tested the CCGP for the three different dichotomies introduced in the previous section (i.e., early vs. late trajectory phase, task sequence IN_R-OUT_L vs. IN_L-OUT_R, and novel vs. familiar environment; Figure 4C, top to bottom). For example, to classify early and late trajectory phases (Figure 4C, top), a linear decoder was trained on 3 out of all 4 trajectory types and then tested on the one trajectory type not used for training. Similarly, we tested the CCGP of the task sequence by holding out a pair of clusters with the same trajectory phase but belonging to different task sequences; for the CCGP of spatial contexts, we tested the decoder trained by neural activity in the novel environment with the activity in the familiar environment (STAR Methods). We found that the CCGP for all three task variables showed high accuracy for PFC but was at or below chance for CA1 with a trial-label permutation test (Figures 4C and 4D), as well as against a geometric random model (STAR Methods; Figures S7A and S7B).³⁵ PFC representation thus has a geometric structure that enables a decoder to classify neural responses to these task variables in novel conditions (i.e., an abstract format). Notably, if we measured the amount of information decodable using the traditional cross-validation decoder for all 35 possible dichotomies (dividing the 8 clusters into 2 groups of 4 conditions),³⁵ with each dichotomy corresponding to a task variable that could be decoded, we found that most of the dichotomies were accurately separated in both CA1 and PFC, suggesting that both regions contain a similar amount of decodable variables (Figures S7C and S7D). Together, these data reveal that although CA1 and PFC representations shared similar information content of the current task, such content was formatted with distinct levels of abstraction in CA1 and PFC.

Figure 4. Distinct abstraction in CA1 and PFC representations.

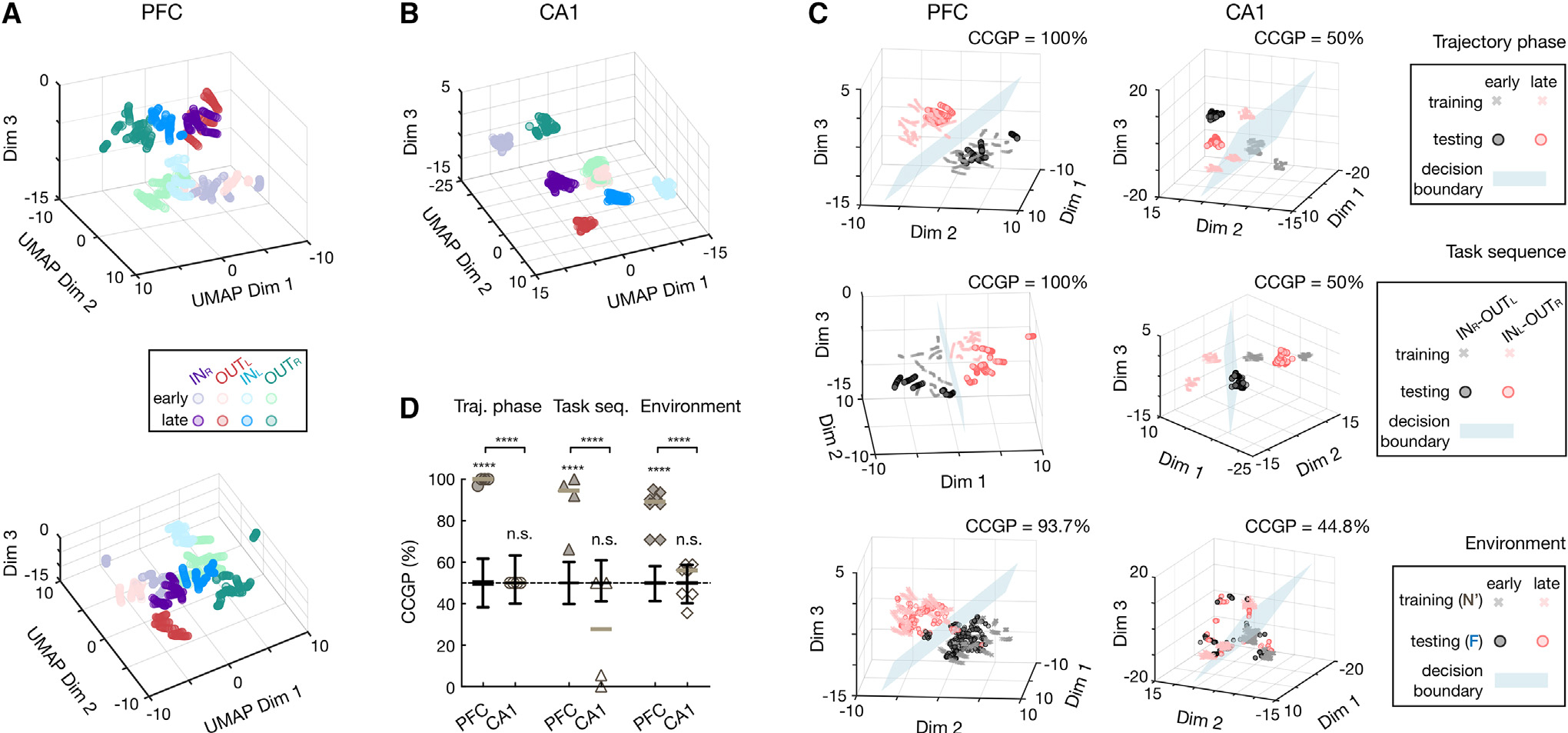
(A and B) UMAP embeddings of 8 clusters for early and late trajectory phases of 4 trajectory types (color coded) in (A) PFC and (B) CA1.

(A) Two different views of PFC clusters shown on top and bottom.

(C) CCGP of example decoding of dichotomies in PFC (left) and CA1 (right). From top to bottom: decoding for trajectory phases, task sequences, and environments, respectively (STAR Methods). A linear classification was implemented by a “decision hyperplane” (blue), trained on a subset of conditions in (A) and (B) (training set, crosses), and divided the space into two classes (red or black). CCGP (denoted on top) was then measured as how well this classifier generalize to an unseen set of conditions (testing set, circles; STAR Methods). Note the good performance on training sets but poor generalization on testing sets for CA1 decoding in contrast to high CCGP for PFC.

(D) CCGP for trajectory phases (circles), task sequences (triangles), and environments (diamonds; horizontal lines, median). Early, early trajectory phase; late, late trajectory phase. Note that all dichotomies can be accurately decoded in PFC (****p < 0.001) but not in CA1 (n.s., $\text{p}>0.05$, trial-label permutation test). Boxplots are for trial-label shuffles ($\mathrm{n}=\mathrm{1,000}\text{times}$) and show median, interquartile range (box), and min-max (whiskers).

See also Figure S7.

DISCUSSION

Here, we have identified neural manifold signatures of memory generalization in the rat hippocampal-prefrontal circuitry using a spatial navigation task across environments with distinct sensory cues. Animals acquired the task significantly faster in the novel environment than during de novo learning (Figures 1 and S1) and thus exhibited behavior reflecting generalization of remembered task knowledge. During memory generalization, we found that the hippocampus remapped and conjunctively linked the task structure with current spatial context, whereas PFC did not remap but organized task knowledge in an abstract format, which is generalizable to novel spatial contexts (Figure 2) and to variable conjunctions relevant to the task rule (Figures 3 and 4).

We note that the generalizable PFC map observed here is broadly consistent with previous reports of its task-rule representation, where PFC neurons respond similarly to different sensory stimuli associated with the same behavioral outcome.^56–58 Our navigational task densely samples the space of task variables, rather than using a few pre-defined task states as in the previous studies,^56–58 and thus reveals the organized cognitive map instantiated by a neural manifold in PFC. Further, the distinct geometry of the prefrontal cognitive map provides a striking contrast to the exemplar cognitive map in the hippocampus for representing episodic details.⁹ Finally, our results provide neurophysiological support to the prevailing theoretical framework regarding the complementary contributions of the hippocampus and PFC to memory generalization.^5–7 Of note, the complementary representations observed here have the capacity to retrieve learned task knowledge in new spatial contexts without losing the separability of different contexts. Proposed models with similar complementary architectures can optimize the trade-off between separability and generalizability in neural computations and thus achieve enhanced flexibility and reduced interference in artificial agents.^7,25,33,59

The use of the W-maze task is motivated by causal evidence that an intact hippocampal-prefrontal network is necessary for optimally learning and performing the task.^37–39,60 In contrast, recent experiments using simple exploratory tasks, such as linear-track running and random foraging, showed that PFC remapped, reminiscent of the hippocampus.^16,19,30,61 Notably, this type of behavior without explicit memory requirements does not require the hippocampal-prefrontal network.^62,63 Together, these results demonstrate that while PFC responds to contextual information, the generalizability of the PFC cognitive map is task dependent. This dependency is further supported by previous evidence that PFC neurons changed their response to similar behaviors across two different tasks in the same environment.^29,64,65 Therefore, shared visual cues and motor patterns alone are insufficient to robustly evoke a generalizable representation of task space in PFC. This idea echoes previous studies, which found that cognitive demands and behavioral engagement can profoundly change hippocampal and prefrontal spatial representations.^{29,40,41,66–68} Given that the hippocampus provides a major input to PFC^69,70 and that hippocampal lesions impair the PFC spatial code,⁶¹ we postulate that the spatial responses in PFC may be passively invoked by hippocampal input when not actively engaged in the behavior, such as during spontaneous locomotion, whereas specific task requirements may necessitate further neural computations of generalizable task knowledge in PFC.

In contrast to the distinct representational formats, we found that the representational content of current task information is largely shared across the hippocampus and PFC, consistent with previous reports of various response types found in both regions, including spatially tuned cells (Figure 2),^14,16,22,28 trajectory-dependent cells (Figures 2 and 3),^{17,22,27,28,52,54} and path-equivalent cells (Figure S5).50–53 Our data also support recent studies demonstrating highly distributed encoding of task variables across diverse brain areas involved in flexible behavior,^71–74 posing the challenge of reconciling highly distributed encoding with specialized functions in distinct brain circuits. Here, we bridged this gap by revealing an important relationship between coding properties of individual neurons and population geometry in the hippocampal-prefrontal circuitry (Figures 3 and S6) and demonstrating how distinct representational geometries can be compatible with hippocampal and PFC specialized functions. Notably, the PFC representation achieved generalization across many task variables (Figure 4) yet did not discard their information (Figure S7). This coding mechanism can confer flexibility for readout of task variables (Figure S7), in agreement with studies in other species, including humans and non-human primates,^35,36,55 suggesting that it may be a conserved computational strategy.

Limitations of the study

The present study did not explore the relationship between the dynamics of geometric properties of neural manifolds (e.g., CCGP) and behavioral improvement due to the limited numbers of different trial types and neurons recorded. Recent developments in optical imaging and high-density electrophysiological recordings offer opportunities to address this question, and our study provides an ideal foundation to characterize the geometric structure of cognitive maps in such data. Also, the effective dimensionality of CA1 and PFC population activity remains to be determined. One common strategy to measure dimensionality is to apply linear dimensionality reduction methods, such as principal-component analysis (PCA), to neural population activity.^75,76 While such “embedding dimensionality” carries important information about manifold structures, it does not correspond to the “intrinsic dimensionality” (i.e., the minimal number of latent variables needed to parametrize the manifold).⁷⁷ Using a non-linear dimensionality reduction method, a recent study has demonstrated that the hippocampal manifold embedded in 4 dimensions of the non-linear space needed a much larger number of dimensions when applying PCA (~29 dimensions).²⁶ Therefore, accurately estimating the dimensions of CA1 and PFC manifolds remains a challenge. Finally, our results open questions not addressed here regarding the circuit mechanisms that govern transformation of hippocampal-PFC representations underlying memory generalization. The hippocampal-PFC interaction involves a broad network via multiple direct and indirect pathways,^69,70 and their functional connectivity is modulated by multiple network patterns, including theta oscillations and sharp-wave ripples.^18,78 Unraveling the roles of these pathways and network patterns in memory generalization is an important avenue for future studies.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dr. Shantanu P. Jadhav (shantanu@brandeis.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• Raw electrophysiological and rat behavioral data have been deposited on servers at Brandeis University, and are available upon request by contacting the lead contact.

• Custom code in MATLAB (R2017a) used for analyses in this study is available on GitHub at http://github.com/JadhavLab/GeometricTransformation.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Eight adult male Long-Evans rats (450–550 g, 4–6 months) were used in this study. Animals were individually housed and kept on a on a 12-hr regular light/dark cycle. All procedures were approved by the Institutional Animal Care and Use Committee at the Brandeis University and conformed to US National Institutes of Health guidelines.

METHOD DETAILS

Experimental design

After habituation to daily handling and resting in a high-walled, opaque sleep box (~30 × 30 cm), animals were food deprived to 85–90% of their ad libitum weight, and pre-trained to run on a linear track (~1-m long) for rewards (sweetened evaporated milk).^17,22 For experiments on the W-maze (~80 × 80 cm with ~7-cm wide tracks), animals were food-deprived and naïve to the W-mazes and the novel experimental room (Figure S1A). Animals were rewarded for performing a hippocampal and PFC-dependent continuous alternation task (Figure 1A, left)^37–39: returning to the center well after visits to either side well (left or right well; inbound, IN_L or IN_R), and choosing the opposite side well from the previously visited side when starting from the center (outbound, OUT_R or OUT_L). Animals learned the W-track alternation rule by trial-and-error. Rewards were automatically delivered in the three reward wells (left well: L; right well: R; center well: C), triggered by crossing of an infrared beam by the animal’s nose. Each W-maze session lasted 15–20 mins, and was interleaved with rest sessions in the sleep box placed near the W-maze (Figures 1A and S1A). The task performance was estimated using a state-space model (Figures 1 and S1).^39,84

We collected behavioral and electrophysiological data from five rats. For these animals, de novo learning of the W-maze task occurred in one room (Figure S1A) with 8 W-maze sessions within a single day.^17,22 Three of the five rats were trained for 2 additional days in the same environment (i.e., familiar environment). On a subsequent day after the de novo learning, rats were first trained to perform the W-maze task in a novel room for one session (denoted as N). In addition to a different size and number of prominent visual cues, the novel room incorporated large cue cards with distinct patterns to increase the discriminability from the familiar room (Figure S1A). After this novel session, rats ran one session in the familiar environment (F), followed by another session in the novel environment (N’; Figure 1A).

To ensure that animals can remember and discriminate the two environments, we analyzed the behavioral data of another three rats from a previous experiment^23,85 (Figure 1C). These animals were well-trained for the W-maze task in one environment for 5 days. Subsequently, for two further days, they ran one session in the familiar environment first, and then one session in the novel environment each day, and thus experienced a test sequence as F-N-F’-N’.

Recording procedures

After linear-track pretraining, animals were implanted with a multi-tetrode drive containing 32–64 independently moveable tetrodes targeting dorsal hippocampal region CA1 (−3.6 mm AP and 2.2 mm ML) and medial PFC (+3.0 mm AP and 0.7 mm ML), both in the right hemisphere (for 32-tetrode drives) or bilaterally (for 64-tetrode drives). On the days following surgery, hippocampal tetrodes were gradually advanced to the desired depths with characteristic EEG patterns (sharp wave polarity, theta modulation) and neural firing patterns.^17,22,23,85 One tetrode in corpus callosum served as the hippocampal reference, and another tetrode in overlying cortical regions with no spiking signal served as the prefrontal reference. The reference tetrodes reported voltage relative to a ground (GND) screw installed in skull overlying cerebellum. The W-maze experiments started at ~21 days after implantation, and electrodes were not moved at least 4 hours before and during the experiments. Following the conclusion of the experiments, micro-lesions were made through each electrode tip to mark recording locations^17,22 (Figures S2A–S2F). PFC recordings were primarily in PreLimbic cortex with a smaller number in rostral Anterior Cingulate Cortex (Figures S2D–S2F).

Data were collected using a SpikeGadgets data acquisition system (SpikeGadgets LLC). Spike data were sampled at 30 kHz and bandpass filtered between 600 Hz and 6 kHz. LFPs were sampled at 1.5 kHz and bandpass filtered between 0.5 Hz and 400 Hz. The animal’s position and running speed were recorded with an overhead color CCD camera (30 fps) and tracked by color LEDs affixed to the headstage. Single units were identified offline using a manual clustering method (MatClust, M. P. Karlsson).^17,22 Only well isolated neurons with stable spiking waveforms (Figures S2G–S2I), and at least 100 spikes in a given session were included in analyses. Putative interneurons were identified and excluded based on spike width and firing rate criterion.^17,22,23,85

QUANTIFICATION AND STATISTICAL ANALYSIS

Spatial fields and linearization

Spatial fields were calculated only during locomotor periods (> 5 cm/s; all SWR times excluded) at positions with sufficient occupancy (> 20 ms). 2D occupancy-normalized rate maps (Figure 2A) was constructed using spike counts and occupancies with 2-cm spatial bins, and smoothed with a 2D Gaussian (σ = 8 cm). To construct the 1D linearized rate maps on the 4 trajectory types (IN_R, OUT_L, IN_L, OUT_R), animal’s linear positions were first estimated by projecting its actual 2D positions onto pre-defined idealized paths along the track, and further classified as belonging to one of the four trajectory types.^17,22 The linearized rate maps were then calculated with 2-cm spatial bins of the linear positions, and smoothened with a 1D Gaussian (s = σ cm; Figure 2B). A peak rate ≥ 3 Hz across linear spatial bins was required for a cell to be considered as a spatially-tuned cell.

Quantification of single-cell remapping

Single-cell activity on the W-maze was compared across different environments. Rate remapping (i.e., change in firing rate) was quantified using “rate overlap”, which was calculated by dividing the mean firing rate in the less active environment to the mean rate in the more active one¹¹ (Figure S3A, top). Global remapping (i.e., change in firing location) was quantified using “spatial similarity”, as Pearson correlation ($r$) between linearized rate maps of two environments (Figure S3A, bottom). These values were also compared to the values expected from independent distributions, by randomly pairing the activity of a cell in the familiar environment to the activity of a different cell in the novel environment (i.e., cell ID shuffles).

Population vector similarity

To measure remapping in population activity, a population vector (PV) was constructed as the activity vector of all spatially-tuned cells in a certain linear spatial bin. The PV similarity was then defined as the Pearson correlation ($\text{r}$) between the PVs across all bins in two environments (Figures 2C, S3B, and S3C).

Ramping response identification

The ramping response was identified using a previous established method⁴⁹ (Figure S4). Session-averaged rate maps were considered as having ramping characteristics toward reward if they have a significantly linear regression coefficient (Pearson’s, $r>0.5$ and $\mathrm{p}<0.05$) over traversed positions to reward. We only included cells with a peak rate ≥ 3 Hz and located within 20 cm around the reward location.

Bayesian decoding

To evaluate neural representations at the ensemble level, Bayesian decoding was implemented.^17,22 A memoryless Bayesian decoder was built to estimate the probability of animals’ position given the observed spikes (Bayesian reconstruction; or posterior probability matrix):

$$P(X,Tr\mid \mathbf{spikes})=\frac{P(\mathbf{spikes}\mid X,Tr)P(X,Tr)}{P\left(\mathbf{spikes}\right)}$$

where $X$ is the set of all linear positions on the track for different trajectory types (i.e., $Tr,Tr\in \left\{{\mathrm{I}\mathrm{N}}_{\mathrm{R}},{\mathrm{O}\mathrm{U}\mathrm{T}}_{\mathrm{L}},{\mathrm{I}\mathrm{N}}_{\mathrm{L}},{\mathrm{O}\mathrm{U}\mathrm{T}}_{\mathrm{R}}\right\}$), and we assumed a uniform prior probability over $X$ and $Tr$. Assuming that all $N$ cells fired independently and followed a Poisson process:

$$P(\mathbf{spikes}\mid X,Tr)=\prod _{i=1}^N \frac{{\left(\tau f_i(X,Tr)\right)}^{{spikes}_i}{e}^{-\tau f_i(X,Tr)}}{{spikes}_i!}$$

where $\tau$ is the duration of the time window, $f_i(X,Tr)$ is the expected firing rate of the i-th cell as a function of sampled location $X$ and trajectory type $Tr$, and ${\mathrm{spikes}}_i$ is the number of spikes of the i-th cell in a given time window. Therefore, the posterior probability matrix can be derived as follows:

$$P\left(X,Tr\mid \mathbf{s}\mathbf{p}\mathbf{i}\mathbf{k}\mathbf{e}\mathbf{s}\right)=C(\prod _{i=1}^N{f}_i{(X,Tr)}^{spike{s}_i})e^{-\tau \sum _{i=1}^N{f}_i\left(X,Tr\right)}$$

where $C$ is a normalization constant such that ${\sum }_{k=1}^4 {\sum }_{j=1}^D P\left(x_j,t{r}_k\mid \mathbf{s}\mathbf{p}\mathbf{i}\mathbf{k}\mathbf{e}\mathbf{s}\right.=1$ ($x_j$ is the j-th spatial bin, $D$ is the total number of spatial bins, and $t{r}_k$ is the k-th trajectory type).

Specifically, linearized rate maps of neural ensembles in the N’ session were used as templates (i.e., $f(X,Tr)$). Spikes were calculated from the population activity in the N or F session binned into 200-ms bins (i.e., τ = 200 ms; moving window with 50 ms overlap), and was restricted to locomotor periods (> 5 cm/s; locations within 15 cm of the reward well were excluded for decoding to prevent contamination from SWR activity). For each time bin, the location with maximum decoded probability was compared to the actual position of the current trajectory that the animal was at in that bin (Figure 2B, bottom). Decoding error was then determined as the linear distance between estimated position and actual position (Figures 2E and 2F), and was compared to distributions from shuffling cell identities of rate maps in the N′ session (Figure 2E).

Trajectory selective index

To measure the trajectory selectivity of single cells, a trajectory selectivity index (SI) was calculated (Figures 3D and 3E) by comparing the mean firing rates on the Left- (or L-) vs. Right- (or R-) side trajectories for outbound (OUT, OUT_L vs. OUT_R) and inbound (IN, IN_L vs. IN_R), respectively:

$$SI=\frac{F{R}_L-F{R}_R}{F{R}_L+F{R}_R}$$

where $F{R}_L$ is the mean firing rate on the L-side trajectory, and $F{R}_R$ is for the R-side trajectory. Only cells that had at least one spatial field (peak rate ≥3 Hz) detected on either the L- or R-side trajectory were considered, and the rate maps in different sessions were analyzed separately.

Path-equivalent coefficient

Path equivalent coefficient of single cells was calculated using a previously established method.⁵⁰ We calculated the Pearson correlation of rate maps between two trajectory types. The median of the Pearson correlations across all possible pair combinations was reported as path-equivalent coefficient ($R$; Figure S5).

Characterization of neural manifold

In each region, all spatially-tuned units that were active in both environments were pooled across animals to build a pseudo-population of neurons ($n=98$ CA1 and 171 PFC cells, respectively). For each trajectory type, the minimal number of trials (or passes) across animals starting from the first trial in a given session was used as the trial number. For each population, single-trial linearized rate map of each cell was calculated and binned at a resolution of 1 cm. Bins with spikes from less than 5 neurons were discarded. Uniform Manifold Approximation and Projection (UMAP)^80,81 was then run on these n-dimensional data to extract low-dimensional neural manifolds (Figures 3J and 3G). The hyperparameters for UMAP were: ‘n_dims’ = 3, ‘metric’ = ‘cosine’, ‘n_neighbours’ = 50, and ‘min_dist’ = 0.6, similar to previous studies.^86,87 To compare the neural manifolds between the novel and familiar environment, the UMAP transformation calculated for the N’ session was re-applied to the population activity of the F session, by applying the fitted N’ UMAP transformation as the ‘template_file’ to the ‘run_umap’ function in the UMAP MATLAB toolbox⁸¹ (Figures 3F and 3G, right).⁸⁶

The geometric relationship of CA1 and PFC representations was further estimated using Euclidean distance in this reduced manifold space (Figures 3H–3J), as well as the original n-dimensional state space (Figure S6). In both spaces, distance was computed identically, except for the number of dimensions used. The between-trajectory distance was computed between the single-trial neural trajectories from two different trajectory types (Figures 3H and S6A). For trajectory pairs belong to the same task sequence, the distance between their neural states at the same trajectory phase (defined by the distance from the starting point) was calculated; similarly, for trajectory pairs on the same spatial side of the W-maze, the distance between their neural states at the same spatial location was calculated (Figures 3I and S6B). Finally, the distance between F and N⁰ representations was computed as the average distance of all pairwise distances of neural states from the same trajectory type and location in F and N’ (Figures 3J and S6C). The chance level was estimated by randomly shuffling the cell identities of population activity in N’ (Figures 3J and S6C).

Cross-condition generalization performance

The ability of neural manifolds to generalize to unseen experimental conditions was estimated using cross-condition generalization performance (CCGP).³⁵ For trajectory phase (Figure 4C, top), we first trained the decoders $(n=4)$ to classify the early and late phase of 3 out of 4 trajectory types (early and late phases defined as 20%-30% and 70%-80% trajectory length from the trajectory start, respectively; different phase values yielded similar results), and tested the trained decoders on the remaining trajectory type not used for training. Similarly, for task sequence (Figure 4C, middle), we first trained the decoders $(n=4)$ to classify the IN_R-OUT_L versus IN_L-OUT_R task sequences by holding out two clusters belonging to the same trajectory phase of two different OutSeq trajectories, and tested on the held-out conditions. Finally, these two types of decoders $(n=8)$ trained with neural activity in the N’ session were tested with neural activity in the F session (Figure 4C, bottom).

The CCGP was further compared with traditional cross-validation decoders. For cross-validation decoders, we considered all 35 dichotomies that divide the 8 clusters in Figures 4A and 4B into 2 groups of 4 conditions.³⁵ For each dichotomy, the binary decoder was built using a 4-fold cross-validation, of which data samples of all conditions were split into 4 groups with one group as the test data (Figures S7C and S7D). For all the binary decoders, we used a C-Support Vector Machine (SVM) with a linear kernel through the libsvm library.⁷⁹ Significance was estimated using permutation of trial labels ($n=\mathrm{1,000}\text{times}$).

We also tested the CCGP against a geometric random model that destroys the geometrical structure but preserves within-condition noise structure in the data (Figures S7A and S7B), as in previous studies.^35,55 To achieve this, the noise clouds (the trial-by-trial firing rates of each condition) were rotated by permuting the axes of the firing rate space, and we repeated this procedure for each cluster separately (Figures S7A, left). We then computed the CCGP as described above on these moved clusters to obtain a null model CCGP value (Figures S7A, right), and repeated this 100 times to get a null distribution (Figures S7B).

Statistical analysis

Data analysis was performed using custom routines in MATLAB (MathWorks) and GraphPad Prism 9 (GraphPad Software). We used nonparametric and two-tailed tests for statistical comparisons throughout the paper, unless otherwise noted. We used ANOVA for multiple comparisons of Gaussian distributions, followed by a Tukey’s test, when appropriate. For non-Gaussian distributions of multiple groups, we used Kruskal-Wallis test with post hoc analysis performed using a Dunn’s test. p < 0.05 was considered the cutoff for statistical significance. Boxplots show median, 75th (box), and 90th (whiskers) percentile, unless indicated otherwise. All heat maps were obtained using perceptually uniform colormaps from MatPlotLib.^83,82 No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those generally employed in the field.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Cresyl Violet	Acros Organics	Cat#: AC229630050
Formaldehyde	Fisher	Cat#: 50–00–0,67561,7732–18–5
Isoflurane	Patterson Veterinary	Cat#: 07–806–3204
Ketamine	Patterson Veterinary	Cat#: 07–803–6637
Xylazine	Patterson Veterinary	Cat#: 07–808–1947
Atropine	Patterson Veterinary	Cat#: 07–869–6061
Bupivacaine	Patterson Veterinary	Cat#: 07–890–4881
Beuthanasia-D	Patterson Veterinary	Cat#: 07–807-3963
Sucrose	Sigma-Aldrich	Cat#: S8501–5KG
Experimental models: Organisms/strains
Rat: Long Evans	Charles River	Cat#: Crl:LE 006; RRID: RGD_2308852
Software and algorithms
MATLAB 2017a	Mathworks, MA	RRID: SCR_001622
Trodes	SpikeGadgets	http://www.spikegadgets.com
Matclust	Mattias P. Karlsson	https://www.mathworks.com/matlabcentral/fileexchange/39663-matclust, V1.7
Libsvm	Chang and Lin 201179	https://www.csie.ntu.edu.tw/~cjlin/libsvm/, V3.12
Uniform Manifold Approximation and Projection (UMAP)	McInnes et al., 201880; Meehan et al., 202281	https://www.mathworks.com/matlabcentral/fileexchange/71902-uniform-manifold-approximation-and-projection-umap, V4.2.1
MatPlotLib	Cobeldick, 202282; Nunez et al., 201883	https://www.mathworks.com/matlabcentral/fileexchange/62729-matplotlib-perceptually-uniform-colormaps, V2.1.3
Prism 9	GraphPad Software	RRID: SCR_002798
Other
128 Channel electrophysiology data acquisition system	SpikeGadgets	http://www.spikegadgets.com
12.7 μm NiCr tetrode wire	Sandvik	Cat#: PX000004

Highlights.

• Rats generalize knowledge of a hippocampal-PFC-dependent task to novel environments

• As rules transfer across contexts, CA1 remaps, but PFC representations generalize

• CA1 and PFC neural manifolds encode spatial cognitive maps with distinct geometries

• PFC manifolds organize task knowledge in an abstract, generalizable format