Probing neural tissues at small scales: Recent progress of oscillating gradient spin echo (OGSE) neuroimaging in humans

Abstract

The detection sensitivity of diffusion MRI (dMRI) is dependent on diffusion times. A shorter diffusion time can increase the sensitivity to smaller length scales. However, the conventional dMRI uses the pulse gradient spin echo (PGSE) sequence that probes relatively long diffusion times only. To overcome this, the oscillating gradient spin echo (OGSE) sequence has been developed to probe much shorter diffusion times with hardware limitations on preclinical and clinical MRI systems. The OGSE sequence has been previously used on preclinical animal MRI systems. Recently, several studies have translated the OGSE sequence to humans on clinical MRI systems and achieved new information that is invisible using conventional PGSE sequence. This paper overviews the recent progress of the OGSE neuroimaging in humans, including the technical improvements in the translation of the OGSE sequence to human imaging and various applications in different neurological disorders and stroke. Some possible future directions of the OGSE sequence are also discussed.

Introduction

Diffusion MRI (dMRI) provides a unique means to characterize the microstructure of biological tissues non-invasively. Numerous dMRI methods, including diffusion tensor imaging (DTI) (Basser et al., 1994) and multi-compartment quantitative dMRI models (Kaden et al., 2016; Zhang et al., 2012), have been widely used in neuroimaging for the diagnosis and assessment of treatment in various neurological disorders and stroke. It remains an active research topic nowadays to further develop and validate more advanced dMRI methods. Despite a large variety of different dMRI methods, the majority of dMRI acquisitions use the pulsed gradient spin echo (PGSE) sequence that was originally introduced by Stejskal and Tanner for diffusion measurements (Stejskal, 1965; Stejskal and Tanner, 1965). This method uses two pulsed diffusion gradients each with a duration of $\delta$ and separated by a time interval of $\text{Δ}$. If $\delta \ll \text{Δ}$ (i.e., short pulse approximation), $\text{Δ}$ is approximately the effective diffusion time $t_{diff}$, during which water molecules diffuse and constantly encounter barriers/obstacles that restrict/hinder diffusion. Such restrictions/hindrances reflect tissue microstructures such as the density and permeability of myelin sheaths and cell membranes, which in turns provides an opportunity to probe tissue status non-invasively. Therefore, diffusion time is one important factor for diffusion measurements because it determines the average number of interactions between water molecules and tissue microstructure.

In theory, different $t_{diff}$ values can be achieved by simply adjusting $\text{Δ}$ and $\delta$. However, there are hardware constraints in practice that limit achievable $t_{diff}>30$ ms particularly on human MRI systems. Because the root-mean-square displacement of diffusion is $l=\sqrt{2D{t}_{diff}}$, typical diffusion measurements are more sensitive to length scale > 13 μm, which is much larger than typical axon and cell sizes in the central nervous system (CNS). To overcome the limitations of the PGSE sequence, the oscillating gradient spin echo (OGSE) sequence has been developed to achieve much shorter diffusion times with the presence of hardware constraints (Schachter et al., 2000; Tanner, 1979). The OGSE sequence replaces the pulsed gradients with oscillating gradients and the effective diffusion time $t_{diff}$ is not dependent on the separation of two gradients ($\text{Δ}$) but is determined by the oscillating period $T$ ($=1/f$, the oscillating frequency). Although it is unclear how exactly $t_{diff}$ is related to $f$, a shorter $t_{diff}$ can generally be achieved using a higher $f$. This provides an opportunity for the OGSE sequence to probe much shorter diffusion times with hardware limitations.

Over the last two decades, the OGSE sequence has been widely used in preclinical studies to probe short diffusion times to reveal information at small length scales that are not available for the PGSE sequence. For examples, the OGSE sequence has been used in the measurement of surface-to-volume ratios of beads (Schachter et al., 2000) and cells (Xu et al., 2011b), probing intracellular structure variations during cell dividing (Xu et al., 2011b) and response to treatment (Colvin et al., 2011a; Xu et al., 2009b; Xu et al., 2012), enhancing imaging contrast to mouse brain tissues (Aggarwal et al., 2014; Aggarwal et al., 2012), estimating axon sizes (Drobnjak et al., 2016; Kakkar et al., 2018; Mercredi et al., 2017; Xu et al., 2014), and monitoring tumor response to treatment (Colvin et al., 2011b; Jiang et al., 2019a; Xu et al., 2012). Recently, other than using OGSE alone for short diffusion times, the combination of the OGSE and PGSE acquisitions has shown promise to probe more comprehensive microstructural information over a broader range of diffusion times, such as estimating mean cancer cell sizes and intracellular diffusion coefficients simultaneously (Jiang et al., 2017; Jiang et al., 2016a; Reynaud et al., 2016) This, in turn, provides a tool to monitor more specific tumor response to various treatments at both the cellular and subcellular levels. (Jiang et al., 2016b; Jiang et al., 2019a; Jiang et al., 2019b). However, these preclinical studies were usually performed on animal MRI systems with high gradient strengths $G_{max}$ and slew rates $\text{SR}$ that are usually not available on clinical MRI systems. It remains unclear if these preclinical findings can be directly translated to clinical imaging.

Recently, there is an increasing interest in translating the OGSE sequence to human MRI systems to characterize human tissues at smaller length scales. Due to the remarkable differences between preclinical and clinical hardware, the implementation of the OGSE sequence on human systems is significantly different from those reported on animal systems, including the acquisition protocols, detection sensitivity, and quantification methods. In this review paper, we will give an overview of the recent progress of OGSE neuroimaging in humans, including the technical translation of OGSE to human imaging and the recent applications of OGSE imaging in various diseases in patients. We will provide some opinions on possible future directions for OGSE imaging. Note that this review will focus on the practical aspects of OGSE imaging in humans only. Previous reviews have already covered the basics of the OGSE sequence including the frequency domain analysis (Gore et al., 2010) and the theories of the diffusion time dependency (Novikov et al., 2019).

Translation to human imaging

It is not trivial to translate preclinical imaging methods to clinical settings (Hormuth et al., 2019). This is particularly true for OGSE imaging. Because of $b~G^2/f^3$, achieving a higher frequency $f$ (i.e., a shorter $t_{diff}$) while keeping a reasonable $b$ value requires a stronger gradient strength $G$ and a fast $\text{SR}$, both of which are very limited to human systems. To overcome this problem, several efforts have been made to develop new gradient coils and optimize the OGSE sequence while both of which require further improvements such as gradient calibration and deriving new quantification models.

Hardware: Gradients

The typical $G_{max}$ and $\text{SR}$ are ⩽ 80 mT/m and ⩽ 200 T/m/s, respectively, for most clinical MRI systems. Because $G_{max}$ on preclinical systems is usually at least fivefold larger (e.g., ⩾ 400 mT/m), this results in a very limited achievable $f$ and $t_{diff}$ on clinical MRI systems. Moreover, because the OGSE sequence usually maximizes the usage of gradients, the duty cycle of the gradient amplifier becomes a limiting factor that requires a larger TR and hence effectively increases the total scan time. The total duration of all gradient lobes on one side of the refocusing RF pulse is usually long (e.g., > 30 ms) for the OGSE acquisitions on clinical MRI systems so that this results in a long echo time (TE) typically ~ 110 ms which reduces the signal-to-noise ratios (SNR). Despite these disadvantages, several studies have reported the implementation of the OGSE imaging on current human systems of major MRI vendors. Table 1 summarizes the representative OGSE protocols and hardware in some previous OGSE human imaging studies. Most OGSE studies to date can only probe $f$ ⩽ 60 Hz with a relatively lower $b$ value < 450 s/mm². However, the high-performance, head-only gradient coil insert developed recently by Tan et al. significantly enhances the ability to probe $f$ up to 100 Hz, corresponding to an effective $t_{diff}$ ≈ 2.5 ms (Tan et al., 2020), which opens an avenue to push the limit of detection sensitivity to much shorter length scales in humans.

Table 1.

A summary of representative protocols and hardware in previous OGSE imaging studies in humans.

Studies	Scanner	Maximum gradient strength ${\mathit{G}}_{\mathit{max}}$ and slew rate $\mathit{S}{\mathit{R}}_{\mathit{max}}$	Gradient waveform used	Gradient duration $\mathit{\delta }$ and echo time TE	Maximum $\mathit{b}$ and $\mathit{f}$ achieved
Hosey et al. (Hosey et al., 2003)	Bruker MedSpec 300 3 T	$G_{max}$= 30 mT/m $S{R}_{max}$= 70 T/m/s	Sine	$\delta$= 50 ms TE = 152 ms	$b$= 650 s/mm2 $f$= 20 Hz
Van et al. (Van et al., 2014)	GE MR750 3 T	$G_{max}$ = 50 mT/m $S{R}_{max}$ = 200 T/m/s	Trapezoid-cosine	$\delta$ = 48 ms TE = 116 ms	$b$ = 200 s/mm2 $f$ = 65 Hz
Baron et al. (Baron and Beaulieu, 2014)	Varian Unity Inova 4.7 T	$G_{max}$ > 57.5 mT/m $S{R}_{max}$ > 70 T/m/s	Trapezoid-cosine	$\delta$ = 41.2 ms TE = 110 ms	$b$ = 300 s/mm2 $f$ = 50 Hz
Xu et al. (Xu et al., 2016)	Philips Achieva 3 T	$G_{max}$ = 80 mT/m $S{R}_{max}$ = 100 T/m/s	Trapezoid-cosine	$\delta$ = 50 ms TE = 124 ms	$b$ = 400 s/mm2 $f$ = 40 Hz
Andica et al. (Andica et al., 2018)	Siemens MAGNETOM Prisma 3 T	$G_{max}$ = 80 mT/m $S{R}_{max}$ > 100 T/m/s	Trapezoid-sine	$\delta$ = 41.3 ms TE = 120 ms	$b$ = 1500 s/mm2 $f$ = 50 Hz
Maekawa et al. (Maekawa et al., 2019)	Siemens MAGNETOM Prisma 3 T	$G_{max}$ = 80 mT/m $S{R}_{max}$ > 100 T/m/s	Trapezoid-cosine	$\delta$ = 33.3 ms TE = 120 ms	$b$ = 1000 s/mm2 $f$ = 30 Hz
Xu et al. (Xu et al., 2020)	Philips Achieva 3 T	$G_{max}$ = 80 mT/m $S{R}_{max}$ = 100 T/m/s	Trapezoid-cosine	$\delta$ = 40 ms TE = 104 ms	$b$ = 300 s/mm2 $f$ = 50 Hz
Arbabi et al. (Arbabi et al., 2020)	Siemens MAGNETOM Terra 7 T*	$G_{max}$ = 80 mT/m $S{R}_{max}$ = 350 T/m/s	Trapezoid-cosine	$\delta$ = 33.3 ms TE = 111 ms	$b$ = 450 s/mm2 $f$ = 60 Hz
Tan et al. (Tan et al., 2020)	GE Signa MR750 3 T*	$G_{max}$ = 200 mT/m $S{R}_{max}$ = 500 T/m/s	Trapezoid-cosine	$\delta$ = 50 ms TE = 122 ms	$b$ = 450 s/mm2 $f$ = 100 Hz
Hennel et al. (Hennel et al., 2020)	Philips Achieva 3 T*	$G_{max}$ = 200 mT/m $S{R}_{max}$ = 600 T/m/s	Modified trapezoid-cosine	$\delta$ = ~40 ms ** TE = 120 ms	$b$ = 975 s/mm2 $f$ = 75 Hz

^*A head-only gradient coil insert was used.

^**the gradient durations vary with different frequencies

Pulse sequence

The early OGSE imaging studies used either sine- or cosine-modulated gradient waveforms. Intuitively, the cosine waveform provides a shorter $t_{diff}$. In theory, the frequency domain analysis (Callaghan and Stepisnik, 1995; Stepisnik, 1981) suggests that cosine waveforms create encoding (sampling) spectra ${\left|F\left(\omega =2\pi f\right)\right|}^2$ consisting of Dirac delta functions at specified frequencies, which is ideal to sample diffusion spectra $D\left(\omega \right)$ for comprehensive microstructural information. For this reason, cosine waveforms are widely used in preclinical OGSE studies on animal MRI systems, despite that it provides one-third of $b$ values compared with the sine waveforms. However, cosine waveforms do not maximize the usage of the whole capacity of gradient coils so that the achievable $b_{max}$ and $f_{max}$ are not optimal. To overcome this, a cosine-modulated trapezoidal waveform (i.e., trapezoid-cosine) was suggested to maximize the usage of gradients (Van et al., 2014). Fig. 1 shows the comparison of the gradient waveforms and corresponding encoding frequency spectra ${\left|F\left(\omega \right)\right|}^2$ of the cosine and trapezoid-cosine waveforms. The trapezoid-cosine waveform always uses higher or equal gradients compared with the cosine waveform, while their ${\left|F\left(\omega \right)\right|}^2$ only differ slightly. This ensures the trapezoid-cosine waveforms provides higher $b$ values than the cosine waveform with the same hardware. Specifically, the $b$ of the apodised cosine waveform is given by

$$b=\left({\gamma }^2{G}_{max}^{2}n\right)/\left(4{\pi }^2{f}^3\right)\left(1-\frac{1}{8n}\right)$$ [1]

while $b$ of the trapezoid-cosine waveform is

$$b={\gamma }^2{G}_{max}^2\left[{\left(t_r+t_p\right)}^2\left(\text{Δ}-\left(t_r+t_p\right)/3\right)+t_r^3/30-\left(t_r+t_p\right)t_r^2/6\right]$$ [2]

where $\gamma$ is the gyromagnetic ratio, $n$ is the number of oscillations in each gradient, $t_r$ is the gradient rise time (i.e., the time allows the gradient increases from 0 to the maximum), and $t_P$ is the duration time of the first gradient plateau. The exact enhancement in $b$ values is hardware dependent. For example, if $G_{max}$ = 80 mT/m, $t_r$= 0.9 ms, $\delta$= 40 ms, and $f$ = 25 Hz, $b_{max}$= 1130 s/mm² for trapezoid-cosine waveform, which is 52% higher than $b_{max}$ = 745 s/mm² for the cosine waveform. Presumably due to the ability to maximize $b$ while keeping similar frequency sampling spectra ${\left|F\left(\omega \right)\right|}^2$, the trapezoid-cosine waveform has been widely used in almost all recent OGSE imaging studies in humans as shown in Table 1.

Fig. 1.

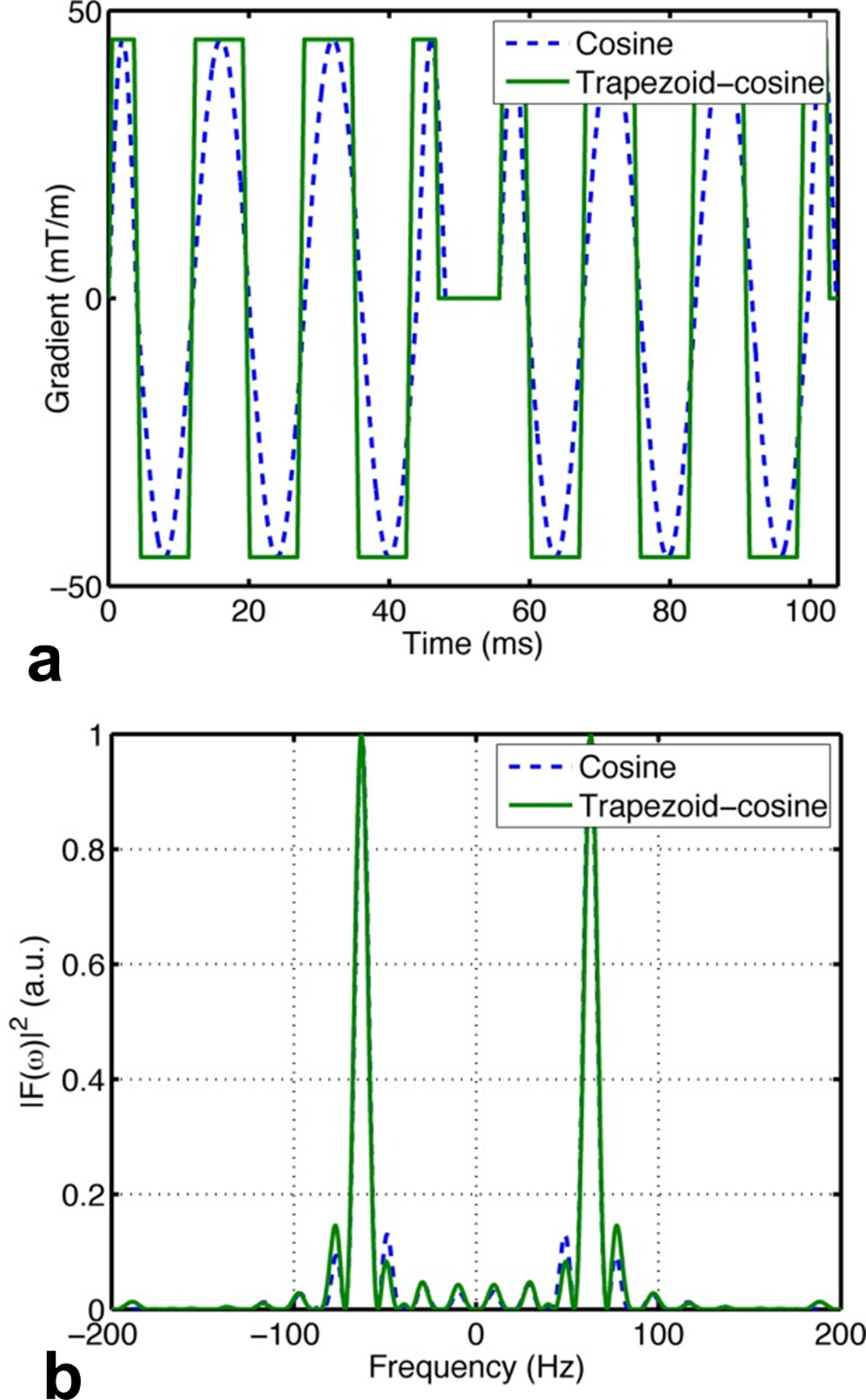
Comparison between the cosine and trapezoid-cosine (a) gradient waveforms and (b) corresponding encoding spectra ${\left|F\left(\omega \right)\right|}^2$. The figure is reprinted with permission from (Van et al., 2014).

Quantification

In addition to the popular DTI, it remains an active research topic to quantitatively characterize tissue microstructural properties such as cell size, density, and diffusivities using dMRI non-invasively. To this end, analytical expressions are usually needed to link dMRI signals to the dMRI sequence parameters and underlying biophysical properties. For the PGSE sequence, analytical equations to predict dMRI signals in a few regular geometries (i.e., planes, cylinders, and spheres) were reported back in the ’70s (Neuman, 1974). For the OGSE sequence, the analytical equations were first derived based on the velocity correction function for infinitely long, ideal OGSE sequences (Stepisnik, 1993). However, there are many limiting factors on OGSE sequences in realistic experiments such as the finite duration of $\delta$ and $\text{Δ}$, and limited $\text{SR}$. The $\delta$ and the number cycles affect the OGSE results (Novikov and Kiselev, 2011; Sukstanskii, 2013). The choice of appropriate $\text{Δ}$ is sometimes overlooked in OGSE experiments but it can play an importantly role to modulate ${\left|F\left(\omega \right)\right|}^2$ (Baron and Beaulieu, 2014). Based on the realistic gradient waveforms with all practical parameters, analytical expressions to predict dMRI signals have been derived for sine and cosine waveforms (Xu et al., 2009a) and the square and general sine-modulated trapezoidal waveforms (Ianus et al., 2013). For the trapezoid-cosine waveforms that are widely used in OGSE imaging studies in humans, the analytical expressions were reported recently (Xu et al., 2020). Because the analytical expressions are usually very complicated and long, we do not show the equations here but encourage readers to refer to the previous papers for details. Note that the above analytical equations have been used in several studies to estimate e.g., cell sizes and diffusivities with comprehensive validations using simulations in silico, cell cultures in vitro, and animals in vivo (Jiang et al., 2017; Jiang et al., 2016a; Jiang et al., 2020; Xu et al., 2020).

It is worth mentioning that the above analytical equations for OGSE sequences are based on a Gaussian approximation for the phase distribution (Stepisnik, 1993). However, studies have shown that this approximation is valid with a broad range of $f$ and $b$ values (Ianus et al., 2013; Xu et al., 2009a). For example, a comparison of simulated and analytical signal echo attenuations suggests < 2.9% of discrepancies occur when $b$ values increase up to 5000 mm²/s (Xu et al., 2009a). Because $b$ values are always limited to human MRI scanners, this Gaussian approximation is not expected to affect the accuracy of analytical equations for OGSE sequences. Moreover, recent analytical equations of trapezoid-cosine waveforms were derived based on the realistic waveforms performed on the human MRI scanners (Xu et al., 2020), which in turn further increases the accuracy of analytical equations to descript realistic signals in measurements.

Calibration

Gradient calibration is essential for any dMRI measurements but is sometimes overlooked. In addition to the gradient nonlinearity that affects all diffusion sequences (Malyarenko et al., 2014), the OGSE sequence is so far not a standard sequence on clinical systems so it requires more attenuation on calibration. One of the most attractive applications of the OGSE sequence is the ability to probe much shorter $t_{diff}$ and smaller length scales, so the diffusion time dependence is key information. Therefore, it is essential to calibrate the sequence and hardware to ensure any dMRI signal variations across different $t_{diff}$ are caused by underlying biophysical properties, not by hardware or sequence inconsistency among different $t_{diff}$ values.

To complicate matters, previous studies have reported a few unique calibration issues related to the OGSE sequence that need extra attention, including

1. Amplifier response. If very high gradient frequencies are acquired with strong gradient strengths and slew rates, the gradient amplifier may lose linear response, resulting in significantly biased ADCs (Xu et al., 2011b).

2. Mechanical vibration. For certain gradient and MRI systems, the OGSE sequence could result in remarkable mechanical vibrations only at a certain diffusion gradient frequency, which can cause serious motion artifacts. For example, severe mechanical vibrations were found in studies of both phantoms and tissues in vivo at 150 Hz only in a wide frequency range of 50 – 250 Hz using a gradient insert on a 4.7 Tesla preclinical scanner (Xu et al., 2012).

3. Signal drift. The dMRI signal drifts may become more severe during the OGSE acquisitions presumably due to the gradient coil heating caused by the heavy usage of gradients. This effect could be minimized by using dynamic stabilization during acquisitions (Xu et al., 2020) and the dMRI signal drift correction (Vos et al., 2017).

Therefore, it is important to perform comprehensive calibration of the OGSE sequence to ensure every gradient axis is well-calibrated with the OGSE sequence. Possible approaches include the use of well-established, temperature-controlled phantoms with known ADC values such as ice-water phantoms (Chenevert et al., 2011) and alkane phantoms with different viscosities (Maekawa et al., 2018). Fiber phantoms have been used to evaluate the accuracy of the OGSE imaging for estimating surface-to-volume ratio (S/V), which can also serve to evaluate the accuracy of OGSE acquisitions on clinical MRI systems (Lemberskiy et al., 2017).

New information obtained using OGSE

OGSE dMRI signals with short diffusion times

It is well-known that $t_{diff}$ plays an important role in restricted diffusion systems and dMRI signals vary with $t_{diff}$ (Tanner and Stejskal, 1968). dMRI signals with different $t_{diff}$ values are sensitive to different length scales and hence convey different microstructural information. This was observed in brain cancer studies in rodents that OGSE dMRI signals with smaller $t_{diff}$ provides an increased contrast and shows more spatial heterogeneity inside brain tumors (Colvin et al., 2008). By contrast, the OGSE sequence with shorter $t_{diff}$ have been found to diminish the imaging contrast of stroke lesions in patients (Baron et al., 2015; Boonrod et al., 2018). Although a reduced contrast may not be desirable for diagnosis, this behavior provides new insights for better understanding of the contrast mechanism of dMRI in stroke (Baron et al., 2015).

Diffusion time-dependent DTI

In addition to the direct usage of OGSE dMRI signals with short diffusion times, it is of great interest to apply the OGSE sequence to detect the $t_{diff}$ dependence of diffusion tensor imaging (DTI) metrics, such as fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), and radial diffusivity (RD). Previously, the $t_{diff}$ dependence was not observed in human DTI studies using the PGSE sequence only, such as the DTI of normal human brains showed no significant changes with the $t_{diff}$ range of 8 – 80 ms (Clark et al., 2001). Presumably, this is because these measurements were acquired using the PGSE sequence with $t_{diff}$ not short enough to allow the movements of water molecules to be appear less restricted. The use of the OGSE sequence pushes the limits to shorter $t_{diff}$ and hence gleans new information at smaller scales that are invisible in typical PGSE imaging. The OGSE DTI study was first performed in a fixed monkey brain (Xu et al., 2010) and later applied to rats (Kershaw et al., 2013) and human (Baron and Beaulieu, 2014) brains in vivo. These studies found that DTI metrics showed a $t_{diff}$ dependence in most brain regions. In general, FA decreases with shorter $t_{diff}$ while MD, AD, and RD increase. Such a $t_{diff}$ dependence reveals additional microstructural information that is not achievable by the PGSE sequence alone. For example, this dependence suggests the existence of diffusion restriction in the laminated keratin layers within the cyst, which is not revealed by the PGSE sequence alone (Andica et al., 2018).

Diffusion dispersion with frequency

The diffusion spectrum $D\left(f\right)$ over a broad range of frequencies and $t_{diff}$ is desirable to characterize comprehensive information on tissue microstructure (Parsons et al., 2006). However, the exact dependence of $D\left(f\right)$ on $f$ is determined by the specific $f$ range (Reynaud, 2017). In the high frequency (short $t_{diff}$) regime, Mitra’s equation is valid so $D\left(f\right) ~f^{-1/2}$ (Novikov and Kiselev, 2011; Xu et al., 2011b). In the low frequency (long $t_{diff}$) regime, there is a power-law relationship between $\text{ADC}$ and $f$ as $\text{ADC}={\text{ADC}}_0+\text{Λ}\cdot f^{\theta }$ (Burcaw et al., 2015; Novikov et al., 2014), where the constant $\text{Λ}$ is defined as diffusion dispersion rate. This relationship has been observed in OGSE imaging in healthy human subjects with fitted $\theta =0.5$ and $f$ from 0 (PGSE) to 60 Hz (Arbabi et al., 2020). However, this study included ADCs achieved by PGSE as ADC($f=0$) in the ADC spectrum analyses, but it remains unclear if this approximation is valid in practice. The PGSE and OGSE have very different gradient waveforms and power spectra, and they have different sensitivities to flow (Wu and Zhang, 2017) and background gradients (Hong and Thomas Dixon, 1992). The differences between PGSE and OGSE signals may not arise just from diffusion time dependence but also from other confounding effects. Although such differences have been found useful to assess the age and sex differences in the human corpus callosum (Tétreault et al., 2020) and to assess neonatal hypoxia-ischemia (Gao et al., 2020), it is plausible to reduce the complexity of ADC spectrum analyses by excluding PGSE data and focused on ADCs achieved by OGSE only (Aggarwal et al., 2014; Aggarwal et al., 2012; Wu et al., 2014a; Xu et al., 2016; Xu et al., 2012). This ensures to minimize the influences of confounding effects. Because the achievable $f$ in the OGSE acquisitions are usually remarkably limited by available hardware, particularly on clinical MRI systems, only a narrow range of $f$ can be acquired in practice. In such a narrow range, the $t_{diff}$ dependence of ADC on $f$ was found to be approximated as a linear function for $f>0$ (i.e., excluding a PGSE acquisition), i.e., $\text{ADC}={\text{ADC}}_0+\text{DDR}\cdot f$, where DDR is the linear diffusion dispersion rate that describes the rate that ADC increases with $t_{diff}$ approximately in a linear manner (Xu et al., 2016; Xu et al., 2012). Note that some groups use ${\text{Δ}}_{f}ADC$ to indicate the same concept (Aggarwal et al., 2014; Aggarwal et al., 2012; Wu et al., 2014a). Fig.2 shows linear $t_{diff}$ dependence in six representative human brain regions with $f$ from 20 to 100 Hz acquired in vivo (Tan et al., 2020). Although it still requires further investigation on how to include PGSE data (particularly those with different $t_{diff}$ values) in the ADC spectrum analyses, either power law or approximated linear relation seem able to describe the $t_{diff}$ dependence because of the narrow ranges of $f$ achievable in practice. However, the approximated linear dependence has been found to provide more reliable data fitting e.g., in cell size estimation in tumors using the OGSE sequence (Jiang et al., 2016a). Even excluding PGSE data, the underlying biophysical meaning of DDR needs more investigation. Evidence has suggested DDR contains microstructural information such as the sizes of intrinsic microstructure (Li et al., 2015) so that it can be used as a simple and fast indicator of cell or axon sizes. For example, DDR has been used to monitor rodent tumor response to treatment (Xu et al., 2012), to enhance imaging contrast to of mouse hippocampus and cerebellum (Aggarwal et al., 2014; Aggarwal et al., 2012; Wu et al., 2014a), and to show correlation with mean axon diameters in fixed rat spinal cords and human corpus callosum in vivo (Xu et al., 2016). Note that the previously reported DDRs in animals and humans are different, which might attribute to different neurite sizes. However, further investigation is required.

Fig. 2.

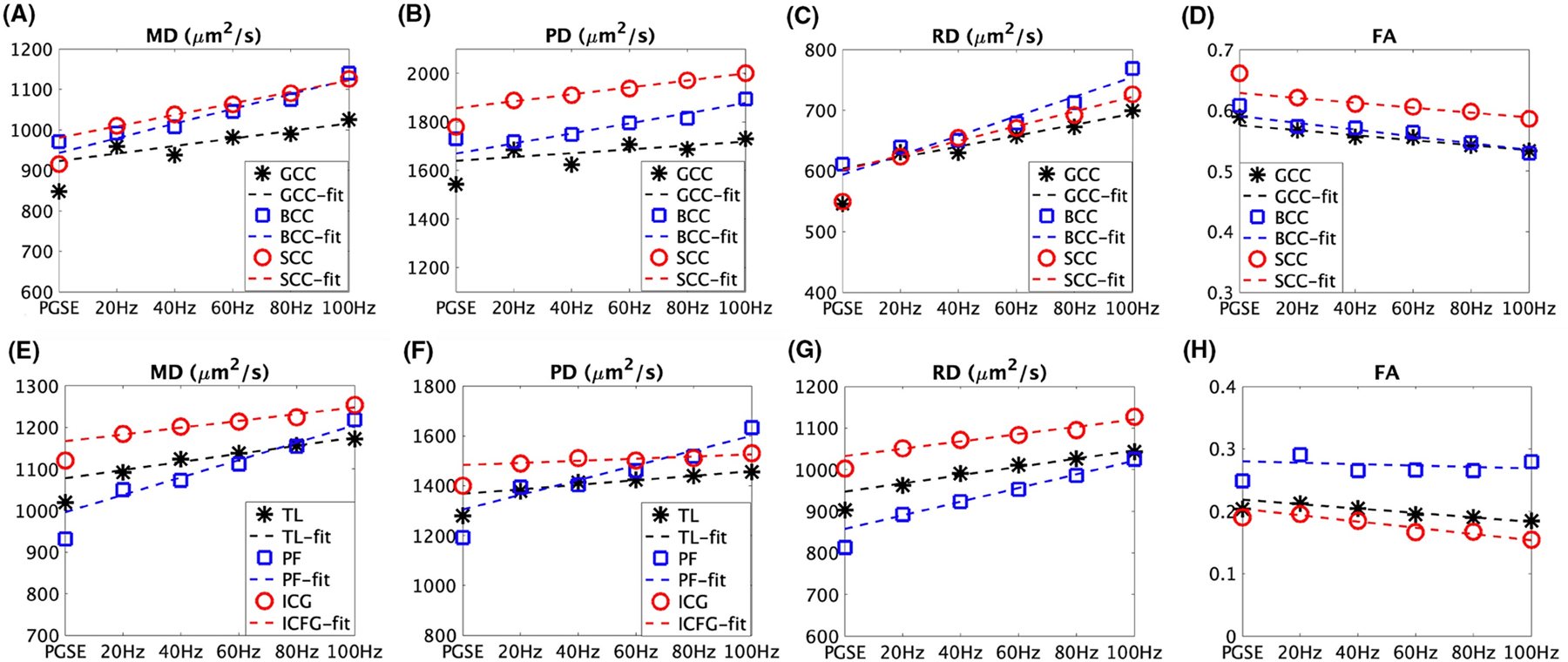
Representative diffusion time dependence of DTI metrics: MD (mean diffusivity), PD (parallel diffusivity), RD (radial diffusivity), and FA (fractional anisotropy) in three white matter regions and three gray matter regions of a healthy subject. GCC: genu, BCC: body, and SCC: splenium of the corpus callosum. TL: temporal lobes. PF: posterior fossa, and ICG: insula/cingulate gyri. The figure is reprinted with permission from (Tan et al., 2020).

Another advantage of DDR is its fast acquisition. In theory, DDR can be achieved using a minimum of two ADC measurements, although more ADCs may enhance the data fitting. A recent study has optimized a fast (~ 6 mins) protocol with one OGSE frequency and one PGSE (Arbabi et al., 2020), suggesting potential for clinical applications.

Intracranial neuroimaging applications

To date, the majority of the reported OGSE applications focus on brain imaging. With much shorter $t_{diff}$, new information can be achieved which may provide new insights into the diagnosis of various diseases or assist in better understanding of the biophysical mechanism of imaging metrics. The intracranial OGSE imaging has been applied to patients with stroke (Baron et al., 2015; Boonrod et al., 2018), NPH (normal pressure hydrocephalus) (Irie et al., 2019), epidermoid cysts (Andica et al., 2018), multiple sclerosis (Li et al., 2017), and brain cancer (Xu et al., 2017). In this review, we will focus on the new information achieved with the OGSE sequence in stroke and NPH.

Stroke

dMRI has been used daily as a sensitive method for the diagnosis of stroke. It is well known for decades that ADC decreases after stroke, but the underlying biophysical mechanism remains elusive. Several theories have been developed to explain the reduction of ADC in strokes, such as brain cell swelling (cytotoxic edema) (Warach et al., 1995) and neurite beading (Budde and Frank, 2010). dMRI has been used daily for the diagnosis of stroke and almost all acquisitions are using the PGSE sequence with relatively long $t_{diff}$. This limits dMRI to convey microstructural information averaged over relatively long length scales, which in turn makes it challenging to entangle signal contributions from different sources in stroke. If a short $t_{diff}$ could be used and push the detection sensitivity to shorter length scales, more microstructural information could be achieved which may assist in elucidating the underlying biophysical mechanism of ADC reduction in stroke. Does et al. first applied the OGSE imaging in globally ischemic rat brains (Does et al., 2003) and Wu et al. reported the use of the OGSE imaging in hypoxia-ischemia injured mouse brains (Wu et al., 2014a). Both studies observed that the contrast between ischemic lesions and normal tissues reduces at shorter $t_{diff}$. These findings were confirmed by Baron et al. in the OGSE imaging in stroke patients (Baron et al., 2015). As shown in Fig.3, the imaging contrast of ischemic stroke lesions reduces with shorter $t_{diff}$ at multiple time points post onset. In white matter, the PGSE MD maps with $t_{diff}=40$ ms show hypointense lesions, but these lesions are nearly isointense in OGSE MD maps. In gray matter, there are no significant differences between PGSE and OGSE. Confirmed with computer simulations, Baron et al. suggested that the reduction of ADC in white matter in stroke is due to neurite beading and axonal swelling. Recently, similar findings were also reported in cerebral infarctions in patients (Boonrod et al., 2018).

Fig. 3.

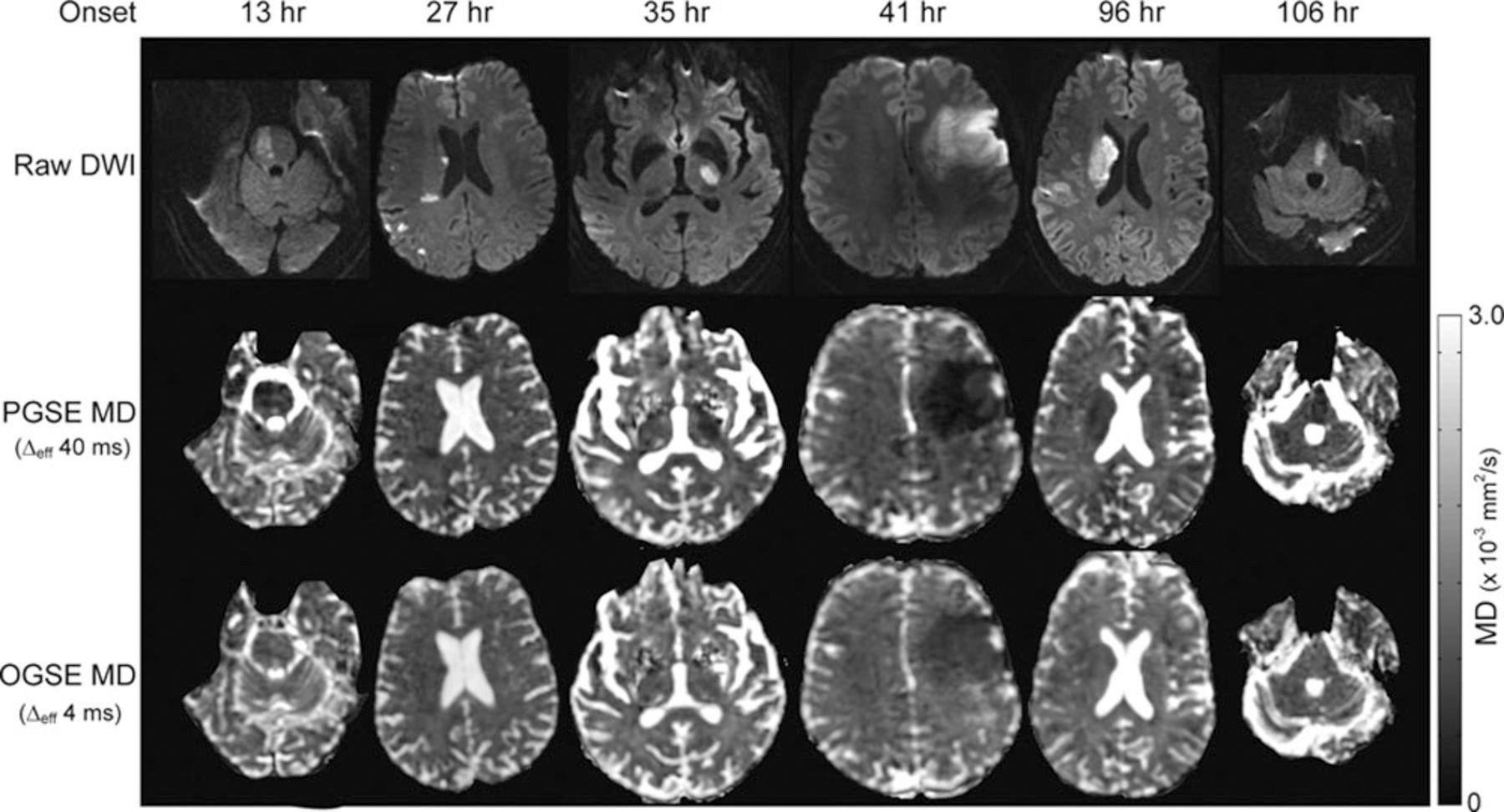
Representative images of raw dMRI, PGSE MD, and OGSE MD maps at multiple time points post-onset of ischemic stroke. The figure is reprinted with permission from (Baron et al., 2015).

Interestingly, a preclinical study (Wu et al., 2019) found out that OGSE MRI, particularly DDR, provides much higher sensitivity to subtle hypoxia-ischemia (HI) brain tissue damages compared with PGSE in a mouse model. Specifically, they found more significant increases (average 64.8% and 48.9% ipsilateral hippocampal CA1 and cortical regions vs. the contralateral side) in DDR than the modest decrease in PGSE ADC’s (average 6.5% and 2.7% decreases). More recently, similar findings have been reported in neonates with hypoxic-ischemic encephalopathy (HIE) using clinical MRI scanners (Gao et al., 2020). These observations suggest, the $t_{diff}$ dependence achieved using OGSE may provide a more sensitive indicator to the microstructural changes in stroke. However, as PGSE already provides high sensitivity to stroke, OGSE imaging with shorter $t_{diff}$ may not be a replacement for stroke diagnosis but may provide new insights into stroke lesions that can assist in elucidating the biophysical contrast mechanism of ADC in stroke.

NPH (normal pressure hydrocephalus)

Normal pressure hydrocephalus (NPH) is a clinical symptom complex caused by the build-up of cerebrospinal fluid (CSF) without increasing CSF pressure (Adams et al., 1965). Previous studies have used DTI to characterize the mechanical compression of white matter presumably due to ventricular enlargement (Assaf et al., 2006; Hattori et al., 2011). They found AD increased (+10%) and RD decreased (-25%) in the patient white matter close to ventricles, particularly in the corticospinal tract (CST). Although these findings were consistent with the theory of mechanical compression, it remains unclear if the variations of DTI metrics reflect such underlying pathological changes because DTI is usually affected by many tissue properties simultaneously. If shorter $t_{diff}$ can be achieved, additional microstructural information can be obtained which may assist in better interpretation of DTI data in NPH. Irie et al. recently reported the OGSE imaging in NPH patients with $f$ up to 30 Hz (effective $t_{diff}\approx 8.3\text{\hspace{0.17em}ms}$) (Irie et al., 2019). They observed that both AD and RD increase with shorter $t_{diff}$ in CST and hence defined $\Delta \text{ADC}$, the ADC differences between the short and long $t_{diff}$ i.e., $\text{ΔADC}=\text{ADC}\left(t_{diff}^{short}\right)-\text{ADC}\left(t_{diff}^{long}\right)$ as in (Gao et al., 2020). They found $\text{ΔADC}$’s in NPH patients are significantly lower than in those in healthy subjects. This trend is opposite to the change of cerebral infarction (Boonrod et al., 2018). A possible explanation is that “nerve fibers are compressed and stretched straight in NPH”. Although this hypothesis needs further validation, the use of OGSE and $t_{diff}$ dependence provide additional sensivity to subtle tissue changes in NPH patients, which serve a new imaging biomarker for future NPH imaging.

Extracranial neuroimaging applications

There is increasing interest in applying the OGSE sequence in extracranial applications, such as spinal cord (By et al., 2019), peripheral nerve (Li et al., 2016), liver (Jiang et al., 2020), head and neck cancer (Iima et al., 2019), and breast cancer (Xu et al., 2020). We here will focus on OGSE neuroimaging in the spinal cord and peripheral nerve.

Spinal cord

By et al. reported the first application of the OGSE imaging in the human spinal cord in vivo with $t_{diff}$ from 8.77 ms to 66.7 ms (By et al., 2019). Unlike that AD dominates the $t_{diff}$ dependence in the brain, AD in the spinal cord of healthy subjects appears to be negligibly affected with $t_{diff}$ with ≤1.53% changes across all $t_{diff}$ acquired. This is very different from the significant $t_{diff}$ dependent AD in the brain (Baron and Beaulieu, 2014). The underlying mechanism remains unclear. By contrast, RD shows a 37% mean increase when $t_{diff}$ decreases from 66.7 ms (acquired using the PGSE sequence) to 8.77 ms (using the OGSE sequence). This results in a 12.9% decrease in FA. By et al. also applied the OGSE sequence in the spinal cord of multiple sclerosis patients. Fig. 4 shows the RD maps of the cervical spine for representative control and MS patient. A larger increase (46.5%) in RD in the MS patient is observed with the OGSE sequence, in comparison to 40.7% with the PGSE sequence. This is opposite to the findings in stroke, in which the imaging contrast decreases with shorter $t_{diff}$. This indicates an increased sensitivity to pathological variations in MS using the OGSE sequence with shorter $t_{diff}$. The reason why OGSE increases the sensitivity to MS remains unclear, but a possible explanation is that the demyelination in MS causes a larger extra-axonal space with an increased restriction size (spacing between axons). Because OGSE with shorter $t_{diff}$ is more sensitive to this subtle change in restriction sizes, RD obtained with OGSE shows a more significant increase, resulting in an increased sensitivity to MS lesions.

Fig. 4.

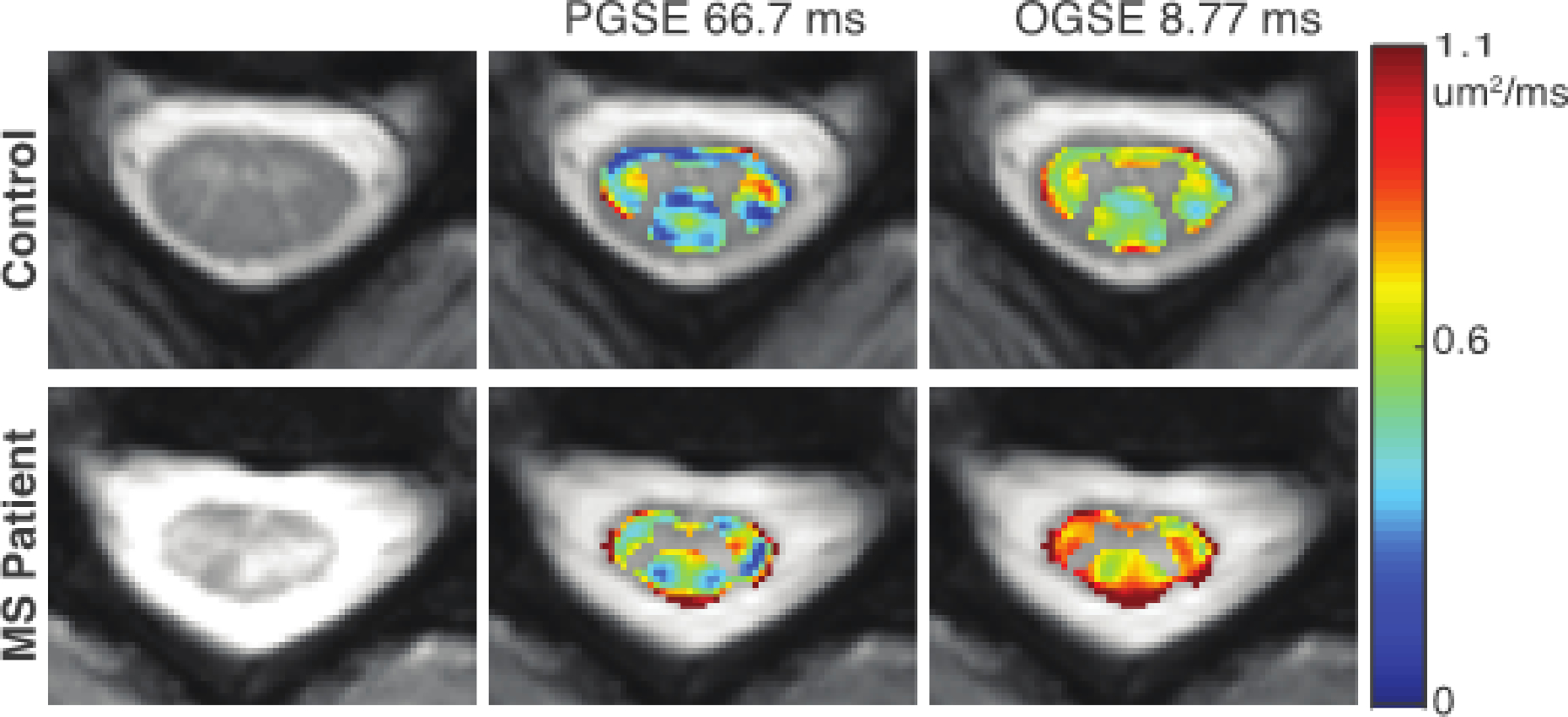
Comparison of RD maps in healthy control (top) and MS patient (bottom). From left to right, the anatomical image, RD map acquired with an effective diffusion time of 66.7 ms, and RD map acquired with an effective diffusion time of 8.77 ms are shown. A larger difference is observed between the healthy control and MS patient with the shorter diffusion times achievable with OGSE. The figure is reprinted with permission from (By et al., 2019).

Peripheral nerve

Peripheral nerves refer to parts of the nervous system outside the brain and spinal cord. They transmit motor/sensory information between the central nervous system (CNS) and other parts of the body. Peripheral nerve injury can disrupt this transmission, resulting in a variety of symptoms (e.g., pain, weakness). The axon sizes in many peripheral nerves are usually much larger than those in the CNS, making it suitable to be estimated using typical dMRI even on clinical MRI systems. Because the OGSE sequence probes shorter $t_{diff}$, it can assist in better estimating the mean axon size in peripheral nerves. Li et al. reported the first application of estimating the mean axon size in the human sciatic nerve in vivo using the OGSE sequence (Li et al., 2016). With the IMPULSED model (Jiang et al., 2016a), they fitted the mean axon diameter of 9.8±0.9 μm and mean axonal signal fraction 47±4%, consistent with previous histological findings (Ikeda and Oka, 2012). Because diseases may affect certain axon populations (e.g. small sensory fibers damaged in diabetic neuropathy), this technique may provide more specific information on neural injury in peripheral nerves, compared with conventional DTI.

Possible future directions

Despite several successful applications of the OGSE sequence on clinical MRI systems, it is still at the very early stage of implementing OGSE for human imaging. Here, we provide a few thoughts on possible future directions to further improve the OGSE imaging in humans.

Hardware

As mentioned above, the majority of the OGSE neuroimaging was performed using the regular clinical MRI systems with e.g., gradient strengths $G_{max}$ up to 80 mT/m and slew rates $\text{SR}$ up to 200 T/m/s. This typically limits the achievable $f$ up to 60 Hz, i.e., with $t_{diff}\sim 4\text{\hspace{0.17em}ms}$. The recent development of the high-performance, head-only gradient coils pushes the limits to $t_{diff}$ ~ 2.5 ms and $b$ = 450 s/mm², which opens an avenue to probe much smaller length scales in human brains. With the rapid development of more cutting-edge gradient coils for humans, even stronger $G_{max}$ and $\text{SR}$ can be achieved. For example, $t_{diff}$ ~ 2 ms and $b$ ~ 420 s/mm² could be achieved theoretically with $G_{max}$ = 300 mT/m and $\text{SR}$ = 200 T/m/s in multi-directional dMRI measurements using the human connectome coil (Setsompop et al., 2013). The connectome 2.0 coil under development could theoretically probe $t_{diff}$ ~ 1.25 ms and $b$ ~ 473 s/mm² with $G_{max}$ = 500 mT/m and $\text{SR}$ = 600 T/m/s. However, due to hardware limitations and physiological constraints (such as peripheral nerve stimulation and cardiac stimulation), maximum $G_{max}$ and $\text{SR}$ are not likely to be achievable simultaneously (Setsompop et al., 2013). This in turn limits the ability of OGSE to achieve the shortest $t_{diff}$ possible with hardware constraints. It is likely the achievable $t_{diff}$ ranges will be machine dependent. However, OGSE achievable shortest $t_{diff}$ should be much shorter than those achievable by PGSE, because the latter should be always larger than the sum of the gradient duration $\delta$ and the duration of the 180° refocusing RF pulse. Therefore, the recent hardware developments will significantly improve the ability of the OGSE sequence to probe much shorter length scales.

Note that the above calculations of maximum $b$ values are based on arbitrary directions. It is worth mentioning the maximum possible $b$ values in OGSE measurements also depend on acquisition strategies with the same hardware limitations. For example, DTI measurements using the minimal six-direction icosahedral scheme can allow two diffusion gradients to be on simultaneously, leading to doubled maximum $b$ values. If only MD is desired, the four-direction tetrahedral scheme can result in tripled maximum $b$ values (Conturo et al., 1996). Another approach of circularly polarized oscillating gradient sequence was developed to extend achievable diffusion times with gradient strength limits for DTI measurements as well (Lundell et al., 2015).

Acquisition

There are a few drawbacks in OGSE acquisitions that require further improvements. First, the limited gradient strengths confine the shortest diffusion time achievable. Second, the gradient duty cycle limited longer TR’s result in longer scan time. Moreover, the relatively long gradient durations (typically $\delta$ > 30 ms) and echo times (typically TE > 100 ms) significantly limit the SNR of OGSE acquisitions, particularly on higher field strength when T₂ is shorter. There are several efforts to tackle these issues. The integration of multiband can remarkably reduce TR and accelerate whole-brain OGSE acquisitions (Xu et al., 2019). However, the inclusion of multi-band will further increase TE and reduce SNR. Recently, Wu et al. reported a diffusion-prepared 3D gradient and spin-echo sequence (GRASE) to tackle both issues by reducing the scan time by a factor of 1.38 and increasing the SNR by a factor of 1.74 – 2.27 compared (Wu et al., 2020). Hennel et al. developed a modified trapezoid-cosine gradient waveform and achieved a range of 30 – 75 Hz with a $b$-value of nearly 1000 s/mm² in DTI measurements in human white matter by using a high-performance gradient insert (Hennel et al., 2020). Moreover, it is possible to further accelerate OGSE acquisitions by combining other emerging techniques such as multi-slab (Engström and Skare, 2013) and compress sensing (Wu et al., 2014b). We emphasize that OGSE is one type of dMRI so that it will benefit from the extensive improvements of dMRI acquisitions.

Biophysical mechanism

One of the main benefits of the OGSE sequence is to achieve much shorter diffusion times $t_{diff}$ so that a $t_{diff}$ dependence can be obtained to characterize the microstructure of tissues (Xu et al., 2011a). The biophysical theories of $t_{diff}$ dependence of dMRI have been investigated comprehensively, particularly in the short and long $t_{diff}$ ranges (Mitra et al., 1992; Novikov et al., 2011; Novikov et al., 2019; Novikov et al., 2014; Novikov et al., 2018). However, biophysical tissues are very complex and heterogeneous so that the exact $t_{diff}$ dependence varies with $t_{diff}$ itself. In another word, the rates of ADC dependence on $t_{diff}$ are different in different $t_{diff}$ ranges. Therefore, it is important to determine in which $t_{diff}$ range the experiments could achieve. For example, $f$ up to 200 Hz (i.e., $t_{diff}$ ~ 1.25 ms) is considered as short for tumors with cancer cell size ~ 16 μm. This provides an opportunity to fit cell size reliably (Jiang et al., 2017; Jiang et al., 2016a; Jiang et al., 2016b). By contrast, the same $f$ up to 200 Hz is considered as long for nerves with axon sizes ~ 2 μm, with which small axon sizes and transverse intra-axonal diffusivities cannot be estimated reliably (Xu et al., 2014). To complicate matters, the variations of tissue during disease progression or response to intervention may change microstructure as well as the $t_{diff}$ dependence. Hence, it is important to investigate the exact $t_{diff}$ dependence for certain combinations of experimental parameters, tissue types, and interventions. This will affect the achievable $t_{diff}$ ranges in low, intermediate, or long time regimes, which may determine the data interpretation and analyses.

Another controversial topic is the effective diffusion time $t_{diff}$ for the OGSE sequence, i.e., how to convert $f$ to $t_{diff}$. Intuitively, the effective $t_{diff}$ of the OGSE sequence should be smaller than the period $\left(1/f\right)$ of sine-modulated waveforms or a half period of cosine-modulated waveforms, i.e., the total duration of a pair of encoding and decoding diffusion gradients. However, this is similar to the violation of the short pulse approximation in the PGSE sequence so that the exact $t_{diff}$ is uncertain. Theoretical analyses suggest that there may not be a single $t_{diff}$ in this case (Fordham et al., 1996), but several OGSE studies both in animals and humans defined effective $t_{diff}=1/\left(4f\right)$ for cosine-modulated waveforms (Baron and Beaulieu, 2014; Does et al., 2003; Parsons et al., 2006; Xu et al., 2011b). This relationship was validated in packed spheres (Schachter et al., 2000), cell cultures (Xu et al., 2011b), and fixed animal nerves (Portnoy et al., 2013). However, a recent fiber phantom study suggested $t_{diff}=9/\left(64f\right)$ with a validation using other MRI modalities (Lemberskiy et al., 2017). One possible explanation of the discrepancy may be the different length scales that result in different $t_{diff}$ ranges. The fiber phantom study used fibers with a diameter of 17 μm combined with the relative loose packing resulting in a short $t_{diff}$ range. By contrast, the $t_{diff}$ was in the long time range becaure of the small nerves with sizes of < 2 μm (Portnoy et al., 2013). This suggests again that it is essential to first determine in which $t_{diff}$ range the experiments are and then the appropriate models can be used.

Perfusion is another confounding effect. Due to the differences in gradient waveforms, the OGSE sequence is much less susceptible to blood perfusion than the PGSE sequence. Although this effect is small in the brain presumably due to a small cerebral blood volume fraction, perfusion plays an important role in e.g., the liver in which perfusion is significant (Jiang et al., 2020). Without correcting for this effect, the ADCs obtained using the PGSE sequence could be mistakenly higher than those obtained using the OGSE sequence, which violates the $t_{diff}$ dependence theory (Jiang et al., 2020). In addition to the appropriate $b$ ranges and corrections in data analyses, modified OGSE sequences could be helpful to address this issue (Wu and Zhang, 2017).

More applications in diseases

Studies have found the OGSE sequence shows significant advantages in human cancer imaging (Bongers et al., 2018; Iima et al., 2019; Xu et al., 2020). For neuroimaging, although the OGSE sequence provides additional information to elucidate the biophysical mechanism of dMRI in stroke, the reduced imaging contrast suggests that it may not be suitable for the diagnosis of stroke (Baron et al., 2015; Boonrod et al., 2018). However, the increased imaging contrast in multiple sclerosis in the spinal cord suggests that the OGSE sequence might be suitable for practical MS imaging (By et al., 2019). Therefore, it is of interest to further implement the OGSE sequence in different diseases to investigate if it provides any advantages. Currently, we are still at the very early stage of this implementation.

Conclusion

The OGSE sequence can probe much shorter diffusion times and smaller length scales with the presence of hardware limitations on clinical MRI systems. Recent progress of the OGSE imaging in humans has shown that it provides an opportunity to provide new microstructural information that is invisible using the conventional PGSE sequence. Further development and more applications are necessary to enable the OGSE sequence as a useful tool in daily clinical imaging.

Highlights.

• The OGSE sequence with short diffusion times is sensitive to small length scales

• The OGSE sequence has been translated to clinical MRI systems for patients

• More technical improvements and clinical applications are needed for OGSE imaging