Regularities of context-dependent codon bias in eukaryotic genes

Abstract

Nucleotides surrounding a codon influence the choice of this particular codon from among the group of possible synonymous codons. The strongest influence on codon usage arises from the nucleotide immediately following the codon and is known as the N₁ context. We studied the relative abundance of codons with N₁ contexts in genes from four eukaryotes for which the entire genomes have been sequenced: Homo sapiens, Drosophila melanogaster, Caenorhabditis elegans and Arabidopsis thaliana. For all the studied organisms it was found that 90% of the codons have a statistically significant N₁ context-dependent codon bias. The relative abundance of each codon with an N₁ context was compared with the relative abundance of the same 4mer oligonucleotide in the whole genome. This comparison showed that in about half of all cases the context-dependent codon bias could not be explained by the sequence composition of the genome. Ranking statistics were applied to compare context-dependent codon biases for codons from different synonymous groups. We found regularities in N₁ context-dependent codon bias with respect to the codon nucleotide composition. Codons with the same nucleotides in the second and third positions and the same N₁ context have a statistically significant correlation of their relative abundances.

INTRODUCTION

The nucleotide composition of a gene coding sequence (CDS) is non-random. First, CDS non-randomness is engendered by the information needed to code for the protein primary structure. Second, CDS non-randomness is effected by the preferences in the choice of synonymous codons representing the same amino acid, the so-called codon bias. In addition to codon bias, neighboring nucleotides surrounding a codon influence the choice of this codon from the synonymous group. This phenomenon is known as context-dependent codon bias (CDCB) (1–3). The most important nucleotide determining CDCB is the first one following the codon (4,5) and is known as the N₁ context. Context N_i stands for the next i nucleotide after the codon, according to the notation of Berg and Silva (4). CDCB has been examined to a much lesser extent than codon bias itself. Regularities in CDCB have been described only fragmentally for a small portion of codons (4,6,7) while the whole picture of CDCB is unknown. Some cases of CDCB could be explained by the bias in the sequence composition of the entire genome. For example, human codons with a C nucleotide in the third position and with a G nucleotide as the N₁ context are significantly under-represented. The major reason for this under-representation is a 4-fold deficiency of the CG dinucleotides characteristic of the entire human genome, due to the methylation of cytosines within CG sites.

Information on codon bias and CDCB is very important for the improvement of gene-finding algorithms. All the available programs for gene prediction are far from perfect. In fact, we still do not have a good estimate of the number of genes in the human genome, as was shown in a recent report by Hogenesch et al. (8). A major part of gene prediction programs is based on the computation of characteristic non-randomness of coding and non-coding sequences. In this computational differentiation of genomic sequences on coding and non-coding pieces, the contribution of codon bias and CDCB is essential. Besides practical significance, knowledge of the CDCB is important in understanding the biological fundamentals of codon bias.

In this paper we have pursued several aims: (i) to carry out a thorough statistical analysis of the distribution of all codons with N₁ context in complete gene sets of different evolutionarily divergent species; (ii) to examine the extent of the influence of genomic sequence non-randomness on CDCB; and (iii) to expose possible regularities in CDCB. We analyzed CDCB by computing R values, where the R value represents the relative abundance for a codon uvw with N₁ context n computed as the ratio R(uvw∼n) = F(uvw∼n)/[F(uvw)F(n)]. F(uvw) denotes the frequency of the codon uvw (u, v, w and n are the nucleotides a, g, t and c, and the codon is underlined), F(n) is the frequency of nucleotide n in the N₁ context and F(uvw∼n) is the frequency of the codon with the n context. Here and elsewhere the tilde character (∼) separates codons (underlined) or oligonucleotides (non-underlined) from their mononucleotide context. The local non-randomness of the genome nucleotide composition was measured by the same approach by computing r values, the relative abundance of tri- di- and mononucleotide y with mononucleotide context n. They were calculated as the ratio r(y∼n) = F(yn)/[F(y)F(n)], where F(y) denotes the frequency of the oligonucleotide y, F(n) the frequency of nucleotide n and F(yn) the frequency of oligonucleotide yn. By comparing R(uvw∼n) values computed for coding sequences with r(uvw∼n), r(uw~n) and r(w~n) values for the genomic sequences, we found that in some cases CDCB could be a consequence of the nucleotide composition characterized for the entire genome (genome bias). Nonetheless, in ∼35–55% of the cases CDCB could not be explained by the genomic bias. In addition, we found regularities in the CDCB with respect to the nucleotide composition of codons and N₁ context. Our data support the hypothesis that the primary reason for codon bias and CDCB is selection for the accuracy of protein synthesis.

MATERIALS AND METHODS

Nucleotide samples

Genomic and CDS sequences of Drosophila melanogaster, Caenorhabditis elegans and Arabidopsis thaliana were downloaded from GenBank release 119 (9) (ftp: ncbi.nlm.nih.gov) as *.fna and *.ffn files, respectively. As a result, the entire genomic and CDS sequences for D.melanogaster and C.elegans and all the sequences from chromosomes I, II and IV of A.thaliana were obtained. Coding sequences with internal stop codons and those that did not start with an ATG codon or end in stop codons were removed from the samples. In the end, we obtained 14 335 coding sequences (21.6 × 10⁶ nt) from D.melanogaster, 14 502 coding sequences (18.1 × 10⁶ nt) from C.elegans and 10 145 (13.8 × 10⁶ nt) from A.thaliana.

Since *.fna and *.ffn files are not available for human sequences, we used human genome contigs (0.5 × 10⁹ nt) obtained from the NCBI (www.nlm.nih.gov/Genomes/index.html) as a source of genomic sequences. The human CDS sample was as published previously (intron-containing plus intronless samples) representing 782 genes (1.1 × 10⁶ nt) (10).

The independent intron-containing CDS sample of D.melanogaster (IC-CDS) was obtained from our Exon-Intron Database (11). We removed all coding sequences with multiple duplications and purged the sample at the 20% amino acid similarity level as described in Fedorov et al. (10). Finally, the IC-CDS sample of D.melanogaster contained 505 coding sequences (0.67 × 10⁶ nt). The entire set of D.melanogaster genes was randomly subdivided into two equally sized samples to generate random subsets 1 and 2.

Calculations of relative abundance of codons with context

For each codon x_i coding for amino acid X we computed M_X(x_i∼n), the number of occurrences of codon x_i with nucleotide n in the N₁ context in the CDS samples. To eliminate the bias in non-random associations of neighboring amino acids in a protein, we analyzed each group of synonymous codons separately. Based on the M_X(x_i∼n) table obtained we calculated M_X(x_i), the number of occurrences of codon x_i in the sample [M_x(x_i) = M_x(x_i∼n)], M_X(n), the number of occurrences of nucleotide n following the codons representing amino acid X [M_x(n) = M_x(x_i∼n)], and M_X, the total number of codons representing amino acid X [M_x = M_x(x_i∼n)].

We then calculated the relative frequency of codon x_i with context n within synonymous group X [F_X(x_i∼n) = M_X(x_i∼n)/M_X], the relative frequency of codon x_i within group X [F_X(x_i) = M_X(x_i)/M_X] and the relative frequency of the context (n) within group X [F_X(n) = M_X(n)/M_X]. Finally, the relative abundance of codon x_i with context n [R(x_i∼n)] was calculated by the formula:

R(x_i∼n) = F_X(x_i∼n)/[F_X(x_i)F_X(n)] 1

Alternatively, we calculated the relative abundance of codon x_i with context n [R(x_i∼n)] for the united pool of all codons with context by the formula:

R(x_i∼n) = F_X(x_i∼n)/[F_X(x_i)F(n)]

where F(n) is now the frequency of nucleotide n in the first position of all codons. The results of this calculation are close to the results obtained using equation 1 and are present on our web page.

Standard deviation for R(x_i∼n)

To estimate the significance of R values, we calculated standard deviations for each R(x_i∼n), using Monte Carlo simulations. For this purpose 100 independent random tests were applied. In each test, using a random number generator, we created M_X^rand(x_i∼n) distributions with the total number of codons within the synonymous group for each random sample equal to the corresponding number in the real sample (M_X^rand = M_X). The random number generator simulated the appearance of codons x_i with n context with the same frequencies as in the real sample, F_X(x_i∼n). For each random sample we calculated R_k^rand(x_i∼n), k = 1, …, 100, according to equation 1. The standard deviation for R(x_i∼n) was calculated by the formula:

σ(x_i∼n) = {∑_{k = 1}¹⁰⁰[R_k^rand (x_i∼n) –²/99}1/2

Calculations of relative abundance of mono-, di- and trinucleotides with context in the genomes

For the studied samples of genomic sequences we calculated the frequencies of each nucleotide F(u), dinucleotide F(uv), trinucleotide F(uvw) and quadranucleotide F(uvwn), where u, v, w and n are each one of the four nucleotides a, c, g and t. Then we calculated the relative abundances (r value) of the mono-, di- and trinucleotides with a single nucleotide context:

r(w∼n) = F(wn)/[F(w)F(n)], for mononucleotide w with context n;

r(vw∼n) = F(vwn)/[F(vw)F(n)], for dinucleotide vw with context n;

r(uvw∼n) = F(uvwn)/[F(uvw)F(n)], for trinucleotide uvw with context n.

The r value of a mononucleotide with context r(w∼n) represents the so-called genomic signature, introduced by Karlin and Burge. (12).

Ranking statistics

We divided groups of synonymous codons into three types, based on their size and nucleotide composition in the third variable position. Type I was composed of those groups that contained four codons: the Ala, Gly, Leu(c) = [cta, ctc, ctg, ctt], Pro, Arg(c) = [cga, cgc, cgg, cgt], Ser(t) = [tca, tcc, tcg, tct], Thr and Val groups. Type II was composed of the groups containing two codons with pyrimidines in the third variable position: the Cys, Asp, Phe, His, Asn, Ser(a) = [agc, agt] and Tyr groups. Type III was composed of the groups containing two codons with purines in the third variable position: the Glu, Lys, Leu(t) = [tta, ttg], Gln and Arg(a) = [aga, agg] groups. Each of the three 6-fold degenerate codon groups (Arg, Leu and Ser) was divided into a group of four degenerate codons and a group of two degenerate codons based on the nucleotide in the first and second codon positions. For instance, we analyzed a 4-fold degenerate group of arginine codons [Arg(c): cga, cgc, cgg, cgt] with a C nucleotide in the first position and a 2-fold degenerate group of arginine codons [Arg(a): aga, agg] with an A nucleotide in the first position separately. CDCB was compared between groups of synonymous codons belonging to the same type using ranking statistics (13). For this purpose, within a group of synonymous codons representing amino acid X, each codon x_i with context n was given a rank on the basis of its relative abundance value R(x_i∼n). The codon with the context which had the minimal R(x_i∼n) value was given rank 1, the codon with the next smallest R(x_i∼n) value was given rank 2, and so on. Then, homologous pairs (A_i and B_i) from synonymous groups A and B, which have the same nucleotide at the third codon position and the same nucleotide in the N₁ context, were compared by counting the absolute difference of their ranks d_i^AB = │rank(A_i) – rank(B_i)│. Finally, to obtain D values all d_i^AB values were summed:

D^AB = ∑_{i = 1}¹⁶d_i^AB 2a

for type I synonymous groups or

D^AB = ∑_{i = 1}⁸d_i^AB 2b

for synonymous groups of types II and III.

We used this D^AB value to measure the difference of CDCB between groups A and B.

We also performed ranking statistics for ranks which were normalized by the genomic signature r(w∼n) value. In this case, we calculated the normalized relative abundance values as R′(uvw∼n) = R(uvw∼n)/r(w∼n), where u, v and w are nucleotides and n is the context of the codon uvw. We then computed ranks on the basis of the R′ values.

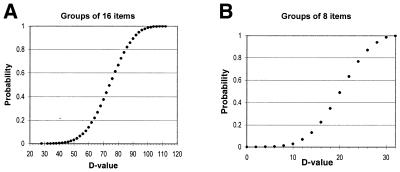
The distribution of the D values of ranking statistics for two groups with non-correlated elements was simulated on a computer for 100 000 groups of 16 or 8 random elements, to which ranks were randomly attributed (see Fig. 3).

Figure 3.

Cumulative probability distributions of D values for groups with randomly assigned ranks. The graphs can be used to assess the significance of D values. Specifically, the y-axis represents the probability that a pair of groups of 8 (A) or 16 (B) elements with randomly assigned ranks will have a D value less than or equal to the corresponding value on the x-axis.

All calculations were performed by Perl scripts on a Pentium III computer running LINUX. The entire set of our data is available from our web site: www.mcb.harvard.edu/gilbert/cdcb.

RESULTS

An example of the calculated R values, the relative abundance of codons with N₁ contexts, obtained for the entire set of D.melanogaster genes is shown in Figure 1. The complete list of R values for all studied CDS samples of four species are presented on our web page: www.mcb.harvard.edu/gilbert/cdcb. The data show that 90% of codons with N₁ context have a statistically significant bias, since their R values differ from 1 by more than 3 SD. Fifty-five percent of the codons uvw with N₁ context n from the entire set of Drosophila genes have the following properties: (i) the R(uvw∼n) value differs by >3 SD from all of the r(uvw∼n), r(vw∼n) and r(w∼n) values representing the genomic bias (relative abundance in the entire genome of the trinucleotide uvw, dinucleotide vw and nucleotide w with the n context, respectively); and (ii) the CDCB is larger than or opposite to the genomic bias. Therefore, the described cases of CDCB cannot be explained by non-random associations of neighboring nucleotides in the studied genome. For example, the alanine codon gct with a c context has a R(gct∼c) value of 1.32 ± 0.005 (Fig. 1). The genomic signature of the tc dinucleotide shows that this dinucleotide is deficient in the Drosophila genome [r(t∼c) = 0.907] and, therefore, cannot cause the excess of gct codons with a c context. The genomic bias of the trinucleotide gct with a c context [r(gct∼c) = 1.03] and the dinucleotide ct with a c context [r(ct∼c) = 1.05] in the Drosophila genome cannot be the reason for the much larger excess of gct codons with a c context either. Similar results were observed for the other three species examined. Forty-two percent of A.thaliana codons, 37% of C.elegans codons and 31% of human codons have a statistically significant CDCB which cannot be explained by genomic bias. The low percentage observed for the human genome is due to the smallest size of the human CDS sample and, thus, the largest values for standard deviation.

Figure 1.

Relative abundance of D.melanogaster codons with N₁ context and genomic oligonucleotides with context. Relative abundance of codons with N₁ context, R values were calculated using equation 1. Relative abundance of genomic oligonucleotides with context, r values were calculated as described in Materials and Methods. The ranking system is also described in Materials and Methods.

Since we deal with sets of genes, the obtained samples of codons are likely to be inhomogeneous and depend on gene composition. Because of this, we compared the R values obtained for several independent sets of Drosophila genes. In addition to the entire sample of Drosophila genes described above, we examined: (i) an experimentally confirmed intron-contained non-redundant set of 505 Drosophila genes; and (ii) two random gene subsets (subsets 1 and 2) representing half the total number of Drosophila genes. The R values for each of the four Drosophila samples were very similar to each other (see our web site). In 95% of the cases │R_i(uvw∼n) – R_j(uvw∼n)│ < 3σ_max(uvw∼n), where uvw is a codon with context n, i and j represent different Drosophila CDS samples and σ_max is the maximal σ_i(uvw∼n) and σ_j(uvw∼n) standard deviation. In 99% of cases │R_i(uvw∼n) – R_j(uvw∼n)│ < 5σ_max(uvw∼n). Therefore, none of the results presented above are affected considerably by the gene sampling.

Ranking statistics

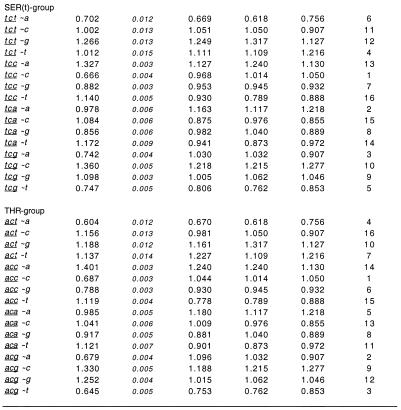
It is clear from Figure 1 that there are regularities in CDCB. If there is a strong bias for a particular codon uvw with nucleotide n in the N₁ context, then it is likely that a similar bias exists for other codons having the same nucleotide w in the third position and with the same n context. This correlation is usually strongest for codons with the same nucleotide v in the second position as well. For instance, the alanine codon gcc with a c context is deficient in Drosophila genes [R(gcc∼c) = 0.779 ± 0.003; Fig. 1]. The corresponding Ser (tcc), Pro (ccc) and Thr (acc) codons with the same c context are also deficient [R(ccc∼c) = 0.484 ± 0.003, R(tcc∼c) = 0.666 ± 0.004 and R(acc∼c) = 0.687 ± 0.003]. The described CDCB has not been caused by biological processes at the genomic level, since the cc dinucleotide is in excess in the Drosophila genome r(c∼c) =1.05. Also the genomic bias for the corresponding di- and trinucleotides with a c context cannot explain the described CDCB (see Fig. 1).

It is sensible to start an investigation of CDCB regularities comparing codons from synonymous groups of the same sizes and similar nucleotide compositions. That is why we divided the synonymous groups into three types, all having the same sizes and nucleotide compositions at the third codon position (see Materials and Methods). We compared R values of codons belonging to synonymous groups of the same type only. The similarity in CDCB between groups of synonymous codons representing amino acids A and B was measured as the D^AB value calculated using equation 2a or 2b. The smaller the D^AB value, the stronger the similarity in CDCB between the A and B groups of synonymous codons. The calculated D values for D.melanogaster and A.thaliana (Fig. 2) are much smaller than the simulated D values for two groups of 16 or 8 random elements shown in Figure 3A and B, respectively. Figure 3A shows that, on average, for two groups of 16 elements to which ranks were assigned randomly, the D value is 74. The D value is <56 for only 10% of the random group pairs, <42 for 1% of the random group pairs, <36 for 0.1% of the pairs and <28 for 0.01% of the pairs. At the same time, all D values calculated for Drosophila type I groups of synonymous codons with the N₁ context (Fig. 2) are less than the average value of 74 for the random groups. In seven of the 28 cases of pairwise comparison of Drosophila type I synonymous codon groups the D values are ≤28 (by chance, each occurrence has a probability of 10^–4). And in 20 of 28 cases these D values are <58 (by chance, each occurrence has a probability of 0.1). Similar ranking statistics results were obtained for the type II and III groups of D.melanogaster synonymous codons, containing two codons per group and hence eight codons with an N₁ context. The data for ranking statistics between random groups of eight elements is shown in Figure 3B. The average D value for two random groups of eight elements is 20. A D value ≤12 was found for only 10% of the random group pairs and ≤8 for 1% of the random group pairs. In 15 of 21 cases of pairwise comparison of Drosophila type II synonymous codon groups and in four of 10 cases of Drosophila type III codon groups the calculated D values were ≤8 (by chance, each occurrence has a probability of 0.01). It is important to stress that most frequently the observed similarity is strongest between groups of synonymous codons with similar nucleotide compositions (those having the same nucleotide in the second position), which are boxed in Figure 2.

Figure 2.

D^AB values measuring the CDCB difference between groups A and B of synonymous codons with N₁ context. Groups of synonymous codons are marked by the letters of the amino acids they code for. Groups are divided into type I, II and III, based on their size and nucleotide composition in the third variable position. The tables present D values of pairwise comparisons for all groups of synonymous codons belonging to the same type. Synonymous group pairs with similar nucleotide compositions (having the same nucleotide in the second codon position) are boxed. Most frequently the minimal D values are located inside boxes and correspond to groups with similar nucleotide compositions. D values calculated for (A) D.melanogaster genes and (B) A.thaliana genes.

In summary, Drosophila codons with the same nucleotides in the second and third positions and the same N₁ context have a statistically significant correlation of their relative abundances. The same types of regularities of CDCB between codons with similar nucleotide compositions are detected for Arabidopsis genes (Fig. 2B) and for H.sapiens and C.elegans. The complete set of our results on the ranking statistics obtained for different types of rank normalization for different species is shown on our web site (www.mcb.harvard.edu/gilbert/cdcb).

DISCUSSION

Codon bias and CDCB are particular manifestations of coding sequence non-randomness, which is utilized in many different cellular processes. The best known use is that of codon bias in achieving efficiency and accuracy in protein synthesis (14–19). Also, in eukaryotic cells, CDS non-randomness is utilized in the splicing process. For many genes, the earliest steps of splicing of the pre-mRNA transcripts start with the binding of a group of SR proteins to the exonic sequences (for reviews see 20,21). The specificity of binding of SR proteins to coding sequences and the avoidance of intronic sequences is due to distinct motifs within the CDS. There is evidence that selection of such motifs within exons modulates the CDS non-randomness (10). After splicing, export of mRNAs to the cytoplasm occurs in complex with different proteins, some of which are SR proteins (22–24). In the cytoplasm, mRNAs exist in tight association with many proteins as a mRNP complex. The association of mRNAs with a variety of proteins, from their appearance during transcription until the time of translation, requires many motifs within the coding sequences and, therefore, creates CDS non-randomness. These motifs regulate mRNA fate in the cell. Because these motifs are involved in many cellular processes, the whole picture of codon bias and CDCB is very diverse and sometimes inconsistent. That is why there are many non-congruent facts about codon bias and CDCB in the literature. For example: (i) eukaryotes have a negative correlation of codon bias with gene length, while prokaryotes have a positive correlation (16,25,26); (ii) the evidence that over-represented codon pairs are translated slower than under-represented pairs (27) contradicts the theory that codon bias and CDCB increase the speed of translation (17–19,28); (iii) the observed congruency of in-frame and out-of-frame trinucleotide preference in Drosophila (6) is contrary to the idea that CDS periodicity is involved in the translation frame monitoring mechanism (29).

Here we would like to summarize the fundamental properties of codon bias and CDCB. First, codon bias is ubiquitous in all organisms, but evolutionarily remote species from different taxa have different patterns of codon bias (see Codon Usage Database, www.kazusa.or.jp/codon). Second, there are distinct regularities in the pattern of codon bias as described by the nucleotide composition of a codon via simple rules, shown by Karlin and Mrazek (5). We show that CDCB is ubiquitous for all organisms and that CDCB has distinct regularities. The CDCB regularities are also dependent on the nucleotide composition of a codon and, therefore, are in accordance with the codon bias regularities.

It is of interest to ascertain the underlying process that causes the appearance of codon bias and CDCB. There is an old hypothesis that the main reason for codon bias is translational efficiency, and the change in the relative concentrations of different isoaccepting tRNAs determines the codon bias. This hypothesis is based on the observation that there is a strong correlation between codon usage and the abundance of the corresponding tRNAs within each pool of isoaccepting tRNAs (18,19). We think that this scenario is highly unlikely, since it cannot explain: (i) the regularities of codon bias shown by Karlin and Mrazek (5); (ii) the existence of CDCB; and (iii) the regularities in CDCB shown in this paper. It is much more probable that the abundance of tRNAs is a consequence of and not a reason for codon bias. At the same time, variations of tRNA abundance should follow and stabilize the codon bias. Our results support the theory that the accuracy of protein synthesis on the ribosome is the primary reason for codon bias (14–16). Spatial interaction of ribosomal proteins with codon–anticodon RNA pairs inside the A and P sites of the ribosome could be preferable for particular codons with context. If such preferences exist they could be the primary reason for the regularities in codon bias and CDCB with respect to codon nucleotide composition.