Abstract
Immune cells adopt a variety of metabolic states to support their many biological functions, which include fighting pathogens, removing tissue debris, and tissue remodeling. One of the key mediators of these metabolic changes is the transcription factor hypoxia-inducible factor 1α (HIF-1α). Single-cell dynamics have been shown to be an important determinant of cell behavior; however, despite the importance of HIF-1α, little is known about its single-cell dynamics or their effect on metabolism. To address this knowledge gap, here we optimized a HIF-1α fluorescent reporter and applied it to study single-cell dynamics. First, we showed that single cells are likely able to differentiate multiple levels of prolyl hydroxylase inhibition, a marker of metabolic change, via HIF-1α activity. We then applied a physiological stimulus known to trigger metabolic change, interferon-γ, and observed heterogeneous, oscillatory HIF-1α responses in single cells. Finally, we input these dynamics into a mathematical model of HIF-1α-regulated metabolism and discovered a profound difference between cells exhibiting high versus low HIF-1α activation. Specifically, we found cells with high HIF-1α activation are able to meaningfully reduce flux through the tricarboxylic acid cycle and show a notable increase in the NAD+/NADH ratio compared with cells displaying low HIF-1α activation. Altogether, this work demonstrates an optimized reporter for studying HIF-1α in single cells and reveals previously unknown principles of HIF-1α activation.
Keywords: hypoxia-inducible factor (HIF), microscopy, fluorescence, systems biology, mathematical modeling
Many immune cells, and in particular T cells and macrophages, need to adopt a variety of metabolic states to perform the diverse functions that are required of them (1, 2, 3). For example, macrophage activation can range from proinflammatory in M1 cells to anti-inflammatory in M2 cells (4, 5, 6, 7). These two activation states have different responsibilities within the body and also exhibit different metabolic signatures (8, 9, 10). For example, M1 macrophages utilize aerobic glycolysis, increase flux through the pentose phosphate pathway, and attenuate oxidative phosphorylation. Moreover, they accumulate the tricarboxylic acid (TCA) cycle intermediates succinate, citrate, and itaconate, which have important metabolic and signaling roles within the cell (9, 11). M2 macrophages, on the other hand, have an increased reliance on oxidative phosphorylation and fatty acid oxidation (9, 12, 13).
One of the key transcription factors involved in mediating these large metabolic changes in immune cells is the transcription factor hypoxia-inducible factor 1α (HIF-1α). HIF-1α has been shown to be required for immune responses in several contexts (14). For example, HIF-1α is known to be essential for bactericidal activity in myeloid cells (15, 16). HIF-1α activity is also required for trained immunity, as mice with a myeloid-specific HIF-1α knockout, unlike wildtype mice, were not protected against infection by Staphylococcus aureus by an initial stimulus of β-glucan (17). In some cases, inhibition of HIF-1α can also lead to a stronger immune response in innate immune cells (18). Beyond an immune context, HIF-1α also has important regulatory roles and is frequently found to be differentially regulated, in cancerous cells and in the context of metabolic or cardiovascular diseases (19, 20, 21, 22).
Single-cell analysis via live-cell imaging has been a powerful tool to elucidate cell behavior in many systems but has only been applied in a limited capacity to HIF-1α signaling (23, 24, 25). Nonetheless, the few studies of single-cell HIF-1α dynamics have already revealed important characteristics of single-cell HIF-1α responses. For example, Bagnall et al. (26) used live-cell microscopy to show that HIF-1α responses are “pulsatile” or transient in response to sustained hypoxic conditions. Their work suggests that the transient responses are likely necessary to avoid induction of proapoptotic genes that would occur with more sustained HIF-1α activation. In a separate example, Moroz et al. (27) observed differences of HIF-1α localization and activation patterns in different cell lines using a luciferase-based reporter. Yet, despite these examples, still relatively little is known about HIF-1α dynamics in single cells, especially in normoxia and in response to nonhypoxia mimetic stimuli. In addition, whether the dynamics of HIF-1α activation can be used to encode information at a single-cell level, and how that information is decoded into a phenotypic response, is still unknown.
Live, single-cell imaging of signaling pathway or transcription factor activity over time has often been paired with systems analysis and mathematical modeling (23). Existing mathematical models of HIF-1α activation have yielded valuable insights (28). For instance, in the example mentioned above, Bagnall et al. (26) combined models of HIF-1α activation and the p53-Mdm2 feedback loop to interrogate how different HIF-1α activation profiles affect the dynamics of p53. In another example, a detailed model of HIF-1α activation was used to suggest that hydroxylation by factor inhibiting HIF can actually confer some protection from proteasomal degradation (29). Finally, in a more recent example, a systems analysis approach was used to explain seemingly paradoxical results regarding HIF-1α activation and adipogenesis (30). Literature results have shown roles for HIF-1α in both promoting and preventing adipogenesis. The authors used experiments and modeling to show that, depending on the strength and timing of the adipogenic differentiation cue and HIF-1α activation, HIF-1α can both increase and decrease the accumulation of lipids in OP9 cells (30).
Nonetheless, measuring single-cell dynamics can be technically challenging and requires making measurements with high spatial and temporal resolution. Live-cell microscopy is a widely used method for studying single-cell signaling but requires a way to connect activity of the protein of interest into a change in fluorescence intensity, wavelength, or localization. Although HIF-1α, like most proteins, can be regulated in many ways, the primary mode of regulation is via posttranslational modifications (31). Specifically, HIF-1α is hydroxylated on two conserved proline residues by a family of O2-dependent prolyl-4-hydroxylases (PHDs) (32, 33). The hydroxylation of HIF-1α is recognized by the von Hippel-Lindau E3 ubiquitin ligase complex, leading to polyubiquitination and subsequent proteasomal degradation of HIF-1α (32, 34). In the absence of oxygen or other required cofactors, however, the PHDs are inactive and HIF-1α accumulates in the cell.
Here, we describe a novel HIF-1α fluorescent reporter, which builds on the work of Bagnall and colleagues by adding a number of improvements, including the addition of the endogenous 5′ UTR, as well as mutations to prevent downstream effects of overexpression of the reporter. We show that this reporter allows accurate quantification of HIF-1α dynamics in single cells. We then use the reporter to characterize single-cell responses to PHD inhibition and show that single cells can theoretically resolve differences in PHD activity levels via HIF-1α accumulation. We then examine single-cell responses to the physiological stimulus interferon gamma (IFN-γ) and observe the presence of previously undescribed HIF-1α oscillations. Finally, we use a mathematical model to examine the potential downstream metabolic consequences in each individual cell and observe that only cells with high HIF-1α activation are able to downregulate mitochondrial metabolism. In all, this work provides a new reporter for use by the broader scientific community and meaningful insights about the activation of HIF-1α in single cells.
Results
A novel fluorescent HIF-1α reporter allows accurate quantification of heterogeneous single-cell HIF-1α activation dynamics
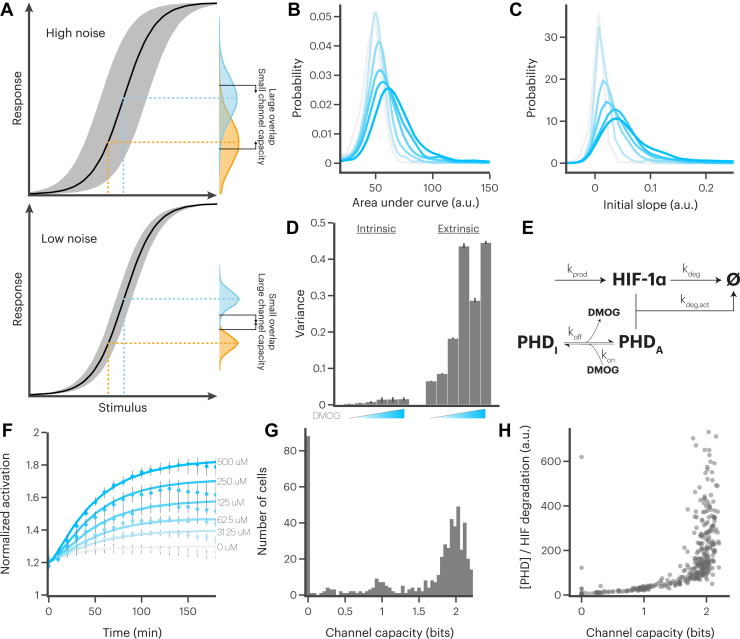
Our decision to construct a novel reporter was based on a preliminary investigation of single-cell HIF-1α activation using immunofluorescence. We stimulated RAW 264.7 cells (a mouse monocyte cell line) with dimethyloxallyl glycine (DMOG), an inhibitor of PHDs, and IFN-γ, a cytokine known to activate HIF-1α, for 10 h, taking samples every hour for immunostaining. As expected, we observed rapid, strong, and nearly ubiquitous HIF-1α activation in cells stimulated with DMOG (Fig. 1, A and B). On the other hand, cells stimulated with IFN-γ exhibited a delayed HIF-1α response, with significant variability within the population (Fig. 1, A and B). In particular, the overall response appeared to be driven by a small portion of the population with very high HIF-1α accumulation (Fig. 1C). The coefficient of variation was also higher for the IFN-γ response than for the DMOG response (Fig. 1D).
Figure 1.
An optimized HIF-1α reporter allows accurate quantification of HIF-1α activity in single cells.A, representative immunofluorescence images showing maximum activation of RAW 264.7 cells stimulated with PBS, 500 μM dimethyloxallyl glycine (DMOG), or 10 ng/ml interferon gamma (IFN-γ). The scale bar represents 50 μm. B, accumulation of HIF-1α normalized to maximum HIF-1α accumulation observed for each stimulus. Error bars are standard deviation from three biological replicates. C, distributions of HIF-1α accumulation in single RAW 264.7 cells 10 h after stimulation with 10 ng/ml IFN-γ. D, coefficient of variation of HIF-1α accumulation in single RAW 264.7 cells stimulated with 500 μM DMOG or 10 ng/ml IFN-γ, as measured at maximum activation using immunofluorescence. Error bars are standard deviation from three biological replicates. E, graphical representation of the HIF-1α reporter construct. Red x’s represent point mutations designed to block HIF-1α binding to binding partners. F, distribution of mean single-cell HIF-1α accumulation for reporters with and without the endogenous HIF-1α 5′ UTR region. G, comparison of HIF-1α activation dynamics as measured using the reporter (lines) and immunofluorescence (markers). Normalized by maximum activation observed. Shaded region and error bars represent standard deviation of three biological replicates.
To explore this heterogeneity further, and to quantify it in more detail, we turned to live-cell microscopy, which offers both a higher temporal resolution and the ability to track individual cells over time (23, 35). We designed and built a novel fluorescent reporter for HIF-1α activity (Fig. 1E). We aimed to build a reporter that would report on the posttranslational regulation of HIF-1α, as this is the primary method of regulation (31). The initial design was based on previously published reporters, which comprised a fluorescent protein linked to the C terminus of the full-length HIF-1α protein (26, 36). Unfortunately, we were unable to measure reporter activity in RAW 264.7 cells using this initial design; thus, we first made a number of changes aimed at increasing expression and brightness (Table S1). In particular, we replaced the original promoter with the murine cytolomegavirus promoter, which has previously been demonstrated to be a strong promoter in RAW 264.7 cells (37, 38). We also changed the primary fluorescent protein to mNeonGreen, which is brighter and matures faster (39).
Several other changes were also made to improve the reporter. We added an H2B nuclear marker, separated by a P2A sequence, to allow for normalization of disparate protein levels and quantification of relative HIF-1α activity (40, 41). Interestingly, the fluorescent protein attached to the nuclear marker had a significant impact on the intensity of the reporter signal: reporters with an H2B-mCerulean nuclear marker were much brighter than reporters with an H2B-mRuby2 or H2B-mCerulean3 nuclear marker, possibly due to the reduced propensity of mCerulean to form aggregates (Fig. S1) (42). We also introduced a number of point mutations (Q320E, V336E, Y340T, L805A) into the HIF-1α protein intended to prevent binding with HIF-1β and p300, thus reducing the chance of effects associated with overexpression of an exogenous protein (43, 44, 45). We also found that moving the fluorescent protein from the C terminus to a disordered loop in the middle of the protein resulted in more consistent localization and a brighter reporter (46).
Together, these changes produced a reporter with measurable expression and predictable localization in the nucleus. However, expression levels were still low for much of the population. Indeed, this reporter did not respond to DMOG stimulation in most cells, in contrast to our immunofluorescence results. We hypothesized that this was in part due to the global decrease in translation that occurs in hypoxic and hypoxia-mimetic conditions (47, 48, 49). To mitigate this, we included the 5′ UTR from the endogenous HIF-1α gene, which contains an efficient ribosome entry site and is required for adequate HIF-1α expression in hypoxic conditions (50). The resulting reporter exhibited a much stronger response to DMOG stimulation (Fig. 1F). In all, our novel reporter produced a strong fluorescent signal in RAW 264.7 in response to known HIF-1α activators. We also examined the reporter in a human cell line (HeLa cells) and found that it was responsive to DMOG stimulation (Fig. S2).
To validate that the reporter was accurately recapitulating HIF-1α activation dynamics, we returned to our earlier time-course immunofluorescence measurements. Measurements in the same single cell are challenging because the reporter is also recognized by HIF-1α antibodies. We found that HIF-1α measurements obtained using our reporter closely matched the immunofluorescence-measured HIF-1α dynamics over several hours (Figs. 1G, S3, and S4). These results confirm that the reporter can be used to accurately determine the dynamics of HIF-1α activation in single cells over time; we note, however, that the reporter only provides information about posttranslational regulation of HIF-1α.
RAW 264.7 cells respond to PHD inhibition primarily in a digital manner, but individual cells still exhibit some analog properties
In the previous literature, single-cell responses have been characterized as either digital, where differing fractions of cells respond with the same intensity, or analog, where cells respond with differing intensities (Fig. 2A). We wondered whether HIF-1α activation exhibited more digital or analog qualities. We therefore ran live-cell imaging experiments to quantify the response characteristics of HIF-1α activation in hundreds of individual RAW 264.7 cells (Fig. 2B). We used DMOG to directly manipulate PHD activity, thus avoiding noise in HIF-1α activation that could be generated by upstream signaling pathways. Even at high DMOG concentrations, a substantial portion of the population did not produce measurable HIF-1α activation (Fig. 2C). We also observed a range of response intensities and speeds in the responding cell population.
Figure 2.
RAW 264.7 cells respond to prolyl hydroxylase inhibition in a primarily digital manner.A, as stimulus concentration increases, digital responses are defined by an increase in the fraction of cells responding, while analog responses are defined by an increase in the mean response of the responding cells. B, representative images of reporter activation over time in RAW 264.7 cells stimulated with 500 μM dimethyloxallyl glycine (DMOG). The scale bar represents 25 μm. C, single-cell traces of responding (blue) and nonresponding (black) cells in response to stimulation with 500 μM DMOG. Distributions represent probability density of mean activation levels in single cells. D, mean population responses of RAW 264.7 cells stimulated with DMOG. Shaded regions represent 95% confidence intervals estimated from 1000 bootstrap replicates. E, fractions of cells responding to stimulation with DMOG. Error bars represent 95% confidence intervals estimated from 1000 bootstrap replicates. F, distributions of mean activation in responding cells in response to stimulation with indicated concentrations of DMOG. G, distributions of mean derivative during first 2 h after stimulation with indicated concentrations of DMOG.
Next, we examined the dependence of HIF-1α activation on concentration of DMOG. We stimulated cells with a log-distributed range of DMOG concentrations from 0 μM to 500 μM. Each concentration produced a distinct HIF-1α activation response at the population level (Fig. 2D). Further analysis showed that higher concentrations of DMOG corresponded to larger fractions of the population responding, a 3.6-fold increase from the smallest nonzero DMOG concentration to the largest (Fig. 2E). This suggests that the single-cell HIF-1α activation response includes a strong digital component. However, responding cells appeared to exhibit some analog capacity as well, as we observed that higher DMOG concentrations produced greater mean activation (1.3× increase), faster responses (2.4× increase), and more sustained responses (2.9× increase) in active cells (Figs. 2, F and G, S5, and S6). Together, these results suggest that activation of HIF-1α in single cells also has analog properties.
A minimal model of HIF-1α activation predicts that analog properties of HIF-1α activation can theoretically encode information in single cells
We next sought to quantify the ability of single cells to encode information about varying amounts of PHD inhibition. We applied the mathematical framework of information theory, which has been used extensively in other cellular systems (51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67). In short, each individual cell may be considered as an information channel that can encode information about an external signal as a response in the internal state of the cell. High levels of noise can preclude the cell from accurately discriminating the signal it receives. In such cases, the distribution of responses to one stimulus exhibits significant overlap with the distribution of responses to a second stimulus, such that the nature of the stimulus cannot be reliably determined from the response (Fig. 3A, top panel). These cells may be thought of as channels with a low capacity for information transfer. Alternatively, cells experiencing lower levels of noise can precisely discriminate the stimuli from experimental outputs and thus may be called channels with a high capacity for information transfer (bottom panel).
Figure 3.
A minimal model predicts that single cells can encode information via HIF-1α activation.A, high amounts of noise can preclude cells for accurately determining the level of stimulus they received as response distributions largely overlap (top panel), while pathways with little noise allow accurate stimulus discrimination (bottom panel). B, distributions of area under the curve of cells responding to dimethyloxallyl glycine (DMOG) stimulation. Darker color indicates higher concentration. Concentrations included are 0, 31.25, 62.5, 125, 250, and 500 μM. C, distributions of mean derivative during the first 2 h after stimulation with DMOG. Darker color indicates higher concentration. Concentrations included are 0, 31.25, 62.5, 125, 250, and 500 μM. D, experimentally measured intrinsic and extrinsic variance for cells stimulated with 0, 31.25, 62.5, 125, 250, or 500 μM DMOG. Note that these data also appear in the left panel of Fig. S10, where they are compared with values derived from simulations. E, schematic of a minimal model of HIF-1α activation and prolyl hydroxylase–mediated HIF-1α degradation. F, model-simulated median HIF-1α activation (lines) compared with experimentally measured responses (markers) in DMOG-stimulated cells. Error bars represent 95% confidence intervals estimated from 1000 bootstrap replicates. G, distribution of estimated single-cell channel capacities for cells stimulated with 500 μM DMOG. Distribution of channel capacities for all concentrations shown in Fig. S11. H, ratio of estimated prolyl hydroxylase concentration to HIF-1α degradation rate for cells stimulated with 500 μM DMOG. Ratio for all concentrations shown in Fig. S11.
A quantity that can be used to describe this effect is the channel capacity (C), which is the maximum achievable mutual information. This value can be conceptualized as the amount of information that can be gained about a set of inputs by measuring the output responses. Equation 1 shows a basic formula for calculating mutual information in a discrete system, where S = {s1, s2, s3, . . ., sN } represents the possible stimuli and R = {r1, r2, r3, . . ., rM } represents the possible responses. Applying this framework to our experimental results, we take S to be the DMOG concentrations used in the experiment and R to be properties of the measured single-cell HIF-1α responses, such as mean activation, area under the curve, or derivative of the initial response. We refer the reader to the Supporting information for a more complete discussion of applying information theory to study cellular systems.
| (1) |
We observed that the distributions of the area under the curve of single-cell HIF-1α responses exhibit substantial overlap for different concentrations of DMOG, with an estimated single-cell channel capacity below 1 bit, suggesting that single cells have a highly limited ability to encode information through HIF-1α (Fig. 3B). We found a similarly low channel capacity using the initial speed of the HIF-1α response (Fig. 3C). Surprisingly, such a low channel capacity suggests that cells cannot even reliably discriminate the presence or absence of PHD inhibition.
Given this counterintuitive result, we sought to understand the source of the noise that confounded the HIF-1α channel capacity of our cells. Noise can be broadly categorized as intrinsic, referring to the stochastic fluctuations associated with low discrete molecule counts inside of individual cells, or extrinsic, referring to intercell variability in the concentrations of important molecules (68, 69). Recent results have suggested that much of the variance observed in cellular populations is due to extrinsic effects and may be better conceptualized as phenotypic variability rather than noise (55, 70, 71, 72, 73). To investigate this possibility in the context of PHD inhibition, we first estimated the contribution of intrinsic and extrinsic noise to the variance, as previously described (52). Briefly, a short time period is defined in which HIF-1α levels may reasonably be expected to be nearly constant. This period is then used to calculate the intracellular variance, which is compared with the total variance in the population (Fig. S7). The intracellular variance is the intrinsic noise combined with experimental error, while the extrinsic noise can be derived by subtracting the intracellular variance from the total variance. Similar to other systems, we observed that the variance in the activation of HIF-1α is dominated by extrinsic noise (Fig. 3D). This suggests that individual cells experience lower noise and may be able to resolve varying amounts of PHD inhibition with higher fidelity than our previous estimates.
To correct for the impact of extrinsic effects on our channel capacity calculations, we would normally need to stimulate the same cell multiple times with different stimulus strengths (54, 55, 56). However, this is generally infeasible, as cells will not return to the same baseline state after stimulation. We therefore used mathematical modeling to run a theoretical experiment in which the same cell begins in the same baseline state and is stimulated with many different stimulus concentrations. For this purpose we built a minimal ordinary differential equation model based on a HIF-1α network shown schematically in Figure 3E and described by Equations (2), (3), (4), (5).
| (2) |
| (3) |
| (4) |
| (5) |
We fit the kinetic parameters of the model to the response of the median cell in the population. We tested the model by running it with the same stimulus concentrations as in our earlier experiments. Our model was able to accurately recapitulate the dose response of the whole population (Fig. 3F).
We reasoned that the extrinsic noise most likely arose from intercellular variance in the concentrations of HIF-1α and PHD. Therefore, we fit the model to each of the individual measured traces by adjusting only the initial PHD and HIF-1α concentration. The HIF-1α concentrations were modified by adjusting kprod and kdeg, resulting in a new steady-state concentration of HIF-1α. The differences in kprod and kdeg can be attributed to differences in the concentration of cellular components, such as ribosomes, mRNAs, and protease complexes. The simulated single-cell traces from our model corresponded reasonably well to our measured traces (Figs. S8 and S9); differences between the measured and modeled traces are largely attributable to cells that divide during the experiment or cells with particularly strong HIF-1α feedback.
Taken together, this set of models, fit to our full collection of individual cell traces, is a representation of the extrinsic noise in the population. To incorporate intrinsic effects, we simply added a Gaussian noise term, where the distribution was defined by the mean intracellular variance in our measured traces. Having incorporated both intrinsic and extrinsic representations of noise, we were able to recapitulate the measured intrinsic and extrinsic noise values at each experimental DMOG concentration (Fig. S10).
We then simulated treating each cell with each DMOG concentration 100 times (a total of 600 simulations for each modeled cell) and analyzed the predicted outcomes to calculate a new channel capacity. Interestingly, this analysis suggested that two subpopulations of cells coexist in the population: one group exhibited a high channel capacity around 2 bits, and the other exhibited a channel capacity that is effectively zero (Figs. 3G and S11). The size of this latter group was likely overestimated, due to the limited dynamic range of our reporter at low activation levels (Fig. S12). That said, this group could also not be called universally nonresponding, as we observed that several cells were still responding to PHD inhibition (Fig. S13). Rather, this group was simply unable to adequately discriminate between different DMOG concentrations. This finding led us to question why some cells could discriminate between DMOG concentrations while others could not. Further analysis shows that the ratio of PHD concentration to the basal HIF-1α degradation rate was a strong indicator of cellular channel capacity, with cells having a higher channel capacity typically also having a higher PHD concentration to HIF-1α degradation ratio (Figs. 3H and S11). This suggests that the primary determinant of channel capacity in the cells is the capacity for active PHD-mediated degradation compared with constitutive HIF-1α degradation. Taken together, these results suggest that single cells could theoretically encode a substantive amount of information about a stimulus that leads to PHD inhibition and HIF-1α activation.
Stimulation of RAW 264.7 cells with IFN-γ leads to a heterogeneous, and often oscillatory, HIF-1α response
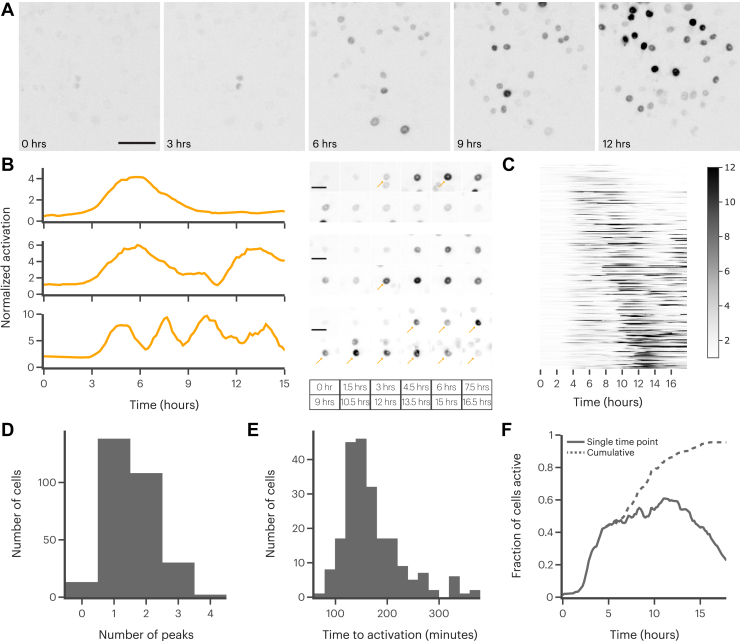
We next turned our attention to HIF-1α activation in response to a more physiological stimulus, IFN-γ. We again used immunofluorescence to confirm that our reporter was able to accurately recapitulate HIF-1α dynamics in response to IFN-γ stimulation (Figs. S14 and S15). The differences between the immunofluorescence and reporter might be due to transcriptional regulation that the reporter cannot capture. We then measured the dynamic HIF-1α response to IFN-γ over 18 h using live-cell microscopy (Fig. 4A and Supplemental Movie). The single-cell responses exhibited significant heterogeneity in both timing and intensity, as we had expected based on our immunofluorescence results. However, we observed many different dynamic patterns of activation, including up to four recurrent peaks of activation, over the time course (Fig. 4, B and C).
Figure 4.
Stimulation of RAW 264.7 cells with interferon gamma (IFN-γ) leads to a heterogeneous, and often oscillatory, HIF-1α response.A, representative images of reporter activation in RAW 264.7 cells stimulated with 10 ng/ml IFN-γ. The scale bar represents 50 μm. B, example single-cell reporter traces and corresponding images of cells stimulated with 10 ng/ml IFN-γ. Arrows indicate cell of interest in images with more than one cell visible. Time points shown at bottom. The scale bar represents 10 μm. C, heatmap showing normalized individual cell reporter traces after stimulation with 10 ng/ml IFN-γ. Darker colors indicate greater reporter accumulation. D, distribution of number of peaks found in cells stimulated with 10 ng/ml IFN-γ. E, distribution of times to first activation in cells stimulated with 10 ng/ml IFN-γ, defined as time to peak activation of first peak in each trace. Does not include cells with no peaks. F, fraction of cells active at the given time point (solid line) and cumulatively for the whole trace (dashed line).
These oscillations were highly variable in periodicity, amplitude, and shape. This variability precluded the use of most readily available peak finding algorithms, so we used a convolutional neural net-based approach recently developed in our laboratory to identify peaks in each individual cell trace (see Supporting information). Using this algorithm, we found that approximately half of cells stimulated with IFN-γ exhibited more than one peak of HIF-1α activity (Fig. 4D). Interestingly, the number of peaks did not correlate with mean or total HIF-1α activation, suggesting that the oscillations do not serve to increase HIF-1α activity (Fig. S16). We also found that many cells took as long as 6 h after IFN-γ stimulation to exhibit measurable HIF-1α activation (Fig. 4E). This delay, combined with our observation of oscillations, again indicates the presence of complex signaling processes required for HIF-1α activation following IFN-γ stimulation. Finally, we observed that approximately 90% of cells exhibit some HIF-1α activation after IFN-γ stimulation. Yet, due to the oscillatory nature of the response, at any given time point only about 50% of cells are active (Fig. 4F). This discrepancy highlights the importance of making dynamic measurements with high temporal resolution for fully describing HIF-1α activation, as our immunofluorescence results were not able to capture the full scope of HIF-1α activation.
A minimal model of mitochondrial metabolism suggests that cells with higher HIF-1α activation inhibit mitochondrial metabolism and generate a high NAD+/NADH ratio
Finally, we wondered whether the heterogeneous HIF-1α dynamics we observed under IFN-γ stimulation conditions would also lead to heterogeneity in the downstream phenotypes of the cells and, in particular, cellular metabolism. Given the challenge of combining measurements of metabolism and signaling in the same single cell we again turned to mathematical modeling for additional insight.
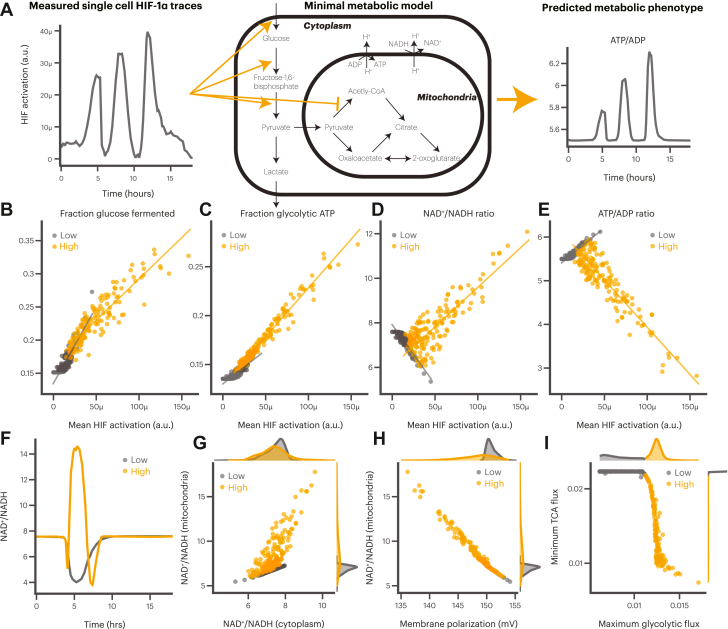
We began by implementing a recently published ordinary differential equation model of HIF-1α-regulated metabolism (74, 75). The model comprises a minimal model of glycolysis, the TCA cycle, and oxidative phosphorylation, with known HIF-1α regulation incorporated as a positive or negative effect on specific reaction rates. The model was originally validated by matching experimentally measured metabolite concentrations in normoxic conditions and expected cell behaviors under hypoxic conditions. For each individual cell trace, we scaled our experimentally measured single-cell HIF-1α activation to the concentrations produced by the model (Fig. 5A shows roughly how this was performed; see Experimental procedures for complete details).
Figure 5.
A minimal metabolic model predicts that only cells with high HIF-1α activation alter mitochondrial metabolism.A, measured single-cell HIF-1α activation was used as an input to a minimal metabolic model to predict the metabolic phenotype of each cell. Not all reactions shown; see Fig. S17 for more details. Mean HIF-1α activation compared with mean fraction of glucose fermented (B), mean fraction of ATP derived from glycolysis (C), mean whole cell NAD+/NADH ratio (D), and mean whole cell ATP/ADP ratio (E) for cells with high (orange) and low (gray) HIF-1α activation. Each point represents a single cell. Lines represent linear regressions for each group of cells. F, example single-cell NAD+/NADH ratio traces showing difference for a cell with high (orange) and low (gray) HIF-1α activation. G, comparison of NAD+/NADH ratio in the mitochondrial and cytoplasmic compartments for cells with high (orange) and low (gray) HIF-1α activation. Distributions are the single-cell probability densities. H, comparison of mitochondrial membrane polarization and the NAD+/NADH ratio for cells with high (orange) and low (gray) HIF-1α activation. Distributions are the single-cell probability densities. I, comparison of the maximum glycolytic flux and minimum tricarboxylic acid flux for cells with high (orange) and low (gray) HIF-1α activation. Distributions are the single-cell probability densities.
Using this approach, we observed that the dynamics of HIF-1α activation correlated with dynamic changes in the metabolic model on approximately the same time scale (Fig. S18). The model also recapitulated expected behaviors, such as the increase in lactate fermentation and ATP derived from glycolysis that results from an increase in HIF-1α activity (Fig. 5, B and C). Cells with high HIF-1α activation also showed a significant increase in their NAD+/NADH ratio (Fig. 5D), consistent with recently published experimental results that show that demand for NAD+ is a driver of aerobic glycolysis (76). We also confirmed that saturation of the glycerol 3-phosphate shuttle in the model led to an increase in fermentation, which is also consistent with recent experimental results (77). Together, these results gave us confidence that the downstream model outputs were representative of HIF-1α-mediated metabolic changes.
We next explored in more detail the impact of HIF-1α dynamics on two important metrics describing the state of the cell, specifically the NAD+/NADH ratio, which reflects the oxidative state of the cell, and the ATP/ADP ratio, which reflects the energy balance in the cell. We observed that increased mean HIF-1α activation was correlated with a decrease in the ATP/ADP ratio and an increase in the NAD+/NADH ratio (Fig. 5, D and E). We wanted to see whether we could discriminate the model results further by using the cell subpopulations based on HIF-1α activation dynamics (see Fig. 4B). We identified no correlation between the number of peaks and either ratio or the amount of fermentation and glycolytically derived ATP (Fig. S19, colored dots). This result is consistent with our earlier observation that the number of peaks does not correlate with mean HIF-1α activation.
In contrast, comparing model outcomes for cells based on their maximum exhibited HIF-1α activation revealed a striking difference between cells with high HIF-1α activation and cells with no or low HIF-1α activation. Although both groups of cells exhibit the same trends we observed in regards to fermentation and glycolytically derived ATP (Fig. 5, B and C), we observed a reversal of trends in regards to the NAD+/NADH ratio and ATP/ADP ratio (Fig. 5, D and E). Specifically, cells with lower HIF-1α activation tended to exhibit a modest decrease in the NAD+/NADH ratio and a modest increase in the ATP/ADP ratio as HIF-1α activity increased. However, cells with high HIF-1α activation exhibited a reversed trend, with a significant increase in the NAD+/NADH ratio and a concomitant decrease in the ATP/ADP ratio as HIF-1α activity increased. We confirmed this observation in individual cell traces where peaks with opposite trends were readily apparent (Figs. 5F and S20).
We wondered what was causing this difference between high- and low-activating cells and so compared the NAD+/NADH ratio and ATP/ADP ratio in the cytoplasmic and mitochondrial compartments in the model. We found strong correlation between the ATP/ADP ratio in each compartment, which is understandable given that ATP and ADP can be transported between the mitochondria and cytoplasm (Fig. S21). Stated differently, the ATP/ADP ratio decreased in both compartments together.
However, there was a substantial difference in the NAD+/NADH ratio between the two compartments. The distribution of the cytoplasmic NAD+/NADH ratios remained largely unchanged by differences in HIF-1α activity (high versus low), while the distributions of the mitochondrial NAD+/NADH ratios clearly correlated with the amount of HIF-1α activation (Fig. 5G, see distributions at top and right). This difference appeared to be mediated by differences in mitochondrial membrane polarization. Cells with low HIF-1α activity did not change the polarization of the mitochondrial membrane and therefore experienced relatively unchanged mitochondrial NAD+/NADH ratios. On the other hand, cells with high HIF-1α activity exhibited a pronounced reduction in the mitochondrial membrane potential, resulting in reduced ATP production and a higher NAD+/NADH ratio (Fig. 5H).
Taken together, these results suggest a dynamic metabolic phenotype in most cells, with two main subpopulations: all cells with measurable HIF-1α activation exhibited an increase in glycolytic flux, but only cells with very high HIF-1α activation were able to substantively decrease flux through the TCA cycle and attenuate ATP production (Fig. 5I). Cells with the highest HIF-1α activation seem to be in a metabolic state requiring significant support for oxidative reactions, resulting in a much higher NAD+/NADH ratio at the expense of ATP production. On the other hand, cells with lower HIF-1α activation do not substantively change their mitochondrial metabolism and instead have only a modest increase in ATP production associated with increased flux through glycolysis. Overall, these results suggest that the heterogeneous HIF-1α dynamics we measured can translate to heterogeneous metabolic states as well, with two distinct phenotypes.
Discussion
Here we describe a novel fluorescent reporter that can be used to study single-cell HIF-1α activation and utilize mathematical modeling to characterize single-cell HIF-1α responses measured using live-cell microscopy. We show that individual cells are able to distinguish multiple degrees of PHD inhibition, suggesting that the activation of HIF-1α could theoretically be used to encode information in single cells. In addition, we made several observations that merit additional consideration.
For instance, our measurements of single-cell HIF-1α responses revealed substantial cell-to-cell variability, even when just using a control stimulus. Mathematical modeling revealed that this variability was likely due to intercell variability in the amount of PHDs. This result may have been expected based on some previous results showing the dominance of extrinsic noise (52, 55, 70, 71, 72) and because our measurements were focused on the last step of the pathway. It is likely true that, if a larger or more complex pathway was considered, such as with IFN-γ activation, that the amount of intrinsic noise would be higher. Nonetheless, it is interesting to note the amount of extrinsic noise at the last step of the pathway. This variability may serve to allow the population to respond robustly to a range of inputs (78). In certain systems, such as adipogenesis, the variability might also engender a mix of phenotypes within a population (30).
As in other systems, the application of an information theoretic framework greatly contributed to our ability to form new insights regarding single-cell HIF-1α activation (51, 53, 54, 67). Although we describe cells distinguishing different amounts of HIF-1α activity, it remains unclear whether these differences are decoded into differences in gene expression. However, the presence of the more complicated HIF-1α dynamics we observed in response to IFN-γ stimulation does suggest that cells have also evolved mechanisms to utilize those dynamics. Indeed, it was recently demonstrated that activation of HIF-1α by an oscillatory stimulus led to differential regulation of specific genes compared with sustained HIF-1α activation, indicating the ability for cells to decode HIF-1α dynamics to specific transcriptional states (79). There is also evidence in the HIF-1α pathway of cells distinguishing different oxygen tensions, as different amounts of hypoxia lead to the differential expression of certain HIF-1α target genes (80, 81). Although the mechanism the authors propose relies on another protein, factor inhibiting HIF, it nonetheless demonstrates that cells are able to discriminate multiple physiological levels of hypoxia.
When using a physiological stimulus, in this case IFN-γ, we observed a far greater amount of heterogeneity and a significant oscillatory component to the response. This is in agreement with a recently published study describing the presence of oscillatory HIF-1α-dependent transcription in response to sustained hypoxia (79). In that work, the authors found that the oscillatory HIF-1α-dependent transcription was associated with cell cycle progression. It is possible that the oscillations mediate a similar phenotype in this system. It is also relevant to consider the role of cross talk, and the possibility that the oscillations observed have downstream consequences for other signaling pathways, such as NF-κB, glucocorticoid signaling, and circadian signaling (82, 83, 84, 85, 86). It is known, for example, that HIF-1α accumulation induces stabilization of p53 (87, 88). Furthermore, as modeled by Bagnall and colleagues, pulsatile, rather than sustained, HIF-1α activity leads to differences in p53 activation profiles (26). Therefore, given the extensive cross talk that is known to exist between HIF-1α and other pathways, it may be that the oscillations we measured have a direct impact on the regulation of other pathways.
It is also interesting to consider the delay of multiple hours in the IFN-γ-induced HIF-1α response, especially considering reports that IFN-γ-induced increase in glycolysis occurs within minutes of stimulation (89). Although these differences are possibly due to different cell types and experimental modalities, it is still valuable to consider the biological implications. It is possible that multiple transcription factors act in unison to regulate metabolism over long periods of time. For example, FOXK1 and FOXK2 are known to regulate aerobic glycolysis on timescales shorter than the time we observed was required for HIF-1α induction (90). This could suggest that HIF-1α has more of a role in sustaining metabolic changes or inducing a different metabolic state at a later time. This is also in accordance with findings that the induced accumulation of succinate is required for HIF-1α accumulation, showing that metabolic changes occur before HIF-1α accumulation (11, 91).
Finally, we use our measured single-cell HIF-1α activation dynamics as an input to a mathematical model of metabolism and show that, while all cells with HIF-1α activation show an increase in glycolysis, only cells with very high HIF-1α activation are able to downregulate mitochondrial metabolism. We note that the model does not expressly account for changes in enzyme concentration or allosteric regulation and therefore may miss important phenomena associated with HIF-1α regulation. Nonetheless, the model was able to recapitulate a number of phenotypic observations. One such result, which has also been reported elsewhere, is a reduction in mitochondrial oxidative phosphorylation associated with HIF-1α activation (92, 93). Our modeling results suggest that this reduction only occurs in cells with high HIF-1α activation. This mitochondrial phenotype has also been associated with an inability of M1 macrophages to reprogram to M2 macrophages (94). One might therefore speculate that the cells with less HIF-1α activity may be more plastic and are able to assume a different phenotype after proinflammatory stimulus. In this manner, while part of the population is ready to assume a tissue-remodeling phenotype, another part of the population could ensure a continued inflammatory response.
Finally, there are many other contexts in which studying single-cell HIF-1α dynamics is likely to be important. For example, other immune cells, such as dendritic cells (95), neutrophils (15), and T cells (96, 97) are known to activate HIF-1α. In addition, some pathogens are also known to directly induce HIF-1α stabilization (98, 99) or use HIF-1α to regulate expression of viral genes (100, 101). Hypoxia is also a common feature of different physiological niches, such as the bone marrow or inflamed tissues, and a recent study has revealed the role of oscillatory HIF-1α-dependent transcriptional activity in the context of sustained hypoxia (79). Therefore, we hope that our reporter will be a useful tool to study HIF-1α activation in a variety of contexts.
Experimental procedures
Cloning
Plasmids and primers were designed using Benchling. All PCR reactions were conducted using PrimeStar Max (Takara Bio, R045A). Murine HIF-1α cDNA was purchased from the Mammalian Gene Collection sold by Horizon (MMM1013-202764365). All reporter constructs were first cloned into a pENTR backbone (Invitrogen K240020) and then moved to a lentiviral backbone using a Gateway LR reaction (Thermo Fisher Scientific 11791020). The lentiviral reporter plasmid has been made available on Addgene.
Mammalian cell culture
RAW 264.7 cells from ATCC (ATCC TIB-71) were used. Cells were grown in Dulbecco’s modified Eagle’s medium (Thermo Fisher Scientific 11965118), supplemented with 1X penicillin/streptomycin, 2 mM L-glutamine, and 10% fetal bovine serum. Cells were incubated at 37 °C and 5% CO2 and subcultured every 2 days upon reaching 80% confluence. Accutase (Sigma-Aldrich A6964) was used to remove adherent cells for subculturing. Cells used for cell line generation and experiments were used at passage numbers well below previously identified limits (102). Stimulation of cells was conducted with DMOG (Cayman Chemical 71210) or IFN-γ (PeproTech 315-05).
Cell line generation
Lentivirus was generated in Lenti-X 293T cells using second-generation viral packaging plasmids (Addgene #12259, 12260). Viral packaging plasmids and the target lentiviral vector, constituting 2 μg of total DNA, were transfected into Lenti-X 293T cells on 6-well tissue culture treated plates using Lipofectamine 2000 (Thermo Fisher Scientific 11668019). Cells were incubated for 48 h at 37 °C and 5% CO2. The medium containing lentivirus was then harvested and filtered through a 0.45-μm filter. Aliquots, 200 μl, of virus were used for infection immediately or stored at −80 °C for up to 2 months. For infection, RAW 264.7 cells were plated at a density of 12,500 cells per well in 12-well tissue culture treated plates 24 h prior to infection. On the day of infection, the medium was replaced to the viral medium harvested before, supplemented with fresh Dulbecco’s modified Eagle’s medium to a volume of 2 ml and 2 μl of polybrene (Sigma-Aldrich TR-1003). Cells were then spun at 2900g and 34 °C for 90 min and then incubated for 4 to 6 h at 37 °C and 5% CO2. Finally, the cells were washed once in PBS and the medium replaced to fresh 10% DFPG. Selection was started the following day using 2 μg/ml puromycin for 24 to 72 h or 1.5 μg/ml blasticidin for 72 to 96 h.
Live-cell imaging
Cells were plated in 10% DFPG at a density of 10,000 to 15,000 cells per well on a fibronectin-coated glass-bottom 96-well plate 24 h prior to imaging. One hour prior to imaging cells were washed once with PBS and the medium replaced to imaging medium: Fluorbrite (Thermo Fisher Scientific A1896701) supplemented with 10 mM Hepes buffer, 2 mM L-glutamine, and 1% fetal bovine serum. Imaging was conducted using a Nikon Eclipse Ti fluorescence microscope equipped with a 20×/0.75 numerical aperture objective. Images were acquired using an Andor Neo 5.5 sCMOS camera with 3 × 3 binning. The microscope was also equipped with environmental and temperature control to maintain the cells at 37 °C and 5% CO2. Imaging was automated using Micro-manager (103). Exact acquisition parameters varied slightly between experiments but typically included 3 to 6 positions per well, an interval of 10 to 15 min between frames, and a total imaging time of 3 to 24 h.
Immunofluorescence
Cells were plated in 10% DFPG at a density of 10,000 to 15,000 cells per well on a fibronectin-coated glass-bottom 96-well plate 24 h prior to the start of the experiment. At the end of the experiment, the cells were washed once in PBS, then fixed with 4% paraformaldehyde for 15 min at room temperature. Cells were then washed in PBS three times followed by permeabilization in 0.1% Triton X-100 in PBS for 15 min at room temperature. Next, blocking was performed using 10% donkey serum (Jackson ImmunoResearch 017-000-001) in PBS for 1 h at 4 °C. All antibody incubations were also done in 10% donkey serum in PBS. First, primary antibody staining was conducted overnight at 4 °C using a rabbit monoclonal anti-HIF-1α antibody (Cell Signaling Technology 36169). Following the primary stain, cells were washed three times in PBS at room temperature, then incubated with a goat anti-rabbit IgG conjugated with Cy5 (Abcam ab97077) for 1 h at 4 °C, followed again by three room temperature PBS washes. If required, cells were then incubated with 50 ng/ml Hoechst 33342 for 15 min and washed with PBS again. Imaging was conducted the same as described for live-cell imaging immediately following the last incubation step.
Image analysis
Images were analyzed using CellTK version 0.4.2 (https://github.com/sjeknic/CellTK). First, images were corrected for illumination bias using reference images collected using fluorescent dyes. Next, images were segmented to mark pixels that corresponded to a cell nucleus and pixels that corresponded to background. To accomplish this, a UNet-based convolutional neural net was first used to predict the probability that each pixel in the nuclear marker image corresponded to a nucleus (104). A constant threshold was applied to create seed regions pixels that had a probability of being a nucleus of at least 0.98. These seed regions were expanded using an iterative watershed-based method to include neighboring pixels with probability at least 0.67. Finally, contiguous regions were labeled with a unique pixel value and only regions within specified area and solidity (ratio of convex area to area) thresholds were kept.
Next, the segmented regions were tracked in consecutive frames. This was accomplished using a recently published approach (105). Cells that were missing or untracked in two or more frames were excluded. Although this tracking approach can account for cell division, in practice only one of the daughter cells was included in the final data set. Finally, pixel intensity values for both fluorescent channels in each tracked region were recorded and used in further downstream analysis. Activation values shown are median FITC intensity divided by median CFP (cyan fluorescent protein) intensity. Peak finding was conducted with a convolutional neural net (Fig. S22, see Supporting information for more details).
Modeling of DMOG-mediated HIF-1α activation
The minimal model of HIF-1α activation was built based on mass-action kinetics and implemented in Python 3.8. Numerical integration was conducted with the solve_ivp function in Scipy using the LSODA solver (106). Parameters were fit to match the median solution at each DMOG concentration. Parameter fitting was first done manually to find a generally correct solution, which was then used as the starting point for gradient descent to optimize the parameter fit. Fitting of individual cell traces was done using the curve_fit function in Scipy, wrapped around the solve_ivp function. HIF-1α-mediated negative feedback through induction of PHDs was not included in the model for a few reasons. One, we found that the model without negative feedback was sufficiently able to capture the behavior we were interested in and thus favored it because it was the simplest model. Two, by focusing only on the first few hours of the HIF-1α response, we observed that the negative feedback did not have a significant effect in most cells. Finally, including negative feedback expands the parameter space and complicates the fitting such that the fitting algorithm failed for more cells.
For all analyses related to active and inactive cells, we normalized all traces to the initial HIF-1α activation. Cells were marked as active if they sustained activation 25% greater than the initial activation for at least ten time points. Intensity thresholds ranging from 15% to 50%, and duration thresholds ranging from 5 to 15 frames, were also tested and led to consistent trends.
Channel capacity calculations
There are multiple methods for estimating channel capacity. We used a binning approach similar to previously published papers (51, 53, 67). Briefly, individual cells were binned into a set number of bins based on their HIF-1α activity or other metric, as stated. The number of bins was selected to be sufficiently high to capture the relationship while also ensuring the mutual information of randomized data was essentially zero (Fig. S23). A contingency table was built and used in accordance with Equation 1 to calculate mutual information. All values presented in this work are corrected for bias due to limited sample size. This bias was estimated by repeatedly jackknife sampling different fractions of the data, fitting a linear regression, and extrapolating to infinite sample size (51) (Fig. S24). Please refer to the Supporting information for more details regarding our information theory calculations.
Metabolic modeling
A previously existing MATLAB model of HIF-1α-regulated metabolism was implemented in Python 3.8. The parameters were fit by the original authors such that the model exhibited experimentally measured steady-state metabolite concentrations. The HIF-1α effects were modeled as a Hill function mediating an increase or decrease in the kinetic rate of the reactions in question. We confirmed that our implementation of the model was equivalent to the original by recreating figures from the original paper.
The measurements from the reporter are relative measurements, therefore we needed to scale the measurements to the range of concentrations used in the model. We scaled each trace to a [0, 1] range and then multiplied by the mean active HIF-1α concentration in the model. The lower bound of the range was set with the smallest HIF-1α value measured. For the upper bound, we used three standard deviations above the mean HIF-1α activation of all cells. In all, this produced a range of HIF-1α concentrations that were well within the relevant range of the model, and nearly all cells with HIF-1α activation registered some metabolic changes in the model. We tested other, similar methods for scaling the concentrations and found consistent results.
For the results in Figure 5, cells with high activation were defined as cells that reached 80% or greater of the maximum possible HIF-1α activation in the model at any time point. All other cells were taken to be cells with low or no activation. Other threshold values were tested as well and provided consistent results.
Data availability
All raw data are included in the article. Experimental arrays are in hdf5 format and can be read using CellTK (https://github.com/sjeknic/CellTK). Images are available upon request. Reporter plasmid is available through Addgene.
Supporting information
This article contains supporting information (26, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 50, 51, 53, 67, 104, 107, 108, 109, 110)
Conflict of interest
The authors declare that they have no conflicts of interest with the contents of this article.
Acknowledgments
The authors thank members of the Covert lab for insightful discussions, advice, and feedback. The authors also thank Keara Lane for experimental guidance and Aditya Mukund for many helpful discussions about information theory. Some of the computing for this project was performed on the Sherlock cluster. We thank Stanford University and the Stanford Research Computing Center for providing computational resources.
Author contributions
S. J., T. K., and M. W. C. conceptualization; S. J. and T. K. methodology; S. J. software; S. J. and J. J. S. investigation; S. J. writing–original draft; T. K. and M. W. C. writing–review & editing; M. W. C. supervision; M. W. C. funding acquisition.
Funding and additional information
The authors gratefully acknowledge funding from several sources, including an Allen Discovery Center Award and an Allen Distinguished Investigator Award to M. W. C., and funding from the NIGMS, National Institutes of Health (NIH) Training Grant in Biotechnology (5T32GM008412) awarded to S. J. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Reviewed by members of the JBC Editorial Board. Edited by Donita Brady
Footnotes
Present addresses for: Takamasa Kudo, Genentech, South San Francisco, California, USA; Joanna J. Song, Morsani College of Medicine, University of South Florida, Tampa, Florida, USA.
Supporting information
References
- 1.O'Neill L.A.J., Kishton R.J., Rathmell J. A guide to immunometabolism for immunologists. Nat. Rev. Immunol. 2016;16:553–565. doi: 10.1038/nri.2016.70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Phan A.T., Goldrath A.W., Glass C.K. Metabolic and epigenetic coordination of T cell and macrophage immunity. Immunity. 2017;46:714–729. doi: 10.1016/j.immuni.2017.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Buck M.D., Sowell R.T., Kaech S.M., Pearce E.L. Metabolic instruction of immunity. Cell. 2017;169:570–586. doi: 10.1016/j.cell.2017.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gordon S., Taylor P.R. Monocyte and macrophage heterogeneity. Nat. Rev. Immunol. 2005;5:953–964. doi: 10.1038/nri1733. [DOI] [PubMed] [Google Scholar]
- 5.Mosser D.M., Edwards J.P. Exploring the full spectrum of macrophage activation. Nat. Rev. Immunol. 2008;8:958–969. doi: 10.1038/nri2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Murray P.J., Wynn T.A. Protective and pathogenic functions of macrophage subsets. Nat. Rev. Immunol. 2011;11:723–737. doi: 10.1038/nri3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xue J., Schmidt S.V., Sander J., Draffehn A., Krebs W., Quester I., et al. Transcriptome-based network analysis reveals a spectrum model of human macrophage activation. Immunity. 2014;40:274–288. doi: 10.1016/j.immuni.2014.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Galván-Peña S., O'Neill L.A.J. Metabolic reprograming in macrophage polarization. Front. Immunol. 2014;5:420. doi: 10.3389/fimmu.2014.00420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jha A.K., Huang S.C.C., Sergushichev A., Lampropoulou V., Ivanova Y., Loginicheva E., et al. Network integration of parallel metabolic and transcriptional data reveals metabolic modules that regulate macrophage polarization. Immunity. 2015;42:419–430. doi: 10.1016/j.immuni.2015.02.005. [DOI] [PubMed] [Google Scholar]
- 10.Viola A., Munari F., Sánchez-Rodríguez R., Scolaro T., Castegna A. The metabolic signature of macrophage responses. Front. Immunol. 2019;10:1–16. doi: 10.3389/fimmu.2019.01462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tannahill G.M., Curtis A.M., Adamik J., Palsson-McDermott E.M., McGettrick A.F., Goel G., et al. Succinate is an inflammatory signal that induces IL-1β through HIF-1α. Nature. 2013;496:238–242. doi: 10.1038/nature11986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vats D., Mukundan L., Odegaard J.I., Zhang L., Smith K.L., Morel C.R., et al. Oxidative metabolism and PGC-1β attenuate macrophage-mediated inflammation. Cell Metab. 2006;4:13–24. doi: 10.1016/j.cmet.2006.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang S.C.C., Everts B., Ivanova Y., O'Sullivan D., Nascimento M., Smith A.M., et al. Cell-intrinsic lysosomal lipolysis is essential for alternative activation of macrophages. Nat. Immunol. 2014;15:846–855. doi: 10.1038/ni.2956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Palazon A., Goldrath A.W., Nizet V., Johnson R.S. HIF transcription factors, inflammation, and immunity. Immunity. 2014;41:518–528. doi: 10.1016/j.immuni.2014.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Peyssonnaux C., Datta V., Cramer T., Doedens A., Theodorakis E.A., Gallo R.L., et al. HIF-1α expression regulates the bactericidal capacity of phagocytes. J. Clin. Invest. 2005;115:1806–1815. doi: 10.1172/JCI23865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cramer T., Yamanishi Y., Clausen B.E., Förster I., Pawlinski R., Mackman N., et al. HIF-1α is essential for myeloid cell-mediated inflammation. Cell. 2003;112:645–657. doi: 10.1016/s0092-8674(03)00154-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheng S.C., Quintin J., Cramer R.A., Shepardson K.M., Saeed S., Kumar V., et al. mTOR- and HIF-1α–mediated aerobic glycolysis as metabolic basis for trained immunity. Science. 2014;345:1250684. doi: 10.1126/science.1250684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ni J., Wang X., Stojanovic A., Zhang Q., Wincher M., Bühler L., et al. Single-cell RNA sequencing of tumor-infiltrating NK cells reveals that inhibition of transcription factor HIF-1α unleashes NK cell activity. Immunity. 2020;52:1075–1087.e8. doi: 10.1016/j.immuni.2020.05.001. [DOI] [PubMed] [Google Scholar]
- 19.Semenza G.L. Signal transduction to hypoxia-inducible factor 1. Biochem. Pharmacol. 2002;64:993–998. doi: 10.1016/s0006-2952(02)01168-1. [DOI] [PubMed] [Google Scholar]
- 20.Semenza G.L. Targeting HIF-1 for cancer therapy. Nat. Rev. Cancer. 2003;3:721–732. doi: 10.1038/nrc1187. [DOI] [PubMed] [Google Scholar]
- 21.Gonzalez F.J., Xie C., Jiang C. The role of hypoxia-inducible factors in metabolic diseases. Nat. Rev. Endocrinol. 2019;15:21–32. doi: 10.1038/s41574-018-0096-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yu B., Wang X., Song Y., Xie G., Jiao S., Shi L., et al. The role of hypoxia-inducible factors in cardiovascular diseases. Pharmacol. Ther. 2022;238:108186. doi: 10.1016/j.pharmthera.2022.108186. [DOI] [PubMed] [Google Scholar]
- 23.Jeknić S., Kudo T., Covert M.W. Techniques for studying decoding of single cell dynamics. Front. Immunol. 2019;10:1–12. doi: 10.3389/fimmu.2019.00755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Purvis J.E., Lahav G. Encoding and decoding cellular information through signaling dynamics. Cell. 2013;152:945–956. doi: 10.1016/j.cell.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vance R.E., Isberg R.R., Portnoy D.A. Patterns of pathogenesis: discrimination of pathogenic and nonpathogenic microbes by the innate immune system. Cell Host Microbe. 2009;6:10–21. doi: 10.1016/j.chom.2009.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bagnall J., Leedale J., Taylor S.E., Spiller D.G., White M.R., Sharkey K.J., et al. Tight control of hypoxia-inducible factor-α transient dynamics is essential for cell survival in hypoxia. J. Biol. Chem. 2014;289:5549–5564. doi: 10.1074/jbc.M113.500405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moroz E., Carlin S., Dyomina K., Burke S., Thaler H.T., Blasberg R., et al. Real-time imaging of HIF-1α stabilization and degradation. PLoS One. 2009;4:e5077. doi: 10.1371/journal.pone.0005077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fábián Z., Taylor C.T., Nguyen L.K. Understanding complexity in the HIF signaling pathway using systems biology and mathematical modeling. J. Mol. Med. 2016;94:377–390. doi: 10.1007/s00109-016-1383-6. [DOI] [PubMed] [Google Scholar]
- 29.Nguyen L.K., Cavadas M.A.S., Scholz C.C., Fitzpatrick S.F., Bruning U., Cummins E.P., et al. A dynamic model of the hypoxia-inducible factor 1-alpha (HIF-1α) network. J. Cell Sci. 2013;128:1454–1463. doi: 10.1242/jcs.119974. [DOI] [PubMed] [Google Scholar]
- 30.Kudo T., Zhao M.L., Kovary K., LaGory E.L., Covert M.W., Teruel M.N. A dynamic HIF1α-PPARγ circuit controls a paradoxical adipocyte regulatory landscape. bioRxiv. 2022 doi: 10.1101/2022.05.17.492374. [preprint] [DOI] [Google Scholar]
- 31.Kaelin W.G., Ratcliffe P.J. Oxygen sensing by metazoans: the central role of the HIF hydroxylase pathway. Mol. Cell. 2008;30:393–402. doi: 10.1016/j.molcel.2008.04.009. [DOI] [PubMed] [Google Scholar]
- 32.Ivan M., Kondo K., Yang H., Kim W., Valiando J., Ohh M., et al. HIFα targeted for VHL-mediated destruction by proline hydroxylation: implications for O2 sensing. Science. 2001;292:464–468. doi: 10.1126/science.1059817. [DOI] [PubMed] [Google Scholar]
- 33.Bruick R.K., McKnight S.L. A conserved family of prolyl-4-hydroxylases that modify HIF. Science. 2001;294:1337–1340. doi: 10.1126/science.1066373. [DOI] [PubMed] [Google Scholar]
- 34.Jaakkola P., Mole D.R., Tian Y.M., Wilson M.I., Gielbert J., Gaskell S.J., et al. Targeting of HIF-alpha to the von Hippel-Lindau ubiquitylation complex by O2-regulated prolyl hydroxylation. Science. 2001;292:468–472. doi: 10.1126/science.1059796. [DOI] [PubMed] [Google Scholar]
- 35.Cuny A.P., Schlottmann F.P., Ewald J.C., Pelet S., Schmoller K.M. Live cell microscopy: from image to insight. Biophys. Rev. 2022;3 doi: 10.1063/5.0082799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bagnall J., Boddington C., Boyd J., Brignall R., Rowe W., Jones N.A., et al. Quantitative dynamic imaging of immune cell signalling using lentiviral gene transfer. Integr. Biol. (Camb.) 2015;7:713–725. doi: 10.1039/c5ib00067j. [DOI] [PubMed] [Google Scholar]
- 37.Dorsch-Häsler K., Keil G.M., Weber F., Jasin M., Schaffner W., Koszinowski U.H. A long and complex enhancer activates transcription of the gene coding for the highly abundant immediate early mRNA in murine cytomegalovirus. Proc. Natl. Acad. Sci. U. S. A. 1985;82:8325–8329. doi: 10.1073/pnas.82.24.8325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Addison C.L., Hitt M., Kunsken D., Graham F.L. Comparison of the human versus murine cytomegalovirus immediate early gene promoters for transgene expression by adenoviral vectors. J. Gen. Virol. 1997;78:1653–1660. doi: 10.1099/0022-1317-78-7-1653. [DOI] [PubMed] [Google Scholar]
- 39.Shaner N.C., Lambert G.G., Chammas A., Ni Y., Cranfill P.J., Baird M.A., et al. A bright monomeric green fluorescent protein derived from Branchiostoma lanceolatum. Nat. Methods. 2013;10:407–409. doi: 10.1038/nmeth.2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lo C.A., Kays I., Emran F., Lin T.J., Cvetkovska V., Chen B.E. Quantification of protein levels in single living cells. Cell Rep. 2015;13:2634–2644. doi: 10.1016/j.celrep.2015.11.048. [DOI] [PubMed] [Google Scholar]
- 41.Kim J.H., Lee S.R., Li L.H., Park H.J., Park J.H., Lee K.Y., et al. High cleavage efficiency of a 2A peptide derived from porcine Teschovirus-1 in human cell lines, zebrafish and mice. PLoS One. 2011;6 doi: 10.1371/journal.pone.0018556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cranfill P.J., Sell B.R., Baird M.A., Allen J.R., Lavagnino Z., De Gruiter H.M., et al. Quantitative assessment of fluorescent proteins. Nat. Methods. 2016;13:557–562. doi: 10.1038/nmeth.3891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Erbel P.J.A., Card P.B., Karakuzu O., Bruick R.K., Gardner K.H. Structural basis for PAS domain heterodimerization in the basic helix-loop-helix-PAS transcription factor hypoxia-inducible factor. Proc. Natl. Acad. Sci. U. S. A. 2003;100:15504–15509. doi: 10.1073/pnas.2533374100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Freedman S.J., Sun Z.Y.J., Kung A.L., France D.S., Wagner G., Eck M.J. Structural basis for negative regulation of hypoxia-inducible factor-1α by CITED2. Nat. Struct. Biol. 2003;10:504–512. doi: 10.1038/nsb936. [DOI] [PubMed] [Google Scholar]
- 45.Lindström I., Andersson E., Dogan J. The transition state structure for binding between TAZ1 of CBP and the disordered Hif-1α CAD. Sci. Rep. 2018;8:7872. doi: 10.1038/s41598-018-26213-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wu D., Potluri N., Lu J., Kim Y., Rastinejad F. Structural integration in hypoxia-inducible factors. Nature. 2015;524:303–308. doi: 10.1038/nature14883. [DOI] [PubMed] [Google Scholar]
- 47.Thomas J.D., Dias L.M., Johannes G.J. Translational repression during chronic hypoxia is dependent on glucose levels. RNA. 2008;14:771–781. doi: 10.1261/rna.857308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Stein I., Itin A., Einat P., Skaliter R., Grossman Z., Keshet E. Translation of vascular endothelial growth factor mRNA by internal ribosome entry: implications for translation under hypoxia. Mol. Cell. Biol. 1998;18:3112–3119. doi: 10.1128/mcb.18.6.3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tinton S.A., Buc-Calderon P.M. Hypoxia increases the association of 4E- binding protein 1 with the initiation factor 4E in isolated rat hepatocytes. FEBS Lett. 1999;446:55–59. doi: 10.1016/s0014-5793(99)00185-4. [DOI] [PubMed] [Google Scholar]
- 50.Lang K.J.D., Kappel A., Goodall G.J. Hypoxia-inducible factor-1α mRNA contains an internal ribosome entry site that allows efficient translation during normoxia and hypoxia. Mol. Biol. Cell. 2002;13:1792–1801. doi: 10.1091/mbc.02-02-0017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cheong R., Rhee A., Wang C.J., Nemenman I., Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science. 2011;334:354–358. doi: 10.1126/science.1204553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Selimkhanov J., Taylor B., Yao J., Pilko A., Albeck J., Hoffmann A., et al. Accurate information transmission through dynamic biochemical signaling networks. Science. 2014;346:1370–1373. doi: 10.1126/science.1254933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Suderman R., Bachman J.A., Smith A., Sorger P.K., Deeds E.J. Fundamental trade-offs between information flow in single cells and cellular populations. Proc. Natl. Acad. Sci. U. S. A. 2017;114:5755–5760. doi: 10.1073/pnas.1615660114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Keshelava A., Solis G.P., Hersch M., Koval A., Kryuchkov M., Bergmann S., et al. High capacity in G protein-coupled receptor signaling. Nat. Commun. 2018;9:876. doi: 10.1038/s41467-018-02868-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wada T., Hironaka K.-I., Wataya M., Fujii M., Eto M., Uda S., et al. Single-cell information analysis reveals that skeletal muscles incorporate cell-to-cell variability as information not noise. Cell Rep. 2020;32:108051. doi: 10.1016/j.celrep.2020.108051. [DOI] [PubMed] [Google Scholar]
- 56.Zhang Q., Gupta S., Schipper D.L., Kowalczyk G.J., Mancini A.E., Faeder J.R., et al. NF-κB dynamics discriminate between TNF doses in single cells. Cell Syst. 2017;5:638–645.e5. doi: 10.1016/j.cels.2017.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tkačik G., Callan C.G., Bialek W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. U. S. A. 2008;105:12265–12270. doi: 10.1073/pnas.0806077105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lestas I., Vinnicombe G., Paulsson J. Fundamental limits on the suppression of molecular fluctuations. Nature. 2010;467:174–178. doi: 10.1038/nature09333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lenaerts T., Ferkinghoff-Borg J., Schymkowitz J., Rousseau F. Information theoretical quantification of cooperativity in signalling complexes. BMC Syst. Biol. 2009;3:9. doi: 10.1186/1752-0509-3-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Garner K.L., Voliotis M., Alobaid H., Perrett R.M., Pham T., Tsaneva-Atanasova K., et al. Information transfer via gonadotropin-releasing hormone receptors to ERK and NFAT: sensing GnRH and sensing dynamics. J. Endocr. Soc. 2017;1:260–277. doi: 10.1210/js.2016-1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Granados A.A., Pietsch J.M.J., Cepeda-Humerez S.A., Farquhar I.L., Tkačik G., Swain P.S. Distributed and dynamic intracellular organization of extracellular information. Proc. Natl. Acad. Sci. U. S. A. 2018;115:6088–6093. doi: 10.1073/pnas.1716659115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Voliotis M., Perrett R.M., McWilliams C., McArdle C.A., Bowsher C.G. Information transfer by leaky, heterogeneous, protein kinase signaling systems. Proc. Natl. Acad. Sci. U. S. A. 2014;111:1–22. doi: 10.1073/pnas.1314446111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mehta P., Goyal S., Long T., Bassler B.L., Wingreen N.S. Information processing and signal integration in bacterial quorum sensing. Mol. Syst. Biol. 2009;5:325. doi: 10.1038/msb.2009.79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Uda S., Saito T.H., Kudo T., Kokaji T., Tsuchiya T., Kubota H., et al. Robustness and compensation of information transmission of signaling pathways. Science. 2013;341:558–561. doi: 10.1126/science.1234511. [DOI] [PubMed] [Google Scholar]
- 65.Tang Y., Adelaja A., Ye F.X., Deeds E., Wollman R., Hoffmann A. Quantifying information accumulation encoded in the dynamics of biochemical signaling. Nat. Commun. 2021;12:1272. doi: 10.1038/s41467-021-21562-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Adelaja A., Taylor B., Sheu K.M., Liu Y., Luecke S., Hoffmann A. Six distinct NFκB signaling codons convey discrete information to distinguish stimuli and enable appropriate macrophage responses. Immunity. 2021;54:916–930.e7. doi: 10.1016/j.immuni.2021.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mukund A., Bintu L. Temporal signaling, population control, and information processing through chromatin-mediated gene regulation. J. Theor. Biol. 2022;535:110977. doi: 10.1016/j.jtbi.2021.110977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Swain P.S., Elowitz M.B., Siggia E.D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. U. S. A. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Elowitz M.B., Levine A.J., Siggia E.D., Swain P.S. Stochastic gene expression in a single cell: supporting online material. Science. 2002;297:1183–1187. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 70.Topolewski P., Zakrzewska K.E., Walczak J., Nienałtowski K., Müller-Newen G., Singh A., et al. Phenotypic variability, not noise, accounts for most of the cell-to-cell heterogeneity in IFN-γ and oncostatin M signaling responses. Sci. Signal. 2022;15:1–10. doi: 10.1126/scisignal.abd9303. [DOI] [PubMed] [Google Scholar]
- 71.Strasen J., Sarma U., Jentsch M., Bohn S., Sheng C., Horbelt D., et al. Cell-specific responses to the cytokine TGFβ are determined by variability in protein levels. Mol. Syst. Biol. 2018;14 doi: 10.15252/msb.20177733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kramer B.A., Sarabia J., Pelkmans L. Multimodal perception links cellular state to decision making in single cells. Science. 2022;4062:1–11. doi: 10.1126/science.abf4062. [DOI] [PubMed] [Google Scholar]
- 73.Nienałtowski K., Rigby R.E., Walczak J., Zakrzewska K.E., Głów E., Rehwinkel J., et al. Fractional response analysis reveals logarithmic cytokine responses in cellular populations. Nat. Commun. 2021;12:4175. doi: 10.1038/s41467-021-24449-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bocharov G., Jäger W., Knoch J., Neuss-Radu M., Thiel M. A mathematical model of HIF-1 regulated cellular energy metabolism. Vietnam J. Math. 2021;49:119–141. [Google Scholar]
- 75.Nazaret C., Heiske M., Thurley K., Mazat J.P. Mitochondrial energetic metabolism: a simplified model of TCA cycle with ATP production. J. Theor. Biol. 2009;258:455–464. doi: 10.1016/j.jtbi.2008.09.037. [DOI] [PubMed] [Google Scholar]
- 76.Luengo A., Li Z., Gui D.Y., Sullivan L.B., Zagorulya M., Do B.T., et al. Increased demand for NAD+ relative to ATP drives aerobic glycolysis. Mol. Cell. 2021;81:691–707.e6. doi: 10.1016/j.molcel.2020.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wang Y., Stancliffe E., Fowle-Grider R., Wang R., Wang C., Schwaiger-Haber M., et al. Saturation of the mitochondrial NADH shuttles drives aerobic glycolysis in proliferating cells. Mol. Cell. 2022;82:3270–3283.e9. doi: 10.1016/j.molcel.2022.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Kellogg R.A., Tay S. Noise facilitates transcriptional control under dynamic inputs. Cell. 2015;160:381–392. doi: 10.1016/j.cell.2015.01.013. [DOI] [PubMed] [Google Scholar]
- 79.Kshitiz, Afzal J., Suhail Y., Chang H., Hubbi M.E., Hamidzadeh A., et al. Lactate-dependent chaperone-mediated autophagy induces oscillatory HIF-1α activity promoting proliferation of hypoxic cells. Cell Syst. 2022;13:1–17. doi: 10.1016/j.cels.2022.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Dayan F., Roux D., Brahimi-Horn M.C., Pouyssegur J., Mazure N.M. The oxygen sensor factor-inhibiting hypoxia-inducible factor-1 controls expression of distinct genes through the bifunctional transcriptional character of hypoxia- inducible factor-1α. Cancer Res. 2006;66:3688–3698. doi: 10.1158/0008-5472.CAN-05-4564. [DOI] [PubMed] [Google Scholar]
- 81.Dayan F., Monticelli M., Pouysségur J., Pécou E. Gene regulation in response to graded hypoxia: the non-redundant roles of the oxygen sensors and FIH in the HIF pathway. J. Theor. Biol. 2009;259:304–316. doi: 10.1016/j.jtbi.2009.03.009. [DOI] [PubMed] [Google Scholar]
- 82.Vanderhaeghen T., Beyaert R., Libert C. Bidirectional crosstalk between hypoxia inducible factors and glucocorticoid signalling in Health and disease. Front. Immunol. 2021;12:1–19. doi: 10.3389/fimmu.2021.684085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.D'Ignazio L., Bandarra D., Rocha S. NF-κB and HIF crosstalk in immune responses. FEBS J. 2016;283:413–424. doi: 10.1111/febs.13578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Peek C.B. Metabolic implications of circadian–HIF crosstalk. Trends Endocrinol. Metab. 2020;31:459–468. doi: 10.1016/j.tem.2020.02.008. [DOI] [PubMed] [Google Scholar]
- 85.Shurin M.R., Umansky V. Cross-talk between HIF and PD-1/PD-L1 pathways in carcinogenesis and therapy. J. Clin. Invest. 2022;132 doi: 10.1172/JCI159473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Ivanov S.V., Salnikow K., Ivanova A.V., Bai L., Lerman M.I. Hypoxic repression of STAT1 and its downstream genes by a pVHL/HIF-1 target DEC1/STRA13. Oncogene. 2007;26:802–812. doi: 10.1038/sj.onc.1209842. [DOI] [PubMed] [Google Scholar]
- 87.Greijer A.E. The role of hypoxia inducible factor 1 (HIF-1) in hypoxia induced apoptosis. J. Clin. Pathol. 2004;57:1009–1014. doi: 10.1136/jcp.2003.015032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Chen D., Li M., Luo J., Gu W. Direct interactions between HIF-1α and Mdm2 modulate p53 function. J. Biol. Chem. 2003;278:13595–13598. doi: 10.1074/jbc.C200694200. [DOI] [PubMed] [Google Scholar]
- 89.Wang F., Zhang S., Jeon R., Vuckovic I., Jiang X., Lerman A., et al. Interferon gamma induces reversible metabolic reprogramming of M1 macrophages to sustain cell viability and pro-inflammatory activity. EBioMedicine. 2018;30:303–316. doi: 10.1016/j.ebiom.2018.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Sukonina V., Ma H., Zhang W., Bartesaghi S., Subhash S., Heglind M., et al. FOXK1 and FOXK2 regulate aerobic glycolysis. Nature. 2019;566:279–283. doi: 10.1038/s41586-019-0900-5. [DOI] [PubMed] [Google Scholar]
- 91.Mills E., O'Neill L.A. Succinate: a metabolic signal in inflammation. Trends Cell Biol. 2014;24:313–320. doi: 10.1016/j.tcb.2013.11.008. [DOI] [PubMed] [Google Scholar]
- 92.Tang K., Yu Y., Zhu L., Xu P., Chen J., Ma J., et al. Hypoxia-reprogrammed tricarboxylic acid cycle promotes the growth of human breast tumorigenic cells. Oncogene. 2019;38:6970–6984. doi: 10.1038/s41388-019-0932-1. [DOI] [PubMed] [Google Scholar]
- 93.Vincent E.E., Sergushichev A., Griss T., Gingras M.C., Samborska B., Ntimbane T., et al. Mitochondrial phosphoenolpyruvate carboxykinase regulates metabolic adaptation and enables glucose-independent tumor growth. Mol. Cell. 2015;60:195–207. doi: 10.1016/j.molcel.2015.08.013. [DOI] [PubMed] [Google Scholar]
- 94.Van den Bossche J., Baardman J., Otto N.A., van der Velden S., Neele A.E., van den Berg S.M., et al. Mitochondrial dysfunction prevents repolarization of inflammatory macrophages. Cell Rep. 2016;17:684–696. doi: 10.1016/j.celrep.2016.09.008. [DOI] [PubMed] [Google Scholar]
- 95.Jantsch J., Chakravortty D., Turza N., Prechtel A.T., Buchholz B., Gerlach R.G., et al. Hypoxia and hypoxia-inducible factor-1α modulate Lipopolysaccharide-induced dendritic cell activation and function. J. Immunol. 2008;180:4697–4705. doi: 10.4049/jimmunol.180.7.4697. [DOI] [PubMed] [Google Scholar]
- 96.Nakamura H., Makino Y., Okamoto K., Poellinger L., Ohnuma K., Morimoto C., et al. TCR engagement increases hypoxia-inducible factor-1α protein synthesis via rapamycin-sensitive pathway under hypoxic conditions in human peripheral T cells. J. Immunol. 2005;174:7592–7599. doi: 10.4049/jimmunol.174.12.7592. [DOI] [PubMed] [Google Scholar]
- 97.Dang E.V., Barbi J., Yang H.Y., Jinasena D., Yu H., Zheng Y., et al. Control of TH17/Treg balance by hypoxia-inducible factor 1. Cell. 2011;146:772–784. doi: 10.1016/j.cell.2011.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Cai Q.L., Knight J.S., Verma S.C., Zald P., Robertson E.S. EC5S ubiquitin complex is recruited by KSHV latent antigen LANA for degradation of the VHL and p53 tumor suppressors. PLoS Pathog. 2006;2:1002–1012. doi: 10.1371/journal.ppat.0020116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Kondo S., Seo S.Y., Yoshizaki T., Wakisaka N., Furukawa M., Joab I., et al. EBV latent membrane protein 1 up-regulates hypoxia-inducible factor 1α through siah1-mediated down-regulation of prolyl hydroxylases 1 and 3 in nasopharyngeal epithelial cells. Cancer Res. 2006;66:9870–9877. doi: 10.1158/0008-5472.CAN-06-1679. [DOI] [PubMed] [Google Scholar]
- 100.Piña-Oviedo S., Khalili K., Del Valle L. Hypoxia inducible factor-1 alpha activation of the JCV promoter: role in the pathogenesis of progressive multifocal leukoencephalopathy. Acta Neuropathol. 2009;118:235–247. doi: 10.1007/s00401-009-0533-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Deshmane S.L., Mukerjee R., Fan S., Del Valle L., Michiels C., Sweet T., et al. Activation of the oxidative stress pathway by HIV-1 vpr leads to induction of hypoxia-inducible factor 1α expression. J. Biol. Chem. 2009;284:11364–11373. doi: 10.1074/jbc.M809266200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Taciak B., Białasek M., Braniewska A., Sas Z., Sawicka P., Kiraga Ł., et al. Evaluation of phenotypic and functional stability of RAW 264.7 cell line through serial passages. PLoS One. 2018;13 doi: 10.1371/journal.pone.0198943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Edelstein A.D., Tsuchida M.A., Amodaj N., Pinkard H., Vale R.D., Stuurman N. Advanced methods of microscope control using μManager software. J. Biol. Methods. 2014;1:e10. doi: 10.14440/jbm.2014.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ronneberger O., Fischer P., Brox T. In: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Volume 9351 of Lecture Notes in Computer Science. Navab N., Hornegger J., Wells W.M., Frangi A.F., editors. Springer International Publishing; Cham: 2015. U-net: convolutional networks for biomedical image segmentation; pp. 234–241. [Google Scholar]
- 105.Ulicna K., Vallardi G., Charras G., Lowe A.R. Automated deep lineage tree analysis using a Bayesian single cell tracking approach. Front. Comput. Sci. 2021;3:1–14. [Google Scholar]
- 106.Virtanen P., Gommers R., Oliphant T.E., Haberland M., Reddy T., Cournapeau D., et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods. 2020;17:261–272. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Cover T.M., Thomas J.A. 2nd Ed. John Wiley & Sons, Inc.; New York, NY: 1991. Elements of Information Theory. [Google Scholar]
- 108.Qin J.Y., Zhang L., Clift K.L., Hulur I., Xiang A.P., Ren B.Z., et al. Systematic comparison of constitutive promoters and the doxycycline-inducible promoter. PLoS One. 2010;5:e10611. doi: 10.1371/journal.pone.0010611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Balleza E., Kim J.M., Cluzel P. Systematic characterization of maturation time of fluorescent proteins in living cells. Nat. Methods. 2018;15:47–51. doi: 10.1038/nmeth.4509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Rechsteiner M., Rogers S.W. PEST sequences and regulation by proteolysis. Trends Biochem. Sci. 1996;21:267–271. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All raw data are included in the article. Experimental arrays are in hdf5 format and can be read using CellTK (https://github.com/sjeknic/CellTK). Images are available upon request. Reporter plasmid is available through Addgene.