Abstract
The purpose of our study was to identify the low-dimensional latent components, defined hereafter as motor unit modes, underlying the discharge rates of the motor units in two knee extensors (vastus medialis and lateralis, eight men) and two hand muscles (first dorsal interossei and thenars, seven men and one woman) during submaximal isometric contractions. Factor analysis identified two independent motor unit modes that captured most of the covariance of the motor unit discharge rates. We found divergent distributions of the motor unit modes for the hand and vastii muscles. On average, 75% of the motor units for the thenar muscles and first dorsal interosseus were strongly correlated with the module for the muscle in which they resided. In contrast, we found a continuous distribution of motor unit modes spanning the two vastii muscle modules. The proportion of the muscle-specific motor unit modes was 60% for vastus medialis and 45% for vastus lateralis. The other motor units were either correlated with both muscle modules (shared inputs) or belonged to the module for the other muscle (15% for vastus lateralis). Moreover, coherence of the discharge rates between motor unit pools was explained by the presence of shared synaptic inputs. In simulations with 480 integrate-and-fire neurons, we demonstrate that factor analysis identifies the motor unit modes with high levels of accuracy. Our results indicate that correlated discharge rates of motor units that comprise motor unit modes arise from at least two independent sources of common input among the motor neurons innervating synergistic muscles.
SIGNIFICANCE STATEMENT It has been suggested that the nervous system controls synergistic muscles by projecting common synaptic inputs to the engaged motor neurons. In our study, we reduced the dimensionality of the output produced by pools of synergistic motor neurons innervating the hand and thigh muscles during isometric contractions. We found two neural modules, each representing a different common input, that were each specific for one of the muscles. In the vastii muscles, we found a continuous distribution of motor unit modes spanning the two synergistic muscles. Some of the motor units from the homonymous vastii muscle were controlled by the dominant neural module of the other synergistic muscle. In contrast, we found two distinct neural modules for the hand muscles.
Keywords: common synaptic input, motor neurons, motor unit, muscle synergies
Introduction
The motor unit, which comprises a motor neuron and the muscle fibers it innervates, is the final common pathway of the neuromuscular system. The motor neuron integrates an extensive array of synaptic inputs and produces an activation signal that is transmitted to muscle fibers (Duchateau and Enoka, 2011). All voluntary actions are accomplished by varying the amount of motor unit activity. Despite claims to the contrary (Harrison and Mortensen, 1962; Basmajian, 1963), it is not possible to control the activation of individual motor units independently (Henneman et al., 1976; Bräcklein et al., 2022). Instead, synaptic inputs are distributed broadly among sets of motor neurons, and the motor units that are activated in response to these inputs depend on their relative excitability (Henneman et al., 1965; Henneman and Olson, 1965; Heckman and Enoka, 2012). As a consequence of this organization, the order in which motor units are recruited during a voluntary action is relatively fixed (Milner-Brown et al., 1973; Desmedt and Godaux, 1977, 1978).
It is the shared synaptic inputs received by the motor neurons that are responsible for the force generated by a muscle (Negro et al., 2009; Thompson et al., 2018). These shared inputs can arise from four sources (cortical, brainstem, spinal, and afferent pathways) and have varying distributions across spinal motor nuclei (Phillips and Porter, 1964; https://onlinelibrary.wiley.com/doi/10.1002/cphy.cp010211; Heckman and Enoka, 2012; Ferreira-Pinto et al., 2018). One advantage of this scheme is that the shared inputs can engage several motor nuclei concurrently and thereby facilitate control of the net muscle torque.
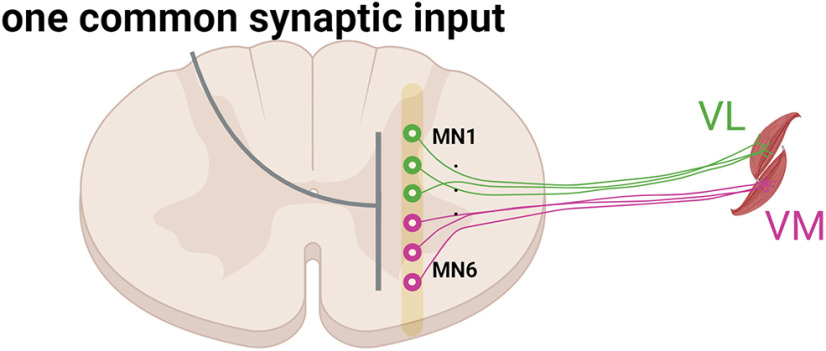
It has been hypothesized that the control of multiple muscles is achieved by the activation of sets of motor neurons that have been referred to as neural modules, motor primitives, or common synaptic inputs (Ivanenko et al., 2004; d'Avella et al., 2006; Lacquaniti et al., 2012; Laine et al., 2015; Santello et al., 2016; Alessandro et al., 2020; Madarshahian et al., 2021; Fig. 1). The modularity of neural control in humans has been estimated by measuring the covariation in muscle activation patterns (EMG signals). The modules extracted by factorization analysis have been termed muscle synergies (d'Avella et al., 2003; Tresch et al., 2006) and are assumed to reflect, albeit indirectly, the synaptic inputs that are common to all the motor neurons contributing to each muscle synergy (Ivanenko et al., 2004; Tresch et al., 2006; d'Avella et al., 2006; Muceli et al., 2010; Laine et al., 2015; Alessandro et al., 2020).
Figure 1.
Classic view of the common synaptic input to motor neurons. Motor neurons in an individual motor nucleus or in synergistic nuclei receive a dominant common synaptic input (gray line). The neural coupling between VL and VM has been performed either by low-pass filtering (<20 Hz) the electromyographic signals from VL and VM and then using a factorization algorithm or by performing the coherence or time-domain correlation analysis between the motor unit spike trains from these two muscles. Both methods identify one main component that explains most of the variance during both isometric and dynamic tasks.
The synaptic inputs shared by motor neurons can be examined more directly by measuring the covariation in the rates at which motor units discharge action potentials. The identified patterns are referred to as motor unit modes (Madarshahian et al., 2021) and neural modules (which refer to the principal component identified by factorization analyses). This can be accomplished by investigating pairwise spike-train correlations of the activated motor units (Schneidman et al., 2006; Shlens et al., 2006; de la Rocha et al., 2007). The purpose of our study was to identify the motor unit modes underlying the discharge rates of the motor units from two knee extensors, vastus medialis (VM) and vastus lateralis (VL) and two hand muscles (index and thumb muscles) during submaximal isometric contractions. We hypothesized that the discharge rates of the motor neurons innervating each muscle would be explained by more than one motor unit mode.
We found that the discharge rates of motor units in individual quadriceps and hand muscles comprised two independent motor unit modes that were specific for each muscle in the synergistic pair. The discharge rates of most motor units were associated with the neural module for the muscle in which they resided, but others were correlated with either the neural module for the synergistic muscle or both motor unit modes. We then simulated the delivery of two independent common synaptic currents into integrate-and-fire motor neurons to validate our approach. Our findings provide a greater level of detail about the distribution of common synaptic input within and across the motor nuclei that innervate synergistic muscles. Moreover, they indicate that the modular (synergistic) organization of movement is not at the muscle level but rather at the motor unit level, and these two levels do not overlap.
Materials and Methods
Participants
Eight subjects were recruited for each experiment (hand and knee extensor muscles). All procedures were approved by the local ethical committees at the University of Rome Foro Italico (approval number 44 680, knee extension experiments) and Imperial College London (approval number 18IC4685, hand experiments) and conformed to the standards set by the Declaration of Helsinki. The subjects provided informed consent before participating in the study. Some of these data have been published previously (Del Vecchio et al., 2019; Nuccio et al., 2021).
As described subsequently, high-density EMG recordings (Quattrocento, OT Bioelettronica) were decomposed (Del Vecchio et al., 2020a) from the signals measured in both experiments.
Experiment 1 (knee extensors)
Eight participants (27.6 ± 2.4 year, all men) visited the laboratory on two occasions. In the first visit, they were familiarized with the experimental procedures by performing a series of maximal and submaximal isometric contractions with the knee extensors. In the second visit, which occurred 24 h after the familiarization session, simultaneous recordings of the force applied by the knee extensors during maximal and submaximal voluntary contractions and high-density surface electromyography (HDsEMG) signals were recorded from vastus lateralis and vastus medialis.
After standardized warm-up contractions, participants were verbally encouraged to push as hard as possible for ∼3–5 s to achieve peak maximal voluntary contraction (MVC) force. They performed fewer than four or four trials with ∼60 s of rest between trials. About 5 min later, they performed steady contractions (2× at 10% MVC for 70 s) and submaximal trapezoidal contractions at three target forces (2× each at 35, 50, and 70% MVC force). The trapezoidal contractions required participants to match a prescribed trajectory that comprised a ramp-up phase (5% MVC s-1), a plateau (10 s of constant force at target), and a ramp-down phase (−5% MVC/s). Three minutes of rest was provided between all submaximal contractions. We only used the steady contractions at 10% of maximum in the current report.
All measurements were taken with each leg in a random order. Participants were asked to avoid exercise and caffeine intake for 48 h before testing. Participants were comfortably seated and secured in a Kin-Com dynamometer by means of three Velcro straps (thigh, chest, pelvis), with the knee joint fixed at 45° of flexion (full knee extension = 0°). HDsEMG signals were acquired from the vastii muscles with two grids of 64 electrodes each (5 columns × 13 rows, gold coated, 1 mm diameter, 8 mm interelectrode distance, OT Bioelettronica; Fig. 1A).
Placement of the electrode grids was based on existing guidelines (Barbero et al., 2012) and adjusted as necessary. After shaving and cleaning the skin (70% ethanol), both electrode grids were attached over the muscles using two layers of disposable double-sided foam (SpesMedica). Skin-electrode contact was ensured by filling the holes of the foam layer with conductive paste (SpesMedica). A ground electrode was placed on the contralateral wrist, whereas the reference electrodes for both vastus lateralis and vastus medialis grids were attached to the skin over the ipsilateral patella and medial malleolus, respectively. Monopolar HDsEMG signals were recorded using a multichannel amplifier (EMG, Quattrocento; A/D converted to 16 bits, bandwidth 10–500 Hz) at a sampling rate of 2048 Hz.
Experiment 2 (hand muscles)
The experimental setup involved a chair, table, and computer monitor. Participants (eight men and one woman, 26 ± 2 years) were comfortably seated with both arms resting on the table. A custom-made apparatus was secured to the table to support the dominant hand (self-reported) with the forearm midway between pronation and supination and both the forearm and wrist immobilized. The index finger was aligned with the longitudinal axis of the forearm, and the thumb was held in a resting position at the same height as the index finger. The applied force was displayed on a monitor that was positioned 60 cm in front of the subject. The visual gain was fixed at 66 pixels per percentages of MVC force for each muscle (axis).
The forces exerted by the index finger and thumb were measured with a three-axis force transducer (Nano25, ATI Industrial Automation), digitized at 2048 Hz (USB-6225, National Instruments), and low-pass filtered with a cutoff frequency of 15 Hz. HDsEMG signals were recorded with a multichannel amplifier (Quattrocento, OT Bioelettronica; A/D converted to 16 bits, bandwidth 10–500 Hz) at a sampling rate of 2048 Hz. Two flexible grids of high-density EMG electrodes (13 × 5 pins, 4 mm interelectrode spacing) were placed on the skin over the first dorsal interosseous (FDI) and thenar muscles (flexor pollicis brevis and abductor pollicis brevis).
Participants performed force-matching tasks (10% MVC force) involving concurrent abduction of the index finger and flexion of the thumb for 60 s (see Fig. 3). Visual feedback was provided as a moving dot cursor in which the x-axis and y-axis corresponded to the thumb and index finger forces, respectively. Subjects were required to maintain the force signal within 10% of the target for each applied force.
Figure 3.
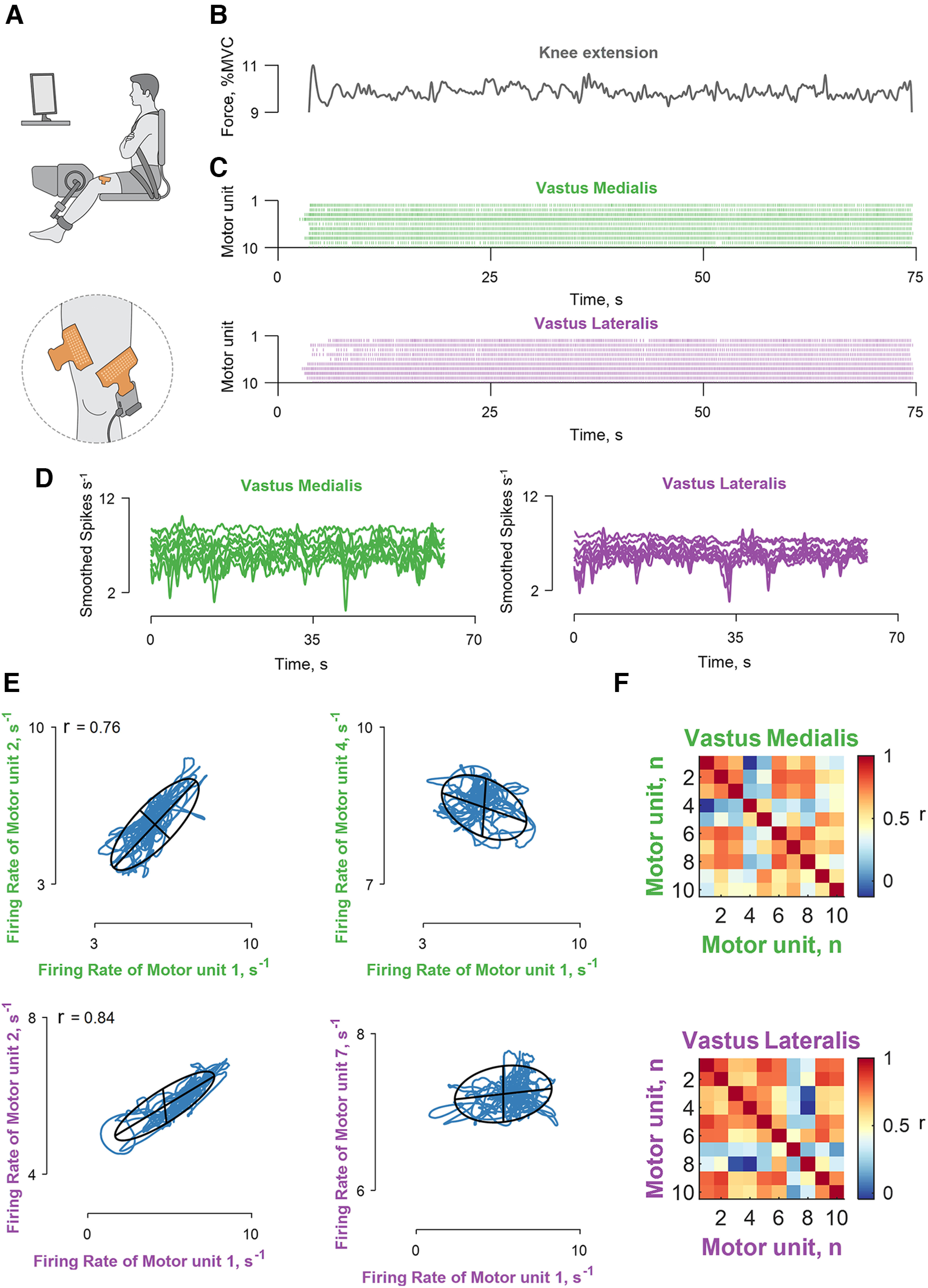
Recordings of muscle force and correlation analysis of motor unit discharge times. A, Experimental setup included high-density EMG grids over the vastus lateralis and medialis muscles during isometric contractions at 10% MVC force. B, The applied force. C, The decomposed motor unit discharge times represented in a raster plot for the vastus lateralis (violet) and medialis (green) muscles. D, The motor unit discharge times (series of 0s and 1s) were convolved with a 400 ms Hann window to yield discharge rates (spikes s−1), which retained the motor unit oscillations responsible for the fluctuations in force during steady contractions. E, Four bivariate correlations (correlation strength, r) between different motor units belonging to the same muscle module (the labels are color coded as indicated in C, D). The blue lines indicate the smoothed discharge rates during the steady contraction. F, Matrix color map of the correlation strength (r) between all the identified motor units for the two muscles. Note that the discharge rates within each muscle module exhibited a range of correlation values. The Pearson's p value was <0.0001 for the reported r values.
The experiments began with MVCs (as described in experiment 1). Subsequently, the required target forces were displayed on a monitor, and participants performed two 60 s trials with 30 s of rest between trials. As noted in the introduction, we designed our tasks to determine the extent to which sets of motor neurons receive common synaptic inputs. To achieve this goal, subjects were instructed to exert forces in the same sagittal plane with the two sets of muscles, which required ∼10 min of practice.
Data Analysis
HDsEMG decomposition
The 64 monopolar HDsEMG signals were filtered off-line with a zero-lag, high-pass (10 Hz) and low-pass filter (500 Hz). The force signals were corrected for the influence of gravity and normalized to MVC force. HDsEMG channels with poor signal-to-noise ratios were inspected with a semiautomated function that identified spurious EMG signals based on the power spectrum. Those channels with a poor signal-to-noise ratio (defined as 3 SDs from the mean of the power spectrum averaged across all signals in the band 10–500 Hz) were visually inspected and removed from the analysis. The number of EMG channels containing noise was low; >95% of the channels had acceptable signal-to-noise ratios.
Subsequently, the HDsEMG signals were decomposed with a gradient convolution kernel compensation algorithm (Holobar and Zazula, 2007). The general decomposition procedures have been described previously (Farina and Holobar, 2016). Briefly, the decomposed signals can be described as a time series of Dirac delta functions that contain the sources (s) representing the discharge times of motor units, which can be described as delta functions as follows:
| (1) |
where corresponds to the spike times of the jth motor unit. Each channel of the HDsEMG signal can then be described as the convolution of the motor unit discharge times (s) into the muscle fiber action potentials. Because each motor unit innervates multiple muscle fibers, we detect a compound action potential from the muscle fibers innervated by the same motor axon. Therefore, the HDsEMG recordings can be described mathematically in a matrix x form as follows:
| (2) |
where (k) = [s1 (k), s2 (k), …, sn (k)]T represents the n motor unit discharge times derived from the HDsEMG signal (10) and n is the noise to for each electrode. The matrix H contains the two-dimensional information of the motor unit action potential and has size m × l with lth sample of motor unit action potentials for the n motor units and m channels.
Before beginning the blind-source separation procedure, the spatial sparsity of the matrix x was enhanced by extending the observed numbers. This procedure improves the decomposition as the gradient descent update rule maximizes the diversity of the motor unit waveform to converge on the discharge times of each motor unit (the sources, s). The shapes of the motor unit action potentials obtained by spike-triggered averaging are then inspected as 2D and 3D waveforms (Vecchio and Farina, 2019; Del Vecchio et al., 2020b).
Factorization analysis
Once the discharge times of the motor units are known, it is possible to predict modulation of muscle force with near perfect correlations (Partridge, 1965; Baldissera et al., 1998). By recording large samples of motor units, the modulation of muscle force can be reconstructed (Negro et al., 2009) because of the low-pass filtering properties of the muscle to a given neural drive (Baldissera et al., 1998; Del Vecchio et al., 2018). When motor unit discharge rates are filtered in the low-frequency range (muscle bandwidth <20 Hz), it is possible to predict oscillations in the applied force close to ∼1% MVC (Del Vecchio et al., 2018). Consequently, the factorization analysis used in the current study focused on the low-pass-filtered motor unit discharge rates. The discharge rates were filtered by convolving with a Hann window of 400 ms (2.5 Hz). Because of late recruitment of motor units, we only analyzed the last 50 s segment of the smoothed discharge rate at the steady contraction. The motor unit discharge times were characterized with three methods, factorization analysis (Jöreskog, 1967; Maxwell and Harman, 1967), principal component analysis, and non-negative matrix factorization.
These factorization methods were applied to the matrix containing the smoothed discharge rates with rows equal to the number of motor units identified for both muscles and columns equal to the smoothed discharge rates. Factorization analysis is based on the rationale that the activated motor units can be represented as time sequences of M dimensional vectors (Eq. 3) in response to various common and independent synaptic inputs delivered to the motor neurons m(t). The response of the motor neuron population, therefore, can be described as combinations of N varying synaptic inputs that are constrained by the nonlinear properties of the motor neuron to produce a motor unit mode, expressed as as follows:
| (3) |
where is a non-negative scaling coefficient of the ith motor unit mode. We were interested in finding the matrix without making any assumptions about the associations between muscles or motor neurons. We found that factor analysis resulted in the strongest correlations between the motor unit modes and the discharge rates of individual motor units. Moreover, we demonstrate with an integrate-and-fire model (see below) that factor analysis can separate the motor unit modes with high levels of accuracy. We also examined the performance of non-negative matrix factorization and principal component analysis by using previous approaches to identify muscle synergies (i.e., >100 iterations and reconstruction of the original signal; D'Avella et al., 2003; Ivanenko et al., 2004; Tresch et al., 2006).
Factor analysis models the associations between variables into a lesser number of latent variables (factors). It assumes that for a collection of observed variables () there are a set factors (f) that explain most of the total variance, which is the common variance. The function factoran in MATLAB computes the maximum likelihood estimate of the factor loadings matrix () as follows:
| (4) |
where is the vector of independent factors. Alternatively, the model can be specified as follows:
| (5) |
where is the common variance matrix, and is the diagonal matrix of specific variances.
The unique variance in the model with no a priori assumption of orthogonality between factors (when allowing for factor rotations, such as promax) makes the factor analysis an appropriate choice to extract the latent discharge rate of synergistic motor nuclei. It is supposed that the model mimics the common () and independent () inputs impinging onto the two motor nuclei.
In our current study, we found that two factors explained much of the variance in the pooled motor unit discharge rates (see below, Results). The two motor unit factors (modes) were further characterized based on the strength of the correlation with the motor units in each muscle; we refer to these factors as “muscle modules.” For instance, the VL module is the factor that showed the stronger correlation of the smoothed compound spike trains of vastus lateralis motor units. Note, however, that the VL module could be associated with either of the two motor unit factors (modes) because the association depended on the variance of the motor unit discharge rates during a trial. Trials in which only one muscle module was identified were discarded from analysis (one trial for the hand muscles and two trials for vastii muscles). Not all motor units showed stronger correlation with the homonymous muscle module; the modulation of discharge rate for some motor units was better explained by the other muscle module, whereas some motor units showed a similar correlation with both muscle modules.
We classified the motor units into three groups, based on the correlation values with specific centroids [pdist2 function, x and y coordinates, (0.65 1.00), (0.60 0.60), (1.00 0.65)]. We arbitrarily selected these centroids based on the variability of the motor unit modes with respect to an individual common input observed in the results of the computer simulations. There are two main limitations with our approach. First, the motor unit discharge rates are smoothed with a Hann window of 400 ms, which may cause spurious correlations. For this reason, the duration of the trial is critical in understanding the statistical significance of our results. From the simulations, we found that 50 s of simulated voluntary contractions were sufficient to cluster two unique inputs and a shared input. In contrast, a 10 s trial resulted in many motor unit modes that converged in the common space, presumably because of the filtering effects described above. Second, it is important to understand how well the factor analysis can distinguish the contribution of specific independent inputs. We found that some motor units had correlation values with the neural module within the 0.1–0.3 range for 50 s of simulated data, but this increased to −0.2–0.6 for 10 s of simulated data. Moreover, the results from the hand experiments identified two muscle-specific motor unit modes that had correlation values >0.8 with the muscle-specific neural module and a range of −2 to 0.5 with the other module. Therefore, by selecting boundaries of [0.65 1.00] for motor unit mode 1, [0.60 0.60] for the shared mode, and [1.00 0.65] for the motor unit mode 2, we could estimate the proportion of the motor units in the two clusters for the vastii muscle, where many motor units also had a strong correlation with both modes. Note that the scope of this analysis is not to define the specific clusters of motor unit modes in the vastii muscles, but rather it provides an estimate that was tuned with a computer model and hand motor unit results about the proportions of the motor unit modes in the vastii muscles.
Tracking motor units
To evaluate the reliability of the motor units being assigned to the same motor unit mode, we tracked the motor units in the two trials performed by each subject. The motor units were considered the same if the two-dimensional correlation of the motor unit action potential waveform from all channels (obtained by spike-triggered averaging on the HDsEMG) was above a threshold of 0.86.
Cross talk and realigning
Up to 95% of the action potentials generated by motor units in first dorsal interosseous can be detected in recordings from the thenar muscles (and vice versa) and similarly from the two vastii muscles (Germer et al., 2021). Consequently, we examined the level of such cross talk with a validated method (Del Vecchio et al., 2019; Germer et al., 2021). Briefly, this procedure takes advantage of the distance from the activated muscle fibers (muscle unit) to the electrode, which is less for motor units in a targeted muscle. Motor units from a targeted muscle are expected to show greater action potential amplitudes with minimal shape distortion (Germer et al., 2021 contains a detailed assessment of statistically significant cross talk of individual motor units.).
Also, we aligned motor unit action potentials relative to the average shape of the motor unit action potentials obtained by spike-triggered averaging. Because action potentials show some variability in time because of surface EMG stochasticity, we convoluted the average action potential to retrieve the discharge times of the motor units. Although this procedure is critical when assessing brain-spinal transmission latencies (Ibáñez et al., 2021), it did not influence our results because of the brief corticospinal latencies (<50 ms). In our study, discharge rate was smoothed in the frequency domain for force production (2.5 Hz, 400 ms). The influence of discharge time, therefore, is removed by low-pass filtering at <2.5 Hz.
Computer simulations
We simulated 480 integrate-and-fire motor neurons, each of which received a computer-generated current input (set at 20 nA). The synaptic currents that were shared among all neurons represented the common synaptic input, but the neurons also received some independent synaptic inputs. Because the discharge times of motor neurons can be synchronized, the common input currents were close to maximal values in the low-frequency range of <2.5 Hz (see below). The resting membrane potential and reset voltage was set at −70 mV, the spike threshold was set at −50 mV, and a membrane time constant was 20 ms. The time step duration was set at 0.1 ms.
Our model comprised randomly distributed Gaussian noises at each time step to represent the common and independent synaptic inputs. Two random uncorrelated Gaussian input currents were created at each time step to represent the motor unit modes that were identified experimentally; one-third of the neurons (160 neurons) received Isyn1 as a unique common input, and Isyn2 comprised another common input at the same strength, but orthogonal to Isyn1; Isyn3 was the average of Isyn1 and Isyn2 plus its unique independent noise (see eq. 5). The input current for each neuron i and population j (j = 1,2,3) can be summarized by the following equation:
| (6) |
where µi is the temporal average of the current that was set at 20 nA and σi sets the global network state by taking into account the unique independent inputs for each neuron () and the Gaussian-distributed random common inputs (). The tuning of these parameters was matched to those observed in vivo. The values of , , and were adjusted to reflect physiological values for the variability in motor unit interspike intervals and common input. Interspike interval variability was examined with histogram distributions as found in the current study and by others (Moritz et al., 2005). The common and independent inputs were tuned based on the cross-correlogram function derived from previously reported motor unit data (Negro et al., 2016). Therefore, each combination of three randomly assigned groups of 160 neurons from the total pool (n = 480) received two independent synaptic currents ( equal to Eq. 6), and a third randomized subpopulation (j = 3) of motor neurons received the average of the two inputs as follows:
| (7) |
Simulations were run for 10, 50, and 80 s. We removed the first and last 2 s of spiking activity in all simulations to minimize the influence of spike-frequency adaptation. The spike trains emitted by the Ith neuron after generating the spike times were stored as a binary time series, which was equal to one when the neuron reached voltage threshold. The successive analysis followed the same steps as the experimental data. Briefly, the binary spike trains were low-pass filtered with a 2.5 Hz Hann window, and the factorization analysis was then performed on the low-pass-filtered signals.
Because the distribution of inputs to each neuron was known (i.e., ), it was possible to determine the performance accuracy of the factorization analysis. Moreover, we investigated the relation between motor neuron responses to increased synaptic currents with changes in common and independent inputs.
Statistical analysis
We performed linear regression analysis between the smoothed motor unit discharge rates within and between muscles. The significance level was extracted from bivariate Pearson correlations, and Bonferroni corrections were applied for multiple comparisons. The same procedure was used to find the modules carried by each neuron (decoding function). Each neural module extracted by the factorization algorithm (Jöreskog, 1967; Maxwell and Harman, 1967) was compared with the firing rate of the individual motor units. Significance was accepted for p values < 0.05.
Data availability
The website https://github.com/alecsdelvecchio/neuralmodules contains the data and functions for the extraction of the motor unit modes.
Results
Muscle modules
Our approach involved extending the classic method for muscle synergy analysis (Lee and Seung, 1999; D'Avella et al., 2003; Ivanenko et al., 2004; Tresch et al., 2006; Alessandro et al., 2020; Sylos-Labini et al., 2020) to motor unit recordings. Instead of treating muscles as individual elements, the discharge times of motor units from different muscles were grouped together. We found that the factor analysis was superior to principal component analysis and non-negative matrix factorization (Tresch et al., 2006; Tanzarella et al., 2020, 2021; Ting et al., 2021) in maximizing the correlation between individual motor unit discharge rates and the muscle modules (Fig. 2).
Figure 2.
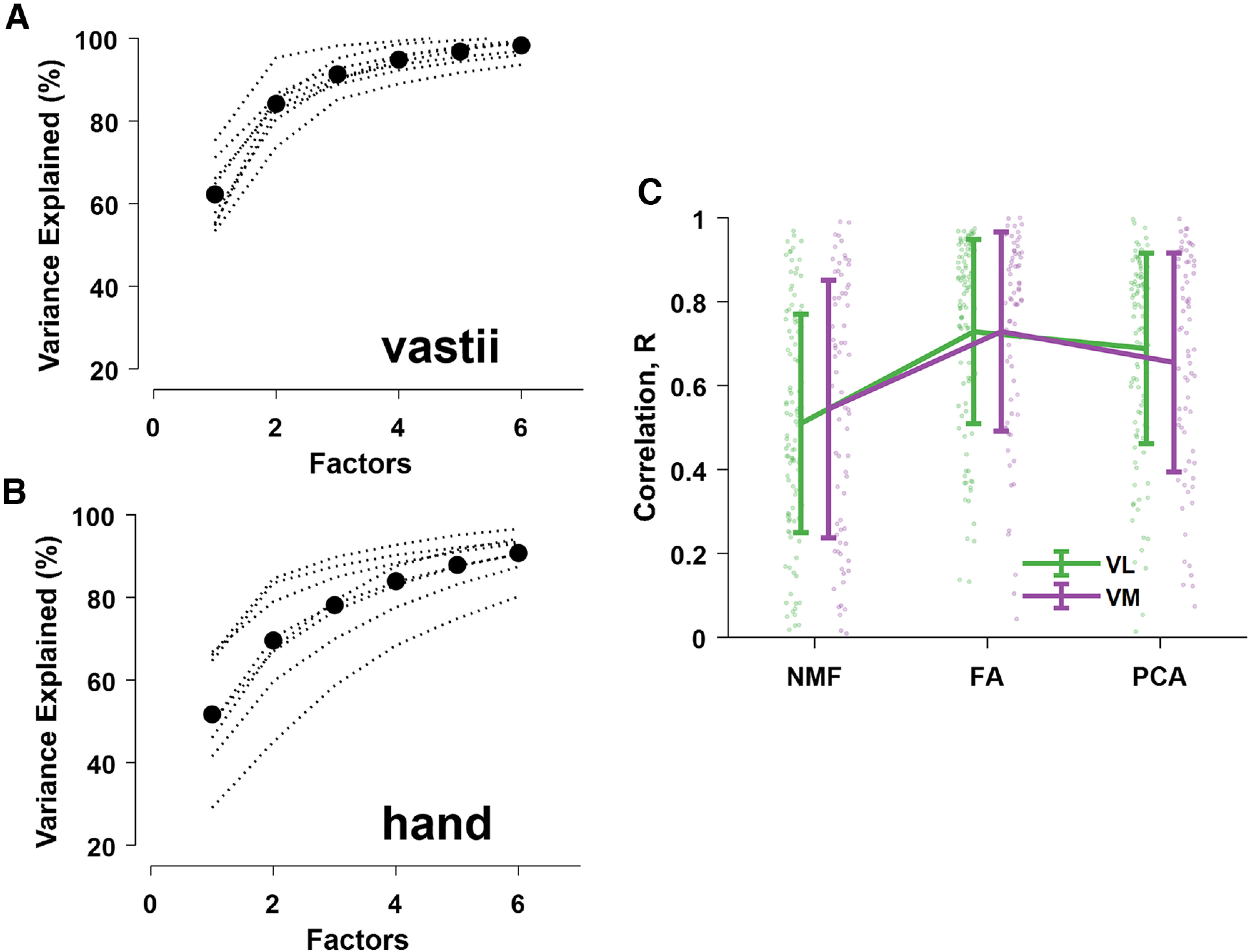
Reconstruction accuracy (percentage of variance explained) for each subject (dotted black lines). A, B, The black dots represent the average motor unit modes across subjects for the vastii and hand muscles. C, The correlation values (mean ± SD) between the muscle modules (VL and VM) and the motor unit discharge rates (dots) as determined by non-negative matrix factorization (NMF), factor analysis (FA), and principal component analysis (PCA).
The experimental setup and correlation analysis for the two vastii muscles is shown in Figure 3. The motor unit discharge times were decomposed with a blind-source separation procedure, which identifies each event with no a priori knowledge on the physiological information conveyed by the individual motor units (Holobar and Zazula, 2007; Farina and Holobar, 2016; Del Vecchio et al., 2020b). We identified an average of 6.9 ± 4.3 and 4.4 ± 2.3 motor units for VL and VM, respectively, across participants during isometric contractions at 10% of MVC force. We subsequently smoothed the motor unit discharge times with a Hann window, which retained all the frequencies responsible for muscle force (<5 Hz; Negro et al., 2009). As the applied force has a cutoff frequency of ≤20 Hz, the low-pass-filtered discharge times (the time series of zeros and ones; Fig. 3C) are strongly correlated with the variance in force during steady contractions (Baldissera et al., 1998; Negro et al., 2009; Del Vecchio et al., 2018; Feeney et al., 2018). Consequently, we focused on finding the latent components (i.e., the motor unit modes) for the low-pass-filtered signals (Fig. 3D).
After converting the discharge times to rates and smoothing the signal, we computed pairwise correlations between each motor unit within the same muscle (Fig. 3E,F). We consistently found correlated and uncorrelated discharge rates of some motor units from the same vastus muscle (muscle module), which indirectly indicates that not all motor neurons in a given nucleus received the same common input (Schneidman et al., 2006; Shlens et al., 2006). Because most previous studies report high correlations among motor units within a motor nucleus (De Luca and Erim, 1994; Farina et al., 2014; Laine et al., 2015), it was necessary to assess the level of cross talk between muscles. We found that the motor units identified in the other muscle had action-potential amplitudes that were statistically similar to those in the homonymous muscle and, therefore, were not the result of cross talk (Del Vecchio et al., 2019; Germer et al., 2021).
The average number of identified motor units for the hand muscles across participants was 12.2 ± 3.0 and 4.3 ± 1.2 for the first dorsal interosseous and thenar muscles, respectively. In contrast to the vastii muscles, Figure 4 shows that the discharge rates of motor units in each hand muscle were strongly correlated (>0.9), and there were few cases of low correlations (see cluster analysis below).
Figure 4.
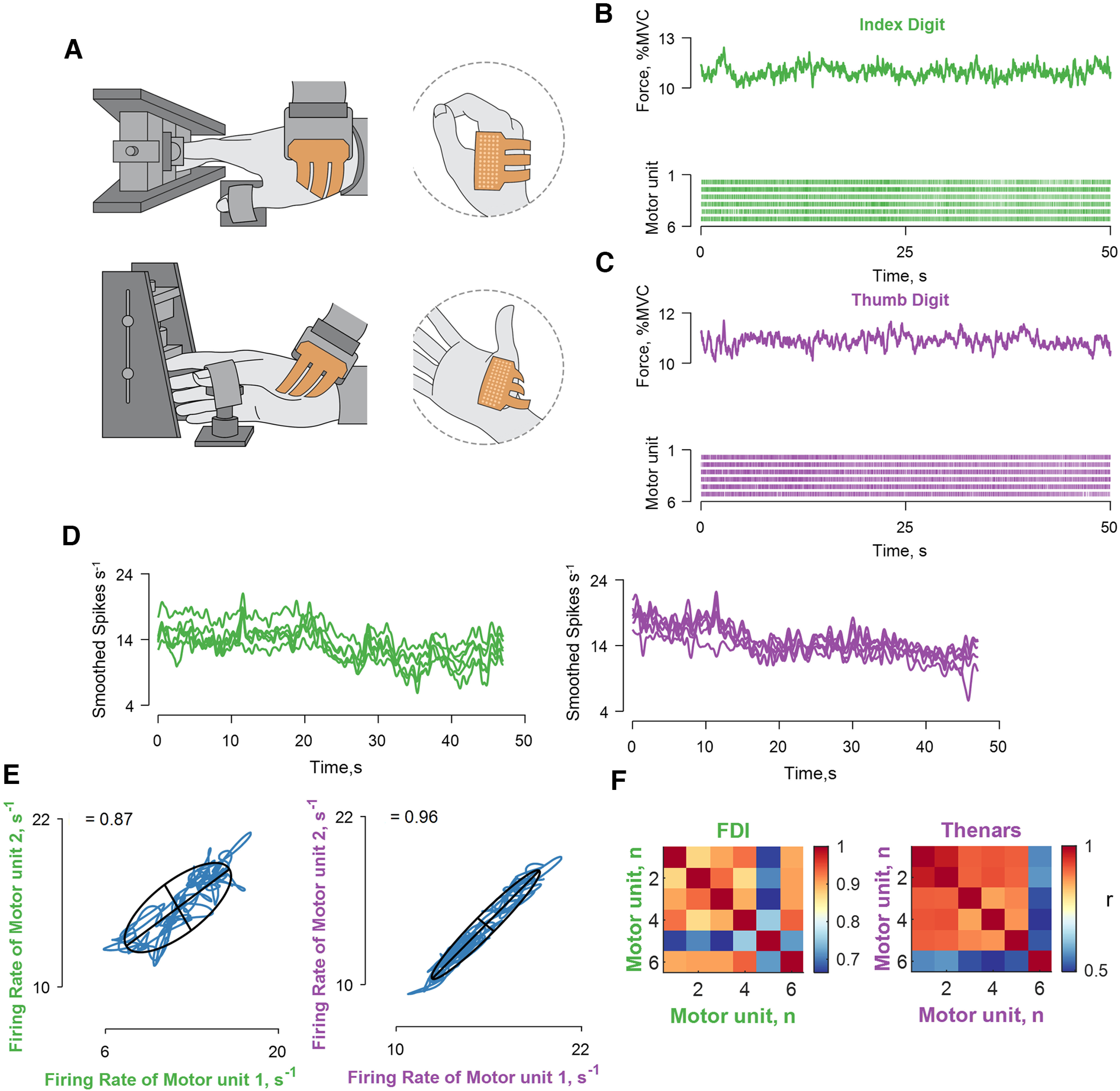
Recordings of muscle force and correlation analysis between the discharge times of motor units in hand muscles. A, Experimental setup involved high-density EMG grids placed over the first dorsal interosseous and thenar muscles. B, C, The applied force and the discharge times of motor units shown in a raster plot for the first dorsal interosseous (green) and thenar muscles (violet). D, The motor unit discharge times (series of 0s and 1s) were convolved with a 2.5 Hz (400 ms) Hann window to yield discharge rates (spikes s−1). E, Two bivariate correlations between different motor units belonging to the same muscle module (the labels are color coded as indicated in C, D). The blue lines indicate the smoothed discharge rates during the steady-state contraction. F, Matrix color map of the correlation strength (r) between all the identified motor units for the two muscles. Note that all motor units are highly correlated within each muscle module. The Pearson's value was <0.0001 for both correlations.
Motor unit modes
Figure 5 shows the results obtained from the factor analysis for the vastii muscles of two participants. The factor analysis was applied to the pooled motor units from both muscles; therefore, the extracted factors did not have any a priori muscle-specific constraint. The factors (motor unit modes) are then superimposed for each muscle (gray lines indicate individual motor unit discharge rates from that muscle; Fig. 5A). The first two modes explained most of the variance in the signal (>80%).
Figure 5.
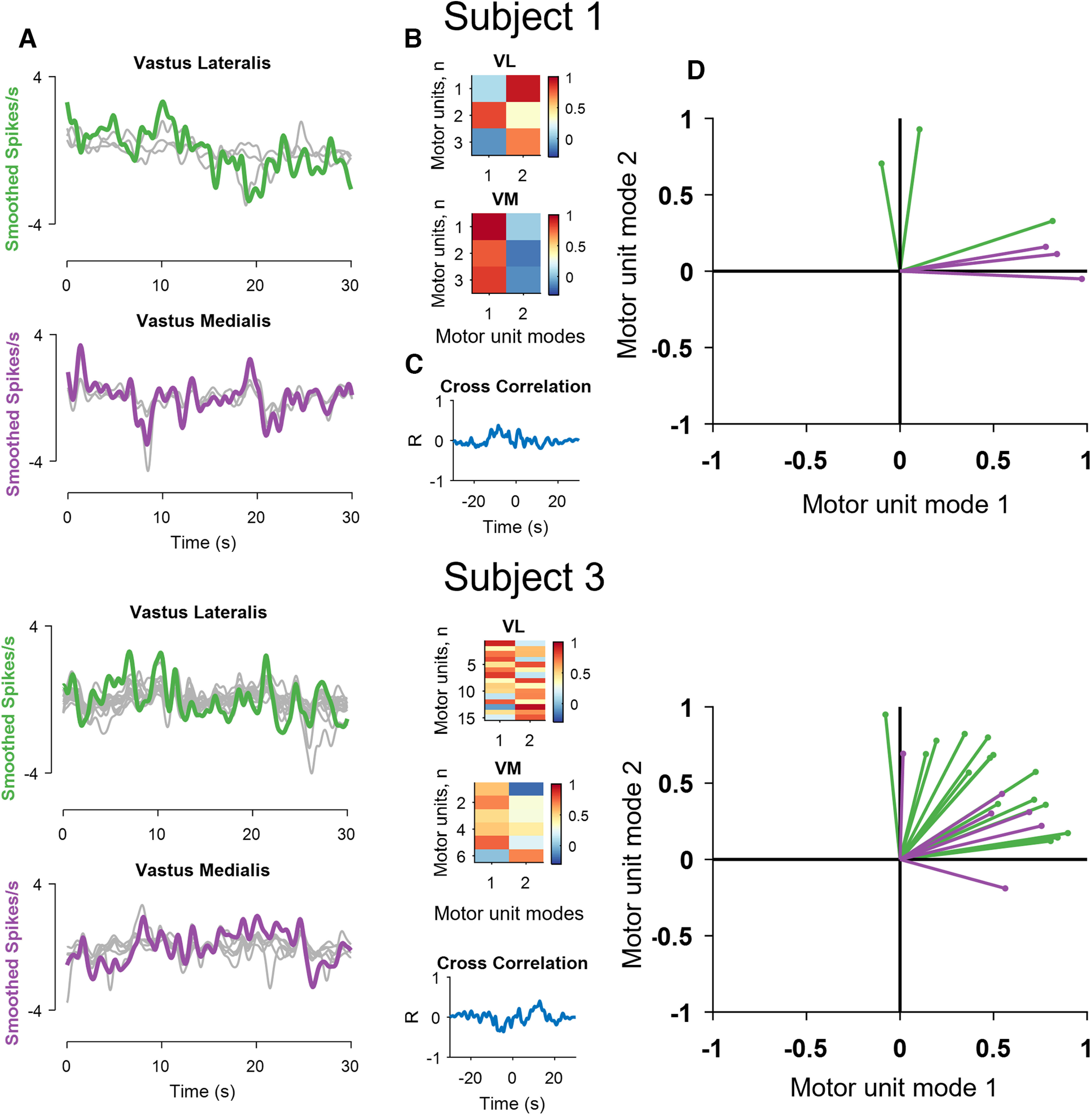
Results of the factorization analysis for the vastii muscles of two subjects. A, The smoothed motor unit discharge rates (gray lines, zeroed mean for visualization) and two muscle modules derived from the factor analysis (green for the vastus lateralis and violet for vastus medialis). Note the high correlation between the two factors and the discharge rates of some, but not all, motor units for the two subjects. B, The two factors were then correlated with the smoothed discharge rates of all motor units and defined the motor unit modes. C, The cross-correlation values between the two modes. D, Projections of the bivariate correlation values for each motor unit with respect to the motor unit modes. Values close to one indicate that a motor unit carries ∼100% of that motor unit mode. Note that some vastus lateralis (green) and medialis (violet) motor units invade the territory of the other motor unit mode; for example, intermingling of the green and violet lines for Subject 3. Also note that some motor units are only correlated with one module.
We then determined the level of correlation between the discharge rate of each motor unit and the two modes (Fig. 5B). This analysis shows, for example, that motor unit number 2 in vastus lateralis for Subject 1 had a stronger correlation with the first mode, whereas the two other motor units were more correlated with the other mode (Fig. 5D). However, the two modes were not correlated (Fig. 5C). We then take the first mode as the vastus medialis module and the second mode as the vastus lateralis module. Projections of the correlations with the two modes (Fig. 5D) indicated that one motor unit in vastus lateralis (green) belonged to the mode of the vastus medialis (violet) motor units. Subject 3 exhibited more intermingling of the motor unit data in the space of the two motor unit modes (Fig. 5; graph, bottom right).
We then examined the overall distribution of the identified motor units within each motor unit mode across participants for the vastii (n = 8) and hand muscles (n = 8). We found that although many motor units from each vastus muscle shared the same modes (Fig. 5A–D), the discharge rates of some motor units were correlated with both motor unit modes. There were also some motor units that showed negative correlations with one of the modes. These negative correlations were more common for the hand muscles.
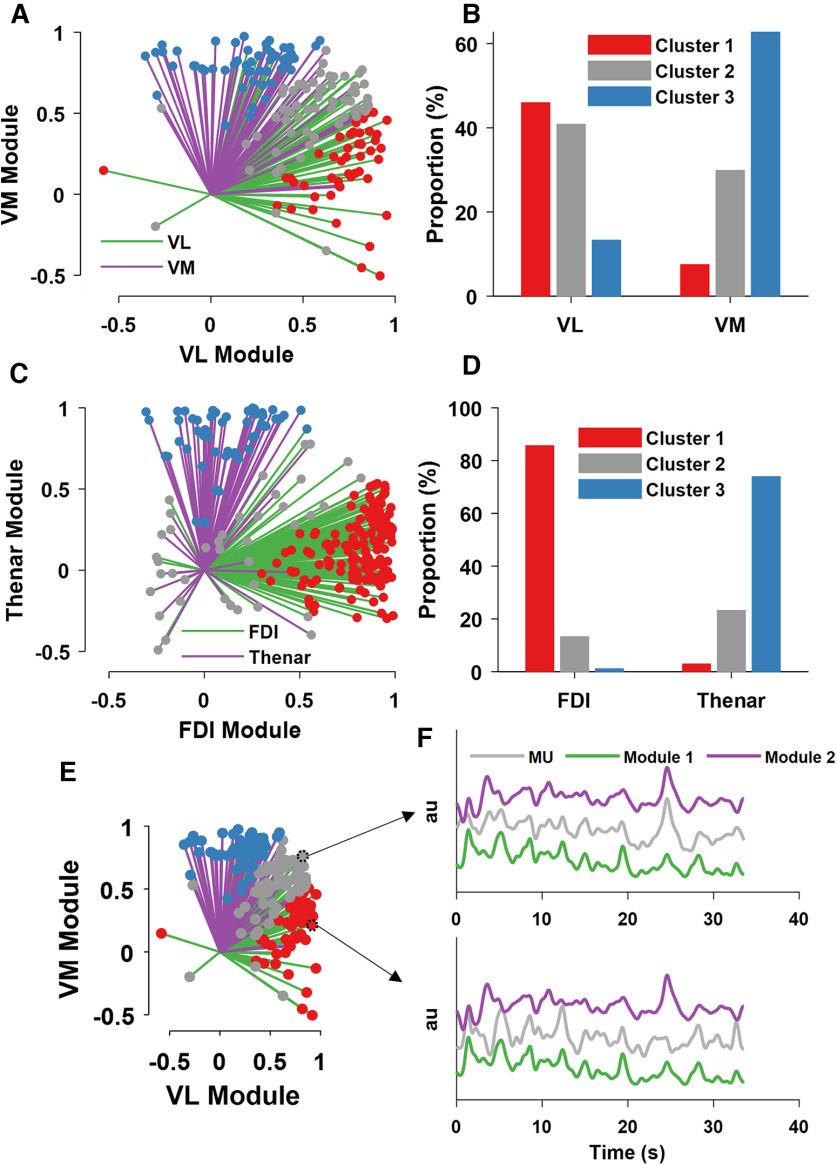
In the vastii muscles, we found a continuous distribution of motor unit modes across the two muscle-specific neural modules. We clustered the correlation values of the motor units with the respective modes based on specific centroids [x and y coordinates, (0.65 1.00), (0.60 0.60), (1.00 0.65); Fig. 6B–D]. We have arbitrarily chosen these clusters because they represent a large proportion of the data in the vastii and not in the hand motor units, so that all motor unit modes that were correlated with an R > 0.6 with both modules represented the shared cluster. This analysis was not intended to identify a specific cluster, but rather to determine the number of the motor units within these boundaries. The largest proportion of motor units for all muscles was the group belonging to the homonymous muscle module (e.g., correlation level ranging from 0.65 to 1.00). Interestingly, the proportion of motor units belonging to the shared cluster was greater for vastus lateralis than vastus medialis (Fig. 6B). The muscle module clusters were stronger for the hand muscles, with few motor units in the shared cluster (<20% for both first dorsal interosseous and thenar muscles). Moreover, there were some motor units for both sets of muscles that diverged from the homonymous module and were more correlated with the synergistic muscle. This was more evident for the vastii (>10% of motor units) than hand muscles (<3% of motor units).
Figure 6.
The output of the factor and cluster analysis across all subjects and motor units. A, The motor units from vastus lateralis (green) and vastus medialis (violet). Each line indicates the strength (line length) and sign of the correlation coefficient (r) ranging from −1 to 1 between the discharge rate of one motor unit and the muscle module. Note that some motor units shared the combined module space (indicated as gray lines and dots), whereas others diverged from synergistic modules (blue and red), and a few invaded the territory of the other module. B, A cluster analysis identified three motor unit modes. Note the gray cluster that indicates the percentage of motor units that shared both motor unit modes. C, D, The same analysis as in A, B but for the hand muscles. Note the smaller proportion of motor units belonging to the shared (gray) cluster in comparison with the vastii muscles. E, F, An example of two motor units that occupy different module space. The discharge rate of the motor unit in F (top) was correlated to both motor unit modes (mode 1 and mode 2), whereas the motor unit in F (bottom) was only correlated with mode 1.
We then removed the motor units that shared both motor unit modes and performed coherence analysis between the motor pools. This analysis was performed only in the subjects with at least three motor units in both modes (total number of subjects, six). We found a twofold decrease in the coherence value when the shared motor units were removed. Among the subjects who had motor units in different modes, the coherence in the physiological bandwidth (0–50 Hz) did not differ from frequencies >50 Hz, which means that there was no coherence between motor units that did not belong to the same mode. Conversely, the coherence for the motor units that shared both modes was similar to previous reports (Laine et al., 2015; Negro et al., 2016). This finding suggests that previous coherence values found between muscles from the thigh and the hand are because of the shared inputs only and do not represent common synaptic input to all motor neurons in the nuclei (Laine et al., 2015; Del Vecchio et al., 2019).
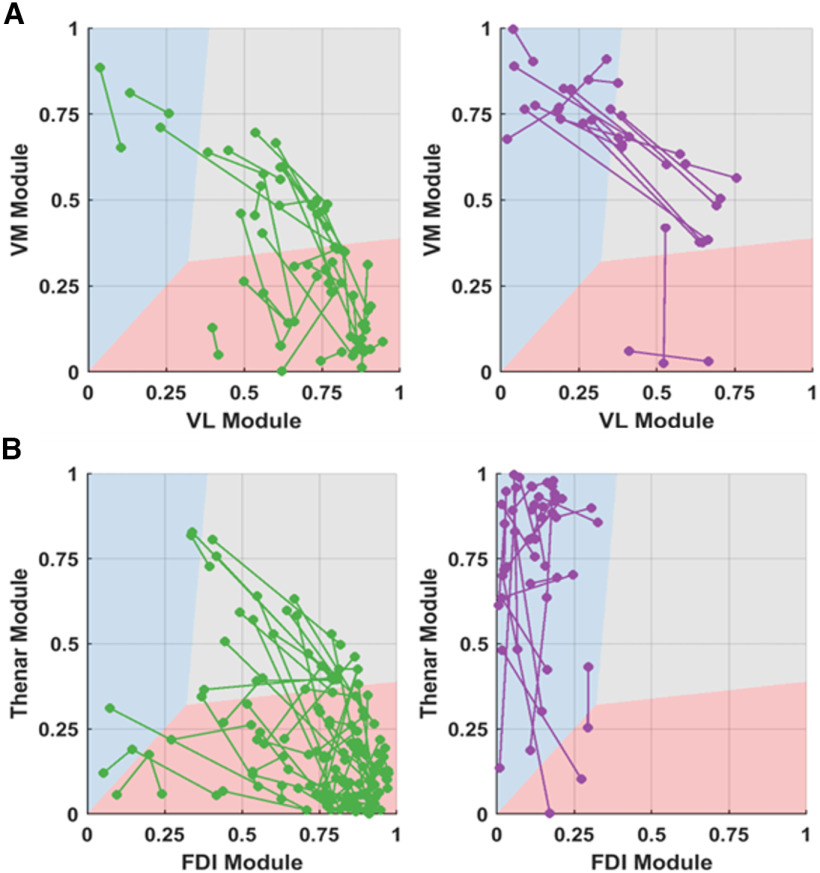
The analysis of the tracked motor units showed higher variability in the correlation values with the neural modules for the vastii muscles than in the hand muscles (Fig. 7). Many of the motor units remained in the same cluster for vastus lateralis (50%, N = 24) and vastus medialis (56%, N = 18), whereas the proportion was significantly higher for the first dorsal interosseous (77%, N = 59) and thenar muscles (96%, N = 23).
Figure 7.
The smoothed discharge rates of the motor units that were tracked across two trials. The variability in the motor unit modes for each motor unit was plotted with a line connecting the same motor units in the first and second trial. The axes of the plot correspond to the correlation coefficient (r, ranging from 0 to 1) of the motor unit discharge rate to the muscle module. A, The variability for the vastii (green for the motor units that resided in VL and violet motor units that resided in VM). B, The thenars and FDI muscle (green for the motor units that resided in FDI and violet motor units that resided in thenars).
Integrate-and-fire model: factor analysis accurately reflects the interplay of two common inputs
We performed computer simulations to generate a set of motor neuron discharge times that could be used to determine the accuracy of factorization analysis on the extraction of motor unit modes (Fig. 8). The aim was to assess the influence of known distributions of two synaptic inputs (Isyn1,2) and their average Isyn3 = (Isyn1 + Isyn2)/2 plus independent inputs on the number of identifiable motor unit modes. The common and independent inputs, as well as the discharge times, were approximated by tuning the parameters of an integrate-and-fire model (Abbott, 1999; de la Rocha et al., 2007).
Figure 8.
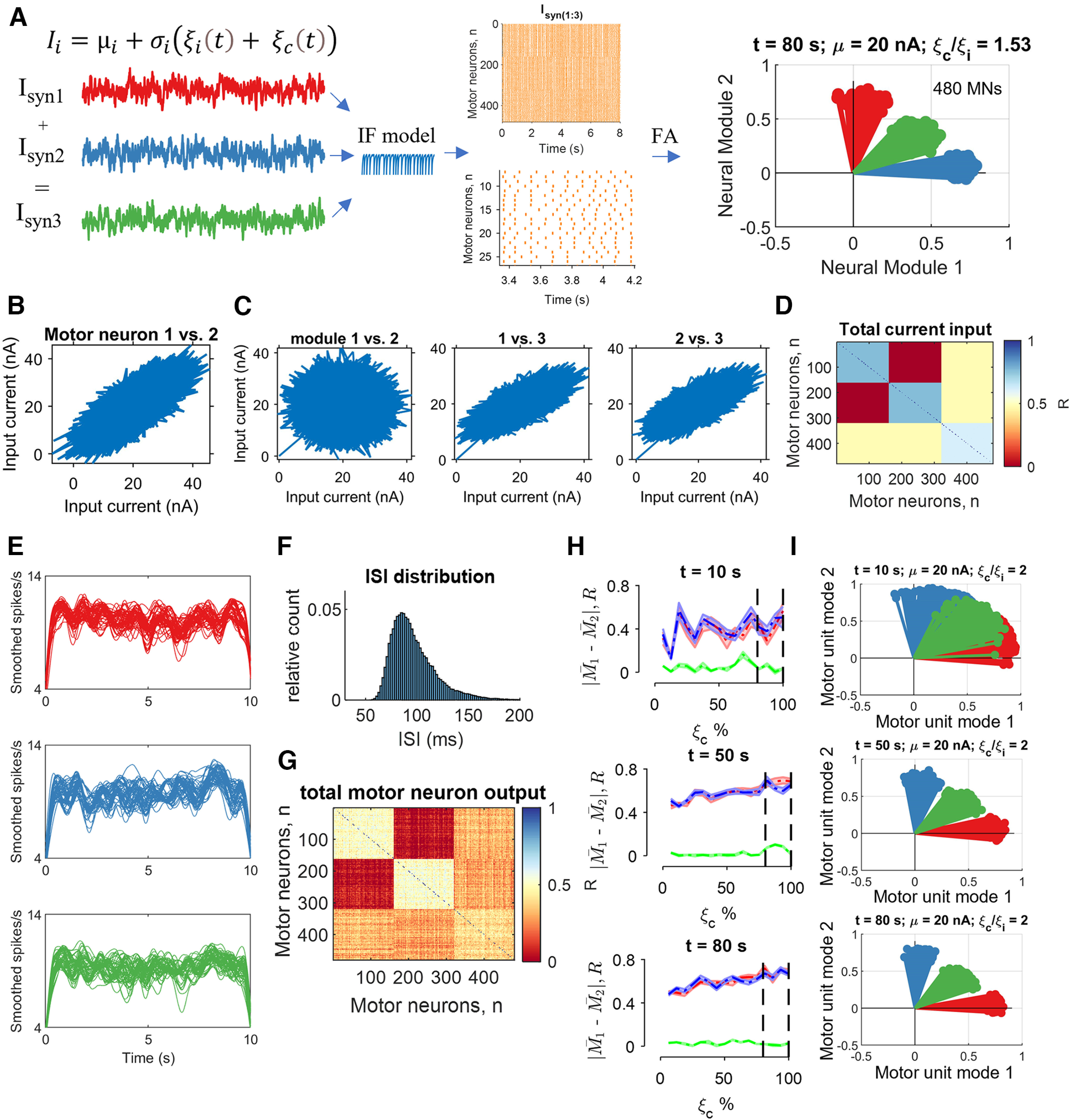
Integrate-and-fire (IF) model. We injected correlated and uncorrelated fluctuating currents () into 480 motor neurons. Two-thirds of the population received two distinct common inputs (), and one-third received the average of the two common inputs plus its own independent noise. The proportion of common and independent inputs reflected the cross-correlation values observed in experimental data. Similarly, the injected current (20 nA) generated interspike intervals that matched in vivo motor unit data. Each neuron received Gaussian synaptic noise reflecting its unique connections (independent input, ). A, Is the temporal average of the current (20 nA), and sets the global network state. Raster plot (orange lines) showing some of the data from an 80 s simulation with the proportion of common-to-independent inputs set at 1.53. Note that the output of the factorization analysis clearly depicts the space of three injected currents (graph, top right), as observed in the experimental recordings. B, Pairwise correlation for the first neural (muscle) module between motor neurons 1 and 2 from a pool of 160 neurons that each received Isyn1. C, The averaged total current across all cells plotted between the motor unit modes. Note that module 1 and module 2 are uncorrelated, whereas there was a high correlation with module 3 because of the shared averaged synaptic current. D, Matrix colormap of the correlation strength across all 480 neurons. E, The computed discharge rates from the integrate-and-fire model were low-pass filtered at 25 Hz for a 10 s trial. The first and last second was excluded when calculating the correlations to avoid the influence of spike frequency adaptation. Each line corresponds to one motor neuron. F, Distribution of interspike intervals across all 480 neurons for an 80 s trial. G, Matrix colormap of the correlation strength across all 480 motor neuron smoothed discharge timings. H, Accuracy of factor analysis computed as the average difference in discharge rate of all neurons belonging to each module (|M1 - M2|) at three time points during the simulation. The absolute difference between the modules corresponds to the accuracy of factor analysis in converging in that specific module. The values for the shared module (green) were close to 0, which indicates perfect separation from the two modules. We injected low percentages of common input (0% indicates that the common and independent inputs are the same). The dashed vertical lines indicate the range of values that reflect in vivo motor unit correlation values. There was a strong influence of time, so that 10 s of data were insufficient to obtain reliable estimates of the proportion of common input, whereas there were no differences for the data at 50 s and 80 s. I, Three representative motor unit modes extracted by factor analysis at three time points (10, 50, and 80 s) when the common input was twice as much as the independent input.
Because we have no information on the dimensions of the synaptic inputs received by the motor neurons, we can model these inputs with an integrate-and-fire model and study the outputs with pairwise correlations and factor analysis. Moreover, the model allowed us to test the influence of time (trial duration), net synaptic currents, and the relative strength of the common and independent inputs.
We simulated 480 integrate-and-fire neurons that were activated by applying an independent input and a common input. Two-thirds of the population of neurons received the uncorrelated inputs, Isyn1 and Isyn2, and a one-third received Isyn3, which represented the average of the two other inputs (Fig. 8A). We examined the correlations between the inputs and outputs (smoothed motor unit discharge rates) as well as the average and SD of the motor unit modes extracted by the factorization method (Fig. 8). Because of the influence of low-pass filtering of the discharge rates, there was a strong influence of trial duration with the 10 s data being unable to distinguish between the unique and shared inputs. With longer simulations, we were able to retrieve the full dimensions of the three common synaptic input signals (Fig. 8H,I) independent of the strength of the common and independent inputs.
Discussion
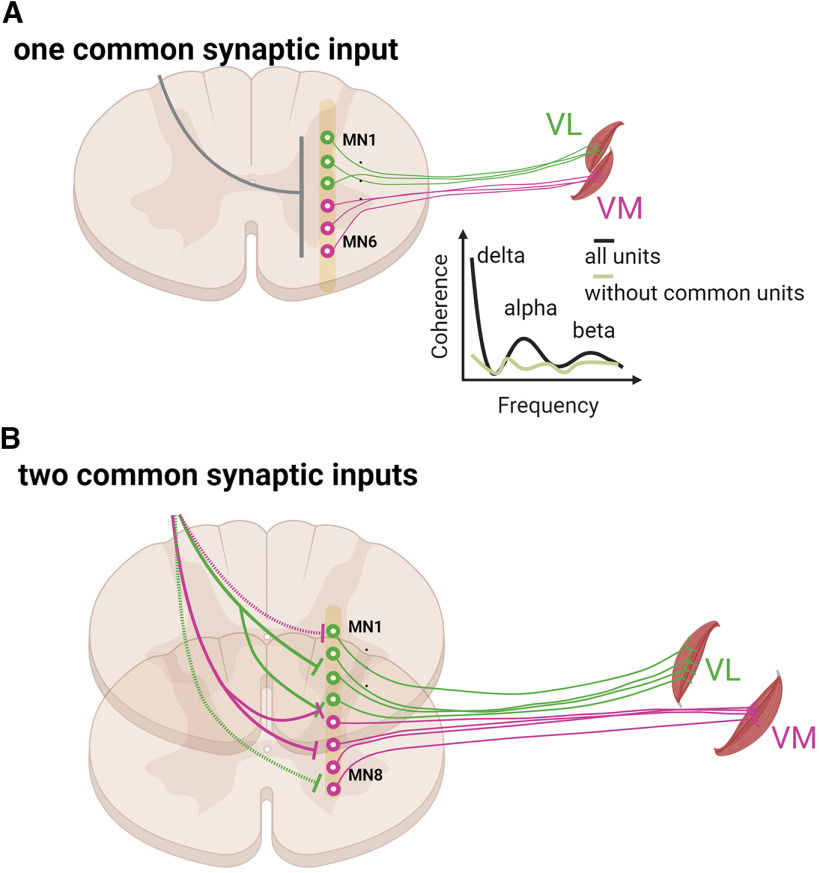
We analyzed the strength of the correlations between the discharge rates of motor units from different synergistic muscles during isometric contractions with the knee extensors and index finger and thumb muscles. We found two motor unit modes for the motor units of the vastii muscles, which contrasts with previous findings of only one dominant common input to individual (De Luca and Erim, 1994) or synergistic muscles (Laine et al., 2015). As conceptualized in Figure 9, large groups of motor units innervating the vastus lateralis and vastus medialis muscles were associated with a specific module for each muscle, but some motor units were associated with both neural modules. In contrast, fewer motor units innervating the hand muscles (<20%) were associated with both neural modules. Moreover, the discharge rates of some motor units were not correlated with the module for the muscle in which they resided but instead were correlated with the module for the synergistic muscle.
Figure 9.
Schematic representation of the results and suggested neural connectivity of voluntary motor commands to motor neuron pools. A, Previous studies that grouped the vastii or hand muscles based on global EMG signals have found strong coherence between the two muscles, indicating a dominant common input across synergistic muscles (Figure 1). After we removed those motor units that shared both motor unit modes (green line showing without common units), the correlation between the two pools of motor units was significantly reduced, as indicated in the coherence graph. This indicates that the coherence found in previous studies is mainly attributable to those motor units that shared two distinct sources of common synaptic. B, Visual representation of our current findings. Factor analysis suggested that there are at least two sources of common synaptic input (motor unit modes) to motor neurons that innervate each pair of synergistic muscles. Most motor neurons, but not all of them, innervating each vastus muscle receive common input from a unique source (green and violet lines), but some motor neurons receive inputs from the source directed to the other muscle (dashed green and violet lines, top graph), and some receive inputs from both sources.
The correlation between each motor unit and its mode reveals the potential nature of shared synaptic inputs by the motor neuron pools that is inevitably obscured in the global EMG signal. With a motor unit analysis, we show that the motor neurons from two hand muscles during an independent task can be fully represented by a unique muscle-specific input, but the motor units for each knee extensor muscle receive common input from two unique sources.
Previous experiments reported a single dominant common input governing coordination of the vastus medialis and lateralis muscles (Laine et al., 2015). Similarly, previous studies on one motor unit pool have identified a single common synaptic input (De Luca and Erim, 1994; Negro et al., 2016). The identification of a single dominant common input in previous studies is not necessarily in contradiction with the present results because the number of inputs received by a motor unit pool may depend on the task that is performed. The sources of common input, such as the type and intensity of feedback from sensory receptors (Nielsen, 2016; Sobinov and Bensmaia, 2021), likely differ depending on the task and type of contraction (isometric and dynamic). For example, in a previous study using similar techniques, we observed that most motor units did share the same neural module when macaque monkeys performed rapid high-force contractions (Del Vecchio et al., 2022), which was probably because of the specificity of the task. At the same time, we also note that it is not possible to identify multiple common inputs when using the motor unit pooled-coherence approach, which masks the presence of more than one input when most motor units in a pool receive a similar input and relatively few a different one. Because we found that the motor units innervating an individual muscle may receive more than one common input, correlation analysis in time and frequency domains should be ideally performed at the level of pairs of motor units rather than using a pooled coherence approach.
Even for isometric contractions, however, the sources of common input may differ with the details of the task being performed (Hug et al., 2021). Based on the interpretation that the fluctuations in force during steady isometric contractions are attributable to the variance in the common synaptic input (Negro et al., 2009; Feeney et al., 2018; Thompson et al., 2018), differences in the coefficient of variation for force during a specific action suggest adjustments in the common input across tasks. For example, the coefficient of variation for force during index finger abduction, which is mainly because of the activity of the first dorsal interosseus muscle, was 2× greater when participants performed index finger abduction and wrist extension at the same time, although the abduction force was the same in both tasks (Almuklass et al., 2016).
Based on the finding of an increase in the coefficient of variation for force during the double-action task (index finger abduction plus wrist extension) in the study by Almuklass et al., (2016), it seems reasonable to predict that the motor unit modes for the two hand muscles in the current study would differ from those observed during independent actions. Consistent with this possibility, Desmedt and Godaux (1981) suggested that the synaptic inputs delivered to the motor neurons that innervate the first dorsal interossei muscle differed when the direction of the force applied by the index finger changed from abduction to flexion. The basis for this conclusion was the finding that the recruitment for some pairs of motor units (∼8%) consistently reversed order when the task was changed from abduction to flexion. They hypothesized that this effect, although relatively modest, was attributable to differences in the distribution of the motor command for each task. We found the presence of three motor unit modes during knee extension that were explained by two independent inputs and the algebraic summation of these two inputs. The motor unit modes that carried both inputs are likely the ones that are ultimately responsible, for example, for precise coordinated activity of both muscles. In contrast, the existence of independent neural modules that control motor unit pools of agonist muscles rather than a single dominant input is likely also important from a functional perspective as it gives more space for flexibility of control, such as changes in the covariation of vastus medialis and lateralis to regulate internal joint stresses (Barroso et al., 2019; Alessandro et al., 2020) or context-dependent separation of activity of other agonist muscles (Sylos-Labini et al., 2017). The CNS can modulate the force at the tendon level with a greater precision by using various combinations of independent and shared motor unit modes.
Despite the limited scope of the tasks examined in our current study, the findings indicate that the derivation of muscle synergies is based on the common synaptic input that is shared by the motor neurons involved in the action but that this common input is not shared by all the neurons within a given motor nucleus. We found, for example, that the modulation of discharge rate for all motor units could be classified into three clusters distributed across two motor unit modes. These results indicate that synergistic motor neuron pools may receive more than one common synaptic input during submaximal isometric contractions.
Footnotes
D.F. was supported by the European Research Council under Synergy Natural BionicS Grant 810346 and the Engineering and Physical Sciences Research Council Transformative Healthcare for 2050 Project Non-Invasive Single Neuron Electrical Monitoring Technology Grant EP/T020970/1.
The authors declare no competing financial interests.
References
- Abbott L (1999) Lapicque's introduction of the integrate-and-fire model neuron (1907). Brain Res Bull 50:303–304. 10.1016/s0361-9230(99)00161-6 [DOI] [PubMed] [Google Scholar]
- Alessandro C, Barroso FO, Prashara A, Tentler DP, Yeh H-Y, Tresch MC (2020) Coordination amongst quadriceps muscles suggests neural regulation of internal joint stresses, not simplification of task performance. Proc Natl Acad Sci U S A 117:201916578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almuklass A, Price R, Gould J, Enoka R (2016) Force steadiness as a predictor of time to complete a pegboard test of dexterity in young men and women. J Appl Physiol 120:1410–1417. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Cavallari P, Cerri G (1998) Motoneuronal pre-compensation for the low-pass filter characteristics of muscle. A quantitative appraisal in cat muscle units. J Physiol 511:611–627. 10.1111/j.1469-7793.1998.611bh.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbero M, Merletti R, Rainoldi A (2012) Atlas of muscle innervation zones: understanding surface electromyography and its applications. Springer Science & Business Media. [Google Scholar]
- Barroso FO, Allessandro C, Tresch MC (2019) Adaptation of muscle activation after patellar loading demonstrates neural control of joint variables. Sci Rep 9:20370. 10.1038/s41598-019-56888-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basmajian JV (1963) Control and training of individual motor units. Science 141:440–441. 10.1126/science.141.3579.440 [DOI] [PubMed] [Google Scholar]
- Bräcklein M, Barsakcioglu DY, Ibáñez J, Eden J, Burdet E, Mehring C, Farina D (2022) The control and training of single motor units in isometric tasks are constrained by a common input signal. Elife 11:e72871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d'Avella A, Saltiel P, Bizzi E (2003) Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci 6:300–308. 10.1038/nn1010 [DOI] [PubMed] [Google Scholar]
- d'Avella A, Portone A, Fernandez L, Lacquaniti F (2006) Control of fast-reaching movements by muscle synergy combinations. J Neurosci 26:7791–7810. 10.1523/JNEUROSCI.0830-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Rocha J, Doiron B, Shea-Brown E, Josić K, Reyes AD (2007) Correlation between neural spike trains increases with firing rate. Nature 448:802–806. 10.1038/nature06028 [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Erim Z (1994) Common drive of motor units in regulation of muscle force. Trends Neurosci 17:299–305. 10.1016/0166-2236(94)90064-7 [DOI] [PubMed] [Google Scholar]
- Del Vecchio A, Úbeda A, Sartori M, Azorín JM, Felici F, Farina D (2018) Central nervous system modulates the neuromechanical delay in a broad range for the control of muscle force. J Appl Physiol (1985) 125:1404–1410. 10.1152/japplphysiol.00135.2018 [DOI] [PubMed] [Google Scholar]
- Del Vecchio A, Germer CM, Elias LA, Fu Q, Fine J, Santello M, Farina D (2019) The human central nervous system transmits common synaptic inputs to distinct motor neuron pools during non-synergistic digit actions. J Physiol 597:5935–5948. 10.1113/JP278623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Vecchio A, Holobar A, Falla D, Felici F, Enoka RM, Farina D (2020a) Tutorial: analysis of motor unit discharge characteristics from high-density surface EMG signals. J Electromyogr Kinesiol 53:102426. 10.1016/j.jelekin.2020.102426 [DOI] [PubMed] [Google Scholar]
- Del Vecchio A, Sylos-Labini F, Mondì V, Paolillo P, Ivanenko Y, Lacquaniti F, Farina D (2020b) Spinal motoneurons of the human newborn are highly synchronized during leg movements. Sci Adv 6:eabc3916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Vecchio A, Jones RHA, Schofield IS, Kinfe TM, Ibáñez J, Farina D, Baker SN (2022) Interfacing motor units in non-human primates identifies a principal neural component for force control constrained by the size principle. J Neurosci 42:7386–7399. 10.1523/JNEUROSCI.0649-22.2022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E (1977) Fast motor units are not preferentially activated in rapid voluntary contractions in man. Nature 267:717–719. 10.1038/267717a0 [DOI] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E (1978) Ballistic contractions in fast or slow human muscles; discharge patterns of single motor units. J Physiol 285:185–196. 10.1113/jphysiol.1978.sp012566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E (1981) Spinal motoneuron recruitment in man: rank deordering with direction but not with speed of voluntary movement. Science 214:933–936. [DOI] [PubMed] [Google Scholar]
- Duchateau J, Enoka RM (2011) Human motor unit recordings: origins and insight into the integrated motor system. Brain Res 1409:42–61. 10.1016/j.brainres.2011.06.011 [DOI] [PubMed] [Google Scholar]
- Farina D, Holobar A (2016) Characterization of human motor units from surface EMG decomposition. Proc IEEE 104:353–373. 10.1109/JPROC.2015.2498665 [DOI] [Google Scholar]
- Farina D, Negro F, Dideriksen JL (2014) The effective neural drive to muscles is the common synaptic input to motor neurons. J Physiol 592:3427–3441. 10.1113/jphysiol.2014.273581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feeney DF, Mani D, Enoka RM (2018) Variability in common synaptic input to motor neurons modulates both force steadiness and pegboard time in young and older adults. J Physiol 596:3793–3806. 10.1113/JP275658 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira-Pinto MJ, Ruder L, Capelli P, Arber S (2018) Connecting circuits for supraspinal control of locomotion. Neuron 100:361–374. 10.1016/j.neuron.2018.09.015 [DOI] [PubMed] [Google Scholar]
- Germer CM, Farina D, Elias LA, Nuccio S, Hug F, Del Vecchio A (2021) Surface EMG cross talk quantified at the motor unit population level for muscles of the hand, thigh, and calf. J Appl Physiol (1985) 131:808–820. 10.1152/japplphysiol.01041.2020 [DOI] [PubMed] [Google Scholar]
- Harrison VF, Mortensen OA (1962) Identification and voluntary control of single motor unit activity in the tibialis anterior muscle. Anat Rec 144:109–116. 10.1002/ar.1091440205 [DOI] [PubMed] [Google Scholar]
- Heckman CJ, Enoka RM (2012) Motor unit. Compr Physiol 2:2629–2682. 10.1002/cphy.c100087 [DOI] [PubMed] [Google Scholar]
- Henneman E, Olson C (1965) Relations between structure and function in the design of skeletal muscles. J Neurophysiol 28:581–598. [DOI] [PubMed] [Google Scholar]
- Henneman E, Somjen G, Carpenter DO (1965) Functional significance of cell size in spinal motoneurons. J Neurophysiol 28:560–580. [DOI] [PubMed] [Google Scholar]
- Henneman E, Shahani B, Young RR (1976) Voluntary control of human motor units. In: The motor system: neurophysiology and muscle mechanisms (Shahani M, ed), pp 73–78. Amsterdam: Elsevier. [Google Scholar]
- Holobar A, Zazula D (2007) Multichannel blind source separation using convolution kernel compensation. IEEE Trans Signal Process 55:4487–4496. [Google Scholar]
- Hug F, Avrillon S, Sarcher A (2021) Networks of common inputs to motor neurons of the lower limb reveal neural synergies that only partly overlap with muscle innervation. bioRxiv 460524. 10.1101/2021.10.13.460524. [DOI] [Google Scholar]
- Ibáñez J, Del Vecchio A, Rothwell JC, Baker SN, Farina D (2021) Only the fastest corticospinal fibers contribute to B corticomuscular coherence. J Neurosci 41:4867–4879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F (2004) Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol 556:267–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jöreskog KG (1967) Some contributions to maximum likelihood factor analysis. Psychometrika 32:443–482. [Google Scholar]
- Lacquaniti F, Ivanenko YP, Zago M (2012) Patterned control of human locomotion. J Physiol 590:2189–2199. 10.1113/jphysiol.2011.215137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laine CM, Martinez-Valdes E, Falla D, Mayer F, Farina D (2015) Motor neuron pools of synergistic thigh muscles share most of their synaptic input. J Neurosci 35:12207–12216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401:788–791. [DOI] [PubMed] [Google Scholar]
- Madarshahian S, Letizi J, Latash ML (2021) Synergic control of a single muscle: the example of flexor digitorum superficialis. J Physiol 599:1261–1279. 10.1113/JP280555 [DOI] [PubMed] [Google Scholar]
- Maxwell AE, Harman HH (1967) Modern factor analysis. Chicago London: The University of Chicago. [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R (1973) The contractile properties of human motor units during voluntary isometric contractions. J Physiol 228:285–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritz CT, Barry BK, Pascoe MA, Enoka RM (2005) Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. J Neurophysiol 93:2449–2459. 10.1152/jn.01122.2004 [DOI] [PubMed] [Google Scholar]
- Muceli S, Boye AT, D'Avella A, Farina D (2010) Identifying representative synergy matrices for describing muscular activation patterns during multidirectional reaching in the horizontal plane. J Neurophysiol 103:1532–1542. [DOI] [PubMed] [Google Scholar]
- Negro F, Holobar A, Farina D (2009) Fluctuations in isometric muscle force can be described by one linear projection of low-frequency components of motor unit discharge rates. J Physiol 587:5925–5938. 10.1113/jphysiol.2009.178509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negro F, Yavuz UŞ, Farina D (2016) The human motor neuron pools receive a dominant slow-varying common synaptic input. J Physiol 594:5491–5505. 10.1113/JP271748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen JB (2016) Human spinal motor control. Annu Rev Neurosci 39:81–101. [DOI] [PubMed] [Google Scholar]
- Nuccio S, Del Vecchio A, Casolo A, Labanca L, Rocchi JE, Felici F, Macaluso A, Mariani PP, Falla D, Farina D, Sbriccoli P (2021) Deficit in knee extension strength following anterior cruciate ligament reconstruction is explained by a reduced neural drive to the vasti muscles. J Physiol 599:5103–5120. [DOI] [PubMed] [Google Scholar]
- Partridge LD (1965) Modifications of neural output signals by muscles: a frequency response study. J Appl Physiol 20:150–156. [DOI] [PubMed] [Google Scholar]
- Phillips CG, Porter R (1964) The pyramidal projection to motoneurones of some muscle groups of the baboon's forelimb. Prog Brain Res 12:222–245. [DOI] [PubMed] [Google Scholar]
- Santello M, Bianchi M, Gabiccini M, Ricciardi E, Salvietti G, Prattichizzo D, Ernst M, Moscatelli A, Jörntell H, Kappers AML, Kyriakopoulos K, Albu-Schäffer A, Castellini C, Bicchi A (2016) Hand synergies: integration of robotics and neuroscience for understanding the control of biological and artificial hands. Phys Life Rev 17:1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman E, Berry MJ, Segev R, Bialek W (2006) Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440:1007–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shlens J, Field GD, Gauthier JL, Grivich MI, Petrusca D, Sher A, Litke AM, Chichilnisky EJ (2006) The structure of multi-neuron firing patterns in primate retina. J Neurosci 26:8254–8266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobinov AR, Bensmaia SJ (2021) The neural mechanisms of manual dexterity. Nat Rev Neurosci 22:741–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sylos-Labini F, Zago M, Guertin PA, Lacquaniti F, Ivanenko YP (2017) Muscle coordination and locomotion in humans. Curr Pharm Des 23:1821–1833. [DOI] [PubMed] [Google Scholar]
- Sylos-Labini F, La Scaleia V, Cappellini G, Fabiano A, Picone S, Keshishian ES, Zhvansky DS, Paolillo P, Solopova IA, D'Avella A, Ivanenko Y, Lacquaniti F (2020) Distinct locomotor precursors in newborn babies. Proc Natl Acad Sci U S A 117:9604–9612. 10.1073/pnas.1920984117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanzarella S, Muceli S, Del Vecchio A, Casolo A, Farina D (2020) Non-invasive analysis of motor neurons controlling the intrinsic and extrinsic muscles of the hand. J Neural Eng 17:046033. 10.1088/1741-2552/aba6db [DOI] [PubMed] [Google Scholar]
- Tanzarella S, Muceli S, Santello M, Farina D (2021) Synergistic organization of neural inputs from spinal motor neurons to extrinsic and intrinsic hand muscles. J Neurosci 41:6878–6891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson CK, Negro F, Johnson MD, Holmes MR, McPherson LM, Powers RK, Farina D, Heckman CJ (2018) Robust and accurate decoding of motoneuron behaviour and prediction of the resulting force output. J Physiol 596: 2643–2659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting JE, Del Vecchio A, Sarma D, Verma N, Colachis SC, Annetta NV, Collinger JL, Farina D, Weber DJ (2021) Sensing and decoding the neural drive to paralyzed muscles during attempted movements of a person with tetraplegia using a sleeve array. J Neurophysiol 126:2104–2118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tresch MC, Cheung VCK, d'Avella A (2006) Matrix factorization algorithms for the identification of muscle synergies: evaluation on simulated and experimental data sets. J Neurophysiol 95:2199–2212. 10.1152/jn.00222.2005 [DOI] [PubMed] [Google Scholar]
- Vecchio AD, Farina D (2019) Interfacing the neural output of the spinal cord: robust and reliable longitudinal identification of motor neurons in humans. J Neural Eng 17:016003. Available at: https://iopscience.iop.org/article/10.1088/1741-2552/ab4d05. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The website https://github.com/alecsdelvecchio/neuralmodules contains the data and functions for the extraction of the motor unit modes.