Abstract
Network neuroscience provides important insights into brain function by analyzing complex networks constructed from diffusion Magnetic Resonance Imaging (dMRI), functional MRI (fMRI) and Electro/Magnetoencephalography (E/MEG) data. However, in order to ensure that results are reproducible, we need a better understanding of within- and between-subject variability over long periods of time. Here, we analyze a longitudinal, 8 session, multi-modal (dMRI, and simultaneous EEG-fMRI), and multiple task imaging data set. We first confirm that across all modalities, within-subject reproducibility is higher than between-subject reproducibility. We see high variability in the reproducibility of individual connections, but observe that in EEG-derived networks, during both rest and task, alpha-band connectivity is consistently more reproducible than connectivity in other frequency bands. Structural networks show a higher reliability than functional networks across network statistics, but synchronizability and eigenvector centrality are consistently less reliable than other network measures across all modalities. Finally, we find that structural dMRI networks outperform functional networks in their ability to identify individuals using a fingerprinting analysis. Our results highlight that functional networks likely reflect state-dependent variability not present in structural networks, and that the type of analysis should depend on whether or not one wants to take into account state-dependent fluctuations in connectivity.
Subject terms: Network models, Imaging, Network topology
Introduction
The introduction of network theory to neuroscience has increased our understanding of the brain’s functional and structural organization. This powerful tool has given new insights into how higher order brain functions arise1,2 and how changes can lead to pathology3. However, questions have been raised regarding the reliability of brain network properties given the effects of noise in the signal, particularly in fMRI4–6. Still, despite the presence of noise, brain networks have been found to exhibit consistent properties over time among individual network connections and in higher order properties, such as the clustering coefficient, characteristic path length, and assortativity, for structural connectivity as measured with dMRI7–11, fMRI12–25 and EEG/MEG18,26,27. Unfortunately, most studies thus far have been limited to the analysis of a single imaging modality and/or few scanning sessions, raising questions about how reliable these properties are over longer times and across modalities.
While it is clear that there is some level of reliability in network properties within an individual over time, it is also important to understand how the state of the brain (e.g., resting wakefulness versus active task situations28), and the neural methodology (e.g., fMRI versus EEG) contributes to this reliability across multiple days. The “resting” brain (e.g., default mode network) is a state that has been shown to be metabolically demanding29 and associated not only with task performance (e.g., Ref.30) but also disease (e.g., Ref.31), very much similar to task-related activity; however, the “resting” brain is fundamentally different from task-related activity, as engagement in a task requires precise recruitment of and coordination between regions of the brain28. Also, in a field with a variety of diverse methodologies (e.g., fMRI, EEG, MEG, PET, etc.), neuroscience researchers draw conclusions from methods that are measuring fundamentally different neural properties. For example, fMRI is an indirect measurement of neural activity, as it measures oxygenation and neural activity is inferred. In contrast, EEG, a “direct” measurement, is measured on the scalp and filtered by a variety of tissues and bone separating the scalp from the brain. In terms of reliability, experimental design and task demands have shown to contribute to reliability in fMRI32,33, and EEG suffers from a large variety of factors that could impact reliability as well34. However, the reliability of networks derived from simulatneous fMRI and EEG has not been extensively studied and comparisons has been limited to resting-state35.
In addition to studying reliability within an individual over time, one can also ask about how network properties differ between individuals. Indeed, recent work has shown that brain networks can provide insight into the unique features associated with a person19,36–38. A giant leap toward the goal of understanding differences in brain networks was made with the finding that functional brain activity has unique features that can identify a person in a group, similar to a fingerprint39. This fingerprinting property has also been found in structural connectomes40,41. Fingerprinting is important because it allows neuroimaging analyses to focus on the individual and not only on group-level differences39.
To further understand reliability in brain networks over time, across different states, and across modalities, we quantified within- and between-subject reliability in a rich longitudinal and multi-modal dataset consisting of dMRI and simultaneous EEG-fMRI recording during resting-state and multiple tasks. Comparing reliability across different imaging modalities is particularly important because in recent years, studies have fused multiple modalities to address outstanding questions in neuroscience. Further, while previous work has shown that diffusion MRI is highly reliable with sufficient images42, other work has shown that structural changes can occur over a short time period with exercise43, working memory training44, and changes in sleep patterns45. Understanding the relationship between structure–function coupling and reliability over time and/or across tasks can therefore aide in studies that incorporate analysis across modalities.
Importantly, the data set studied here was part of a larger study examining naturalistic sleep variability in individuals46. Here, we do not focus on the effects of variation in sleep pressure (i.e., homeostatic sleep drive or the need to sleep), but instead note that due to the study design, subjects varied in the amount of sleep pressure they experienced during each imaging session, presumably augmenting variability within- and between-subjects’ functional brain network over time. We examine both structural and functional brain networks in this data set to study reliability of individual connections and higher order network statistics. To create structural networks, dMRI imaging was used to perform tractography and network connections were defined as the density of streamlines between brain regions. fMRI networks were constructed using the Pearson-Product Correlation to quantify the magnitude of the statistical relationship in the BOLD signal between brain regions. For EEG, the time-series signal from each sensor was first separated into traditional frequency bands of δ (1–3 Hz), θ (4–7 Hz), α (8–13 Hz), β (14–30 Hz) and γ (30–60 Hz), and functional connectivity was calculated using the debiased-weighted Phase-Lag Index (dwPLI) which quantifies phase synchronization between sensors based on the consistency of the lag between the instantaneous phases of two sensors47.
In the current work we evaluate: (1) which brain connections and network measures are most reliable within- and between-individuals; (2) how reliability varies across state and modality; and (3) how the different imaging modalities, dMRI, fMRI, and EEG, perform in a fingerprinting analysis to identify an individual.
Results
We analyzed the reproducibility of brain network properties derived from structural and functional brain imaging using the intra-class correlation (ICC). For the dMRI analysis, this involved analyzing brain networks from 25 subjects across 8 sessions for a total of 200 structural networks. For the fMRI and EEG analysis, a tradeoff between maximizing subjects and sessions was made across resting-state and tasks resulting in a range from 17 to 26 subjects, each with 6 sessions (see “Materials and methods” section for details). For each connection in the network or network measure, the ICC values were calculated using the mean square values for the subject and session terms.
Reliability of individual connections
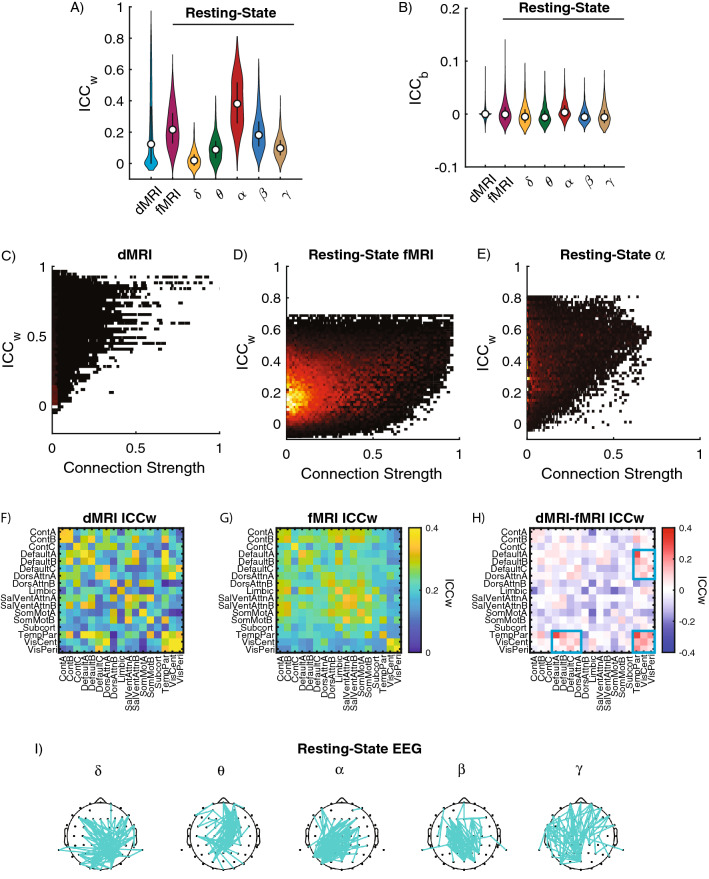
We first assessed the reliability of individual connections between brain regions or sensors. We calculated the ICC within a subject (ICCw) and between subjects (ICCb) for each connection across the three imaging modalities. As expected, we found that across imaging modalities, individual network connections are more reliable within- than between-subjects (Fig. 1A,B). Across imaging modalities, individual edges exhibit high variability in their reliability scores, with ICCw values ranging from poor (< 0.4) to excellent (> 0.8) reliability (Fig. 1A). By contrast, ICCb scores had consistently poor (< 0.2) reliability across all imaging modalities (Fig. 1B). For dMRI, the mean ICCw was 0.21 ± 0.24 (SD) and the mean ICCb score was -1 × 10–4 ± 0.01 (SD). For resting-state fMRI the mean ICCw was 0.23 ± 0.13(SD). Lastly, for the EEG the α-band had the highest mean ICCw (0.39 ± 0.16(SD) compared to the other frequencies [δ: 0.03 ± 0.05(SD); θ: 0.09 ± 0.08(SD); β: 0.20 ± 0.12(SD); γ: 0.10 ± 0.07(SD)]. To assess differences across imaging modalities, we used a one-way ANOVA where dMRI, fMRI, and each EEG frequency band (δ, θ, α, β, γ) were treated as sperate groups, and we found significant differences in the ICCw (F7,85249 = 2241; pcorrected < < 0.001; η2 = 0.18). One important feature is the long-tail distribution in the dMRI ICCw indicating that a small number of connections have excellent (> 0.8) reliability. We additionally looked to see if there was a relationship between connection strength and reliability (Fig. 1C–E).
Figure 1.
Reliability of individual connections. (A) Distribution of ICCw and (B) ICCb for dMRI and resting-state fMRI and EEG frequency bands. For each violin plot, the central dot indicates the median, and the line indicates the 25th–75th percentiles. (C–E) Distribution plots showing the connection strength of ICCw scores for (C) dMRI; (D) Resting-State fMRI and (E) EEG-α. (F–H) Average reliability of connection within and between cognitive systems for (F) dMRI and (G) resting-state fMRI. (H) Differences in average ICCw scores across cognitive systems between dMRI minus the fMRI. Blue boxes highlight connections between cognitive systems in which reliability was stronger in dMRI. (I) Connections with ICCw scores in top 5% for δ, θ, α, β and γ frequency bands plotted on the scalp for resting-state EEG. Cognitive systems are defined as Cont: Control A/B/C, Default: Default Mode A/B/C, DorsAttn: Dorsal Attention A/B, Limbic, SalVentAtt: Salience/Ventral Attention A/B, SomMot: Somatomotor A/B, Subcortical, TempPar: Temporal Parietal, VisCent: Visual Central, VisPer: Visual Peripheral.
We next assessed if for dMRI and resting-state fMRI there was an association between ICCw scores and cognitive systems. First, we mapped edgewise scores and then averaged over edges within each of the 17 cognitive systems from the Schaefer 200 layout combined with 21 subcortical regions from Harvard–Oxford atlas. As a trend, connections within a cognitive system for dMRI and resting-state fMRI exhibited the strongest reliability as can be seen from the figure because of the high values along the diagonal (Fig. 1F,G, respectively). However, a direct comparison between dMRI and fMRI showed distinct distribution of reliability across cognitive systems. dMRI reliability was stronger within and between the Temporal Parietal Network, Visual, and Default Mode Networks (Fig. 1H, blue boxes). For the EEG data we could not perform the same mapping to cognitive systems, so instead resting-state ICCw scores from the top 5% ICCw distribution are plotted onto the scalp (Fig. 1I).
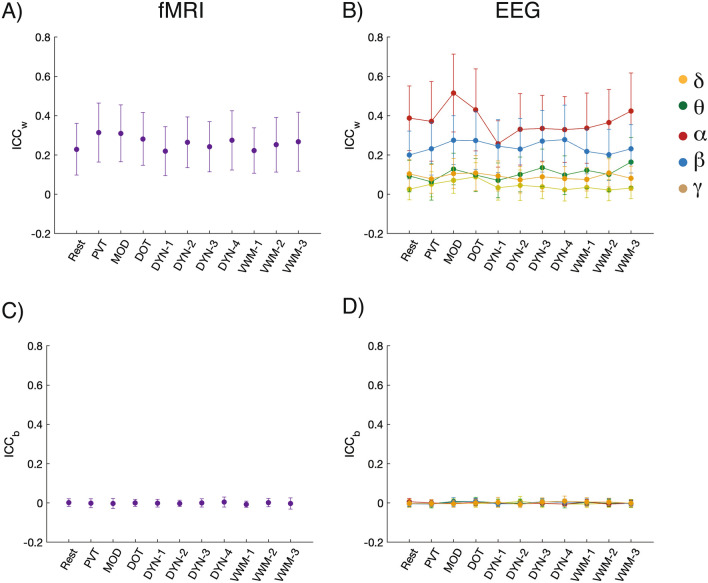
Given the different cognitive demands associated with task performance, one might expect reliability scores during task states to differ from those at rest. However, when we examined task induced changes in reliability, we found that task associated ICCw and ICCb values for fMRI and EEG scores exhibited a similar pattern to resting-state (Fig. 2). We found significant differences when comparing within- and between-subject reliability for fMRI (F1,501389 = 1701, p << 0.001, η2 = 0.003; one-way ANOVA; Fig. 2A,C) and EEG (F4,628 = 2547, p < < 0.001, η2 = 16.2; one-way ANOVA; Fig. 2B,D).
Figure 2.
Reliability of individual connections (A and B) within-subjects (ICCw) and (C and D) between-subjects (ICCb) for fMRI and EEG frequency bands across tasks: DOT, PVT, MOD, VWM-1:3, and DYN-1:4. For each plot, the figure shows the mean and standard deviation. DOT dot probe task, DYN dynamic attention task, MOD modular math task, PVT psychomotor vigilance task, VWM 1–3 visual working memory.
We then focused on the effect a task had on within-subject reliability. For this, we limited our analysis to the ICCw because ICCb values were close to zero. We compared task differences in fMRI using a one-way ANOVA where each task is treated as a variable, and we found significant differences between tasks (F10,501389 = 256, pcorrected << 0.001, η2 = 0.005). It is worth noting that these differences were small, but, for example, resting-state fMRI had consistently lower ICCw values than the other tasks (Fig. 2A). For the EEG, we additionally added each frequency band (δ, θ,α, β, γ) as a variable to the ANOVA design and found that the Task (Rest, Dot, Mod, Pvt, Dyn1-4, VWM1-3) x Frequency(δ, θ, α, β, γ) interaction was significant (F40,201190 = 291, pcorrected << 0.001, η2 = 0.06). Overall, EEG frequency exhibited larger differences in reliability than task effects, with the α-band having the highest ICCw scores.
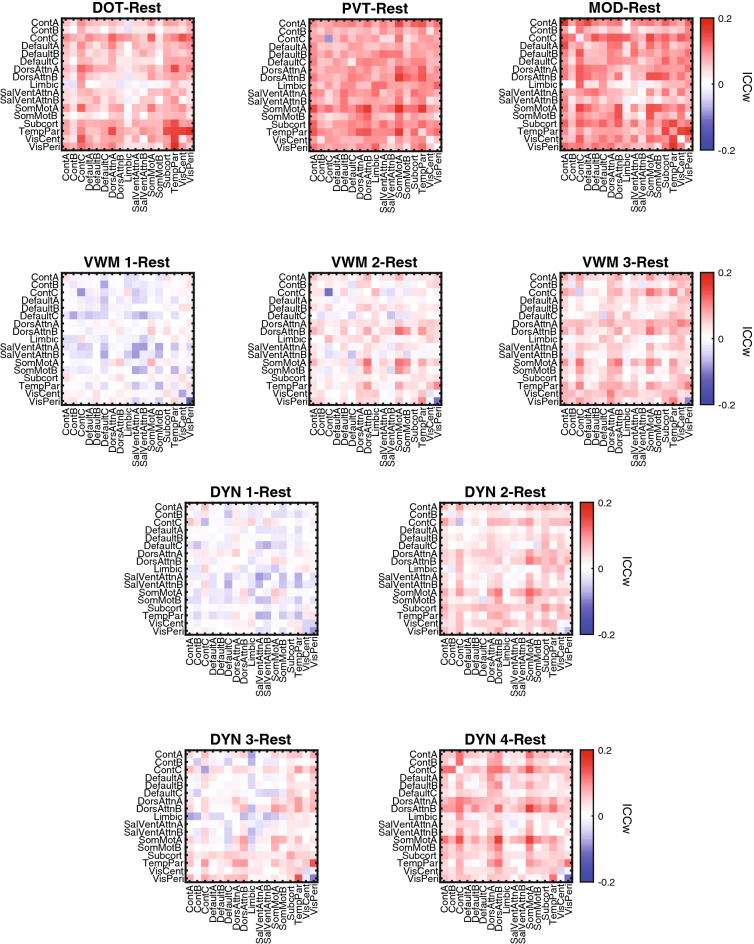
Further, we assessed if for task fMRI there was an association between ICCw scores and cognitive systems. We mapped edgewise scores to the 17 cognitive systems in the same manner as for the resting-state and plotted the difference between the ICCw values during task and resting-state in Fig. 3. Confirming the edgewise results, we generally observed higher reliability during task states. For task EEG data, ICCw scores from the top 5% of the ICCw distribution were plotted onto the scalp and we did not notice any overt reconfiguration in scalp distribution from resting-state to task (Fig. 4).
Figure 3.
fMRI changes in reliability from resting-state for each task: DOT, PVT, MOD, VWM-1:3, and DYN-1:4. Connections are mapped unto 17 cognitive systems from Schaefer cortical and Harvard–Oxford subcortical atlas. DOT dot probe task, DYN dynamic attention task, MOD modular math task, PVT psychomotor vigilance task, VWM 1–3 visual working memory.
Figure 4.
Scalp distribution across tasks for top 5% of ICCw scores. For Resting-State and each task: DOT, PVT, MOD, VWM-1:3, and DYN-1:4, (11 in total), connections with ICCw scores in top 5% for δ, θ, α, β and γ frequency bands are plotted on the scalp. DOT dot probe task, DYN dynamic attention task, MOD modular math task, PVT psychomotor vigilance task, VWM 1–3 visual working memory.
However, these effects in the fMRI and EEG could be impacted by intra-session reliability19,20,22 and motion artifacts in fMRI specifically6,48. We estimated the intra-session reliability by splitting the fMRI and EEG data into two halves and separately calculating the functional connectivity for each half of the session. The intra-session similarity between functional connectivity matrices was assessed using the Pearson Correlation. We found moderate intra-session similarity for fMRI data (r > 0.68 for all tasks; Supplementary Fig. S1A) and strong intra-session similarity for EEG data (r > 0.96 for all tasks; Supplementary Fig. S1B).
The lower intra- and inter-session reliability observed in the fMRI data could be due to the limited time of the recordings. Thus, the inter-session fMRI reliability could potentially be increased with more data per subject, as shown in previous work by Gratton et al.22 and Laumann et al.20, or this issue could be mitigated by combining data across sessions using a “background connectivity” approach49–51. However, given that both modalities were recorded for the same amount of time, this suggests that the sampling rate could also have an impact on intra-session reliability. Further, we note that many of the EEG frequency bands have a high intra-session reliability (Fig. S1), yet still show lower ICCw scores than that of the fMRI data (Fig. 1A). This highlights the fact that relationship between inter-and intra-session reliability is complex and potentially modality dependent. Future work should take care when assessing inter-session reliability, especially in data sets with limited time of recordings.
Additionally, since motion can have a significant impact on fMRI functional connectivity, we evaluated how well our preprocessing pipeline accounted for motion. We in general, found weak correlations between motion (as measured using frame displacement) and functional connectivity (Supplementary Fig. S2). Further, since the relationship between motion and functional connectivity has been found to be distance dependent48, we evaluated this relation and found no such relation (r < 0.04; all panels in Supplementary Fig. S3).
Reliability of network measures
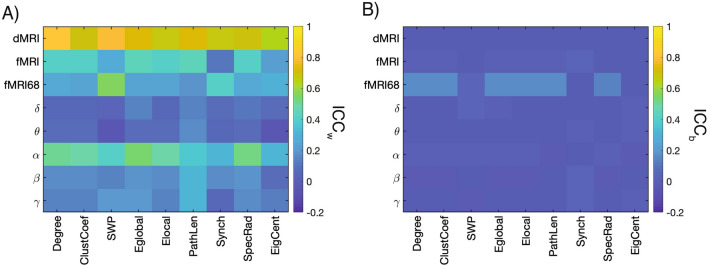
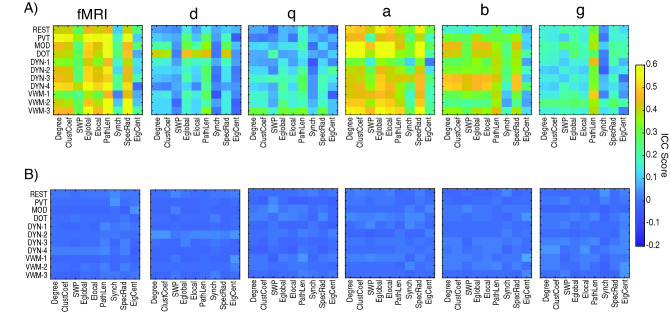
We next assessed the reliability of higher order network properties. For each brain network, nine measures were calculated along with their corresponding ICCw and ICCb scores. Since the functional connectivity was estimated on 200 regions for the fMRI and 62 sensors in the EEG, this difference could be a confound when comparing between the two modalities. To more closely match the number of EEG sensors, we estimated fMRI functional connectivity and network measures using the Desikan-Killiany brain atlas which contains 68 regions (fMRI68).
We first assessed differences among ICCw and ICCb scores using a one-way ANOVA where all network measures across imaging modalities were pooled together and grouped based on whether they are a within- or between-subject measure. As expected, we found stronger values for the ICCw compared to the ICCb (F1,125 = 104, pcorrected << 0.001, η2 = 0.83; Fig. 5).
Figure 5.
Graph Measures for dMRI and Resting-State fMRI and EEG for (A) ICCw and (B) ICCb values. For fMRI data, the analysis was conducted using both the Schaefer 200 (fMRI) and Desikan-Killiany (fMRI68) atlases.
Focusing on the within-subject measures, as shown in Fig. 5A, across all imaging modalities and network properties, the dMRI exhibited the highest ICCw scores [0.71 ± 0.06 (SD)]. By comparison, resting-state fMRI exhibited relatively poor reproducibility [fMRI: 0.35 ± 0.12 (SD); fMRI68: 0.30 ± 0.11 (SD)], and the EEG reproducibility was frequency dependent with the α-band having the highest ICCw scores [0.43 ± 0.09 (SD)]. These results were tested with a one-way ANOVA in which dMRI, fMRI, fMRI68, and each EEG frequency bands (δ, θ,α, β, γ) were treated as separate groups, and we found significant differences between them (F7,62 = 65, pcorrected << 0.001, η2 = 7.33; Fig. 6A). The same analysis for the ICCb scores found significant difference across all modalities (F7,62 = 15, pcorrected < < 0.001, η2 = 1.69; Fig. 5A), but these differences were driven by the fMRI68 having a stronger ICCb [0.11 ± 0.08 (SD)] whereas the other modalities had ICCb close to zero (Fig. 5B). These ICCb results suggest that, for fMRI, the choice of atlas could be an important factor in identifying consistent measures across subjects.
Figure 6.
ICC values for network measures across task and resting-state. (A) ICCw and (B) ICCb values across tasks for fMRI and EEG frequency bands.
We then asked if performing a task alters the reliability of network measures (Fig. 6). To evaluate how a task alters the within- and between-subject reliability, for fMRI we designed an ANOVA that assessed changes across tasks, network measures, and ICC. We found significant effects for Task x ICC (F8,80 = 99, pcorrected << 0.001, η2 = 9.90) and Network Measure x ICC (F10,80 = 9.88, pcorrected << 0.001, η2 = 0.12; Fig. 6A). For the EEG, we added frequency as a factor to the ANOVA design and evaluated a Task x Frequency x Network Measure x ICC ANOVA design, and we found a significant interaction between Task x Frequency (F32,792 = 5.35, pcorrected < 0.001, η2 = 0.22) and Frequency x Network Measure (F40,792 = 6.33, pcorrected < 0.001, η2 = 0.32; Fig. 6A). From Fig. 6 it is apparent that the α-band is the most consistent across resting- and task-state, while the β-band shows an increase in ICCw in the task-states. It is also worth noting that Synchronizability and Eigenvector Centrality exhibited weaker ICCw scores relative to the other metrics across resting- and task-states for both fMRI and EEG.
Further, we conducted the intra-session half-split similarity analysis for the network measures. Overall, we found stronger half-split similarity values across the EEG frequencies for each network measure and task when compared to half-split similarity values for the fMRI (Fig. S4). It is worth noting that the half-split reliability was lower for small-world propensity and synchronizability, reflecting their lower ICC values.
Fingerprinting analysis
Our analysis so far has confirmed that dMRI networks are more reliable within a subject than fMRI and EEG networks. Therefore, we expect that dMRI networks will have a higher probability of being able to identify an individual from a group, similar to a fingerprint39. For functional networks, we would similarly expect the same for the α-band EEG, given the relatively higher reliability scores. In order to fingerprint an individual, brain networks from the individual should be more similar to each other across runs relative to networks obtained from other individuals. To formally assess the similarity between brain networks, we measured the similarity using the Euclidian distance (“Materials and methods”). Our results indicate that fingerprinting was not uniform across all derived networks (F7,236 = 285, pcorrected << 0.001, η2 = 8.45). As expected, structural dMRI networks had the highest accuracy. However, the performance of fMRI networks was dependent on the number of regions, with connectivity based on the Schaefer 200 brain regions outperforming the 68 regions from the Desikan-Killiany atlas. Additionally, both fMRI atlases performed better than α-band EEG derived networks, despite the α-band exhibiting stronger reliability values. In fact, in the EEG, the β-band networks had the highest fingerprinting accuracy (Fig. 7A).
Figure 7.
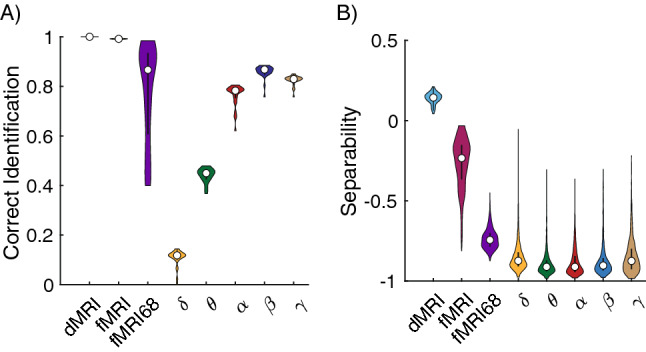
Fingerprinting performance across imaging modalities. (A) Proportion of networks that were correctly matched to the corresponding individual for dMRI, fMRI, and EEG derived brain networks. (B) Separability of each network in being matched to corresponding individual. fMRI indicates results using the Schafer 200 atlas whereas fMRI68 indicates results using the 68 regions Desikan-Killiany atlas. For each violin plot, the central dot indicates the median, and the line indicates the 25th–75th percentiles.
However, this analysis does not tell us about the separability across the networks derived from the different imaging modalities. Here, we define separability as the difference in similarity between the minimum within-subject value for a network to the maximum between subject similarity for that network (see Materials and methods). Therefore, positive separability values indicate that a particular network for an individual is always more similar to other networks from that individual and negative values indicate the opposite. Separability values across imaging modalities were found to be significantly different (F7,10093 = 7898, pcorrected << 0.001, η2 = 5.48). In addition, despite dMRI and fMRI having similar accuracy in fingerprinting, dMRI networks were more separable than fMRI and EEG [dMRI: 0.14 ± 0.04 (SD); fMRI: -0.26 ± 0.27 (SD); fMRI68: − 0.74 ± 0.06 (SD); δ, θ, α, β and γ: < -0.85 (mean)] (Fig. 7B).
Discussion
In the current work, we analyzed the reproducibility of multimodal and multi-task structural and functional brain networks in a unique longitudinal and multi-modal dataset with simultaneous EEG-fMRI recordings. In our analysis, each subject contained brain networks derived from dMRI, fMRI and EEG data, allowing us to assess how reliability differed in brain networks derived from different modalities and across task states.
We first assessed the reliability of individual connections in the structural and functional brain networks and found stronger within- than between-subject reliability across all imaging modalities, in line with previous results12,13,24,52–54. The most reliable connections were also the ones that tended to be the strongest, corroborating previous findings in fMRI networks12,24. In addition, when mapped onto cognitive systems, these connections exhibited distinct patterning. As a trend, for dMRI and resting-state fMRI, connections within a cognitive system exhibited the strongest reliability, consistent with previous studies in functional networks12,52–54. However, a direct comparison between dMRI and resting-state fMRI showed distinct distribution of reliability across cognitive systems. dMRI reliability was strongest within the Frontal-Parietal Control system and between the Visual to Default Mode and Temporal Parietal system, while in resting-state fMRI stronger values were distributed between cognitive systems.
When assessing task mediated changes, we found an increase in reliability across most tasks relative to resting-state in fMRI networks. In addition, we observed an increase in this reliability across multiple sessions of a given task, potentially indicative of an effect of learning the task. This finding complements results from a previous study that found adding task-state fMRI networks improves predictive outcomes relative to resting-states fMRI55. Here, we take care to note that the patterns of functional activity observed during a given task are expected to be different than those observed during rest, as they are likely the result of co-occurring BOLD responses across different regions of the brain that are specific to performing the task. As such, we also expect the patterns to be different between tasks that invoke different brain circuitry. While some studies consider these task-dependent signals in functional connectivity to artificially increase the observed underlying relationships between regions56, here, we instead want to emphasize the observed differences between task-dependent patterns of functional connectivity, noting that the specific task being performed can differentially affect reliability measurements of task-dependent functional connectivity.
For EEG, the α- and β-bands had the highest reliability scores for both resting- and task-states, confirming previous results26. The strong reliability for the α- and β-band could be due to the fact that these frequencies are consistently active, while the other frequency bands tend to have transient activity. In a similar manner to fMRI, EEG reliability increased during a task, but this increase was primarily in the α- and β-bands. In addition, we found no major changes when we mapped connections on the scalp from resting-state to task-state. This could be due to the low spatial resolution of EEG57. Additionally, an inherent limitation of such EEG-fMRI data is the higher-than-normal noise in the EEG, thus requiring a larger number of channels to be interpolated. As a result, this could affect the reliability results in the EEG signal.
When examining the reliability of higher order network properties, we found that network properties had overall stronger reliability scores than individual connections in line with previous findings of Braun et al.21. This might lead one to ask how the prevalence of low reliability scores across most connections could produce fair to excellent reliability in higher order network properties? This result could be due to the fact that edges with higher reliability scores are associated with the stronger connections. Our graph theoretical properties are dependent on connection strength, and the stronger the connection, the more variance it accounts for in the higher order network values. Thus, despite most connections having poor reliability, the few strong connections with good to excellent reproducibility have a disproportionately higher impact on the reliability of a network measure. The notable exception is that in fMRI and EEG, synchronizability and eigenvector centrality had lower reliability scores than the other network properties. One possible reason for this is that these measures, particularly eigenvector centrality, are very sensitive to the state of the subject58. These results indicate these measures might be more sensitive to detecting meaningful differences between individuals in studies where one is attempting to link functional brain connectivity to task performance or behavior.
We also found task associated differences in reliability for the fMRI and EEG. However, for the EEG, the strongest increases in reliability were in the α- and β-bands. However, in contrast to Deuker et al.18 we did not find a corresponding increase in ICCw scores in the δ and θ bands with task.
We found that dMRI and fMRI outperformed EEG derived networks in fingerprinting. However, the separability was not equal across these networks, with dMRI outperforming all functional networks. This is likely due to the fact that, unlike functional connectivity, structural connectivity is not state dependent. Also, despite the fact that the α-band EEG showed higher reliability, all EEG frequency bands performed worse than fMRI in our fingerprinting analysis. This is likely driven by the fact that the fMRI data has a larger number of strong connections than EEG data, and these strong connections will have a greater impact in the similarity calculations used in the analysis.
It has been found that brain activity measured with fMRI is stable over time20,22,59,60 and in fMRI, within-subject variance can be reduced with high quality data with long scan times (~ 15 min) and multiple sessions20,24,53,61. It has been argued that large amounts of data are needed in order to differentiate between true and artifact induced variance6,19 and previous studies have found that reliability increases with more data12,20,53,62,63. This high quality data is important because Horien et al.60 found that motion characteristics can be unique to an individual and can fingerprint a subject at a level greater than chance. In our data, individual scan times were limited to approximately 5 min, but data was collected over multiple sessions for a relatively large number of subjects, suggesting that we might expect more reliable results. However, our observation of the relatively weak accuracy and separability of EEG (a more direct measure of neuronal activity than fMRI) in fingerprinting an individual raises questions as to whether the increase in fingerprinting performance in fMRI on long time scans is based on neuronal activity. Also, respiration induced artifacts in fMRI exhibit the same stability over time64, which could also lead to increased reliability measurements.
Our direct comparison of fingerprinting between structural and functional networks indicates that structural networks are more sensitive. In addition, these results indicate that the patterning in structural connectivity is far more unique to an individual than those in corresponding functional networks. These results suggest that structural networks might have more discriminative power than functional networks.
Unique brain connectivity features have previously been proposed to play a role in differences underlying behavior and cognition65. Specifically, difference in behavioral performance in motor and decision associated tasks are correlated with fractional anisotropy of the corpus callosum66,67, optic radiation68 and grey matter density69. Cortical thickness within the superior parietal lobes has been found to be correlated with the rate of switching in a perception based task70. In addition, structural features unique to an individual lead to characteristic brain functional activity in modeling analysis and task performance38,71.
Is a connection with poor reliability good or bad? To answer this, we need to be mindful of the goal at hand. First and foremost, we need to make sure that reliability values are not due to noise in the signal or artificially low due to short lengths of recordings. On the other hand, if we are confident that low reliability is a genuine part of the signal, then that is also a very informative finding. The seminal work of Poldrack et al.72 found that functional connectivity exhibits a high level of variability within the same person over the course of a year. Along these lines, Noble et al.61 found that functional connections with strong reliability are not very informative when it pertains to predicting behavior. However, we need to be mindful that this is an effect limited to functional connectivity. Therefore, structural connections and/or higher-order network metrics might exhibit a stronger association between reliability and behavior. Also, finding highly reproducible brain connections and/or measures might be very important if we are looking for deviations from expected values that could be used as biomarkers for disease identification/progression. Alternatively, connections and/or measures with low reliability might be useful for studying individual differences and making correlations between structure and performance/behavior.
But, even beyond reliability and noise, our functional results could, along with previous literature, reflect the natural day-to-day changes in our brain. Neuroplastic changes in the brain are the hallmark of learning and memory73, and these changes or natural fluctuations and modifications in the neural code74, reflecting learning and memory could be reflected in functional connectivity. Indeed, there are many examples of rapid neuroplastic changes in the brain that results in functional connectivity changes (e.g., Nierhaus et al., 2019), but see Perich et al.76 as an alternative theory. Moreover, in this particular dataset, individuals were recruited to capture substantial variability in sleep without experimental manipulation. While there is a substantial literature on brain related decrements due to sleep deprivation77,78 little is known about naturalistic fluctuations in sleep46,79. These individuals instead could be more “plastic” (or “stationary”) than other individuals. Future studies will hopefully work to disentangle the effects of neuroplasticity from experimental factors that affect reliability estimates.
fMRI-based analysis has been around for over two decades, but its clinical use has been limited, raising questions about its usefulness as a diagnostic tool. In addition, given that the effectiveness of any diagnostic tool is only as useful as it can be applied to an individual, then in this regard, structural networks should take a more prominent role in medicine. Regardless, one must consider how measures of reliability relate to the modality being studied, the state of the brain, and the question at hand in order to meaningfully ask questions about how brain networks change with disease or how individual differences in structure relate to performance and behavior.
Materials and methods
Participants
The University of California, Santa Barbara (UCSB) Human Subjects Committee (#16-0154) and Army Research Laboratory Human Research Protections Office (#14-098) approved all procedures, and all participants provided informed written consent. Research was conducted in accordance with the declarations of Helsinki. The data presented in this manuscript represent a subset of data collected as part of a large-scale, longitudinal experimental that collected bi-weekly structural and functional brain data. A full description of the study can be found in46. Here we analyze data from 27 healthy participants who were recruited by word of mouth and local advertisements. Note that by study design, participants were excluded from the multi-session segment of the study if they did not experience sleep variability. Data is accessible upon request as far as allowed by the security policy and guidelines established with the ethics committee of the US Army Research Laboratory Human Research Protection Program.
Data description
Over the course of 16 weeks, subjects were asked to complete 8 recording sessions involving dMRI and simultaneous EEG-fMRI. For each session, simultaneous EEG-fMRI recording consisted of a 5-min resting state and 10 tasks with varying levels of cognitive demand; specifically:
Dot Probe Task (Dot)80;
Dynamic Attention Task (DYN 1–4) with four repetitions of the same task81;
Modular Math (MOD)82;
Psychomotor Vigilance Task (PVT)83, and;
Visual Working Memory (VWM 1–3) with three repetitions of the same task84.
Table 1 shows the number of subjects and sessions included in the analysis for each imaging modality and task. Although 27 participants were included in the data set, not all participants participated in all 8 imaging sessions, and some subjects’ fMRI data was excluded due to artifacts. We therefore selected 25 subjects with all 8 sessions of dMRI data for analysis, and for EEG-fMRI data, we analyzed only six sessions of data in order to make a trade-off between maximizing the number of subjects and number of sessions in our data set. As shown in Table 2, for the fingerprinting analysis using dMRI data, we again used 25 subjects, all of which had an equal number of sessions (8 sessions). For the fingerprinting analysis using fMRI data, 15 subjects were included with all 6 sessions of resting-state and task recordings, and for the EEG data, we used 26 subjects with resting-state and all tasks over 6 sessions.
Table 1.
Number of subjects, sessions, task length, and inter-session interval.
| Task | dMRI subject | EEG subject | fMRI subject | Session | Time (min) | Interval (days) | Bad channels |
|---|---|---|---|---|---|---|---|
| n/a | 25 | n/a | n/a | 8 | n/a | 14 | n/a |
| Resting-state | n/a | 27 | 26 | 6 | 5 | 14 | 6.7 |
| DOT | n/a | 27 | 25 | 6 | 14 | 14 | 7.5 |
| DYN-1 | n/a | 27 | 27 | 6 | 5 | 14 | 6.6 |
| DYN-2 | n/a | 27 | 27 | 6 | 5 | 14 | 6.5 |
| DYN-3 | n/a | 27 | 26 | 6 | 5 | 14 | 6.5 |
| DYN-4 | n/a | 27 | 20 | 6 | 5 | 14 | 6.5 |
| MOD | n/a | 27 | 17 | 6 | 14 | 14 | 8.2 |
| PVT | n/a | 27 | 19 | 6 | 12 | 14 | 7.5 |
| VWM-1 | n/a | 27 | 27 | 6 | 6 | 14 | 6.6 |
| VWM-2 | n/a | 27 | 23 | 6 | 6 | 14 | 7.3 |
| VWM-3 | n/a | 27 | 17 | 6 | 6 | 14 | 7 |
Table 2.
Number of subjects and sessions for fingerprinting analysis.
| Modality | Subjects | Sessions | Task included |
|---|---|---|---|
| dMRI | 25 | 8 | n/a |
| fMRI | 15 | 6 | Yes |
| EEG | 27 | 6 | Yes |
fMRI acquisition and preprocessing
Functional neuroimaging data were acquired on a 3 T Siemens Prisma MRI using an echo-planar imaging (EPI) sequence (3 mm slice thickness, 64 coronal slices, field of view (FoV) = 192 × 192 mm, repetition time (TR) = 910 ms, echo time (TE) = 32 ms, flip angle = 52º, and voxel size: 3 × 3 × 3 mm). For repeated scans, a T1-weighted structural image was also acquired using a high-resolution magnetization prepared rapid acquisition gradient echo (MPRAGE) sequence (TR = 2500 ms, TE = 2.22 ms, and FoV = 241 × 241 mm with a spatial resolution of 0.9 × 0.9 × 0.9 mm), for use in coregistration and normalization.fMRI BOLD images were preprocessed using Advanced Normalization Tools (ANTs)85. Physiological artifacts including respiration and cardiac cycle effects were corrected using the retrospective correction of physiological motion effects method, RETROICOR86, implemented in MEAP v1.587. Head motion was estimated using antsMotionCorr, and the motion correction was completed as follows: (1) An unbiased BOLD template was created within each session by averaging the motion-corrected BOLD time series from each run. (2) The BOLD templates were coregistered to the corresponding T1-weighted high resolution structural images, collected in each session. (3) Each session was spatially normalized to a custom study-specific multi-modal template which included T1-weighted, T2-weighted and GFA images from twenty-four quasi-randomly selected participants chosen to match the study population. (4) The template was then affine-transformed to the coordinate space of the MNI152 Asymmetric template. (5) Finally, the fMRI volumes were transformed using the estimated head motion correction, BOLD template coregistration, BOLD-to-T1w coregistration and spatial normalization into MNI space using a single Hamming weighted sinc interpolation. After these transformations, the final step in the preprocessing was to extract time-series from fMRI scans for functional connectivity analyses. Two atlases were used to reduce the 3D volume data into 221 nodal time series data: (1) the cortical Schaefer 200 atlas88 which was derived from intrinsic functional connectivity in resting state fMRI and (2) 21 subcortical regions from the Harvard–Oxford atlas based on anatomical boundaries89. As the atlases are in MNI coordinate space, voxels within each labelled region of the atlases were simply averaged, and time series were extracted for the following connectivity analyses.
To assess functional connectivity among ROIs, mean regional time-courses were extracted and standardized using the nilearn package90 in Python 2.7, and confound regression was then conducted. In particular, the time series for each region was detrended by regressing the time series on the mean as well as both linear and quadratic trends. There were a total of 16 confound regressors, which included: head motion, global signal, white matter, cerebrospinal fluid and derivatives, quadratics and squared derivatives. This functional connectivity preprocessing pipeline was selected based on conclusions from prior work that examined performance across multiple commonly used preprocessing pipelines for mitigating motion artifact in functional BOLD connectivity analyses48,91.
To construct the fMRI networks, the signal from all voxels within a brain region were averaged, and the Pearson Product Correlation (R) between two brain regions was calculated as
| 1 |
where x and y represent the time-series data from two different regions and σ is the variance of the time series. To account for negative correlations, the absolute value of the correlations was used to construct weighted functional connectivity matrices.
EEG acquisition and preprocessing
Continuous EEG recordings were captured simultaneously with an fMRI-compatible EEG equipped with standard Ag/AgCI electrodes from 64 sites on the scalp oriented in a 10–20 scheme system (Brain Products, Gilching, Germany). Initial fMRI pulse and ballistocardiographic artifact correction was completed in BrainAnalyzer 2 (Brain Products, Gilching, Germany) using classic subtraction and filtering approaches92,93. These mid-level processed EEG measurements were then further processed using in-house software in MATLAB (Mathworks, Inc., Natick, MA, USA) and the EEGLAB toolbox94,95. Despite the subtraction and filtering approaches applied, residual artifact from the fMRI pulse persisted. To remove these lingering artifacts, we developed a new cleaning pipeline.
Our cleaning pipeline included steps tailored to remove common EEG artifact (e.g., eye blinks, muscle-related activity) and then targeted the high frequency noise in the 16–19 Hz and 34–38 Hz range. EEG data were bandpass filtered between 0.75 and 50 Hz using a Finite Impulse Response (FIR) filter. Next, EEGLAB’s automated clean_rawdata function was used to determine channels that differed substantially from the estimated signal (derived from other channels) or had consistent flat-lining. Then, the EEG data were subjected to an Independent Component Analysis (ICA) decomposition and the ADJUST algorithm96 was used to remove ICA components associated with stereotyped noise. Following ICA decomposition, bad channels were interpolated using spherical interpolation. As a final step in EEG preprocessing, the EEG data were subjected to Artifact Subspace Reconstruction (ASR)97,98, which we used to target the aforementioned residual high frequency noise from the fMRI artifact. This method, in combination with the ICA cleaning method allows for the targeting of both stationary and non-stationary persistent artifacts. To deploy ASR on the dataset, we first created a “clean” reference signal from each subject’s EEG data by: 1) concatenating EEG segments that were at least 1000 ms long with amplitude below 100 µV, (2) and notch filtering (FIR) the EEG between 16–19 and 34–38 Hz. Following the creation of the reference signal, ASR was then used to reconstruct the EEG that contained large fluctuations greater than 5 standard deviations beyond the reference signal (in 500 ms chunks). Lastly, the data were re-referenced to a common average reference.
To construct EEG networks, the signal from each sensor was separated into standard frequency bands corresponding to δ (1–3 Hz), θ (4–7 Hz), α (8–13 Hz), β (15–30 Hz) and γ (30–60 Hz) with a Butterworth filter (8th order) followed by Hilbert transformation. Weighted functional connectivity adjacency matrices were constructed for each frequency band using the de-biased weighted phase-lag index (dwPLI)47. Each node in the adjacency matrix corresponds to a channel with the weight representing the strength (phase-lag) of the connection. Specifically, dwPLI is calculated as,
| 2 |
where I(Xi) corresponds to the imaginary component of time series data (X) from channel i. Thus, dwPLI is the sum of all pairwise products of the magnitudes of the imaginary components and accounts for any bias due to the number of data points.
dMRI acquisition and preprocessing
Diffusion spectrum imaging (DSI) scans were acquired for each session. DSI scans sampled 258 directions using a Q5 half-shell acquisition scheme with a maximum b-value of 5000 and an isotropic voxel size of 2.4 mm. Minimal preprocessing was carried out on the DSI scans and was restricted to motion correction. Following a similar procedure to the fMRI motion correction, motion was first assessed and applied for all of the b0 volumes, and a template was created for each scan composed of the average of the b0 volumes. Next, the b0 volumes and vectors were transformed using the estimated head motion correction, b0 template coregistration, b0 template-to-T1w coregistration and spatial normalization into MNI space using a single Hamming weighted sinc interpolation.
Fiber tracking was performed in DSI Studio (www.dsi-studio.labsolver.org) with an angular cutoff of 35°, step size of 1.0 mm, minimum length of 10 mm, spin density function smoothing of 0, and a maximum length of 250 mm. Deterministic fiber tracking was performed until 500,000 streamlines were reconstructed for each session. As with the fMRI volume data, streamline counts were estimated in 200 nodes using the same Schaefer 200 atlas88 and 21 subcortical regions part of the Harvard–Oxford atlas89. Connectivity matrices were then normalized by dividing the number of streamlines (T) between region i and j, by the combined volumes (v) of region i and j,
| 3 |
Graph theoretical analysis
We calculated nine commonly used and diverse graph metrics on each weighted dMRI, fMRI and EEG network. The graph metrics are: degree, clustering coefficient, characteristic path length, small-world propensity, global and local efficiency, synchronizability, spectral radius, and eigenvector centrality. See supplemental for detailed description of each network measure.
Degree
The weighted node degree (ki) is defined as the sum of all connections of a node99,
| 4 |
where W is the weighted adjacency matrix of a network with N nodes.
Clustering coefficient
The weighted clustering coefficient (C) for node i is the intensity of triangles in a network100 and is calculated as,
| 5 |
where W is the weighted adjacency matrix and b is the number of edges for node i.
Characteristic path length
The characteristic path length (L) is the average shortest path length between all nodes99,
| 6 |
where is the is the distance between nodes i and j. To calculate , we first take the inverse of the edge weights to transform the weight to a measure of length (i.e., to transform a strong connection strength to a short length). We then determine the shortest path between nodes i and j (using the inverted weights), and is the sum of the inverse of the edge weights along this shortest path.
Small-world propensity
Small-world propensity (φ) quantifies the extent to which a network displays small-worldness, a network property that combines the presence of local clustering with a short path length, while factoring in variation in network density101. Small-worldness is calculated as,
| 7 |
| 8 |
| 9 |
where Cobs is the observed clustering coefficient and Lobs is the observed characteristic path length of the network; Clatt, Llatt, Crand, and Lrand are clustering coefficient and characteristic path length from lattice and random networks with the same number of nodes and edge distribution.
Global and local efficiency
The efficiency of a node is the inverse of the path length99. Global efficiency (Eg) is the inverse shortest path length,
| 10 |
where is the previously defined distance between node i and j.
Local efficiency (El) is the global efficiency computed on the neighborhood of node i,
| 11 |
where wij and wih is strength of the connection between node i to j and h, respectively, and djh (Ni) is the length of the shortest path between nodes j and h that contains only neighbors of node i.
Synchronizability
Synchronizability is a measure of linear stability for a network of coupled dynamical systems102,
| 12 |
where λ2 is the second smallest eigenvalue of the unnormalized Laplacian matrix (L) and λn is its largest eigenvalue. The Laplacian is calculated as,
| 13 |
where D is the degree matrix of the weighted adjacency matrix, W.
Spectral radius
The spectral radius measures the ease with which diffusion process can occur in a network. The spectral radius is calculated as,
| 14 |
where |λ| corresponds to the absolute value of the eigenvalues of a network.
Eigenvector centrality
Eigenvector centrality (ECi) measures how influential a node is in a network, with a high value indicating a node is connected to other highly influential nodes103. The eigenvector centrality of node i is given by the i-th entry in the dominant eigenvector, which is the vector v = [v1,…vN] that solves
| 15 |
where is the largest eigenvalue of the weighted adjacency matrix, W.
Intra-class correlation
The intra-class correlation (ICC) is a measure used to quantify the test–retest reliability of a measure. We used the ICC to measure the consistency of individual connections across the dMRI, fMRI and EEG networks and across the graph metrics for each network. To accomplish this, we calculated two variants of the ICC, the within (ICCw)- and between (ICCb)-subjects104. ICCw and ICCb are, respectively, calculated as,
| 16 |
| 17 |
where I is the number of subjects and J is the number of sessions, SMS, RMS and EMS represent the ANOVA measures of mean square error between sessions, subjects, and due to error, respectively. The reliability of a measurement is considered: (1) “poor” if the ICC values is less than 0.4; (2) “fair” for ICC values between 0.4 and 0.6; (3) “good” for ICC values between 0.6 and 0.8; and (4) “excellent if ICC values exceed 0.8.
Fingerprinting analysis
To perform a fingerprinting analysis, as in Finn et al., 2015, we quantified the degree of similarity between networks. This analysis was performed separately for each of the dMRI, fMRI and EEG modalities. For each individual, connectivity matrices were converted for each individual and run into a vector using the values from the upper triangle of the matrix resulting in vectors of 1 × 24,310 for dMRI and fMRI, and 1 × 2016 for EEG. Thus, each vector, p, represents a single connectivity matrix for a given subject during a given session, and for functional matrices, in a given state (task/rest).
Next, separately within each modality, for each connectivity matrix (representing a subject, session, and state), we calculated the pairwise similarity between two vectors, p and q, using the Euclidian distance to create a dis-similarity matrix (D), where
| 18 |
and each entry in Dpq, corresponds to the dis-similarity between the brain network p to q. However, since the Euclidian distance formally assesses dis-similarity and we were interested in evaluating similarity, we converted from a dis-similarity to a similarity (S) measure by
| 19 |
where max(D) corresponds to the largest value in matrix D. This normalization ensures that the similarity matrix S [0 1].
In order to perform a fingerprinting analysis, for each vector, p, we then looked for the entry Spq with the highest similarity value. If for this entry, the vectors p and q were from the same individual (but could be from different sessions or states), then the fingerprinting analysis was classified to be successful at identifying the individual.
Fingerprinting performance for each imaging modality was assessed using two measures. The first measure quantifies the overall fingerprinting accuracy across subjects and was calculated as the percentage of matrices which were successful in identifying an individual. While this measure is useful from a classification standpoint, we were also interested in the level of separation between matrices within versus between individuals. Therefore, in the second measure, we assessed the separability (T) of each modality. The separability of each matrix, Tp, was defined to be
| 20 |
where the first term is constrained to q from the same subject as p, and the second term is constrained to q from all subjects other than p. The resulting values of T [− 1 1], where a value of 1 indicates perfect similarity within a subject across sessions and no similarity to other subjects and, conversely, -1 indicates no similarity across runs within a subject.
Statistical tests
Analysis of variance (ANOVA) was used to quantify the magnitude difference in ICC scores and the difference in the magnitude of the network similarity. Corresponding p-values were corrected for multiple comparison using Bonferroni correction. The Brain Connectivity Toolbox was used to calculate network measures99. All analyses were conducted in MATLAB 2017b.
Supplementary Information
Author contributions
J.N. and S.F.M. designed the analysis wrote the first draft. N.W., M.C., K.B., and J.O.G. preprocessed the data. M.C. and J.C.E. collected the data collection. J.C.E., B.G., and S.T.G. designed the experiment S.T.G. and J.M.V. secured the funding.
Funding
This research was supported by mission funding to the US CCDC Army Research Laboratory as well as sponsored by the Army Research Office and accomplished under Cooperative Agreement Numbers W911NF-10-D-0022 and W911NF-10-D-0002. Additional support was provided through University at Buffalo startup funding. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the US Government.
Data availability
Data is available upon reasonable request to the corresponding authors and consequent approval by the US DEVCOM Army Research Laboratory and University of California, Santa Barbara.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Johan Nakuci, Email: jnakuci3@gatech.edu.
Sarah F. Muldoon, Email: smuldoon@buffalo.edu
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-023-33441-3.
References
- 1.Park HJ, Friston K. Structural and functional brain networks: From connections to cognition. Science. 2013 doi: 10.1126/science.1238411. [DOI] [PubMed] [Google Scholar]
- 2.Bassett DS, Sporns O. Network neuroscience. Nat. Neurosci. 2017;20:353–364. doi: 10.1038/nn.4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat. Rev. Neurosci. 2015;16:159–172. doi: 10.1038/nrn3901. [DOI] [PubMed] [Google Scholar]
- 4.Laumann, T. O. et al. On the Stability of BOLD fMRI correlations. Cerebral Cortex 1–14 (2016). 10.1093/cercor/bhw265. [DOI] [PMC free article] [PubMed]
- 5.Power JD, et al. Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proc. Natl. Acad. Sci. 2018 doi: 10.1073/pnas.1720985115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012 doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bassett DS, Brown JA, Deshpande V, Carlson JM, Grafton ST. Conserved and variable architecture of human white matter connectivity. Neuroimage. 2011 doi: 10.1016/j.neuroimage.2010.09.006. [DOI] [PubMed] [Google Scholar]
- 8.Bonilha L, et al. Reproducibility of the structural brain connectome derived from diffusion tensor imaging. PLoS ONE. 2015 doi: 10.1371/journal.pone.0135247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Buchanan CR, Pernet CR, Gorgolewski KJ, Storkey AJ, Bastin ME. Test-retest reliability of structural brain networks from diffusion MRI. Neuroimage. 2014 doi: 10.1016/j.neuroimage.2013.09.054. [DOI] [PubMed] [Google Scholar]
- 10.Bürgel U, et al. White matter fiber tracts of the human brain: Three-dimensional mapping at microscopic resolution, topography and intersubject variability. Neuroimage. 2006 doi: 10.1016/j.neuroimage.2005.08.040. [DOI] [PubMed] [Google Scholar]
- 11.Malykhin N, Concha L, Seres P, Beaulieu C, Coupland NJ. Diffusion tensor imaging tractography and reliability analysis for limbic and paralimbic white matter tracts. Psychiatry Res. Neuroimaging. 2008 doi: 10.1016/j.pscychresns.2007.11.007. [DOI] [PubMed] [Google Scholar]
- 12.Noble S, et al. Influences on the test-retest reliability of functional connectivity MRI and its relationship with behavioral utility. Cereb. Cortex. 2017 doi: 10.1093/cercor/bhx230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Noble S, Scheinost D, Constable RT. A decade of test-retest reliability of functional connectivity: A systematic review and meta-analysis. Neuroimage. 2019;203:116157. doi: 10.1016/j.neuroimage.2019.116157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Elliott ML, et al. General functional connectivity: Shared features of resting-state and task fMRI drive reliable and heritable individual differences in functional brain networks. Neuroimage. 2019;189:516–532. doi: 10.1016/j.neuroimage.2019.01.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mangin JF, et al. A framework to study the cortical folding patterns. Neuroimage. 2004 doi: 10.1016/j.neuroimage.2004.07.019. [DOI] [PubMed] [Google Scholar]
- 16.Amunts K, Malikovic A, Mohlberg H, Schormann T, Zilles K. Brodmann’s areas 17 and 18 brought into stereotaxic space—Where and how variable? Neuroimage. 2000 doi: 10.1006/nimg.1999.0516. [DOI] [PubMed] [Google Scholar]
- 17.Rypma, B. & D’Esposito, M. The roles of prefrontal brain regions in components of working memory: Effects of memory load and individual differences. Proc. Natl. Acad. Sci. U S A (1999). [DOI] [PMC free article] [PubMed]
- 18.Deuker L, et al. Reproducibility of graph metrics of human brain functional networks. Neuroimage. 2009;47:1460–1468. doi: 10.1016/j.neuroimage.2009.05.035. [DOI] [PubMed] [Google Scholar]
- 19.Gordon EM, et al. Precision functional mapping of individual human brains. Neuron. 2017 doi: 10.1016/j.neuron.2017.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Laumann TO, et al. Functional system and areal organization of a highly sampled individual human brain. Neuron. 2015;87:657–670. doi: 10.1016/j.neuron.2015.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Braun U, et al. Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage. 2012;59:1404–1412. doi: 10.1016/j.neuroimage.2011.08.044. [DOI] [PubMed] [Google Scholar]
- 22.Gratton C, et al. Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation. Neuron. 2018;98:439–452. doi: 10.1016/j.neuron.2018.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Du HX, et al. Test-retest reliability of graph metrics in high-resolution functional connectomics: A resting-state functional MRI study. CNS Neurosci. Ther. 2015 doi: 10.1111/cns.12431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pannunzi M, et al. Resting-state fMRI correlations: From link-wise unreliability to whole brain stability. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.06.006. [DOI] [PubMed] [Google Scholar]
- 25.Shah LM, Cramer JA, Ferguson MA, Birn RM, Anderson JS. Reliability and reproducibility of individual differences in functional connectivity acquired during task and resting state. Brain Behav. 2016 doi: 10.1002/brb3.456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kuntzelman K, Miskovic V. Reliability of graph metrics derived from resting-state human EEG. Psychophysiology. 2017;54:51–61. doi: 10.1111/psyp.12600. [DOI] [PubMed] [Google Scholar]
- 27.Hardmeier M, et al. Reproducibility of functional connectivity and graph measures based on the phase lag index (PLI) and weighted phase lag index (wPLI) derived from high resolution EEG. PLoS ONE. 2014 doi: 10.1371/journal.pone.0108648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fox MD, et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. USA. 2005 doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Raichle ME, et al. A default mode of brain function. Proc. Natl. Acad. Sci. U S A. 2001 doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tian L, Ren J, Zang Y. Regional homogeneity of resting state fMRI signals predicts Stop signal task performance. Neuroimage. 2012;60:539–544. doi: 10.1016/j.neuroimage.2011.11.098. [DOI] [PubMed] [Google Scholar]
- 31.Sorg, C. et al. Selective changes of resting-state networks in individuals at risk for Alzheimer’s disease. Proc. Natl. Acad. Sci.104, 18760 LP–18765 (2007). [DOI] [PMC free article] [PubMed]
- 32.Bennett CM, Miller MB. FMRI reliability: Influences of task and experimental design. Cogn. Affect. Behav. Neurosci. 2013 doi: 10.3758/s13415-013-0195-1. [DOI] [PubMed] [Google Scholar]
- 33.Bennett CM, Miller MB. How reliable are the results from functional magnetic resonance imaging? Ann. N. Y. Acad. Sci. 2010 doi: 10.1111/j.1749-6632.2010.05446.x. [DOI] [PubMed] [Google Scholar]
- 34.McEvoy, L. K., Smith, M. E. & Gevins, A. Test–retest reliability of cognitive EEG. Clin. Neurophysiol.111, (2000). [DOI] [PubMed]
- 35.Wirsich, J. et al. The relationship between EEG and fMRI connectomes is reproducible across simultaneous EEG-fMRI studies from 1.5T to 7T. bioRxiv 2020.06.16.154625. 10.1101/2020.06.16.154625 (2021). [DOI] [PubMed]
- 36.Seitzman BA, et al. Trait-like variants in human functional brain networks. Proc. Natl. Acad. Sci. U S A. 2019 doi: 10.1073/pnas.1902932116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bansal K, Nakuci J, Muldoon SF. Personalized brain network models for assessing structure-function relationships. Curr. Opin. Neurobiol. 2018;52:1–13. doi: 10.1016/j.conb.2018.04.014. [DOI] [PubMed] [Google Scholar]
- 38.Bansal K, Medaglia JD, Bassett DS, Vettel JM, Muldoon SF. Data-driven brain network models differentiate variability across language tasks. PLoS Comput. Biol. 2018 doi: 10.1371/journal.pcbi.1006487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Finn ES, et al. Functional connectome fingerprinting: Identifying individuals based on patterns of brain connectivity HHS Public Access. Nat. Neurosci. 2015;18:1664–1671. doi: 10.1038/nn.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Powell MA, Garcia JO, Yeh FC, Vettel JM, Verstynen T. Local connectome phenotypes predict social, health, and cognitive factors. Netw. Neurosci. 2018 doi: 10.1162/netn_a_00031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yeh FC, et al. Quantifying differences and similarities in whole-brain white matter architecture using local connectome fingerprints. PLoS Comput. Biol. 2016 doi: 10.1371/journal.pcbi.1005203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Seider NA, et al. Accuracy and reliability of diffusion imaging models. Neuroimage. 2022;254:119138. doi: 10.1016/j.neuroimage.2022.119138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Takeuchi, H. et al. Training of working memory impacts structural connectivity. J. Neurosci.30, 3297 LP–3303 (2010). [DOI] [PMC free article] [PubMed]
- 44.Won J, et al. Evidence for exercise-related plasticity in functional and structural neural network connectivity. Neurosci. Biobehav. Rev. 2021;131:923–940. doi: 10.1016/j.neubiorev.2021.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Amorim, L. et al. Poor sleep quality associates with decreased functional and structural brain connectivity in normative aging: A MRI multimodal approach. Front. Aging Neurosci. 10. 10.3389/fnagi.2018.00375 (2018). [DOI] [PMC free article] [PubMed]
- 46.Thurman SM, et al. Individual differences in compliance and agreement for sleep logs and wrist actigraphy: A longitudinal study of naturalistic sleep in healthy adults. PLoS ONE. 2018 doi: 10.1371/journal.pone.0191883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Vinck M, Oostenveld R, Van Wingerden M, Battaglia F, Pennartz CMA. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage. 2011;55:1548–1565. doi: 10.1016/j.neuroimage.2011.01.055. [DOI] [PubMed] [Google Scholar]
- 48.Ciric R, et al. Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kraus BT, et al. Network variants are similar between task and rest states. Neuroimage. 2021;229:117743. doi: 10.1016/j.neuroimage.2021.117743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fair DA, et al. A method for using blocked and event-related fMRI data to study “resting state” functional connectivity. Neuroimage. 2007;35:396–405. doi: 10.1016/j.neuroimage.2006.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Al-Aidroos N, Said CP, Turk-Browne NB. Top-down attention switches coupling between low-level and high-level areas of human visual cortex. Proc. Natl. Acad. Sci. 2012;109:14675–14680. doi: 10.1073/pnas.1202095109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shehzad Z, et al. The resting brain: Unconstrained yet reliable. Cereb. Cortex. 2009 doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Birn RM, et al. The effect of scan length on the reliability of resting-state fMRI connectivity estimates. Neuroimage. 2013 doi: 10.1016/j.neuroimage.2013.05.099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.O’Connor D, et al. The healthy brain network serial scanning initiative: A resource for evaluating inter-individual differences and their reliabilities across scan conditions and sessions. GigaScience. 2017 doi: 10.1093/gigascience/giw011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gao S, Greene AS, Constable RT, Scheinost D. Combining multiple connectomes improves predictive modeling of phenotypic measures. Neuroimage. 2019 doi: 10.1016/j.neuroimage.2019.116038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Cole MW, et al. Task activations produce spurious but systematic inflation of task functional connectivity estimates. Neuroimage. 2019;189:1–18. doi: 10.1016/j.neuroimage.2018.12.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nunez PL, et al. EEG coherency I: Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalogr. Clin. Neurophysiol. 1997 doi: 10.1016/S0013-4694(97)00066-7. [DOI] [PubMed] [Google Scholar]
- 58.Lohmann G, et al. Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain. PLoS ONE. 2010 doi: 10.1371/journal.pone.0010232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Braga RM, Buckner RL. Parallel interdigitated distributed networks within the individual estimated by intrinsic functional connectivity. Neuron. 2017 doi: 10.1016/j.neuron.2017.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Horien C, Shen X, Scheinost D, Constable RT. The individual functional connectome is unique and stable over months to years. Neuroimage. 2019 doi: 10.1016/j.neuroimage.2019.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Noble S, et al. Influences on the test–retest reliability of functional connectivity MRI and its relationship with behavioral utility. Cereb. Cortex. 2017 doi: 10.1093/cercor/bhx230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Shou H, et al. Quantifying the reliability of image replication studies: The image intraclass correlation coefficient (I2C2) Cogn. Affect Behav. Neurosci. 2013 doi: 10.3758/s13415-013-0196-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Anderson JS, Ferguson MA, Lopez-Larson M, Yurgelun-Todd D. Reproducibility of single-subject functional connectivity measurements. Am. J. Neuroradiol. 2011 doi: 10.3174/ajnr.A2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Power JD, et al. Distinctions among real and apparent respiratory motions in human fMRI data. Neuroimage. 2019 doi: 10.1016/j.neuroimage.2019.116041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kanai R, Rees G. The structural basis of inter-individual differences in human behaviour and cognition. Nat. Rev. Neurosci. 2011 doi: 10.1038/nrn3000. [DOI] [PubMed] [Google Scholar]
- 66.Westerhausen R, et al. Interhemispheric transfer time and structural properties of the corpus callosum. Neurosci. Lett. 2006 doi: 10.1016/j.neulet.2006.09.028. [DOI] [PubMed] [Google Scholar]
- 67.Johansen-Berg H, Della-Maggiore V, Behrens TEJ, Smith SM, Paus T. Integrity of white matter in the corpus callosum correlates with bimanual co-ordination skills. Neuroimage. 2007 doi: 10.1016/j.neuroimage.2007.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Tuch DS, et al. Choice reaction time performance correlates with diffusion anisotropy in white matter pathways supporting visuospatial attention. Proc. Natl. Acad. Sci. USA. 2005 doi: 10.1073/pnas.0407259102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Van Gaal S, Scholte HS, Lamme VAF, Fahrenfort JJ, Ridderinkhof KR. Pre-SMA graymatter density predicts individual differences in action selection in the face of conscious and unconscious response conflict. J. Cogn. Neurosci. 2011 doi: 10.1162/jocn.2010.21444. [DOI] [PubMed] [Google Scholar]
- 70.Kanai R, Bahrami B, Rees G. Human parietal cortex structure predicts individual differences in perceptual rivalry. Curr. Biol. 2010 doi: 10.1016/j.cub.2010.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Bansal K, et al. Cognitive chimera states in human brain networks. Sci. Adv. 2019 doi: 10.1126/sciadv.aau8535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Poldrack RA, et al. Long-term neural and physiological phenotyping of a single human. Nat. Commun. 2015 doi: 10.1038/ncomms9885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lamprecht R, LeDoux J. Structural plasticity and memory. Nat. Rev. Neurosci. 2004 doi: 10.1038/nrn1301. [DOI] [PubMed] [Google Scholar]
- 74.Fairhall, A. L., Lewen, G. D., Bialek, W. & De Ruyter van Steveninck, R. R. Efficiency and ambiguity in an adaptive neural code. Nature. 10.1038/35090500 (2001). [DOI] [PubMed]
- 75.Nierhaus, T., Vidaurre, C., Sannelli, C., Mueller, K.-R. & Villringer, A. Immediate brain plasticity after one hour of brain–computer interface (BCI). J. Physiol. (2019). [DOI] [PubMed]
- 76.Perich MG, Gallego JA, Miller LE. A neural population mechanism for rapid learning. Neuron. 2018 doi: 10.1016/j.neuron.2018.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Hudson AN, Van Dongen HPA, Honn KA. Sleep deprivation, vigilant attention, and brain function: A review. Neuropsychopharmacology. 2020 doi: 10.1038/s41386-019-0432-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Boonstra TW, Stins JF, Daffertshofer A, Beek PJ. Effects of sleep deprivation on neural functioning: An integrative review. Cell. Mol. Life Sci. 2007 doi: 10.1007/s00018-007-6457-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Moturu, S. T., Khayal, I., Aharony, N., Pan, W. & Pentland, A. Using social sensing to understand the links between sleep, mood, and sociability. in 2011 IEEE Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing 208–214. 10.1109/PASSAT/SocialCom.2011.200 (2011).
- 80.Sipos ML, Bar-Haim Y, Abend R, Adler AB, Bliese PD. Postdeployment threat-related attention bias interacts with combat exposure to account for PTSD and anxiety symptoms in soldiers. Depress Anxiety. 2014 doi: 10.1002/da.22157. [DOI] [PubMed] [Google Scholar]
- 81.Yantis S, et al. Transient neural activity in human parietal cortex during spatial attention shifts. Nat. Neurosci. 2002 doi: 10.1038/nn921. [DOI] [PubMed] [Google Scholar]
- 82.Mattarella-Micke A, Mateo J, Kozak MN, Foster K, Beilock SL. Choke or thrive? The relation between salivary cortisol and math performance depends on individual differences in working memory and math-anxiety. Emotion. 2011 doi: 10.1037/a0023224. [DOI] [PubMed] [Google Scholar]
- 83.Loh, S., Lamond, N., Dorrian, J., Roach, G. & Dawson, D. The validity of psychomotor vigilance tasks of less than 10-minute duration. Behav. Res. Methods Instrum. Comput.10.3758/BF03195580 (2004). [DOI] [PubMed]
- 84.Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997 doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- 85.Avants BB, Tustison NJ, Song G, Gee JC. ANTS: Open-source tools for normalization and neuroanatomy. IEEE Trans. Biomed. Eng. 2009 doi: 10.1007/s12021-011-9109-y. [DOI] [Google Scholar]
- 86.Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn. Reson. Med. 2000 doi: 10.1002/1522-2594(200007)44:1<162::AID-MRM23>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 87.Cieslak M, et al. Quantifying rapid changes in cardiovascular state with a moving ensemble average. Psychophysiology. 2018 doi: 10.1111/psyp.13018. [DOI] [PubMed] [Google Scholar]
- 88.Schaefer A, et al. Local-global parcellation of the human cerebral cortex from intrinsic functional connectivity MRI. Cereb. Cortex. 2018;28:3095–3114. doi: 10.1093/cercor/bhx179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Makris N, et al. Decreased volume of left and total anterior insular lobule in schizophrenia. Schizophr. Res. 2006 doi: 10.1016/j.schres.2005.11.020. [DOI] [PubMed] [Google Scholar]
- 90.Abraham A, et al. Machine learning for neuroimaging with scikit-learn. Front. Neuroinform. 2014 doi: 10.3389/fninf.2014.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Lydon-Staley DM, Ciric R, Satterthwaite TD, Bassett DS. Evaluation of confound regression strategies for the mitigation of micromovement artifact in studies of dynamic resting-state functional connectivity and multilayer network modularity. Netw. Neurosci. 2018 doi: 10.1162/netn_a_00071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Allen PJ, Josephs O, Turner R. A method for removing imaging artifact from continuous EEG recorded during functional MRI. Neuroimage. 2000 doi: 10.1006/nimg.2000.0599. [DOI] [PubMed] [Google Scholar]
- 93.Allen PJ, Polizzi G, Krakow K, Fish DR, Lemieux L. Identification of EEG events in the MR scanner: The problem of pulse artifact and a method for its subtraction. Neuroimage. 1998 doi: 10.1006/nimg.1998.0361. [DOI] [PubMed] [Google Scholar]
- 94.Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods. 2004 doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- 95.Mullen, T. et al. Real-time modeling and 3D visualization of source dynamics and connectivity using wearable EEG. in Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS (2013). 10.1109/EMBC.2013.6609968. [DOI] [PMC free article] [PubMed]
- 96.Mognon A, Jovicich J, Bruzzone L, Buiatti M. ADJUST: An automatic EEG artifact detector based on the joint use of spatial and temporal features. Psychophysiology. 2011 doi: 10.1111/j.1469-8986.2010.01061.x. [DOI] [PubMed] [Google Scholar]
- 97.Mullen TR, et al. Real-time neuroimaging and cognitive monitoring using wearable dry EEG. IEEE Trans. Biomed. Eng. 2015 doi: 10.1109/TBME.2015.2481482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Chang CY, Hsu SH, Pion-Tonachini L, Jung TP. Evaluation of artifact subspace reconstruction for automatic artifact components removal in multi-channel EEG recordings. IEEE Trans. Biomed. Eng. 2020 doi: 10.1109/TBME.2019.2930186. [DOI] [PubMed] [Google Scholar]
- 99.Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 100.Onnela JP, Saramäki J, Kertész J, Kaski K. Intensity and coherence of motifs in weighted complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005 doi: 10.1103/PhysRevE.71.065103. [DOI] [PubMed] [Google Scholar]
- 101.Muldoon SF, Bridgeford EW, Bassett DS, Moreno Y, Zhou CS. Small-world propensity and weighted brain networks. Sci. Rep. 2016;6:22057. doi: 10.1038/srep22057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Motter AE, Zhou C, Kurths J. Network synchronization, diffusion, and the paradox of heterogeneity. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2005 doi: 10.1103/PhysRevE.71.016116. [DOI] [PubMed] [Google Scholar]
- 103.Newman MEJ. The mathematics of networks. N. Palgrave Dict. Econ. 2008 doi: 10.1057/9780230226203.1064. [DOI] [Google Scholar]
- 104.Wei X, et al. Functional MRI of auditory verbal working memory: Long-term reproducibility analysis. Neuroimage. 2004 doi: 10.1016/j.neuroimage.2003.10.039. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data is available upon reasonable request to the corresponding authors and consequent approval by the US DEVCOM Army Research Laboratory and University of California, Santa Barbara.