Abstract
Lung cancer is considered the most common and the deadliest cancer type. Lung cancer could be mainly of 2 types: small cell lung cancer and non-small cell lung cancer. Non-small cell lung cancer is affected by about 85% while small cell lung cancer is only about 14%. Over the last decade, functional genomics has arisen as a revolutionary tool for studying genetics and uncovering changes in gene expression. RNA-Seq has been applied to investigate the rare and novel transcripts that aid in discovering genetic changes that occur in tumours due to different lung cancers. Although RNA-Seq helps to understand and characterise the gene expression involved in lung cancer diagnostics, discovering the biomarkers remains a challenge. Usage of classification models helps uncover and classify the biomarkers based on gene expression levels over the different lung cancers. The current research concentrates on computing transcript statistics from gene transcript files with a normalised fold change of genes and identifying quantifiable differences in gene expression levels between the reference genome and lung cancer samples. The collected data is analysed, and machine learning models were developed to classify genes as causing NSCLC, causing SCLC, causing both or neither. An exploratory data analysis was performed to identify the probability distribution and principal features. Due to the limited number of features available, all of them were used in predicting the class. To address the imbalance in the dataset, an under-sampling algorithm Near Miss was carried out on the dataset. For classification, the research primarily focused on 4 supervised machine learning algorithms: Logistic Regression, KNN classifier, SVM classifier and Random Forest classifier and additionally, 2 ensemble algorithms were considered: XGboost and AdaBoost. Out of these, based on the weighted metrics considered, the Random Forest classifier showing 87% accuracy was considered to be the best performing algorithm and thus was used to predict the biomarkers causing NSCLC and SCLC. The imbalance and limited features in the dataset restrict any further improvement in the model’s accuracy or precision. In our present study using the gene expression values (LogFC, P Value) as the feature sets in the Random Forest Classifier BRAF, KRAS, NRAS, EGFR is predicted to be the possible biomarkers causing NSCLC and ATF6, ATF3, PGDFA, PGDFD, PGDFC and PIP5K1C is predicted to be the possible biomarkers causing SCLC from the transcriptome analysis. It gave a precision of 91.3% and 91% recall after fine tuning. Some of the common biomarkers predicted for NSCLC and SCLC were CDK4, CDK6, BAK1, CDKN1A, DDB2.
Keywords: Lung cancer, biomarkers, supervised machine learning, random forest classifier, RNA-Seq
Introduction
Lung cancer is indeed the most prevalent and the deadliest cancer. There are 2 forms of lung cancer: small cell lung cancer (SCLC) and non-small cell lung cancer (NSCLC). 1 Non-small cell lung cancer affects about 85% of people, whereas small cell lung cancer affects almost 14%. In non-small cell lung cancer (NSCLC), lung adenocarcinoma (LUAD) and lung squamous cell carcinoma (LUSC) are commonly recorded. While adenocarcinoma is more frequently found in women, non-smokers, and most Asian ethnicities, small cell lung cancer is more frequently detected in Caucasian men. Tobacco use may be the main cause of this. Patients with small cell lung cancer are not just those who smoke; they are also those who are heavily exposed to second-hand smoke, pollution, occupational toxins and hereditary genetics. Precautions can be taken by using nicotine without the use of drugs like varenicline or agonists for the nicotine acetylcholine receptor. Use of e-cigarettes is one of the alternatives to prevent cancer. 2
RNA sequencing would be preferable for detecting the beneficial genes since it provides biological information about the cells as well as a few in-silico analytical details, these techniques can predict future problems and more information about cancer application. 3 Next-generation sequencing plays a major role in RNA sequencing as the study includes applications of differential gene expression analysis, cancer biomarkers, cancer heterogeneity and evolution, cancer drug resistance, the microenvironment and immunotherapy. 4 Many techniques for analysing cancer data have recently become available, allowing researchers and doctors to access vast amounts of data to benefit cancer patients and add to existing research expertise. Mutaxome, as the name implies, is a database that was created for variants of 5 distinct cancer kinds utilising 20 different cancer exomes and contains thorough information about each sort of detected variant. 5 Despite the availability of credible sources for extracting this information, the database aids in the task of accurately analysing and forming conclusions based on all available facts. 6 A comprehensive analysis of cancer genomes and how they are regulated into proteins is necessary for understanding how cancer spreads. In this, a proteogenomic approach is used, in which protein variations are investigated using mass spectrometry-based proteomics to interpret structural changes and transition order of proteins, as well as the identification and validation of cancer-related mutations to explain the effects of mutations on genes and the identification of Oncogenes and tumour suppressor genes. 7
Artificial intelligence (AI) is the computer-programmed simulation of human intelligence. Artificial intelligence software tools have been used in genetics, patient demographics and medical imaging for research and clinical applications with the least amount of human intervention. Artificial intelligence tools are usually used to interpret, determine and provide clinical information regarding the patient. Machine learning (ML) is a part of artificial intelligence, this technique teaches algorithms to learn how to make conclusions. Thus, NSCLC and SCLC are 2 major lung cancer forms detected worldwide. Identifying biomarkers with respect to lung cancer is easier using machine learning techniques. The following section discusses studies conducted in the domain of machine learning for gene expression analysis, with a focus on the ones related to lung cancer.
Related Study
Radiomics is a branch of medicine that applies machine learning to quantitative data derived from medical pictures for purposes such as staging, therapy selection and response evaluation. Segmentation, feature extraction and machine learning modelling can all help with this. 4 The region of interest, which is usually a tumour, is segmented first, and then evaluated for numerical data known as handcrafted characteristics. These characteristics are usually made up of first-order, texture, size, and form characteristics that may be combined with genetics, histology, blood biomarkers and patient demographics to develop prediction models. 8 Some studies conducted on using machine learning for lung cancer classification were reviewed and they are discussed below.
Previous attempts at finding a solution to diagnosis of lung cancer has led to the development of Prostate, Lung, Colorectal and Ovarian Cancer Screening Trial risk model (mPLCOm2012). In this study, 9 the author has tried to use machine learning to predict lung cancer diagnosis. The data they used for this prediction as features were general clinical and lab data. The authors compared both the techniques and concluded that a machine learning model was more accurate for the early diagnosis of NSCLC. Previously developed models using machine learning techniques for early lung cancer detection gave accuracy which was not close to 90%. Therefore, a better model needs to be employed to increase the accuracy level, demonstrating the need for better ML approaches to help prevent lung cancer deaths through early detection. 10
Extensive research has been performed using machine learning techniques such as detection of sound and the study of CT Scan images for tracking down the infection.11,12 In the study 13 authors reviewed the recent progress of Support Vector Machine (SVM), an ML classification model, in cancer genomic studies and concluded the paper by listing the downsides of the SVM classifier along with suggestions for improving the performance of the classifier. 11
Further, neural networks on CT images attained higher accuracies of around 77%. 14 In one of the research, 15 the authors present 2 machine learning models for classifying cell subtypes from different pathological regions of NSCLC. They developed a Random Forest and a decision tree classifier which achieved a Mathews correlation coefficient of 0.786 between model predictions and actual results. To recognise the pattern for 4181 cancer polymorphisms that were identified across multiple cancer exome datasets that revealed common nucleotide base substitutions that happened most frequently, a Decision Support System based on a Random Forest classifier was constructed. The technique can also be used to diagnose other genetic illnesses early, allowing for more efficient decision-making in healthcare and medicine. 16 Though this algorithm supports the decision-making of identifying the mutation patterns, there is no focus on finding the biomarkers specific to cancer-based on the expression values analysed obtained from transcriptome analysis.
The objective of the present study is to develop and predict biomarkers of lung cancer using its semantic features and make a comparison between NSCLC and SCLC models. To achieve this, the paper compares 4 machine learning algorithms namely; Logistic regression (LR), K Nearest Neighbours(KNN), Support vector machine(SVM) and Random Forest Classifiers (RFC) was performed and more focus on the random forest technique was given as it performs regression and classification tasks, its prediction is easily understandable and most importantly it can handle large datasets effectively and has the high-level accuracy and the hypothesis of predicting a model using semantic and radiomic feature with high accuracy for NSCLC and SCLC is achieved using Random Forest Classifier.
Methodology and Implementation
Dataset collection
The dataset used for the transcriptome analysis is available on NCBI SRA under the project ID SRP117020. This dataset was collected from patients suffering from non-small cell lung cancer. The analysis was started from raw sequencing data in fastq format. The selected samples were representing male and female with age criteria more than 50 years. The data consisted of RNA sequences with distribution of poor to well differentiated adenocarcinomas and squamous cell cancers which were sequenced using Illumina Hiseq2500. The reference genome was obtained from the following page in NCBI (https://www.ncbi.nlm.nih.gov/assembly/GCF_000001405.26/).
Quality check
Quality of the RNAseq reads was inspected using FastQC software. 17
Read alignment and assembly of transcripts
RNA-seq reads were aligned to the human reference genome using a fast and sensitive alignment programme called HISAT2. 18 The experiment is carried out using a standard protocol of tuxedo suite tools for which is useful for analysis of RNA-Seq data. The protocol is well described by different processes which are more convenient to analyse raw sequences 19 of large data in the context here with the human genome.
Differential gene expression analysis
The transcripts and expression levels obtained from Stringtie were subjected to get the differentially expressed genes which was performed using DESeq2 package.20,21 The package uses statistical methods to get the differentially expressed genes. A collective gene expression data for 19777 genes were obtained in our study which was compressed and given as data for the current study. The differential expression table was obtained with 7 columns.
The first column classifies them either as UP or DOWN, or unclassified Gene. The fold-change and the natural logarithm of the fold-change value are the next 2 columns, the dataset also contains the natural logarithm of CPM (counts per million), P-value, and False Discovery Rate (FDR) value.
Where fold change indicates the gene expression level, it is the ratio between the final value and initial value. The log of the fold change value, >1 indicates that it is expressed at a lower level and values <1 indicate that it is expressed at a higher level. P-value indicates the probability of the expression value. 21 While CPM is the count sequence fragments library and multiplies the result by a million. And FDR measures the proportion of false discoveries among a set of hypothesis tests. 22 Thus, the algorithm is designed for gene names, up and down-regulated, fold value, log fold value and P-values and the table is given as Supplemental S1
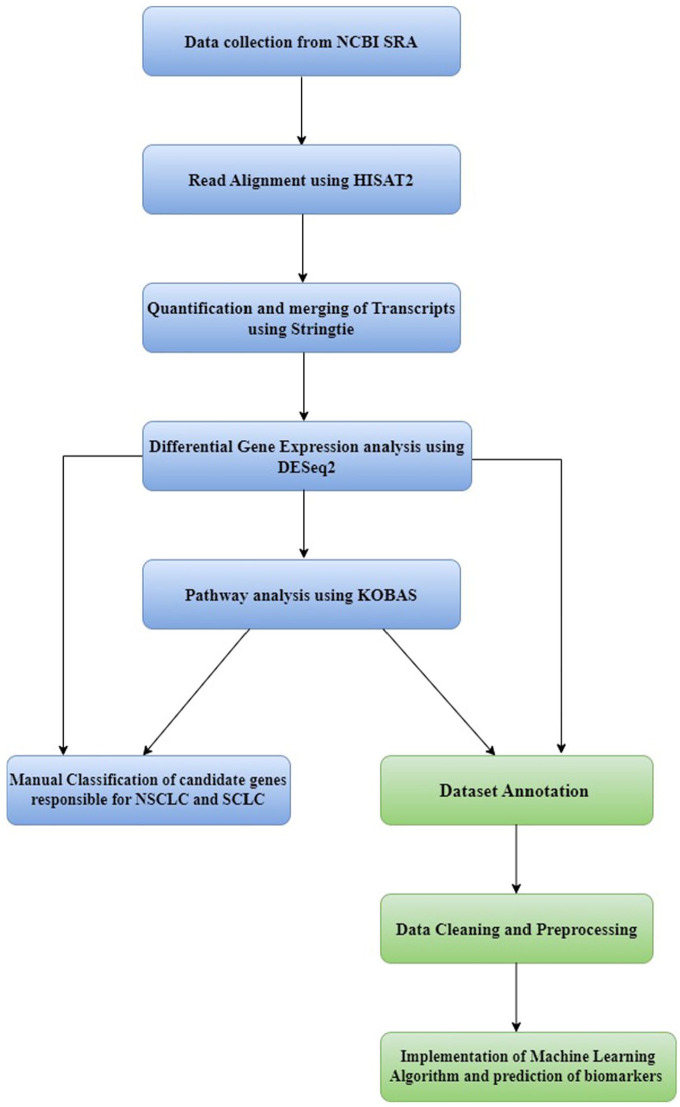
The differential gene expression analysis results were subjected to pathway analysis using KOBAS. The execution of the transcriptomics pipeline is given as a flowchart in Figure 1.
Figure 1.
Implementation of transcriptome analysis.
Dataset annotation
Annotating data is an important step as we intended to use supervised machine learning algorithms to automate the process of classification. The methods followed for classifying genes, was to identify literature in the domain of NSCLC and SCLC that relate to pathways causing the 2 diseases and review23-28 them. Then to identify the key pathways that are conclusively shown to cause NSCLC and SCLC of Lung cancer, respectively.
The genes considered for the study are processed using the KOBAS gene Oncology index to obtain the pathways they are involved in related to cancer. 29 This is then compared with the pathways that are shown to cause NSCLC and SCLC. For every gene if it is involved in a pathway that causes either NSCLC or SCLC it is annotated as ‘NSCLC’ or ‘SCLC’, respectively, and ‘Both’ if it is causing both or ‘None’ if it is involved in none of the pathways.
As annotated feature is a categorical value One-Hot Encoding is used to convert the categorical value to 2 binary features, NSCLC and SCLC. It is understood that if the value of both SCLC and NSCLC is 0 then it causes none of the diseases, and if the value of both is 1 then it causes both the diseases.
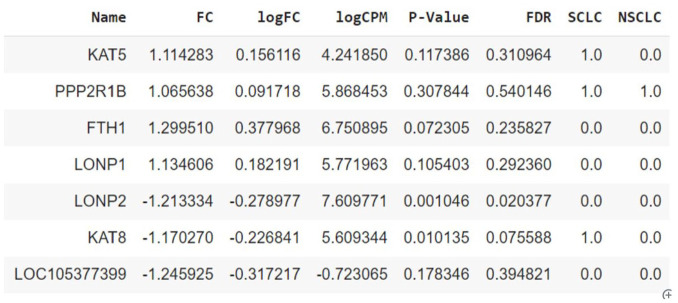
After One-Hot encoding the dataset has 19 777 records with 8 columns. A randomly chosen sample of the dataset is shown in Figure 2. The complete dataset can be found here.
Figure 2.
Randomly chosen sample of the dataset with 19 777 records and 8 columns.
After annotation, 691 genes were classified as causing NSCLC, and 921 genes were classified as causing SCLC.
Dataset Pre-processing
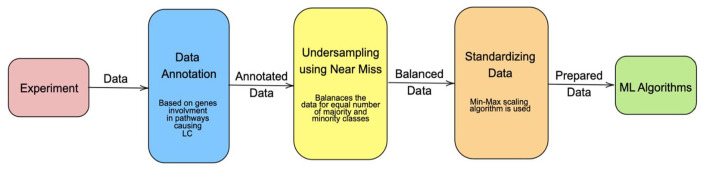
The complete process of data processing before analysis is represented as a flowchart in Figure 3.
Figure 3.
Flowchart chart for data preprocessing.
(1) Under-sampling using Near Miss: The number of genes classified as NSCLC and genes not classified as NSCLC is of the ratio 1:27.5 and the number of genes classified as SCLC and genes not classified as SCLC is of the ratio 1:21, which is known as the class weight ratio. To address the imbalance in the dataset, 3 options are available: using a downsampling algorithm to reduce the number of majority class data points to balance the dataset, using an up-sampling algorithm to synthetically generate new data points of the minority class to increase the number of samples and balance the class weight ratio. 30
Each of these algorithms has its own disadvantage, down sampling causes loss in information and up-sampling may corrupt the data. Therefore, a combination of both algorithms is used in most cases. 31 But for the dataset selected, up sampling is not a feasible option because the number of minority class data points is very less, which means the number of synthetically generated data points will be more than the actual number of real data points. This is undesirable and will result in the model being overfitted, because on average the synthetically generated data will be the same as the original data, when the number generated is comparable to the original number of available data points. Therefore, a down-sampling technique, called Near Miss, which is a heuristic sampling method that is based on the nearest neighbour’s algorithm is used to reduce the number of data points in the majority class (non-NSCLC or non-SCLC). 32 This algorithm was selected because it transforms the classes such that the width between the 2 classes is maximised, by removing data points close to the boundary.
(2) Standardised Scaling of Data: Initially, an exploration of data was performed to verify if the dataset warranted data cleaning, as shown in Table 1. It was found that there were no null values and outliers in any one feature were limited to a few samples. These were not discarded as they may contain valuable information about the dataset. However, the features set had values ranging between 2 arbitrary values. To avoid this difference from creating bias in the model, the values for all the features were scaled using a Gaussian scalar function, which subtracts the mean of the feature set from each value and then scales the set to unit variance. The equation (1) describes how each value (zi) is calculated from its initial value xi
Table 1.
Data Exploration results showing mean, standard deviation, minimum and maximum values for all the features.
| FC | logFC | logCPM | P-Value | FDR | |
|---|---|---|---|---|---|
| Count | 19 778.0 | 19 778.0 | 19 778.0 | 19 778.0 | 19 778.0 |
| Mean | 0.349 | 0.11 | 3.176 | 0.327 | 0.472 |
| Std | 2.277 | 0.604 | 3.037 | 0.31 | 0.317 |
| Min | −65.958 | −6.043 | −2.46 | 0.0 | 0.0 |
| Max | 119.924 | 6.906 | 14.555 | 1.0 | 1.0 |
| (1) |
where μ is the mean of values of a feature, and standard deviation is represented as σ. The processed dataset used is given as Supplemental Table S1.
Machine learning techniques
For training the Machine Learning model for the dataset, the following features were selected, FC, logFC, and P-value. The data was split into a training, testing and validation set in the proportion 60:20:20, respectively. Four types of Classification models were implemented and tested, Logistic Regression, KNN Classifier, Support Vector Machine Classifier and Random Forest Classifier. Precision is considered an appropriate performance metric for comparing the classifiers, because of the imbalance in the dataset. All the machine learning algorithms were implemented with Python using the scikit-learn library and the pre-processing of the data using the imbalance library.33,34 Code can be found in the GitHub repository (https://github.com/abhayhk2001/NSCLC-Gene-Classification). In the following subsections, we will discuss each technique and how it was implemented, fine-tuned and tested.
Python provides many model selection API’s, out of which we have used GridSearchCV()or RandomSearchCV() for hyper-tuning the model.35,36 Both the methods require the following parameters.
(1) The machine learning model instance
(2) Parameter space: set of parameters to be optimised and their values
(3) Method for evaluating
(4) score function
GridSearchCV() performs an exhaustive search of all the parameter combinations and evaluates the score function and returns the combination which gives the best results.
RandomSearchCV() searches the parameter space in an optimised way so the number of computations performed is minimal.
The score function is the evaluation metric that has to be maximised or minimised. Due to the unbalanced nature of the dataset average precision was chosen as the score function.
(1) Logistic Regression: Logistic Regression is a simple classification algorithm used for modelling a probability distribution of a discrete outcome of a variable. It is commonly used for binary classification, such as true/false, and yes/no. Logistic regression can be used for multinomial regression problems. 37 Despite being an extension of a linear regression to solve classification problems, the Logistic regression performs effectively with most problems.
The given data is in the form of (X, Y) where X is the matrix of features for every sample (m samples and n features) and Y is the target variable which is considered to be binary (0, 1). Logistic Regression trains a model to predict the class(Y) of a new vector Xq. To achieve this the logistic regressor approximates the conditional probability given by:
| (2) |
| (3) |
Equation (2) calculates the probability that the value of the target function is 1 given the values of the features and the weights and equation (3) calculates the probability that the value of the target function is 0 given the values of the features and the weights. 38 The function which separates the classes is chosen to be a linear combination of all the features. Let X = x1, x2 . . ., xn
where each xi is a vector of m values. Then the weight matrix is:
| (4) |
The output of the first iteration is calculated using the logistic function.
| (5) |
The loss function used by the logistic regression can be the cross-entropy loss function or the maximum likelihood estimate. 39 In the paper’s implementation the loss function used is the cross-entropy loss function given by equation (6) and the weight matrix is updated using equation (7).
| (6) |
| (7) |
This implementation of the Logistic Regression uses the API Logistic Regression () from Python’s sklearn.linear model library. The model was trained, then validated with the processed dataset and produces the following results after fine tuning. The fine-tuning hyperparameters used are inverse of regularisation strength(C), norm of the penalty (penalty) and algorithm to use in the optimization problem (solver). For Logistic regression the size of the parameter space is small and thus an exhaustive search for all the combinations was performed using GridSearchCV(). The best results were given when C = 1, penalty = ‘l1’ and solver = ‘liblinear’. In this case, the validation sets gave the following results (weighted average): accuracy 74%, precision 75%, recall 75% and F1 score 75%.
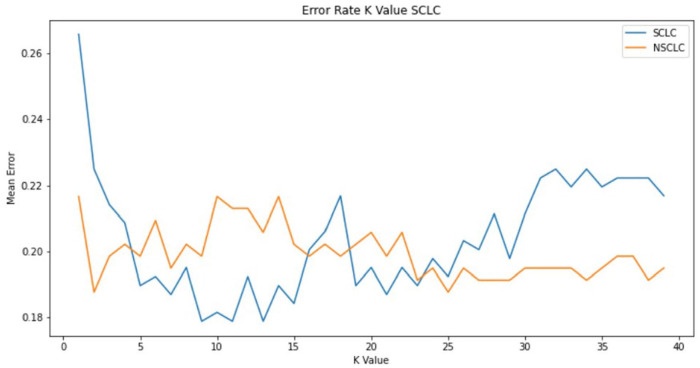
(2) kNN Classifier: K Nearest Neighbors Classification is one of the most common machine learning classifiers which can be easily understood visually. It is a non-parametric, lazy learning classification method, which classifies by first finding the k nearest neighbours of the given data point using euclidean distance and then using majority voting among those samples to estimate the class of the given data point. 40 kNN has proven to be an effective algorithm in multiple cases. However, the model is dependent on k, and its value has a major impact on the accuracy of the algorithm. The model is also dependent on the distance metric used to find the nearest neighbours. To tune the value of k the elbow method is used internally by Syakur et al. 41 This method plots the error of the model as a function of k as shown in Figure 4. The graph plotted is assumed to be a bent hand viewed from the side. When a steep decline is observed (the upper arm bend) the lower point of that steep decline is the optimal value of k (at the point where the elbow is present).
Figure 4.
Plot of error of model vs value of k – used by elbow method to find the optimal value of k for NSCLC (Orange) and SCLC (blue) models.
The distance metric used in the paper’s implementation is Euclidean distance. The distance between 2 points is given by:
| (8) |
where, x = {x1, x2, . . . xn}and y = {y1, y2, . . . yn} are 2 vectors describing the point’s position in Euclidean space. For any new point, xq the distance to all the points in the training set is calculated and the k nearest neighbours are found. The class of the new point is then estimated by finding the majority class of the k nearest neighbours. The equation describing the above steps is:
| (9) |
In equation (9) the function I returns 1 if the yi is of category j or 0 otherwise. kNN also has a high cost for classifying new data points, because all the computation takes place during testing, and verification and not during training. 42 Being simple, non-linear and not having intrinsic parameters are some of its advantages. It can perform poorly in higher-dimensional space but for our purpose, that will not be an issue.
This implementation of the KNN Classifier uses the API KNeighborsClassifier() from Python’s sklearn.neighbors library. 43 The model was trained, then validated with the processed dataset and produces the following results after fine tuning. The fine tuning hyperparameters for the kNN model are the number of neighbours to use (n neighbours) and the power parameter for the Minkowski metric (p).
For KNN classifiers the size of the parameter space is small and thus an exhaustive search for all the combinations was performed using GridSearchCV(). The best results were given when n neighbours = 9 and P = 1. In this case, the validation sets gave the following results (weighted average): accuracy 79%, precision 75%, recall 82% and F1 score 77%.
(3) Support Vector Classifier: Support vector machine classifier works by finding a decision boundary such that the data points, when plotted, are separated into classes by that hyperplane in the feature space, and the separation is the largest possible. Thus, it is called a maximum margin classifier. 44
The kernel trick is the advantage of using SVMs, this technique maps the features in a higher dimensional space in which the classes are well-separated by a hyperplane. 45 For a particular vector of features (x) the kernel function ϕ is applied and the result is a new vector with a different number of dimensions.
The mapping is described in equation (10).
| (10) |
Finding the hyperplane for classification is the task for the model. Due to low dimensionality, the performance of SVM models can be hindered. Any hypothesised hyperplane is described by:
| (11) |
where H represents the hyperplane equation, w is the vector of weights, b is the bias term of the hyperplane equation and x is the vector of features.
An SVM classifier with a radial basis function as its kernel function has to optimise the width of the Gaussian (γ = 0.5 × σ2, where σ is the width) and the soft margin parameter (C). 46 The value of C is a trade-off between a smooth decision surface (small C, less biassed) and a better fit (large C, more accurate). 47
This implementation of the Support vector machine classifier uses the API SVC () from Python’s sklearn.svm library. 48 The model was trained, then validated with the processed dataset and produces the following results after fine tuning. Fine Tuning was done with cross-validation where the training set is split randomly into n equal sets of data points. Sequentially the classifier is show n−1 of these sets, and then the remaining set is used to calculate the error in prediction. 49 This process is repeated n times with different choices for n and the average error is calculated for every parameter, Regularization parameter (C) and Kernel coefficient (gamma). 50 The pair of values which minimises the cross-validation error is selected as the best parameters. GridSearchCV() is used to perform this hyper parameter tuning. The best results were given when C = 1000 and gamma = 1, with the RBF kernel. In this case, the validation sets gave the following results: accuracy 81%, precision 83%, recall 82% and F1 score 82%.
(4) Random Forest Classifier: A random forest classifier, which is a collection of decision trees, is an ensemble learning method. It is a simple structure, simple to understand, and better efficient than similar approaches. The capacity to adapt to problem space settings and independence from the data domain is the most demanding concern with different types of classifiers 51 and this is where the Random Forest classifier performs better. They classify a datapoint by combining the predictions of multiple trees.
The Random Forest algorithm works based on Bagging. Bagging is a method of ensemble which divides the dataset into random subsets and each of these ‘bagged’ set is used to construct a basic decision tree. 52 This process is repeated multiple times to get a large enough set of trees, called a forest to give reasonable predictions. At each node of a tree, the algorithm decides the way of splitting the data based on one or more feature values. For classification problems, the output of the random forest is the output selected by most trees. They usually outperform decision trees. 53 Adding more trees does not improve test performance beyond a certain point, thus random forests are robust against overfitting.
To construct a decision tree the feature that has to be split is selected. To decide which split will be optimal a split measure is used. The Gini index, one such split measure, is calculated as shown in equation (12) and used as a measure for the impurity of a node, that is, if a split is performed based on the value, how distributed would each of the split datasets be. 48
| (12) |
This metric for measuring the impurity of a node is much more computationally efficient than Entropy. The lower the Gini index, the more optimal the node is for splitting. After the split, the separated nodes each have a subset of the dataset with lesser columns and one less feature. This process is repeated multiple times to construct a tree, and then a forest.
The random forest implementation in Scikit-Learn calculates the importance of a node using Gini Importance; it always generates a decision tree with 2 nodes. The Gini importance is calculated with:
| (13) |
where, GIj = the importance of node j, wj = weighted number of samples reaching node j, Cj = the impurity value of node j, left(j) = child node from left split on node j, right(j) = child node from right split on node j.
The importance of each feature vector is calculated as given in equation (14).
| (14) |
where fi = the importance of feature i, GIi = the importance of node j. Based on this metric the tree is built and then the next set of input vectors(bag) is selected and the same process is repeated. The final forest is a collection of generated trees. This implementation of the Support vector machine classifier uses the API RandomForestClassifier() from Python’s sklearn.ensemble library. 54 The model was trained, then validated with the processed dataset and produces the following results after fine tuning. The hyperparameters for a random forest classifier are: number of trees built during training (n estimators), the maximum number of features each node considers (max features), number of leaves required to split a node (min sample leaf), number of the processor to be used (n jobs) and the maximum depth of the tree (max depth).
The number of hyperparameters for random forest classifiers is large and thus the parameter space is also large. Using GridSearchCV() is an efficient method for hyperparameter tuning. Therefore, RandomSearchCV() was used to perform the hyperparameter tuning.
The best results were given when n estimators = 1200, max features = sqrt, min sample leaf = 4, n jobs = −1 and max depth = 100. In this case, the training and validation sets gave the following results: accuracy 87%, precision 86%, recall 84% and F1 score 85%.
Ensemble algorithms
Ensembling is a method by which many machine learning models are combined to form one better performing predictive model or ensemble model. 55 If we consider the based model to be a decision tree. An ensemble algorithm made of decision trees uses each tree’s output and aggregates the results. Similarly for other algorithms the ensembled version of that algorithm is more robust to small changes in the dataset and produces better results. 56
The paper implements 2 ensemble algorithms XgBoost and Adaboost algorithm and compares the result with the machine learning algorithms.
(1) XgBoost Algorithm: XGBoost stands for Extreme Gradient Boosting. Gradient Boosting is a popular boosting algorithm which evaluates the predictor produced, evaluates its errors and rectifies them in further iterations of the algorithm. XgBoost uses decision trees as its base model. It combines a linear model with a boosting tree model. 57 XgBoost rectifies errors created by previous decision trees and new trees are formed. Each tree is dependent on the previous tree. After a tree is formed the algorithm does not modify the weights of the decision tree.
The model is initialised as
| (15) |
Here f is the predictor, and L is the loss function. Then the gradient and hessian vector are calculated for the loss function with respect to the f.
Then the optimal predictor for the current iteration is calculated as shown in 17:
| (16) |
| (17) |
where, h is hessian matrix, g is gradient, and alpha is the learning rate.
All output variables have weights based on their priority. These values are changed after every iteration, and this variation leads to the ensembling nature of the algorithm. But due to its forest kind structure and aggregation, the interpretability of the algorithm is reduced. 58
Output of this algorithm is the predictor f, such that,
| (18) |
This implementation of the XGBoost Classifier uses the API XGBClassifier() from Python’s xgboost library. The model was trained, then validated with the processed dataset and produces the following results after fine tuning. The hyper parameter chosen to optimise XgBoost were: learning task (objective), the learning rate (learning rate), Maximum depth allowed for one decision tree (max depth), minimum sum of weight required in a child (min child weight), Sample ratio for training (subsample), number of boosting rounds (n estimators). Here the parameter space is large, so RandomSearchCV() is used to get the optimal parameters. The best results were given when ‘learning rate = 0.05, max depth = 5, min child weight = 11, n estimators = 7, objective = ‘reg:squarederror’, subsample = 0.7. The model gave a precision of
(2) AdaBoost Algorithm: AdaBoost stands for Adaptive Boosting. It is an ensemble algorithm used mainly for binary classification. It can be used to combine both weak learners and strong base models. In both cases if the performance of one is better than the previous iteration, it can be proven to converge to a better model than the base. 59 In some cases, AdaBoost is less susceptible to overfitting compared to other machine learning and ensemble algorithms. Generally, AdaBoost is used with decision trees with only one split as its base learner. This type of tree is called a decision stump. It works similarly to XGboost by assigning higher points to mis-classified data points and iterating the algorithm again. After a number of iterations, when the error is minimised, the algorithm is complete. 60
This implementation of the AdaBoost Classifier uses the API AdaBoostClassifier() from Python’s sklearn.ensemble library. 61 The model was trained, then validated with the processed dataset and produces the following results after fine tuning. The hyper parameters chosen to optimise AdaBoost were the learning rate (learning rate), number of boosting rounds (n estimators). Here the parameter space is small, so an exhaustive search was performed using GridSearchCV() to get the optimal parameters. The best results were given when ‘learning rate = 0.05, n estimators = 100. Table 7 shows the performance metrics for the AdaBoost model when tested with the validation set. The 3 metrics precision, recall and F1 score are shown for predicting NSCLC (1) or non-NSCLC (0) under the NSCLC column and similarly for SCLC.
Table 7.
Predicted biomarkers for SCLC from the ML Algorithm.
| Predicted genes for SCLC | Fold change | Log FC | P value |
|---|---|---|---|
| ATF6 | −1.074288737 | −0.10338 | .260387 |
| ATF3 | −1.197652552 | −0.26021 | .301848 |
| PIP5K1C | 1.009868788 | 0.014168 | .907544 |
| PDGFA | −1.243269508 | −0.31414 | .088348 |
| PDGFC | −1.506741298 | −0.59143 | .000298 |
| PDGFD | −1.260622972 | −0.33414 | .125071 |
Results and Discussion
Quality check and read alignment
The datasets collected when subjected to quality assessment. The reads showed good per base quality (ranging between 32 and 38) and average spot length of 199. The sequence length showed an average of 6-7 Giga base pairs (Gbp). Alignment of the reads to the human reference genome gave SAM files whose alignment rates were above 85% which was later converted to BAM which is the compressed binary version of SAM files. The alignment files were subjected to transcriptome reconstruction using StringTie resulting in an annotation file (gtf format). The transcript file and the alignment files are given as input for obtaining the differential gene expression.
Differential expression analysis
The relevant packages were installed to run DESeq2, and the phenotype data was loaded in .csv format which contained sample ID and Gender of the sample. The transcriptome pipeline was run between 2 sample sets (male and female). DESeq2 has the requirement namely reference and sample condition. Females were chosen to be the reference condition and Males were chosen to be the sample condition as this experimental design gives a comparison between the 2 conditions. Differential gene expression was run between the male and female samples which gave a table with 3 main values. One, fold change value referring to the ratio between expression levels in male and female. Two, the log of the fold changes value. The fold change values that are <1 indicate that it is expressed at a lower level and values >1 indicate that it is expressed at a higher level. The fold change values indicate the up and downregulation of the genes (1 indicating upregulation and −1 indicating down regulation). Lastly, P-value indicates the probability of the expression value. When all the differentially expressed genes obtained from DeSeq2 were subjected to pathway analysis using KOBAS the field organism was set to be Homo sapiens and method as Gene symbol ID. The differentially expressed genes were involved in different pathways. Manual analysis for classifying the genes from transcriptome analysis causing non-small cell lung cancer and small cell lung cancer was performed before the implementation of ML algorithm. The genes that had the hit specific to NSCLC and SCLC were considered and shortlisted as possible biomarkers from the transcriptome analysis performed. The genes with specific pathway hit to only non-small cell lung cancer and small cell lung cancer were taken which is shown in Tables 2 and 3. The table shows the genes which are differentially expressed with the fold change. The biomarkers shortlisted have fold change values of 1 and -1 indicating the up and down regulation.
Table 2.
Genes classified to cause non-small cell lung cancer based on fold change values and Pathway hit specific to NSCLC.
| GENE name | Fold change | LogFC | P-value |
|---|---|---|---|
| BRAF | −1.175047077 | −0.232718558 | .018633125 |
| MAP2K1 | −1.022807008 | −0.03253395 | .744522768 |
| KRAS | 1.127233255 | 0.172786079 | .188553802 |
| EGFR | −1.414885263 | −0.500685065 | .058563585 |
| NRAS | 1.30453481 | 0.383535442 | .011449642 |
Table 3.
Genes classified to cause small cell lung cancer based on fold change values and Pathway hit specific to SCLC.
| Gene name | Fold change | LogFC | P-value |
|---|---|---|---|
| E2F3 | 1.009993658 | 0.014346234 | .913188853 |
| FHIT | −1.15175616 | −0.203835313 | .164771745 |
| ATF6 | −1.074288737 | −0.103381799 | .260386661 |
| GADD45A | −1.136079068 | −0.184063246 | .346845743 |
| CDK6 | 1.11646539 | 0.158938528 | .397918418 |
| PDGFA | −1.243269508 | −0.314139069 | .088348324 |
| PDGFC | −1.506741298 | −0.591431732 | .000298007 |
Once Transcriptome analysis was performed and the genes responsible for NSCLC and SCLC were classified, the differential gene expression table was subjected to ML implementation.
ML model results
For a classification problem, the performance evaluation is done through the confusion matrix. It is a 2 × 2 matrix with the primary diagonal representing the True positive (TP), predicted and actual are positive and true negative (TN), predicted and actual are negative. The other diagonal has False positive (FP) predicted is negative but actual is negative and False negative (FN) predicted is negative but actual is negative. The performance metrics are accuracy, precision, recall (sensitivity) and F1 score, which are defined by the equations (19)–(22), respectively.
| (19) |
| (20) |
| (21) |
| (22) |
For each algorithm accuracy, precision, recall and F1 score for classes 0 and 1 with the weighted average are given in Tables 4 and 5 for NSCLC and SCLC respectively.
Table 4.
Table of performance metrics of different ML algorithms for NSCLC.
| ML model | Class | NSCLC | |||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 score | ||
| Logistic regression | 0 | 0.68 | 0.68 | 0.68 | 0.71 |
| 1 | 0.68 | 0.68 | 0.68 | 0.81 | |
| W. Avg | 0.68 | 0.68 | 0.68 | 0.77 | |
| k-Nearest neighbours | 0 | 0.7 | 0.84 | 0.76 | 0.76 |
| 1 | 0.76 | 0.79 | 0.77 | 0.76 | |
| W. Avg | 0.73 | 0.82 | 0.77 | 0.76 | |
| Support vector machine | 0 | 0.74 | 0.88 | 0.8 | 0.84 |
| 1 | 0.87 | 0.71 | 0.78 | 0.86 | |
| W. Avg | 0.8 | 0.79 | 0.79 | 0.85 | |
| Random forest classifier | 0 | 0.79 | 0.87 | 0.86 | 0.84 |
| 1 | 0.88 | 0.79 | 0.82 | 0.89 | |
| W. Avg | 0.85 | 0.84 | 0.84 | 0.86 | |
| XgBoost algorithm | 0 | 0.86 | 0.80 | 0.83 | 0.82 |
| 1 | 0.79 | 0.85 | 0.82 | 0.79 | |
| W. Avg | 0.83 | 0.82 | 0.82 | 0.81 | |
| AdaBoost algorithm | 0 | 0.80 | 0.84 | 0.83 | 0.80 |
| 1 | 0.83 | 0.79 | 0.81 | 0.85 | |
| W. Avg | 0.81 | 0.81 | 0.81 | 0.83 | |
Table 5.
Table of performance metrics of different ML algorithms for SCLC.
| ML model | Class | SCLC | |||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 score | ||
| Logistic regression | 0 | 0.83 | 0.76 | 0.68 | 0.68 |
| 1 | 0.7 | 0.75 | 0.68 | 0.68 | |
| W. Avg | 0.76 | 0.76 | 0.68 | 0.68 | |
| k-nearest neigh-bours | 0 | 0.85 | 0.77 | 0.7 | 0.84 |
| 1 | 0.79 | 0.76 | 0.76 | 0.79 | |
| W. Avg | 0.82 | 0.77 | 0.73 | 0.82 | |
| Support vector machine | 0 | 0.88 | 0.86 | 0.74 | 0.88 |
| 1 | 0.82 | 0.84 | 0.87 | 0.71 | |
| W. Avg | 0.85 | 0.85 | 0.8 | 0.79 | |
| Random forest classifier | 0 | 0.88 | 0.87 | 0.79 | 0.87 |
| 1 | 0.77 | 0.83 | 0.88 | 0.79 | |
| W. Avg | 0.85 | 0.85 | 0.85 | 0.84 | |
| XgBoost algorithm | 0 | 0.80 | 0.81 | 0.86 | 0.80 |
| 1 | 0.79 | 0.80 | 0.79 | 0.85 | |
| W. Avg | 0.81 | 0.81 | 0.83 | 0.82 | |
| AdaBoost algorithm | 0 | 0.85 | 0.82 | 0.80 | 0.84 |
| 1 | 0.81 | 0.83 | 0.83 | 0.79 | |
| W. Avg | 0.83 | 0.83 | 0.81 | 0.81 | |
Precision and F1 score were taken as the most important performance metric. This is because of the imbalance in the dataset and precision is used to get a class wise performance of the algorithm rather than the overall performance which is offered by accuracy, f1 score combines the precision and recall results to get an overall performance without losing information about the class wise divide. The paper focuses on the True positives because they are the biomarkers for the NSCLC and SCLC respectively. Considering these metrics, the Random Forest classifier performed well as its prediction is based on the feature values. kNN classifier and Support vector machine classifier’s performance was similar and they perform worse than the random forest classifier. The worst performer was the logistic regressor, possibly because of the limited number of features.
ROC curve for the models
The Receiver Operating Characteristic (ROC) curve is a graph used in a binary classification model to determine the optimal threshold for the classification curve. It is a plot of True Positive Rate vs False Positive Rate (TPR vs FPR). The value of TPR is calculated as in Equation 23 which is equal to sensitivity of the model, equation (21) and the value of FPR is calculated as in equation (24).
| (23) |
| (24) |
In Figure 5, the ROC curve is plotted for the Logistic Regression (Logistic), K-Nearest Neighbours (kNN), Support Vector Machine (SVM) and Random Forest Classifier (RFC) classifiers. Their respective AUC values are also mentioned. The ROC curve for the Random Forest Classifier flattens above all other classifier’s curves, therefore it can be concluded that Random Forest Classifier is best performing classifier. The AUC values for the classifiers will justify this statement. AUC (Area Under the curve) measures the 2D area under the ROC curve. The ROC curve, along with the Area under the curve (AUC) values for each of the 4 classifiers is shown in Figure 3, based on their performance on the final test set.
Figure 5.
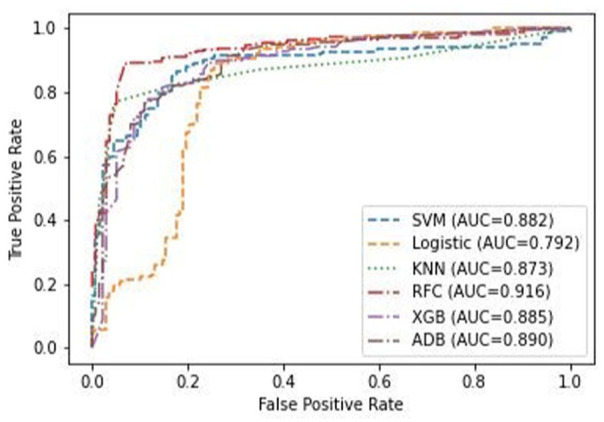
ROC curve and AUC values for the 4 different classifiers: Support Vector Machine (blue), Logistic Regression (orange), KNN Classifier (green) and Random Forest Classifier (red).
Best performing algorithm
If ROC curves for two different models do not intersect when plotted, their AUC values can be used to compare the model’s performance [41,62,63]. An ideal ROC curve has a steep increase (large TPR for low FPR) in the beginning and then flattens out, i.e., it will have a high AUC value (≈ 1). Therefore, the higher the AUC value the better the performance of the model. In this case, the Random Forest Classifier has the highest AUC value of 0.9. Thus, from observation and the AUC values, it can be conclusively stated that Random Forest Classifier is the best-performing algorithm for the dataset used in the experiment, and has been shown to perform well for similar classification problems in bioinformatics.
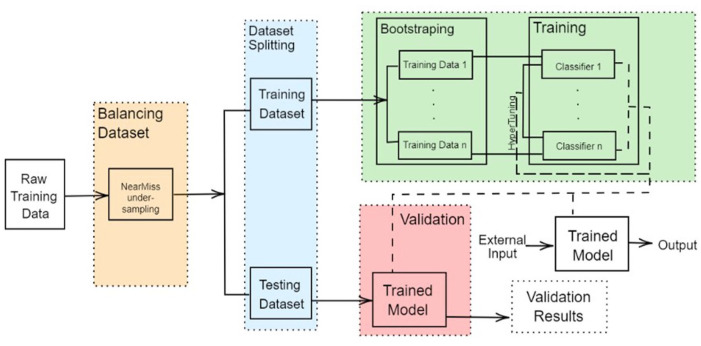
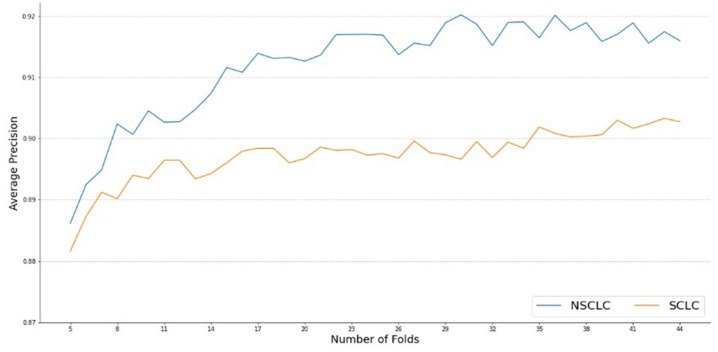
Therefore, the model was validated using the validation set on the Random Forest classifier to get the best possible result without overfitting. This was done through a cross-validation technique with different values of n, to see if the performance flattens. Figure 6 shows this process as a flowchart with the Bootstrapping method used to run multiple trainings on the model to improve it each time. The algorithm was able to increase its average precision by 0.4 units and the model gave an average precision of 0.91 and F1 score of 0.92. Figure 7 shows the plot of average precision vs the cross-validation fold value (n). This graph has one line showing the performance on the SCLC classification and the other showing performance of the NSCLC classification.
Figure 6.
Flowchart for the Bootstrapping method used to improve Random Forest Classifier model.
Figure 7.
Average Precision of Random Forest Classifier after using Bootstrapping method to improve the model for NSCLC (blue) and SCLC (orange).
Therefore, this technique can be used to identify if a gene is involved in a pathway that causes either NSCLC or SCLC or not, with feature values such as FC value, the logarithm of FC value and p-Value. The Random Forest Model will be able to identify the genes with reasonable accuracy.
Prediction of the Genes responsible for non-small cell lung cancer and small cell lung cancer
Differential expression analysis of the transcriptome sequence showed BRAF, MAP2K1, KRAS, EGFR, NRAS to be the possible markers for NSCLC and E2F3, FHIT, ATF6, GADD45A, CDK6, PDGFA, PDGFC to be the genes causing SCLC.
The ML algorithm implemented with the features logFC and p-value showed some of the candidate genes that could be possible biomarkers for NSCLC, SCLC and common biomarkers. The biomarker prediction from the ML algorithm is shown in Tables 6 to 8.
Table 6.
Predicted biomarkers for NSCLC from ML algorithm.
| Predicted genes for NSCLC | Fold change | LogFC | P value |
|---|---|---|---|
| BRAF | −1.17505 | −0.23272 | .01863 |
| KRAS | 1.12723 | 0.17279 | .18855 |
| NRAS | 1.30453 | 0.38354 | .01145 |
| EGFR | −1.41489 | −0.50069 | .05856 |
Table 8.
Common biomarkers for NSCLC and SCLC from ML Algorithm.
| Common markers for NSCLC and SCLC | Fold change | Log FC | P value |
|---|---|---|---|
| CDK4 | 1.122603645 | 0.166849 | .432725 |
| BAK1 | −1.034605696 | −0.04908 | .74456 |
| CDK6 | 1.11646539 | 0.158939 | .397918 |
| CDKN1A | −1.015498272 | −0.02219 | .895518 |
| DDB2 | 1.140508189 | 0.189677 | .110408 |
| E2F3 | 1.009993658 | 0.014346 | .913189 |
| FHIT | −1.15175616 | −0.20384 | .164772 |
| GADD45A | −1.136079068 | −0.18406 | .346846 |
Conclusion
Lung cancer is one of the most lethal cancers on the globe. There are 2 forms of lung cancer: non-small cell lung cancer and small cell lung cancer. Genes that regulated up and down were identified using RNA-seq. The massive data was assembled using artificial intelligence and machine learning, and a random forest was created to simplify and make it easier to grasp. Non-small cell lung cancer and small cell lung cancer are the 2 types of lung cancer that the model was created to classify. This is done to find the genes that correspond to one of the pathways in each category. These genes that were discovered are lung cancer biomarkers.
Four Machine Learning Algorithms were compared, and each algorithm had a marginal difference in accuracy. Random Forest Classifier showed 87% accuracy and helped us in classifying the biomarkers causing non-small cell lung cancer and small cell lung cancer. With an external system the code will be able to detect any genes that may be involved in either SCLC or NSCLC pathways and then return the names of these genes, these are the biomarkers for the disease. From the study BRAF, KRAS, NRAS and EGFR could be the possible biomarkers for NSCLC and ATF6, ATF3, PGDFA, PGDFD, PGDFC and PIP5K1C could be the possible biomarkers for SCLC. Additionally, the model also predicted a few possible common markers for NSCLC and SCLC; CDK1, CDK6, BAK1, DDB2, E2F3, FHIT, GADD45A, CDKN1A. The authors intend to expand their research in order to increase the model's accuracy in the near future which will be performed using multi-layer artificial neural networks and Generative Adversarial Network (GAN) analysis. Therefore, the current study offers significant insights on biomarkers for lung cancer.
Supplemental Material
Supplemental material, sj-xlsx-1-cix-10.1177_11769351231167992 for Novel Biomarker Prediction for Lung Cancer Using Random Forest Classifiers by Lavanya C, Pooja S, Abhay H Kashyap, Abdur Rahaman, Swarna Niranjan and Vidya Niranjan in Cancer Informatics
Acknowledgments
The authors would like to acknowledge Mr. Akshay Uttarkar for reviewing the manuscript and providing valuable suggestions. We would like to thank Dr. Anala, Department of Information Science and Engineering, R V College of Engineering for providing access to NVIDIA TITANX GPU for analysis.
Footnotes
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author Contributions: Author Vidya Niranjan conceptualised the idea for the project and was involved in data analysis and project implementation. Authors Abhay H Kashyap and Abdur Rahaman were involved in implementing the algorithms, data analysis and writing the manuscript. Authors Lavanya C and Pooja S and Swarna Niranjan were involved in writing the manuscript, data analysis and collecting preliminary data required for this project.
Data availability Statement: Raw Data used for performing the transcriptome analysis and obtaining the log2fold values is available in NCBI SRA under the Project ID SRP117020. The input dataset for implementing the machine learning algorithm is given in Supplemental Table S1.
Supplemental Material: Supplemental material for this article is available online.
References
- 1.Herbst RS, Morgensztern D, Boshoff C.The biology and management of non-small cell lung cancer. Nature. 2018;553:446-454. [DOI] [PubMed] [Google Scholar]
- 2.Fagerström K, Hughes J.Varenicline in the treatment of tobacco dependence. Neuropsychiatr Dis Treat. 2008;4:353-363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou M, Leung A, Echegaray S, et al. Non-small cell lung cancer radiogenomics map identifies relationships between molecular and imaging phenotypes with prognostic implications. Radiology. 2018;286:307-315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hong M, Tao S, Zhang L, et al. RNA sequencing: new technologies and applications in cancer research. J Hematol Oncol. 2020;13:166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Padmavathi P, Setlur AS, Chandrashekar K, Niranjan V.A comprehensive in-silico computational analysis of twenty cancer exome datasets and identification of associated somatic variants reveals potential molecular markers for detection of varied cancer types. Inform Med Unlocked. 2021;26:100762. doi: 10.1016/j.imu.2021.100762 [DOI] [Google Scholar]
- 6.Padmavathi P, Chandrashekar K, Setlur AS, Niranjan V.MutaXome: a novel database for identified somatic variations of in silico analyzed cancer exome datasets. Cancer Inform. 2022;21:11769351221097593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ramesh P, Nagarajan V, Khanchandani V, Desai VK, Niranjan V.Proteomic variations of esophageal squamous cell carcinoma revealed by combining RNA-seq proteogenomics and G-PTM search strategy. Heliyon. 2020;6:e04813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Christie JR, Lang P, Zelko LM, Palma DA, Abdelrazek M, Mattonen SA.Artificial intelligence in lung cancer: bridging the gap between computational power and clinical decision-making. Can Assoc Radiol J. 2020;72:86-97. [DOI] [PubMed] [Google Scholar]
- 9.Gould MK, Huang BZ, Tammemagi MC, Kinar Y, Shiff R.Machine learning for early lung cancer identification using routine clinical and laboratory data. Am J Respir Crit Care Med. 2021;204:445-453. [DOI] [PubMed] [Google Scholar]
- 10.Stephen E, Joshua SEN, Bhattacharyya D, Janarthanan M.An extensive review on lung cancer detection using machine learning techniques. J Crit Rev. 2020;7:2020. doi: 10.31838/jcr.07.14.68 [DOI] [Google Scholar]
- 11.Poreva A, Karplyuk Y, Vaityshyn V.Machine learning techniques application for lung diseases diagnosis. Paper presented at: 2017 5th IEEE Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE); November 24-25, 2017; Riga, Latvia. [Google Scholar]
- 12.Yu L, Tao G, Zhu L, et al. Prediction of pathologic stage in non-small cell lung cancer using machine learning algorithm based on CT image feature analysis. BMC Cancer. 2019;19:464-464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang S, Cai N, Pacheco PP, Narrandes S, Wang Y, Xu W.Applications of support vector machine (SVM) learning in cancer genomics. Cancer Genomics Proteomics. 2018;15:41-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wu Q, Zhao W.Small-cell lung cancer detection using a supervised machine learning algorithm. Paper presented at: 2017 International Symposium on Computer Science and Intelligent Controls (ISCSIC); October 20-22, 2017; Budapest, Hungary. [Google Scholar]
- 15.Huang G-H, Zhang Y-H, Chen L, Li Y, Huang T, Cai Y-D.Identifying lung cancer cell markers with machine learning methods and single-cell RNA-seq data. Life (Basel). 2021;11:940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chaudhuri R, Deb S.Machine learning approaches for microscopic image analysis and microbial object detection (MOD) as a decision support system. Paper presented at: 2022 First International Conference on Artificial Intelligence Trends and Pattern Recognition (ICAITPR); March 10-12, 2022; Hyderabad, India. [Google Scholar]
- 17.Leggett RM, Ramirez-Gonzalez RH, Clavijo BJ, Waite D, Davey RP.Sequencing quality assessment tools to enable data-driven informatics for high throughput genomics. Front Genet. 2013;4:288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim D, Langmead B, Salzberg SL.HISAT: a fast spliced aligner with low memory requirements. Nat Methods. 2015;12:357-360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pertea M, Kim D, Pertea GM, Leek JT, Salzberg SL.Transcript-level expression analysis of RNA-seq experiments with HISAT, StringTie and Ballgown. Nat Protoc. 2016;11:1650-1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Frazee AC, Pertea G, Jaffe AE, Langmead B, Salzberg SL, Leek JT.Ballgown bridges the gap between transcriptome assembly and expression analysis. Nat Biotechnol. 2015;33:243-246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Love MI, Huber W, Anders S.Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15:550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Benjamini Y, Hochberg Y.Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B (Methodol). 1995;57:289-300. [Google Scholar]
- 23.Pennell NA, Lynch TJ.Combined inhibition of the VEGFR and EGFR signaling pathways in the treatment of NSCLC. Oncologist. 2009;14:399-411. [DOI] [PubMed] [Google Scholar]
- 24.Tsoukalas N, Aravantinou-Fatorou E, Baxevanos P, et al. Advanced small cell lung cancer (SCLC): new challenges and new expectations. Ann Transl Med. 2018;6:145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cristea S, Sage J.Is the canonical RAF/MEK/ERK signaling pathway a therapeutic target in SCLC? J Thorac Oncol. 2016;11:1233-1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sabari JK, Lok BH, Laird JH, Poirier JT, Rudin CM.Unravelling the biology of SCLC: implications for therapy. Nat Rev Clin Oncol. 2017;14:549-561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reungwetwattana T, Weroha SJ, Molina JR.Oncogenic pathways, molecularly targeted therapies, and highlighted clinical trials in non–small-cell lung cancer (NSCLC). Clin Lung Cancer. 2012;13:252-266. [DOI] [PubMed] [Google Scholar]
- 28.Gupta A, Soto D, Feldman M, et al. Signaling pathways in NSCLC as a predictor of outcome and response to therapy. Lung. 2004;182:151-162. [DOI] [PubMed] [Google Scholar]
- 29.Bu D, Luo H, Huo P, et al. KOBAS-i: intelligent prioritization and exploratory visualization of biological functions for gene enrichment analysis. Nucleic Acids Res. 2021;49:W317-W325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gosain A, Sardana S.Handling class imbalance problem using oversampling techniques: a review. Paper presented at: 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI); September 13-16, 2017; Udupi, India. [Google Scholar]
- 31.Speed FM, Hocking RR, Hackney OP.Methods of analysis of linear models with unbalanced data. J Am Stat Assoc. 1978;73:105-112. [Google Scholar]
- 32.Bej S, Davtyan N, Wolfien M, Nassar M, Wolkenhauer O.LoRAS: an oversampling approach for imbalanced datasets. Mach Learn. 2020;110:279-301. [Google Scholar]
- 33.Abraham A, Pedregosa F, Eickenberg M, et al. Machine learning for neuroimaging with scikit-learn. Front Neuroinform. 2014;8:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dorn M., Grisci B. I., Narloch P. H., Feltes B. C., Avila E., Kahmann A., Alho C. S. (2021). Comparison of machine learning techniques to handle imbalanced COVID-19 CBC datasets. PeerJ Computer Science, 7, e670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pirjatullah KD, Nugrahadi DT, Muliadi FA.Hyperparameter tuning using GridsearchCV on the comparison of the activation function of the ELM method to the classification of pneumonia in toddlers. Paper presented at: 2021 4th International Conference of Computer and Informatics Engineering (IC2IE); September 14-15, 2021; Depok, Indonesia. [Google Scholar]
- 36.Rahman AA, Siraji MI, Khalid LI, et al. Detection of mental state from EEG signal data: an investigation with machine learning classifiers. Paper presented at: 2022 14th International Conference on Knowledge and Smart Technology (KST); January 26-29, 2022; Chon buri, Thailand. [Google Scholar]
- 37.Tolles J, Meurer WJ.Logistic regression. JAMA. 2016;316:533. [DOI] [PubMed] [Google Scholar]
- 38.Hosmer DW, Lemeshow S, Sturdivant RX.Applied Logistic Regression. Wiley Series in Probability and Statistics. Wiley; 2013. [Google Scholar]
- 39.Gourieroux C, Monfort A.Asymptotic properties of the maximum likelihood estimator in dichotomous logit models. J Econom. 1981;17:83-97. [Google Scholar]
- 40.Cunningham P, Delany SJ.K-nearest neighbour classifiers: a tutorial. ACM Comput Surv. 2021;54:1-25. [Google Scholar]
- 41.Syakur MA, Khotimah BK, Rochman EMS, Satoto BD.Integration K-means clustering method and elbow method for identification of the best customer profile cluster. IOP Conf Ser: Mater Sci Eng. 2018;336:012017. [Google Scholar]
- 42.Guo G, Wang H, Bell D, Bi Y, Greer K.KNN model-based approach in classification. Meersman R, Tari Z, Schmidt DC, eds. On the Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE. Springer; Berlin Heidelberg; 2003:986-996. [Google Scholar]
- 43.Pandya VJ.Comparing handwritten character recognition by AdaBoostClassifier and KNeighborsClassifier. Paper presented at: 2016 8th International Conference on Computational Intelligence and Communication Networks (CICN); December 23-25, 2016; Tehri, India. [Google Scholar]
- 44.Cortes C, Vapnik V.Support-vector networks. Mach Learn. 1995;20:273-297. [Google Scholar]
- 45.Multi-Layer Support Vector Machines. Regularization, Optimization, Kernels, and Support Vector Machines. Chapman and Hall/CRC; 2014:475-494. [Google Scholar]
- 46.Schölkopf B, Tsuda K, Vert J-P, eds. Kernel Methods in Computational Biology. The MIT Press; 2004. [Google Scholar]
- 47.Molina-Cabello MA, Luque-Baena RM, Lopez-Rubio E, Deka L, Thurnhofer-Hemsi K.Road pollution estimation using static cameras and neural networks. Paper presented at: 2018 International Joint Conference on Neural Networks (IJCNN); July 8-13, 2018; Rio de Janeiro, Brazil. [Google Scholar]
- 48.Nordhausen K.The elements of statistical learning: data mining, inference, and prediction, second edition by Trevor Hastie, Robert Tibshirani, Jerome Friedman. Int Stat Rev. 2009;77:482. [Google Scholar]
- 49.Chang C-C, Lin C-J.LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol. 2011;2:1-27. [Google Scholar]
- 50.Stone M.An asymptotic equivalence of choice of model by cross-validation and Akaike’s criterion. J R Stat Soc: Ser B (Methodol). 1977;39:44-47. [Google Scholar]
- 51.Crammer K, Gentile C.Multiclass classification with bandit feedback using adaptive regularization. Mach Learn. 2012;90:347-383. [Google Scholar]
- 52.Lambin P, Leijenaar RTH, Deist TM, et al. Radiomics: the bridge between medical imaging and personalized medicine. Nat Rev Clin Oncol. 2017;14:749-762. [DOI] [PubMed] [Google Scholar]
- 53.Opitz D, Maclin R.Popular ensemble methods: an empirical study. J Artif Intell Res. 1999;11:169-198. [Google Scholar]
- 54.Lerman RI, Yitzhaki S.A note on the calculation and interpretation of the Gini index. Econ Lett. 1984;15:363-368. doi: 10.1016/0165-1765(84)90126-5 [DOI] [Google Scholar]
- 55.Breiman L.Random forests. Mach Learn. 2001;45:5-32. [Google Scholar]
- 56.Sagi O, Rokach L.Ensemble learning: a survey. WIREs Data Min Knowl Discov. 2018;8:e1249. [Google Scholar]
- 57.Rokach L.Ensemble-based classifiers. Artif Intell Rev. 2009;33:1-39. [Google Scholar]
- 58.Chen T, Guestrin C.XGBoost. Paper presented at: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; August 13-17, 2016; San Francisco, CA, USA. [Google Scholar]
- 59.Nokeri T. C., Nokeri T. C. (2022). Tree Modeling and Gradient Boosting with Scikit-Learn, XGBoost, PySpark, and H2O. Data Science Solutions with Python: Fast and Scalable Models Using Keras, PySpark MLlib, H2O, XGBoost, and Scikit-Learn, 59-74. [Google Scholar]
- 60.Schapire RE. Explaining AdaBoost. Empirical Inference. Springer; Berlin Heidelberg; 2013:37-52. [Google Scholar]
- 61.Sevinç E. An empowered AdaBoost algorithm implementation: a COVID-19 dataset study. Comput Ind Eng. 2022;165:107912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Demir S, Sahin EK.An investigation of feature selection methods for soil liquefaction prediction based on tree-based ensemble algorithms using AdaBoost, gradient boosting, and XGBoost. Neural Comput Appl. 2023;35:3173-3190. [Google Scholar]
- 63.Vihinen M.How to evaluate performance of prediction methods? Measures and their interpretation in variation effect analysis. BMC Genomics. 2012;13:S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, sj-xlsx-1-cix-10.1177_11769351231167992 for Novel Biomarker Prediction for Lung Cancer Using Random Forest Classifiers by Lavanya C, Pooja S, Abhay H Kashyap, Abdur Rahaman, Swarna Niranjan and Vidya Niranjan in Cancer Informatics