Abstract
Graph contrastive learning has been developed to learn discriminative node representations on homogeneous graphs. However, it is not clear how to augment the heterogeneous graphs without substantially altering the underlying semantics or how to design appropriate pretext tasks to fully capture the rich semantics preserved in heterogeneous information networks (HINs). Moreover, early investigations demonstrate that contrastive learning suffer from sampling bias, whereas conventional debiasing techniques (e.g., hard negative mining) are empirically shown to be inadequate for graph contrastive learning. How to mitigate the sampling bias on heterogeneous graphs is another important yet neglected problem. To address the aforementioned challenges, we propose a novel multi-view heterogeneous graph contrastive learning framework in this paper. We use metapaths, each of which depicts a complementary element of HINs, as the augmentation to generate multiple subgraphs (i.e., multi-views), and propose a novel pretext task to maximize the coherence between each pair of metapath-induced views. Furthermore, we employ a positive sampling strategy to explicitly select hard positives by jointly considering semantics and structures preserved on each metapath view to alleviate the sampling bias. Extensive experiments demonstrate MCL consistently outperforms state-of-the-art baselines on five real-world benchmark datasets and even its supervised counterparts in some settings.
Subject terms: Applied mathematics, Computer science, Information technology
Introduction
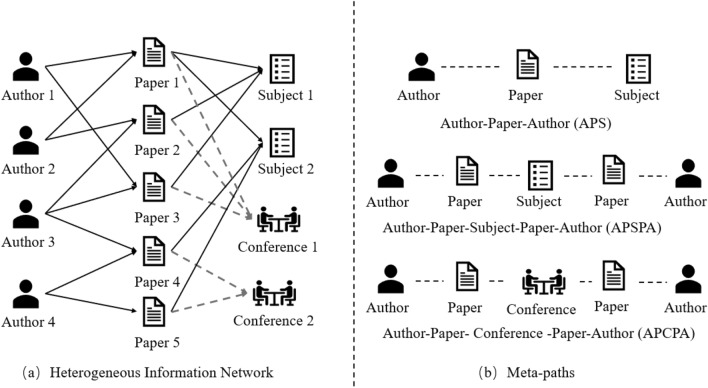
Considering the capacity for modeling complex systems, Heterogeneous Information Networks (HINs) that preserves rich semantic information have become a powerful tool for analyzing real-world graphs1–5. As illustrated in Fig. 1, we present a concise example of a heterogeneous bibliography network with four types of nodes and three types of relations. Recently, Graph Neural Networks (GNNs)6 have emerged as a dominant technique in mining graph structure datasets, and its variant, Heterogeneous Graph Neural Networks (HGNNs)4,7, has occupied the mainstream of HIN analysis8. In general, HGNNs are trained in an end-to-end manner, which requires abundant, various, and dedicated-designed labels for different downstream tasks. However, in the majority of real world scenarios, it is highly expensive and difficult to collect labels9.
Figure 1.
An example of heterogeneous information network.
Contrastive learning (CL)10–13 that automatically generates supervised signals from data itself is a promising solution to learn representations in selfsupervised manner. By maximizing the confidence (mutual information)14 between positive pairs and minimizing the confidence between negative pairs, CL is capable to learn discriminative embeddings without explicit labels. Inspired by the success of CL in Computer Vision11,12,15, many Graph Contrastive Learning (GCL) methods have been proposed. For example, DGI10 exploits a contrast between graph patches (i.e., nodes) and graph summary, and GRACE16 maximizes the mutual information between the same node in two augmented views. Despite some works generalizing the key idea of CL to homogeneous graphs, there are still fundamental challenges that needs to be addressed in exploring the great potential of CL in heterogeneous graphs.
How to design distinct views? Data augmentation that creates corrupted views is shown to be an essential technique to improve the quality of representations15,17. In GCL, prevalent augmentations include edge dropping/adding, node dropping/adding, feature shuffling, and so forth. Although these methods excel in homogeneous graphs16,18, we argue that they materially change the latent semantics of HINs. Take a bibliographic network as an example (Fig. 1); if the link between Author 3 (A3) and Paper 4 (P4) is dropped, the closest path between Author 3 (A3) and Author 4 (A4) will be changed from 2-hop (A3-P4-A4) to 4-hop (A3-P4-S2-P5-A4). To prevent the knowledge altering brought by simple augmentations, we propose to leverage metapath, the composition of semantic relations, to augment datasets. By applying metapaths, we create multiple different yet complementary subgraphs, referred to as metapath views, without changing the underlying semantics while also capturing the high-order relationships on HINs.
How to set proper pretext tasks? The choice of pretext tasks (contrastive objective) determines the informativeness of representations in downstream tasks for GCL19. For HIN, the best choice of pretext tasks is still unclear and each work presents its own solution. For example, Park et al.20 proposes to use metapaths to learn a shared consensus vector as node representation, Wang et al.21 performs contrast between the aggregation of metapaths (view 1) and network schema (view 2), and Zhu et al.22 iteratively maximize the mutual information between a single metapath and the aggregation of them. Despite these approaches attempting to incorporate the universal knowledge across all metapaths, we argue that they actually assume metapaths are independent (different from the complementary nature), failing to capture the consistency between metapaths and thus leading to sub-optimality. To directly model the correlation between metapaths, we propose an intuitive yet unexplored pretext task that performs contrast between each pair of metapaths. To be specific, the contrast between two augmented views of a metapath (intra-metapath) aims to learn discriminative node representations and the contrast between two views generated on two sources (inter-metapath) ensures the alignment across metapaths.
How to mitigate the sampling bias? Sampling bias indicates that the negative samples randomly selected from the original datasets are potential to share the same class with the anchor (i.e., act as false negatives), which lead to a significant performance drop. Existing works23–25 select or synthesize true hard negatives to mitigate the issue. However, these methods are demonstrated to bring limited benefits or even impose adverse impacts on GCL17, because of the message passing26. To alleviate the false negative issue, we propose a positive sampling strategy that collaboratively considers topological and semantic information across metapaths to explicitly decide the positive counterparts for each anchor.
To summarize, we propose Multi-view Heterogeneous Graph Contrastive learning (MCL) to learn informative node representations for HINs. To the best of our knowledge, our work is the pioneer that treats metapaths as multi-views15 under the GCL framework and captures the complementarity between metapaths. In particular, we first apply metapath to create multiple views and leverage parameter-sharing GNNs to encode node representations. Then, we propose a novel contrastive objective that maximizes the mutual information between any pairs of metapath views (for both intra-metapath and inter-metapath) to explicitly model the complementarity among metapaths, which is neglected in other works. Specifically, we maximize the confidence between two metapaths at node-level and graph-level to acquire local and global knowledge. To further enhance the expressiveness, we propose a positive sampling strategy that directly picks hard positives for each node based on graph-specific topology and semantics to mitigate the sampling bias inherent in CL. We highlight the contributions as follows:
We propose a heterogeneous graph contrastive learning framework, called MCL, which is the first attempt to treat metapaths in HIN as multiple views and leverages a novel pretext task to model the consistency between any pairs of metapath views at node- and graph-levels.
We propose a positive sampling strategy, which selects the most similar nodes as positive counterparts for each anchor by considering semantics and topology across metapath views, to remedy the sampling bias.
We conduct extensive experiments on five real-world datasets to evaluate the superiority of our model. Experimental results show MCL outperforms state-of-the-art self-supervised and even supervised baselines.
The remainder of this paper is organized as follows. In “Related work” section, work related to the heterogeneous network embedding technique is introduced; “Preliminary” section describes some preliminaries; “Multi-view heterogeneous graph contrastive learning” section describes the implementation of the multi-view contrastive learning for heterogeneous network embedding; “Multi-view heterogeneous graph contrastive learning” section provides the experimental results; finally, the research is summarized in “Experiments” section.
Related work
GCL that marries the power of GNN and CL has emerged as an important paradigm to learn representations on graphs without annotations. As a pioneering work, DGI10 treats node embedding and graph summary as positive pairs and utilizes InfoMAX14 to optimize the objective. Following this line, MVGRL27 proposes to use graph diffusion as augmentations to generate multiple views and GraphCL18 further analyzes the role of augmentations in introducing prior knowledge. Inspired by instance discrimination28, GRACE16 and GCA17 proposes to leverage node-level objective in contrasting, preserving node-level discrimination. In addition, BGRL29 and its variants26,30 adopts the key idea of31 to perform contrast without negative samples via bootstrapping to save memory consumption.
Meanwhile, some studies have generalized the key idea of GCL on HINs. For instance, HDGI32 extends DGI to heterogeneous graphs and DMGI20 utilizes metapath encoder to train consensus vectors as node representations. CKD33 models the regional and global knowledge between each pair of metapaths, failing to capture node-level properties. CPT-HG34 applies relation-level and subgraph-level pretext tasks to pre-train HGNN on large-scale HINs, and HDMI35 introduces a triplet loss to further enhance generalization. However, these methods do not consider the sampling bias inherent in GCL, inevitably leading to sub-optimality. STENCIL22 and HeCo21 treat the aggregation of metapath-induced subgraphs as a novel view, and propose to apply metapath similarity to measure the hardness between nodes to synthesize hard negatives. However, they still fail to model the consistency and complementarity between metapath views. Our model remedies these deficiencies through (1) applying metapath as augmentation, (2) performing contrast between any pairs of metapaths at node-level and graph-level, (3) explicitly selecting positives for each node by considering topology and semantics.
Preliminary
Definition 1
Heterogeneous Information Network (HIN) refers as to the graph consisting of various types of nodes and edges, represented as , where V and E are node set and edge set, respectively, and T and R denote node types and relation types, associated with a node mapping function and a edge mapping function . Note that .
Definition 2
(Metapath) Meta-path , is the composition of relations in HINs, defined as , where M is the set of meta-paths. R represents the type of relationship between nodes, and the subscripts 0,1,2,,n represent the types between different nodes. For example, represents the relationship between and , and represents the relationship between and . For example, we illustrate three meta-paths extracted from DBLP in Fig. 1, which describe co-author (APA), cosubject (APSPA), and co-conference (APCPA) relationships.
Definition 3
(Metapath-based neighbors) Given a metapath , meta-path-based neighbors is defined as a set of nodes connected to the target node through metapath . For example, in Fig. 1, the meta-path-based neighbors of Author 1 via meta-path APA is Author 2.
Multi-view heterogeneous graph contrastive learning
Data augmentation
For HIN, collectively applying metapaths to construct multi-views is a natural way to supplement the dataset in opposition to simple augmentation techniques. The created multiviews are actually additive to each other because metapaths depict various facets of the same HIN. Given a set of metapaths , where is the number of metapaths. We extract multiple subgraphs (i.e., metapath views) from the original graph to sustain the rich semantics preserved in HINs. For the subgraph generated through meta-path , we construct the direct neighborhoods for each node v as its metapath-based neighbors . Each metapath view is associated with a node feature matrix and an adjacent matrix . We leverage parameter-sharing GNN encoders to learn node representation from each metapath induced view, where . In practice, we leverage additional data augmentation (i.e., feature masking and edge dropping) with specific probabilities and to further corrupt metapath views to make the task more difficult.
Contrastive objectives
To distill rich semantics in HINs, we propose a novel contrastive objective to maximize the correlation between any pair of metapath views. In particular, the contrastive objective is collaboratively performed in intra-metapath (i.e., contrast between two corrupted versions of a metapath view) and inter-metapath (i.e, contrast between two views from different metapaths). We argue that the intra-metapath contrast independently learns the augmentation-invariant latent for each metapath view and the inter-metapath contrast is to align the representations gained from various sources to acquire the complementarity inherent in metapaths. Thus, we thoroughly gain the underlying knowledge maintained in individual metapath views and explicitly model the dependencies between pairs of different metapath views. In addition, the pretext task between two views jointly learns from node and graph-level knowledge to enhance representativeness. Notice that in the node-level contrasting, we select hard positives via the proposed sampling strategy to mitigate the sampling bias.
Node–node contrast
Node-node contrast aims to learn discriminative node representations to boost node-level downstream tasks. Specifically, we perform contrast between the anchor and its positive counterparts in two views to maximize (resp. minimize) the confidence between similar (resp. unassociated) nodes:
| 1 |
where is the representation for node u in view m, denotes the selected positive samples for u. We use similarity function to compute distance between node representations, where measures the cosine distance between two vectors, denotes a nonlinear projector head that increases the expressiveness, and controls the data distribution. This objective function that pulls semantically similar nodes close and pushes dissimilar nodes away contributes to the discrimination of node representations.
Node–graph contrast
Different from node-node contrast that learns local semantics across multi-views, we also perform node-graph contrast as the auxiliary task to facilitate the representation learning by injecting metapath-specific knowledge. We define the following objective:
| 2 |
where is the graph summary of metapath view calculated via the function READOUT() (mean pooling in the paper), and , where is a discriminator that consists of a bilinear layer and a sigmoid function . By imparting global knowledge brought by metapaths, we ensure the representations of nodes are more informative.
Overall objective
The overall objective to be maximized is defined as the aggregation of all pairs of metapaths, formally given by
| 3 |
where M is the set of metapaths. After optimizing the contrastive objective, we perform late fusion (sum or concatenation) on node representations learned from multiple metapath views to get the unified node representations for downstream tasks.
| 4 |
Positive sampling strategy
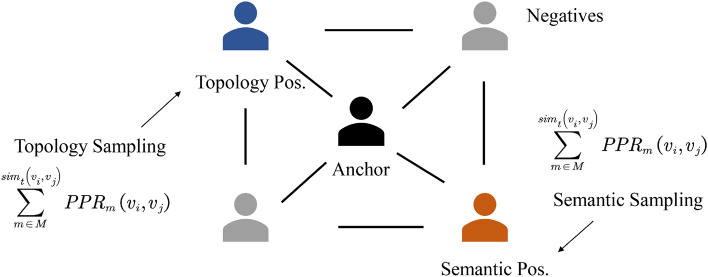
Sampling bias is an important problem in CL since false negatives will generate adverse signals. However, existing debiasing techniques are theoretically and empirically verified to bring severer sampling bias on GCL because the message passing smooths the node representations. To overcome the deficiency, we propose to leverage two different yet reciprocal similarity measurements (i.e., topology and semantics) to define the distance between nodes, shown in Fig. 2, and explicitly select the most similar nodes as positive samples.
Figure 2.
The positive sampling strategy. Personalized PageRank (PPR) is used to measure the topological similarity between nodes, and L2 distance is leveraged to compute the distance between nodes in semantic space to discover semantic associations.
Topology positive sampling
To analyze the similarity between nodes based on topological structure, we propose to use diffusion kernel that assesses the global node importance to compute the distance between two arbitrary nodes. In practice, we apply Personalized PageRank (PPR) score to measure the node-level relationship for each metapath view.
| 5 |
where , , are diffusion matrix, adjacent matrix and diagonal degree matrix for metapath m, respectively, and denotes teleport probability (default is 0.85). Formally, we define the PPR similarity between two nodes and under semantic view as the i-th row and j-th column in the diffusion matrix . The value in fact describes the stationary probability of starting from to reach via an infinite random walk in the metapath view m. Then, we aggregate the PPR scores computed on all metapath-induced views to determine the topological similarity.
| 6 |
and select the top-k similar nodes for each anchor as the topology positives .
Semantic positive sampling
Apart from structural information, graph datasets also preserve rich semantics on the node itself. To measure the semantical similarity between nodes, we propose to utilize a simple metric (i.e., l2 distance) to compute the distance between attributes of nodes
| 7 |
where and denote attributes on nodes and , respectively. The attributes for each node will not change across metapath views, thus we only need to process once to calculate the distance between pairs of nodes. Finally, we also select the top-k similar nodes for each anchor as the semantic positives . At the time, we define the positive samples for node u across metapath views as
| 8 |
Note that the positive sampling phase is performed in preprocessing, therefore, the module will not significantly increase the computational complexity.
Experiments
Datasets and baselines
To demonstrate the superiority of MCL over state -of-the-art algorithms, we conduct extensive experiments on five public benchmark datasets, including ACM, DBLP, IMDB, Aminer, and FreeBase. The statistics of five benchmark datasets as follows (Table 1).
Table 1.
The statistics of five benchmark datasets.
| Dataset | Nodes | Relations | Meta-paths |
|---|---|---|---|
| ACM | Author(A):7167 | P-A:13407 | PAP |
| Paper(P):4025 | P-S:4025 | PSP | |
| Subject(S):60 | |||
| DBLP | Author(A):4057 | P-A:19645 | APA |
| Paper(P):14528 | P-C:14328 | APCPA | |
| Subject(S):7723 | P-S:85810 | APSPA | |
| Conference(C):20 | |||
| IMDB | Actor(A):5257 | M-A:12828 | MAM |
| Movie(M):4278 | M-D:4278 | MDM | |
| Director(D):2081 | |||
| AMiner | Paper(P):6564 | P-A:18007 | PAP |
| Author(A):13329 | P-R:58831 | PRP | |
| Reference(R):35890 | |||
| FreeBase | Movie(M):3492 | M-A:65341 | MAM |
| Actor(A):33401 | M-D:3762 | MDM | |
| Direct(D):2502 | M-W:6414 | MWM | |
| Writer(W):4459 |
ACM36 is a bibliographic network which contains author, paper, and subject. According to the published conference, papers are labelled into three classes, i.e., data mining, database, and communication.
DBLP8 is extracted from a computer science bibliography website. Authors are divided into four groups based on research interests, including database, data mining, artificial intelligence, and information retrieval.
IMDB8 collects movies with actor and director information from online movie database. Movies are categorized according to genres, including action, comedy, and drama.
AMiner21 is another bibliographic graph where papers are labeled into 17 classes. We select a subset of the original graph with 4 types of papers. The initial node features are generated by DeepWalk.
FreeBase21 is a large knowledge network consisting of movie, actor, director, and writer. The movies are labeled into 3 genres. The initial node features are generated by DeepWalk.
We evaluate the performance of our model against various baselines from shallow graph representation learning algorithms, including DeepWalk37, Metapath2vec38, HIN2vec39, HERec40, to GCL methods (e.g., DGI41, GRACE16, DMGI20, STENCIL22, HeCo21) to supervised GNNs, like GCN42, GAT10, HAN36. Note that DMGI, STENCIL, HeCo are three GCL models dedicated for HIN.
Evaluation protocol
We evaluate MCL on node classification and node clustering. For node classification, we use Micro-F140 as the metric and follow the linear protocol that utilizes the learned graph encoder as a feature extractor to train an SVM classifier with 20% random samples as the training set. For node clustering, we apply K-means to generate clusters and utilize NMI as the metric. To mitigate the impact of initialized centroids, we perform 10 times clustering and report the average results. For all baselines, we run 10 times and present the average scores with standard deviations. For DGI, GRACE, GCN, GAT, we create homogeneous graphs based on metapaths and report the best results.
Implementation details
We leverage a 2-layer GCN as the encoder for each metapath-induced view. The parameters are initialized via Xavier initialization43 and we apply Adam as the optimizer44. We perform grid search to tune the learning rate from 5e-4 to 5e-3, the value of temperature from 0.2 to 0.8, the corrupt rate from 0.1 to 0.7, the number of positives from 0 to 128. Moreover, we set early stop to 20 epochs, node dimension to 64, activation function to ReLU() = max(,0), and use concatenation as fusion function in ACM and DBLP, and summation in other datasets. We present settings on baselines in the appendix.
Quantitative results
We report the quantitative result of node classification and node clustering with standard deviations in Tables 2 and 3. From the tables, we observe that GCL methods generally perform better than shallow unsupervised baselines, since the instance discrimination applied on CL captures underlying semantics preserved in HINs but the graph reconstruction adopted in classical methods only considers the topological structure. Our models (MCL and MCL-P) consistently outperform state-of-the-art self-supervised graph learning methods across all datasets by a large margin on supervised classification and unsupervised clustering tasks, and even achieve competitive results compared to supervised baselines. Beyond that, the performance of MCL-P (positive sampling version) is commonly better than its vanilla version that performs contrast between the same node in different views, demonstrating the necessity of introducing correlated nodes as positives to mitigate the sampling bias. Compared with heterogeneous graph contrastive learning methods (DMGI, STENCIL, HeCo), our model always acquires higher scores in both classification and clustering. We argue that it is because (1) the intra-metapath contrast is performed between nodes on two corrupted views induced from the same metapath to learn the discriminative representations and (2) inter-metapath contrast captures the complementarity between metapaths instead of treating the aggregation of them as a single view under the independent assumption applied in mentioned baselines.
Table 2.
Performance of node classification on five benchmark datasets.
| Methods | ACM | DBLP | IMDB | Aminer | FreeBase |
|---|---|---|---|---|---|
| DeepWalk | 81.78 | 88.09 | 56.36 | 84.93 | 69.63 |
| MP2vec | 79.82 | 87.67 | 50.78 | 84.14 | 69.66 |
| HIN2vec | 85.23 | 91.45 | 50.73 | 80.77 | 67.42 |
| HERec | 67.15 | 90.75 | 49.12 | 80.63 | 68.04 |
| DGI | 88.44 | 90.16 | 52.07 | 83.43 | 69.25 |
| GRACE | 87.64 | 91.28 | 54.80 | 83.43 | 69.25 |
| DMGI | 76.76 | 91.62 | 51.16 | 79.19 | 67.69 |
| STENCIL | 88.23 | 92.56 | 57.83 | 84.61 | 68.26 |
| HeCo | 88.97 | 92.24 | 52.12 | 85.22 | 69.02 |
| MCL | 91.02 | 93.29 | 60.75 | 86.63 | 71.41 |
| MCL-P | 91.34 | 93.44 | 61.02 | 87.03 | 71.53 |
| GCN | 89.87 | 92.04 | 58.42 | 85.42 | 69.13 |
| GAT | 88.84 | 92.51 | 54.78 | 84.37 | 70.42 |
| HAN | 89.53 | 93.27 | 54.78 | 85.91 | 70.98 |
Boldfaces denote the best performance among self-supervised and supervised methods, respectively. For our model, we use the suffix -P to indicate the positive sampling version.
Table 3.
Performance of node clustering on five benchmark datasets.
| Methods | ACM | DBLP | IMDB | Aminer | FreeBase |
|---|---|---|---|---|---|
| DeepWalk | 41.15 | 20.13 | 5.97 | 30.17 | 14.56 |
| MP2vec | 37.74 | 73.77 | 2.71 | 26.52 | 14.93 |
| HIN2vec | 40.79 | 68.83 | 3.88 | 23.76 | 14.26 |
| HERec | 45.39 | 70.38 | 4.39 | 31.05 | 15.32 |
| DGI | 43.47 | 54.44 | 4.09 | 29.82 | 15.16 |
| GRACE | 46.51 | 67.98 | 1.58 | 24.12 | 16.23 |
| DMGI | 52.53 | 67.41 | 5.45 | 28.32 | 12.35 |
| STENCIL | 56.67 | 71.41 | 8.25 | 29.99 | 13.19 |
| HeCo | 56.93 | 70.03 | 7.41 | 30.61 | 12.07 |
| MCL | 65.13 | 73.28 | 9.34 | 36.12 | 15.46 |
| MCL-P | 65.75 | 74.53 | 8.95 | 35.62 | 16.26 |
| GCN | 58.14 | 77.71 | 8.59 | 37.82 | 15.77 |
| GAT | 62.22 | 72.06 | 8.04 | 36.81 | 15.44 |
| HAN | 60.98 | 78.21 | 6.83 | 35.37 | 16.38 |
Boldfaces denote the best performance among self-supervised and supervised methods, respectively. For our model, we use the suffix -P to indicate the positive sampling version.
Ablation study
Pretext task
To verify the role of each component in the contrastive objective, we perform ablation studies, shown in Table 4, to compare the performance of multiple variants on node classification. From the table, we observe that (1) Node-node contrast provides better discrimination ability compared with node-graph contrast since the fine grained information (patches) is leveraged in learning representations. When the node-level and graph-level objectives are jointly optimized, the performance is significantly improved, showing the necessity of simultaneously modeling local-level and global-level dependencies. (2) The intra-metapath contrast is essential in promoting the learning procedure, reflected in the competitive performance obtained in the initialized variant (Intra- & Node) against state-of-the-art self-supervised baselines. (3) The variant with full components persistently achieves the best performance since the intra-metapath contrast captures the latent semantics of each metapath-induced view and the inter-metapath contrast aligns the consistency between metapaths. If one of them is removed, we cannot thoroughly model the relationship between metapaths, thus encountering model degradation.
Table 4.
Ablation study of pretext tasks on node classification where the intra- and inter- are abbreviations of intra-metapath and inter-metapath contrasts, and local and global indicate node-node and node-graph contrasts, respectively.
| Intra- | Inter- | Local | Global | ACM | DBLP | IMDB | Aminer | FreeBase |
|---|---|---|---|---|---|---|---|---|
| – | – | 89.21 | 91.94 | 58.71 | 84.95 | 69.61 | ||
| – | – | 83.21 | 90.95 | 48.56 | 83.42 | 69.38 | ||
| – | 90.52 | 92.52 | 60.12 | 86.17 | 71.16 | |||
| – | 88.32 | 92.44 | 59.83 | 85.92 | 70.65 | |||
| 91.02 | 93.29 | 60.75 | 86.63 | 71.41 |
Positive sampling strategy
We also conduct experiments to evaluate the impact of positive sampling, presented in Table 5. We can find that the selected positives indeed improve the performance by implicitly defining hard negatives. In addition, the significance of these two positive sampling strategies depends on the choice of datasets, i.e, there is no obvious superiority between topology positives and semantic positives. However, when they are simultaneously leveraged, our model achieves the best scores. We argue the phenomenon demonstrates that the selected positives based on different strategies are distinct yet complementary.
Table 5.
Ablation study of positive sampling strategy on node classification with four variants; denotes the specific type of positives are selected.
| Topology Pos. | Senamtic Pos. | ACM | DBLP | IMDB | Aminer | FreeBase |
|---|---|---|---|---|---|---|
| – | – | 91.02 | 93.29 | 60.75 | 86.63 | 71.41 |
| – | 91.17 | 93.34 | 59.92 | 86.88 | 71.43 | |
| – | 90.88 | 93.35 | 58.28 | 86.91 | 71.45 | |
| 91.34 | 93.44 | 61.02 | 87.03 | 71.53 |
Hyperparameter analysis
Positive sampling thresholds
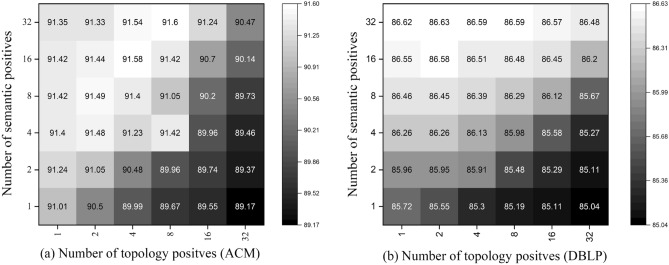
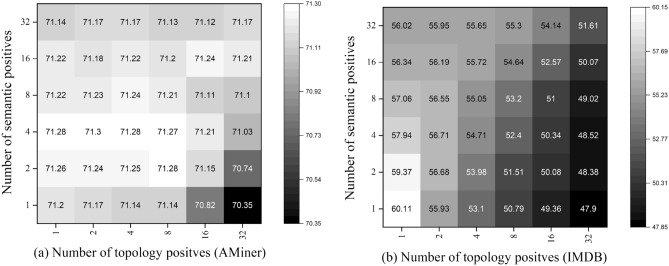
In the above section, we analyze the impact of positive sampling strategies in enhancing the quality of representations, here we delve into the positive sampling thresholds to provide a further examination.We illustrate multiple heatmaps that show the correlation between topology positives and semantic positives in Figs. 3 and 4. As we can see, the best performance is achieved with a large number of semantic positives and a small number of topology positives (ACM, DBLP, IMDB). When the number of topology positives is too large, the performance generally encounters a drop. We assume the phenomena derive from the inherent property of defined similarity functions. To be specific, the semantical similarity is independently measured on attributes of nodes in the representation space, whereas the topological similarity is calculated based on the adjacent matrix, which makes the function naturally biased to nodes with dense connections. Thus, when the number of topology positives is too large, there will contain too many noisy nodes. The Aminer does not follow the observation on the other datasets, whose best performance is achieved when the number of semantic and topology positives are both small. It is because the attributes on Aminer are generated by DeepWalk, a random walk-based algorithm that is biased to hub nodes in the learning procedure.
Figure 3.
Hyperparameter sensitivity of positive sampling thresholds on node classification (ACM and DBLP).
Figure 4.
Hyperparameter sensitivity of positive sampling thresholds on node classification (AMiner and IMDB).
Augmentation probabilities
We evaluate the impact of node dimension on ACM and DBLP where the value varies in {8, 16, 32, 64, 96, 128}, illustrated in Figs. 5 and 6. As we can see, the best choice of node dimension is different across datasets. For ACM, the performance consistently increases with the increase of node dimension, whereas the curve of DBLP goes up first and then declined. However, they both perform well on a typical node embedding 64.
Figure 5.
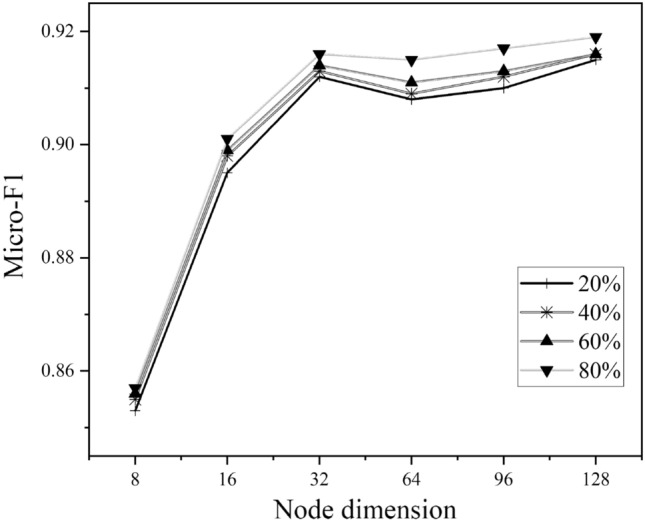
Hyperparameter sensitivity analysis on ACM.
Figure 6.
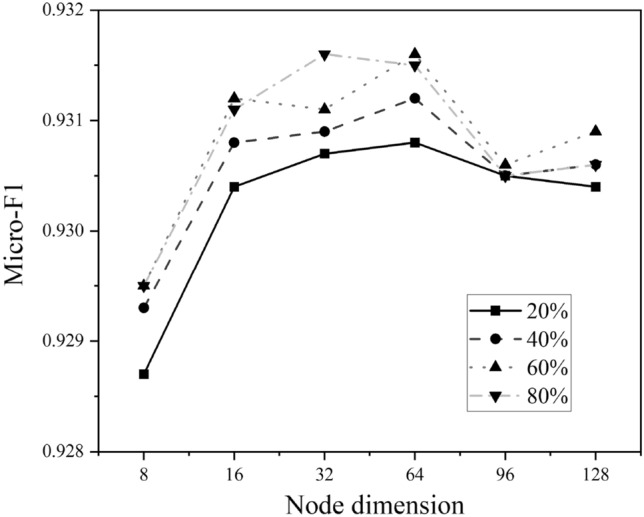
Hyperparameter sensitivity analysis on DBLP.
Temperature
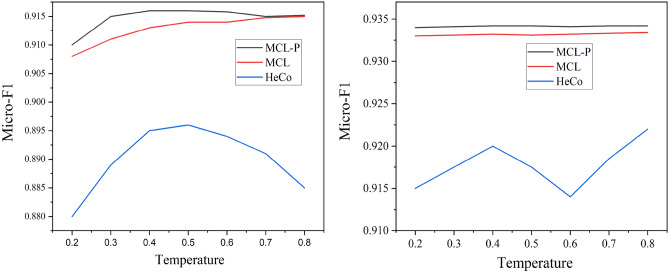
The value of temperature determines the data distribution when measuring the distance between data points in contrasting. As illustrated in Fig. 7, we can see that our model is not sensitive to the temperature and have higher scores with lower variance against HeCo, showing its robustness. In addition, we observe that if the value of temperature is smaller, the gap between MCL-P and MCL will be larger. It is because the data distribution between positives and negatives will be smoother with the increase in temperature. The observation further proves the effectiveness of the proposed positive sampling strategy, especially with a small temperature.
Figure 7.
Hyperparameter sensitivity of temperature terms of Micro-F1.
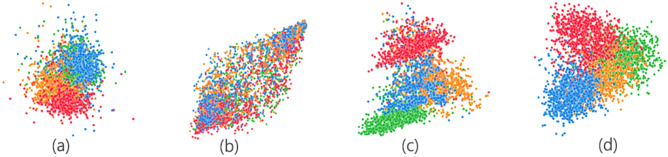
Visualization
To profoundly study the expressiveness of MCL, we visualize the learned node representations of DBLP through t-SNE. In Fig. 8, we visualize node representations obtained from four algorithms, including Metapath2vec, DMGI, HeCo, and MCL. As we can see, DMGI presents blurred boundaries between different classes, failing to learn discriminative low-dimensional node representations. For Metapath2vec and HeCo, despite some types of nodes being categorized clearly, there still exists a large proportion of overlapped data points that cannot be clearly identified. Our model separates nodes into different types, achieving the best performance.
Figure 8.
Visualization of node representations on DBLP (a) Metapath2vec (b) DMGI (c) HeCo (d) MCL.
Conclusion
In this paper, we propose a multi-view heterogeneous graph contrastive learning framework named MCL. By treating metapaths as data augmentation, we create multi-views without impairing the underlying semantics in HINs. Then, we propose a novel objective that jointly performs intra-metapath and inter-metapath contrast to model the consistency between metapaths. Specifically, we iteratively utilize graph patches and graph summary to generate supervision signals to acquire local and global knowledge. To further enhance the quality of representations, we employ a positive sampling strategy that simultaneously considers node attributes and centrality to explicitly select positive samples to mitigate the sampling bias. Experimental results demonstrate the superiority of MCL across five real-world datasets on node classification and node clustering.
Supplementary Information
Acknowledgements
This work was supported by Natural Sciences Foundation of Zhejiang Province under Grant No. LY22F020003, National Natural Science Foundation of China under Grant No. 62002226 and Zhejiang Provincial Natural Science Foundation of China under Grant No. LHQ20F020001.
Experimental settings
The architecture of GCN is defined as
| 9 |
Where is encoded node representation at l-layer, is the adjacent matrix with self-loops, is the degree matrix, is a non-linear activation function, e.g., ReLU, and is the training weight for the l-th layer.
For random-walk-based and proximity-based methods, we set the walk length to 40, the context size to 10, walks per node to 20, the number of negative samples to 5. For homogeneous graph neural network, we test all metapaths and report the best performance. For fair comparison, we set node embedding to 64 for most baselines, the patience in early stopping to 20 epochs. To alleviate the instability derived from initialization, we repeat the experiments 10 times and report the average performance. For other settings, we follow the existing unsupervised heterogeneous graph learning.
Author contributions
Q.L. and Z.F. wrote the main manuscript text, C.Y. prepared figures, and C.W. prepared tables. W.C. and Z.F. Wrote responses to reviewers and modified the experiments. All authors reviewed the manuscript.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author by request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-023-33324-7.
References
- 1.Li Z, Lu C, Yi Y, Gong J. A hierarchical framework for interactive behaviour prediction of heterogeneous traffic participants based on graph neural network. IEEE Trans. Intell. Transp. Syst. 2021;6:66. [Google Scholar]
- 2.Yu, J. et al. Self-supervised multi-channel hypergraph convolutional network for social recommendation. In Proceedings of the Web Conference 2021 413–424 (2021).
- 3.Yang D, Qu B, Yang J, Cudré-Mauroux P. Lbsn2vec++: Heterogeneous hypergraph embedding for location-based social networks. IEEE Trans. Knowl. Data Eng. 2020;6:66. [Google Scholar]
- 4.Schlichtkrull, M., Kipf, T. N., Bloem, P., van den Berg, R., Titov, I., & Welling, M. Modeling relational data with graph convolutional networks. In European Semantic Web Conference 593–607 (Springer, 2018).
- 5.Long, X., Huang, C., Xu, Y., Xu, H., Dai, P., Xia, L., & Bo, L. Social recommendation with self-supervised metagraph informax network. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management 1160–1169.
- 6.Zonghan W, Pan S, Chen F, Long G, Zhang C, Philip SY. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020;32(1):4–24. doi: 10.1109/TNNLS.2020.2978386. [DOI] [PubMed] [Google Scholar]
- 7.Tang, J., Qu, M., & Mei, Q. Pte: Predictive text embedding through large-scale heterogeneous text networks. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1165–1174 (2015).
- 8.Xinyu, F., Zhang, J., Meng, Z. & King, I. Magnn: Metapath aggregated graph neural network for heterogeneous graph embedding. In Proceedings of the Web Conference 2020 2331–2341 (2020).
- 9.Ziniu, H., Dong, Y., Wang, K. & Sun, Y. Heterogeneous graph transformer. In Proceedings of the Web Conference 2020 2704–2710 (2020).
- 10.Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. Graph attention networks. arXiv preprint arXiv:1710.10903 (2017).
- 11.He, K., Fan, H., Wu, Y., Xie, S., & Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 9729–9738 (2020).
- 12.Chen, T., Kornblith, S., Norouzi, M., & Hinton, G.. A simple framework for contrastive learning of visual representations. In International Conference on Machine Learning PMLR, 1597–1607. (2020).
- 13.Yang, L., Wu, F., Zheng, Z., Niu, B., Gu, J., Wang, C., Cao, Xi., & Guo, Y. Heterogeneous graph information bottleneck. In IJCAI 1638–1645 (2021).
- 14.Belghazi, M. I., Baratin, A., Rajeswar, S., Ozair, S., Bengio, Y., Courville, A., & Hjelm, R. D. Mine: Mutual information neural estimation. arXiv preprint arXiv:1801.04062 (2018).
- 15.Tian, Y., Krishnan, D., & Isola, P. Contrastive multiview coding. In European Conference on Computer Vision 776–794 (Springer, 2020).
- 16.Zhu, Y., Xu, Y., Yu, F., Liu, Q., Wu, S., & Wang, L. Deep graph contrastive representation learning. arXiv preprint arXiv:2006.04131 (2020).
- 17.Zhu, Y., Xu, Y., Liu, Q., & Wu, S. An empirical study of graph contrastive learning. arXiv preprint arXiv:2109.01116 (2021).
- 18.You Y, Chen T, Sui Y, Chen T, Wang Z, Shen Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020;33(2020):5812–5823. [Google Scholar]
- 19.Wu L, Lin H, Tan C, Gao Z, Li SZ. Self-supervised learning on graphs: Contrastive, generative, or predictive. IEEE Trans. Knowl. Data Eng. 2021;6:66. [Google Scholar]
- 20.Park, C., Kim, D., Han, J. & Hwanjo, Y. Unsupervised attributed multiplex network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence vol. 34, 5371–5378 (2020).
- 21.Wang, X., Liu, N., Han, H., & Shi, C. Self-supervised heterogeneous graph neural network with co-contrastive learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining 1726–1736 (2021).
- 22.Zhu, Y., Xu, Y., Cui, H., Yang, C., Liu, Q., & Wu, S. Structure-enhanced heterogeneous graph contrastive learning. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM) 82–90 (SIAM, 2022).
- 23.Kalantidis Y, Sariyildiz MB, Pion N, Weinzaepfel P, Larlus D. Hard negative mixing for contrastive learning. Adv. Neural Inf. Process. Syst. 2020;33(2020):21798–21809. [Google Scholar]
- 24.Chuang C-Y, Robinson J, Lin Y-C, Torralba A, Jegelka S. Debiased contrastive learning. Adv. Neural Inf. Process. Syst. 2020;33(2020):8765–8775. [Google Scholar]
- 25.Ho C-H, Nvasconcelos N. Contrastive learning with adversarial examples. Adv. Neural Inf. Process. Syst. 2020;33(2020):17081–17093. [Google Scholar]
- 26.Xia, J., Wu, L., Wang, G., Chen, J., & Li, S. Z. ProGCL: Rethinking hard negative mining in graph contrastive learning. In International Conference on Machine Learning, PMLR 24332–24346 (2022).
- 27.Hassani, K., & Khasahmadi, A. H. Contrastive Multi-View Representation Learning on Graphs (2020).
- 28.Wu, Z., Xiong, Y., Yu, S. X., & Lin, D. Unsupervised feature learning via non-parametric instance discrimination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 3733–3742 (2018).
- 29.Thakoor, S., Tallec, C., Azar, Mohammad Gheshlaghi, A., Mehdi, D., Eva, L., Munos, R., Veličković, P., & Valko, M. Large-scale representation learning on graphs via bootstrapping. arXiv preprint arXiv:2102.06514 (2021).
- 30.Lee, N., Lee, J. & Park, C. Augmentation-free self-supervised learning on graphs. In Proceedings of the AAAI Conference on Artificial Intelligence vol. 36, 7372–7380 (2022).
- 31.Grill J-B, Strub F, Altché F, Tallec C, Richemond P, Buchatskaya E, Doersch C, Pires BA, Guo Z, Azar MG, et al. Bootstrap your own latent—A new approach to self-supervised learning. Adv. Neural Inf. Process. Syst. 2020;33(2020):21271–21284. [Google Scholar]
- 32.Ren, Y., Liu, B., Huang, C., Dai, P., Bo, L., & Zhang, J. Heterogeneous deep graph infomax. arXiv preprint arXiv:1911.08538 (2019).
- 33.Wang, C. et al. Collaborative Knowledge Distillation for Heterogeneous Information network embedding. In Proceedings of the ACM Web Conference 2022, 1631–1639 (2022).
- 34.Jiang, X., Lu, Y., Fang, Y., & Shi, C. Contrastive pre-training of GNNs on heterogeneous graphs. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management 803–812 (2021).
- 35.Jing, B., Park, C. & Tong, H. Hdmi: High-order deep multiplex infomax. In Proceedings of the Web Conference 2021 2414–2424 (2021).
- 36.Wang, X., Ji, H., Shi, C., Wang, B., Ye, Y., Cui, P., & Yu, P. S. Heterogeneous graph attention network. In The World Wide Web Conference 2022–2032 (2019)
- 37.Perozzi, B., Al-Rfou, R., & Skiena, S. DeepWalk: Online Learning of Social Representations (ACM, 2014).
- 38.Dong, Y., Chawla, N. V., & Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 135–144. (2017).
- 39.Fu, T., Lee, W.-Ch., & Lei, Z. Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management 1797–1806 (2017).
- 40.Shi C, Hu B, Zhao WX, Philip SY. Heterogeneous information network embedding for recommendation. IEEE Trans. Knowl. Data Eng. 2018;31(2):357–370. doi: 10.1109/TKDE.2018.2833443. [DOI] [Google Scholar]
- 41.Velickovic P, Fedus W, Hamilton WL, Liò P, Yoshua B, Hjelm RD. Deep graph infomax. ICLR (Poster) 2019;2(3):4. [Google Scholar]
- 42.Kipf, T. N., Welling, M. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016)
- 43.Glorot, X., & Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (Proceedings of Machine Learning Research), Y. W. Teh and M. Titterington (Eds.), Vol. 9. PMLR, Chia Laguna Resort, Sardinia, Italy, 249–256 (2010).
- 44.Kingma D, Ba J. Adam: A method for stochastic optimization. Comput. Sci. 2014;6:66. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author by request.