Single-molecule dynamics of DNA gyrase in evolutionarily distant bacteria Mycobacterium tuberculosis and Escherichia coli

Abstract

DNA gyrase is an essential nucleoprotein motor present in all bacteria and is a major target for antibiotic treatment of Mycobacterium tuberculosis (MTB) infection. Gyrase hydrolyzes ATP to add negative supercoils to DNA using a strand passage mechanism that has been investigated using biophysical and biochemical approaches. To analyze the dynamics of substeps leading to strand passage, single-molecule rotor bead tracking (RBT) has been used previously to follow real-time supercoiling and conformational transitions in Escherichia coli (EC) gyrase. However, RBT has not yet been applied to gyrase from other pathogenically relevant bacteria, and it is not known whether substeps are conserved across evolutionarily distant species. Here, we compare gyrase supercoiling dynamics between two evolutionarily distant bacterial species, MTB and EC. We used RBT to measure supercoiling rates, processivities, and the geometries and transition kinetics of conformational states of purified gyrase proteins in complex with DNA. Our results show that E. coli and MTB gyrases are both processive, with the MTB enzyme displaying velocities ∼5.5× slower than the EC enzyme. Compared with EC gyrase, MTB gyrase also more readily populates an intermediate state with DNA chirally wrapped around the enzyme, in both the presence and absence of ATP. Our substep measurements reveal common features in conformational states of EC and MTB gyrases interacting with DNA but also suggest differences in populations and transition rates that may reflect distinct cellular needs between these two species.

DNA gyrase is ubiquitous to all bacterial genomes (1). Gyrase is the primary target of fluoroquinolones, which are one of the most commonly prescribed family of antibiotics worldwide (2). Knocking out any subunit of the A₂B₂ heterotetrametric structure of gyrase prevents Escherichia coli (EC) growth because gyrase plays an essential role in controlling the topology of the genome (3, 4). All organisms face DNA topology problems during cellular processes such as replication, which causes a build up of positive supercoils ahead of the replication fork as well as intertwining of duplicated helices behind the forks (5, 6). Similarly, positive supercoils build up ahead of the advancement of RNA polymerase during transcript elongation (5, 6). Topoisomerases are enzymes that change the linking number of DNA to maintain supercoiling status and resolve other topological problems. Gyrase is the only known topoisomerase to couple the hydrolysis of ATP to the introduction of negative supercoils in DNA.

Important structural and mechanistic features of DNA gyrase have been elucidated through bulk biochemical assays (7, 8), x-ray crystallography (9, 10, 11), cryo-EM, and single-molecule methods, including FRET (12). Gyrase supercoils DNA using a duplex strand passage mechanism that relies on three subunit interfaces, or “gates,” that can open and close during the mechanochemical cycle (Fig. 1A). The GyrA (97 kDa) and GyrB (90 kDa) dimers come together to form the “DNA gate,” which binds a DNA duplex (the “G-segment”) that is cleaved to permit strand passage. GyrB contains an ATPase domain that dimerizes to form the “N-gate” through which a second double-stranded DNA (the “T-segment”) enters prior to passage through the G-segment. GyrA contains a globular C-terminal domain (CTD) (13), which can chirally wrap DNA to present the T-segment for directional strand passage (14). GyrA also contains the “exit gate” through which the T-segment of DNA is released after strand passage (15, 16).

Figure 1.

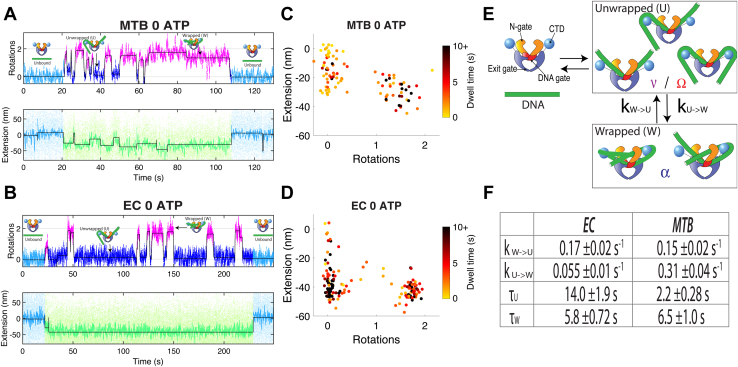
Rotor bead tracking to detect supercoiling dynamics in two evolutionarily distinct species.A, simplified mechanochemical model of DNA:gyrase conformational states previously observed by RBT (17). B, experimental diagram of tethers used for RBT tracking, highlighting the two major modes of information gathering: DNA contraction and DNA rotation caused by enzyme binding and activity below the rotor bead. C, phylogenetic tree of gyrases from previously studied model organisms and several common pathogenic species, populated using a consensus of trees of species divergence dates using the online Time-Tree tool (58). D, depictions of extension and rotation changes to DNA during the gyrase topoisomerization reaction and the response of the rotor bead. E, example single-molecule trace for a DNA tether in the presence of Mycobacterium tuberculosis (MTB) gyrase. The extension data (color) shows a period prior to enzyme binding (blue), then a period during gyrase binding and DNA supercoiling (warmer colors) until dissociation (blue). F, example single-molecule trace for a DNA tether in the presence of Escherichia coli (EC) gyrase, showing a binding and supercoiling event. MTB, Mycobacterium tuberculosis; EC, Escherichia coli; RBT, rotor bead tracking.

Single-molecule measurements can complement high-resolution structures by probing conformations of actively cycling complete nucleoprotein complexes and by revealing dynamics that connect structural snapshots with the overall mechanism of a macromolecular machine (Fig. 1A) (14). To understand the details of gyrase supercoiling, single-molecule studies of EC gyrase have been performed using rotor bead tracking (RBT), which enables high-speed measurements of changes in DNA contraction and rotation in the presence of gyrase, by tracking a bead attached to the side of a single DNA molecule (Fig. 1, B and D) (17, 18, 19, 20, 21). In RBT assays of EC gyrase, processive bursts of activity are seen in which the linking number of the DNA is changed in multiples of (−) 2, without backsteps. RBT has also been used to detect three major observable conformational states—termed α, ν, and Ω—that are visited by the EC gyrase:DNA complex during processive supercoiling events (Fig. 1A) and distinguished by the degree to which DNA contour length and supercoils are trapped within the enzyme complex. The G-segment is bound with minimal sequestration of DNA contour in the ν state (14, 17, 20), where modest contraction of the DNA under tension is explained (17) by bending within the central ∼30 bp of the G-segment (22, 23). DNA is more highly sequestered, but not chirally wrapped, in the Ω state, where >100 bp are thought to be bent around the enzyme through interactions with the CTDs (17, 18, 20). In the α state, the DNA remains sequestered and is chirally wrapped; here, the T-segment is thought to be poised for strand passage (17, 18). The high-resolution structures of these intermediate states are not definitively known, but a recently reported cryo-EM structure of the full EC gyrase in complex with DNA and Gepotidacin, a novel bacterial topoisomerase inhibitor (24), closely resembles the proposed geometry of the Ω state (25), with ∼130 bp of DNA resolved and bent in a path around the enzyme without presenting a T-segment. Previous work in EC gyrase has shown that the transition from Ω to α, forming the chiral wrap, dominates the kinetics of the cycle across all ATP concentrations (17). However, no single-molecule work yet exists to link the mechanistic details of these findings with gyrases from other species.

Many bacterial species such as EC have both gyrase and the related topoisomerase IV (topo IV), which does not actively introduce supercoils but can decatenate duplexes and relax positive supercoils (26). Other species such as Mycobacterium tuberculosis (MTB) and Clostridium difficile, separated from EC by ∼3 billion years of evolution (Fig. 1C), do not express topo IV, and in these cases, gyrase is thought to fulfill functions that would otherwise be shared between the two enzymes (27). DNA gyrase function may differ between species depending on whether topoisomerase IV is also present, which allows for specialization of the gyrase enzyme, as well as due to other cellular constraints such as growth rate. Bulk biochemical assays have reported that the ATPase and supercoiling rates for EC gyrase are both 10 to 50× faster than those of MTB and that MTB supercoils DNA to a much lower extent at steady state, reaching a lower superhelical density “set point” (28, 29, 30, 31, 32). Differences between the CTDs of EC and MTB gyrase have been investigated as a possible basis for functional specialization. The crystal structures of the two CTDs are very similar (1.45 Å root mean square deviation), but the differing sequence and length of unstructured CTD tails have been found to be functionally important (32). When the EC gyrase CTD tail was truncated to resemble the MTB enzyme, the supercoiling setpoint of the enzyme was reduced (31). The specialized CTD tail was also found to be required for coordination between nucleotide state and DNA wrapping in EC gyrase (31). Structural work on MTB gyrase has shown that it can adopt an “extremely open” N-gate conformation and possesses a unique structural element that slows ATPase rate (9). A recent study of heterologous gyrase complexes also showed that the ATPase-containing GyrB subunit limits the activities of MTB gyrase: among other results, the MTB holoenzyme was found to have low ATPase and supercoiling activities in comparison with EC gyrase, but these activities could be accelerated by combining the GyrA subunit from MTB with the GyrB subunit from EC (33). All of these structural and functional differences, however, have yet to be contextualized with comparisons of detailed conformational dynamics between the MTB and EC enzymes.

EC gyrase is a fast, processive, and tightly coupled molecular motor that may have been optimized during evolution for the fast-growing EC bacterium. Previous literature has suggested that MTB gyrase is primarily a distributive enzyme, binding to DNA and performing a single cycle before leaving (34) or at least lacking the robust processivity of the EC enzyme (33). Understanding the processive versus distributive nature of gyrase across species is relevant to the dynamics by which gyrase modulates genomic supercoiling levels and for understanding the impact of drug inhibition (35). In addition to single-molecule supercoiling rates and processivities, we set out to characterize substeps within the gyrase supercoiling cycle, answering questions such as whether the central Ω to α conformational transition is seen in another species distant from EC, and if so, whether the Ω state always dominates the kinetics of the cycle or if other conformational states become prominent in the cycles of enzymes from another species. Observing the unique conformational dynamics of gyrase from different bacterial species helps to understand how structural differences in gyrase optimizations are coupled to functions unique to each species.

Results

MTB gyrase supercoils DNA processively at slower rates than EC gyrase

We used RBT to observe DNA gyrase single-molecule supercoiling behavior across evolutionarily distant species, examining the interaction between DNA and gyrase purified from M. tuberculosis (MTB) and E. coli (EC) (Fig. 1, E and F). First, we observed isolated processive bursts (Fig. 2A) to assess supercoiling rates (Fig. 2B) and processivities (Fig. S1) for the two enzymes assayed under the same solution conditions. Our results show that with saturating (1.3 mM) and intermediate (130 μM) ATP concentrations, 0.8 pN tension, and torsionally relaxed DNA, both species showed processive bursting behavior (Fig. 2A). This direct single-molecule measurement contrasts with a previous suggestion that MTB is distributive (36), but we do observe quantitative differences in processivity, with EC gyrase on average completing more cycles per burst than MTB (Fig. S1). As expected from bulk comparisons of enzymatic rates, the single-molecule supercoiling rates differ between the two enzymes: DNA gyrase from MTB supercoiled DNA ∼5.5× slower than EC gyrase (Fig. 2B) under both ATP concentrations tested.

Figure 2.

Single-molecule burst data and supercoiling velocities.A, example single-molecule processive bursts for EC and MTB DNA gyrase. The starting angle for each trace is offset by an arbitrary multiple of two rotations in order to fit many examples into a single panel. B, average velocity of DNA gyrase by bacterial species and [ATP]. Bars represent the weighted mean and the weighted SD (both weighted by burst duration); text displays the weighted mean. Total number of cycles for each condition: MTB 1.3 mM ATP, N = 167 cycles; EC 1.3 mM ATP, N = 316 cycles; MTB 130 μM ATP, N = 110 cycles; EC 130 μM ATP, N = 59 cycles. Examples of longer EC bursts at 1.3 mM ATP are included in Fig. S4. EC, Escherichia coli; MTB, Mycobacterium tuberculosis.

EC and MTB have distinct distributions of DNA:gyrase conformational states

To examine the ubiquity of gyrase conformations and substep dynamics, we compared RBT data between the previously well-characterized EC gyrase and the MTB enzyme. Previous models for the EC gyrase supercoiling mechanism (Fig. 1A) have been informed by RBT measurements of the DNA:gyrase complex with and without nucleotide (17). These measurements provide two kinds of information about DNA:gyrase conformations: contour length sequestered by the enzyme (extension) and supercoils trapped by the enzyme due to chiral wrapping (rotations). We analyzed nucleoprotein conformational states by plotting two-dimensional histograms of paired rotation and extension values (Fig. 3).

Figure 3.

DNA:gyrase complex conformations at varying nucleotide conditions for EC and MTB enzymes. Distributions of angle and extension measurements are shown as 2D histograms, where (0,0) represents free DNA without gyrase interaction. A and B, fitted 2D Gaussian centers are labeled. The number of gyrase encounters with DNA recorded are as follows: A, MTB gyrase, 0 ATP, N = 19 traces, taken across 3 days and three different tethers; B, MTB gyrase, 130 μM ATP, N = 16 traces, taken across 2 days and three different tethers; C, MTB gyrase, 1.3 mM ATP, N = 17 traces, taken across 5 days and five different tethers; D, EC gyrase, 0 ATP, N = 21 traces, taken across 2 days and two different tethers; E, EC gyrase, 130 μM ATP, N = 7 traces, taken across 2 days and two different tethers; F, EC gyrase, 1.3 mM ATP, N = 8 traces, taken across 3 days and three different tethers. Traces with 5 s of free DNA before and after each run are also shown in Fig. S5 to visualize the free DNA population at (0,0). EC, Escherichia coli; MTB, Mycobacterium tuberculosis.

Without nucleotide, there were two major distinct populations for EC and MTB gyrase interacting with DNA. In each case, one state showed the rotational signature of a chirally wrapped conformation, while the other state we refer to here as “unwrapped” because it shows an angle close to ∼0 rotations, as expected for a conformation that does not trap substantial DNA writhe. Note that in this context, “unwrapped” means only that no supercoils have been trapped; there may still be substantial interactions between the DNA and the surface of the protein. As expected, the dominant unwrapped state for EC gyrase was highly contracted (∼40 nm), attributed to sequestering of extensive DNA contour length within the complex. Extensive DNA sequestration is a hallmark of the previously described Ω state (Fig. 1A) and consistent with a conformation similar to the EC cryo-EM structure in which 130 bp of DNA are resolved in a path that bends around the CTDs (25). The unwrapped state for MTB gyrase, however, was centered at a much smaller level of contraction (∼17 nm), which may be explained by a ν state (Fig. 1A) in which the central G-segment is bent but the flanking DNA is not sequestered by the CTDs. The contraction due to a DNA bend depends on the tension in the DNA and the extent of the bend (37, 38, 39). We may estimate the contraction expected under 0.8 pN (the tension used for this study) assuming a 150° bend as seen in topo II crystal structures (22) or the central region of the EC gyrase cryo-EM structure (25). We expect ∼16 nm of contraction for these conditions, based on interpolating reported Brownian dynamics simulation results (39) or applying the approximate discrete kink model of Kulic (37) corrected for the finite extent of the bend as in prior work (17). In a previous measurement for the EC enzyme (17), a smaller level of contraction in ν was explained by higher tension used to stabilize the state along with a smaller inferred bend angle. Unlike EC, the dominant unwrapped population for nucleotide-free MTB is consistent with the ν conformation, although there may also be some sequestration of DNA by the CTDs within the unwrapped ensemble.

The wrapped state for EC showed a similar level of contraction to the unwrapped state and was positioned at an angle of ∼1.7 rotations, explained by trapping of extensive writhe as DNA is chirally wrapped around both CTDs (17, 18). Under the conditions used for this side-by-side comparison, the wrapped state was more populated for MTB gyrase than for EC gyrase in the absence of nucleotide and was positioned at a smaller angle (consistent with slightly less trapped writhe) and a lower level of contraction, which could reflect less complete wrapping of the DNA around the CTDs. The difference in population of the wrapped state for MTB versus EC is quantified further in kinetic analysis below. We note that the observed EC states are qualitatively similar to prior work (17) but have some quantitative differences. These differences include a larger measured contraction and the lack of a noticeable population at ∼1 rotation that was previously ascribed to partially wrapped α states. The differences might arise from the solution conditions used in this study, which were applied consistently between MTB and EC and include higher [KGlu] than in previous RBT measurements; increasing [KGlu] has been reported to favor DNA wrapping (30).

We also examined the conformations visited during active supercoiling, by plotting histograms of paired rotation (now modulo 2 to account for the repeating 2-rotation reaction coordinate) and extension values in the presence of ATP. We saw a prominent population centered at ∼0 rotations for EC gyrase, as documented in previous work (17, 21) and attributed to the dominance of the Ω state within the kinetic cycle across all ATP concentrations. For MTB gyrase, however, there is a substantial population of intermediate angles consistent with chiral wrapping, even at saturating ATP. These findings (elaborated in more detail below) indicate that previous depictions of the DNA gyrase cycle with a dominant Ω state may in fact be specific to EC gyrase as compared to its MTB counterpart.

EC gyrase transitions to the chirally wrapped state more slowly than MTB gyrase in the absence of nucleotide

A difference between gyrase species in the relative populations of the wrapped and unwrapped states could in principle arise from a difference in the rate of wrapping, the rate of unwrapping, or both. To investigate the kinetic differences underlying the observed distributions of conformations, we applied automated change-point detection to the RBT traces collected in the zero-ATP condition, where states were well-resolved. We chose the Steppi change-point detection method to score apparent changes in state; this method has previously been used to analyze RBT data on Cas9 dynamics, taking advantage of its ability to model noise as an Ornstein-Uhlenbeck process (40, 41). We observed distinguishable dwells for wrapped and unwrapped states in both EC and MTB gyrase (Fig. 4, A–D). We characterized the dynamics using a simple model relative to some previous work (17) in order to focus on wrapping and unwrapping transitions, since the detailed state geometries differ between species. In this model, we combined the states previously described as Ω and ν, which are both unwrapped states; states at intermediate extensions that could correspond to partial sequestering of DNA by CTDs are also included. We similarly grouped all chirally wrapped states (Fig. 4E), without distinguishing between states that trap differing numbers of supercoils.

Figure 4.

DNA:gyrase conformational dynamics in the absence of ATP. Data replicates are the same as for Figure 3. A and B, example traces of MTB and EC gyrase interacting with DNA without nucleotide. Color changes in the plotted angle denote detected changes in mean angle, where magenta signifies detected states beyond 0.65 rotations and blue signifies all other states. The black lines in the angle and extension plots show the Steppi idealizations of the trajectories (41). Light green extension data indicates where a detected contraction has occurred. Darker color extension data has been filtered with a 2.5 Hz low-pass Butterworth filter applied separately to Steppi-detected bound and unbound states. C and D, one data point is plotted for each detected dwell at either the unwrapped or wrapped state. E, simplified model for DNA:gyrase conformations pooled into detected states. F, rates calculated for simplified model and dwell times in wrapped and unwrapped states. All binding events started and ended in detected unwrapped states. For EC, N_free->U and N_U->free = 21, N_W->U and N_U->W = 65; for MTB, N_free->U and N_U->free = 19, N_W->U and N_U->W = 41 (N for total binding events shown in Fig. 3). EC, Escherichia coli; MTB, Mycobacterium tuberculosis.

After scoring transitions between unwrapped and wrapped states along with dissociation events, we extracted dwell times between states and transition probabilities in order to populate our simple kinetic model (Fig. 4F). We found that in the absence of ATP, EC gyrase has an ∼6× slower transition rate from the unwrapped to the wrapped states, but EC and MTB gyrase share a similar rate of transition from wrapped to unwrapped. While formation of a chiral wrap is rate-limiting for supercoiling across all ATP concentrations for EC (18), the spontaneous wrapping rate is in fact faster for the slower MTB enzyme, suggesting that MTB supercoiling may be limited by other factors rather than simply a higher barrier to wrap formation. The properties of wrapped and unwrapped states observed under nucleotide-free conditions are further summarized in Table 1.

Table 1.

States observed in nucleotide-free RBT measurements

Species	State category	Predominant conformation	ΔExtension (nm)	Angle (rotations)	Population (%)
EC	Unwrapped	Ω	−40	0.15	76
EC	Wrapped	α	−42	1.7	24
MTB	Unwrapped	ν	−17	0.1	33
MTB	Wrapped	α	−31	1.5	67

For each gyrase species, the properties of two categories of observed states are shown: unwrapped states do not trap supercoils and have angle values close to 0 rotations, while wrapped states trap supercoils and have corresponding higher angle values. Fit values of (Δextension, angle) are shown from Figure 3, A and D alongside the inferred predominant conformations (Fig. 1A) and the population fractions in the unwrapped and wrapped states calculated from kinetic analysis (Fig. 4F).

MTB gyrase dwells in wrapped states during active supercoiling

Our kinetic model determined in the absence of ATP reflects spontaneous transitions in the conformational landscape of DNA gyrase, which may be modulated by the nucleotide cycle during the ATP-dependent supercoiling. In the presence of ATP, conformational transitions are more difficult to confidently resolve, and a complete understanding of species-dependent substep dynamics will require future high-resolution nucleotide-dependent measurements. However, we asked whether some information about conformational cycling during supercoiling could be obtained from the current data within the resolution of our assay. To approximately characterize the states visited during processive runs in the presence of ATP, we applied the same automated change-point detection methods to these data for EC and MTB gyrase (Fig. 5, A and B). While states are not always well-resolved due to faster kinetics and the proximity of the wrapped angle with the subsequent unwrapped dwell, we found that rotational angle dwells for EC gyrase were characteristically localized to the canonical Ω state, around 0 rotations. In contrast, long dwells for MTB gyrase can frequently be observed at intermediate rotations (Fig. 5, C and D), closely resembling the α states depicted in Figure 4C. Mean levels of DNA contraction were also greater for EC gyrase than for MTB (Fig. S2). Together with our previous observation that highly contracted dwells at ∼0 rotations were rare to observe in MTB even without nucleotide (Fig. 3A), these substep dynamics suggest that the MTB enzyme does not strongly populate the fully contracted Ω state. Accounting for the observed differences in dominant dwells between species in the absence and presence of ATP, we propose an updated simple mechanochemical supercoiling model in Figure 6.

Figure 5.

DNA:gyrase conformational dynamics with ATP. Data replicates same as Figure 3. A and B, example traces of MTB and EC gyrase interacting with DNA with intermediate (130 μM) ATP. Color changes in the angle plot denote detected changes in mean angle, where magenta signifies detected dwells between 0.85 and 1.85 rotations (angle coordinate mod 2) and blue signifies all other detected dwell angles. The black lines in the angle and extension plots show the Steppi idealizations of the trajectories. Light green extension data indicates where a detected contraction has occurred. Darker color extension data has been filtered with a 2.5 Hz low-pass Butterworth filter applied separately to Steppi-detected bound and unbound states. C and D, every detected dwell by species and nucleotide condition, histogrammed along the angle coordinate; magenta signifies detected states between 0.85 and 1.85 rotations (angle coordinate mod 2) and blue signifies all other states. EC, Escherichia coli; MTB, Mycobacterium tuberculosis.

Figure 6.

Summary model for differences in dominant states between species.

Discussion

We have measured gyrase structural dynamics across two evolutionarily distant bacterial species and found both shared processive supercoiling and different substep dynamics. While both gyrases appear to supercoil DNA in processive bursts, the EC enzyme, which derives from a fast-growing bacterium, supercoils at higher rates. Previous single-molecule work has shown that EC and Salmonella typhimurium gyrase are processive motors and that the Bacillus anthracis enzyme processively relaxes positive supercoils (36, 42). The ∼5× faster EC gyrase speed than MTB may relate to the difference in doubling time for their respective host cells in vivo. Whereas M. tuberculosis divides on timescales of several hours to a day (43, 44), E. coli doubles in tens of minutes, placing high demands on gyrase and topoisomerase IV to keep pace with replication (45). Bulk biochemical measurements have also shown that MTB gyrase consumes ATP ∼10× slower than EC gyrase when stimulated by DNA, a difference that is within a factor of two of the observed single-molecule supercoiling rates reported here, implying that the two enzymes may couple ATP hydrolysis to supercoiling at fairly similar efficiencies on relaxed DNA (32). The low DNA-stimulated ATPase activity of MTB can be enhanced when MTB gyrB is replaced with EC gyrB in a heterologous complex with MTB gyrA, indicating that MTB gyrB limits activity in the holoenzyme (33).

Although both chirally wrapped and unwrapped states are important nucleoprotein conformations in the mechanisms of EC and MTB gyrase, the dominant waiting states differ between the two enzymes. In both gyrases, the formation of a chiral wrap is a slow process, as evidenced by dwells at unwrapped angles (near 0 rotations along the repeating 2-rotation reaction coordinate) in both species during processive supercoiling (Fig. 3, C and F). The Ω state plays a central role in the EC gyrase cycle, dominating the kinetics of supercoiling and potentially coordinating N-gate closure with T-segment capture by a well-ordered transition to the chirally wrapped α state (18). However, we found that substep dynamics in MTB gyrase differ greatly from the EC enzyme. Unlike EC, the unwrapped states in MTB appear to have incompletely sequestered DNA, since the degree of contraction during processive runs is smaller (Fig. S2) and fully contracted Ω states are rare without nucleotide in MTB (Fig. 4B). This difference in DNA sequestration suggests that in MTB, chiral wrapping to present a T-segment may occur simultaneously with DNA capture by the CTDs—in contrast to EC where there is an ordered progression through the Ω state and chiral wrapping occurs by rearranging DNA that has already been captured (Fig. 6). In addition, MTB gyrase appears to have one or more additional slow step(s) subsequent to T-segment capture since we can identify dwells at wrapped angles even at saturating ATP (Fig. 5, C and D). Dwells at ∼1.5 rotations during processive bursts for MTB gyrase may reflect wrapped states awaiting ATP hydrolysis, cleavage, product release, and/or conformational steps associated with strand passage. In future studies, the dwells may be more precisely resolved using high-resolution RBT with gold nanoparticles (20), and the associated slow conformational and/or chemical steps, which may limit the rate of MTB supercoiling, can be dissected by varying [ATP] and [ADP] and employing nonhydrolyzable ATP analogs (17) and by following gate dynamics using combined RBT and FRET (46). Since replacing the GyrB subunit of MTB with that of EC results in an increased supercoiling rate (33), single-molecule measurements of heterologous complexes may also help elucidate the structural basis of differences in state distributions.

Physiological functions of DNA gyrase include relieving excess positive supercoils, actively maintaining the negative superhelical density of the genome, and decatenating daughter DNA strands postreplication. EC gyrase appears to have specialized for fast relief of positive supercoils and the ability to quickly add negative supercoils up to a high limiting superhelical density when compared to some distantly related species such as MTB (28, 29, 31, 32, 35, 47, 48, 49, 50, 51). Previous comparisons of DNA gyrase function across species have suggested that EC gyrase can specialize in supercoiling, while gyrase in MTB (and other species that lack the paralogous type II topoisomerase, topo IV, which is EC’s primary decatenase in vivo) may compromise supercoiling activity to balance its roles (25, 29). EC gyrase is able to decatenate DNA but at much lower rates than EC topo IV (8, 26, 52) unless the enzyme is modified by deletion of the CTDs (53). Biochemical studies comparing the decatenation activities of EC gyrase and MTB gyrase have differed in their conclusions, with some reporting stronger decatenation activity for MTB (28, 47) in support of the multifunctional hypothesis, but others reporting that decatenation by MTB is comparable to or even slower than EC (32, 33). In MTB, gyrase binding has been found to be enriched near the Ter domain, where daughter DNA molecules are entangled after DNA replication, requiring decatenation (54). Mycobacterium smegmatis gyrase (an analog for MTB gyrase) can strongly trap two DNA segments in a trans configuration, like EC topo IV but unlike EC gyrase (50). MTB gyrase possesses a unique second potential DNA-binding motif in its CTD that resembles the canonical GyrA-box that wraps DNA in EC (47). This unique motif may enable a different wrapping path around the CTD, which may explain the difference in wrapped angle and contraction depth we see in MTB versus EC gyrase (Fig. 4, B and E) and support its cellular ability to decatenate DNA. Our measurements further suggest that EC gyrase’s function as a specialized supercoiling enzyme may arise from stabilization of the deeply contracted Ω state, which may act as a checkpoint for efficient chiral wrapping (14, 17, 18). Conversely, MTB’s apparent suppression of the Ω state may support decatenation at the expense of supercoiling activity.

Collectively, our findings point to how different evolutionary paths taken by MTB and EC gyrase have yielded differences in the dynamics of the DNA:gyrase nucleoprotein complex. EC gyrase appears to have specialized in supercoiling DNA; it can processively supercoil DNA at a fast rate (Fig. 2) and previous work has highlighted that the enzyme is able to coordinate wrapping at a higher supercoiling setpoint (against back-pressure from highly underwinding the DNA) (32). Magnetic tweezers measurements of EC gyrase demonstrated positive supercoil relaxation continues, even at high force (2–3 pN) and in the presence of fluoroquinolone inhibitors, while negative supercoiling is highly force sensitive and diminishes to zero at ∼50 μM ciprofloxacin (55, 56). Future work could compare the effect of force, torsional backpressure, and/or fluoroquinolones on MTB gyrase. The present study demonstrates that a specialized feature of the EC gyrase mechanochemical cycle is the dominance of the highly contracted Ω state, which may be a key intermediate for the coordinated wrapping of DNA in the presence of torsional backpressure. We have demonstrated differences in the way this complex molecular machine interacts with DNA given different natural selection pathways. Our findings show that when describing the single-molecule behavior of a class of motors, observations should be made across evolutionarily distant species before generalizing dominant states into a universal mechanism. Further work beyond the scope of this study will be required to build a detailed kinetic model of the MTB enzyme in the presence of ATP (17, 20), but the measurements presented here are sufficient to highlight key differences from EC within a simplified framework. This work also highlights the dominant states unique to MTB versus EC gyrase (Fig. 6), which may prove useful to those attempting to investigate specific states through cryo-EM or crystallography.

Experimental procedures

Preparation of DNA, gyrase protein, and beads

DNA tethers (Fig. 1B) with a variant of the μ phage strong gyrase site (57) were prepared via individual PCRs of three segments with modified nucleotides and primers, then subsequent ligation as previously described (17, 18). One μm diameter magnetic beads (ThermoFisher, Dynabeads, MyOne, Carboxylic Acid) were crosslinked with an antibody to Fluorescein/Oregon Green (ThermoFisher) via EDC as previously described (18, 19). Streptavidin-coated rotor beads were purchased (Power-Bind, ThermoFisher, 300 nm diameter). EC and MTB gyrase GyrA and GyrB subunits were individually expressed and purified as previously described (31, 32). Tetramers were formed by mixing monomers for 30 min at room temperature in 50 mM Tris–HCl, pH 7.5, 100 mM potassium glutamate (KGlu), 2 mM DTT, 1 mM EDTA, and 10% (v/v) glycerol and stored at −80 °C.

Single-molecule assays

Flow chambers were assembled with Parafilm or Nescofilm gaskets and hole-punch coverslips, with the objective side of the coverslip spin-coated with 0.1% (w/v) nitrocellulose in amyl acetate. Beads were washed twice with blocking buffer (5 mg/ml bovine serum albumin, 40 mM Tris–Hcl pH 8, 0.5 M NaCl, 0.2% Tween-20, 0.01% sodium azide), centrifuged at 13,200g for 3 min between washes, and incubated overnight with DNA tethers at 4 °C in blocking buffer (46). Chambers were incubated with 50 μl 12 μg/ml anti-digoxigenin in PBS (137 mM NaCl, 2.7 mM KCl, 10 mM Na₂HPO₄, and 2 mM KH₂PO₄, pH 7.5) overnight at 4 °C. On the day of the experiment, chambers were (1) incubated with 90 μl blocking buffer (1 h), (2) incubated with 25 μl DNA-rotor bead solution (1 h), (3) washed with 200 μl binding buffer (1.6 mg/ml bovine serum albumin, 40 mM Tris–Hcl pH 8, 0.5 M NaCl, 0.2% Tween-20, 0.01% sodium azide), (4) incubated with 20 μl magnetic bead solution in binding buffer (1 h), and (5) washed with 200 μl binding buffer. Wash flow steps were conducted at 25 μl/min, and all other flow steps were conducted at 15 μl/min by syringe pump. Once a molecule was selected for imaging, gyrase imaging solution (35 mM Tris–HCl pH 7.2, 92 mM KGlu, 4 mM MgCl₂, 250 μg/ml bovine serum albumin, 0.2 mM Spermidine, 2 mM DTT, 0.1% Tween-20, 10 mM phosphocreatine, and 1.23 μM phosphokinase) with gyrase enzyme (∼250 pM) and nucleotide was flowed into the chamber on the microscope at 10 μl/min.

Instrumentation

The instrumentation used to collect data and correct for drift were the same as those used in previous work to image single-molecule gyrase activity (17, 20). Magnetic tweezers were implemented on a modified Nikon Ti-S inverted microscope (20). The rotor beads were imaged via dark-field evanescent scattering using an 845-nm single-mode diode laser (Lumics, LU0845M200). A custom mount was used to hold diametrically opposed mirrors below the back pupil of the objective (0.13-0.21 WD, Nikon, TIRF, 60×/1.43) to provide separate paths for excitation path and the totally internally reflected return beam. The return beam was directed to a position-sensitive detector (Pacific Silicon) to provide a signal for focus stabilization feeding back to an xyz piezo stage (Mad City Labs). The light scattered by the rotor bead was imaged through an optical path splitter (Optosplit III, Cairn Research) onto a high-speed CMOS camera (Mikrotron, EoSens CL).

Data acquisition and position fitting

Images of rotor beads were acquired at 250 Hz. A quasi-real-time acquisition and analysis loop from previous work was implemented in Matlab at a loop rate of 1 Hz (20). During each loop, images were fit using a 2D Gaussian fitting function. Fit parameters included an additive offset c, peak height A, x position x₀, y position y₀, x sd σ_x, and y sd σ_y.

$$\mathrm{f}=\mathrm{c}+{\mathrm{A}\mathrm{e}}^{\left(-\frac{{\left(\mathrm{x}-{\mathrm{x}}_0\right)}^2}{{2\mathrm{\sigma }}_{\mathrm{x}}^2}-\frac{{\left(\mathrm{y}-{\mathrm{y}}_0\right)}^2}{{2\mathrm{\sigma }}_{\mathrm{y}}^2}\right)}$$

Conversion of rotor bead tracking measurements to angle and contraction coordinates was performed as previously described (17, 20, 46). Spatiotemporal resolution is limited by thermal fluctuations of harmonically constrained rotors, which can be described by an angular variance <Δθ²> = kT/κ and a relaxation time τ = γ/κ, where κ is the torsional stiffness of the tether and γ is the rotational drag of the rotor. For these assays performed at 0.8 pN, measurements of these parameters were <Δθ²> = 4.3 ± 0.8 rad² and τ = 0.15 ± 0.03 s (mean ± sd, N = 84, taken from 15-s regions before each run or binding event; the values of τ and <Δθ²> were obtained by fitting the mean square deviation of the rotor angle as a function of lag time). Evanescent nanometry was used to measure DNA contraction with decay length determined via dual focus imaging on each DNA tether that provided experimental data as previously described (20).

Substep analysis

Dwell states were identified using the Steppi change-point analysis tool (40, 41). Angular noise was modeled as an Ornstein-Uhlenbeck process. We determined the stiffness and coupling parameters for each trace on each tether using a segment of data containing only thermal fluctuations of the rotor bead (no gyrase bound). Estimated Steppi parameters approximately correspond with torsional stiffness and relaxation time above (τ ∼ 0.16 s and <Δθ²> ∼ 3.8 rad²) as expected. The free model parameters were the change point times and mean positions of states visited. When Steppi results are plotted over angle and extension traces, the idealization is plotted as generated by Steppi, producing an exponential decay from the final point of the previous raw data to the susequent mean.

For traces taken at 0 ATP, we were interested in transitions between wrapped and unwrapped states, so we chose to merge transitions between adjacent wrapped states or between adjacent unwrapped states as into clearly defined wrapped versus unwrapped states. To choose a threshold between wrapped and unwrapped states, we first plotted the states (Fig. S3) and manually chose a cutoff with good separation for both species at 0.65 rotations. All states above or below the threshold were merged.

For traces with nucleotide present, data were not pooled because transitions between high rotational angle states and the completions of cycles are indistinguishable for short dwells. Therefore, unpooled dwell data are presented. Dwell positions are presented modulo 2 rotations to indicate the position within the 2-rotation cycle. For approximate assignment of ‘wrapped’ versus ‘unwrapped’ states during bursts, where states are not always well-resolved, ‘wrapped’ were defined to be those between 0.85 and 1.85 rotations (modulo 2). Those angles account for much of the observed ‘wrapped states’ in both EC and MTB without ATP, and this division assigns equal rotational space to ‘wrapped’ and ‘unwrapped’ states.

Burst analysis and selection criteria

Cycles were defined to be completed sets of two rotations. Mean contraction values were calculated with the Steppi algorithm using the mean from the unfiltered raw extension data. Processive bursts were defined to be instances where gyrase bound to DNA causing a contraction of >10 nm for greater than 1 s until the DNA returns to an uncontracted state (<5 nm contracted) for more than 3.5 s and completed at least two cycles. Average burst speeds were calculated as the arithmetic weighted mean (mean velocity in cycles/s, weighted by burst duration, defined by contraction time), and error bars shown represent the weighted SD.

We only included runs where before and after the run, the DNA remained uncontracted for at least 30 s for TB gyrase and at least 5 s for EC gyrase. Single-cycle events were omitted from analysis. Since selected bursts were required to contain at least two cycles, when reporting the average number of cycles per burst, we shifted the reported mean by −1.

Binding events in the absence of nucleotide were defined similarly. Mean contraction values were calculated with the Steppi algorithm using the mean from the unfiltered raw extension data. Binding events were defined to be instances where gyrase bound to DNA causing a contraction of >10 nm for greater than 1 s until the DNA returns to an uncontracted state (<5 nm contracted) for more than 4 s. Binding events were considered regardless of angle change. States were scored based on angle change (Fig. 4A).

Angle-extension two dimensional histograms

Two dimensional histograms were created using Matlab’s hist3 and contourf functions. Extension data were first filtered by applying a low-pass filter with a cutoff frequency of 2.5 Hz. Angle data were not filtered. For histograms in the absence of ATP, the centers of two-dimensional Gaussians fit using maximum likelihood estimation to the unbinned data are shown (Fig. 4, A and D). Histograms in the presence of ATP display periodic repetition of the angle modulo 2 data, corresponding to the repeating reaction coordinate for processive bursts of gyrase activity.

Kinetic modeling

Simple kinetic modeling was performed on the traces with no nucleotide present to determine the rates of transition between wrapped and unwrapped states. Our simplified model of the gyrase:DNA complex interaction (Fig. 4C) is a 3-state continuous time Markov process. Kinetic parameters were measured and computed via:

$${\mathrm{k}}_{\left\{\mathrm{W}\to \mathrm{U}\right\}}=\frac{1}{{\mathrm{\tau }}_{\mathrm{W}}}$$

$${\mathrm{k}}_{\left\{\mathrm{U}\to \mathrm{W}\right\}}=\frac{1}{{\mathrm{\tau }}_{\mathrm{U}}}/\left(\frac{{\mathrm{N}}_{\left\{\mathrm{U}\to \mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\right\}}}{{\mathrm{N}}_{\left\{\mathrm{U}\to \mathrm{W}\right\}}}+1\right)$$

where W and U signify wrapped (rotational angle >0.65 rotations) and unwrapped states, respectively, and ${\mathrm{N}}_{\left\{\mathrm{U}\to \mathrm{free}\right\}}$ and ${\mathrm{N}}_{\left\{\mathrm{U}\to \mathrm{W}\right\}}$ are the number of dissociation and wrapped events, respectively. ${\mathrm{\tau }}_{\mathrm{U}}$ and ${\mathrm{\tau }}_{\mathrm{W}}$ are the average dwell times at each state. Errors for dwell times were calculated as SEM. Errors for observed transition probabilities were calculated as standard errors of proportions.

Data availability

All data and code available upon request.

Supporting information

This article contains supporting information.

Conflict of interest

The authors declare that they have no conflicts of interest with the contents of this article.

Reviewed by members of the JBC Editorial Board. Edited by Enrique De La Cruz

Supporting information

Supporting Figure S1

Mean processive burst lengths, in number of cycles. Bars represent the standard error and the mean, text displays the mean. Number of gyrase runs per condition: MTB 1.3 mM ATP, N = 17 bursts; EC 1.3 mM ATP, N = 8 bursts; MTB 130 μM ATP, N = 16 bursts; EC 130 μM ATP, N = 7 bursts. (Numbers of tethers and experimental days are given in the legend to Fig. 3).

Supporting Figure S2

DNA:gyrase conformational dynamics with ATP.A and B, every Steppi-detected dwell for MTB and EC gyrase during processive runs. (Numbers of runs, tethers, and experimental days are given in the legend to Fig. 3).

Supporting Figure S3

DNA:gyrase conformational dynamics in the absence of ATP with unpooled state definitions. One data point is plotted for each Steppi-detected dwell at either the unwrapped or wrapped state; dashed line indicates the angle threshold used to separate the two states for subsequent pooled analysis (Fig. 4).

Supporting Figure S4

Additional, longer example EC gyrase bursts.

Supporting Figure S5

2D histograms with free DNA included. Histograms constructed from the same traces as Figure 3, but with the inclusion of 5 seconds of the flanking regions from each binding event to capture the free DNA state.