Renal surface reconstruction and segmentation for image-guided surgical navigation of laparoscopic partial nephrectomy

Abstract

An unpredictable dynamic surgical environment makes it necessary to measure morphological information of target tissue real-time for laparoscopic image-guided navigation. The stereo vision method for intraoperative tissue 3D reconstruction has the most potential for clinical development benefiting from its high reconstruction accuracy and laparoscopy compatibility. However, existing stereo vision methods have difficulty in achieving high reconstruction accuracy in real time. Also, intraoperative tissue reconstruction results often contain complex background and instrument information that prevents clinical development for image-guided systems. Taking laparoscopic partial nephrectomy (LPN) as the research object, this paper realizes a real-time dense reconstruction and extraction of the kidney tissue surface. The central symmetrical Census based semi-global block stereo matching algorithm is proposed to generate a dense disparity map. A GPU-based pixel-by-pixel connectivity segmentation mechanism is designed to segment the renal tissue area. An in-vitro porcine heart, in-vivo porcine kidney and offline clinical LPN data were performed to evaluate the accuracy and effectiveness of our approach. The algorithm achieved a reconstruction accuracy of ± 2 mm with a real-time update rate of 21 fps for an HD image size of 960 × 540, and 91.0% target tissue segmentation accuracy even with surgical instrument occlusions. Experimental results have demonstrated that the proposed method could accurately reconstruct and extract renal surface in real-time in LPN. The measurement results can be used directly for image-guided systems. Our method provides a new way to measure geometric information of target tissue intraoperatively in laparoscopy surgery.

Supplementary Information

The online version contains supplementary material available at 10.1007/s13534-023-00263-1.

Introduction

Minimally invasive surgery (MIS) is a way for surgeons to manipulate instruments inserted into a patient through three-to-four abdominal channels to complete the operation based on the images provided by a laparoscope. Owing to the greater clinical benefits, like less trauma and low infection risk, MIS has become a standard of care for certain abdominal tumor surgeries [1]. For example, laparoscopic partial nephrectomy (LPN) is the standard procedure for the treatment of early-stage renal cancer (kidney tumor < 4 mm). However, narrow operable space and video-based surgical processes lead to a limited surgical field of view and less intraoperative perception, which makes the outcome of the operation depend on the experience and visuospatial awareness of the surgeon. Image-guided surgical navigation can effectively alleviate the limited surgical perception [2]. It guides surgeons' operation by overlaying virtual key anatomy structures (blood vessels, tumors, etc.) on the surgical field/laparoscopic video and has been reported in many files of laparoscopic surgeries over the last decade [3, 4]. Unlike in a rigid environment, abdominal tissue in laparoscopic surgery has dynamic unstructured deformation. This makes the overlaid images need to be updated in real-time according to the morphological changes of the intraoperative tissue during the navigation. Therefore, intraoperative measurement of geometric information of target tissue becomes a necessary and important step in image-guided surgical navigation system.

The traditional intraoperative measurement methods of 3D information of target tissue can be roughly divided into two types: segmentation modeling based on intraoperative CT, ultrasound, or other scanning images, and optical 3D reconstruction based on the laparoscopic video. The former, based on intraoperative CT or MRI, is expensive and can only be performed in a hybrid operating room (Hybrid-OR) equipped with the equipment [5]. Although ultrasound is easier to implement intraoperatively, it has difficulties in image recognition and imaging [6]. The latter, video-based optical 3D reconstruction also has two categories: active measurement and passive measurement. Active measurement algorithms have better reconstruction robustness, mainly including shape-from-polarization (SfP) [7], structured light [8], and time-of-flight (ToF) [9], but the algorithms require new or improved laparoscopic hardware support due to the need for imaging auxiliary equipment. It requires considerable trade-offs in minimally invasive surgical standards and resolution leading to limited clinical application. Passive measurement is a type of technology that only relies on analyzing endoscopic images for optical reconstruction. It is compatible with the most common endoscopes and has become the most popular intraoperative reconstruction method. There are four main methods, including: stereo vision [10], simultaneous localization and mapping (SLAM) [11], structure from motion (SfM) [12] and shape-from-shading (SfS) [13]. Among them, stereo vision can complete the depth calculation through the feature matching of the left and right images without motion scenes needed for SFM and SLAM. Moreover, by comparing most organs in the abdomen, Groch et al. pointed out that the reconstruction accuracy of the stereo vision algorithm is higher than that of ToF or SFM [14]. Maier-Hein et al. later verified that the reconstruction accuracy of stereo vision is higher than that of structured light and ToF [9]. With the popularization of stereo laparoscopy in clinics, the stereo vision reconstruction method has the most potential for clinical application.

Physical 3D reconstruction of stereo image pixels can be directly computed from the disparities using stereo camera calibration parameters. The disparities are estimated through stereo matching, which has developed a lot of research algorithms as the critical technology of stereo vision. Readers can refer to the Middlebury website. However, not all the algorithms fulfill the specific requirements within a laparoscopic environment, such as the need for real-time performance, the problem of specular reflections, periodic textures, and occlusions due to surgical instruments.

Related works

In the application of laparoscopy, many stereo matching approaches are developed based on feature matching and tracking. Stoyanov et al. proposed a semi-dense reconstruction approach for robotic-assisted minimally invasive surgery by local optimization to propagate disparity information around correspondence seeds obtained [10, 15]. This algorithm had been extended to recover temporal motion [16], reduce noise artifacts [17], and performed more fast using a multi-resolution pyramidal approach [18]. Marques et al. obtained sparse 3D points by matching points on the tissue surface, and then established a tissue deformation model to interpolate the tissue surface to complete the reconstruction [19]. Such methods can be implemented in scenes lacking texture or periodic textures to realize disparity estimation and even avoid instrument occlusions. However, the robustness of these reconstruction methods can be influenced much by the availability of stable features, which is difficult to detect in the complex environments of laparoscopic surgery. With the success of deep learning, learning-based or data-driven algorithms have been approved for laparoscopic dense reconstruction [20–22]. One limitation of such algorithms is the reconstruction accuracy depends heavily on the training dataset. Due to the difficulty in obtaining ground truth data in the surgical domain, few datasets exist and are typically much smaller or focus on phantom or non-realistic environments [23], which makes the training model overfitting and poor generalization performance. For example, the 3D reconstruction will be inaccurate when the test data have different camera parameters [24]. Recently, Luo et al. proposed an unsupervised depth estimation method without ground truth labels and achieved the mean absolute error (MAE) of 3.054 mm [25].

Another approach, as the conventional stereo matching algorithm, transforms the disparity map estimation into a function optimization problem to achieve pixel-by-pixel matching to complete dense reconstruction. The optimization function generally includes a cost function term for calculating pixel similarity and a disparity smoothing constraint term. This pixel-based algorithm is generally more suitable for tissues with clear texture representation. Thanks to the development of high-definition stereo laparoscopic hardware systems, this approach is increasingly applied in soft tissue, such as kidney [26, 27], liver [28]. Devernay et al. proposed the first dense stereo reconstruction method by using normalized cross correlation (NCC) for cost computation without any global optimization and with a field programmable gate arrays (FPGA) implementation [29]. Vagvolgyi et al. developed semi-global optimization using dynamic programming (DP) with SAD as block matching similarity cost function [30], and it was applied to acquire disparity map during surgery to pre-operative models in robotic partial nephrectomy [26]. But this algorithm is sensitive to image noise. Chang et al. proposed to compute pixel matching cost in terms of zero-mean normalized cross-correlation (ZNCC) with convex optimization to get a smooth disparity map [31]. The ZNCC matching cost is robust to illumination changes and it has been used in many laparoscopic reconstructions for disparity estimation [32]. Hirschmuller et al. evaluated 15 cost matching functions and confirmed that the cost matching function Census has higher robustness and matching accuracy than ZNCC [33]. Penza et al. applied a modified Census matching method combined with a simple linear iterative clustering super-pixel algorithm for disparity refinement [34]. This method got a high reconstruction accuracy (around 1.7 mm) excepting not in real time.

In addition, the above dense matching methods are applied to the whole laparoscope image that the reconstructed point cloud contains both the target tissue and its background. Although some researchers used the reconstruction results directly [35] or selected target points manually [30, 34] for image-guided systems, these undoubtedly reduce the processing efficiency of the system. In our previous work, we performed a deep learning algorithm of Mask R-CNN to segment the kidney tissue in laparoscopic images [27]. However, we found that the segmentation performance of these algorithms is poor when having instrument occlusions.

To realize the real-time dense reconstruction and extraction of the renal tissue surface in laparoscopic scenes of LPN, this paper proposes to use a center-symmetric Census transform (CSCT) block stereo matching algorithm combined with semi-global dynamic programming to generate the dense matching disparity map. This algorithm provides high accuracy as Census while with real-time performance achievement [35, 36]. Meanwhile, a GPU-based pixel-by-pixel connectivity segmentation method is designed to complete the real-time segmentation of kidney tissue in laparoscopic images. The main contributions of this paper are as follows. (a) Applying CSCT to partial nephrectomy achieved a high accuracy dense reconstruction of surgical laparoscopic scenes with real-time performance. (b) A GPU pixel-by-pixel segmentation algorithm dealing with complex surgical environment is proposed and realized the real-time extraction of kidney tissue surface under laparoscopy. (c) The obtained real-time reconstruction and segmentation results provide a data basis for the registration of subsequent surgical navigation. Our method can be used in other laparoscopic procedures, such as livers.

Methods

In the following pages, we describe the necessary methods for reconstructing a renal surface from laparoscopic images which can be registered to a preoperative model.

Stereo matching and reconstruction

A semi-global block matching (SGBM) strategy is adapted to generate the disparity map for 3D reconstruction. The SGBM is derived from the semi-global matching algorithm (SGM) [37, 38] with the matching speed improved, which uses the CSCT as a local matching cost function and the SGM semi-global cost aggregation.

Local matching cost computation of CSCT

The CSCT local matching cost transforms pixels in a window centered with the pixel that to be matched as a 0/1 bit-vector. Then the matching cost of the two pixels to be matched in the left and right images is computed by the Hamming distance of the two CSCT bit-vectors:

$$\mathit{C}(\mathit{p},d)=Hamming[CSC{T}_l(\mathbf{p}),CSC{T}_r(\mathbf{p}+d)]$$ 1

where d represents the estimated disparity of the corresponding pixel. CSCT(p), CSCT(p + d) corresponding to the two CSCT bit-vectors of the pixel p in the left and right images respectively. The bit-vector encoding of CSCT is obtained by comparing the symmetrical pixels by the center pixel to each other in the transformation window. Assume the location of p in the image I is (x,y), then the CSCT bit-vector of p is transformed by

$$CSC{T}_{m,n}(x,y)=\underset{(i,j)\in L}{\otimes }\xi (I(x-i,y-j),I(x+i,y+j))$$ 2

mxn is the size of the transformation window centered with p. $\otimes$ represents a bitwise concatenation operation. L is the symmetrical area of the front part of the transformation window, and $\xi (\bullet ,\bullet )$ is the judgment function of the symmetrical pixels.

$$\begin{array}{cc}\xi (I(x-i,y-i),I(x+i,y+j))=1,& \text{if}I(x-i,y-i)>I(x+i,x+j),\\ 0,& \mathit{otherwise}\end{array}$$ 3

As shown in Fig. 1, the CSCT bit-vector of the center pixel p in a 9 × 7 transformation window is encoded as CSCT(p) = 00,000,000,00,011,110,11,111,111,0,001,110. It uses 31 bits to describe 55 pixels, which greatly reduced the computational complexity compared to the traditional Census transform and improved the computation efficiency.

Fig. 1.

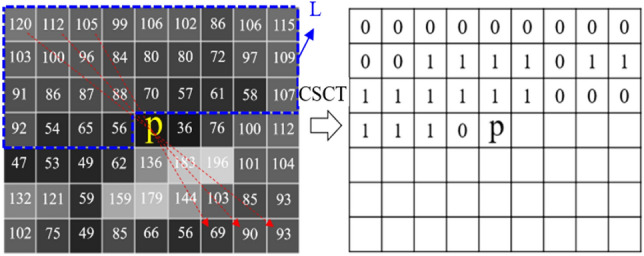
Center-symmetric census transform for a 9 × 7 patch

Semi-global cost aggregation

The semi-global cost aggregation seeks to approximate a global 2D smoothness constraint by combining multidirectional 1D paths L in several directions r through the image. DP approach is used to calculate the minimum cost along each path L_r. L_r represents the cost aggregate value on the current path r.

$${\mathbf{L}}_{\mathit{r}}(\mathbf{p},d)=\mathbf{C}(\mathit{p},d)+min\left(\begin{array}{c}{\mathbf{L}}_{\mathit{r}}(\mathbf{p}-\mathit{r},d),\\ {\mathbf{L}}_{\mathit{r}}(\mathbf{p}-\mathit{r},d-1)+P_1,\\ {\mathbf{L}}_{\mathit{r}}(\mathbf{p}-\mathit{r},d+1)+P_1,\\ \underset{i=d_{min},...,d_{max}}{min}{\mathbf{L}}_{\mathit{r}}(\mathbf{p}-\mathit{r},i)+P_2\end{array}\right)-\underset{i=d_{min},...,d_{max}}{min}{\mathbf{L}}_{\mathit{r}}(\mathbf{p}-\mathit{r},i)$$ 4

where p−r refers to all pixels along with direction r with a distance p of one unit, two units, …, until to the end. C represents the local matching cost of CSCT. P₁ and P₂ are constant penalty coefficients controlling the disparity smoothness. The matching cost of pixel p with disparity d is the cost aggregation of all paths, i.e.,$E(\underset{\mathit{p},d}{D})=\sum _{\mathit{r}}{\mathbf{L}}_{\mathit{r}}(\mathbf{p},d)$. The disparity d (d ∈ [d_min, d_max]) that minimizes E(D) is taken for pixel p in left (or right) laparoscopic image. The disparity estimation pipeline is implemented on embedded GPU and the GPU architecture can be seen in [39]. Finally, the disparity map D is calculated after finishing disparity estimation of every pixel, and the 3D information of every point in the image can be calculated with the calibrated camera parameters using the principle of triangulation reconstruction.

Kidney segmentation and extraction based on GPU

Although the stereo matching based on the CSCT improves the computation efficiency, it increases the difficulty of segmentation of kidney from the disparity map due to blurred boundaries (Fig. 2b). In this regard, a GPU-based pixel-by-pixel connectivity segmentation method applying of the disparity gradient information is designed. As shown in Fig. 2, edges in the disparity map are first extracted. After degradation of invalid edges, a partition-merged connected domain labeling method is carried out to complete the kidney segmentation.

Fig. 2.

Segmentation of Kidney from disparity map, a laparoscopic image; b disparity map; c edge-detected image; d edge extraction map; e connected domain labeling; f segmentation result

Edge detection and degradation

A modified Canny edge detection algorithm is applied for edge detection. The traditional Canny edge detection algorithm has 5 steps containing Gaussian blur, determining the intensity gradients, non-maximum suppression, double thresholding, and edge tracking by hysteresis [40]. The modified canny algorithm replaces the Gaussian filter in the original algorithm with a median filter to eliminate outliers while maintaining effective edge information in the image. Also, to simplify the calculation process, the gradient sum of squares from x and y direction is calculated to represent the gradient feature of point. Thirdly, a novel edge degradation is used when finalizing the detection of edges in the last step to remove the false edges avoiding edge breakage.

Specifically, after obtaining the edge-detected image (Fig. 2c) by double thresholding process, each edge pixel, that value 0, is discriminated within its 8 neighborhoods. If the pixel cannot connect edges, it will be degraded, i.e., its value will be set to 1. This process proceeds iteratively until there are no valid points that need to be degraded. However, since each pixel is calculated in parallel in a single thread, it is easy to cause edge breakage. As shown in Fig. 3, in the two parallel threads the two points p₁ and p₂ will be discriminated with no role of connection, and their value will be set to 1. That will result in fracture of the original continuous edge. Therefore, in this paper, only the six forms and their rotation or axisymmetric forms shown in Fig. 4 will proceed with degradation. After finishing the edge detection and degradation processing, the edge extraction map is finally obtained (Fig. 2d).

Fig. 3.

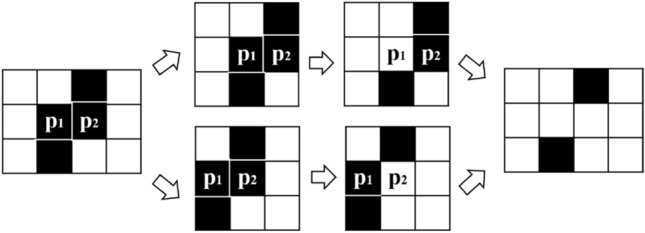
Parallel degradation causes edge breakage

Fig. 4.

Six forms proceed degradation

Connected region labeling and extraction

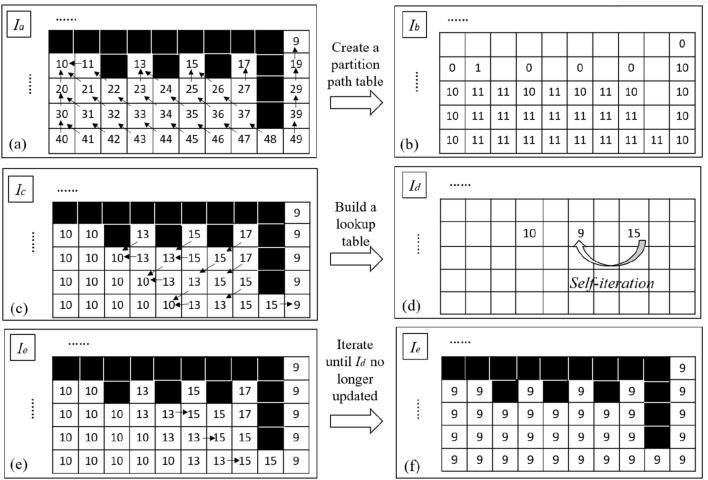
The traditional connected domain labeling method of region growth by setting seed points is hardly to realize real-time application. Inspired by labeling connected component method designed by Štava [41], we propose a GPU-based method for labeling connected regions by partition merging (Fig. 5). The steps are as follows.

Fig. 5.

Diagram of the region labeling process

(a) Create a partition path table and obtain a partition map. All non-edge points in the edge extraction map are set index value with the upper left corner of the image as the coordinate origin: Index = y*width + x. y is the column coordinate where the pixel is located, x is the row coordinate, and width is the width of the image. Then, a partition path table I_b is established by using the edge extraction map I_a.

$$I_b(\mathbf{p})=I_{\text{a}}(\mathbf{p})-\underset{\mathbf{q}\in \mathit{N}}{min}{I}_{\text{a}}(\mathbf{q})$$ 5

where q is the pixel point within the 8-neighborhood interval N with p as the center. Based on the partition path table I_b, the partition map I_c (Fig. 5c) is obtained by path iteration on every pixel of I_a parallelly.

$$\begin{array}{cc}{I}_{\text{c}}(\mathbf{p})=I_{\text{a}}(\mathbf{p})-\sum I_b(\mathbf{p}-\widehat{\mathit{L}}),& I_b(\mathbf{p}-\widehat{\mathit{L}})>0\end{array}$$ 6

$\widehat{\mathit{L}}$ represents the direction in which the marked value changes the most, i.e., the path direction of the partition in this paper (indicated by the arrow in Fig. 5a). For example, I_c(4,5) = I_a(4,5)-I_b(4,5)-I_b(3,4)-I_b(2,3) = 13.

(b) Build a lookup table based on the partition map. Calculate the minimum value of the 8-neighborhood of each point of I_c and record the minimum value in the look-up table according to the converted coordinates. The converted coordinates of I_c(p) corresponding to the lookup table I_d are (I_c(p)/width, I_c(p)%width). In this way, all points with the same label in I_c correspond to one coordinate position in I_d. When the same pixel label (such as 15) has multiple 8-neighbor minimum values, 15 → 13,15 → 9, then the minimum value min (13,9) = 9 will be taken and filled in the lookup table at the coordinates of (15/10, 15%10) = (1, 5), as shown in Fig. 5(d).

(c) Self-iteration of the lookup table. Self-iteration of the lookup table is used to merge the region of the partition map faster by chain update of values. Specifically, update the value of valid point I_d(p) in I_d by the value under the coordinates at (I_d(p)/width, I_d(p)%width) if the value is non-zero. As shown in Fig. 5(d), for example, the coordinate of the value 15 is (1,5), in which there is a non-zero value 9. Then the 15 will be updated to 9.

(d) Partition merges using the lookup table. The transformed coordinates of each label value in I_c are calculated, and the new label value is retrieved in I_d with the coordinates. Each pixel in I_c corresponds to one computation thread. After finishing updating the partition map I_c, the new label map I_e is obtained (Fig. 5e).

Iterate steps (b), (c), and (d) until the lookup table I_d corresponding to I_c is no longer updated. A statistical histogram is used to find the label value with the largest number in the histogram. Then the position of the label value is marked to extract the renal tissue region in the disparity map (Fig. 2f). Finally, the extracted target point cloud is obtained by 3D reconstruction by using of the segmented disparity map.

Evaluation and results

Experiments were conducted respectively for 3D reconstruction and segmentation and the evaluation data used include in-vitro porcine heart images, in-vivo porcine kidney, and off-line clinical LPN video. The porcine heart data has structure ground truth and similar texture characteristics to the human kidney, which was used for evaluating the stereo matching and reconstruction accuracy in our paper. CT scans were performed to obtain the morphology of the heart with slice spacing of 0.6 mm and pixel spacing of 0.6\0.6 mm. The ground truth surface information of the heart was from mesh model generated using the 3D Slicer. The laparoscopic used was Karl Storz HD stereo laparoscopic with a single image resolution of 960 × 540. The image processing workstation used is equipped with Intel Xeon 2.9 GHz CPU, Nvidia RTX A4000 GPU. All algorithm acceleration was applied with CUDA 11.1 general parallel computing architecture, and the run time of processing is recorded statistically at last.

Evaluation of stereo matching and 3D reconstruction

An in-vitro porcine heart tissue was placed in a standard abdominal model of the human body to simulate a sufficiently realistic intraoperative scene. Intraoperative video was captured using the Karl Storz HD stereo laparoscopic at surgeons' operating angle and the actual clinical workspace (about 2–15 cm away from the tissue). In the acquired intraoperative laparoscopic images, a total of four sets of images at different distances were selected to evaluate the proposed stereo matching algorithm. We compared our proposed algorithm (window size of 9 × 7) with a ZNCC-based block matching algorithm (window size of 17 × 17) and the BT-based SGBM algorithm. The results are shown in Fig. 6. It can be seen the estimation disparity map from ours is more complete and more effective for stereo matching of laparoscopic images than the latter two.

Fig. 6.

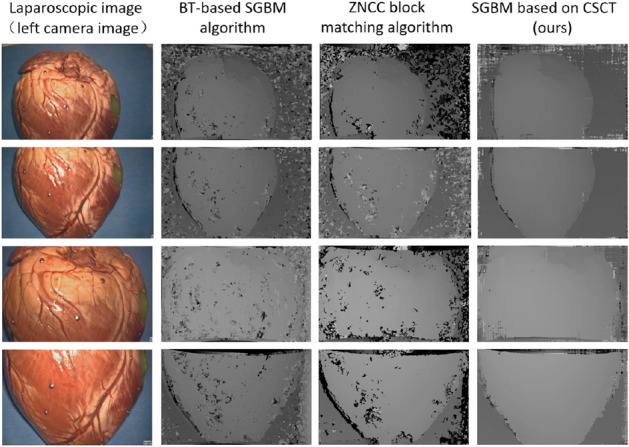
Comparison of stereo matching results from different algorithms

Meanwhile, the reconstruction error of the reconstructed points was evaluated quantitatively by measuring the Euclidean distance from the ground truth, i.e., the heart CT model. As shown in Fig. 7(a), the Iterative Closest Point (ICP) registration with a point-based initial transformation was applied to align the CT model and the reconstructed points [42]. A total of 21 pairs of LPN images were analyzed and the average maximum reconstruction error is ± 1.86 mm. The mean absolute error is 0.23 ± 0.33 mm. Some of the analysis results are shown in Fig. 7(b). It can be seen the error is mainly concentrated in the boundary area with occlusions, and the overall error distribution is around ± 2 mm.

Fig. 7.

Reconstruction error, a framework of error measurement b reconstruction error distribution of example data

Accuracy of automatic segmentation

The LPN data was processed to verify the accuracy of the segmentation algorithm. To quantitatively evaluate the accuracy of the segmentation algorithm, artificial segmentation results were used as ground truth. However, segmenting the target area in images would introduce a lot of noises in the boundary part of the 3D reconstructed point cloud (Fig. 8c). To evaluate the effective segmentation region more accurately, the 3D point cloud after removing noises was used as the manually segmented ground truth (Fig. 8d). As shown in the Fig. 8(f), the yellow points are the overlapping area (O-lap), red points are the false negative area (dividing the target tissue area into non-target areas, FN), and green is the false positive area (dividing the non-target tissue area into the target tissue area, FP). we calculated segmentation accuracy by

$$r=\frac{N(\text{O - lap})}{N(\text{O - lap}+\text{FN}+\text{FP})}\times 100\%$$ 7

where N is the sum of the number of all pixels in the area.

Fig. 8.

Precision analysis of the segmentation, a laparoscopic image; b manual segmentation of image; c reconstructed points corresponding to the image segmented area; d reconstructed points after removing noises by manually segmentation; e reconstructed points by our automatic segmentation; f comparison result; g segmentation accuracy comparison of different algorithms

A total of 20 pairs of LPN images were collected randomly and 17 were in the context of tissue-tool interaction. The mean segmentation accuracy of the proposed method was 91.0% compared with 82.9% of the Mask R-CNN segmentation method [27]. Figure 8(g) shows the comparison result. Adding more training data containing instrument interaction scenes may further improve the accuracy of Mask-RCNN, but our proposed algorithm has higher generalization. In the segmentation results, most of the FN areas are fat that adheres to the surface of the kidney, and most FP areas are the parts where the surgical instrument contacts the tissue. A higher segmentation accuracy would be obtained if the fat were peeling before the measurement.

The final renal surface reconstruction results were obtained after rending by the visualization toolkit (VTK). Two videos, an offline LPN clinic data and a public in-vivo porcine kidney laparoscopy data with tissue-tool interaction from Hamlyn Centre [43], showing the reconstruction results are given in Online Resource 1. They verify the effectiveness of our proposed algorithm to achieve automatic reconstruction and segmentation of intraoperative renal tissue even with occlusion of surgical instruments at any angle.

Processing time

We report the average runtime of the main steps of the proposed method in Table 1. The results list is the average time of 1000 key frames on 960 × 540 laparoscopy videos. The average computational time to process a key frame is 47.1 ms, which suggests that the proposed method is realtime.

Table 1.

Average runtime of the proposed method

Images reading and rectified	15.3 ms
Stereo mathcing	2.6 ms
Segmentation	18.3 ms
Reconstruction	10.9 ms
Total	47.1 ms

Discussion

In this paper, we describe and evaluate a dense reconstruction and segmentation method for tissue geometric measurements intraoperatively of LPN. Compared with previously reported reconstruction algorithms in laparoscopic surgery, our approach achieves a real-time reconstruction with target tissue extraction automatically. The reconstruction achieved a real-time update rate (21 fps) for an HD image size of 960 × 540 and the results could be used directly in following registration step for image-guided navigation systems. Experiments were performed to evaluate our algorithms. The reconstruction error was distributed mainly within ± 2 mm, and the target tissue segmentation was found to be 91.0% with surgical instrument occlusions. The algorithm proposed in this paper has reference significance for intraoperative measurements of other tissues in laparoscopic surgery. Higher performance could be achieved in the future by focusing on the following investigations: pre-processing the laparoscopic stereo images, introducing region-based 2D area information in the cost aggregation part of the stereo matching function, and reconstruction compensation for occlusion or missing highlight reflection.

Supplementary Information

Below is the link to the electronic supplementary material.

Author’s contribution

All authors contributed to the study conception and design. XZ: Performed the research, Designed the reconstruction method, Analyzed the results. XJ: Designed the segmentation method, Coding the parallel computing. JW: Reviewed the manuscript, Acquired image data and project funding. YF: Supervised the project, Reviewed the final manuscript, Worked on the manuscript with support. CT: Supervised the project, Reviewed the final manuscript, Worked on the manuscript with support.

Funding

This work was supported by Natural Science Foundation of China (Grant No. 62173014) and Natural Science Foundation of Beijing Municipality (Grant No. L192057).

Declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Consent to participate

Informed consent was obtained from all individual participants included in the study.

Consent to publish

The authors affirm that human research participants provided informed consent for publication of the images in Figs. 2a, 8a, b and Online Resource video.