Abstract
Purpose
The aim of this study was to examine measured and calculated dose distributions in a thin-chest-wall phantom and estimate the variations in the dose-volume histogram (DVH) parameters used in plan evaluation for patient geometries with chest-wall thicknesses <15 mm with and without bolus implementation.
Methods and Materials
Measurements were made using thermoluminescent dosimeters in a chest-wall phantom. The Monte Carlo method, anisotropic analytical algorithm, and Acuros XB Eclipse algorithms were used to calculate dose distributions for clinical plans. DVH parameters for clinical target volume tumor (CTVT) and planning target volume (PTV) and mean doses were evaluated for 15 patients with a chest-wall thickness of 8 to 15 mm with and without partial bolus and for 10 patients with a chest-wall thickness of 20 to 25 mm without bolus.
Results
Measurements showed that the dose at a depth of 2 to 12 mm at the beam entrance and laterally was within 90% of the dose at 8 mm depth. Monte Carlo and Acuros XB calculations were well aligned with the experimental data, whereas the anisotropic analytical algorithm underestimated the beam entrance and lateral doses. The DVH parameters for the patients with a thin chest wall were sensitive to calculation algorithm, resolution, body structure definition, and patient geometry. The parameters CTVTV95%, CTVTD98%, and PTVD98% were much lower than the tolerance criteria. Partial bolus improved the values for all algorithms and decreased the variations due to patient geometry. Dose calculations for patients with a chest-wall thickness of 20 to 25 mm resulted in sufficient target coverage and low dependence on patient geometry and calculation algorithm without the use of bolus.
Conclusions
Dose calculations using advanced algorithms and resolution <2 mm are recommended for patients with a thin chest wall. Specific DVH criteria or the implementation of partial bolus was needed to facilitate plan development and evaluation for this patient group.
Introduction
Adjuvant postmastectomy radiation therapy is used to reduce the risk of local recurrences and to increase the patient survival.1, 2, 3 In general, the treatment is administered to the chest wall and regional nodes. The chest-wall irradiation geometry is highly inhomogeneous, comprising a soft-tissue layer a few centimeters thick, ribs behind this, and finally low-density lung tissue. Guidelines for target delineation specify an anterior border of 2 to 5 mm below the skin surface and a posterior border at the rib (or middle of the rib)–pleural interface.2,4 A significant part of the target thus belongs to regions in which lack of electron equilibrium and incomplete scatter conditions are present. Some patients’ chest-wall thickness may be comparable with the buildup region of the photon depth dose distribution, and the chest target volume may be considered a superficial region. Accurate dose determination under these conditions requires advanced dose calculation algorithms and appropriate description of the geometry.
Despite the challenges, few studies have explored dosimetry issues concerning chest-wall irradiation. Mean dose, voxel dose values, and detailed dose-volume histogram (DVH) parameters have usually been used in plan evaluations, comparisons of treatment techniques, and radiobiological evaluations without discussion of dose distributions and calculation uncertainties.2,4, 5, 6, 7 Patients with different chest-wall thicknesses were grouped together; target coverage was not provided and explicitly not related to the clinical outcomes.8, 9, 10
In general, treatment planning guidelines for postmastectomy radiation treatment provide common dosimetry criteria irrespective of the chest-wall thickness or dose calculation algorithm. The previous praxis of using a 5-mm thick and 60-mm bread partial bolus around the scar, for all patients treated in our hospital has recently been updated by recommending bolus in specific cases. Effects on target coverage are of interest, especially for target volumes in the superficial region.
A chest wall with a thickness of 15 mm or less, observed in the target region, was considered thin in this work. The choice of this thickness was motivated by physical aspects. It is associated with the buildup region of the depth dose distribution in water of a 6-MV accelerator beam. In a previous work, the occurrence of a thin chest wall in 160 consecutive patients receiving radiation therapy after mastectomy at our institution was found to be 14%.11
The aim of this study was to examine measured and calculated dose distributions in a thin-chest-wall phantom and to estimate the variations in dose determination and DVH parameters used in plan evaluation for patient geometries with chest-wall thicknesses <15 mm with and without bolus implementation. Measurements were made using thermoluminescent dosimeters (TLDs) in a cylindrical phantom. The Monte Carlo (MC) method and the analytical anisotropic algorithm (AAA) and Acuros XB clinical algorithms in Eclipse Treatment Planning System (TPS) (Varian Medical Systems, Palo Alto, CA) were used for the dose calculations, as described herein.
Methods and Materials
Measurements and calculations in a cylindrical chest wall phantom
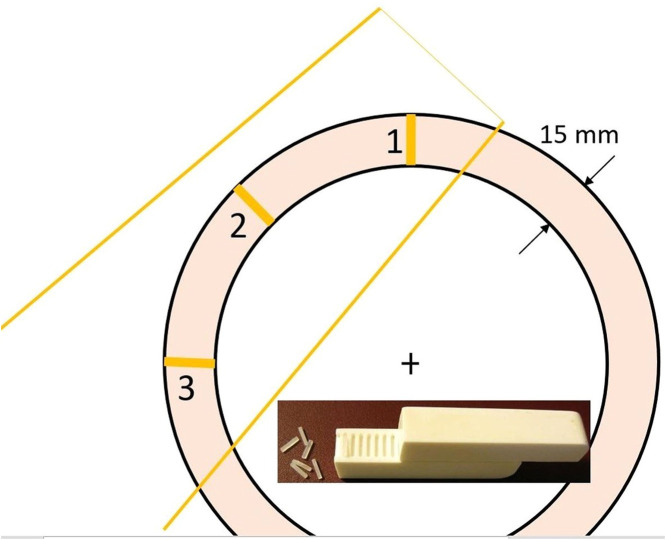
Measurements were made of a 6-MV 100 × 100 mm2 open field from a TrueBeam accelerator (Varian Medical Systems), tangentially (45°) incident on a 200-mm-diameter and 300-mm-long custom-made cylindrical “plastic water” phantom (PTW RW3) with a central air cavity 170 mm in diameter and 80 mm long. Dose profiles from the surface toward the geometric center of the phantom were obtained using Harshaw TLD-100 (LiF:Mg,Ti) square rods (1 × 1 × 6 mm) (Thermo Scientific, Waltham, MA) in 3 positions, that is, the beam axis entrance and exit as well as laterally (Fig. 1). The dosimeters were embedded in the plastic water material 1 mm from one another. Individual calibration factors and individual uncertainties, in terms of one standard deviation from the mean, were estimated from 6 independent irradiations. The dose was determined in absolute units (Gy) by delivering a known dose to reference dosimeters.
Figure 1.
Transverse view of the cylindrical chest wall phantom with the tangential beam indicated. Dose profiles from the surface toward the geometric center of the phantom: (1) at beam axis entrance, (2) laterally, and (3) at beam axis exit. Insert: TLDs embedded in the solid water holder. Abbreviation: TLD = thermoluminescent dosimeter.
MC dose calculations were made using a software system based on the EGSnrc code package.12 The system was developed in our hospital and used clinically for pretreatment quality controls.13,14 Dose distributions were also determined using the clinical algorithms available in the Eclipse TPS: the AAA v. 16.1 and the Acuros XB v.15.6.
A computed tomography (CT) scan of the cylindrical phantom was used in the calculations. Automatic body search was performed using the default clinical settings (–350 HU, smoothing level 3). CT numbers were set to 0 HU in the plastic water part inside body and to –1000 HU in the central air cavity. An outer margin of 3 mm was then applied to the body structure to include the whole superficial region of the phantom visible on the CT scan. The calculation matrix was set to 2 × 2 × 2 mm3. The MC dose distribution was determined with statistical uncertainty (one standard deviation) of up to 1.5% in the irradiated plastic water region and imported to the Eclipse TPS for analysis and comparison with data from the clinical algorithms. Profiles at the beam entrance and exit were extracted using the Eclipse line dose tool. A hypothetical target volume of 230 cm3 was delineated with a 2-mm margin for the default body structure and a 2-mm margin for the default lung delineation. DVH parameters for the hypothetical target were estimated assuming irradiation with 2 opposite tangential beams.
Calculations in patient geometries
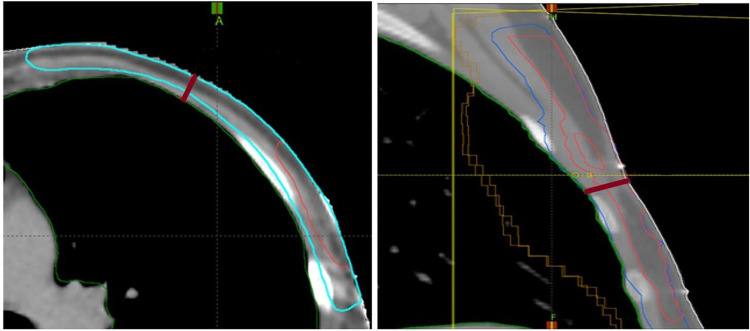
Fifteen patients with a chest-wall thickness of 8 to 15 mm were identified (Fig. 2) for analysis; an additional 10 patients with a chest-wall thickness of 20 to 25 mm were selected for comparative results. CT scans were acquired on an Aquilion LB scanner (Toshiba Medical Systems, Otawara, Japan). The clinical target volume tumor (CTVT) and planning target volume (PTV) were delineated according to national guidelines.15 The recommendations for posterior and anterior borders could not be entirely fulfilled in the thin-chest-wall cases, whereas the 5-mm target distance from the body structure was attained in the thick-chest-wall cases. The target volumes were 4 to 236 cm3 for CTVT and 236 to 470 cm3 for PTV in thin-chest-wall patients, and 12 to 95 cm3 for CTVT and 371 to 773 cm3 for PTV in thick-chest-wall patients.
Figure 2.
Smallest chest-wall thicknesses of 0.88 and 1.45 cm found in 2 patients: transverse view of patient (a) showing PTV and CTVT; sagittal view of patient (b) showing PTV, CTV, and CTVT. Abbreviations: CTV = clinical target volume; CTVT = clinical target volume tumor; PTV = planning target volume.
The 3-dimensional conformal radiation technique was applied with anterior–posterior photon irradiation of the lymph nodes and tangential photon beams encompassing the chest wall part of the target. The clinical plans were generated in Eclipse TPS using the AAA algorithm and were recalculated using the Acuros XB algorithm and the MC method, keeping the same beam parameters, monitor units, and a calculation matrix with 2.5 × 2.5 mm2 resolution. The CT calibration curve was used to extract mass density information. The AAA interpreted the patient tissues as water material of different densities. Acuros XB implemented 5 biologic tissues and air in the automatic CT-to-material conversion. The CT numbers in the MC simulations were correlated to 9 tissues: air, lung, adipose, and muscle tissues, as well as 5 bone tissues obtained by interpolating bone mass density and composition between trabecular and cortical bone.13 Dose was reported in dose-to-water and dose-to-medium terms using the MC method and Acuros XB (denoted MCw, AXBw, MCm, and AXBm) and in dose-to-water terms using AAA. The statistical uncertainty of the MC dose in the target region was within 2%. The distributions obtained in the MC system were imported into Eclipse TPS for comparison with the clinical algorithm data and for DVH analysis.
The effects of the calculation matrix resolution and surface conditions on the DVH values were studied by means of case calculations with a 1.5 × 1.5 mm2 grid and implementing a 3-mm outer margin for the default body. The effect of bolus implementation was investigated by comparing dose distributions with and without bolus for the thin-chest-wall patient group. Partial 5-mm bolus was assumed with a 60-mm width placed at the scar. Bolus was not considered for the thick-chest-wall patients.
Statistics
The DVH parameters CTVTD98%, CTVTV95%, PTVD98%, and PTVV105% as well as the mean dose values to CTVT and PTV were evaluated for each plan in the Eclipse TPS. The common interpretation of the notations was used. For example, CTVTV95% indicated the percentage of the total CTVT volume receiving 95% of the prescribed dose. PTVD98% indicated the dose (in percentage of the prescribed dose) that 98% of the PTV volume received. The mean values of the aforementioned parameters and the corresponding minimum–maximum variations were obtained for a patient group. These were compared with the tolerance criteria for plan evaluation implemented in our hospital: CTVTmean > 100%, CTVTV95% > 100%, CTVTD98% > 95%, PTVD98% > 93%, and PTVV105% < 20%.
Results
Cylindrical chest wall phantom
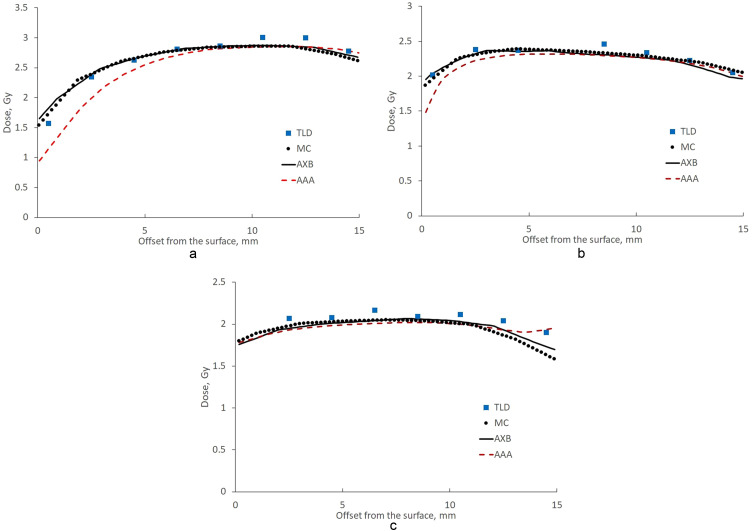
Experimentally measured and calculated dose profiles at the beam entrance, beam exit, and laterally are presented in Fig. 3. TLD data showed a dose increase up to a 10-mm depth at the beam entrance, whereas a maximum dose was reached at a 2-mm depth laterally. The dose reduction at the plastic water–air cavity interface (at a 14.5-mm depth) was 3%, 9%, and 17% for the TLD profiles at the beam entrance, beam exit, and laterally, respectively. There was good agreement between the MC data and experimental data: deviations within statistical and TLD uncertainty were observed, except at 2 TLDs at a 10- to 12-mm depth at the beam entrance and at 2 TLDs at depths greater than 12 mm at the beam exit. Acuros XB results followed the MC data. Small deviations exceeding the MC statistical uncertainty were observed at 2 mm depth at the superficial and water-air cavity interfaces. The AAA profiles were inferior to the others at the beam entrance and laterally. The AAA algorithm underestimated the dose by more than 19%, 8%, and 3% at 2-, 4-, and 6-mm depth, respectively, at the beam entrance with the MC estimated dose as a reference. The underestimation of the lateral dose laterally was smaller: 5% to 3% at 2- to 4-mm depth. An inconsistent tendency for the AAA dose to increase at around a 14-mm depth was seen at the beam exit.
Figure 3.
Experimental and theoretical profiles (a) at the beam axis entrance, (b) laterally, and (c) at the beam axis exit. Boxes = TLD data, dots = MC data, black line = Acuros XB data, and red dotted line = AAA. The error bars indicate 1 standard deviation for each TLD. The 0-mm depth is at the surface–air interface; the 15-mm depth is at the phantom–air cavity interface. Abbreviations: AAA = analytical anisotropic algorithm; MC = Monte Carlo; TLD = thermoluminescent dosimeter.
Profiles at the beam entrance, beam exit, and laterally were derived from the measured data for 2 opposite tangential fields with equal dose contributions and normalized to the corresponding dose at an 8-mm depth. The dose exceeded 90% at depths greater than 2 mm from the surface at the beam entrance and exit and at depths of 2 to 12 mm laterally. The calculated DVH parameters D98%, V95%, and V105% for the hypothetical target assuming 2 opposite fields were 75.5% to 82%, 73.7% to 80.5%, and 18.2% to 20%, respectively.
Patient geometries
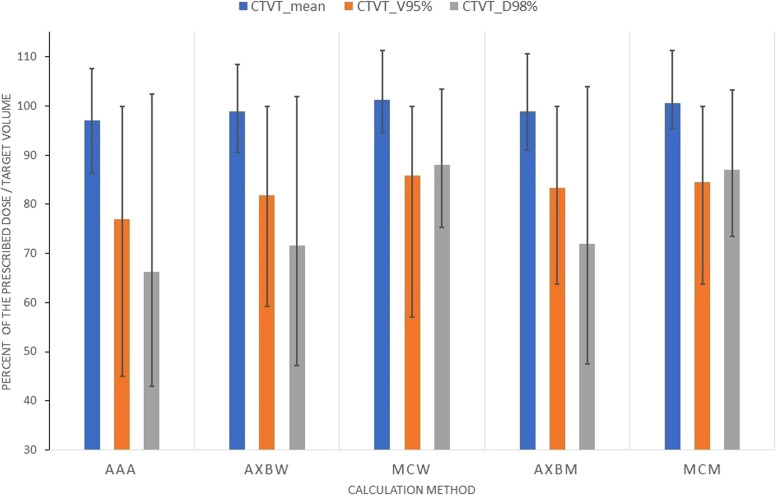
Results for the patient group with the smallest chest-wall thickness, that is, <15 mm, are presented in Fig. 4. The average values of the mean dose to CTVT, calculated using the different algorithms, ranged from 96.5% (calculated with AAA) to 101% (calculated with the MC method) (Fig. 4). The minimum–maximum deviation from the average was within 12%. The tolerance criterion of 100% for the CTVT mean dose was met in 4, 6, and 8 of the 15 patient geometries for AAA, Acuros XB, and MC dose-to-water results, respectively. The mean values of CTVTV95% ranged from 78% (calculated with AAA) to 86% (calculated with the MC method), with a minimum–maximum spread of up to 30%. The 100% tolerance criterion was met in 2 patient geometries.
Figure 4.
DVH parameters for CTVT estimated using the MC method and the different algorithms in the Eclipse TPS for 15 patients with the smallest chest-wall thickness (ie, <15 mm). AXBw and MCw denote Acuros XB and MC doses in dose-to-water terms, whereas AXBm and MCm refer to doses in dose-to-medium terms. Error bars indicate minimum–maximum values obtained. Tolerances: mean and V95% values >100%, D98% >95%. Abbreviations: CTVT = clinical target volume tumor; DVH = dose-volume histogram; MC = Monte Carlo.
The estimated CTVTD98% indicates greater sensitivity to the calculation algorithm and patient geometry. Values of 64.5% to 87.5% were obtained by applying different algorithms, with a spread of up to 37% in individual geometries (Fig. 4). The 95% tolerance criterion was met in 2 patient geometries. Similar sensitivities were found for the DVH parameters PTVD98% and PTVV105% (not shown). The 93% tolerance criterion for PTVD98% was met in one patient geometry for Acuros XB and MC calculations but was not fulfilled in any patient geometry for AAA. The PTVV105% values were <20% in 13, 9, and 4 patient geometries for AAA, Acuros XB, and MC calculations, respectively. The mean dose to PTV was around 100% with small variations within 3% for the different algorithms and patient geometries.
The effect of the calculation matrix resolution and body structure definition on the dose distribution in thin-chest-wall targets is illustrated in Table 1 for test calculations made using Acuros XB. Refining the grid improved the target coverage, particularly for the parameters CTVTV95%, CTVTD98%, and PTVD98%. Implementing a 3-mm outer margin for the default body structure defined by an automatic body search (CT number = –350 HU) improved CTVTD98% and PTVD98% by 30% and 15%, respectively.
Table 1.
Patient case
| Calculation grid, mm (default body) | CTVTmean% | CTVTV95% | CTVTD98% | PTVD98% | PTVV105% | PTVmean% |
|---|---|---|---|---|---|---|
| 2.5 | 91.0 | 63.7 | 47.5 | 67.9 | 7.4 | 99.3 |
| 1.5 | 92.8 | 67.8 | 49.0 | 74.5 | 6.2 | 99.4 |
| 1.5 3 mm margin |
96.5 | 70.2 | 80.6 | 90.3 | 6.5 | 100.2 |
Abbreviations: CTVT = clinical target volume tumor; DVH = dose-volume histogram; PTV = planning target volume.
DVH results obtained by Acuros XB for different calculation matrix resolution and body structure locations. Dose distribution in terms of dose-to-medium.
Use of a partial 5-mm bolus enhanced the energy deposition in the superficial targets. Mean values of CTVTV95% and PTVD98% close to 100% and 95%, respectively, were achieved in the thin-chest-wall group (Table 2). The presence of bolus improved the agreement between the different algorithms: the variations in the mean values of CTVTD98% and PTVD98% calculated using the different algorithms decreased from 18% and 14% to 2% (see columns showing mean values in Table 2). Also, the variations due to patient anatomy decreased (see columns showing intervals in Table 2). Results obtained for a patient group with a chest-wall thickness of 20 to 25 mm indicated sufficient target coverage and low dependence on the calculation algorithm and the patient geometry without the use of bolus (Table 2). Bolus presence and chest-wall thickness did not influence the behavior of the DVH parameter PTV105%.
Table 2.
Mean values and minimum–maximum intervals for CTVTD98%, PTVD98%, and PTV105% calculated using MC and Eclipse algorithms for patients with a chest-wall thickness <15 mm, without and with bolus, and for patients with a chest-wall thickness of 20 to 25 mm without bolus
| CTVTD98%, thin chest |
Chest wall 20-25 mm |
|||||
|---|---|---|---|---|---|---|
| Mean |
Range |
Mean |
Range |
|||
| Calculation method | No bolus | With bolus | No bolus | With bolus | No bolus | |
| AAA | 70.1 | 97.6 | [–25.3, 32.2] | [–2.7, 2.8] | 100.2 | [–5.2, 3.8] |
| AXBw | 75.0 | 97.3 | [–23.9, 26.9] | [–2.6, 2.9] | 99.6 | [–4.3, 4.6] |
| MCw | 88.0 | 97.2 | [–12.6, 15.4] | [–2.3, 2.4] | 99.9 | [–5.2, 3.6] |
| AXBm | 75.3 | 96.9 | [–24.0, 28.6] | [–3.0, 3.4] | 99.6 | [–5.3, 3.5] |
| MCm | 87.0 | 96.1 | [–13.5, 16.3] | [–2.9, 3.0] | 99.2 | [–5.4, 3.6] |
| PTVD98%, thin chest |
Chest wall 20-25 mm |
|||||
|---|---|---|---|---|---|---|
| Mean |
Range |
Mean |
Range |
|||
| Calculation method | No bolus | With bolus | No bolus | With bolus | No bolus | |
| AAA | 72.0 | 94.7 | [–11.7, 20.1] | [–1.6, 1.2] | 94.6 | [–2.7, 1.1] |
| AXBw | 77.6 | 94.5 | [–9.9, 15.7] | [–1.8, 1.1] | 94.2 | [–2.7, 2.4] |
| MCw | 86.7 | 94.4 | [–5.2, 6.6] | [–4.2, 0.5] | 94.2 | [–2.9, 2.2] |
| AXBm | 77.4 | 93.4 | [–10.5, 14.7] | [–1.8, 0.6] | 93.4 | [–2.5, 1.7] |
| MCm | 84.4 | 92.7 | [–13.6, 7.2] | [–3.3, 1.2] | 92.9 | [–2.9, 1.7] |
Abbreviations: CTVT = clinical target volume tumor; MC = Monte Carlo; PTV = planning target volume.
AXBw and MCw denote Acuros XB and MC doses in dose-to-water terms, whereas AXBm and MCm refer to doses in dose-to-medium terms.
Discussion
Results for the cylindrical chest-wall phantom showed that the conditions for achieving a certain dose coverage depended on the location of the region relative to the beam incidence (ie, dependent on the irradiation geometry). The TLD measurements indicated a negligible dose decrease at the air–cavity interface at the beam entrance (Fig. 2). This implies, for example, that internal mammary lymph nodes, located at the chest–lung interface, may receive 95% of the dose. The lateral part of the target at the same interface, however, may receive a 17% dose reduction according to the experimental data.
The comparison between measured and calculated dose profiles illustrated the weakness of AAA for dose determination in a superficial region where materials with different densities were present. The algorithm uses beam convolution–superposition and density correction approximations and is regarded as a class B algorithm. The next-generation algorithm, Acuros XB, and the MC method demonstrated high capability for accurate dose estimation under highly inhomogeneous nonreference conditions. Acuros XB and the MC method apply deterministic and stochastic approaches when solving the linear Boltzmann transport equation, achieving comparable radiation transport accuracy. Their implementation was independent with respect to beam source and patient description. The accelerator head was explicitly modeled in the MC calculations, whereas an analytical multiple-source model was used by Acuros XB. The tissue segmentation tables also differed (see Methods and Materials section). The agreement of the results in phantom and patient geometries increased the confidence in the obtained dose distributions, especially when high resolution was used (Table 1).
The tolerance criteria were not fulfilled in most of the geometries for patients with a thin chest wall. DVH parameters such as D98% and V95% depended on the shape of the DVH; their values displayed considerable algorithmic and anatomic dependency. The values obtained using the reference MC method and the advanced Acuros XB algorithm were less than the recommended ones. The applicability of these DVH parameters to plan development and evaluation could therefore be questioned. The mean values of the target dose were more robust and relevant. The DVH parameters obtained for the hypothetical target volume in the chest-wall phantom and the simplified tangential irradiation of the phantom were within the spread of the corresponding parameters for clinical plans.
The use of bolus for patients with a thin chest wall increased the distance between the target and the air interface, reduced the target underdosage, and enabled the tolerance criteria to be met. For this patient group, bolus implementation may facilitate the plan generation and evaluation. The use of bolus was reported to cause excessive skin toxicity, pain, and treatment interruptions.10,16,17 The effect of the bolus on the risk of local recurrence could not be confirmed.10,17 However, patients with a thin chest wall were not investigated as a separate group. For these patients, the dosimetry aspects of the target coverage may justify the usage of partial bolus. Interruption of treatment due to acute skin toxicity was not recorded in our hospital during the previous praxis of using bolus around the scar for all patients.
Our evaluation showed that bolus use was not needed for patients with chest walls thicker than 20 mm (Table 2), where target delineation with a 5-mm distance to the skin surface was possible. The target volumes for these patients were larger and the superficial region constituted less of the whole volume. The results agreed with an experimental study where the increase of a chest phantom wall thickness from 5 to 20 mm was found to improve the dose coverage.18
Dose distributions calculated using the MC method resulted in the highest target coverage and best DVH parameters. Additional analysis demonstrated the influence of the differences in patient modeling between using the Eclipse algorithms and the MC method. The default body search in Eclipse, with a low threshold of –350 HU, resulted in a structure intersecting nonair material (CT numbers >–1000 HU), present in the CT images as part of patient geometry. The image information for the outside of the body and the surrounding air was not considered by the Eclipse algorithms and could not contribute to the energy deposition. The MC patient model, however, was independent of the body structure definition and included the material outside the default body structure as well as the surrounding air medium. The MC dose near the surface was therefore higher than the corresponding one obtained using the Eclipse algorithms. Comparing the test calculation results with the default and expanded body structure results (Table 1) confirmed the effect of surface settings on the superficial dose.
The dose estimated using MC and Acuros XB, expressed in dose-to-medium terms, tended to be lower than that expressed in dose-to-water terms, especially when larger rib volumes were included in the target. The conversion coefficient related to the water-to-bone stopping power ratio for a 6-MV beam at a 10-cm depth is nearly 1 for lung tissue, 1.01 for soft tissue, 1.035 for soft bone, and 1.116 for cortical bone.19 Thus, comparing dose distributions for targets including lung and soft tissue was relatively straightforward, whereas larger corrections were introduced in dose-to-medium algorithms for targets involving ribs.
There is no literature consensus as to which presentation of the dose is the correct one. Some clinical algorithms, such as Acuros XB, allow choice, whereas others allow only dose-to-medium or dose-to-water presentations. The requirements for target coverage are more general and should apply to different hospitals with different TPSs and algorithms. The dose properties of the skin–air interface can be altered by adding a bolus, but the target–lung region cannot be influenced. Guidelines about the posterior border of the target play a significant role in achieving the required coverage. The evaluation is more accurate for a target with a posterior border in the middle of the ribs than for a target reaching the pleural interface.
Conclusion
Dose calculations using advanced algorithms, like Acuros XB and the MC method, and calculation grid up to 2 mm are recommended for patients with a thin (<15 mm) chest wall. Implementation of a partial bolus may be needed for this patient group to facilitate plan development and evaluation and to meet the DVH criteria. Sufficient target coverage and low dose dependence on the patient geometry and calculation algorithm could be achieved for a patient group with a chest-wall thickness >20 mm without bolus use.
Acknowledgments
We express our gratitude to Henrik Svensson and Maria Hällje for their help in the initial stage of the study and to Jozsef Mihai for optimizing the chest wall phantom.
Footnotes
Sources of support: This study was supported by grants (2017:151) from the King Gustav V Jubilee Clinic Cancer Research Foundation, the Swedish Research Council (2021-0138), and the Swedish governmental ALF-agreement (ALFGBG-965020).
Disclosures: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Research data are not available at this time.
References
- 1.McGale P, Taylor C, Correa C, et al. Effect of radiotherapy after mastectomy and axillary surgery on 10-years recurrence and 20-years breast cancer mortality: Meta-analysis of individual patient data for 8135 women in 22 randomised trials. Lancet. 2014;383:2127–2135. doi: 10.1016/S0140-6736(14)60488-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Remick J, Amin NP. StatPearls Publishing; Treasure Island, FL: 2022. Postmastectomy Breast Cancer Radiation Therapy. [PubMed] [Google Scholar]
- 3.Recht A, Comen EA, Fine RE, et al. Postmastectomy radiotherapy: An American Society of Clinical Oncology, American Society for Radiation Oncology, and Society of Surgical Oncology focused guideline update. Pract Radiat Oncol. 2016;6:e219–e234. doi: 10.1016/j.prro.2016.08.009. [DOI] [PubMed] [Google Scholar]
- 4.Ma J, Li J, Xie J, et al. Post mastectomy linac IMRT irradiation of chest wall and regional nodes: Dosimetry data and acute toxicities. Radiat Oncol. 2013;8:81. doi: 10.1186/1748-717X-8-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.MacDonald SM, Jimenez R, Paetzold P, et al. Proton radiotherapy for chest wall and regional lymphatic radiation; dose comparisons and treatment delivery. Radiat Oncol. 2013;8:71. doi: 10.1186/1748-717X-8-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xu H, Hatcher G. Treatment planning study of volumetric modulated arc therapy and three-dimensional field-in-field techniques for left chest-wall cancers with regional lymph nodes. Rep Pract Oncol Radiother. 2016;21:517–524. doi: 10.1016/j.rpor.2016.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bjöhle J, Onjukka E, Rintelä N, et al. Post-mastectomy radiation therapy with or without implant-based reconstruction is safe in terms of clinical target volume coverage and survivalࣧA matched cohort study. Radiother Oncol. 2019;131:229–236. doi: 10.1016/j.radonc.2018.07.005. [DOI] [PubMed] [Google Scholar]
- 8.Yap ML, Tieu M, Sappiatzer J, et al. Outcomes in patients treated with post-mastectomy chest wall radiotherapy without the routine use of bolus. Clin Oncol. 2018;30:427–432. doi: 10.1016/j.clon.2018.03.005. [DOI] [PubMed] [Google Scholar]
- 9.Nichol A, Narinesingh D, Raman S, et al. The effect of bolus on local control for patients treated with mastectomy and radiation therapy. Int J Radiat Oncol Biol Phys. 2021;110:1360–1369. doi: 10.1016/j.ijrobp.2021.01.019. [DOI] [PubMed] [Google Scholar]
- 10.Dahn HM, Boersma LJ, de Ruysscher D, et al. The use of bolus in postmastectomy radiation therapy for breast cancer: A systematic review. Crit Rev Oncol Hematol. 2021;163 doi: 10.1016/j.critrevonc.2021.103391. [DOI] [PubMed] [Google Scholar]
- 11.Chakarova R, Lundstedt D, Svensson H, et al. EP-1726 Utilization of bolus in post-mastectomy radiation therapy. Radiother Oncol. 2019;133(Suppl. 1):S930. [Google Scholar]
- 12.Kawrakow I, Mainegra-Hing E, Rogers DWO, et al. The EGSnrc Code System: Monte Carlo simulation of electron and photon transport. Available at: https://nrc-cnrc.github.io/EGSnrc/doc/pirs701-egsnrc.pdf. Accessed February 18, 2023.
- 13.Chakarova R, Cronholm R, Krantz M, et al. An automated Monte Carlo QC system for volumetric modulated arc therapy: possibilities and challenges. Phys Med. 2018;51:32–37. doi: 10.1016/j.ejmp.2018.03.010. [DOI] [PubMed] [Google Scholar]
- 14.Andersson P, Pettersson N, Lindberg A, et al. Effects of lung tissue characterization in radiotherapy of breast cancer under deep inspiration breath hold when using Monte Carlo dosimetry. Physica Medica. 2021;90:83–90. doi: 10.1016/j.ejmp.2021.09.009. [DOI] [PubMed] [Google Scholar]
- 15.Riktlinjer för volymer och teknik vid strålbehandling av bröstcancer. 2021;5. Available at: http://www.swebcg.se/wp-content/uploads/2022/04/Riktlinjer-f%C3%B6r-volymer-och-teknik-vid-br%C3%B6stcancer_Version-5.pdf. Accessed April 11, 2023.
- 16.Pignol J-P, Vu TTT, Mitera G, et al. Prospective evaluation of severe skin toxicity and pain during postmastectomy radiation therapy. Int J Radiat Oncol Biol Phys. 2015;91:157–164. doi: 10.1016/j.ijrobp.2014.09.022. [DOI] [PubMed] [Google Scholar]
- 17.Abel S, Renz P, Trombetta M, et al. Local failure and acute radiodermatological toxicity in patients undergoing radiation therapy with and without postmastectomy chest wall bolus: Is bolus ever necessary? Pract Radiat Oncol. 2017;7:167–172. doi: 10.1016/j.prro.2016.10.018. [DOI] [PubMed] [Google Scholar]
- 18.Shiau A-C, Chiu M-C, Chen T-H, et al. Surface and superficial dose dosimetric verification for postmastectomy radiotherapy. Med Dosim. 2012;37:417–424. doi: 10.1016/j.meddos.2012.03.005. [DOI] [PubMed] [Google Scholar]
- 19.Siebers JV, Keall PJ, Nahum AE, Mohan R. Converting absorbed dose to medium to absorbed dose to water for Monte Carlo based beam dose calculations. Phys Med Biol. 2000;45:983–995. doi: 10.1088/0031-9155/45/4/313. [DOI] [PubMed] [Google Scholar]