Abstract
The goal of present study is to explore how the size and functionalization of graphene quantum dots (GQDs) affect their sensing capabilities. Specifically, we investigated the adsorption of SO2, SOF2, SO2F2, and SF6 on GQDs that were functionalized with –CH3, –COCH3, and –NH2. We used density functional theory to analyse the electronic properties of these functionalized GQDs and found that the functionalization significantly altered their electronic properties. For example, the B3LYP H-L gap of pristine triangulene was 3.9eV, while the H-L gap of functionalized triangulene ranged from 2.8 eV to 3.6 eV (using the B3LYP functional). Our results indicate that –NH2 functionalized phenalenyl and triangulene provide strong interaction with SO2, with adsorption energies of −0.429 eV and −0.427 eV, respectively. These adsorption properties exhibit physisorption, leading to high gas sensitivity and superior recovery time. The findings of this study provide new insights into the potential use of GQDs for detecting the decomposed constituents of sulfur hexafluoride, which can be beneficial for assessing the operation status of SF6 insulated devices. Overall, our calculations suggest that functionalized GQDs can be employed in gas insulated systems for partial discharge detection.
Keywords: Graphene quantum dot, Sulfur hexafluoride, Density functional theory, Chemical functionalization, Electronic properties
1. Introduction
Sulfur hexafluoride (SF6) is an odourless, nontoxic, non-flammable, colourless and inert gas that possesses excellent insulation and strong chemical stability [1,2]. Its dielectric strength and chemical inertness make it a crucial medium for electrical insulators and in gas-insulated switchgear (GIS) for power systems as an arc-quenching medium [3,4]. However, in certain cases, partial discharge can occur when the electric field is intensified over time, leading to the decomposition of SF6. The resulting products, such as SO2, H2S, SO2F2, CF4, and SOF2, are responsible for equipment corrosion and can potentially lead to system failure [[5], [6], [7], [8], [9]]. Current methods used to detect these decomposed products of SF6 include ultrasonic, ultrahigh frequency, gas sensing and optical measurement methods [[10], [11], [12]]. Among these, the gas sensing method is highly recommended due to its high sensitivity in less volume and the most important thing, it is cost effective [[13], [14], [15], [16]]. However, gases such as SO2, SOF2, and SO2F2, which have extremely low concentrations on the order of parts per million (PPM), are challenging to detect with conventional sensors [17].
Nanomaterials based on graphene have received significant attention in the scientific community following the successful fabrication of graphene [18]. For both fundamental science and practical applications, graphene oxide (GO), reduced graphene oxide (rGO), and graphene quantum dots (GQD) have been extensively studied [[19], [20], [21], [22]]. Within the graphene family, GQD possess superior properties such as chemical inertness, low cytotoxicity, size and shape dependent photoluminescence etc. [[23], [24], [25]], make them useful for various applications in electronics (super capacitor, flash memory etc.), optical (photodetector, phototransistor etc.), medical (drug delivery, cancer phototherapy etc.) and energy [[26], [27], [28], [29], [30], [31], [32]]. Due to large surface-to-volume ratio, GQD also have superior sensing properties [24,33] making them useful in electrical and optical gas sensing devices [33,34]. A group of GQD have closed-shell electronic structures, while some, due to their unique topology, may have open-shell structure with high-spin ground states [35,36]. Open-shell GQD with π-electrons near the Fermi level have a delocalized radical character, which is useful for spintronics [[37], [38], [39]] and energy-related applications [40]. Closed-shell graphene fragments have closed-shell electronic configuration (no unpaired electrons) with π-electrons in bonding orbitals. However, open-shell graphene fragments have unpaired electrons or partially unpaired electrons, which results in non-bonding single occupied molecular orbitals (SOMO) in molecular orbital theory. For example, graphene fragments with two unpaired electrons are also known as biradical hydrocarbons, in which the ground state has two nonbonding molecular orbitals filled by two unpaired electrons [41]. Open-shell graphene fragments are unique in nature, possessing intriguing optical, electronic, magnetic properties and crystalline structures compared to their closed-shell counterparts. As a result, open-shell graphene fragments have numerous potential applications in photovoltaic devices [42], spintronic devices [43,44] etc. As stated by Lambert, “The future of these biradical PAHs clearly lies in materials science” [45]. Although useful in their pristine form, oxygen (−OH, –O−, –OCH3, –COOH, etc.), amine (−NH2) and methyl (−CH3) functionalized GQDs generally have improved solubility and superior quantum yield (QY) due to changes in their electronic structure caused by functionalization [[46], [47], [48]].
The study of sensing SF6 decomposition products on GQDs is motivated by the need to monitor and detect the breakdown of SF6, a commonly used gas in electrical equipment such as switchgear and circuit breakers. SF6 is a powerful insulator and arc quencher, but it is also a potent greenhouse gas with a global warming potential of 23,500 times that of CO2. SF6 decomposition products can indicate the presence of partial discharges, corona discharges, or other electrical faults in the equipment, which can lead to equipment failure if left unaddressed. Sensing SF6 decomposition products on GQDs can provide a sensitive and selective method for detecting these breakdowns, and thus, enabling early maintenance and preventing equipment failure. In this work, we computationally study the sensing properties of three different GQDs (phenalenyl, triangulene, and extended triangulene) for gases SO2, SOF2, SO2F2 and SF6 using a DFT methodology.
2. Computational methodology
As mentioned earlier, we employed the Gaussian16 suit of programs [49] to perform all the DFT calculations presented in this work. In the first step, we optimized the geometries of –CH3, –COCH3 and –NH2 functionalized phenalenyl, triangulene and extended triangulene. In the simulation process, the charge is neutral for all the considered structures along with the molecules adsorbated. The multiplicity of doublet, triplet and quartet is utilized for phenalenyl, triangulene and extended-triangulene, respectively, due to presence of one, two and three unpaired electrons. To address the significant role played by van der Waals (vdW) interactions in systems involving adsorption, we utilized the ωB97XD functional. This functional incorporates London dispersion corrections that account for the long-range interactions that arise during the adsorption process. The ωB97XD functional includes Grimme's van der Waals (vdW) correction term of –C6/R6, also known as the GD2 dispersion model. The mathematical expression for the dispersion correction term is as follows:
| (1) |
Here, represents the damping function. is the sum of vdW radii of the atomic pair ij, and the parameter, , governs the power of dispersion corrections. The number of atoms in the system is denoted by in Eq. (1). Additionally, represents the dispersion coefficient for the atom pair , while denotes the interatomic distance between them. The value of the fitting parameter S6, used in the damping function to account for the correlation of this additive dispersion term, was included in the ωB97XD functional, and set to 1.0 [50].
In addition, we utilized the hybrid functional B3LYP [51,52], which is a combination of the Becke exchange functional (Becke three parameter) with the Hartree-Fock exchange term. The B3LYP hybrid functional incorporates a non-local correlation functional from LYP (Lee, Yang and Parr) and a local correlation functional of the form VWN (Vosko, Wilk, and Nusair). We employed a 6-31G (D) split-valence basis set, which consists of six Gaussian functions for describing inner-shell orbitals and a split-valence set of four Gaussians for the valence orbitals, with subsets of 3 and 1. The gases to be adsorbed were initially placed parallel to the surfaces of the functionalized GQDs, and the whole systems (GQD + adsorbed gas) were then permitted to relax until the gradient forces achieved the predetermined threshold of 0.00045 Hartree. The optimized structure and the molecular orbitals were visualized with GaussView (version 6). The adsorption energy (Ead) of SO2, SOF2, SO2F2 and SF6 molecules on the three functionalized GQDs was computed using the equation [53,54]:
| (2) |
where is the optimized total energy for the gas molecule = SO2, SOF2, SO2F2 and SF6 adsorbed over = phenalenyl, triangulene and extended triangulene, is the optimized total energy of individual gas molecule and is the optimized energy of pristine GQDs (phenalenyl, and triangulene and extended triangulene). Using the definition, negative value of value shows a stable adsorption complex on the GQD. To further check the effect of higher basis set, we have evaluated the using def2-TZVPP triple zeta basis set and the discussion is presented in supplementary material. The formation energy Ef are calculated using equation:
| (3) |
where is the total energy of the functionalized phenalenyl, triangulene and extended triangulene system, and is the total energy of individual carbon, hydrogen, oxygen or nitrogen. N represents total number of atoms in the system while, represents individual number of atom respectively. We observed negative formation energy for all systems, conforming thermodynamical stability and also suggest finite possibility of these materials to be synthesize experimentally. The results obtained using ωB97XD functional are presented in the main text, while those corresponding to B3LYP are presented in the supplementary material.
3. Results and discussion
In this study, we focus on three triangular GQDs with unique topology (i) phenalenyl, which has three fused benzene rings and a total spin quantum number of 1/2, (ii) triangulene which has six fused benzene rings and a total spin quantum number of, and (iii) extended triangulene, which has ten fused benzene rings and a total spin quantum number of 3/2. These GQDs have unusual topologies that prevent the formation of an aromatic structure without the presence of unpaired electrons, resulting in high-spin ground states. Additionally, to investigate the effect of different functional groups on the sensing of gases SO2, SOF2, SO2F2 and SF6 gases, we functionalize phenalenyl, triangulene and extended triangulene with three different groups: methyl (CH3), ketone (COCH3) and amino (NH2). These functional groups are chosen based on previous experimental and theoretical studies [23,48,55]. For simplicity, phenalenyl with functional group is denoted as Phe + CH3, Phe + COCH3 and Phe + NH2, triangulene with functional group is denoted as Tri + CH3, Tri + COCH3 and Tri + NH2, and the extended triangulene as Ex-Tri + CH3, Ex-Tri + COCH3 and Ex-Tri + NH2. Our results were obtained using the ωB97XD functional, which includes long-range corrections for a more accurate description of adsorption properties. The results of the B3LYP functional can be found in the supplementary material.
3.1. Structural properties
Before examining the adsorption process, the structures of the four gas molecules and the three GQDs functionalized with various groups were optimized individually to obtain their most stable configurations. First, we will discuss the optimized structures of the individual gas molecules SO2, SOF2, SO2F2 and SF6 (see Fig. 1(a–d)). In the case of the SO2 molecule, the bond length of S–O bond is 1.469 Å with bond angle of 119.127°. In SOF2, sulfur is the centre atom bonding with both fluorine atoms and oxygen atom, comprising sp2 hybridization. The S–O and S–F bond lengths are 1.445 Å and 1.627 Å respectively. The F–S–O bond angle is 107.07°, while F–S–F bond angle is 92.652°. In the case of SO2F2, sulfur is the centre atom bonding with both fluorine atoms and oxygen atoms leading to sp3 hybridization. The S–O and S–F bond lengths are 1.434 Å and 1.586 Å, respectively. In the case of SF6, sulfur is the central atom bonding with six fluorine atoms comprising F–S bond length of 1.6 Å and F–S–F bond angles 90°. These results are in good agreement with the previous reports [56,57].
Fig. 1.
Optimized structures of SO2, SOF2, SO2F2, and SF6 molecules. The green, red and purple balls represent sulfur, oxygen and fluorine atoms respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Next, we will discuss the optimized structures of the functionalized GQDs both with and without the adsorbed molecules, followed by their electronic properties. For the adsorption process, initially the molecules are placed parallel to the GQDs so as to provide them with more access to the surface areas.
3.1.1. Molecule adsorption on phenalenyl
In Fig. 2, we present the optimized structures of isolated Phe + CH3, and the structures with various gas molecules adsorbed on it. For the SO2 molecule, it is located slightly towards the centre of phenalenyl with its oxygen atoms over both hexagonal rings with S–C bond distance of 3.1 Å. The SO2 structure does not present any noticeable modification in the bond lengths, however, the O–S–O bond angle has decreased from 119.127° to 118.42°. In the case of SOF2 adsorption on Phe + CH3, the S–C adsorption distance changes from 2 Å to 3.2 Å with no modification in S–O and S–F bond lengths. The bond angle of F–S–O decreases from 107.07° to 106.50° and the bond angle of F–S–F changes from 92.652° to 92.126°. When SO2F2 is adsorbed on Phe + CH3, the S–C adsorption distance becomes 3.5 Å with minor to no change in bond lengths and bond angles of the gas molecule. The SO2F2 molecule is slightly shifted with fluorine atom tilting towards the carbon atoms. In the case of SF6 adsorption on Phe + CH3, the S–C adsorption distance is the highest with 4.47 Å, as compared to all other cases considered here. The bond lengths and bond angles of SF6 depict no change in its structure as molecule is shifted far away and towards the edge of Phe + CH3.
Fig. 2.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over CH3 edge-functionalized phenalenyl calculated with wB97XD functional.
In Fig. 3, we present the optimized structure of Phe + COCH3 with various gas molecules (SO2, SOF2, SO2F2 and SF6) adsorbed on it. Similar to the case of SO2 adsorption on Phe + CH3, the molecule is located slightly towards the edge, closer to the oxygen atom of functional group. The O–S–O bond angle has decreased from 119.127° to 118.35° (lower than Phe + CH3). In the case of SOF2 adsorption on Phe + COCH3, the molecule is slightly shifted with S–C distance 3.2 Å, similar to the case of SOF2 over Phe + CH3. The bond angle of F–S–O decrease from 107.07° to 106.62°, and bond angle of F–S–F changes from 92.652° to 92.28°. In the case of SO2F2 molecule over Phe + COCH3, the adsorbed molecule has not been shifted, but the adsorption distance changes to 3.5 Å with fluorine atom facing the GQD. Similar to SF6 adsorption over Phe + CH3, SF6 is attracted towards the functional group making the initial S–C distance of 4.7 Å with no noticeable alteration in bond lengths and bond angles.
Fig. 3.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over COCH3 edge-functionalized calculated with wB97XD functional.
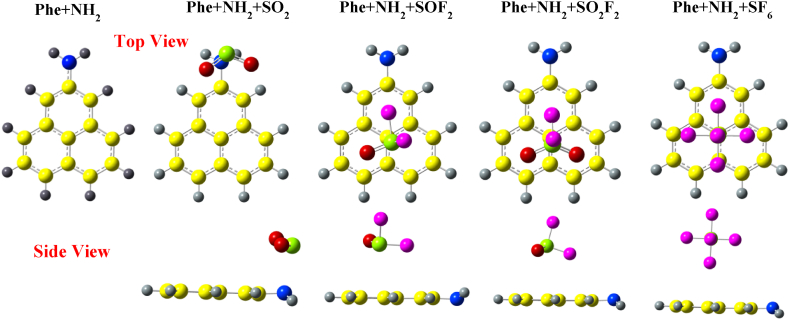
Fig. 4 shows the optimized structures of gas molecules on Phe + NH2. In the case of SO2 adsorption, the molecule positions itself slightly towards the edge of the GQD, with the sulfur atom facing the hydrogen atom of –NH2 functional group. The adsorption distance between the sulfur and nitrogen atom is 2.62 Å and the O–S–O bond angle has decreased from 119.127° to 117.88°. For the SOF2 molecule, the adsorption is similar to that on both –CH3 and –COCH3 group, but on the opposite side of the Phe + NH2 GQD. The bond angle of F–S–O decreases from 107.07° to 106.5° and the bond angle of F–S–F changes from 92.652° to 92.09°. The SO2F2 molecule adsorbed on Phe + NH2 presents similar results as on Phe + CH3. In contrast, SF6 adsorption on Phe + NH2 results in contrasting structural outcomes as compared to the other two functional groups, –CH3 and –COCH3. The molecule is repelled away from the GQD, with the S–F distance increasing from 2 Å to 2.9 Å.
Fig. 4.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over NH2 edge-functionalized phenalenyl calculated with wB97XD functional.
3.1.2. Molecule adsorption on triangulene
Fig. 5 presents the optimized structures of Tri + CH3 with and without gas molecules. The adsorption of SO2 on Tri + CH3 is similar to that on Phe + CH3, with a similar adsorption distance and position after optimization. The bond angles are also analogous to those of the SO2 molecule adsorbed on Phe + CH3. The SOF2 molecule realigns itself to the opposite edge of functional group –CH3 with no changes in the S–O and S–F bond lengths. The bond angle of F–S–O decreases from 107.07° to 106.64° and bond angle of F–S–F changes from 92.652° to 92.23°. Similarly, to SOF2, SO2F2 is also repelled from the –CH3 functional group to the edges of Tri + CH3. In contrast to the SF6 adsorption on Phe + CH3, SF6 on Tri + CH3 is moved slightly away from the functional group with the adsorption distance of 2.9 Å. However, similar to SF6 on Phe + CH3, there are no obvious changes in bond lengths or bond angles.
Fig. 5.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over CH3 edge-functionalized triangulene calculated with wB97XD.
Fig. 6 presents the optimized structures of Tri + COCH3 along with gases. Unlike the adsorption of SO2 over Phe + COCH3, the molecule positions itself towards the methyl group of Tri + COCH3. The O–S–O bond angle has decreased from 119.127° to 118.42°. The structure of SOF2 and SO2F2 are similar to their adsorption on Tri + CH3. In contrast to SF6 adsorption over Phe + COCH3, SF6 is repelled away from the system, with a final adsorption distance of 3.9 Å.
Fig. 6.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over COCH3 edge-functionalized triangulene calculated with wB97XD.
Fig. 7 presents the optimized structures of SO2, SOF2, SO2F2 and SF6 adsorbed over Tri + NH2. The sulfur atom of SO2 molecule is attracted towards the nitrogen atom of the –NH2 group in Tri + NH2 with an adsorption distance of 2.62 Å. The O–S–O bond angle has decreased from 119.127° to 117.87°. The structural properties of SOF2 are similar to its adsorption on Tri + COCH3. Additionally, the structure of SO2F2 molecule when adsorbed on Tri + NH2 is similar to its adsorption on Tri + COCH3. The adsorption of SF6 on Tri + NH2 is similar to its adsorption on Phe + NH2, with the SF6 molecule slightly attracted towards the edge of Tri + NH2, with an adsorption distance of 4.6 Å.
Fig. 7.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over NH2 edge-functionalized triangulene calculated with wB97XD functional.
3.1.3. Molecule adsorption on extended triangulene
Fig. 8 presents the optimized structures of pristine Ex-Tri + CH3, along with those with the gas molecules adsorbed on it. For SO2, the molecule slightly tilts over the carbon atom, resulting in an S–C bond distance of 3.1 Å, which is similar to the case of Phe + CH3. The SO2 structure does not lead to any noticeable changes in the bond lengths, but the O–S–O bond angle decreases from 119.127° to 118.48°. SOF2 adsorption over Ex-Tri + CH3 is similar to that of SOF2 over Tri + CH3.
Fig. 8.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over CH3 edge-functionalized extended-triangulene calculated with wB97XD functional.
When SO2F2 is adsorbed over Ex-Tri + CH3, the S–C adsorption distance becomes 3.4 Å with minor to no change in bond lengths and bond angles of the gas molecule. Analogous to Phe + CH3, the SO2F2 molecule slightly shifts towards the edges of Ex-Tri + CH3. The SF6 adsorption on Ex-Tri + CH3 results in a similar structure as in the case of Phe + CH3. Similar adsorption properties are observed when SO2 and SOF2 are adsorbed over Ex-Tri + COCH3 (See Fig. 9). However, both SO2F2 and SF6 are shifted towards the edge of GQD after adsorption, with similar adsorption distances as in case of Ex-Tri + CH3.
Fig. 9.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over COCH3 edge-functionalized extended-triangulene calculated with wB97XD.
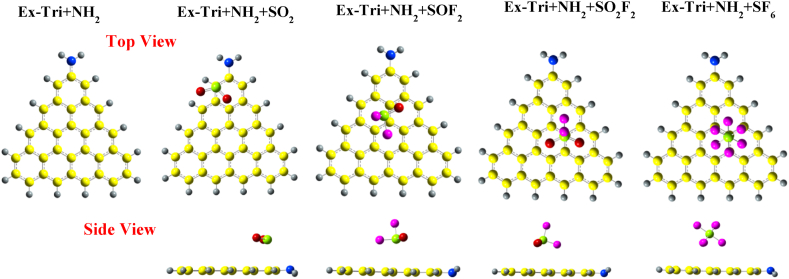
Fig. 10 presents the optimized structures of SO2, SOF2, SO2F2 and SF6 adsorption over Ex-Tri + NH2. SO2 is attracted towards the NH2 functional group with adsorption distance between S and C atom 3.01 Å. The adsorption of SOF2, SO2F2 and SF6 results in similar configurations except for the adsorption distances, which, for the three molecules become 3.19 Å, 3.4 Å, and 3.9 Å, respectively.
Fig. 10.
Optimized structures of SO2, SOF2, SO2F2, and SF6 over NH2 edge-functionalized extended-triangulene calculated with wB97XD functional.
To confirm the thermodynamical stability, we have calculated the formation energy (Ef) using Eq. (3) for functionalized GQDs. The Ef for phenalenyl functionalized with –CH3, –COCH3 and –NH2 are −6.314 eV, −6.957 eV and −6.388 eV, respectively. While in case of Ef for triangulene functionalized with –CH3, –COCH3 and –NH2 are −6.729 eV, −7.153 eV and −6.79 eV, respectively. Further, Ef for extended triangulene functionalized with –CH3, –COCH3 and –NH2 are −7.029 eV, −7.072 eV and −7.090 eV, respectively. The negative Ef for all GQDs confirms their thermodynamical stability and possible fabrication experimentally. Raman calculation is a powerful analytical tool for characterizing the structural stability of materials. The Raman spectrum is sensitive to the vibrational modes of a material and can provide information about the chemical bond structure and symmetry of a material. By monitoring changes in the Raman plot, researchers can determine if a material is undergoing structural changes or if its structure is remaining stable. The Raman plot can be used as a measure of the stability of the structure of a material over time. Raman analysis (presented in Fig. S8 of Supplementary material) suggests that all the systems are dynamically stable as there are no imaginary frequencies.
3.2. Electronic and adsorption properties
Calculations regarding the sensing ability are made using the principle that as the adsorbed gas molecules interact with the GQDs, the electron distribution in the system must change. This electron reorganization should manifest as a measurable change in the ability to conduct an electrical current, known as conductivity. The fundamental parameter that can be calculated using this is the molecular orbits or HOMO-LUMO (H-L) gap. The electron donating and accepting ability of a system can be defined using the value of HOMO and LUMO energy. These molecular orbitals play vital role in electronic and optical properties, luminescence, photochemical reaction, UV-VIS, quantum chemistry etc. The molecular orbitals help in predicting the most reactive position of the studied system. Further, Mulliken charge transfer is calculated and tabulated in Table 1, Table 2, Table 3, confirming the sensitivity of gas molecules SO2, SOF2, SO2F2 and SF6 over phenalenyl, triangulene and extended triangulene.
Table 1.
Energy H-L gap (Eg), Adsorption Energy (Ead) and Recovery time (τ) of structure of SO2, SOF2, SO2F2, and SF6 adsorption on phenalenyl.
| Structure | Charge (e) | Eg (eV) |
Ead (eV) |
τ (ps) |
|||
|---|---|---|---|---|---|---|---|
| B3LYP | ωB97XD | B3LYP | ωB97XD | B3LYP | ωB97XD | ||
| Phe + CH3 | – | 3.913 | 7.511 | – | – | – | – |
| Phe + CH3 + SO2 | +0.03462 | 3.595 | 7.544 | −0.124 | −0.256 | 121 | 19,988 |
| Phe + CH3 + SOF2 | +0.02214 | 3.907 | 7.516 | −0.137 | −0.268 | 200 | 31,796 |
| Phe + CH3 + SO2F2 | +0.00311 | 3.901 | 7.537 | −0.066 | −0.227 | 12 | 6509 |
| Phe + CH3 + SF6 | −0.00998 | 3.696 | 7.502 | −0.074 | −0.184 | 17 | 1233 |
| Phe + COCH3 | – | 4.083 | 7.71 | – | – | – | – |
| Phe + COCH3 + SO2 | +0.04581 | 4.108 | 7.40 | −0.26 | −0.241 | 23,332 | 11,188 |
| Phe + COCH3 + SOF2 | +0.01746 | 3.956 | 7.71 | −0.128 | −0.252 | 141 | 17,121 |
| Phe + COCH3 + SO2F2 | +0.00183 | 4.041 | 7.724 | −0.064 | −0.223 | 11 | 5576 |
| Phe + COCH3 + SF6 | −0.01299 | 4.08 | 7.714 | −0.032 | −0.201 | 3 | 2381 |
| Phe + NH2 | – | 2.847 | 6.38 | – | – | – | – |
| Phe + NH2 + SO2 | +0.09231 | 3.359 | 7.01 | −0.37 | −0.429 | 1,644,093 | 16,112,404 |
| Phe + NH2 + SOF2 | +0.02352 | 2.924 | 6.562 | −0.247 | −0.33 | 14,110 | 349,899 |
| Phe + NH2 + SO2F2 | +0.00294 | 3.002 | 6.62 | −0.122 | −0.28 | 112 | 50,579 |
| Phe + NH2 + SF6 | −0.0028 | 2.549 | 6.58 | −0.141 | −0.166 | 233 | 614 |
Table 2.
Energy H-L gap (Eg), Adsorption Energy (Ead) and Recovery time (τ) of structure of SO2, SOF2, SO2F2, and SF6 adsorption on triangulene.
| Structure | Charge(e) | Eg (eV) |
Ead (eV) |
τ (ps) |
|||
|---|---|---|---|---|---|---|---|
| B3LYP | ωB97XD | B3LYP | ωB97XD | B3LYP | ωB97XD | ||
| Tri + CH3 | – | 3.669 | 7.182 | – | – | – | – |
| Tri + CH3 + SO2 | +0.03745 | 3.23 | 7.025 | −0.119 | −0.261 | 99 | 24,253 |
| Tri + CH3 + SOF2 | +0.01667 | 3.62 | 7.192 | −0.111 | −0.282 | 73 | 54,644 |
| Tri + CH3 + SO2F2 | +0.00028 | 3.653 | 7.190 | −0.065 | −0.257 | 12 | 20,774 |
| Tri + CH3 + SF6 | −0.00356 | 3.668 | 7.180 | −0.021 | −0.145 | 2 | 272 |
| Tri + COCH3 | – | 3.734 | 7.267 | – | – | – | – |
| Tri + COCH3 + SO2 | +0.03396 | 3.261 | 6.93 | −0.109 | −0.247 | 67 | 14,110 |
| Tri + COCH3 + SOF2 | +0.0145 | 3.698 | 7.301 | −0.127 | −0.275 | 136 | 41,680 |
| Tri + COCH3 + SO2F2 | −0.0048 | 3.72 | 7.288 | −0.061 | −0.261 | 10 | 24,253 |
| Tri + COCH3 + SF6 | −0.01106 | 3.73 | 7.265 | −0.03 | −0.243 | 3 | 12,088 |
| Tri + NH2 | – | 2.808 | 6.312 | – | – | – | – |
| Tri + NH2 + SO2 | +0.09266 | 3.275 | 6.853 | −0.365 | −0.427 | 1,354,983 | 14,912,345 |
| Tri + NH2 + SOF2 | +0.01645 | 2.918 | 6.488 | −0.177 | −0.335 | 940 | 424,556 |
| Tri + NH2 + SO2F2 | +0.00027 | 3.017 | 6.504 | −0.162 | −0.389 | 526 | 3,428,728 |
| Tri + NH2 + SF6 | −0.00811 | 2.973 | 6.493 | −0.09 | −0.254 | 32 | 18,499 |
Table 3.
Energy H-L gap (Eg), Adsorption Energy (Ead) and Recovery time (τ) of structure of SO2, SOF2, SO2F2, and SF6 adsorption on extended triangulene.
| Structure | Charge (e) | Eg (eV) |
Ead (eV) |
τ (ps) |
|||
|---|---|---|---|---|---|---|---|
| B3LYP | ωB97XD | B3LYP | ωB97XD | B3LYP | ωB97XD | ||
| Ex-Tri + CH3 | – | 1.342 | 4.566 | – | – | – | – |
| Ex-Tri + CH3 + SO2 | +0.04094 | 1.329 | 4.432 | −0.180 | −0.261 | 1055 | 24,253 |
| Ex-Tri + CH3 + SOF2 | +0.01486 | 1.367 | 4.527 | −0.133 | −0.285 | 171 | 61,371 |
| Ex-Tri + CH3 + SO2F2 | −0.00064 | 1.429 | 4.555 | −0.102 | −0.260 | 51 | 23,332 |
| Ex-Tri + CH3 + SF6 | −0.01252 | 1.404 | 4.570 | −0.039 | −0.256 | 4 | 19,988 |
| Ex-Tri + COCH3 | – | 1.386 | 4.544 | – | – | – | – |
| Ex-Tri + COCH3 + SO2 | +0.0358 | 1.183 | 4.407 | −0.142 | −0.246 | 242 | 13,575 |
| Ex-Tri + COCH3 + SOF2 | +0.01236 | 1.448 | 4.520 | −0.077 | −0.273 | 19 | 38,580 |
| Ex-Tri + COCH3 + SO2F2 | −0.00098 | 1.382 | 4.503 | −0.042 | −0.262 | 5 | 25,210 |
| Ex-Tri + COCH3 + SF6 | −0.01315 | 1.401 | 4.543 | −0.034 | −0.261 | 3 | 24,253 |
| Ex-Tri + NH2 | – | 2.767 | 6.22 | – | – | – | – |
| Ex-Tri + NH2 + SO2 | +0.05453 | 2.491 | 6.215 | −0.23 | −0.320 | 7310 | 237,660 |
| Ex-Tri + NH2 + SOF2 | +0.01644 | 2.873 | 6.395 | −0.219 | −0.344 | 4777 | 601,390 |
| Ex-Tri + NH2 + SO2F2 | −0.000093 | 2.968 | 6.405 | −0.161 | −0.324 | 506 | 277,423 |
| Ex-Tri + NH2 + SF6 | −0.01191 | 2.927 | 6.394 | −0.067 | −0.324 | 13 | 277,423 |
Fig. 11(a–c) depicts total density of states (TDOS) to further analyse the electronic structure from the perspective of size of the GQDs (phenalenyl, triangulene and extended triangulene), functional groups, and adsorbed molecules SO2, SOF2, SO2F2 and SF6. The total density of states gives the number of states present per energy range. The discrete levels are modified using Gaussian as the broadening function. The adsorption of these gas molecules on Phe + CH3 leads to minor changes in highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO). However, the highest peak of Phe + CH3 located around −13 eV in valence band shifts and even splits in case of Phe + CH3 + SF6. The HOMO and LUMO in Phe + CH3 + SOF2 and Phe + CH3 + SO2F2 depict minor changes attributable to slight alteration in their structural properties. The energy HOMO-LUMO gap (H-L gap) of all considered systems are presented in Table 1.
Fig. 11.
Density of states of adsorption of SO2, SOF2, SO2F2, and SF6 with (a) phenalenyl (b) triangulene and (c) extended-triangulene systems with wB97XD functional.
The DOS plots of the gas molecules adsorbed on Phe + COCH3 show that the HOMO exhibit trivial difference in all cases except Phe + COCH3 + SO2. However, the LUMOs are shifted slightly towards higher energies. The molecules adsorbed over Phe + NH2 largely show similar features except that a shift in HOMO is observed for the case of Phe + NH2 + SO2. In all three cases of functionalized phenalenyl, SF6 adsorbed systems acquire the highest peak in the valence region. The H-L gap changes significantly in case of Phe + NH2 as compared to others.
The middle row in Fig. 11 shows the results of DOS for triangulene functionalized systems. The energy gap changes noticeably only in case of Tri + CH3+SO2, from 7.18 eV to 7.02 eV. The minimum change in the gap is observed in case of Tri + CH3+SF6. Similar changes are also seen also in SO2, SOF2, SO2F2 and SF6 adsorbed Tri + COCH3 systems. In the case of Tri + NH2, a drastic modification is observed when SO2 is adsorbed, leading to a change in the energy H-L gap from 6.31 eV to 6.85 eV. The minimum H-L gap change is observed in SOF2 adsorbed systems. The energy H-L gap values of Ex-Triangulene are presented in Table 3 with B3LYP and ωB97XD. The largest H-L gap is found for Ex-Tri + NH2 among all functionalized GQDs. The ωB97XD (long range corrected) predicted energy gaps are considerably larger than the B3LYP predicted gap values. This is mainly due to the inclusion of full Hartree–Fock exchange term in the ωB97XD functional at long distances [58]. It is concluded that for electronic properties such as the H-L gaps, B3LYP shows better results; however, ωB97XD shows better results for studying the adsorption mechanism. The sizes and functionalization of GQDs strongly influence its structural and electronic properties. The energy gap value is a crucial parameter in defining the electrical conductivity (σ) of materials because the energy required to take out an electron from the outer shell to become a free portable charge carrier is proportional to the H-L gap. The link between the Eg and σ of a material can be mathematically represented by the following formula [59]:
| (4) |
where k and T are the Boltzmann's constant and the temperature respectively. The conductivity of a material is inversely proportional to its H-L gap, as shown by Eq. (4). Therefore, a smaller H-L gap value leads to higher σ at a given temperature T. Consequently, when gas molecules are adsorbed onto the surfaces of graphene quantum dots, a significant decrease in their H-L gap value leads to an increase in their conductivity. The reduction of Eg is observed in case of Phe + CH3+SF6, Phe + COCH3 + SO2, Tri + CH3 + SO2, Tri + COCH3 + SO2, Ex-Tri + CH3 + SO2 and Ex-Tri + COCH3 + SO2. As a result, the conductivity of the functionalized GQDs increases, providing evidence of the robust interaction between the adsorbed gas molecule and the GQDs. This alteration in the molecular orbitals of the GQDs because of the adsorbed molecules could be identified electronically, which suggests its potential application in sensor technology. The adsorption energies calculated through Eq. (2) for all optimized systems are given in Table 1, Table 2, Table 3. The gas molecules get adsorbed on the energetically stable structures of functionalized GQDs, typically at distances in the range 2.46–4.47 Å. These considerably large adsorption distances prohibit the formation of chemical bonds, resulting in physisorption [[60], [61], [62], [63], [64]].
The adsorption energy (Ead) calculated for SO2, SOF2, SO2F2 and SF6 over Phe + CH3 is −0.256 eV, −0.268 eV, −0.227 eV and −0.184 eV respectively. The lower adsorption energy in SO2F2 and SF6 can be attributed to the relatively larger adsorption distances. In Phe + COCH3, the highest adsorption energy is observed for the sensing of SOF2 with the value −0.252 eV. Of all the gas molecules adsorbed on various functionalized GQDs, the largest adsorption energy of −0.429 eV is achieved for the case of SO2 over Phe + NH2. The adsorption energies of functionalized triangulene for various gas molecules are presented in Table 2. For sensing of SO2, Tri + NH2 (−0.427 eV) provides superior adsorption energy as compared to Tri + CH3 (−0.261 eV) and Tri + COCH3 (−0.247 eV). Similarly, Tri + NH2 is energetically better for sensing of SOF2, SO2F2 and SF6 in comparison with other triangulene functionalizations. In Table 3, we present the adsorption energies of all the functionalized GQDs for various gas molecules. It is obvious from the table that for GQDs functionalized with the groups CH3, COCH3 and NH2, SOF2 shows high adsorption energies −0.285 eV, −0.273 eV, and −0.344 eV, respectively. To understand the electronic interaction between the gas molecules and functionalized GQDs, we plot in Fig. 12 the frontier molecular orbitals.
Fig. 12.
HOMO-LUMO plot of adsorption of SO2, SOF2, SO2F2, and SF6 with phenalenyl, triangulene and extended-triangulene systems with wB97XD functional.
It is clear from the figure that SOF2, SO2F2 and SF6 molecules do not contribute to the formation of either HOMO or LUMO. Instead, these orbitals are completely confined to the surfaces of the functionalized GQDs, confirming the physisorption character of the adsorption processes. Furthermore, the H-L gap of SOF2, SO2F2 and SF6 over the functionalized GQDs is close to the corresponding pristine values (see Table 1, Table 2, Table 3). In contrast, the behaviour of SO2 on the functionalized GQDs is qualitatively different (as shown in Fig. 12). The HOMO (in the case of Phe + CH3, Phe + COCH3, Phe + NH2, Tri + NH2) and LUMO (in the case of Tri + CH3, Tri + COCH3, Ex-Tri + CH3, Ex-Tri + COCH3, Ex-Tri + NH2) are shared indicating strong hybridization.
As a result, the H-L gap is altered for these cases. Additionally, non-covalent interaction (NCI) analyses were performed using Multiwfn [64] and VMD [65] packages at the same level of theory to account for H-bonds and non-covalent interactions and are presented in Fig. 13. The strong attraction and repulsion are represented by blue and red region respectively. The van der Waals interaction is shown by the green region. The coloration of the isosurfaces is determined by the values of sign (λ2)ρ (a.u.), ranging from 0.03 to 0.02 a. u. It is observed that strong attractions (blue region) are found in SO2 over NH2 functionalized phenalenyl and triangulene. Steric effect or strong repulsion is found between the hexagonal rings in GQDs, however, van der Waals interaction were observed between the gas molecules and GQDs systems.
Fig. 13.
NCI plots with wB97XD functional. Blue represents strong attractive interactions, green indicates interactions and red indicates repulsive/steric interactions. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
3.3. Recovery time
The recovery characteristics of a gas sensor are crucial for determining its usefulness and reusability. The traditional method for evaluating recovery time is by heating the substrate, however, strong chemical reactions or chemisorption between gases and the substrate can result in long recovery times. Theoretical calculations to determine recovery time (τ) can be performed using transition state theory and the Van't-Hoff-Arrhenius expression [66,67], resulting in the expression:
| (5) |
Here, is defined as the attempt frequency, K and T denote Boltzmann constant (∼8.318∗10−3 kJ/mol K), and temperature respectively. In the present cases, 1012 s−1 of attempt frequency and 298 K temperature is taken for the recovery time calculation [68,69].
The van der Waals interactions between functionalized GQDs and gas molecules have a significant impact on the recovery time of a gas sensor. This is because van der Waals interactions can strongly influence the adsorption and desorption of gas molecules on the surface of the GQDs. The strength of these interactions can determine the amount of energy required for a gas molecule to adsorb or desorb from the surface, which in turn can affect the recovery time of the sensor. Additionally, the van der Waals interactions can also contribute to a shift in the adsorption energy, which can further impact the performance of the sensor. Therefore, understanding and controlling the van der Waals interactions between functionalized GQDs and gas molecules is crucial for optimizing the performance of gas sensors. Comparing the –CH3, –COCH3 and –NH2 functionalized GQDs according to recovery time, the gas molecules are challenging to desorb from Phe + NH2, Tri + NH2 and Ex-Tri + NH2. The recovery times calculated through Eq. (5) are given in Table 1, Table 2, Table 3. In Phe + CH3, SO2F2 and SF6 have lower recovery times of 6509 ps and 1233 ps, resulting in better desorption property. Similarly for Phe + COCH3, SO2F2 and SF6 have lower recovery time of 5576 ps and 2381 ps. In summary, both Phe + CH3 and Phe + COCH3 have superior recovery properties and therefore perform better at lower temperatures as compared to Phe + NH2. For sensing SO2 and SOF2, Phe + NH2 and Phe + COCH3 are not very suitable as they require relatively high working temperature for desorption. Similarly to –NH2 functionalized phenalenyl system, Tri + NH2 and Ex-Tri + NH2 also have high recovery times for SO2, SOF2, SO2F2 and SF6 gases making them unsuitable for use. In order to put the performance of functionalized GQDs in perspective, we briefly discuss the recovery times of a few other adsorbing materials for the same gas molecules. The α-arsenene with SO2, SOF2 and SO2F2 shows recovery times of 0.23s, 0.68 ms and 0.44μs, however β-arsenene with SO2, SOF2 and SO2F2 provides 3.65 μs, 0.33 μs and 0.05 μs of recovery times, respectively [70]. The SO2, SOF2 and SO2F2 have long recovery times of 400 s, 669 μs and 5.9 ns at 298 K, respectively for Ni-BNNT system [71]. It is found that in Pt–MoS2 and Au–MoS2, SO2 and SOF2 are difficult to desorb unless increasing the working temperature [72]. These recovery times are higher as compared to GQDs (in ps) in the present study leading to their superiority and high detection limit.
4. Conclusions
In this study, we employed density functional theory (DFT) to investigate the adsorption behaviour and gas sensing properties of size and edge-functionalized graphene quantum dots (GQDs), specifically phenalenyl, triangulene, and extended triangulene. We analyzed properties such as adsorption energy, adsorption distance, recovery time, and density of states. Our results show that functionalization of phenalenyl, triangulene, and extended triangulene alters their electronic properties. However, the adsorption of SO2, SOF2, SO2F2, and SF6 gases on Phe + CH3 leads to minor changes in HOMO and LUMO. A significant change is observed when SO2 is adsorbed on –NH2 functionalized triangulene, resulting in a change in the energy gap. Furthermore, –NH2 functionalized phenalenyl, triangulene, and extended triangulene show superior adsorption energies for SO2 sensing compared to other functionalizations. In terms of recovery time, it is challenging to desorb the gases (SO2, SOF2, SO2F2, and SF6) from Phe + NH2, Tri + NH2, and Ex-Tri + NH2 when using –CH3, –COCH3, and –NH2 functionalized phenalenyl and triangulene. In conclusion, this study offers a microscopic understanding of the ultrafast recovery times of GQDs and their potential applications in sensing toxic environmental gases.
Author contribution statement
Vaishali Roondhe; Basant Roondhe: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Sumit Saxena; Rajeev Ahuja; Alok Shukla: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Authors VR and BR would like to acknowledge the supported by the Institute Post-Doctoral Fellowship (IPDF) of Indian Institute of Technology Bombay. This article is financially supported by the Swedish Research Council (VR-2016-06014 & VR-2020-04410) and J. Gust. Richert Stiftelse, Sweden (2021-00665).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e15388.
Contributor Information
Vaishali Roondhe, Email: oshivaishali@gmail.com.
Rajeev Ahuja, Email: rajeev.ahuja@physics.uu.se.
Alok Shukla, Email: shukla@phy.iitb.ac.in.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Tang J., Liu F., Zhang X., Meng Q., Zhou J. Partial discharge recognition through an analysis of SF6 decomposition products part 1: decomposition characteristics of SF6 under four different partial discharges. IEEE Trans. Dielectr. Electr. Insul. 2012;19:29–36. [Google Scholar]
- 2.You H., Zhang Q., Guo C., Xu P., Ma J., Qin Y., et al. Motion and discharge characteristics of metal particles existing in GIS under DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2017;24:876–885. [Google Scholar]
- 3.Suehiro J., Zhou G.B., Hara M. Detection of partial discharge in SF6 gas using a carbon nanotube-based gas sensor. Sens. Actuators, B. 2005;105:164–169. [Google Scholar]
- 4.Ph R.-J., Yousfi M. New breakdown electric field calculation for SF6 high voltage circuit breaker applications. Plasma Sci. Technol. 2007;9:690–694. [Google Scholar]
- 5.Zhang X., Yang B., Liu W., Zhang J. Detection of partial discharge in SF6 decomposition gas based on modified carbon nanotubes sensors. Procedia Eng. 2012;29:4107–4111. [Google Scholar]
- 6.Irawan R., Scelsi G.B., Woolsey G.A. Optical fiber sensing of SF6 degradation in high-voltage switchgear. J. Nonlinear Opt. Phys. Mater. 2012;10:181–195. [Google Scholar]
- 7.Ju T., Min F., Tan Z., Sun C. Crossover response processing technology of photoacoustic spectroscopy signal of SF6 decomposition components under partial discharge. High Volt. Eng. 2013;39:257–264. [Google Scholar]
- 8.Beyer C., Jenett H., Klockow D. Influence of reactive SFxgases on electrode surfaces after electrical discharges under SF6 atmosphere. IEEE Trans. Dielectr. Electr. Insul. 2000;7:234–240. [Google Scholar]
- 9.Braun J.M., Chu F.Y., Seethapathy R. Characterization of GIS spacers exposed to SF6 decomposition products. IEEE Trans. Electr. Insul. EI. 1987;22:187–193. [Google Scholar]
- 10.Li J., Han X., Liu Z., Yao X. A novel GIS partial discharge detection sensor with integrated optical and UHF methods. IEEE Trans. Power Delivery. 2018;33:2047–2049. [Google Scholar]
- 11.Ma G.-m., Zhou H.-y., Zhang M., Li C.-r., Cui B.-y., Wu Y.-y. Optical Sensors and Sensing Congress (ES, FTS, HISE, Sensors) Optical Society of America; San Jose, California: 2019. Optical fiber acoustic emission sensor for GIS partial discharge detection. STh3A.5. [Google Scholar]
- 12.Zhang X., Cui H., Gui Y. Synthesis of graphene-based sensors and application on detecting SF6 decomposing products: a review. Sensors. 2017;17:363. doi: 10.3390/s17020363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhou X., Lee S., Xu Z., Yoon J. Recent progress on the development of chemosensors for gases. Chem. Rev. 2015;115:7944–8000. doi: 10.1021/cr500567r. [DOI] [PubMed] [Google Scholar]
- 14.Gui Y., Shi J., Yang P., Li T., Tang C., Xu L. Platinum modified MoS2 monolayer for adsorption and gas sensing of SF6 decomposition products: a DFT study. High Volt. 2020;5:454–462. [Google Scholar]
- 15.Xu L., Gui Y., Li W., Li Q., Chen X. Gas-sensing properties of Ptn-doped WSe2 to SF6 decomposition products. J. Ind. Eng. Chem. 2021;97:452–459. [Google Scholar]
- 16.Gui Y., Shi J., Xu L., Ran L., Chen X. Aun (n = 1–4) cluster doped MoSe2 nanosheet as a promising gas-sensing material for C2H4 gas in oil-immersed transformer. Appl. Surf. Sci. 2021;541 [Google Scholar]
- 17.Chen D., Zhang X., Tang J., Cui Z., Cui H. Pristine and Cu decorated hexagonal InN monolayer, a promising candidate to detect and scavenge SF6 decompositions based on first-principle study. J. Hazard Mater. 2019;363:346–357. doi: 10.1016/j.jhazmat.2018.10.006. [DOI] [PubMed] [Google Scholar]
- 18.Novoselov K.S., Geim A.K., Morozov S.V., Jiang D., Zhang Y., Dubonos S.V., et al. Electric field effect in atomically thin carbon films. Science. 2004;306:666–669. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- 19.Hernández Rosas J.J., Ramírez Gutiérrez R.E., Escobedo-Morales A., Anota E.C. First principles calculations of the electronic and chemical properties of graphene, graphane, and graphene oxide. J. Mol. Model. 2011;17:1133–1139. doi: 10.1007/s00894-010-0818-1. [DOI] [PubMed] [Google Scholar]
- 20.Shi S., Chen F., Ehlerding E.B., Cai W. Surface engineering of graphene-based nanomaterials for biomedical applications. Bioconjugate Chem. 2014;vol. 25:1609–1619. doi: 10.1021/bc500332c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sharma V., Som N.N., Pillai S.B., Jha P.K. Utilization of doped GQDs for ultrasensitive detection of catastrophic melamine: a new SERS platform. Spectrochim. Acta. 2020;224 doi: 10.1016/j.saa.2019.117352. [DOI] [PubMed] [Google Scholar]
- 22.Sharma V., Kagdada H.L., Singh D.K., Jha P.K. In: Advances in Spectroscopy: Molecules to Materials. Singh D., Das S., Materny A., editors. vol. 236. Springer; Singapore: 2019. (Springer Proceedings in Physics). [Google Scholar]
- 23.Li L., Wu G., Yang G., Peng J., Zhao J., Zhu J.-J. Focusing on luminescent graphene quantum dots: current status and future perspectives. Nanoscale. 2013;5:4015–4039. doi: 10.1039/c3nr33849e. [DOI] [PubMed] [Google Scholar]
- 24.Shen J., Zhu Y., Yang X., Li C. Graphene quantum dots: emergent nanolights for bioimaging, sensors, catalysis and photovoltaic devices. Chem. Commun. 2012;48:3686–3699. doi: 10.1039/c2cc00110a. [DOI] [PubMed] [Google Scholar]
- 25.Bacon M., Bradley S.J., Nann T. Graphene quantum dots. Part. Part. Syst. Char. 2014;31:415–428. [Google Scholar]
- 26.Liu W.-W., Feng Y.-Q., Yan X.-B., Chen J.-T., Xue Q.-J. Superior micro-supercapacitors based on graphene quantum dots. Adv. Funct. Mater. 2013;23:4111–4122. [Google Scholar]
- 27.Joo S.S., Kim J., Kang S.S., Kim S., Choi S.-H., Hwang S.W. Graphene-quantum-Dot nonvolatile charge-trap flash memories. Nanotechnology. 2014;25 doi: 10.1088/0957-4484/25/25/255203. [DOI] [PubMed] [Google Scholar]
- 28.Kim C.O., Hwang S.W., Kim S., Shin D.H., Kang S.S., Kim J.M., et al. High- performance graphene-quantum-dot photodetectors. Sci. Rep. 2014;4:5603. doi: 10.1038/srep05603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nurunnabi M., Khatun Z., Reeck G.R., Lee D.Y., Lee Y. Photoluminescent graphene nanoparticles for cancer phototherapy and imaging. ACS Appl. Mater. Interfaces. 2014;6:12413–12421. doi: 10.1021/am504071z. [DOI] [PubMed] [Google Scholar]
- 30.Wang X., Sun X., Lao J., He H., Cheng T., Wang M., et al. Multifunctional graphene quantum dots for simultaneous targeted cellular imaging and drug delivery. Colloids Surf., B. 2014;122:638–644. doi: 10.1016/j.colsurfb.2014.07.043. [DOI] [PubMed] [Google Scholar]
- 31.Fei H., Ye R., Ye G., Gong Y., Peng Z., Fan X., et al. Boron- and nitrogen-doped graphene quantum dots/graphene hybrid nanoplatelets as efficient electrocatalysts for oxygen reduction. ACS Nano. 2014;8:10837–10843. doi: 10.1021/nn504637y. [DOI] [PubMed] [Google Scholar]
- 32.Sharma V., Kagdada H.L., Wang Jinlan, Jha P.K. Hydrogen adsorption on pristine and platinum decorated graphene quantum dot: a first principle study. Int. J. Hydrogen Energy. 2020;45:23977–23987. [Google Scholar]
- 33.Sun H., Wu L., Wei W., Qu X. Recent advances in graphene quantum dots for sensing. Mater. Today. 2013;16:433–442. [Google Scholar]
- 34.Basu S., Bhattacharyya P. Recent developments on graphene and graphene oxide based solid state gas sensors. Sens. Actuators, B. 2012;173:1–21. [Google Scholar]
- 35.Haddon R.C. Design of organic metals and superconductors. Nature. 1975;256:394–396. [Google Scholar]
- 36.Sun Z., Wu J. Open-shell polycyclic aromatic hydrocarbons. J. Mater. Chem. 2012;22:4151–4160. [Google Scholar]
- 37.Son Y.-W., Cohen M.L., Louie S.G. Half-metallic graphene nanoribbons. Nature. 2006;444:347–349. doi: 10.1038/nature05180. [DOI] [PubMed] [Google Scholar]
- 38.Barone V., Hod O., Peralta J.E., Scuseria G.E. Accurate prediction of the electronic properties of low-dimensional graphene derivatives using a screened hybrid density functional. Acc. Chem. Res. 2011;44:269–279. doi: 10.1021/ar100137c. [DOI] [PubMed] [Google Scholar]
- 39.Tao C., Jiao L., Yazyev O.V., Chen Y.-C., Feng J., Zhang X., et al. Spatially resolving edge states of chiral graphene nanoribbons. Nat. Phys. 2011;7:616–620. [Google Scholar]
- 40.Morita Y., Nishida S., Murata T., Moriguchi M., Ueda A., Satoh M., et al. Organic tailored batteries materials using stable open-shell molecules with degenerate frontier orbitals. Nat. Mater. 2011;10:947–951. doi: 10.1038/nmat3142. [DOI] [PubMed] [Google Scholar]
- 41.Kolc J., Michl J. pi.,.pi.-Biradicaloid hydrocarbons. Pleiadene family. I. Photochemical preparation from cyclobutene precursors. J. Am. Chem. Soc. 1973;95:7391–7401. [Google Scholar]
- 42.Smith M.B., Michl J. Singlet fission. Chem. Rev. 2010;110:6891–6936. doi: 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
- 43.Coronado E., Epstein A.J. Molecular spintronics and quantum computing. J. Mater. Chem. 2009;19:1670–1671. [Google Scholar]
- 44.Yazyev O.V., Katsnelson M.I. Magnetic correlations at graphene edges: basis for novel spintronics devices. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.047209. [DOI] [PubMed] [Google Scholar]
- 45.Lambert C. Towards polycyclic aromatic hydrocarbons with a singlet open-shell ground state. Angew. Chem., Int. Ed. 2011;50:1756. doi: 10.1002/anie.201006705. [DOI] [PubMed] [Google Scholar]
- 46.Wang L., Zhu S.-J., Wang H.-Y., Qu S.-N., Zhang Y.-L., Zhang J.-H., et al. Common origin of green luminescence in carbon nanodots and graphene quantum dots. ACS Nano. 2014;8:2541–2547. doi: 10.1021/nn500368m. [DOI] [PubMed] [Google Scholar]
- 47.Jin S.H., Kim D.H., Jun G.H., Hong S.H., Jeon S. Tuning the photoluminescence of graphene quantum dots through the charge transfer effect of functional groups. ACS Nano. 2013;7:1239–1245. doi: 10.1021/nn304675g. [DOI] [PubMed] [Google Scholar]
- 48.Li Y., Shu H., Niu X., Wang J. Electronic and optical properties of edge-functionalized graphene quantum dots and the underlying mechanism. J. Phys. Chem. C. 2015;119:24950–24957. [Google Scholar]
- 49.Frisch M.J., et al. Gaussian Inc. Gaussian, Inc.; Wallingford CT: 2016. Gaussian 16, Revision C.01. [Google Scholar]
- 50.Chai J.-D., Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008;10:6615–6620. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 51.Becke A.D. Completely numerical calculations on diatomic molecules in the local-density approximation. Phys. Rev. A. 1986;33:2786–2788. doi: 10.1103/physreva.33.2786. [DOI] [PubMed] [Google Scholar]
- 52.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 53.Deji R., Jyoti R., Verma A., Choudhary B.C., Sharma R.K. A theoretical study of HCN adsorption and width effect on co-doped armchair graphene nanoribbon. Comput. Theor. Chem. 2022;1209 113592-11. [Google Scholar]
- 54.Deji R., Verma A., Kaur N., Choudhary B.C., Sharma R.K. Adsorption chemistry of co-doped graphene nanoribbon and its derivatives towards carbon based gases for gas sensing applications: quantum DFT investigation. Mater. Sci. Semicond. Process. 2022;146 106670-13. [Google Scholar]
- 55.Tetsuka H., Asahi R., Nagoya A., Okamoto K., Tajima I., Ohta R., et al. Optically tunable amino‐functionalized graphene quantum dots. Adv. Mater. 2012;24:5333–5338. doi: 10.1002/adma.201201930. [DOI] [PubMed] [Google Scholar]
- 56.Cui H., Zhang X., Zhang J., Tang J. Adsorption behaviour of SF6 decomposed species onto Pd4-decorated single-walled CNT: a DFT study. Mol. Phys. 2018;116:1749. [Google Scholar]
- 57.Pi S., Zhang X., Chen D., Tang J. Sensing properties of Ni-doped boron nitride nanotube to SF6 decomposed components: a DFT study. AIP Adv. 2019;9:95101–95109. [Google Scholar]
- 58.Samanta P.N., Das K.K. Structural and electronic properties of covalently functionalized 2-aminoethoxy-metallophthalocyanine–graphene hybrid materials: a computational study. RSC Adv. 2015;5:85730–85740. [Google Scholar]
- 59.Li S.S. Springer Science; United States: 1997. Semiconductor Physical Electronics. [Google Scholar]
- 60.Deji R., Choudhary B.C., Sharma R.K. Novel hydrogen cyanide gas sensor: a simulation study of graphene nanoribbon doped with boron and phosphorus. Physica E Low Dimens. Syst. Nanostruct. 2021;134:114844–114849. [Google Scholar]
- 61.Deji R., Jyoti R., Choudhary B.C., Singh R., Sharma R.K. Enhanced sensitivity of graphene nanoribbon gas sensor for detection of oxides of nitrogen using boron and phosphorus co-doped system: a first principles study. Sens. Actuator A Phys. 2021;331 112897-10. [Google Scholar]
- 62.Deji R., Choudhary B.C., Sharma R.K. Hydrogen sulfide gas sensor using osmium doped graphene nanoribbon: an insights from DFT study. Mater. Lett. 2022;306 130986-5. [Google Scholar]
- 63.Deji R., Verma A., Choudhary B.C., Sharma R.K. New insights into NO adsorption on alkali metal and transition metal doped graphene nanoribbon surface: a DFT approach. J. Mol. Graph. Model. 2022;111:108109–108112. doi: 10.1016/j.jmgm.2021.108109. [DOI] [PubMed] [Google Scholar]
- 64.Lu T., Chen F. Multiwfn: a multifunctional wavefunction analyser. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 65.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 66.Zhang Y.H., Chen Y.B., Zhou K.G., Liu C.H., Zeng J., Zhang H.L., et al. Improving gas sensing properties of graphene by introducing dopants and defects: a first-principles study. Nanotechnology. 2009;20 doi: 10.1088/0957-4484/20/18/185504. [DOI] [PubMed] [Google Scholar]
- 67.Roondhe B., Jha P.K. “Haeckelite”, a new low dimensional cousin of boron nitride for biosensing with ultra-fast recovery time: a first principles investigation. J. Mater. Chem. B. 2018;6:6796–6807. doi: 10.1039/c8tb01649f. [DOI] [PubMed] [Google Scholar]
- 68.Patel K., Roondhe B., Dabhi S.D., Jha P.K. A new flatland buddy as toxic gas scavenger: a first principles study. J. Hazard Mater. 2018;351:337–345. doi: 10.1016/j.jhazmat.2018.03.006. [DOI] [PubMed] [Google Scholar]
- 69.Roondhe B., Patel K., Jha P.K. Two-dimensional metal carbide comrade for tracing CO and CO2. Appl. Surf. Sci. 2019;496 [Google Scholar]
- 70.X. Wang, G. Fan, X. Tu, X. Liu, C. Li, H. Xu, Sc doped arsenene as adsorbent for the detection and removal of SF6 decomposition gases: a DFT study, Appl. Surf. Sci., 552, 149449.
- 71.Pi S., Zhang X., Chen D., Tang J. Sensing properties of Ni-doped boron nitride nanotube to SF6 decomposed components: a DFT study. AIP Adv. 2016;9 [Google Scholar]
- 72.Chen D., Zhang X., Tang J., Cui H., Li Y. Noble metal (Pt or Au)-doped monolayer MoS2 as a promising adsorbent and gas-sensing material to SO2, SOF2 and SO2F2: a DFT study. Appl. Phys. A. 2018;124:194. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.