Abstract
Efficient delivery of anticancer drugs into tumor tissues at maximally effective and minimally toxic concentrations is vital for therapeutic success. At present, no method exists that can predict the spatial and temporal distribution of drugs into a target tissue after administration of a specific dose. This prevents accurate estimation of optimal dosage regimens for cancer therapy. Here we present a new method that predicts quantitatively the time-dependent spatial distribution of drugs in tumor tissues at sub-micrometer resolution. This is achieved by modeling the diffusive flow of individual drug molecules through the three-dimensional network of blood-vessels that vascularize the tumor, and into surrounding tissues, using molecular mechanics techniques. By evaluating delivery into tumors supplied by a series of bl ood-vessel networks with varying degrees of complexity, we show that the optimal dose depends critically on the precise vascular structure. Finally, we apply our method to calculate the optimal dosage of the cancer drug doxil into a section of a mouse ovarian tumor, and demonstrate the enhanced delivery of liposomally administered doxorubicin when compared to free doxorubicin. Comparison with experimental data and a multiple-compartment model show that the model accurately recapitulates known pharmacokinetics and drug-load predictions. In addition, it provides, for the first time, a detailed picture of the spatial dependence of drug uptake into tissues surrounding tumor vasculatures. This approach is fundamentally different to current continuum models, and reveals that the target tumor vascular topology is as important for therapeutic success as the transport properties of the drug delivery platform itself. This sets the stage for revisiting drug dosage calculations.
Keywords: Tumor model, molecular mechanics, personalized medicine, vasculature, drug delivery, doxil
Graphical Abstract
1. Introduction
Knowledge of the efficiency of drug delivery from the vasculature into target tissues is important for estimating the optimal dosage regimen for a given drug[1]. This is particularly significant for anticancer drugs, which are generally very toxic[2].
Drug dosing for humans is often derived from animal studies, which are refined in human clinical trials[3]. Adaptation to individual patients is achieved by scaling the standard dose based on weight or body surface area (BSA) using empirical calculations, with the DuBois and Mosteller formulas being the most commonly used[4]. BSA based regimens have been criticized, as they cannot account for the 4 to 10-fold variation in drug clearance typically observed within any particular patient pool [5], nor do they consider the variability of maximally tolerated doses among individuals[6]. Furthermore, BSA calculations differ depending on the empirical formula used. This may considerably impact patients’ health due to under- or overdosing, especially for children[7]. In cancer patients, calculations based on these methodologies have resulted in both increased toxicity due to overdosing[8] as well as decreased efficacy and possible development of drug-resistance due to underdosing during chemotherapy[9]. Furthermore, BSA derived dosimetry fails to individualize the effects of the majority of the most commonly used cytotoxics[10]. This highlights the need for better tools to predict effective doses when discussing nonspecific chemotherapeutic agents[11].
Systemic delivery of therapeutics into tissues relies upon the vascular network, which also delivers oxygen and nutrients. In healthy human tissues (e.g. liver, kidney, muscle), cells are typically located ~50 μm from a blood vessel[12], which results in good tissue distribution of pharmaceuticals with high permeability. In contrast, drug delivery into tumor tissue is complicated by the leaky and defective tumor vasculature. The growth of the neovasculature recruited to supply tumor cells is typically slower than the proliferation rate of cells inside a tumor[13], [14]. This results in a significant increase in the average normal distance to the nearest vessel for cancer cells (>100 μm) and a lower overall density of blood vessels inside a tumor [15], [16]. Together with reduced lymphatic drainage, this creates an acidic and hypoxic extracellular environment for tumor cells at larger distances from the vasculature due to accumulation of by products of cell metabolism (e.g. lactic acid and carbonic acid) and oxygen starvation[17]. Targeting cells in these deeply buried microenvironments with chemotherapy is challenging, because drugs may not diffuse efficiently enough through the interstitial space to reach them[18], and the drugs that do reach deep into these tissues may be less active due to the acidic microenvironment[19].
The ability of anticancer therapeutics to come into contact with all proliferating cells within an inoperable tumor is vital for prolonging remission or preventing relapse. To improve delivery into solid tumors nanoparticle-based cancer drugs have been developed that exploit the enhanced permeability and retention (EPR) effect[20] by penetrating the leaky junctions of the tumor vasculature and accumulating inside tumor tissues[21]. In this study we compare the efficacy of tissue penetration of the anthracycline doxorubicin, a commonly use anticancer drug, to doxil, an FDA-approved nanoparticle formulation, which encapsulates ~48,000 doxorubicin molecules in a liposome[22]. Typical intravenously administered doses are 50 mg/m2 every 28 days for doxil and 60 to 75 mg/m2 every 21 days up to a typical maximum dose of 300-600 mg/m2 for doxorubicin. Inter-individual clearance rates of doxorubicin are uncorrelated with BSA[23], while cardiotoxic side effects increase proportionally to the cumulative administered dose, with 6-20% cardiotoxicity at 500 mg/m2. This makes accurate prediction of the optimal administered dose desirable.
Simple drug delivery models typically divide the organism into a number of compartments such as blood vessel, peripheral tissue, and tumor tissue. How much of a given compound was delivered to the tumor is calculated by assigning first order rate constants to model the transport between the various compartments and by taking into account clearance[24]. While these models can be parameterized to capture uptake in the tumor microenvironment implicitly, the spatial resolution of the drug in the target tissue and hence the overall effectiveness of a particular chemotherapeutic dose remain undetermined.
Here, we present a new method that predicts the spatial drug delivery efficiency into a target tissue. To achieve this, we simulate the diffusive transport of compounds through a vasculature towards target tissues using molecular mechanics methods in complex geometrical volumes. The model works for both molecular solutes as well as nanoparticle-based delivery systems that carry thousands of individual pharmaceutically active compounds. The ultimate goal of this model is to provide new insights into the relative efficacies of different pharmacophores, enabling systematic optimization of therapeutics for specific tumor and healthy tissue vasculatures.
2. Material and Methods
2.1. Modeling the vasculature, endothelium, and surrounding tissues
Stochastic drug transport towards target tissues is modeled by pseudo-random diffusion through a micrometer-resolution three-dimensional (3D) model of vasculature and surrounding tissue (see Figure 1) in an algorithm that scales linearly with the number of particles.
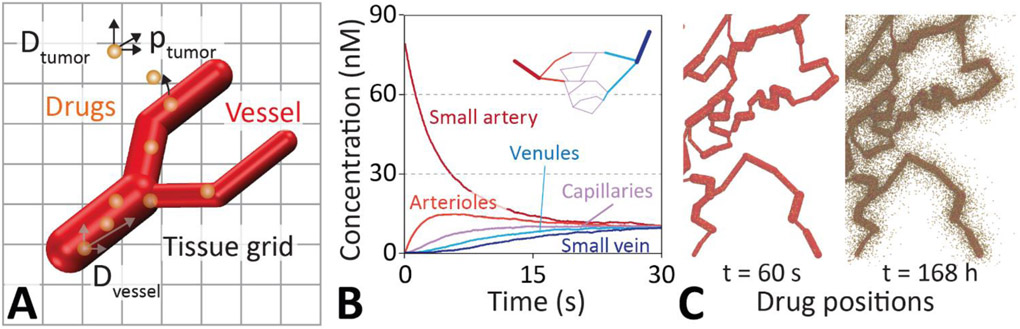
Figure 1 ∣. Drug diffusion model schematic and drug equilibration inside a vasculature.
A. Drug delivery is modeled by diffusive flow of particles through the vasculature and into the tissues using Brownian dynamics. Drugs incident on the walls of the vasculature are transferred back and forth between the vessel and the tissue with a given probability () via a kinetic Monte Carlo scheme. The vasculature is modeled by an interconnected network of cylinders. These are connected via spheres to allow branching as well as changing of the direction and radius of blood vessels. Interstitial space and tissues are represented as a micrometer resolution cubic grid. B. Rapid diffusive equilibration of an injected drug dosage throughout the small arteries (red), arterioles (light red), capillaries (pink), venules (light blue), and veins (blue) of a simple vascular network (inset). C. Three dimensional distribution of drugs in a vasculature and surrounding tissue at t = 60s and 168h. The model captures the position of individual drug molecules (brown spheres) as they transfer out of the vessel and disperse into the tissue.
Corrosion casts and micro-computed tomography (μCT) scans of tumor vasculatures show branched networks of arteries, capillaries, and veins that are approximately cylindrical in cross section[15]. In order to capture the vascular network efficiently we modeled veins and arteries as linked cylinders of constant radius, with a sphere at either end to allow map bends and branches as well as changes in radius (see Figure 1). This greatly facilitates tracking of drug diffusion through the various compartments representing the vasculature and surrounding tissues, which makes the simulation of a large number of particles tractable with reasonable computational effort. Blood vessel networks are defined in a text file that specifies the Cartesian coordinates of the cylinders and spheres. This information is loaded at runtime during the setup of the simulation (c.f. Figure S1). Different physical parameters can be assigned for each geometric element without loss of computational efficiency to model leakier vessel segments or to capture changes in diffusivity due to tortuous vascular structures. Each vascular network (e.g. Figure 1C) was mapped by manually specifying starting and ending locations of each vessel section. A realistic vasculature was traced by a reference image[25]. In the absence of 3D information from the image, the blood vessels were traced in a plane.
Tissues surrounding the vasculature are modeled as a mesh of rectangular prisms that are connected in three-dimensions. Each prism is ~3.33 μm long on each side, with a volume of ~37.0 μm3. All simulations presented here have physical volume of 1 mm3, consisting of a cubic grid of 300x300x300 prisms. This allows tracking the flow and spatial distribution of individual molecules in tissues. For the present study, we have assigned the particle diffusivity to be isotropic for the vasculature and tissues. However, different diffusivities in x, y, and z can be assigned for each element of the tissue or vasculature (e.g. dependent of vessel radius or related to the distance from the closest vessel), and there is no major computational overhead associated to adding microscopic structural features, such as individual tumor cells or blood lakes, to these tissues. While the mesh allows for full spatial and temporal tracking of particle concentrations within tissues, the particles themselves are able to move freely in three dimensions and their position is not constrained by the grid (Figure 1A). Peripheral tissues were modeled as a virtual compartment with exchange particles with the blood vessels via an effective forward () and backward rate constant (), which were taken from Wong et al.[24].
Tumor vasculatures have complex structures, which are abundant in chaotically branched microvessels that form loops and dead ends[15], [16], [26]-[28]. These malformed vascular networks typically have microvessels that vary greatly in diameter when compared to healthy tissues. Often there is no preferred blood flow direction or the vasculature is connected only to feeder arteries with no draining veins [29]. To explore the effect of these structural features on drug delivery we modeled a section of vasculature of a mouse ovarian tumor. This was accomplished by manually specifying the vasculature coordinates based on the pixel data in the reference image[25]. Because we have little 3D information from this image, we flattened it to 2D. This simplification is much easier to present and visualize, while still demonstrating the effect of the vascular topology on delivery, despite the constraint of the 3D blood vessels to a 2D plane.
2.2. Drug diffusion in the vasculature and surrounding tissues
Diffusion of the drugs and the delivery system was modeled by a fixed step-size () spherical random walk in combination with a Metropolis Monte Carlo scheme to hop between vasculature and surrounding tissues (summarized in Figure 1). A time-step of Δt = 1 second was chosen with a fixed Einstein diffusion length (i.e. step-size) inside the vasculature of in a spherically random direction.
For the vasculature, a diffusion coefficient of was chosen for doxil, which corresponds to the theoretical random diffusion of a spherical liposome of 100 nm diameter through capillary blood. For the small molecule drug doxorubicin was chosen, which is the same order of magnitude as other molecules of similar size[30]. Regarding the surrounding tissues, diffusivity measurements in vivo are challenging at present. The diffusivity of doxorubicin inside the interstitial space of tumor tissues was chosen to be . This value is consistent with a drug that delivers well in tissues with dense vasculature[31], and is comparable values used in other models[32]. The diffusive lengths of nanoparticles are certainly much lower. The diffusivity of doxil liposomes was based on broad-field fluorescence measurements of nanoparticles of similar size and mass within agar gel phantoms (in vitro)[33]. Many nanoparticles diffuse on the order of 10−11 cm2/s in mucus covered epithelial tissues[34], but the selection of is closer line with previous simulations of doxil[35], and yields a similar drug penetration in the tumor, due to the square root dependence on diffusivity on permeation length.
For the present study, we model only diffusive flow of liposomes through the vasculature, across the endothelium, and into and across surrounding tissue. Time-dependent blood flow and viscosity, as well as more fine-grained tissue structures can be implemented straight forwardly to refine this model. We show below that equilibration inside the vasculature is much faster than trans-endothelial transport and diffusion in surrounding tissues. Thus, flow was ignored for the present study.
2.3. Clinically relevant dosing
All tumor models were chosen to have a fixed volume of 1 mm3. This allows us to directly compare the variation of drug uptake into tumor tissues with different vascular structures. In order to explore the effect of the tumor vascular structure on delivery, the model patient BSA and body mass index (BMI) are kept fixed.
We can relate the simulated dose to a standard clinical dose of 50 mg/m2, corresponding to ~90 mg of doxorubicin, for a model human being (mass = 70 kg, height = 1.70 m, volume = 0.07 m3). This human’s BSA, calculated from the Dubois formula, is 1.81 m2. As each doxil liposome contains ~48,000 doxorubicin molecules (M.W. = 543.52 g/mol)[22], equivalent to 2.6 x 107 g of doxorubicin per mol of doxil liposomes, typical dose administered is ~3.47 nanomoles of doxil liposomes.
Further assuming that the body is roughly uniformly vascularised, after distributive equilibration the blood vessels of a 1 mm3 tumor contain ~2.98x107 doxil liposomes, hence each of the 107 particles in the simulations represents ~3 doxil liposomes. Delivering the same dose of free doxorubicin (50 mg/m2) to the same human equates to an average concentration of ~2.38 μM in the body, or ~1.43x1012 doxorubicin molecules in a 1 mm3 tumor, hence each particle in doxorubicin simulations corresponds to ~143,000 doxorubicin molecules. One particle of either formulation within a ~37 μm3 voxel corresponds to a localized concentration of ~6 μM clinical doxorubicin for a simulated dose of 50 mg/m2 statistically represented by 107 total particles.
2.4. Trans-endothelial transport
Tumor endothelia have leaky junctions between cells, resulting in increased transport of large complexes including liposomes up to around 500 nm in diameter[36]-[38]. This can be modeled by adjusting the permeability for individual segments of the vasculature. Since we are simulating the delivery of individual molecules the first-order rate constant for transport between compartments must be converted into a perparticle transport probability. This is achieved using a kinetic Monte Carlo approach. In brief, the experimentally determined first-order rate constant of a drug exiting a compartment (e.g. doxil moving from blood into tissue) was converted to a corresponding Monte Carlo probability for this process. A first-order population decay of particles at some time , which was obtained from fits to clinical pharmacokinetic data for doxil[39] (Figure 2A):
| (Eq. 1) |
can be transformed into a rate-equivalent Monte Carlo extravasation probability, p, using:
| (Eq. 2) |
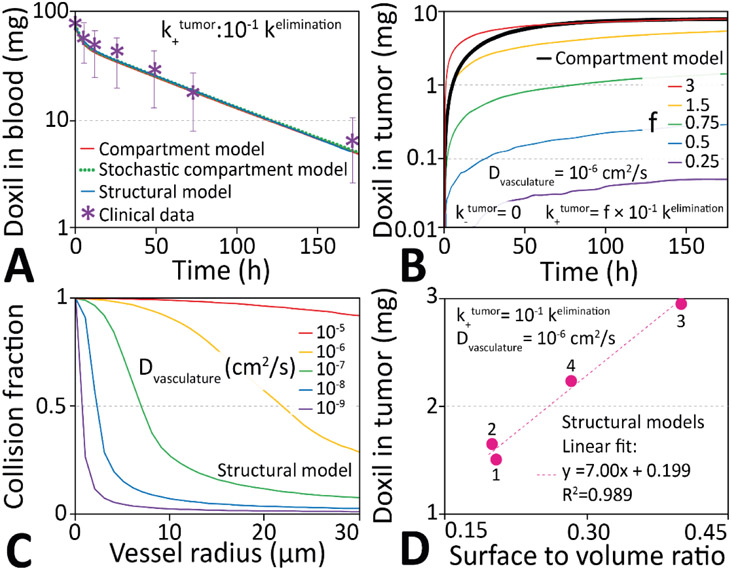
Figure 2 ∣. Compartment-based pharmacokinetics of doxil delivery into tumors.
A. Comparison of the modeled time dependence of the amount of doxil liposomes in blood with clinical data. B. Time dependent uptake of doxil in the tumor. A scale factor f can match the total amount of drug delivered via the structural model to the value obtained from the compartment model. C. Fraction of particles that can reach the walls and potentially exit a vessel segment as a function of vessel radius and particle diffusivity in blood, a quantity inversely proportional to f in panel B. D: The surface-to-volume ratio of all vasculatures scales linearly with the delivered concentration for the vascular structures in Figure 3.
Here is the initial population, is the first-order rate constant, is the number of simulation steps, is the simulation time-step, and is the Monte Carlo probability of a change of state (i.e. transport event or clearance event ). The solution of this equation gives the rate-derived transport probability:
| (Eq. 3) |
This Monte Carlo scheme quantitatively replicates the pharmacokinetic compartment model (c.f. Figure 2A).
2.5. Drug injection, clearance, and delivery
Injection is simulated by placing all drug molecules at a point source in the artery and allowing them to diffuse. As most drugs extravasate slowly compared to vascular circulation times we first equilibrate to uniform concentration throughout the vasculature, before enabling trans-endothelial transport and clearance. This is a good approximation for doxil and doxorubicin, which exhibit negligible extravasation and clearance in the <5 minute timeframe the drug takes to equilibrate in the vasculature. However, some drugs have very high extravasation and clearance rates, we therefore also performed simulations without pre-equilibration (See Figure S2). Clearance by macrophages, liver, and kidneys is simulated as a random removal using a kinetic Monte Carlo scheme with a rate .
Delivery from the large vessels (arteries or veins) into surrounding tissues is modeled using a kinetic Monte Carlo approach outlined above (Eq. 2) with a rate constant of . This value is based on the observation of a much slower clearance (plasma half-life t½ > 180 hrs) of fluorescently loaded nanoparticles and free drug within mouse tissues when compared to the normalized plasma bound concentration of nanoparticles and free drugs[40]-[43].
2.6. Definition of the minimum effective dose
To achieve a therapeutic dose in a patient a drug has to be administered at the minimum effective dose (MED). We chose 5 μM as the MED. This value was derived from the Genomics of Drug Sensitivity in Cancer database, which report half maximal inhibitory concentrations (IC50) for doxorubicin ranging from 4.4 nM to 32.2 μM for 928 cancer cell lines[44].
Due to the non-specificity of anticancer chemotherapeutics like doxorubicin, toxic side effects to off-target tissues in the body are common and currently unavoidable even at minimal therapeutic dosages. The maximally tolerated dose (MTD), which accumulates over the entire treatment cycle, for doxorubicin can be estimated to be ~50 μM. This was calculated for a model human being (see Section 2.4) and defined as an 18% incidence of doxorubicin cardiomyopathy, which is primarily related to the cumulative dose and increases from 4% at 500 mg/m2 to 36% above 600 mg/m2 [2]
2.7. Doxil and doxorubicin parameters
Doxil is modeled as a spherical particle with 100 nm diameter, a tissue diffusivity of 10−9 cm2/s (See supplement for a calculation using the Stokes-Einstein equation), trans-endothelial transport probability into tumor tissues of 6.33x10−5 s−1, and a clearance rate of . Doxorubicin on the other hand is modeled as a particle with 1.7 nm diameter, tissue diffusivity of 10−7 cm2/s, trans-endothelial permeability of 4.36x10−4 s−1, and a clearance rate of . These values were derived from Wong et al. and equation 3 [24]. All model parameters and their source are summarized in Table 1.
Table 1.
Key parameters used in the structural model.
| Parameter | Value | Source |
|---|---|---|
| Tissue diffusivities (Fig 4) | 1x10−10 − 1x10−6 cm2/s | [30], [46], [48] |
| Transfer probabilities (Fig 4) | 10−5 – 10−3 | |
| 0 − 2 x 107 | Section 2.4 | |
| 1 mm3 | ||
| 2.7 x 107 | ||
| 37.0 mm3 | ||
| (Doxil) | 1 x 10−7 cm2/s | Supplementary Calculation A |
| (Doxorubicin) | 1 x 10−5 cm2/s | Supplementary Calculation A |
| (Doxil) | 1 x 10−9 cm2/s | [32], [35], [41] |
| (Doxorubicin) | 1 x 10−7 cm2/s | [32], [41], [49] |
| (Doxil) | 0.0204 - 0.0228 (hr−1) | [24], [39] |
| (Doxorubicin) | 1.57 (hr−1) | [24], [39] |
| (Doxil) | 0.0956 (hr−1) | [24], [39] |
| (Doxil) | 0.198 (hr−1) | [24], [39] |
| (Doxorubicin) | 9.57 (hr−1) | [24], [39] |
| (Doxorubicin) | 0.494 (hr−1) | [24], [39] |
| (Doxil) | 0.0000228 - 0.00228 (hr−1) | [24], [39] |
| (Doxil) | 0 – 0.00228 (hr−1) | [24], [39] |
| (Doxorubicin) | 0.0157 (hr−1) | [24], [39] |
| (Doxorubicin) | 0.0157 (hr−1) | [24], [39] |
| (Doxil) | 0.000228 (hr−1) | / 100 |
| (Doxorubicin) | 0.0157 (hr−1) | / 100 |
| (Doxil) | 5.67 − 6.33 x 10−6 | from (Eq. 3) |
| (Doxorubicin) | 4.36 x 10−4 | from (Eq. 3) |
| (Doxil) | 2.66 x 10−5 | from (Eq. 3) |
| (Doxil) | 5.50 x 10−5 | from (Eq. 3) |
| (Doxorubicin) | 2.66 x 10−3 | from (Eq. 3) |
| (Doxorubicin) | 1.37 x 10−4 | from (Eq. 3) |
| (Doxil) | 6.33 x 10−9 – 6.33 x 10−7 | from (Eq. 3) |
| (Doxil) | 0 − 6.33 x 10−7 | from (Eq. 3) |
| (Doxorubicin) | 4.36 x 10−6 | from (Eq. 3) |
| (Doxorubicin) | 4.36 x 10−6 | from (Eq. 3) |
| (Doxil) | 6.33 x 10−8 | from (Eq. 3) |
| (Doxorubicin) | 4.36 x 10−6 | from (Eq. 3) |
= Number of liposomes simulated during the majority of the study, = the approximate mass of the therapeutic doses provided as a dosimetry reference, = simulated volume of tissue and vasculature. = diffusion coefficient of therapeutics in the vasculature, = number of tissue components which makes for the tissue grid for detailed concentration tracking. = (i.e. the volume of each tissue grid component, = diffusion coefficient of therapeutics in the both tumorous and healthy tissues, = first-order rate constant for eliminating therapeutics from the system, = first-order rate constant for therapeutics to transfer from blood to peripheral tissues, = first-order rate constant for therapeutics to transfer from peripheral tissues to blood, = first-order rate constant for therapeutics to transfer from blood to tumor, = first-order rate constant for therapeutics to transfer from tumor to blood, = first-order rate constant for therapeutics to finish releasing their payload within the tumor, = Monte Carlo elimination probability within a simulation time-step of one second. = Monte Carlo probability of transfer between blood and peripheral tissue within a simulation time-step of one second. = Monte Carlo probability of transfer between peripheral tissue and blood within a simulation time-step of one second. = Monte Carlo probability of transfer between peripheral tissue and blood within a simulation time-step of one second. = Monte Carlo probability for for therapeutics to finish releasing their payload within the tumor within a simulation time-step of one second.
3. Results
3.1. Particle injection and equilibration in the vasculature
Figure 1B shows that random diffusion alone is sufficient to equilibrate the concentration in the vasculature within 30 seconds of simulated time. All vasculatures tested here efficiently equilibrated within 24 hours on a single CPU for an injection of 10 million liposomes. A movie and snapshots of the equilibration process is provided in the Supplement. However, other chemotherapeutics such as 5-Fluorouracil (5-FU) with high extravasation or clearance rates may not reach uniform concentrations in the bloodstream. To investigate this we simulated a drug with a high extravasation probability of 1x10−4 s−1, clearance rate of 3.22 hr−1 [45], and tissue diffusivity of 1x10−8 cm2/s [46]. Figure S2 shows that this results in uneven drug penetration across the vasculature, suggesting that drugs like this may be unsuitable to treat certain tumors. Doxorubicin and doxil have pharmacokinetics (see below) that suggest that the amount of drugs that extravasate before vascular equilibration is negligible, we hence proceed with pre-equilibrated simulations.
3.2. Pharmacokinetics of structural versus compartment models
Figure 2A compares clinical measurements of the blood concentration of doxil liposomes, after injections of 50 mg/m2, with best fits to a simple multi-compartment model[24], a stochastic compartment model, and the structural model presented here, with clinical data[39]. All three models are able to reproduce the functional form of the clinical data reproduce the clinical clearance half-time of 30.4 h [24], [47].
In the simple compartment model drugs move between four dimensionless compartments (blood, tumor, peripheral tissue, and clearance), while in the stochastic compartment model individual drug molecules are placed in a 3D vasculature, but each drug still has the same probability of passing into the tissue, irrespective of physical position. Figure S3 shows that these models are essentially identical.
In the structural model presented here, drugs extravasate by diffusion across the walls of a three-dimensional vasculature. This means only particles close to the walls can exit a vessel. Figure 2B shows the simulated tumor uptake of doxil liposomes for different extravasation and clearance ratios (:), which can be thought of as a measure of the strength of the EPR effect, for both the compartment and structural models. While the total amount of drugs that eventually cross the endothelia can be multiplied by a scale factor f to match the number obtained via a compartment model, the mathematical curve describing the number of drugs leaving the vessel as function of time is different and cannot be reproduced by scaling (Figure 2B). The functional form of time-dependent tumor drug uptake of a compartment model can only be recaptured by allowing any drug in the vasculature to exit with an equal probability (Figure S3). However, in a structural model, the fraction of particles being able to exit varies with vessel diameter (Figure 2C), and the final location of a molecule in the system depends on the precise trajectory through the vasculature and surrounding tissues.
Only molecules within a volume element surrounding the vascular surface may traverse the endothelium. For each cylindrical vascular segment this volume element is: , where is the mean speed of the drug in the blood vessel, and c is a constant that depends on the diameter and length of the vessel segment. The sum of all volume elements of the vasculature scales non-trivially with the total volume of the entire blood vessel compartment (Figure S3). This means that for a compartment model to accurately reproduce a structural model the rate-derived probability (Eq. 1) would ultimately need to be scaled in each vascular segment.
For any given drug with known kinetic properties (i.e. , , ), the final delivered dose scales linearly with the surface area to volume ratio of the blood vessel (Figure 2D), which demonstrates that the delivery depends on the three-dimensional structure of the vasculature. Tables S1 to S4 indicate the structural parameters of the vascular networks simulated in this paper.
Comparison of the time-dependent uptake kinetics of doxil in all three vasculatures shown in Figure 3 was found to be similar in functional form (Figure S3), yet the ultimate dose delivered is different for all vasculatures. The key parameters used in this study are reported in Table 1.
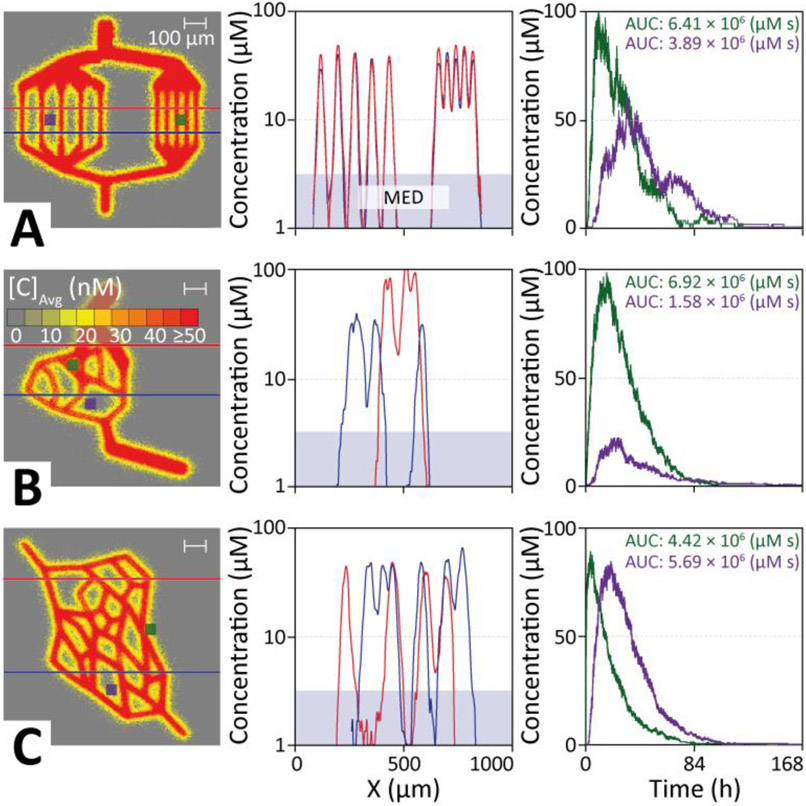
Figure 3 ∣. Simulated doxorubicin delivery into model tissues of different complexity.
The heat map of each vascular model is analysed using two tissue cross sections (horizontal lines, data potted in middle panels) and target areas (blue and green squares, data plotted in right panels). A. Doxorubicin delivery via parallel blood vessels (structure 1) shows that increasing the capillary distance results in therapeutic gaps, resulting in an up to 50% smaller AUC for target areas as well as a delay in reaching peak concentration. B. A simple branched micro-tumor model (structure 2) with uneven capillary spacing results in much larger regions that are outside the therapeutic window in the cross-sectional analysis. Tissue areas close to vessels show high drug loads, whereas areas near the center of large loops receive up to five times lower doses. C. A more complex branched and looped capillary web (structure 3) shows similar behavior than the branched model in panel B. Despite a time-lag, target areas located further from vessels in an acute angle (purple) show better drug penetration compared to areas closer to the capillaries in an obtuse branching angle (green).
3.3. How vascular structure impacts tissue penetration
Figure 3 shows diffusion of doxorubicin through three vascular structures of 1 mm3 of different complexity. To simplify visualization, analysis, and model validation, all vasculatures in the present study are constructed in a plane. However, all vasculatures exist as full 3D objects and our model and software implementation does not require them to be confined to a plane.
Each system was injected with 107 doxorubicin particles, and the diffusion into tissue recorded. Figure 3 shows heat maps, that record the accumulated final resting positions of doxorubicin together with the distribution of drugs along two different cross sections through the tissue (indicated by red & blue lines in the heat map, respectively), and the time-evolution of the drug concentration within two target regions over the course of the delivery simulation (green & purple indicated in the first column).
The concentration profile across parallel capillaries shows 99% delivery above the MED for capillaries spaced 50 μm apart, representing healthy tissues. Increasing the inter-capillary distance to 100 μm, a level common in tumor tissues[16], reveals therapeutic gaps between the capillaries, with 27% of the tissue receiving an ineffective dose. Target areas located midway between these 100 μm spaced capillaries show ~50% smaller AUCs, as well as a time-lag in reaching peak concentration compared to capillaries with 50 μm spacings.
Figure 3B shows that for a simple branched network micro-tumor model with similar but uneven capillary spacing ~32% of the cross sections remains below MED. A target area close to vessels shows very high drug AUCs (>1000 μg h mL−1), while the center of large loops receives a ~4x lower dose (~250 μg h mL−1).
A more complex branched and looped web of capillaries in a micro-tumor (Figure 3C) shows similar behavior and highlights that vessel geometry greatly influences how drugs are distributed across the tissue. Choosing a target site (purple) located further away from the capillaries (~10 μm) in an acute angle (~30°) shows better drug delivery, despite a ~30 minute time-lag for drugs arriving, compared to a site (green) that is closer to the capillaries (~20 μm), but in an obtuse branching angle (~150°).
This indicates that the average spacing of capillaries is a poor predictor of drug delivery. Instead, the distance-weighted vascular volume surrounding a target tissue is the key indicator of delivery efficiency. Indeed, drug concentrations are particularly high at the branching points of capillaries. To investigate this, we ran simulations over a range of branching angles (Figure S4). This revealed that in the proximity of small branching angles (<30°) concentrations are increased 3-fold compared to similar distances from straight capillaries, and are still 15% larger at 90° branches. This is due to a higher vessel surface to tissue volume ratio close to an angled vessel.
3.4. Trans-endothelial transport and tissue diffusivity
Drug delivery depends strongly on clearance kinetics from blood, tissue diffusivity, and trans-endothelial permeability. The latter two are physical properties of the drug itself. This suggests that a model that can predict the spatiotemporal distribution of a drug after administration can be used to identify drugs with kinetic properties that are optimal for treating a particular tumor. Figure 4 shows the results of a systematic scan of trans-endothelial permeabilities and tissue diffusivities for a fixed clearance rate. The figure demonstrates graphically that, while trans-endothelial permeability is vital in getting drugs into the tumor, tissue diffusivity is the key determinant for efficient delivery into deeply buried tissues.
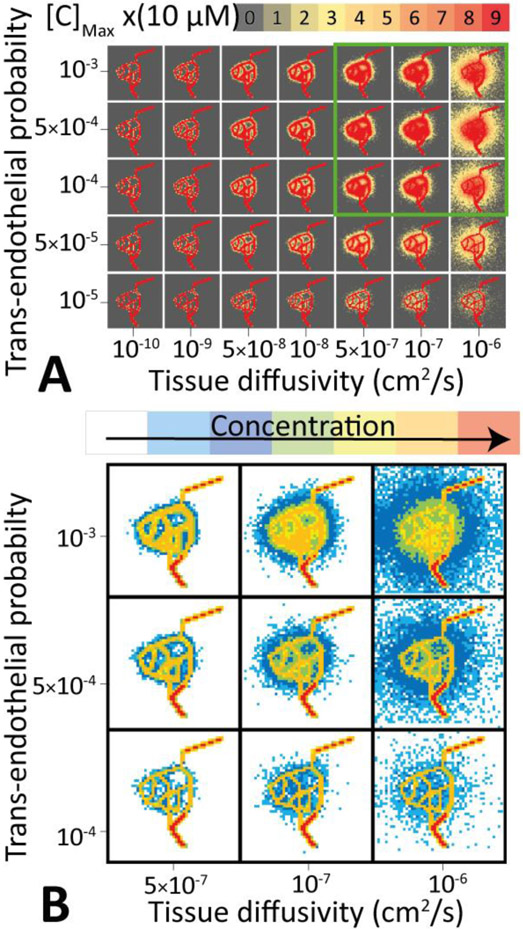
Figure 4 ∣. Three-dimensional final distribution of drugs in tumor tissues as a function of the trans-endothelial transport probability and tissue diffusivity of drugs in the tumor.
A: A heat map plot shows the drug concentration inside the tissue and vasculature for a range of trans-endothelial transport probabilities and tissue diffusivities. The optimal range of parameters is highlighted by a green box. B: Analysis of the drug distribution across the tumor tissue allows precise spatial mapping of the therapeutic efficiency.
Quantitative analysis of the drug distribution in the tissue allows precise spatial mapping of the therapeutic efficiency across the tumor. For this particular vascular structure, a range of good drug properties is highlighted by a green box. Outside this parameter range the structure of the vasculature effectively prevents delivery of drugs at sufficient concentrations to treat the tumor. For a fixed trans-endothelial transport probability the total number of drug molecules released into the tissue is approximately constant. However, the diffusive length into the tissue varies with an expected square-root-dependence of the diffusion coefficient. Thus, tissue diffusivity, rather than trans-endothelial transport propensity is essential for increasing the volume of tissue with effective drug delivery concentrations.
Comparison of the delivery of doxil with doxorubicin reveals that the latter, due to its small size, penetrates much deeper into the tumor tissues. However, we show below that this does not result in a higher overall dose ending up in the tumor (see Section 3.7).
If the trans-endothelial permeability is very high, there will be an extravasation gradient along the vasculature, that results in uneven delivery of drugs into the tumor. Figure S2 shows a drug with exceptionally high . This results in a steep decline in drug delivery along the vasculature, with 5% of drugs delivered to the 18% of tumor tissue. While the area near the injection site is well treated, large sections of the tumor receiving a very low dosage.
3.5. Delivery of doxorubicin through realistic tumor vasculatures
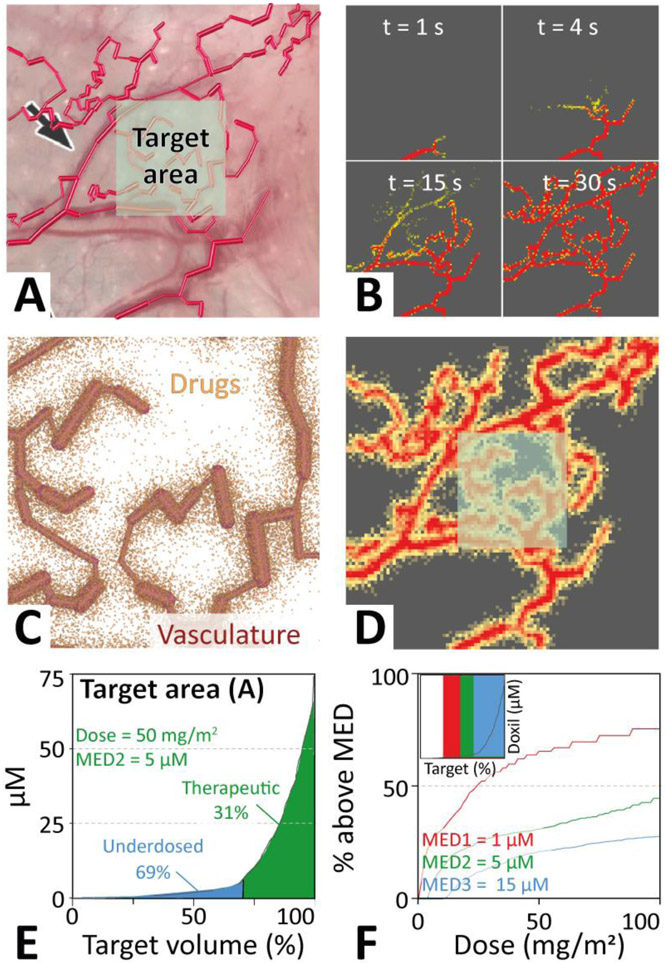
Figure 5 shows a model of a real tumor vasculature that was traced from a mouse ovarian tumor image (see Methods). As no data was available for the whole tumor we model only the subset provided and concentrate our analysis on a target area. Uniform equilibration of doxil across this blood vessel is achieved within 5 minutes, despite the complexity of the branched vascular network (see Supplemental movie). Simulation of spontaneous drug diffusion out of this vasculature shows that the key barrier to treating this tumor is the wide and uneven spacing of the blood vessels. This results in <46% of the tumor tissue being exposed to therapeutic concentrations for drugs with the smallest MED (Figure 5E).
Figure 5 ∣. Application of the three-dimensional molecular mechanics model to a realistic vascular system.
A. The vasculature (structure 4) was modeled by tracing blood vessels from an image of a mouse ovarian tumor[25]. A target area monitored in the analyses is indicated. B. Equilibration of the drug is rapid, with uniform concentration across the vasculature achieved within 5 minutes of simulated time. C. Resting position of doxil liposomes 168 hours after injection of 5x107 liposomes, equivalent to ~15 nanomol of doxil. D. Equivalent doxorubicin concentration in the tissue surrounding the vasculature. E. Quantitative analysis of the therapeutic efficiency as a function of the total volume of the tumor target area (highlighted in panels A and C). F. Scanning the initial dose for a reduced (MED3) or increased (MED1) minimum effective dose (MED) compared to that of doxorubicin (MED2) allows estimating the therapeutic improvement achieved for particular MED (highlighted by arrows).
For doxorubicin regions close to the vasculature are generally well saturated, while many regions buried deeply inside the tumor tissue remain effectively untreated with few or no drugs reaching this far. Increasing the injection dose to treat these deeply buried parts of the tumor tissue may result in toxic side-effects, thus rendering portions of the tumor untreatable for drugs with insufficient tissue diffusivities.
Figure 5C shows the resting position of doxil liposomes 168 hours after injection of 5x107 liposomes, equivalent to ~15 nanomol of doxil. When scaled up to the whole body this corresponds roughly to a typical clinical dose of 50 mg/m2 for an average human. From the positions a heat map can be calculated, showing the local concentrations of doxorubicin across the tumor tissue (Figure 5D).
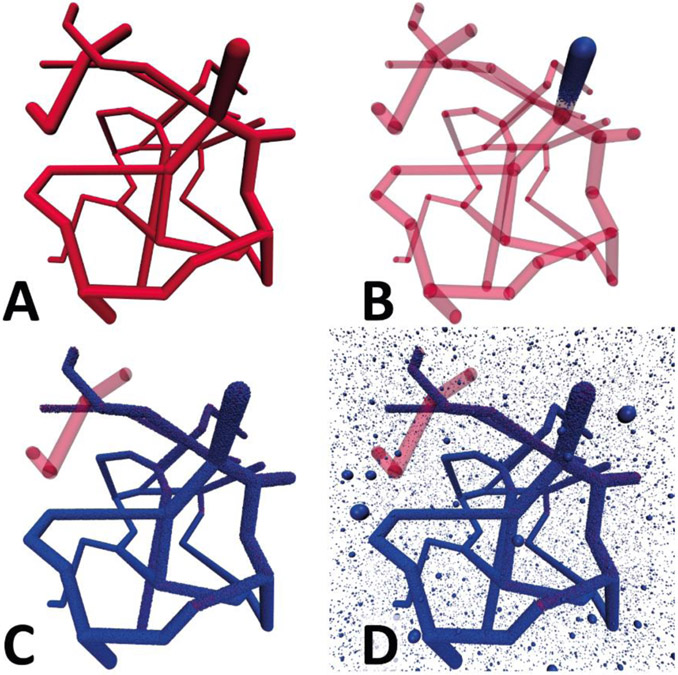
The simple geometrical blood vessel representation of our model allows loading of existing microvascular structures. Figure 6A shows a 3D vasculature acquired from a rat brain named brain99 [50], which was used as a tumor scaffold. This structure was mapped by Secombe and coworkers from scanning electron microscopy data[51] from the superficial rat cortex [48],[49]. The tissue dimensions are 150 x 160 x 140 μm. After injection and equilibration of 106 doxorubicin clusters, the delivery of drugs into the system was simulated for 24 h (see movie in Supplement). Figure 6D shows the final positions of the delivered clusters in the tissue. The relatively high tissue diffusivity of doxorubicin () and small brain tissue volume results in a nearly homogeneous drug distribution across the tissue with an average concentration of ~70 μM. The ~50% thinner blood vessel diameters of the brain99 (average vessel diameter = 5.52 μm) structure resulted in a significantly higher amount of drug delivered (2.12% of the initial dose) compared to the mouse ovarian tumor (1.15% of the initial dose, average vessel diameter = 12.8 μm). This effect is a direct result of a structural model (c.f. Figure 2C).
Figure 6 ∣. Simulation of drug delivery through the three-dimensional rat brain vasculature.
A. Structural model of the brain99 vasculature mapped from rat brain by Secombe and coworkers. B. Drug molecules diffusing near the injection site. C. After drug equilibration drugs are uniformly distributed throughout the connected vasculature. Note, a disconnected segment remains drug-free. D. Final resting position of the drugs at the end of the delivery simulation.
3.6. Dosage optimization for a specific vasculature and MED
Drugs like doxorubicin have a trans-endothelial permeability of at least 10−9 cm/s corresponding to an extravasation probability of ~10−6 when there a collision with blood vessel walls in a 1 second simulation time step. Improving therapeutic efficacy (i.e. increasing the tumor volume above the MED), which is constrained by the tumor vasculature, can be achieved by enhancing the trans-endothelial transport rate and tissue diffusivity. For the target area indicated in Figure 5A and the MED of doxorubicin (derived in Section 2.7) ~44% of the target tissue reached a dose sufficient to kill tumor cells (Figure 5E).
In order to analyse the effect of improved MED on tissue delivery we chose three MEDs (MED 1, 2, & 3), corresponding to 1, 5, and 15 μM, respectively. Figure 5F shows how an decrease (MED1: 1 μM) or increase (MED3: 15 μM) of the MED of doxorubicin (MED2: 5 μM) affects the amount of target area treated therapeutically. The inset of Figure 5F shows rectangles, where vertical area indicates the therapeutic range of the drug, and the width represents the fraction of the tumor with concentrations above the MED. Scanning of the delivered dose from 0 to 100 mg/m2 allows determination of the treatment efficiency (i.e. % of tumor reaching the MED) as a function of MED. Figure 5F shows that for MED1, the tumor volume treated at therapeutic concentrations increases to a maximum of 76%, while it successively decreases to 44% for MED2 and 28% for MED3 at a dose of 50 mg/m2. Thus a five-fold improvement in MED results in an absolute 32% increase in tumor tissue above the MED. This demonstrates that delivery efficiency depends on all inputs to our model (i.e. vascular and tissue fine-structure, trans-endothelial transfer probabilities, tissue diffusivities, clearance rates, and MED).
To evaluate the dependence on the choice of target area we repeated the analysis for a less well vascularized target area (Figure S5). This shows that at a dose of 50 mg/m2 improving the MED of an anticancer therapeutic from 5 μM to 1 μM results in a 2-fold increase in treated target tissue. This corresponding to 43% of the target volume receiving an MED.
3.7. Comparison of free versus liposomal doxorubicin formulations
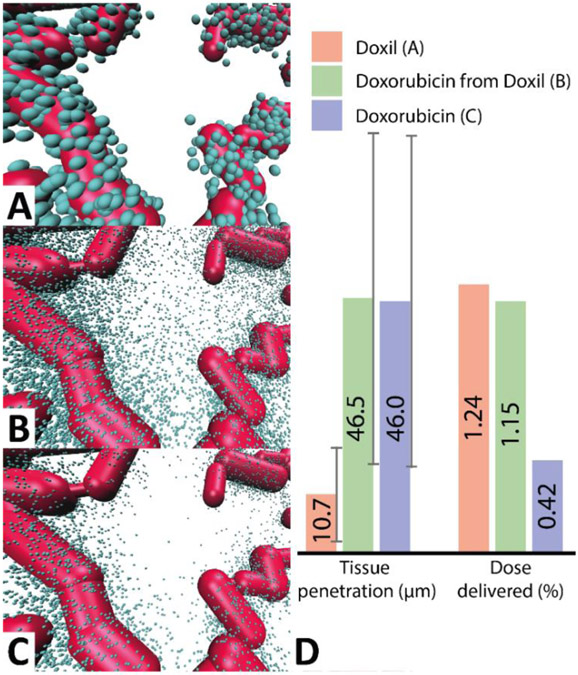
We calculated the tumor delivery efficiency of equivalent molar quantities of doxorubicin for two different formulations: doxil liposomes and free doxorubicin molecules. Figure 6 shows that 168h after administration of 107 doxil liposomes (, , , ), ~1% of the initial dose accumulated in the tumor, resulting in a delivered dose of 0.3 nanomol doxorubicin into the tissue. The average tissue penetration depth, defined as the average distance of a doxil molecule from the surface of the nearest blood vessel, was 10.7±8.7 μm.
To mimic liposomal drug release the final location of each doxil particle with in the tissue was replaced with 48 ‘doxorubicin clusters’, each simulated as a single doxorubicin molecule, but statistically representing 1000 doxorubicin molecules being released as a burst from the doxil liposome. Even though most doxil liposomes remained close to the vasculature the subsequent dispersive release of doxorubicin resulted in only minimal back-transfer of doxorubicin into the bloodstream (less than 3% of the population which reached the tissues). This corresponded to an overall delivered dose of ~30 femtomol doxorubicin to the 1 mm3 tissue (i.e. an average doxorubicin concentration in the tumor of ~30 nM), with average tissue penetration depth of 46.5±29.4 μm (Figure 7BD). Even though both the trans-endothelial permeability and tumor tissue diffusivity are much lower for free doxorubicin than for of doxil (c.f. Table 1), the lower clearance of doxil in combination with the very low back-transfer of released doxorubicin into the vasculature results in a superior overall delivery into the tumor at the same doxorubicin dose.
Figure 7 ∣. Comparison of doxorubicin delivery into tumor using direct injection and doxil after 168 hours.
A. This panel shows the final position of doxil liposomes that spontaneously diffused from the vasculature into the tissue after 168 hours. B. Final position of doxorubicin clusters, each representing 1000 actual doxorubicin molecules, released from the doxil liposomes of panel A. C. Final position of 107 doxorubicin clusters injected into the same vasculature. ~42,200 doxorubicin clusters reached the tumor compared to ~115,000 after simulation B. D. Comparison of the mean tissue penetration (i.e. the average distance of each drug to the nearest vascular segment) and the percentage of initial dose delivered.
In contrast, direct injection of 107 representative doxorubicin clusters (each representing ~143,000 molecules, or ~3 doxil liposomes) in uniform concentration throughout the vasculature resulted in a dose delivered to the 1 mm3 tumor of ~11 femtomol (average tumor concentration 11 nM), and an average tissue penetration of 46.0±29.1 micrometers, with an overwhelming large majority (>2.60 of the 2.62 picomol) of the dose being cleared by blood (Figure 6CD).
This demonstrates that injection of doxil almost triples the dose of doxorubicin delivered into this tumor, while tissue penetration of doxorubicin remain roughly identical. However, clearance of doxorubicin is on the timescale of minutes, while doxil clearance is over the timescale of days resulting in a reduction of toxic side-effects. At present it is unclear how doxorubicin is released from doxil liposomes upon accumulation in tumor tissue. However, the present simulations provide a quantitative estimate of the EPR effect, irrespective of the liposomal release mechanism, which is consistent with pharmacokinetic data obtained from patients in clinical trials[47]. We note that improved tumor accumulation may not necessarily result in improved clinical outcomes [52].
To further explore why the larger doxil has favoured tumor uptake compared to doxorubicin, despite having a lower extravasation rate, we built a simple blood vessel of 10 μm diameter, consisting of a square loop with 100 μm edge length, with one side having uniformly spaced fenestrations of 2 μm, representing the average fenestration size observed in tumor vasculatures[53]. Figure S6 shows that this fenestrated vasculature favors particles that clear more slowly (i.e. doxil), irrespective of the particle diffusivity in blood or tissue.
3.8. The effect of the doxorubicin leakage rate from doxil
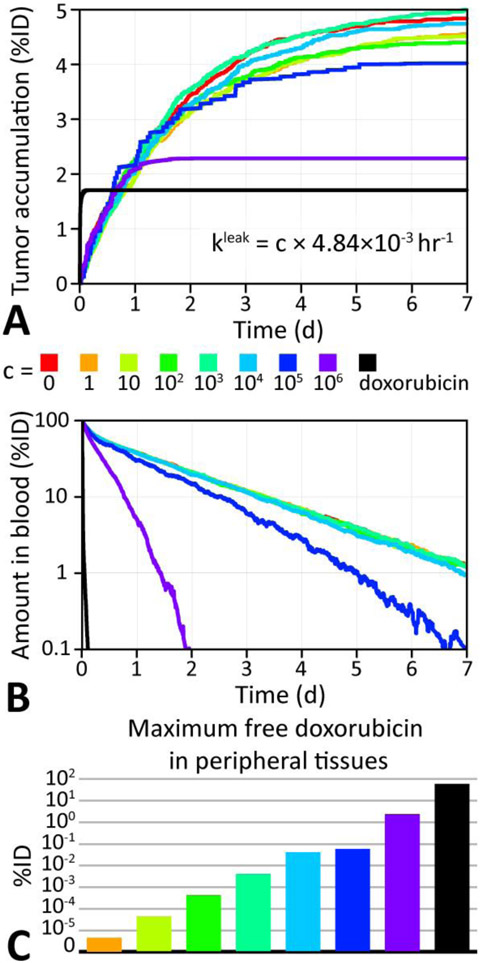
To investigate how the kinetics of doxorubicin leakage from doxil liposomes affects tumor accumulation we ran simulations with different leakage rates. In vitro experiments by Russell et al. found that doxorubicin leakage from doxil liposomes can be described by a first-order rate constants proportional to the liposome surface area to volume ratio[54]. Using their mean observed rate of 2.2 × 10−12 cm s−1 for commercial 100 nm diameter doxil liposomes with an estimated surface area to volume ratio of 16.7 nm, the reference leakage rate was determined to be ~4.8 x 10−3 h−1.
Figure 8 summarizes the effect of leakage rate variation on tumor accumulation as a function of time of 9 simulations of 48,000 doxorubicin molecules loaded into 10,000 doxil liposomes (i.e. 4.8x108 doxorubicin molecules) placed in a cylindrical microvessel of 10 μm diameter and 1 mm length. This shows that the slow leakage rate of doxil results in higher tumor accumulation by protecting the doxorubicin payload from being cleared. A surprising result was that intermediate rates (4.8 h−1), which are 1000 times higher than commercial doxil [54], can offer a marginally increased tumor delivery, but also result in higher doxorubicin loads in peripheral tissues, which may outweigh the benefit of improved tumor delivery (Figure 8C).
Figure 8 ∣. Comparison of doxorubicin delivery for different leakage rates from doxil.
A. Doxorubicin tumor accumulation as a percentage of the initially injected doxorubicin dose (%ID) for various leakage rate from doxil liposomes. The accumulation for free doxorubicin is also shown (black). B. Total %ID of doxorubicin in the blood as a function of time, showing the effect of leakage on clearance. C. Maximum %ID of doxorubicin in the peripheral compartment (see section 2.1) as a function of leakage rate.
4. Discussion
4.1. Drug equilibration in the vasculature
A human red blood cell takes less than one minute to circulate through the body[55]. For many small molecule drugs and most larger delivery vehicles, equilibration inside the vasculature is orders of magnitude faster than extravasation. Doxorubicin and doxil liposomes have clearance half-lives of ~27 minutes and ~30 hrs in blood, respectively, which indicates both drugs are well-equilibrated across the vasculature before significant extravasation takes place[31], [56]. This is especially true for doxil liposomes, which have a ~70-fold lower clearance rate than doxorubicin. This means that the rate-limiting step for doxil delivery is extravasation into the tissues[24], [39]. For compounds such as doxil, which circulate through the body many times without significant clearance or extravasation, blood flow will play only a minor role. This assumption holds as long as the vasculature network structure of the tumor in question supplies all tissues at an equal rate. This is more like to not be the case in tumours due to their broader variation in vessel diameters compared to healthy tissues[57].
On the other hand, chemotherapeutics with high extravasation rates, such as 5-Fluoruracil (5-FU), will exhibit drug tissue concentrations that decrease with distance from the injection site (Figure S2). For these drugs the rate limiting step is how close they can be administered to the tumor itself. Blood flow is likely to reduce the extravasation gradient, as drugs are distributed much more rapidly across the vasculature, and must be included for accurate modeling. These drugs will be largely concentrated in high-velocity segments of the microvasculature, and may not reach effective concentrations in nearby regions of slower blood flow[57]. However, Figure S2 suggests that tuning extravasation rates to maximize drug delivery to the tumor while minimizing extravasation into healthy tissues may be a viable strategy to limit adverse effects of chemotherapies, as long as injection close to a solid tumor is a viable treatment option.
4.2. Importance of the vascular structure
The third column in Figure 3 shows the time-evolution of the drug concentration within two target regions over the course of the delivery simulation. Numerical integration provides a pharmacokinetic area under the curve for each target area in the tissue. These plots show that the time-evolution of the concentration, peak concentration (), area under the curve (AUC), and rates of change vary not just with the distance of the target area relative to the vasculature, but also the vessel’s branching density and angles.
Simulation of 107 doxil liposomes diffusing through a realistic tumor vasculature, traced from a mouse ovarian tumor image, permitted calculation of the percentage of tumor tissues receiving drug doses above the MED of a tumor patch (see Figure 5). This simulation revealed that the 3D structure of the vasculature is important for drug delivery efficiency due to two key factors: first, the diameter of the blood vessel scales inversely with the rate of diffusion of drugs into tumor tissues; and secondly, the weighted distance of tissue areas to surrounding capillaries determines the final drug concentration. Both effects depend directly, significantly, and non-trivially on the actual vascular structure.
When treating a tumor with looped vasculature (see Figure 3BC), the size of the loop impacts the AUC and for the pharmacophores reaching the tumor tissues inside the loop. Therefore, tumors with very sparse vasculature or large loops may be better served by two different drugs in order to average out the advantages of both modes of therapy.
4.3. Doxil versus doxorubicin delivery to tumor tissues via the EPR effect
The initial distributive pharmacokinetic phase of doxorubicin has a half-life of ~5 minutes, whereas the terminal elimination half-life ranges between 20-48 minutes[56]. Conversely, doxil liposomes have a distributive phase of approximately 5 hours and an elimination half-life of between 47 and 59 hours[31]. The pharmacokinetic profile suggests that doxil liposomes are largely confined to the vasculature during the distributive and circulation-elimination stages, whereas free doxorubicin shows a large volume of distribution () with considerably more side-effects due to indiscriminate tissue uptake[24], [39].
Temporal release of drugs from liposomes roughly follows an exponential decay of drug released over time, as measured in vitro [54], [58], [59] and described via mathematical models [60]. The half-life of doxorubicin release from doxil, measured via dialysis, is 118.4±18.8 h [61]. Another study measuring liposomal doxorubicin release kinetics shows a maximal release of 20-30% of the doxorubicin over the course of 2 weeks, indicating liposomal release is much slower than the clearance rate of doxil [54], [62], suggesting that the majority of the doxorubicin will remain inside the doxil liposomes until it is delivered into the tissue. Figure 8 shows, that as suggested by El Kareh et al. and Charrois et al. [61], [63], the doxorubicin leakage rate from doxil directly affects the amount of drug delivered to the tumor. This suggests that it may be advantageous to tune the leakage rate from doxil to optimize doxorubicin delivery.
At present, the mechanistic details of how doxil kills cells via release of its toxic doxorubicin warhead inside the tumor are not fully understood[62]. Assuming a final tumor delivery range of 0.1% to 1.0% of the administered dose, a 1 cm3 tumor, consisting of approximately 109 cells, will take up 1011–1012 doxil liposomes, outnumbering the cells in the tumor by 2–3 orders of magnitude. Comparison of the simulated delivery of doxorubicin versus doxil (see Figure 6) suggests a mechanism where doxil, due to its long half-life, high tumor endothelium permeability (i.e. the EPR effect), and low tissue diffusivity, accumulates just behind the tumor endothelium. Our model shows that extravasated doxil liposomes remain close to the vasculature in tumors. This result is consistent with Yuan et al., who observed liposomes in human colon cancer xenografts accumulating in perivascular clusters that remained stationary for up to one week[36].
Key to the efficiency of the EPR effect in tumors is that once a liposome has extravasated, even though it remains close to the vasculature, the backflow into the vasculature is small. We show here that this is due to the small solid angle of the vasculature compared to the surrounding tumor tissue (Figure S7), even if the drug is spaced close to the blood vessel, and therefore works especially well for fenestrated tumor vasculatures (Figure S6). This is consistent with Ngoune et al. who observed no significant change in the fluorescence signal coming from extravasated liposomes in a tumor when the vasculature was drained of liposomes, demonstrating that the liposomes remain in the tumor[64]. The simulations demonstrate that the reverse flow of drugs from tissue back into the vasculature is almost negligible, due to the small solid angle presented by the vasculature, even for drugs very close to blood vessels. In fact, our simulations show that the vast majority (97.4 %) of doxorubicin released from extravasated doxil liposomes diffuses into the tumor (Figure 6), despite an initial average nearest vessel distance of just 10.7 μm.
Killing of cells buried in the tumor is then achieved by release of doxorubicin, which has a much higher tissue diffusivity than doxil and is able to penetrate deeply into the tumor without getting cleared by MPS, the kidneys, or the liver. While the simulation cannot reveal how the doxorubicin molecules leave the liposomes, the results are consistent with doxil being taken up by the cell (e.g. via endocytosis), and subsequent release of doxorubicin molecules upon cell death as suggested by literature [54], [62].
4.4. Applicability of the model to other compounds and systems
Estimating the transport barrier of drugs across a unit area of tumor vasculature is non-trivial. Extravasation is dominated by the leaky tumor vasculature and hence expected to be similar for most drugs, especially if delivered via a nanoparticle formulation. Varying the trans-endothelial probability between 10−3 s−1 and 10−5 s−1, a range considerably higher than doxil’s rate-derived parameter of ~6 x 10−7 s−1, indicates that a transport probability exceeding 10−4 s−1 is desirable for therapeutic efficiency, particularly for slowly diffusing drugs or drug delivery vehicles (see Figure 4).
In principle, the kinetic parameters (, , , etc.) used in the present model capture the behavior of clinical pharmacokinetic parameters, such as the volume of distribution () and pharmaceutical parameters such as the octanol-water partitioning coefficient (log(P)) for the neutral species of a molecule. However, directly relating and log(P) to the clearance rate, extravasation probability, and tissue diffusivity of a drug is non-trivial. This is because captures a range of physiological effects, such as drug binding, tissue penetration, and clearance. In our model is related to the probability of a molecule exiting the blood vessel, , as well as the clearance rate , but has virtually no relation to , which provides a measure of how rapidly a drug can diffuse through the interstitial space and how deep into body tissues it can penetrate.
Log(P) is used to assess a drug’s lipophilicity, and serves to estimate solubility and how well a molecule will cross lipid bilayers to reach cytosolic targets. In our model, Log(P) is also related to the trans-endothelial transport probability, , especially for vessels such as those found in the brain and central nervous system, which have tight endothelial junctions that preclude para-cellular transport. However, leaky tumor vasculatures permit efficient extravasation of >100 nm diameter liposomes with hydrophilic surfaces, suggesting that Log(P) may not play a major role in tumor delivery.
4.5. Comparison with experimental pharmacokinetics
Drug clearance data is typically available from clinical studies that measure the mean blood concentration of drugs in patients as a function of injection dosage[9], [39]. However, within hours of monitoring plasma concentrations can differ by over one order of magnitude between individual patients[5].
The area under the curve (AUC) is calculated by integrating the blood plasma concentration of a drug over the course of an administered dose. This provides a measure of the exposure to a given drug. In general, the AUC is inversely proportional to the clearance rate and directly proportional to the dose. Variation of AUC and Cmax in plasma are due to differences in clearance and extravasation, which do not correlate well with BSA[10]. In fact, the clinical clearance rate alone does not allow estimating the rate of uptake for tumor and peripheral tissue. Ultimately what is needed are clinical methods that allow independent measurements of patient specific clearance and extravasation rates, which currently cannot be separated by measurements of plasma drug concentrations. This presents a challenge to all models.
In the present study, we fitted the drug concentration in blood to clinical clearance data from patients that were injected with 25 or 50 mg/m2 of doxil[39], respectively, to obtain the clearance rate, in agreement with previous studies[24]. Indeed, the compartment model of Wong et al. used the same averaged clinical plasma drug concentration data to calibrate their model. This allows them to estimate the total amount of drug accumulated in the tumor for a range of putative rate constants for clearance (), extravasation into tumour and peripheral tissues (, ), and drug backflow from tissues into the vasculature (, ) [24]. In our model we use the same approach, which is the only viable option in the absence of quantitative clinical measurements (see Figure 2 and 3).
When all drugs are moved randomly between the vasculature and tissues the time dependent accumulation of drugs in tumor as well as variation due to EPR effect (i.e. varying the ratio of to ) predicted from the four-compartment model can be replicated quantitatively. However, drug extravasation into tumors via a three-dimensional vasculature has a different functional form (Figure 2B). This is because extravasation probabilities depend on the location of the drug in the vessel. This effect is particularly prominent for vessels with larger diameters, as the transport probability for a structural model scales approximately with the surface area of the vessel (i.e. the number of particles near the vessel walls, see Figure S3), while compartment models scale with vessel volume (i.e. the total number of particles).
This highlights the importance of the vascular structure for drug delivery. Pharmacokinetics alone are poor indicators of effective drug doses at target sites and cannot provide information on how evenly drugs are distributed within a tumor.
The spatiotemporal model presented here provides high-resolution time series of localized drug concentrations in tumor vasculatures and tissues (Figure 3). At present no experimental data exists that provides similar spatial and temporal resolutions. What is typically measured clinically is drug AUC, and in plasma, with values for target and off-target tissues usually coming from pre-clinical studies in animal models. While drug plasma concentrations are generally dominated by clearance and extravasation, and are used to fit pharmacokinetic models, whole tumor AUCs, and are available from pre-clinical trials and can be compared to our model. A numerical sum of the concentrations within all tissue mesh prisms at each time -step during the realistic vasculature simulation (see Figure 5D) gives a tumor AUC on the order of ~5000 (mg h / L). This value is reasonably close to an experimental AUC for various PEG-ylated liposomal doxorubicin formulations injected into C-26 tumor bearing mice, which ranged between ~1000-7000 (mg h / L)[65]. The possibility of a tumor-specific determination of a concentration-time profile of drug delivery is significant, as conventional dose determination methods are increasingly recognized as problematic [6]-[11]. These factor determining delivery depend on a patient’s vascular structure (see Figure 2D), as well as on the patient-specific pharmacokinetics of the drug, which are uncorrelated with BSA[5].
4.6. Comparison with in vitro and in vivo studies
Diffusion constants for drugs in a tumor have been measured in pre-clinical studies and range from D = 10−5 – 10−9 cm2/s in rabbits for doxorubicin HCl (MW = 580 Da)[56] to D = 10−9 – 10−13 cm2/s for the 100 nm diameter PEGylated liposomal formulation doxil[41]. Molecular diffusion constants through the interstitial space of living tissues are more difficult to obtain and are likely to vary between different tissue types. For the present study, we estimated tissue diffusivity for doxil liposomes to be 1x10−9 cm2/s, in line with previous studies[35], [36], [66]. Varying the diffusivity by five orders of magnitude (10−10 – 10−5 cm2/s) allowed us to implicitly investigate the impact of drug weight, size, polarity, and interaction with endothelia and tissue environments (see Figure 4). This suggests that anticancer agents with clearance and distribution pharmacokinetics similar to doxorubicin should have a tissue diffusivity of at least 10−8 cm2/s to allow sufficiently deep penetration to treat at least 50% of the tumor tissue (assuming an MED of 1 μM).
Figure S6 shows that the tissue penetration of free doxorubicin and doxil liposomes declines rapidly with distance from a fenestrated vessel. This is consistent in functional form with intra-vital fluorescence microscopy studies of free doxorubicin and doxil liposomes, with most of the drugs remaining within 40 μm from the vessel[67], [68].
4.7. Applications and comparison with previous structural models
Previous efforts at modeling the spatial distribution of drugs have applied continuum finite-element[69][25] and finite-difference methods[18], fluid-mechanics formalisms[70], [71], time evolution of differential equations[35], [63], [72], and other methods[73]. These models generally treat both blood vessels and tissues as homogeneous continua and some have been shown to capture detailed advection and diffusion continuum physics including Michaelis-Menten kinetics within 3D networks of cylindrical blood vessels[74]. While this approach works well for simple systems, solving the boundary conditions of realistic tumor vasculatures, which are typically extremely complex, is computationally prohibitive.
The key goal of the present study was to develop a computational model that can replicate the results of continuum models, but dramatically improve computation efficiency and capture the complexity of the physiological micro-environment of tumors. A particle based approach was chosen, where the vasculature is mapped by an interconnected web of cylinders and spheres, embedded in a tissue grid, allowing extremely rapid assignment of particles to a spatial compartment. The computational efficiency of this model therefore scales linearly with the number of particles only, with the addition of even very complex and large vascular networks entailing negligible additional computational costs.
While we have concentrated here solely on the structure of the vasculature, the heterogeneous nature of tumor tissues can be included into our model and mapped at micrometer resolution. Specifically, simulating tortuous vascular structures, and adding tumor fine-structures, such as poorly vascularized areas, blood lakes, and necrotic tissues, different cell types, endothelial layers, etc. is straight forward and does not change the linear scaling with the number of particles of the model.
4.8. Model utility, current limitations, and future improvements
At present our methodology can be used to screen the effectiveness of any medication, especially where uptake into different tissues and microenvironments varies, using non-clinical μCT tissue scans. In particular, the present model identifies pharmacological drug property combinations (i.e. the drug’s trans-endothelial permeability, tissue diffusion coefficient, and vascular clearance) that provide optimal distribution in a tumor with a particular vascular structure. This has a broad range of potential applications including such as selecting drugs that have tissue penetration properties that are more suited to a particular type of tumor. Future improvements in clinical CT and MRI technology will ultimately allow prediction of the optimal drug dosage regimen for a particular patient and target tissue using structural imaging and modeling of drug delivery.
Quantitative validation of this model requires precise experimental knowledge of a drug or delivery system’s vascular and tissue diffusivities, trans-endothelial permeabilities (into healthy and tumor tissues), and pharmacokinetic clearance rates, as well as 3D structural data at micrometer resolution, which are extremely challenging to obtain at present. While conventional clinical CT scanners have a typical resolution of 240 μm, too coarse to capture the fine structure of 10-100 μm capillaries inside a tumor, advanced clinical scanners exist which provide resolutions of down to 30 μm [75], [76]. For research purposes μCT machines are available with sub-micrometer resolutions, allowing full visualization of even the smallest capillaries. However, experimentally tracking drugs at this resolution in 3D tissues remains challenging.
Future improvements in algorithm parallelization and computational hardware performance suggest that the ability to simulate the actual number of particles is well within reach for a tumor of this size. In addition, mechanistic and physiological details such as increased extravasation within predefined leaky endothelial regions or vessel sub-sections can be implemented without loss of efficiency. Furthermore, anisotropic diffusivities in different vessel segments, drag forces, and other biases can be straight forwardly incorporated.
5. Conclusions
Chemotherapy outcomes depend critically upon the ability of an anticancer drug to penetrate tumor tissues and cancerous cells at therapeutic concentrations. Systematic optimization of delivery necessitates the development of a more detailed understanding of how molecules enter tissues. The present study shows that there is scope for improvement in dosing drugs for optimal therapeutic effect. The present study shows that: (i.) the 3D structure of the vasculature is an important factor in determining the distribution of a given drug in the tumor tissue it supplies and that correlation with average capillary spacings is poor, (ii.) choosing drugs with optimal extravasation probability and tissue diffusivity can improve overall delivery for a particular vascular structure and MED, and (iii.) the EPR effect makes the liposomal nanoparticle formulation doxil ~3x more effective at delivering doxorubicin into the tumor than free doxorubicin itself, even though doxil nanoparticles have both a lower trans-endothelial permeability and a lower tissue diffusivity.
We note that compartment models cannot capture the fact that the vasculature structure is a 3D object, and we show here that the time-dependent transport kinetics from a 3D structure cannot be captured accurately with a one-dimensional rate constant, even if a scale factor is introduced. While pure pharmacokinetic models are generally based on fits, which offer valuable insights into correlations between key clinical or physical variables, they provide little information into the fundamental mechanistic, topological, or physical effects driving drug delivery. The latter can only be obtained with a realistic spatial model that accurately captures the key natural phenomena, which we show here is important for optimizing dosage.
Supplementary Material
Acknowledgements
This project has been supported by a pilot grant from the Johns Hopkins University Institute for NanoBioTechnology to M.B.U. (CCNE Pilot Project Grant #90058409). We thank the MARCC supercomputer facility at Johns Hopkins University for computational resources.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflicts of Interest: All authors declare that they have no conflicts of interest.
7. References
- [1].Prokop A and Davidson JM, “Nanovehicular Intracellular Delivery Systems,” J. Pharm. Sci, vol. 97, no. 9, pp. 3518–3590, Sep. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Chatterjee K, Zhang J, Honbo N, and Karliner JS, “Doxorubicin Cardiomyopathy,” Cardiology, vol. 115, no. 2, pp. 155–162, Jan. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Perel P et al. , “Comparison of treatment effects between animal experiments and clinical trials: systematic review,” BMJ, vol. 334, no. 7586, p. 197, Jan. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gao B, Klumpen H-J, and Gurney H, “Dose calculation of anticancer drugs,” Expert Opin. Drug Metab. Toxicol, vol. 4, no. 10, pp. 1307–1319, Oct. 2008. [DOI] [PubMed] [Google Scholar]
- [5].Gurney H, “How to calculate the dose of chemotherapy,” Br. J. Cancer, vol. 86, no. 8, pp. 1297–1302, Apr. 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Beumer JH, Chu E, and Salamone SJ, “Body-Surface Area–Based Chemotherapy Dosing: Appropriate in the 21st Century?,” J. Clin. Oncol, vol. 30, no. 31, pp. 3896–3897, Nov. 2012. [DOI] [PubMed] [Google Scholar]
- [7].Redlarski G, Palkowski A, and Krawczuk M, “Body surface area formulae: an alarming ambiguity,” Sci. Rep, vol. 6, p. srep27966, Jun. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Wallington M et al. , “30-day mortality after systemic anticancer treatment for breast and lung cancer in England: a population-based, observational study,” Lancet Oncol., vol. 17, no. 9, pp. 1203–1216, Sep. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Verbraecken J, Van de Heyning P, De Backer W, and Van Gaal L, “Body surface area in normal-weight, overweight, and obese adults. A comparison study,” Metabolism, vol. 55, no. 4, pp. 515–524, Apr. 2006. [DOI] [PubMed] [Google Scholar]
- [10].Felici A, Verweij J, and Sparreboom A, “Dosing strategies for anticancer drugs: the good, the bad and body-surface area,” Eur. J. Cancer, vol. 38, no. 13, pp. 1677–1684, Sep. 2002. [DOI] [PubMed] [Google Scholar]
- [11].Levêque D, “Body Weight and Body Surface Area in Chemotherapy,” in Handbook of Anthropometry, Springer, New York, NY, 2012, pp. 1735–1743. [Google Scholar]
- [12].Chow DC, Wenning LA, Miller WM, and Papoutsakis ET, “Modeling pO(2) distributions in the bone marrow hematopoietic compartment. I. Krogh’s model.,” Biophys. J, vol. 81, no. 2, pp. 675–684, Aug. 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Folkman J, “Role of angiogenesis in tumor growth and metastasis,” Semin. Oncol, vol. 29, no. 6, Supplement 16, pp. 15–18, Dec. 2002. [DOI] [PubMed] [Google Scholar]
- [14].Folkins C and Kerbel RS, “Tumor Angiogenesis and the Cancer Stem Cell Model,” in Angiogenesis, Figg WD and Folkman J, Eds. Springer US, 2008, pp. 249–258. [Google Scholar]
- [15].Konerding MA et al. , “Evidence for characteristic vascular patterns in solid tumours: quantitative studies using corrosion casts,” Br. J. Cancer, vol. 80, no. 5, pp. 724–732, May 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Folarin AA, Konerding MA, Timonen J, Nagl S, and Pedley RB, “Three-dimensional analysis of tumour vascular corrosion casts using stereoimaging and micro-computed tomography,” Microvasc. Res, vol. 80, no. 1, pp. 89–98, Jul. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Bellone M, Calcinotto A, Filipazzi P, Milito AD, Fais S, and Rivoltini L, “The acidity of the tumor microenvironment is a mechanism of immune escape that can be overcome by proton pump inhibitors,” OncoImmunology, vol. 2, no. 1, p. e22058, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Baish JW et al. , “Scaling rules for diffusive drug delivery in tumor and normal tissues,” Proc. Natl. Acad. Sci, vol. 108, no. 5, pp. 1799–1803, Feb. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Wojtkowiak JW, Verduzco D, Schramm KJ, and Gillies RJ, “Drug Resistance and Cellular Adaptation to Tumor Acidic pH Microenvironment,” Mol. Pharm, vol. 8, no. 6, pp. 2032–2038, Dec. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Fang J, Nakamura H, and Maeda H, “The EPR effect: Unique features of tumor blood vessels for drug delivery, factors involved, and limitations and augmentation of the effect,” Adv. Drug Deliv. Rev, vol. 63, no. 3, pp. 136–151, Mar. 2011. [DOI] [PubMed] [Google Scholar]
- [21].Heneweer C, Holland JP, Divilov V, Carlin S, and Lewis JS, “Magnitude of Enhanced Permeability and Retention Effect in Tumors with Different Phenotypes: 89Zr-Albumin as a Model System,” J. Nucl. Med, vol. 52, no. 4, pp. 625–633, Apr. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Abraham SA, Waterhouse DN, Mayer LD, Cullis PR, Madden TD, and Bally MB, “The Liposomal Formulation of Doxorubicin,” in Methods in Enzymology, vol. 391, Supplement C vols., Academic Press, 2005, pp. 71–97. [DOI] [PubMed] [Google Scholar]
- [23].Freyer G et al. , “Population pharmacokinetics of doxorubicin, etoposide and ifosfamide in small cell lung cancer patients: results of a multicentre study,” Br. J. Clin. Pharmacol, vol. 50, no. 4, pp. 315–324, Oct. 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Wong AD, Ye M, Ulmschneider MB, and Searson PC, “Quantitative Analysis of the Enhanced Permeation and Retention (EPR) Effect,” PLOS ONE, vol. 10, no. 5, p. e0123461, May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Nagy JA and Dvorak HF, “Heterogeneity of the tumor vasculature: the need for new tumor blood vessel type-specific targets,” Clin. Exp. Metastasis, vol. 29, no. 7, pp. 657–662, Oct. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Carmeliet P, “VEGF as a Key Mediator of Angiogenesis in Cancer,” Oncology, vol. 69, no. Suppl. 3, pp. 4–10, 2005. [DOI] [PubMed] [Google Scholar]
- [27].Bullitt E, Wolthusen PA, Brubaker L, Lin W, Zeng D, and Dyke TV, “Malignancy-Associated Vessel Tortuosity: A Computer-Assisted, MR Angiographic Study of Choroid Plexus Carcinoma in Genetically Engineered Mice,” Am. J. Neuroradiol, vol. 27, no. 3, pp. 612–619, Mar. 2006. [PMC free article] [PubMed] [Google Scholar]
- [28].Shelton SE et al. , “Quantification of Microvascular Tortuosity during Tumor Evolution Using Acoustic Angiography,” Ultrasound Med. Biol, vol. 41, no. 7, pp. 1896–1904, Jul. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Nagy JA, Chang S-H, Dvorak AM, and Dvorak HF, “Why are tumour blood vessels abnormal and why is it important to know?,” Br. J. Cancer, vol. 100, no. 6, pp. 865–869, Feb. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Wang J and Hou T, “Application of Molecular Dynamics Simulations in Molecular Property Prediction II: Diffusion Coefficient,” J. Comput. Chem, vol. 32, no. 16, pp. 3505–3519, Dec. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].“DOXIL - Prescribing Information - fda.gov [Patient Package Insert].” [Online]. Available: https://www.accessdata.fda.gov/drugsatfda_docs/label/2007/050718s029lbl.pdf. [Accessed: 12-May-2018].
- [32].Weinberg BD, Patel RB, Exner AA, Saidel GM, and Gao J, “Modeling Doxorubicin Transport to Improve Intratumoral Drug Delivery to RF Ablated Tumors,” J. Control. Release Off. J. Control. Release Soc, vol. 124, no. 1–2, pp. 11–19, Dec. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Markovic S, Kumar R, Belz J, Sridhar S, and Niedre M, “Fluorescence quantification of nanoparticle diffusion from smart brachytherapy spacers in vivo,” in 2014 40th Annual Northeast Bioengineering Conference (NEBEC), 2014, pp. 1–2. [Google Scholar]
- [34].Lai SK et al. , “Rapid transport of large polymeric nanoparticles in fresh undiluted human mucus,” Proc. Natl. Acad. Sci, vol. 104, no. 5, pp. 1482–1487, Jan. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Zhan W and Xu XY, “A Mathematical Model for Thermosensitive Liposomal Delivery of Doxorubicin to Solid Tumour,” J. Drug Deliv, vol. 2013, p. e172529, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Yuan F, Leunig M, Huang SK, Berk DA, Papahadjopoulos D, and Jain RK, “Mirovascular Permeability and Interstitial Penetration of Sterically Stabilized (Stealth) Liposomes in a Human Tumor Xenograft,” Cancer Res, vol. 54, no. 13, pp. 3352–3356, Jul. 1994. [PubMed] [Google Scholar]
- [37].Petros RA and DeSimone JM, “Strategies in the design of nanoparticles for therapeutic applications,” Nat. Rev. Drug Discov, vol. 9, no. 8, pp. 615–627, Aug. 2010. [DOI] [PubMed] [Google Scholar]
- [38].Kobayashi H, Watanabe R, and Choyke PL, “Improving Conventional Enhanced Permeability and Retention (EPR) Effects; What Is the Appropriate Target?,” Theranostics, vol. 4, no. 1, pp. 81–89, Dec. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Gabizon A and Papahadjopoulos D, “Liposome formulations with prolonged circulation time in blood and enhanced uptake by tumors.,” Proc. Natl. Acad. Sci. U. S. A, vol. 85, no. 18, pp. 6949–6953, Sep. 1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Kumar R et al. , “In Vivo Biodistribution and Clearance Studies Using Multimodal Organically Modified Silica Nanoparticles,” ACS Nano, vol. 4, no. 2, pp. 699–708, Feb. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Toley BJ, Lovatt ZGT, Harrington JL, and Forbes NS, “Microfluidic technique to measure intratumoral transport and calculate drug efficacy shows that binding is essential for doxorubicin and release hampers Doxil,” Integr. Biol, vol. 5, no. 9, pp. 1184–1196, Aug. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Barapatre N et al. , “Quantitative detection of drug dose and spatial distribution in the lung revealed by Cryoslicing Imaging,” J. Pharm. Biomed. Anal, vol. 102, pp. 129–136, Jan. 2015. [DOI] [PubMed] [Google Scholar]
- [43].Dicheva BM, Seynhaeve ALB, Soulie T, Eggermont AMM, ten Hagen TLM, and Koning GA, “Pharmacokinetics, Tissue Distribution and Therapeutic Effect of Cationic Thermosensitive Liposomal Doxorubicin Upon Mild Hyperthermia,” Pharm. Res, vol. 33, no. 3, pp. 627–638, Mar. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Yang W et al. , “Genomics of Drug Sensitivity in Cancer (GDSC): a resource for therapeutic biomarker discovery in cancer cells,” Nucleic Acids Res, vol. 41, no. Database issue, pp. D955–961, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Heggie GD, Sommadossi J-P, Cross DS, Huster WJ, and Diasio RB, “Clinical Pharmacokinetics of 5-Fluorouracil and Its Metabolites in Plasma, Urine, and Bile,” Cancer Res, vol. 47, no. 8, pp. 2203–2206, Apr. 1987. [PubMed] [Google Scholar]
- [46].Tongwen X and Binglin H, Mechanism of sustained drug release in diffusion-controlled polymer matrix-application of percolation theory. 1997. [Google Scholar]
- [47].Gabizon A, Shmeeda H, and Barenholz Y, “Pharmacokinetics of Pegylated Liposomal Doxorubicin,” Clin. Pharmacokinet, vol. 42, no. 5, pp. 419–436, Apr. 2003. [DOI] [PubMed] [Google Scholar]
- [48].Lankelma J, Fernández Luque R, Dekker H, Schinkel W, and Pinedo HM, “A Mathematical Model of Drug Transport in Human Breast Cancer,” Microvasc. Res, vol. 59, no. 1, pp. 149–161, Jan. 2000. [DOI] [PubMed] [Google Scholar]
- [49].Qian F, Stowe N, Liu EH, Saidel GM, and Gao J, “Quantification of in vivo doxorubicin transport from PLGA millirods in thermoablated rat livers,” J. Controlled Release, vol. 91, no. 1, pp. 157–166, Aug. 2003. [DOI] [PubMed] [Google Scholar]
- [50].Secomb TW, Hsu R, Braun RD, Ross JR, Gross JF, and Dewhirst MW, “Theoretical Simulation of Oxygen Transport to Tumors by Three-Dimensional Networks of Microvessels,” in Oxygen Transport to Tissue XX, Springer, Boston, MA, 1998, pp. 629–634. [DOI] [PubMed] [Google Scholar]
- [51].Motti EDF, Imhof H-G, and Yaşargil MG “The terminal vascular bed in the superficial cortex of the rat,” J. Neurosurg, vol. 65, no. 6, pp. 834–846, Dec. 1986. [DOI] [PubMed] [Google Scholar]
- [52].Shi J, Kantoff PW, Wooster R, and Farokhzad OC, “Cancer nanomedicine: progress, challenges and opportunities,” Nat. Rev. Cancer, vol. 17, no. 1, pp. 20–37, Jan. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Hashizume H et al. , “Openings between Defective Endothelial Cells Explain Tumor Vessel Leakiness,” Am. J. Pathol, vol. 156, no. 4, pp. 1363–1380, Apr. 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Russell LM, Hultz M, and Searson PC, “Leakage kinetics of the liposomal chemotherapeutic agent Doxil: The role of dissolution, protonation, and passive transport, and implications for mechanism of action,” J. Controlled Release, vol. 269, pp. 171–176, Jan. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Sheilagh B, “Chapter 4 - Red Blood Cell Antigens and Human Blood Groups,” in Handbook of Pediatric Transfusion Medicine, Hillyer CD, Strauss RG, and Luban NLC, Eds. San Diego: Academic Press, 2004, pp. 45–61. [Google Scholar]
- [56].“Doxorubicin Hydrochloride for Injection, USP - fda.gov [Patient Package Insert].” [Online]. Available: https://www.accessdata.fda.gov/drugsatfda_docs/label/2003/050467s068lbl.pdf. [Accessed: 12-May-2018].
- [57].Dewhirst MW and Secomb TW, “Transport of drugs from blood vessels to tumour tissue,” Nat. Rev. Cancer, vol. 17, no. 12, pp. 738–750, Dec. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Chouhan R and Bajpai A, “Real time in vitro studies of doxorubicin release from PHEMA nanoparticles,” J. Nanobiotechnology, vol. 7, p. 5, Oct. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Dadsetan M, Taylor KE, Yong C, Bajzer Ž, Lu L, and Yaszemski MJ, “Controlled release of doxorubicin from pH-responsive microgels,” Acta Biomater, vol. 9, no. 3, pp. 5438–5446, Mar. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Modi S and Anderson BD, “Determination of Drug Release Kinetics from Nanoparticles: Overcoming Pitfalls of the Dynamic Dialysis Method,” Mol. Pharm, vol. 10, no. 8, pp. 3076–3089, Aug. 2013. [DOI] [PubMed] [Google Scholar]
- [61].Charrois GJR and Allen TM, “Drug release rate influences the pharmacokinetics, biodistribution, therapeutic activity, and toxicity of pegylated liposomal doxorubicin formulations in murine breast cancer,” Biochim. Biophys. Acta BBA - Biomembr, vol. 1663, no. 1–2, pp. 167–177, May 2004. [DOI] [PubMed] [Google Scholar]
- [62].Seynhaeve ALB, Dicheva BM, Hoving S, Koning GA, and ten Hagen TLM, “Intact Doxil is taken up intracellularly and released doxorubicin sequesters in the lysosome: Evaluated by in vitro/in vivo live cell imaging,” J. Controlled Release, vol. 172, no. 1, pp. 330–340, Nov. 2013. [DOI] [PubMed] [Google Scholar]
- [63].El-Kareh AW and Secomb TW, “A Mathematical Model for Comparison of Bolus Injection, Continuous Infusion, and Liposomal Delivery of Doxorubicin to Tumor Cells,” Neoplasia N. Y. N, vol. 2, no. 4, pp. 325–338, Jul. 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Ngoune R, Peters A, von Elverfeldt D, Winkler K, and Pütz G, “Accumulating nanoparticles by EPR: A route of no return,” J. Controlled Release, vol. 238, pp. 58–70, Sep. 2016. [DOI] [PubMed] [Google Scholar]
- [65].Hong R-L et al. , “Direct Comparison of Liposomal Doxorubicin with or without Polyethylene Glycol Coating in C-26 Tumor-bearing Mice: Is Surface Coating with Polyethylene Glycol Beneficial?,” Clin. Cancer Res, vol. 5, no. 11, pp. 3645–3652, Nov. 1999. [PubMed] [Google Scholar]
- [66].Eikenberry S, “A tumor cord model for Doxorubicin delivery and dose optimization in solid tumors,” Theor. Biol. Med. Model, vol. 6, p. 16, Aug. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Li L et al. , “Triggered content release from optimized stealth thermosensitive liposomes using mild hyperthermia,” J. Controlled Release, vol. 143, no. 2, pp. 274–279, Apr. 2010. [DOI] [PubMed] [Google Scholar]
- [68].Manzoor AA et al. , “Overcoming Limitations in Nanoparticle Drug Delivery: Triggered, Intravascular Release to Improve Drug Penetration into Tumors,” Cancer Res, Sep. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Rim JE, Pinsky PM, and van Osdol WW, “Finite Element Modeling of Coupled Diffusion with Partitioning in Transdermal Drug Delivery,” Ann. Biomed. Eng, vol. 33, no. 10, pp. 1422–1438, Oct. 2005. [DOI] [PubMed] [Google Scholar]
- [70].Hosie EMPK, Gilbert JA, Kerr D, Brown CB, “Fluid Dynamics in Man of an Intraperitoneal Drug Delivery Solution: 4% Icodextrin,” Drug Deliv., vol. 8, no. 1, pp. 9–12, Jan. 2001. [DOI] [PubMed] [Google Scholar]
- [71].Chen XB, Lee HP, Chong VFH, and Wang DY, “A Computational Fluid Dynamics Model for Drug Delivery in a Nasal Cavity with Inferior Turbinate Hypertrophy,” J. Aerosol Med. Pulm. Drug Deliv, vol. 23, no. 5, pp. 329–338, Aug. 2010. [DOI] [PubMed] [Google Scholar]
- [72].Jaramillo-Botero A, Abrol R, van Duin A, and Goddard W, “Multiscale-Multiparadigm Modeling and Simulation of Nanometer Scale Systems and Processes for Nanomedical Applications,” in Nanomedicine, 0 vols., Pan Stanford Publishing, 2009, pp. 245–300. [Google Scholar]
- [73].Liu Y, Shah S, and Tan J, “Computational Modeling of Nanoparticle Targeted Drug Delivery,” Rev. Nanosci. Nanotechnol, vol. 1, no. 1, pp. 66–83, Mar. 2012. [Google Scholar]
- [74].Secomb TW, Hsu R, Park EYH, and Dewhirst MW, “Green’s Function Methods for Analysis of Oxygen Delivery to Tissue by Microvascular Networks,” Ann. Biomed. Eng, vol. 32, no. 11, pp. 1519–1529, Nov. 2004. [DOI] [PubMed] [Google Scholar]
- [75].Zagorchev L et al. , “Micro computed tomography for vascular exploration,” J. Angiogenesis Res, vol. 2, p. 7, Mar. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Starosolski Z et al. , “Ultra High-Resolution In vivo Computed Tomography Imaging of Mouse Cerebrovasculature Using a Long Circulating Blood Pool Contrast Agent,” Sci. Rep, vol. 5, May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.