The effect of voxelization in Monte Carlo simulation to validate Bragg peak characteristics for a pencil proton beam

Abstract

Background

The purpose of this research was to show how the Bragg peak (BP) characteristics were affected by changing the voxel size in longitudinal and transverse directions in Monte Carlo (MC) simulations by using Geant4 and to calculate BP characteristics accurately by considering the voxel size effect for 68 MeV and 235.81 MeV.

Materials and methods

Different interpolation techniques were applied to simulation data to find the closest results to the experimental data.

Results

When the x-size of the voxel was increased 2 times at low energy, the maximum dose increase in the entrance and plateau regions were 17.8% and 17%, respectively, while BP curve shifted to the shallower region, resulting in a 0.5 mm reduction in the curable tumor width (W_80pd). At high energy, the maximum dose increase at the entrance and plateau regions were 0.4% and 0.6%, respectively, while it was observed that W_80pd did not change. When the y-z sizes of the voxel were increased 2 times at low energy, the maximum dose reduction at the entrance and plateau regions was 3.4%, but no change was observed in W_80pd. At high energy, when the y-z sizes of the voxel were increased 2.2 times, the maximum dose reduction at the entrance and plateau regions were 8.9% and 9.1%, respectively, while W_80pd increased by 0.5 mm. When linear, cubic spline, and Akima interpolations were applied to the simulation data, it was found that the results closest to the experimental data were obtained for Akima interpolations for both energies.

Conclusion

it has been shown that the voxel size effect for the longitudinal direction was more effective at low energy than at high energy. However, the voxel size effect for the transverse direction was more effective for high energy.

Introduction

During the past decade advancements in proton therapy have grown considerably, especially for cancer treatment [1, 2]. The shape of the proton depth dose distribution, with its low entrance dose and well-defined range ending with the high dose Bragg peak (BP), is without doubt critical to these advancements [3]. Protons can deliver a high dose to the target without inflicting any surrounding normal tissue [4], so this ability allows proton therapy to spare healthy tissue and have a conformal dose distribution [5–7]. Use of protons in radiation therapy was first treated in 1954 at the Lawrence Berkeley Laboratory [8]. Proton therapy centres are now appearing more widespread across the world and treatment modality is becoming very well known.

Different proton therapy centres substantially vary from one to another, which affects the beam line design and the primary part of the depth dose characteristics of the proton beam [9]. Determination of characteristics of all radiation beams is vital. In proton therapy, the quality of a proton beam is mostly expressed in terms of its physical properties; the deposition of the major proportion of the dose within a few millimetres in a well-defined depth (BP), followed by a sharp dose fall-off and a subsequent negligible dose deposition thereafter, but one of the biggest factors affecting BP dosimetric characteristics is a geometrical collection efficiency [10], which can be defined as the partial volume effect associated with the process of voxelization [11]. BP is defined by its characteristics. Percentage dose ranges, such as proximal depth of the 50% dose (R_50p) and distal depth of the 50% dose (R_50d), proximal depth of the 80% dose (R_80p), distal depth of the 80% dose (R_80d), distal depth of the 90% dose (R_90d), depth of the peak (R_peak), distal depth of the 20% dose (R_20d), a width of 80–20% distal fall-off (W_80–20dd), full with at half maximum (FWHM) of BP, width between proximal and distal depth of the 80% dose (W_80pd) and peak to entrance dose ratio (a division of maximum dose of the BP by entrance dose), are parameters for depth dose characteristics [2].

Monte Carlo (MC) dose calculation is considered to be a gold standard for simulating doses delivered in radiation therapy. MC simulations have increasingly been used for dose calculations in proton therapy due to inherent accuracy. Several MC transport codes have been published for proton radiotherapy [12, 13]. MC simulations, based on the particles using theoretical models and experimental data section, take into account the physics of particle interaction particle by particle. In photon therapy, the difference between dose distributions obtained with pencil beam (PB) algorithms and MC generated dose distributions can be significant for certain treatment areas and beam configurations. This may be even more significant in proton therapy because of steep dose gradients, which are often near critical structures. MC simulation has a much larger clinical impact in proton therapy than in photon therapy [14]. The main reason for the increased interest in proton therapy is the physical characteristics of the depth dose curve with a dose peak (BP) at a well-defined depth in tissue.

Different MC codes, such as GEANT4 [15] (Geometry and Tracking), FLUCA [16], PENELOPE [17], and MCNPX [18] have been used by several authors for proton therapy. GEANT4 is a MC particle physics simulation toolkit, implemented in object-oriented C++. It is very important to find an optimum value of ionization potential energy and to define voxel dimensions for Geant4 MC toolkit at energies of interest in particles. The proton range of energetic ions depends on the mean ionization potential (I-value) of the stopping medium which has a strong influence on the BP spatial position [19]. Uncertainties in the mean ionization potential energy are presumably significant. International Committee for Radiological Units (ICRU) Report 49 [20] recommends mean ionization potential energy, or I-value of water as 75 ± 3 eV. Another study has reported 80 ± 2 eV [21]. The stopping power tables by Janni [22] are based on a value of 81.8 eV while a more recent experimental study resulted in a value of 78.4 ± 1.0 eV [23]. Andreo [24] has demonstrated that a variation of I-values between 67.2 eV and 80 eV can have a substantial impact on the proton beam range in water. The value I = 75 ± 3 eV for water from ICRU Reports 37 [25] and 49 [20] has been accepted as the norm for many years. Then, a lower value I = 67.2 eV has been assumed in ICRU Report 73 [26] for water. Increased I values for water have also been suggested by Kramer (I = 77 eV) [27], Faddegon (I = 80–83 eV) [28], Dingfelder [29] (I = 81.8 eV), and Emfietzoglou et al. [30] (I = 80–85 eV) for different proton energies. Researchers have also suggested different I of water in literature [24, 31, 32]. The I value of water is a subject of growing interest and values between 67.2 eV and 85 eV were reported [21–24, 33, 34]. It was concluded that the range uncertainty due to uncertainties in I values is in the order of ± 1.5–2.0% [24].

The other important parameter is voxel size which, if not taken into consideration, can give erroneous results, like statistical errors, as well as prolong the computational time for commissioning. The effect of voxel size was studied for photon therapy [35–37] but to our knowledge, this effect has not been extensively studied for proton therapy. It has been reported in the literature that the voxel size effect on dose distribution in photon therapy varies between 12% and 17% [36]. The voxel size effect has been utilized to establish a relationship with both efficiency [10] and step size [38] by using different ion chambers. When calculating dose distribution, the choice of voxel size is a compromise between computational time and accuracy. Larger voxels affect the computational time and smaller voxels, should be the same size as that of the CT data about 1mm, affect the accuracy of depth dose calculation due to reduced spatial resolution [35]. Hence, simulations used for evaluation should be performed with excellent resolution to avoid any bias. While the voxel size was chosen as 0.5 × 1 × 1 mm³, 1 × 1 × 1 mm³ in some studies [39, 40], an effective radius of 4.1 cm and 6. 0 cm was used in another study [10] for energies between 90 and 226 MeV proton therapy. In the literature, possible lengths in the transverse direction of the voxel dimension for an ideal proton PB are defined [41]. The transverse length can vary between 0.85 cm and 1.35 cm at low proton energies such as 68 MeV, and between 0.75 cm and 11.47 cm at high proton energies such as 235.38 MeV [41].

The aim of this study was to investigate how BP characteristics were affected by changing the voxel size in the longitudinal and transverse directions and to calculate BP characteristics accurately by considering the voxel size effect for 68 MeV and 235.81 MeV. By applying different interpolation techniques to the simulation results, it was also aimed to investigate which of these techniques would be the most suitable for simulation data to evaluate BP characteristics.

Materials and methods

Experimental set-up

The experimental data, which was supplied by the manufacturer of VARIAN for ProBeam system (Munich, Germany), was used to choose a suitable I value of water for the proton energies used in MC simulations. Depth-dose measurements were taken for 68 MeV and 235.81 MeV proton energies at the surface of the water tank by the manufacturer. The measurement was performed with PTW 34070 Bragg Peak Chamber. Measured depth–doses were normalized to the maximum doses.

MC simulation geometry

In the following study, MC simulations were performed using Geant4 v10.01.p02 [42]. G4Em-StandardPhysics_option3 standard electromagnetic package [15] was used. In this study, energy type was selected as mono [43, 44] and 68 MeV and 235.81 MeV energies were used to model a proton PB to evaluate the impact of voxelization on the characteristics of BP curve. Initial beam energy spread σ_E was accepted as zero [45]. Nozzle wasn’t modelled, proton beam source was placed at the entrance surface of the water tank. For production thresholds, a range cut of 0.1 mm was used for photons, electrons, and positrons. There was no range cut on protons [46]. Protons were tracked to the end of their range.

The transportation of particles in Geant4 was done in steps. One step was defined by the distance between two voxel boundaries if there was no discrete interaction in the present voxel [47]. Very small steps need to be used in order to ensure accurate simulation [48]. Range cut and maximum allowed step size should be equal to or lower than the voxel size, around 1 mm for clinical applications [49]. Maximum step size was set to 1 mm. ρ_water = 0.998 g/cm³ was set in the source file according to ICRU 2016 [50].

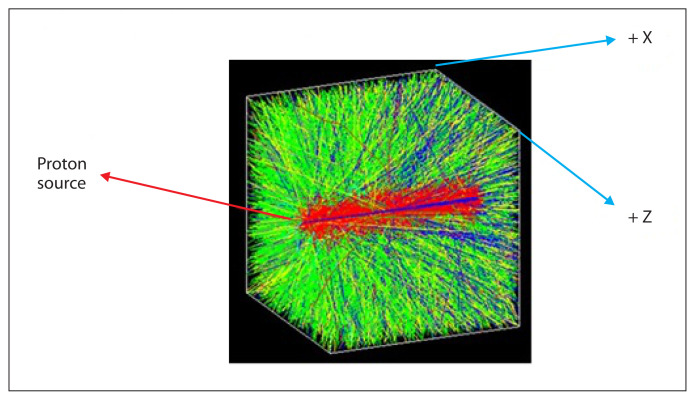
The beam was modelled using several parameters, which were defined by beam source position and structure, beam direction, angular distribution, and energy spectra. The parameters related to the visualization of the beam were defined in the macro file. Beam direction was set from −x direction to +x direction. Protons in a beamlet incident on a patient or a phantom are very nearly monoenergetic and are distributed laterally, essentially as a narrow Gaussian function of position relative to the beamlet’s central axis [44]. Therefore, beam energy was selected as mono-energetic and it was defined in Gaussian profile. The incident surface was in the y–z plane and the beam was traveling along the x axis without any angular dispersion. The proton source was set at d = −20 cm depth on the x-axis in the y-z plane. The beam shape was set to circle. The monoenergetic proton source used is entirely a point source, therefore the beam radius was defined as r = 0 mm in the macro file. The beam thickness σ_r = 3 mm, which was found as a result of proton fluence measurements taken in air, was added to the macro file. 2 × 10⁷ protons were traced to obtain less than 1% statistical accuracy. The homogenous water phantom was cubic with dimensions of 40 × 40 × 40 cm³. Simulation results were deposited in a voxelized (small cubic volumes) water phantom. Dose from all primary and secondary particles was considered. The coordinates of the modelled water phantom shown in Figure 1 were expressed in a Cartesian coordinate system.

Figure 1.

Voxelized water phantom with an incident proton beam in the y–z plane. The beam was travelling along the x-axis denoted as “Depth” in the plots shown later. Colours: protons in blue, gammas in green, neutrons in yellow, electrons in red

Selection of voxel dimension

Firstly, the suitable I value of water was selected for the high and low proton energies to be used in the study. For 235.81 MeV proton energy 76 eV, 77 eV and 78 eV and for 68 MeV proton energy 85 eV, 86 eV and 87 eV mean ionization potential energies were tested. BP characteristics were measured for different voxel sizes by selecting the most appropriate I according to the results of the graphs obtained.

The water phantom was divided into voxels. In the setup geometry, x side of the voxel was varied between 0.05 cm and 0.2 cm. Voxel sizes at transverse direction (y–z size of the voxel) were varied between 1 cm to 7.4 cm to understand the contribution of Multiple Coulomb scattering to the Bragg Peak. Profiles were obtained with 0.5 mm resolution for 68 MeV and 1 mm resolution for 235.81 MeV in the beam direction (longitudinal direction). In MC simulations, plenty of voxel variations were tested and the selected ones were listed in Table 1. These voxel dimensions were chosen to test the voxel effect at 86 eV and 77 eV of I values for 68 MeV and 235.81 MeV, respectively.

Table 1.

Voxel dimensions used in the study for low and high proton energies

Voxel dimensions [cm3]	Proton energy/Ionization potential energy
	E = 68 MeV I = 86 eV	E = 235.81 MeV I = 77 eV
0.05 × 1 × 1	v
0.1 × 1 × 1	v
0.1 × 2 × 2	v
0.1 × 3.4 × 3.4		v
0.2 × 3.4 × 3.4		v
0.2 × 7.4 × 7.4		v

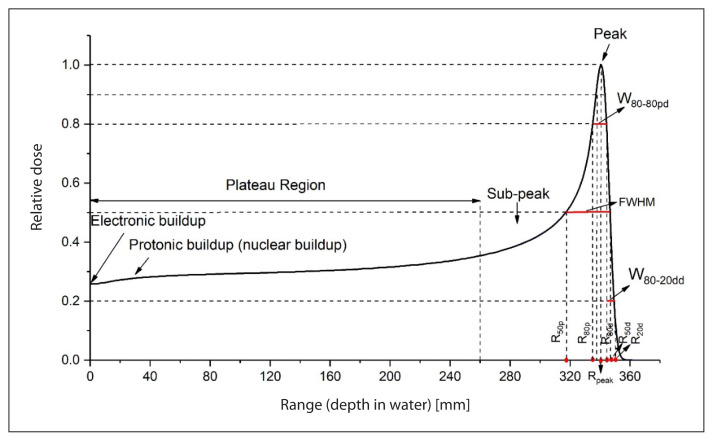
The characteristics of Bragg peak

In this study eleven dose range parameters were used to characterize the shape of a BP (as shown in Figure 2): R_peak, R_90d, R_80p, R_80d, R_50p, R_50d, R_20d, FWHM, W_80–20dd, W_80pd, and peak-to-entrance dose ratio was used for comparison between the experimental and simulation data. The maximum doses in the plateau region were also compared. The plateau region is defined as the region from the entrance to the proximal depth of the 36% dose point. Characteristic parameters and regions of a BP curve are shown in Figure 2.

Figure 2.

Beam characteristics of Bragg peak (BP)

Statistical methods

All data processing, analysis, and visualization were performed using OriginPro 2017 SR2 [51]. In this study, the comparison between dose values has been done using a percentage dose normalization equation (1)

$$\mathrm{\Delta }=\frac{|D_i-{Dref}_i|}{{Dref}_i}\times 100$$ (1)

D_i represents evaluated doses in measurement, D_ref represents the reference doses in simulation and is the dose difference between the simulation and measurement. Doses are normalised to the maximum dose. To obtain BP characteristics, three different interpolation techniques were also used: linear (L), cubic spline (CS), and Akima (A) interpolations. All comparisons were assessed according to ICRU Report 78 [43].

Results and Discussion

In this study, the effect of voxel size on BP characteristics was examined. To calculate BP characteristics, the value at the x % dose point indicated by R_x must be known. If these points are not calculated in the simulation data set, the missing data is completed by applying the interpolation technique. L, CS, and A techniques were tested for low and high proton energies. Simulation data sets with values of 0.1 × 1 × 1 cm³ and I = 86 eV for 68 MeV and 0.2 × 3.4 × 3.4 cm³ and I = 77 eV for 235.81 MeV were selected. The difference between interpolations was examined for W_80pd, which indicates the treatable tumor thickness and it was also an important parameter in clinical practice because it was known that the 80% dose range (R_80d) does not change with varying initial energy spread [52]. For 68 MeV, the maximum difference between L and A, L and CS and A and CS were 5.9%, 7.7% and 2.6%, respectively. For 235.81 MeV in the same region, the difference between A and CS was less than 0.5% while the maximum difference between L-A and L-CS was 1.2%. When the experimental data and the interpolated simulation data were compared for 68 MeV for W_80pd, there was a 0.1 mm difference between L and experimental data and a 0.2 mm difference between CS and experimental data while there was no difference between A and experimental data. When experimental data was compared with the interpolated simulation data for 235.81 MeV for W_80pd, there was a 0.6 mm difference between L and experimental data, 0.8 mm difference between CS and experimental data and A and experimental data. When peak to entrance dose ratios was compared between experimental data and the interpolated simulation data for 235.81 MeV, 2.6% and 1.3% differences were seen between L and experimental data and CS and experimental data, respectively, while there was no difference between A and experimental data. Therefore, the A interpolation technique was used in all mathematical calculations in this study.

Selection of ionization energy

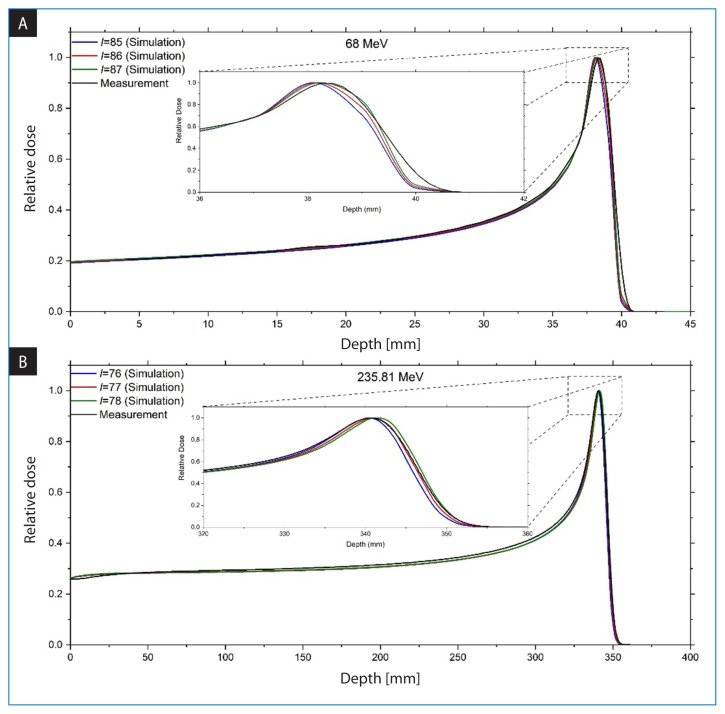
In this study, the characteristics of BP curves were obtained as a result of changing the voxel sizes used in dose deposit examined. To do this, at the first step, different mean ionization potential energies were tested for 2 therapeutic proton energies 68 MeV and 235.81 MeV by using 0.1 × 1 × 1 cm³ and 0.2 × 3.4 × 3.4 cm³ voxel dimensions, respectively. As can be seen in Figure 3, BP curves were obtained for low and high proton energies using different I values and simulation data were compared with the measurement. The I values were changed to obtain a relevant sensitivity curve for BP position.

Figure 3.

Bragg peak (BP) curves obtained using different ionisation energies for 68 MeV (A), 235.81 MeV (B)

In Figure 3A, the peak to entrance dose ratio differences between the experimental data and the simulations were 4.0%, 2% and 0% and maximum dose differences at the plateau region were 4.1%, 2.5%, and 1.6% for I of 85, 86 and 87eV, respectively. R_peak (BP position) differences were 0.3 mm, 0.2 mm and 0.1 mm for 85, 86 and 87 eV, respectively. While there was a 0.1 mm and 1.2 mm difference in W_80pd for 85 and 87 eV, respectively, there was no difference in W_80pd for 86 eV. The differences in the peak to entrance dose ratio, the maximum dose at the plateau region, and R_peak value seemed small when compared with the experimental data for I = 87 eV. Since treatable tumor thickness was an important parameter in clinical practice, I value was chosen as 86 eV for 68 MeV proton energy.

In Figure 3B, there was not any difference for the peak to entrance dose ratio between the experimental data and the simulations for I of 76 eV, 77 eV, and 78 eV. Maximum dose differences at the plateau region were 3.3%, 3.2% and 2.9% and R_peak (BP position) differences were 0.2 mm, 0.1 mm and 0.6 mm for I of 76 eV, 77 eV and 78 eV, respectively. While there was a 0.8 mm difference in W_80pd for 76 eV, a 0.6 mm difference was calculated for both 77 eV and 78 eV. When evaluating the calculation results for 235.81 MeV proton energy, the closest I value to the experimental data was chosen as 77 eV.

In the present study, water was used as a stopping medium. One of the parameters required for a precise calculation of the BP position was the I value of the stopping medium. In this study, it was observed that as I increases, the BP curve shifts to the right (deeper region) due to the relationship between range and stopping power and the result was consistent with the literature [53].

Effect of voxel size

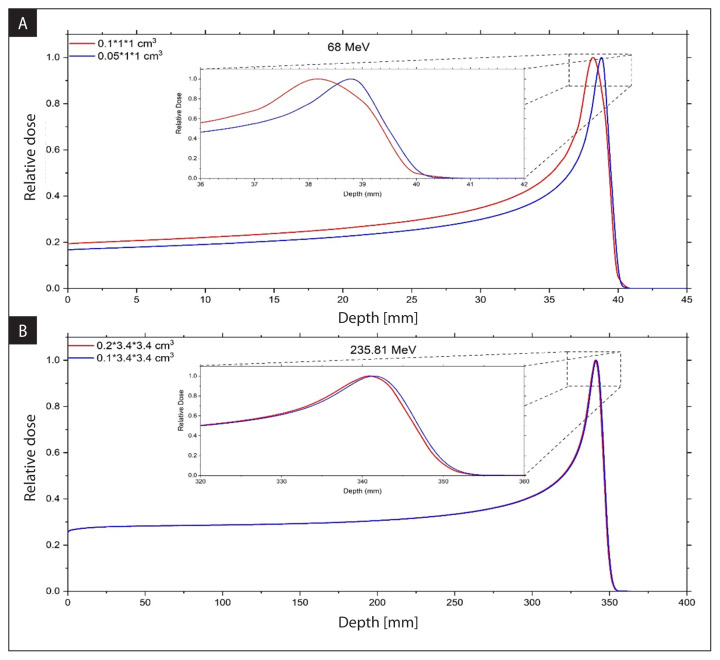
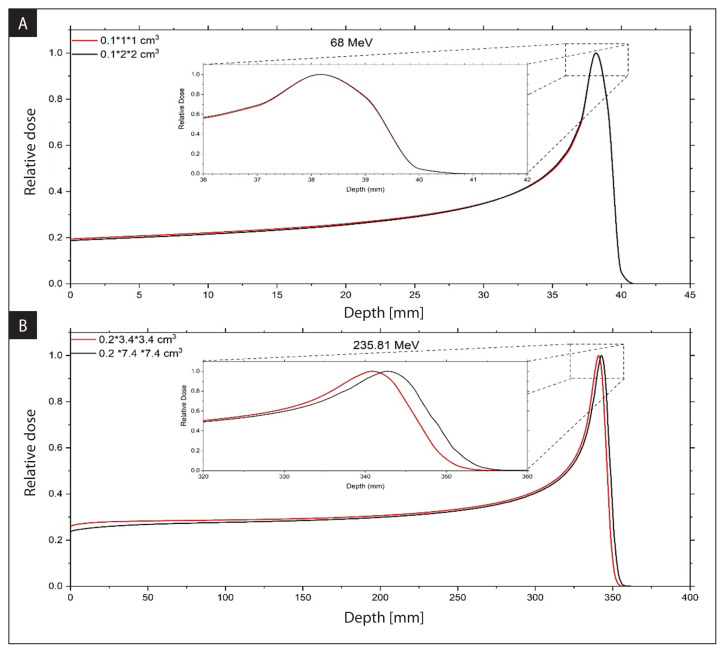
In this section, the effect of voxel size on BP curves was tested using Geant4 MC software. First by keeping the voxel sizes constant in the y–z directions (in transverse direction), and selecting the voxel sets with different x sizes (in the same direction as the proton beam), the effect of voxel size in the longitudinal direction was examined for low and high proton energies (Fig. 4). Then by keeping the x length of the voxel constant (in longitudinal direction) and increasing the lengths in the y–z directions, the effect of voxel size in the transverse direction was examined for both energies (Fig. 5).

Figure 4.

Bragg peak (BP) curves from Monte Carlo (MC) simulation were obtained using different x dimensions for 68 MeV (A), 235.81 MeV (B)

Figure 5.

Bragg peak (BP) curves from Monte Carlo (MC) simulation were obtained using different y–z sizes for 68 MeV (A), 235.81 MeV (B)

To investigate x size effect on the BP curve for 68 MeV, 0.05 × 1 × 1 cm³ and 0.1 × 1 × 1 cm³ voxel sizes were used. By keeping the y–z lengths of the voxel constant and increasing the x length of the voxel from 0.05 cm to 0.1 cm, it was observed that the dose at the entrance increased by 17.8% and the maximum dose difference at the plateau region was 17%. BP shifted to the left so range characteristics were observed in the shallower region. When it was examined in terms of characteristics, R_peak value shifted 0.5 mm to the left. The difference for R_80d was 0.2 mm and 1.4 mm for R_50p. W_80pd, FWHM and W_80–20dd increased 0.5 mm, 1.2 mm and 0.1 mm, respectively.

For 235.81 MeV, 0.1 × 3.4 × 3.4 cm³ and 0.2 × 3.4 × 3.4 cm³ voxel sets were used to analyze x size effect on the BP curve by keeping the length of the y-z size of the voxels constant and increasing the x size from 0.1 cm to 0.2 cm. BP curves showed similar behaviour to that observed at low energy, but the differences between BP curves were not as large and sharp as they were at low energy. It was observed that the dose at the entrance increased by 0.4% and the maximum dose difference at the plateau region was 0.6%. BP shifted to the left so range characteristics were observed in the shallower region. When it was examined in terms of characteristics, R_peak value shifted 0.6 mm to the left. The difference was 0.5 mm for R_80d and 0.6 mm for R_50p. W_80pd, FWHM, and W_80–20dd values remained same.

To investigate the y-z size effect on the BP curve for 68 MeV, 0.1 × 1 × 1 cm³ and 0.1 × 2 × 2 cm³ voxel sizes were used (Fig. 5A). When the x length of the voxel was kept constant and the lengths in the y-z directions were increased 2 times, a dose reduction was observed at the entrance and plateau region. The maximum dose difference was 3.4% at both the entrance and plateau region. It was observed that BP curve range characteristics shifted to the shallow region only less than 0.1 mm. FWHM increased 0.1 mm, while W_80pd and W_80-20dd remained the same.

To investigate y–z size effect on the BP curve for 235.81 MeV, 0.2 × 3.4 × 3.4 cm³ and 0.2 × 7.4 × 7.4 cm³ voxel sets were used (Fig. 5B). When the x length of the voxel was kept constant and the length in the y-z sizes were increased 2.2 times, a dose reduction was observed at the entrance and plateau region. At the entrance, the dose difference was 8.9% and the maximum dose difference was 9.1% at the plateau region. R_peak, R_80d, and R_50p shifted less than 1.8 mm to the right. W_80pd and FWHM increased 0.5 mm and 0.2 mm, respectively, while W_80-20dd remained the same.

To perform the geometrical collection efficiency in the simulations, the voxel size should be large enough to ensure the entire beam laterally broadened by scattered and secondary contributions. The decrease in the entrance and plateau was due to primary protons undergoing nuclear interactions whereas the sharp decrease at BP is mainly due to the stopping power of primary protons. In this study, it has been seen that by increasing the y-z lengths of the voxel, BP curve was broadened by 0.5 mm for high proton energy. This will reflect the contribution from scattering and secondary particle production on the BP curve when the proton enters the phantom.

Analytical dose calculation algorithms typically project the range based on the water equivalent depth in the patient neglecting the position of inhomogeneities relative to the Bragg peak depth [54–56]. Furthermore, such algorithms are less sensitive to complex geometries and density variations, e.g. at bone-soft tissue interfaces. Consequently, analytical algorithms are not able to correctly predict the effect of range degradation caused by multiple Coulomb scattering [57–60]. In these cases, MC techniques might reduce the range uncertainty by several mm [61]. Hence, MC technique’s advantages were used in this study. When the x size of the voxel was increased, an increase in the entrance and plateau dose was observed due to the inclusion of energy deposition from non-elastic nuclear interactions, because secondaries deposit their energy further upstream and BP range characteristics have shifted to the left (shallow) region. Therefore, these interactions raise the entrance dose. While a slight increase was observed in each of W_80pd, FWHM, and W_80–20dd at low energy, no increase was observed in W_80pd, FWHM, and W_80–20dd at high energy. This could be due to increasing the voxel size and would reduce the relative uncertainty but may introduce errors due to reduced spatial resolution.

Comparison of BP characteristics with chosen voxel sizes

After investigating the effect of voxel size in longitudinal and transverse directions, simulations that were the closest to the experimental results were selected. BP characteristics obtained in the simulation results using 0.1 ×1 × 1 cm³ for 68 MeV and 0.2 × 3.4 × 3.4 cm³ for 235.81 MeV voxel sets were compared with the experimental ones and the results were given in Table 2.

Table 2.

The difference between simulation results and the experimental data of BP characteristics

	E = 68 MeV			E = 235.81 MeV
	Simulation	Experimental	Difference	Simulation	Experimental	Difference
Peak to Ent.	4.9	4.8	1%	3.9	3.9	0.0
Dose ratio
R50p [mm]	35.2	35.1	0.1	319.4	317.2	2.2
R80p [mm]	37.4	37.6	0.2	335.8	335.0	0.8
Rpeak [mm]	38.2	38.4	0.2	340.8	340.7	0.1
R90d [mm]	38.7	38.9	0.2	343.2	343.2	0.0
R80d [mm]	38.9	39.1	0.2	344.2	344.2	0.0
R50d [mm]	39.4	39.5	0.1	346.3	346.6	0.3
R20d [mm]	39.7	40.0	0.3	348.9	349.2	0.3
W80pd [mm]	1.5	1.5	0.0	8.4	9.2	0.8
FWHM [mm]	4.2	4.4	0.2	26.9	29.4	2.5
W80–20dd [mm]	0.8	0.9	0.1	4.7	5.0	0.3

FWHM — full with at half maximum

As seen in Table 2, when the simulation results were compared with the experimental data for low and high energies, the difference was found to be acceptable according to the protocol [43]. In the protocol, the dose differences between experiment and simulation should be less than 2.3% and range differences should be less than 1 mm. In this study, while the difference in peak to entrance ratio was 1% for 68 MeV, there was no difference for 235.81 MeV.

For a monoenergetic proton beam, the 80% fall-off position coincides with the mean projected range of a proton, i.e. the range at which 50% of the protons have stopped. Furthermore, the 80% fall-off position is independent of the beam’s energy spread [61] and it was also demonstrated in the literature that initial energy spreads had a minimum effect on R_80d so R_80d can be used as a good index to represent the initial incident mean beam energy [9]. When differences in R_80d (clinical range) were calculated, it was seen that while the difference was 0.2 mm for 68 MeV, there was no difference for 235.81 MeV. In proton therapy applications, another important parameter was W_80pd. For this parameter, the difference was 0.8 mm for high energy while there was no difference for low energy. In this study, the only parameter that was not in good agreement with the protocol was the FWHM which was obtained for high energy. The treatment nozzle was not modelled in this study; therefore, 0–1% of the initial energy was not added into the simulations as an initial energy spread. The slight shift of FWHM was influenced by the change of R_50p and R_50d; in other words, the width between R_50p and R_50d depends on the magnitude of the added initial energy spread which varies between 0–1% of the mean initial energy [45, 61].

Conclusion

In this paper, we investigated how BP characteristics were affected by changing the voxel size in the longitudinal and transverse directions for 68 MeV and 235.81 MeV. The mean ionization potential energies that have been consistent with experimental results were determined. It has also been shown that the interpolation effect was lower at high energies, while it was higher at low energies. Additionally, BP characteristic parameters obtained from simulation for chosen voxel size (0.1 × 1 × 1 cm³ for 68 MeV and 0.2 × 3.4 × 3.4 cm³ for 235 MeV) were compared with experimental results.

It has been shown that the voxel size effect for the longitudinal direction was more effective at low energy than at high energy. However, the voxel size effect for the transverse direction was more effective for high energy. When the voxel size in the beam direction was increased at both low and high energy, the doses at the entrance and plateau regions increased and BP curves shifted towards the shallow region, but when the voxel size was increased in the transverse direction, it was observed that the dose at the entrance and plateau regions decreased in both high and low energy. The difference between BP’s obtained as a result of increasing the voxel size at low energy was quite higher compared to the one at high energy. When BP characteristic parameters obtained from simulation for a chosen voxel size were compared with experimental results, differences were in good agreement with the ICRU 78 protocol except for FWHM value. The result of this study may be helpful in improving dose calculation accuracy for high and low energy pencil proton beams by choosing suitable voxelization.