Abstract
Collagen is the main load-bearing component of cornea and sclera. When stretched, both of these tissues exhibit a behavior known as collagen fiber recruitment. In recruitment, as the tissues stretch the constitutive collagen fibers lose their natural waviness, progressively straightening. Recruited, straight, fibers bear substantially more mechanical load than non-recruited, wavy, fibers. As such, the process of recruitment underlies the well-established nonlinear macroscopic behavior of the corneoscleral shell. Recruitment has an interesting implication: when recruitment is incomplete, only a fraction of the collagen fibers is actually contributing to bear the loads, with the rest remaining “in reserve”. In other words, at a given intraocular pressure (IOP), it is possible that not all the collagen fibers of the cornea and sclera are actually contributing to bear the loads.
To the best of our knowledge, the fraction of corneoscleral shell fibers recruited and contributing to bear the load of IOP has not been reported. Our goal was to obtain regionally-resolved estimates of the fraction of corneoscleral collagen fibers recruited and in reserve. We developed a fiber-based microstructural constitutive model that could account for collagen fiber undulations or crimp via their tortuosity. We used experimentally-measured collagen fiber crimp tortuosity distributions in human eyes to derive region-specific nonlinear hyperelastic mechanical properties. We then built a three-dimensional axisymmetric model of the globe, assigning region-specific mechanical properties and regional anisotropy. The model was used to simulate the IOP-induced shell deformation. The model-predicted tissue stretch was then used to quantify collagen recruitment within each shell region. The calculations showed that, at low IOPs, collagen fibers in the posterior equator were recruited the fastest, such that at a physiologic IOP of 15 mmHg, over 90% of fibers were recruited, compared with only a third in the cornea and the peripapillary sclera. The differences in recruitment between regions, in turn, mean that at a physiologic IOP the posterior equator had a fiber reserve of only 10%, whereas the cornea and peripapillary sclera had two thirds. At an elevated IOP of 50 mmHg, collagen fibers in the limbus and the anterior/posterior equator were almost fully recruited, compared with 90% in the cornea and the posterior sclera, and 70% in the peripapillary sclera and the equator. That even at such an elevated IOP not all the fibers were recruited suggests that there are likely other conditions that challenge the corneoscleral tissues even more than IOP. The fraction of fibers recruited may have other potential implications. For example, fibers that are not bearing loads may be more susceptible to enzymatic digestion or remodeling. Similarly, it may be possible to control tissue stiffness through the fraction of recruited fibers without the need to add or remove collagen.
Keywords: collagen, crimp, tortuosity, cornea, sclera, recruitment, biomechanics
1. Introduction
Collagen fibers are the main load-bearing component of the eye. (Boote et al., 2020) From simple fiber embedded models (Amini and Barocas, 2009) to more complex ones (Grytz and Meschke, 2010), the anisotropy and microstructural architecture of ocular collagen fibers have been shown to significantly affect the biomechanics of the corneoscleral shell. Hence, great efforts have been devoted to developing imaging tools for mapping collagen fibers. (Campbell et al., 2015; Danford et al., 2013; Girard et al., 2011; Ho et al., 2014; Jan et al., 2015; Ling et al., 2019; Pijanka et al., 2019; Winkler et al., 2011; Zhang et al., 2015; Zhou et al., 2019b) The fiber maps are then translated into mechanical models. The underlying assumption being that the collagen maps directly translate into the local capability of the tissues to bear load. (Grytz and Meschke, 2010) However, as we, (Gogola et al., 2018a; Jan et al., 2018; Jan et al., 2017a) and others, (Boote et al., 2020; Liu et al., 2014) have shown, the tissues of the eye exhibit natural undulations called crimp. Wavy fibers, in turn, lead to an important behavior of the tissues: recruitment. When under load, the initially wavy fibers straighten. While the wavy fibers bear almost no load, the straightened ones bear substantial loads. The process of progressively straightening fibers is known as fiber recruitment (Figure 1). Fiber recruitment has been shown to underlie the nonlinear mechanical behavior of many soft tissues, not only sclera and cornea. (Cheng et al., 2018; Fata et al., 2014; Hansen et al., 2002; Hill et al., 2012; Jan and Sigal, 2018; Mattson et al., 2017; Roy et al., 2010; Weisbecker et al., 2015)
Figure 1. Diagram of collagen fiber recruitment.
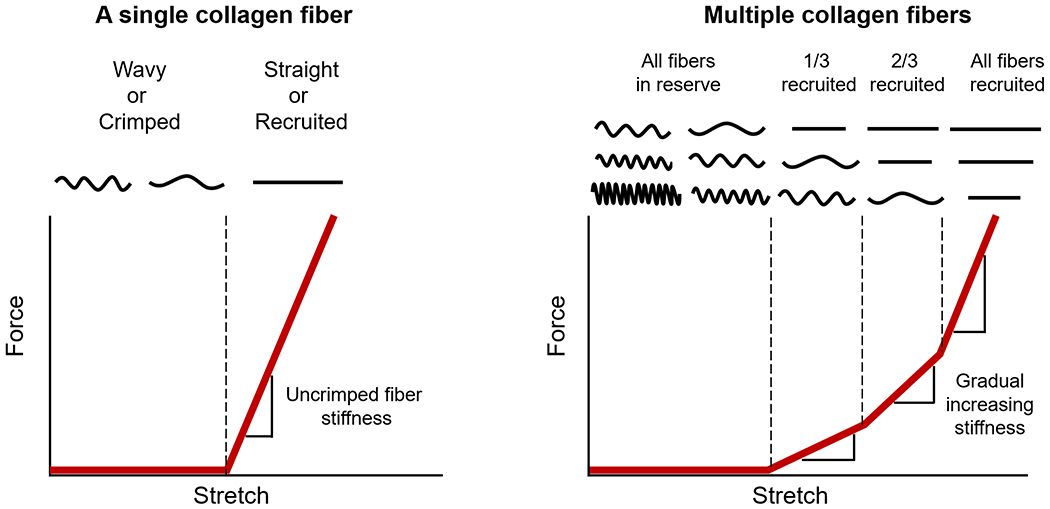
(Left) A single fiber is easy to stretch when it is crimped or wavy. However, once the fiber is straightened or recruited, the fiber becomes much stiffer, requiring more force to elongate the fiber. (Right) When many crimped fibers with different amount of slack are stretched together, the gradual straightening of the fibers creates a gradual, nonlinear stiffening, where more and more force is required to continue stretching the tissue. A fiber that is straightened is referred to as recruited. Conversely, a fiber that is not recruited, but would at higher stretch, is referred to as in reserve. The proportion of fibers recruited to those in reserve is directly related to the rate of recruitment. Adapted from (Jan and Sigal, 2018).
During the process of recruitment, only a fraction of tissue collagen fibers are load-bearing, while the rest remains in “reserve”. In other words, similar to the dormancy of cells, the undulated fibers are “off”. When straightened, the fibers turn “on” and are considered recruited to bear mechanical loads. For example, we have recently shown that at normal IOP, only about three-quarters of the fibers of the peripapillary sclera and lamina cribrosa in sheep eyes are contributing to bearing the load, with one-fourth in reserve. (Jan and Sigal, 2018) Peripapillary sclera and lamina cribrosa had distinct recruitment curves, with different fractions of fibers recruited at sub-physiologic and supra-physiologic pressures. With the rest of the corneoscleral shell exhibiting the same fundamental mechanism of recruitment, it follows that at normal pressures also only a fraction of the fibers is contributing to bear the load of IOP. This can have important implications. First, from a fundamental perspective it is interesting and worthwhile to note that it is not necessarily correct to assume that collagen fibers will help bear a load simply because they “are there”. Hence, fibers discernible in stained sections or by other imaging tools, may or may not contribute to bear a particular load. Second, the recruitment may also have important implications for remodeling and treatments aimed at modifying tissue properties. For instance, fibers not bearing load are likely to be more susceptible to degradation, whereas fibers under load are more likely to remodel. Similarly, fiber cross-linking likely affects fibers differently depending on whether they are bearing load or not. Moreover, given the regional variations in micro and macrostructure and mechanics over the globe, (Gogola et al., 2018a; Jan et al., 2018; Voorhees et al., 2017a; Whitford et al., 2016) it seems reasonable to expect that the fraction of recruited fibers likely also varies. Further, the fraction of fibers in reserve when under load can indicate the extent to which a region is able to adapt to further loads or if it has reached a limit.
Despite the abovementioned reasons, to the best of our knowledge, there is no information on the fraction of corneoscleral fibers bearing load at a given IOP. Our goal in this study was to obtain regionally-resolved estimates of the fraction of corneoscleral collagen fibers recruited, hence “turned-on” for bearing IOP-related loads. To achieve this goal, we used computational modeling based on experimentally obtained measures of collagen fiber undulations. (Gogola et al., 2018a) As a first step, in this work, we focused on estimating the fiber recruitment fraction in young healthy eyes.
2. Methods
Our general strategy was as it follows (Figure 2): using polarized light microscopy (PLM), we measured collagen crimp tortuosity in seven regions across the corneoscleral shell. The results were then fed into a fiber-based microstructural constitutive model to obtain region-specific nonlinear hyperelastic mechanical properties. A three-dimensional axisymmetric model was developed to simulate the IOP-induced deformation of the corneoscleral shell. The model-predicted tissue stretch was used to quantify collagen fiber recruitment over the corneoscleral shell. Below we describe each step in detail.
Figure 2. General strategy.
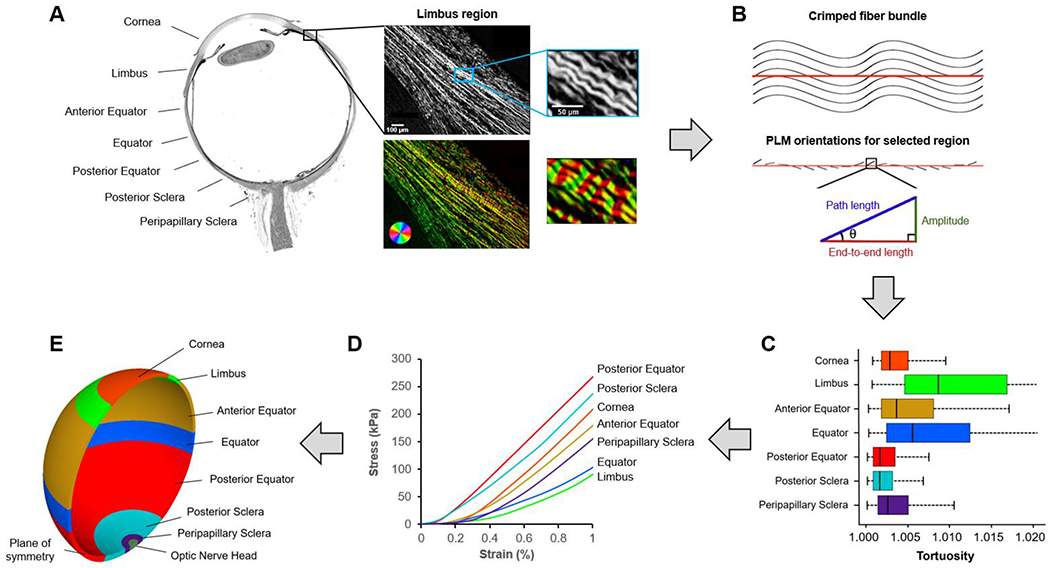
We divided the corneoscleral shell into seven regions (A). Each region was imaged using polarized light microscopy (PLM). The close-up images show the collagen fibers in the limbus region. The wavy pattern of collagen fibers is discernible and emphasized using a color map of orientation. To quantify collagen crimp, a straight line was marked manually along a fiber bundle (B). Trigonometric identities were then used pixel by pixel along the line to calculate local amplitude, path length, and end-to-end length based on the orientation information derived from PLM as described in detail in (Brazile et al., 2018; Gogola et al., 2018a; Jan et al., 2018). The local amplitude and lengths were then integrated to compute those of the fiber bundle. The crimp tortuosity of the fiber bundle was calculated as its integrated path length divided by the end-to-end length. We measured collagen crimp tortuosity in seven regions across the corneoscleral shell and the results (C) were fed into a fiber-based microstructural constitutive model to obtain region-specific nonlinear hyperelastic mechanical properties (D). A three-dimensional axisymmetric model (E) was then developed to simulate the IOP-induced deformation of the corneoscleral shell. The model-predicted tissue stretch was used to quantify collagen fiber recruitment over the corneoscleral shell.
2.1. Measuring collagen crimp across the corneoscleral shell: a review
Details of sample preparation, imaging, and crimp quantification were given in our previous report. (Gogola et al., 2018a) A brief description of these methods are provided here:
Sample preparation.
Nine normal eyes of nine human donors (ages ranging from 1 month to 17 years) were fixed unpressurized (0 mmHg IOP) in 10% neutral buffered formalin for a week. The eyes were then bisected into superior and inferior portions without cutting through the optic nerve head. The superior portion, which contained the optic nerve head, was embedded in paraffin and cryosectioned axially at 5-μm thickness. A total of 42 sections, which passed through both the optic nerve head and the cornea and were free of artifacts, such as tears and folds, were selected for imaging.
Imaging.
The selected sections were imaged with PLM using a previously reported method to visualize and quantify collagen fiber orientations. (Brazile et al., 2018; Gogola et al., 2018b; Jan et al., 2017a; Jan et al., 2015; Jan et al., 2017b) For each section, images were collected from seven regions across the corneoscleral shell: the cornea, limbus, anterior equator, equator, posterior equator, posterior sclera, and peripapillary sclera (Figure 2A).
Crimp quantification.
Crimp tortuosity was measured in at least 20 collagen fiber bundles in each region, distributed throughout depth (Figure 2B). For each bundle, we manually placed a line segment with a length of 60 pixels (~ 45 μm). This line segment was used to sample the collagen fiber orientation values within the bundle for calculating the crimp tortuosity. We refer readers to our previous papers for full details of the calculation of crimp tortuosity. (Brazile et al., 2018; Gogola et al., 2018a; Jan et al., 2018) The distribution of crimp tortuosity in the seven regions across the corneoscleral shell is shown in Figure 2C.
2.2. Crimp-informed nonlinear hyperelastic mechanical properties
For tissue consisting of fibers with various tortuosities, the gradual straightening of the fibers creates a nonlinear stiffening. (Brazile et al., 2018; Cacho et al., 2007; Jan and Sigal, 2018) To obtain the region-specific mechanical behavior of the corneoscleral shell, we pooled crimp tortuosity measurements in each region and then calculated the corresponding stress-strain curve (Figure 2D). Specifically, the mechanical response of the corneoscleral shell was modeled using a fiber-based constitutive equation of the form
| (1) |
where is the total strain energy density; is the isotropic strain energy density of the ground substance; is the strain energy density of the anisotropic fibers; and are the probability density functions used to describe the percentage of fibers with a given orientation and tortuosity, respectively; is the preferred fiber orientation relative to a local coordinate system. is the tortuosity of a crimped fiber (≥ 1); is the maximum tortuosity in a specific region of the tissue.
The strain energy density equation for the ground substance was modeled as a Neo-Hookean material which has the form
| (2) |
where is the first invariant of the right Cauchy-Green deformation tensor; is the first Mooney-Rivlin coefficient, which is also equivalent to the matrix shear modulus divided by two. We chose to be 150 kPa. (Girard et al., 2009a; Hua et al., 2020; Voorhees et al., 2017c)
As shown in Figure 1, we assumed a fiber is easy to stretch when it is crimped or wavy, and its stress is zero; once the fiber is straightened, it starts to bear load, and its stress increases linearly with stretch. (Brazile et al., 2018; Cacho et al., 2007; Jan and Sigal, 2018) Based on this assumption, the strain energy associated with a single collagen fiber at a given orientation and tortuosity satisfies the following relationship
| (3) |
where is the fourth invariant of the right Cauchy-Green deformation tensor associated with the collagen fiber family aligned in the orientation , which is equivalent to the squared fiber stretch is the tortuosity of a crimped fiber (≥ 1); is the elastic modulus of a straightened fiber, which was set to 30 MPa. (Grytz and Meschke, 2009)
We then obtained the Cauchy stress tensor as follows
| (4) |
where is the Lagrange multiplier to enforce incompressibility (similar to the hydrostatic pressure in fluids); is the second-order identity tensor; is the left Cauchy-Green deformation tensor; is a unit vector representing the local fiber direction in the deformed configuration. and are expressed as
| (5) |
| (6) |
We checked the convexity requirements for the proposed constitutive model to ensure its reliable mechanical and mathematical behavior (Supplementary Material).
2.3. Finite element modeling
Model geometry.
To reduce computational cost, we modeled the only one hemisphere of the corneoscleral shell with a simplified optic nerve head (Figure 2E). The inner radius of the shell was 12 mm. (Sigal et al., 2005a; Sigal et al., 2004) The shell thickness was non-uniform, with a maximum thickness of 996 μm adjacent to the scleral canal and a minimum thickness of 491 μm at the equator. (Norman et al., 2010; Norman et al., 2011) A spline fit was performed to ensure a smooth transition in thickness. (Wold, 1974) The shell was then partitioned circumferentially into seven regions, matching those in the experiment. (Gogola et al., 2018a)
Mechanical properties.
An anisotropic hyperelastic constitutive equation was used to describe the region-specific mechanical behavior of the corneoscleral shell, (Girard et al., 2009b) with parameters determined by fitting the crimp-informed nonlinear stress-strain curves (Figure 2D). The collagen fibers of the corneoscleral shell followed the semi-circular von Mises distribution. In the limbus and the peripapillary sclera, the collagen fibers were aligned circumferentially; while in the cornea, we defined two preferred collagen fiber orientations orthogonal to each other. (Abahussin et al., 2009) The collagen fibers in the other regions of the corneoscleral shell were assumed to be randomly distributed. A bulk modulus of 0.1 GPa was defined to ensure tissue incompressibility. (Girard et al., 2009b) Note that the bulk modulus does not directly correspond to the tissue compressibility. Instead, it acts as a penalty factor that helps define how strict the incompressibility constraint is enforced. The value selected provides reliable model convergence while keeping volume changes low. A summary of the hyperelastic parameters is listed in Table 1.
Table 1.
Region-specific hyperelastic parameters used in finite element modeling. Please see the main text for more details of how the parameters were obtained.
| Mooney-Rivlin parameter c1 (kPa) | Exponential multiplier c3 (kPa) | Fiber scale factor c4 (−) | Fiber concentration factor kf (−) | |
|---|---|---|---|---|
| Cornea | 150 | 39 | 184 | 2 |
| Limbus | 150 | 6 | 275 | 2 |
| Anterior equator | 150 | 35 | 181 | 0 |
| Equator | 150 | 16 | 196 | 0 |
| Posterior equator | 150 | 232 | 76 | 0 |
| Posterior sclera | 150 | 135 | 100 | 0 |
| Peripapillary sclera | 150 | 15 | 240 | 2 |
The optic nerve head was modeled as an incompressible, linear isotropic material with an elastic modulus fixed to 0.3 MPa. (Sigal et al., 2005a; Sigal et al., 2004)
Loading and boundary conditions.
A uniform pressure load was applied to the inner surface of the corneoscleral shell to simulate the effects of increasing IOP from 0 to 50 mmHg. The node at the apex of the cornea was constrained in all directions to prevent displacement or rotation, as done previously. (Sigal, 2009, 2011; Sigal and Grimm, 2012) The nodes on the plane of symmetry (Figure 2E) were constrained to deform so that they remained on the symmetry plane.
Solutions.
The model was solved using the FEBio software package (Musculoskeletal Research Laboratories, University of Utah, Salt Lake City, UT, USA) with eight-node hexahedral elements. Convergence tests were performed and adequate accuracy (relative strain differences under 1%) was achieved with an average element length of 100 μm. We computed the maximum principal strain as a measure of tissue stretch in response to changes in IOP.
2.4. Quantification of collagen fiber recruitment
We tracked the percentage of recruited fibers in each region as IOP increased from 0 to 50 mmHg. We used the model-predicted tissue stretch to determine whether a wavy fiber was recruited. Specifically, if the magnitude of tissue stretch is larger than the tortuosity of a fiber, the fiber is considered recruited; otherwise, the fiber is considered reserved. For each region, we used the number of tortuosity measurements that were smaller than the stretch as an indication of the number of recruited fibers. We then divided this number by the total number of tortuosity measurements in this region, as an indication of the total number of fibers, to calculate the percentage of recruited fibers. The recruitment curve was fitted to the log-normal distribution function using least square method.
3. Results
The model-predicted maximum principal strain over the whole globe at an IOP of 50 mmHg is shown in Figure 3. The strain distribution was nonuniform throughout the corneoscleral shell. In general, the pattern of strain variations across the shell was similar to that of tortuosity variations shown in Figure 2C. For example, regions with large crimp tortuosities experience large strains (i.e., limbus, anterior equator, and equator), and regions with small tortuosities (i.e., posterior equator and posterior sclera) experience small strains.
Figure 3. The maximum principal strain over the whole globe at an IOP of 50 mmHg.

(A) Contour plot of the maximum principal strain. The strain was not uniform across the globe. The highest strain was in the optic nerve head region as this region was more compliant than the other regions. In the corneoscleral shell, the limbus region experienced higher strains than the other regions. (B) Box plot of the maximum principal strain in the seven regions across the corneoscleral shell. Note that the strains were weighted by the volume of elements. Overall, the pattern of strain variations across the shell was similar to that of tortuosity variations shown in Figure 2C, but there are also some interesting differences. For example, the equator region had a wide distribution of collagen crimp tortuosity, but the strain distribution was narrow.
Figure 4 shows the contour plots of collagen fiber recruitment over the corneoscleral shell at various IOP levels, with colors corresponding to the percentage of recruited fibers. As IOP increases, collagen fibers of the corneoscleral shell were not recruited simultaneously, suggesting a region-dependent rate of tissue stiffening with IOP. At either normal or elevated IOP, collagen fibers of the corneoscleral shell were not fully recruited. A detailed quantitative analysis of the IOP-induced collagen fiber recruitment over the corneoscleral shell is shown in Figure 5.
Figure 4.
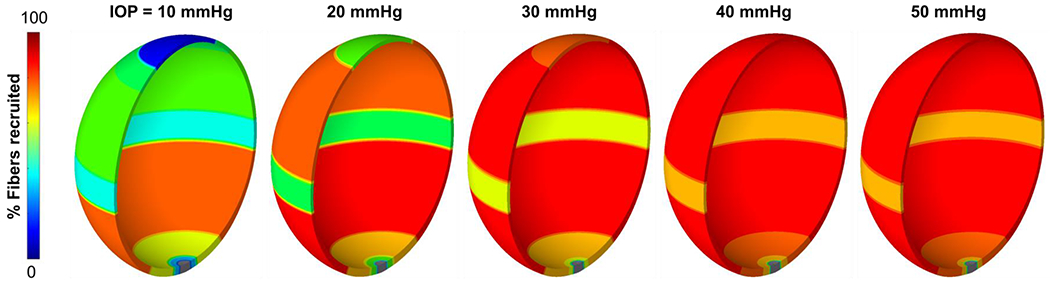
Contour plots of collagen fiber recruitment over the corneoscleral shell at various IOP levels. The shell was colored according to the percentage of recruited fibers, with blue indicating no recruitment and red indicating fully recruitment. Collagen fibers of the corneoscleral shell were not recruited simultaneously, suggesting a region-dependent rate of tissue stiffening with IOP. At either normal or elevated IOP, collagen fibers of the corneoscleral shell were not fully recruited. Note: the scleral canal region is shown in grey since we did not calculate a fiber recruitment for this region.
Figure 5.
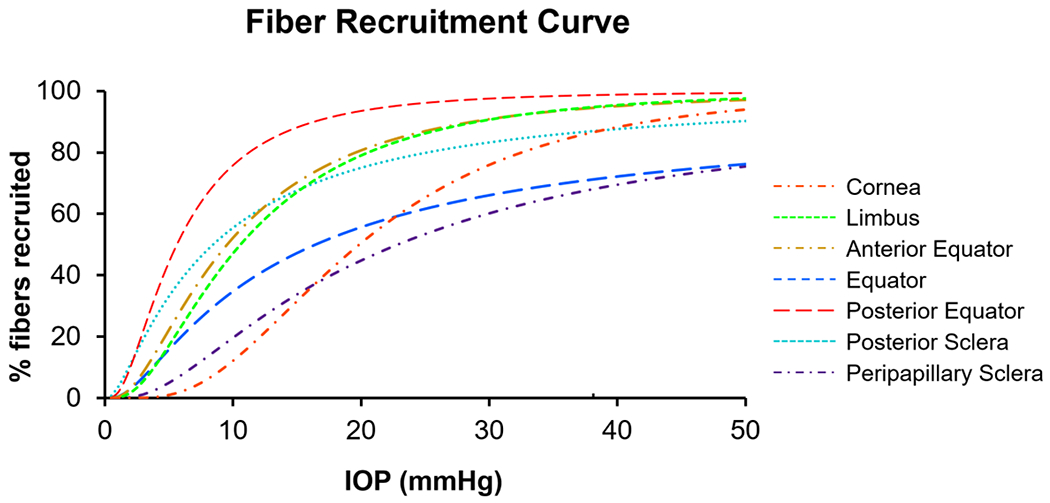
The IOP-induced collagen fiber recruitment over the corneoscleral shell. The curves were colored by regions across the corneoscleral shell. All regions exhibited sigmoid recruitment curves, but the recruitment rates varied substantially. At low IOPs, collagen fibers in the posterior equator were recruited the fastest, such that at a physiologic IOP of 15 mmHg, over 90% of fibers were recruited, compared with only a third in the cornea and the peripapillary sclera. At an elevated IOP of 50 mmHg, collagen fibers in the limbus and the anterior/posterior equator were almost fully recruited, compared with 90% in the cornea and the posterior sclera, and 70% in the peripapillary sclera and the equator.
4. Discussion
Our goal was to obtain regionally-resolved estimates of the fraction of corneoscleral collagen fibers recruited, hence contributing to bearing IOP-related loads. The results show that, at low IOPs, collagen fibers in the posterior equator were recruited the fastest, such that at a physiologic IOP of 15 mmHg, over 90% of fibers were recruited, compared with only a third in the cornea and the peripapillary sclera. This, in turn, means that at a physiologic IOP the posterior equator had a fiber reserve of only 10%, whereas the cornea and peripapillary sclera had two thirds. At an elevated IOP of 50 mmHg, collagen fibers in the limbus and the anterior/posterior equator were almost fully recruited, compared with 90% in the cornea and the posterior sclera, and 70% in the peripapillary sclera and the equator. Two main findings can be drawn from these results. First, collagen fibers of the corneoscleral shell were not recruited simultaneously with increasing IOP. Second, collagen fibers of the corneoscleral shell were not fully loaded or recruited at either normal or elevated IOP. Below we discuss each finding in detail.
Our results show that collagen fibers of the corneoscleral shell were not recruited simultaneously with increasing IOP. This suggests that the rate of tissue stiffening with IOP differs in different regions of the corneoscleral shell. We found that collagen fibers in the posterior equator of sclera were recruited the fastest. This could be attributed to the small collagen crimp tortuosity in this region, in which fibers only require a small amount of stretch to straighten. A biomechanical advantage of fast recruitment is to resist large deformations at moderate IOPs, which could help maintain the shape of globe. On the other hand, collagen fibers in cornea were recruited the slowest, suggesting that cornea stiffens at higher IOPs. In this sense, cornea likely behaves as a “mechanical absorber” to protect tissues in other regions from large acute volume or IOP increases. Note that uncrimping or recruitment only relates to the rate of tissue stiffening with IOP, which is different from tissue stiffness. Therefore, our results should not be interpreted to mean that the posterior equator of sclera is stiffer than cornea.
It is important to note that, in addition to collagen crimp, other factors may affect the percentage of collagen recruitment, including, but not limited to, fiber type, composition, alignment, and slip conditions, fiber-to-fiber interactions, proteoglycan and elastin content and distribution, the amount and type of cross-linking between fibers, and the presence of blood vessels within fibers. (Birch et al., 2013; Brazile et al., 2020; Ethier et al., 2004; Fratzl, 2008; Holzapfel, 2001; Wang et al., 2020) Further research is needed to quantify additional microstructural characteristics to be able to fully characterize the IOP-induced collagen fiber recruitment over the corneoscleral shell.
Our results also show that collagen fibers of the corneoscleral shell were not fully loaded or recruited at either normal or elevated IOP. Note that collagen fibers in other connective tissues, such as artery, (Hill et al., 2012; Roy et al., 2010; Weisbecker et al., 2015) heart valve, (Mattson et al., 2017) and bladder, (Cheng et al., 2018) are also not fully recruited under physiological loading. However, most models developed to study connective tissue mechanics only consider the fiber density, orientation, and degree of anisotropy or fiber concentration, assuming all fibers are recruited or loaded. (Coudrillier et al., 2013; Hua et al., 2020; Pandolfi and Holzapfel, 2008; Thomas et al., 2019; Voorhees et al., 2017c; Zhang et al., 2015; Zhou et al., 2019a) This may overestimate the stiffness of connective tissues, resulting in a relatively low physiological accuracy of the estimates obtained from models.
We understand that an IOP of 50 mmHg is high. In our study, we aimed to investigate the biomechanics of the eye under extreme conditions and provide insight into how the eye responds to different mechanical stresses. Moreover, it is not uncommon for studies in ocular biomechanics, particularly those related to ONH biomechanics, to consider high or extremely high pressures, such as those that reach 45 or 50 mmHg. (Amini et al., 2011; Brazile et al., 2020; Gsellman and Amini, 2016; Ho et al., 2014; Sigal et al., 2004; Sigal et al., 2009a; Wang et al., 2016b) By extending our work to such pressures, we intended to relate to those studies and provide further insight into the biomechanics of the eye under various conditions. Interestingly, even at the extremely high IOP of 50 mmHg, not all fibers are recruited. This suggests that some fibers may be optimized to bear forces that are not due to IOP, such as from intracranial pressure, (Feola et al., 2016; Feola et al., 2018; Hua et al., 2017; Hua et al., 2018) gaze, (Sibony et al., 2018; Wang et al., 2016a; Wang et al., 2016b) muscle tension, (Jafari et al., 2021) or impact. This conclusion would not be possible if we had only considered normal or mildly elevated IOPs.
It should be noted that the peripapillary sclera recruitment curve as a function of IOP derived in this study is generally lower than that observed in our previous study. (Jan and Sigal, 2018) For example, at a normal IOP, this study observed approximately 1/3 recruitment, compared to 75% in the previous study. Interestingly, however, at a high IOP of 50 mmHg, both studies showed similar results with about 70% recruitment. It is important to keep in mind that the differences and similarities between the two studies should be interpreted with caution due to several factors that could have impacted the results. First, in the two studies different species were investigated: in the previous one sheep, and in this one humans. Although the species are similar, it cannot be assumed that the results will be identical. Second, the direction of measurement is different, with the previous study using coronal sections and this study using longitudinal sections. This difference could potentially impact the visibility of crimp and recruitment as the measurements represent fibers aligned with the plane of sectioning. Third, in the previous study we directly measured crimp from eyes fixed at various IOPs, whereas in this study we used crimp from eyes at no pressure to estimate the recruitment resulting from increases in IOP. As noted elsewhere, fiber recruitment is not the only factor affecting tissue stiffness. Since we have not incorporated all these factors, predictions made in this study may be off. Fourth, in the microstructural model used in this study, we assumed a monotonic increase in the fraction of recruitment with IOP. In contrast, in the previous study, we observed a maximum recruitment fraction of 82% at approximately 25 mmHg of IOP, followed by a decrease to 75% at 50 mmHg.
The relationship between collagen microstructure and the overall tissue mechanical properties is complex. (Amini et al., 2014; Thomas et al., 2019) We developed a fiber-based microstructural constitutive model that considered crimp tortuosity of collagen fibers. Collagen fibers were assumed as linear elastic, and the nonlinear stiffening behavior was derived from a load-dependent recruitment of collagen fibers based on a distribution of crimp tortuosities. A similar approach has been adopted by others. (Cacho et al., 2007; Liu et al., 2014; Raz and Lanir, 2009) Inversely, Grytz et al. predicted collagen crimp morphology in the corneoscleral shell using the stress-strain curves gathered from mechanical tests. (Grytz and Meschke, 2009, 2010) They assumed that collagen fibers in the corneoscleral shell had uniform helical spring morphology and were never straightened under stretch. In their constitutive model, the nonlinearity of the stress-strain curve arose from fiber uncrimping, rather than recruitment. These are related but not the same. We found direct experimental evidence that the peripapillary sclera gradually recruited its collagen fibers with increasing IOP-induced stretch. (Jan et al., 2017a; Jan and Sigal, 2018; Lee et al., 2022)
We used tortuosity, i.e., the path length divided by the end-to-end length (≥ 1), as a measure of crimp morphology in this study. When the tortuosity of a fiber drops to one under stretch, the fiber is considered recruited. It is important to note that tortuosity is only one measure of crimp morphology. Other measures, such as period (the length of one wave), waviness (the standard deviation of orientations), and amplitude (half the peak to trough distance), can also be used to quantify crimp morphology, and could vary in different ways than tortuosity. (Gogola et al., 2018a; Jan et al., 2018; Jan et al., 2017a; Jan and Sigal, 2018) Future work should incorporate additional crimp measures in the constitutive model to fully characterize the relationship between collagen crimp morphology and the nonlinear mechanical behavior of tissues.
The crimp tortuosity incorporated in our constitutive model was quantified using PLM. (Gogola et al., 2018a) Others have visualized the crimp in the eye with other imaging modalities, including transmitted electron microscopy, (Liu et al., 2014) brightfield microscopy, (Ostrin and Wildsoet, 2016) nonlinear microscopy, (Quantock et al., 2015) and MRI. (Ho et al., 2014) The advantages of PLM have been detailed in our previous work. (Gogola et al., 2018a; Jan et al., 2018; Jan et al., 2017a; Jan and Sigal, 2018; Jan et al., 2015) Briefly, PLM has the appropriate sensitivity, resolution, and field of view to quantify crimp over the whole globe. In addition, sample preparation for the crimp analysis is relatively simple as tissue can be visualized without dehydration, labels, or stains, reducing tissue processing and the likelihood of introducing artifacts, such as deformation.
The three-dimensional axisymmetric model presented in this study is a simplification of the corneoscleral shell. It follows the general idea of generic parametric models we have published previously. (Hua et al., 2017; Hua et al., 2018; Sigal, 2009; Sigal et al., 2005a; Sigal et al., 2004; Sigal and Grimm, 2012; Sigal et al., 2011a; Sigal et al., 2011b; Voorhees et al., 2016) Although the simplifications may not capture every aspect of the complex mechanical behavior of the corneoscleral shell, they are well-suited to test the fundamental behavior of the parameters of interest, without the overlying complexity of inter-eye variability that the specimen-specific models imply. (Sigal et al., 2005b; Sigal et al., 2009a, b; Sigal et al., 2010a; Sigal et al., 2010b; Voorhees et al., 2020; Voorhees et al., 2017b; Voorhees et al., 2017c) In addition, these simplifications help provide fundamental new insight into how collagen fibers of the corneoscleral shell were recruited with increasing IOP, which would otherwise be challenging to obtain through experiment. A thorough discussion of the limitations of this modeling approach can be found in our previous studies, (Hua et al., 2017; Hua et al., 2018; Sigal, 2009; Sigal et al., 2005a; Sigal et al., 2004; Sigal and Grimm, 2012; Sigal et al., 2011a; Sigal et al., 2011b; Voorhees et al., 2016) and was recently discussed in detail. (Roberts et al., 2018) Below we summarize the limitations more relevant to this study.
First, the crimp tortuosity incorporated in our constitutive model was measured in tissues that had been histologically processed. (Gogola et al., 2018a) Some artifacts, such as tissue distortion or shrinkage, could result from fixation or sectioning. However, because all the globes were treated the same way, the regional differences in crimp tortuosity as we measured must still be valid. Further studies could measure crimp in tissues fixed with 10% formalin, as it has shown to have minimal effects on the size or shape of ocular tissues at large and small scales, (Jan et al., 2015; Tran et al., 2017) or study crimp without sectioning. (Ho et al., 2014)
Second, we measured the crimp tortuosity based on the in-plane collagen fiber orientations derived from 2D histological sections of the corneoscleral shell. (Gogola et al., 2018a) Although we were careful to measure collagen fibers and bundles in the section plane, it is likely that they had small out-of-plane angles. In this case, our 2D measures of crimp tortuosity would be underestimated relative to the three-dimensional variations. Future studies should include examination of any potential differences with three-dimensional measurements. This examination could be done, for example, by using sections made with different orientations, or using extensions of PLM that allow three-dimensional measurement of fiber orientation. (Yang et al., 2018)
Third, our constitutive model did not consider the elastic responses of cells, proteoglycans, elastin, glycosaminoglycans, and other extracellular tissue constituents. (Hatami-Marbini and Pachenari, 2020; Midgett et al., 2020; Murienne et al., 2016) As a result, the contribution of these constituents to the tissue mechanical properties or the interaction of these constituents with the collagen fiber network was ignored in our constitutive model. We remind readers that our intention was not to accurately quantify the IOP-induced deformation of the globe, but to understand how collagen fibers of the corneoscleral shell bear loads as IOP increases. In this sense, it is acceptable for our constitutive model to focus on the elastic response of collagen fibers.
Fourth, collagen fibers of the corneoscleral shell are interwoven. (Gogola et al., 2018b; Jan et al., 2017b; Komai and Ushiki, 1991; Lee et al., 2022; Meek, 2009; Morishige et al., 2007; Nguyen, 2016) We and others have demonstrated that collagen interweaving plays an important role in determining the structural stiffness of ocular connective tissues. (Pandolfi et al., 2019; Petsche and Pinsky, 2013; Wang et al., 2020; Winkler et al., 2011) However, such interweaving was not considered in our constitutive model. Future constitutive models might benefit from incorporating measures of collagen interweaving from experiments to better characterize the IOP-induced collagen fiber recruitment over the corneoscleral shell.
Fifth, our finite element model did not incorporate depth-dependent variations in fiber distributions. Using wide-angle x-ray scattering, Pijanka et al. found that fiber concentration factors varied with depth. (Pijanka et al., 2012) Another study by Danford et al., using small angle light scattering, confirmed depth dependence of the fiber concentration factor in both normal and glaucoma human sclera. (Danford et al., 2013) More advanced finite element models will be required to understand the implication of depth-dependent fiber concentration factors on the IOP-induced globe deformation and collagen recruitment.
Sixth, our model did not incorporate prestresses.(Grytz and Downs, 2013) It is unclear how exactly prestresses would change the conclusions, especially since the magnitudes of the prestresses likely also vary over the globe and are anisotropic. Although it has been shown that residual strains in soft tissues can be measured experimentally, (Amini et al., 2012; Wang et al., 2015) to the best of our knowledge the techniques have yet to be applied over the whole globe.
Seventh, the experimental data on collagen fiber tortuosity on which we based this study only accounted for variations along the axial length of the globe, aggregating measurements over equatorial lines. Hence the models and analysis in this work were axisymmetric, which may be useful as a first approximation, (Hua et al., 2018) but it also means that this work cannot account for more complex conditions. (Chung et al., 2016) More detailed experimental information on the anisotropy of the sclera, both in terms of its mechanical behavior and collagen components, will be necessary for more comprehensive models. (Hua et al., 2022; Jan et al., 2022)
Eighth, we modeled the ONH tissues as linearly elastic. We did this for simplicity to avoid more complex boundary conditions that could affect the interpretation of our results, which were primarily focused on the sclera.
Lastly, experimental measurement of whole-globe collagen fiber recruitment with IOP is not possible yet with current imaging techniques, making it difficult to validate our model predictions. With the development of more advanced imaging techniques, such as polarization-sensitive optical coherence tomography, (Baumann et al., 2014; Tang et al., 2021; Willemse et al., 2020) we expect relevant experimental data to be available in the near future.
In conclusion, by developing a fiber-based microstructural constitutive model that could account for the collagen fiber crimp via their tortuosity, we obtained regionally-resolved estimates of the fraction of corneoscleral collagen fibers recruited and in reserve. An accurate measure of the fraction of the fibers bearing load can help improve our understanding and ability to predict and control tissue remodeling and/or treatments based on fiber cross-linking.
Supplementary Material
Highlights.
Under load, the collagen fibers of eye tissues lose their natural waviness, or crimp, progressively straightening and becoming recruited to bear elastic loads
We developed a constitutive model of corneoscleral tissues based on collagen crimp and fiber recruitment
We used the model to compute the fraction of recruited fibers contributing to bear the load of IOP in seven regions of the globe
The fibers of the posterior equator recruited the fastest at low IOPs such that at 15mmHg over 90% of fibers were recruited.
The fibers of the peripapillary sclera recruited slower with only 34% of the fibers recruited at 15mmHg. At 50mmHg 75% of the peripapillary sclera fibers had been recruited, leaving 25% in reserve.
Acknowledgements
Supported in part by National Institutes of Health grants R01-EY023966, R01-EY028662, P30-EY008098, and T32-EY017271; Eye and Ear Foundation (Pittsburgh, PA); Research to Prevent Blindness (unrestricted grant to UPMC Ophthalmology and Stein Innovation Award to Sigal IA); BrightFocus Foundation; National Science Foundation (CAREER 2049088).
Footnotes
Disclosures: None.
References
- Abahussin M, Hayes S, Cartwright NEK, Kamma-Lorger CS, Khan Y, Marshall J, Meek KM, 2009. 3D collagen orientation study of the human cornea using X-ray diffraction and femtosecond laser technology. Investigative Ophthalmology & Visual Science 50, 5159–5164. [DOI] [PubMed] [Google Scholar]
- Amini R, Barocas VH, 2009. Anterior chamber angle opening during corneoscleral indentation: the mechanism of whole eye globe deformation and the importance of the limbus. Investigative Ophthalmology & Visual Science 50, 5288–5294. [DOI] [PubMed] [Google Scholar]
- Amini R, Barocas VH, Kavehpour HP, Hubschman JP, 2011. Computational simulation of altitude change-induced intraocular pressure alteration in patients with intravitreal gas bubbles. Retina 31, 1656–1663. [DOI] [PubMed] [Google Scholar]
- Amini R, Eckert CE, Koomalsingh K, McGarvey J, Minakawa M, Gorman JH, Gorman RC, Sacks MS, 2012. On the in vivo deformation of the mitral valve anterior leaflet: effects of annular geometry and referential configuration. Annals of biomedical engineering 40, 1455–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amini R, Voycheck CA, Debski RE, 2014. A method for predicting collagen fiber realignment in non-planar tissue surfaces as applied to glenohumeral capsule during clinically relevant deformation. Journal of Biomechanical Engineering 136, 031003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumann B, Rauscher S, Glösmann M, Götzinger E, Pircher M, Fialová S, Gröger M, Hitzenberger CK, 2014. Peripapillary rat sclera investigated in vivo with polarization-sensitive optical coherence tomography. Investigative Ophthalmology & Visual Science 55, 7686–7696. [DOI] [PubMed] [Google Scholar]
- Birch HL, Thorpe CT, Rumian AP, 2013. Specialisation of extracellular matrix for function in tendons and ligaments. Muscles, Ligaments and Tendons Journal 3, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boote C, Sigal IA, Grytz R, Hua Y, Nguyen TD, Girard MJA, 2020. Scleral structure and biomechanics. Progress in Retinal and Eye Research 74, 100773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brazile BL, Hua Y, Jan N-J, Wallace J, Gogola A, Sigal IA, 2018. Thin lamina cribrosa beams have different collagen microstructure than thick beams. Investigative Ophthalmology & Visual Science 59, 4653–4661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brazile BL, Yang B, Waxman S, Lam P, Voorhees AP, Hua Y, Loewen RT, Loewen NA, Rizzo JF III, Jakobs TC, Sigal IA, 2020. Lamina cribrosa capillaries straighten as intraocular pressure increases. Investigative Ophthalmology & Visual Science 61, 2–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cacho F, Elbischger P, Rodriguez J, Doblaré M, Holzapfel GA, 2007. A constitutive model for fibrous tissues considering collagen fiber crimp. International Journal of Non-Linear Mechanics 42, 391–402. [Google Scholar]
- Campbell IC, Coudrillier B, Mensah J, Abel RL, Ethier CR, 2015. Automated segmentation of the lamina cribrosa using Frangi’s filter: A novel approach for rapid identification of tissue volume fraction and beam orientation in a trabeculated structure in the eye. Journal of The Royal Society Interface 12, 20141009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng F, Birder LA, Kullmann FA, Hornsby J, Watton PN, Watkins S, Thompson M, Robertson AM, 2018. Layer-dependent role of collagen recruitment during loading of the rat bladder wall. Biomechanics and Modeling in Mechanobiology 17, 403–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung CW, Girard MJ, Jan N-J, Sigal IA, 2016. Use and misuse of Laplace’s law in ophthalmology. Investigative Ophthalmology & Visual Science 57, 236–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudrillier B, Boote C, Quigley HA, Nguyen TD, 2013. Scleral anisotropy and its effects on the mechanical response of the optic nerve head. Biomechanics and Modeling in Mechanobiology 12, 941–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danford FL, Yan D, Dreier RA, Cahir TM, Girkin CA, Geest JPV, 2013. Differences in the region-and depth-dependent microstructural organization in normal versus glaucomatous human posterior sclerae. Investigative Ophthalmology & Visual Science 54, 7922–7932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ethier CR, Johnson M, Ruberti J, 2004. Ocular biomechanics and biotransport. Annual Review of Biomedical Engineering 6, 249–273. [DOI] [PubMed] [Google Scholar]
- Fata B, Zhang W, Amini R, Sacks MS, 2014. Insights into regional adaptations in the growing pulmonary artery using a meso-scale structural model: effects of ascending aorta impingement. Journal of Biomechanical Engineering 136, 021009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feola AJ, Myers JG, Raykin J, Mulugeta L, Nelson ES, Samuels BC, Ethier CR, 2016. Finite element modeling of factors influencing optic nerve head deformation due to intracranial pressure. Investigative ophthalmology & visual science 57, 1901–1911. [DOI] [PubMed] [Google Scholar]
- Feola AJ, Nelson ES, Myers J, Ethier CR, Samuels BC, 2018. The impact of choroidal swelling on optic nerve head deformation. Investigative ophthalmology & visual science 59, 4172–4181. [DOI] [PubMed] [Google Scholar]
- Fratzl P, 2008. Collagen: structure and mechanics, an introduction, Collagen. Springer, pp. 1–13. [Google Scholar]
- Girard MJ, Dahlmann-Noor A, Rayapureddi S, Bechara JA, Bertin BM, Jones H, Albon J, Khaw PT, Ethier CR, 2011. Quantitative mapping of scleral fiber orientation in normal rat eyes. Investigative Ophthalmology & Visual Science 52, 9684–9693. [DOI] [PubMed] [Google Scholar]
- Girard MJ, Downs JC, Bottlang M, Burgoyne CF, Suh J-KF, 2009a. Peripapillary and posterior scleral mechanics—part II: experimental and inverse finite element characterization. Journal of Biomechanical Engineering 131, 051012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJ, Downs JC, Burgoyne CF, Suh J-KF, 2009b. Peripapillary and posterior scleral mechanics—part I: development of an anisotropic hyperelastic constitutive model. Journal of Biomechanical Engineering 131, 051011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogola A, Jan N-J, Brazile B, Lam P, Lathrop KL, Chan KC, Sigal IA, 2018a. Spatial patterns and age-related changes of the collagen crimp in the human cornea and sclera. Investigative Ophthalmology & Visual Science 59, 2987–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogola A, Jan N-J, Lathrop KL, Sigal IA, 2018b. Radial and circumferential collagen fibers are a feature of the peripapillary sclera of human, monkey, pig, cow, coat, and sheep. Investigative Ophthalmology & Visual Science 59, 4763–4774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grytz R, Downs JC, 2013. A forward incremental prestressing method with application to inverse parameter estimations and eye-specific simulations of posterior scleral shells. Computer methods in biomechanics and biomedical engineering 16, 768–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grytz R, Meschke G, 2009. Constitutive modeling of crimped collagen fibrils in soft tissues. Journal of the Mechanical Behavior of Biomedical Materials 2, 522–533. [DOI] [PubMed] [Google Scholar]
- Grytz R, Meschke G, 2010. A computational remodeling approach to predict the physiological architecture of the collagen fibril network in corneo-scleral shells. Biomechanics and Modeling in Mechanobiology 9, 225–235. [DOI] [PubMed] [Google Scholar]
- Gsellman L, Amini R, 2016. Patients with intravitreal gas bubbles at risk of high intraocular pressure without exceeding elevation of surgery: theoretical analysis. Investigative ophthalmology & visual science 57, 3340–3347. [DOI] [PubMed] [Google Scholar]
- Hansen KA, Weiss JA, Barton JK, 2002. Recruitment of tendon crimp with applied tensile strain. Journal of Biomechanical Engineering 124, 72–77. [DOI] [PubMed] [Google Scholar]
- Hatami-Marbini H, Pachenari M, 2020. The contribution of sGAGs to stress-controlled tensile response of posterior porcine sclera. PLOS One 15, e0227856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill MR, Duan X, Gibson GA, Watkins S, Robertson AM, 2012. A theoretical and non-destructive experimental approach for direct inclusion of measured collagen orientation and recruitment into mechanical models of the artery wall. Journal of Biomechanics 45, 762–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho LC, Sigal IA, Jan N-J, Squires A, Tse Z, Wu EX, Kim S-G, Schuman JS, Chan KC, 2014. Magic angle–enhanced MRI of fibrous microstructures in sclera and cornea with and without intraocular pressure loading. Investigative Ophthalmology & Visual Science 55, 5662–5672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzapfel GA, 2001. Biomechanics of soft tissue. The handbook of materials behavior models 3, 1049–1063. [Google Scholar]
- Hua Y, Quinn M, Ji F, Salinas S, Amini R, Sigal IAJIO, Science V, 2022. Mechanical anisotropy of the equatorial sclera does not concur with its preferred fiber orientation. 63, 2731–A0095–2731–A0095. [Google Scholar]
- Hua Y, Tong J, Ghate D, Kedar S, Gu L, 2017. Intracranial pressure influences the behavior of the optic nerve head. Journal of Biomechanical Engineering 139, 031003. [DOI] [PubMed] [Google Scholar]
- Hua Y, Voorhees AP, Jan N-J, Wang B, Waxman S, Schuman JS, Sigal IA, 2020. Role of radially aligned scleral collagen fibers in optic nerve head biomechanics. Experimental Eye Research 199, 108188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua Y, Voorhees AP, Sigal IA, 2018. Cerebrospinal fluid pressure: Revisiting factors influencing optic nerve head biomechanics. Investigative Ophthalmology & Visual Science 59, 154–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jafari S, Lu Y, Park J, Demer JL, 2021. Finite element model of ocular adduction by active extraocular muscle contraction. Investigative Ophthalmology & Visual Science 62, 1–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan N-J, Brazile BL, Hu D, Grube G, Wallace J, Gogola A, Sigal IA, 2018. Crimp around the globe; patterns of collagen crimp across the corneoscleral shell. Experimental Eye Research 172, 159–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan N-J, Gomez C, Moed S, Voorhees AP, Schuman JS, Bilonick RA, Sigal IA, 2017a. Microstructural crimp of the lamina cribrosa and peripapillary sclera collagen fibers. Investigative Ophthalmology & Visual Science 58, 3378–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan N-J, Lee P-Y, Wallace J, Iasella M, Gogola A, Wang B, Sigal IA, 2022. Stretch-Induced Uncrimping of Equatorial Sclera Collagen Bundles. Journal of Biomechanical Engineering, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan N-J, Sigal IA, 2018. Collagen fiber recruitment: A microstructural basis for the nonlinear response of the posterior pole of the eye to increases in intraocular pressure. Acta Biomaterialia 72, 295–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan NJ, Grimm JL, Tran H, Lathrop KL, Wollstein G, Bilonick RA, Ishikawa H, Kagemann L, Schuman JS, Sigal IA, 2015. Polarization microscopy for characterizing fiber orientation of ocular tissues. Biomedical Optics Express 6, 4705–4718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jan NJ, Lathrop K, Sigal IA, 2017b. Collagen architecture of the posterior pole: High-resolution wide field of view visualization and analysis using polarized light microscopy. Investigative Ophthalmology & Visual Science 58, 735–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komai Y, Ushiki T, 1991. The three-dimensional organization of collagen fibrils in the human cornea and sclera. Investigative Ophthalmology & Visual Science 32, 2244–2258. [PubMed] [Google Scholar]
- Lee P-Y, Yang B, Hua Y, Waxman S, Zhu Z, Ji F, Sigal IA, 2022. Real-time imaging of optic nerve head collagen microstructure and biomechanics using instant polarized light microscopy. Experimental Eye Research 217, 108967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ling YTT, Shi R, Midgett DE, Jefferys JL, Quigley HA, Nguyen TD, 2019. Characterizing the collagen network structure and pressure-induced strains of the human lamina cribrosa. Investigative Ophthalmology & Visual Science 60, 2406–2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Wang L, Ji J, Yao W, Wei W, Fan J, Joshi S, Li D, Fan Y, 2014. A mechanical model of the cornea considering the crimping morphology of collagen fibrils. Investigative Ophthalmology & Visual Science 55, 2739–2746. [DOI] [PubMed] [Google Scholar]
- Mattson JM, Turcotte R, Zhang Y, 2017. Glycosaminoglycans contribute to extracellular matrix fiber recruitment and arterial wall mechanics. Biomechanics and Modeling in Mechanobiology 16, 213–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meek KM, 2009. Corneal collagen - its role in maintaining corneal shape and transparency. Biophysical Reviews 1, 83–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Midgett DE, Jefferys JL, Quigley HA, Nguyen TD, 2020. The inflation response of the human lamina cribrosa and sclera: Analysis of deformation and interaction. Acta Biomaterialia 106, 225–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morishige N, Wahlert AJ, Kenney MC, Brown DJ, Kawamoto K, Chikama T. i., Nishida T, Jester JV, 2007. Second-harmonic imaging microscopy of normal human and keratoconus cornea. Investigative Ophthalmology & Visual Science 48, 1087–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murienne BJ, Chen ML, Quigley HA, Nguyen TD, 2016. The contribution of glycosaminoglycans to the mechanical behaviour of the posterior human sclera. Journal of The Royal Society Interface 13, 20160367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TD, 2016. Biomechanics of the Cornea and Sclera, Structure-Based Mechanics of Tissues and Organs. Springer, pp. 285–315. [Google Scholar]
- Norman RE, Flanagan JG, Rausch SM, Sigal IA, Tertinegg I, Eilaghi A, Portnoy S, Sled JG, Ethier CR, 2010. Dimensions of the human sclera: thickness measurement and regional changes with axial length. Experimental Eye Research 90, 277–284. [DOI] [PubMed] [Google Scholar]
- Norman RE, Flanagan JG, Sigal IA, Rausch SM, Tertinegg I, Ethier CR, 2011. Finite element modeling of the human sclera: influence on optic nerve head biomechanics and connections with glaucoma. Experimental Eye Research 93, 4–12. [DOI] [PubMed] [Google Scholar]
- Ostrin LA, Wildsoet CF, 2016. Optic nerve head and intraocular pressure in the guinea pig eye. Experimental Eye Research 146, 7–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandolfi A, Gizzi A, Vasta M, 2019. A microstructural model of cross-link interaction between collagen fibrils in the human cornea. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 377, 20180079. [DOI] [PubMed] [Google Scholar]
- Pandolfi A, Holzapfel GA, 2008. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. Journal of Biomechanical Engineering 130. [DOI] [PubMed] [Google Scholar]
- Petsche SJ, Pinsky PM, 2013. The role of 3-D collagen organization in stromal elasticity: a model based on X-ray diffraction data and second harmonic-generated images. Biomechanics and Modeling in Mechanobiology 12, 1101–1113. [DOI] [PubMed] [Google Scholar]
- Pijanka JK, Coudrillier B, Ziegler K, Sorensen T, Meek KM, Nguyen TD, Quigley HA, Boote C, 2012. Quantitative mapping of collagen fiber orientation in non-glaucoma and glaucoma posterior human sclerae. Investigative Ophthalmology & Visual Science 53, 5258–5270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijanka JK, Markov PP, Midgett D, Paterson NG, White N, Blain EJ, Nguyen TD, Quigley HA, Boote C, 2019. Quantification of collagen fiber structure using second harmonic generation imaging and two‐dimensional discrete Fourier transform analysis: application to the human optic nerve head. Journal of Biophotonics 12, e201800376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quantock AJ, Winkler M, Parfitt GJ, Young RD, Brown DJ, Boote C, Jester JV, 2015. From nano to macro: studying the hierarchical structure of the corneal extracellular matrix. Experimental Eye Research 133, 81–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raz E, Lanir Y, 2009. Recruitment viscoelasticity of the tendon. Journal of Biomechanical Engineering 131, 111008. [DOI] [PubMed] [Google Scholar]
- Roberts CJ, Dupps WJ, Downs JC, 2018. Biomechanics of the Eye. Kugler Publications. [Google Scholar]
- Roy S, Boss C, Rezakhaniha R, Stergiopulos N, 2010. Experimental characterization of the distribution of collagen fiber recruitment. Journal of Biorheology 24, 84–93. [Google Scholar]
- Sibony PA, Wei J, Sigal IA, 2018. Gaze-evoked deformations in optic nerve head drusen: repetitive shearing as a potential factor in the visual and vascular complications. Ophthalmology 125, 929–937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, 2009. Interactions between geometry and mechanical properties on the optic nerve head. Investigative Ophthalmology & Visual Science 50, 2785–2795. [DOI] [PubMed] [Google Scholar]
- Sigal IA, 2011. An applet to estimate the IOP-induced stress and strain within the optic nerve head. Investigative Ophthalmology & Visual Science 52, 5497–5506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Ethier CR, 2005a. Factors influencing optic nerve head biomechanics. Investigative Ophthalmology & Visual Science 46, 4189–4199. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR, 2004. Finite element modeling of optic nerve head biomechanics. Investigative ophthalmology & visual science 45, 4378–4387. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR, 2005b. Reconstruction of human optic nerve heads for finite element modeling. Technology and Health Care 13, 313–329. [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR, 2009a. Modeling individual-specific human optic nerve head biomechanics. Part I: IOP-induced deformations and influence of geometry. Biomech Model Mechanobiol 8, 85–98. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR, 2009b. Modeling individual-specific human optic nerve head biomechanics. Part II: influence of material properties. Biomech Model Mechanobiol 8, 99–109. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR, 2010a. 3D morphometry of the human optic nerve head. Experimental eye research 90, 70–80. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Grimm JL, 2012. A few good responses: which mechanical effects of IOP on the ONH to study? Investigative Ophthalmology & Visual Science 53, 4270–4278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Yang H, Roberts MD, Burgoyne CF, Downs JC, 2011a. IOP-induced lamina cribrosa displacement and scleral canal expansion: an analysis of factor interactions using parameterized eye-specific models. Investigative ophthalmology & visual science 52, 1896–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Yang H, Roberts MD, Downs JC, 2010b. Morphing methods to parameterize specimen-specific finite element model geometries. Journal of biomechanics 43, 254–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Yang H, Roberts MD, Grimm JL, Burgoyne CF, Demirel S, Downs JC, 2011b. IOP-induced lamina cribrosa deformation and scleral canal expansion: independent or related? Investigative ophthalmology & visual science 52, 9023–9032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang P, Kirby MA, Le N, Li Y, Zeinstra N, Lu GN, Murry CE, Zheng Y, Wang RK, 2021. Polarization sensitive optical coherence tomography with single input for imaging depth-resolved collagen organizations. Light: Science & Applications 10, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas VS, Lai V, Amini R, 2019. A computational multi-scale approach to investigate mechanically-induced changes in tricuspid valve anterior leaflet microstructure. Acta Biomaterialia 94, 524–535. [DOI] [PubMed] [Google Scholar]
- Tran H, Jan N-J, Hu D, Voorhees A, Schuman JS, Smith MA, Wollstein G, Sigal IA, 2017. Formalin fixation and cryosectioning cause only minimal changes in shape or size of ocular tissues. Scientific Reports 7, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees A, Grimm J, Bilonick R, Kagemann L, Ishikawa H, Schuman J, Wollstein G, Sigal I, 2016. What is a typical optic nerve head? Experimental eye research 149, 40–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees AP, Ho LC, Jan N-J, Tran H, van der Merwe Y, Chan K, Sigal IA, 2017a. Whole-globe biomechanics using high-field MRI. Experimental Eye Research 160, 85–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees AP, Hua Y, Brazile BL, Wang B, Waxman S, Schuman JS, Sigal IA, 2020. So-called lamina cribrosa defects may mitigate IOP-induced neural tissue insult. Investigative Ophthalmology & Visual Science 61, 15–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees AP, Jan NJ, Austin ME, Flanagan JG, Sivak JM, Bilonick RA, Sigal IA, 2017b. Lamina cribrosa pore shape and size as predictors of neural tissue mechanical insult. Investigative Ophthalmology & Visual Science 58, 5336–5346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees AP, Jan NJ, Sigal IA, 2017c. Effects of collagen microstructure and material properties on the deformation of the neural tissues of the lamina cribrosa. Acta Biomaterialia 58, 278–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Hua Y, Brazile BL, Yang B, Sigal IA, 2020. Collagen fiber interweaving is central to sclera stiffness. Acta Biomaterialia 113, 429–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Raykin J, Gleason RL Jr, Ethier CR, 2015. Residual deformations in ocular tissues. Journal of The Royal Society Interface 12, 20141101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Beotra MR, Tun TA, Baskaran M, Perera S, Aung T, Strouthidis NG, Milea D, Girard MJ, 2016a. In vivo 3-dimensional strain mapping confirms large optic nerve head deformations following horizontal eye movements. Investigative ophthalmology & visual science 57, 5825–5833. [DOI] [PubMed] [Google Scholar]
- Wang X, Rumpel H, Lim WEH, Baskaran M, Perera SA, Nongpiur ME, Aung T, Milea D, Girard MJ, 2016b. Finite element analysis predicts large optic nerve head strains during horizontal eye movements. Investigative Ophthalmology & Visual Science 57, 2452–2462. [DOI] [PubMed] [Google Scholar]
- Weisbecker H, Unterberger MJ, Holzapfel GA, 2015. Constitutive modelling of arteries considering fibre recruitment and three-dimensional fibre distribution. Journal of The Royal Society Interface 12, 20150111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitford C, Joda A, Jones S, Bao F, Rama P, Elsheikh A, 2016. Ex vivo testing of intact eye globes under inflation conditions to determine regional variation of mechanical stiffness. Eye and Vision 3, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willemse J, Gräfe MG, Verbraak FD, de Boer JF, 2020. In vivo 3D determination of peripapillary scleral and retinal layer architecture using polarization-sensitive optical coherence tomography. Translational Vision Science & Technology 9, 21–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler M, Chai D, Kriling S, Nien CJ, Brown DJ, Jester B, Juhasz T, Jester JV, 2011. Nonlinear optical macroscopic assessment of 3-D corneal collagen organization and axial biomechanics. Investigative Ophthalmology & Visual Science 52, 8818–8827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wold S, 1974. Spline functions in data analysis. Technometrics 16, 1–11. [Google Scholar]
- Yang B, Jan NJ, Brazile B, Voorhees A, Lathrop KL, Sigal IA, 2018. Polarized light microscopy for 3‐dimensional mapping of collagen fiber architecture in ocular tissues. Journal of biophotonics 11, e201700356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Albon J, Jones H, Gouget CL, Ethier CR, Goh JC, Girard MJ, 2015. Collagen microstructural factors influencing optic nerve head biomechanics. Investigative Ophthalmology & Visual Science 56, 2031–2042. [DOI] [PubMed] [Google Scholar]
- Zhou D, Abass A, Eliasy A, Studer HP, Movchan A, Movchan N, Elsheikh A, 2019a. Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue. Journal of the Royal Society Interface 16, 20180685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D, Eliasy A, Abass A, Markov P, Whitford C, Boote C, Movchan A, Movchan N, Elsheikh A, 2019b. Analysis of X-ray scattering microstructure data for implementation in numerical simulations of ocular biomechanical behaviour. PLOS One 14, e0214770. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


