Minimising Tibial Fracture after Unicompartmental Knee Replacement: A Probabilistic Finite Element Study

Abstract

Background

Periprosthetic tibial fracture after unicompartmental knee replacement is a challenging post-operative complication. Patients have an increased risk of mortality after fracture, the majority undergo further surgery, and the revision operations are less successful. Inappropriate surgical technique increases the risk of fracture, but it is unclear which technical aspects of the surgery are most problematic and no research has been performed on how surgical factors interact.

Methods

Firstly, this study quantified the typical variance in surgical cuts made during unicompartmental knee replacement (determined from bones prepared by surgeons during an instructional course). Secondly, these measured distributions were used to create a probabilistic finite element model of the tibia after replacement. A thousand finite element models were created using the Monte Carlo method, representing 1000 virtual operations, and the risk of tibial fracture was assessed.

Findings

Multivariate linear regression of the results showed that excessive resection depth and making the vertical cut too deep posteriorly increased the risk of fracture. These two parameters also had high variability in the prepared synthetic bones. The regression equation calculated the risk of fracture from three cut parameters (resection depth, vertical and horizonal posterior cuts) and fit the model results with 90% correlation.

Interpretation

This study introduces the application of a probabilistic approach to predict the aetiology of fracture after unicompartmental knee replacement and has quantified the potential importance of surgical saw cut variations for the first time. Targeted changes to operative technique can now be considered to seek to reduce the risk of periprosthetic fracture.

1. Introduction

Periprosthetic tibial fracture after unicompartmental knee replacement (UKR) is a severe complication which can be challenging to treat and manage [1]. Fracture is associated with increased mortality and significant morbidity, and is increasing in incidence [2]. Of the cases of tibial fracture after UKR reported in the literature [1; 3–11], approximately half of the fractures occurred during the operation, and half occurred within 6 weeks post-operatively. More than 50% of the reported case studies end with revision to total knee replacement, requiring removal of the cruciate ligament(s) and leading to reduced knee function [1; 3–11].

The reported incidence of tibial fracture after UKR ranges from 0.8% [1] to 5.0 % [11]. The absolute number of patients at risk of fracture is rising [2] as a result of increasing numbers of UKRs being performed each year [12], greater life expectancy [13], higher cases of osteoporosis [14], and increasing patient activity [15]. It is, therefore, important to identify which aspects of UKR surgery put patients at the greatest risk of fracture, so that the operative technique can be optimised to minimise the occurrence of this serious complication.

The issue of periprosthetic fracture has been reported in several different unicompartmental knee designs, so it appears the issue is not design-specific [1; 3–4; 6; 8; 11], though one study suggested cementless components are at greater risk [16]. There is uncertainty in the literature regarding the most important surgical risk factors for tibial fracture after UKR. The surgical errors that have been proposed to cause tibial plateau fracture include:

• excessive depth of surgical cuts made for the tray, tray keel, or pegs [1; 4; 9; 17; 18]

• too many holes in the cortex for alignment guides [6; 10]

• perforation of the tibial cortex [5]

• under-sizing of the tibial tray [1; 3]

• use of excessive force when impacting the plateau [1]

• excessive removal of bone [1].

However, of these studies, Clarius et al. were the only authors to base their conclusions on experimental evidence and showed that extended vertical cuts reduced the force required to cause tibial fracture by 30% [18].

Finite element analysis (FEA) is a useful tool for predicting bone fracture, and it has been applied most commonly to fractures of the femoral neck. Schileo et al. proposed a Risk Of Fracture (ROF) criterion (Equation 1) which has been validated for hip fracture cases [19]. The ROF is calculated from the maximum principal strain (ε) within the bone divided by elastic limit strain values. The criterion distinguishes between tensile and compressive loading states, and high ROF values in a localised region indicate a higher risk of fracture.

$$\text{ROF}=\{\begin{array}{ll}\epsilon /0.0073\hfill & \hfill \mathit{if}\mathit{tensile}\hfill \\ \hfill \epsilon /0.0104\hfill & if\mathit{compressive}\hfill \end{array}$$ (1)

An advantage of using FEA to examine risk factors for bone fracture is that the uncertainty resulting from confounding factors is removed, enabling the study to focus on the parameters of interest. The aim of this study was apply Schileo’s fracture criterion and utilise probabilistic FEA methods to assess which surgical parameters increase the risk of periprosthetic fracture after unicompartmental knee replacement.

2. Methods

The study first quantified the surgical variability in the preparation of tibia for UKR, then used the Monte Carlo method to virtually implant 1000 UKRs, representing that variability.

The risk of fracture for the finite element models was found and multivariate linear regression used to assess the influence of each surgical cut parameter.

2.1. Quantification of variability in surgical cuts

Twenty three right tibial Sawbones (custom anatomic design made for Zimmer-Biomet UK Ltd. by Sawbones, Pacific Research Laboratories Inc., Vashon Island, Washington, USA) were prepared for medial mobile UKR (Oxford Partial Knee, Biomet, Bridgend, UK) as part of an instructional course. The attendees were a mixture of experienced and inexperienced orthopaedic surgeons who each prepared a Sawbone tibia after receiving training in the operative technique. Measurements were then taken of the positions and depths of the surgical cuts (Figure 1). The parameters examined were:

• the resection depth (the superior-inferior distance from the tibial plateau on the lateral side to the resected medial horizontal cut, where the distance was parallel to the mechanical axis)

• the angle between the horizontal and vertical cuts

• the depth of the vertical cuts, both at the posterior and anterior cortex

• the depth of the horizontal cuts, both at the posterior and anterior cortex

• the depth of the pin hole (used to hold the cutting guide)

Figure 1.

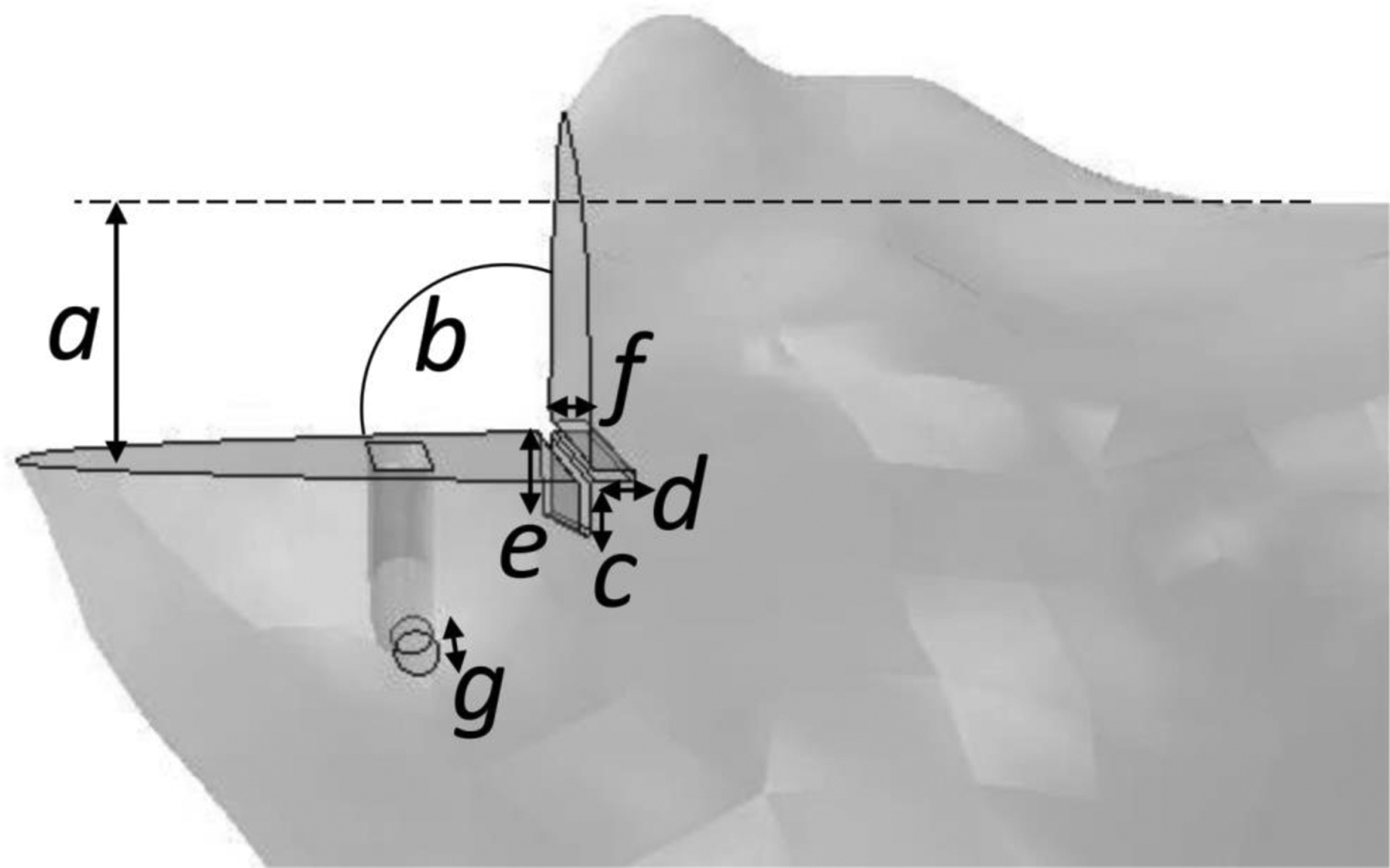
The surgical cut parameters measured from synthetic sawbone tibia were: the resection depth (a), the angle between the horizontal and vertical cuts (b), the extension of the vertical and horizontal cuts posteriorly (e, f) and anteriorly (c, d), and the depth of the pin hole required to hold the cutting guide (g).

2.2. Finite element model

2.2.1. Geometry

The finite element model was based on a previously published UKR tibial model that was validated against cadaveric tests [20]. The tibial geometry was segmented from a CT scan of a cadaveric tibia obtained from a male donor aged 60 years with a body mass index of 22.5.

The geometry was segmented using Mimics software (version 14.1, Materialise, Leuven, Belgium) and smoothed using the Scanto3D function in SolidWorks software (version 2012, Simulia, Waltham, MA, USA). The tibia was aligned so that the tibial mechanical axis was the Z-axis, anterior-posterior was the X-axis, and medial-lateral was the Y-axis. Previous work verified that use of a shortened tibia improves computational speed without affecting the strain in the periprosthetic region [21]. Therefore, the length of the tibia was shortened to 100 mm proximally.

The UKR was implanted virtually using Boolean functions within ABAQUS software (Version 6.12, Dassault-Systèmes, Rhode Island, USA). A Python script (version 2.6, Python Software Foundation) was created to automate the implantation for different surgical and loading parameters. The width of all saw cuts used was 1 mm, which is the width of the saw blade used during surgery [22]. The base of the Oxford Unicompartmental Knee tibial tray was fully fixed to the tibia, and frictionless contact was defined between the tray wall and the bone. Neither the effect of interference fit nor loosening was examined in this study.

2.2.2. Mesh

The finite element mesh was created using ABAQUS software. Quadratic tetrahedral elements (C3D10) were used to mesh the bone and the tibial tray was meshed with quadrilateral rigid elements (R3D4). A smaller element size (a third of the overall element size) was assigned to; the muscle attachment sites, the edges created by the saw cuts, and the drilled pin-hole.

A mesh convergence study was performed to determine the optimal mesh density, where convergence was defined as when the output was within 5% of the next three finer element sizes (0.1 mm mesh size intervals). The model converged for both output parameters at an overall element size of 2.4 mm.

2.2.3. Material properties

The tray was modelled as a rigid cobalt chromium-molybdenum alloy with a density of 8.4 g cm⁻³ [23]. The tibia was modelled as a heterogeneous linear elastic material, where the modulus of each element was assigned based on the corresponding gray scale value of that element in the CT scan of the tibia. The bone material assignment was performed with Mimics software (400 material intervals with a modulus range of 1 to 22 GPa, consistent with previous work [20]).

2.2.4. Musculoskeletal model

The muscle and contact loads applied to the tibia throughout the gait cycle were estimated using data from an instrumented total knee replacement (TKR) implanted in a male subject (age: 83 years, BMI: 22.5, alignment: neutral) at the Shiley Center for Orthopaedic Research and Education at the Scripps Clinic in California [24]. The data were recorded while the patient performed overground walking trials at a self-selected speed [25; 26] and included the following quantities: contact forces on the tibial tray, ground reaction forces and moments, surface marker positions, and electromyographic (EMG) data. Medial and lateral tibial contact forces were calculated from the implant load cell data using an elastic foundation contact model [27]. Muscle force estimates were generated using static optimization of a subject-specific knee model which minimized (the sum of the squares of) muscle activations. The measured tibio-femoral contact forces and net (inverse-dynamic) knee loads were also matched as part of this optimization [28] constructed in OpenSim [29]. The musculoskeletal knee model and muscle force estimation approach have been described in detail in a previous study [23].

2.2.5. Boundary conditions

The muscle and contact loads from the musculoskeletal model were applied to the FE model using distributed coupling to the tibial attachment site (Figure 2). On the lateral side the compartment loads were applied to the tibial articular surface in the same manner, while on the medial side the compartment load was applied to the upper surface of the tibial tray using an equation derived in a previous study to represent the pressure field [23]. The distal end of the tibia was fixed in all degrees of freedom.

Figure 2.

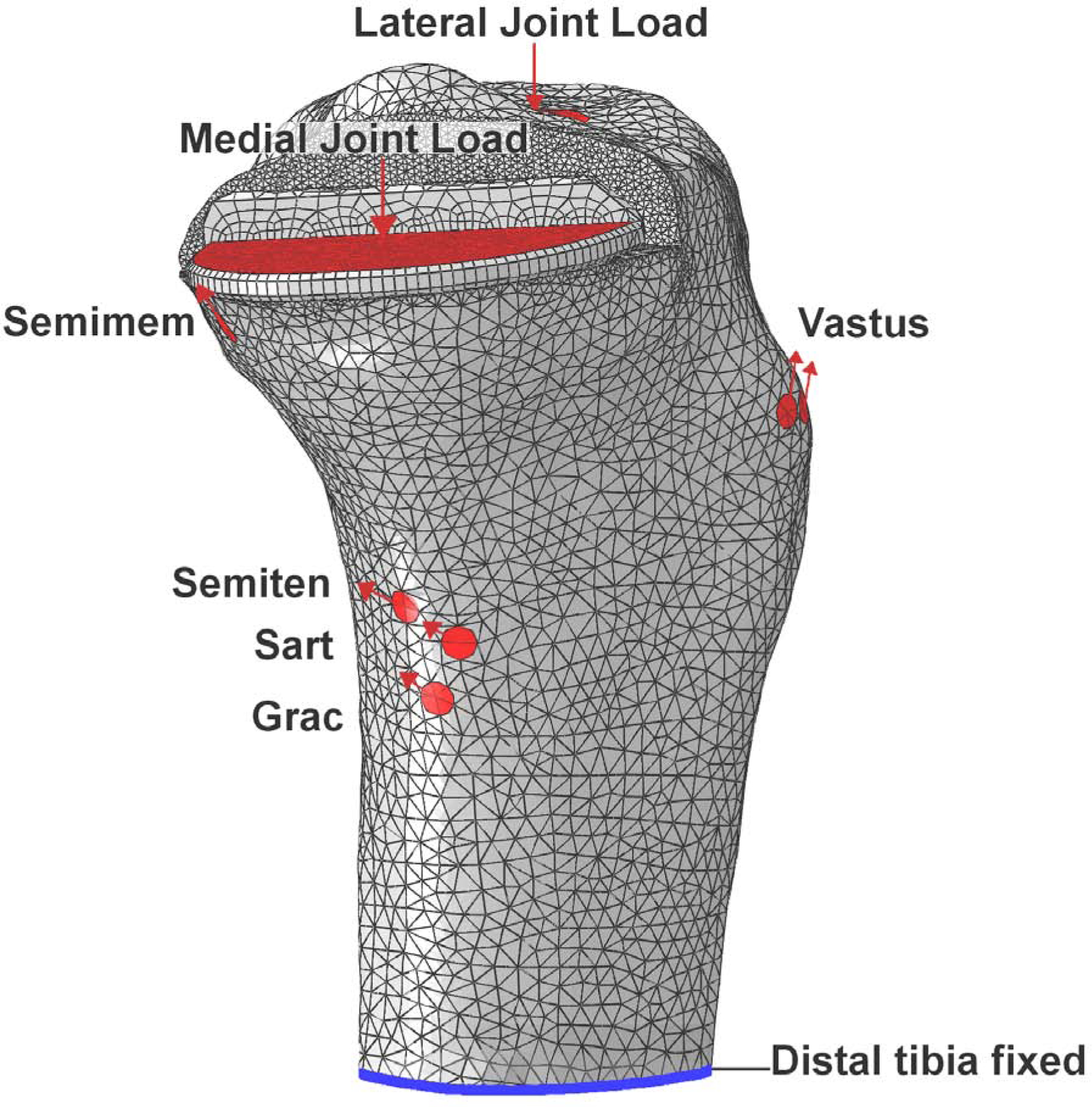
The constraint (blue), load locations, and vectors (red) applied to the model at 16% of the gait cycle. The medial view shown includes the gracilis (Grac), sartorius (Sart), semiteninosus (Semiten), semimembranosus (Semimem), vastus medialis, vastus intermedius and vastus lateralis (Vastus) muscles forces; the tensor fasciae latae muscle forces were also applied on the lateral side.

The cadaveric tibia used for the finite element model in the present study was different from the instrumented knee subject tibia. Both tibias were from male subjects with a similar body mass index (instrumented tibia: 22.5 and cadaveric tibia: 25.9) and size (instrumented tibia: 75.0 mm tibial width, and cadaveric tibia: 76.5 mm tibial width) but different age (instrumented tibia: 83, cadaveric tibia: 60). An iterative closest point (ICP) algorithm was used to register the two tibias and determine the muscle attachment sites and vectors for the new geometry.

2.2.6. Post-processing

The risk of fracture parameter described by Schileo et al. [19] (Equation 1) is not automatically calculated by ABAQUS software, so a custom Python script was written to interact with ABAQUS and calculate the new field output. The two outputs used for the analysis were: (1) the maximum ROF value (omitting artificially high results at muscle attachment sites), and (2) the total volume of elements exceeding an ROF of 1 (threshold for fracture defined by Schileo).

2.3. Application of the Monte Carlo method

The measurements taken from the tibia prepared during the surgical training course (Section 2.1, Figure 1) were used to define the envelope of surgical cut variation for the models. A thousand finite element models were then created to represent the variance in surgical technique.

The distribution of each surgical cut parameter was categorised from the measured data using the Kernel Density function from the ‘scikit-learn’ machine learning module implemented in Python [30]. A Gaussian kernel (K(x; h)) was applied with a bandwidth (h) of 0.75, to create the function representing the distribution of cut parameters measured from the sawbones. The kernel has the form given in Equation (2) where the density estimate at point y is found from the provided group of points x_i; i = 1 … N.

$${\rho }_K\left(y\right)=\sum _{i=1}^{N}K\left(\frac{y-x_i}{h}\right)$$ (2)

An ABAQUS-python script was then used to automate the creation of each finite element model. The script involved the following steps:

1. Randomly select each surgical cut parameter from its calculated distribution, using Python ‘random’ and ‘scikit-learn’ packages.

2. Prepare tibia using Boolean operations

3. Assemble tibia and UKR components

4. Apply muscle loading, joint loading, constraints. and materials

5. Mesh and solve

To confirm that 1000 models were sufficient to achieve convergence of the Monte Carlo method, we used the method described by Fishman et al. [31]. Convergence was defined when the mean and coefficient of variance of both risk of fracture output parameters were within 3% of their values from the last 10% of valid instantiations [31; 32].

2.4. Model verification

The finite element model was verified two ways: (1) the location of elements at risk of fracture were compared to typical clinical fracture locations [1] and (2) the maximum ROF in the periprosthetic region was compared with failure loads reported by Clarius et al. [18]. To replicate the experiments performed by Clarius an increasing load (max 10 kN) was applied to the medial compartment while the two risk of fracture criteria were recorded. The tibia was analysed with, and without an extended vertical cut (cut angled at 10 degrees [18]). No muscle or lateral compartment loading was applied.

2.5. Statistical analysis

Which parameters influenced the risk of fracture was determined by performing an analysis of variance (ANOVA) test. The parameters which significantly (p<0.05) influenced the risk of fracture were then input into a generalised linear regression (GLM) model. All statistical analyses were implemented in R (www.r-project.org). To ensure the dependent variables (maximum ROF and Volume of failed elements) were normally distributed for the ANOVA and GLM model, we transformed the data by taking the logarithm of the maximum ROF and the cube root of the volume of failed elements.

3. Results

3.1. Quantification of variability in surgical cuts

The measurements of the prepared tibial Sawbones highlighted large variability in the vertical and horizontal cuts posteriorly (Table 1). The standard deviation in the anterior cut depths was half that of the posterior cuts. Furthermore, in 14 of the 23 Sawbone tibias, the pin hole had gone into the keel slot, greatly increasing the hole depth and producing a bi-modal distribution with a high standard deviation. The cut angle had very low variability (percent deviation 1.6%) and so was not included in the Monte Carlo models.

Table 1.

The surgical cut parameters measured from 23 synthetic tibias prepared by surgeons during an instructional course. The mean value, standard deviation and distribution percentiles for each parameter are summarised.

Parameter	Mean	Standard Deviation	0%	25%	50%	75%	100%
a (resection depth, mm)	8.8	1.7	5.0	8.0	9.0	10.0	11.0
b (angle between cuts, deg)	90.6	1.4	88.0	90.0	90.0	91.0	95.0
c (vertical cut anterior, mm)	0.5	1.0	0.0	0.0	0.0	0.3	4.0
d (horizontal cut anterior, mm)	0.7	0.9	0.0	0.0	0.0	1.0	3.0
e (vertical cut posterior, mm)	4.2	3.9	0.0	0.0	4.0	7.0	12.0
f (horizontal cut posterior, mm)	1.3	2.1	0.0	0.0	1.0	1.3	7.5
g (pin depth, mm)	28.6	6.8	8.0	25.0	30.0	33.5	36.0

3.2. Application of the Monte Carlo method

A linear relationship was found between medial contact force and the maximum ROF when loaded through the whole gait cycle (R² = 0.83), despite the varying muscle loads and load vectors from the musculoskeletal model (Figure 3). The maximum ROF value and the maximum volume of failed elements occurred at 16% of the gait cycle, so these results were used for the regression analysis.

Figure 3.

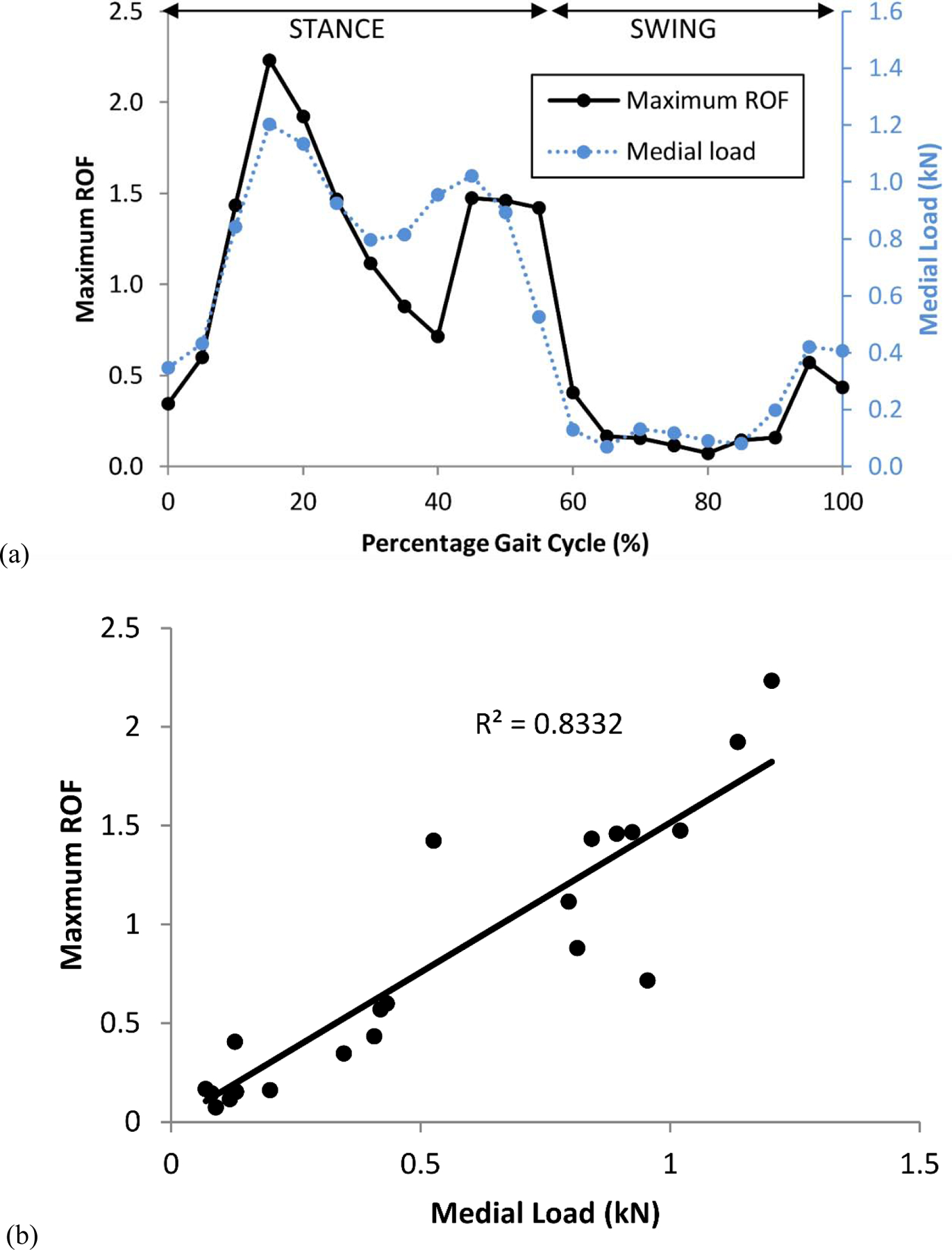
The risk of fracture (ROF) varied through the gait cycle (a) and a linear correlation was observed with medial load (b).

The ANOVA results (Table 2) found the extension of the vertical cut posteriorly (e), the resection depth (a), and extension of the horizontal cut posteriorly (f) to significantly influence both the maximum ROF value and the volume of failed elements. Consequently, these parameters were used to create the regression model. The correlation between both output variables and the posterior vertical and horizontal cuts and the resection depth was also confirmed visually (Figure 4).

Table 2.

ANOVA test of the null hypotheses that the surgical cut parameters do not influence the maximum ROF value, and the volume of failed elements. The ANOVA F-value (F), p-value (p) and significance (Sig) results (*=p<0.05, **=p<0.01, ***=p<0.001, NS=p>0.5) are shown.

Parameter	Maximum ROF value			Volume of failed elements
	F	p	Sig	F	p	Sig
a (resection depth, mm)	183.4	2.2e-16	***	1295.5	2.2e-16	***
c (vertical cut anterior, mm)	0.1	0.028	*	0.04	0.843	NS
d (horizontal cut anterior, mm)	21.2	0.709	NS	21.3	4.3e-06	***
e (vertical cut posterior, mm)	4.9	2.2e-16	***	2859.7	2.2e-16	***
f (horizontal cut posterior, mm)	628.8	4.8e-06	***	315.4	2.2e-16	***
g (pin depth, mm)	0.8	0.365	NS	0.3	0.565	NS

Figure 4.

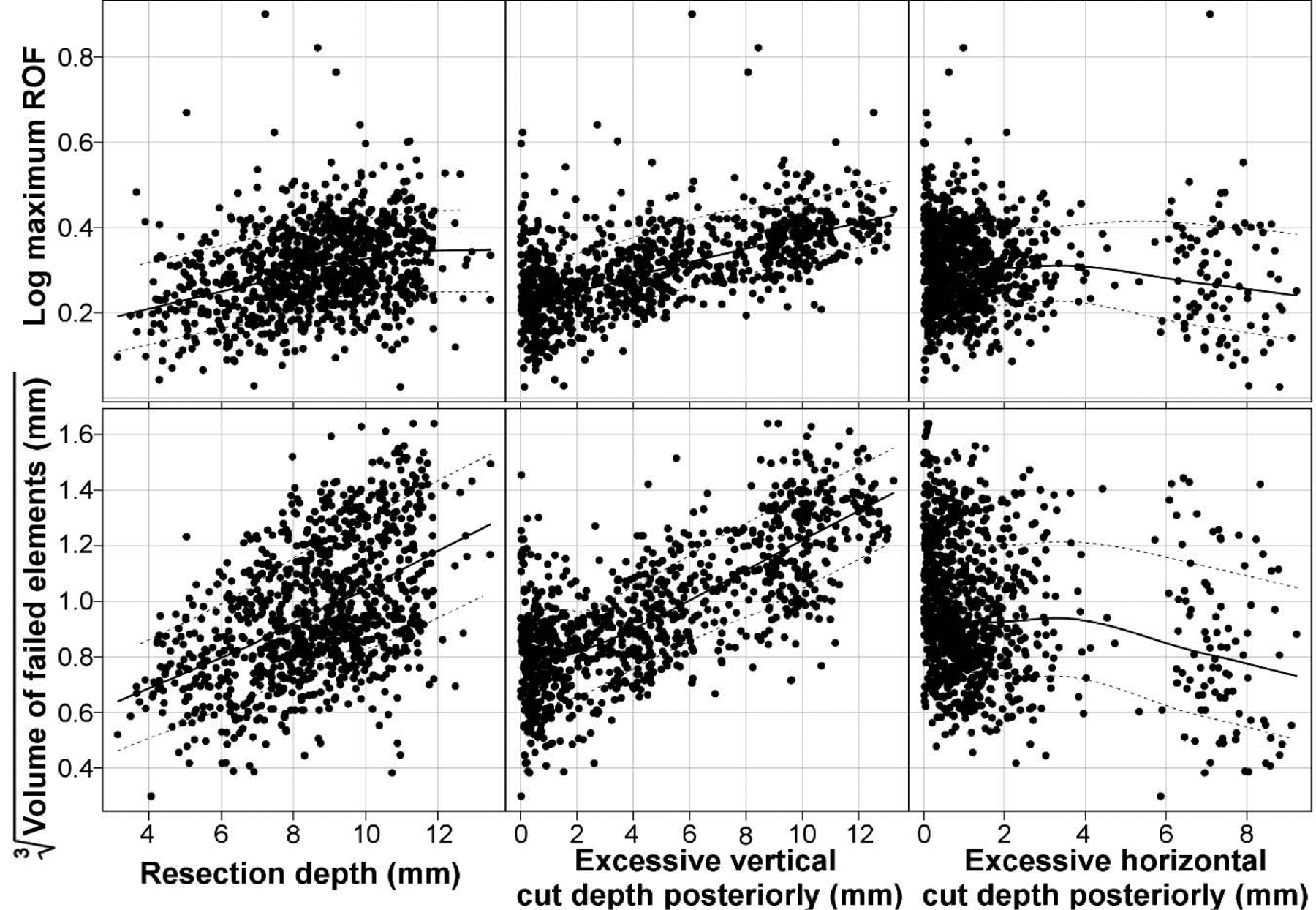
Scatterplots of regression parameters which were found to significantly influence the maxim ROF value (log) and volume of failed elements (cube root). The lines in each plot represent the mean and the interquartile range.

The multivariate linear regression model found that the greater the resection depth and the more extended the posterior vertical cut, the greater the risk of fracture in terms of both the maximum ROF and the volume of failed elements. In contrast, extension of the horizontal cut posteriorly reduced the risk of fracture slightly. The parameters which most influenced the risk of fracture were the resection depth and extension of the vertical cut posteriorly, as can be seen from the 3-dimensional scatterplot shown in Figure 5.

Figure 5.

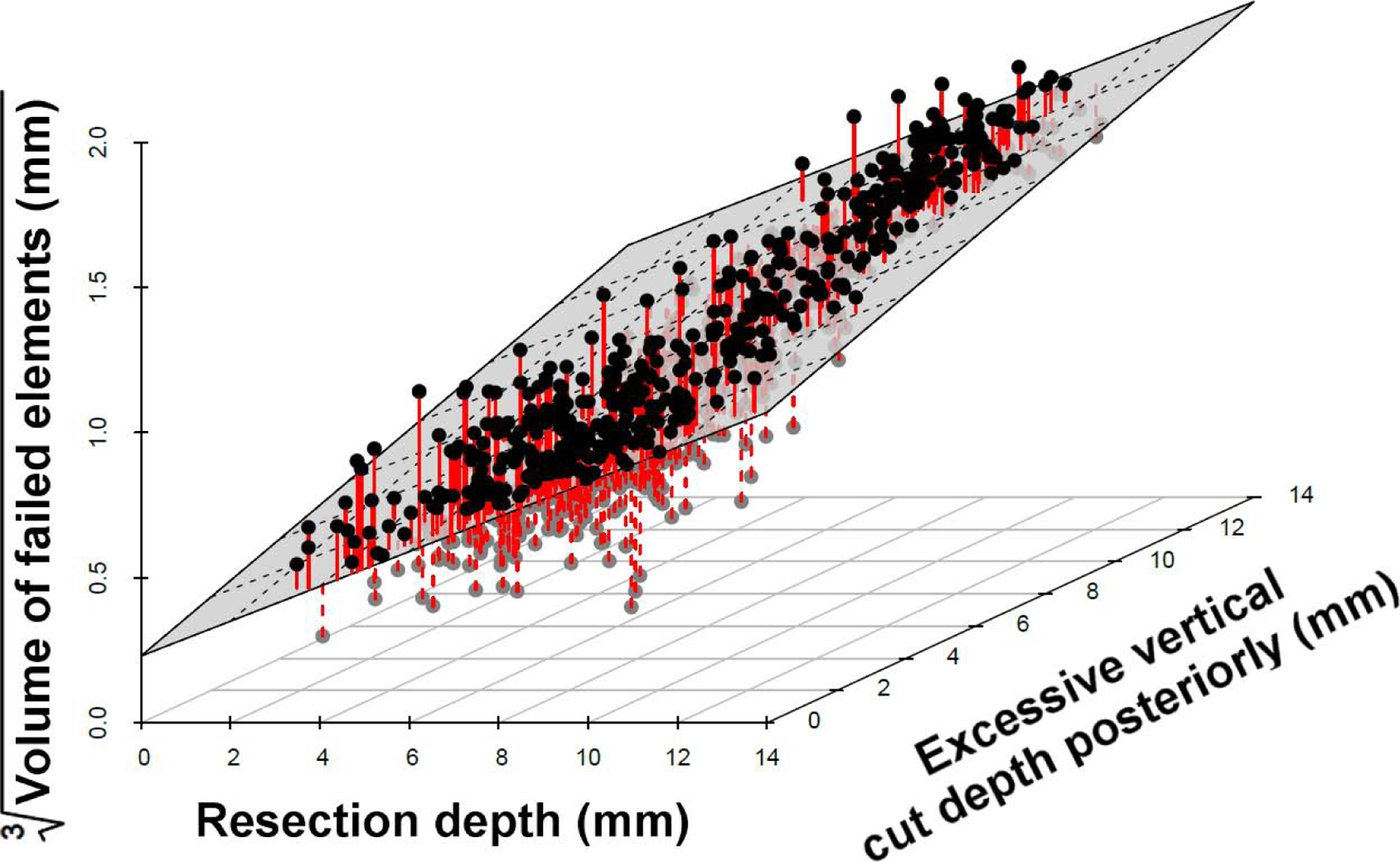
Scatterplot illustrating the dependence of the volume of failed elements on the resection depth and the vertical cut. The multivariate regression model fit is represented by the plane and the red lines indicate the residuals.

From the known resection depth, posterior vertical cut, and posterior horizontal cut for each of the 1000 models, the regression equations were used to calculate the maximum ROF value (Equation (3)) and the volume of failed elements (Equation (4)). The equations were able to predict the finite element maximum ROF with a Pearson’s correlation coefficient of 0.59 and the volume of failed elements with a 90% correlation, indicating a reasonable regression model fit.

$$MaxROF={10}^{\wedge }\left(0.0152e+0.0161a-0.0052f+0.102\right)$$ (3)

$$\mathit{Volume}\mathit{of}\mathit{failed}\mathit{elements}={\left(0.0454e+0.061a-0.029f+0.267\right)}^{\wedge }3$$ (4)

Where: (a) is the resection depth, (e) is the extension of the vertical cut posteriorly, and (f) is the extension of the horizontal cut posteriorly.

3.3. Model Verification

When the tibia was prepared and loaded in the same manner as described by Clarius et al. [18], regions of high ROF were observed in the corner between the horizontal and the vertical cut and in the region surrounding the keel. At high loads, these two regions combined to create a line of high fracture risk extending to the tibial cortex (Figure 6). The line matched the path of fractures observed clinically [1], confirming that the ROF parameter is an indicator of tibial fracture risk.

Figure 6.

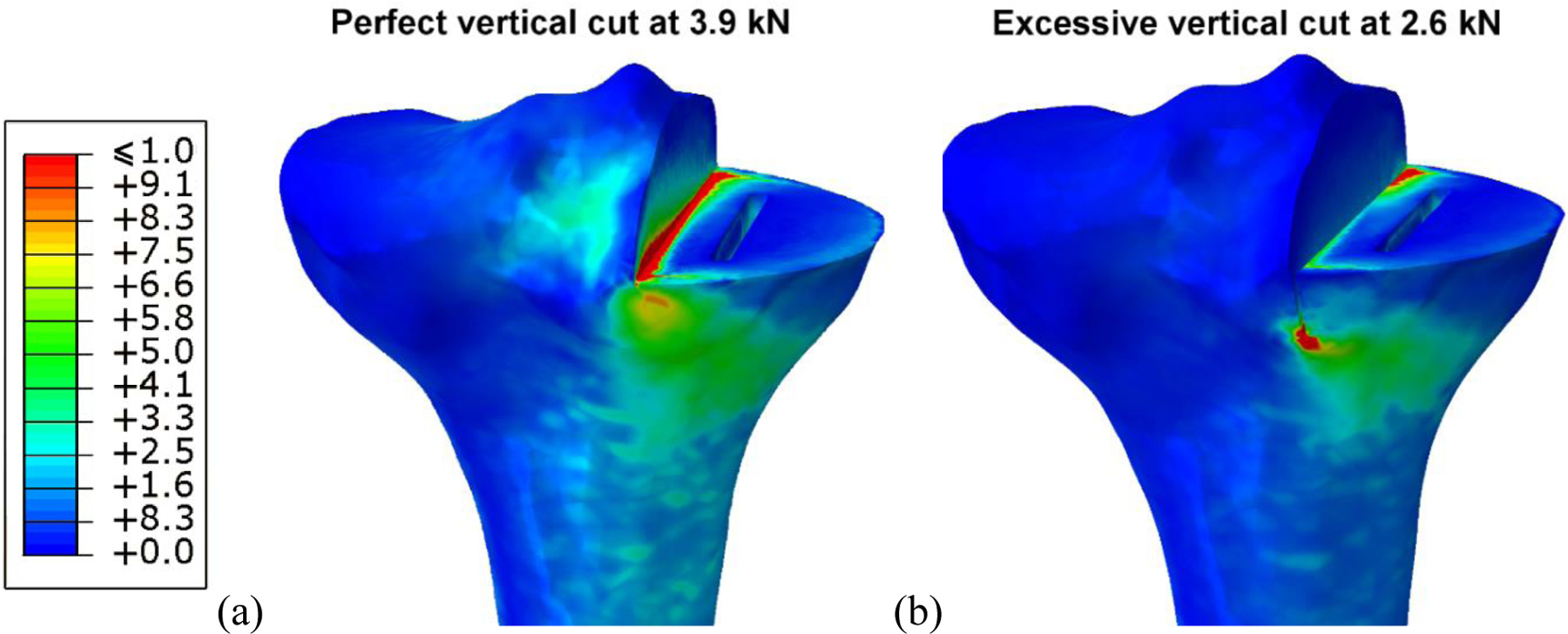
Distribution of the risk of fracture through a perfectly cut tibia loaded at 3.9 kN (a), and a tibia with excessive vertical cut loaded at 2.6 kN (b). Both models represent conditions which caused tibial fracture in experiments performed by Clarius et al.. The region most at risk of fracture extends diagonally from the vertical cut to the tibial cortex, via the keel.

The average failure load reported by Clarius et al. for a tibia with an excessive vertical cut was 2.6 kN (range 1.08–5.04), and 3.9 kN (range 2.35–8.50) for a the tibia with a perfect cut [18]. The finite element models when loaded under these conditions had corresponding maximum ROF values of 5.2 and 5.6, and volume of failed elements of 128 mm³ and 177 mm³, respectively. These results indicate that a maximum ROF value above 5, with a failure volume greater than 128 mm³, would represent a high fracture risk. From the 1000 models examined in the Monte Carlo simulation, 0.3% had a maximum ROF greater than 5; none reached the volume threshold.

4. Discussion

This study used a probabilistic finite element modelling approach to investigate the influence of different surgical cuts used to prepare the tibia for unicompartmental knee replacement on the risk of periprosthetic fracture. Of the surgical parameters investigated, excessive resection depth and an extended posterior vertical saw cut were found to significantly increase the risk of fracture according to the regression model. Furthermore, based on measurements of the Sawbone tibias prepared by surgeons as part of an instructional course, the depths of the vertical saw cuts posteriorly are highly variable. This combination of results is concerning, as high variability in a factor believed to increase the risk of fracture increases uncertainty in the surgical outcome.

The tibial saw guide is an important part of the surgical instrumentation for making the vertical saw cut. The guide comprises a rectangular block, which is pinned to the anterior side of the tibia (causing the pin holes described) and provides a horizontal surface to stop the saw blade when making the vertical cut. Although the guide provides a stop anteriorly, there is no such stop posteriorly, and the surgeon is required to estimate the correct cut angle (7 degrees). The guide is also used to aid the horizontal cut, where the flat side of the reciprocating saw rests on the top of the block which ensures the cut is straight and has a 7 degree posterior slope [22]. If the surgeon under-estimates the slope of the vertical cut, the horizontal and vertical cuts will not meet and the vertical cut will need to be extended to enable the worn tibial plateau to be removed. If the surgeon over-estimates the slope, the vertical cut will be excessive, causing a posterior notch. It is, therefore, difficult for a surgeon to ensure that the vertical cut is not excessive with the current operative technique, and limited posterior visibility makes it hard to identify cut depth intra-operatively.

The resection depth is controlled by the height at which the tibial guide is pinned. The operative technique suggests the level should be 2 to 3 mm lower than the eroded bone [22]. Several studies have suggested that errors in the vertical cut increase the risk of fracture [1; 9; 17], and Clarius et al. demonstrated this relationship experimentally [18]. However, resection depth has been proposed by only one other publication as a critical parameter and is largely overlooked in the literature [1]. If clinicians were made aware that excessive resection can contribute to fracture, it would be simple for them to modify their surgical practice accordingly.

Regardless of the manufacturer or implant type, all UKR designs require an L-shaped space to be created for the tibial component, which requires a horizontal resection cut and a vertical cut to be made by the surgeon. This consistency in UKR surgical technique may explain why tibial plateau fracture is not restricted to only one device design [3; 5; 6; 8]. By knowing the surgical factors which may increase tibial fracture risk, surgeons and orthopaedic manufacturers can begin to propose solutions that can minimise the risk of fracture after UKR.

Interestingly, the finite element model which simulated loading throughout a whole gait cycle found a linear relationship between the risk of fracture and the medial load. Rudol et al. suggested that peri-prosthetic fracture after UKR may be linked to patient weight [9], and our results indicate it could be a risk factor. Whether high body mass index should be considered a contraindication for UKR is a controversial topic, with evidence both for [33] and against [34; 35]. Some case studies in the literature have mentioned limiting weight-bearing and using medial unloading braces to offset the medial load in cases of peri-prosthetic fracture to aid healing [3; 10], but not as a preventative measure. In patients considered at risk, bracing could be used as a non-invasive treatment.

Periprosthetic tibial fractures after UKR can occur intraoperatively or post-operatively [1; 9]. Reports of intraoperative fracture describe a high strain-rate impact load which causes the bone to fracture [3; 5]. Post-operative fractures are associated with a combination of intra-operative damage and cumulative damage from cyclic loading of the bone [36]. Studies of patient activities after knee replacement have shown that in a typical day a patient will stand for 21% of the time, walk for 8%, and climb stairs for 1%; the remaining time is non-weight bearing [37]. In terms of cyclic loading, gait is therefore the most likely activity to cause post-operative peri-prosthetic fracture, though the largest medial contact forces occur for stair ascent and descent [38]. Our finite model did not examine the development of cumulative strains within the bone, but both static [19] and fatigue mechanisms of bone fracture [36] have been related to strain.

It is important to consider the limitations of this work. The model has been created to represent the strains after UKR for one tibia to a high degree of accuracy, but no conclusions can be made regarding variation within the population (e.g. in gait, bone shape, or bone density). The load data which were applied to the model were based on results from an instrumented total knee replacement, rather than from a unicompartmental knee replacement. As UKR forces have never been measured directly in vivo, it is not possible to know whether the load distribution between the condyles is equivalent. However, an anatomic approach was used to implant the instrumented TKR [38], and therefore alignment should have been similar to an implanted UKR with a similar load distribution between the condyles. This study also makes the assumption that the cuts made during an instructional course are representative of a surgical scenario, but there will be differences. For example, the Sawbone tibias will feel different to real bone so feedback from the saw will be different, and the saw itself may be a different model to that used in theatre. Since this study was performed new Microplasty instrumentation has also been introduced by the manufacturers which assist the surgeon with selecting an appropriate horizontal cut height, so should reduce the risk of fracture. Furthermore, at the instructional course the surgeons will be new to the technique and more likely to make errors and have increased variability. Therefore the results of this study can be considered to represent a worst-case scenario. Finally, our model assumed perfect fixation of the base of the tibial tray to the bone and so could not consider component loosening or interference fit. Incorporating loosening and interference fit adds significant complexity to the model and is planned for inclusion in future work.

In conclusion, the results of this study have highlighted the importance of careful surgical preparation of the tibial plateau prior to UKR implantation. This study suggests that the cause of fracture is multifactorial and that to minimise the risk of fracture, a surgeon should;

• ensure that the vertical cut does not go too deep posteriorly

• be conservative with resection of the tibia

It may be possible to reduce the likelihood of an excessively deep vertical cut by altering the surgical technique. If the horizontal cut were made before the vertical cut, a shim could be inserted into the horizontal saw cut to stop the vertical cut from going too deep. Surgeon training and better communication of the fracture risks could encourage surgeons to be more conservative when resecting the tibia. If orthopaedic manufacturers and surgeons worked to implement these changes in operative technique, our results suggest that the risk of tibial plateau fracture after UKR could be reduced.

Highlights.

• 1000 probabilistic models created with varying unicompartmental surgical cuts

• Tibia fracture risk increased for excessive resection or posterior vertical cut depth

• Regression fitted finite element results with 90% correlation using 3 cut parameters

• Predicted instrumentation modifications may reduce the likelihood of fracture