Abstract
We present here the use of a new statistical segmentation method on the Bacillus subtilis chromosome sequence. Maximum likelihood parameter estimation of a hidden Markov model, based on the expectation-maximization algorithm, enables one to segment the DNA sequence according to its local composition. This approach is not based on sliding windows; it enables different compositional classes to be separated without prior knowledge of their content, size and localization. We compared these compositional classes, obtained from the sequence, with the annotated DNA physical map, sequence homologies and repeat regions. The first heterogeneity revealed discriminates between the two coding strands and the non-coding regions. Other main heterogeneities arise; some are related to horizontal gene transfer, some to t-enriched composition of hydrophobic protein coding strands, and others to the codon usage fitness of highly expressed genes. Concerning potential and established gene transfers, we found 9 of the 10 known prophages, plus 14 new regions of atypical composition. Some of them are surrounded by repeats, most of their genes have unknown function or possess homology to genes involved in secondary catabolism, metal and antibiotic resistance. Surprisingly, we notice that all of these detected regions are a + t-richer than the host genome, raising the question of their remote sources.
INTRODUCTION
Numerous factors are known to affect statistical composition of chromosome DNA sequences, such as constraints related to coding properties (1), gene transfers (2) and statistical biases related to replication (3). Horizontal gene transfer between bacteria species (4), often due to mobile elements, is now recognized as playing an important role in the acquisition of adaptive traits, such as pathogenicity (5–7), resistance to antibiotics (8) or heavy metals, such as mercury (9,10) or arsenic (11). Horizontal transfer has been shown to occur in a wide variety of ecosystems (12), raising questions about the consequences of dispersion of genetic constructions from genetically modified organisms. More generally, horizontal transfer is considered as a driving force of bacterial evolution (13–15). Bacteria are known to integrate prophages (16), and to have other ways of integrating foreign DNA sequences (17–19). These transfers can correspond to DNA segments, which have different statistical properties from those of the host. A classical method of horizontal transfer detection, based on codon usage frequencies, has been introduced by Médigue et al. (20), and some other approaches have been recently reviewed in Karlin (21).
Hidden Markov models (HMMs) are good statistical tools for the analysis of this heterogeneity (22–27). We applied them to the Bacillus subtilis chromosome (4.2 Mb long). In these models, one assumes that a DNA sequence is made up of successive segments, each one belonging to one of a finite number q of types.
Other statistical models could be used for sequence segmentation (28), in particular change point models (29,30). In these models there are no segment types; each segment of the sequence has its own set of composition parameters. In our study, we consider these models to be less realistic because we typically expect the same composition to be found in different segments of the chromosome.
In HMMs, each type of segment is characterized by its own statistical oligonucleotide composition, and the succession of types along the sequence is represented by an unobservable q-state Markov chain (the hidden chain). The aim is first to reconstruct these segments from the DNA sequence, and characterize the identified segment types, then to find correlations between segment types and biological DNA features, such as horizontal transfers.
MATERIALS AND METHODS
Hidden Markov models
A DNA sequence can be represented by a finite series y1, . . . , yn , each base yt being taken from the alphabet Y = {a, c, g, t}. HMMs are characterized by two processes [see for instance Rabiner (32)]. The hidden state process s = (s1, . . . , sn), such that st ε S = {1, . . . , q}, which in our set-up governs the succession of the segment types along the sequence, and the observed process y = (y1, . . . , yn ) which corresponds to the observed DNA sequence. Hidden states are generated according to a homogeneous first order Markov chain (M1) with transition probabilities P(st = v │ st – 1 = u), u, v ε S. Conditional on the hidden process s = (s1, . . . , sn), the observed process y = (y1, . . . , yn ) is a heterogeneous Markov chain: base yt appears in the sequence with a probability distribution that depends on the actual hidden state st, as well as on previous bases yt – k, . . . , yt – 1. Higher order Markovian dependencies will not be considered for the hidden chain, as we expect to identify large compositional segments, but the number q of hidden states will vary; similarly the order and other structural features of the observed chain will also vary. Thus, according to the characteristics of these Markov chains, several models of interest can be constructed.
The M1-M0 model assumes that, conditional on the hidden state st, nucleotides yt are drawn independently with a probability P(yt = j │ st = u), j ε Y, u ε S. Hence, this model takes into account the local base composition of the sequence, and corresponds to the classical HMM described in the literature. More generally, the M1-Mk model assumes, conditional on the actual hidden state, a k order Markovian dependence between observations, with a transition probability P(yt = j │ yt – 1 = ik, . . . , yt – k = i1, st = u). This model, introduced by Churchill (22), accounts for the local k +1 nucleotide frequencies of the DNA sequence. We denote the whole set of model parameters by θ i.e. transition probabilities between states and between bases.
Given the sequence y, we consider the maximum likelihood estimator of θ. Consistency and normality results, which justify the maximum likelihood approach, were proved in the M1-M0 model by Baum and Petrie (31), and extended to the M1-Mk model by Muri (23). Several methods exist for estimating the parameters of HMMs, including stochastic likelihood maximization algorithm and Bayesian estimation (23,24,32–36). All these methods do not require any learning set of pre-segmented sequences to estimate θ. They only require specification of the model structure (number of states, q, and order of the model, k). In our study we chose not to introduce prior information, and choose the expectation-maximization algorithm (EM) to maximize likelihood P(y │ θ ) (25), which proved to be one of the most effective.
Hidden states are missing data, and the likelihood is a sum over all hidden state paths P(y │ θ ) = ΣsεSn P(y, s │ θ ), which makes it not directly tractable. The EM algorithm is useful in many estimation problems involving missing data, including HMM. It is an iterative procedure that alternates two steps, see Churchill (22), Rabiner (32) and Durbin et al. (35) for detailed description of the HMM case and Dempster et al. (37) for mathematical proof of the convergence toward the maximum likelihood estimator. Given the current value θ (m), the expectation E(logP(y, s │ θ ) │ y, θ (m)) is computed during the E-step and maximized over θ during the M-step. In the HMM context, the E-step consists of computing the probability of two consecutive hidden states P(st – 1 = u, st = v │ y, θ (m)) from which follows P(st = v │ y, θ (m)). These probabilities are computed using the Baum–Welch forward–backward recurrence. A new value θ (m + 1) is obtained in the M-step which increases the likelihood:
where 1{...} is equal to 1 if the sentence between the brackets is true and 0 otherwise. E and M steps are alternated until we come to an iteration M for which numerical convergence is reached.
Every limit point of a sequence (θ (m))m ≥ 0, generated by EM, satisfies the log-likelihood equations, and (θ (m))m ≥ 0 converges towards the maximum likelihood estimator, if the starting point θ (0) is not too far from the true value of the parameter θ (23). This is why we run EM with multiple random initializations, and then select the final result presenting the highest likelihood. Computational cost of the algorithm is proportional to sequence length and to the square of the number of states. Obviously cost also grows proportionally to the number of required iterations which depends on the smoothness of the likelihood landscape. Memory requirement is proportional to sequence length and the number of states, but approximations of the E-step could be done to bypass this problem; they were implemented but not used here.
In order to identify homogeneous segments in y, probabilities of each hidden state were computed at each position P(st = u │ y, θ (M)), using the forward–backward recurrence with the maximum likelihood estimator θ (M). We did not use the popular Viterbi algorithm (38–41), which consists, given the sequence, of computing the most probable path of the hidden states. In the case of our poorly structured model Viterbi reconstruction is less informative than the one obtained by forward–backward recurrence. Nevertheless, for results interpretation and discussion, we will need to recognize segments. Hence, contiguous positions having v as the most probable hidden state [i.e. where v maximizes P(st = u │ y, θ (M))] are identified as a homogeneous segment of class v. In the M1-Mk model, all the homogeneous segments of type v are characterized by the same k + 1 nucleotide composition P(M)(yt = j │ yt – 1 = ik, . . . , yt – k = i1, st = v).
Processing the chromosome
Results were obtained with the software RHOM (Research of HOMogeneous regions in DNA sequences), C++ sources are freely available for UNIX/Linux, at http://www-mig.versailles.inra.fr/ssb/rhom/. RHOM implements the algorithms needed to estimate the parameters of a M1-Mk HMM and to produce a segmentation in the way presented in the previous section. Concerning the model, the user only chooses the number of hidden states and the length of the oligonucleotides taken into account. Different model orders, 0 ≤ k ≤ 3, and different hidden state numbers, 2 ≤ q ≤ 8, were used. All models were fitted to the whole sequence of the B.subtilis chromosome (4.2 Mb) through likelihood maximization. To give an idea of the computational cost, processing the chromosome according to the five states M1-Mk model with 25 different start points, requires ∼24 h and 550 MB of active memory on a SUN-SPARC 400 MHz.
RHOM produces a graphical display of the estimated hidden state probabilities for all sequence positions. In our case, we relied on a more sophisticated graphical presentation of the results: chromosome contigs were viewed as ‘featured DNA physical maps’, using appropriate graphical symbols for existing annotations of the sequence. Hidden state probabilities for each position were superimposed on the map, enabling a precise interpretation. Sequences and annotations were taken from MICADO (http://locus.jouy.inra.fr/micado), a relational database dedicated to microbial genomes (42), containing a translation of EMBL/GenBank sequence records.
Segment borders found with RHOM were compared with gene annotation coordinates. The different segment types were compared to previously described codon usage classes of B.subtilis coding sequences (18). As previously found in Escherichia coli (20), codon usage classes of B.subtilis are linked to biological characteristics of the genes: class I contains the majority of the genes, class II is enriched with genes that belong to translational processes, intermediate metabolism and other highly expressed genes and, finally, class III corresponds to genes with properties of horizontally transferred sequences. Attempts to correlate RHOM heterogeneities with finer functional classes of genes were made using the metabolic classification of B.subtilis gene products, given in the publication of the complete genome (16), and maintained on the SubtiList WWW server (http://genolist.pasteur.fr/SubtiList/). For this purpose, each gene was given the type of the homogeneous segment spanning the largest part of it, usually all the gene, or a high proportion of it.
Another kind of heterogeneity we have been looking for is related to gene transfer. In our opinion, a strong assumption that a DNA sequence segment arises from a horizontal gene transfer relies on the simultaneous occurence of three features. First, it has a singular oligonucleotide composition, compared with the context of the B.subtilis chromosome. Secondly, it bears genes with functions known to be transferred between bacterial species, such as pathogenicity and resistance factors. Thirdly, it is surrounded by repeated sequences, or large intergenic regions (the ‘gray holes’), revealing probable chromosomal rearrangements.
For all atypical composition segments revealed by the statistical analysis, homologies for genes with an unknown function were systematically searched for. This was done by protein homology searching against the nr non-redundant protein database at the NCBI using BLAST (43). In this publication we report only highly significant similarities (i.e. when the expectation value is <1 × 10–10). To detect repeated sequences, we produced dot plots of the segments, and compared them with repetitions revealed by systematic search (19).
RESULTS
Program behavior
An interesting segmentation of the B.subtilis chromosome is obtained with the M1-M2 model. Segments are long and coincide with genes or groups of them. In contrast, M1-M0 and M1-M1 models give very short segments of a few base pairs, which do not appear related to biological features. Thus, hidden state probabilities plotted along the sequence give intermingled profiles. M1-M2 and higher order Markov models integrate short-range heterogeneities in each segment type, so that the hidden state chain can fit long-range heterogeneities. Therefore the M1-M2 model is a good choice to perform chromosome segmentation. Higher order models do not seem to significantly modify the results, while the number of parameters increases geometrically.
With the two-state M1-M2 model, hidden states fit gene orientation. With the three state M1-M2 model, we typically get two states matching gene orientations (sensitivity, 86.48%; specificity, 90.60% at the nucleotide level), and the third one matching intergenic regions. Such a strong observation may be an indication of the appropriateness of a three-state model for segmenting the chromosome. In terms of oligonucleotide composition, coding strands are a + g rich whereas intergenic regions are a + t rich. Actually, intergenic regions, computed according to GenBank annotation, have an a + t content of 63.2%, and coding strands have an a + g content of 54.0%, in comparison with 56.4% a + t content and 49.9% a + g content for the whole chromosome. In this context, some genes, systematically found associated to the state matching the intergenic regions, appear as atypical. More generally, genes were assigned to the class corresponding to their main hidden state in terms of base pairs.
Searching for gene transfers
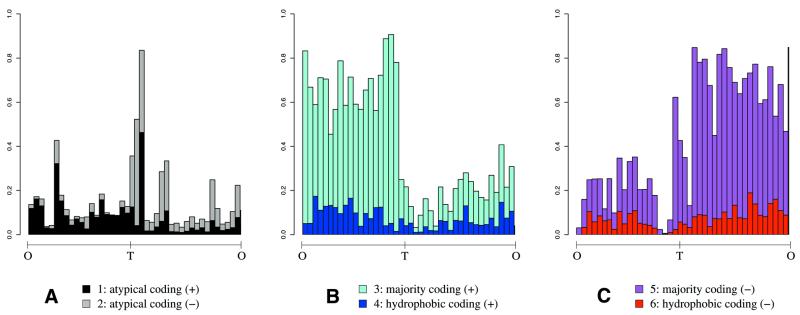
In its search for three states RHOM was able to detect a first level of heterogeneity revealing previously identified prophages, and other DNA segments potentially arising from horizontal transfer, both containing genes that we call atypical (for details, see below). Atypical genes belong to the so-called a + t-rich type (a + t content 66.0%) which also contains most of the intergenic regions. These genes have a highly heterogeneous distribution along the chromosome, with a peak at the replication terminus, as shown in Figure 5A.
Figure 5.
State repartition along the chromosome. Proportion of coding sequences of each hidden state in a sliding window of 100 kb, B.subtilis chromosome is 4215 kb long, O is the replication origin, T the replication terminus at 2017 kb. (B and C) Asymmetrical repartition of coding sequence preferentially located on leading strand. This is already true for atypical coding sequences displayed in (A), which are moreover highly concentrated near the replication terminus.
These a + t-rich regions contain 539 genes, of which 68% have unknown functions, compared with 42% for the complete genome. Here, the term unknown function means genes similar to unknown proteins or without similarities, taken from the functional classification of the bacterium. Genes without any similarity represent 56%, in comparison with 26% for the complete genome. A cross comparison with the codon usage classification reveals that 80% of the genes in the a + t-rich type belong to class III (specificity), while genes of class III represent 13% of the B.subtilis genes. On the other hand, 81% of these genes belong to the atypical state (sensitivity). Thus, there is a strong correspondence between our atypical regions and the codon usage class III genes.
Prophage detection. Literature reports 10 prophages integrated into the B.subtilis chromosome. Seven are putative, or prophage-like sequences P1–P7 (16), since their identification is only based on a + t composition, and all these ‘prophages’ are a + t rich. There is experimental evidence for the three other prophages: PBSX (44), skin (45) and SPβ (46). In this context, the ability of the program to detect experimentally identified prophages and prophage-like sequences provides a biological validation of our approach.
The RHOM software was able to detect all these prophages, except PBSX. The latter is not detectable by RHOM because its content is too close to the local B.subtilis DNA composition, nor is it detectable by simple a + t content analysis. At least two distinct explanations may be provided for the non-detection of PBSX, the first being that it was integrated a long time ago, resulting in the adaptation of its DNA composition to the host context, and the second being that its DNA composition was originally close to that of B.subtilis.
Our detection of SPβ and of the three prophage-like sequences P1, P3 and P7 is in keeping with the literature. For the remaining prophage-like sequences, the detection works, although some boundaries are located differently, or some of their genes remain in the types associated with B.subtilis. These differences are probably related to a better segmentation accuracy using HMM than that produced by 10 kb sliding windows with a 5 kb step used in the calculation of the a + t content (16).
New detection of gene transfers. In a similar manner to prophage detection, we found 14 DNA segments identified as a + t rich, and thus potentially arising from horizontal transfer. These segments are presented in Table 1 together with the prophages. In addition to this compositional observation, some other signs exist which strengthen our conclusions.
Table 1. Coordinates (kb) of potential horizontal transfer regions on the chromosome of B.subtilis.
| Functions | HMM | Repeats |
|---|---|---|
| P1 ‘prophage∍ | 202–220 | 202–213 |
| P2 ‘prophage∍ | 529–570 | 555–567 |
| See Table 2 | 570–600 | – |
| P3 ‘prophage∍ | 651–664 | – |
| Site-specific recombinase | 738–747 | – |
| Multidrug-efflux transporter | 818–822 | – |
| – | 1124–1130 | – |
| P4 ‘prophage∍ | 1262–1270 | – |
| PBSX prophage (1320–1348) | – | – |
| – | 1397–1399 | 1385–1424 |
| – | 1442–1447 | – |
| – | 1478–1482 | – |
| P5 ‘prophage∍ | 1879–1891 | – |
| – | 2038–2041 | – |
| P6 ‘prophage∍ | 2046–2073 | 2050–2060 |
| SPβ prophage | 2151–2286 | – |
| Skin prophgage | 2652–2701 | 2654–2701 |
| P7 ‘prophage∍ | 2707–2756 | 2725–2735 |
| Competence | 3253–3257 | – |
| Arsenic resistance regul. | 3463–3467 | 3462–3469 |
| – | – | 3608–3634 |
| Cell wall synthesis | 3658–3685 | 3665–3672 |
| ABC transporter | 4123–4134 | – |
| ABC transporter | 4171–4176 | 4170–4176 |
| Streptothricin, tetracycline, mercury regul. | 4184–4190 | 4189–4190 |
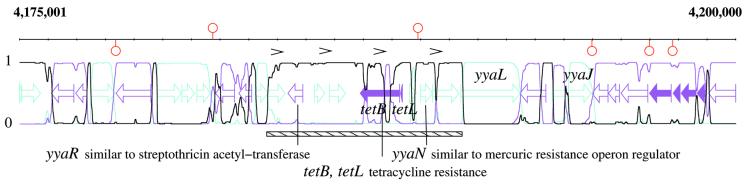
As reported in Table 1, there is a high correlation between detected segment locations and repeats described in Rocha et al. (19). In particular, only one of these repeats was found not to be associated with the detection of some atypical genes. For example, the 3463–3467 kb segment (Fig. 1) is flanked on both sides by long direct repeats which probably signal a chromosomal rearrangement. These duplicated fragments are larger than the transferred segment and contain five genes, four of which belong to the ABC transporter family. In this case, the putative transfer contains an unknown gene similar to an arsenical resistance operon repressor (yvbA). Figure 2 shows another kind of repetition, associated with the 4184–4190 kb region of the a + t-rich type. These sequences are short, ∼100 bp long, and repeated four times. These repeats are regularly spaced, but not correlated with gene borders, and therefore do not present the characteristics of an integron. Nevertheless, the four repeats surround four resistance related genes, two of them are experimentally proven to confer tetracycline resistance (tetB, tetL), and the other two are similar to streptothrycin acetyl-transferase (yyaR), and to the mercuric resistance operon regulator (yyaN), respectively.
Figure 1.
Detection using a three-state M1-M2 model of an atypical segment (3463–3467 kb, underlined) surrounded by ABC transporter gene duplication (thin black arrows). Segment reconstruction on 25 kb is shown. At each position, probabilities P(st = u │ y, θ (M)), u = 1, 2, 3 (color curves) are plotted on the DNA featured physical map. Filled arrows represent genes of known function, empty arrows, those of unknown function, and red hairpins represent transcriptional terminators. The magenta state matches genes on the (+) strand whereas cyan denotes genes on the (–) strand. The black state (a + t rich) fits either intergenic regions or atypical genes.
Figure 2.
Detection of an atypical segment (4184–4190 kb) using a three-state M1-M2 model, containing the tetracyclin resistance, and four direct repeats each ∼100 bp in length, shown by small black brackets.
The 818–822, 1442–1447 and 4171–4176 kb segments are surrounded by intergenic regions larger than usual, compared with sizes expected in bacterial chromosomes. Another segment located at 3658–3685 kb contains ‘gray holes’. This segment, including teichoic acid metabolism genes, is described in the literature as potentially arising from horizontal gene transfer (17) but the segment detected by the program is larger because it encompasses other genes also coding enzymes involved in cell wall synthesis.
The occurrence of genes having imprecisely known function in these a + t-rich regions, whose homologies are related to resistance functions, reinforces the hypothesis of gene transfer events. In addition to those previously mentioned in the 3463–3467 and 4184–4190 segments, we found a homology to a multidrug-efflux transporter in 818–822 (yfmI), and many other significant homologies in the largest newly detected 570–600 region. Remarkably, this 30 kb segment, adjacent to the P2 ‘prophage’, bears genes with numerous homologies, either related to resistance functions, or to mocR, the rhizopine catabolism regulator of Sinorhizobium meliloti. Rhizopine is a compound found in root nodules resulting from plant–bacteria symbiosis. All homologies of this segment are reported in Table 2.
Table 2. Homologies found in the 30 kb long atypical 570–600 kb region, downstream of the P2 prophage.
| Genes | Homologies |
|---|---|
| ydeL | Transcriptional regulator MocR (GntR family) |
| ydeP | Cinnamoyl ester hydrolase |
| ydeQ | General stress protein 14 of B.subtilis |
| ydeR | Antibiotic resistance translocase |
| ydeS | Transcriptional regulator (TetR/AcrR family) |
| ydeT | Transcriptional regulator (ArsR family) |
| ydfA | Arsenical pump membrane protein |
| ydfB | Antibiotic resistance protein |
| ydfC | Permease |
| ydfD | Transcriptional regulator MocR (GntR family) |
| ydfF | Transcriptional regulator (ArsR family) |
| ydfH | Nitrates/nitrites sensor protein |
| ydfI | Nitrates/nitrites sensor protein |
| ydfJ | Antibiotic transport-associated protein |
| ydfK | Putative transport protein |
| nap | Naproxen carboxylesterase (experimental evidence) |
| ydfL | Multidrug-efflux transcriptional regulator |
| ydfM | Cation efflux system cobalt–zinc–cadmium |
| ydfN | Nitroreductase |
| ydfO | ABC transporter |
| ydfQ | Thioredoxin |
Homologies have been found using BLAST against the non-redundant protein database at the NCBI and only highly significant homologies are reported (with E-value <1 × 10–10).
Finally, a new potential mobile element was found, located between 738 and 747 kb. Genes yefB and yefC, belonging to this segment, are homologous to site-specific recombinases. Moreover, yeeA shows similarity with a DNA modification methyltransferase suggesting the presence of a restriction–modification system. These systems are known to be often horizontally transferred (47).
Heterogeneities and functional classes
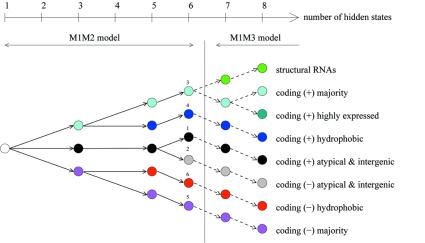
After identifying the coding strand of genes and atypical segments related to horizontal transfer as being the main heterogeneities, our aim was to find additional ones that can be linked to significant biological features. For example, can we find other kinds of horizontal transfer that are not a + t rich? We thus fitted HMMs with more than three states to the chromosome. As a consequence of incrementally adding one more state, the heterogeneity detected is not completely reorganised, but on the contrary, is refined: one of the previously identified states is split. This enables us to present the results in a tree structure as shown in Figure 3. In the following section, we describe the new hidden states in the order in which they appear.
Figure 3.
Tree representation of state subdivisions as a function of the number of hidden states. Numeric labels for the six-state HMM correspond to those used in Figures 4 and 5. (+) and (–) indicate the coding strand.
Hydrophobic proteins. With the introduction of the fourth and fifth hidden states into the model, we distinguish a minority class of coding sequences, borne by both DNA strands of the chromosome. Compared with the usual a + g-rich coding strand composition, this new class is t enriched (31.9 versus 25.7% computed from annotations for the coding strand), and a depleted (21.8 versus 29.9%), in fact it appears as 56.4% t + g rich. When compared with the functional classification, these two hidden states are found to be strongly enriched in genes annotated as coding for transport/binding proteins (TBPs). These TBP coding genes represent 9.5% of B.subtilis genes, 58% of which belong to the minority class of coding sequences, while TBP genes constitute 36% of the minority class.
The TBP category contains a lot of hydrophobic membrane proteins. Therefore, we looked for amino acid biased composition. Actually, we noticed that proteins belonging to this minority state present differences, compared with the majority state. Their amino acid composition is enriched in: phenylalanine (frequency 0.072 versus 0.039) for which codons, when ordered by B.subtilis preference (18), are ttt, ttc; isoleucine (0.096 versus 0.068) att, atc, ata; and leucine (0.13 versus 0.091) ctg, ctt, tta, ttg, ctc, cta. Their composition is simultaneously depleted in: glutamate (0.031 versus 0.080) gaa, gag; aspartate (0.025 versus 0.057) gat, gac; and lysine (0.045 versus 0.073) aaa, aag. These amino acid biases of the minority class respectively correspond to a t nucleotide/hydrophobic amino acid enrichment, and an a nucleotide/charged amino acid depletion. Thus these two states appear to be associated with genes that code hydrophobic proteins.
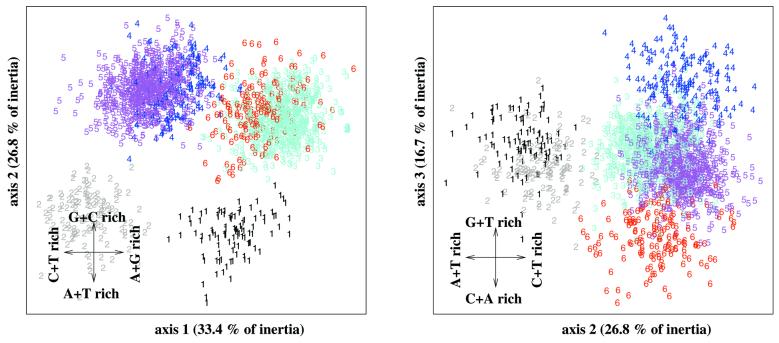
A sixth state leads to the separation of atypical a + t-rich coding sequences according to their transcriptional direction. Thus sensitivity of coding sense detection reaches 98.35% (previously 86.48%) but specificity drops to 85.35% since intergenic regions are counted together with atypical coding sequences. We investigated the trinucleotide composition of the segments obtained with a six-state M1-M2 model, by principal component analysis (Fig. 4). The first three axes explain 77% of the total inertia. The first axis divides the cloud according to coding sense, the second axis distinguishes a + t-rich segments (atypical coding and intergenic) from the others, while the third axis separates hydrophic coding sequences. The display of the distribution of the segments according to their associated type along the chromosome (Fig. 5) reports the asymmetrical distribution of coding sequences between leading and lagging strands even for the atypical a + t-rich segments.
Figure 4.
Principal component analysis on trinucleotide composition of segments (M1-M2, six states). The a + t-rich intergenic and atypical coding (+) and (–) senses are labeled 1 and 2. Labels 3 and 5 correspond to the (+) and (–) majority coding, while 4 and 6 are associated with the (+) and (–) hydrophobic coding states. The crosses display main compositional trends of the principal axes. Hidden state mononucleotide compositions are: 1 (a, 0.36; t, 0.28; c, 0.15; g, 0.21); 2 (a, 0.30; t, 0.37; c, 0.20; g, 0.14); 3 (a, 0.30; t, 0.24; c, 0.21; g, 0.25); 4 (a, 0.22; t, 0.32; c, 0.22; g, 0.24); 5 (a, 0.24; t, 0.30; c, 0.25; g, 0.21); 6 (a, 0.32; t, 0.22; c, 0.24; g, 0.22).
RNA genes. Introducing a seventh hidden state requires increasing the model order from M1-M2 to M1-M3. Otherwise, two hidden states remain melted, giving very short segments and intermingled probability profiles, as described in Results for M1-M0 and M1-M1 models. The newly identified composition type corresponds to structural RNA genes. In terms of base pairs, these genes cover 1.28% of the chromosome. We identified structural RNA genes with a sensitivity and a specificity which, at the nucleotide level are 96.6 and 90.8%, respectively. At the gene level, we found all rRNA genes and 78 out of the 88 annotated tRNA genes. Thus the correspondence of this compositional type to structural RNA is highly accurate.
Highly expressed genes. An eighth state extracts a subcategory from majority coding sequences from the (+) strand (the one given in the sequence file, in opposition to its reverse complement). This subcategory contains most of the codon usage class II genes, which have been characterized as highly expressed. Genes of class II on the (+) strand cover 2.5% of the chromosome, 92% are found in this new state, but they only represent 44% of the subcategory that might interestingly extend class II. It is well known that such highly expressed proteins exhibit greater codon biases than others (48), producing a different statistical composition from the remaining genes in bacteria [see Makrides (49) for a review on high-level expression strategies in E.coli]. They are especially concentrated within the 118–156 kb region close to the replication origin, where most of them are related to transcription and translation: ribosomal proteins, RNA polymerase α and β subunits, translation initiation and elongation factors.
The highly expressed genes in this region were already detected with a two-state M1-M2 model fitted to the 100–200 kb segment of the chromosome, while we had to go up to eight states when running on the complete chromosome. This exemplifies the interest and complementarity of using both local and complete genome analyses.
DISCUSSION
General trends of nucleotide compositions
To summarize, general trends are an a + t enrichment for intergenic regions and those we identified as resulting from gene transfer, and a coding strand enrichment in a + g (purine) for the majority class of genes, as opposed to a coding strand enriched in t + g (keto) for a minority class of genes corresponding to those coding hydrophobic proteins. The trends are mixed; for instance, we were able to distinguish transcriptional orientation of a + t-rich horizontally transferred genes, according to their a + g content.
The gc-skew (Ng – Nc)/(Ng + Nc) and the at skew are positive on the replication leading strand in this species, as previously described (3). These skews are linked to a + g enrichment of coding strands, due to a high preference in B.subtilis for encoding of proteins on the leading strand (Fig. 5B and C). These compositional biases violate the second Chargaff rule. This empirical statement assumes that the relations Na = Nt and Ng = Nc are not only valid on double-stranded DNA but also on each of the strands, if the sequence is long enough. Thus, two violation levels are clearly observed due to asymmetrical evolutionary pressure: the first is related to transcription (kilobase scale), the second to replication (megabase scale). Whereas some work noticed that results of asymmetric pressure related to the replication is observable (50,51), our study does not notice asymmetric bias that could not be due to the transcription, probably because of its low magnitude. Hypotheses explaining strand asymmetry compositions as results of mutation or selection pressures have been extensively discussed by Frank and Lobry (52).
Whereas the positive gc skew of the leading strand is a general characteristic of bacterial genomes, a positive at skew is more exceptional, and depends on the codon base position referred to (3,53). Moreover, the preferred choice of a versus t at the third codon position is not the same for all the encoded amino acids (54).
Gene transfers
Concordance between atypical nucleotide composition, occurence of repetitions, and presence of genes related to resistances or unknown functions, makes the horizontally transferred origin of the detected regions very likely. Overrepresentation of genes of unknown function within these regions could then be due to adaptive characters of these genes, which are only expressed in natural soil surroundings of the bacteria, and not required by them in the laboratory.
All prophages, plus 14 other segments we identified, are a + t rich in comparison with the chromosome composition. We cannot explain this general property, as we expected nucleotide composition heterogeneity among these horizontal transfers due to their supposedly diverse origins. This is intriguing, particulary since a + t enrichment of horizontal transfers seems common in genomes presenting compositional heterogeneity, including E.coli. However, we know of some cases where horizontal transfer is g + c richer than the host genome, see for example the mu-like prophage integrated in the Haemophilus influenzae genome (55) or the E.coli yagH gene (56).
The widespread hypothesis is to explain the compositional heterogeneity of a genome as a snapshot of transferred DNA fragments progressively adapting to the host composition (2), these transfers having originally a distinct nucleotide composition related to the source organism. If this assumption is correct, horizontal transfers should generally come from source organisms which are a + t richer than the host.
According to the analysis results on E.coli and Salmonella sequences of Syvanen (4), an alternative interpretation may be suggested, whereby horizontal transfers essentially occur among strains of the same or close species. In this case, we can imagine a pool of adaptive genes that are shared by recurrent transfers. This may explain the relative homogeneity in a + t richness of the detected fragments, because their shared nucleotide content could then be due to the same evolutionary pressure. Possible origins of the a + t composition bias have been extensively discussed from different angles, not only in relation to gene transfers (4), but also in the interpretation of the interspecific a + t content differences (57), of the isochore existence among vertebrates (58), or even of bacterial intraspecific a + t content heterogeneity (54), the latter relating to the context of our study.
Protein hydrophobicity
The t + g richness of hydrophobic proteins appears as one of the main heterogeneity factors at the DNA composition level, coming just after heterogeneities derived from coding properties (coding/non coding, and the transcription direction), and atypical a + t richness related to gene transfers. This is due to the preferential occurrence of t in the second codon position of hydrophobic amino acids.
Influence of amino acid hydrophobicity at the nucleotide composition level has been previously considered (52), because global hydrophobicity has been shown as a main factor for protein variation in amino acid content (59). We were surprised about the importance of this phenomenon on nucleotide composition, even without introducing any frame consideration. It could be interesting to take this heterogeneity into account to improve gene detection based on Markov models, as is done for genes of codon usage class III (41,60).
Perspectives
Fitting parameters of a HMM to the oligonucleotide composition of the chromosome, by likelihood maximization through the EM algorithm, leads to a segmentation correlated to biological features of the DNA sequence. It is somewhat remarkable that such structures could be identified without having to specify a window length, or any learning set. From here, the mathematical challenge would be to choose adequate selection criteria of the Markov order and of the number of states that define the model structure.
Initially considered as a tool for detecting horizontal gene transfers, this approach enables one to reveal many more heterogeneities, mainly linked to characteristics of coding sequences. On the basis of these results, it would be interesting to extend the model to phased sequences using a HMM that changes the hidden state periodically according to the codon position. These models allows for a more realistic representation of coding sequences. One promising feature of using such a model is to enable the combination of gene detection and heterogeneity description, in a similar manner to Besemer et al. (61). In addition, focusing the analysis on the heterogeneity of intergenic regions appears to be very promising. To summarize, our general goal is to produce a finer integrated description of the structure of the chromosome, in terms of the statistical composition of biological features.
Acknowledgments
ACKNOWLEDGEMENTS
We are grateful to Annie Bouvier and Fabrice Lepage for their extensive participation in the RHOM program development and we thank Kevin Bryson for his careful reading of the manuscript.
REFERENCES
- 1.Staden R. (1994) Measurements of the effects that coding for a protein has on a DNA sequence and their use for finding genes. Nucleic Acids Res., 12, 551–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lawrence J.G. and Ochman,H. (1998) Molecular archeology of the Escherichia coli genome. Proc. Natl Acad. Sci. USA, 95, 9413–9417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lobry J.R. (1996) Asymmetric substitution patterns in the two DNA strands of bacteria. Mol. Biol. Evol., 13, 660–665. [DOI] [PubMed] [Google Scholar]
- 4.Syvanen M. (1994) Horizontal gene transfer: evidence and possible consequences. Annu. Rev. Genet., 28, 237–261. [DOI] [PubMed] [Google Scholar]
- 5.Hacker J., Blum-Oehler,G., Muhldorfer,I. and Tschape,H. (1997) Pathogenicity islands of virulent bacteria: structure, function and impact on microbial evolution. Mol. Microbiol., 23, 1089–1097. [DOI] [PubMed] [Google Scholar]
- 6.Groisman E.A. and Ochman,H. (1997) How Salmonella became a pathogen. Trends Microbiol., 5, 343–349. [DOI] [PubMed] [Google Scholar]
- 7.Hacker J. and Kaper,J.B. (2000) Pathogenicity islands and the evolution of microbes. Annu. Rev. Microbiol., 54, 641–679. [DOI] [PubMed] [Google Scholar]
- 8.Davies J. (1994) Inactivation of antibiotics and the dissemination of resistance genes. Science, 264, 375–382. [DOI] [PubMed] [Google Scholar]
- 9.Osborn A.M., Bruce,K.D., Strike,P. and Ritchie,D.A. (1997) Distribution, diversity and evolution of the bacterial mercury resistance (mer) operon. FEMS Microbiol. Rev., 19, 239–262. [DOI] [PubMed] [Google Scholar]
- 10.Liebert C.A., Hall,R.M. and Summers,A.O. (1999) Transposon Tn21, flagship of the floating genome. Microbiol. Mol. Biol. Rev., 63, 2925–2929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cervantes C., Ji,G., Ramirez,J.L. and Silver,S. (1994) Resistance to arsenic compounds in microorganisms. FEMS Microbiol. Rev., 15, 355–367. [DOI] [PubMed] [Google Scholar]
- 12.Davison J. (1999) Genetic exchange between bacteria in the environment. Plasmid, 42, 73–91. [DOI] [PubMed] [Google Scholar]
- 13.Lawrence J.G. (1999) Selfish operons: the evolutionary impact of gene clustering in prokaryotes and eukaryotes. Curr. Opin. Genet. Dev., 9, 642–648. [DOI] [PubMed] [Google Scholar]
- 14.Ochman H., Lawrence,J.G. and Groisman,E.A. (2000) Lateral gene transfer and the nature of bacterial innovation. Nature, 405, 299–304. [DOI] [PubMed] [Google Scholar]
- 15.de la Cruz I. and Davies,I. (2000) Horizontal gene transfer and the origin of species: lessons from bacteria. Trends Microbiol., 8, 128–133. [DOI] [PubMed] [Google Scholar]
- 16.Kunst F., Ogasawara,N., Moszer,I., Albertini,A.M., Alloni,G., Azevedo,V., Bertero,M.G., Bessières,P., Bolotin,A., Borchert,S. et al. (1997) The complete genome of the gram-positive bacterium Bacillus subtilis. Nature, 390, 249–256. [DOI] [PubMed] [Google Scholar]
- 17.Lazarevic V., Mauel,C., Soldo,P., Freymond,P.P., Margot,P. and Karamata,D. (1995) Sequence analysis of the 308 to 311 segment of the Bacillus subtilis 168 chromosome, a region devoted to cell wall metabolism, containing non-coding grey holes which reveal chromosomal rearrangements. Microbiology, 141, 329–335. [DOI] [PubMed] [Google Scholar]
- 18.Moszer I., Rocha,E. and Danchin,A. (1999) Codon usage and lateral gene transfer in Bacillus subtilis. Curr. Opin. Microbiol., 2, 524–528. [DOI] [PubMed] [Google Scholar]
- 19.Rocha E., Danchin,A. and Viari,A. (1999) Analysis of long repeats in bacterial genomes reveals alternative evolutionary mechanisms in Bacillus subtilis and other competent prokaryotes. Mol. Biol. Evol., 16, 1219–1230. [DOI] [PubMed] [Google Scholar]
- 20.Médigue C., Rouxel,T., Vigier,P., Hénaut,A. and Danchin,A. (1991) Evidence for horizontal gene transfer in Escherichia coli speciation. J. Mol. Biol., 222, 851–856. [DOI] [PubMed] [Google Scholar]
- 21.Karlin S. (2001) Detecting anomalous gene clusters and pathogenicity islands in diverse bacterial genomes. Trends Microbiol., 9, 335–343. [DOI] [PubMed] [Google Scholar]
- 22.Churchill G.A. (1989) Stochastic models for heterogeneous DNA sequences. Bull. Math. Biol., 51, 79–94. [DOI] [PubMed] [Google Scholar]
- 23.Muri F. (1997) Comparaison d’algorithmes d’identification de chaînes de Markov cachées et application à la détection de régions homogènes dans les séquences d’ADN. PhD thesis Université René Descartes, Paris V.
- 24.Muri F. (1998) Searching gene transfers on Bacillus subtilis using hidden Markov models. In Physica-Verlag, (ed.), Compstat’98 Proceedings in Computational Statistics, pp. 98–100.
- 25.Bize L., Muri,F., Samson,F., Rodolphe,F., Ehrlich,S.D., Prum,B. and Bessières,P. (1999) Modelling bacterial genomes using hidden Markov models. In Recomb’99 Proceedings of 3rd Annual International Conference on Computational Molecular Biology, pp. 43–49.
- 26.Peshkin L. and Gelfand,M.S. (1999) Segmentation of yeast DNA using hidden Markov models. Bioinformatics, 15, 980–986. [DOI] [PubMed] [Google Scholar]
- 27.Boys R.J., Henderson,D.A. and Wilkinson,D.J. (2000) Detecting homogenous segments in DNA sequences by using hidden Markov models. Appl. Stat., 49, 269–285. [Google Scholar]
- 28.Braun J.V. and Muller,H.G. (1998) Statistical methods for DNA sequence segmentation. Stat. Sci., 13, 142–162. [Google Scholar]
- 29.Oliver J.L., Roman-Roldan,R., Perez,J. and Bernaola-Galvan,P. (1999) Segment: identifying compositional domains in DNA sequences. Bioinformatics, 15, 974–979. [DOI] [PubMed] [Google Scholar]
- 30.Liu J.S. and Lawrence,C.E. (1999) Bayesian inference on biopolymer models. Bioinformatics, 15, 38–52. [DOI] [PubMed] [Google Scholar]
- 31.Baum L.E. and Petrie,T. (1996) Statistical inference for probabilistic functions of finite state Markov chains. Ann. Math. Stat., 37, 1554–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rabiner L.R.A. (1989) Tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE, 77, 257–286. [Google Scholar]
- 33.Qian W. and Titterington,D.M. (1990) Parameter estimation for hidden Gibbs chains. Stat. Prob. Lett., 10, 49–58. [Google Scholar]
- 34.Robert C.P., Celeux,G. and Diebolt,J. (1993) Bayesian estimation of hidden Markov chains: a stochastic implementation. Stat. Prob. Lett., 16, 77–83.
- 35.Durbin R., Eddy,S.R., Krogh,A. and Mitchison,G. (1998) Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, Cambridge, UK.
- 36.Baldi P. and Brunak,S. (1998) Bioinformatics. The Machine Learning Approach. MIT Press, Cambridge, MA, USA.
- 37.Dempster A., Laird,N. and Rubin,D. (1977) Maximum likelihood from incomplete data via the EM algorithm J. R. Stat. Soc. Ser. B, 39, 1–38. [Google Scholar]
- 38.Krogh A., Mian,I.S. and Haussler,D. (1994) A hidden Markov model that finds genes in Escherichia coli DNA. Nucleic Acids Res., 22, 4768–4778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Burge C. and Karlin,S. (1997) Prediction of complete gene structures in human genomic DNA. J. Mol. Biol., 268, 801–807. [DOI] [PubMed] [Google Scholar]
- 40.Henderson J., Salzberg,S. and Fasman,K.H. (1997) Finding genes in DNA with a hidden Markov model. J. Comput. Biol., 4, 127–141. [DOI] [PubMed] [Google Scholar]
- 41.Lukashin A.V. and Borodovsky,M. (1998) GeneMark.hmm: new solutions for gene finding. Nucleic Acids Res., 26, 1107–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Biaudet V., Samson,F. and Bessières,P. (1997) Micado—a network-oriented database for microbial genomes. Comput. Appl. Biosci., 13, 431–438. [DOI] [PubMed] [Google Scholar]
- 43.Altschul S.F., Madden,T.L., Schäffer,A.A., Zhang,J., Zhang,Z., Miller,W. and Lipman,D.J. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res., 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wood H.E., Dawson,M.T., Devine,K.M. and McConnell,D.J. (1990) Characterization of PBSX, a defective prophage of Bacillus subtilis. J. Bacteriol., 172, 2667–2674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Takemaru K., Mizuno,M., Sato,T., Takeuchi,M. and Kobayashi,Y. (1995) Complete nucleotide sequence of a skin element excised by DNA rearrangement during sporulation in Bacillus subtilis. Microbiology, 141, 323–327. [DOI] [PubMed] [Google Scholar]
- 46.Zahler S.A., Korman,R.Z., Rosenthal,R. and Hemphill,H.E. (1977) Bacillus subtilis bacteriophage SPβ: localization of the prophage attachment site and specialized transduction. J. Bacteriol., 129, 556–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kobayashi I., Nobusato,A., Kobayashi-Takahashi,N. and Uchiyama,I. (1999) Shaping the genome—restriction-modification systems as mobile genetic elements. Curr. Opin. Genet. Dev., 9, 645–656. [DOI] [PubMed] [Google Scholar]
- 48.Gouy M. and Gautier,C. (1982) Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res., 10, 7055–7074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Makrides S.C. (1996) Strategies for achieving high-level expression of genes in Escherichia coli. Microbiol. Rev., 60, 512–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rocha E.P., Danchin,A. and Viari,A. (1999) Universal replication biases in bacteria. Mol. Microbiol., 32, 11–16. [DOI] [PubMed] [Google Scholar]
- 51.Tillier E.R. and Collins,R.A. (2000) The contributions of replication orientation, gene direction and signal sequences to base-composition asymmetries in bacterial genomes. J. Mol. Evol., 50, 249–257. [DOI] [PubMed] [Google Scholar]
- 52.Frank A.C. and Lobry,J.R. (1999) Asymmetric substitution patterns: a review of possible underlying mutational or selective mechanisms. Gene, 238, 65–77. [DOI] [PubMed] [Google Scholar]
- 53.McLean M.J., Wolfe,K.H. and Devine,K.M. (1998) Base composition skews, replication orientation and gene orientation in 12 prokaryote genomes. J. Mol. Evol., 47, 691–696. [DOI] [PubMed] [Google Scholar]
- 54.Sueoka N. (1999) Two aspects of DNA base composition: G+C content and translation-coupled deviation from intra-strand rule A=T and G=C. J. Mol. Evol., 49, 49–62. [DOI] [PubMed] [Google Scholar]
- 55.Fleischmann R.D., Adams,M.D., White,O., Clayton,R.A., Kirkness,E.F., Kerlavage,A.R., Bult,C.J., Tomb,J.F., Dougherty,B.A., Merrick,J.M. et al. (1995) Whole-genome random sequencing and assembly of Haemophilus influenzae Rd. Science, 269, 496–512. [DOI] [PubMed] [Google Scholar]
- 56.Garcia-Vallvé S., Palau,J. and Romeu,A. (1999) Horizontal gene transfer in glycosyl hydrolases inferred from codon usage in Escherichia coli and Bacillus subtilis. Mol. Biol. Evol., 16, 1125–1134. [DOI] [PubMed] [Google Scholar]
- 57.Galtier N. and Lobry,J.R. (1997) Relationships between genomic G+C content, RNA secondary structures and optimal growth temperature in prokaryotes. J. Mol. Evol., 44, 632–636. [DOI] [PubMed] [Google Scholar]
- 58.Bernardi G. (2000) Isochores and the evolutionary genomics of vertebrates. Gene, 241, 3–17. [DOI] [PubMed] [Google Scholar]
- 59.Lobry J.R. and Gautier,C. (1994) Hydrophobicity, expressivity and aromaticity are the major trends of amino-acid usage in 999 Escherichia coli chromosome-encoded genes. Nucleic Acids Res., 15, 3174–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Borodovsky M., McIninch,J.D., Koonin,E.V., Rudd,K.E., Médigue,C. and Danchin,A. (1995) Detection of new genes in a bacterial genome using Markov models for three gene classes. Nucleic Acids Res., 23, 3554–3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Besemer J., Lomsadze,A. and Borodovsky,M. (2001) GeneMarkS: a self-training method for prediction of gene starts in microbial genomes. Implications for finding sequence motifs in regulatory regions. Nucleic Acids Res., 29, 2607–2618. [DOI] [PMC free article] [PubMed] [Google Scholar]