Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Apr 4;23(8):3152–3158. doi: 10.1021/acs.nanolett.2c04696

Scannable Dual-Focus Metalens with Hybrid Phase

Gi-Hyun Go 1, Chung Hyun Park 1, Kie Young Woo 1, Minho Choi 1, Yong-Hoon Cho 1,*
PMCID: PMC10141419  PMID: 37015348

Abstract

graphic file with name nl2c04696_0005.jpg

Metalenses with two foci in the longitudinal or transverse direction, called bifocal or dual-focus metalenses, are promising building blocks in tomography techniques, data storage, and optical tweezers. For practical applications, relative movement between the beam and specimen is required, and beam scanning is highly desirable for high-speed operation without vibration. However, dual-focus metalenses employ a hyperbolic phase that experiences off-axis aberrations, which is not suitable for beam scanning. Here, we demonstrated a scannable dual-focus metalens by employing a new phase called “hybrid phase”. The hybrid phase consists of a hyperbolic phase inside and a quadratic phase outside to reduce off-axis aberrations while maintaining a high numerical aperture. We show that the two foci of the scannable dual-focus metalens move together without severe distortion for incident angles of up to 2.5°. Our design easily extends to the case of multifocusing, which is essential for various applications ranging from imaging to manipulation.

Keywords: dielectric metalens, high numerical aperture, wide field of view, dual-focus metalens

Metalenses are the most promising optical elements that can replace or improve bulk optical systems.1−8 The recent research on broadband or tunable metalenses has led to increased interest of the metalenses.9−12 The advantages of their ultracompact properties have already been discussed in numerous applications, including mobile phone cameras, endoscopes, and ultrathin microscope objectives.13−16 In addition, their capability to manipulate a wavefront provides additional functionalities for various applications that cannot be realized in a traditional optical system or require a complex setup. In particular, metalenses making two focal spots in the longitudinal or transverse direction, called bifocal or dual-focus metalens, are promising building blocks for various applications, including optical communications,17−19 multi-imaging systems,20,21 tomography technique,22−24 data storage,25,26 and optical tweezers.27−29 In these applications, relative movement between the light beam and specimen is often required. For instance, one-dimensional nanoparticles, such as nanowires, which act as probes for high-resolution photonic force microscopy, should be stably trapped by dual focusing and displaced to measure a single-molecule force or scan a biological specimen.27−30 Fundamentally, this movement can be achieved by employing a specimen translation stage with a stationary light beam (stage scanning) or a scanned light beam with a stationary stage (beam scanning). Stage scanning is built in the early stages of new idea development, owing to its simplicity. However, stage scanning is prone to vibration, which deforms the specimen, and the speed of the stage movement is relatively slow. Therefore, most modern instruments employ beam-scanning mechanisms. Dual-focus scanning is highly desirable for high-speed, low-vibration bifocal applications.

However, scannable dual-focus metalenses have not been demonstrated, because of the problems caused by off-axis aberrations and spherical aberrations. Metalenses using a hyperbolic phase, which is free from spherical aberrations, experience off-axis aberrations, which severely limit the scan range (SR) of the focal spot. Meanwhile, metalenses using a quadratic phase achieve a wide SR but introduce large spherical aberrations, which hinder dual-focusing in the longitudinal direction.31−36 The aplanatic metalens, a metalens with an aperture, and a combination of metalenses have been proposed to address the problem of aberrations.31,37−40 However, these approaches require a nontrivial fabrication process and a large volume. A phase profile to reduce both aberrations is not only crucial for the metalens in a single planar element but also opens unprecedented opportunities for various applications, including scannable dual-focus metalenses.

In this study, we demonstrated a scannable dual-focus metalens by employing a new phase profile, namely, a hybrid phase profile. The hybrid phase consists of a hyperbolic phase inside and a quadratic phase outside to reduce off-axis aberrations while maintaining a high numerical aperture (NA). The optical properties of the hyperbolic, quadratic, and hybrid phase profiles were characterized by using ray traces and the calculated focal spots. We confirmed that the hybrid phase profile is suitable for a scannable dual-focus metalens. Subsequently, we fabricated single-focus and dual-focus metalenses to verify the results. In a micrometer SR, the single-focus metalens achieved a NA >0.9, and the dual-focus metalens made two focal spots that moved together for oblique incidence. Our scannable dual-focus metalens easily extends to the case of multifocusing, which has a significant impact on various applications in tomography techniques, data storage, and optical tweezers.

Results

Design of a Metalens with a Hybrid Phase Profile

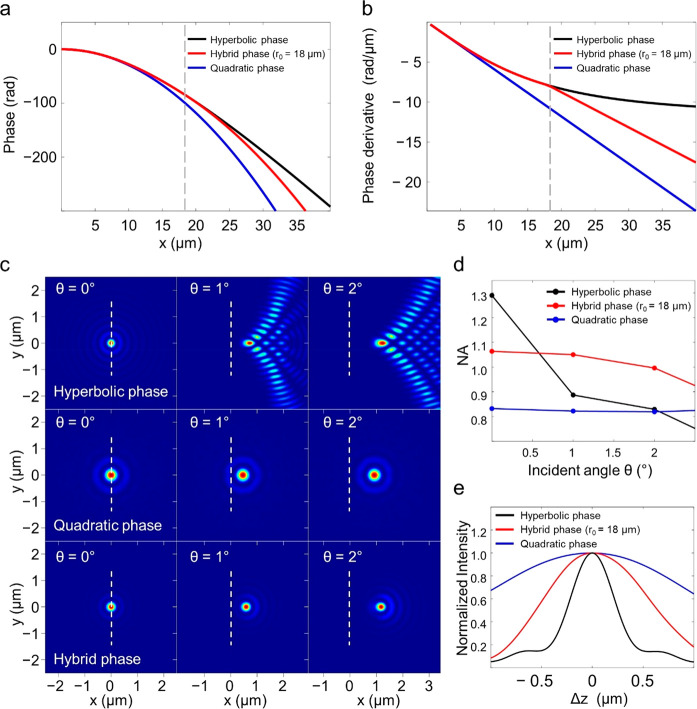
We designed a hybrid phase for a scannable dual-focus metalens to create two focal spots that move together for oblique incidence, as shown in Figure 1a. We consider metalenses comprising crystalline silicon nanopillars that operate in an aqueous environment (Figure 1b,c). The hybrid phase consists of a hyperbolic phase inside and a quadratic phase outside. The effects of each phase were investigated by ray analysis, as shown in Supplementary Figure 1. In the case of the hyperbolic phase, the metalenses are free from spherical aberrations at normal incidence. The chief ray from the central region and the marginal ray from the edge meet at exactly one point. Meanwhile, for oblique incidence, the marginal ray on the left edge is more abruptly bent than the chief ray. Therefore, the chief ray and marginal ray do not meet at a point, resulting in off-axis aberrations. In the case of the quadratic phase at normal incidence, the chief ray and marginal ray do not focus at the same point, resulting in spherical aberrations. The rays that contribute to the focus emerge only from a limited area, inducing an effective aperture that reduces the NA. The phase modulation outside of the effective aperture is so rapid that the beam becomes evanescent. For oblique incidence, the effective aperture is laterally displaced, and rays that cause off-axis aberrations do not influence the focus. Therefore, a metalens with the quadratic phase achieves wide SR. These results imply that the hyperbolic phase in the central region reduces spherical aberrations, whereas the quadratic phase in the outer region reduces off-axis aberration. Consequently, we designed a hybrid phase consisting of a hyperbolic phase inside and quadratic phase outside. Quadratic phase modulation can be obtained through the first-order Taylor polynomial of the hyperbolic phase with respect to the square of the radial coordinate. The hybrid phase profile with the boundary at r = r0 is expressed as

Figure 1.

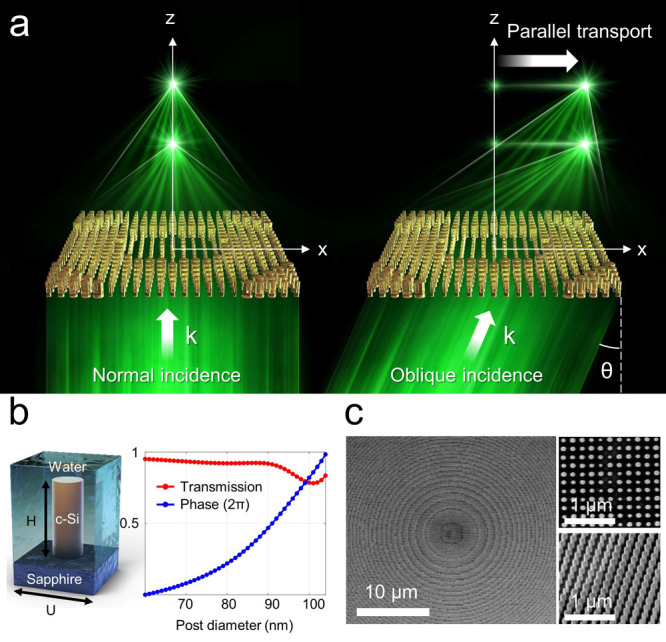
Figure 1

Open in a new tab

Scannable dual-focus metalens design. (a) Schematic of a scannable dual-focus metalens using a hybrid phase profile with an incident angle θ. (b) Crystalline silicon nanopillars with a height of H = 503 nm are arranged on a subwavelength square lattice with a periodicity of U = 200 nm in an aqueous environment. The transmittance and phase delay imparted by the nanopillar are retrieved using rigorous coupled-wave analysis. (c) Scanning electron micrographs of the fabricated metalens with a diameter of 160 μm.

for r ≤ r0,

graphic file with name nl2c04696_m001.jpg 1

for r > r0,

graphic file with name nl2c04696_m002.jpg 2

where nw, λ, f, and r are the refractive index of water, wavelength, focal length, and radial coordinate, respectively. Here, we consider a water-immersion metalens with a front-immersion geometry (Figure 1b) to eliminate the restriction on the working distance (Supplementary Figure 2). Figure 2a,b shows line profiles for a hyperbolic, quadratic, and hybrid phase with a boundary r0 = 18 μm and their derivatives. The hybrid phase followed a hyperbolic phase in the central region and a quadratic phase outside the boundary: r0 = 18 μm. We compared the optical properties of the hyperbolic, quadratic, and hybrid phases using ray traces, as shown in Supplementary Figure 3. Here, the incident angle was defined in the sapphire substrate (n = 1.76). The results show that the rays of the quadratic and hybrid phases are virtually unchanged for an incident angle as high as 2° and are much more tolerant than those of the hyperbolic phase. Note that the aperture size of the hybrid phase is larger than that of the quadratic phase for delivering the high-k components. We also calculate the focal spots for metalenses with diameters D = 160 μm and a focal lengths f = 20 μm using the Kirchhoff diffraction integral, a physically rigorous form of the Huygens-Fresnel principle.41 We define NA for our metalens as NA = 0.51λ/fwhm, where fwhm is the full width at half-maximum of the focal spot. Supplementary Note 4 shows NAs and displacements of the focal spot that are obtained from the calculation. Here, we find two interesting facts regarding the focal spots of a hybrid phase profile for different boundaries. First, the trade-off between NA and SR depends on the position of the boundary, r0 (Supplementary Figure 4a). As r0 increased, it became similar to the hyperbolic phase, and as r0 decreased, it became similar to the quadratic phase. This result provides a methodology that controls the trade-off between the aberrations. The most favorable boundary value depends on the specific application. Second, the displacements of the focal spots for oblique incidence depend on the boundaries and focal lengths (Supplementary Figure 4b). These results can be interpreted in terms of the phase profile outside the boundary (eq 2) for oblique incidence. The effect of oblique incidence is described as

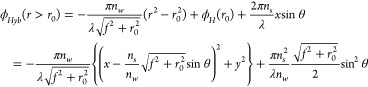graphic file with name nl2c04696_m003.jpg 3

where ns is the refractive index of the sapphire substrate. eq 3 shows that the effect of oblique incidence is a spatial translation of the focal spot, where the displacement of the focal spot depends on the position of the boundary r0, as 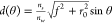Inline graphic. This result implies that the same displacements of the two spots at different axial positions are possible if the f2 + r02 values are the same. The parallel movement of the focal spots at different axial positions is useful for the movement of multifocusing holograms formed in 3D space without distortion. Figure 2c shows the calculated focal spots for the hyperbolic, quadratic, and hybrid phases with a boundary of r0 = 18 μm. The boundary was determined to maximize the space-bandwidth product in the field of view of 3 μm, which can cover the size of a bacterium, a representative biological specimen (Supplementary Note 5). The results from the ray traces were even more apparent from the focal spot. The position where the intensity is maximum for normal incidence is defined as the focal position. Owing to the spherical aberration, the focal positions are slightly changed for the metalenses with quadratic and hybrid phase profiles. As expected, the calculated focal spot of the hybrid phase is virtually unchanged for an incident angle as high as 2°, whereas that of the hyperbolic phase is badly distorted, even at the 1° incidence. In addition, the spot size of the hybrid phase was much smaller than that of the quadratic phase for the incoming angles. Figure 2d shows the NAs for the three phases with varying angles of incidence. The calculated NA of the hyperbolic phase is the highest at normal incidence, but it decreases abruptly for an angle of only 1°. The NA of the hybrid phase was significantly higher than that of the quadratic phase and decreased more slowly than that of the hyperbolic phase. We conclude that a metalens with a hybrid phase can achieve an NA higher than 0.9, while minimizing other aberrations inside an angular cone <2.5°. Figure 2e shows the intensity distribution in the axial direction. The spot size of the hybrid phase was much smaller than that of the quadratic phase, even in the axial direction, which is useful for constructing focal spots in the axial direction.

Figure 2.

Figure 2

Open in a new tab

Comparison of hyperbolic, quadratic and hybrid phases. (a) Line profile for a hyperbolic phase, quadratic phase, and hybrid phase. (b) Phase derivatives of three phases. Hybrid phase consists of the hyperbolic phase inside and quadratic phase outside to reduce both spherical and off-axis aberrations. (c) Focal spots are calculated for the water-immersion metalens of a diameter D = 160 μm and a focal length f = 20 μm, at the wavelength of 532 nm. The focal spot of the hyperbolic phase profile is perfect at normal incidence, but the spot is badly distorted for an angle of only 1°. The focal spots of the quadratic and hybrid phases are virtually unchanged for an incident angle as high as 2°. Note that the spot size of the hybrid phase is much smaller than that of the quadratic phase. (d) NAs of different phase profiles for different angles of incidence. (e) Axial intensity distributions for normal incidence.

Implementation of a Single-Focus Metalens with a Hybrid Phase

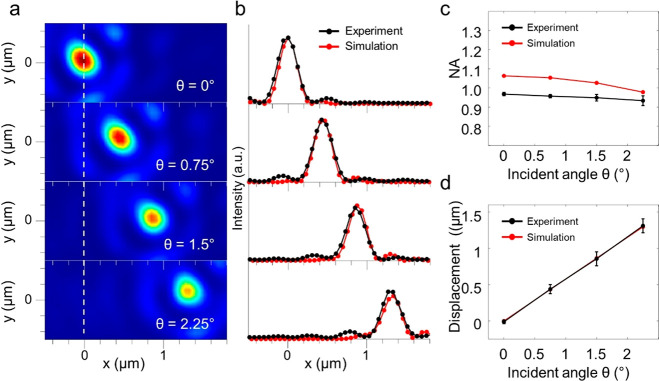
To verify the hybrid phase of r0 = 18 μm, a single-focus metalens with a focal length of f = 20 μm and a diameter of D = 160 μm was fabricated on 503 nm-thick crystalline silicon on 460 μm-thick sapphire, as described in the Methods section. The metalens consisted of cylindrical nanopillars arranged on a subwavelength square lattice with a periodicity of 200 nm to satisfy the Nyquist–Shannon sampling criterion. The transmittance and phase delay imparted by the nanopillars were retrieved by using rigorous coupled-wave analysis, as shown in Figure 1b. We chose a diameter range of 60–110 nm to achieve full 2π phase coverage with a high transmission. The hybrid phase profile is wrapped to [0, 2π] (i.e., modulo 2π) and is matched to the phase of nanopillar as closely as possible. Since rigorous coupled-wave analysis works with the assumption of a perfectly periodic array, the undesired effects caused by large phase gradients for high NA should be investigated. The diffraction angles of nanopillar arrays with linear phase change along the x-direction were computed using the finite-difference time-domain method. The results confirmed that the desired diffraction is the major portion of the diffracted field (Supplementary Figure 6). The fabricated metalens was characterized using a collimated beam from a 532 nm laser. The incidence angles were controlled using Galvano mirrors. The measured focal spots and their line profiles for different angles of incidence show that the spot shape remains undistorted inside an angular cone <2.25° (Figure 3a,b). Figure 3c shows the measured NA values at different angles of incidence. The measured values of NA are 0.97 ± 0.01, 0.96 ± 0.01, 0.95 ± 0.02, and 0.93 ± 0.03, respectively, and the error bars represent the standard deviation for 5 consecutive repetitions. Even though the measured NA is slightly smaller than the designed NA, the values are 0.9 or higher and are quite tolerant at oblique incidence. Furthermore, we also fabricated and characterized the single-focus metalenses using hyperbolic and quadratic phases. Even though the measured NAs are slightly smaller than the designed NAs, qualitative trends are well matched to the simulations (Supplementary Note 7). Figure 3d shows the measured displacement of the focal spot, which is consistent with the calculations, indicating that it has an SR of 2.6 μm. The SR can increase as the size of the metalens increases. Here, we refer the size of metalens as the diameter with keeping the ratio of the focal length to the diameter (Supplementary Figure 10). We also examined the relationship between an SR and the size of the metalens (Supplementary Note 8). For a large-diameter metalens, the region of the quadratic phase should occupy more area than the hyperbolic phase. Therefore, the fwhm of the focal spot depends on the diameter of the metalens. Here, we choose the diameter of 160 μm for the smaller fwhm than 250 nm, corresponding to a NA higher than 1.0, because higher NA than 1.0 is extremely important in the optical tweezers and biological applications.

Figure 3.

Figure 3

Open in a new tab

Optical characteristics of the metalens using the hybrid phase profile. (a) Experimentally measured focal spot and (b) its line profile. (c) NAs for different angles of incidence. (d) Displacement of the focal spot for different angles of incidence.

Implementation of a Dual-Focus Metalens with a Hybrid Phase

In the Gerchberg–Saxton algorithm, the phase generating two focal spots is assumed to be the superposition of the phases generating individual spots. We also created a dual-focus phase by superposing the two-hybrid phase profiles:

graphic file with name nl2c04696_m005.jpg 4

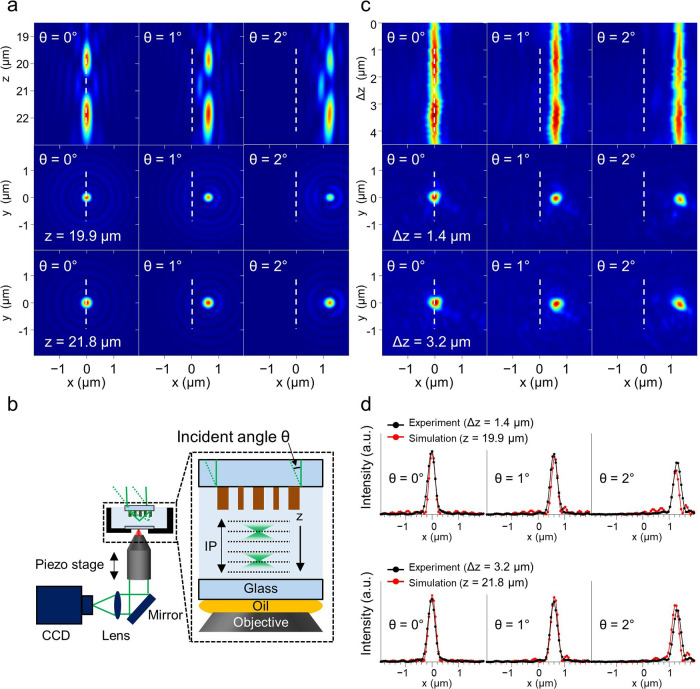
where δ is the constant phase determined to separate the two spots distinctly, and ϕHyb2 are the phases for the two spots. We choose a hybrid phase profile of f1 = 20 μm and r0,1 = 20 μm and a hybrid phase profile of f2 = 22 μm and r0,2 = 17.8 μm to have the same f2 + r02 for parallel movements of two spots from the previous analysis of eq 3. Figure 4a shows the simulated focusing behaviors of the dual-focus metalens in a plane containing the optical axis and two focal planes for different angles of incidence. The positions of the focal planes are determined at z = 19.9 μm and z = 21.8 μm, respectively, where the peak intensities are local maxima. The calculated focal spots were virtually undistorted and well separated for incident angles as high as 2°. The dual-focus metalens was fabricated using the same process as that for the single-focus metalens. The optical properties of the dual-focus metalens were investigated by using the experimental setup in Figure 4b. The setup was built on a custom-made inverted microscope with optical components, including a high NA oil immersion objective lens mounted on a piezo stage to achieve an image along the z-direction (details in the Methods section). Figure 4c shows the measured focusing behavior in a plane containing the optical axis and two focal planes. The positions of the focal planes are Δz = 1.4 μm (corresponding to f1) and Δz = 3.2 μm(corresponding to f2), where the peak intensities are the local maxima for normal incidence. Even though the intensities of both spots decreased, both focal spots were well separated for an incident angle as high as 2°. Furthermore, the measured focal spots in the focal planes were virtually undistorted for oblique incidences. Figure 4d shows the line profiles of the two focal spots in the x-direction. The results are in good agreement with the simulation, indicating the parallel movement of the two focal spots. The measured focal spots are more spread out than the calculated results due to the fabrication error and the point spread function broadening of the imaging system (Supplementary Note 9). We also examined the dual-focus metalens with hyperbolic and quadratic phases (Supplementary Note 10). From the results of the simulation and experiment, we confirmed that the hybrid phase is most adequate for the scannable dual-focus metalens.

Figure 4.

Figure 4

Open in a new tab

Optical characteristics of the dual-focus metalens using the hybrid phase profile. (a) Calculated focal spots of the scannable dual-focus metalens in the xz-plane and the focal planes. The positions of the focal plane are z = 19.9 μm (corresponding to f1) and 21.8 μm (corresponding to f2), where the peak intensities are local maxima. (b) Experimental setup to characterize the optical properties of the scannable dual-focus metalens. (c) Measured focal spots of the dual-focus metalens in the xz-plane and focal planes. The positions of the focal plane are Δz = 1.4 μm (corresponding to f1) and 3.2 μm (corresponding to f2), where the peak intensity is the local maximum. Even though the intensities decrease, both focal spots are virtually undistorted for an incident angle of as high as 2°. (d) Line profiles of the focal spots at f1 and f2. The displacements of the experiment are well matched with the simulation results.

Discussion

We designed a hybrid phase consisting of a hyperbolic phase inside and a quadratic phase outside to achieve a high NA while minimizing other aberrations. The hyperbolic phase inside reduces the spherical aberration, and the quadratic phase outside reduces the off-axis aberrations. We calculated the focal spots of the hyperbolic, quadratic, and hybrid phases to compare their optical properties. The focal spot of the hybrid phase profile was virtually unchanged for an incident angle as high as 2°, whereas that of the hyperbolic phase was badly distorted even at 1° incidence. In addition, the spot size of the hybrid phase was much smaller than that of the quadratic phase for incoming angles. To verify these results, single-focus and dual-focus metalenses with a diameter of 160 μm were fabricated on 503 nm-thick crystalline silicon on 460 μm-thick sapphire. In a micrometer SR, the single-focus metalens achieved a NA >0.9, and the dual-focus metalens made two focal spots that moved together for oblique incidence. The metalens with a diameter of 160 μm can cover an SR of 2.6 μm, which can cover the size of a bacterium, a representative biological specimen. Note that the SR can increase as the size of the metalens increases. Our metalenses have significant applications in tomographic techniques, data storage, and optical tweezers. Furthermore, our design easily extends to the case of multifocusing, which would open unprecedented opportunities for various applications from imaging to manipulation.

Methods

Metalens Fabrication

Single-focus and dual-focus metalenses were fabricated on 503 nm-thick crystalline silicon on 460 μm-thick sapphire. The thickness and refractive index of the crystalline silicon were measured using a scanning electron microscope and ellipsometer (Supplementary Figures 16 and 17). The sample was spin-coated with a 150 nm-thick positive electron beam resist (PMMA), and the pattern was generated using electron beam lithography. After development, an electron-beam-evaporated aluminum oxide layer was used to reverse the generated pattern using a lift-off process and was used as a hard mask for dry etching of the underlying crystalline silicon layer. The dry etching was performed using an inductively coupled plasma reactive ion etching process. The aluminum oxide layer was then dissolved in buffered oxide etchant. Supplementary Figure 18 shows the fabrication flow.

Characterization of Metalens

Figure 4b shows a schematic of the optical setup. A single-mode laser (λ = 532 nm) was used to characterize the optical properties of the metalens. A set of Galvano mirrors was used to control the angle of incidence. The metalenses were placed in the sample chamber to create focal spots. The focal spots were measured using a homemade inverted microscope with a high-NA oil immersion objective lens (Olympus; Plan APO 100× , NA = 1.4) mounted on a 1D piezo scanning stage (Figure 4b). By scanning along the optical axis, the 3D images of the focal spots were reconstructed. See the Supplementary Figure 19 for more details on the experimental setup.

Acknowledgments

This work was supported by the National Research Foundation (NRF-2022R1A2B5B03002560 and NRF-2020M3E4A1080112) and Institute of Information and Communications Technology Planning and Evaluation (IITP-2020-0-00841) of the Korean government, and the Samsung Science and Technology Foundation under project number SSTF-BA1602-05.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c04696.

  • Details of the design of a hybrid phase profile, geometry of the metalens, ray analysis, space-bandwidth product, finite-difference time-domain simulation, experimental results of single- and dual-focus metalens using hyperbolic and quadratic phase, fabrication process and optical setup to chracterize dual-focus metalenses (PDF)

Author Contributions

Y.-H.C. and G.-H.G. initiated the study and designed all experiments. G.-H.G. designed and fabricated the metalenses. K.W. and M.C. provided experimental guidance and support for the fabrications. G.-H.G. and Y.-H.C. performed optical characterizations and numerical simulations. G.-H.G. and C.H.P. analyzed and interpreted the experimental data. Y.-H.C. conceived and supervised this project. G.-H.G. and Y.-H.C. wrote the manuscript, supported by all co-authors.

The authors declare no competing financial interest.

Supplementary Material

nl2c04696_si_001.pdf (1.9MB, pdf)

References

  1. Genevet P.; Capasso F.; Aieta F.; Khorasaninejad M.; Devlin R. Recent advances in planar optics: from plasmonic to dielectric metasurfaces. Optica 2017, 4 (1), 139–152. 10.1364/OPTICA.4.000139. [DOI] [Google Scholar]
  2. Khorasaninejad M.; Capasso F. Metalenses: Versatile multifunctional photonic components. Science 2017, 358 (6367), aam8100. 10.1126/science.aam8100. [DOI] [PubMed] [Google Scholar]
  3. Liang H.; Martins A.; Borges B.-H. V.; Zhou J.; Martins E. R.; Li J.; Krauss T. F. High performance metalenses: numerical aperture, aberrations, chromaticity, and trade-offs. Optica 2019, 6 (12), 1461–1470. 10.1364/OPTICA.6.001461. [DOI] [Google Scholar]
  4. Rubin N. A.; D’Aversa G.; Chevalier P.; Shi Z.; Chen W. T.; Capasso F. Matrix Fourier optics enables a compact full-Stokes polarization camera. Science 2019, 365 (6448), aax1839. 10.1126/science.aax1839. [DOI] [PubMed] [Google Scholar]
  5. Yoon G.; Kim K.; Huh D.; Lee H.; Rho J. Single-step manufacturing of hierarchical dielectric metalens in the visible. Nat. Commun. 2020, 11 (1), 1–10. 10.1038/s41467-020-16136-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Yoon G.; Kim K.; Kim S.-U.; Han S.; Lee H.; Rho J. Printable nanocomposite metalens for high-contrast near-infrared imaging. ACS Nano 2021, 15 (1), 698–706. 10.1021/acsnano.0c06968. [DOI] [PubMed] [Google Scholar]
  7. Moon S.-W.; Kim Y.; Yoon G.; Rho J. Recent progress on ultrathin metalenses for flat optics. Iscience 2020, 23 (12), 101877. 10.1016/j.isci.2020.101877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Moon S.-W.; Lee C.; Yang Y.; Kim J.; Badloe T.; Jung C.; Yoon G.; Rho J. Tutorial on metalenses for advanced flat optics: Design, fabrication, and critical considerations. J. Appl. Phys. 2022, 131 (9), 091101. 10.1063/5.0078804. [DOI] [Google Scholar]
  9. Badloe T.; Kim I.; Kim Y.; Kim J.; Rho J. Electrically tunable bifocal metalens with diffraction-limited focusing and imaging at visible wavelengths. Advanced Science 2021, 8 (21), 2102646. 10.1002/advs.202102646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kim J.; Seong J.; Yang Y.; Moon S.-W.; Badloe T.; Rho J. Tunable metasurfaces towards versatile metalenses and metaholograms: a review. Advanced Photonics 2022, 4 (2), 024001–024001. 10.1117/1.AP.4.2.024001. [DOI] [Google Scholar]
  11. Baek S.; Kim J.; Kim Y.; Cho W. S.; Badloe T.; Moon S.-W.; Rho J.; Lee J.-L. High numerical aperture RGB achromatic metalens in the visible. Photonics Research 2022, 10 (12), B30–B39. 10.1364/PRJ.470004. [DOI] [Google Scholar]
  12. Ren H.; Jang J.; Li C.; Aigner A.; Plidschun M.; Kim J.; Rho J.; Schmidt M. A.; Maier S. A. An achromatic metafiber for focusing and imaging across the entire telecommunication range. Nat. Commun. 2022, 13 (1), 4183. 10.1038/s41467-022-31902-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Khorasaninejad M.; Chen W. T.; Devlin R. C.; Oh J.; Zhu A. Y.; Capasso F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352 (6290), 1190–1194. 10.1126/science.aaf6644. [DOI] [PubMed] [Google Scholar]
  14. Decker M.; Chen W. T.; Nobis T.; Zhu A. Y.; Khorasaninejad M.; Bharwani Z.; Capasso F.; Petschulat J. r. Imaging performance of polarization-insensitive metalenses. Acs Photonics 2019, 6 (6), 1493–1499. 10.1021/acsphotonics.9b00221. [DOI] [Google Scholar]
  15. Pahlevaninezhad H.; Khorasaninejad M.; Huang Y.-W.; Shi Z.; Hariri L. P.; Adams D. C.; Ding V.; Zhu A.; Qiu C.-W.; Capasso F.; et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photonics 2018, 12 (9), 540–547. 10.1038/s41566-018-0224-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Li Z.; Tang F.; Shang S.; Wu J.; Shao J.; Liao W.; Kong B.; Zeng T.; Ye X.; Jiang X.; et al. Compact metalens-based integrated imaging devices for near-infrared microscopy. Opt. Express 2021, 29 (17), 27041–27047. 10.1364/OE.431901. [DOI] [PubMed] [Google Scholar]
  17. Wang W.; Guo Z.; Zhou K.; Sun Y.; Shen F.; Li Y.; Qu S.; Liu S. Polarization-independent longitudinal multi-focusing metalens. Opt. Express 2015, 23 (23), 29855–29866. 10.1364/OE.23.029855. [DOI] [PubMed] [Google Scholar]
  18. Zhang F.; Pu M.; Luo J.; Yu H.; Luo X. Symmetry breaking of photonic spin-orbit interactions in metasurfaces. Opto-Electronic Engineering 2017, 44 (3), 319–325. [Google Scholar]
  19. Ji R.; Chen K.; Ni Y.; Hua Y.; Long K.; Zhuang S. Dual-focuses metalens for copolarized and cross-polarized transmission waves. Advances in Condensed Matter Physics 2018, 2018, 1. 10.1155/2018/2312694. [DOI] [Google Scholar]
  20. Chen X.; Chen M.; Mehmood M. Q.; Wen D.; Yue F.; Qiu C. W.; Zhang S. Longitudinal multifoci metalens for circularly polarized light. Advanced Optical Materials 2015, 3 (9), 1201–1206. 10.1002/adom.201500110. [DOI] [Google Scholar]
  21. Khorasaninejad M.; Chen W.; Zhu A.; Oh J.; Devlin R.; Rousso D.; Capasso F. Multispectral chiral imaging with a metalens. Nano Lett. 2016, 16 (7), 4595–4600. 10.1021/acs.nanolett.6b01897. [DOI] [PubMed] [Google Scholar]
  22. Adams D. C.; Suter M. J. Processing-based approach for resolving the sample optic axis in endoscopic polarization-sensitive optical coherence tomography. Opt. Express 2018, 26 (19), 24917–24927. 10.1364/OE.26.024917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Chen L.-Y.; Pan M.-C.; Pan M.-C. Flexible near-infrared diffuse optical tomography with varied weighting functions of edge-preserving regularization. Appl. Opt. 2013, 52 (6), 1173–1182. 10.1364/AO.52.001173. [DOI] [PubMed] [Google Scholar]
  24. Tong S.; Han B.; Tang J. Edge-guided TVp regularization for diffuse optical tomography based on radiative transport equation. Inverse Problems 2018, 34 (11), 115009. 10.1088/1361-6420/aadb23. [DOI] [Google Scholar]
  25. Salinga M.; Kersting B.; Ronneberger I.; Jonnalagadda V. P.; Vu X. T.; Le Gallo M.; Giannopoulos I.; Cojocaru-Mirédin O.; Mazzarello R.; Sebastian A. Monatomic phase change memory. Nat. Mater. 2018, 17 (8), 681–685. 10.1038/s41563-018-0110-9. [DOI] [PubMed] [Google Scholar]
  26. Horiuchi S.; Fukumoto A.; Yamamoto M. Analysis of crosstalk-free conditions for a cross-shift multiplexing method in holographic data recording. Appl. Opt. 2018, 57 (27), 7805–7810. 10.1364/AO.57.007805. [DOI] [PubMed] [Google Scholar]
  27. Wang F.; Toe W. J.; Lee W. M.; McGloin D.; Gao Q.; Tan H. H.; Jagadish C.; Reece P. J. Resolving stable axial trapping points of nanowires in an optical tweezers using photoluminescence mapping. Nano Lett. 2013, 13 (3), 1185–1191. 10.1021/nl304607v. [DOI] [PubMed] [Google Scholar]
  28. Simpson S. H.; Hanna S. Holographic optical trapping of microrods and nanowires. JOSA A 2010, 27 (6), 1255–1264. 10.1364/JOSAA.27.001255. [DOI] [PubMed] [Google Scholar]
  29. Phillips D. B.; Carberry D. M.; Simpson S.; Schäfer H.; Steinhart M.; Bowman R.; Gibson G. M.; Padgett M. J.; Hanna S.; Miles M. Optimizing the optical trapping stiffness of holographically trapped microrods using high-speed video tracking. Journal of Optics 2011, 13 (4), 044023. 10.1088/2040-8978/13/4/044023. [DOI] [Google Scholar]
  30. Go G.-H.; Heo S.; Cho J.-H.; Yoo Y.-S.; Kim M.; Park C.-H.; Cho Y.-H. Real-time monitoring and visualization of the multi-dimensional motion of an anisotropic nanoparticle. Sci. Rep. 2017, 7 (1), 1–10. 10.1038/srep44167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Aieta F.; Genevet P.; Kats M.; Capasso F. Aberrations of flat lenses and aplanatic metasurfaces. Opt. Express 2013, 21 (25), 31530–31539. 10.1364/OE.21.031530. [DOI] [PubMed] [Google Scholar]
  32. Aieta F.; Genevet P.; Kats M. A.; Yu N.; Blanchard R.; Gaburro Z.; Capasso F. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 2012, 12 (9), 4932–4936. 10.1021/nl302516v. [DOI] [PubMed] [Google Scholar]
  33. Arbabi A.; Horie Y.; Ball A. J.; Bagheri M.; Faraon A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 2015, 6 (1), 1–6. 10.1038/ncomms8069. [DOI] [PubMed] [Google Scholar]
  34. Khorasaninejad M.; Zhu A. Y.; Roques-Carmes C.; Chen W. T.; Oh J.; Mishra I.; Devlin R. C.; Capasso F. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 2016, 16 (11), 7229–7234. 10.1021/acs.nanolett.6b03626. [DOI] [PubMed] [Google Scholar]
  35. Pu M.; Li X.; Guo Y.; Ma X.; Luo X. Nanoapertures with ordered rotations: symmetry transformation and wide-angle flat lensing. Opt. Express 2017, 25 (25), 31471–31477. 10.1364/OE.25.031471. [DOI] [PubMed] [Google Scholar]
  36. Martins A.; Li K.; Li J.; Liang H.; Conteduca D.; Borges B.-H. V.; Krauss T. F.; Martins E. R. On metalenses with arbitrarily wide field of view. Acs Photonics 2020, 7 (8), 2073–2079. 10.1021/acsphotonics.0c00479. [DOI] [Google Scholar]
  37. Arbabi A.; Arbabi E.; Kamali S. M.; Horie Y.; Han S.; Faraon A. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 2016, 7 (1), 1–9. 10.1038/ncomms13682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Groever B.; Chen W. T.; Capasso F. Meta-lens doublet in the visible region. Nano Lett. 2017, 17 (8), 4902–4907. 10.1021/acs.nanolett.7b01888. [DOI] [PubMed] [Google Scholar]
  39. Engelberg J.; Zhou C.; Mazurski N.; Bar-David J.; Kristensen A.; Levy U. Near-IR wide-field-of-view Huygens metalens for outdoor imaging applications. Nanophotonics 2020, 9 (2), 361–370. 10.1515/nanoph-2019-0177. [DOI] [Google Scholar]
  40. Kalvach A.; Szabó Z. Aberration-free flat lens design for a wide range of incident angles. JOSA B 2016, 33 (2), A66–A71. 10.1364/JOSAB.33.000A66. [DOI] [Google Scholar]
  41. Shalaginov M. Y.; An S.; Zhang Y.; Yang F.; Su P.; Liberman V.; Chou J. B.; Roberts C. M.; Kang M.; Rios C.; et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat. Commun. 2021, 12 (1), 1–8. 10.1038/s41467-021-21440-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl2c04696_si_001.pdf (1.9MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES