Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Apr 12;23(8):3362–3368. doi: 10.1021/acs.nanolett.3c00367

Demonstration of a Plasmonic Nonlinear Pseudodiode

Sergejs Boroviks 1,*, Andrei Kiselev 1, Karim Achouri 1, Olivier J F Martin 1,*
PMCID: PMC10141562  PMID: 37043888

Abstract

graphic file with name nl3c00367_0005.jpg

We demonstrate a nonlinear plasmonic metasurface that exhibits strongly asymmetric second-harmonic generation: nonlinear scattering is efficient upon excitation in one direction, and it is substantially suppressed when the excitation direction is reversed, thus enabling a diode-like functionality. A significant (approximately 10 dB) extinction ratio of SHG upon opposite excitations is measured experimentally, and those findings are substantiated with full-wave simulations. This effect is achieved by employing a combination of two commonly used metals—aluminum and silver—producing a material composition asymmetry that results in a bianisotropic response of the system, as confirmed by performing homogenization analysis and extracting an effective susceptibility tensor. Finally, we discuss the implications of our results from the more fundamental perspectives of reciprocity and time-reversal asymmetry.

Keywords: plasmonics, metasrufaces, bianisotropy, second-harmonic generation, nonlinear optics

High-performance nanoscale devices that allow transmission of light only in one direction—optical isolators—remain a long-coveted research objective for optical engineers. This problem is nontrivial due to the fundamental property of electromagnetic waves: in linear time-invariant (LTI) media and in the absence of an external time-odd bias, such as a magnetic field, they propagate reciprocally, i.e. the same way in the forward and backward directions. This property is linked with the time-reversal symmetry of the macroscopic Maxwell equations and can be shown via the Lorentz reciprocity theorem, which specifically applies to LTI media.1−3 However, despite recent comprehensive publications on this topic,1,2,4−6 there remains a tangible confusion in the community about the difference between true nonreciprocity and the deceptively similar time-reversal asymmetric response. For example, time-invariant and bias-less lossy systems may exhibit contrast upon excitation from opposite directions, but they do not qualify as optical isolators since they possess a symmetric scattering matrix and thus obey Lorentz reciprocity.7 Furthermore, in the case of devices based on nonlinear effects, the distinction between true and pseudoisolators is even more intricate. In particular, devices based on Kerr-type nonlinearities8 are intrinsically limited by dynamic reciprocity: they can only perform as pseudoisolators, since they do not exhibit unidirectional transmission upon simultaneous excitation from opposite directions.9,10 One aim of this letter is to explore possibilities to overcome this limitation and demonstrate how it can be turned into an advantage with an appropriate application.

In that context, photonic metasurfaces—artificial planar materials constituted of subwavelength elements—have been identified as a promising platform for the realization of miniature optical isolators or asymmetric devices.11 To this end, let us highlight recent progress in the development of two classes of metasurfaces—nonlinear and bianisotropic metasurfaces. These two classes are particularly relevant to the scope of our work, since combining their features enables the realization of unconventional functionalities, such as the aforementioned nonlinearly induced nonreciprocity,12−17 directional harmonic generation,18−20 and nonlinear beam shaping.21,22

Nonlinear metasurfaces23−25 have the potential to replace bulky optical crystals and thus miniaturize nonlinear optical devices. Among other applications, plasmonic metasurfaces have proven to be interesting for second-harmonic generation (SHG),26−28 which is a second-order nonlinear optical process in which an excitation wave with frequency ω is converted into a wave with double frequency 2ω.29 However, the second-order nonlinear response of plasmonic metals is weak due to their centrosymmetric crystal structure, which is only broken at the surface, giving rise to a nonvanishing surface normal component of the second-order susceptibility tensor χ⊥⊥⊥(2). Yet, the overall SHG efficiency remains small due to the reduced interaction volume: essentially, the nonlinear process occurs within the few atomic layers at the metal surface, since the bulk metal is opaque for visible and infrared light and its bulk second-order response is vanishing. Nevertheless, this limitation can be partially overcome by virtue of the field enhancement associated with surface plasmon resonances at metal surfaces. Thus, various SHG enhancement schemes were proposed for plasmonic metasurfaces, based on multipolar resonances,30−36 plasmonic lattice resonances,37,38 and even light-induced centrosymmetry breaking.39

On the other hand, bianisotropic metasurfaces allow engineering the polarization response to realize highly efficient refraction devices through the combination of electric and magnetic effects.40,41 The bianisotropic response, which emerges in structures with broken spatial symmetries,42 implies that the material effectively acquires magnetic polarization upon excitation with an electric field, and vice versa, electric polarization is produced by a magnetic field. Such a magneto-electric coupling gives rise to the spatial dispersion (i.e., wavevector-dependent response) that enables an excitation-angle-dependent operation.43 For example, in lossy systems, it may lead to asymmetric reflection and absorption, which will be discussed further in relation to our work.

In this letter, we demonstrate theoretically and experimentally a plasmonic metasurface that exhibits asymmetric SHG. The operation of the device is conceptually depicted in Figure 1: in contrast to a conventional nonlinear crystal, a second harmonic (SH) is efficiently generated only upon one excitation direction. This, essentially, enables a nonlinear optical pseudodiode functionality, since a nonlinear signal is transmitted only in one direction (though it has to be distinguished from true optical isolators and pseudoisolators, as we discuss in detail further in the letter). Such an asymmetric response imposes a structural asymmetry of the system, and previously proposed theoretical designs with similar functionalities have relied on a geometric asymmetry, which might be difficult to realize experimentally.44−48 Here, we take a different route and implement a structural asymmetry through the utilization of two common plasmonic materials—silver (Ag) and aluminum (Al)—in a metasurface and show substantial direction-dependent SHG (up to approximately 16.9 dB in theory and approximately 10 dB in experiment). A major advantage of this two-dimensional design is that such a material asymmetry is relatively easy to implement using standard nanofabrication techniques: e.g., single-exposure electron-beam lithography (EBL).49 Furthermore, the combination of plasmonic metals is known to enhance nonlinear processes.50,51 To the best of our knowledge, this is the first experimental demonstration of a plasmonic metasurface for asymmetric SHG, although we note that in a recent experimental demonstration Kruk et al. utilized a combination of dielectric nonlinear materials for third-harmonic generation.52 Additionally, we perform a homogenization analysis of the metasurface to extract effective susceptibilities and reveal the bianiostropic property of our metasurface. Finally, we discuss the fundamental implications of our results in the context of nonreciprocity.

Figure 1.

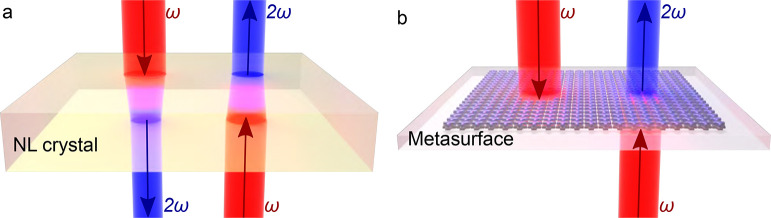
Figure 1

Open in a new tab

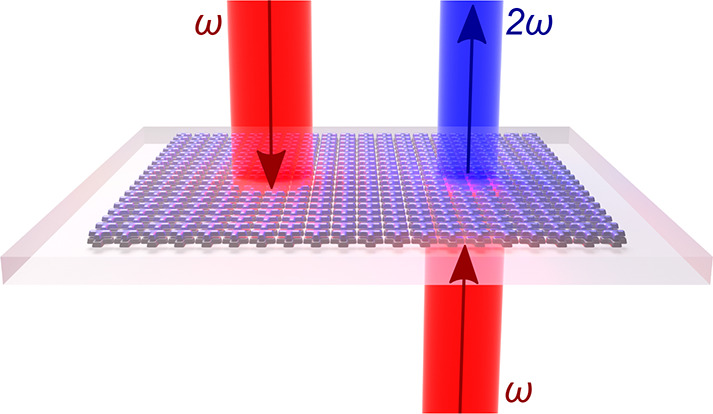
Comparison of conventional and asymmetric SHG: (a) symmetric SHG from a nonlinear (NL) crystal; (b) asymmetric SHG from a nonlinear bianisotropic metasurface.

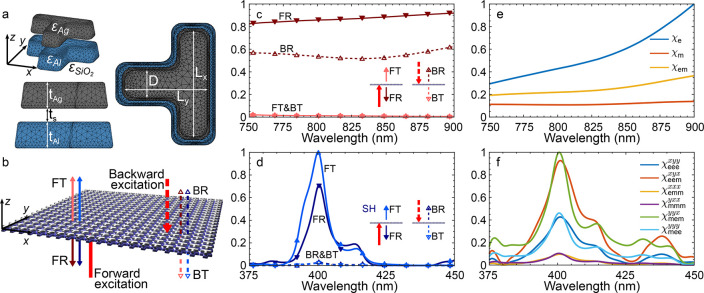
The building block of the metasurface—the meta-atom—is schematically depicted in Figure 2a. It is comprised of two T-shaped nanostructures made of Al and Ag that are stacked one on top of the other and separated by a thin silicone dioxide (SiO2) spacer. These nanostructures are embedded in SiO2 and arranged in a square lattice with the period of Λ = 250 nm. Such a periodicity is sufficiently small to avoid diffraction in both linear and nonlinear regimes, as the metasurface is designed for the excitation with the vacuum wavelength of λ0 = 800 nm (the effective wavelength in SiO2 is ∼537 nm) and SHG at λSH = 400 nm (∼268 nm in SiO2).

Figure 2.

Figure 2

Open in a new tab

Design and simulated performance of the nonlinear bianisotropic metasurface. (a) Schematics of the considered system: the solid/dashed arrows indicate forward/backward excitations and the arrows colors designate linear (red) and nonlinear (blue) regimes, whereas shades of the colors indicate the transmitted (light) and reflected (dark) waves. Simulated metasurface reflectance and transmittance (c) in the linear regime and (d) at the SH frequency with the same color and line style convention as in (b). Relevant components of the extracted (e) linear and (f) nonlinear effective susceptibility tensors.

As shown in Figure 2b, we consider two different excitation conditions that are indicated with thick red arrows: forward (in the direction along the +z-axis, designated with solid lines) and backward (along the −z-axis, designated with dashed lines) propagating plane waves that are x-polarized. In the linear regime (shown in red), each of the two waves gives rise to transmitted (light shaded lines) and reflected waves (dark shaded lines), which are labeled as forward-excited reflection (FR) and transmission (FT), or backward-excited reflection (BR) and transmission (BT). Additionally, both excitations produce signals at the SH frequency (shown in blue, where the light shade indicates transmission and the dark shade indicates reflection). For the SH waves, we use the same naming convention as the waves produced by linear scattering, and we use the same convention of colors, line styles, and triangular upward/downward arrows throughout the rest of the letter. Also, we note that for the reflected and transmitted waves in the linear regime, we measure the copolarized x-component of the electric field, whereas for the SHG waves, the cross-polarized y-component is measured, as it is found to be dominant (see Figure S3 in the Supporting Information).

T-shaped meta-atoms provide almost independent control of the spectral positions for the resonances at both the excitation and SH frequencies by varying the lateral dimensions Lx and Ly.53 As can be seen from Figure S1 in the Supporting Information, for a fixed wavelength, the transmission in the linear regime is tuned by varying Lx. In the nonlinear regime, the transmission and reflection are controlled by both Lx and Ly. Importantly, for forward excitation, the maximum in SHG transmission coincides with the minimum in linear transmission (compare (a) and (b) in Figure S1 in the Supporting Information). The other geometric parameters Ls, D, tAg, and tAl do not have a strong influence on the resonance wavelength of the fundamental mode; however, they affect the scattering cross-section of the meta-atoms via retardation effects,54 which in turn determine the overall transmission and SHG intensity (see Figure S2 in the Supporting Information). The sidewalls of the meta-atom are tilted by 10°, and the edges and corners are rounded with a 5 nm radius to mimic the experimentally fabricated structures, as discussed below.

We select Lx = 135 nm, Ly = 195 nm, Ls = 25 nm, and D = tAg = tAl = 50 nm, since these parameters maximize SHG upon forward excitation at the design wavelength, minimize transmission in the linear regime, and result in a sufficiently high extinction ratio of SHG upon forward and backward excitation (see the parametric sweeps in Figure S1 in the Supporting Information). Furthermore, in the Lx and Ly parameter space, the forward-excitation SHG peak is broad, which implies that the metasurface efficiency is weakly sensitive to deviations from the nominal dimensions, thus easing nanofabrication tolerances.

The simulations are performed in two steps using a custom-developed numerical electromagnetic solver based on the surface integral equation.55,56 First, the linear fields are computed with a plane wave excitation and periodic boundary conditions. For the SHG simulations, the nonlinear surface polarization P⊥(2ω) = χ⊥⊥⊥E⊥ωE⊥ is used as a source, where the normal components of the surface fields E⊥ω are obtained from the linear simulations.

The simulated reflectance and transmittance in the linear and SHG regimes are shown in Figure 2c,d. In the simulations, we use interpolated values εAl and εAg of the experimental permittivity data from McPeak et al.,57 and for the permittivity of the background medium we use 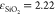Inline graphic. Among the noble metals, Ag is known to have the lowest losses at optical frequencies, whereas Al has recently attracted attention as a low-cost alternative plasmonic material.58−61 Apart from its low cost, Al is known to have the highest second-order nonlinear susceptibility among the plasmonic materials, in particular its surface normal component χ⊥⊥⊥(2);62 it also exhibits an interband transition-related absorption peak at 800 nm (see Figure S4 in the Supporting Information).

As shown in Figure 2c, in the linear regime, the transmission T for both forward and backward excitations is exactly the same, as imposed by reciprocity. However, the reflection R and absorption A, which are related to transmission as A + R = 1 – T, depend on the excitation direction, as they are not restricted by reciprocity and depend on the spatial asymmetry of the system. The asymmetric reflection and absorption of the system can be analyzed by considering an isolated meta-atom. As can be seen in Figure S5c,d in the Supporting Information, forward and backward excitations give rise to two distinct electric field distributions. In particular, the electric field concentration in the Al part of the structure is strongly dependent on the excitation direction. Although the response is primarily dipolar for both excitations (see Figure S6a,b in the Supporting Information), this results in asymmetric linear scattering and absorption cross sections, which is a characteristic of bianisotropic systems.17 In fact, it is the presence of the losses that enables asymmetric scattering when the structure is illuminated from opposite directions, whereas the extinction cross-section remains exactly the same, as imposed by reciprocity.63

In turn, the SHG response that is plotted in Figure 2d has an even stronger dependence on the excitation direction: both nonlinear FT and RT are more than 2 orders of magnitude stronger than the BT and BR at 400 nm. A multipolar analysis of an isolated meta-atom (see Figure S6c,d in the Supporting Information) shows that the electric dipolar and quadruplar modes are excited more efficiently at 400 nm upon forward excitation. This is due to the aforementioned different electric-field distributions at the surface of the T-shaped particles, which become the sources for the SHG.

To further elucidate the significance of bianisotropy in such an asymmetric response, we extracted the effective susceptibilities from the simulated electromagnetic fields following the previously documented procedure of metasurface homogenization analysis.64−66 Briefly, the expressions for nonlinear susceptibilities are derived from the generalized sheet transition conditions and are calculated using the simulated reflected and transmitted fields upon different excitation conditions at ω and 2ω frequencies.

In Figure 2e,f we plot the extracted effective susceptibility tensor elements that are relevant to the considered excitation conditions. For both linear and nonlinear susceptibilities, the magneto-electric coupling (corresponding to the terms with mixed “e” and “m” subscripts in Figure 2e,f) is non-negligible. The asymmetric response becomes apparent by noting that the induced linear and nonlinear polarizations are given by

graphic file with name nl3c00367_m002.jpg 1a
graphic file with name nl3c00367_m003.jpg 1b

In the linear regime, the non-negligible magneto-electric coupling term χme results in an asymmetric absorption and reflection. As for the nonlinear effective susceptibility tensors, the dominant components are χmemyyx and χeem, which relate magnetic/electric excitations with electric/magnetic responses along orthogonal directions and result in strongly asymmetric SHG.

To verify experimentally this asymmetric nonlinear response, we fabricated and characterized a metasurface device. Instead of the widespread lift-off process, we employ the ion beam etching (IBE) technique, which enables the fabrication of stratified nanostructures, in particular metal–dielectric composites, with sharper features.49,67 The schematic flowchart of the fabrication process is shown in Figure 3a. We use a 150 μm thick D 263 glass wafer (Schott) which is coated with 50 nm thick Al and 25 nm SiO2 films using RF sputtering (Pfeiffer SPIDER 600). Next, we deposit a 50 nm thick Ag layer using an e-beam-assisted evaporator (Alliance-Concept EVA 760). The T-shaped pattern arrays are exposed in the hydrogen silsesquioxane (HSQ, XR-1541-006 from DuPont), which is a negative tone e-beam resist, using electron beam lithography (Raith EBPG5000+). The formation of the exposed patterns in the thin films is performed using a low-power argon IBE (Veeco Nexus IBE350, operated at a 300 V acceleration voltage). An important point for this last step is the pulsed IBE operation: 10 s of etching followed by 30 s of cooling to avoid damaging the sample by substrate overheating. The typical overall IBE process time is 160 s, and the etching depth is controlled in situ using a mass spectrometer, which allows real-time monitoring of the etched material composition: the etching process is stopped as soon as the Al flux drops to a minimum. The fabrication results are shown in the scanning electron microscope (SEM) images in Figure 3b–d. The morphology of the fabricated structure can be inspected in Figure 3c: intrinsically, the IBE process results in tilted sidewalls (approximately 10°) and rounded corners and edges. Although such features are typically undesirable, they are not expected to degrade the performance of the metasurface, as these were taken into account in the simulations. In turn, the layered material composition can be well identified in the image acquired with the backscattered electron (BSE) detector in Figure 3d. In the last fabrication step, we cover the metallic nanostructures with a thick SiO2 layer (approximately 300 nm), which serves two purposes: it acts as a protective layer preventing degradation of the Al and Ag nanostructures and simplifies the physical conditions by having identical permittivities above and below the metasurface.

Figure 3.

Figure 3

Open in a new tab

Fabrication of the bimetallic metasurface. (a) Flowchart of the fabrication: (1) initial substrate; (2) Al, SiO2, Ag, and HSQ thin film deposition; (3) e-beam exposure; (4) IBE; (5) covering with a thick SiO2 film. SEM images of the fabricated structure acquired using different detectors and tilt angles: (b) top view SE (scale bar: 1 μm); (c) 45°-tilted view SE (scale bar: 200 nm); (d) 45°-tilted view BSE (scale bar: 200 nm).

The experimental setup and the results for the optical characterization of the fabricated sample are shown in Figure 4. As an excitation light source, we use a mode-locked Ti:sapphire laser that outputs approximately 120 fs pulses with a central wavelength of 800 nm. The excitation light is weakly focused onto the metasurface with a low-magnification objective (NA = 0.1), which results in a focal spot with a 10 μm full width at half maximum mimicking the plane wave excitation used in the simulations. Additionally, in Figure S7 we show white light linear transmission and reflection spectra upon forward and backward excitations. As expected, FR and BR spectra show asymmetric linear reflection, whereas FT and BT spectra are practically identical. The spectrum of the nonlinear light is shown in Figure 4c. Apart from the characteristic SHG peak at 400 nm, it has a tail at longer wavelengths, which is attributed to nonlinear photoluminescence (NPL).

Figure 4.

Figure 4

Open in a new tab

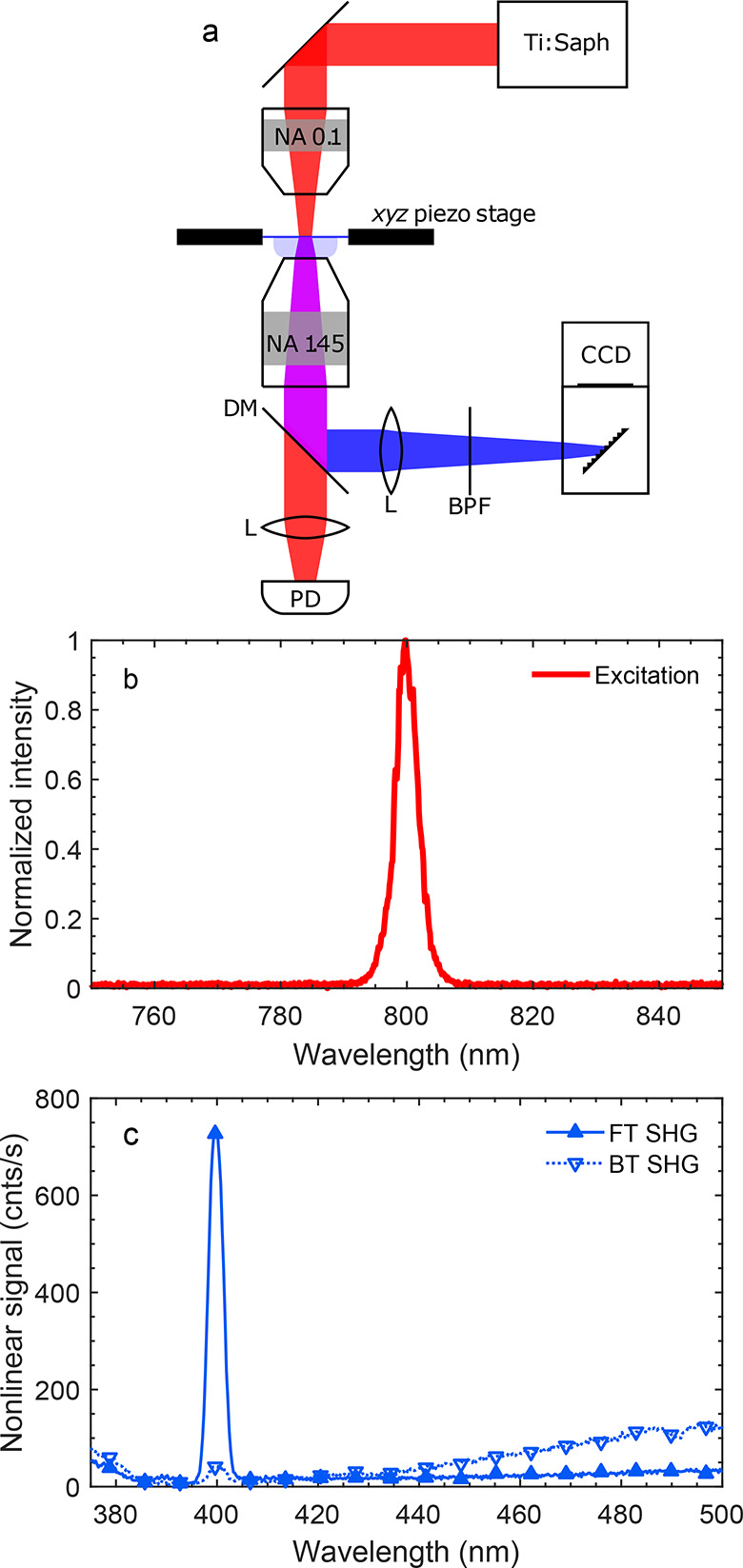
Optical characterization of the metasurface. (a) Measurement setup: a dichroic mirror (DM) in combintation with a short-pass filter (SPF) is used to filter out the excitation light; lenses (L) are used to focus the excitation and nonlinear light onto the photodiode (PD) and the camera (CCD). (b) Excitation spectrum. (c) Nonlinear transmission spectra upon forward and backward excitations.

As an interesting side effect, we note that the NPL signal is substantially larger for BT than for FT. This fact can be explained by the peculiarity of the two-photon absorption mechanism in metals that induces the NPL. As opposed to the coherent nature of two-photon absorption in molecules or dielectrics, in metals it can be regarded as a cascaded process. Specifically, two photons are absorbed sequentially rather than simultaneously.68−70 Absorption of the first photon gives rise to an intraband transition in the conduction band and creates a vacancy below the Fermi level. Thus, the second photon results in an interband transition that fills the vacancy in the conduction band and creates one in the valence band. Both of these photon absorption steps are linear but result in an effective nonlinearity. Thus, higher linear absorption upon backward excitation (see Figure S5 and discussion above) results in a higher probability of two-photon absorption and subsequent NPL, which is consistent with our observations.

Such asymmetric behavior is sometimes referred to as “nonreciprocal SHG”, both in the metasurface13,44 and solid-state physics71,72 communities. We share the view that such a nomenclature is improper in the case of SHG, since the concept of nonrecipocity is not well-defined for nonlinear optics.65,73,74 For any N-port system, the Lorentz reciprocity implies the symmetry of the scattering matrix 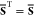Inline graphic, where T denotes the transpose operator. In the case of a two-port system like the one considered in this work in the linear regime, the scattering matrix is given by

graphic file with name nl3c00367_m005.jpg 2

and reciprocity requires that the transmission coefficients S12 and S21 are equal. However, it does not impose any limitations on the reflection coefficients S11 and S22. This is true for our system in the linear regime, since the transmissions for forward and backward excitations are equal, while the reflections are asymmetric.

However, in the nonlinear regime, our metasurface can no longer be regarded as a two-port system, since the SH emission represents a distinct electromagnetic mode. Therefore, this system must be at least considered as a four-port system (assuming that higher-order harmonic generation is negligible), represented with the scattering matrix

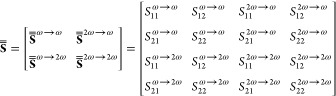graphic file with name nl3c00367_m006.jpg 3

which describes both linear transmission/reflection at frequencies ω and 2ω, as well as nonlinear processes ω → 2ω and 2ω → ω.

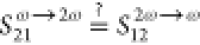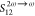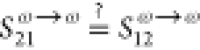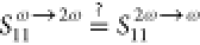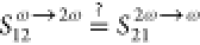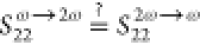In our experiment, we do not directly probe Inline graphic, where Inline graphic parameters corresponds to the excitation at SH frequency and generation of a wave at frequency ω. 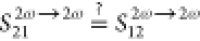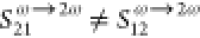In fact, this process is known as parametric downconversion and it has an extremely low efficiency in comparison with SHG.29 Probing this equality, as well as equality of eight other parameters that are flipped by the transpose operation, namely Inline graphic, Inline graphic, Inline graphic, Inline graphic and Inline graphic stand for a true reciprocity test in a four-port system. Instead, within our experiment we show that Inline graphic, which corresponds to an asymmetric nonlinear scattering process that is reciprocal. Yet, a rigorous probing of reciprocity in a nonlinear system would require sophisticated experiments that involve simultaneous excitation with the two waves at frequencies ω and 2ω and precise control over their amplitude and phase.73 Nevertheless, we assert that our device essentially functions as a nonlinear optical pseudodiode, allowing efficient excitation of SHG only upon one excitation direction and thus enabling unidirectional SH signal transmission, which is a desired functionality for various signal processing applications.75

In summary, we have demonstrated that strongly asymmetric SHG can be achieved in a plasmonic metasurface that is comprised of two common plasmonic metals—aluminum and silver. Our approach in creating structural asymmetry via the material contrast allows us to engineer spatial dispersion, which is required to achieve the asymmetric nonlinear response. The tailored designed meta-atoms produce a dependence on the excitation direction, with an extinction ratio of approximately 16.9 dB in theory and approximately 10 dB in the experiment. We anticipate that our findings can pave the way for further developments in the field of nanoscale bianisotropic and nonreciprocal devices, as well as inspire novel nonlinear plasmonic devices with unrivaled functionalities.

Acknowledgments

The authors thank Christian Santschi and Zdenek Benes for their valuable advises on nanofabrication. We also gratefully acknowledge funding from the European Research Council (ERC-2015-AdG-695206 Nanofactory) and from the Swiss National Science Foundation (project PZ00P2_193221).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c00367.

  • Additional results of the numerical simulations, including control over the linear and SH transmission via variation of the geometrical parameters of the meta-atom, SH electric field polarization, permittivity data of the used materials, and scattering, absorption, and multipole analysis of the isolated meta-atom (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl3c00367_si_001.pdf (3.3MB, pdf)

References

  1. Caloz C.; Alù A.; Tretyakov S.; Sounas D.; Achouri K.; Deck-Léger Z.-L. Electromagnetic Nonreciprocity. Phys. Rev. Applied 2018, 10, 047001. 10.1103/PhysRevApplied.10.047001. [DOI] [Google Scholar]
  2. Asadchy V. S.; Mirmoosa M. S.; Díaz-Rubio A.; Fan S.; Tretyakov S. A. Tutorial on Electromagnetic Nonreciprocity and its Origins. Proceedings of the IEEE 2020, 108, 1684–1727. 10.1109/JPROC.2020.3012381. [DOI] [Google Scholar]
  3. Achouri K.; Martin O. J. F. Extension of Lorentz reciprocity and Poynting theorems for spatially dispersive media with quadrupolar responses. Phys. Rev. B 2021, 104, 165426. 10.1103/PhysRevB.104.165426. [DOI] [Google Scholar]
  4. Jalas D.; Petrov A.; Eich M.; Freude W.; Fan S.; Yu Z.; Baets R.; Popovic M.; Melloni A.; Joannopoulos J. D.; Vanwolleghem M.; Doerr C. R.; Renner H. What is - and what is not - an optical isolator. Nat. Photonics 2013, 7, 579–582. 10.1038/nphoton.2013.185. [DOI] [Google Scholar]
  5. Sounas D. L.; Alu A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. 10.1038/s41566-017-0051-x. [DOI] [Google Scholar]
  6. Sigwarth O.; Miniatura C. Time reversal and reciprocity. AAPPS Bulletin 2022, 32, 23. 10.1007/s43673-022-00053-4. [DOI] [Google Scholar]
  7. Fan S.; Baets R.; Petrov A.; Yu Z.; Joannopoulos J. D.; Freude W.; Melloni A.; Popović M.; Vanwolleghem M.; Jalas D.; Eich M.; Krause M.; Renner H.; Brinkmeyer E.; Doerr C. R. Comment on “Nonreciprocal Light Propagation in a Silicon Photonic Circuit. Science 2012, 335, 38–38. 10.1126/science.1216682. [DOI] [PubMed] [Google Scholar]
  8. Cotrufo M.; Mann S. A.; Moussa H.; Alù A. Nonlinearity-Induced Nonreciprocity—Part I. IEEE Transactions on Microwave Theory and Techniques 2021, 69, 3569–3583. 10.1109/TMTT.2021.3079250. [DOI] [Google Scholar]
  9. Shi Y.; Yu Z.; Fan S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photonics 2015, 9, 388–392. 10.1038/nphoton.2015.79. [DOI] [Google Scholar]
  10. Fernandes D. E.; Silveirinha M. G. Asymmetric Transmission and Isolation in Nonlinear Devices: Why They Are Different. IEEE Antennas and Wireless Propagation Letters 2018, 17, 1953–1957. 10.1109/LAWP.2018.2868044. [DOI] [Google Scholar]
  11. Shaltout A. M.; Shalaev V. M.; Brongersma M. L. Spatiotemporal light control with active metasurfaces. Science 2019, 364, eaat3100 10.1126/science.aat3100. [DOI] [PubMed] [Google Scholar]
  12. Menzel C.; Helgert C.; Rockstuhl C.; Kley E.-B.; Tünnermann A.; Pertsch T.; Lederer F. Asymmetric Transmission of Linearly Polarized Light at Optical Metamaterials. Phys. Rev. Lett. 2010, 104, 253902. 10.1103/PhysRevLett.104.253902. [DOI] [PubMed] [Google Scholar]
  13. Valev V. K.; et al. Nonlinear Superchiral Meta-Surfaces: Tuning Chirality and Disentangling Non-Reciprocity at the Nanoscale. Adv. Mater. 2014, 26, 4074–4081. 10.1002/adma.201401021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Mahmoud A. M.; Davoyan A. R.; Engheta N. All-passive nonreciprocal metastructure. Nat. Commun. 2015, 6, 1–7. 10.1038/ncomms9359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lawrence M.; Barton D. R.; Dionne J. A. Nonreciprocal Flat Optics with Silicon Metasurfaces. Nano Lett. 2018, 18, 1104–1109. 10.1021/acs.nanolett.7b04646. [DOI] [PubMed] [Google Scholar]
  16. Chen X.; Zhang J.; Wen C.; Liu K.; Zhu Z.; Qin S.; Yuan X. Optical nonlinearity and non-reciprocal transmission of graphene integrated metasurface. Carbon 2021, 173, 126–134. 10.1016/j.carbon.2020.10.076. [DOI] [Google Scholar]
  17. Cheng L.; Alaee R.; Safari A.; Karimi M.; Zhang L.; Boyd R. W. Superscattering, Superabsorption, and Nonreciprocity in Nonlinear Antennas. ACS Photonics 2021, 8, 585–591. 10.1021/acsphotonics.0c01637. [DOI] [Google Scholar]
  18. Yang K.-Y.; Verre R.; Butet J.; Yan C.; Antosiewicz T. J.; Käll M.; Martin O. J. F. Wavevector-Selective Nonlinear Plasmonic Metasurfaces. Nano Lett. 2017, 17, 5258–5263. 10.1021/acs.nanolett.7b01412. [DOI] [PubMed] [Google Scholar]
  19. Xu L.; et al. Forward and Backward Switching of Nonlinear Unidirectional Emission from GaAs Nanoantennas. ACS Nano 2020, 14, 1379–1389. 10.1021/acsnano.9b07117. [DOI] [PubMed] [Google Scholar]
  20. Nauman M.; Yan J.; de Ceglia D.; Rahmani M.; Zangeneh Kamali K.; De Angelis C.; Miroshnichenko A. E.; Lu Y.; Neshev D. N. Tunable unidirectional nonlinear emission from transition-metal-dichalcogenide metasurfaces. Nat. Commun. 2021, 12, 1–11. 10.1038/s41467-021-25717-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Tymchenko M.; Gomez-Diaz J. S.; Lee J.; Nookala N.; Belkin M. A.; Alù A. Advanced control of nonlinear beams with Pancharatnam-Berry metasurfaces. Phys. Rev. B 2016, 94, 214303. 10.1103/PhysRevB.94.214303. [DOI] [PubMed] [Google Scholar]
  22. Bar-David J.; Levy U. Nonlinear Diffraction in Asymmetric Dielectric Metasurfaces. Nano Lett. 2019, 19, 1044–1051. 10.1021/acs.nanolett.8b04342. [DOI] [PubMed] [Google Scholar]
  23. Minovich A. E.; Miroshnichenko A. E.; Bykov A. Y.; Murzina T. V.; Neshev D. N.; Kivshar Y. S. Functional and nonlinear optical metasurfaces. Laser & Photonics Reviews 2015, 9, 195–213. 10.1002/lpor.201400402. [DOI] [Google Scholar]
  24. Li G.; Zhang S.; Zentgraf T. Nonlinear photonic metasurfaces. Nature Reviews Materials 2017, 2, 1–14. 10.1038/natrevmats.2017.10. [DOI] [Google Scholar]
  25. Krasnok A.; Tymchenko M.; Alù A. Nonlinear metasurfaces: a paradigm shift in nonlinear optics. Mater. Today 2018, 21, 8–21. 10.1016/j.mattod.2017.06.007. [DOI] [Google Scholar]
  26. Lee J.; Tymchenko M.; Argyropoulos C.; Chen P.-Y.; Lu F.; Demmerle F.; Boehm G.; Amann M.-C.; Alu A.; Belkin M. A. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions. Nature 2014, 511, 65–69. 10.1038/nature13455. [DOI] [PubMed] [Google Scholar]
  27. Kauranen M.; Zayats A. V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. 10.1038/nphoton.2012.244. [DOI] [Google Scholar]
  28. Butet J.; Brevet P.-F.; Martin O. J. F. Optical Second Harmonic Generation in Plasmonic Nanostructures: From Fundamental Principles to Advanced Applications. ACS Nano 2015, 9, 10545–10562. 10.1021/acsnano.5b04373. [DOI] [PubMed] [Google Scholar]
  29. Boyd R. W.Nonlinear Optics, 4th ed.; Academic Press: 2020. [Google Scholar]
  30. Chandrasekar R.; Emani N. K.; Lagutchev A.; Shalaev V. M.; Ciracì C.; Smith D. R.; Kildishev A. V. Second harmonic generation with plasmonic metasurfaces: direct comparison of electric and magnetic resonances. Opt. Mater. Express 2015, 5, 2682–2691. 10.1364/OME.5.002682. [DOI] [Google Scholar]
  31. Kruk S.; Weismann M.; Bykov A. Y.; Mamonov E. A.; Kolmychek I. A.; Murzina T.; Panoiu N. C.; Neshev D. N.; Kivshar Y. S. Enhanced Magnetic Second-Harmonic Generation from Resonant Metasurfaces. ACS Photonics 2015, 2, 1007–1012. 10.1021/acsphotonics.5b00215. [DOI] [Google Scholar]
  32. Smirnova D.; Kivshar Y. S. Multipolar nonlinear nanophotonics. Optica 2016, 3, 1241–1255. 10.1364/OPTICA.3.001241. [DOI] [Google Scholar]
  33. Bernasconi G. D.; Butet J.; Martin O. J. F. Mode analysis of second-harmonic generation in plasmonic nanostructures. J. Opt. Soc. Am. B 2016, 33, 768–779. 10.1364/JOSAB.33.000768. [DOI] [Google Scholar]
  34. Butet J.; Bernasconi G. D.; Petit M.; Bouhelier A.; Yan C.; Martin O. J. F.; Cluzel B.; Demichel O. Revealing a Mode Interplay That Controls Second-Harmonic Radiation in Gold Nanoantennas. ACS Photonics 2017, 4, 2923–2929. 10.1021/acsphotonics.7b01027. [DOI] [Google Scholar]
  35. Yang K.-Y.; Butet J.; Yan C.; Bernasconi G. D.; Martin O. J. F. Enhancement Mechanisms of the Second Harmonic Generation from Double Resonant Aluminum Nanostructures. ACS Photonics 2017, 4, 1522–1530. 10.1021/acsphotonics.7b00288. [DOI] [Google Scholar]
  36. Kiselev A.; Bernasconi G. D.; Martin O. J. F. Modes interplay and dynamics in the second harmonic generation of plasmonic nanostructures. Opt. Express 2019, 27, 38708–38720. 10.1364/OE.382041. [DOI] [PubMed] [Google Scholar]
  37. Das Gupta T.; Martin-Monier L.; Butet J.; Yang K.-Y.; Leber A.; Dong C.; Nguyen-Dang T.; Yan W.; Martin O. J. F.; Sorin F. Second harmonic generation in glass-based metasurfaces using tailored surface lattice resonances. Nanophotonics 2021, 10, 3465–3475. 10.1515/nanoph-2021-0277. [DOI] [Google Scholar]
  38. Abir T.; Tal M.; Ellenbogen T. Second-Harmonic Enhancement from a Nonlinear Plasmonic Metasurface Coupled to an Optical Waveguide. Nano Lett. 2022, 22, 2712–2717. 10.1021/acs.nanolett.1c04584. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Li G.-C.; Lei D.; Qiu M.; Jin W.; Lan S.; Zayats A. V. Light-induced symmetry breaking for enhancing second-harmonic generation from an ultrathin plasmonic nanocavity. Nat. Commun. 2021, 12, 4326. 10.1038/s41467-021-24408-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Asadchy V. S.; Díaz-Rubio A.; Tretyakov S. A. Bianisotropic metasurfaces: physics and applications. Nanophotonics 2018, 7, 1069–1094. 10.1515/nanoph-2017-0132. [DOI] [Google Scholar]
  41. Achouri K.; Caloz C.. Electromagnetic Metasurfaces: Theory and Applications; Wiley: 2021. [Google Scholar]
  42. Achouri K.; Tiukuvaara V.; Martin O. J. F.. Spatial Symmetries in Multipolar Metasurfaces: From Asymmetric Angular Transmittance to Multipolar Extrinsic Chirality. 2022, 2208.12504. arXiv. https://arxiv.org/abs/2208.12504 (accessed April 5, 2023).
  43. Overvig A.; Alù A. Diffractive Nonlocal Metasurfaces. Laser & Photonics Reviews 2022, 16, 2100633. 10.1002/lpor.202100633. [DOI] [Google Scholar]
  44. Poutrina E.; Urbas A. Multipolar interference for non-reciprocal nonlinear generation. Sci. Rep. 2016, 6, 1–10. 10.1038/srep25113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Mobini E.; Alaee R.; Boyd R. W.; Dolgaleva K. Giant Asymmetric Second-Harmonic Generation in Bianisotropic Metasurfaces Based on Bound States in the Continuum. ACS Photonics 2021, 8, 3234–3240. 10.1021/acsphotonics.1c01038. [DOI] [Google Scholar]
  46. Jin B.; Argyropoulos C. Self-Induced Passive Nonreciprocal Transmission by Nonlinear Bifacial Dielectric Metasurfaces. Phys. Rev. Applied 2020, 13, 054056. 10.1103/PhysRevApplied.13.054056. [DOI] [Google Scholar]
  47. Kim K.-H. Asymmetric Second-Harmonic Generation with High Efficiency from a Non-chiral Hybrid Bilayer Complementary Metasurface. Plasmonics 2021, 16, 77–82. 10.1007/s11468-020-01261-0. [DOI] [Google Scholar]
  48. Liu W.; Huang L.; Ding J.; Xie C.; Luo Y.; Hong W. High-Performance Asymmetric Optical Transmission Based on a Dielectric–Metal Metasurface. Nanomaterials 2021, 11, 2410. 10.3390/nano11092410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Abasahl B.; Santschi C.; Raziman T. V.; Martin O. J. F. Fabrication of plasmonic structures with well-controlled nanometric features: a comparison between lift-off and ion beam etching. Nanotechnology 2021, 32, 475202. 10.1088/1361-6528/ac1a93. [DOI] [PubMed] [Google Scholar]
  50. Wang J.; Butet J.; Bernasconi G. D.; Baudrion A.-L.; Lévêque G.; Horrer A.; Horneber A.; Martin O. J. F.; Meixner A. J.; Fleischer M.; Adam P.-M.; Zhang D. Strong second-harmonic generation from Au–Al heterodimers. Nanoscale 2019, 11, 23475–23481. 10.1039/C9NR07644A. [DOI] [PubMed] [Google Scholar]
  51. Wang J.; Baudrion A.-L.; Béal J.; Horneber A.; Tang F.; Butet J.; Martin O. J. F.; Meixner A. J.; Adam P.-M.; Zhang D. Hot carrier-mediated avalanche multiphoton photoluminescence from coupled Au–Al nanoantennas. J. Chem. Phys. 2021, 154, 074701. 10.1063/5.0032611. [DOI] [PubMed] [Google Scholar]
  52. Kruk S. S.; Wang L.; Sain B.; Dong Z.; Yang J.; Zentgraf T.; Kivshar Y. Asymmetric parametric generation of images with nonlinear dielectric metasurfaces. Nat. Photonics 2022, 16, 561–565. 10.1038/s41566-022-01018-7. [DOI] [Google Scholar]
  53. Czaplicki R.; Mäkitalo J.; Siikanen R.; Husu H.; Lehtolahti J.; Kuittinen M.; Kauranen M. Second-Harmonic Generation from Metal Nanoparticles: Resonance Enhancement versus Particle Geometry. Nano Lett. 2015, 15, 530–534. 10.1021/nl503901e. [DOI] [PubMed] [Google Scholar]
  54. Kottmann J. P.; Martin O. J. F. Retardation-induced plasmon resonances in coupled nanoparticles. Opt. Lett. 2001, 26, 1096–1098. 10.1364/OL.26.001096. [DOI] [PubMed] [Google Scholar]
  55. Gallinet B.; Kern A. M.; Martin O. J. F. Accurate and versatile modeling of electromagnetic scattering on periodic nanostructures with a surface integral approach. J. Opt. Soc. Am. A 2010, 27, 2261–2271. 10.1364/JOSAA.27.002261. [DOI] [PubMed] [Google Scholar]
  56. Butet J.; Gallinet B.; Thyagarajan K.; Martin O. J. F. Second-harmonic generation from periodic arrays of arbitrary shape plasmonic nanostructures: a surface integral approach. J. Opt. Soc. Am. B 2013, 30, 2970–2979. 10.1364/JOSAB.30.002970. [DOI] [Google Scholar]
  57. McPeak K. M.; Jayanti S. V.; Kress S. J. P.; Meyer S.; Iotti S.; Rossinelli A.; Norris D. J. Plasmonic Films Can Easily Be Better: Rules and Recipes. ACS Photonics 2015, 2, 326–333. 10.1021/ph5004237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Castro-Lopez M.; Brinks D.; Sapienza R.; van Hulst N. F. Aluminum for Nonlinear Plasmonics: Resonance-Driven Polarized Luminescence of Al, Ag, and Au Nanoantennas. Nano Lett. 2011, 11, 4674–4678. 10.1021/nl202255g. [DOI] [PubMed] [Google Scholar]
  59. Knight M. W.; King N. S.; Liu L.; Everitt H. O.; Nordlander P.; Halas N. J. Aluminum for Plasmonics. ACS Nano 2014, 8, 834–840. 10.1021/nn405495q. [DOI] [PubMed] [Google Scholar]
  60. Gérard D.; Gray S. K. Aluminium plasmonics. J. Phys. D: Appl. Phys. 2015, 48, 184001. 10.1088/0022-3727/48/18/184001. [DOI] [Google Scholar]
  61. Thyagarajan K.; Santschi C.; Langlet P.; Martin O. J. F. Highly Improved Fabrication of Ag and Al Nanostructures for UV and Nonlinear Plasmonics. Advanced Optical Materials 2016, 4, 871–876. 10.1002/adom.201500740. [DOI] [Google Scholar]
  62. Krause D.; Teplin C. W.; Rogers C. T. Optical surface second harmonic measurements of isotropic thin-film metals: Gold, silver, copper, aluminum, and tantalum. J. Appl. Phys. 2004, 96, 3626–3634. 10.1063/1.1786341. [DOI] [Google Scholar]
  63. Sounas D. L.; Alù A. Extinction symmetry for reciprocal objects and its implications on cloaking and scattering manipulation. Opt. Lett. 2014, 39, 4053–4056. 10.1364/OL.39.004053. [DOI] [PubMed] [Google Scholar]
  64. Achouri K.; Vahabzadeh Y.; Caloz C. Mathematical synthesis and analysis of a second-order magneto-electrically nonlinear metasurface. Opt. Express 2017, 25, 19013–19022. 10.1364/OE.25.019013. [DOI] [PubMed] [Google Scholar]
  65. Achouri K.; Bernasconi G. D.; Butet J.; Martin O. J. F. Homogenization and Scattering Analysis of Second-Harmonic Generation in Nonlinear Metasurfaces. IEEE Transactions on Antennas and Propagation 2018, 66, 6061–6075. 10.1109/TAP.2018.2863116. [DOI] [Google Scholar]
  66. Achouri K.; Kiselev A.; Martin O. J. F. Modeling of second-order nonlinear metasurfaces. New J. Phys. 2022, 24, 025006. 10.1088/1367-2630/ac5130. [DOI] [Google Scholar]
  67. Ray D.; Raziman T. V.; Santschi C.; Etezadi D.; Altug H.; Martin O. J. F. Hybrid Metal-Dielectric Metasurfaces for Refractive Index Sensing. Nano Lett. 2020, 20, 8752–8759. 10.1021/acs.nanolett.0c03613. [DOI] [PubMed] [Google Scholar]
  68. Beversluis M. R.; Bouhelier A.; Novotny L. Continuum generation from single gold nanostructures through near-field mediated intraband transitions. Phys. Rev. B 2003, 68, 115433. 10.1103/PhysRevB.68.115433. [DOI] [Google Scholar]
  69. Mühlschlegel P.; Eisler H.-J.; Martin O. J. F.; Hecht B.; Pohl D. W. Resonant Optical Antennas. Science 2005, 308, 1607–1609. 10.1126/science.1111886. [DOI] [PubMed] [Google Scholar]
  70. Biagioni P.; Celebrano M.; Savoini M.; Grancini G.; Brida D.; Mátéfi-Tempfli S.; Mátéfi-Tempfli M.; Duò L.; Hecht B.; Cerullo G.; Finazzi M. Dependence of the two-photon photoluminescence yield of gold nanostructures on the laser pulse duration. Phys. Rev. B 2009, 80, 045411. 10.1103/PhysRevB.80.045411. [DOI] [Google Scholar]
  71. Toyoda S.; Fiebig M.; hisa Arima T.; Tokura Y.; Ogawa N. Nonreciprocal second harmonic generation in a magnetoelectric material. Science Advances 2021, 7, eabe2793 10.1126/sciadv.abe2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Mund J.; Yakovlev D. R.; Poddubny A. N.; Dubrovin R. M.; Bayer M.; Pisarev R. V. Toroidal nonreciprocity of optical second harmonic generation. Phys. Rev. B 2021, 103, L180410. 10.1103/PhysRevB.103.L180410. [DOI] [Google Scholar]
  73. Trzeciecki M.; Hübner W. Time-reversal symmetry in nonlinear optics. Phys. Rev. B 2000, 62, 13888–13891. 10.1103/PhysRevB.62.13888. [DOI] [Google Scholar]
  74. Sounas D. L.; Alù A. Time-Reversal Symmetry Bounds on the Electromagnetic Response of Asymmetric Structures. Phys. Rev. Lett. 2017, 118, 154302. 10.1103/PhysRevLett.118.154302. [DOI] [PubMed] [Google Scholar]
  75. Willner A. E.; Khaleghi S.; Chitgarha M. R.; Yilmaz O. F. All-Optical Signal Processing. J. Lightwave Technol. 2014, 32, 660–680. 10.1109/JLT.2013.2287219. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl3c00367_si_001.pdf (3.3MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES