Missing Outcome Data in Epidemiologic Studies

Abstract

Missing data are pandemic and a central problem for epidemiology. Missing data reduce precision and can cause notable bias. There remain too few simple published examples detailing types of missing data and illustrating their possible impact on results. Here we take an example randomized trial that was not subject to missing data and induce missing data to illustrate 4 scenarios in which outcomes are 1) missing completely at random, 2) missing at random with positivity, 3) missing at random without positivity, and 4) missing not at random. We demonstrate that accounting for missing data is generally a better strategy than ignoring missing data, which unfortunately remains a standard approach in epidemiology.

Abbreviations

17p

17α-hydroxyprogesterone caproate

HIV

human immunodeficiency virus

IPOP

Improving Pregnancy Outcomes With Progesterone

Editor’s note: The opinions expressed in this article are those of the authors and do not necessarily reflect the views of the American Journal of Epidemiology.

The future of epidemiology depends on widespread and deepened understanding of missing data. Missing data cause big problems for epidemiology (1, 2). At best, missing data reduce precision because there are fewer observed data points to analyze. At worst, missing data induce a large amount of bias that cannot be ameliorated given the observed data.

While missing data abound, there remain few simple published examples detailing types of missing data and illustrating their impact on results. We provide a summary data set taken from a recent randomized trial conducted in Zambia which was not subject to missing data (3). We induce missing outcomes to illustrate 4 scenarios—namely, data missing 1) completely at random, 2) at random with positivity, 3) at random without positivity, and 4) not at random. Then we analyze the modified data sets using both a naive method and a principled missing-data method, and we close with a brief discussion.

METHODS

The IPOP Trial

The Improving Pregnancy Outcomes With Progesterone (IPOP) Trial was a double-masked placebo-controlled randomized trial of weekly injections of 17α-hydroxyprogesterone caproate (17p) to reduce the composite outcome of preterm birth (birth at <37 weeks’ gestation) or stillbirth among 800 human immunodeficiency virus (HIV)-seropositive women seeking antenatal care in Lusaka, Zambia (3, 4). Eligible women were aged 18 years or older, had a viable singleton pregnancy at less than 24 weeks’ gestation, had confirmed HIV infection, and were currently receiving or intended to commence the use of antiretroviral therapy. Those reporting a prior spontaneous preterm birth were excluded. To aid interpretation, we present results with the 17p arm as the reference group, such that risk ratios remain (mostly) above 1, and risk ratios are interpreted as the effect of no 17p treatment on preterm birth.

The outcome was ascertained for all 800 trial participants, and adherence to weekly injections was 98% in both treatment arms. Data are provided in Table 1. The risk of preterm birth was 9% in both arms, with a risk ratio of 1.00 (95% confidence interval: 0.63, 1.67). Cervical length was measured by ultrasound before randomization. A short cervix is typically defined as one that is less than 2.5 cm long, but here it was defined as less than 4 cm, to maximize the association with risk of preterm birth while maintaining adequate group sizes (i.e., risk ratio = 1.89, 95% confidence interval: 1.20, 2.98). Having a short cervix was not associated with the randomly assigned 17p treatment (i.e., risk ratio = 1.04, 95% confidence interval: 0.91, 1.20), as expected. The IPOP Trial full data set provides a reference against which to compare scenarios with varying missing-data mechanisms.

Table 1.

Distribution of Data From the IPOP Trial and Possible Missing-Data Scenarios (n = 800), Zambia, 2018–2020

		Cervix Length and 17p Treatment Arm
Data Set	Total No.	Cervix ≥4 cm		Cervix <4 cm
		No 17p	17p	No 17p	17p
Observed IPOP data
No. of women	800	215	222	186	177
No. of preterm births	72	15	13	21	23
No. of missing data points	0	0	0	0	0
Missing-data mechanism
MCARa
No. of women	601	161	167	140	133
No. of preterm births	54	11	10	16	17
No. of missing data points	199	54	55	46	44
MAR with positivityb
No. of women	605	108	222	186	89
No. of preterm births	54	8	13	21	12
No. of missing data points	195	107	0	0	88
MAR without positivityc
No. of women	623	215	222	186	0
No. of preterm births	49	15	13	21	0
No. of missing data points	177	0	0	0	177
MNARd
No. of women	583	100	216	186	81
No. of preterm births	55	15	7	21	12
No. of missing data points	217	115	6	0	96

Abbreviations: 17p, 17α-hydroxyprogesterone caproate; IPOP, Improving Pregnancy Outcomes With Progesterone; MAR, missing at random; MCAR, missing completely at random; MNAR, missing not at random.

^a Approximately 25% missing data from each stratum.

^b Approximately 50% missing data from the first and fourth strata.

^c All women from the fourth stratum were missing outcome data.

^d Approximately 50% of term births were missing from the first and fourth strata and 50% of preterm births were missing from the second and fourth strata.

Data deformations

We induced approximately 25% missing outcome data under the 4 mechanisms detailed below. The proportion of missing data was approximate, to allow integer patient counts for each scenario. Data for each scenario are also provided in Table 1, and software code is provided on GitHub (https://github.com/pzivich/publications-code). Causal diagrams depicting each scenario are shown in Figure 1. Note that in Figure 1 we included an arrow denoting the parameter of interest, from 17p treatment to the outcome of preterm birth, even though there was no relationship demonstrated in the IPOP Trial.

Figure 1.

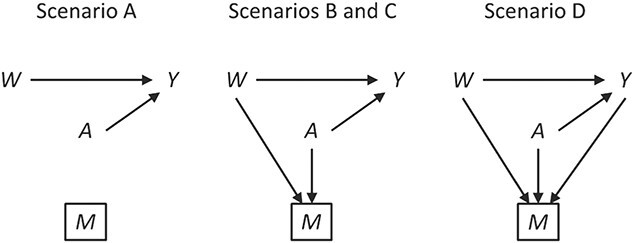
Causal diagrams for possible missing-data scenarios in the IPOP Trial. W denotes the covariate short cervix, A denotes treatment with 17α-hydroxyprogesterone caproate, Y denotes preterm birth outcome, and M denotes a missing value for the outcome. Boxes denote restriction to observed data. IPOP, Improving Pregnancy Outcomes With Progesterone.

The 4 missing-data mechanisms were as follows.

• 1. Missing completely at random: 25% of patients had their outcome set to missing, independent of 17p treatment, short cervix, or the value of the outcome itself. Therefore, no bias should be incurred even with a naive analysis, but a loss in precision is to be expected.

• 2. Missing at random with positivity: 50% of patients with both 17p treatment and a short cervix and 50% of patients with neither 17p treatment nor a short cervix had their outcomes set to missing. Other patients had complete data. Therefore, among the patients with the outcome observed, the odds ratio for the association between short cervix and no 17p treatment was 4.3. This relationship is expected to cause positive bias because the no-17p treatment group is enriched with patients with a short cervix, and short cervix was associated with a nearly 2-fold increased risk of preterm birth. Regarding missing data, positivity is the condition that each woman has a positive probability of having observed data given measured covariates, or formally 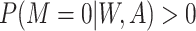, where , 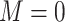denotes observed data, and W and A denote covariates and treatment, respectively.

• 3. Missing at random without positivity: All patients with both 17p treatment and a short cervix had their outcomes set to missing. Other patients had complete data. Therefore, the probability of being observed was 0 (nonpositive) for patients with both 17p treatment and a short cervix.

• 4. Missing not at random: Among women who did not have a preterm birth, 50% with both 17p treatment and a short cervix and 50% with neither 17p treatment nor a short cervix had their outcomes set to missing. Additionally, 50% of women with preterm birth who were treated with 17p had their outcomes set to missing. Therefore, a bias is induced which cannot be removed without knowledge of the data that are missing.

Statistical methods

For the naive method, risk ratios were estimated using a log binomial model fitted to the complete records by maximum likelihood, with Wald-type 95% confidence intervals computed using the model-based standard error. Principled approaches with which to account for missing data include imputation, weighting, or direct maximum likelihood (5). Here, with only the outcome missing, we accounted for missing data using a direct maximum likelihood approach. Specifically, we used generalized computation (g-computation) to estimate the treatment effect accounting for the missing outcome data (6). The generalized formula (7) can be used to construct a g-computation algorithm that provides a maximum likelihood estimator of the risk under binary treatment a, given as

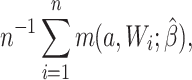where 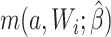is the probability of the potential outcome 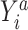estimated using the observed data, 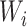is a set of covariates (where i indexes the n participants), and β is a set of parameters from the model m. For completeness, we provide imputation and weighting results in Web Table 1 (available at https://doi.org/10.1093/aje/kwac179).

To implement the g-computation approach, first, we construct the 2 potential outcomes and add them to the data set. We set 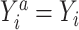when 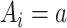, by invoking the causal consistency assumption (8). When 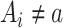, the constructed potential outcome 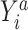is missing. When the observed outcome 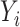is missing, then both constructed potential outcomes 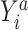are missing. The data set with the 2 constructed potential outcomes is illustrated in Web Table 2. Second, we fit a pair of logistic regression models, one with each potential outcome as the outcome, both conditional on short cervix status. Third, the fitted logistic regression models are used to predict the probability of the potential outcome under plan a, which is 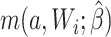. Finally, we estimate the preterm birth risk under treatment a by taking the average of the predicted values .

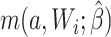There are 2 exchangeability assumptions being invoked. First, women treated with 17p are assumed to be marginally exchangeable with women treated with placebo given the randomized design. However, in our implementation we assume that 17p is exchangeable given short cervix status, which we table until the discussion. Second, women who are missing data are assumed to be exchangeable with women with observed data, conditional on short cervix and 17p treatment. Conceptually, g-computation imputes missing potential outcome data, whether those data are missing because the outcome is missing or missing because the woman received the alternate treatment (i.e., 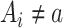) (9). Wald-type 95% confidence intervals were computed with the bootstrap standard error—that is, the standard deviation of 500 bootstrap random samples, each of size n, taken with replacement from the observed data (10). We compared the risk ratios, both naive and accounting for missing data in a principled manner, using the IPOP full-data estimate as a gold standard. We also calculated the root mean squared error (i.e., the square root of the sum of squared bias and variance).

RESULTS

When data were missing completely at random, the naive complete-case analysis had no bias but there was a loss of precision, with the standard error for the log risk ratio being 1.16 (= 0.260/0.225) times larger than the full-data standard error (Table 2). While accounting for data that are missing completely at random can improve precision in comparison with a complete-case analysis, a reduction in the standard error upon accounting for the missing data was not seen in this simple example.

Table 2.

Effect of No 17p Use on Preterm Birth Under Various Missing-Data Mechanisms in the IPOP Trial (n = 800), Zambia, 2018–2020

	Analysis
	Naive				Imputed  a
Missing-Data Mechanism	RR	95% CI	RMSE	SE for    Log RR	RR	95% CI	RMSE	SE for    Log RR
No missing data	1.00	0.65, 1.56	0.225	0.225	N/A	N/A	N/A	N/A
MCAR	1.00	0.60, 1.66	0.260	0.260	0.98	0.58, 1.67	0.273	0.273
MAR with positivity	1.23	0.74, 2.04	0.339	0.261	0.98	0.57, 1.70	0.280	0.280
MAR without positivity	1.53	0.83, 2.83	0.536	0.313	1.52	0.78, 2.97	0.547	0.340
MNAR	1.97	1.16, 3.35	0.740	0.271	1.56	0.88, 2.78	0.540	0.292

Abbreviations: 17p, 17α-hydroxyprogesterone caproate; CI, confidence interval; IPOP, Improving Pregnancy Outcomes With Progesterone; MAR, missing at random; MCAR, missing completely at random; MNAR, missing not at random; N/A, not applicable; RMSE, root mean squared error; RR, risk ratio; SE, standard error.

^a Generalized computation accounting for cervix length <4 cm, with the SE estimated by the standard deviation of 500 bootstrap samples.

When data were missing at random, given 17p treatment and a short cervix with positivity, there was notable bias when using the naive complete-case estimator (Table 2). The bias was ameliorated upon accounting for the missing data, with some cost in precision, as the standard error for the log risk ratio was 1.07 (= 0.280/0.261) times larger than it was without bias correction. Taking the estimated risk ratio from the full data set as the truth, the root mean squared error was 0.339 for the naive log risk ratio and 0.280 for the imputed risk ratio, suggesting that here the reduction in bias outweighed any loss of precision in terms of squared error.

When data were missing at random, given 17p treatment and a short cervix without positivity, there was again notable bias when using the naive complete-case estimator (Table 2). Here the bias was not ameliorated upon accounting for the missing data. In this example, the effect of no 17p treatment on preterm birth is homogeneous on the ratio scale (as well as the difference scale, since there is no effect) for women with and without a short cervix, as can be verified in the full data. Therefore, we can restrict analysis to the subset in which we have positivity (i.e., where the cervix is ≥4 cm long) and obtain an unbiased estimate of the effect of no 17p treatment on preterm birth, albeit with loss of precision.

Finally, when data were missing not at random (i.e., depended on values of the missing variables themselves), there was again notable bias when using the naive complete-case estimator (Table 2). Here, accounting for the missing data reduced but did not eliminate bias.

DISCUSSION

Missing data were an important problem 50 years ago (11), and we suspect they will remain so. Why are missing data so important? Everything you don’t know is missing data; and much of what you think you know is affected by missing data. If we don’t have a formal way to represent and analyze missing data, we may not be able to even recognize what is missing, let alone make accurate inferences when there are missing data. Missing data are arguably the central analytical problem for epidemiology, because both confounding and measurement error may be framed as implicit missing-data problems (12, 13). Ignoring missing data stubbornly remains standard practice in epidemiology (14, 15).

There are limitations to this illustration. As noted above regarding the 2 exchangeability conditions, the g-computation approach taken here to account for missing outcome data does not easily allow one to have different covariate sets for the missing data and treatment exchangeability assumptions (16). When this is desired, inverse probability weighting can be used instead. Furthermore, the variance for the imputation estimator was estimated using the bootstrap, but M-estimation (17) could have been used instead, which avoids the computationally intensive resampling procedure.

Missing data come in many forms. One way to classify missing data is as data missing completely at random, missing at random, or missing not at random. In empirical work, we rarely know which form of missingness is operating. If data are missing completely at random, then accounting for missing data may improve precision (2), though this is not guaranteed, as is seen in the example. If data are missing at random with positivity, then accounting for missing data can remove bias. However, data can be missing at random without positivity. Without positivity, we may not be able to obtain unbiased estimates of the parameter of interest (18, 19). Here, we could have chosen to restrict the parameter to a population in which positivity was met (i.e., effect of 17p treatment on preterm birth among women without a short cervix). However, this revised parameter addresses a different research question than the original question (i.e., effect of 17p treatment on preterm birth) because there is a change in the population of interest. Finally, in this example, the bias induced when data were missing not at random was reduced by accounting for missing data in the analysis. While such scenarios are possible (and perhaps common), one can envision scenarios where accounting for data missing not at random increases bias. Bounds and sensitivity analysis ought to be used when we suspect data are missing not at random (20). To summarize, it seems better to account for, rather than ignore, missing data. Ignorance is bliss until a bridge collapses.