Abstract
Active comparator studies are increasingly common, particularly in pharmacoepidemiology. In such studies, the parameter of interest is a contrast (difference or ratio) in the outcome risks between the treatment of interest and the selected active comparator. While it may appear treatment is dichotomous, treatment is actually polytomous as there are at least 3 levels: no treatment, the treatment of interest, and the active comparator. Because misclassification may occur between any of these groups, independent nondifferential treatment misclassification may not be toward the null (as expected with a dichotomous treatment). In this work, we describe bias from independent nondifferential treatment misclassification in active comparator studies with a focus on misclassification that occurs between each active treatment and no treatment. We derive equations for bias in the estimated outcome risks, risk difference, and risk ratio, and we provide bias correction equations that produce unbiased estimates, in expectation. Using data obtained from US insurance claims data, we present a hypothetical comparative safety study of antibiotic treatment to illustrate factors that influence bias and provide an example probabilistic bias analysis using our derived bias correction equations.
Keywords: active comparator study, information bias, treatment misclassification
Abbreviations
- AOM
acute otitis media
- PPV
positive predictive value
- RD
risk difference
- RR
risk ratio
Much epidemiologic research ignores potential exposure misclassification (1, 2). When acknowledged, authors commonly invoke the well-known result that independent nondifferential misclassification of an exposure produces bias toward the null (3–6). However, this result applies only to misclassification of a binary exposure (3, 7). When the exposure is polytomous, the resulting bias may be in any direction (3, 5, 7).
In active comparator studies, our target parameter is a causal contrast between 2 active treatments: the treatment of interest (index treated) and an active comparator (comparator treated). However, the cohorts in active comparator studies are drawn from a population with at least 3 levels of treatment—index, comparator, and no treatment (untreated)—and misclassification may occur in this polytomous variable. Therefore, bias from nondifferential treatment misclassification in active comparator studies may be in any direction (5).
Active comparator studies have been used across a range of research areas but are particularly common in pharmacoepidemiology, where they are strongly recommended to reduce confounding by indication (8, 9). In such studies, treatment misclassification occurs for a variety of reasons and may occur between any of the treatment groups. For example, individuals who are truly treated but are misclassified as untreated are false negatives. Individuals who are truly untreated but are misclassified as treated are false positives. False negatives and false positives occur when sensitivity and specificity, respectively, for a treatment are less than 1.
While it has been shown that independent nondifferential misclassification in an active comparator study may result in bias away from the null (5), this type of systematic bias has not been thoroughly described. Our objective was to describe bias from independent nondifferential misclassification of treatment in active comparator studies by identifying factors that influence the magnitude and direction of bias and deriving equations for bias and bias correction.
NOTATION
We examined treatment misclassification that was independent (i.e., independent of measurement error of other variables) and nondifferential with respect to the outcome (i.e., misclassification was independent of the true outcome) and that occurred between each treated group (index or comparator treated) and the untreated. Let subscripts  ,
,  , and
, and  denote index treated, comparator treated, and untreated, respectively. Let
denote index treated, comparator treated, and untreated, respectively. Let 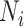 ,
, 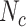 , and
, and  be the true number of individuals and
be the true number of individuals and 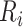 ,
, 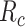 , and
, and 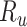 be the true risk (incidence) of a binary outcome,
be the true risk (incidence) of a binary outcome,  , in each treatment group. Table 1 is the cross-tabulation of true treatment and outcome. The parameters of interest are the outcome risks for index treatment (
, in each treatment group. Table 1 is the cross-tabulation of true treatment and outcome. The parameters of interest are the outcome risks for index treatment (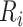 ) and comparator treatment (
) and comparator treatment (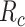 ) and the index-comparator risk difference (RD,
) and the index-comparator risk difference (RD,  ) or risk ratio (RR,
) or risk ratio (RR, 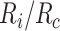 ).
).
Table 1.
Cross-Tabulation of True Treatment and Outcome to Introduce Notation
| Treatment | |||
|---|---|---|---|
| Outcome | Index | Comparator | Untreated |

|
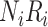
|
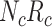
|

|
|

|

|
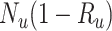
|
| Total |
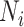
|

|
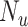
|
Abbreviations: Y, outcome; Nc, true number of individuals treated with comparator; Ni, true number of individuals treated with index; Nu, true number of individuals untreated; Rc, true outcome risk for the comparator treatment; Ri, true outcome risk for the index treatment; Ru, true outcome risk for no treatment.
Table 2 is the observed (misclassified) cross-tabulation with each cell denoted by letters 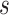 ,
, 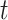 ,
, 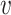 ,
,  ,
,  ,
, 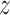 . From the observed data, the estimates of the parameters of interest are
. From the observed data, the estimates of the parameters of interest are 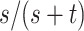 (risk for index),
(risk for index), 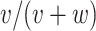 (risk for comparator),
(risk for comparator),  (RD), and
(RD), and 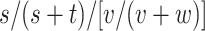 (RR). For index and comparator, respectively, let
(RR). For index and comparator, respectively, let 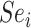 and
and 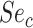 be the sensitivities (proportion of truly treated who were observed to be treated) and
be the sensitivities (proportion of truly treated who were observed to be treated) and 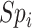 and
and 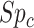 be the specificities (proportion of truly untreated who were correctly observed to be not treated with index for
be the specificities (proportion of truly untreated who were correctly observed to be not treated with index for 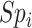 or with comparator for
or with comparator for 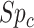 ). Web Appendix 1 (including Web Tables 1–3 and available at https://doi.org/10.1093/aje/kwac131), includes the misclassification table comparing true and observed treatment that illustrates calculation of sensitivity and specificity. Table 2 includes equations for obtaining the value in each cell from the true number of individuals in each treatment group, the true outcome risk, sensitivity, and specificity. For example, the observed number of individuals treated with index,
). Web Appendix 1 (including Web Tables 1–3 and available at https://doi.org/10.1093/aje/kwac131), includes the misclassification table comparing true and observed treatment that illustrates calculation of sensitivity and specificity. Table 2 includes equations for obtaining the value in each cell from the true number of individuals in each treatment group, the true outcome risk, sensitivity, and specificity. For example, the observed number of individuals treated with index, 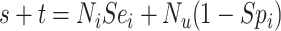 , and the observed number of individuals treated with comparator,
, and the observed number of individuals treated with comparator, 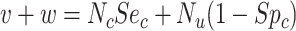 . Finally, the positive predictive value (PPV) is the proportion of observed (misclassified) treated who were truly treated (true positives):
. Finally, the positive predictive value (PPV) is the proportion of observed (misclassified) treated who were truly treated (true positives): 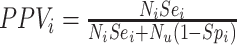 and
and 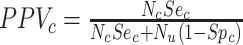 . The complement of PPV (
. The complement of PPV (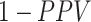 , the false-positive predictive value) is the proportion of the observed treated who were truly untreated (false positives) and can be expressed as
, the false-positive predictive value) is the proportion of the observed treated who were truly untreated (false positives) and can be expressed as  and
and 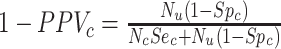 . See Web Appendix 2 (including Web Tables 4 and 5) for equation derivations.
. See Web Appendix 2 (including Web Tables 4 and 5) for equation derivations.
Table 2.
Cross-Tabulation of Observed (Misclassified) Treatment and Outcome to Illustrate Relationships With True Cell Counts, Sensitivity, and Specificity
| Treatment | |||
|---|---|---|---|
| Outcome | Index | Comparator | Untreated |
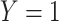
|
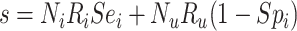
|

|

|
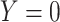
|
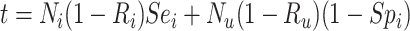
|
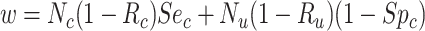
|

|
| Total |
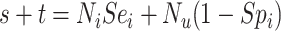
|
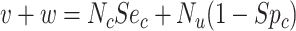
|

|
Abbreviations: Y, outcome; Nc, true number of individuals treated with comparator; Ni, true number of individuals treated with index; Nu, true number of individuals untreated; Rc, true outcome risk for the comparator treatment; Ri, true outcome risk for the index treatment; Ru, true outcome risk for no treatment; Sec, sensitivity for comparator treatment; Sei, sensitivity for index treatment; Spc, specificity for comparator treatment; Spi, specificity for index treatment.
Bias in the estimated risks
The outcome risk for the index treatment estimated using the observed (misclassified) data is
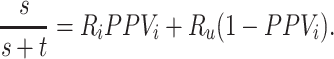 |
The estimated risk based on the observed data is a weighted average of: 1) the true outcome risk for the index treatment (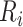 ), weighted by the proportion of true positives among those observed to be index treated (
), weighted by the proportion of true positives among those observed to be index treated (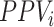 ); and 2) the true outcome risk without treatment (
); and 2) the true outcome risk without treatment (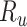 ), weighted by the proportion of false positives among those observed to be index treated (
), weighted by the proportion of false positives among those observed to be index treated (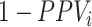 ). The bias in the estimated outcome risk for index treatment,
). The bias in the estimated outcome risk for index treatment,
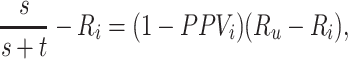 |
has 2 components: 1) a misclassification component, the complement of PPV (i.e., the false positive predictive value); and 2) a scaling component, the difference in outcome risk without treatment and the outcome risk for the index treatment. The first component quantifies the misclassification while the second component quantifies the impact of each false positive on the observed risk.
Based on the equations above, note that there will be no bias in the estimated risk for index treatment when: 1) there are no false positives (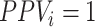 ), which will occur when
), which will occur when 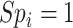 ; or 2) the outcome risk for index treatment and no treatment are equal (
; or 2) the outcome risk for index treatment and no treatment are equal (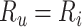 , i.e., index treatment has no effect on the outcome risk compared with no treatment so false positives have the same outcome risk as the true positives). Bias increases as 1) index treatment has a greater effect on the outcome risk and 2) the proportion of false positives, among those observed to be index treated, increases. Figure 1 illustrates what factors influence the proportion of false positives among those observed to be index treated,
, i.e., index treatment has no effect on the outcome risk compared with no treatment so false positives have the same outcome risk as the true positives). Bias increases as 1) index treatment has a greater effect on the outcome risk and 2) the proportion of false positives, among those observed to be index treated, increases. Figure 1 illustrates what factors influence the proportion of false positives among those observed to be index treated, 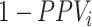 . The proportion of false positives increases as specificity (
. The proportion of false positives increases as specificity (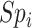 ) decreases. At a given specificity, false positives decrease as the ratio of the true number of individuals treated with index to the true number of untreated individuals (
) decreases. At a given specificity, false positives decrease as the ratio of the true number of individuals treated with index to the true number of untreated individuals (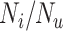 ) increases. The proportion of false positives is particularly inflated when
) increases. The proportion of false positives is particularly inflated when 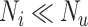 (i.e., when the ratio is very small on the left-hand side of the figure). At a given specificity, the proportion of false positives increases as sensitivity (
(i.e., when the ratio is very small on the left-hand side of the figure). At a given specificity, the proportion of false positives increases as sensitivity (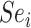 ) decreases, although the impact is comparatively small. A plot of the bias in the estimated outcome risk for index treatment, as opposed to
) decreases, although the impact is comparatively small. A plot of the bias in the estimated outcome risk for index treatment, as opposed to 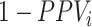 , would be identical to Figure 1, except the y-axis would be scaled by
, would be identical to Figure 1, except the y-axis would be scaled by  . When
. When 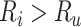 , which may be the case in a study of adverse effects of treatment, bias is downward (
, which may be the case in a study of adverse effects of treatment, bias is downward (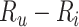 would be negative and
would be negative and 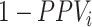 is always positive) and the estimated risk is an underestimate. When
is always positive) and the estimated risk is an underestimate. When 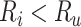 , which may be the case in an efficacy study, bias is upward and the estimated risk is an overestimate. The estimated outcome risk for the comparator treatment can be expressed analogously (Web Appendix 2). For the comparator treatment, the relationship of the proportion of false positives (
, which may be the case in an efficacy study, bias is upward and the estimated risk is an overestimate. The estimated outcome risk for the comparator treatment can be expressed analogously (Web Appendix 2). For the comparator treatment, the relationship of the proportion of false positives (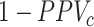 ) with specificity (
) with specificity (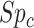 ), true ratio of comparator treated to untreated individuals (
), true ratio of comparator treated to untreated individuals (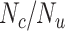 ), and sensitivity (
), and sensitivity (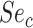 ) are equivalent.
) are equivalent.
Figure 1.

Influence of specificity, sensitivity, and true ratio of index treated (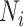 ) to true untreated (
) to true untreated (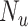 ) on the proportion of the observed index treated who are false positives (1 − positive predictive value).
) on the proportion of the observed index treated who are false positives (1 − positive predictive value).
Bias in the estimated risk contrast
The bias in the index-comparator RD is the difference between the bias in the outcome risk for the index treatment and the bias in the outcome risk for the comparator treatment,
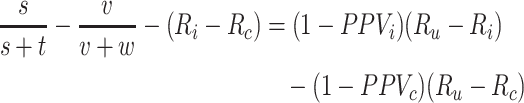 |
See Web Appendix 2 for bias of the RR. There is no bias in the RD when 1) both risks are unbiased or 2) the bias in each risk is equal and cancels out,
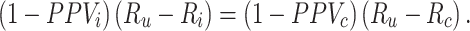 |
There is a special case when 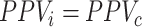 . When PPV for index treatment and comparator treatment are equal (
. When PPV for index treatment and comparator treatment are equal (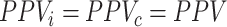 ), then the estimated RD is
), then the estimated RD is
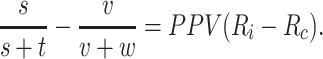 |
The PPV, bounded by 0 and 1, is an attenuation factor and the estimated RD will be biased toward the null and will not cross the null.
Bias correction equations
We inverted the bias equation for the outcome risk for index treatment to obtain a formula to recover the unbiased (bias-corrected) risk in the index treated,
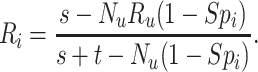 |
The formula requires the observed number of individuals treated with index (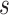 and
and 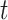 ), the specificity of the classification of index treatment (
), the specificity of the classification of index treatment (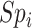 ), the true outcome risk without treatment (
), the true outcome risk without treatment (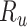 ), and the true number of untreated individuals (
), and the true number of untreated individuals (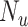 ). An analogous formula was obtained for the outcome risk for the comparator treatment (Web Appendix 2) using observed number of individuals treated with comparator (
). An analogous formula was obtained for the outcome risk for the comparator treatment (Web Appendix 2) using observed number of individuals treated with comparator (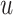 and
and  ), the specificity of the classification of comparator treatment (
), the specificity of the classification of comparator treatment (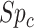 ), the true outcome risk without treatment (
), the true outcome risk without treatment (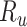 ), and the true number of untreated individuals (
), and the true number of untreated individuals (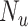 ). A bias-corrected risk contrast can be estimated from the bias-corrected risks.
). A bias-corrected risk contrast can be estimated from the bias-corrected risks.
Illustration of a hypothetical study
We examined the impact treatment misclassification could have on estimates from a hypothetical comparative safety study of adverse events within 30 days after treatment with azithromycin (index) or cefdinir (comparator) for acute otitis media (AOM) or acute sinusitis in children. We examined 2 indications to illustrate how resulting bias differs between populations with different true treatment distributions. We used data from the IBM Watson Health MarketScan Commercial Claims and Encounters database (IBM Corporation, Armonk, New York). We identified children older than 24 months and younger than 18 years, with a new outpatient diagnosis of AOM or acute sinusitis in 2019 and no recent antibiotic fills, with continuous insurance coverage for the prior 60 days. For illustration, we used antibiotic prescription fills from the day of or day subsequent to diagnosis as the true treatment distribution ( and
and 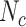 ). Children with a diagnosis without an antibiotic prescription fill were considered untreated (
). Children with a diagnosis without an antibiotic prescription fill were considered untreated (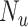 ). The true outcome risks were set deterministically: azithromycin at 0.08, cefdinir at 0.07, and no treatment at 0.01. The true index-comparator RD was 0.01 (or 1.0 percentage points) and RR was 1.14. Specificity for azithromycin and cefdinir was varied between 0.8 and 1.0 (10). Sensitivity was set at 0.7. We examined sensitivities ranging from 0.6 to 0.9 in additional scenarios. We used the bias equations presented above to calculate PPV and bias.
). The true outcome risks were set deterministically: azithromycin at 0.08, cefdinir at 0.07, and no treatment at 0.01. The true index-comparator RD was 0.01 (or 1.0 percentage points) and RR was 1.14. Specificity for azithromycin and cefdinir was varied between 0.8 and 1.0 (10). Sensitivity was set at 0.7. We examined sensitivities ranging from 0.6 to 0.9 in additional scenarios. We used the bias equations presented above to calculate PPV and bias.
Table 3 shows the true treatment distribution for the illustration. For both diagnoses, approximately 50% of children were untreated, so the number of children receiving any active treatment was smaller than the number untreated (ratios with untreated < 1). For sinusitis, a similar number of individuals used azithromycin and cefdinir, while azithromycin use was less common than cefdinir for AOM. For specificities ranging from 0.8 to 1.0, Figure 2 illustrates the expected proportion of false positives among the observed treated (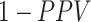 ) for each treatment (Figure 2A and 2B), the expected bias in each risk (Figure 2C and 2D), and the expected bias in the RD (Figure 2E and 2F) for each treatment. In Figure 2A and 2B, the proportion of false positives increases with decreasing specificity for each treatment. For AOM, at each specificity, azithromycin had a greater proportion of false positives than cefdinir because there were fewer individuals truly treated with azithromycin than with cefdinir (i.e., azithromycin had a smaller ratio with untreated in Table 3). For sinusitis, at each specificity, the proportion of false positives was similar for both treatments because the number of individuals truly treated with azithromycin and cefdinir were similar (i.e., similar ratios with untreated in Table 3).
) for each treatment (Figure 2A and 2B), the expected bias in each risk (Figure 2C and 2D), and the expected bias in the RD (Figure 2E and 2F) for each treatment. In Figure 2A and 2B, the proportion of false positives increases with decreasing specificity for each treatment. For AOM, at each specificity, azithromycin had a greater proportion of false positives than cefdinir because there were fewer individuals truly treated with azithromycin than with cefdinir (i.e., azithromycin had a smaller ratio with untreated in Table 3). For sinusitis, at each specificity, the proportion of false positives was similar for both treatments because the number of individuals truly treated with azithromycin and cefdinir were similar (i.e., similar ratios with untreated in Table 3).
Table 3.
True Treatment Distribution, for Hypothetical Comparative Safety Study of 2 Antibiotics, Using Data Obtained From MarketScan, United States, 2019
| Acute Otitis Media | Acute Sinusitis | |||||
|---|---|---|---|---|---|---|
| Treatment | No. | % | Ratio to Untreated | No. | % | Ratio to Untreated |
| Azithromycin | 15,072 | 13 | 0.26 | 21,488 | 23 | 0.48 |
| Cefdinir | 42,465 | 37 | 0.74 | 27,936 | 30 | 0.63 |
| Untreated | 57,633 | 50 | 45,068 | 48 | ||
| Othera | 210,180 | 114,374 | ||||
a Includes multiple antibiotic fills.
Figure 2.
Illustration of the proportion of observed treated who are false positives (1 − positive predictive value) (A and B), bias in the risks (in percentage points) (C and D), and bias in the risk difference (in percentage points) (E and F) as specificity varies in a hypothetical comparative safety study of azithromycin (index) versus cefdinir (comparator) for treatment of acute otitis media and sinusitis in children.
In the illustration, the formula for bias in the risk was 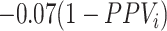 for azithromycin and
for azithromycin and 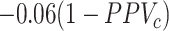 for cefdinir. Recall that the equation for the bias in the outcome risks for each treatment includes a misclassification component (the complement of the PPV) and a scaling component (the difference in the true outcome risk without treatment and the true outcome risk for treatment). The plot of bias in the risks in Figure 2C and 2D are thus scaled versions of the Figure 2A and 2B plots. The azithromycin lines are scaled by −0.07 and the cefdinir lines are scaled by −0.06. Panels Figure 2E and 2F present heat maps illustrating the direction and magnitude of bias in the RD for (see Web Figure 1 for RR results). The white diagonal path through each plot marks the specificities when the RD is unbiased. The differing patterns in magnitude and direction of bias for each diagnosis, resulting from the differing true treatment distributions, indicate that treatment misclassification can result in heterogeneity between populations even when misclassification does not vary across those populations. For example, when azithromycin specificity was 0.92 and cefdinir specificity was 0.81, there was the same magnitude of bias for each diagnosis, but in opposite directions: downward bias for AOM (observed RD = 0.5 percentage points) and upward bias (away from the null) for sinusitis (RD = 1.5). When azithromycin specificity was 0.95 and cefdinir specificity was 0.82, there was no bias for AOM (cancellation of bias in each risk, RD = 1.0) and upward bias for sinusitis (RD = 1.8). Finally, when azithromycin specificity was 0.90 and cefdinir specificity was 0.95, there was downward bias for both diagnoses. For AOM, the bias pushed the RD past the null making azithromycin appear more harmful than cefdinir (RD = –0.9). For sinusitis, bias pushed the RD to the null making the treatments appear equivalent (RD = 0.0). This illustration was deterministic and utilized the bias equations to produce results. See Web Appendix 3 (including Web Tables 6 and 7 and Web Figure 2) for a stochastic Monte Carlo simulation of these 3 scenarios.
for cefdinir. Recall that the equation for the bias in the outcome risks for each treatment includes a misclassification component (the complement of the PPV) and a scaling component (the difference in the true outcome risk without treatment and the true outcome risk for treatment). The plot of bias in the risks in Figure 2C and 2D are thus scaled versions of the Figure 2A and 2B plots. The azithromycin lines are scaled by −0.07 and the cefdinir lines are scaled by −0.06. Panels Figure 2E and 2F present heat maps illustrating the direction and magnitude of bias in the RD for (see Web Figure 1 for RR results). The white diagonal path through each plot marks the specificities when the RD is unbiased. The differing patterns in magnitude and direction of bias for each diagnosis, resulting from the differing true treatment distributions, indicate that treatment misclassification can result in heterogeneity between populations even when misclassification does not vary across those populations. For example, when azithromycin specificity was 0.92 and cefdinir specificity was 0.81, there was the same magnitude of bias for each diagnosis, but in opposite directions: downward bias for AOM (observed RD = 0.5 percentage points) and upward bias (away from the null) for sinusitis (RD = 1.5). When azithromycin specificity was 0.95 and cefdinir specificity was 0.82, there was no bias for AOM (cancellation of bias in each risk, RD = 1.0) and upward bias for sinusitis (RD = 1.8). Finally, when azithromycin specificity was 0.90 and cefdinir specificity was 0.95, there was downward bias for both diagnoses. For AOM, the bias pushed the RD past the null making azithromycin appear more harmful than cefdinir (RD = –0.9). For sinusitis, bias pushed the RD to the null making the treatments appear equivalent (RD = 0.0). This illustration was deterministic and utilized the bias equations to produce results. See Web Appendix 3 (including Web Tables 6 and 7 and Web Figure 2) for a stochastic Monte Carlo simulation of these 3 scenarios.
Web Figure 3 presents heat maps illustrating bias in the RD for 2 additional scenarios: Web Figure 3A, azithromycin sensitivity 0.9 and cefdinir sensitivity 0.6, and Web Figure 3B, azithromycin sensitivity 0.6 and cefdinir sensitivity 0.9. As the sensitivity differs between treatments, there are changes in the pattern of direction and magnitude of bias that differ by diagnosis.
Example simulated probabilistic bias analysis
To illustrate use of the bias correction equations in a probabilistic bias analysis, we simulated a single cohort of 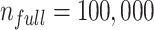 (the full cohort) from the AOM population. The true treatment distribution was simulated using the proportions observed in MarketScan (IBM) (index P = 0.13, comparator P = 0.37, and untreated P = 0.50). The outcome was simulated from a Bernoulli distribution using the probabilities from the illustration (
(the full cohort) from the AOM population. The true treatment distribution was simulated using the proportions observed in MarketScan (IBM) (index P = 0.13, comparator P = 0.37, and untreated P = 0.50). The outcome was simulated from a Bernoulli distribution using the probabilities from the illustration (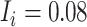 ,
, 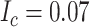 , and
, and 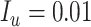 ) for a true index-comparator RD of 1.0 percentage points. Then we simulated the observed (misclassified) treatment using sensitivity 0.7, index specificity 0.9, and comparator specificity 0.95 (data-generation code in Web Appendix 4).
) for a true index-comparator RD of 1.0 percentage points. Then we simulated the observed (misclassified) treatment using sensitivity 0.7, index specificity 0.9, and comparator specificity 0.95 (data-generation code in Web Appendix 4).
From the full cohort, we randomly sampled a single hypothetical validation cohort (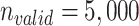 ) in which data on the misclassified and true treatment and on the outcome were available. We used the validation cohort to estimate the true number of untreated individuals in the full data (
) in which data on the misclassified and true treatment and on the outcome were available. We used the validation cohort to estimate the true number of untreated individuals in the full data (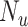 ), the true outcome risk in the untreated (
), the true outcome risk in the untreated ( ), the specificity for index treatment (
), the specificity for index treatment (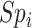 ), and the specificity for comparator treatment (
), and the specificity for comparator treatment (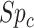 ). For each parameter, we defined triangular distributions using the validation cohort point estimate as the mode and the lower and upper confidence limits as the minimum and maximum, respectively. Other distributions, such as trapezoidal, could also have been chosen (11, 12). We drew each parameter 10,000 times from the triangular distributions (Web Figure 4 shows histograms).
). For each parameter, we defined triangular distributions using the validation cohort point estimate as the mode and the lower and upper confidence limits as the minimum and maximum, respectively. Other distributions, such as trapezoidal, could also have been chosen (11, 12). We drew each parameter 10,000 times from the triangular distributions (Web Figure 4 shows histograms).
For each draw, we corrected the outcome risks for index treatment and comparator treatment for misclassification using the bias correction equations and the observed (tabular) data from the full cohort. We estimated the corrected risk difference by taking the difference in the corrected risks. Estimates were summarized by the median and 2.5th and 97.5th percentiles. We also incorporated uncertainty from random error by taking a random draw from a zero-centered normal distribution for each of the 10,000 parameter draws and adding this to the bias corrected risk difference (11). The normal distribution standard deviation was the standard error of the observed risk difference in the full cohort.
In the full cohort, the RD estimate using the unknown true treatment was 1.15 percentage points (95% CI: 0.61, 1.69) (Table 4). See Web Tables 8 and 9 for cross-tabulation for the true and misclassified full cohort. The estimated RD ignoring measurement error was −0.86 (95% CI: –1.34, −0.39). The estimated RD corrected for measurement error was 1.51 (95% CI: 1.08, 1.99). Incorporating random error, the confidence interval widened to 0.86 to 2.20 (Table 4). Note that these results are from a single analysis using one validation cohort, and therefore the corrected point estimate may not be exactly equal to the estimate using the unknown true treatment.
Table 4.
Estimated Risk Difference (in Percentage Points) From an Example Simulated Probabilistic Bias Analysis Accounting for Random Error and Systematic Error
| Analysis | Point Estimate (Median) | 95% Interval (2.5th, 97.5th Percentile) |
|---|---|---|
| With unknown true treatmenta | 1.15 | 0.61, 1.69 |
| Random error (conventional result)b | −0.86 | −1.34, −0.39 |
| Systematic error | 1.51 | 1.08, 1.99 |
| Total error analysisc | 1.51 | 0.86, 2.20 |
a Estimated using the true treatment classification that would be unknown in a real-data analysis.
b Estimated using the observed misclassified treatment.
c Incorporates uncertainty from random error by adding random draws from zero centered normal distribution with standard deviation equal to standard error from observed full cohort analysis (0.0024).
DISCUSSION
Independent nondifferential treatment misclassification in active comparator studies may result in bias toward the null, bias away from the null, or no bias at all. The direction of bias in risk contrasts is the result of a complex relationship between misclassification probabilities for each treatment, the true distribution of treated and untreated populations, and the true outcome risks for each treatment and no treatment. This complexity makes it challenging to predict the direction of bias in real world settings. Well-supported prior knowledge of these factors, validation data, or strong assumptions are thus needed to infer the direction of bias. In the simple scenario examined here, bias in the RD is guaranteed to be toward the null only when PPV is the same for index and comparator. However, equal PPVs requires a balancing of misclassification probabilities with treatment distribution that is highly unlikely. In the absence of specific exposure validation data, we conclude that it is generally inappropriate to assume that independent nondifferential treatment misclassification results in bias toward the null in active comparator studies.
Previous work has described bias resulting from independent nondifferential misclassification of a polytomous exposure, typically focusing on polytomous categorization of continuous exposures (7, 13–15). In contrast to prior work, the exposure in active comparator studies is typically truly categorical (as opposed to ordinal), misclassification between certain exposure categories is more likely than others (e.g., between an active treatment and untreated as opposed to between active treatments), and our parameter of interest is typically a contrast between only 2 of the categories. In this sense, our work can be viewed as a special case of the previous work by Birkett (14) and Correa-Villaseñor et al. (15).
Treatment misclassification in active comparator studies may occur for a variety of reasons. The data source and data-collection procedures should be considered when speculating about potential misclassification. The active comparator design is often used in pharmacoepidemiology research leveraging insurance claims, electronic health records, or self-report data. Sensitivity is reduced when an individual who was truly treated is misclassified as untreated (false negative). In claims data, false negatives occur if no claim was generated because of out-of-pocket payment, physician samples, over-the-counter use, or use of supplemental insurance (16–20). In electronic health record data, similar misclassification occurs when prescriptions are provided outside of a documented encounter or provided by a practitioner outside the electronic health record’s network (21, 22).
Specificity is reduced when an individual who was truly untreated is misclassified as treated (false positive). This may occur because of some error in the data, such as an adjustment record in claims or incorrect documentation in a medical record. False positives may also occur because of nonadherence. In electronic health record data, false positives occur when prescriptions are written but not filled (primary nonadherence) or filled but not taken (secondary nonadherence) (10, 23, 24). Secondary nonadherence also produces false positives in claims data (10). It may be possible to reduce false positives by requiring more than one filled prescription (5). Using self-report data, a false positive may occur if an individual reports using a treatment that they did not use, possibly because of perceived social desirability of compliance, or that they used at a different time (25–27).
Of note, whether or not nonadherence is considered misclassification depends on the study question and the estimand (i.e., the parameter of interest) (28). If the objective is to estimate the effect of a treatment decision (to prescribe one medication vs. another) then someone with a prescription who does not take the medication is not misclassified. This is analogous to the intention-to-treat effect in a clinical trial. Alternatively, if the objective is to estimate the effect of taking one medication vs. another, then nonadherence can be considered misclassification. A priori we were interested in examining potential bias from nondifferential treatment misclassification—that is, treatment misclassification that is marginally independent of the outcome. However, when considering nonadherence as the cause of misclassification specifically, it may be difficult to justify a nondifferential assumption. Rather, there may be common causes of adherence and outcomes resulting in differential misclassification (28).
Misclassification (and whether false positives or false negatives are more common) is highly related to the data source and the treatment under study including the indication and cost. In one study examining medical records and using patient report as the gold standard, sensitivity was as low as 0.33 and was commonly below 0.8. The investigators observed that sensitivity was usually lower than specificity; however, there were some medications where specificity was lower (29). When patient report is the gold standard, studies have observed specificity of medical records or electronic prescription records as low as 0.63, although most often specificity was between 0.88 and 0.98 (10, 29). Studies comparing prescription-fill data with electronic prescription records have found that primary nonadherence for some medication classes may be quite high, but there is likely notable variability by specific medications within classes (24, 30). There is little information on secondary nonadherence for claims data. Our work showed that both sensitivity and specificity affect bias from treatment misclassification; however, there will be no bias if specificity is perfect, and reductions in specificity have a greater influence on bias in the risks than similar reductions in sensitivity.
We derived algebraic equations that can be used to correct for bias from nondifferential treatment misclassification in active comparator studies. These equations essentially attempt to restrict analysis to true positives. When considering nonadherence specifically, this would be akin to restricting analysis to adherers. Such an analysis is valid only when adherence is truly nondifferential with respect to the outcome; otherwise, the restriction results in selection bias, and alternative methods are required (28, 31, 32). Algebraic approaches to address misclassification in 2 × 2 tables have been available since at least 1954, and several investigators have provided easy-to-use tools for leveraging such equations (11, 33). We illustrated a probabilistic bias analysis using such tools leveraging our derived equations that require the true number of untreated individuals, the true outcome risk in the untreated, and the true index and comparator specificities. These inputs are typically unknown but could be estimated in validation studies, as in our example. Outside of validation studies, the true outcome risk in the untreated could be obtained from literature on the natural course of an indication or background occurrence in the population. The true number of untreated may be harder to glean from prior literature and may be estimated given knowledge of the treatment guidelines and the inclusion/exclusion criteria. Alternatively, a wide range of plausible values could be examined and summarized in a sensitivity analysis. Incorporation of adjustment for other biases (e.g., confounding) would require record-level correction, instead of tabular level as in our example (12, 34). Approaches to correct for misclassification in analysis, as opposed to sensitivity analysis, include regression calibration and imputation (35–39).
In our illustration there was a large untreated population. As the untreated population becomes much smaller than the treated population, PPV is less sensitive to declines in specificity (Figure 1). In that setting, bias from treatment misclassification may be minimal unless sensitivity and specificity are very low.
We limited ourselves to studying simple scenarios that may not reflect realistic settings. First, we did not consider the setting where individuals truly treated with index are misclassified as comparator treated and vice versa. Second, we assumed that no one truly received dual therapy but was misclassified as monotherapy or vice versa. Third, we did not consider other systematic biases such as confounding or missing data and how these other biases may interact with misclassification. Also, it is important to remember that bias is a measure of expectation across many studies, and so our equations for bias cannot be used to draw conclusions about the error in any single study.
CONCLUSION
In active comparator studies, bias from independent nondifferential treatment misclassification may be toward or away from the null. Bias from treatment misclassification may be addressed in sensitivity analyses leveraging the derived bias correction equations we provide here or using other bias analyses that accommodate adjustment for other biases. Validation studies are an essential source of supplemental data to quantify the occurrence of treatment misclassification and to inform realistic sensitivity analyses or implement correction approaches.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Gillings School of Global Public Health, University of North Carolina, Chapel Hill, North Carolina, United States (Rachael Ross, I-Hsuan Su, Michael Webster-Clark, Michele Jonsson Funk); and Department of Epidemiology, Biostatistics, and Occupational Health, McGill University, Montreal, Canada (Michael Webster-Clark).
R.K.R. was supported by a training grant from the Eunice Kennedy Shriver National Institute of Child Health and Development (grant T32 HD52468).
Code for this work is available in the Web Material.
Presented at the 2021 Society for Epidemiologic Research annual meeting (online), June 22–25, 2021, and the 2021 International Conference on Pharmacoepidemiology and Therapeutic Risk Management (online), August 23–25, 2021.
Conflict of interest: none declared.
REFERENCES
- 1. Jurek AM, Maldonado G, Greenland S, et al. Exposure-measurement error is frequently ignored when interpreting epidemiologic study results. Eur J Epidemiol. 2006;21(12):871–876. [DOI] [PubMed] [Google Scholar]
- 2. Brakenhoff TB, Mitroiu M, Keogh RH, et al. Measurement error is often neglected in medical literature: a systematic review. J Clin Epidemiol. 2018;98:89–97. [DOI] [PubMed] [Google Scholar]
- 3. Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3rd ed. Philadelphia, PA: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 4. Jurek AM, Greenland S, Maldonado G, et al. Proper interpretation of non-differential misclassification effects: expectations vs observations. Int J Epidemiol. 2005;34(3):680–687. [DOI] [PubMed] [Google Scholar]
- 5. Jonsson Funk M, Landi SN. Misclassification in administrative claims data: quantifying the impact on treatment effect estimates. Curr Epidemiol Reports. 2014;1(4):175–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Copeland KT, Checkoway H, Mcmichael AJ, et al. Bias due to misclassification in the estimation of relative risk. Am J Epidemiol. 1977;105(5):488–495. [DOI] [PubMed] [Google Scholar]
- 7. Dosemeci M, Wacholder S, Lubin JH. Does nondifferential misclassification of exposure always bias a true effect toward the null value? Am J Epidemiol. 1990;132(4):746–748. [DOI] [PubMed] [Google Scholar]
- 8. Food and Drug Administration . Guidance document: best practices for conducting and reporting pharmacoepidemiologic safety studies using electronic healthcare data. 2013. https://www.fda.gov/regulatory-information/search-fda-guidance-documents/best-practices-conducting-and-reporting-pharmacoepidemiologic-safety-studies-using-electronic. Accessed Juy 29, 2022.
- 9. Cox E, Martin BC, Van Staa T, et al. Good research practices for comparative effectiveness research: approaches to mitigate bias and confounding in the design of nonrandomized studies of treatment effects using secondary data sources: International Society for Pharmacoeconomics and Outcomes Research Good Research Practices for Retrospective Database Analysis Task Force Report—Part II. Value Heal. 2009;12(8):1053–1061. [DOI] [PubMed] [Google Scholar]
- 10. Joseph RM, van Staa TP, Lunt M, et al. Exposure measurement error when assessing current glucocorticoid use using UK primary care electronic prescription data. Pharmacoepidemiol Drug Saf. 2019;28(2):179–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lash TL, Fox MP, Fink AK. Applying Quantitative Bias Analysis to Epidemiologic Data. New York, NY: Springer; 2009. [Google Scholar]
- 12. Fox MP, Lash TL, Greenland S. A method to automate probabilistic sensitivity analyses of misclassified binary variables. Int J Epidemiol. 2005;34(6):1370–1376. [DOI] [PubMed] [Google Scholar]
- 13. Marshall JR, Priore R, Graham S, et al. On the distortion of risk estimates in multiple exposure level case-control studies. Am J Epidemiol. 1981;113(4):464–473. [DOI] [PubMed] [Google Scholar]
- 14. Birkett NJ. Effect of nondifferential misclassification on estimates of odds ratios with multiple levels of exposure. Am J Epidemiol. 1992;136(3):356–362. [DOI] [PubMed] [Google Scholar]
- 15. Correa-Villaseñor A, Stewart WF, Franco-Marina F, et al. Bias from nondifferential misclassification in case-control studies with three exposure levels. Epidemiology. 1995;6(3):276–281. [DOI] [PubMed] [Google Scholar]
- 16. Delaney JAC, Biggs ML, Kronmal RA, et al. Demographic, medical, and behavioral characteristics associated with over the counter non-steroidal anti-inflammatory drug use in a population-based cohort: results from the Multi-Ethnic Study of Atherosclerosis. Pharmacoepidemiol Drug Saf. 2011;20(1):83–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Soriano LC, Soriano-Gabarro M, Garcia Rodriguez LA. Validation of low-dose aspirin prescription data in the Health Improvement Network: how much misclassification due to over-the-counter use? Pharmacoepidemiol Drug Saf. 2016;25(4):392–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Cepeda MS, Fife D, Denarié M, et al. Quantification of missing prescriptions in commercial claims databases: results of a cohort study. Pharmacoepidemiol Drug Saf. 2017;26(4):386–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Gamble J-M, Jonson JA, Majumdar SR, et al. Evaluating the introduction of a computerized prior-authorization system on the completeness of drug exposure data. Pharmacoepidemiol Drug Saf. 2013;22(5):551–555. [DOI] [PubMed] [Google Scholar]
- 20. Jacobus S, Schneeweiss S, Chan KA. Exposure misclassification as a result of free sample drug utilization in automated claims databases and its effect on a pharmacoepidemiology study of selective COX-2 inhibitors. Pharmacoepidemiol Drug Saf. 2004;13(10):695–702. [DOI] [PubMed] [Google Scholar]
- 21. West SL, Ritchey ME, Poole C. Validity of pharmacoepidemiologic drug and diagnosis data. In: Strom BL, ed. Pharmacoepidemiology. 3rd ed. Hoboken, NJ: John Wiley & Sons, Ltd; 2000:661–705. [Google Scholar]
- 22. Lin KJ, Glynn RJ, Singer DE, et al. Out-of-system care and recording of patient characteristics critical for comparative effectiveness research. Epidemiology. 2018;29(3):356–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Huber D, Wikén C, Henriksson R, et al. Statin treatment after acute coronary syndrome: adherence and reasons for non-adherence in a randomized controlled intervention trial. Sci Rep. 2019;9(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Jackevicius CA, Li P, Tu JV. Prevalence, predictors, and outcomes of primary nonadherence after acute myocardial infarction. Circulation. 2008;117(8):1028–1036. [DOI] [PubMed] [Google Scholar]
- 25. Choo PW, Rańd CS, Inui TS, et al. Validation of patient reports, automated pharmacy records, and pill counts with electronic monitoring of adherence to antihypertensive therapy. Med Care. 1999;37(9):846–857. [DOI] [PubMed] [Google Scholar]
- 26. Stirratt MJ, Dunbar-Jacob J, Crane HM, et al. Self-report measures of medication adherence behavior: recommendations on optimal use. Transl Behav Med. 2015;5(4):470–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Atkinson TM, Rodríguez VM, Gordon M, et al. The association between patient-reported and objective oral anticancer medication adherence measures: a systematic review. Oncol Nurs Forum. 2016;43(5):576–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Li X, Cole SR, Westreich D, et al. Primary non-adherence and the new-user design. Pharmacoepidemiol Drug Saf. 2018;27(4):361–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Palmsten K, Hulugalle A, Bandoli G, et al. Agreement between maternal report and medical records during pregnancy: medications for rheumatoid arthritis and asthma. Paediatr Perinat Epidemiol. 2018;32(1):68–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Fischer MA, Stedman MR, Lii J, et al. Primary medication non-adherence: analysis of 195,930 electronic prescriptions. J Gen Intern Med. 2010;25(4):284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Mo Y, Lim C, Watson JA, et al. Non-adherence in non-inferiority trials: pitfalls and recommendations. BMJ. 2020;370:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Murray EJ, Caniglia EC, Petito LC. Causal survival analysis: a guide to estimating intention-to-treat and per-protocol effects from randomized clinical trials with non-adherence. Res Methods Med Heal Sci. 2020;2(1):39–49. [Google Scholar]
- 33. Bross I. Misclassification in 2 × 2 tables. Biometrics. 1954;10(4):478–486. [Google Scholar]
- 34. Lash TL, Fink AK. Semi-automated sensitivity analysis to assess systematic errors in observational data. Epidemiology. 2003;14(4):451–458. [DOI] [PubMed] [Google Scholar]
- 35. White IR. Commentary: dealing with measurement error: multiple imputation or regression calibration? Int J Epidemiol. 2006;35(4):1081–1082. [DOI] [PubMed] [Google Scholar]
- 36. Klebanoff MA, Cole SR. Use of multiple imputation in the epidemiologic literature. Am J Epidemiol. 2008;168(4):355–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Cole SR, Chu H, Greenland S. Multiple-imputation for measurement-error correction. Int J Epidemiol. 2006;35(4):1074–1081. [DOI] [PubMed] [Google Scholar]
- 38. Edwards JK, Cole SR, Fox MP. Flexibly accounting for exposure misclassification with external validation data. Am J Epidemiol. 2020;189(8):850–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Blackwell M, Honaker J, King G. A unified approach to measurement error and missing data: overview and applications. Sociol Methods Res. 2017;46(3):303–341. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



