Quantification of cross-relaxation in downfield ¹H MRS at 7 T in human calf muscle

Abstract

Purpose

The purpose of this study was to characterize the ¹H downfield MR spectrum from 8.0 to 10.0 ppm of human skeletal muscle at 7 T and determine the T₁ and cross-relaxation rates of observed resonances.

Methods

We performed downfield MRS in the calf muscle of 7 healthy volunteers. Single-voxel downfield MRS were collected using alternately selective or broadband inversion recovery sequences and spectrally-selective 90° E-BURP RF pulse excitation centered at 9.0 ppm with bandwidth=600 Hz (2.0 ppm). MRS were collected using inversion times 50-2500 ms. We modeled recovery of the longitudinal magnetization of three observable resonances using two models: 1) a 3-parameter model accounting for the apparent T₁ recovery and 2) a Solomon model explicitly including cross-relaxation effects.

Results

Three resonances were observed in human calf muscle at 7 T at 8.0, 8.2 and 8.5 ppm. We found broadband (broad) and selective (sel) inversion recovery T₁=mean±std (ms): T_{1-broad,8.0ppm}=2108.2±664.5, T_1-sel,8.0ppm=753.6±141.0 (P=0.003); T_{1-broad,8.2ppm}=2033.5±338.4, T_1-sel,8.2ppm=135.3±35.3 (P<0.0001); T_{1-broad,8.5ppm}=1395.4±75.4, T_1-sel,8.5ppm=107.1±40.0 (P<0.0001). Using the Solomon model, we found T₁=mean±std (ms): T_1-8.0ppm=1595.6±491.1, T_1-8.2ppm=1737.2±963.7, T_1-8.5ppm=849.8±282.0 (P=0.04). Post-hoc tests corrected for multiple comparisons showed no significant difference in T₁ between peaks. The cross-relaxation rate σ_AB=mean±std (Hz) of each peak was: σ_AB,8.0ppm=0.76±0.20, σ_AB,8.2ppm=5.31±2.27, σ_AB,8.5ppm=7.90±2.74 (P<0.0001); post-hoc t-tests revealed the cross-relaxation rate of the 8.0 ppm peak was significantly slower than the peaks at 8.2 (P=0.0018) and 8.5 ppm (P=0.0005).

Conclusion

We found significant differences in effective T₁ and cross-relaxation rates of ¹H resonances between 8.0 and 8.5 ppm in the healthy human calf muscle at 7 T.

Introduction

The majority of proton magnetic resonance spectroscopy (¹H MRS) studies measure the metabolite resonances in the up-field region (<4.7 ppm) of the ¹H spectrum (1-3), yet there is emerging interest in the downfield portion of the MR spectrum (>4.7 ppm). Recent studies have determined that the downfield MR spectrum includes resonances from the nicotinamide protons of nicotinamide adenine dinucleotide (NAD⁺) in the range of 8.9-9.3 ppm, protons of the adenosine moiety in molecules such as adenosine triphosphate (ATP) at 8.2 and 8.5 ppm, and the protons of the imidazole ring of carnosine at 7.0 and 8.0 ppm (4,5). The detection of these downfield metabolites is difficult in part due to their inherent low concentrations. Also, the assignments of resonances from many of these metabolites, as well as the relaxation times and other MR properties of these resonances, are yet to be determined (6,7). Moreover, it is likely that several peaks observed in the downfield region include a number of overlapping resonances from multiple metabolites. Studies at ultra-high fields (7 T and higher) potentially address some of the challenges of downfield MRS. Specifically, ultra-high magnetic fields can increase the signal-to-noise ratio (SNR) and chemical shift dispersion of downfield metabolite resonances, providing improved sensitivity and separability (7).

Another challenge is that the water suppression techniques employed in most MRS experiments hinder detection of downfield metabolites, as many of these resonances exhibit magnetization transfer with water through chemical exchange or cross-relaxation. Perturbation of the water signal can therefore indirectly lead to the loss of signal from many downfield metabolites. Techniques that avoid water suppression include metabolite cycling (8), which alternatingly inverts metabolites upfield or downfield of water and removes the water signal through spectral subtraction, and spectrally-selective radio frequency (RF) pulses, which use a narrow bandwidth to avoid excitation of water. Application of these techniques have recently allowed the detection of downfield resonances in vivo (6,9-11).

Faster T₁ recovery has consistently been observed in downfield metabolite signals when water suppression is not used (5,11-13). Shemesh et al. used progressive saturation to measure apparent T₁ relaxation times of downfield peaks in excised mouse brains and observed that T₁ decreased from 2030 ms with water suppression to 740 ms without water suppression at 9.4 T (13). de Graaf et al. used an inversion recovery (IR) scheme in the presence and absence of water inversion on rat brains in situ at 11.7 T and found the T₁ of NAD⁺ to decrease from 1136 ms to 280 ms (5). Furthermore, MacMillan et al., investigated magnetization exchange rates between downfield peaks and water in the human brain at 3 T (11).

In the current study, we sought to measure the cross-relaxation rates of non-exchangeable downfield proton resonances with bulk water in human calf muscle in the range of 8.0-8.5 ppm at 7 T. We compared the T₁ relaxation times of downfield metabolite resonances measured with both spectrally-selective and broadband inversion recovery ¹H MRS experiments in human calf muscle. Furthermore, we determined the cross-relaxation rates with water using a two-spin model. We use spectrally-selective excitation to minimize excitation of water.

Methods

Participants and recruitment

This study was approved by the local Institutional Review Board (IRB) at the University of Pennsylvania. All participants gave written, informed consent. We collected inversion recovery single-voxel ¹H downfield MRS data from 7 healthy male and female volunteers (5 male, 2 female) with no history of musculoskeletal disease between the ages of 24 and 31 years (26.1±2.5 years).

In vivo magnetic resonance spectroscopy

Non-water-suppressed spectra were collected on a 7 T (Terra, Siemens Healthcare, Erlangen, Germany) using a 28-channel knee RF coil (Quality Electrodynamics, Mayfield Village, OH, USA). T₂-weighted axial images (TR: 12 ms, TE: 2.48 ms, resolution: 0.2x0.2x0.5 mm) were acquired to localize the spectroscopy voxel at the center of the calf muscle. A large voxel of 40 x 40 x 40 mm³, or 30 x 30 x 30 mm³ in subjects with smaller calf sizes, in order to increase SNR. In each subject, the voxel was placed over the gastrocnemius and soleus muscles. Manual shimming over the voxel was performed, with an average reference water peak full-width half-maximum (FWHM) of 24.1±2.2 Hz.

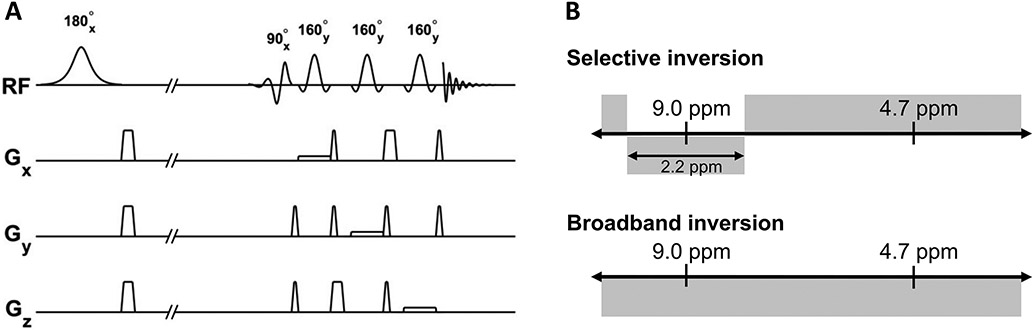
Each subject underwent a water reference acquisition, selective inversion (metabolite only) recovery experiment, and a broadband inversion (metabolite and water) recovery experiment. Water reference spectra were collected using TR=8 s, TE=18 ms, number of averages (NA)=16, with excitation and refocusing pulses centered at 4.7 ppm. Inversion pulses were added to our previously-reported sequence (9) that uses a spectrally-selective uniform phase E-BURP excitation pulse as shown in Figure 1 (14,15), with TR= 7 s, TE=20 ms, NA=32. This protocol was developed for the quantification of the cross-relaxation of metabolites with water in the range of 8.0-10.0 ppm, including NAD⁺ (peaks at 8.9, 9.1, and 9.3 ppm) which was observed by de Graaf et al. (5), and thus the bandwidth was limited to 600 Hz (2 ppm) to avoid water contamination and the excitation was centered at 9.0 ppm.

Figure 1:

A, Pulse sequence schematic for measurement of ¹H cross-relaxation in downfield MRS. First, the magnetization is inverted using a spectrally selective (not shown) or broadband inversion pulse (shown). A spectrally selective uniform phase excitation pulse is followed by a spin echo localization using three spatially-selective refocusing pulses. B, Schematic showing the spectrally-selective inversion (scan 1) and broadband inversion recovery (scan 2) experiments. MRS data from both experiments is used to determine T₁ and cross-relaxation rates of observed resonances.

Either selective or broadband inversion was implemented with varying delay times (TI) prior to excitation. Spectra were collected using seven TIs ranging from 50-2500 ms. The selective inversion pulse was a 180° Sinc pulse with bandwidth=660 Hz, chosen for its low bandwidth-time product in order to limit the pulse duration for inversion of the 8.0-10.0 ppm range. The broadband inversion pulse was a 180° hyperbolic secant pulse with bandwidth=4000 Hz. Voxel localization was achieved using three spatially-selective refocusing 180° Shinnar-Le Roux pulses centered at 9.0 ppm with bandwidth=800 Hz. To ensure the observed peaks were not artifactual, water reference (excitation centered at 4.7 ppm) and downfield spectra (excitation centered at 9.0 ppm), with the same parameters described above except the use of an inversion module, were acquired from a single volunteer utilizing a VAPOR (variable pulse power and optimized relaxation delays) water suppression scheme (16). Additionally, these same sequences were run in a cylindrical water phantom to investigate the behavior of water sidebands.

MRS data analysis

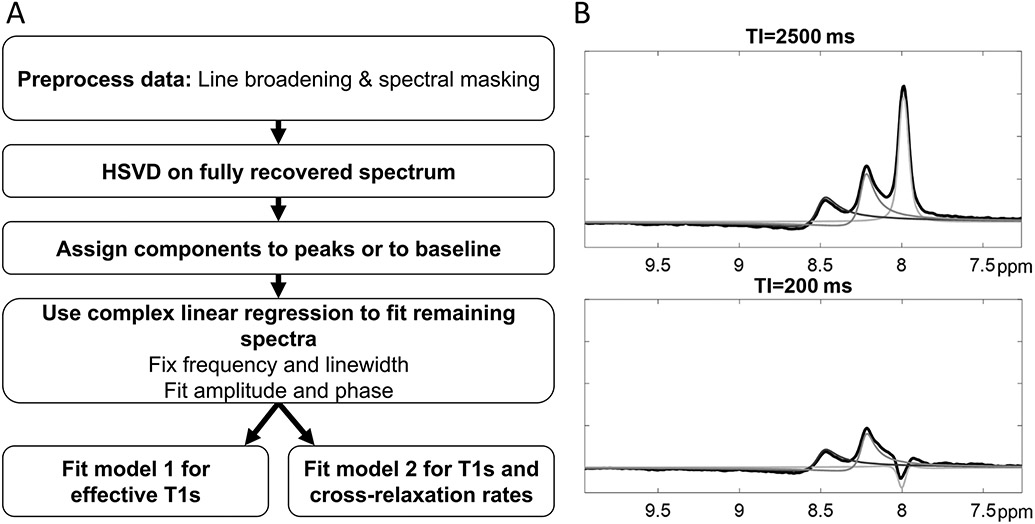
All spectroscopic data were processed offline using custom software (Matlab, The Mathworks, Natick, MA, USA). A flow chart illustrating the processing pipeline is shown in Figure 2. Spectra were line-broadened (5 Hz) and masked over the spectral range of interest (8.0 to 10.0 ppm). Hankel-singular value decomposition (HSVD)(17,18) was applied in the time-domain to the signal acquired at the longest TI time, when all the resonances have maximally recovered their longitudinal magnetization, and consequently have their highest SNR. Peaks of interest at were then assigned to one or more components of the HSVD fit. Components found by HSVD were assigned to the targeted resonances, based on empirically determined constraints for the component frequencies, line widths and phases. When more than one component fell within the limits for a particular resonance, the complex sum of the components was used for the fit to the resonance. In all data sets, the moieties at 8.2 and 8.5 ppm were found to require only a single HSVD component. The moiety at 8.0 ppm, attributed to carnosine, was found to comprise of as many as 3 components in some spectra, and in other cases 2 or 1. The specific constraint criteria are reported in Supporting Information Table S1. NAD⁺ resonances were excluded from analysis due to low SNR. Additional components were assigned to fit the baseline or peaks of unknown origin. Next, the frequencies and linewidths of the peaks of interest were fixed, and complex linear regression of this “spectral basis set” was performed on the remaining TI time signals for to measure amplitude and phase of each peak.

Figure 2:

A, Schematic of MRS data processing to determine effective T₁ and cross-relaxation rates. After line broadening and spectral masking, the Hankel SVD is applied to the fully recovered (TI>>T₁) spectrum to determine the MRS resonances chemical shift, linewidth, phase and amplitude non-parametrically. Components of the Hankel SVD are then assigned to the spectral resonances or baseline. Then, complex linear regression is used to fit the remaining spectrum (B, example modeled peak fits). Finally, the determined parameters are used to fit the spectrum at other inversion times and fit using either the 3-parameter model or the cross-relaxation model.

T₁ relaxation model

In the first model, the amplitude estimates at each TI were then used to measure the effective T₁ measured from both selective and broadband IR curves using a 3-parameter fit with least-squares minimization of: S(TI) = M₀(1 − 2ke^−TI/TI), where S is the observed signal and M₀ is the equilibrium magnetization and k is the efficiency of inversion (range [0,1]). For each subject, each pair of broadband and selective inversion curves was normalized to signal of the longest selective TI for each peak.

Cross-relaxation model

In the second model, T₁ and cross-relaxation rates were estimated using modified 2-spin Bloch equations accounting for cross-relaxation (19,20):

$$\text{Spin A:}\frac{d{M}_{z,A}(t)}{dt}=-\frac{[M_{z,A}(t)-M_{z,A,0}]}{T_{1,A}}-{\sigma }_{AB}(M_{z,A}(t)-M_{z,A,0})+{\sigma }_{BA}(M_{z,B}(t)-M_{z,B,0})$$ [1a]

$$\text{Spin B:}\frac{d{M}_{z,B}(t)}{dt}=-\frac{[M_{z,B}(t)-M_{z,B,0}]}{T_{1,B}}-{\sigma }_{BA}(M_{z,B}(t)-M_{z,B,0})+{\sigma }_{AB}(M_{z,A}(t)-M_{z,A,0})$$ [1b]

where spin A and spin B are the metabolite and water protons, respectively. M_z,X(t) is the longitudinal magnetization of a spin, M_z,X,0 is the equilibrium magnetization, and σ_AB and σ_BA are the forward and reverse cross-relaxation rates, related by σ_AB = σ_BA(M_z,B,0/M_z,A,0). The initial conditions M_z,A(0) and M_z,B(0) are controlled with the inversion conditions. Two additional parameters were included to account for incomplete inversion in both the broadband and selective inversion experiments. The model was evaluated using Python version 3.6.8 (Python Software Foundation, https://www.python.org/). Equation [1] was solved using odeint from the Python library SciPy (v1.5.4)(21) sub-package integrate.

To estimate the cross-relaxation rate, we minimized the sum-of-squared residual values between measured inversion recovery data S_m and an estimate of the signals obtained using Eq. [1]:

$$mi{n}_x\Vert s_m-s_p{\Vert }_{SIR}+\Vert s_m-s_p{\Vert }_{NSIR}$$ [2]

with x the model unknowns to be determined. For selective IR, the initial conditions are M_z,A(0) = (1 − 2k_Sel)M_z,A,0 and M_z,B(0) = M_z,B,0 and where k = 1 indicates perfect inversion and k = 0 indicates no inversion. The broadband IR, initial conditions are M_z,A(0) = (1 − 2k_Broad)M_z,A,0 and M_z,B(0) = (1 − 2k_Broad)M_z,B,0. In general, there are eight unknowns T_1,A, T_1,B, σ_AB, M_z,A,0, M_z,B,0, k_Sel, and k_Broad. We can reduce the number of unknowns to four by assuming the water relaxation rate T_1,B to be 1800 ms (22) and estimating the magnetization ratio M_z,A,0/M_z,B,0 to be 10 mM/55 M (22,23). T_1,A, σ_AB, k_Sel, and k_Broad were modeled without constraint.

Using a least-squares approach, a native T₁ time and the cross-relaxation rate (σ_AB) for each peak was estimated using a 2-parameter fit to the solution of the Bloch equations with the Python library SciPy sub-package optimize.

Statistical analysis

Statistical analysis was conducted using R 4.0.2 (R Foundation for Statistical Computing, Vienna, Austria). Paired Student’s t-tests were used to compare effective T₁ relaxation times measured with selective and broadband inversion, and results were Bonferroni corrected. T₁ relaxation time and σ_AB measured from the modified Bloch equations were compared between the peaks in the 8.0-10.0 ppm range using analysis of variance (ANOVA) and Bonferroni-correct t-tests were performed post-hoc.

Results

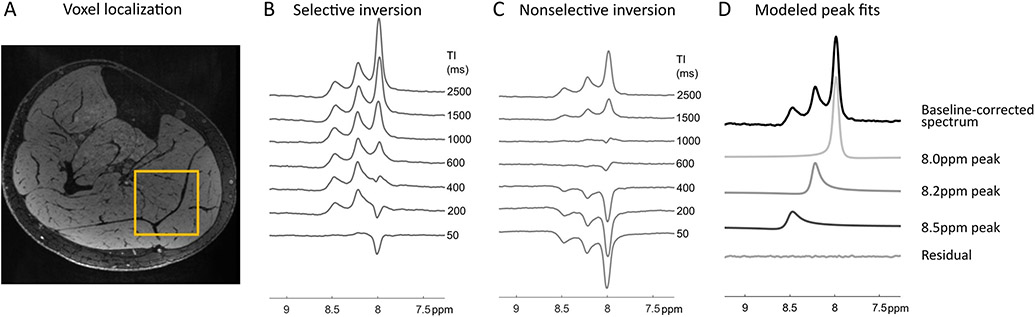
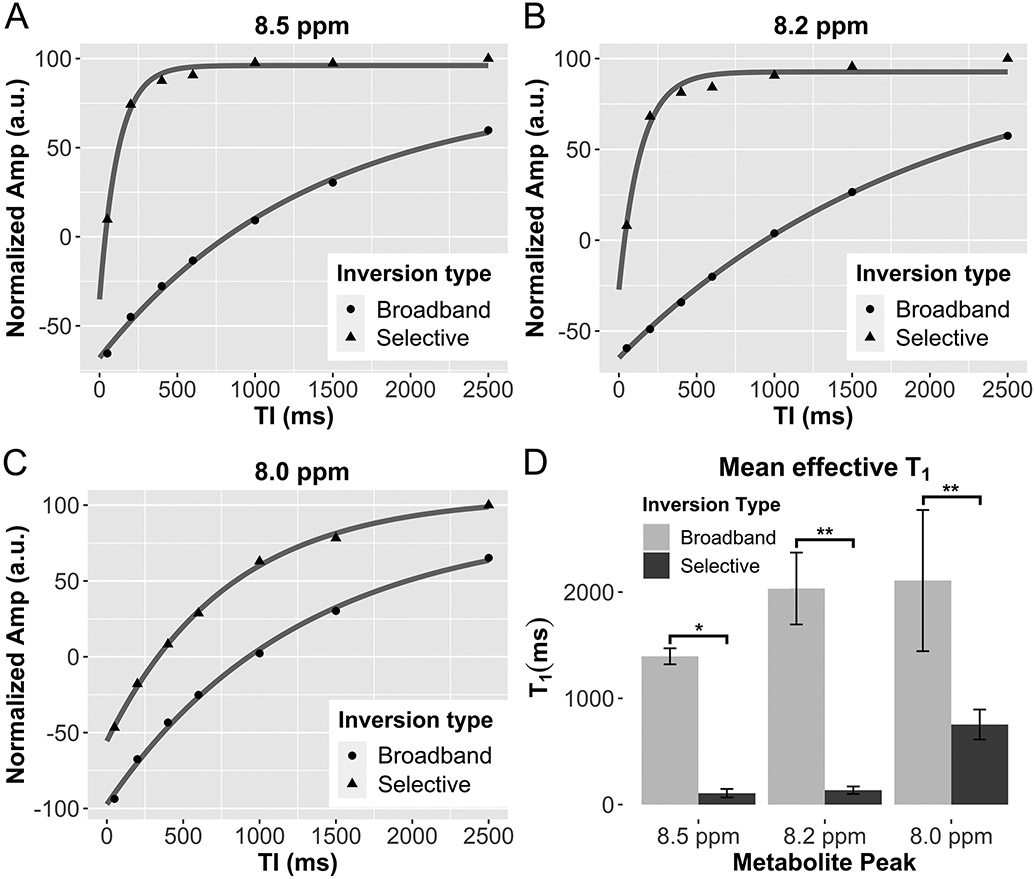
Downfield peaks were observed at 8.0, 8.2, and 8.5 ppm. Representative spectra of the downfield region under selective and broadband inversion conditions are shown in Figure 3. When water-suppression is turned on, the peaks are present but severely attenuated (Supporting Information Figure S1). Antisymmetric water sidebands are visible in the water reference spectra acquired in the water phantom and in vivo, but not in spectra acquired with the excitation centered at 9.0 ppm (Supporting Information Figure S2). Under broadband inversion recovery conditions, all three peaks were nulled at approximately TI=1000 ms. Under selective inversion recovery, the magnetization was observed to recover much faster. The null TI of the 8.2 and 8.5 ppm peaks were 29 and 36 ms while the 8.0 ppm null TI is 324 ms, an order of magnitude longer, under selective inversion recovery conditions. The magnetization recovery of the three peaks following selective and broadband inversion from all subjects is shown in Supporting Information Figure S3. The modeled T₁ recovery curve is also shown. There was a significant difference in the effective T₁ under selective and broadband inversion recovery conditions for each metabolite peak. The broadband (broad) and selective (sel) values of T₁=mean±std (ms) of each peak were: T_{1-broad,8.0ppm}=2108.2±664.5, T_1-sel,8.0ppm=753.6±141.0 (P=0.003); T_{1-broad,8.2ppm}=2033.5±338.4, T_1-sel,8.2ppm=135.3±35.3 (P<0.0001); and T_{1-broad,8.5ppm}=1395.4±75.4, T_1-sel,8.5ppm=107.1±40.0 (P<0.0001) (Table 1, Fig. 4). There was more variability in the measured effective T₁ of the 8.0 ppm peak than the 8.2 and 8.5 ppm peaks.

Figure 3:

A, Representative region for SVS experiments in leg skeletal muscle. B, data in a single subject showing MR spectra at TI = 50-2500 ms under selective inversion recovery and C, broadband inversion recovery conditions. D, Resonances determined using Hankel SVD from fully recovered data in the selective inversion recovery experiment.

Table 1.

Effective T₁ of peaks located at 8.0, 8.2, and 8.5 ppm of all subjects measured by broadband and selective inversion recovery.

	Broadband inversion T1 [ms] (R1 [Hz])			Selective inversion T1 [ms] (R1 [Hz])
	8.0 ppm	8.2 ppm	8.5 ppm	8.0 ppm	8.2 ppm	8.5 ppm
Subject 1	3289.7 (0.30)	1484.3 (0.67)	1416.8 (0.71)	706.5 (1.42)	112.4 (8.90)	96.0 (10.42)
Subject 2	1255.4 (0.80)	1958.9 (0.51)	1356.5 (0.74)	791.4 (1.26)	139.5 (7.17)	118.3 (8.45)
Subject 3	1742.4 (0.57)	2106.7 (0.47)	1313.1 (0.76)	469.2 (2.13)	187.2 (5.34)	191.3 (5.23)
Subject 4	2654.9 (0.38)	2071.8 (0.48)	1448.1 (0.69)	737.0 (1.36)	89.7 (11.15)	105.2 (9.51)
Subject 5	1938.6 (0.52)	2339.6 (0.43)	1504.2 (0.66)	829.6 (1.21)	174.6 (5.73)	82.6 (12.11)
Subject 6	1995.1 (0.50)	2495.7 (0.40)	1431.2 (0.70)	896.5 (1.12)	110.5e (9.05)	76.1 (13.14)
Subject 7	1881.0 (0.53)	1777.3 (0.56)	1297.9 (0.77)	844.7 (1.18)	132.9 (7.52)	80.4 (12.44)
Mean±Std	2108.2±664.5 (0.51±0.16)	2033.5±338.4 (0.50±0.09)	1395.4±75.4 (0.72±0.04)	753.6±141.0 (1.38±0.35)	135.3±35.3 (7.84±2.03)	107.1±40.0 (10.18±2.76)

Figure 4:

A-C, Representative inversion recovery data for selective and broadband inversion recovery experiments from 8.0, 8.2 and 8.5 ppm resonances. D, The magnetization recovery under selective IR conditions appears more rapid than under broadband conditions. *P<0.0001, **P<0.0001, ***P=0.003.

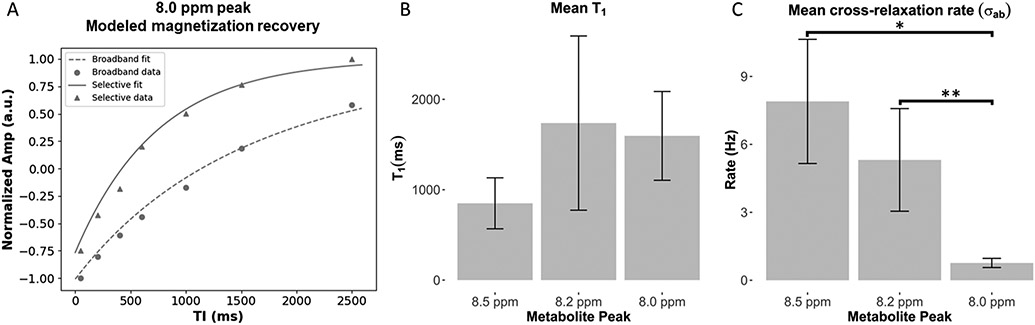
We report the results from the numerical solution to the Bloch equations during the magnetization recovery under selective and broadband inversion conditions as shown in Figure 5A. The fit models native T₁, as well as the cross-relaxation rate with water. The modeled T₁=mean±std (ms) of each peak was: T_1-8.0ppm=1595.6±491.1, T_1-8.2ppm=1737.2±963.7, T_1-8.5ppm=849.8±282.0 (Table 2, Fig. 5B). Analysis of variance (ANOVA) showed there was a significant difference between the T₁’s of each peak (P=0.04), however post-hoc tests revealed no significant difference after correction for multiple comparisons. The cross-relaxation rate σ_AB=mean±std (Hz) of each peak was: σ_AB,8.0ppm=0.76±0.20, σ_AB,8.2ppm=5.31±2.27; σ_AB,8.5ppm=7.90±2.74 (Table 2, Fig. 5C). There was a significant difference between the cross-relaxation rate of each peak (P<0.0001), and post-hoc t-tests revealed that the cross-relaxation rate of the 8.0 ppm peak was significantly slower than the peaks at 8.2 (P=0.0018) and 8.5 ppm (P=0.0005).

Figure 5:

A, Representative inversion recovery data from a single subject under selective and broadband IR conditions. The fit to the modified Bloch equations model is shown overlaid. B, boxplots showing T₁ and C, cross-relaxation rate in n=7 subjects. *P=0.0005, **P=0.0018.

Table 2.

T₁ and cross-relaxation rates of peaks located at 8.0, 8.2, and 8.5 ppm of all subjects estimated using 2-pool Bloch equations.

	T1 [ms] (R1 [Hz])			Cross-relaxation rate [Hz]
	8.0 ppm	8.2 ppm	8.5 ppm	8.0 ppm	8.2 ppm	8.5 ppm
Subject 1	1483.2 (0.67)	512.0 (1.95)	1040.8 (0.96)	0.79	3.25	7.45
Subject 2	1228.8 (0.81)	1736.6 (0.58)	853.9 (1.17)	0.56	4.56	5.96
Subject 3	1221.2 (0.82)	1839.4 (0.54)	1393.9 (0.72)	1.02	3.60	3.34
Subject 4	2664.9 (0.38)	1209.5 (0.83)	650.5 (1.54)	1.06	9.67	7.45
Subject 5	1518.0 (0.66)	1929.7 (0.52)	733.2 (1.36)	0.69	3.92	9.21
Subject 6	1508.2 (0.66)	3624.4 (0.28)	664.9 (1.50)	0.56	6.76	10.73
Subject 7	1544.9 (0.65)	1308.9 (0.76)	611.0 (1.64)	0.67	5.43	11.13
Mean±Std	1595.6±491.1 (0.66±0.15)	1737.2±963.7 (0.78±0.55)	974.3±333.4 (1.27±0.34)	0.76±0.20	5.31±2.27	7.90±2.74

Discussion

The significance of this work is the quantification of relaxation times and cross-relaxation rates of resonances in the downfield MR spectrum of human skeletal muscle in vivo at 7 T. Though there have been some recent investigations of resonances in the downfield MR spectrum, the cross-relaxation properties of metabolites with resonances in this region are not well characterized. We designed a protocol to quantify cross-relaxation rates from resonances in the 8.0-10.0 ppm range, including NAD⁺. However, due to the time constraint of scanning human subjects, the number of averages was limited to 32 and only peaks at 8, 8.2, and 8.5 were detectable. The presence of water sidebands in the water reference spectra, and absence of them in the downfield excitation spectra support that these peaks are not artifacts. Our results show that there are enormous (order of magnitude) differences in the cross-relaxation properties of resonances within the 8.0-8.5 ppm range.

It is not fully clear what metabolites can be assigned to the observed resonances between 8.0-8.5 ppm. While the 8.0 ppm peak has been attributed to carnosine (22,24,25), the peaks found at 8.2-8.5 ppm remain poorly characterized. The adenosine moiety of multiple metabolites, including ATP, likely contribute to the signals detected at 8.2 and 8.5 ppm. Because the H2 proton of the carnosine imidazole ring and the H8 and H2 protons of the ATP adenosine rings do not rapidly exchange with water, the decrease in effective T₁ under the selective inversion condition suggests a cross-relaxation effect and not chemical exchange, though this is complicated by unknown contributions to the peaks.

We investigated several models for characterizing the relaxation properties of the downfield resonances in human skeletal muscle at 7 T. First, we considered a simple description of relaxation that assumes that relaxation can be characterized by an ‘effective T₁’, which implicitly includes cross-relaxation. In this model, the recovery of the magnetization is modeled using a model with 3 unknown parameters, which is commonly applied in other T₁ recovery experiments. One reason that a 2-parameter fit may fail is due to an imperfect inversion pulse, arising from many factors that include B₁ inhomogeneity and T₂ relaxation during inversion. A 3-parameter fit reports more accurate T₁ measurements even when inversion efficiency is imperfect (26). Using this model, relaxation rate enhancement is large for resonances appearing at 8.2 and 8.5 ppm and effective T₁ is shortened by a factor of 5-10, from approximately 1 s to between 100-200 ms using broadband inversion or spectrally selective inversion, respectively. By distinction, the resonance at 8.0 ppm showed more moderate relaxation rate enhancement, with effective T₁ shortening from approximately 2 s to 1 s under the same two experimental conditions. This suggests that cross-relaxation has a larger contribution to effective T₁ for the 8.2 and 8.5 ppm peaks than the 8.0 ppm peak. de Graaf et al. similarly measured a difference in T₁ in the absence and presence of water inversion (~200-300 ms and 1000-1200 ms, respectively) of NAD⁺ resonances at 8.8, 9.1, and 9.3 ppm in the downfield range (5). However, this was measured in situ in rat brains, and cannot be directly compared to our measurements of T₁ of other downfield metabolites in human skeletal muscle.

In the relaxation coupled spin model, we explicitly modeled the cross-relaxation properties of these resonances. In this model, it is presumed that each resonance has a single T₁ relaxation time, and that the recovery rate is amplified by cross-relaxation. This contrasts with the earlier model in a few ways. First, in the previous model, effective T₁ was short or long depending on the conditions of the experiment, and thus separate effective T₁ relaxation times were found under the experimental conditions of selective or broadband inversion recovery. Using the second model, there was only a single T₁ for each resonance, which is measured by jointly modeling the selective and broadband inversion recovery data. As with the first model, the second model includes parameters to correct for imperfect inversion pulses. However, we do not expect the intercept of the recovery curve at t=0 (which changes with inversion efficiency) to greatly impact the estimate of cross-relaxation rate, which drives the difference between the selective and broadband recovery curves. The T₁ for all 3 resonances were longer (~900-1700 ms) than what would be expected under the spectrally selective conditions producing the ‘relaxation rate enhancement’ effect. The cross-relaxation rate effects are significant; we found that the 8.2 and 8.5 ppm resonances showed cross-relaxation rates about an order of magnitude larger than the 8.0 ppm resonance.

The cross-relaxation rates of the 8.2 and 8.5 ppm peaks were significantly more rapid than that of the 8.0 ppm peak. MacMillan et al. found the magnetization transfer rates of the 8.2 and 8.5 ppm peaks in the brain to be 7.5 and 8.9 Hz at 3 T (11), similar to the 6.7 and 9.2 Hz cross-relaxation rates we observed in skeletal muscle. As cross-relaxation is a 2-spin dipole-dipole interaction, it is proportional to 1/r⁶, where r is the distance between the two spins. Additionally, cross-relaxation is dependent on the correlation time τ_c, which is affected by both translational and rotational motion. As ω₀τ₀ approaches 1, where ω₀ is the Larmor frequency, cross-relaxation becomes a more efficient mechanism of longitudinal magnetization recovery. The faster cross-relaxation rate for metabolite peaks at 8.2 and 8.5 ppm may suggest that a larger proportion of adenosine-containing metabolites are bound to large proteins in vivo, which would decrease the rotational correlation time and enhance the cross-relaxation effect. The cross-relaxation rate of carnosine is significantly slower and may contribute to the visibility of carnosine in the downfield region even when water suppression is used. These differences in cross-relaxation may be exploited to enhance or suppress signals from downfield resonances. Characterization of T₁ and cross-relaxation rate of downfield metabolites in muscle will be useful for further studies of these resonances, including their assignment. Additionally, these properties will aid in the absolute quantification of these resonances by serving as correction factors, though further work is needed to also characterize their T₂ relaxation properties.

Several limitations in this work exist. While we considered the effects of cross-relaxation, due to the unknown contribution of amide protons to the 8.2-8.5 ppm range, our measured cross-relaxation rate may indeed be accounting somewhat for other modes of magnetization transfer such as chemical exchange. Further studies are needed to determine the molecular mechanisms contributing to downfield metabolite signal loss seen with water perturbation. Furthermore, as this work was conducted as an adjunct to studies of the downfield targeting NAD⁺, the excitation pulse is centered at 9.0, causing the carnosine peak to appear at the edge of the excitation bandwidth. While this may decrease the SNR of the carnosine peak, we do not expect the measured cross-relaxation rate to change. The size of the voxel chosen in these experiments may also result in contributing partial volume effects, as muscle fiber type and orientation differ between the gastrocnemius and soleus muscles, though we do not expect to observe fiber type-dependent spectral changes due to pH (27), as the subjects were at rest in the scanner. There may be orientation-dependent effects on the carnosine peak at 8.0 ppm, though this effect is expected to be reduced for the C2 proton at 8.0 ppm in comparison to the C4 proton at 7.0 ppm (28,29). The influence of angled muscle fibers is therefore uncertain and remains to be investigated. These factors together could contribute to one to three HSVD components being found in the prescribed carnosine peak region. Additionally, further work is needed to improve the assumptions made in the model of the 2-spin Bloch equations, including relative water/metabolite concentrations, and direct measurements of T₁ of skeletal muscle water at 7 T, as well as optimization of inversion times. Specifically, longer inversion times may be more reflective of M₀ and could aid in fitting a more accurate T₁.

Additionally, the current approach used a non-adiabatic sinc RF pulse (duration 2 ms) for selective inversion of the metabolites, which is susceptible to B₁ inhomogeneity effects and may result in reduced inversion efficiency. We thus assessed the robustness of the models to imperfect inversion using a Monte Carlo analysis of simulated datasets with a range of inversion efficiencies, known selective apparent T₁ and known cross-relaxation rate. The simulation was used to determine the relative errors in the apparent T₁ and cross-relaxation rates measured using the two models (see Supporting Information Methods). Relative error of the measured selective apparent T₁ and cross-relaxation rate were both less than 16% across a large range of inversion efficiencies (Supporting Information Figure S4 and Figure S5). Nonetheless, selective inversion pulses that are more B₁ insensitive, such as the sech/tanh pulse developed by Balchandani, et al. (30) for lipid suppression, could be used instead. However, such pulses have longer durations because of their larger bandwidth-time products on the order of 15-30 ms and are less efficient for short T₂ species. In comparison, the selective sinc pulse used in this study had a duration of 2 ms. The T₂ of downfield metabolites is expected to very short (25-40 ms in brain) (6) and the T₂ relaxation times of muscle metabolites tend to be shorter than those in brain (31). Optimization of such protocol parameters was beyond the scope of this work, and future investigations of RF pulse design for short T₂ species in the downfield are needed.

Conclusion

Downfield metabolites in ¹H MRS exhibited cross-relaxation with water in human skeletal muscle, as evidenced by shorter effective T₁ relaxation times for metabolites in the 8-8.5 ppm range. The cross-relaxation rate was quantified and found to be similar to magnetization transfer rates measured in the brain for peaks at 8.2 and 8.5 ppm. Peaks at 8.2-8.5 ppm exhibited faster rates of cross-relaxation with water than the carnosine peak at 8.0 ppm.

Supplementary Material

supinfo

Supporting Information Table S1. Empirically determined constraints [min, max] for the component frequencies, line widths, and phases used to assign HSVD components. The 8.2 and 8.5 peaks were always assigned one component, the 8.0 component was assigned between 1 and 3 components.

Supporting Information Figure S1: The 1H downfield region in a single subject after frequency selective excitation (E-BURP 90° pulse centered at 9.0 ppm with BW = 2 ppm, 40x40x40 mm voxel, TR/TE = 7 s/ 20 ms), without water suppression (left), and with VAPOR water suppression showing attenuated metabolite peaks (right).

Supporting Information Figure S2: Antisymmetric water sidebands are visible (solid arrows) in the 1H spectrum of a water phantom (top row) and in vivo (bottom row) with frequency selective excitation (E-BURP 90° pulse with BW=2 ppm, 40x40x40 mm voxel, TR/TE = 1 s/ 20 ms) centered at 4.7 ppm on water (left column). Sidebands are not visible in the same frequency locations (dashed arrows) when the same sequence is applied with excitation centered at 9.0 ppm (right column, zoomed x140) in either the phantom (top row) or in vivo (bottom row).

Supporting Information Figure S3: Recovery of magnetization and 3-parameter fits for all subjects (n=7) using broadband and selective inversion recovery data. Both selective and broadband data for each subject were normalized to the magentization of the subject’s last selective inversion time (TI=2500 ms) for each resonance.

Supporting Information Figure S4: Percent error between estimated T₁ and true T₁ in 1000 simulated selective IR datasets, plotted versus selective inversion efficiency k (k=0 indicating no inversion, k=1 indicating perfect inversion). The maximum error across the three resonances is <16%. The average percent error was 2.01±1.56%, 1.79±1.40%, and 2.12±2.00% for the 8.0, 8.2, and 8.5 ppm peaks respectively.

Supporting Information Figure S5. Percent error between estimated cross-relaxation rate σ_AB and true σ_AB of 1000 simulated datasets plotted versus selective (k_sel) and broadband (k_broad) inversion efficiencies (k=0 indicating no inversion, k=1 indicating perfect inversion). The maximum error across the three resonances is <16%. The average percent error was 2.18±1.68%, 2.23±1.77%, and 2.45±1.95% for the 8.0, 8.2, and 8.5 ppm peaks respectively.