Only-Train-Once MR Fingerprinting for B₀ and B₁ Inhomogeneity Correction in Quantitative Magnetization Transfer Contrast

Abstract

Purpose:

To develop a fast, deep-learning approach for quantitative MTC-MRF that simultaneously estimates multiple tissue parameters and corrects the effects of B₀ and B₁ variations.

Methods:

An only-train-once recurrent neural network was designed to perform the fast tissue parameter quantification for a large range of different MRF acquisition schedules. It enabled a dynamic scan-wise linear calibration of the scan parameters using the measured B₀ and B₁ maps, which allowed accurate, multiple-tissue parameter mapping. MRF images were acquired from eight healthy volunteers at 3T. Estimated parameter maps from the MRF images were used to synthesize the MTC reference signal (Z_ref) through Bloch equations at multiple saturation power levels.

Results:

The B₀ and B₁ errors in MR fingerprints, if not corrected, would impair the tissue quantification and the subsequently corrupt the synthesized MTC reference images. Bloch equation-based numerical phantom studies and synthetic MRI analysis demonstrated that the proposed approach could correctly estimate water and semisolid macromolecule parameters, even with severe B₀ and B₁ inhomogeneities.

Conclusion:

The only-train-once deep-learning framework can improve the reconstruction accuracy of brain tissue parameter maps and be further combined with any conventional MRF or CEST-MRF method.

1. INTRODUCTION

Magnetization transfer contrast (MTC) provides an indirect measurement of semisolid macromolecular protons based on the transfer of magnetization to the surrounding free bulk water molecules, which is not directly detectable with conventional MRI sequences, because the semisolid protons have an extremely short T₂ relaxation times (< 100 μs) (1–4). The cumulative saturation with repeated radiofrequency (RF) irradiation of macromolecular protons results in a decrease in the water signal through the magnetization transfer, thereby allowing the assessment of semisolid macromolecules with improved sensitivity. MTC imaging has been shown to be a powerful biomarker for the clinical diagnosis of disorders in tissues (e.g., multiple sclerosis), which provides a profound insight into the brain-tissue microstructure (5–8). A conventional MTC experiment as measured by the MT ratio (MTR) has been widely used for clinical studies (9–11). However, the MTR contrast is highly dependent on scan parameters and water tissue relaxation effects. To overcome the poor specificity, quantitative imaging techniques have been developed by fitting MTC-weighted signals to the analytical solution of the Bloch equations using a series of image acquisitions with various saturation powers and frequency offsets (12–15). However, these model-based methods sometimes suffer from long imaging times, due to the repeated acquisitions necessary with various experimental settings, and the computationally expensive fitting process.

Magnetic resonance fingerprinting (MRF) was introduced as a time-efficient quantification technique that can simultaneously estimate multiple tissue parameters (16). The time-varying signal evolution, the so-called fingerprint, is achieved by intentionally varying imaging parameters for each scan and this is then used to probe the characteristics of tissues. A conventional approach to map a fingerprint space into a tissue parameter space is to match the fingerprint with a pre-defined dictionary (17–20). Recent studies using learning-based techniques have shown their powerful ability to map the two different domains of the MR fingerprint space and the tissue parameter space, bypassing the exhaustive dictionary search and circumventing the curse of dimensionality (21–24). Furthermore, learning-based MRF reconstruction techniques have been adopted for quantitative MTC imaging with various training schemes (25–27).

B₀ and B₁ inhomogeneities that originate from system imperfections hinder MRF reconstruction that solves the complex inverse problem of Bloch equations (28–31). Particularly, MRF sequences for MTC and chemical exchange saturation transfer (CEST) imaging use a pulsed or continuous RF saturation schemes with various saturation powers, and are, thus, vulnerable to B₁ variation. Since the MTC and CEST measurements are based on the RF saturation of specific proton pools, errors in the B₀ and B₁ values directly propagate to tissue quantification errors (32–36). Consequently, B₀ and B₁ correction are essential in MTC- and CEST-MRF imaging. Typically, experimentally acquired B₀ and B₁ maps can be used to calibrate an off-resonance frequency and to scale the power of an RF pulse, respectively. In MRF with a subgrouping proton exchange model (MRF-SPEM) framework (37), B₀ shifts and B₁ scaling factors obtained from additional scans were used to linearly compensate for the MRF schedule for the CEST and MTC quantification. However, it is challenging to apply such compensation methods to a deep-learning-based MRF technique, because neural networks are trained on a simulated dataset with numerous combinations of tissue parameters for a specific MRF schedule without considering B₀ and B₁ inhomogeneities. Consequently, B₀ and B₁ errors would result in unpredictable quantification errors from the conventional deep-learning approach.

Recently, we introduced a novel deep-learning approach for MTC-MRF, which can quantify tissue parameters for a myriad of different MRF schedules, and dubbed Only-Train-Once MRF (OTOM) (38). The OTOM scheme trained with numerous acquisition patterns and lengths of MRF sequence can be applied to a large range of MRF schedules without compromising MRF reconstruction accuracy. In this study, we developed a linear compensation scheme for B₀ and B₁ correction on the OTOM framework. To validate the proposed correction method, digital phantom studies and synthetic MRI analysis were performed with a two-pool Bloch equations-based simulation. The performance of the B₀ and B₁ correction was demonstrated in the brain of healthy volunteers.

2. THEORY

2.1. Transient-state MTC-MRF model

A two-pool MTC exchange model (w: a free bulk water pool, m: a semisolid macromolecule pool) is used to simulate MTC-MRF signals in the presence of proton exchange and RF irradiation. The magnetization of each pool can be described with the modified Bloch-McConnell equations in a matrix format as follows (39,40):

$$dM(t)/dt=AM(t)+C$$ [1]

where

$$M(t)={\left[M^w\text{(t) }{M}^m\text{(t)}\right]}^T$$ [2]

$$A=\left[\begin{array}{cc}{D}^{wm}& E^{mw}\\ E^{wm}& D^{mw}\end{array}\right]$$ [3]

$$D^{ij}=\left[\begin{array}{ccc}-k_{ij}-1/T_2^i& -2\pi \Omega & 0\\ 2\pi \Omega & -k_{ij}-1/T_2^i& -\gamma B_1\\ 0& \gamma B_1& -k_{ij}-1/T_1^i\end{array}\right]$$ [4]

$$E^{ij}=\left[\begin{array}{ccc}{k}_{ij}& 0& 0\\ 0& k_{ij}& 0\\ 0& 0& k_{ij}\end{array}\right]$$ [5]

$$C={\left[C^w{C}^m\right]}^T$$ [6]

$$C^i={\left[0\text{ 0 }{M}_0^i/T_1^i\right]}^T$$ [7]

where T₁ⁱ and T₂ⁱ are the longitudinal and transverse relaxation times of a pool i, respectively; Ω is the frequency offset of the RF saturation; B₁ is the RF saturation power; γ is the gyromagnetic ratio (for ω₁/B₁= γ = 267.5 rad/(μT×s)); k_ij is the proton exchange rate from a pool i to a pool j; and M₀ⁱ is the equilibrium magnetization of a pool i. By solving the coupled differential equations (Eq. [1]), the longitudinal magnetization of the free bulk water pool can be written as:

$$M_z^w(t)=\left[M_0^w-M_{ss}^w\left(B_1,\Omega \right)\right]e^{\lambda t}+M_{ss}^w\left(B_1,\Omega \right)$$ [8]

where

$$M_{ss}^w\left(B_1,\Omega \right)=M_0^w\frac{\frac{(k_{mw}{M}_0^m{T}_1^w)}{T_1^m}+\alpha }{(k_{mw}{M}_0^m{T}_1^w)\left(L_m+\frac{1}{T_1^m}\right)+\alpha \left[1+{\left(\frac{\gamma B_1}{2\pi \Omega }\right)}^2\left(\frac{T_1^w}{T_2^w}\right)\right]}$$ [9]

$$\lambda =-\frac{1}{2}\left(\alpha +\beta -\sqrt{{(\alpha -\beta )}^2+4k_{mw}^2{M}_0^m}\right)$$ [10]

$$\alpha =1/T_1^m+k_{mw}+L_m$$ [11]

$$\beta =1/T_1^w+k_{wm}+L_w$$ [12]

$$L_i=\frac{{\left(\gamma B_1\right)}^2\cdot T_2^i}{1+{(2\pi \Omega T_2^i)}^2}$$ [13]

where M_ss^w is the steady-state longitudinal magnetization of the free bulk water, and L_i denotes a Lorentzian line-shape function of the RF absorption rate of a pool i. According to Eq. [8], the characteristics of the RF saturation are determined by three scan parameters: RF saturation power (B₁); frequency offset (Ω); and saturation time (t = Ts). A relaxation delay time (Td) is also defined to consider the relaxation of the longitudinal magnetization in the absence of RF irradiation, changing an initial value of the magnetization for the next dynamic scan. Therefore, the transient-state MTC-MRF signal evolution (S_MTC-MRF) can be described as follows:

$$S_{MTC-MRF}(p_{\mathit{\text{tissue}}};p_{\mathit{\text{scan}}})=[S_{MTC}(p_{\mathit{\text{tissue}}};p_{\mathit{\text{scan}},1}),\cdots ,S_{MTC}(p_{\mathit{\text{tissue}}};p_{\mathit{\text{scan}},N})]$$ [14]

where

$$S_{MTC}(p_{\mathit{\text{tissue}}};B_1,\Omega ,Ts,Td)=[M_0^w(1-e^{-Td/T_1^w})-M_{ss}^w\left(B_1,\Omega \right)]e^{-\lambda Ts}+M_{ss}^w\left(B_1,\Omega \right)$$ [15]

$$p_{\mathit{\text{tissue}}}=[k_{mw},M_0^m,T_2^m,T_1^w],p_{\mathit{\text{scan}},k}=[B_{1,k},{\Omega }_k,T{s}_k,T{d}_k]$$ [16]

where p_tissue is a set of tissue parameters and p_scan,k is a set of scan parameters of the k^th scan. The analytical solution of the MTC-MRF signal model is used to understand the complex relation among the fingerprint space (S_MTC-MRF), the scan parameter space (p_scan), and the tissue parameter space (p_tissue). The complex relation can be solved by a deep neural network.

2.2. B₀ and B₁ correction

A linear compensation scheme was used to compensate the B₀ and B₁ inhomogeneities in a pixel-wise manner. In the presence of B₁ inhomogeneity, the saturation power (B₁) is linearly scaled according to the relative B₁ (rB₁, a scaling factor of B₁, not to be confused with gamma γ, the gyromagnetic ratio) map per pixel. Similarly, the frequency offset (Ω) is shifted with the ΔB₀ map. Therefore, the correction can be accomplished by B₀ shifting and B₁ scaling as follows (41,42):

$$B_{1,i}^{\mathit{\text{corr}}}=B_{1,i}^{nom}\times r{B}_1,i=1,\cdots ,N$$ [17]

$${\Omega }_i^{\mathit{\text{corr}}}={\Omega }_i^{nom}+\gamma \Delta B_0/2\pi ,i=1,\cdots ,N$$ [18]

$$p_{\mathit{\text{scan}}}^j=\left[B_1^j,{\Omega }^j,T{s}^{nom},T{d}^{nom}\right],j\in \{\mathit{\text{corr}},nom\}$$ [19]

where ${\text{B}}_{1,i}^{\text{corr}}$ and ${\text{B}}_{1,i}^{\text{nom}}$ are the corrected and nominal RF saturation power of i^th scan, respectively; ${\Omega }_{\text{i}}^{\text{corr}}$ and ${\Omega }_{\text{i}}^{\text{nom}}$ are the corrected and nominal frequency offset of i^th scan, respectively; rB₁ is a scaling factor of B₁; ΔB₀ is a field inhomogeneity offset; ${\text{p}}_{\text{scan}}^{\text{corr}}$ represents the corrected scan parameters; and ${\text{p}}_{\text{scan}}^{\text{nom}}$ represents the nominal scan parameters. Note that the ΔB₀ and rB₁ values of each pixel were equally applied to the entire MRF schedule for B₀ and B₁ correction.

3. METHODS

An overview of the OTOM method for B₀ and B₁ correction is described in Fig. 1. In the training phase, the recurrent neural network (RNN) was trained to solve the complex inverse problem of mapping an MR fingerprint into tissue parameters in accordance with the MRF schedule. Millions of different MRF schedules were applied to the training, and thus, the trained RNN model can estimate tissue parameters for a variety of different MRF schedules in the test phase. This enables a dynamic scan-wise modification of the MRF schedule, which can be utilized to compensate for B₀ and B₁ errors. The corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$), in lieu of the nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$), were calibrated using experimentally obtained ΔB₀ and rB₁ maps and fed to the trained RNN to estimate the field inhomogeneity artifact-free tissue parameter maps.

Figure 1.

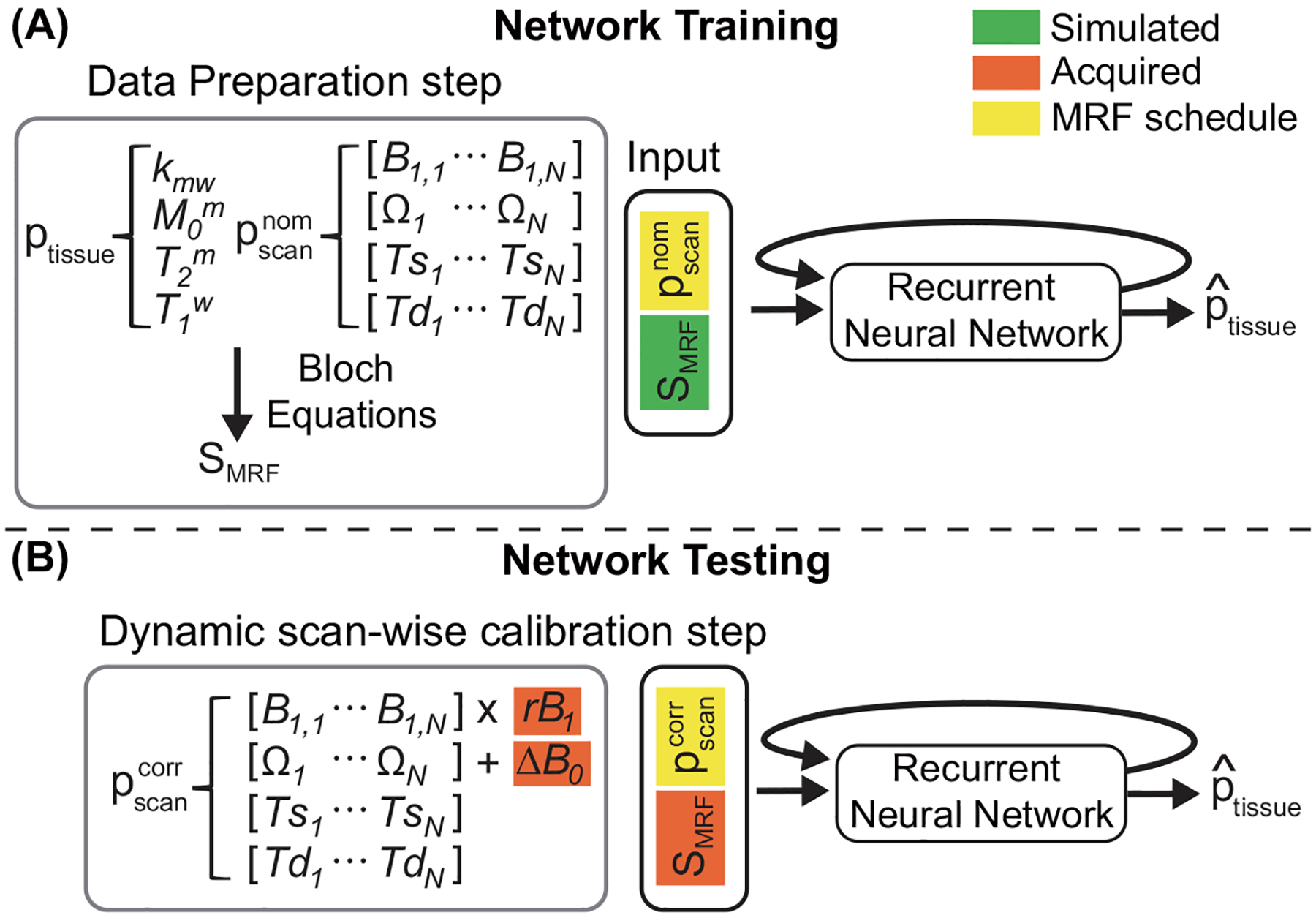
An overview of the MTC-MRF quantification scheme with B₀ and B₁ correction. (A) In the training phase, MR fingerprints are simulated using two-pool Bloch equations with randomly selected tissue and nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$) within the pre-defined ranges. The simulated fingerprints and the corresponding scan parameters are fed to the recurrent neural network to estimate the tissue parameters. (B) In the test phase, the corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$) are calibrated using the acquired ΔB₀ and relative B₁ (rB₁) values, and fed to the trained RNN model.

3.1. Data preparation: Training dataset

To train the RNN model that can be successfully applied to various MRF schedules, such as acquisition pattern and length, MTC-MRF signals (S_MTC-MRF) were simulated using the analytical solution of the Bloch-McConnell equations (Eq. [14]). A random MRF schedule was generated by varying the scan parameters (p_scan) for each MR fingerprint. As shown in Fig. 2A, the number of dynamic scans (N) was determined and then four scan parameters (B₁, Ω, Ts, and Td) were randomly sampled N times within the pre-defined ranges (Table 1). Similarly, tissue parameters were sampled for the simulation within the corresponding ranges, as shown in Table 1. In addition, T₁^m was chosen to be a constant value of 1 s due to its negligible contribution to the two-pool MTC signal. Note that T₂^w was indirectly defined from the T₁^w/T₂^w ratio, which referred to a line-shape of direct water saturation, thus, a key parameter in the two-pool model. To generate the training dataset, 80 million combinations of scan and tissue parameters were randomly chosen. Finally, white Gaussian noise (SNR = 46 dB), whose SNR was similar to the obtained in vivo images, was added to the simulated MTC-MRF signals. The Bloch simulations were performed on a 64-bit Windows operating system (12-CORE, 3.8-GHz AMD Ryzen 9 3900XT processor and 32 GB of memory) using MATLAB (MathWorks, Natick, MA).

Figure 2.

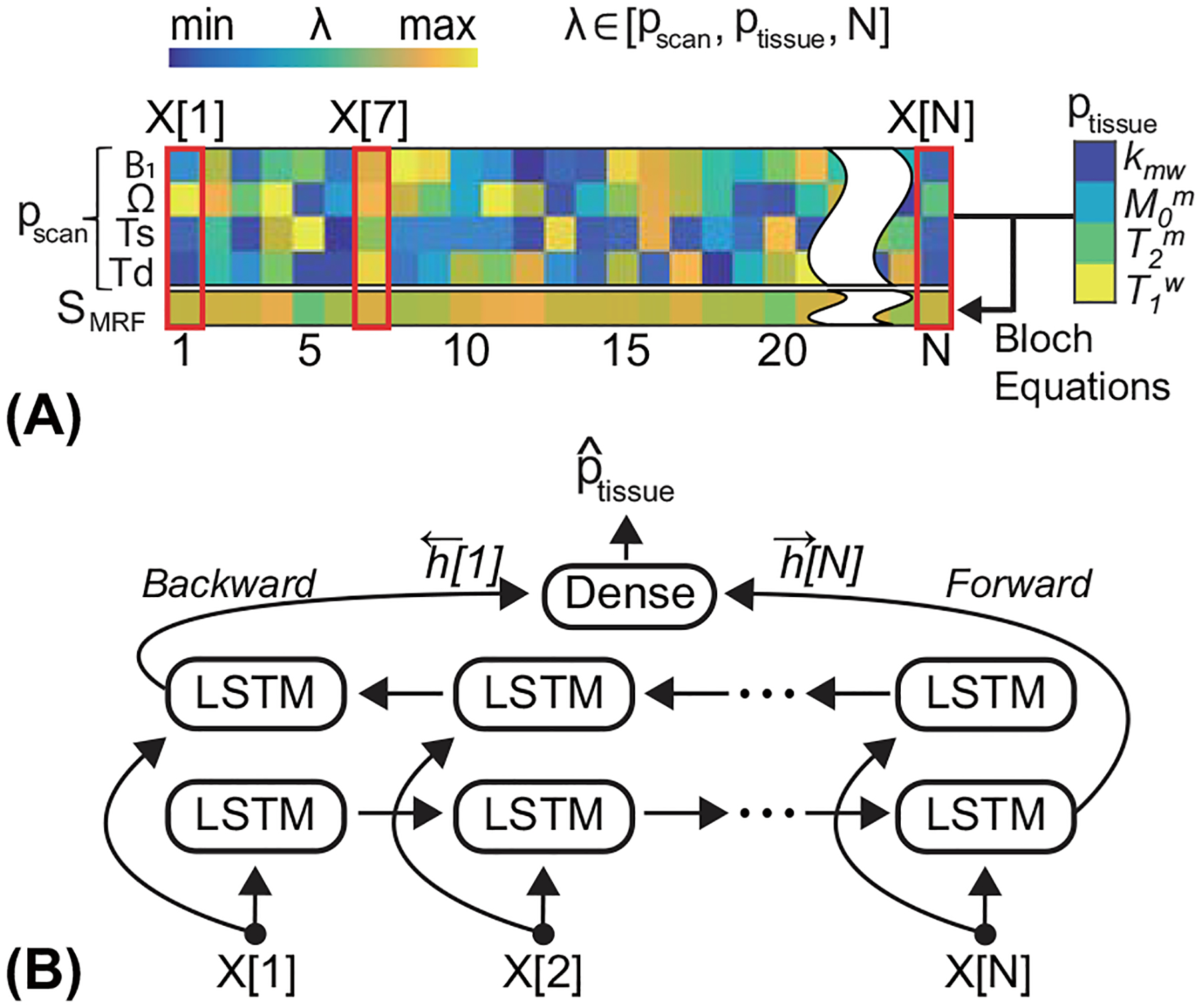
(A) The illustration of the data preparation step in the training phase. The input sequence consists of four scan parameters (p_scan) and simulated fingerprints (S_MRF). (B) The LSTM model takes the input sequence per time-point (X[n]) and updates the hidden state. The bi-directional LSTM processes the input sequence in two ways: moving forward from the start to the end of the sequence, and vice versa.

Table 1.

The characteristics of tissue and scan parameters used in the data preparation step (training dataset).

	Tissue parameters					Scan parameters
	kmw (Hz)	M0m (%)	T2m (μs)	T1w (s)	T1w/T2w	B1 (μT)	Ω (ppm)	Ts (s)	Td (s)	N (#)
Upper bound	100.0	17.0	100.0	3.0	30.0	3.0	50	2.0	5	40
Lower bound	5.0	2.0	1.0	0.2	1.0	0.4	8	0.4	3.5	10
Interval	1.0	0.1	1.0	0.03	0.2	0.1	1	0.1	0.1	1

3.2. Recurrent neural network (RNN)

The RNN architecture was designed to analyze the input data of the MTC fingerprints and the corresponding scan parameters and to output the free bulk water and semisolid MTC parameters. As shown in Fig. 2B, the architecture consisted of bi-directional LSTM (long short-term memory) (43,44) and a single fully connected layer. The RNN extracted features from each time point, not considering the input MR fingerprint all at once, and accumulated them in a hidden state. The finally updated hidden states of the forward and backward directions were concatenated, and fed to the fully connected layer to estimate the four tissue parameters of k_mw, M₀^m, T₂^m, and T₁^w, as follows:

$$\overrightarrow{h}[i]=LST{M}_{\mathit{\text{forward}}}(X[i],\overrightarrow{h}[i-1])$$ [20]

$$\overleftarrow{h}[i]=LST{M}_{\mathit{\text{backward}}}(X[i],\overleftarrow{h}[i+1])$$ [21]

$${\widehat{p}}_{\mathit{\text{tissue}}}=\mathit{\text{Dense}}(\stackrel{\rightharpoonup }{h}[N],\overleftarrow{h}[1])$$ [22]

where

$$X[i]=[S_{MTC-MRF,i},B_{1,i},{\Omega }_i,T{s}_i,T{d}_i],i=1,\cdots ,N$$ [23]

where $\overrightarrow{h}[i]$ and $\overleftarrow{h}[i]$ are the forward and backward hidden states of i^th time point, respectively; X[i] is the input vector of i^th time point; S_MIC–MRF,i is the MRF signal of i^th time point; and N is the number of dynamic scans of the MRF sequence. The LSTM consisted of three layers with 512 hidden units each, which led to 1024 hidden units after the concatenation of the forward and backward hidden states, and the fully connected layer had 1024×4 neurons followed by rectified linear units (ReLU) as an activation function. The RNN was trained by minimizing the l₁-norms of difference between the label parameters, p_tissue, and the estimated parameters, ${\widehat{p}}_{\mathit{\text{tissue}}}$, as follows:

$$\mathit{\text{Loss}}={\left|p_{\mathit{\text{tissue}}}-{\widehat{p}}_{\mathit{\text{tissue}}}\right|}_1$$ [24]

The network was implemented using Pytorch on an NVIDIA TITAN RTX GPU (Santa Clara, CA). The network was trained for 20 epochs with the adaptive moment estimation (ADAM) optimizer (45) and a batch size of 256. The initial learning rate was 10⁻³ and decreased by a factor of 0.1 for every three epochs. The training dataset was randomly divided into two parts: 90% for training and 10% for validation. The RNN model that showed the lowest validation loss was saved for our experiments. In addition, the validation loss was monitored for early stopping of training. OTOM was trained for 100 hours on 80 million dataset whereas it took 6 hours to train the FCNN with 10 million dataset. OTOM consumed 2459MB and FCNN consumed 1159MB with the batch size of 256 on NVIDIA TITAN RTX GPU.

3.3. Digital phantom study: Bloch simulation

The proposed method was validated with digital phantoms simulated from the two-pool Bloch-McConnell equations. Two phantom studies were designed to investigate the effect of B₀ and B₁ correction on the accuracy of tissue parameter quantification (k_mw, M₀^m, T₂^m, and T₁^w).

In the first digital phantom study, ΔB₀ and rB₁ values were randomly sampled to simulate the effect of field inhomogeneities. The parameter ranges were given as −1.2 to 1.2 ppm for ΔB₀ and 50 to 150% for rB₁. As shown in Fig. 3A, four digital phantoms (PH1, PH2, PH3, PH4) were constructed, each of which had five circular compartments to evaluate each of the four tissue parameters, while the other three tissue parameters were randomly chosen within the pre-defined ranges (Table 1). The five tissue parameter values for each phantom were: 5, 20, 40, 60, and 80 Hz for k_mw; 2, 6, 10, 14, and 17% for M₀^m; 1, 25, 50, 75, and 100 μs for T₂^m; and 0.2, 0.9, 1.6, 2.3, and 3.0 s for T₁^w. Longitudinal magnetization evolutions of the free bulk water protons (MTC-MRF) were encoded to the four digital phantom images using a Bloch simulation with an MRF schedule of 40 dynamic scans. The simulated fingerprints were fed to the RNN in accordance with the nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$) and the corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$), respectively. The estimated tissue parameters were compared to ground-truths and the normalized root mean square errors (nRMSE) were calculated. The MRF schedule was optimized from the learning-based optimization of the acquisition schedule (LOAS) method (46). In the second digital phantom study, the quantification accuracy was evaluated with various numbers of dynamic scans (#10, #20, #30, and #40). Quantification results from the nominal scan parameters were compared with those from the B₀ and B₁-corrected scan parameters.

Figure 3.

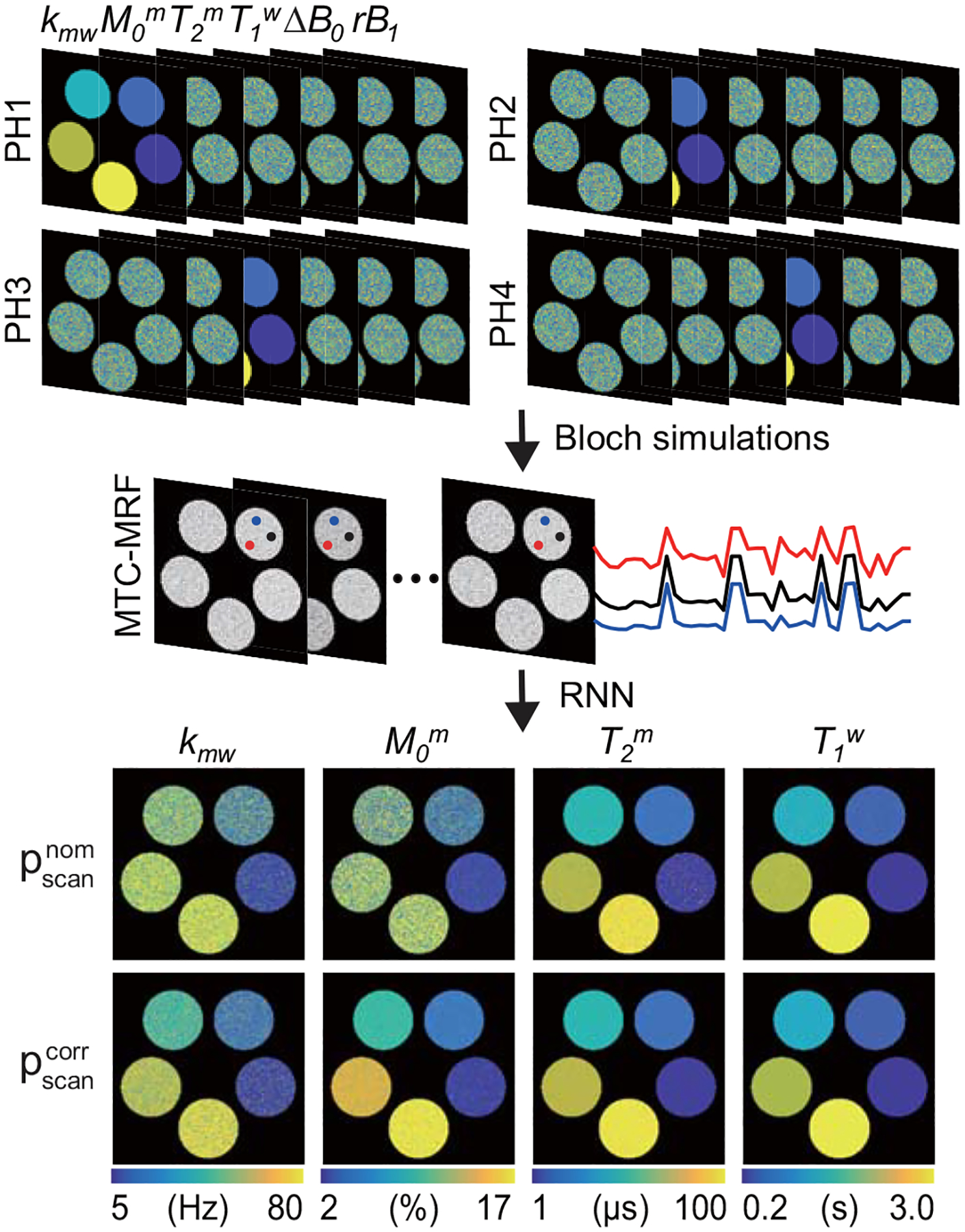
Bloch-McConnell equation based digital phantom studies using simulated B₀ and B₁ errors. Four digital phantoms (PH1, PH2, PH3, and PH4) and the MRF schedule optimized with the learning-based optimization of acquisition schedule (LOAS) were used to simulate MTC-MRF images. Three fingerprints (red, black and blue) encode the same tissue parameters but with different saturation powers due to rB1. The simulated fingerprints and scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$ or ${\text{p}}_{\text{scan}}^{\text{corr}}$) were fed to the trained RNN to quantify the tissue parameters.

3.4. In vivo MRI measurements

Eight healthy volunteers (three females and five males; age 38.1 ± 4.1) were scanned on a 3T MRI system (Achieva dStream, Philips Healthcare, Best, the Netherlands). All subjects were examined with the approval of the institutional review board, and written, informed consent was obtained prior to the MRI experiments. The 3D MTC-MRF images were acquired from a fat-suppressed (spectral pre-saturation with inversion recovery) multi-shot turbo spin echo (TSE) pulse sequence with 2×2 compressed sensing (CS) accelerations in the two phase-encoding directions (ky-kz) (47). The imaging parameters were TE = 6 ms, FOV = 212 × 186 × 60 mm³, spatial resolution = 1.8 × 1.8 × 4 mm³, slice-selective 120° refocusing pulses, turbo factor = 104, and slice oversampling factor = 1.4. The two-channel, time-interleaved, parallel RF transmission (pTX) technique through the body coil was applied to achieve pseudo-continuous RF saturation with a 100% duty-cycle. The pTX-based saturation allowed a high degree of freedom for RF sequence design and highly sensitive saturation effects (48,49). Forty dynamic scans were acquired with a PR (pseudo-random) schedule for six subjects and an LOAS schedule for two subjects. To normalize MTC-MRF images, an unsaturated image (S₀) was acquired. In addition, multi-echo gradient-spin-echo (GRASE) images with five echoes (TE = 20, 40, 60, 80, and 100 ms) were acquired for the T₂ map (50). For B₀ mapping, the water saturation shift referencing (WASSR) method (51) was used with the following RF saturation parameters: 26 frequency offsets (from −1.5 to 1.5 ppm at intervals of 0.125 ppm); Ts = 800 ms; and B₁ = 0.5 μT. For B₁ mapping, the dual refocusing echo acquisition mode (DREAM) method (52) was used with the simulated echo acquisition mode (STEAM) with a flip angle of 40°.

3.5. Validation of B₀ and B₁ correction using synthetic MRI analysis

A synthetic MRI analysis was performed to gauge how tissue estimates can be corrupted by the influence of B₀ and B₁ errors and how well the proposed method corrects B₀ and B₁ inhomogeneities. The field inhomogeneities were simulated with synthetic ΔB₀ and relative B₁ (rB₁) maps. Both maps were constructed to have nine constant values (60, 70, 80, 90, 100, 110, 120, 130, and 140% for rB₁; −0.8, −0.6, −0.4, −0.2, 0.0, 0.2, 0.4, 0.6, and 0.8 ppm for ΔB₀). The tissue parameter maps estimated from in vivo MTC-MRF images obtained with the PR schedule of forty dynamic scans were defined as the reference (namely, Ref). Corresponding 3D MTC-MRF images were synthesized by inserting the reference tissue parameters, ΔB₀, rB₁ maps, and the LOAS schedule into the forward Bloch transform. Then, the synthesized 3D MTC-MRF images were fed to the RNN model. The percent error maps were calculated for all tissue parameters. To further evaluate the performance of the field inhomogeneity correction using the proposed method, nRMSE was calculated as a measure of the quantification accuracy for various numbers of scans (#10, #20, #30, and #40). In addition, the estimated tissue parameter maps and the experimentally acquired water T₂ map were used to synthesize the MTC reference signal intensity (Z_ref) through Bloch equations.

4. RESULTS

4.1. Digital phantom studies

The performance of the RNN-based B₀ and B₁ correction method was evaluated using digital phantoms simulated from two-pool Bloch equations, as shown in Fig. 3. The MRF schedule optimized by LOAS was encoded to each phantom. The saturation power (B₁) was scaled with the relative B₁ (rB₁) map and the frequency offset was shifted with the ΔB₀ map (See supporting Figure S1). The estimated tissue parameter maps using the corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$) were much more accurate than those using the nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$) for all tissue parameters. The nRMSE values with the nominal and corrected scan parameters were 32.5% and 20.1% for K_mw, 28.1% and 7.4% for M₀^m, 9.7% and 3.0% for T₂^m, and 3.9% and 0.9% for T₁^w, respectively. Specifically, the accuracy of the exchange rate and the concentration parameters was greatly improved by reducing more than 12% and 20% of nRMSE, respectively. Overall, the nRMSE values of free bulk water T₁ and the semisolid macromolecules T₂ were lower than those of the exchange rate and the concentration.

Figure 4 illustrates the performance of B₀ and B₁ correction for various MRF schedule lengths. MTC-MRF images were generated using the two-pool Bloch equations with four MRF acquisition schedules with different dynamic scan numbers (LOAS #10, LOAS #20, LOAS #30, and LOAS #40) and fed to the RNN model to quantify the tissue parameters. The MRF reconstruction accuracy substantially increased after B₀ and B₁ correction (See supporting Figure S2). While the nRMSE values decreased with the number of dynamic scans after B₀ and B₁ correction, no significant correlation was observed between the number of dynamic scans and nRMSE values without B₀ and B₁ correction.

Figure 4.

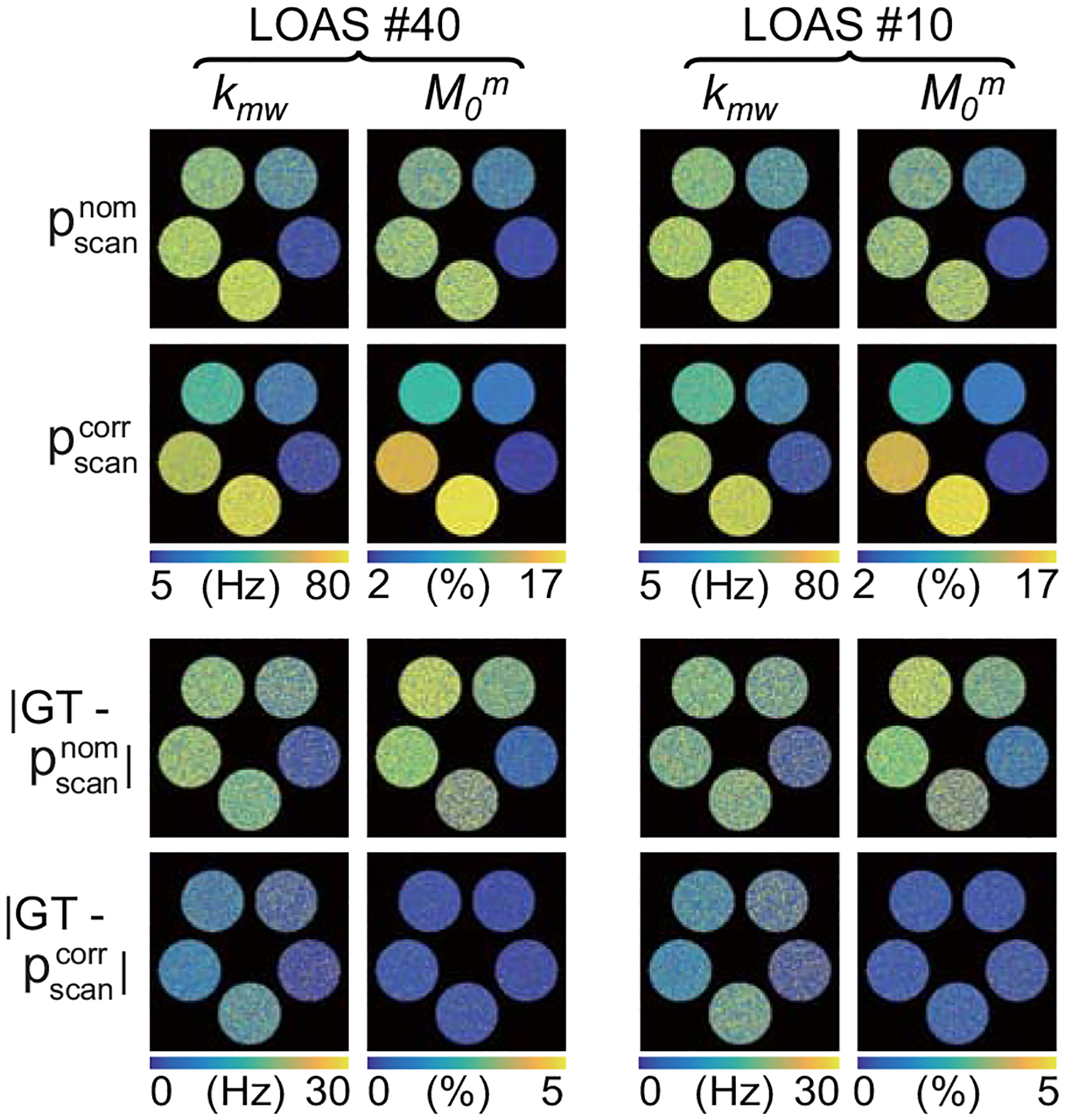
Bloch-McConnell equation based digital phantom studies using various MRF schedule lengths. An example of the B₀ and B₁-uncorrected (${\text{p}}_{\text{scan}}^{\text{nom}}$) and -corrected (${\text{p}}_{\text{scan}}^{\text{corr}}$) quantitative maps of the exchange rate and concentration estimated with MRF schedules of 10 and 40 dynamic scans.

4.2. Synthetic MRI analysis

To assess the proposed correction method with in vivo images, a simulated relative B₁ map (nine values of rB₁ from 60 to 140% at intervals of 10%) and reference tissue parameter maps were assigned to synthesize MTC-MRF images, as shown in Fig. 5A. The synthetic images were fed to the trained RNN with the nominal and corrected scan parameters to estimate B₁-corrupted and B₁-corrected tissue parameter maps, respectively. There was excellent agreement between the reference tissue parameter maps and the estimated tissue parameter maps from the corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$). However, a poor agreement was observed between the reference maps and the estimated maps from the nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$). The Pearson correlation coefficients for ${\text{p}}_{\text{scan}}^{\text{corr}}$ and ${\text{p}}_{\text{scan}}^{\text{nom}}$ were 0.742 and 0.253 for K_mw, 0.995 and 0.503 for M_o^m, 0.985 and 0.976 for T₂^m, and 0.998 and 0.923 for T₁^w, respectively. The B₁ inhomogeneity highly impaired the quantification of the exchange rate and the concentration of the semisolid macromolecules, whereas the free bulk water T₁ and the semisolid macromolecule T₂ relaxation times were relatively robust to the B₁ inhomogeneity. Specifically, the error maps of k_mw and M₀^m were exacerbated by relative B₁ values lower than 80% and higher than 120%. Figure 6 shows the accuracy of tissue parameters and MTC signals at 3.5 ppm (= 1 - Z_ref(3.5 ppm)) estimated from various numbers of dynamic scans. As the number of dynamic scans increased, the nRMSE values decreased when B₁ inhomogeneity was corrected (gray bars). MTC reference signals at 3.5 ppm were relatively insensitive to the number of dynamic scans, whose nRMSE value was less than 0.8%, even with 10 dynamic scans.

Figure 5.

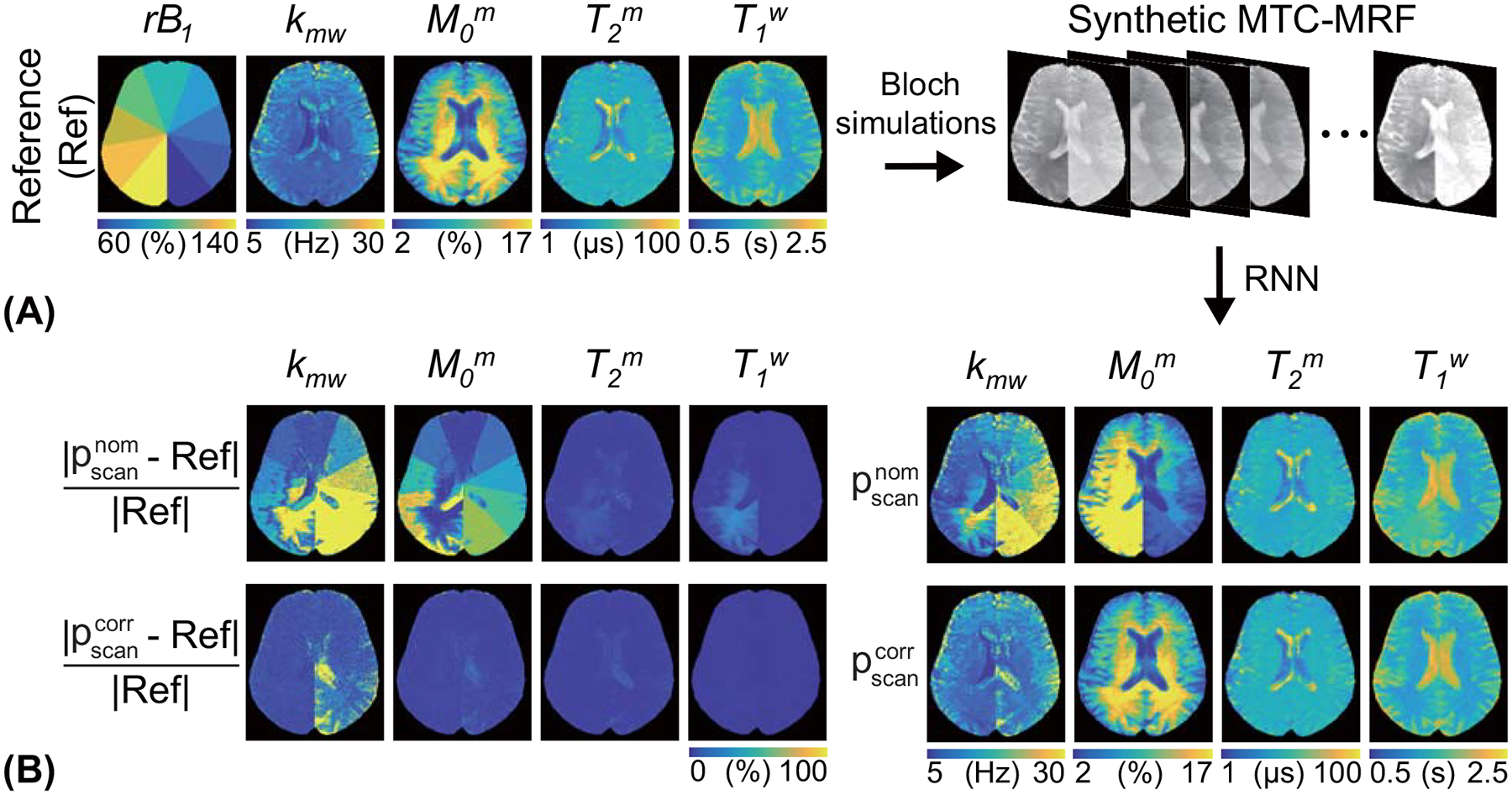
The sensitivity of the MTC quantification to B₁ inhomogeneity was evaluated using a synthetic MRI technique. (A) An illustration of the validation process. The synthetic MTC-MRF images were generated with the simulated relative B₁ (rB₁) and the reference tissue maps and fed to the trained RNN. The nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$) and corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$) were used to estimate the quantitative water and MTC maps. (B) Difference images between the reference and the estimated tissue maps are shown.

Figure 6.

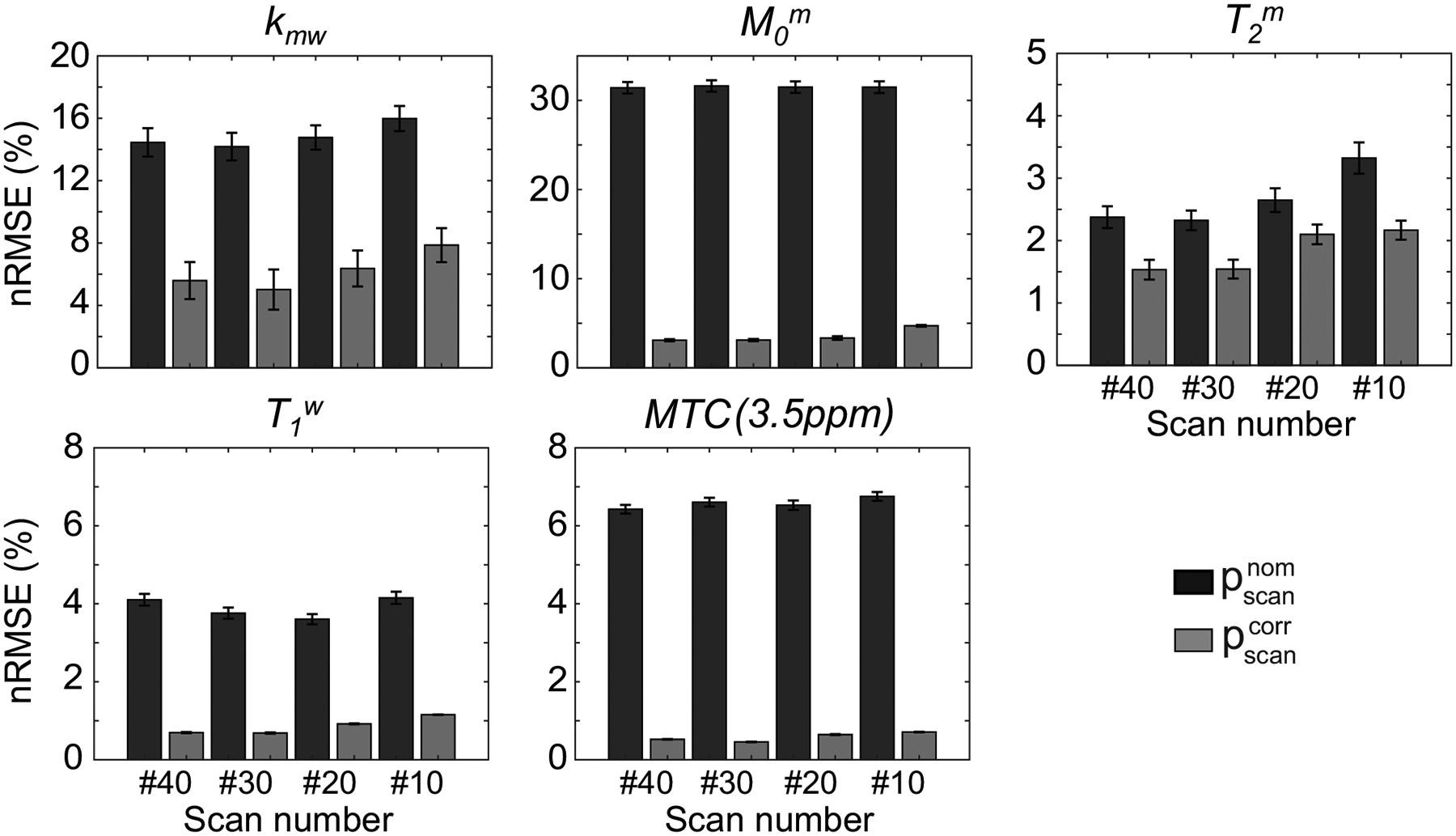
Quantification accuracy of the proposed correction method with respect to the number of dynamic scans (#10, #20, #30, and #40) for tissue parameters and MTC (3.5 ppm) signals. The MTC images were synthesized with an RF saturation power of 1.2 μT, a saturation time of 2 seconds, and a relaxation delay time of 4 seconds. The graphs show the mean and variance of nRMSE from six healthy volunteers.

In addition, the B₀ correction was validated using a synthetic MRI analysis (see Supporting Fig. S3). Good agreement was observed between the reference maps and the estimated tissue parameter maps with and without B₀ correction. The Pearson correlation coefficients for ${\text{p}}_{\text{scan}}^{\text{cor}}$ and ${\text{p}}_{\text{scan}}^{\text{nom}}$ were 0.900 and 0.900 for K_mw, 0.997 and 0.996 for M_o^m, 0.991 and 0.991 for T₂^m, and 0.998 and 0.998 for T₁^w, respectively.

4.3. In vivo experiments

The RNN network trained with the simulated MTC-MRF signals using numerous sets of scan and tissue parameters was applied to human brain images of healthy volunteers. MTC-MRF images were experimentally acquired using LOAS schedules of 40 dynamic scans (LOAS #40). The nominal scan parameters and corrected scan parameters, compensated with the acquired ΔB₀ from WASSR and rB₁ maps from the DREAM methods, were fed to the trained RNN with the in vivo MTC-MRF images to estimate water and MTC parameter maps. Figure 7 shows the quantitative water and MTC parameter maps obtained from the RNN-based MRF reconstruction in accordance with the nominal and corrected scan parameters and difference images between the estimated maps with and without B₀ and B₁ correction. The B₁ inhomogeneity pattern obviously reflected the tissue parameter maps, particularly as seen in the difference images of the exchange rate and the concentration, whereas the B₀ inhomogeneity had less impact on the MTC-MRF reconstruction. The field inhomogeneity error further propagated to the synthesized MTC images at 3.5 ppm, as shown in Fig. 8. A 17% error in B₁ (ROI 2 in Fig. 8) produced a water saturation signal change of up to 5%. The proposed correction method appeared to mitigate the errors that originated from the field inhomogeneities and improved reconstruction accuracy.

Figure 7.

(A) Quantitative MTC parameters and water T₁ maps of a representative brain scan from a healthy human volunteer using the nominal (${\text{p}}_{\text{scan}}^{\text{nom}}$) and corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$). The acquired ΔB₀ and relative B₁ (rB₁) maps used for correction are shown. (B) Difference images between tissue parameter maps with and without B₀ and B₁ correction are also shown. The mean difference values (white color) are displayed in the difference images.

Figure 8.

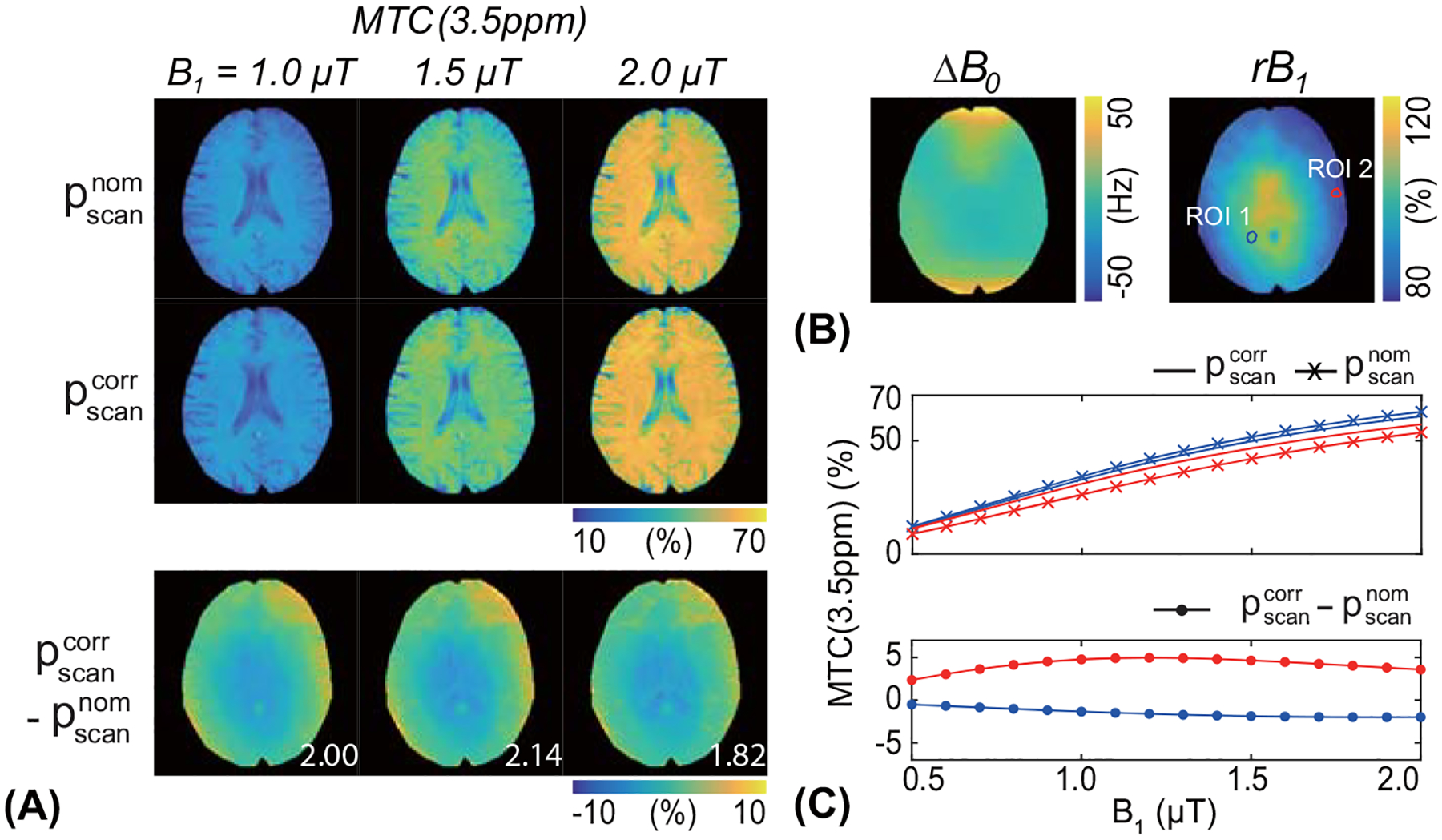
(A) Representative MTC (3.5 ppm) images from the brain of a healthy volunteer, reconstructed with the nominal (${\text{p}}_{\text{scan}}^{\text{nom}}$) and corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{cor}}$). The MTC images were synthesized with a saturation time of 2 s, a relaxation delay time of 5 s, and RF saturation powers of 1.0, 1.5, and 2.0 μT, respectively (top left). Difference images between the B₀, B₁-corrected and -uncorrected maps are shown (bottom left). The mean difference value of each map is shown in the difference image. (B) Two ROIs (ROI 1 and ROI 2) were drawn in the rB₁ map, one ROI with an rB₁ of 105% and the other ROI with an rB₁ of 83%. (C) The MTC signals and the signal difference at drawn ROIs are plotted as a function of RF saturation power (0.5 to 2.0 μT at intervals of 0.1 μT).

5. DISCUSSION

The main and transmit magnetic field inhomogeneities alter MTC-MRF signal profiles, which leads to substantive errors in the estimated tissue parameters. Here, we developed a fast and effective technique to correct the field inhomogeneity-induced artifacts and errors. The linear compensation scheme was adopted to correct the quantification errors from the local B₀ and B₁ variations. The performance of the correction technique was evaluated using numerical phantom studies and synthetic MRI analysis, and demonstrated a high degree of accuracy in quantifying water and semisolid macromolecule parameters, even with severe B₀ and B₁ inhomogeneities. The proposed network enabled fast tissue parameter estimations of the human brain due to its simple feed-forward deployments in the test phase.

MRF allows direct mapping of unique magnetization evolutions into tissue parameters by solving the ill-posed, non-linear inverse problem of MR physics models with dictionary-matching (53), model-based (37), or learning-based (25,27) methods. The MR signal model involves three different spaces: fingerprint; tissue parameter; and scan parameter spaces. The dictionary-matching and learning-based MRF techniques solve the inverse-mapping problem between the fingerprint space and the tissue parameter space. Thus, the scan parameter space is fixed for the dictionary-matching and learning-based methods. Although the model-based approach fully explores MR signal models, becoming independent of the MRF sequence, high computational complexity limits its clinical usefulness. In this work, various tissue parameters, as well as scan parameters, were exploited during the training of neural networks, so that it could be applied to MTC-MRF images obtained with any scan parameters. The deep-learning approaches have been the most effective methods with which to circumvent the curse of dimensionality in MR fingerprinting (54). Our results reiterate the effectiveness of a neural network in MR fingerprinting by expanding the parameter dimension beyond tissue parameters to scan parameters. In addition, a recurrent neural network was adopted, which is suitable for time series data, i.e., signal evolution of the MR fingerprint over time (55,56). Only the hidden state is updated throughout every time point of the input sequence and used for next step analysis, allowing the input sequence of any scan number. It is noteworthy that the single RNN model was trained only once and applied to different types of MRF acquisition schedule (pseudorandom and LOAS-optimized) with various schedule lengths in this study. In addition, it is very important to define the range of scan parameters not to fall outside the range of training data after correction, because the learning-based methods could fail to generalize beyond the parameter values encountered in the training (See Supporting Fig. S4).

Several deep-learning approaches have been applied to MTC-MRF reconstruction by training networks with simulated or in vivo MRF profiles (25,26). However, the deep-learning approaches did not consider the B₁ correction. It would be beneficial to develop a network that corrects B₀ and B₁ error without explicit image acquisition to measure B₀ and rB₁ maps. However, the network trained with B₁-inhomogeneity-involved dataset failed to estimate accurate tissue parameters without an explicit rB₁ map as an input (57), particularly the concentration of semisolid tissues, when there was moderate-to-severe B₁ inhomogeneity (see Supporting Fig. S5). When the rB₁ map was given as an input, neural network was able to correct B₁ inhomogeneity accurately. This emphasizes the need for B₁ inhomogeneity correction in MTC-MRF using the rB1 map. In this study, we utilized the OTOM framework to support a large range of different acquisition schedules, and thereby, enabled the linear compensation of the scan parameters. The proposed approach effectively corrected B₀ and B₁ errors, while maintaining the fast tissue parameter quantification due to the feed-forward mechanism of the neural network. The reconstruction time for an image matrix of 256 × 256 × 9 (slices) × 40 (scans) was less than two minutes, whereas the fitting method required hours.

The exchange rate and the concentration maps of the semisolid macromolecular protons were highly corrupted with severe B₁ inhomogeneity. Interestingly, a linear relationship was observed between the rB₁ value and the concentration estimation. Low values of rB₁ (relative to nominal B₁) underestimated the concentration of semisolid tissues and high values of rB₁ overestimated the concentration of semisolid tissues, which is in line with a previous observation (58). It is not surprising that B₁ errors can influence MRF signal intensities and be mistaken as the saturation effect from the semisolid proton concentration, which results in incorrect tissue quantification. The exchange rate map from the proposed correction method showed high error with low values of rB₁, presumably due to the insufficient saturation. Therefore, the field inhomogeneity correction resulted in somewhat different MTC values compared to previous studies without correction (25,26). Especially, the estimated MTC exchange rates of gray matter (~8 Hz) were lower than those reported previously (~15 Hz) and the concentration of the gray matter (~14 %) was significantly higher with B₁ correction compared to previous reported value (~10 %), which was consistent with the values before B₁ correction (See Supporting Table S1). In addition, the Intrinsic water T₁ relaxation times estimated in this study were longer than the observed T₁ relaxation times estimated from conventional inversion-recovery studies because of the interaction between the free bulk water and semisolid macromolecules (26). Although water T₁ estimation was less affected by small B₁ errors, very high rB₁ values (> 120%) caused a substantial error in water T₁ estimation (Fig. 5B) due to small MRF signal discrimination between different T₁^w values. The MTC-MRF signal becomes less dependent on the longitudinal relaxation term ($1-e^{-Td/T_1^w}$) when the higher saturation (e^λTs, where λ is negative and includes B₁) is applied (Eq. [15]). On the other hand, the semisolid macromolecular T₂ was relatively robust to B₁ inhomogeneity. Interestingly, the effect of B₁ errors on MTC-MRF reconstruction is influenced by a B₁ power schedule (see Supporting Fig. S6). In addition, the MTC-MRF signal was less sensitive to the exchange rate and therefore the estimated exchange rate could easily be distorted by B₁ inhomogeneity (25). This could be even exacerbated by a different MRF schedule, leading to inconsistent rRMSE values with respect to the number of dynamic scans (See Supporting Fig. S7). Thus, the robustness of tissue parameter estimation to B₁ errors could be improved by optimizing the acquisition protocol (59). The optimization of an MRF acquisition schedule that is more resilient to B₀ and B₁ errors may be an important future study direction.

A conventional MTC-MRF approach is relatively less sensitive to B₀ error than B₁ error (Supporting Fig. S3 and Supporting Fig. S8) because of a very broad line-shape as a result of the microsecond T₂ of semisolid macromolecules. However, B₀ inhomogeneity is not trivial in CEST parameter quantification because the chemical shift of the solute protons is sufficiently close to the water frequency and the location of CEST peaks is easily shifted by B₀ error. Therefore, the proposed OTOM-based B₀ and B₁ correction could benefit CEST-MRF reconstruction or imaging of the brainstem, frontal lobes, and temporal lobes, where severe B₀ inhomogeneity in the air-tissue interfaces remains. In addition to the B₀ and B₁ correction, OTOM could be further extended to MRF schedule optimization by analyzing the quantification error of a given schedule (46,60,61). The feasibility was already demonstrated (62).

6. Conclusion

A fast, deep-learning approach was developed to simultaneously estimate multiple tissue parameters and correct B₀ and B₁ errors, validated in digital phantoms, and demonstrated in healthy volunteers. The proposed method could achieve a high degree of accuracy for tissue parameter quantification in the presence of severe B₀ and B₁ inhomogeneities. The only-train-once deep-learning framework can be combined with any conventional MRF or CEST-MRF method, and improve the reconstruction accuracy of tissue parameter maps.

Supplementary Material

supinfo

Supporting Information Table S1. Estimated free bulk water T₁ relaxation time, semisolid MTC parameters, MTC at 3.5 ppm (1.5 uT), APT, and NOE signal intensities for white matter and gray matter of the healthy volunteer human brain. Regions of interest (ROIs) were shown in Supporting Figure S9.

Supporting Information Figure S2. Bloch-McConnell equation based digital phantom studies using various MRF schedule lengths. The reconstruction accuracy was evaluated for each tissue parameter with respect to the number of dynamic scans by calculating the nRMSE values.

Supporting Information Figure S3. The sensitivity of the MTC quantification to B₀ inhomogeneity was evaluated using a synthetic MRI technique. (A) An illustration of the validation process. The synthetic MTC-MRF images were generated with the simulated ΔB₀ and the reference tissue maps and fed to the trained RNN. The nominal scan parameters (${\text{p}}_{\text{scan}}^{\text{nom}}$) and corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{cor}}$), respectively, were used to estimate the quantitative water and MTC maps. (B) Difference images between the reference and the estimated tissue parameter maps are shown.

Supporting Information Figure S4. Bloch equation-based digital phantom studies. (A) One has an optimized B1 power schedule (red) from a LOAS algorithm and the other six have different B1 power schedules by adding 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 μT, respectively. (B) The nRMSE values were calculated for each tissue parameter estimated by OTOM. This study shows that OTOM can fail to correct B1 inhomogeneity if the scan parameters after correction are out of range for training data (Out-of-distribution inputs).

Supporting Information Figure S5. A synthetic MRI technique was performed to analyze the importance of explicit rB1 as an input. (A) Illustration of the validation process. The synthetic MTC-MRF images were generated with the simulated relative B1 (rB1) and the reference tissue maps, and fed to the trained RNN. Three FCNNs trained differently and OTOM were used to estimate the quantitative water and MTC maps. (B) Difference images between the reference and the estimated tissue maps are shown.

Supporting Information Figure S6. Bloch equation-based digital phantom studies using simulated B₁ inhomogeneity. One B₁ power schedule (black) was optimized by an LOAS algorithm and two additional B₁ power schedules were generated by adding 0.5 μT (LOAS+, blue) and −0.5 μT (LOAS-, red). Note that LOAS schedule was optimized for the RF saturation range of [0.9 1.9] μT. Then, B₁ errors were encoded in the digital phantoms. The nRMSE values were calculated for each tissue parameter with and without correction of B₁ inhomogeneity. This simulation study shows that the effect of B₁ errors on tissue parameter quantification is influenced by B₁ power schedules.

Supporting Information Figure S7. Bloch-McConnell equation based digital phantom studies using the simulated B₁ errors. The nRMSE values were calculated for each tissue parameter with the corrected scan parameters (${\text{p}}_{\text{scan}}^{\text{corr}}$) using four OTOM networks. The variance of exchange rate with LOAS#40 was particularly large and most vulnerable to B₁ inhomogeneity.

Supporting Information Figure S8. Bloch equation-based digital phantom studies using simulated B₀ inhomogeneity (−1.2 ~ 1.2 ppm). (A) The tissue parameter maps were reconstructed from the fingerprints simulated with and without B₀ inhomogeneity. (B) nRMSE was calculated for two cases with and without B₀ inhomogeneity when the tissue parameters were estimated by the proposed method without B₀ correction.

Supporting Information Figure S9. ROIs were carefully drawn on a center slice of 3D T2 maps. The ROIs of white matter (black) and gray matter (yellow) for two subjects are shown.