ADOPT: intrinsic protein disorder prediction through deep bidirectional transformers

Abstract

Intrinsically disordered proteins (IDPs) are important for a broad range of biological functions and are involved in many diseases. An understanding of intrinsic disorder is key to develop compounds that target IDPs. Experimental characterization of IDPs is hindered by the very fact that they are highly dynamic. Computational methods that predict disorder from the amino acid sequence have been proposed. Here, we present ADOPT (Attention DisOrder PredicTor), a new predictor of protein disorder. ADOPT is composed of a self-supervised encoder and a supervised disorder predictor. The former is based on a deep bidirectional transformer, which extracts dense residue-level representations from Facebook’s Evolutionary Scale Modeling library. The latter uses a database of nuclear magnetic resonance chemical shifts, constructed to ensure balanced amounts of disordered and ordered residues, as a training and a test dataset for protein disorder. ADOPT predicts whether a protein or a specific region is disordered with better performance than the best existing predictors and faster than most other proposed methods (a few seconds per sequence). We identify the features that are relevant for the prediction performance and show that good performance can already be gained with <100 features. ADOPT is available as a stand-alone package at https://github.com/PeptoneLtd/ADOPT and as a web server at https://adopt.peptone.io/.

INTRODUCTION

Modern biochemistry is based on the assumption that proteins fold into a three-dimensional structure, which defines their biological function (1). However, in the past 20 years a novel class of biologically active polypeptides was identified that defies the structure–function paradigm. Intrinsically disordered proteins (IDPs) constitute a broad class that encompasses proteins that do not fold into a defined three-dimensional structure, undergo transitions between multiple unstructured or partially structured conformations or fold upon binding (2). IDPs play a fundamental role in biological processes such as cell signalling and regulation (3) and were implicated in numerous debilitating human disorders, including various cancers (4), diabetes (5), cardiovascular diseases (6) and neurodegenerative conditions such as Alzheimer’s or Parkinson’s disease (7). Consequently, IDPs are considered prime targets for drug development, yet very limited success of IDP-targeting compounds has been reported to date (8). The development of therapeutic molecules that target full-length IDPs or unstructured regions of folded proteins (IDRs) is particularly challenging because unfolded regions are depleted in hydrophobic residues, which stabilize druggable protein regions. Instead, IDPs contain many charged and polar residues, whose repulsive interactions drive intrinsic protein disorder. Thus, amino acid sequence composition of IDPs holds key to precise prediction and assessment of structural disorder in high-value and unmet medical targets. The rational design of IDP-targeting compounds is hindered by the lack of a well-defined structure and by the challenges posed by the experimental characterization of the broad conformational ensembles they populate. The big amount of potential IDP drug targets is presently not approachable with traditional structure-based drug design tools and needs the development of new methods. Experimental techniques used to characterize intrinsic disorder include X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, small-angle X-ray scattering, circular dichroism and Förster resonance energy transfer. The resolution of the information and nature itself of the disorder probed depend on the experimental technique used to characterize it. NMR chemical shifts depend uniquely on the local environment and provide a probe, at single amino acid level, of the structure and dynamics of IDPs.

Since the first disorder predictor was proposed in 1997 (9), numerous protein disorder predictors have been developed. In general, they can be divided into four categories: physicochemical predictors, machine learning (ML)-based predictors, template-based predictors and meta predictors. Physicochemical property-based predictors (10–15) utilize chemical features of amino acids, especially hydrophobicity and net charge, to predict whether a residue belongs to an ordered or a disordered region. Disorder predictions can be straightforwardly interpreted in terms of physical properties of underlying amino acid sequence. However, the accuracy and sensitivity of such predictors are limited to the features they use to differentiate between order and disorder. ML-based predictors (16–30) use positive and negative samples to distinguish between ordered and disordered regions. They can be used to search for the most important among many features. In comparison to physicochemical predictors, ML-based predictors are more flexible in their search of features, yet may suffer from poor ‘explainability’ of extracted features and their relevance for disorder. Template-based predictors (31–33) search for homologous structures (templates) and use these to distinguish between structured and unstructured regions in proteins. Their results can be easily interpreted, but homologous structures might not be found or their disorder prediction might not be transferable to the query protein. Finally, meta predictors (33) aggregate the output of multiple other disorder prediction tools and report a composite disorder score. In general, this leads to a better prediction accuracy than individual predictors, but at the cost of an increased computational effort, which in turn may hamper their effectiveness against proteome-size surveys.

Despite the progress in disorder prediction in the last 25 years, a systematic assessment of the different predictors did not exist until a few years ago. Recently, two comparisons have been established. The critical assessment of protein intrinsic disorder prediction (CAID) (34) is a community-based blind test of state-of-the-art prediction of intrinsically disordered regions based on 643 proteins from DisProt (35). DisProt, the most comprehensive database of disordered proteins, provides manually curated annotations of currently ∼2400 IDPs and IDRs of at least 10 residues likely to be associated with a biological function. The data are based on multiple experimental measurements, but not all IDRs of a protein are contained in DisProt. Furthermore, the annotations in the DisProt database are binary; e.g. they do not report on the strength of disorder of a specific residue in the protein.

CheZOD is a small database (36) of 117 proteins known to contain disorder for which NMR chemical shifts are available from the BMRB database (37). The CheZOD Z-score (referred to as Z-score below), based on secondary chemical shifts and defined in (36), quantifies the degree of local disorder on a continuous scale. Secondary chemical shifts, e.g. differences in chemical shifts of nuclei between the actual structure and a random coil structure, are a precise indicator of local protein disorder (38). It was demonstrated that the Z-score scale, besides being a reliable measure of disorder, also agrees well with other measures of disorder. The histogram of all Z-scores calculated for an expanded CheZOD database (39) containing 1325 proteins and constructed in a way to ensure balanced amounts of disordered and ordered residues fits a bimodal distribution; residues with Z-scores <3.0 can be considered fully disordered, whereas 3.0 < Z < 8.0 corresponds to cases with fractional formation of local, ordered structure.

A systematic comparison of 43 predictors in CAID (34) and 27 predictors on Z-scores (39) showed that deep learning techniques clearly outperform physicochemical methods. For example, SPOT-Disorder (27,40) was the second best predictor in both competitions, slightly beaten by flDPnn (30) in CAID and by ODiNPred (39) on Z-scores. All three predictors use deep neural networks to predict protein disorder.

The elucidation of information from protein sequences is one of the most formidable challenges in modern biology. A comparable task in artificial intelligence (AI) research is natural language processing (NLP), in which ML and linguistic models are used to study how properties of language, including semantics, phonetics, phonology, morphology, syntax, lexicon and pragmatics, arise and interact. To accomplish this, NLP models must be able to find common patterns in variable length and non-linear correlations in language constituents as letters, words and sentences (41). The final goal of NLP is to find regularities of natural language and universal language creation rules.

Supervised learning, a rapidly emerging branch of AI research, is of particularly high importance to computational biology where vast and well-annotated data repositories are available. Its more sophisticated variant, self-supervised learning, enables AI systems to learn from orders of magnitude more data than supervised ones, which is important for recognizing and understanding patterns of more subtle and less common representations. Self-supervised neural models such as the transformer (42) have recently proven to be especially effective for these tasks, e.g. vastly improving language modelling and next sentence prediction in BERT (43) or generating high-quality human-like text in GPT (44).

Motivated by recent developments in self-supervised learning and its application to protein language models (45,46), we developed a novel structural disorder predictor that benefits from the transformer architecture. We demonstrate here the relative benefit of ADOPT (Attention DisOrder PredicTor) software on the expanded version of the CheZOD database. ADOPT outperforms the state-of-the-art tools, ODiNPred, SPOT-Disorder and Metapredict v2, in a number of benchmarks. Finally, we provide an analysis of the residue-level representations used in the development of ADOPT and discuss in detail the features that contribute to an accurate prediction of protein disorder from sequence alone.

MATERIALS AND METHODS

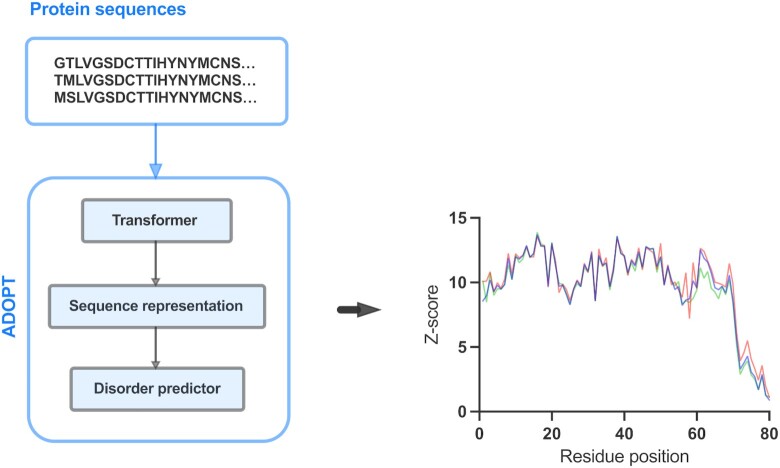
ADOPT is composed of two blocks: a self-supervised encoder and a supervised disorder predictor. The encoder takes a protein input sequence and uses information from a large database of sequences to generate feature information for every residue in the sequence. The decoder uses this information and predicts a disorder score. We used Facebook’s Evolutionary Scale Modeling (ESM) library to extract dense amino acid residue-level representations, which feed into the supervised ML-based predictor. The ESM library exploits a set of deep transformer encoder models (42,43), which processes character sequences of amino acids as inputs. A high-level representation of the ADOPT architecture is shown in Figure 1.

Figure 1.

Schematic view of the ADOPT architecture. A protein sequence is fed into the transformer encoder block that generates a residue-level representation of the input. The embedding vector serves as an input to the disorder predictor block that predicts the level of disorder of each residue, given in terms of Z-scores.

The encoder maps each element x_i ∈ V of an input sequence of symbol representations x = (x₁, …, x_n) to a dense vector z_i, where 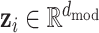. This means that the context of every residue within the input sequence is encoded in a vector with d_mod features . Here, 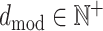is the embedding dimension that is set at training time, 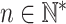is the length of the protein p represented by x and

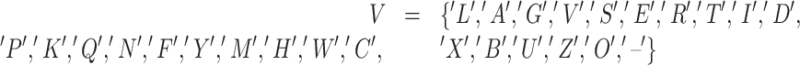represents the vocabulary, where 'X’ stands for unknown amino acid and ‘−’ is the gap symbol in the event of a multi-sequence aligned input. Furthermore, ‘B and Z’ are ambiguous and ‘U and O’ are non-natural amino acids, and the remaining 20 are standard ones. Therefore, a protein p, represented by the sequence vector x, will be encoded on an embedding matrix 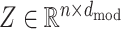obtained by stacking z_i for i = 1, 2, …, n.

ADOPT computes residue-level Z-scores (36), which quantify the degree of local disorder related to each residue, on a continuous scale, based on NMR secondary chemical shifts (47). The input of the disorder predictor is given by the dense representations (embeddings) Z of each protein sequence x, whereas the output is the predicted Z-score of each element x_i of x.

In order to strike a balance between readability and details, while keeping the paper self-contained, we provide more details on the transformer block, including the attention mechanism (see Supplementary Figure S1).

Datasets

Pre-training datasets

Pre-training datasets were based on UniRef (48). UniRef50 and UniRef90 were extracted from UniParc (49) by clustering at 50% and 90% sequence identity, respectively. The UR90/S dataset represents a high-diversity and sparse subset of UniRef90 dated March 2020 and contains 98 million proteins, while the UR50/S dataset represents a high-diversity and sparse subset of UniRef50 representative sequences from March 2018 with 27.1 million proteins. The MSA-UR50 dataset was generated with multiple sequence alignment (MSA) to each UniRef50 sequence by searching the UniClust30 (50) database in October 2017 with HHblits 3.1.0 (51) and contained 26 million MSAs. Default settings were used for HHblits except for the number of search iterations (-n), which was set to 3. Sequences longer than 1024 residues were removed and the average depth of the MSAs was 1192.

Disorder prediction datasets

The disorder prediction datasets were the CheZOD ‘1325’ and the CheZOD ‘117’ databases (39) containing 1325 and 117 sequences, respectively, together with their residue-level Z-scores. Note that throughout this paper we refer to the ‘1325’ and ‘117’ sets as base and validation sets, respectively.

Although Z-scores can be transformed into probabilities of disorder that report on the likelihood of a residue being disordered, we decided to adhere to Z-scores primarily reported in ODiNPred (39).

Pre-trained transformer models

ADOPT utilizes three different pre-trained transformers: ESM-1b, ESM-1v and ESM-MSA. The architectures of ESM-1b and ESM-1v were described earlier and pre-trained on UR50/S and UR90/S, respectively. A complete review of ESM-MSA architecture is given in (52). The aforementioned transformer was pre-trained on MSA-UR50 (see Table 1).

Table 1.

Hyperparameters, dataset and number of parameters related to each ESM model employed

Transformer	Dataset	l	d mod	h	Parameters
ESM-1v	UR90/S	33	1280	20	650 M
ESM-1b	UR50/S	33	1280	20	650 M
ESM-MSA	MSA-UR50	12	768	12	100 M

Disorder predictors

We built four different variants of ADOPT, which differed in the underlying ESM model. We used ESM-1v, ESM-1b, ESM-MSA and ESM-combined, where the last one referred to the concatenation of the representations given by ESM-1v and ESM-1b. The input dimension d_mod, which was equivalent to the dimension of the residue-level representation, was dependent on the ESM transformer used (Table 1), e.g. d_mod = 2560 for ESM-combined and d_mod = 1280 for ESM-1b. Note that ESM-combined is an artificial concept and just a label that does not represent a stand-alone transformer model. In fact, it is only a reference to the concatenated outputs extracted from the two pre-trained transformers ESM-1v and ESM-1b.

Not all four predictors were tested in every benchmark exercise due to the fact that some of them, e.g. ESM-1v and ESM-1b, have similar performances. We indicate in each result discussed which predictor is used.

To predict Z-scores using the residue-level representations, we used a simple Lasso regression model with shrinkage parameter λ = 0.0001, which is considered a well-known, standard technique; see e.g. Chapter 3 in (53). The optimal value for λ was found experimentally by a search across the interval [0.0001, 0.5].

In the binary case, i.e. predicting order/disorder only, we used a simple logistic regression with a L₂ penalty term; for details, see Chapter 4 in (53).

As a benchmark with AlphaFold2, we correlated rolling averages of the predicted local distance difference test (pLDDT) and solvent accessible surface area (SASA), defined in the ‘Benchmark on order/disorder classification’ section, with Z-scores. In both metrics, the window lengths were ranging from 5 to 30 in steps of 5. In the three cases of sequences containing unknown amino acids, the unknown amino acid was replaced with glycine. SASA was calculated using FreeSASA 2.0.3 (https://freesasa.github.io/) with default parameters, with the total relative per residue used for correlations.

Supervised training and evaluation

Our predictors were trained on a reduced part of base dataset. We filtered out all sequences from the base set that showed 20% or higher pairwise sequence similarity with the sequences in the test set, i.e. the 117 CheZOD dataset. These sequences were identified with the tool MMSeqs2 [mmseqs search was used with sensitivity -s 7.5 and number of iteration 3; fident (fraction of identical matches) was used as a pairwise similarity metric]; see (54) and https://github.com/soedinglab/MMseqs2. We further reduced our training set and kept only those sequences that appeared in the training set of Ilzhoefer et al. (55), which also used the CheZOD dataset to develop a disorder predictor (after the original release of our work in a bioRxiv manuscript on 26 May 2022). This means that there were 1159 sequences in our final training set. We used the validation set containing 117 sequences as the test set. The performance of our regression models was measured by Spearman correlation (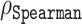) between predicted and experimental Z-scores. To further assess model performance, we also provided mean absolute errors (MAEs) and average prediction errors. Where relevant, we also added P-values. However, given that these were consistently 0.0, i.e. detecting e.g. correlation falsely had zero probability, we omitted them from most tables.

Following the cross-validation settings used in (39), we performed a similar 10-fold cross-validation (CV), separately, using only a filtered version of the base dataset, i.e. 1325 sequences. We removed sequences that showed pairwise identity ≥50%. This time, similarity was computed only within the base set, and we used the same setting as described earlier, i.e. mmseqs search routine with sensitivity -s 7.5 and number of iterations 3; similarity was assessed using fident. This procedure resulted in a set with 1168 sequences, which we will refer to as a cross-validation set. Note that the overlap between this set, which we used for all subsequent cross-validation exercises, and the training set described in the above paragraph is only 1069 sequences. As per standard practice, in a fold 9/10th of the base dataset was used as the training set, where model was fitted, and the remaining 1/10th as the test set. We used randomized 10-fold CV; that is, the folds were selected randomly. A new regression was trained for each fold and we report the average correlation 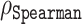, average MAE and average prediction errors, together with standard deviations, taken across the folds. For the regression task, we performed two cross-validation exercises: one based on residue-level and another on sequence-level fold selection. In the former case, whether a residue was in the training or test set was decided on amino acid level. The latter meant that training and test sets were assembled by sequences; i.e. all residues in a sequence were either in the training or in the test set. Note that despite mentioning some of the results from the related ODiNPred paper (39), we omit any direct comparison between the cross-validation tasks presented here and those appearing in the ODiNPred, due to differences in the datasets used.

In the order/disorder classification tasks, we used the area under the receiver operating characteristic curve (ROC AUC) and Matthews correlation coefficient (MCC) as standard evaluation metrics. Furthermore, we provided precision scores, whereby ordered residues were treated as ‘positives’ (Z-scores >8.0). Our classifiers were evaluated in two settings: a residue-level 10-fold CV on the cross-validation set, and a training using the filtered base set and testing on the validation set.

Feature selection

Two methods were used to identify a subset of relevant coordinates or features of the residue-level representation vectors, as shown in Figure 5. Recall that we used Lasso regression as our disorder predictor.

Figure 5.

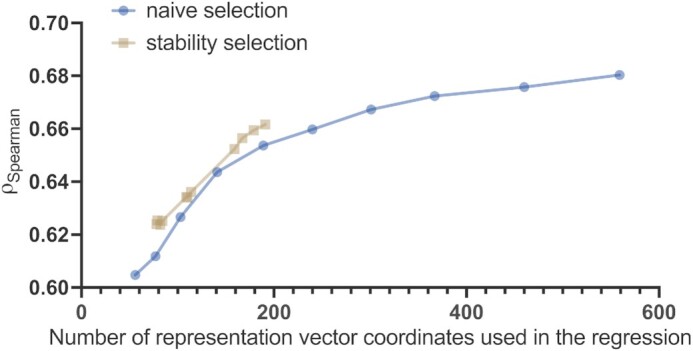
Predictive power of the residue-level representation vectors as a function of the number of their coordinates used in the regression. Here, the transformer ESM-1b was used, and the predictive power was quantified in terms of 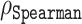between actual and predicted Z-scores on the validation set containing 117 sequences. Naive selection (blue line) is based on the magnitude of the regression coefficients and stability selection (red line) is a more robust technique based on resampling; more details are provided in the ‘Discussion’ section.

In naive selection, we selected only those coordinates whose coefficients were above a certain threshold in terms of their absolute value; that is, the subset S ⊂ {1, 2, …, 1280} was given by

where β_i for i ∈ {1, 2, …, 1280} are the Lasso coefficients for the fixed shrinkage parameter λ = 0.0001. We fitted a new linear regression (Lasso with the same parameter λ = 0.0001) on the reduced set of features and reported the correlation ρ_Spearman between predicted and actual Z-scores on the test set. We repeated this procedure for 10 different cut-off values, equally spaced ranging from 0.5 to 0.2. This selection method is called naive, as it throws away coordinates whose coefficients are below the cut-off in absolute terms, which may still be relevant, and the set of selected features may contain a fair amount of noise. As an alternative method, we used stability selection to identify relevant subsets of the representation vector coordinates. We defined 30 different shrinkage parameters λ. These were equally spaced points of the interval [5 × 10⁻⁵, 0.1], endpoints included. For each λ, we carried out the following procedure. From the initial test set, we chose a random subset, whose size was half of the original one. We fitted a Lasso regression and recorded the features, whose coefficients were non-zero. We repeated this 500 times and for each vector coordinate i ∈ {1, 2, …, 1280} we estimated the selection probability Π_i(λ) by the number of times the coordinate got selected divided by 500.

In order to arrive at the relevant subsets, we applied cut-off values at two different stages. First, we put a threshold c_p on the selection probabilities. Second, we counted for how many λ values this particular threshold c_p has been exceeded. We refer to the latter quantity as frequency cut-off and denote it by c_f. We used the following values:

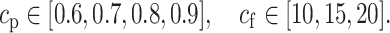As an example, for c_p = 0.6 and c_f = 15, a representation vector coordinate i was deemed relevant if the selection probability Π_i(λ) > 0.6 for at least 15 different λ values. The estimated probabilities Π_i(λ) as a function of λ ∈ Λ can be depicted as paths. We use the term stability paths to describe those that pass the aforementioned two thresholds c_p and c_f, as shown in Figure 6. For more details and discussions on stability selection in general, we refer to (56).

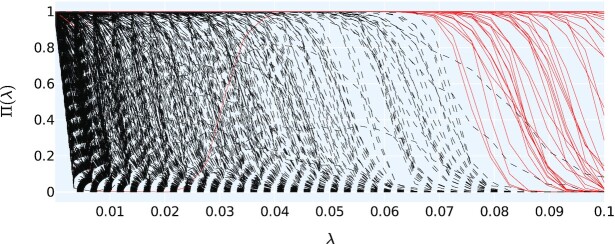
Figure 6.

Stability path examples given by stability selection, as described in the ‘Materials and Methods’ section; see the ‘Feature selection’ subsection. Here, we used the transformer ESM-1b and applied the probability and frequency cut-offs c_p = 0.9 and c_f = 20, respectively. A particular line represents one coordinate or feature of the representation vector and shows the selection probability Π_i(λ) (on the y-axis) as a function of the shrinkage parameter λ (on the x-axis). The red, solid lines represent the coordinates that made the final subset selection and the black, dashed lines represent all remaining coordinates. In this particular example, there are 78 red lines. Interestingly, there is one red line (coordinate) buried in the black lines in the region of lower shrinkage values λ. This means that even though more coordinates were selected in Lasso for a lower λ, this particular coordinate, which typically was picked for higher λ, was not selected.

Implementation

ADOPT is available as a command-line utility at https://github.com/PeptoneLtd/ADOPT. The software uses Facebook’s ESM 0.4 (https://github.com/facebookresearch/esm) for the pre-training phase, Sklearn 1.0 (https://scikit-learn.org/stable/) for the disorder predictor, BertViz 1.2 (https://github.com/jessevig/bertviz) for the multi-head attention visualization, HHblits 3.1.0 (https://github.com/soedinglab/hh-suite) for extracting the MSAs and ONNX 1.10.2 (https://onnx.ai/) for the inference phase. The embedding representations were extracted in bulk with the ESM command-line utility specifying the --include per_tok option from both CheZOD ‘1325’ and CheZOD ‘117’ FASTA files. The embedding vectors’ extraction and tool development (training and inference) were performed on a single Nvidia DGX A100.

RESULTS

Disorder predictor developed using the CheZOD datasets

In order to compare ADOPT to the current state-of-the-art disorder predictor ODiNPred, we adopted the benchmarking protocol found in (39). The CheZOD database was split into two parts, a base and a validation set, containing 1325 and 117 sequences, respectively, with their residue-level Z-scores, which are NMR-based measures of disorder. We used Z-scores to compute the probability of disorder 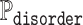at residual level. A probability close to 1 indicates that the residue is likely disordered. Throughout this paper, we are only considering Z-scores as a measure of disorder and omit any further quantification of probabilities of disorder. Furthermore, for classification tasks residues with Z-scores below/above 8 were assumed to be disordered/ordered, respectively.

Training on the base set and performance evaluation on the validation set

We evaluated the variants of ADOPT on four different representations obtained from ESM transformers: ESM-1b, ESM-1v, ESM-MSA and also an ESM-combined that used the concatenated representations from ESM-1b and ESM-1v. Note that the choice of the transformer model changes the input of our disorder predictor and therefore influences its performance. The reduced base and validation sets consisted of 1236 and 117 sequences, respectively. Here, sequences that are part of both sets of the CheZOD database were removed from the base set. We found that disorder predictors had a tendency to overestimate the experimental Z-scores, which was a phenomenon universally observed across the whole spectrum of predictors (39). On the validation set, ODiNPred e.g. displayed an average prediction error of −2.723, meaning that it typically predicted higher Z-scores and an MAE of 3.735. Although our ESM-based predictors also overestimated Z-scores, their prediction errors were considerably lower; e.g. for ESM-1b the average prediction error and MAE were −2.179 and 3.417, respectively. Spearman correlation coefficients (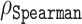) between the predicted and actual Z-scores were used to benchmark performance against ODiNPred. Our ESM transformer-based predictors showed the following Spearman correlation coefficients between predicted and experimental Z-scores: 0.686 (ESM-1b), 0.677 (ESM-1v), 0.604 (ESM-MSA) and 0.688 (ESM-combined), compared to the reported Spearman correlation coefficient of 0.649 for ODiNPred and 0.64 for SPOT-Disorder given the same prediction task (39) (see Table 2). We note that these results have been reproduced by Ilzhoefer et al. (55) after the original release of our work in a bioRxiv manuscript on 26 May 2022. Note that the difference between correlation coefficients of ESM-1b and ODiNPred was found to be significant (one-sided P-value = 0.0122, compared to ODiNPred’s 0.671) by using Fisher r-to-Z transformation. At the same time, the difference between the correlations of ESM-1b and ESM-1v is less significant (one-sided P-value = 0.0869). We also performed the same benchmark test on a recent disorder predictor, Metapredict v2 (57). Metapredict v2 was generated by training a neural network on the disorder scores of a hybrid version of the original Metapredict disorder predictor (58) and predicted pLDDT scores. While the original predictor was highly competitive in the last CAID competition, the successor clearly outperforms the performance of the original predictor with faster execution time. The Spearman correlation coefficient between predicted disorder scores from Metapredict v2 and experimentally derived scores was 0.6581, slightly better than ODiNPred and SPOT-Disorder, but worse than ADOPT. In summary, ADOPT predicted protein disorder more accurately than current state-of-the-art predictors and the overestimation of experimental Z-scores observed across all the tested disordered predictors indicates that these ML-based algorithms display high sensitivity to sequence patterns present in ordered regions.

Table 2.

Spearman correlations between actual Z-scores and predicted pLDDT₅ scores along with actual Z-scores and predicted SASA₁₅ scores, obtained by AlphaFold2

Disorder predictor	Spearman correlation coefficient (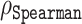)	Average prediction error	MAE
AlphaFold2, pLDDT5	0.555
AlphaFold2, SASA15	0.630
Metapredict v2	0.658
ODiNPred	0.649	−2.723 ± 3.95	3.735 ± 3.01
ESM-1v	0.677	−2.377 ± 3.94	3.559 ± 2.93
ESM-1b	0.686	−2.179 ± 3.85	3.417 ± 2.81
ESM-MSA	0.604	−2.973 ± 4.16	4.035 ± 3.14
ESM-combined	0.688	−2.189 ± 3.91	3.442 ± 2.86

Spearman correlations between actual and predicted Z-scores, average prediction error (actual − predicted) and MAE obtained by ODiNPred and our ESM transformer-based predictors. These correlations have been collected for the task linked to the model evaluated on the validation set consisting of 117 sequences. Given that the P-values in all cases were 0.0, we omitted them.

The prediction of local disorder in a residue is dependent on the neighbourhood of this residue. In order to estimate whether our predictor is able to correctly identify disordered regions, we computed the disordered regions’ prediction recall score, i.e. the fraction of correctly predicted disordered regions from all disordered regions in the dataset. First, the Z-score related to each residue in all proteins of the validation set has been predicted with the ESM-1b model as upstream task. After converting the Z-scores of both, the ground truth and the predicted ones, into a binary class, i.e. Z < 8 for a residue belonging to a disordered region and Z ≥ 8 for a residue in an ordered region (39), we identify for each sequence the related disordered regions defined as those areas where the number of consecutive disordered residues is ≥3 in the ground truth and 70% of the residues in those areas are disordered in the prediction. The recall computed over the binary class of disordered regions is 66%. This means that the ADOPT disorder predictor trained on the ESM-1b transformer is able to correctly find most disordered regions.

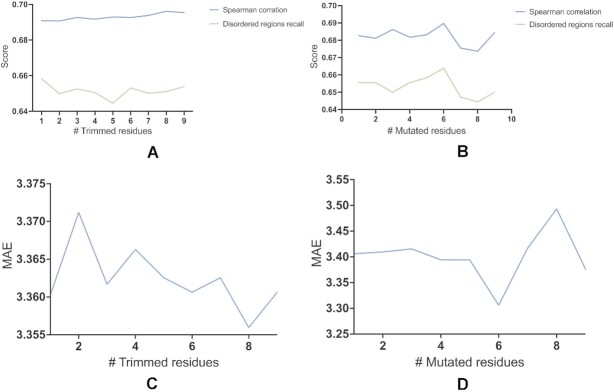
Furthermore, we test the robustness of our methods. Therefore, we introduce two small changes in the sequence and measure the change in disorder prediction. First, we predict how the termini of a protein sequence that are less structured and more flexible influence our predictions. We trim between 1 and 10 residues at both termini of each sequence and measure the difference between predicted and actual Z-scores for the rest of the protein. Second, we randomly mutated up to 10 residues in the validation dataset. In both cases, we report the differences in terms of MAE and Spearman correlation computed on the related ground truth and predicted Z-scores as well as recall score computed over disordered regions’ binary class. The results in Figure 2 show that the accuracy of ADOPT is not influenced by the inclusion of random residues and changes in the number of termini residues showing that ADOPT is robust upon small changes in the given input protein sequence.

Figure 2.

Reliability study on ADOPT predictions. Spearman correlations and disordered regions’ prediction recall computed on trimmed and randomly mutated sequences are shown in panels (A) and (B), respectively. MAEs computed on trimmed and randomly mutated sequences are shown in panels (C) and (D), respectively.

In order to understand the origin of improvement observed in ADOPT, we compared the performance of one of our ESM transformer-based predictors ESM-1b against ODiNPred by visualizing the contour plots of the 2D density of actual versus predicted Z-scores (see Figure 3). Here, the reference lines indicate the idealized case, where predicted values are equal to the actual values. The more probability mass lies closer to these reference lines, the better the accuracy of the predictor. Figure 3 demonstrates that both predictors identify correctly the bimodal Z-score distribution of ordered and disordered regions. This distribution has been chosen in the development of the CheZOD database in order to have a good mixture of both protein classes. The average mass is above the reference line in both regions and for both predictors, which shows that the bias to ordered regions is not limited to a specific strength of protein disorder. The contour lines are tighter around the reference line for the ESM transformer-based predictor (on the left), than for ODiNPred (on the right). The data for ODiNPred were obtained via the publicly available web service (https://st-protein.chem.au.dk/odinpred). Note that using these predicted Z-scores a slightly higher Spearman correlation coefficient of 0.671 was found for ODiNPred, than 0.649 as reported in the paper (39). The result shows that the ESM transformer produces less outliers in comparison to ODiNPred. While the prediction of the ESM transformer is far from perfect, the probability of returning a bad Z-score prediction, defined by a difference of ΔZ = 5 from the experimental Z-score, is significantly lower than that for ODiNPred (see Figure 3).

Figure 3.

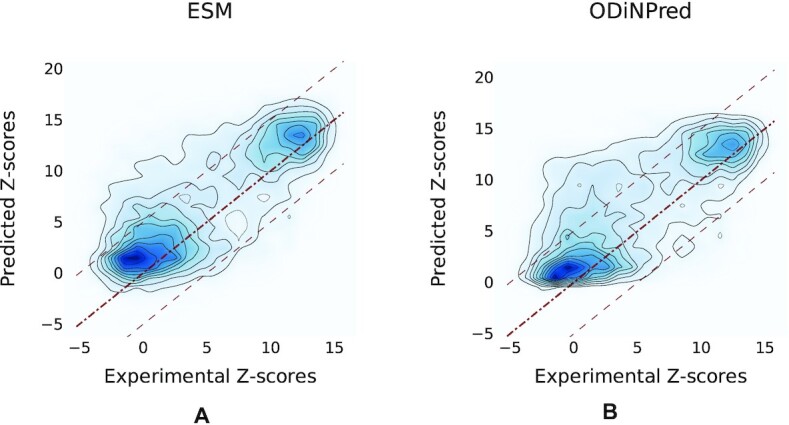
Contour plots showing the density levels of experimental versus predicted Z-scores for the validation set containing 117 sequences: panel (A) shows results obtained with ESM transformer-based predictor (here ESM-1b was used) and panel (B) shows the results obtained with ODiNPred. Diagonal reference lines indicate the idealized ‘perfect’ prediction; i.e. predicted values are equal to the experimental values. As the probability mass around the reference line is tighter for the ESM-based predictor on the left, its accuracy is better than that of ODiNPred. This is further supported by the average prediction error and MAE for the two predictors (see Table 2). Z-scores predicted by ODiNPred were retrieved via the publicly available web service referenced in (39). Note that using these predicted Z-scores a slightly higher Spearman correlation of 0.671 was found, rather than 0.649 as reported in (39). Recall that the Spearman correlation for ESM-1b was 0.686. Note that the difference between correlation coefficients 0.671 and 0.686 was found to be significant (one-sided P-value = 0.0122) based on the Fisher r-to-Z transformation.

Our amino acid level analysis reveals further details about the biophysical origin of the prediction accuracy. We compared two of our proposed disorder predictors, ESM-1b and ESM-combined, to ODiNPred (Figure 4). Keeping the same setting as described earlier, i.e. 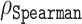between the predicted and experimental Z-scores for the validation set, we observed that the ESM transformer-based predictors displayed better than or similar correlation levels to that of ODiNPred for most amino acids. Some notable exceptions were histidine and methionine. In these cases, ODiNPred was significantly weaker with correlation coefficients 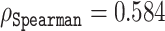and 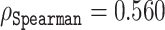compared to e.g. ESM-1b with 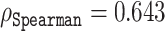and 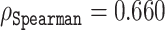for histidine and methionine, respectively. Curiously, all three predictors had considerable difficulties with glycine, cysteine and proline. In fact, for glycine, ODiNPred’s 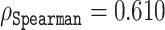outperformed both ESM transformer-based predictors by ∼0.03 (see Figure 4). The distribution of Z-scores for these amino acids (Supplementary Figures S2 and S3) demonstrates that especially the Z-scores of ordered glycine and proline residues are shifted to higher Z-scores in the predictions of ESM-1b and ODiNPred in comparison to the actual values. While this trend is observed for all residues, it has a more pronounced effect on the correlation coefficient of glycine and proline because these amino acids are under-represented in ordered regions. The distribution of Z-scores from cysteine (see Supplementary Figure S3) is clearly different from the distribution of the other amino acids with a higher relative amount of cysteines with intermediate Z-scores around 8. ODiNPred and ESM-1b, however, predict a much higher amount of ordered cysteine residues. Glycine, cysteine and proline are structurally different from the other 17 naturally occurring amino acids. Proline is the only amino acid with a secondary α amino group. Glycine is the smallest and most flexible amino acid, i.e. the only residue that has no chiral C^α atom. Both amino acids are commonly referred to as α-helix breakers and thus are crucial for a correct prediction of disordered protein regions (59). Cysteine has a thiol group and is therefore the only residue that is able to form disulfide bonds within the protein over long distances in sequence. Disulfide bonds are particularly important for the stability of proteins (60). The forming or breaking of disulfide bonds depends on the oxidation state of the protein. This renders a correct prediction of its disorder state particularly challenging because the data we use to learn from and train on do not explicitly include the effect of oxidation. Moreover, the prediction of protein disorder remains especially challenging for amino acids that are important for the breaking of ordered regions. The newly developed ESM transformer improves the prediction of disordered segments for 19 out of 20 amino acids. This shows that the improvement of the ESM transformer is not limited to amino acid-specific biophysical properties.

Figure 4.

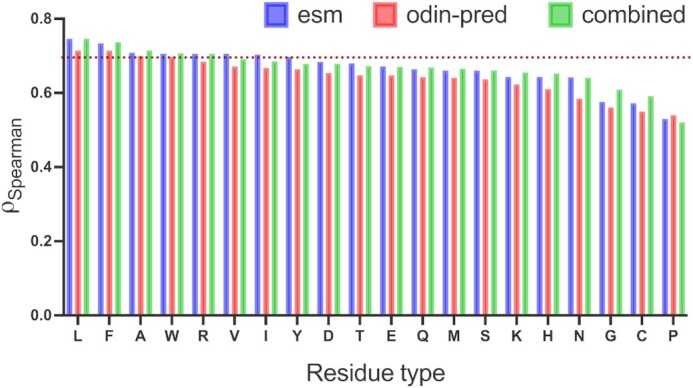
Residue-level comparison of Spearman correlations between actual and predicted Z-scores for the validation set containing 117 sequences. Two of the ESM transformer-based predictors were used, ESM-1b and ESM-combined, which is based on the concatenated representations of ESM-1v and ESM-1b. The dotted reference line indicates the overall Spearman correlation of 0.649 obtained by ODiNPred as reported in (39).

Performance of the ESM transformer-based disorder predictors assessed by 10-fold CV

To gain further insights into the performance of our predictors, we carried out two different 10-fold CV following the protocol proposed in (39); a detailed description of these tests is provided in the ‘Materials and Methods’ section. Cross-validation gives information on how the predictor generalizes to an independent dataset by resampling the validation set in different portions to avoid overfitting or selection bias. In the residue-level 10-fold CV, the Spearman correlations averaged across the 10 folds were as follows: 0.746 (ESM-1b), 0.745 (ESM-1v) and 0.719 (ESM-MSA). The same correlations for the sequence-level 10-fold CV showed slightly lower values: 0.718 (ESM-1b), 0.717 (ESM-1v) and 0.702 (ESM-MSA). Even though a similar 10-fold CV was reported by ODiNPred to have a correlation of 0.6904 [see (39)], we highlight again that due to differences in datasets we used for CV and the one used by ODiNPred, we omit direct comparisons. These results are summarized in Tables 3 (residue level) and 4 (sequence level) and show that our predictor does not suffer from selection bias, e.g. from the specific choice of the validation set, but rather gives an overall balanced performance independent of the constitution of the validation set.

Table 3.

Spearman correlations, MAE and average prediction error between predicted and actual Z-scores obtained by our ESM transformer-based predictors for the residue-level 10-fold CV on the cross-validation set consisting of 1168 sequences only

Residue-level 10-fold CV
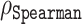
Disorder predictor		MAE	Average prediction error
ESM-1v	0.746	2.285 ± 0.012	0.0001 ± 0.029
ESM-1b	0.745	2.292 ± 0.019	0.0001 ± 0.016
ESM-MSA	0.719	2.62 ± 0.023	−0.0004 ± 0.034

Table 4.

Spearman correlations, MAE and average prediction error between predicted and actual Z-scores obtained by our ESM transformer-based predictors for the sequence-level 10-fold CV on the cross-validation set consisting of 1168 sequences only

Sequence-level 10-fold CV
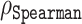
Disorder predictor		MAE	Average prediction error
ESM-1v	0.717	2.438 ± 0.076	0.0004 ± 0.168
ESM-1b	0.718	2.428 ± 0.081	0.004 ± 0.151
ESM-MSA	0.702	2.716 ± 0.111	−0.012 ± 0.268

Benchmark on order/disorder classification

Experimental Z-scores from the sequences in the CheZOD database exhibit traits of a bimodal distribution, as shown in Figure 3. In (39), a mixture of two skew-normal distributions was fitted to the distribution of observed Z-scores with a reasonably high accuracy quantified by a Hellinger distance of 0.00367. This means that the distribution of Z-scores of all sequences in the CheZOD database can be approximated by two distributions that are separated in Z-score. This motivates a binary classification task, where a Z-score below/above 8 is interpreted as disorder/order, respectively. To remain aligned with (39), a 10-fold CV was performed on the cross-validation set. Accuracy was measured using standard metrics: the ROC AUC and the MCC that measure dependence between binary outcomes. Here, a simple logistic regression was used on the representations extracted from the ESM transformers. The ROC AUC/MCC averaged across the 10-folds were as follows: 0.964/0.798 (ESM-1b), 0.964/0.799 (ESM-1v) and 0.947/0.765 (ESM-MSA) (see Table 5). Although these results clearly exceed the values of ROC AUC = 0.914 and MCC = 0.690 ODiNPred reported for the same task in (39), we omit any direct comparison for this task, given that the cross-validation set we used is different from that of ODiNPred. In the aforementioned table, we also present precision scores for disorder for ESM-based predictors. Given that we labelled disordered residues with 0 (i.e. treated as ‘negatives’), precision in this case means the percentage of the correctly predicted disordered residues. Our predictors are able to predict ∼88% of disordered residues. Note that considering a majority-based random classifier, which takes the most frequent class from the training set and uses that as prediction in a test set, in this 10-fold CV the majority class is always ordered (∼70%); accordingly, its prediction on the test fold will be ordered, which amounts to an ROC AUC value of 0.5. This can be compared to an ROC AUC value of 0.94 of the ESM-based predictors.

Table 5.

ROC AUC, MCC and precision for disorder by our ESM transformer-based predictors for order/disorder classification given by the residue-level 10-fold CV on the cross-validation set consisting of 1168 sequences only

	Residue-level 10-fold CV
Disorder predictor	ROC AUC	MCC	Precision
ESM-1v	0.964	0.799	0.880 ± 0.005
ESM-1b	0.964	0.798	0.881 ± 0.007
ESM-MSA	0.947	0.765	0.865 ± 0.007

In order to support these results further, a similar logistic regression was fitted to the filtered base dataset. As described earlier, this dataset contains 1159 sequences. The performance of the ESM transformer-based (here ESM-1b) order/disorder classifier was evaluated on the validation set containing 117 sequences. The results of ROC AUC = 0.895 and MCC = 0.610 obtained on this task can still be considered strong. Our analysis demonstrates that the ESM transformer not only predicts better Z-scores than ODiNPred, but also performs better on a binary classification of ordered and disordered regions, a topic that is very relevant in biology. This result is further reinforced by the lower mass of the ESM transformer in comparison to ODiNPred in the intermediate region with Z-scores around 8 in Figure 3.

Additionally, it is worth mentioning that there are well-known frameworks, e.g. CASP10, for disorder prediction assessment. As described in (39), the datasets in CASP10 were heavily imbalanced and <10% of the residues were disordered. To put this in context, in the overall CheZOD dataset, this percentage was 36.3%. The authors in (39) make two further observations. ODiNPred was not the best-performing predictor in the CASP10 dataset, which may be due to the over-representation of ordered residues. Second, other disorder predictors overall performed much better on the CheZOD dataset.

The scientific community has shown great interest in AlphaFold2. Recent work has demonstrated that the pLDDT (61), a per-residue metric of local confidence of the prediction, is correlated with disorder, outperforming IUPred2 (62), SPOT-Disorder2 (63) and other disorder predictors (64,65). Further work has proved that the SASA per residue of models produced by AlphaFold2 shows better correlation to protein disorder than the pLDDT and that using a smoothing window improves accuracy further (62). To benchmark performance, AlphaFold2 structural models were predicted for the validation set of 117 proteins using the full database. For the rolling averages of pLDDT and of SASA, we observed that the largest correlations (0.5546 and 0.6299) were given by window sizes 5 and 15, respectively, as reported in Table 2. We note that predicting the structure from pre-calculated features derived from the MSAs took ∼40 h on one NVIDIA A100 GPU in total. It is worth highlighting that AlphaFold2 is a template-based predictor; that is, it uses templates as ingredients in making predictions. Hence, it is more nuanced than pure sequence-based methods. Curiously, for disordered proteins finding a suitable template is problematic. Broadly speaking, this may also be the reason why pLDDT correlates reasonably well with disorder; i.e. where AlphaFold2 is less certain about a well-defined structure, there will likely be disorder.

A fast inference tool

From an end user perspective, obtaining accurate disorder predictions quickly and easily is important. In this aspect, ADOPT offers unmatched performance. We demonstrate this through comparisons with two other tools. ODiNPred currently is available through the web service (https://st-protein.chem.au.dk/odinpred). Querying 117 proteins took overnight. We also made an attempt to use SPOT-Disorder2 (https://sparks-lab.org/server/spot-disorder2/), which is considered at least as accurate as ODiNPred. However, a maximum of 10 sequences can be submitted at a time and the output is returned in 12 h in the best case. In contrast, ADOPT, with a single command line, takes a few seconds to produce disorder predictions for 117 sequences and there is no cap on the number of sequences used in inference.

To prove that the ADOPT performance is the best in class not only in terms of disorder prediction but even in terms of inference time, we used the ADOPT to predict the Z-scores of the 20 600 unique protein-coding genes from the reference human proteome (https://www.uniprot.org/proteomes/UP000005640) that encode for 79 038 protein transcript variants. The protein sequences longer than 1024 units were split into two subsequences, due to the ESM context window length constraint mentioned earlier. The whole procedure takes roughly 15 min to be completed on a single NVIDIA DGX A100, which demonstrates that the ADOPT inference phase is three orders of magnitude faster than those of ODiNPred and AlphaFold2. However, this comparison is limited taking advantage of the fact that ADOPT runs as a fast command-line tool, while ODiNPred and SPOT-Disorder2 have been used as a web service. To give a fairer comparison, we repeated the speed benchmark with Metapredict v2 on one CPU core, which reflects the standard usage of an end user of this predictor. Running the human proteome took 15 and 46 min on an Apple M1 chip and on a Colab instance, respectively, and is therefore of comparable speed to ADOPT using a GPU. Note that Metapredict v2 has been generated to reproduce the pre-calculated results of another disorder predictor, Metapredict hybrid, for 363 265 protein sequences from 21 proteomes in order to increase its speed. Performing a similar task, e.g. training a neural network on pre-predicted protein sequences from ADOPT, could be an opportunity to increase the speed of our predictor. Both on a single NVIDIA DGX and on an Apple M1 chip, I/O time represents ∼15% of the inference time and computation time constitutes the remaining ∼85%.

We believe that these aspects—accuracy and ease of use—will not just appeal to a wider audience, but also facilitate disorder-related research projects that were previously not possible due to scale.

DISCUSSION

Remarks on the residue-level representations produced by ESM transformers

There is a set of questions that naturally and frequently arise in the domain of NLP and recently in language models in biological applications: How much information is encoded in these representations? What exactly do they encode? Are bigger representations always better? In general, how do we make sense of them?

To motivate these questions, recall that ODiNPred uses 157 hand-engineered biophysical features as inputs in its prediction model (39). By design, these input features are straightforward to interpret and there is sound rationale as to why they may help predict disorder. In contrast, the input of our ESM-based predictor is much bigger, 1280, which is the size of the representation vectors given by e.g. ESM-1b, and its features are, albeit real numbers, abstract, and they are hard to make sense of in physical terms, e.g. residue interaction entropy or net charge.

Answers to the above questions also depend on the downstream task the representations are used for, e.g. predicting fluorescence, contact maps, disorder, sequence/amino acid level classification, etc. This implies a dependence on the prediction model too. In the case of disorder prediction, we use Lasso regression, which is a linear method (53). It is a continuous feature selection technique that means that varying the shrinkage parameter λ will influence the number of non-zero coefficients. The higher the λ, the greater the L₁ penalty term, and hence, the number of non-zero coefficients decreases. In a fitted model with a given λ, only those features are used that have non-zero coefficients. In other words, these features are the ones that carry significant information. Therefore, Lasso can help us understand which coordinates of the representation vectors are relevant.

Are all the 1280 coordinates, e.g. in the case of ESM-1b, needed? We used two different approaches to address this question. The first one was a naive selection, whereby only those features are considered whose coefficients were above a certain threshold in absolute terms. This analysis showed that e.g. with 141 coordinates a correlation of ρ_Spearman = 0.643 could be achieved, as shown in Figure 5.

A better, yet computationally more demanding approach is stability selection, which uses resampling and in this aspect is similar to bootstrapping (56). Using this more robust technique, we found that choosing only 84 coordinates of the representation vectors and using those to predict Z-scores already showed an acceptable correlation 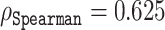on the validation set containing 117 sequences. The predictive power of the representation vectors could be further enhanced by taking additional coordinates, e.g. 114, which yielded a correlation 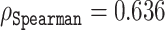, as depicted by the markers on the red line in Figure 6. Interestingly, this method identified 167 coordinates, which gave a correlation of 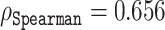, which is markedly better than the subset of the same size selected by the naive approach. In comparison to ODiNPred that relies on 157 biophysical features and achieves a correlation of 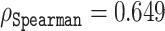(39), already a subset of 114 coordinates of the ESM-1b representations could offer a very similar performance.

This analysis answers, at least partly, the question whether bigger representations are necessarily better. The ESM-MSA-based predictor, which uses smaller sized representations, 768, performs relatively poorly with a correlation 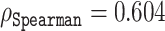(see Table 2), compared to all of the alternatives based on the reduced ESM-1b representations presented earlier. This clearly suggests that, at least regarding disorder prediction, the quality of the representations given by ESM-1b is genuinely better not purely because of the size of the representation. This is because we could select a subset of coordinates from the ESM-1b representations that was much smaller in size than the ESM-MSA representations (768), and yet had better prediction power than ESM-MSA.

Remarks on the current state of protein disorder predictions

Protein disorder prediction is a challenging task. Even with the methodological advancements of ADOPT, Spearman rank correlation coefficients (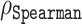) of up to 0.7 demonstrate that there is still a significant room for further improvement. Besides their different architectures, the most performant protein disorder predictors use deep neural networks to predict the disorder of a residue within a sequence. While these tools identify the features important for disorder prediction, they do not necessarily give a direct indication about the connection of these features to the biophysical origin of protein disorder. Here, we compared two state-of-the-art predictors, ODiNPred (39) and our new ESM transformer, and found several similarities in their ability to predict certain biophysical features. For example, we could show that both predictors could accurately separate ordered from disordered residues, whose definition is based on the simple observation that experimental Z-scores follow a bimodal distribution. While such a classification performance is promising, applying the predictors to a more diverse dataset, as e.g. used in CAID (34), is more challenging.

We observed that both predictors predict slightly too ordered Z-scores. Interestingly, this observation is independent of the actual Z-score; e.g. ordered and disordered regions are both predicted, on average, to be too ordered. This indicates that there might be a general feature that contributes to the ‘orderness’ of a residue, which is not completely learned by either of the predictors. Our amino acid analysis reveals that especially the Z-scores of these amino acids, which are known as breakers or stoppers of ordered regions like α helices or β sheets, e.g. glycine and proline, are less accurately predicted than the other amino acids (Figure 4 and Supplementary Figures S2 and S3). This suggests that the prediction of protein disorder might be enhanced if the predictors are trained on well-labelled data of these residues as their occurrence within a protein sequence plays an important role in the formation of ordered regions.

Furthermore, we observe that it is particularly difficult to predict cysteine residues. Long-range contacts formed from disulfide bridges hold proteins together and are therefore of tremendous importance for the formation of the hydrophobic core of folded proteins. This observation is in line with the analysis of the 157 biophysical features from ODiNPred (39). They observed that the most important features for protein disorder prediction are hydrophobic clusters, the predicted secondary structure and the evolutionary relationship. While the last one was used to extract the features in this study, it is interesting to see that the other two biophysical features have been learned implicitly by our ESM transformer, even though it does not use any biophysical features during its training. This shows that the evolutionary information in pre-trained datasets such as UniRef (48) already contains these features and transformers are able to unveil this information.

Finally, negligible differences in terms of key performance metrics described in the reliability study under the ‘Results’ section clearly illustrate the efficacy of ADOPT in terms of reliability and accuracy.

CONCLUSIONS

Understanding and accurately predicting protein disorder have been an area of active research in computational biology for more than two decades. Here, we present a sequence-based approach to predict disorder using ESM transformers. These NLP-based methods applied to vast protein databases, e.g. UniProt90, which at the time of writing of this paper consisted of 135 301 051 sequences (see https://www.uniprot.org/uniref/). These transformers produce amino acid level representations of protein sequences that we use as inputs in our disorder predictors. We show in various tasks (predicting Z-scores, classifying residues in order/disorder classes) that our predictors offer superior performance compared to the previous state-of-the-art disorder predictor (39) and per-residue score correlations to protein disorder of models produced by AlphaFold2 (46). We study the quality of these residue-level representations by analysing which coordinates of the residue-level representations are relevant in terms of predictive power. We highlight two main advantages of our proposed approach. First, it does not require additional feature engineering or selection of potentially relevant biophysical inputs. Second, its inference capabilities are remarkably fast compared to other publicly available tools. This could aid large-scale studies that were previously not possible.

In a broader context, our work complements the most recent developments in NLP-based computational biology [see e.g. (66,67)]. The common theme of such approaches can be summarized in two steps. First, the aim is to find suitable embeddings or representations of protein sequences. The second aspect is to use these in relevant downstream tasks, e.g. contact map prediction, stability prediction, etc. Downstream use cases are typically less data intense, and this approach is expected to work already reasonably well with datasets of size around 10 000 or above. Note that in the CheZOD training set alone, which was used in this paper, there are >140 000 observations, given that disorder is a residue-level property of interest. In contrast, large transformer models ideally require millions of data points to achieve their full potential. Note that the data points used by transformers are not necessarily experimental observations, but they are purely sequences.

There are many directions for future research related to this particular approach; however, we would highlight three of them specifically. Clearly, great potential lies in the exploration of other relevant downstream tasks. Reiterating the point made in (67), a promising way to improve NLP-based techniques, in particular, transformers, in protein science, is to utilize priors, e.g. known protein structures, into these models. This could be a key to enhance the quality of sequence representations. The third area requires novel ideas, but could be invaluable to connect large transformers to molecular dynamics (MD) methods in order to improve simulations and the quality of computed biophysical features. Atomic MD simulations could be used to sample the heterogeneous ensemble of structures in intrinsically disordered regions. The distribution of NMR chemical shifts in these ensembles is directly related to the Z-score and can be used to improve the data used to train transformers, while transformers can be used to improve MD force fields.

DATA AVAILABILITY

The data underlying this article are available in Zenodo at https://doi.org/10.5281/zenodo.7822077.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

No external funding.

Conflict of interest statement. All authors are employees of and shareholders in Peptone Ltd.