Abstract
Rapid accumulation of temporal Electronic Health Record (EHR) data and recent advances in deep learning have shown high potential in precisely and timely predicting patients’ risks using AI. However, most existing risk prediction approaches ignore the complex asynchronous and irregular problems in real-world EHR data. This paper proposes a novel approach called Knowledge-guIded Time-aware LSTM (KIT-LSTM) for continuous mortality predictions using EHR. KIT-LSTM extends LSTM with two time-aware gates and a knowledge-aware gate to better model EHR and interprets results. Experiments on real-world data for patients with acute kidney injury with dialysis (AKI-D) demonstrate that KIT-LSTM performs better than the state-of-the-art methods for predicting patients’ risk trajectories and model interpretation. KIT-LSTM can better support timely decision-making for clinicians.
Keywords: Machine learning, Deep Learning, Electronic Health Record, Acute Kidney Injury, Continuous Prediction
I. Introduction
Clinical risk prediction using Electronic Health Record (EHR) data provides accurate and timely individualized patient outcomes, allowing early interventions for high-risk patients and better-allocating hospital resources [1], [2]. It is particularly critical to predicting risks for patients with Acute Kidney Injury requiring Dialysis (AKI-D), a severe complication associated with a very high mortality rate for critically ill patients [3], [4].
Artificial intelligence (AI), esp. deep learning (DL) models, have drawn increasing attention to patients’ outcome predictions using temporal EHR data [5], [6]. However, due to complicated data collection procedures and strict data management, EHR data are not generally AI-ready, which hinders the adaption of AI tools directly in the clinical settings [7]-[9].
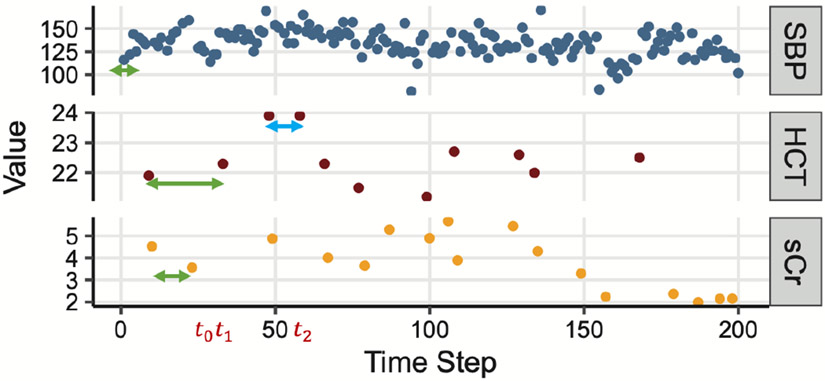
Firstly, EHR data are collected daily in hospitals for efficient patient care delivery but are usually not in ideal shape for ML/DL models [5], with temporal irregularity and asynchrony being the most common problems encountered when building ML/DL applications in clinical settings [10], [11]. Irregularity refers to the uneven time gaps between measurements of a single feature. Asynchrony refers to the unaligned measurements across multiple features. Fig. 1 shows an example of EHR data with three clinical variables (SBP, HCT, and sCr) collected in the ICU. The green and blue lines in HCT show irregular time gaps between the measurements of a single clinical parameter, while the three green lines in SBP, HCT, and sCr show unaligned observations across the three clinical variables with different measurements frequency.
Fig. 1.
An example of real-world EHR data in the ICU. “SBP” stands for systolic blood pressure, “HCT” for Hematocrit, and “sCr” for serum creatinine. Arrows highlight irregular and asynchronous gaps between measurements.
Early DL methods ignore the irregularity and asynchrony problem. For example, the standard LSTM [12] assumes equal temporal gaps between time steps, and the original Transformer [13] uses absolute positions encoding. Recent LSTM variants have been focused on addressing the irregularity problem. T-LSTM [14] considered time elapse between patients’ visits. Phased-LSTM [15] introduced a time gate in the LSTM cell to update cell states and hidden states only if the time gate is open. Nevertheless, most of the existing LSTM models still ignore the asynchrony problem, as illustrated in Fig. 1. With recurrent neural networks (RNN), the irregularity and asynchrony problems have been addressed using missingness patterns and time elapsed between measurements. The GRU-D model updates GRU cells using missing patterns and decayed input/hidden state according to the elapsed time [16]. The BRITS model estimates missing values by introducing a complement input variable in the RNN unit when the variable is missing and also uses the hidden time decayed state of the RNN unit [17]. However, the missingness patterns are not always informative and are challenging to interpret.
Secondly, the accountability of DL models in terms of model interpretation in healthcare practice is critical for clinicians to make decisions based on the model results and rationale [18]. Model-agnostic methods, such as LIME [19] and SHAP [20], support the interpretation of any ML/DL method in a post-hoc fashion. Nevertheless, using these methods needs an extra and separate step to training the actual ML/DL models. Self-interpretable DL models such as RETAIN [21] use two-level attention scores for model interpretation, but cannot address the irregularity and asynchrony problem in EHR. ATTAIN [22] builds time-wise attention based on all/some previous cell states of LSTM plus a time-aware decay function for resolving the irregular time gaps issues. The trade-off between interpretability and prediction power invokes the development of self-interpretable ML/DL models without sacrificing prediction power, promoting a better adoption in routine uses in practical healthcare settings [23].
Another model interpretation approach uses domain-specific knowledge encoded in medical or biological ontologies databases as prior knowledge [24]. A knowledge-driven ML model that utilizes ontologies databases may gain better interpretation and potentially higher prediction power [5], [25]. Recent studies [26]-[28] have incorporated medical knowledge graphs into medical applications using translation-based graph embeddings methods [29], [30]. Moreover, medical knowledge-graph-based attention models such as GRAM [25], DG-RNN [31], and KGDAL [32] have demonstrated comparable performance as well as the power of result interpretation. Nevertheless, these methods do not embed knowledge for numerical features or lack a mechanism for handling irregular and asynchronous EHR data.
In this article, we present a Knowledge guIded Time-aware LSTM model (KIT-LSTM), which handles irregular and asynchronous time series EHR data, and uses medical ontology to guide the attention between multiple numerical clinical variables, and provides knowledge-based model interpretation.
KIT-LSTM extends LSTM with two time-aware gates and a knowledge-aware gate. The time-aware gates adjust the memory content according to two types of elapsed time, i.e., the elapsed time since the last visit for all variable streams and the elapsed time since the last measured values for each variable stream. The knowledge-aware gate uses medical ontology to guide attention between multiple numerical variables at each time step. To the best of our knowledge, KIT-LSTM is the first LSTM variant that incorporates medical ontology with the addition of two time-aware gates to guide the attention mechanism inside the LSTM cell. As a result, the proposed model provides better guidance for attention and interpretation and handles both irregular and asynchronous problems simultaneously. Our contributions are summarized as follows:
1) KIT-LSTM adds to the original LSTM cell two unique time-aware gates. The time-ware gates adjust different proportions of the LSTM cell memory contents, which address irregularity and asynchrony.
2) KIT-LSTM adds to the original LSTM cell a knowledge-aware gate. It uses the relationship between concepts learned from medical ontology to guide attention between multiple variables at each time step, and the loss function enforces the learned attention aligned with the medical ontology, enabling knowledge-based model interpretation.
3) Using EHR data, KIT-LSTM continuously and accurately predicts mortality risks in the next 24 hours for critically ill AKI-D patients in the ICU.
4) KIT-LSTM shows high robustness in subpopulation distribution shift.
II. Method
A. Notations
EHR features:
A patient’s EHR data at time step can be represented as a vector of clinical parameters (e.g., heart rate) denoted as , where is the number of features.
Time-related features:
denotes the time elapsed since the last time step, and RNf denotes the time elapsed since the last measured value of the same feature. The value of for each feature can be different since features are possibly measured at different frequencies.
Knowledge-related features
KIT-LSTM uses Human Phenotype Ontology (HPO) [33] as the prior knowledge to guide the model learning process. We extract ontology concepts related to the selected clinical features and call them feature concepts (e.g., “elevated systolic blood pressure” (HP:0004421) is a concept related to systolic blood pressure in HPO). In addition, we extract a concept related to the study population, i.e., “acute kidney injury” (HP:0001919), which is called the target concept. The total number of ontology concepts is , where is the number of feature concepts. Note that is not the same as the number of features because some features can be mapped to more than one related ontology concept, and some can only be mapped to one. All concepts are encoded as one-hot vectors as the initial embeddings denoted as .
Based on the feature values and the ontology concepts at time step , we extract the physiological status denoted as . The value of for each concept is either 0 or 1. For example, for concept “high systolic blood pressure” means patient systolic blood pressure is greater than 130. Thresholds of all features are defined based on clinical practice and are validated by clinicians.
B. KIT-LSTM Cell
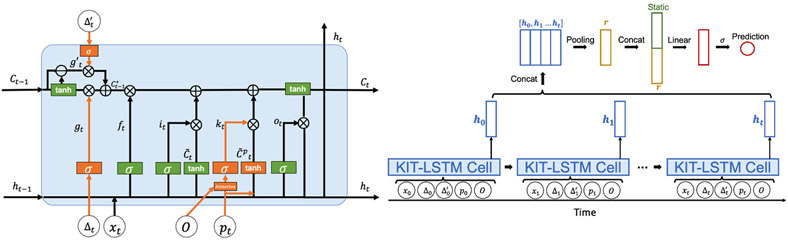
The architecture of KIT-cell is illustrated in Fig. 2. The input to a KIT-LSTM cell consists of five components: clinical feature , elapsed time since last time step, elapsed time since the last measured values, physiological status , and initial concept embedding .
Fig. 2.
The architecture of KIT-LSTM cell (left), orange represents the unique gates in KIT-LSTM, and green represents the original gates in LSTM. The prediction layers (right) combine all the hidden states learned from KIT-LSTM and the static features, such as patient demographics, for the final prediction.
KIT-LSTM kept the original three gates (forget, input, output) from LSTM and added three additional gates (two time-aware gates and one knowledge-aware gate).
The first time gate, the long-term time-aware gate, is a time decay function that adjusts long-term memory by using the elapsed time since the last measured value of the same clinical parameter. For example, the green and blue arrows in Fig. 1 for the “HCT” indicate that the previous memory will be more likely to be discounted when the green arrow ends than the time when the blue arrow ends .
The second time gate, the short-term time-aware gate, is a time decay function to adjust short-term memory. It is measures the elapsed time since the last time step (e.g, in Fig. 1), similar to the time decay function in T-LSTM [14].
The long and short time-aware gates control how the previous short or long-term memories can be passed into the current memory. Intuitively, the longer the elapsed times, the less likely the long or short-term memory gate will open.
The knowledge-aware gate uses concepts embeddings and physiological features to control which feature should be paid more attention to at each time step. Intuitively, if the physiological status is abnormal and there is a strong relationship between a feature concept and the target concept, more attention will be paid to the corresponding feature.
Gate update:
We denoted the forget gate as , the input gate as , the output gate as , the time-aware gates as and , and the knowledge-aware gate as , where , , , , , , is the dimension of the hidden vectors, and is the time step. The short-term time-aware gate is updated by the elapsed time since the last time step, and the long-term time-aware gate is updated by the elapsed time since last measured value for each feature. The knowledge-aware gate is updated by the attention scores learned from the concept embeddings as well as physiological status . Gates at time step are:1
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where , , , , , , , , and , , , , are the learnable parameters. is a sigmoid function.
The attention score for each physiological feature at time is computed using:
| (7) |
| (8) |
| (9) |
where and are the learnable parameters; and is the learned concepts embedding from initial embeddings using a linear function. includes both the feature concepts embeddings and the target concept embedding denoted as . Note that is not shown in above equation, but will be used in loss regularization described in Section II-C.
The attention score can be used to interpret the prediction behavior of KIT-LSTM. For detailed interpretation steps and results, please refer to our GitHub link at the end of this section.
Memory cell update:
Following the definition in T-LSTM [14], we extracted the short and long-term memory from the previous memory cell , denoted as and respectively. Then, the short- and long-term memory are adjusted separately by their corresponding time-aware gates and . In particular, the short-term memory is discounted by the elapsed time since last time step, and the long-term memory is discounted by the elapsed time since last measured values. We denote the discounted short-term and long-term memory cell as and respectively. Finally, the total adjusted previous memory cell denoted as is the sum of all the discounted short- and long-term memories. Memory cells are computed as:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where , are the learnable parameters, and is the Hadamard product.
Candidates memory cells:
While the original feature candidate cell, denoted as , computed from the feature value and the previous hidden state , a new candidate cell is added, denoted as , which also considers the physiological status . Candidate memory cells can be computed using:
| (15) |
| (16) |
where , , , , , and , , are the learnable parameters.
Current memory cell and hidden state:
and represent the current memory cell and its corresponding hidden state. is a combination of adjusted previous memory multiplied by the forget gate, the feature candidate memory multiplied by the input gate, and the physiological candidates memory multiplied by the knowledge-aware gate. The current cell and hidden state are computed using:
| (17) |
| (18) |
C. Patient Outcome Prediction
Prediction layer:
All the hidden states are concatenated and passed into a pooling layer for taking the sum/max along time steps. The resulting hidden representation is denoted as . Then the static features (e.g, demographics) are concatenated with followed by a fully connected layer with a sigmoid function for the binary prediction. The process of final prediction is shown in Fig. 2.
Loss function:
Let the ground truth label be and the predicted label be , we use the binary cross entropy as the part of the final prediction loss denoted as . We add a regularization term to ensure the relationship between the learned feature concept embeddings and the target concept embedding aligns to the observed relations in a medical ontology. Thus, the regularization term counts the discrepancy at the knowledge level, i.e. the difference between the learned concept embedding distance and the corresponding concept distance in a medical ontology. The regularization term , cross entropy loss , and final prediction loss are:
| (19) |
| (20) |
| (21) |
| (22) |
where is the total number of samples. represents the learned distance between feature concept embedding and the target embedding ; similarly represents the observed distance between feature concepts and the target concept in medical ontology. The observed distance can be obtained directly from the ontology graph by computing node-based distances or it can be obtained from the pre-trained initial embedding using graph embedding methods [29]. For detailed implementation of computing the knowledge-related embeddings and distances, please refer to our previous work KGDAL [32].
The source code of KIT-LSTM is available at https://github.com/lucasliu0928/KITLSTM. The information about hyperparameter tuning can be found in the link.
III. Experiment Settings
The experiment aims to continuously predict AKI-D patients’ mortality risk in their dialysis/renal replacement therapy (RRT) duration. More specifically, given any period of EHR in dialysis duration before time , we will continuously predict the mortality risk at , i.e., 24 hours after .
A. Experiment Data
Patient cohort:
The study population consists of 570 AKI-D adult patients admitted to ICU at the University of Kentucky Albert B. Chandler Hospital from January 2009 to October 2019. Among them, 237 (41.6%) died in hospital, and 333 (58.4%) survived. Patients were excluded if they were diagnosed with end-stage kidney disease (ESKD) before or at the time of hospital admission, were recipients of a kidney transplant, or had RRT less than 72 or greater than 2,000 hours.
EHR data:
Data features include twelve temporal features (systolic blood pressure, diastolic blood pressure, serum creatinine, bicarbonate, hematocrit, potassium, bilirubin, sodium, temperature, white blood cells (WBC) count, heart rate, and respiratory rate) and six static features (age, race, gender, admission weight, body mass index (BMI), and Charlson comorbidity score). All outliers greater than 97.5 or lower than 2.5 percentile were excluded. Measurement frequencies vary dramatically, ranging from 0.2 to 21.7 observations per day.
Sample generation:
To continuously predict patient’s mortality risks, we generate 30 samples from each patient’s EHR data with a random start and end time as long as the length of the sample is greater than 10 time steps where a time step refers to the time when any feature has a value. The class label of a sample is whether the patient died (positive) or survived (negative) in the next 24 hours from the end of the sample.
Training, validation and testing data:
From 570 AKI-D patients, 13,333 EHR samples were extracted, including 1,456 positives and 11,877 negatives. As shown in Table I, the data were split into training (75%), validation (5%), and testing data (20%) patient-wise to ensure that the samples from the same patients only appeared in one of the three datasets.
TABLE I.
Training, Validation and Testing Data.
| Total N Samples (Patient) |
Alive N Samples (Patient) |
Death in the next 24 hours N Samples (Patient) |
Negative to Positive Ratio (Patient) |
|
|---|---|---|---|---|
| Train (75% of patients) | 9979 (432) | 8843 (424) | 1136 (125) | 8:1 (3:1) |
| Validation (5% of patients) | 642 (24) | 586 (24) | 56 (6) | 10:1 (6:1) |
| Test (20 % of patients) | 2712 (114) | 2448 (113) | 264 (25) | 9 :1 (5:1) |
B. Baseline Algorithms
We compared KIT-LSTM with eight existing algorithms, including two traditional ML algorithms (XGBoost and SVM) and six DL models (LSTM, T-LSTM, Phased-LSTM, RETAIN, ATTAIN, and Transformer). For all DL models, static features are concatenated with the hidden states before the prediction layer, as described in Section II-C. Moreover, all missing temporal features are imputed with the last observation carried forward (LOCF) method.
C. Model Robustness Evaluation Metric
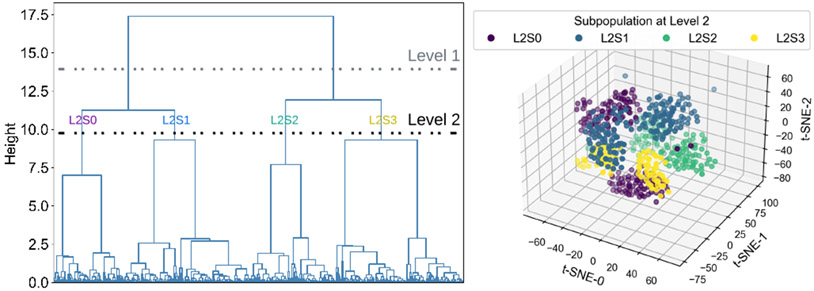
Robustness is one of the most important performance metrics for clinical applications, which can be assessed using the subpopulation distribution shift approach [34], [35]. First, patient subpopulations were identified using demographics and comorbidity in EHR. Second, subpopulations at different levels of granularity were obtained using hierarchical clustering and applying thresholds at the dendrogram. Third, the clustering dendrogram and the corresponding t-SNE plot of subpopulations were visualized to identify distinct subpopulations. Fig. 3 shows four subpopulations at the second level (green) of dendrogram have distinctly different distributions.
Fig. 3.
Identified subpopulation using hierarchical clustering. In the clustering dendrogram (left), the horizontal lines show two different subpopulations levels. The four resulting subpopulations at level two (right) are shown on a three-dimensional t-SNE space. ‘L_X S_Y’ represents the subpopulation Y at level X.
IV. Results and Discussion
The following section briefly discusses the performance comparison between all methods and the ablation study. Please refer to our GitHub link for more details.
A. Performance Comparison to Baselines
Table II shows the overall performance on both balanced and imbalanced test data (pos: neg ratio being 1:1 and 1:9) of our proposed model KIT-LSTM compared with other baseline models. The scores are shown in average and standard deviation across pre-defined subpopulations. KIT-LSTM has the best overall performance with the highest ROCAUC, F-3, and recall on both test data. The DL method Transformer has the highest precision on the balanced test data and the same highest ROCAUC on the imbalanced test data, but the scores on other metrics are at the lower end. The traditional ML method XGBoost has the highest precision on imbalanced test data, but the scores on all other metrics are the lowest.
TABLE II.
Overall Performance of KIT-LSTM and seven compared algorithms on balanced and imbalance test data.
| Balanced Test (Pos:Neg = 1:1) | Imbalanced Test (Pos:Neg = 1:9) | |||||||
|---|---|---|---|---|---|---|---|---|
| ROCAUC | F-3 | Recall | Precision | ROCAUC | F-3 | Recall | Precision | |
| XGBoost | 0.55(0.05) | 0.11(0.11) | 0.10(0.10) | 0.66(0.46) | 0.55(0.05) | 0.11(0.11) | 0.10(0.10) | 0.47(0.36) |
| SVM | 0.65(0.06) | 0.58(0.09) | 0.58(0.10) | 0.62(0.11) | 0.69(0.06) | 0.47(0.07) | 0.58(0.10) | 0.19(0.08) |
| LSTM | 0.70(0.14) | 0.52(0.24) | 0.51(0.25) | 0.74(0.11) | 0.71(0.14) | 0.46(0.22) | 0.51(0.25) | 0.29(0.14) |
| Transformer | 0.74(0.12) | 0.34(0.26) | 0.33(0.27) | 0.81(0.08) | 0.75(0.11) | 0.32(0.26) | 0.33(0.27) | 0.37(0.18) |
| T-LSTM | 0.74(0.12) | 0.52(0.24) | 0.50(0.25) | 0.73(0.10) | 0.74(0.11) | 0.44(0.22) | 0.50(0.25) | 0.24(0.14) |
| Phased-LSTM | 0.69(0.17) | 0.51(0.24) | 0.50(0.25) | 0.74(0.12) | 0.70(0.16) | 0.45(0.21) | 0.50(0.25) | 0.29(0.10) |
| RETAIN | 0.72(0.12) | 0.48(0.23) | 0.47(0.24) | 0.76(0.08) | 0.71(0.12) | 0.43(0.21) | 0.47(0.24) | 0.25(0.08) |
| ATTAIN | 0.66(0.12) | 0.37(0.28) | 0.36(0.28) | 0.65(0.14) | 0.64(0.14) | 0.31(0.24) | 0.36(0.28) | 0.18(0.10) |
| KIT-LSTM (Ours) | 0.75(0.10) | 0.62(0.20) | 0.62(0.21) | 0.70(0.10) | 0.75(0.10) | 0.51(0.17) | 0.62(0.21) | 0.23(0.11) |
To further assess model robustness using subpopulation shift, we measured performance variability across clustered subpopulations at different levels of granularity. Results show that KIT-LSTM outperforms all the compared methods on almost all tested subpopulations at every level of granularity.
B. Ablation Study
We conducted an ablation study to test how each component of KIT-LSTM performed by removing several components of KIT-LSTM. The results show that the version without any time-aware gates or knowledge-aware gates has the lowest performance, whereas models that maintained time-aware gates had better performance. The results also indicate that the physiological status itself is inadequate for enhancing model prediction power. KIT-LSTM, with all components, has the best performance for all subpopulations, indicating that the two time-aware gates and the knowledge-aware gate substantially improve the prediction power.
V. Conclusion
In this work, we presented KIT-LSTM, a new LSTM variant that uses two time-aware gates to address irregular and asynchronous problems in multi-variable temporal EHR data. In addition, KIT-LSTM uses a knowledge-aware gate to infuse medical knowledge for better prediction and interpretations. Experiments on real-world healthcare data demonstrated that KIT-LSTM outperforms the state-of-art ML methods on continuous mortality risk prediction for critically ill AKI-D patients. In the future, we will further investigate the separate contribution of the individual time-ware gate, the model fairness problem, and approaches to incorporate biomedical knowledge better.
Acknowledgments
This work is supported by NIDDK R56 DK126930 (PI JAN) and P30 DK079337.
Footnotes
is repeated for every hidden dimension, thus
References
- [1].Cheng Y, Wang F, Zhang P, and Hu J, “Risk prediction with electronic health records: A deep learning approach,” in Proceedings of the 2016 SIAM International Conference on Data Mining. SIAM, 2016, pp. 432–440. [Google Scholar]
- [2].Shawwa K, Ghosh E, Lanius S, Schwager E, Eshelman L, and Kashani KB, “Predicting acute kidney injury in critically ill patients using comorbid conditions utilizing machine learning,” Clinical Kidney Journal, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Malhotra R, Kashani KB, Macedo E, Kim J, Bouchard J, Wynn S, Li G, Ohno-Machado L, and Mehta R, “A risk prediction score for acute kidney injury in the intensive care unit,” Nephrology Dialysis Transplantation, vol. 32, no. 5, pp. 814–822, 2017. [DOI] [PubMed] [Google Scholar]
- [4].Kang M, Kim J, Kim D, Oh K, Joo K, Kim Y, and Han SS, “Machine learning algorithm to predict mortality in patients undergoing continuous renal replacement therapy,” Critical Care, vol. 24, no. 1, pp. 1–9, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Rose S, “Machine learning for prediction in electronic health data,” JAMA network open, vol. 1, no. 4, pp. e181 404–e181 404, 2018. [DOI] [PubMed] [Google Scholar]
- [6].Solares J, Raimondi F, Zhu Y, Rahimian F, Canoy D, Tran J, Gomes A, Payberah A, Zottoli M, Nazarzadeh M et al. , “Deep learning for electronic health records: A comparative review of multiple deep neural architectures,” Journal of biomedical informatics, vol. 101, p. 103337, 2020. [DOI] [PubMed] [Google Scholar]
- [7].Yu K-H, Beam AL, and Kohane IS, “Artificial intelligence in healthcare,” Nature biomedical engineering, vol. 2, no. 10, pp. 719–731, 2018. [DOI] [PubMed] [Google Scholar]
- [8].Kim H-S, Kim D-J, and Yoon K-H, “Medical big data is not yet available: why we need realism rather than exaggeration,” Endocrinology and Metabolism, vol. 34, no. 4, pp. 349–354, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Noorbakhsh-Sabet N, Zand R, Zhang Y, and Abedi V, “Artificial intelligence transforms the future of health care,” The American journal of medicine, vol. 132, no. 7, pp. 795–801, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Yadav P, Steinbach M, Kumar V, and Simon G, “Mining electronic health records (ehrs) a survey,” ACM Computing Surveys (CSUR), vol. 50, no. 6, pp. 1–40, 2018. [Google Scholar]
- [11].Wu S, Liu S, Sohn S, Moon S, Wi C, Juhn Y, and Liu H, “Modeling asynchronous event sequences with rnns,” Journal of biomedical informatics, vol. 83, pp. 167–177, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hochreiter S and Schmidhuber J, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997. [DOI] [PubMed] [Google Scholar]
- [13].Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A, Kaiser Ł, and Polosukhin I, “Attention is all you need,” in Advances in neural information processing systems, 2017, pp. 5998–6008. [Google Scholar]
- [14].Baytas I, Xiao C, Zhang X, Wang F, Jain A, and Zhou J, “Patient subtyping via time-aware lstm networks,” in Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, 2017, pp. 65–74. [Google Scholar]
- [15].Neil D, Pfeiffer M, and Liu S-C, “Phased lstm: Accelerating recurrent network training for long or event-based sequences,” arXiv preprint arXiv:1610.09513, 2016. [Google Scholar]
- [16].Che Z, Purushotham S, Cho K, Sontag D, and Liu Y, “Recurrent neural networks for multivariate time series with missing values,” Scientific reports, vol. 8, no. 1, pp. 1–12, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Cao W, Wang D, Li J, Zhou H, Li L, and Li Y, “Brits: Bidirectional recurrent imputation for time series,” Advances in neural information processing systems, vol. 31, 2018. [Google Scholar]
- [18].Ahmad MA, Eckert C, and Teredesai A, “Interpretable machine learning in healthcare,” in Proceedings of the 2018 ACM international conference on bioinformatics, computational biology, and health informatics, 2018, pp. 559–560. [Google Scholar]
- [19].Ribeiro MT, Singh S, and Guestrin C, “” why should i trust you?” explaining the predictions of any classifier,” in Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 2016, pp. 1135–1144. [Google Scholar]
- [20].Lundberg SM and Lee S-I, “A unified approach to interpreting model predictions,” in Advances in Neural Information Processing Systems 30, Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, and Garnett R, Eds. Curran Associates, Inc., 2017, pp. 4765–4774. [Google Scholar]
- [21].Choi E, Bahadori MT, Kulas JA, Schuetz A, Stewart W, and Sun J, “Retain: An interpretable predictive model for healthcare using reverse time attention mechanism,” arXiv preprint arXiv:1608.05745, 2016. [Google Scholar]
- [22].Zhang Y, “Attain: Attention-based time-aware lstm networks for disease progression modeling.” in In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI-2019), pp. 4369–4375, Macao, China., 2019. [Google Scholar]
- [23].Vellido A, “The importance of interpretability and visualization in machine learning for applications in medicine and health care,” Neural computing and applications, vol. 32, no. 24, pp. 18 069–18 083, 2020. [Google Scholar]
- [24].Kulmanov M, Smaili FZ, Gao X, and Hoehndorf R, “Machine learning with biomedical ontologies,” biorxiv, 2020. [Google Scholar]
- [25].Choi E, Bahadori MT, Song L, Stewart W, and Sun J, “Gram: graph-based attention model for healthcare representation learning,” in Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, 2017, pp. 787–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Lin Z, Yang D, and Yin X, “Patient similarity via joint embeddings of medical knowledge graph and medical entity descriptions,” IEEE Access, vol. 8, pp. 156 663–156 676, 2020. [Google Scholar]
- [27].Srinivas Bharadhwaj V, Ali M, Birkenbihl C, Mubeen S, Lehmann J, Hofmann-Apitius M, Tapley Hoyt C, and Domingo-Fernández D, “Clep: A hybrid data-and knowledge-driven framework for generating patient representations,” Bioinformatics, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Gong F, Wang M, Wang H, Wang S, and Liu M, “Smr: Medical knowledge graph embedding for safe medicine recommendation,” Big Data Research, vol. 23, p. 100174, 2021. [Google Scholar]
- [29].Bordes A, Usunier N, Garcia-Duran A, Weston J, and Yakhnenko O, “Translating embeddings for modeling multi-relational data,” in Neural Information Processing Systems (NIPS), 2013, pp. 1–9. [Google Scholar]
- [30].Lin Y, Liu Z, Sun M, Liu Y, and Zhu X, “Learning entity and relation embeddings for knowledge graph completion,” in Twenty-ninth AAAI conference on artificial intelligence, 2015. [Google Scholar]
- [31].Yin C, Zhao R, Qian B, Lv X, and Zhang P, “Domain knowledge guided deep learning with electronic health records,” in 2019 IEEE International Conference on Data Mining (ICDM). IEEE, 2019, pp. 738–747. [Google Scholar]
- [32].Liu L, Ortiz-Soriano V, Neyra J, and Chen J, “Kgdal: knowledge graph guided double attention lstm for rolling mortality prediction for aki-d patients,” in Proceedings of the 12th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics, 2021, pp. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Köhler S, Gargano M, Matentzoglu N, Carmody L, Lewis-Smith D, Vasilevsky N, Danis D, Balagura G, Baynam G, Brower A et al. , “The human phenotype ontology in 2021,” Nucleic acids research, vol. 49, no. D1, pp. D1207–D1217, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Santurkar S, Tsipras D, and Madry A, “Breeds: Benchmarks for subpopulation shift,” arXiv preprint arXiv:2008.04859, 2020. [Google Scholar]
- [35].Chaudhary K, Vaid A, Duffy Á, Paranjpe I, Jaladanki S, Paranjpe M, Johnson K, Gokhale A, Pattharanitima P, Chauhan K et al. , “Utilization of deep learning for subphenotype identification in sepsis-associated acute kidney injury,” Clinical Journal of the American Society of Nephrology, vol. 15, no. 11, pp. 1557–1565, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]