Significance
In the quest for collective phases of matter that can lead to novel quantum properties, a long-sought example is the excitonic insulator—an exotic state where excitons spontaneously form in thermodynamic equilibrium and undergo Bose–Einstein condensation. In the past decades, Ta2NiSe5 has been identified as the most promising candidate to host this electronically driven phase at a critical temperature of 328 K, which makes it ideal for the coherent control of an exciton condensate in ambient conditions. Here, we use nonequilibrium spectroscopy tools and first-principles calculations to show that the spontaneous symmetry breaking in Ta2NiSe5 has a predominantly structural rather than electronic character. Our results establish a protocol to clarify elusive phase transitions in solids with intricate electron–phonon couplings.
Keywords: excitonic insulator, structural phase transitions, time- and angle-resolved photoemission spectroscopy
Abstract
The excitonic insulator is an electronically driven phase of matter that emerges upon the spontaneous formation and Bose condensation of excitons. Detecting this exotic order in candidate materials is a subject of paramount importance, as the size of the excitonic gap in the band structure establishes the potential of this collective state for superfluid energy transport. However, the identification of this phase in real solids is hindered by the coexistence of a structural order parameter with the same symmetry as the excitonic order. Only a few materials are currently believed to host a dominant excitonic phase, Ta2NiSe5 being the most promising. Here, we test this scenario by using an ultrashort laser pulse to quench the broken-symmetry phase of this transition metal chalcogenide. Tracking the dynamics of the material’s electronic and crystal structure after light excitation reveals spectroscopic fingerprints that are compatible only with a primary order parameter of phononic nature. We rationalize our findings through state-of-the-art calculations, confirming that the structural order accounts for most of the gap opening. Our results suggest that the spontaneous symmetry breaking in Ta2NiSe5 is mostly of structural character, hampering the possibility to realize quasi-dissipationless energy transport.
The excitonic insulator (EI) is an elusive state of matter predicted theoretically in 1965 (1–3) and proposed to exhibit many unusual properties, such as superfluid energy transport (4), electronic ferroelectricity (5), and superradiant emission (6). In several ways the EI is analogous to a superconductor, both being many-body phenomena beyond the scope of noninteracting electron theory and both involving the spontaneous emergence of a condensate. In the EI, the condensate is formed by excitons, bound states of electron–hole pairs (7, 8). While this exotic instability is electronically driven in nature (i.e., triggered by the Coulomb interaction), it is in general accompanied by a structural phase transition with the same symmetry (9). As a result, the system develops two linearly coupled order parameters that have no symmetry distinction, and the question of whether the transition is excitonic or structural in nature is quantitative rather than qualitative, involving a comparison of energy scales. In particular, a phase can be classified as predominantly excitonic on the basis of two theoretically defined criteria (Appendix A): i) the instability occurs in the electronic subsystem alone, at fixed ionic positions (1, 2), and ii) the symmetry breaking leads to the emergence of a pseudo-Goldstone collective mode (phason) with much smaller energy than the Higgs-like mode (10). From these considerations, it follows that assessing the size of the excitonic and structural contributions to the instability is crucial to establishing the energetics of the EI state and its putative phase mode. Indeed, if the symmetry breaking had mostly structural character, the phason would be pinned at the high energy scale of the structural gap, hindering any possibility of realizing dissipationless transport and excitonic superfluidity even upon application of tailored external stimuli.
There are only few EI candidates, of which Ta2NiSe5 is one of the most extensively studied. Above a critical temperature TC = 328 K, this material crystallizes in a layered orthorhombic unit cell that consists of parallel Ta and Ni chains (Fig. 1A). At TC, a second-order phase transition lowers the crystalline symmetry to monoclinic, and the material simultaneously undergoes a semimetal-to-semiconductor transition (11, 12). Of note is the breaking of mirror symmetry (10, 13) and the development of spontaneous strain below TC (13, 14). In the semiconducting phase, a gap opens in the electronic structure (11, 15), and the valence band (VB) top acquires an M-like flat shape around the Γ point of the Brillouin zone (as schematically represented in Fig. 1B) (12, 16). Since this band flattening is expected from the Bogoliubov transformation for an electron–hole pair, it has been quoted as evidence for an electronic origin of the phase transition in Ta2NiSe5. In this scenario, the changes in the lattice degrees of freedom accompanying the electronic structure reconstruction are interpreted in terms of linear coupling of the lattice to the putative EI order parameter (10, 17). Nevertheless, the opening of the hybridization gap and the M-shaped dispersion could also follow from a fundamentally distinct effect: the lowering of the crystal symmetry alone (12, 18). Under this circumstance, the primary order parameter would be structural in nature, with relevant consequences on the energy of the phason and the fate of the EI.
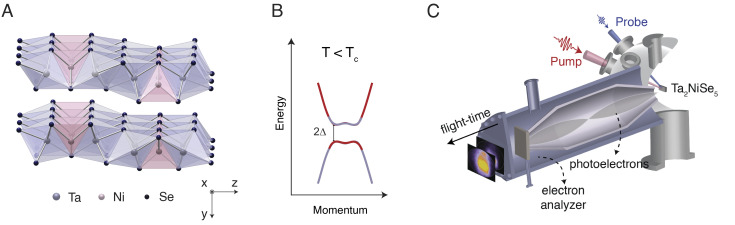
Fig. 1.
(A) High-temperature orthorhombic crystal structure of Ta2NiSe5 showing the layered nature of the system along the y axis and the quasi-one dimensional Ta- and Ni chains running along the x axis. The TaSe6 octahedra and NiSe4 tetrahedra are represented in light blue and pink, respectively. (B) Schematic band diagram for gap formation in a candidate EI. The concomitant action of interband Coulomb interaction and the lowering of the crystal symmetry lead to band hybridization and result in the opening of an excitation gap 2Δ for T < TC. (C) Schematic of the trARPES experiment. An ultrashort near-infrared pump pulse illuminates the sample and a delayed ultraviolet probe pulse photoejects electrons at different energies and momenta. The photoelectrons are finally detected in a time-of-flight analyzer.
Such an underlying complexity in Ta2NiSe5 so far has posed significant challenges to disentangling different contributions to gap formation in experiments performed under equilibrium conditions. Advanced nonequilibrium schemes can in principle separate the time dependence of the electronic and structural components of the instability and determine their relative importance to gap formation (19–22). In particular, time- and angle-resolved photoemission spectroscopy (trARPES) has emerged as a powerful technique for mapping the temporal evolution of electronic bandgaps in response to the laser-induced quench of broken-symmetry phases. However, to draw conclusions on the underlying symmetry breaking in Ta2NiSe5, trARPES must operate in a parameter space (e.g., sample temperature, pump fluence, and repetition rate) that keeps the electronic and lattice temperatures well separated (23–25); in addition, as the bandgap of Ta2NiSe5 is predicted to be weakly indirect in the kx-kz plane, a systematic study of both valence and conduction bands over a wide portion of the two-dimensional (2D) Brillouin zone is required. All these conditions have not been met by previous trARPES studies (SI Appendix, section S4 for a detailed comparison with our results) (23–29), thus calling for the design of tailored experiments.
Here, we present a joint experimental–theoretical study aimed at uncovering the nature of the phase transition in Ta2NiSe5. Experimentally, we investigate the quench dynamics driven by an ultrashort laser pulse when the material is kept deep in the low-temperature broken-symmetry phase. By using two distinct trARPES setups operating at 30 to 100-kHz repetition rate, we observe that intense photoexcitation is not sufficient to induce bandgap collapse in the 2D kx-kz plane, even though the electronic temperature largely exceeds TC and the depletion of the electronic states near the VB maximum is strong; moreover, we reveal that the dominant response proceeds over a phononic rather than electronic timescale. Advanced first-principles calculations performed in the realistic low-temperature unit cell clarify that the leading contribution to gap opening in Ta2NiSe5 is of structural origin, as encountered in phonon-driven displacive transitions.
1. Experimental Results
We investigate the origin of the phase transition in the candidate EI Ta2NiSe5 via trARPES (Fig. 1C), choosing the experimental parameters so that the excitonic and structural contributions to gap formation can be clearly separated. Specifically, we drive a single crystal of Ta2NiSe5 deep in the low-temperature phase (T = 11 K) with an intense near-infrared laser pulse that rapidly changes the electronic distribution, in effect increasing the electronic temperature (Te) well above the transition temperature (Te ≫ TC) while keeping the lattice cold (TL ≪ TC). The combination of a vacuum ultraviolet probe beam and a time-of-flight electron analyzer allows us to access a large portion of the in-plane Brillouin zone, elucidating how the electronic gap reacts to photoexcitation along both kx—the direction parallel to the chains in the orthorhombic cell—and kz, the one perpendicular to it. This feature, which had never been explored by previous trARPES studies on Ta2NiSe5 (23, 24, 26–29), is of relevant interest because the material’s electronic structure is not purely one-dimensional, with the interchain coupling establishing a well-defined dispersion along kz (12). Details of the methods are reported in SI Appendix, section S1. Within this experimental protocol, the light-induced renormalization of the electronic gap reflects the origin of the instability: Indeed, if the gap was purely excitonic in nature, one would expect its complete melting on an electronic timescale; conversely, in the presence of a predominantly structural gap, the change in gap size would be governed by the electron–phonon coupling and lattice anharmonicity effects.
Fig. 2 A and B show snapshots of trARPES spectra along kx for kz = 0 Å−1. Before photoexcitation (Fig. 2A), the flat antibonding VB is observed around an energy of −0.16 eV relative to the Fermi level (EF) at Γ, whereas the bonding VB appears at −0.65 eV (16). Photoexciting electron–hole pairs with Te of several hundred kelvins above TC, while keeping TL well below TC induces a modification of the band structure that is the strongest around 0.3 to 0.4 ps (Fig. 2B). The flat VB is depleted in intensity and broadened substantially, but its peak energy remains nearly unchanged at all momenta (SI Appendix, Fig. S4). This is in stark contrast to the behavior observed in equilibrium upon increasing the lattice temperature in the vicinity of TC, which involves a prominent energy shift of the VB toward EF (12, 16); it also differs from the behavior reported in trARPES measurements performed under experimental conditions different from ours (SI Appendix, section S4 for a thorough discussion about the effects of lattice temperature, laser fluence, and repetition rate on the trARPES response of Ta2NiSe5) (23, 26, 28, 29).
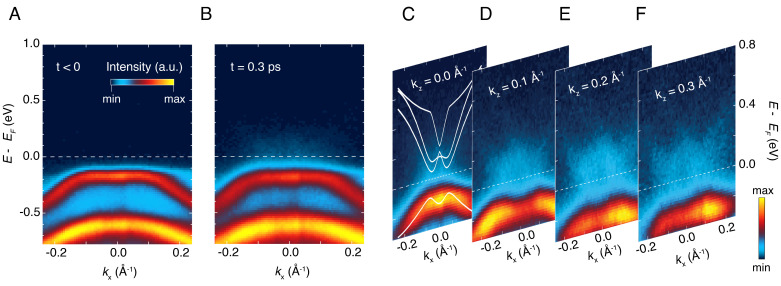
Fig. 2.
(A and B) Snapshots of the trARPES spectra along the kx momentum direction and for kz = 0 Å−1. The data have been measured at 11 K with a probe photon energy of 10.75 eV and an absorbed pump fluence of 0.4 mJ/cm2. (A) Snapshot before photoexcitation (t < 0). At the Γ point of the Brillouin zone (kx = 0 Å−1), the flat antibonding VB is located around −0.16 eV, whereas the bonding VB appears around −0.65 eV. (B) Snapshot measured at the maximum of the pump–probe response (t = 0.3 ps). Upon photoexcitation, the VB is depleted in intensity and broadens significantly. Spectral weight is transferred above EF and accumulates close to Γ. (C–F) Evolution of the photoexcited state (at t = 0.3 ps) along kx at representative kz momenta, as indicated in the labels. Note that the color scale is different from that of panels A and B. The spectral weight above EF assumes a W-like shape consistent with the dispersion of the CB. The VB and CB never cross each other, and thus, the gap size remains finite in the whole kx-kz momentum space around Γ. The white lines denote the energy–momentum dispersion calculated at the GW level (Fig. 4B). A rigid shift of −84 meV has been applied to the VB to account for the underestimated gap resulting from the GW method. The calculated dispersions have an excellent match with the experimental findings.
Another important feature in the pump–probe spectrum is found above EF, where spectral weight accumulates around the Γ point. To investigate the nature of these states, we acquire data at 0.3 ps with improved sensitivity around EF and show them in Fig. 2 C–F at representative kz values. At kz = 0 Å−1 and an energy of ∼50 to 75 meV (Fig. 2C), we observe an upward-dispersing band with a characteristic W shape, which we identify as the lowest conduction band (CB). While the exact estimate of the nonequilibrium gap is hindered by energy resolution constraints, the relevant aspect for our discussion is that the gap along kx remains always open, with an approximate size (210 to 240 meV) that is comparable to the most accurate experimental estimate of the equilibrium gap available to date (SI Appendix, section S8C). Direct inspection of the snapshots simultaneously taken at finite kz (Fig. 2 D–F) confirms that the VB and CB never cross each other throughout the 2D momentum space around Γ. Thus, already at this stage, our data indicate that the size of the putative excitonic gap is at least an order of magnitude smaller than that of the structural gap. We remark that this behavior occurs in the presence of a clear separation between the electronic and lattice temperatures, differing from the response observed in several trARPES studies performed at high fluence and samples temperature (a condition that leads the lattice to transiently heat up above TC) (26, 27, 29).
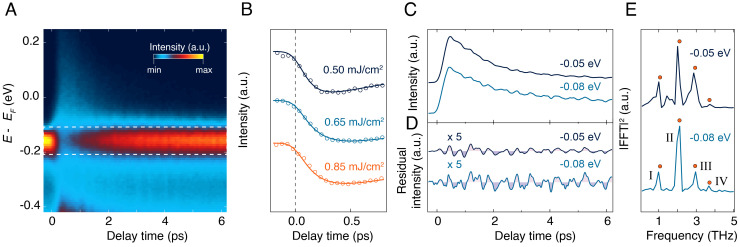
To elucidate whether the electronic or ionic degrees of freedom control the dynamics, we measure the trARPES signal with a high time resolution setup. Fig. 3A displays the energy distribution of the photoemission intensity around Γ (integrated over ±0.05 Å−1 in the kx-kz plane) as a function of pump–probe delay. Tracking the evolution of the VB intensity at different pump fluences (Fig. 3B) allows us to observe a response that is complete within ∼0.3 to 0.4 ps, a timescale longer than our instrument response function. This behavior is incompatible with the very short timescale (i.e., few fs; SI Appendix, section S5) that characterizes the plasma-induced screening of the Coulomb interaction. The latter effect plays an important role in the bandgap renormalization of conventional semiconductors and, in the case of a model two-band EI, it is expected to modify the excitonic gap amplitude on timescales of 10 to 100 fs (30–32). Direct inspection of our raw data and a combined analysis of the VB amplitude, broadening, and peak position (SI Appendix, Fig. S7) indicates that plasma screening in Ta2NiSe5 provides only a small contribution to the gap renormalization compared to the phenomenon evolving on the slower timescale. (Details are given in SI Appendix, section S5.) The same analysis suggests that the dominant process involves the emission of optical phonons, a behavior usually observed in materials with a gap of structural origin (19, 33, 34). To assess the validity of this scenario, we search for an unambiguous signature of strongly coupled phonon modes in Ta2NiSe5. Fig. 3C displays the momentum-integrated photoemission response as a function of time at representative energies of −0.05 eV and −0.08 eV. Both curves refer to the upper edge of the VB and show the presence of oscillations in the photoemission intensity due to coherent phonons. Subtracting the multiexponential background from the data of Fig. 3C allows us to isolate the signal of the collective response (Fig. 3D). The residuals reveal that the coherent phonon oscillations already emerge during the rise of the pump–probe signal, confirming that the maximum gap response is locked to a phononic timescale. Applying a Fourier filter to the signal of Fig. 3D yields the frequency spectrum of Fig. 3E. The peaks (labeled as I–IV) match the frequencies of four Raman-active phonons previously observed in other ultrafast studies (17, 27, 28, 35, 36). The presence of mode IV deserves special attention, as this is a characteristic fingerprint of the monoclinic phase of Ta2NiSe5 (SI Appendix, section S6). It indicates that the crystal maintains the low-temperature structure even if the electronic distribution becomes strongly nonequilibrium, another feature incompatible with a symmetry breaking of purely excitonic origin.
Fig. 3.
(A) Map of the photoelectron intensity at the Γ point as a function of energy and pump–probe delay. The data have been acquired at 14 K with a probe photon energy of 6.20 eV and an absorbed pump fluence of 0.85 mJ/cm2. (B) Excitation-density dependence rise of the photoelectron intensity response at Γ (dotted lines). Fits to the experimental traces are overlapped in solid lines. The traces are selected at an energy of −0.158 eV with respect to EF and averaged over an energy window of ±0.05 eV, as indicated by the dashed rectangle in panel A. (C) Time dependence of the momentum-integrated photoelectron intensity in selected energy intervals referenced to EF. Intensities are normalized to the average intensity I0 in the delay interval [−300,−50] fs; curves are offset for clarity and smoothed. The energy interval over which the intensity is integrated is ±0.05 eV around the indicated energy. (D) Oscillatory component singled out from the temporal traces of panel C by subtracting the nonoscillatory transient. For visualization purposes, the residuals have been multiplied by a factor of 5 and smoothed. (E) Fourier transform analysis of the oscillatory signal in D. Four frequency components (labeled as I–IV) appear in the spectrum, and they are identified as Raman-active phonons of Ta2NiSe5. The corresponding frequencies detected in spontaneous Raman scattering (17) are indicated by orange dots.
In summary, our low-temperature (10 to 15 K) and high-precision ultrafast study shows that the above-gap photoexcitation of Ta2NiSe5 leads to: i) a substantial and sudden change in the electronic distribution; ii) a small renormalization in the electronic gap size at all time delays; iii) a temporal evolution of the band structure that proceeds on a timescale set by the electron–phonon coupling; and iv) the retention of the monoclinic crystal structure. Altogether, these results suggest that the instability of Ta2NiSe5 is driven mainly by phonons and not by a pure EI order of electronic origin.
2. First-Principles Calculations
In the following, we rationalize these findings by performing state-of-the-art calculations based on density functional theory (DFT) and its Hartree–Fock-like generalizations. As a first step, we establish the crystal structure that is favored at low temperatures by relaxing the material’s unit cell. We find that this structure is monoclinic, in agreement with previous results (12, 14, 18). We then study how the low-symmetry monoclinic distortion reacts to an increase in Te by performing a series of calculations in which we vary the Fermi smearing on the electronic eigenvalues. To quantify this effect, we optimize the structure using the given Fermi smearing and density functional, use the spglib library (37) to find a structure with the orthorhombic symmetry Cmcm, and calculate the statistical distance between the original and the symmetrized structures (38). The statistical distance is defined as . In this expression, where Rij(r) is the standard radial distribution function for specific ionic species (in our case i = {Ni, Ta, Se}, which yields a total of 6 radial distribution functions).
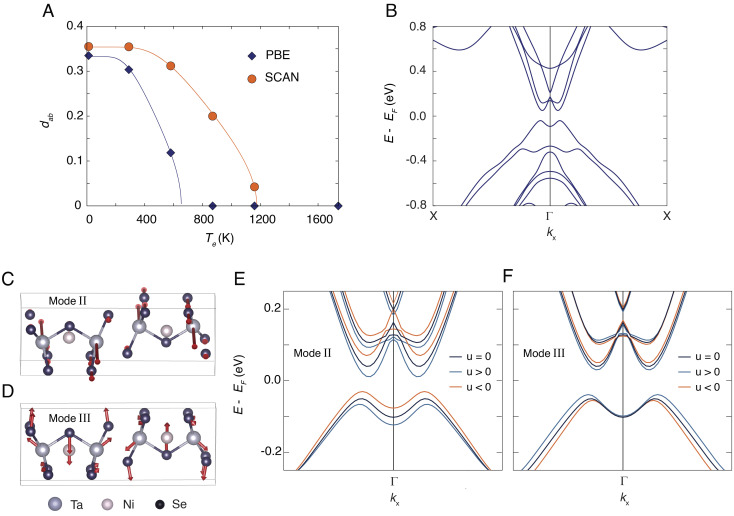
In order to estimate the effect of the choice of the density functional, we perform DFT calculations using the Perdew–Burke–Ernzerhof (PBE) functional (39) and the Strongly Constrained and Appropriately Normed (SCAN) functional (40). The results are shown in Fig. 4A and indicate that electron heating does not remove the monoclinic distortion even at Te ≫ TC. This is consistent with the experimental finding that the phonon modes of highly photoexcited Ta2NiSe5 are those characteristic of the low-temperature monoclinic phase (Fig. 3E). The amplitude of the distortion is gradually reduced, albeit never to zero. While the zero-temperature structures hardly depend on the choice of the functional, SCAN leads to about twice as high temperatures for structural instability. Regardless of this detail, already at this stage, we could conclude that the orthorhombic-to-monoclinic transition in Ta2NiSe5 is primarily driven by ion dynamics and not by excitonic effects.
Fig. 4.
(A) Distance between the calculated monoclinic structure and the nearest orthorhombic structure, evaluated as a function of Te. In the computation, we used two different density functionals: PBE (blue symbols) and SCAN (orange symbols). The lines are fits to the standard mean-field behavior, , where TC = 328 K. (B) Calculated electronic structure of Ta2NiSe5 in the low-temperature monoclinic unit cell along the X-Γ-X momentum direction (parallel to the Ta and Ni chains). The electronic structure is computed using GW calculations. A bandgap opens in the single-particle band structure, and its lower value is close to the Γ point of the Brillouin zone (SI Appendix, section S8 for details). The VB (CB) dispersions acquire an M-like (W-like) shape around Γ, consistent with the dispersion found in experiments. (C and D) Calculated eigenvectors of the dynamical matrix of Ta2NiSe5 corresponding to modes II and III, respectively. Violet atoms refer to Ta, pink atoms to Ni, and blue atoms to Se. The phonon spectrum has been computed using DFT. To enhance the visibility of the atomic motion, the amplitude is scaled by a factor of 8. (E and F) Calculated electronic structure of Ta2NiSe5 displaced along the eigenvectors of the modes showed in panels C and D. The dark blue lines refer to the electronic structure of the initial (undisplaced, u = 0) low-temperature unit cell, whereas the light blue (orange) lines indicate the band structure for positive (negative) displacements. The electronic structures are computed on the GW level of theory.
To possibly reproduce the salient features of the equilibrium electronic structure of Ta2NiSe5, we then perform advanced ab initio calculations on the realistic unit cell of the material. In particular, we examine the evolution of the electronic structure as the lattice is varied between the orthorhombic and monoclinic phases. To capture the electronic structure in the monoclinic phase, DFT alone is not sufficient, as the standard functionals routinely yield severely underestimated gaps and inaccurate band dispersions in semiconductors. Nevertheless, this fact is not related to any EI physics and stems from an incomplete description of the long-range exchange interaction in DFT (41). One can circumvent this problem by including the lowest-order correction in the screened electron-electron interaction. This is the essence of the so-called GW method, which largely improves the description of semiconductors (42). Importantly, this method does not account for any ladder-diagrammatic effects (such as the EI order) and thus can serve as a crucial test for the EI hypothesis in Ta2NiSe5.
We compute the material’s electronic structure at the GW level in the monoclinic unit cell and show the results in Fig. 4B. (Details are given in SI Appendix, sections S1 and S8.) We observe that the monoclinic distortion alone profoundly affects the electronic structure, changing it from semimetallic to semiconducting. Specifically, a hybridization gap opens around the Γ point, with its size being 90 to 169 meV (depending on the starting DFT functional and related wavefunctions) (11); the change in structure also leads to large systematic modifications in band offsets, with the CBs moving upward in energy with respect to the VBs. Further corrections in the description of the screening and the inclusion of the electron–phonon coupling would likely refine the gap size to larger values. Indeed, while our GW approach does not include the full electron–phonon coupling matrix elements, we show below that frozen-phonon calculations demonstrate a 10-meV increase of the gap size upon the static displacement of the most strongly coupled phonon modes. More importantly, our GW calculations show that along kx, the topmost VB acquires an M-like flat shape, and the lowest CB develops a W-like structure, both consistent with the experimental dispersions (as shown by the white lines overlapped to the experimental data of Fig. 2D). These shapes are expected when two intersecting electron and hole bands hybridize, with the degree of flattening set by the strength of the hybridization potential.
Starting from this electronic structure, we establish how it evolves upon increasing Te. There are two mechanisms through which electron heating can modify the GW gap: i) screening of the long-range exchange interaction, which proceeds on the electronic timescale set by the plasma frequency, and ii) the dependence of the structural distortion (involving the monoclinic angle and the internal displacements) on Te, an effect that proceeds on phononic timescales. At our values of Te, the former mechanism has a small impact on the electronic structure of Ta2NiSe5, consistent with our experimental findings (SI Appendix, section S8D). In contrast, a small decrease in the monoclinic distortion would cause a larger shrinkage of the GW gap (43). In our trARPES data, the phononic timescale associated with the largest gap response reinforces the idea that the dynamics is governed by a small reduction of the structural distortion. During this time, the electron–phonon coupling plays a key role in equilibrating the electron and the ion subsystems. We can quantify this coupling for each of the coherent phonons emerging in trARPES by computing the GW band structure while statically displacing the ions along the mode coordinates (44). Fig. 4 C and F shows representative results for modes II and III. In agreement with the experiment, our calculations show that the VB undergoes a substantial modulation around Γ, confirming a strong deformation potential coupling between the low-energy electronic states and the atomic displacements. Such deformation potential coupling involves, together with band offsets, strong changes in band hybridization.
3. Conclusions
Our experimental data and theoretical calculations point toward a scenario wherein the instability in Ta2NiSe5 is mostly of structural nature. In particular, the trARPES data allow us to estimate that most of the quasiparticle bandgap in the material can be best described as a one-electron hybridization gap driven by ion–ion interactions. This estimate has a profound consequence on the energetics of the EI state, determining a bound for the energy of its putative phase mode. While our calculations and those in ref. 18 predict that a zone-center soft phonon leads to a quadrupolar order below TC, only advanced structural probes will clarify the complex lattice dynamics responsible for symmetry breaking in Ta2NiSe5. Recently, systematic Raman scattering studies have provided key insights into the zone-center lattice dynamics by identifying the emergence of a Fano lineshape for relevant B2g modes around TC (45–48). This observation suggests the presence of a strong coupling between the B2g phonon modes and a continuum of states, most likely of electronic nature (13). However, spontaneous Raman scattering cannot distinguish whether phonons are dressed in simple electron or hole continuum (via the electron–phonon coupling) or in a continuum of electron–hole pairs bounded exclusively by direct Coulomb attraction. Accurate studies of the energy- and momentum-resolved lattice dynamics—possibly in the presence of stimuli such as gate voltage or uniaxial strain—will be key to providing the missing information on the lattice dynamics. Looking beyond the physics of Ta2NiS5, we envision that the joint experimental–theoretical strategy presented in our work can serve as a protocol to establish the role of the crystal structure in future candidate EIs.
Appendix A: Fate of the Excitonic Insulator in the Presence of Phonons
In this Appendix, we discuss the fate of the EI state in the two limiting cases where the transition is driven either by electronic instability or by structural instability. Starting from a simple two-band model of an EI, the order parameter is given by the hybridization between the two bands , where creates an electron in band 1, c2(x) annihilates an electron in band 2, and ⟨...⟩ indicates the expectation value. The structural instability is described by an optical phonon coordinate Xphon. One can then derive a low-energy effective theory from this microscopic model. Using the symmetry of the phonon and the excitonic order parameter and expanding in the lowest order terms of the relevant fields (which should be justified not too far from the transition temperature TC), we obtain the Lagrangian
| [A1a] |
| [A1b] |
where Mphon is the ionic mass associated with the phonon. The quartic terms g, u, and v, have a positive sign. The quadratic coefficients in the potential, r and κ, respectively, drive the excitonic and structural instability as they approach zero. Here, for simplicity, we neglect the U(1) symmetry breaking that, as noted in ref. 10, is intrinsic to solid-state realizations of the EI phenomenon, on the grounds that this symmetry breaking is very small in practice. In the dynamics, we neglect dissipative terms arising from particle–hole excitations. As pointed out by Pekker and Varma (49), in this case, the lowest-order time-derivative term for the order parameter is second order due to particle–hole symmetry. The theory is thus valid only for frequencies less than twice the quasiparticle gap. Finally, λ couples the two modes linearly.
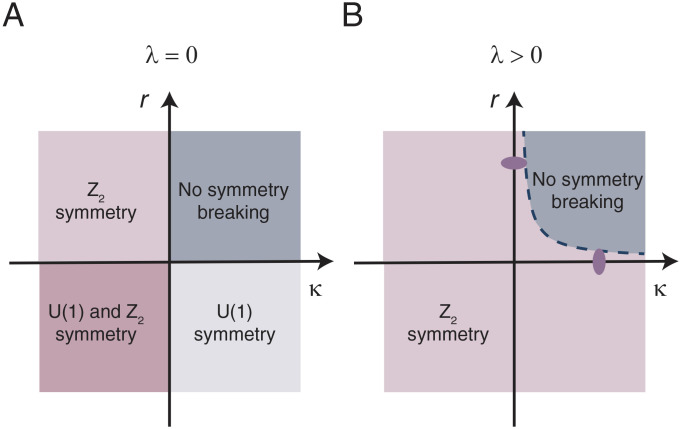
A. Phase Diagram.
For λ = 0, the above problem factorizes into a U(1) × Z2 symmetry sector. The phase diagram for this case is presented in Fig. 5A, and it comprises four distinct phases: i) r > 0, κ > 0, with no symmetry breaking, ii) r < 0, κ > 0, an EI phase with U(1) symmetry breaking, iii) r > 0, κ < 0, a phase with Z2 symmetry breaking in the form of a structural phase transition, and iv) r < 0, κ < 0, with both U(1) and Z2 symmetry breaking. However, for λ> 0, the U(1) symmetry of the electron system is explicitly broken by linear coupling to the phonon, and all three symmetry-broken phases for λ = 0 merge into a single phase of spontaneous Z2-symmetry breaking (shown in Fig. 5B). First, we express the order parameter in terms of its real and imaginary parts: Δ = Δ1 + iΔ2. Then, due to the presence of the phonon, we can set Δ2 = 0 and find the minimum of Δ1. The resulting equations are
| [A2a] |
| [A2b] |
Fig. 5.
(A) Phase diagram without coupling of electrons to phonons (λ = 0). In this case, there is a U(1) symmetry in the electronic sector and a Z2 symmetry in the structural sector which can be broken independently, leading to four distinct phases. (B) Phase diagram with finite electron–phonon coupling (λ > 0). U(1) symmetry is explicitly broken by linear coupling to the phonons, leading to the three symmetry-broken phases to merge into only one Z2 phase. The purple dots signify the two limiting cases where the transition is driven by the excitonic order parameter or the crystal structure.
For small λ, we can perturbatively find the correction to the phase diagram near the two extreme scenarios |r|≪1, κ > 0 (corresponding to an electronically driven transition) and |κ|≪1, r > 0 (corresponding to a structurally driven transition):
for |r|≪1 and k > 0: and ,
for |κ|≪1 and r > 0: and .
In both limits, the transition occurs at r = λ2/κ, which defines the new phase transition boundary. In both cases, the transition corresponds to a Z2-type of symmetry breaking.
B. Phason Dispersion.
Next, we show how the dispersion of the phason mode—an important feature in the definition of the EI phase—is modified in the two case scenarios described above. When the excitonic order parameter and the phonon fields are linearly coupled as in Eq. A1, there is no rigorous symmetry distinction between different types of symmetry breaking. Furthermore, since the continuous U(1) symmetry is reduced to the Z2 symmetry, there may not be a gapless Goldstone mode (10, 31, 50). However, as discussed in detail in ref. 51, the phason dispersion should give indications of the leading mechanism of instability. In particular, when λ is small and the transition is primarily driven by the excitonic part of the model, there are pseudo-Goldstone modes, i.e., modes with a nonzero but small gap that may be understood as arising from the proximity of the U(1) symmetry. From the Lagrangian in Eq. A1, the energy of the phason in the symmetry broken phase is given by
| [A3] |
In the case of an electronically driven scenario, ωphas2(q = 0)≈λ2/κ. For small λ, this is a pseudo-Goldstone mode, i.e., a remnant of the massless Goldstone mode in the U(1) theory that has been gapped by interactions with phonons. On the other hand, in the case of a structurally driven transition, ωphas2(q = 0)≈r, and the energy of the phason is as high as that of the amplitude (Higgs) mode.
C. Other Collective Modes.
We then compute the dispersion of the remaining Higgs mode and phonon mode, which are now coupled. This is done by expanding the Lagrangian in Eq. A1 around the mean-field expectation value, |Δ|=Δ0 + δΔ and Xphon = ⟨Xphon⟩ + u to quadratic order in the fluctuations. This derivation assumes that the mode energies are less than the quasiparticle gap, so that damping by particle–hole pairs need not be considered.
| [A4] |
On the frequency-momentum basis, the equations of motion are given by
| [A5] |
The dispersion relation of the collective modes can be found by solving the secular equation
| [A6a] |
| [A6b] |
where C1(k2) = r + 3gΔ02 + v⟨Xphon⟩2 + ξq2, and . The two collective mode energies are expressed as
| [A7] |
Taking the limit of a weakly coupled system (where λ is small but finite), the two modes are ω1, 22 = C1, 2(q2). Approaching the phase boundary either from the electronically driven direction (|r|≪1, κ > 0) or the structurally driven direction (|κ|≪1, r > 0), we find that there is one mode in each case that goes to zero at the transition, either the amplitude mode or the phonon mode respectively, while the other modes’ frequency is hardly affected by the transition. A detailed account of the influence of these modes on the linear and nonlinear optical response is given in ref. 51.
4. Materials and Methods
Single crystals of Ta2NiSe5 were synthesized by chemical vapor transport. A time-of-flight analyzer was used to acquire the trARPES data in the two-dimensional kx-kz plane around the Γ point of the Brillouin zone without rotating the sample or the detector. Systematic measurements were reproduced on a total of 10 samples with two different laser schemes. The first scheme used a setup based on an amplified Yb:KGW laser system operating at 100 kHz. The pump beam was directed into an optical parametric amplifier to produce a near-infrared pulse at 1.55 eV. The probe pulse was frequency tripled to 3.58 eV and directed into a hollow fiber filled with Xe gas. Pulses centered around 10.75 eV were obtained through nonlinear conversion of the 3.58-eV beam. The time resolution of the setup was 230 fs, and the energy resolution was 43 meV. The second laser scheme consisted of an amplified Ti:sapphire system, emitting ultrashort pulses around 1.55 eV and at 30 kHz. A portion of the output beam was used directly as the pump pulse at 1.55 eV, whereas the ultraviolet probe was obtained by frequency-quadrupling the laser fundamental to 6.20 eV. The time resolution was ∼160 fs, and the energy resolution was 31 meV. More details about the sample preparation, trARPES experiments, ultrafast electron diffraction experiments, and computational calculations are reported in SI Appendix, section S1.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank F. Boschini, S. Kaiser, D. Chowdhury, A. Georges, G. Mazza, and A. Subedi for insightful discussions. We are grateful to F. Mahmood, E. J. Sie, T. Rohwer, and B. Freelon for early instrumentation work of the trARPES and UED setups at MIT. The work at MIT was supported by DARPA DSO under DRINQS program grant number D18AC00014 (trARPES data taking and analysis), Army Research Office Grant No. W911NF-15-1-0128 (instrumentation for the trARPES setup), and the US Department of Energy BES DMSE (UED measurements). The work at Harvard was supported by Harvard-MIT CUA, AFOSR-MURI: Photonic Quantum Matter (award FA95501610323), and DARPA DRINQS program (award D18AC00014). E.B. acknowledges additional support from the Swiss NSF under fellowships P2ELP2-172290 and P400P2-183842. The theory work was supported by the European Research Council (ERC-2015-AdG694097), the Cluster of Excellence “Advanced Imaging of Matter” (AIM), Grupos Consolidados (IT1249-19), and SFB925. The Flatiron Institute is a division of the Simons Foundation. Support by the Max Planck Institute - New York City Center for Non-Equilibrium Quantum Phenomena is acknowledged. S. L. acknowledges support from the Alexander von Humboldt foundation. I.I.M. acknowledges support from the Office of Naval Research (ONR) through the grant #N00014-20-1-2345. A.J.M. acknowledges support from DOE BES Pro-QM EFRC (DE-SC0019443). Part of the calculations used resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. A.Z. and A.K. thank Y. Zhang for assisting us at the MRSEC Shared Experimental Facilities at MIT, supported by the NSF under award number DMR-14-19807. A.Z. and A.K. also thank C. Marks for the assistance in preparing UED samples at the Center for Nanoscale Systems, a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported by the NSF under NSF award no. 1541959. CNS is part of Harvard University.
Author contributions
E.B. designed research; E.B., A.Z., D.C., C.L., M.H.M., L.W., I.I.M., S.L., D.A., B.L., A.K., Y.S., Y.W., Y.L., T.T., H.T., A.J.M., A.R., and E.D. performed research; E.B., A.Z., I.I.M., A.J.M., A.R., and E.D. analyzed data; and E.B., I.I.M., A.J.M., A.R., E.D., and N.G. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Raw data corrected for artifacts, analysis. Data have been deposited (in to be decided). All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Keldysh L. V., Kopaev Y. V., Possible instability of semimetallic state toward Coulomb interaction. Soviet Phys. Solid State, USSR 6, 2219 (1965). [Google Scholar]
- 2.Des Cloizeaux J., Exciton instability and crystallographic anomalies in semiconductors. J. Phys. Chem. Sol. 26, 259–266 (1965). [Google Scholar]
- 3.Halperin B. I., Rice T. M., Possible anomalies at a semimetal-semiconductor transistion. Rev. Mod. Phy. 40, 755 (1968). [Google Scholar]
- 4.Snoke D., Spontaneous Bose coherence of excitons and polaritons. Science 298, 1368–1372 (2002). [DOI] [PubMed] [Google Scholar]
- 5.Batista C. D., Gubernatis J. E., Bonča J., Lin H. Q., Intermediate coupling theory of electronic ferroelectricity. Phys. Rev. Lett. 92, 187601 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Mazza G., Georges A., Superradiant quantum materials. Phys. Rev. Lett. 122, 017401 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Safaei S., Mazziotti D. A., Quantum signature of exciton condensation. Phys. Rev. B 98, 045122 (2018). [Google Scholar]
- 8.Schouten A. O., Sager-Smith L. M., Mazziotti D. A., Large cumulant eigenvalue as a signature of exciton condensation. Phys. Rev. B 105, 245151 (2022). [Google Scholar]
- 9.Jérome D., Rice T., Kohn W., Excitonic insulator. Phys. Rev. 158, 462 (1967). [Google Scholar]
- 10.Mazza G., et al. , Nature of symmetry breaking at the excitonic insulator transition: Ta2NiSe5. Phys. Rev. Lett. 124, 197601 (2020). [DOI] [PubMed] [Google Scholar]
- 11.Lu Y. F., et al. , Zero-gap semiconductor to excitonic insulator transition in Ta2NiSe5. Nat. Commun. 8, 14408 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Watson M. D., et al. , Band hybridization at the semimetal-semiconductor transition of Ta2NiSe5 enabled by mirror-symmetry breaking. Phys. Rev. Res. 2, 013236 (2020). [Google Scholar]
- 13.Nakano A., et al. , Antiferroelectric distortion with anomalous phonon softening in the excitonic insulator Ta2NiSe5. Phys. Rev. B 98, 045139 (2018). [Google Scholar]
- 14.Di Salvo F. J., et al. , Physical and structural properties of the new layered compounds Ta2NiS5 and Ta2NiSe5. J. Less Comm. Met. 116, 51–61 (1986). [Google Scholar]
- 15.Lee J., et al. , Strong interband interaction in the excitonic insulator phase of Ta2NiSe5. Phys. Rev. B 99, 075408 (2019). [Google Scholar]
- 16.Wakisaka Y., et al. , Excitonic insulator state in Ta2NiSe5 probed by photoemission spectroscopy. Phys. Rev. Lett. 103, 026402 (2009). [DOI] [PubMed] [Google Scholar]
- 17.Werdehausen D., et al. , Coherent order parameter oscillations in the ground state of the excitonic insulator Ta2NiSe5. Sci. Adv. 4, eaap8652 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Subedi A., Orthorhombic-to-monoclinic transition in ta2nise5 due to a zone-center optical phonon instability. Phys. Rev. Mater. 4, 083601 (2020). [Google Scholar]
- 19.Hellmann S., et al. , Time-domain classification of charge-density-wave insulators. Nat. Commun. 3, 1069 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Porer M., et al. , Non-thermal separation of electronic and structural orders in a persisting charge density wave. Nat. Mater. 13, 857–861 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Zhang W., et al. , Ultrafast quenching of electron-boson interaction and superconducting gap in a cuprate superconductor. Nat. Commun. 5, 1–6 (2014). [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y., et al. , Coherent modulation of the electron temperature and electron-phonon couplings in a 2D material. Proc. Natl. Acad. Sci. U.S.A. 117, 8788–8793 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mor S., et al. , Ultrafast electronic band gap control in an excitonic insulator. Phys. Rev. Lett. 119, 086401 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Mor S., Fundamental Interactions Governing the (Non-) Equilibrium Electronic Structure in Low Dimensions (Freie Universitaet Berlin, Germany, 2019). [Google Scholar]
- 25.Mor S., Herzog M., Monney C., Stähler J., Ultrafast charge carrier and exciton dynamics in an excitonic insulator probed by time-resolved photoemission spectroscopy. Prog. Surface Sci. 97, 100679 (2022). [Google Scholar]
- 26.Okazaki K., et al. , Photo-induced semimetallic states realised in electron-hole coupled insulators. Nat. Commun. 9, 4322 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Suzuki T., et al. , Detecting electron-phonon coupling during photoinduced phase transition. Phys. Rev. B 103, L121105 (2021). [Google Scholar]
- 28.Tang T., et al. , Non-Coulomb strong electron-hole binding in Ta2NiSe5 revealed by time- and angle-resolved photoemission spectroscopy. Phys. Rev. B 101, 235148 (2020). [Google Scholar]
- 29.Saha T., et al. , Photoinduced phase transition and associated timescales in the excitonic insulator Ta2nise5. Phys. Rev. B 103, 144304 (2021). [Google Scholar]
- 30.Golež D., Werner P., Eckstein M., Photoinduced gap closure in an excitonic insulator. Phys. Rev. B 94, 035121 (2016). [Google Scholar]
- 31.Murakami Y., Golež D., Eckstein M., Werner P., Photoinduced enhancement of excitonic order. Phys. Rev. Lett. 119, 247601 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Ning H., et al. , Signatures of ultrafast reversal of excitonic order in Ta 2 NiSe 5. Phys. Rev. Lett. 125, 267602 (2020). [DOI] [PubMed] [Google Scholar]
- 33.Schmitt F., et al. , Transient electronic structure and melting of a charge density wave in TbTe3. Science 321, 1649–1652 (2008). [DOI] [PubMed] [Google Scholar]
- 34.Petersen J. C., et al. , Clocking the melting transition of charge and lattice order in 1T-TaS2 with ultrafast extreme-ultraviolet angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 107, 177402 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Mor S., et al. , Inhibition of the photoinduced structural phase transition in the excitonic insulator Ta2NiSe5. Phys. Rev. B 97, 115154 (2018). [Google Scholar]
- 36.Bretscher H. M., et al. , Imaging the coherent propagation of collective modes in the excitonic insulator Ta2nise5 at room temperature. Sci. Adv. 7, eabd6147 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Togo A., Tanaka I., Spglib: A software library for crystal symmetry search. arXiv [Preprint] (2018). http://arxiv.org/abs/1808.01590. (Accessed 6 July 2020).
- 38.Kolmogorov A. N., Shah S., Margine E. R., Kleppe A. K., Jephcoat A. P., Pressure-driven evolution of the covalent network in CaB6. Phys. Rev. Lett. 109, 075501 (2012). [DOI] [PubMed] [Google Scholar]
- 39.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
- 40.Sun J., Ruzsinszky A., Perdew J. P., Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Maksimov E. G. II, Mazin SY Savrasov., Uspenski Y. A., Excitation spectra of semiconductors and insulators: A density-functional approach to many-body theory. J. Phys. Condens. Matter 1, 2493 (1989). [Google Scholar]
- 42.Hedin L., New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 139, A796 (1965). [Google Scholar]
- 43.Faleev S. V., van Schilfgaarde M., Kotani T., Léonard F., Desjarlais M. P., Finite-temperature quasiparticle self-consistent GW approximation. Phys. Rev. B 74, 033101 (2006). [Google Scholar]
- 44.Gerber S., et al. , Femtosecond electron-phonon lock-in by photoemission and X-ray free-electron laser. Science 357, 71–75 (2017). [DOI] [PubMed] [Google Scholar]
- 45.Kim M. J., et al. , Phononic soft mode behavior and a strong electronic background across the structural phase transition in the excitonic insulator Ta2NiSe5. Phys. Rev. Res. 2, 042039 (2020). [Google Scholar]
- 46.Kim K., et al. , Direct observation of excitonic instability in Ta 2 NiSe 5. Nat. Commun. 12, 1–8 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Volkov P. A., et al. , Critical charge fluctuations and emergent coherence in a strongly correlated excitonic insulator. npj Q. Mater. 6, 1–9 (2021). [Google Scholar]
- 48.Ye M., et al. , Lattice dynamics of the excitonic insulator Ta 2 Ni (Se 1–x s x) 5. Phys. Rev. B 104, 045102 (2021). [Google Scholar]
- 49.Pekker D., Varma C. M., Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 6, 269–297 (2015). [Google Scholar]
- 50.Zenker B., Fehske H., Beck H., Fate of the excitonic insulator in the presence of phonons. Phys. Rev. B 90, 195118 (2014). [Google Scholar]
- 51.Murakami Y., et al. , Collective modes in excitonic insulators: Effects of electron-phonon coupling and signatures in the optical response. Phys. Rev. B 101, 195118 (2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
Raw data corrected for artifacts, analysis. Data have been deposited (in to be decided). All study data are included in the article and/or SI Appendix.