Accurate Reproduction of Quantum Mechanical Many-Body Interactions in Peptide Main-Chain Hydrogen-Bonding Oligomers by the Polarizable Gaussian Multipole Model

Abstract

A key advantage of polarizable force fields is their ability to model the atomic polarization effects that play key roles in the atomic many-body interactions. In this work, we assessed the accuracy of the recently developed polarizable Gaussian Multipole (pGM) models in reproducing quantum mechanical (QM) interaction energies, many-body interaction energies, as well as the nonadditive and additive contributions to the many-body interactions for peptide main-chain hydrogen-bonding conformers, using glycine dipeptide oligomers as the model systems. Two types of pGM models were considered, including that with (pGM-perm) and without (pGM-ind) permanent atomic dipoles. The performances of the pGM models were compared with several widely used force fields, including two polarizable (Amoeba13 and ff12pol) and three additive (ff19SB, ff15ipq, and ff03) force fields. Encouragingly, the pGM models outperform all other force fields in terms of reproducing QM interaction energies, many-body interaction energies, as well as the nonadditive and additive contributions to the many-body interactions, as measured by the root-mean-square errors (RMSEs) and mean absolute errors (MAEs). Furthermore, we tested the robustness of the pGM models against polarizability parameterization errors by employing alternative polarizabilities that are either scaled or obtained from other force fields. The results show that the pGM models with alternative polarizabilities exhibit improved accuracy in reproducing QM many-body interaction energies as well as the nonadditive and additive contributions compared with other polarizable force fields, suggesting that the pGM models are robust against the errors in polarizability parameterizations. This work shows that the pGM models are capable of accurately modeling polarization effects and have the potential to serve as templates for developing next-generation polarizable force fields for modeling various biological systems.

INTRODUCTION

Development of molecular mechanical force fields has been at the forefront of molecular modeling research due to the critical roles that force fields play in applications such as molecular dynamics (MD) simulations, Monte Carlo (MC) simulations, and protein structure prediction.^1-4 Force fields that have the ability to provide accurate energy calculations and are highly transferable to a wide range of molecular systems have become highly desirable. With graphical processing unit (GPU)-accelerated and specialized high-performance computational platforms,^5,6 it becomes increasingly feasible to conduct simulations at time scales of biological relevance. The extensively used point-charge additive force fields, such as Amber ff19SB,⁷ CHARMM,⁸ and OPLS,⁹ share similar functional forms. In the additive Amber force fields, the following general functional form is used to calculate the potential energies of molecular systems:

$$E_{\text{total}}=E_{\text{bond}}+E_{\text{angle}}+E_{\text{dihedral}}+E_{\text{ele}}+E_{\text{vdW}}$$ (1)

The first three terms are short-range bonded terms, including the bond stretching terms $E_{\text{bond}}$, the angle bending terms $E_{\text{angle}}$, and the dihedral angle torsion terms $E_{\text{dihedral}}$, with the following formulas:

$$E_{\text{bond}}=\sum _{\text{bonds}}{k}_{\mathrm{b}}(r-r_0{)}^2$$ (2)

$$E_{\text{angle}}=\sum _{\text{angles}}{k}_{\theta }(\theta -{\theta }_0{)}^2$$ (3)

$$E_{\text{dihedral}}=\sum _{\text{dihedrals}}{V}_{\mathrm{n}}[1+\cos (n\varphi -\gamma )]$$ (4)

The last two terms are nonbonded terms between any two atoms $i$ and $j$. The electrostatic term $E_{\text{ele}}$, usually modeled by the interactions between fixed atom-centered partial charges (Coulomb’s law), is a long-range term; whereas the van der Waals term $E_{\text{vdW}}$, modeled by the 6–12 Lennard-Jones potential, is nominally also a long-range term, although it decays rather quickly with increasing distance. $E_{\text{ele}}$ and $E_{\text{vdW}}$ are formulated as

$$E_{\text{vdW}}=\sum _{i<j}\left(\frac{A_{ij}}{R_{ij}^{12}}-\frac{B_{ij}}{R_{ij}^6}\right)$$ (5)

$$E_{\text{ele}}=\sum _{i<j}\frac{q_i{q}_j}{\epsilon R_{ij}}$$ (6)

both of which are pairwise and additive. Therefore, in this framework, the interaction between any two atoms is not affected by the presence or absence of other nonbonded atoms.

While additive force fields will continue to play important roles, polarizable force fields are expected to extend our ability to study biomolecular systems more adequately due to their ability to model the atomic polarization effects, which are the redistribution of atomic electron density due to the electric field produced by nearby atoms.¹⁰ Polarization effects are important in biological processes such as ligand–receptor interactions,^11-14 the interactions of ions with nucleic acids,^15,16 the dielectric environmental changes during protein folding,^17,18 and enzymatic mechanisms.¹⁹ If more than two atoms are involved, polarization effects lead to nonadditivity, since when polarized by a third atom, any two atoms interact differently from the situation where the third atom is absent. Lacking proper representation of the polarization effects is considered a major shortcoming of the additive force fields. For over five decades, many attempts have been directed to properly incorporate polarization effects into polarizable force fields. A variety of methods have been explored, including the induced dipole models,^20-28 the fluctuating charge models,^29,30 the Drude oscillator models,^31,32 and the continuum dielectric models.^33,34

The induced point dipole model is one of the most studied approaches with a long history since the 1970s.^35,36 In this approach, the induced dipole of atom $i$, subject to the external electric field ${\mathit{E}}_i$, is

$${\mu }_{{}_i}={\alpha }_{{}_i}\left[{\mathit{E}}_{{}_i}-\sum _{j\ne i}^{\mathit{n}}{\mathit{T}}_{{}_{ij}}{\mu }_{{}_j}\right]$$ (7)

where ${\alpha }_i$ is the isotropic polarizability of atom $i$ and ${\mathit{T}}_{ij}$ is the dipole field tensor with the matrix form

$${\mathit{T}}_{{}_{ij}}=\frac{f_{{}_{\mathrm{e}}}}{r_{{}_{ij}}^{{}^3}}\mathit{I}-\frac{3f_{{}_{\mathrm{t}}}}{r_{{}_{ij}}^{{}^5}}\left[\begin{array}{ccc}\hfill x^2\hfill & \hfill xy\hfill & \hfill xz\hfill \\ \hfill xy\hfill & \hfill y^2\hfill & \hfill yz\hfill \\ \hfill xz\hfill & \hfill yz\hfill & \hfill z^2\hfill \end{array}\right]$$ (8)

where $\mathit{I}$ is the identity matrix; $x$, $y$, and $z$ are the Cartesian components along the vector between atoms $i$ and $j$ at distance $r_{ij}$; and $f_{\mathrm{e}}$ and $f_{\mathrm{t}}$ are distance-dependent damping functions that modify ${\mathit{T}}_{ij}$ to avoid the so-called “polarization catastrophe” problem, i.e., the phenomenon that induced dipole diverges due to the cooperative induction between induced dipoles at short distances.^10,37 Several damping schemes have been proposed by Thole using a smeared charge distribution $\rho (u)$, where $u=r_{ij}∕({\alpha }_i{\alpha }_j{)}^{1∕6}$ is the effective distance.^38,39 Thole’s damping schemes have been incorporated into several important polarizable force fields. For example, in the ff12pol force field,^22-25 the linear damping scheme is adopted

$$\rho (u)=\{\begin{array}{cc}\frac{3}{\pi }\frac{(a-u)}{a^4},\hfill & u<a\hfill \\ 0,\hfill & u\ge a\hfill \end{array}\phantom{\}}$$ (9)

and the damping functions $f_{\mathrm{e}}$ and $f_{\mathrm{t}}$ have the form

$$\begin{gathered} v=u∕a \\ {f}_{{}_e}=\{\begin{array}{cc}4v^3-3v^4,\hfill & v<1\hfill \\ 1.0,\hfill & v\ge 1\hfill \end{array}\phantom{\}} \\ {f}_{{}_t}=\{\begin{array}{cc}{v}^{{}^4},\hfill & v<1\hfill \\ 1.0,\hfill & v\ge 1\hfill \end{array}\phantom{\}} \end{gathered}$$ (10)

In the Amoeba polarizable force field,^26-28 an exponential damping scheme is used

$$\rho (u)=\frac{3a}{4\pi }\text{exp}(-a{u}^3)$$ (11)

and the damping functions $f_{\mathrm{e}}$ and $f_{\mathrm{t}}$ become

$$\begin{gathered} v=a{u}^3 \\ {f}_{{}_{\mathrm{e}}}=1-\text{exp}(-v) \\ {f}_{{}_{\mathrm{t}}}=1-(v+1)\text{exp}(-v) \end{gathered}$$ (12)

However, since Thole’s schemes only screen the interactions between induced dipoles, leaving the polarization due to fixed charges and permanent multipoles unaffected, one caveat is the possibility of producing large atomic induced dipoles when other highly charged species are nearby. About a decade ago, Elking et al. developed a scheme that models atomic electric multipoles using Gaussian electron densities,^40-42 which was originally proposed by Wheatley,^43,44 and this model was later named as the polarizable Gaussian Multipole (pGM) model.^45-47 The pGM model can overcome the potential problem of Thole’s scheme by screening all short-range electrostatic interactions in a consistent manner, including the interactions of charge—charge, charge—dipole, charge—quadrupole, dipole—dipole, and so on, eliminating a potential source of singularity in the electrostatic term $E_{\text{ele}}$. Consequently, it has been shown that the pGM model notably improves the prediction of molecular polarizability anisotropy compared with that of Thole models.⁴⁵ In the pGM model, the nth order Gaussian multipole at distance r with atom i is defined as

$${\rho }^{(n)}(r)={\Theta }^{(n)}\cdot {\nabla }^{(n)}{\left(\frac{{\beta }_{{}_i}}{\sqrt{\pi }}\right)}^3\text{exp}(-{\beta }_{{}_i}^{{}^2}{r}^{{}^2})$$ (13)

where ${\Theta }^{(n)}$ is the nth rank momentum tensor, ${\nabla }^{(n)}$ is the nth rank gradient operator, and ${\beta }_i$ is the Gaussian exponent controlling the “radius” of the distribution with the following formula:

$${\beta }_{{}_i}=s{\left(\frac{2{\alpha }_{{}_i}}{3\sqrt{2\pi }}\right)}^{-1∕3}$$ (14)

where ${\alpha }_i$ is the atomic polarizability and s is a constant screening factor. Although any order of multipoles can be modeled by the pGM model, only charges (zeroth order multipole, eq 15) and dipoles (first order multipole, eq 16) are considered in the current pGM model design

$${\rho }^{(0)}(r)=q_{{}_i}{\left(\frac{{\beta }_{{}_i}}{\sqrt{\pi }}\right)}^3\text{exp}(-{\beta }_{{}_i}^{{}^2}{r}^{{}^2})$$ (15)

$${\rho }^{(1)}(r)={\mathbf{p}}_{{}_i}\cdot \nabla {\left(\frac{{\beta }_{{}_i}}{\sqrt{\pi }}\right)}^3\text{exp}(-{\beta }_{{}_i}^{{}^2}{r}^{{}^2})$$ (16)

where $q_i$ is the permanent charge and ${\mathit{p}}_i$ is the permanent dipole of atom $i$. Replacing ${\mathit{p}}_i$ in eq 16 with ${\mu }_i$ in eq 7 will give the pGM distribution of the induced dipole, which has the same form as that of the permanent dipole. For the pGM model, we have the following formula of damping functions $f_{\mathrm{e}}$ and $f_{\mathrm{t}}$:

$$\begin{gathered} S_{{}_{ij}}=\frac{{\beta }_{{}_i}{\beta }_{{}_j}{r}_{{}_{ij}}}{\sqrt{2({\beta }_{{}_i}^{{}^2}+{\beta }_{{}_j}^{{}^2}})} \\ {f}_{{}_e}=\text{erf}(S_{{}_{ij}})-\frac{2}{\sqrt{\pi }}{S}_{{}_{ij}}\text{exp}(-S_{{}_{ij}}^{{}^2}) \\ {f}_{{}_t}=\text{erf}(S_{{}_{ij}})-\frac{2}{\sqrt{\pi }}{S}_{{}_{ij}}\text{exp}(-S_{{}_{ij}}^{{}^2})\left(1+\frac{2}{3}{S}_{{}_{ij}}^{{}^2}\right) \end{gathered}$$ (17)

where erf($\text{erf}(S_{ij})$) is the error function of $S_{ij}$.

In a series of recent works, the functional form and parameterization schemes for the pGM model have been designed and implemented. First, a set of isotropic atomic polarizabilities and radii for the pGM model were obtained by fitting to molecular polarizability tensors of 1405 molecules or dimers calculated at the B3LYP/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ level of theory using an optimization method based on the genetic algorithm (GA).⁴⁵ Second, a local frame for the pGM permanent dipoles formed by covalent basis vectors (CBVs), which are unit vectors along the direction of covalent bonds or virtual bonds, has been proposed based on the observation that atomic permanent dipole moments mainly result from covalent bonding interactions.⁴⁶ Third, the analytical formula of the electrostatic term of the pGM models has been derived,⁴⁶ which is the sum of a permanent electrostatic term $E_{\text{ele}-\text{perm}}$ and an induced electrostatic term $E_{\text{ele}-\text{ind}}$

$$E_{\text{ele}}=E_{\text{ele}-\text{perm}}+E_{\text{ele}-\text{ind}}$$ (18)

with the following formula

$$E_{\text{ele}-\text{perm}}=\sum _{i<j}(q_{{}_i}+{\mathit{p}}_{{}_i}\cdot {\nabla }_{{}_i})(q_{{}_j}+{\mathit{p}}_{{}_j}\cdot {\nabla }_j)\frac{\text{erf}(S_{{}_{ij}})}{r_{{}_{ij}}}$$ (19)

$$E_{\text{ele}-\text{ind}}=\sum _{i<j}{\mu }_{{}_i}(q_{{}_j}+{\mathit{p}}_{{}_j}\cdot {\nabla }_{{}_j}){\nabla }_i\frac{\text{erf}(S_{{}_{ij}})}{r_{{}_{ij}}}$$ (20)

Therefore, in the functional form of the pGM models, the electrostatic term in eq 6 is replaced by eqs 18-20, and the rest of the terms remain unchanged (eqs 2-5). In addition, the pGM electrostatic term has been interfaced with the particle mesh Ewald (PME) method for molecular simulations under periodic boundary conditions.^46,48-51 Fourth, the pGM internal stress tensor expression for constant pressure MD simulations of both the flexible and rigid-body molecular system has been derived.⁴⁷ Finally, the PyRESP program enabling parameterizations for the pGM models with and without atomic permanent dipoles by reproducing quantum mechanical (QM) electrostatic potential (ESP) around molecules has been implemented.⁵² All of the components mentioned above, including the pGM polarizabilities and radii, the sander program enabling MD simulations for the pGM models, and the PyRESP parametrization program, are available in the AmberTools22 program suite that can be downloaded from http://ambermd.org/.⁵³

In this work, we assessed the ability of the pGM models to reproduce QM many-body interaction energies in peptide oligomers, specifically the influences of neighboring peptides upon a pair of interacting peptide monomers. For polarizable force fields, the many-body interaction energies can be decomposed into nonadditive and additive contributions. The detailed definitions of the many-body interaction energy, as well as its nonadditive and additive contributions, will be presented in the Theory section. Glycine dipeptide oligomers arranged in three main-chain hydrogen-bonding conformations were used as the model peptide systems because glycine has the minimalist side chain so that we can focus on main-chain hydrogen-bonding interactions. Two types of pGM models were considered, including pGM-perm, in which the atomic dipoles are represented by a combination of both induced and permanent dipoles, and pGM-ind, in which the atomic dipoles are represented by the induced dipoles only. We compared the performances of the pGM-perm and pGM-ind models with several other widely used force fields in terms of reproducing QM interaction energies and many-body interaction energies, including four Amber force fields: ff12pol,^22-25 ff19SB,⁷ ff15ipq,⁵⁴ and ff03,⁵⁵ as well as the 2013 version of the Amoeba protein force field (Amoeba13).²⁸ Among the seven force fields tested, pGM-perm, pGM-ind, Amoeba13, and ff12pol are polarizable force fields, while ff19SB, ff15ipq, and ff03 are classical point-charge additive force fields. The results show that the pGM models perform significantly better than all other force fields in terms of reproducing QM interaction energies, many-body interaction energies, and the nonadditive and additive contributions to the many-body interactions. In addition, we tested the robustness of the pGM models against parameterization errors by employing alternative atomic polarizabilities, including the pGM polarizabilities scaled by a factor of 0.9,⁴⁵ the Amoeba polarizabilities,²⁶ and the ff12pol polarizabilities.²² The results show that the pGM models are highly robust and perform well even with those “wrong” polarizabilities.

THEORY

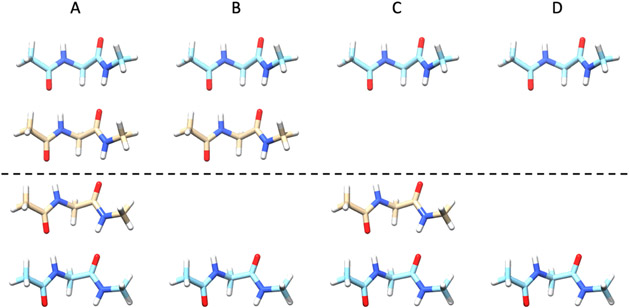
In this work, each oligomer is arranged in a general form of $m$ glycine dipeptides interacting with $n$ glycine dipeptides, named ${\text{Gly}}_m{\text{:Gly}}_n$, where $m$ and $n$ are ranged from 1 to 3. Each “Gly” in this work represents a glycine dipeptide (ACE-GLY-NME) capped with an N-acetyl (ACE) group at the N-terminal and an N-methylamide (NME) group at the C-terminal. For example, Figure 1A shows the ${\text{Gly}}_2{\text{:Gly}}_2$ oligomer.

Figure 1.

Glycine dipeptide oligomers (in the parallel $\beta$-sheet conformation) used to calculate the interaction energy, many-body interaction energy, and the nonadditive and additive contributions to the many-body interaction of the ${\text{Gly}}_2{\text{:Gly}}_2$ oligomer. For each oligomer, the interaction energies between glycine dipeptides above and below the dashed line are calculated using eq 21. (A) ${\text{Gly}}_2{\text{:Gly}}_2$, (B) ${\text{Gly}}_2\text{:XGly}$, (C) ${\text{GlyX:Gly}}_2$, and (D) $\text{GlyX:XGly}$. Refer to the Theory section for detailed descriptions.

The interaction energy $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ between ${\text{Gly}}_m$ and ${\text{Gly}}_n$ of the ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer can be calculated by the following equation:

$$\text{IE}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=E({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})-E({\text{Gly}}_{{}_m})-E({\text{Gly}}_{{}_n})$$ (21)

where $E({\text{Gly}}_m{\text{:Gly}}_n)$ is the potential energy of the entire ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer and $E({\text{Gly}}_m)$, $E({\text{Gly}}_n)$ are the potential energies of isolated ${\text{Gly}}_m$ and ${\text{Gly}}_n$, respectively.

More importantly, we intend to study the many-body effects in the ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer, specifically, the influence of the neighboring glycine dipeptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$ upon the interaction between the two middle glycine dipeptides Gly:Gly in the ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer. Here, we define the many-body interaction energy $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ as the difference between $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ and $\text{IE}(\text{Gly:Gly})$. That is,

$$\text{ME}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{IE}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})-\text{IE}(\text{Gly}:\text{Gly})$$ (22)

Taking the ${\text{Gly}}_2{\text{:Gly}}_2$ oligomer in Figure 1A as an example, the difference between $\text{IE}({\text{Gly}}_2{\text{:Gly}}_2)$ and $\text{IE}(\text{Gly:Gly})$ of the two middle peptides (displayed in brown) is the many-body interaction energy $\text{ME}({\text{Gly}}_2{\text{:Gly}}_2)$ caused by the presence of the two neighboring peptides (displayed in cyan).

The many-body interaction energy $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ can be decomposed into the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and the additive contribution ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$. Before showing their formulas, we first need to define the interaction energies of the two middle peptides ${\text{IE}}_{\text{mid}}({\text{Gly}}_m{\text{:Gly}}_n)$ in the presence of the neighboring peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$.

$$\begin{gathered} {\text{IE}}_{\text{mid}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{IE}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})-\text{IE}({\text{Gly}}_{{}_m}:{\text{XGly}}_{{}_{n-1}}) \\ -\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{Gly}}_{{}_n}) \\ +\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{XGly}}_{{}_{n-1}}) \end{gathered}$$ (23)

where X indicates the absence of either one of the two middle peptides. $\text{IE}({\text{Gly}}_m{\text{:XGly}}_{n-1})$ is the interaction energy between ${\text{Gly}}_m$ and the neighboring peptides ${\text{Gly}}_{n-1}$; $\text{IE}({\text{Gly}}_{m-1}X:{\text{Gly}}_n)$ is the interaction energy between the neighboring peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_n$; and $\text{IE}({\text{Gly}}_{m-1}X:{\text{XGly}}_{n-1})$ is the interaction energy between the neighboring peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$ on both sides. Then, we have the formulas of ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$, the proof of which can be found in the Appendix.

$${\text{ME}}_{{}_{\text{NA}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})={\text{IE}}_{\text{mid}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})-\text{IE}(\text{Gly}:\text{Gly})$$ (24)

$${\text{ME}}_{{}_{\mathrm{A}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{ME}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})-{\text{ME}}_{{}_{\text{NA}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})$$ (25)

For the ${\text{Gly}}_2{\text{:Gly}}_2$ oligomer example, Figure 1B shows the oligomer ${\text{Gly}}_2\text{:XGly}$ with the interaction energy $\text{IE}({\text{Gly}}_2\text{:XGly})$; Figure 1C shows the oligomer $\text{GlyX:}{\text{Gly}}_2$ with the interaction energy $\text{IE}(\text{GlyX:}{\text{Gly}}_2)$; and Figure 1D shows the oligomer $\text{GlyX:XGly}$ with the interaction energy $\text{IE}(\text{GlyX:XGly})$. The interaction energy of the two middle peptides in the presence of the neighboring peptides is ${\text{IE}}_{\text{mid}}({\text{Gly}}_2{\text{:Gly}}_2)=\text{IE}({\text{Gly}}_2{\text{:Gly}}_2)-\text{IE}({\text{Gly}}_2\text{:XGly})-\text{IE}({\text{GlyX:Gly}}_2)+\text{IE}(\text{GlyX:XGly})$. The nonadditive and additive contributions to the many-body interaction energy $\text{ME}({\text{Gly}}_2{\text{:Gly}}_2)$ are ${\text{ME}}_{\text{NA}}({\text{Gly}}_2{\text{:Gly}}_2)={\text{IE}}_{\text{mid}}({\text{Gly}}_2{\text{:Gly}}_2)-\text{IE}(\text{Gly:Gly})$ and ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_2{\text{:Gly}}_2)=\text{ME}({\text{Gly}}_2{\text{:Gly}}_2)-{\text{ME}}_{\text{NA}}({\text{Gly}}_2{\text{:Gly}}_2)$, respectively.

For additive force fields, ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ is guaranteed to be zero, so that $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ is equivalent to ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$, while for polarizable force fields, ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ is nonzero, so that $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ has both additive and nonadditive contributions.

COMPUTATIONAL DETAILS

Geometry Preparations.

The formamide dimer and three glycine dipeptide dimers were used to select density functional theory (DFT) methods for subsequent QM energy calculations. The formamide dimer was first arranged into hydrogen-bonding conformation, and the geometry was optimized at the B3LYP/6-311++G(d,p) level of theory. A total of 15 glycine dipeptide oligomers were constructed. First, three glycine dipeptide dimers were configured and arranged into $\alpha$-helix, anti-parallel $\beta$-sheet, and parallel $\beta$-sheet hydrogen-bonding conformations observed in proteins. Then, the geometries were optimized at the B3LYP/6-311++G(d,p) level of theory with the main-chain torsion angles fixed at ($\varphi$, $\psi$) = (−57, −47°), (−140, 135°) and (−119, 113°), corresponding to the $\alpha$-helix, anti-parallel $\beta$-sheet, and parallel $\beta$-sheet conformations, respectively. Higher-order oligomers were constructed from these three optimized dimers by rigid-body translations and rotations. For example, to produce a ${\text{Gly}}_3{\text{:Gly}}_3$ dipeptide hexamer (in the conformation of an interacting pair of trimers) while maintaining the central dimer in the optimized conformation, both dipeptides of the $\text{Gly:Gly}$ dimer are rotated and moved toward both sides along the hydrogen bond direction. The structures of formamide dimer and glycine dipeptide oligomers are presented in Figures S1-S6, and the detailed coordinates of glycine dipeptide oligomers are available in the Supporting Information.

Quantum Mechanical Calculations.

Three DFT methods were tested to calculate the QM interaction energies of the formamide dimer and the glycine dipeptide dimers, including $\omega \text{B97X}-\mathrm{D}$,⁵⁶ M062X,⁵⁷ and B3LYP,^58,59 all with the aug-cc-pVTZ (aTZ) basis set. The basis set superposition errors (BSSEs) were corrected through the counterpoise corrections.⁶⁰ To select the most suitable DFT method for our systems, the CCSD(T)/CBS interaction energies ${\text{IE}}_{\text{CCSD}(\mathrm{T})∕\text{CBS}}$ were calculated as the reference energies using Helgaker’s extrapolation method.^61,62 First, the HF and MP2 interaction energies were calculated with aug-cc-pVTZ (aTZ) and aug-cc-pVQZ (aQZ) basis sets, and the correlation (CORR) energies ${\text{IE}}_{\text{CORR}}$ were defined as the difference between the MP2 and HF energies ${\text{IE}}_{\text{CORR}}={\text{IE}}_{\text{MP2}}-{\text{IE}}_{\text{HF}}$. Next, ${\text{IE}}_{\text{HF}∕\text{CBS}}$ and ${\text{IE}}_{\text{CORR}∕\text{CBS}}$ were calculated using the following equations:

$$\begin{gathered} {\text{IE}}_{{}_{\text{HF}∕\text{CBS}}}= \\ \frac{{\text{IE}}_{{}_{\text{HF}∕\text{aTZ}}}\text{exp}(-1.63\times 4)-{\text{IE}}_{{}_{\text{HF}∕\text{aQZ}}}\text{exp}(-1.63\times 3)}{\text{exp}(-1.63\times 4)-\text{exp}(-1.63\times 3)} \end{gathered}$$ (26)

$${\text{IE}}_{{}_{\text{CORR}∕\text{CBS}}}=\frac{{\text{IE}}_{{}_{\text{CORR}∕\text{aTZ}}}\times 3^3-{\text{IE}}_{{}_{\text{CORR}∕\text{aQZ}}}\times 4^3}{3^3-4^3}$$ (27)

and ${\text{IE}}_{\text{MP2}∕\text{CBS}}$ can be calculated as

$${\text{IE}}_{{}_{\text{MP}2∕\text{CBS}}}={\text{IE}}_{{}_{\text{HF}∕\text{CBS}}}+{\text{IE}}_{{}_{\text{CORR}∕\text{CBS}}}$$ (28)

Note that the average of ${\text{IE}}_{\text{MP2}∕\text{CBS}}$ with and without counterpoise correction was used as the final ${\text{IE}}_{\text{MP2}∕\text{CBS}}$. Finally, ${\text{IE}}_{\text{CCSD}(\mathrm{T})∕\text{CBS}}$ were calculated by adding a CCSD(T) correction calculated at a small basis set to the averaged ${\text{IE}}_{\text{MP2}∕\text{CBS}}$

$$\begin{gathered} {\text{IE}}_{{}_{\text{CCSD}(\mathrm{T})∕\text{CBS}}}={\text{IE}}_{{}_{\text{MP}2∕\text{CBS}}} \\ +({\text{IE}}_{{}_{\text{CCSD}(\mathrm{T})}}-{\text{IE}}_{{}_{\text{MP}2}}{)}_{{}_{\text{small basis set}}} \end{gathered}$$ (29)

For formamide dimers, aug-cc-pVTZ was used as the small basis set; for glycine dipeptide dimers, cc-pVTZ was used as the small basis set.

Following the strategy that has been successfully used in Amber force field development in which the partial charges were fit to QM electrostatic potentials (ESPs), the QM ESPs were calculated at the MP2/aug-cc-pVTZ level of theory for a set of points in the solvent-accessible region around each glycine dipeptide molecule in the $\alpha$-helix, anti-parallel $\beta$-sheet, and parallel $\beta$-sheet conformations. The points were generated using the method developed by Singh et al. on molecular surfaces (with a density of 6 points/Ų) at each of 1.4, 1.6, 1.8, and 2.0 times the van der Waals radii.^63,64 All QM calculations were performed using the Gaussian 16 software.⁶⁵

pGM Parameterizations.

To assess the robustness of the pGM models against errors in polarizability parameterization, four sets of atomic polarizabilities were employed to parameterize the pGM models, including the pGM polarizabilities,⁴⁵ the pGM polarizabilities scaled by a factor of 0.9, the Amoeba polarizabilities,²⁶ and the ff12pol polarizabilities,²² for a combined total of two pGM models and six variants. The recently developed PyRESP program was used to parameterize the point charges and permanent point dipoles of the glycine dipeptide molecule for the pGM-perm and pGM-ind models, and a two-stage parameterization procedure was adopted.⁵² In the first stage, all charges and permanent dipoles were set free to change, and a weak restraining strength of 0.0005 was applied. In the second stage, intra-molecular equivalencing was enforced on all charges and permanent dipoles that share an identical chemical environment with others, such as those of methyl and methylene hydrogens. A stronger restraining strength of 0.001 was applied, and all other fitting centers were set frozen to keep the values obtained from the first stage. In both stages, the restraints were only applied to non-hydrogen-heavy atoms. Only the total charge constraint was enforced in the parameterization process, and no additional intra-molecular charge constraint was applied. Inter-molecular equivalencing was enforced in both the first and the second stages for the three conformations of glycine dipeptides. For the parameterizations of both the pGM-perm and pGM-ind models, both 1–2 and 1–3 polarization interactions were included for reasons elucidated before.^45,66

The parameters of bonded terms (bond stretching terms, angle bending terms, dihedral angle torsion terms) and the van der Waals terms for both the pGM-perm and pGM-ind models were obtained from the ff12pol force field without any change.²⁵

Molecular Mechanics Calculations.

Seven force fields were explored for calculating the molecular mechanics energies of glycine dipeptide oligomers, including four polarizable force fields: pGM-perm, pGM-ind, ff12pol,^22-25 and Amoeba13,²⁸ and three additive force fields: ff19SB,⁷ ff15ipq,⁵⁴ and ff03.⁵⁵ The parameter and topology files for the Amber force fields (pGM-perm, pGM-ind, ff12pol, ff19SB, ff15ipq, and ff03) were generated using the tleap program from the AmberTools22 program suite.⁵³ The coordinate files for the Amber force fields and the .xyz files for the Amoeba13 force field were generated from the geometries optimized by Gaussian 16 software.⁶⁵ The single-point energies of the Amber force fields were calculated by the sander program with extensions to accommodate the pGM models.^46,53 The dynamic program from the Tinker 8.6.1 software package was used to calculate the single-point energies of the Amoeba13 force field.⁶⁷ All nonbonded interactions were calculated in gas phase without distance cutoff.

The performance of each force field in each energy calculation task was evaluated by the root-mean-squared error (RMSE) and mean absolute error (MAE) given by

$$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^N(E_{{}_i}^{{}^{\text{QM}}}-E_{{}_i}{)}^{{}^2}}{N}}$$ (30)

$$\text{MAE}=\frac{{\sum }_{i=1}^N\mid E_{{}_i}^{{}^{\text{QM}}}-E_{{}_i}\mid }{N}$$ (31)

where $E_{\mathrm{i}}^{\text{QM}}$ is the energy given by QM calculations and $E_{\mathrm{i}}$ is the energy calculated by molecular mechanics force fields.

RESULTS AND DISCUSSION

$\omega B97X-\mathsf{D}$ without Counterpoise Correction Most Accurately Reproduces CCSD(T)/CBS Interaction Energies.

There have been numerous works documenting the performances of various DFT methods in their ability to model the dispersion effect. Among these DFT methods, $\omega \text{B97X}-\mathrm{D}$⁵⁶ and M062X⁵⁷ exhibit great trade-offs between computation speed and accuracy.⁶⁸ One observation is that the accuracy of DFT methods depends on the particular molecular systems being studied. To determine which one of these DFT methods is the most suitable to our systems, we compared the interaction energies of the formamide dimer and the glycine dipeptide dimers obtained from three DFT methods, including $\omega \text{B97X}-\mathrm{D}$,⁵⁶ M062X,⁵⁷ and B3LYP,^58,59 with those calculated at the CCSD(T)/CBS level of theory, which have been considered as the “gold standard” of computational chemistry. Table 1 shows the interaction energies calculated with these DFT methods with and without counterpoise BSSE corrections. We can see that the interaction energies by $\omega \text{B97X}-\mathrm{D}$ without counterpoise correction are the closet to the CCSD(T)/CBS results (eq 29), with an RMSE of 0.17 kcal/mol and an MAE of 0.12 kcal/mol. Not surprisingly, B3LYP interaction energies consistently exhibit the highest deviations from the CCSD(T)/CBS results, since B3LYP lacks proper consideration of dispersion contributions. Without counterpoise corrections, the RMSEs of M062X and B3LYP are 0.32 and 3.37 kcal/mol, respectively, and the MAEs are 0.30 and 3.12 kcal/mol, respectively. With counterpoise corrections, the RMSEs of $\omega \text{B97X}-\mathrm{D}$, M062X, and B3LYP are 0.31, 0.71, and 3.70 kcal/mol, respectively, and the MAEs are 0.29, 0.67, and 3.42 kcal/mol, respectively. Therefore, for the formamide dimer and the glycine dipeptide dimers, $\omega \text{B97X}-\mathrm{D}$ without counterpoise BSSE correction best reproduces the CCSD(T)/CBS interaction energies. For this reason, $\omega \text{B97X}-\mathrm{D}$ without counterpoise correction was chosen as the QM reference method to evaluate various molecular mechanical force fields in the following discussions.

Table 1.

Quantum Mechanical Interaction Energies of the Formamide Dimer and the Glycine Dipeptide Dimers Calculated by the CCSD(T)/CBS and Density Functional Theory Methods (kcal/mol)

		$\omega \text{B97X}-\mathrm{D}$/aTZ		M062X/aTZ		B3LYP/aTZ
CCSD(T)/CBSa		noCpb	CPb	noCpb	CPb	noCPb	CPb
Formamide Dimer
	−7.04	−6.96 (0.08)d	−6.83 (0.21)	−6.91 (0.13)	−6.77 (0.27)	−6.15 (0.89)	−6.05 (0.99)
Glycine Dipeptide Dimer (Gly:Gly)
$\alpha \mathrm{R}$ c	−14.40	−14.73 (−0.33)	−14.29 (0.11)	−14.00 (0.40)	−13.57 (0.83)	−10.37 (4.03)	−10.01 (4.39)
$\mathrm{a}\beta$ c	−14.49	−14.53 (−0.04)	−14.10 (0.39)	−14.22 (0.27)	−13.77 (0.72)	−10.54 (3.95)	−10.17 (4.32)
$\beta$ c	−17.34	−17.36 (−0.02)	−16.91 (0.43)	−16.93 (0.41)	−16.47 (0.87)	−13.75 (3.59)	−13.37 (3.97)
RMSE		0.17	0.31	0.32	0.71	3.37	3.70
MAE		0.12	0.29	0.30	0.67	3.12	3.42

^aThe formula for the CCSD(T)/CBS interaction energies is shown in eq 29.

^bnoCP means no counterpoise BSSE corrections; CP means with counterpoise BSSE corrections.

^c$\alpha \mathrm{R}$, $\mathrm{a}\beta$, and $\beta$ represent $\alpha$-helix, anti-parallel $\beta$-sheet, and parallel $\beta$-sheet conformations, respectively.

^dThe values in parentheses are differences between the values calculated by DFT methods and corresponding values calculated by the CCSD(T)/CBS method.

pGM Models Show the Best Performances in Interaction Energy Calculations.

Listed in Table 2 are the interaction energies calculated at the $\omega \text{B97X}-\mathrm{D}$/aug-cc-pVTZ level of theory without counterpoise corrections and seven molecular mechanical force fields. The interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ between ${\text{Gly}}_m$ and ${\text{Gly}}_n$ of the ${\text{Gly}}_m{\text{:Gly}}_n$ oligomers were calculated following eq 21 without consideration of the deformation energies to avoid complications in energy calculations that may arise from structural changes. The interaction energies calculated by the $\omega \text{B97X}-\mathrm{D}$ method exhibit an increasing trend in the order of $\text{Gly:Gly}$, ${\text{Gly:Gly}}_2$, ${\text{Gly:Gly}}_3$, ${\text{Gly}}_2{\text{:Gly}}_2$, and ${\text{Gly}}_3{\text{:Gly}}_3$ for all three conformations. It is notable that $\text{IE}({\text{Gly}}_3{\text{:Gly}}_3)$ is 11.00 kcal/mol stronger than $\text{IE}(\text{Gly:Gly})$ in the $\alpha$-helix conformation. In comparison, for the anti-parallel $\beta$-sheet and parallel $\beta$-sheet conformations, $\text{IE}({\text{Gly}}_3{\text{:Gly}}_3)$ are only 3.50 and 4.11 kcal/mol stronger than $\text{IE}(\text{Gly:Gly})$, respectively. The larger difference of the $\alpha$-helix conformation is attributable to the strong polarization effect caused by the alignments of the main-chain peptide hydrogen bonds. Another observation is that although ${\text{Gly:Gly}}_3$ and ${\text{Gly}}_2{\text{:Gly}}_2$ are both tetramers, ${\text{Gly}}_2{\text{:Gly}}_2$ consistently shows stronger interaction energies than ${\text{Gly:Gly}}_3$ in all three conformations. This shows that the inner parts of the peptide secondary structures are expected to have stronger main-chain hydrogen bonding than the outer parts.

Table 2.

Interaction Energies $\mathbf{IE}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ of Glycine Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by $\omega B97X-\mathbf{D}$/aTZ and Molecular Mechanical Force Fields (kcal/mol)^a

$\omega \text{B97X}-\mathrm{D}$/aTZ		pGM-perm	pGM-ind	Amoeba13	ff12pol	ff19SB	ff15ipq	ff03
$\text{Gly:Gly}$
$\alpha \mathrm{R}$ b	−14.73	−16.21 (−1.48)d	−16.09 (−1.36)	−12.98 (1.75)	−12.91 (1.81)	−16.04 (−1.31)	−19.08 (−4.35)	−15.35 (−0.62)
$\mathrm{a}\beta$ b	−14.53	−16.01 (−1.48)	−16.13 (−1.60)	−13.82 (0.71)	−14.67 (−0.15)	−13.60 (0.92)	−16.31 (−1.78)	−11.83 (2.70)
$\beta$ b	−17.36	−19.24 (−1.88)	−19.28 (−1.92)	−14.16 (3.20)	−17.82 (−0.46)	−15.69 (1.67)	−18.85 (−1.48)	−14.78 (2.58)
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$ b	−17.90	−19.21 (−1.31)	−19.11 (−1.22)	−15.38 (2.52)	−14.94 (2.96)	−17.90 (−0.01)	−21.30 (−3.40)	−17.09 (0.80)
$\mathrm{a}\beta$ b	−16.00	−17.26 (−1.26)	−17.38 (−1.38)	−14.89 (1.11)	−15.68 (0.32)	−14.06 (1.94)	−16.83 (−0.83)	−12.28 (3.72)
$\beta$ b	−18.99	−20.64 (−1.65)	−20.67 (−1.69)	−15.42 (3.57)	−18.97 (0.02)	−16.19 (2.80)	−19.45 (−0.46)	−15.26 (3.73)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$ b	−19.06	−20.32 (−1.26)	−20.23 (−1.18)	−16.26 (2.80)	−15.68 (3.37)	−18.42 (0.63)	−21.93 (−2.87)	−17.57 (1.48)
$\mathrm{a}\beta$ b	−16.12	−17.36 (−1.24)	−17.47 (−1.35)	−14.95 (1.17)	−15.74 (0.38)	−14.09 (2.03)	−16.86 (−0.74)	−12.31 (3.81)
$\beta$ b	−19.16	−20.79 (−1.63)	−20.83 (−1.67)	−15.56 (3.61)	−19.08 (0.08)	−16.25 (2.91)	−19.52 (−0.36)	−15.31 (3.85)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$ b	−22.11	−23.20 (−1.09)	−23.12 (−1.01)	−18.54 (3.57)	−17.71 (4.40)	−20.30 (1.81)	−24.16 (−2.04)	−19.36 (2.75)
$\mathrm{a}\beta$ b	−17.72	−18.75 (−1.03)	−18.85 (−1.13)	−16.21 (1.51)	−16.88 (0.84)	−14.61 (3.11)	−17.49 (0.23)	−12.80 (4.92)
$\beta$ b	−21.02	−22.34 (−1.33)	−22.40 (−1.38)	−16.98 (4.03)	−20.27 (0.75)	−16.77 (4.25)	−20.14 (0.87)	−15.80 (5.22)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$ b	−25.73	−26.68 (−0.96)	−26.63 (−0.90)	−21.27 (4.45)	−20.09 (5.64)	−21.91 (3.82)	−26.11 (−0.39)	−20.86 (4.87)
$\mathrm{a}\beta$ b	−18.03	−18.99 (−0.97)	−19.09 (−1.07)	−16.37 (1.66)	−17.04 (0.98)	−14.69 (3.33)	−17.57 (0.46)	−12.90 (5.12)
$\beta$ b	−21.47	−22.74 (−1.27)	−22.80 (−1.32)	−17.33 (4.14)	−20.56 (0.91)	−16.92 (4.55)	−20.33 (1.14)	−15.94 (5.53)
RMSE		1.35	1.37	2.91	2.28	2.67	1.87	3.78
MAE		1.32	1.34	2.65	1.54	2.34	1.43	3.45
max devc		−0.96	−0.90	4.45	5.64	4.55	1.14	5.53
min devc		−1.88	−1.92	0.71	−0.46	−1.31	−4.35	−0.62

^aThe formula for the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ is shown in eq 21.

^b$\alpha \mathrm{R}$, $\mathrm{a}\beta$, and $\beta$ represent $\alpha$-helix, anti-parallel $\beta$-sheet, and parallel $\beta$-sheet conformations, respectively.

^cThe maximum and minimum deviations with $\omega \text{B97X}-\mathrm{D}$/aTZ results.

^dThe values in parentheses are differences between the values calculated by molecular mechanical force fields and corresponding values calculated by the $\omega \text{B97X}-\mathrm{D}$/aTZ method.

The interaction energies calculated by the pGM-perm and pGM-ind models stand out as the closest to the DFT results, with RMSEs of 1.35 and 1.37 kcal/mol, respectively. The similarity between the performances of the pGM-perm and pGM-ind models indicates that, with the pGM damping schemes, the induced dipoles are sufficient for calculating the interaction energies of glycine dipeptides. The next best performance is given by the ff15ipq force field with an RMSE of 1.87 kcal/mol, which is an additive force field whose charges were fit to the ESP of peptides in the presence of explicit solvent water.⁵⁴ The polarizable force field ff12pol, the additive force field ff19SB, and the polarizable force field Amoeba13 are ranked fourth to sixth, with RMSE of 2.28, 2.67, and 2.91 kcal/mol, respectively. The observation that Amoeba13 performs worse than ff12pol in this test set is somewhat surprising, given that Amoeba13 is such an elaborate force field that includes atomic permanent dipoles and quadrupoles, in addition to the polarizable induced dipoles.^26,28 In contrast, the ff12pol force field is a minimalist polarizable induced dipole force field with neither permanent dipoles nor quadrupoles.^22-25

Another interesting observation is that, compared with the $\omega \text{B97X}-\mathrm{D}$ results, the pGM-perm and pGM-ind models systematically overestimate the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$. On average, pGM-perm and pGM-ind overestimate the interaction energies by 1.32 and 1.34 kcal/mol, respectively. Also interesting is the consistency of the deviations between the interaction energies of $\omega \text{B97X}-\mathrm{D}$ and the pGM models across different conformations. Since the main-chain hydrogen bonds contribute to peptide secondary structure formations, the balance across different conformations can influence the peptide secondary structure preference and the capability of modeling the relative strength of different hydrogen-bonding systems and in peptide main-chain secondary structures. In this regard, both pGM models show good balance and their differences in the interaction energies are about the same magnitude across the three conformations, with pGM-perm exhibiting slightly better consistency than pGM-ind. For example, the Gly:Gly interaction energies are overestimated by 1.48–1.88 kcal/mol by pGM-perm and overestimated by 1.36–1.92 kcal/mol by pGM-ind. In contrast, all other force fields show nonuniform deviations across different conformations. Taking ff12pol as an example, the largest deviation of interaction energies among the three conformations consistently comes from the oligomers in the $\alpha$-helix conformation. For Amoeba13, the deviations of $\alpha$-helix and parallel $\beta$-sheet conformers are comparable, whereas the deviations of anti-parallel $\beta$-sheet conformer are notably smaller. Since uniform deviations across different conformers naturally avoid introducing conformational bias, it is much more preferable than nonuniform deviations. Furthermore, when taking all ${\text{Gly}}_m{\text{:Gly}}_n$ oligomers into account, the deviations of interaction energies range between −0.96 and −1.88 kcal/mol for pGM-perm, and between −0.90 and −1.92 kcal/mol for pGM-ind, which are more consistent than other force fields. On the other hand, all other force fields (except ff15ipq) exhibit a tendency of growing deviations with increasing size of oligomers, suggesting that they underestimate the many-body interactions when there are multiple peptides in the oligomers. Therefore, it is encouraging that the pGM models outperform all other five force fields in terms of interaction energy calculations across oligomers with different conformations and with different sizes.

pGM Models Most Accurately Reproduce QM Many-Body Interaction Energies.

Subtracting corresponding rows of the Gly:Gly dimers from other rows in Table 2 gives Table 3, which lists the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ calculated by the seven force fields compared with those calculated by the $\omega \text{B97X}-\mathrm{D}$ method. The many-body interaction energies defined in eq 22 describe the overall (additive and nonadditive) contributions from the neighboring glycine dipeptides (${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$, excluding the Gly:Gly at the interface) to the dimerization energy at the interface of ${\text{Gly}}_m{\text{:Gly}}_n$. As shown in the $\omega \text{B97X}-\mathrm{D}$ results, the many-body interaction energies again increase in the order of ${\text{Gly:Gly}}_2$, ${\text{Gly:Gly}}_3$, ${\text{Gly}}_2{\text{:Gly}}_2$, and ${\text{Gly}}_3{\text{:Gly}}_3$ for all three conformations. Comparing oligomers in the anti-parallel and parallel $\beta$-sheet conformations, we can see that the addition of outer peptides does not significantly increase the many-body interactions. Thus, the cross-strand effects in the $\beta$-sheet conformations are mainly limited to those in close contact and diminish rather quickly with distance. For the $\alpha$-helix conformation, notably, a stronger many-body interaction is observed because the hydrogen bonds are aligned in the same directions. An interesting observation is that the many-body interaction energy of tetramer ${\text{Gly:Gly}}_3$ is only marginally stronger than that of trimer ${\text{Gly:Gly}}_2$ by 1.16 kcal/mol, which is a much smaller increase compared to the 4.21 kcal/mol increase of tetramer ${\text{Gly}}_2{\text{:Gly}}_2$. By adding one more peptide at each side, the many-body interaction energy of hexamer ${\text{Gly}}_3{\text{:Gly}}_3$ becomes stronger by 3.62 kcal/mol than that of tetramer ${\text{Gly}}_2{\text{:Gly}}_2$. Therefore, for the $\alpha$-helix conformation, in contrast to the marginal effect of adding peptides to one side of the interface, symmetric addition makes the interaction at the interface significantly stronger, so that a much stronger many-body interaction is expected in the inner part of $\alpha$-helices. Therefore, the outer and inner parts of $\alpha$-helices could have considerably different stabilities. This effect could be significant in nonpolar environments such as transmembrane proteins.

Table 3.

Many-Body Interaction Energies $\mathbf{ME}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ of Glycine Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by $\omega B97X-\mathbf{D}$/aTZ and Molecular Mechanical Force Fields (kcal/mol)^a,b

$\omega \text{B97X}-\mathrm{D}$/aTZ		pGM-perm	pGM-ind	Amoeba13	ff12pol	ff19SB	ff15ipq	ff03
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$	−3.17	−3.00 (0.17)	−3.02 (0.15)	−2.40 (0.77)	−2.03 (1.14)	−1.87 (1.30)	−2.22 (0.95)	−1.75 (1.42)
$\mathrm{a}\beta$	−1.47	−1.25 (0.22)	−1.24 (0.23)	−1.07 (0.40)	−1.00 (0.47)	−0.46 (1.02)	−0.53 (0.95)	−0.44 (1.03)
$\beta$	−1.63	−1.39 (0.23)	−1.39 (0.23)	−1.25 (0.37)	−1.14 (0.48)	−0.50 (1.12)	−0.60 (1.02)	−0.48 (1.15)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$	−4.33	−4.11 (0.22)	−4.14 (0.19)	−3.28 (1.05)	−2.77 (1.56)	−2.39 (1.94)	−2.85 (1.48)	−2.23 (2.10)
$\mathrm{a}\beta$	−1.59	−1.35 (0.24)	−1.34 (0.25)	−1.14 (0.46)	−1.07 (0.52)	−0.49 (1.11)	−0.55 (1.04)	−0.48 (1.11)
$\beta$	−1.80	−1.55 (0.25)	−1.55 (0.25)	−1.39 (0.41)	−1.26 (0.54)	−0.56 (1.24)	−0.67 (1.13)	−0.53 (1.27)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$	−7.38	−6.99 (0.39)	−7.03 (0.35)	−5.57 (1.82)	−4.80 (2.58)	−4.27 (3.12)	−5.08 (2.31)	−4.01 (3.37)
$\mathrm{a}\beta$	−3.19	−2.74 (0.45)	−2.72 (0.47)	−2.39 (0.80)	−2.20 (0.99)	−1.01 (2.19)	−1.19 (2.01)	−0.97 (2.22)
$\beta$	−3.66	−3.10 (0.55)	−3.12 (0.54)	−2.82 (0.84)	−2.45 (1.21)	−1.08 (2.57)	−1.30 (2.36)	−1.02 (2.64)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$	−11.00	−10.47 (0.53)	−10.53 (0.47)	−8.29 (2.71)	−7.18 (3.82)	−5.88 (5.12)	−7.03 (3.97)	−5.51 (5.49)
$\mathrm{a}\beta$	−3.50	−2.98 (0.51)	−2.96 (0.53)	−2.55 (0.95)	−2.37 (1.13)	−1.09 (2.41)	−1.26 (2.24)	−1.07 (2.43)
$\beta$	−4.11	−3.50 (0.61)	−3.52 (0.59)	−3.17 (0.94)	−2.74 (1.37)	−1.23 (2.87)	−1.48 (2.63)	−1.16 (2.95)
RMSE		0.40	0.38	1.16	1.62	2.45	2.04	2.58
MAE		0.37	0.35	0.96	1.32	2.17	1.84	2.26
max dev		0.61	0.59	2.71	3.82	5.12	3.97	5.49
min dev		0.17	0.15	0.37	0.47	1.02	0.95	1.03

^aThe formula for the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ is shown in eq 22.

^bSee Table 2 and text for notation.

Among the seven force fields tested, pGM-perm and pGM-ind again show the lowest RMSEs (0.40 and 0.38 kcal/mol, respectively) and the lowest MAEs (0.37 and 0.35 kcal/mol, respectively), making them the best force fields in terms of many-body interaction energy calculations. It is encouraging that the RMSEs and MAEs of both pGM models are lower than the thermal fluctuation energy of 0.60 kcal/mol at 300 K. Similar to the case of interaction energy calculations, both pGM models give similar performances in terms of many-body interaction energy calculations. This indicates a potential advantage of the ESP fitting strategy employed for pGM parameterizations. Both the interaction energies and many-body interaction energies between molecules are largely dependent on the electrostatic interactions, and the ESP surrounding molecules are one of the most important electrostatic properties. Since both the pGM-ind and pGM-perm models are able to reproduce QM ESPs with low errors,⁵² it is expected that both models can accurately reproduce QM interaction energies and many-body interaction energies, therefore giving similar performances.

The next best-performing force field is the Amoeba13 force field, which exhibits the largest improvement compared with interaction energy calculations in Table 2, with the RMSE reduced from 2.91 to 1.16 kcal/mol. The significant improvement of Amoeba13 shows that the short-range interactions are the main cause of the large errors observed in the interaction energies. The ff12pol force field is ranked the third best-performing force field, with an RMSE of 1.62 kcal/mol. It is remarkable that all polarizable force fields perform better than all additive force fields. In fact, all additive force fields notably underestimate the many-body interactions by more than 2.00 kcal/mol. Among the additive force fields tested, ff15ipq once again shows the best performance, with an RMSE of 2.04 kcal/mol. However, this RMSE is slightly higher than that of interaction energies (1.87 kcal/mol) given by ff15ipq.

Another observation in Table 3 is that all force fields consistently underestimate the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ when compared with the $\omega \text{B97X}-\mathrm{D}$ results. For the pGM models, this is in sharp contrast to the systematic overestimations in the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$, as shown in Table 2, indicating that the long-range terms are still under-represented in the pGM models. Moreover, this suggests that the overestimations of $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ of the pGM models are primarily due to the short-range van der Waals terms. Because of this, we anticipate that the present van der Waals parameters, which were taken directly from ff12pol without optimization, need to be tuned to make the short-range terms less attractive. For Amoeba13 and ff12pol, however, since their $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ and $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ are systematically weaker than the $\omega \text{B97X}-\mathrm{D}$ results and the errors in $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ are larger than $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$, it appears that these two force fields could be improved by strengthening both their short-range and polarization terms.

Similar to the case of interaction energies, the underestimations of the pGM models compared to $\omega \text{B97X}-\mathrm{D}$ across different conformations and across different oligomers are consistent, which range between 0.17 and 0.61 kcal/mol for pGM-perm and between 0.15 and 0.59 kcal/mol for pGM-ind. In contrast, all other force fields once again show nonuniform deviations across different conformations, and the deviations increase with the size of oligomers. It is notable that the additive ff15ipq force field, which exhibits relatively consistent deviations in terms of interaction energies, also shows gradually increasing deviations with the oligomer size in terms of many-body interaction energies. Based on the above observations, we conclude that the polarization effects play critical roles in the many-body interactions, and the additive force fields are, in general, incapable of modeling them accurately.

pGM Models Perform the Best in Reproducing QM Nonadditive and Additive Contributions to the Many-Body Interactions.

The many-body interaction energies in Table 3 depend on the nonbonded terms in the functional form of each molecular mechanical force field. For additive force fields such as Amber ff19SB, ff15ipq, and ff03, the many-body interactions only have contributions from the additive electrostatic and van der Waals terms. In polarizable force fields ff12pol and pGM-ind, the nonadditive induced dipole polarization energy is also involved. The pGM-perm model has additional energy contributions from atomic permanent dipoles, and the Amoeba13 force field also has contributions from atomic permanent quadrupoles, which are both additive terms. It is difficult to decipher which of these terms plays a more important role if we just look at the total many-body interaction energies shown in Table 3. Therefore, we decompose the many-body interaction energies into nonadditive and additive contributions to gain insight into these force fields. For each ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer, the formulas of the nonadditive contributions ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and the additive contributions ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$ are given in eqs 24 and 25, respectively. The proof of the decomposition is shown in the Appendix. Note that the functional forms of additive force fields only have additive terms, so that the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ of any additive force field is guaranteed to be zero. For this reason, we will only compare the performances of polarizable force fields pGM-perm, pGM-ind, Amoeba13, and ff12pol in this section.

The interaction energies of the two peptides at the interface, ${\text{IE}}_{\text{mid}}({\text{Gly}}_m{\text{:Gly}}_n)$, in the presence of the neighboring peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$ defined in eq 23, calculated by the four polarizable force fields and by $\omega \text{B97X}-\mathrm{D}$, are shown in Table S1. For additive force fields, the values will be identical to those of $\text{IE}(\text{Gly:Gly})$ in the absence of neighboring peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$, as shown in Table 2, if listed. For polarizable force fields, a trend similar to that in Table 2 is observed. First, the pGM-perm and pGM-ind models outperform the other two polarizable force fields, with RMSEs of 1.39 and 1.43 kcal/mol, respectively. The RMSEs of the Amoeba13 force field and the ff12pol force field are 2.54 and 1.69 kcal/mol, respectively. Second, compared with the $\omega \text{B97X}-\mathrm{D}$ results, the pGM-perm and pGM-ind models systematically overestimate the interaction energies (by 1.37 and 1.41 kcal/mol, respectively), whereas both Amoeba13 and ff12pol underestimate (by 2.31 and 1.18 kcal/mol, respectively). Third, the deviations between the interaction energies given by $\omega \text{B97X}-\mathrm{D}$ and the pGM models across different conformations and different oligomers are highly consistent. For pGM-perm, the largest spread (0.41 kcal/mol) comes from ${\text{Gly:Gly}}_3$ between the anti-parallel $\beta$-sheet (−1.25 kcal/mol) and parallel $\beta$-sheet (−1.66 kcal/mol) conformers. For pGM-ind, the largest spread (0.56 kcal/mol) is between the $\alpha$-helix (−1.36 kcal/mol) and parallel $\beta$-sheet (−1.92 kcal/mol) conformers of Gly:Gly. Overall, the deviations range between −1.02 and −1.88 kcal/mol for pGM-perm, and between −1.15 and −1.92 kcal/mol for pGM-ind, for all five oligomers and all three conformations. However, Amoeba13 and ff12pol show nonuniform deviations across different conformations, and these deviations tend to increase with the size of oligomers.

Table 4 shows the nonadditive contributions ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ of $\omega \text{B97X}-\mathrm{D}$ and the four polarizable force fields obtained by subtracting corresponding rows of the Gly:Gly dimers from other rows in Table S1, and Table 5 shows the additive contributions ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$ obtained by subtracting the corresponding nonadditive contributions ME_NA(Gly_m:Gly_n) from the many-body interaction energies ME(Gly_m:Gly_n) in Table 3. For nonadditive contributions ME_NA(Gly_m:Gly_n), pGM-ind produces the lowest RMSE (0.30 kcal/mol) among all four polarizable force fields, and pGM-perm is the second best, with an RMSE of 0.33 kcal/mol. However, for additive contributions ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$, pGM-perm performs the best with an RMSE of 0.09 kcal/mol, and pGM-ind is the second-best, with an RMSE of 0.10 kcal/mol. The significantly lower RMSEs of the additive contributions of the pGM models than other polarizable force fields show the robustness of the ESP fitting scheme of PyRESP since the additive contribution is mainly due to the interactions involving fixed point charges and permanent dipoles.⁵² For both nonadditive and additive contributions, the ff12pol force field gives the worst performance, with RMSEs of 0.95 and 0.72 kcal/mol for the nonadditive and additive contributions, respectively. Amoeba13 yields RMSEs of 0.59 kcal/mol for both the nonadditive and additive contributions, which are better than ff12pol in terms of both contributions, but still notably worse than the pGM models.

Table 4.

Nonadditive Contributions ${\mathbf{ME}}_{\mathbf{NA}}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ to the Many-Body Interaction Energies of Glycine Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by $\omega B97X-\mathbf{D}$/aTZ and Polarizable Force Fields (kcal/mol)^a,b

$\omega \text{B97X}-\mathrm{D}$/aTZ		pGM-perm	pGM-ind	Amoeba13	ff12pol
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$	−1.70	−1.57 (0.12)	−1.61 (0.09)	−1.30 (0.39)	−0.98 (0.71)
$\mathrm{a}\beta$	−1.04	−0.83 (0.21)	−0.83 (0.21)	−0.76 (0.28)	−0.64 (0.40)
$\beta$	−1.12	−0.91 (0.21)	−0.92 (0.20)	−0.86 (0.26)	−0.73 (0.40)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$	−2.17	−2.02 (0.15)	−2.07 (0.10)	−1.65 (0.52)	−1.27 (0.90)
$\mathrm{a}\beta$	−1.12	−0.89 (0.23)	−0.89 (0.22)	−0.80 (0.31)	−0.68 (0.44)
$\beta$	−1.21	−0.99 (0.22)	−1.00 (0.21)	−0.95 (0.26)	−0.79 (0.42)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$	−3.52	−3.27 (0.26)	−3.34 (0.18)	−2.68 (0.84)	−2.10 (1.43)
$\mathrm{a}\beta$	−2.13	−1.71 (0.42)	−1.72 (0.42)	−1.56 (0.57)	−1.32 (0.81)
$\beta$	−2.48	−1.99 (0.49)	−2.02 (0.47)	−1.90 (0.58)	−1.51 (0.97)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$	−4.62	−4.32 (0.31)	−4.41 (0.21)	−3.48 (1.14)	−2.79 (1.83)
$\mathrm{a}\beta$	2.29	−1.83 (0.46)	−1.83 (0.45)	−1.65 (0.64)	−1.40 (0.89)
$\beta$	−2.68	−2.16 (0.52)	−2.19 (0.49)	−2.05 (0.63)	−1.62 (1.06)
RMSE		0.33	0.30	0.59	0.95
MAE		0.30	0.27	0.54	0.85
max dev		0.52	0.49	1.14	1.83
min dev		0.12	0.09	0.26	0.40

^aThe formula for the nonadditive contributions ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ to the many-body interaction energies is shown in eq 24.

^bSee Table 2 and text for notation.

Table 5.

Additive Contributions ${\mathbf{ME}}_{\mathbf{A}}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ to the Many-Body Interaction Energies of Glycine Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by $\omega B97X-\mathbf{D}$/aTZ and Polarizable Force Fields (kcal/mol)^a,b

$\omega \text{B97X}-\mathrm{D}$/aTZ		pGM-perm	pGM-ind	Amoeba13	ff12pol
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$	−1.47	−1.43 (0.05)	−1.41 (0.06)	−1.10 (0.38)	−1.04 (0.43)
$\mathrm{a}\beta$	−0.43	−0.42 (0.01)	−0.41 (0.02)	−0.31 (0.12)	−0.36 (0.07)
$\beta$	−0.50	−0.48 (0.02)	−0.47 (0.03)	−0.39 (0.11)	−0.42 (0.08)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$	−2.16	−2.09 (0.07)	−2.08 (0.08)	−1.63 (0.53)	−1.50 (0.66)
$\mathrm{a}\beta$	−0.48	−0.46 (0.02)	−0.45 (0.03)	−0.33 (0.15)	−0.39 (0.09)
$\beta$	−0.59	−0.56 (0.03)	−0.55 (0.04)	−0.44 (0.14)	−0.47 (0.11)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$	−3.86	−3.73 (0.14)	−3.69 (0.17)	−2.88 (0.98)	−2.70 (1.16)
$\mathrm{a}\beta$	−1.06	−1.03 (0.03)	−1.01 (0.05)	−0.83 (0.23)	−0.88 (0.17)
$\beta$	−1.17	−1.11 (0.06)	−1.10 (0.07)	−0.92 (0.25)	−0.94 (0.23)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$	−6.37	−6.16 (0.22)	−6.12 (0.25)	−4.81 (1.57)	−4.38 (1.99)
$\mathrm{a}\beta$	−1.21	−1.15 (0.06)	−1.13 (0.08)	−0.90 (0.31)	−0.97 (0.24)
$\beta$	−1.43	−1.34 (0.09)	−1.33 (0.10)	−1.11 (0.32)	−1.12 (0.31)
RMSE		0.09	0.10	0.59	0.72
MAE		0.06	0.08	0.42	0.46
max dev		0.22	0.25	1.57	1.99
min dev		0.01	0.02	0.11	0.07

^aThe formula for the additive contributions ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$ to the many-body interaction energies is shown in eq 25.

^bSee Table 2 and text for notation.

Interestingly, compared with the $\omega \text{B97X}-\mathrm{D}$ results, all four polarizable force fields underestimate both the nonadditive and additive contributions to varying degrees. As measured by MAE, the nonadditive contributions are underestimated by 0.30, 0.27, 0.54, and 0.85 kcal/mol by pGM-perm, pGM-ind, Amoeba13, and ff12pol, respectively, and the additive contributions are underestimated by 0.06, 0.08, 0.42, and 0.46 kcal/mol by pGM-perm, pGM-ind, Amoeba13, and ff12pol, respectively. Therefore, MAEs show the same performance trend as RMSEs, where pGM-ind performs the best for calculating the nonadditive contributions, and pGM-perm performs the best for calculating the additive contributions. The consistent underestimations could potentially come from two sources: inadequate short-range damping and smaller-than-needed polarizabilities, both of which may be improved by further parameterizations. Encouragingly, the pGM models again exhibit consistent deviations from the $\omega \text{B97X}-\mathrm{D}$ results for both contributions across different conformations and different sized oligomers. For the pGM-perm model, the deviations range between 0.12 and 0.52 kcal/mol for the nonadditive contributions, and between 0.01 and 0.22 kcal/mol for the additive contributions; For the pGM-ind model, the deviations range between 0.09 and 0.49 kcal/mol for the nonadditive contributions, and between 0.02 and 0.25 kcal/mol for the additive contributions. In contrast, Amoeba13 and ff12pol show significant variations in the deviations from the $\omega \text{B97X}-\mathrm{D}$ results for both nonadditive and additive contributions across different conformations. Overall, Tables 4 and 5 show that compared with the other two polarizable force fields tested here, the pGM models (with or without permanent atomic dipoles) perform the best in terms of reproducing QM nonadditive and additive contributions to the many-body interaction energies.

pGM Models Are Robust with Altered Atomic Polarizabilities.

Because of the inherent approximations to either experimental observations or QM calculations, all mechanical force fields are subject to errors that can come from both the functional forms and parameterization processes. In the development of Amber force fields, a consistent electrostatic parameterization approach is to fit the QM calculated ESPs of small molecules or fragments of large molecules to obtain atomic charges and multipoles. Technically, this approach is rather straightforward and allows the development of consistent parameters across a wide variety of chemistry. In the cases of polarizable force fields, another advantage is that the errors in the initial fitting of polarizabilities can be partially compensated at the stage when charges and permanent multipoles are calculated, yielding a more robust force field. This feature is potentially advantageous because of the nonlinear nature of the polarization energy.

In our previous work, the pGM atomic polarizabilities and radii were obtained by fitting QM molecular polarizability tensors of 1405 molecules or dimers.⁴⁵ In this work, we further evaluated the robustness of the pGM models by re-parameterizing the glycine dipeptide charges and permanent dipoles using the recently developed PyRESP program,⁵² with alternative polarizabilities, including the pGM polarizabilities scaled by a factor of 0.9, the Amoeba13 polarizabilities,²⁶ and the Amber ff12pol polarizabilities.²² These alternative polarizability sets are either scaled or taken from different sources and have been developed for different polarization schemes. Therefore, we expect that the energies related to polarization calculated with these three polarizability sets be less accurate than those produced by the pGM models with original pGM polarizabilities shown in Tables 2-5. Our objective is to see whether these “wrong” polarizabilities would lead to intolerable errors in energy calculations.

The interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ as well as the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ of each ${\text{Gly}}_m{\text{:Gly}}_n$ oligomer of the pGM-perm and pGM-ind models calculated with the alternative polarizabilities are shown in Tables 6 and S2, respectively. Interestingly, for both pGM models, the “wrong” polarizabilities produce interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ with lower RMSEs compared with those obtained by the “correct” pGM polarizabilities shown in Table 2. For the pGM-perm model, the overall RMSE of interaction energies decreased from 1.35 kcal/mol to 0.80, 0.82, and 0.62 kcal/mol for the scaled pGM, Amoeba13, and ff12pol polarizabilities, respectively. For the pGM-ind model, the overall RMSE of interaction energies decreased from 1.37 kcal/mol to 0.81, 0.97, and 0.57 kcal/mol for the scaled pGM, Amoeba13, and ff12pol polarizabilities, respectively. The higher RMSEs associated with the “correct” pGM polarizabilities compared with that of the “wrong” polarizabilities might be explained by the fact that the van der Waals parameters for the pGM models were taken directly from the ff12pol force field without any optimization. As shown in Table 2, with the original polarizabilities, both pGM-perm and pGM-ind overestimate the interaction energies. Since the interaction energies can be decomposed to the electrostatic and van der Waals contributions, the overestimation in the interaction energies can be explained by the overestimation of the van der Waals term in the current pGM models. Specifically, the dispersion effect of the van der Waals term might be too attractive. As shown in Tables 6 and S2, the amount of overestimation in the interaction energies is reduced with the alternative polarizabilities, indicating weaker electrostatic attractions. Consequently, the overestimation of the van der Waals term is compensated by the underestimation of the electrostatic term with the alternative polarizabilities, leading to lower overall RMSEs. Therefore, there is a need to reparameterize the van der Waals terms, and we anticipate the pGM models with re-parameterized van der Waals terms will give interaction energies with better agreement with QM results than those with the “wrong” polarizabilities.

Table 6.

Interaction Energies $\mathbf{IE}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ and Many-Body Interaction Energies $\mathbf{ME}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ of Glycin Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by the pGM-perm Model with the Alternative Polarizabilities (kcal/mol)^a,b

	pGM-perm/scaledc		pGM-perm/Amoebac		pGM-perm/ff12polc
	$\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$	$\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$	$\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$	$\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$	$\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$	$\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$
$\text{Gly:Gly}$
$\alpha \mathrm{R}$	−16.06 (−1.33)		−16.13 (−1.40)		−15.86 (−1.13)
$\mathrm{a}\beta$	−15.58 (−1.06)		−15.60 (−1.07)		−15.01 (−0.48)
$\beta$	−18.64 (−1.28)		−18.62 (−1.26)		−17.75 (−0.39)
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$	−18.89 (−0.99)	−2.83 (0.34)	−18.93 (−1.04)	−2.80 (0.36)	−18.44 (−0.54)	−2.58 (0.59)
$\mathrm{a}\beta$	−16.72 (−0.72)	−1.13 (0.34)	−16.75 (−0.75)	−1.14 (0.33)	−15.99 (0.01)	−0.98 (0.49)
$\beta$	−19.90 (−0.91)	−1.26 (0.37)	−19.89 (−0.90)	−1.27 (0.36)	−18.84 (0.15)	−1.09 (0.54)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$	−19.91 (−0.85)	−3.85 (0.48)	−19.96 (−0.91)	−3.83 (0.50)	−19.35 (−0.30)	−3.49 (0.84)
$\mathrm{a}\beta$	−16.80 (−0.68)	−1.21 (0.38)	−16.83 (−0.71)	−1.23 (0.36)	−16.06 (0.06)	−1.05 (0.54)
$\beta$	−20.04 (−0.88)	−1.40 (0.40)	−20.03 (−0.87)	−1.41 (0.39)	−18.96 (0.20)	−1.21 (0.59)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$	−22.64 (−0.53)	−6.58 (0.80)	−22.67 (−0.56)	−6.54 (0.84)	−21.86 (0.25)	−6.00 (1.38)
$\mathrm{a}\beta$	−18.06 (−0.34)	−2.47 (0.72)	−18.10 (−0.38)	−2.50 (0.69)	−17.15 (0.57)	−2.14 (1.05)
$\beta$	−21.43 (−0.42)	−2.79 (0.86)	−21.43 (−0.41)	−2.81 (0.85)	−20.15 (0.87)	−2.40 (1.25)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$	−25.85 (−0.12)	−9.79 (1.21)	−25.90 (−0.17)	−9.77 (1.23)	−24.72 (1.01)	−8.86 (2.14)
$\mathrm{a}\beta$	−18.27 (−0.25)	−2.69 (0.81)	−18.33 (−0.30)	−2.73 (0.77)	−17.33 (0.69)	−2.32 (1.17)
$\beta$	−21.78 (−0.31)	−3.14 (0.97)	−21.80 (−0.33)	−3.18 (0.93)	−20.45 (1.02)	−2.71 (1.40)
RMSE	0.80	0.70	0.82	0.69	0.62	1.11
MAE	0.71	0.64	0.74	0.63	0.51	1.00
max dev	−0.12	1.21	−0.17	1.23	1.02	2.14
min dev	−1.33	0.34	−1.40	0.33	−1.13	0.49

^aSee Table 2 and text for notation.

^bThe values in parentheses are differences between the values calculated by the pGM-perm model with the alternative polarizabilities and corresponding values calculated by the $\omega \text{B97X}-\mathrm{D}$/aTZ method, which can be found in Tables 2 and 3, respectively.

^cpGM-perm/scaled, pGM-perm/Amoeba, and pGM-perm/ff12pol represent the pGM-perm models with the pGM polarizabilities scaled by a factor of 0.9, the Amoeba13 polarizabilities, and the ff12pol polarizabilities, respectively.

In contrast to the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$, as expected, the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ calculated by the pGM models with the “wrong” polarizabilities are consistently worse than those with the “correct” pGM polarizabilities shown in Table 3. For the pGM-perm model, the overall RMSE of the many-body interaction energies increased from 0.40 kcal/mol to 0.70, 0.69, and 1.11 kcal/mol for the scaled pGM, Amoeba13, and ff12pol polarizabilities, respectively. Similarly, for the pGM-ind model, the overall RMSE increased from 0.38 kcal/mol to 0.69, 0.68, and 1.10 kcal/mol for the scaled pGM, Amoeba13, and ff12pol polarizabilities, respectively. Remarkably, the many-body interaction energies produced by the pGM models with alternative polarizabilities consistently outperform the Amoeba13 and ff12pol force fields, with their respective native polarizabilities shown in Table 3. With the Amoeba13 polarizabilities, the RMSEs of the Amoeba13 force field, the pGM-perm, and pGM-ind models are 1.16, 0.69, and 0.68 kcal/mol, respectively; with the ff12pol polarizabilities, the RMSEs of the ff12pol force field, the pGM-perm, and pGM-ind models are 1.62, 1.11, and 1.10 kcal/mol, respectively. Because short-range terms contribute much less to $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ than to $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$, these improvements are likely attributable to the differences in the treatment of long-range terms, including the electrostatic and polarization terms. This shows that the pGM models are highly robust in terms of modeling the many-body interactions of peptide main-chain hydrogen-bonding structures. The improvement is remarkable, given the substantial differences among the different force fields in their functional forms of the electrostatic and polarization terms. Both the Amoeba13 and ff12pol force fields are based on the Thole screening schemes, in which only the cross induction between the induced dipoles is screened to avoid polarization catastrophe. In the pGM models, all electrostatic terms are represented as Gaussian densities. Consequently, all electrostatic interactions are screened, including charge—charge, charge—dipole, and dipole—dipole interactions. The improvement observed in this comparison is likely attributable to the inherent consistency of the treatment of electrostatic terms in the pGM models.

The nonadditive and additive contributions to the many-body interactions calculated by the pGM-perm and pGM-ind models with the alternative polarizabilities are shown in Tables 7 and S3, respectively. With the scaled pGM polarizabilities, the RMSEs of the nonadditive contributions of the pGM-perm and pGM-ind models increase from 0.33 and 0.30 kcal/mol to 0.60 and 0.58 kcal/mol, respectively. Despite the fact that the functional forms of the polarization terms of the pGM models are different from those of the Amoeba13 and ff12pol force fields, the nonadditive contributions of the pGM models with the Amoeba13 and ff12pol polarizabilities are remarkably similar to Amoeba13 and ff12pol with their respective native polarizabilities. With the Amoeba13 polarizabilities, the RMSEs of the Amoeba13 force field, the pGM-perm, and pGM-ind models are 0.59, 0.59, and 0.57 kcal/mol, respectively; with the ff12pol polarizabilities, the RMSEs of the ff12pol force field, the pGM-perm, and pGM-ind models are 0.95, 0.96, and 0.95 kcal/mol, respectively. We therefore conclude that the changes in the functional forms in the calculations of induction energies from their respective native forms did not lead to an intolerable level of error.

Table 7.

Nonadditive Contributions ${\mathbf{ME}}_{\mathbf{NA}}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ and Additive Contributions ${\mathbf{ME}}_{\mathbf{A}}({\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}})$ to the Many-Body Interaction Energies of Glycine Dipeptide Oligomers ${\mathbf{Gly}}_{\mathit{m}}{:\mathrm{Gly}}_{\mathit{n}}$ Calculated by the pGM-perm Model with the Alternative Polarizabilities (kcal/mol)^a,b

	pGM-perm/scaledc		pGM-perm/Amoebac		pGM-perm/ff12polc
	${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$	${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$	${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$	${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$	${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$	${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$
${\text{Gly:Gly}}_2$
$\alpha \mathrm{R}$	−1.38 (0.31)	−1.44 (0.03)	−1.37 (0.33)	−1.44 (0.04)	−1.12 (0.58)	−1.46 (0.01)
$\mathrm{a}\beta$	−0.71 (0.33)	−0.42 (0.01)	−0.73 (0.32)	−0.42 (0.01)	−0.56 (0.48)	−0.42 (0.01)
$\beta$	−0.78 (0.35)	−0.48 (0.02)	−0.79 (0.33)	−0.48 (0.02)	−0.61 (0.51)	−0.48 (0.02)
${\text{Gly:Gly}}_3$
$\alpha \mathrm{R}$	−1.77 (0.40)	−2.08 (0.08)	−1.75 (0.42)	−2.08 (0.08)	−1.42 (0.75)	−2.07 (0.09)
$\mathrm{a}\beta$	−0.76 (0.36)	−0.46 (0.02)	−0.78 (0.34)	−0.45 (0.02)	−0.60 (0.52)	−0.45 (0.03)
$\beta$	−0.84 (0.37)	−0.55 (0.03)	−0.86 (0.35)	−0.55 (0.03)	−0.66 (0.55)	−0.55 (0.04)
${\text{Gly}}_2{\text{:Gly}}_2$
$\alpha \mathrm{R}$	−2.87 (0.65)	−3.71 (0.15)	−2.84 (0.68)	−3.70 (0.16)	−2.31 (1.21)	−3.69 (0.17)
$\mathrm{a}\beta$	−1.46 (0.67)	−1.02 (0.04)	−1.49 (0.64)	−1.01 (0.05)	−1.15 (0.99)	−1.00 (0.06)
$\beta$	−1.69 (0.79)	−1.10 (0.07)	−1.71 (0.77)	−1.10 (0.07)	−1.32 (1.17)	−1.08 (0.09)
${\text{Gly}}_3{\text{:Gly}}_3$
$\alpha \mathrm{R}$	−3.76 (0.86)	−6.03 (0.35)	−3.74 (0.89)	−6.03 (0.34)	−3.00 (1.62)	−5.86 (0.52)
$\mathrm{a}\beta$	−1.55 (0.73)	−1.13 (0.08)	−1.59 (0.69)	−1.13 (0.08)	−1.22 (1.07)	−1.10 (0.11)
$\beta$	−1.82 (0.85)	−1.32 (0.11)	−1.86 (0.82)	−1.32 (0.11)	−1.42 (1.26)	−1.29 (0.14)
RMSE	0.60	0.12	0.59	0.12	0.96	0.17
MAE	0.56	0.08	0.55	0.09	0.89	0.11
max dev	0.86	0.35	0.89	0.34	1.62	0.52
min dev	0.31	0.01	0.32	0.01	0.48	0.01

^aSee Table 6 and text for notation.

^bThe values in parentheses are differences between the values calculated by the pGM-perm model with the alternative polarizabilities and corresponding values calculated by the $\omega \text{B97X}-\mathrm{D}$/aTZ method, which can be found in Tables 4 and 5, respectively.

^cpGM-perm/scaled, pGM-perm/Amoeba, and pGM-perm/ff12pol represent the pGM-perm models with the pGM polarizabilities scaled by a factor of 0.9, the Amoeba13 polarizabilities, and the ff12pol polarizabilities, respectively.

For the additive contribution calculations, the RMSEs of the pGM-perm and pGM-ind models with the scaled pGM polarizabilities increase from 0.09 and 0.10 kcal/mol to 0.12 and 0.13 kcal/mol, respectively, which are essentially unchanged. Remarkably, both pGM models with the Amoeba13 and ff12pol polarizabilities notably outperform their respective native counterparts (Amoeba13 and ff12pol force fields) in the calculation of the additive contributions. With the Amoeba13 polarizabilities, the RMSEs of the Amoeba13 force field, the pGM-perm, and pGM-ind models are 0.59, 0.12, and 0.13 kcal/mol, respectively; with the ff12pol polarizabilities, the RMSEs of the ff12pol force field, the pGM-perm, and pGM-ind models are 0.72, 0.17, and 0.18 kcal/mol, respectively. In fact, for the additive contribution calculations, the RMSEs of both pGM models with the alternative polarizabilities are comparable to those with the original polarizabilities. The notably better performance of the pGM models with the Amoeba13 and ff12pol polarizabilities than the Amoeba13 and ff12pol force fields in the additive contribution calculations suggests that the PyRESP scheme of fitting charges and permanent multipoles from QM calculated ESPs is a reliable approach in the development of molecular mechanical force fields and has the ability to compensate the errors in the initial parameterization of polarizabilities.

CONCLUSIONS

In this work, we assessed the capabilities of the recently developed pGM models^46,47 in modeling the many-body interactions of glycine dipeptides main-chain hydrogen-bonding conformers. Two types of pGM models were considered, including that with (pGM-perm) and without (pGM-ind) permanent atomic dipoles. The performances of the pGM models were compared with several other widely used force fields, including Amoeba13,²⁸ ff12pol,^22-25 ff19SB,⁷ ff15ipq,⁵⁴ and ff03.⁵⁵ The glycine dipeptide oligomers were selected as the model systems since glycine has the minimalist side chain so that we can focus on main-chain hydrogen-bonding interactions.

We first identified $\omega \text{B97X}-\mathrm{D}$/aug-cc-pVTZ without counterpoise BSSE correction as the most suitable DFT method for our molecular systems. Compared with other DFT methods tested (M062X and B3LYP) with and without counterpoise corrections, $\omega \text{B97X}-\mathrm{D}$ without counterpoise correction produced the interaction energies of the formamide dimer and the glycine dipeptide dimers with the best agreement to those calculated at the CCSD(T)/CBS level of theory.

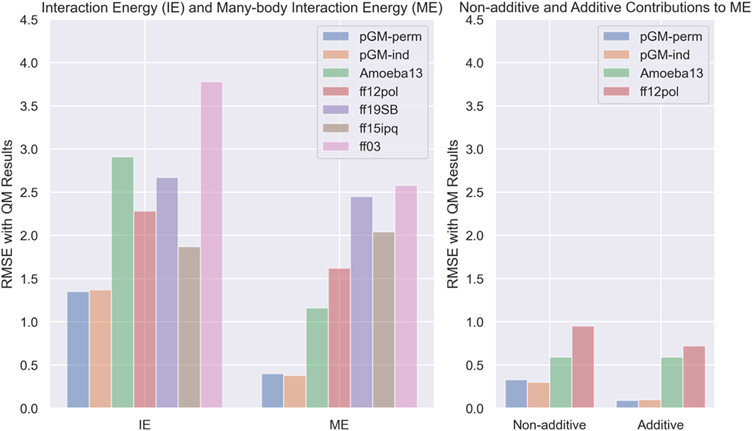
Next, we compared the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ and many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ calculated at the $\omega \text{B97X}-\mathrm{D}$/aug-cc-pVTZ level of theory and those calculated by the seven molecular mechanical force fields. The overall RMSEs of the interaction energies and many-body interaction energies of the seven force fields are shown in Figure 2. Encouragingly, the overall RMSEs of the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$ calculated by the pGM-perm and pGM-ind models are 1.35 and 1.37 kcal/mol, respectively, which significantly outperform other polarizable (Amoeba13, 2.91 kcal/mol; ff12pol, 2.28 kcal/mol) and additive (ff19SB, 2.67 kcal/mol; ff15ipq, 1.87 kcal/mol; ff03, 3.78 kcal/mol) force fields. For the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$, the overall RMSEs of the pGM-perm and pGM-ind models are 0.40 and 0.38 kcal/mol, respectively. In comparison, the RMSEs of other polarizable (Amoeba13, 1.16 kcal/mol; ff12pol, 1.62 kcal/mol) and additive (ff19SB, 2.45 kcal/mol; ff15ipq, 2.04 kcal/mol; ff03, 2.58 kcal/mol) force fields are notably higher than those of the pGM models. In addition, for both interaction energies and many-body interaction energies, the deviations between the $\omega \text{B97X}-\mathrm{D}$ results and the pGM models results across different conformations and oligomers with different sizes are highly consistent, while all other force fields exhibit nonuniform deviations across different conformations, and these deviations increase with the size of oligomers. Therefore, our data show that the pGM models perform the best among all seven tested force fields in terms of calculating interaction energy and many-body interaction energy.

Figure 2.

Overall RMSEs of the interaction energies $\text{IE}({\text{Gly}}_m{\text{:Gly}}_n)$, many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ (left), as well as the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and the additive contribution ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$ to the many-body interaction energies (right) of the tested force fields with the $\omega \text{B97X}-\mathrm{D}$/aug-cc-pVTZ calculated results.

For polarizable force fields, the many-body interaction energy can be decomposed into the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and the additive contribution ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$, so that we compared both contributions calculated by the four polarizable force fields with those of ωB97X-D calculations. Figure 2 shows the overall RMSEs of the nonadditive and additive contributions to the many-body interaction energies of the four polarizable force fields. Encouragingly, the pGM models result in the lowest RMSEs for both nonadditive (pGM-perm, 0.33 kcal/mol; pGM-ind, 0.30 kcal/mol) and additive (pGM-perm, 0.09 kcal/mol; pGM-ind, 0.10 kcal/mol) contributions. In comparison, the Amoeba13 force field gives RMSEs of 0.59 kcal/mol for both the nonadditive and additive contributions. The ff12pol force field gives RMSEs of 0.95 kcal/mol for the nonadditive contribution and 0.72 kcal/mol for the additive contribution. Therefore, the pGM models perform the best among all tested polarizable force fields in terms of modeling both the nonadditive and additive contributions to the many-body interactions.

Finally, we tested the robustness of the pGM models against parameterization errors by employing alternative polarizabilities. Interestingly, the pGM models with the alternative polarizabilities produce interaction energies with lower RMSEs compared with those produced by the original pGM polarizabilities. This might be explained by the fact that the current pGM models share identical van der Waals parameters as the ff12pol force field, and the overestimation of the van der Waals term is compensated by the underestimation of the electrostatic term with the alternative polarizabilities. In future works, the van der Waals parameters of the pGM models will be re-parameterized using similar ways as we did for parameterizing the ff12pol force field.²⁵ On the other hand, the pGM models with the alternative polarizabilities produce many-body interaction energies as well as the nonadditive and additive contributions to the many-body interactions with higher RMSEs compared with those with the original pGM polarizabilities. Even so, both pGM models with the alternative polarizabilities still give better or similar performances compared with the Amoeba13 and ff12pol force fields. Our data show that the pGM models are robust against polarizability errors and perform well even with those “wrong” polarizabilities.

In summary, this work validates that the pGM models have the capabilities to accurately model the interaction energies, many-body interaction energies, as well as the nonadditive and additive contributions to the many-body interactions of peptide main-chain hydrogen-bonding structures. We expect that the pGM models have the potential to serve as templates for developing the next-generation polarizable force fields for modeling various polarization-sensitive biological processes.

APPENDIX: PROOF OF MANY-BODY INTERACTION ENERGIES DECOMPOSITION

In the Theory section, we claim that the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ (eq 22) can be decomposed into the nonadditive contributions ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ and the additive contributions ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$, whose formulas are given in eqs 24 and 25, respectively. We first prove the formula of the nonadditive contributions in Appendix A1 and then prove the formula of the additive contributions in Appendix A2.

A1. Nonadditive Contributions

The nonadditive effect refers to that for a molecular system with more than two atoms involved; any two atoms will interact differently compared with the situation where other atoms were not present.¹⁰ For additive force fields, the nonadditive effect does not exist, i.e., ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ defined in eq 24 is always zero. Therefore, the interaction energy of the two middle peptides ${\text{IE}}_{\text{mid}}({\text{Gly}}_m{\text{:Gly}}_n)$ in the presence of the neighbor peptides ${\text{Gly}}_{m-1}$ and ${\text{Gly}}_{n-1}$ defined in eq 23 should be the same as the interaction energy of the two middle peptides $\text{IE}(\text{Gly:Gly})$ in the absence of the neighbor peptides. The key to prove this is that, for additive force fields, the interaction energy IE(A,B:C,D) of a four-body system A,B:C,D can be decomposed into

$$\begin{gathered} \text{IE}(\mathrm{A},\mathrm{B}:\mathrm{C},\mathrm{D})=\text{IE}(\mathrm{A}:\mathrm{C})+\text{IE}(\mathrm{B}:\mathrm{C})+\text{IE}(\mathrm{A}:\mathrm{D}) \\ +\text{IE}(\mathrm{B}:\mathrm{D}) \end{gathered}$$ (A1)

Therefore, the first three terms in eq 23 can be decomposed to

$$\begin{gathered} \text{IE}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{XGly}}_{{}_{n-1}}) \\ +\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:\text{Gly})+\text{IE}(\text{Gly}:{\text{XGly}}_{{}_{n-1}}) \\ +\text{IE}(\text{Gly}:\text{Gly}) \end{gathered}$$ (A2)

$$\begin{gathered} \text{IE}({\text{Gly}}_{{}_m}:{\text{XGly}}_{{}_{n-1}}) \\ =\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{XGly}}_{{}_{n-1}})+\text{IE}(\text{Gly}:{\text{XGly}}_{{}_{n-1}}) \end{gathered}$$ (A3)

$$\begin{gathered} \text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{Gly}}_{{}_n}) \\ =\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{XGly}}_{{}_{n-1}})+\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:\text{Gly}) \end{gathered}$$ (A4)

Substituting eqs A2-A4 into eq 23 gives

$${\text{IE}}_{{}_{\text{mid}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{IE}(\text{Gly}:\text{Gly})$$ (A5)

Therefore, for additive force fields, the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ in eq 24 becomes zero. For polarizable force fields, the difference between ${\text{IE}}_{\text{mid}}({\text{Gly}}_m{\text{:Gly}}_n)$ and $\text{IE}(\text{Gly:Gly})$ is naturally the nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$, which is a nonzero value.

A2. Additive Contributions

For either additive or polarizable force fields, the additive contribution can be expressed in the following alternative formula by substituting eqs 22-24 into eq 25

$$\begin{gathered} {\text{ME}}_{{}_{\mathrm{A}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})=\text{IE}({\text{Gly}}_{{}_m}:{\text{XGly}}_{{}_{n-1}}) \\ +\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{Gly}}_{{}_n}) \\ -\text{IE}({\text{Gly}}_{{}_{m-1}}\mathrm{X}:{\text{XGly}}_{{}_{n-1}}) \end{gathered}$$ (A6)

For additive force fields, we need to show that the many-body interaction energies $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ only have the additive contribution ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$. This can be done by substituting eq A2 into the formula of the many-body interaction energy in eq 22 and substituting eq A3-A4 into the formula of the additive contribution in eq A6. Therefore, we have proved that for additive force fields, we have

$$\text{ME}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})={\text{ME}}_{{}_{\mathrm{A}}}({\text{Gly}}_{{}_m}:{\text{Gly}}_{{}_n})$$ (A7)

For polarizable force fields, the difference between the many-body interaction energy $\text{ME}({\text{Gly}}_m{\text{:Gly}}_n)$ and the nonzero nonadditive contribution ${\text{ME}}_{\text{NA}}({\text{Gly}}_m{\text{:Gly}}_n)$ naturally gives the additive contribution ${\text{ME}}_{\mathrm{A}}({\text{Gly}}_m{\text{:Gly}}_n)$.