Abstract
Accuracy and transferability are the two highly desirable properties of molecular mechanical force fields. Compared with the extensively used point-charge additive force fields that apply fixed atom-centered point partial charges to model electrostatic interactions, polarizable force fields are thought to have the advantage of modeling the atomic polarization effects. Previous works have demonstrated the accuracy of the recently developed polarizable Gaussian multipole (pGM) models. In this work, we assessed the transferability of the electrostatic parameters of the pGM models with (pGM-perm) and without (pGM-ind) atomic permanent dipoles in terms of reproducing the electrostatic potentials surrounding molecules/oligomers absent from electrostatic parameterizations. Encouragingly, both the pGM-perm and pGM-ind models show significantly improved transferability than the additive model in the tests (1) from water monomer to water oligomer clusters; (2) across different conformations of amino acid dipeptides and tetrapeptides; (3) from amino acid tetrapeptides to longer polypeptides; and (4) from nucleobase monomers to Watson–Crick base pair dimers and tetramers. Furthermore, we demonstrated that the double-conformation fittings using amino acid tetrapeptides in the αR and β conformations can result in good transferability not only across different tetrapeptide conformations but also from tetrapeptides to polypeptides with lengths ranging from 1 to 20 repetitive residues for both the pGM-ind and pGM-perm models. In addition, the observation that the pGM-ind model has significantly better accuracy and transferability than the point-charge additive model, even though they have an identical number of parameters, strongly suggest the importance of intramolecular polarization effects. In summary, this and previous works together show that the pGM models possess both accuracy and transferability, which are expected to serve as foundations for the development of next-generation polarizable force fields for modeling various polarization-sensitive biological systems and processes.
Graphical Abstract
INTRODUCTION
Molecular modeling techniques at the atomic level such as molecular dynamics (MD) simulations and Monte Carlo (MC) simulations rely on the development of accurate and transferable molecular mechanical force fields.1-3 The ability to transfer parameters from one molecule to another molecule or across different conformations of the same molecule is crucial for general-purpose force fields that aim at applications to a wide range of molecular systems. For this type of force fields, it is of critical importance to accurately reproduce the properties and behaviors of not only the training molecules and conformations used for parameterizations but also larger testing systems (such as oligomer clusters, molecule complexes, or polymers) and different conformations that are absent from the parameterization process. For example, Amber force fields are general-purpose force fields that were designed for modeling biomolecules such as proteins and nucleic acids,4 whose parameterizations were performed on smaller training molecules such as amino acid dipeptides and nucleotides in selected representative conformations.5-7
One of the most important components of force field development is the treatment of electrostatic interactions. In the extensively used point-charge additive force fields, the electrostatic terms are modeled by the interactions between fixed atom-centered point partial charges that obey Coulomb’s law. One commonly used parameterization method for obtaining the atomic partial charges is to use least-squares fitting to reproduce the quantum mechanically (QM) determined electrostatic potential (ESP) at a large number of grid points around the molecule.8-12 However, these fixed-point charges suffer from two disadvantages of lacking both accuracy and transferability. First, charges on atoms that are buried by the other atoms are often poorly determined, and their values often have a high degree of uncertainty while fitting to QM ESPs. Consequently, unphysically large charges may be assigned to these buried atoms. Second, the ESP-derived atomic charges are often sensitive to molecular conformations, leading to a lack of transferability of the charges across different conformations of identical molecules, as well as among common functional groups in related molecules. The problems of the ESP fitting strategy have been addressed by the restrained electrostatic potential (RESP) method developed by Bayly et al., which restrains the atomic charges towards zero using a hyperbolic penalty function to avoid impractically large charges.13,14 Additionally, the multiple-conformation fitting strategy further improved the transferability of the ESP-fitted charges.15,16 Using the combination of the multiple-conformation fitting strategy and the RESP method, Cieplak et al. derived the charges for all the ribonucleotides, deoxyribonucleotides, and amino acids using ESPs calculated at the HF/6-31G* level of theory, which were incorporated into the Amber ff94 force field.5,6 Since then, the charge set of the ff94 force field has become the foundation of various subsequent Amber force fields, including the Amber ff99 force field,7 the Amber SB (Stony Brook) family force fields for modeling proteins,17-19 and the Amber OL (Olomouc) family force fields for modeling nucleic acids.20-22 The changes made by these subsequent force fields are mainly in torsional parameters, while the charges remain mostly unchanged.
Despite the improved accuracy and transferability of the additive Amber force fields with the charge parameters derived using the RESP method, the additive force fields suffer from a major disadvantage of being unable to model the atomic polarization effects, that is, the redistribution of the atomic electron density due to the electric field produced by nearby charged atoms.23 Polarization effects are important in various biological processes such as protein–ligand bindings,24-26 nucleic acid–ion interactions,27,28 the dielectric environmental changes during protein folding,29,30 and ion transport through transmembrane ion channels.31,32 Therefore, a variety of methods have been proposed to properly incorporate polarization effects into polarizable force fields, including the induced dipole models,33-40 the fluctuating charge models,41,42 the Drude oscillator models,43,44 and the continuum dielectric models.45,46.
The induced dipole model is one of the most studied polarizable models, which has been incorporated into various Amber polarizable force fields, including ff02,33 ff02rl,34 and ff12pol.35-38 In this model, the induced dipole of atom subject to the external electric field that comes from all the atoms other than is
| (1) |
where is the isotropic polarizability of atom and is the dipole field tensor with the matrix form
| (2) |
where is the identity matrix; , , and are the Cartesian components along the vector between atoms and at distance ; and and are distance-dependent damping functions that modify to avoid the so-called “polarization catastrophe” problem, which is the phenomenon that induced dipole diverges due to the cooperative induction between induced dipoles at short distances.23,47 Various damping schemes have been proposed by Thole,48 which have been incorporated into the Amber ff12pol force field.35-38 However, one disadvantage of Thole’s schemes is that they only screen the interactions between induced dipoles, leading to an inconsistent treatment of the polarizations due to fixed charges and permanent multipoles. About a decade ago, a damping scheme that models atomic electric multipoles using Gaussian electron densities was proposed by Elking et al.,49-51 which was later named the polarizable Gaussian multipole (pGM) model.52-55 The pGM model overcomes the disadvantage of Thole’s schemes by screening all short-range electrostatic interactions in a physically consistent manner, including the interactions of charge–charge, charge–dipole, charge–quadrupole, dipole–dipole, and so on. The formula of damping functions and for the pGM model is as follows
| (3) |
where is the inverse of the pGM “radius” of the Gaussian density distribution of atom ; is a constant screening factor; and is the error function of .
In the current pGM model design, the atomic charges and atomic induced dipoles are always present, while the inclusion of the atomic permanent dipoles is optional, leading to two distinct pGM models. The pGM model without atomic permanent dipoles is named pGM-ind, indicating that the atomic dipoles of this pGM model only have contributions from atomic induced dipoles. The pGM model with atomic permanent dipoles is named pGM-perm, indicating that the atomic dipoles of this pGM model have contributions from both induced dipoles and permanent dipoles. Based on the observation that atomic permanent dipole moments mainly exist along the direction of covalent bonding interactions, a local frame for the permanent dipoles formed by covalent basis vectors (CBVs) that are unit vectors along the directions of covalent bonds has been proposed for the pGM-perm model, so that the atomic permanent dipoles of the pGM-perm model always exist along the directions of covalent bonds.53 An alternative pGM-perm model is called pGM-perm-v, where “v” stands for “virtual”. In the pGM-perm-v model, the CBVs exist not only along the directions of covalent bonds (1–2 connecting atoms) but also along the directions of virtual bonds (1–3 connecting atoms) such as between the two hydrogen atoms of a water molecule. Consequently, in the pGM-ind model, the electric field at the position of atom in eq 1 is only produced by fixed-point charges of all atoms other than , while in the pGM-perm and pGM-perm-v models, the electric field is produced by both point charges and permanent dipoles of all atoms other than i. The formula of the electric field for the pGM-ind model is shown in eq 4 and that for the pGM-perm and pGM-perm-v models is shown in eq 5.
| (4) |
| (5) |
where is the point charge of atom , is the permanent dipole of atom in the global frame, and is the unit vector pointing in the direction from atom to atom .
In a series of recent works, the pGM models have been further developed and made available to the molecular modeling community. First, using an optimization method based on the genetic algorithm, we obtained a set of isotropic atomic polarizabilities and radii for the pGM models by fitting to molecular polarizability tensors of 1405 molecules or dimers calculated at the B3LYP/aug-cc-pVTZ level of theory.52 Second, the closed-form analytical formula of the electrostatic energy and forces of the pGM models have been derived and has been interfaced with the particle mesh Ewald method for molecular simulations under periodic boundary conditions.53 Third, the pGM internal stress tensor expression for constant-pressure MD simulations of both flexible and rigid body molecular systems has been derived.54 Finally, following the idea of charge parameterization by reproducing QM ESPs of the RESP method, we implemented the PyRESP program, enabling the electrostatic parameterizations of the point-charge additive model and various induced dipole polarizable models, including the pGM-ind, pGM-perm, and pGM-perm-v models.56
The accuracy of the pGM models has been demonstrated by various previous works. It has been shown that even without atomic permanent dipoles, the pGM-ind model can notably improve the prediction of molecular polarizability anisotropy compared with the Amber ff12pol force field that is based on Thole’s damping schemes.52 Moreover, the electrostatic parameterizations on various molecules with various electrostatic models using the PyRESP program show that the pGM models consistently produce ESPs and molecular electric moments with a better agreement with QM-calculated results than the point-charge additive model.56 A recent work assessed the accuracy of the pGM models in reproducing QM interaction energies, many-body interaction energies, as well as the nonadditive and additive contributions to the many-body interactions for peptide main-chain hydrogen-bonding conformers, which showed that the pGM models outperform all other tested and widely used polarizable and additive force fields.55
However, there has been no work assessing the transferability of the pGM models, that is, whether the pGM models can accurately reproduce the electrostatic properties of larger molecular systems or different molecular conformations other than the molecules or conformations used for parametrizations. This is the primary focus of this work. Another focus of this work is to find the optimal parameterization strategy for developing the next-generation polarizable force fields based on the pGM models. Specifically, we aim to identify how many and what conformations should be applied for parameterizing amino acids for the pGM-ind and pGM-perm models that can give optimal accuracy and transferability for modeling polypeptides or proteins. The performances of the pGM models were compared with that of the point-charge additive model, which we call “additive model” for short. The electrostatic parameterizations of the additive, pGM-ind, and pGM-perm models were performed by fitting them to the same QM ESPs of each data set. One caveat of the pGM-perm and pGM-perm-v models is that their parameterizations suffer from the so-called “singularity problem”, which originates from the use of the permanent dipole local frame formed by CBVs. Fortunately, the restrained fitting strategy and the multiple-conformation fitting strategy implemented in the PyRESP program can theoretically address the singularity problem, both of which have been demonstrated to successfully improve the accuracy and transferability of the electrostatic parameters of the additive model. The details of the singularity problem of the pGM-perm and pGM-perm-v models as well as the discussion of how restrained fitting and multiple-conformation fitting can address this problem can be found in the Appendix. Therefore, extra attention has been paid to the performance of the pGM-perm and pGM-perm-v models with different parametrization strategies in this work.
COMPUTATIONAL DETAILS
Data Sets and Geometry Preparations.
A total of nine data sets were generated and used for testing the transferability of the pGM models in this work, including WAT4, WAT6, WAT8, WAT10, ALA-di, ALA-tet, ALA-poly, GLY-poly, and BASE. The WAT4, WAT6, WAT8, and WAT10 data sets comprise 100 water tetramer clusters, 72 water hexamer clusters, 13 water octamer clusters, and 10 water decamer clusters, respectively. The initial geometries of the water clusters were extracted from 1 ns of MD simulations of a periodic box of 322 TIP3P waters.57 A total of 100 snapshots were saved at 10 ps intervals, and all the clusters were extracted from these 100 TIP3P water boxes by randomly selecting a water molecule together with the closest water molecules. The MD simulation was conducted using the sander program from the AmberTools22 program suite.58 Next, the WAT4 data set was optimized at the MP2/6-311++G(d, p) level of theory, and the WAT6, WAT8, and WAT10 data sets were optimized at the B3LYP/6-311++G(d, p) level of theory.
The ALA-di data set comprises 14 alanine dipeptides (ACE-ALA-NME) capped with an N-acetyl (ACE) group at the N-terminal and an N-methylamide (NME) group at the C-terminal. The ACE and NME caps are used to mimic the chemical environment within peptides. Each alanine dipeptide was optimized at the MP2/6-311++G(d, p) level of theory with the main-chain torsional angles ϕ and ψ fixed according to Table 1. The ALA-tet data set comprises a total of 16 alanine tetrapeptides (ACE-ALA3-NME), including (1) those in the conf1–conf10 conformations optimized at the HF/6-31G** level of theory by Beachy et al.,59 which were further optimized at the MP2/6-311++G(d, p) level of theory without any constraints and (2) those in the aβ, αL, αR, α2, β, and pII conformations optimized at the MP2/6-311++G(d, p) level of theory with all the main-chain torsional angles ϕ and ψ constrained. The main-chain torsional angles ϕ and ψ of each of the optimized conf1–conf10 conformations and the torsional angle constraints of the aβ, αL, αR, α2, β, and pII conformations are given in Table 2.
Table 1.
Main-Chain Torsional Angle Constraints for Geometry Optimizations of the Alanine Dipeptides from the ALA-di Data Set and Their QM Molecular Dipole Moments
| conformation | ϕ/° | ψ/° | μ/Debyea |
|---|---|---|---|
| C5 | −140 | 120 | 1.8190 |
| C7eq | −80 | 80 | 2.5090 |
| C7ax | 60 | −70 | 3.1220 |
| α 1 | −60 | −40 | 5.9446 |
| α 2 | −52 | −53 | 5.9848 |
| αl | 70 | 30 | 5.5989 |
| αp | 7 | −40 | 5.1311 |
| β 1 | −161.9 | 166.4 | 3.0836 |
| β 2 | −130 | 20 | 4.5831 |
| aβ | −140 | 135 | 2.2315 |
| αL | 57 | 47 | 5.7158 |
| αR | −57 | −47 | 5.9860 |
| β | −119 | 113 | 0.8758 |
| pII | −79 | 150 | 2.0894 |
The QM molecular dipole moments are calculated at the MP2/aug-cc-pVTZ level of theory.
Table 2.
Main-Chain Torsional Angles of the Optimized Alanine Tetrapeptides in the Conf1–Conf10 Conformations and the aβ, αL, αR, α2, β, and pII Conformations from the ALA-tet Data Set and Their QM Molecular Dipole Moments
| conformation | ϕ1/° | ψ1/° | ϕ2/° | ψ2/° | ϕ3/° | ψ3/° | μ/Debyea |
|---|---|---|---|---|---|---|---|
| Conf1 | −158.4 | 157.1 | −158.1 | 156.5 | −157.5 | 154.0 | 6.8721 |
| Conf2 | −158.3 | 155.7 | −158.9 | 152.6 | −80.1 | 84.7 | 2.1669 |
| Conf3 | −76.9 | 95.1 | 73.8 | −59.0 | −75.4 | 85.1 | 2.2505 |
| Conf4 | −159.1 | 156.0 | −79.9 | 87.9 | −160.7 | 143.3 | 4.2586 |
| Conf5 | −157.4 | 164.0 | −59.9 | −35.8 | −76.7 | 90.1 | 2.8701 |
| Conf6 | −85.5 | 64.8 | 51.8 | 28.1 | −179.0 | 139.2 | 5.8466 |
| Conf7 | 52.2 | −160.6 | −88.0 | 71.2 | −166.6 | −53.3 | 9.2910 |
| Conf8 | 69.3 | −74.8 | −52.8 | 134.4 | 54.3 | 33.9 | 3.2394 |
| Conf9 | 74.3 | −54.9 | 74.5 | −53.4 | 74.4 | −50.5 | 8.3039 |
| Conf10 | 66.8 | 20.1 | 45.6 | 42.3 | 68.6 | −74.5 | 8.0954 |
| aβ | −140.0 | 135.0 | −140.0 | 135.0 | −140.0 | 135.0 | 5.3779 |
| αL | 57.0 | 47.0 | 57.0 | 47.0 | 57.0 | 47.0 | 12.7255 |
| αR | −57.0 | −47.0 | −57.0 | −47.0 | −57.0 | −47.0 | 13.2536 |
| α 2 | −52.0 | −53.0 | −52.0 | −53.0 | −52.0 | −53.0 | 13.3017 |
| β | −119.0 | 113.0 | −119.0 | 113.0 | −119.0 | 113.0 | 1.9427 |
| pII | −79.0 | 150.0 | −79.0 | 150.0 | −79.0 | 150.0 | 5.4174 |
The QM molecular dipole moments are calculated at the MP2/aug-cc-pVTZ level of theory.
The ALA-poly and GLY-poly data sets comprise 60 alanine polypeptides (ACE-ALAn-NME) and 60 glycine polypeptides (ACE-GLYn-NME), respectively, where n is the number of repetitive ALA or GLY residues, ranging from 1 to 20. ACE-ALAn-NME and ACE-GLYn-NME have three conformations each: aβ, αR, and β. To prepare the ALA-poly and GLY-poly data sets, three alanine dipeptides (ACE-ALA-NME) and three glycine dipeptides (ACE-GLY-NME) were optimized at the ωB97X-D/6-311++G(d, p) level of theory with the main-chain torsional angles fixed at (ϕ, ψ) = (−140°, 135°), (−57°, −47°), and (−119°, 113°), corresponding to the aβ, αR and β conformations, respectively. Next, all the ACE-ALAn-NME and ACE-GLYn-NME with n greater than or equal to 2 were generated from optimized alanine and glycine dipeptides by rigid body translation and rotation with the same ϕ and ψ torsional angles.
The BASE data set comprises four individual DNA nucleobases, including adenine (A), thymine (T), guanine (G), and cytosine (C), each capped with a methyl group to mimic the chemical environment within nucleosides, two Watson–Crick (WC) base pairs (A-T and C-G), and eight stacked WC base pair tetramers (A-T/A-T, A-T/T-A, A-T/C-G, A-T/G-C, G-C/A-T, G-C/T-A, G-C/C-G, and G-C/G-C). The WC base pair tetramers are named as follows: the A-T/C-G tetramer means an A-T base pair is stacked onto a C-G base pair, where A and T are stacked with C and G, respectively. To prepare the BASE data set, the two WC base pair dimers were first optimized at the MP2/6-311++G(d, p) level of theory. The individual nucleobases were extracted from the WC base pair dimers without further optimization. The tetramers were constructed from the WC base pairs by rigid body alignment of the base pair dimers to the B-DNA geometry created using the nucgen program,60 without further optimization.
All the QM geometry optimizations were performed using the Gaussian 16 software.61
Electrostatic Parameterizations.
The electrostatic parameterizations of the additive, pGM-ind, pGM-perm, and pGM-perm-v models require the QM ESPs of a set of points in the solvent-accessible region around molecules as input. The QM ESPs of the molecules from the data sets WAT4, WAT6, WAT8, WAT10, ALA-di, and ALA-tet were calculated at the MP2/aug-cc-pVTZ level of theory and those of the data sets ALA-poly, GLY-poly, and BASE were calculated at the ωB97X-D/aug-cc-pVTZ level of theory. The points were generated using the strategy developed by Singh et al. on molecular surfaces (with a density of 6 points/Å2) at each of 1.4, 1.6, 1.8. and 2.0 times the van der Waals radii.62,63 The QM molecular dipole moments of alanine dipeptides and alanine tetrapeptides from the ALA-di and ALA-tet data sets are shown in Tables 1 and 2, and the QM molecular dipole moments of alanine polypeptides, glycine polypeptides, and WC base pair tetramers from the ALA-poly, GLY-poly, and BASE data sets are shown in Tables S1-S3. All QM ESPs and molecular dipole moments were calculated using the Gaussian 16 software.61
The recently developed PyRESP program was used to parameterize the atomic charges (and permanent dipoles) of the molecules from each data set for each electrostatic model.56 For polarizable models pGM-ind, pGM-perm and pGM-perm-v, the isotropic atomic polarizabilities derived in our previous work were used to calculate the induced dipoles.52 A two-stage parameterization procedure was adopted.56 In the first stage, all charges (and permanent dipoles) were set free to change, and a weak restraining strength of 0.0005 was applied. In the second stage, intramolecular equivalencing was enforced on all charges (and permanent dipoles) that share an identical chemical environment with others, such as those of methyl and methylene hydrogens. A stronger restraining strength of 0.001 was applied, and all other fitting centers were set frozen to keep the values obtained from the first stage. In both stages, the restraints were only applied to nonhydrogen heavy atoms. The parameters of the individual water molecule for the WAT4, WAT6, WAT8, and WAT10 data sets have been derived in our previous work.56 The parameters for the ALA-di, ALA-tet, ALA-poly, and GLY-poly data sets were obtained by constraining the total molecular charge to be zero, and the intramolecular charge of the ACE and NME groups sum to zero in order to ensure zero net charges of the central amino acid fragments (─NH─CHR─CO─). For the parameterizations of amino acid tetrapeptides, intramolecular equivalencing was enforced in both the first and second stages to ensure identical parameters across the three repetitive central amino acid fragments. For multiple-conformational fittings, intermolecular equivalencing was enforced in both stages to ensure identical atomic charges and permanent dipoles of the same molecule in different conformations. The parameters for the BASE data set were derived using single-conformation fittings with constraints to enforce net zero molecular charges and no additional intramolecular charge constraint. For the parameterizations of the pGM-ind, pGM-perm, and pGM-perm-v models, both 1–2 and 1–3 polarization interactions were included for reasons elucidated before.52,64
Transferability Tests.
The transferability of the electrostatic parameters of all electrostatic models were measured by the relative-root-mean-square errors of the overall molecular dipoles of each data set and the relative-root-mean-square errors of ESPs (RRMSV) of each molecule (or molecule oligomer), given by
| (6) |
| (7) |
and the average-relative-root-mean-square errors of ESPs of each data set is
| (8) |
where is the number of molecules for each data set; is the number of ESP points surrounding the molecule (or molecule oligomer) ; and are the overall molecular dipoles of the molecule/oligomer given by QM calculations and molecular mechanics (MM) calculations, respectively; and and are the ESP values at point of the molecule/oligomer given by QM calculations and MM calculations, respectively.
To calculate the total molecular dipole and ESP values of molecule A with the electrostatic parameters transferred from the parameterization results of molecule B, the input file (-i) and qin file (-q) of molecule A are created manually using the parameters from molecule B, which are provided as the inputs for the PyRESP program. The control parameter irstrnt of the PyRESP program is set to 2 so that no parameterization on molecule A is carried out, and the total molecular dipole and ESP values of molecule A with the transferred parameters from molecule B are printed in the output file (-o) of the PyRESP56 program.
All scatterplots, boxplots, and line plots are plotted using the Python package Matplotlib. The QM ESPs surrounding water tetramer clusters and the differences between QM- and MM-calculated ESPs are visualized using the UCSF Chimera software.65
RESULTS AND DISCUSSION
pGM-perm and pGM-perm-v Models Show the Best Transferability from Water Monomer to Water Oligomer Clusters.
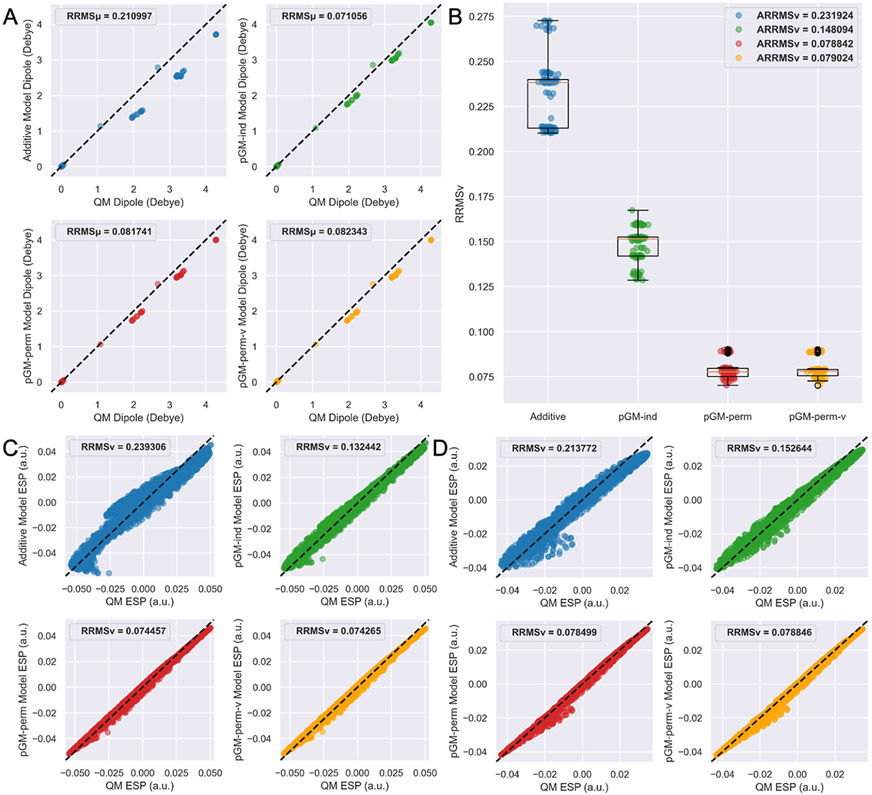
The transferability of the additive, pGM-ind, pGM-perm, and pGM-perm-v models from water monomer to water oligomer clusters is tested by investigating the quality of the overall water cluster dipoles and ESPs calculated by MM calculations in comparison to those calculated at the MP2/aug-cc-pVTZ QM level of theory, as measured by and , respectively. The parameters of the water monomer for each electrostatic model have been derived in the original PyRESP work. As discussed in the Appendix, the water molecule is nonsingular, so a single-conformation fitting is sufficient for the parameterization of the pGM-perm and pGM-perm-v models for the water molecule. The single set of water monomer parameters is used in testing all WAT4, WAT6, WAT8, and WAT10 data sets. Figure 1A shows the scatterplots of MM dipoles calculated by each electrostatic model for the 100 water tetramer clusters from the WAT4 data sets versus those calculated by QM methods. It can be observed that all three pGM models outperform the additive model, as the of the pGM-ind (0.0711), pGM-perm (0.0817), and pGM-perm-v (0.0823) models are only 34, 39, and 39% of that of the additive model (0.2110), respectively. Figure 1B shows the boxplots of the of each electrostatic model for the WAT4 data sets, and we can see that the of both the pGM-perm (0.0788) and pGM-perm-v (0.0790) models are 34% of that of the additive (0.2319) model and 53% of that of the pGM-ind (0.1481) model. Interestingly, adding the virtual dipoles along the H─H direction in the pGM-perm-v model does not improve the quality of calculated overall dipoles and ESPs, as both the and of the pGM-perm-v model are slightly higher than those of the pGM-perm model. To further explore the transferability difference among different models, the scatterplots of MM versus QM ESPs for the water tetramer clusters with the highest QM overall dipole (Figure 1C, dipole = 4.2850 Debye) and with the lowest QM overall dipole (Figure 1D, dipole = 0.0008 Debye) are shown. The pGM-perm and pGM-perm-v models produce the lowest for both water clusters. For the water cluster with the highest QM dipole, the pGM-perm and pGM-perm-v models produce of 0.0745 and 0.0743, respectively, both of which are 31% of that of the additive model (0.2393) and 56% of that of the pGM-ind model (0.1324). For the water cluster with the lowest QM dipole, the pGM-perm and pGM-perm-v models produce of 0.0785 and 0.0788, respectively, both of which are 37% of that of the additive model (0.2138) and 52% of that of the pGM-ind model (0.1526). Once again, the of the pGM-perm and pGM-perm-v models are very similar.
Figure 1.
Transferability tests of the additive, pGM-ind, pGM-perm, and pGM-perm-v models from water monomer to water tetramer clusters. (A) Scatterplots of MM dipoles of each electrostatic model versus QM dipoles. Each plot shows a total of 100 data points, with each point representing a water tetramer. (B) Boxplots of the of each electrostatic model with QM results. Each plot shows a total of 100 data points, with each point representing a water tetramer. (C) Scatterplots of MM ESPs of each electrostatic model versus QM ESPs for the water tetramer with the highest QM dipole (dipole = 4.2850 Debye). Each plot shows a total of 4660 data points, with each point representing an ESP point. (D) Scatterplots of MM ESPs of each electrostatic model versus QM ESPs for the water tetramer with the lowest QM dipole (dipole = 0.0008 Debye). Each plot shows a total of 4339 data points, with each point representing an ESP point. For (A,C,D), the dashed lines correspond to perfect matching.
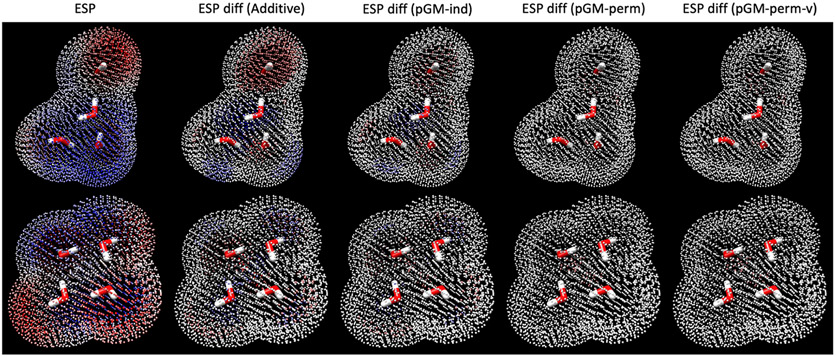
Figure 2 illustrates the QM ESPs surrounding the water tetramer clusters with the highest and lowest QM overall dipoles, as well as the differences between QM ESPs and MM ESPs calculated by each electrostatic model. It can be observed that the additive model is unable to accurately reproduce the ESP of polar regions, that is, regions with high ESP absolute values. Specifically, the additive model tends to generate ESPs with lower values than QM results where the QM ESPs have large positive values but generate ESPs with higher values than QM results where the QM ESPs have large negative values. The pGM-ind model improves the ESP fitting significantly. It is noteworthy that both the pGM-ind and additive models have an identical number of electrostatic parameters. Therefore, the significant improvement observed in the pGM-ind model over the additive model is a piece of strong evidence for the critical roles that intramolecular polarization plays in transferability. The pGM-perm and pGM-perm-v models give ESPs nearly identical to those of QM results in both polar and nonpolar regions. Note that the ESP differences with QM results given by the pGM-perm and pGM-perm-v models are almost indistinguishable. Therefore, we conclude that the additional dipoles along the H─H virtual bond in the pGM-perm-v model do not improve the ESP fitting quality and transferability compared with the pGM-perm model for the water tetramer clusters.
Figure 2.
Visualization of QM ESPs surrounding water tetramer clusters and the differences between QM- and MM-calculated ESPs of the additive, pGM-ind, pGM-perm, and pGM-perm-v models. The upper panel shows the water tetramer with the highest QM dipole (4.2850 Debye) and the lower panel shows the water tetramer with the lowest QM dipole (0.0008 Debye). The leftmost column shows the QM ESPs, with red color indicating a positive ESP value and blue color indicating a negative ESP value. All other columns show the differences between QM ESPs and MM ESPs, with red color indicating that QM ESP is greater than MM ESP and blue color indicating that QM ESP is less than MM ESP.
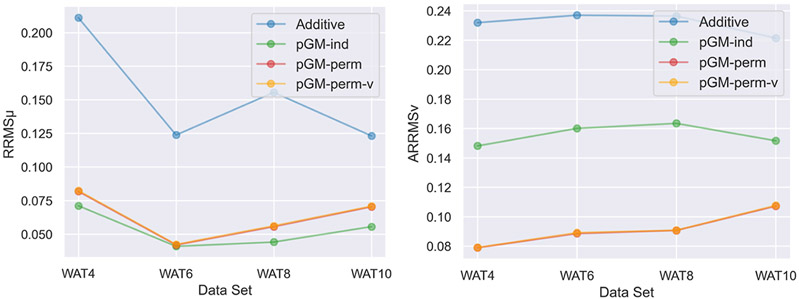
After analyzing the transferability from water monomer to water tetramer clusters, we examined the transferability of each electrostatic model from water monomer to water oligomers with larger sizes, including hexamer, octamer, and decamer clusters from the WAT6, WAT8, and WAT10 data sets, respectively. The scatterplots of MM dipoles of each electrostatic model versus QM dipoles, the boxplots of the of each electrostatic model with QM results, and the scatterplots of MM ESPs of each electrostatic model versus QM ESPs for the water hexamer, octamer, and decamer clusters with the highest and lowest QM dipoles are shown in Figures S1-S3. The and of each water oligomer cluster size produced by each electrostatic model are summarized in Figure 3. The pGM-ind, pGM-perm, and pGM-perm-v models consistently outperform the additive models in terms of both and , regardless of the water oligomer cluster sizes. Although the pGM-ind model performs slightly better than the pGM-perm and pGM-perm-v models in terms of , the latter two models significantly outperform the pGM-ind model in terms of . Another observation is that the and of each water oligomer cluster data set produced by the pGM-perm and pGM-perm-v models are essentially indistinguishable, as their plots overlap each other, consistent with the earlier observations in the case of water tetramers. In fact, as discussed in the original PyRESP work,56 the virtual dipoles in the pGM-perm-v model may lead to the overfitting problem and is expected to increase the computational time in simulations. Furthermore, the virtual dipole may cause additional singularity problems during parameterization, as discussed in the Appendix. For these reasons, the transferability test of the pGM-perm-v model will only be performed for the water oligomer clusters for illustration purposes. For other data sets, we will only test the transferability of the additive, pGM-ind, and pGM-perm models.
Figure 3.
and of the WAT4, WAT6, WAT8, and WAT10 data sets of the additive, pGM-ind, pGM-perm, and pGM-perm-v models parameterized with the water monomer. Note that the plots of the pGM-perm and pGM-perm-v models overlap each other.
Electrostatic Parameters of the pGM Models Derived with Amino Acid Dipeptides Transfer Well across Different Conformations and to Tetrapeptides.
In the previous subsection, we have shown that the pGM-perm and pGM-ind models outperform the additive model in terms of the transferability from water monomer (training molecule) to water oligomer clusters (testing molecules). Next, we move on to compare the transferability of the additive, pGM-ind, and pGM-perm models across different conformations of amino acids, as well as from short amino acid dipeptides (training molecules) to longer amino acid tetrapeptides (testing molecules). The reason why we are interested in amino acids is that they are the building blocks of proteins, so the electrostatic parameterizations of amino acids are of critical importance for the development of force fields for modeling biomolecules. Therefore, we aim to explore the best parametrization strategy of amino acids for developing the next-generation polarizable Amber force field based on the pGM models. As discussed in the Appendix, every amino acid molecule is singular in the context of parameterization of the pGM-perm model due to the existence of the sp3 α-carbon in every amino acid backbone. Therefore, the combination of restrained fitting and multiple-conformation fitting implemented in the PyRESP program will be explored for the electrostatic parameterizations of each model, which are expected to improve the transferability of each model and to mitigate the singularity problem of the pGM-perm model. Alanine was selected as the model amino acid for testing the transferability of each electrostatic model. In this test, five alanine dipeptides (ACE-ALA-NME) in αR (QM dipole = 5.9860 Debye), β (0.8758 Debye), C7eq (2.5090 Debye), aβ (2.2315 Debye), and C5 (1.8190 Debye) conformations from the ALA-di data set were used for electrostatic parameterization because of their wide range of molecular dipole moments, as shown in Table 1. A total of nine parameterization combinations of the five conformations were tested, including three single-conformation fittings (αR, β, and C7eq), three double-conformation fittings (αR/β, αR/C7eq, and β/C7eq), one triple-conformation fitting (αR/β/C7eq), one four-conformation fitting (αR/β/C7eq/aβ), and one five-conformation fitting (αR/β/C7eq/aβ/C5).
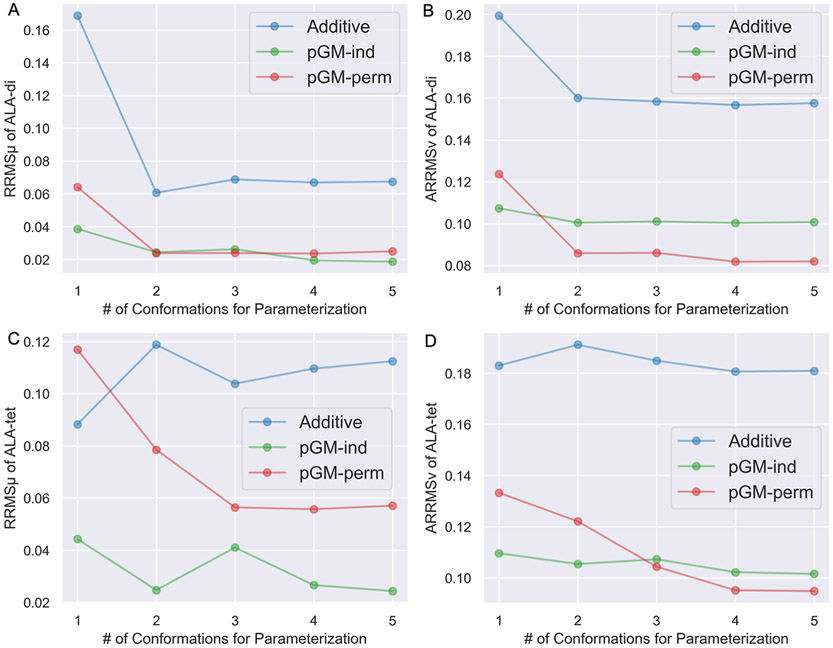
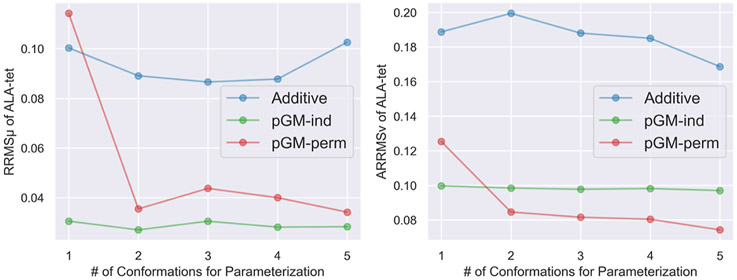
We first tested the transferability of the additive, pGM-ind, and pGM-perm models across different conformations of alanine dipeptides within the ALA-di data set, which contains a total of 14 conformations. The transferability test results are shown in Figures S4-S12. Among all the three single-conformation fittings, the C7eq conformation gives the best overall performance for the transferability of the pGM-ind and pGM-perm models, with of 0.0386 and 0.0641, and of 0.1074 and 0.1237, respectively. Among all the three double-conformation fittings, the combination of the αR and β conformations gives the best overall performance for the pGM-ind and pGM-perm models, with of 0.0244 and 0.0239, and of 0.1004 and 0.0858, respectively. Figure 4A,B summarizes the and of the ALA-di data set of each electrostatic model parameterized with alanine dipeptides in one to five conformations, where the single-conformation fitting and double-conformation fitting are C7eq and αR/β, respectively. One observation is that for all the additive, pGM-ind, and pGM-perm models, both and reached convergence with double-conformation fittings, and multiple-conformation fittings with more than two conformations do not significantly improve the transferability across different conformations of alanine dipeptides in the ALA-di data set. Another observation is that the pGM-perm model performs the best among the three models in terms of both and . Taking double-conformation fitting as an example, the and of the pGM-perm model are 0.0239 and 0.0858, respectively, which are 98 and 85% of those of the pGM-ind model (0.0244 and 0.1004), and 39 and 54% of those of the additive model (0.0607 and 0.1601). One exception is the case of single-conformation fitting, where the pGM-perm model shows worse transferability than the pGM-ind model, as the and of the pGM-ind model (0.0386 and 0.1074) are 60 and 87% of those of the pGM-perm model (0.0641 and 0.1237). The worse performance of the pGM-perm model with single-conformation fitting might be explained by its singularity problem, suggesting that multiple conformations should be used in the parameterization of amino acids. Even so, the pGM-perm model still performs much better than the additive model, as the and of the pGM-perm model are only 38 and 62% of those of the additive model (0.1687 and 0.1994).
Figure 4.
and of the ALA-di and ALA-tet data sets of the additive, pGM-ind, and pGM-perm models parameterized with alanine dipeptides from the ALA-di data set in one to five conformations. (A,B) and of the ALA-di data set. The one to five conformations are C7eq, αR/β, αR/β/C7eq, αR/β/C7eq/aβ, and αR/β/C7eq/aβ/C5, respectively. (C,D) and of the ALA-tet data set. The one to five conformations are β, αR/β, αR/β/C7eq, αR/β/C7eq/aβ, and αR/β/C7eq/aβ/C5, respectively.
Next, we tested the transferability of each electrostatic model from alanine dipeptides (ACE-ALA-NME) to longer alanine tetrapeptides (ACE-ALA3-NME). Specifically, the electrostatic parameters derived with the nine combinations of alanine dipeptides in the previously used five conformations (αR, β, C7eq, αR/β, αR/C7eq, β/C7eq, αR/β/C7eq, αR/β/C7eq/aβ, and αR/β/C7eq/aβ/C5) from the ALA-di data set were used to calculate the and of alanine tetrapeptides from the ALA-tet data set, which contains a total of 16 conformations. The transferability test results are shown in Figures S13-S21. Among all the three single-conformation fittings, the β conformation gives the best overall performance for the transferability of the pGM-ind and pGM-perm models, with of 0.0443 and 0.1169, and of 0.1096 and 0.1333, respectively. This is in contrast to the transferability test across alanine dipeptides in different conformations where the best performance is given by the C7eq conformation. Among all the three double-conformation fittings, the combination of αR and β conformations gives the best overall performance for the pGM-ind and pGM-perm models, with of 0.0247 and 0.0785 and of 0.1054 and 0.1221, respectively. This is consistent with the transferability test across different alanine dipeptide conformations. Figure 4C,D summarizes the and of the ALA-tet data set of each electrostatic model parameterized with alanine dipeptides in one to five conformations, where the single-conformation fitting and double-conformation fitting are β and αR/β, respectively. It can be observed that the transferability of the additive, pGM-ind, and pGM-perm models from alanine dipeptides to alanine tetrapeptides shows somewhat different patterns compared with the transferability across alanine dipeptides in different conformations. First, the pGM-ind model consistently gives the lowest , and it gives the lowest when less than three conformations were used for parameterizations. The superior performance shown by the pGM-ind model is somewhat surprising, given that the pGM-ind model does not take atomic permanent dipoles into account, in contrast to the pGM-perm model. Second, for the pGM-perm model, both and reached convergence with triple-conformation fitting. In the case of single-conformation fitting, it performs even worse than the additive model. This again illustrates the impact of the singularity problem of the pGM-perm model.
Electrostatic Parameterization of the pGM Models with Amino Acid Tetrapeptides Leads to Improved Transferability across Different Conformations and to Longer Polypeptides.
The transferability of the electrostatic parameters derived from dipeptides is unsatisfactory for the pGM-perm model, particularly from dipeptides to tetrapeptides. In addition to the potential singularity problem, we hypothesize that part of the reason is that there are two terminal groups (ACE and NME) in each dipeptide, making the terminal/amino acid ratio to be 2, much higher than that in polypeptides in which this ratio can be orders of magnitude lower. Therefore, we attempted to perform parameterizations using tetrapeptides in which three repetitive amino acid residues are present, making it possible to mimic multiple chemical environments and multiple conformations. The alanine tetrapeptides (ACE-ALA3-NME) in αR (QM dipole = 13.2536 Debye), β (1.9427 Debye), pII (5.4174 Debye), aβ (5.3779 Debye), and αL (12.7255 Debye) conformations from the ALA-tet data set were selected for parameterizations because of their wide range of molecular dipole moments as shown in Table 2. A total of nine parameterization combinations of the above five conformations were tested, including three single-conformation fittings (αR, β, and pII), three double-conformation fittings (αR/β, αR/pII, and β/pII), one triple-conformation fitting (αR/β/pII), one four-conformation fitting (αR/β/pII/aβ), and one five-conformation fitting (αR/β/pII/aβ/αL).
We first tested the transferability of each electrostatic model across different conformations of alanine tetrapeptides within the ALA-tet data set, which contains a total of 16 conformations. The transferability test results are shown in Figures S22-S30. Among all the three single-conformation fittings, the pII conformation gives the best overall performance for the transferability of the pGM-ind and pGM-perm models, with of 0.0305 and 0.1143 and of 0.0997 and 0.1253, respectively. Among all the three double-conformation fittings, the combination of αR and β conformations gives the best overall performance for the pGM-ind and pGM-perm models, with of 0.0270 and 0.0354, and of 0.0984 and 0.0846, respectively. Figure 5 summarizes the and of each electrostatic model of the ALA-tet data set parameterized with alanine tetrapeptides using one to five conformations, where the single-conformation fitting and double-conformation fitting are pII and αR/β, respectively. Similar to the transferability test across different conformations of the ALA-di data set, both the and of the additive and pGM-perm models reached convergence with double-conformation fittings, and multiple-conformation fitting with more than two conformations do not significantly improve the transferability across different conformations in the ALA-tet data set. As in the transferability test from alanine dipeptides to alanine tetrapeptides, the pGM-ind model consistently shows the lowest (around 0.03) among all the three models, regardless of the number of alanine tetrapeptide conformations used for parameterizations. In terms of , the pGM-perm model shows the best performance with multiple-conformation fittings. In contrast, with single-conformation fitting, the pGM-ind model again outperforms the pGM-perm model, as the of the pGM-ind model (0.0997) is 80% of that of the pGM-perm model (0.1253). This is consistent with the transferability test across different conformations of the ALA-di data set, which can be explained again by the singularity problem of the pGM-perm model. Encouragingly, for the pGM-perm model, double-conformation fitting using tetrapeptides leads to significantly improved transferability than using dipeptides, as the reduced from 0.0785 to 0.0354, and the reduced from 0.1221 to 0.0846. Finally, the additive model consistently gives the worst transferability as measured by both and . For example, with double-conformation fittings, the of the pGM-ind (0.0270) and pGM-perm (0.0354) models are only 21 and 28% of that of the additive model (0.0891), and the of the pGM-ind (0.0984) and pGM-perm (0.0846) models are 46 and 39% of that of the additive model (0.1994).
Figure 5.
and of the ALA-tet data set of the additive, pGM-ind, and pGM-perm models parameterized with alanine tetrapeptides from the ALA-tet data set in one to five conformations. The one to five conformations are pII, αR/β, αR/β/pII, αR/β/pII/aβ, and αR/β/pII/aβ/αL, respectively.
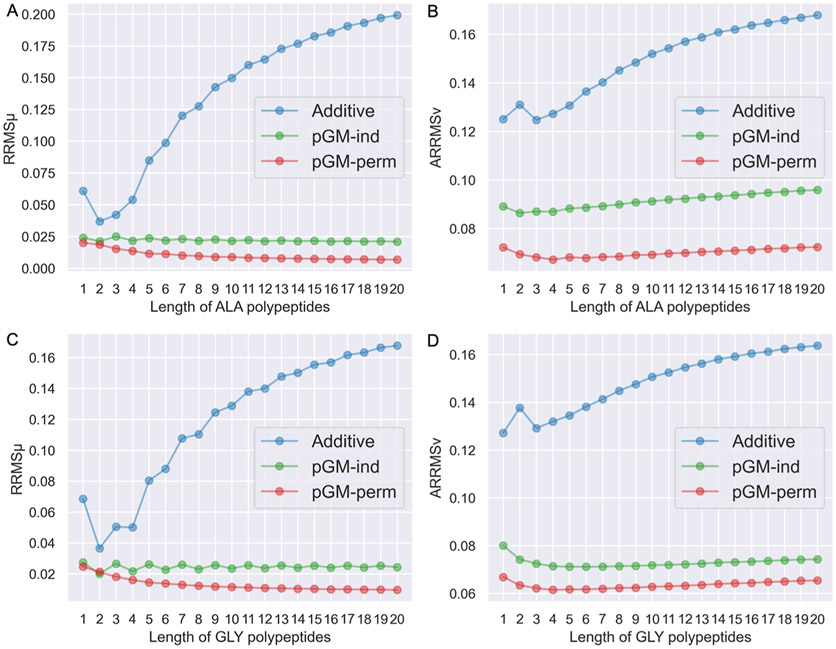
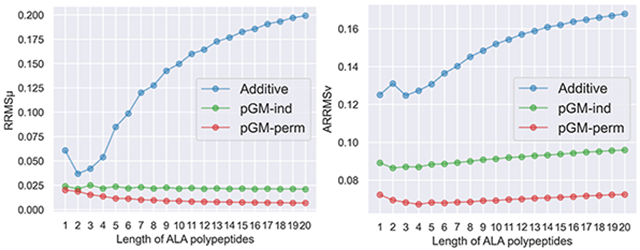
In addition to the transferability across different conformations, another question that needs to be addressed is the transferability across polypeptide chains with different lengths. This is a rather critical question because, for practical purposes, all protein force fields are parameterized using short peptides or model compounds and are applied to proteins that can be hundreds of amino acids long. Therefore, we need to know how well the electrostatic parameters obtained from parameterizing tetrapeptides transfer to longer polypeptides. To answer this question, transferability tests were performed using the ALA-poly and GLY-poly data sets containing a total of 60 alanine polypeptides (ACE-yALAn-NME) and 60 glycine polypeptides (ACE-GLYn-NME), respectively, where n ranges between 1 and 20. ACE-ALAn-NME and ACE-GLYn-NME are each represented by three conformations: aβ, αR, and β. Due to the large molecular size of long polypeptides such as ACE-ALA20-NME (212 atoms) and ACE-GLY20-NME (152 atoms), the ωB97X-D DFT method was used for both geometry preparations and ESP calculations for the two data sets to save computational resources. The electrostatic parameters (atomic charges and permanent dipoles) of alanine polypeptides and glycine polypeptides were both obtained by αR/β double-conformation fittings to the ESPs calculated at the ωB97X-D/aug-cc-pVTZ level of theory, using alanine tetrapeptides (ACE-ALA3-NME) from the ALA-poly data set and glycine tetrapeptides (ACE-GLY3-NME) from the GLY-poly data set, respectively. The reparameterization of alanine tetrapeptides is necessary to ensure that the parameters are consistent with other alanine polypeptides, since the ESPs of alanine tetrapeptides in the ALA-tet data set were calculated using a different QM method (MP2/aug-cc-pVTZ), which leads to slightly different ESPs. The and of the ALA-poly data set and the GLY-poly data set of each electrostatic model are shown in Figure 6A-D, respectively. Encouragingly, with αR/β double-conformation fittings, both the pGM-ind and pGM-perm models show great transferability to alanine and glycine polypeptides with lengths ranging from 1 to 20, although the pGM-perm model performs slightly better than the pGM-ind model. Interestingly, both the pGM-ind and pGM-perm models exhibit higher at the shorter end compared to longer polypeptides. This indicates that the underlying chemical environment in peptides of one to two amino acids is somewhat different from that of longer polypeptides, likely due to the unrealistically high terminal/amino acid ratio in short peptides. This explains why electrostatic parameterization with dipeptides leads to unsatisfactory transferability to longer tetrapeptides. The additive model consistently shows the worst transferability to alanine and glycine polypeptides among all the three electrostatic models. In general, the longer the polypeptides are, the higher the and the additive model produces. Therefore, we conclude that double-conformation fitting using amino acid tetrapeptides in the αR and β conformations is a sound strategy for amino acid electrostatic parametrizations for the pGM models. In the future development of the pGM force fields for proteins, this strategy is expected to be applied to the systematic electrostatic parameterizations for all amino acids.
Figure 6.
and of the ALA-poly and GLY-poly data sets of the additive, pGM-ind, and pGM-perm models parameterized with alanine or glycine tetrapeptides. (A,B) and against the length of alanine polypeptides from the ALA-poly data set. Each model is parameterized with alanine tetrapeptides from the ALA-poly data set using the αR/β double-conformation fitting. (C,D) and against the length of glycine polypeptides from the GLY-poly data set. Each model is parameterized with glycine tetrapeptides from the GLY-poly data set using αR/β double-conformation fitting.
The pGM models outperform the additive model in transferability from nucleobase monomers to WC base pair dimers and tetramers.
Besides amino acids, another key component of force field development for modeling biomolecules is the electrostatic parameterizations of nucleotides, the building blocks of nucleic acids including DNA and RNA. Nucleotides are composed of three subunits, including a nucleobase, a five-carbon sugar, and a phosphate group. The ability of nucleobases to form hydrogen-bonding WC base pairs and to stack upon each other through π─π interactions leads directly to the double-stranded helical structures of DNA molecules. Therefore, in this subsection, we aim to compare the transferability of the additive, pGM-ind, and pGM-perm models from the DNA nucleobase monomers, including adenine (A), thymine (T), guanine (G), and cytosine (C), to the WC base pair dimers and stacked WC base pair tetramers formed by the four DNA nucleobases. All monomers, dimers, and tetramers used in this work are from the BASE data set. Each nucleobase is capped with a methyl group to mimic the chemical environment within nucleosides. The two WC base pair dimers include the A-T base pair with two hydrogen bonds and the G-C base pair with three hydrogen bonds. The eight stacked WC base pair tetramers include A-T/A-T, A-T/T-A, A-T/C-G, A-T/G-C, G-C/A-T, G-C/T-A, G-C/C-G, and G-C/G-C. For instance, the A-T/C-G tetramer is formed by stacking the A-T base pair onto the C-G base pair, where A and T are stacked with C and G, respectively.
Since the nucleobases are rigid molecules in nature, each DNA nucleobase monomer was parameterized using single-conformation fitting to ESPs calculated at the ωB97X-D/aug-cc-pVTZ level of theory. Table 3 shows the molecular dipole and quadrupole moments calculated by each electrostatic model and QM methods as well as the RRMSV of the A-T and G-C WC base pair dimers. It can be seen that the pGM-ind and pGM-perm models produce molecular dipole moments and quadrupole moments with better agreement with the QM moments than the additive model. However, nucleobases are also singular molecules in terms of the parameterizations of the pGM-perm model due to the existence of sp2 carbons in all nucleobases (see Appendix), which can explain the observation that the pGM-ind model gives slightly better agreement with the QM-calculated electric moments than the pGM-perm model. On the other hand, the RRMSV consistently decreases with the order of the additive, pGM-ind, and pGM-perm models for both WC base pairs. For the A-T base pairs, the RRMSV of the pGM-ind (0.1250) and pGM-perm (0.0904) models are 86 and 62% of that of the additive model (0.1454); for the G-C base pairs, the RRMSV of the pGM-ind (0.1183) and pGM-perm (0.0766) models are 71 and 46% of that of the additive model (0.1657). Therefore, the pGM models outperform the additive model significantly in terms of transferability to WC base pairs with the single-conformation fitting with the A, T, G, and C monomers. Note that the G-C base pair (QM dipole = 6.0874 Debye) has a much higher overall dipole moment than the A-T base pair (1.9010 Debye). The observation that the additive model gives higher RRMSV for the G-C base pair than for the A-T base pair, while the pGM models give lower RRMSV for the G-C base pair than for the A-T base pair indicates that the pGM models can better model the polarization effects in the highly polar G-C base pairs.
Table 3.
Molecular Dipole/Quadrupole Moments and of the A-T and G-C WC Base Pair Dimers Fitted with the A, T, G, and C Monomers with the Additive, pGM-ind, and pGM-perm Models
| WC base pair |
additive |
pGM-ind |
pGM-perm |
QM |
|
|---|---|---|---|---|---|
| Dipole Moments/Debyea | |||||
| A-T | 2.3174 | 1.8483 | 1.9134 | 1.9010 | |
| G-C | 4.6236 | 5.9753 | 5.9603 | 6.0874 | |
| Quadrupole Moments/Debye Angstromsb | |||||
| A-T | Qxx | 46.5515 | 41.0910 | 40.7533 | 43.5328 |
| Qyy | −19.7216 | −17.9977 | −17.5097 | −18.6448 | |
| Qzz | −26.8299 | −23.0933 | −23.2436 | −24.8879 | |
| G-C | Qxx | 46.5542 | 43.6740 | 43.6416 | 46.3355 |
| Qyy | −20.9126 | −19.4755 | −19.1479 | −20.4689 | |
| Qzz | −25.6416 | −24.1985 | −24.4937 | −25.8666 | |
| A-T | 0.1454 | 0.1250 | 0.0904 | ||
| G-C | 0.1657 | 0.1183 | 0.0766 | ||
Dipole moment relative to the center of mass.
Quadrupole moments along the principal axes.
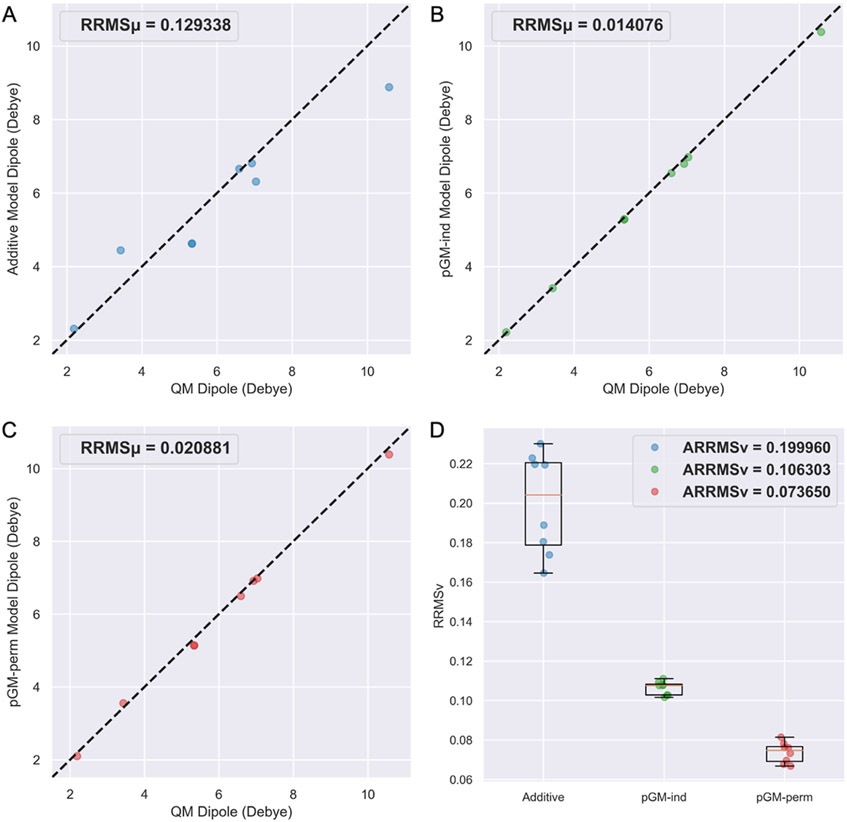
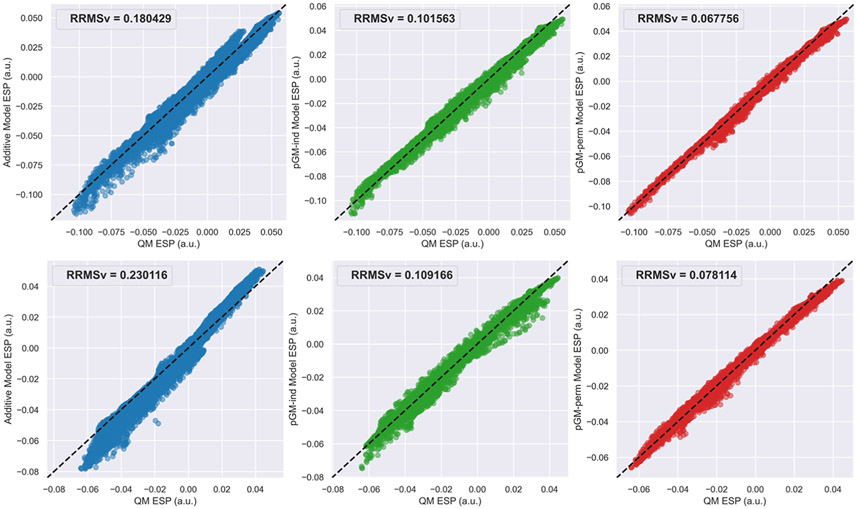
Figure 7A-C shows the scatterplot of MM dipoles of the eight WC base pair tetramers from the BASE data set calculated by each electrostatic model versus those calculated at the ωB97X-D/aug-cc-pVTZ level of theory. It can be observed that the of the pGM-ind (0.0141) and pGM-perm (0.0209) models are much lower than that of the additive model (0.1293), as the of the pGM-ind and pGM-perm models are only 11 and 16% of that of the additive model. The slightly better performance of the pGM-ind model than the pGM-perm model is consistent with the better electric moment agreement with QM results given by the pGM-ind model for WC base pair dimers, which might be caused by the singularity problem of the pGM-perm model. Figure 7D shows the boxplots of the of the WC base pair tetramers of each electrostatic model, and we can see that the decreases in the order of the additive (0.2000), pGM-ind (0.1063), and pGM-perm (0.0737) models, as the of the pGM-ind and pGM-perm models are 53 and 37% of that of the additive model. To further explore the transferability difference among different models, the scatterplots of MM ESPs versus the QM ESPs for the G-C/G-C tetramer with the highest QM overall dipole (dipole = 10.5748 Debye) and the A-T/T-A tetramer with the lowest QM overall dipole (dipole = 2.1904 Debye) are shown in Figure 8. Once again, for both WC base pair tetramers, the of the pGM-perm model are the lowest and those of the pGM-ind model are the second lowest. For the G-C/G-C tetramer, the of the additive, pGM-ind, and pGM-perm models are 0.1804, 0.1016, and 0.0678, respectively. For the A-T/T-A tetramer, the of the additive, pGM-ind, and pGM-perm models are 0.2301, 0.1092, and 0.0781, respectively.
Figure 7.
Transferability tests of the additive, pGM-ind, and pGM-perm models from A, T, G, and C monomers to WC base pair tetramers. (A–C) Scatterplots of MM dipoles of each electrostatic model versus QM dipoles. (D) Boxplots of of each electrostatic model with QM results. Each scatterplot or boxplot shows a total of eight data points, with each point representing a WC base pair tetramer.
Figure 8.
Scatterplots of the MM ESPs of the additive, pGM-ind, and pGM-perm models versus QM ESPs for representative WC base pair tetramers. The upper panel is for the G-C/G-C tetramer with the highest QM dipole (dipole = 10.5748 Debye). Each plot shows a total of 14015 data points, with each point representing an ESP point. The lower panel is for the A-T/T-A tetramer with the lowest QM dipole (dipole = 2.1904 Debye). Each plot shows a total of 14 196 data points, with each point representing an ESP point.
DISCUSSION AND CONCLUSIONS
Two desirable properties of molecular mechanical force fields are accuracy and transferability. Various previous works have demonstrated the accuracy of the pGM models.52,55,56 In this work, we assessed the transferability of the electrostatic parameters of the pGM-ind and pGM-perm models by exploring whether the pGM models can accurately reproduce the electrostatic properties of larger molecular systems or different molecular conformations other than the molecules or conformations used for parametrizations. Encouragingly, as measured by and , both the pGM-ind and pGM-perm models show significantly better transferability than the point-charge additive model. This has been demonstrated in the transferability tests (1) from water monomer to water oligomer clusters with various sizes; (2) across different conformations of amino acid dipeptides or tetrapeptides with widespread distributions of molecular dipole moments; (3) from amino acid tetrapeptides to longer polypeptides with up to 20 amino acid residues; and (4) from nucleobase monomers to WC base pair dimers and tetramers, which play key roles in the formation of double-stranded helical structures of DNA molecules. This and previous assessments together show that the accurate and transferable pGM models have the potential to serve as foundations for developing the next-generation polarizable force fields for modeling various biological processes that are sensitive to polarization effects.
Another focus of this work is to identify the optimal parameterization strategy of amino acids for developing the next-generation polarizable force fields based on the pGM models. Taking previous Amber force fields as examples, the amino acid charge sets of the ff94 additive force field5,6 and the ff02 polarizable force field33 were both derived with C5/αR double-conformation fittings using amino acid dipeptides and that of the ff12pol polarizable force field35-38 was derived with the αR/β/pII triple-conformation fittings, also using amino acid dipeptides. The electrostatic terms of the ff94 force field were parameterized using the RESP program,13,14 which have remained unchanged in various subsequent additive Amber force fields for almost 30 years.6,7,17-22 The electrostatic terms of the ff02 and ff12pol force fields were parameterized using an iterative charge fitting program named i_RESP.23 Recently, the PyRESP program that performs electrostatic parameterizations for the pGM models using a direct matrix form solvation approach has been implemented.56 Therefore, we aim to identify the amino acid conformations and the number of conformations for parameterizing the pGM models that lead to optimal transferability. We first tested parametrizations using dipeptides in 1–5 conformations, and the electrostatic parameters derived by fitting dipeptides transfer well across the 14 different dipeptide conformations. However, the pGM-perm model gives unsatisfactory transferability from dipeptides to tetrapeptides. Therefore, we moved on to test parametrizations using tetrapeptides directly. Encouragingly, the αR/β double-conformation fitting with tetrapeptides shows great transferability not only across different tetrapeptide conformations but also from tetrapeptides to longer polypeptides with lengths ranging from 1 to 20 repetitive amino acid residues for both the pGM-ind and pGM-perm models. In the future development of the pGM force fields for proteins, the αR/β double-conformation fittings with tetrapeptides are expected to be applied to derive the electrostatic parameters of all amino acids systematically.
An important question is, between the pGM-ind and pGM-perm models, which one has better transferability. In theory, the more elaborate pGM-perm model with atomic permanent dipoles has a higher degree of freedom for parametrization, which can better reproduce the ESPs used for fitting and give a better description for molecular electrostatic properties such as electric moments, leading to better transferability. This is indeed the case for water molecules as shown in Figures 1-3, where the pGM-perm and pGM-perm-v models yield much lower than the pGM-ind model, regardless of the water oligomer cluster size. Additionally, all pGM models give similar for each water oligomer cluster data set. However, as discussed in the Appendix, the parameterization of the pGM-perm model suffers from the singularity problem for most biomolecules due to the use of the permanent dipole local frame formed by CBVs. In contrast, the pGM-ind model does not have this problem since it does not take atomic permanent dipoles into account. In theory, the singularity problem can be addressed by the restrained fitting strategy as well as the multiple-conformation fitting strategy implemented in the PyRESP program. As shown in Figures 4-7, for single-conformation fittings of alanine dipeptides, alanine tetrapeptides, and nucleobases, which are all singular molecules, the pGM-ind model consistently shows better transferability than the pGM-perm model, as measured by both and . With multiple-conformation fittings, the pGM-perm model generally outperforms the pGM-ind model, especially in the transferability from amino acid tetrapeptides to longer amino acid polypeptides. Therefore, we conclude that the pGM-perm model can be expected to give better transferability than the pGM-ind model for nonsingular molecules such as water. For singular molecules such as amino acids and nucleotides, if there are more than one conformation available for multiple-conformation fittings, the pGM-perm model is expected to give better transferability; otherwise, the pGM-ind model is expected to give better transferability for single-conformation fittings.
Another important question for future users who wish to parameterize nonstandard molecules (such as small-molecule ligands) is as follows: What types of conformations should be used for parameterizing the pGM models in general? For molecules that have rigid conformations such as nucleobases, there are probably not too many choices. However, the transferability tests on amino acids provide some insights for the parameterizations of flexible molecules. For the parameterizations of both the alanine dipeptides and alanine tetrapeptides, we tested the single-conformation fittings and double-conformation fittings using conformations with the highest (αR for both dipeptide and tetrapeptide), lowest (β for both dipeptide and tetrapeptide), and intermediate (C7eq for dipeptide and pII for tetrapeptide) molecular dipole moments. As shown in Figures S4-S6 and S22-S24, among all single-conformation fittings, the conformations with intermediate dipole moments (C7eq or pII) consistently give the best overall performance for the transferability of the pGM-ind and pGM-perm models. In contrast, as shown in Figures S7-S9 and S25-S27, among all double-conformation fittings, the best overall performance is consistently given by the combination of the conformations with the highest (αR) and lowest (β) dipole moments. Therefore, for selecting conformations for the parameterizations of flexible molecules, conformations with intermediate molecular dipole moments are recommended for single-conformation fittings, while the combination of conformations with widespread molecular dipole moments (such as conformations with the highest and lowest dipoles from all available conformations) is recommended for multiple-conformation fittings.
Our goal is to develop applicable and accessible pGM force fields for the molecular modeling community to perform simulation works on biomolecular systems that are sensitive to polarization effects. In future works, the electrostatic parameters of all standard amino acids (in any protonation states) and nucleotides for the pGM models will be derived using the strategy of restrained fitting in combination with multiple-conformation fitting provided by the PyRESP program.56 A polarizable water model based on the pGM models will also be developed and analyzed. In addition, the van der Waals parameters for the pGM models need to be reoptimized using a similar strategy as was used in the development of the ff12pol force field.38
Supplementary Material
ACKNOWLEDGMENTS
The authors would like to thank Dr. Haixin Wei for providing insights into the singularity problem of the pGM-perm model. The authors also gratefully acknowledge the research support from NIH (GM79383 to Y.D. and GM130367 to R.L.).
APPENDIX
Singularity Problem of the pGM-perm and pGM-perm-v Models and Solutions
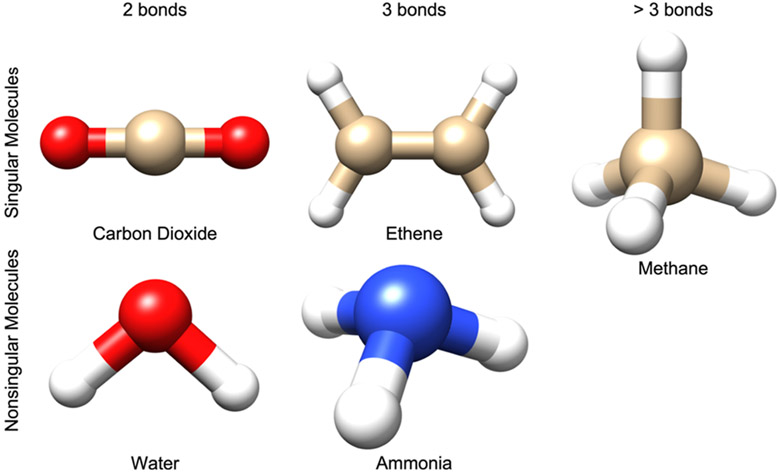
The parameterizations of the pGM-perm and pGM-perm-v models suffer from the singularity problem that originates from the use of the permanent dipole local frame formed by CBVs. Since CBVs are along the direction of covalent bonds (and virtual bonds for pGM-perm-v), some molecules are “singular molecules” due to the existence of “singular atoms”. Taking carbon dioxide (CO2) as an example, the two covalent bonds associated with the central carbon atom are colinear, so the two permanent C─O dipoles oriented in opposite directions can be assigned any value to give zero net dipole to the carbon atom. Therefore, the carbon atom in CO2 is a singular atom, and the CO2 molecule is a singular molecule. Figure A1 gives several examples of singular and nonsingular molecules. The water (H2O) molecule is nonsingular. Similar to the case of CO2, there are two covalent bonds associated with the central oxygen atom of water. However, the permanent O─H dipoles are not colinear, so there only exists one solution for the value of the O─H dipole to give the correct atomic dipole for oxygen. The carbon atom of the ethene (C2H4) molecule and the nitrogen atom of the ammonia (NH3) molecule both have three covalent bonds associated. However, ethene is singular, but ammonia is nonsingular. The two C─H dipoles and the C─C dipole of each carbon atom in the ethene molecule are coplanar, so the net atomic dipole of the ethene molecule can be produced by infinitely many linear combinations of the three dipoles. In contrast, the three N─H dipoles of the nitrogen atom in the ammonia molecule are not coplanar, so there only exists one solution for the value of the N─H dipole to give the correct atomic dipole for nitrogen. For atoms associated with more than three covalent bonds (and virtual bonds), such as the central carbon of the methane (CH4) molecule, regardless of how these bonds are oriented, there will always be infinitely many linear combinations of the dipoles on these bonds that can produce the net atomic dipole for the atom. Therefore, any atoms associated with more than three bonds are singular atoms, and any molecules containing this type of atoms are singular molecules. Furthermore, the virtual dipoles of the pGM-perm-v model may cause additional singularity problems during parameterization. For example, the oxygen atoms in CO2 are nonsingular atoms in the pGM-perm model but they are singular atoms in the pGM-perm-v model, since the O─C covalent dipole and O─O virtual dipole are colinear.
Figure A1.
Several examples of singular and nonsingular molecules in the context of parameterization of the pGM-perm model. The upper panel shows examples of singular molecules, and the lower panel shows examples of nonsingular molecules. In the left column, the singular carbon atom of the carbon dioxide (CO2) molecule has two covalent bonds; in the middle column, the singular carbon atom of the ethene molecule has three covalent bonds; and in the right column, the singular carbon atom of the methane molecule has four covalent bonds.
The general rule for checking whether an atom is singular in the context of pGM-perm and pGM-perm-v models is as follows: first, count the number of covalent bonds and virtual bonds associated with this atom. If there is only one bond, the atom is nonsingular; if there are more than three bonds, the atom is singular. In the case of two bonds, the atom is singular if the two bonds are colinear and nonsingular if the two bonds are not colinear. In the case of three bonds, the atom is singular if the three bonds are coplanar and nonsingular if the two bonds are not coplanar. In fact, most biomolecules are singular molecules due to the widespread existence of sp3 carbons, such as the α-carbon in every amino acid backbone and the five carbons in the sugar unit of every nucleotide. If there is at least one singular atom in the molecule, the molecule is a singular molecule.
The mathematical explanation of the singularity problem is that the electrostatic parameterization of a molecule using the PyRESP program essentially computes the least-squares solution of the following equation56
| (A1) |
where is a vector for all the point charges and permanent point dipoles of the molecule being parameterized, and the details of the equation can be found in our original PyRESP work.56 The least-squares solution can be obtained by solving the following equation, the proof of which can be found in most linear algebra textbooks
| (A2) |
If eq A2 has a unique solution, the square symmetric matrix needs to be positive, definite, and invertible. However, for the parameterization of singular molecules such as methane with the pGM-perm or pGM-perm-v models, the matrix contains linearly dependent columns, and the matrix becomes a singular matrix, which is not invertible.
One solution to the singularity problem is the restrained fitting implemented in the PyRESP program, which was originally implemented in its ancestor program RESP.13,14 The RESP program applies the following hyperbolic restraining function χ to the least-squares fitting of additive models
| (A3) |
where is the point charge of atom ; is the scale factor that defines the restraining strength; and determines the “tightness” of the hyperbola around its minimum, which has been recommended to be set to 0.1 to make the restraint appropriately tight.13 The PyRESP program extends the restraining functions of the RESP program by applying an additional penalty function with the same format as eq A3 for restraining atomic permanent dipoles and allowing the users to choose different restraining strength for point charges and permanent dipoles. In the restrained fitting process, the partial derivative of the penalty function χ to each electrostatic parameter is added to the diagonal terms of the matrix , introducing nonlinearity into the singular matrix. Therefore, the matrix becomes invertible, and eq A2 has a unique solution.
Another solution to the singularity problem is the multiple-conformation fitting. By enforcing intermolecular equivalences among multiple conformations of the same molecule, the rows and columns of the matrix corresponding to equivalent permanent dipoles are added up to form a single row and column, giving rise to a smaller matrix . This operation essentially eliminates the linear dependence of the linearly dependent columns of the matrix , and the resulting smaller matrix becomes invertible. However, the disadvantage of the multiple-conformation fitting strategy is that it may be difficult, if not impossible, to construct multiple optimized conformations for small rigid singular molecules such as CO2, ethene, and methane. It is only an appropriate strategy for parameterizing large singular molecules such as amino acids and nucleotides.
Footnotes
The authors declare no competing financial interest.
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c01048.
QM molecular dipole moments of alanine polypeptides (ACE-ALAn-NME) from the ALA-poly data set, of glycine polypeptides (ACE-GLYn-NME) from the GLY-poly data set, and of WC base pair tetramers from the BASE data set; transferability tests of the additive, pGM-ind, pGM-perm, and pGM-perm-v models from water monomer to water hexamer clusters, from water monomer to water octamer clusters, and from water monomer to water decamer clusters; and transferability tests of the additive, pGM-ind, and pGM-perm models across alanine dipeptide conformations, from alanine dipeptides to alanine tetrapeptides, and across alanine tetrapeptide conformations (PDF)
Contributor Information
Shiji Zhao, Departments of Molecular Biology and Biochemistry, Chemical and Biomolecular Engineering, Materials Science and Engineering, and Biomedical Engineering, University of California, Irvine, Irvine, California 92697, United States; Present Address: Nurix Therapeutics, Inc., 1700 Owens Street Suite 205, San Francisco, CA 94158, United States.
Piotr Cieplak, SBP Medical Discovery Institute, La Jolla, California 92037, United States.
Yong Duan, UC Davis Genome Center and Department of Biomedical Engineering, University of California, Davis, Davis, California 95616, United States.
Ray Luo, Departments of Molecular Biology and Biochemistry, Chemical and Biomolecular Engineering, Materials Science and Engineering, and Biomedical Engineering, University of California, Irvine, Irvine, California 92697, United States.
REFERENCES
- (1).Leach AR, Molecular Modelling: Principles and Applications. 2nd ed.; Pearson education: 2001. [Google Scholar]
- (2).Vitalis A; Pappu RV Chapter 3 Methods for Monte Carlo Simulations of Biomacromolecules. Annu. Rep. Comput. Chem 2009, 5, 49–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Monticelli L; Tieleman DP Force fields for classical molecular dynamics. Biomolecular simulations 2013, 924, 197–213. [DOI] [PubMed] [Google Scholar]
- (4).Salomon-Ferrer R; Case DA; Walker RC An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev.: Comput. Mol. Sci 2013, 3, 198–210. [Google Scholar]
- (5).Cieplak P; Cornell WD; Bayly C; Kollman PA Application of the multimolecule and multiconformational RESP methodology to biopolymers: Charge derivation for DNA, RNA, and proteins. J. Comput. Chem 1995, 16, 1357–1377. [Google Scholar]
- (6).Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- (7).Wang J; Cieplak P; Kollman PA How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem 2000, 21, 1049–1074. [Google Scholar]
- (8).Momany FA Determination of partial atomic charges from ab initio molecular electrostatic potentials. Application to formamide, methanol, and formic acid. J. Phys. Chem 1978, 82, 592–601. [Google Scholar]
- (9).Cox S; Williams D Representation of the molecular electrostatic potential by a net atomic charge model. J. Comput. Chem 1981, 2, 304–323. [Google Scholar]
- (10).Chirlian LE; Francl MM Atomic charges derived from electrostatic potentials: A detailed study. J. Comput. Chem 1987, 8, 894–905. [Google Scholar]
- (11).Besler BH; Merz KM Jr; Kollman PA Atomic charges derived from semiempirical methods. J. Comput. Chem 1990, 11, 431–439. [Google Scholar]
- (12).Breneman CM; Wiberg KB Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem 1990, 11, 361–373. [Google Scholar]
- (13).Bayly CI; Cieplak P; Cornell W; Kollman PA A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem 1993, 97, 10269–10280. [Google Scholar]
- (14).Cornell WD; Cieplak P; Bayly CI; Kollman PA Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc 1993, 115, 9620–9631. [Google Scholar]
- (15).Reynolds CA; Essex JW; Richards WG Atomic charges for variable molecular conformations. J. Am. Chem. Soc 1992, 114, 9075–9079. [Google Scholar]
- (16).Stouch T; Williams DE Conformational dependence of electrostatic potential derived charges of a lipid headgroup: Glycerylphosphorylcholine. J. Comput. Chem 1992, 13, 622–632. [Google Scholar]
- (17).Tian C; Kasavajhala K; Belfon KA; Raguette L; Huang H; Migues AN; Bickel J; Wang Y; Pincay J; Wu Q; Simmerling C ff19SB: Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J. Chem. Theor. Comput 2019, 16, 528–552. [DOI] [PubMed] [Google Scholar]
- (18).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theor. Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hornak V; Abel R; Okur A; Strockbine B; Roitberg A; Simmerling C Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Zgarbová M; Šponer J; Jurečka P Z-DNA as a Touchstone for Additive Empirical Force Fields and a Refinement of the Alpha/Gamma DNA torsions for AMBER. J. Chem. Theory Comput 2021, 17, 6292–6301. [DOI] [PubMed] [Google Scholar]
- (21).Zgarbová M; Šponer J; Otyepka M; Cheatham TE III; Galindo-Murillo R; Jurečka P Refinement of the Sugar-Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA. J. Chem. Theor. Comput 2015, 11, 5723–5736. [DOI] [PubMed] [Google Scholar]
- (22).Zgarbová M; Otyepka M; Šponer J. i.; Mládek A. t.; Bansáš P; Cheatham TE III; Jursečka P Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theor. Comput 2011, 7, 2886–2902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Cieplak P; Dupradeau F-Y; Duan Y; Wang J Polarization effects in molecular mechanical force fields. J. Phys.: Condens. Matter 2009, 21, 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Gresh N; Cisneros GA; Darden TA; Piquemal J-P Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and Ligand–Macromolecule Complexes. A Bottom-Up Strategy. J. Chem. Theor. Comput 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Zhao S; Schaub AJ; Tsai S-C; Luo R Development of a Pantetheine Force Field Library for Molecular Modeling. J. Chem. Inf. Model 2021, 61, 856–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).King E; Qi R; Li H; Luo R; Aitchison E Estimating the roles of protonation and electronic polarization in absolute binding affinity simulations. J. Chem. Theor. Comput 2021, 17, 2541–2555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Draper DE; Grilley D; Soto AM Ions and RNA folding. Annu. Rev. Biophys. Biomol. Struct 2005, 34, 221–243. [DOI] [PubMed] [Google Scholar]
- (28).Gkionis K; Kruse H; Platts JA; Mládek A; Koča J; Šponer J Ion binding to quadruplex DNA stems. Comparison of MM and QM descriptions reveals sizable polarization effects not included in contemporary simulations. J. Chem. Theor. Comput 2014, 10, 1326–1340. [DOI] [PubMed] [Google Scholar]
- (29).Fitch CA; Karp DA; Lee KK; Stites WE; Lattman EE; García-Moreno EB Experimental pKa values of buried residues: analysis with continuum methods and role of water penetration. Biophys. J 2002, 82, 3289–3304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Lin Z; van Gunsteren WF Effects of Polarizable Solvent Models upon the Relative Stability of an α-Helical and a β-Hairpin Structure of an Alanine Decapeptide. J. Chem. Theory Comput 2015, 11, 1983–1986. [DOI] [PubMed] [Google Scholar]
- (31).Peng X; Zhang Y; Chu H; Li Y; Zhang D; Cao L; Li G Accurate evaluation of ion conductivity of the gramicidin a channel using a polarizable force field without any corrections. J. Chem. Theor. Comput 2016, 12, 2973–2982. [DOI] [PubMed] [Google Scholar]
- (32).Sun R-N; Gong H Simulating the activation of voltage sensing domain for a voltage-gated sodium channel using polarizable force field. J. Phys. Chem. Lett 2017, 8, 901–908. [DOI] [PubMed] [Google Scholar]
- (33).Cieplak P; Caldwell J; Kollman P Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. J. Comput. Chem 2001, 22, 1048–1057. [Google Scholar]
- (34).Wang ZX; Zhang W; Wu C; Lei H; Cieplak P; Duan Y Strike a balance: optimization of backbone torsion parameters of AMBER polarizable force field for simulations of proteins and peptides. J. Comput. Chem 2006, 27, 781–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Wang J; Cieplak P; Li J; Hou T; Luo R; Duan Y Development of polarizable models for molecular mechanical calculations I: parameterization of atomic polarizability. J. Phys. Chem. B 2011, 115, 3091–3099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Wang J; Cieplak P; Li J; Wang J; Cai Q; Hsieh M; Lei H; Luo R; Duan Y Development of polarizable models for molecular mechanical calculations II: induced dipole models significantly improve accuracy of intermolecular interaction energies. J. Phys. Chem. B 2011, 115, 3100–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Wang J; Cieplak P; Cai Q; Hsieh M-J; Wang J; Duan Y; Luo R Development of polarizable models for molecular mechanical calculations. 3. Polarizable water models conforming to Thole polarization screening schemes. J. Phys. Chem. B 2012, 116, 7999–8008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Wang J; Cieplak P; Li J; Cai Q; Hsieh M-J; Luo R; Duan Y Development of polarizable models for molecular mechanical calculations. 4. van der Waals parametrization. J. Phys. Chem. B 2012, 116, 7088–7101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Ren P; Ponder JW Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. J. Comput. Chem 2002, 23, 1497–1506. [DOI] [PubMed] [Google Scholar]
- (40).Ren P; Ponder JW Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar]
- (41).Banks JL; Kaminski GA; Zhou R; Mainz DT; Berne B; Friesner RA Parametrizing a polarizable force field from ab initio data. I. The fluctuating point charge model. J. Chem. Phys 1999, 110, 741–754. [Google Scholar]
- (42).Patel S; Brooks CL III CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. J. Comput. Chem 2004, 25, 1–16. [DOI] [PubMed] [Google Scholar]
- (43).Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD Jr. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem. Phys. Lett 2006, 418, 245–249. [Google Scholar]
- (44).Lopes PE; Lamoureux G; Roux B; MacKerell AD Polarizable empirical force field for aromatic compounds based on the classical drude oscillator. J. Phys. Chem. B 2007, 111, 2873–2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Tan Y-H; Luo R Continuum treatment of electronic polarization effect. J. Chem. Phys 2007, 126, 094103. [DOI] [PubMed] [Google Scholar]
- (46).Tan Y-H; Tan C; Wang J; Luo R Continuum Polarizable Force Field within the Poisson–Boltzmann Framework. J. Phys. Chem. B 2008, 112, 7675–7688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Applequist J; Carl JR; Fung K-K Atom dipole interaction model for molecular polarizability. Application to polyatomic molecules and determination of atom polarizabilities. J. Am. Chem. Soc 1972, 94, 2952–2960. [Google Scholar]
- (48).Thole BT Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys 1981, 59, 341–350. [Google Scholar]
- (49).Elking D; Darden T; Woods RJ Gaussian induced dipole polarization model. J. Comput. Chem 2007, 28, 1261–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Elking DM; Cisneros GA; Piquemal J-P; Darden TA; Pedersen LG Gaussian multipole model (GMM). J. Chem. Theor. Comput 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Elking DM; Perera L; Duke R; Darden T; Pedersen LG Atomic forces for geometry-dependent point multipole and Gaussian multipole models. J. Comput. Chem 2010, 31, 2702–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Wang J; Cieplak P; Luo R; Duan Y Development of polarizable Gaussian model for molecular mechanical calculations I: Atomic polarizability parameterization to reproduce ab initio anisotropy. J. Chem. Theor. Comput 2019, 15, 1146–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Wei H; Qi R; Wang J; Cieplak P; Duan Y; Luo R Efficient formulation of polarizable Gaussian multipole electrostatics for biomolecular simulations. J. Chem. Phys 2020, 153, 114116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Wei H; Cieplak P; Duan Y; Luo R Stress tensor and constant pressure simulation for polarizable Gaussian multipole model. J. Chem. Phys 2022, 156, 114114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Zhao S; Wei H; Cieplak P; Duan Y; Luo R Accurate Reproduction of Quantum Mechanical Many-Body Interactions in Peptide Main-Chain Hydrogen-Bonding Oligomers by the Polarizable Gaussian Multipole Model. J. Chem. Theory Comput 2022, 18, 6172–6188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Zhao S; Wei H; Cieplak P; Duan Y; Luo R PyRESP: A Program for Electrostatic Parameterizations of Additive and Induced Dipole Polarizable Porce Pields. J. Chem. Theory Comput 2022, 18, 3654–3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (58).Case DA; Aktulga HM; Belfon K; Ben-Shalom I; Berryman JT; Brozell SR; Cerutti DS; Cheatham TE III; Cisneros GA; Cruzeiro VWD; Darden TA; Duke RE; Giambasu G; Gilson MK; Gohlke H; Goetz AW; Harris R; Izadi S; Izmailov SA; Kasavajhala K; Kaymak MC; King E; Kovalenko A; Kurtzman T; Lee T; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Machado M; Man V; Manathunga M; Merz KM; Miao Y; Mikhailovskii O; Monard G; Nguyen H; O’Hearn KA; Onufriev A; Pan P; Pantano S; Qi R; Rahnamoun A; Roe DR; Roitberg A; Sagui C; Schott-Verdugo S; Shajan A; Shen J; Simmerling CL; Skrynnikov NR; Smith J; Swails J; Walker RC; Wang J; Wang J; Wei H; Wolf RM; Wu X; Xiong Y; Xue Y; York DM; Zhao S; Kollman PA Amber 2022; University of California: San Francisco, 2022. [Google Scholar]
- (59).Beachy MD; Chasman D; Murphy RB; Halgren TA; Priesner RA Accurate ab initio quantum chemical determination of the relative energetics of peptide conformations and assessment of empirical force fields. J. Am. Chem. Soc 1997, 119, 5908–5920. [Google Scholar]
- (60).Bansal M; Bhattacharyya D; Ravi B NUPARM and NUCGEN: software for analysis and generation of sequence dependent nucleic acid structures. Bioinformatics 1995, 11, 281–287. [DOI] [PubMed] [Google Scholar]
- (61).Prisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ Gaussian 16, Revision A. 03. 2016; Gaussian Inc.: Wallingford CT, 2016; Vol. 2 (4). [Google Scholar]
- (62).Connolly ML Analytical molecular surface calculation. J. Appl. Crystallogr 1983, 16, 548–558. [Google Scholar]
- (63).Singh UC; Kollman PA An approach to computing electrostatic charges for molecules. J. Comput. Chem 1984, 5, 129–145. [Google Scholar]
- (64).Xie W; Pu J; Gao J A coupled polarization-matrix inversion and iteration approach for accelerating the dipole convergence in a polarizable potential function. J. Phys. Chem. A 2009, 113, 2109–2116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Pettersen EF; Goddard TD; Huang CC; Couch GS; Greenblatt DM; Meng EC; Ferrin TE UCSF Chimera? A visualization system for exploratory research and analysis. J. Comput. Chem 2004, 25, 1605–1612. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.