The benefits of a metacognitive lesson on children’s understanding of mathematical equivalence, arithmetic, and place value

Abstract

Metacognition is theorized to play a central role in children’s mathematics learning. The primary goal of the current study was to provide experimental evidence in support of this role with elementary school students learning about mathematical equivalence. The final sample included 135 children (59 first-graders and 76 second-graders) who participated in the study across three sessions in their classrooms. They completed a pretest during session one, a lesson and posttest during session two, and a two-week delayed retention test during session three. For session two, children were randomly assigned to receive a lesson on mathematical equivalence with or without integrated metacognitive questions. Relative to the control lesson, children who received the metacognitive lesson demonstrated higher accuracy and higher metacognitive monitoring scores on the posttest and retention test. Further, these benefits sometimes extended to uninstructed items targeting arithmetic and place value. No condition effects were observed for children’s metacognitive control skills within any of the topics. These findings suggest a brief metacognitive lesson can improve children’s mathematics understanding.

Successful learning often depends on students’ metacognition – their ability to conceptualize and regulate their own knowledge (Flavell, 1979). Two key skills include students’ monitoring of their own performance (e.g., I think I solved that correctly) and students’ control of their study behaviors (e.g., I need to study that problem again; Nelson & Narens, 1994). These components of metacognition have been shown to predict academic achievement in a variety of domains (e.g., Ohtani & Hisasaka, 2018; Veenman & Spaans, 2005). The goal of the current study was to focus on these metacognitive skills for children learning mathematics. The first aim was to quantify children’s monitoring and control skills and examine how they are related within and across three mathematics topics (equivalence, arithmetic, and place value). The second aim was to experimentally evaluate the causal effect of a metacognitive lesson relative to a control lesson on children’s understanding of mathematical equivalence. The third aim was to determine whether the benefits of the metacognitive lesson were specific to the instructed topic of equivalence or whether they generalized to the other topics of arithmetic and place value.

Metacognition in Mathematics Education

The importance of metacognition in mathematics has both theoretical and empirical support (see Desoete & De Craene, 2019 and Schneider & Artelt, 2010 for reviews). For example, Schoenfeld (1992) argued that metacognition has the potential to move students beyond the use of rote mathematical formulas toward more meaningful mathematical experiences. By reflecting on their knowledge and problem-solving processes, students may be able to make connections between mathematical concepts and develop more effective self-regulated learning strategies (see also Rinne & Mazzocco, 2014).

A variety of correlational studies demonstrate positive links between metacognition and mathematics performance (e.g., Bellon et al., 2019; Carr & Jessup, 1995; Lucangeli & Cornoldi, 1997; Nelson & Fyfe, 2019). For example, Vo and colleagues (2014) assessed children ages five to eight and found a strong correlation between their monitoring skills and their performance on a standardized mathematics test. Also, Rinne and Mazzocco (2014) found that metacognitive monitoring in fifth grade (approximately age 10) not only predicted students’ current arithmetic performance, but also their growth in arithmetic performance from fifth to eighth grade.

Several intervention studies indicate that the positive link may be causal – that is, training children’s metacognitive skills can influence their mathematics achievement (see Baten et al., 2017). One example is the IMPROVE intervention (Mevarech & Kramarski, 1997), which is an acronym standing for Introducing concepts, Metacognitive questioning, Practicing, Reviewing and reducing difficulties, Obtaining mastery, Verification, and Enrichment. A core component of the intervention is the use of metacognitive questions that students are taught to use as they engage in problem solving (e.g., what strategy can be used? does my solution make sense?). Although primarily implemented with older students in seventh and eighth grade (e.g., Mevarech & Kramarski, 1997; 2003), the IMPROVE intervention has been used successfully with students in third grade. Kramarski et al. (2010) assigned two third-grade classes to the IMPROVE intervention for lessons on arithmetic and assigned two other third-grade classes to a business-as-usual control. Students in the IMPROVE classes exhibited better mathematical problem solving.

Additional studies also highlight metacognitive questions as playing a key role. For example, the Solve It! intervention (Montague, 2003) teaches students to use metacognitive strategies while solving mathematics word problems, including the use of reflective questioning (e.g., does my answer make sense? have I checked every step?). The intervention was shown to facilitate seventh-grade students’ mathematics problem solving relative to a business-as-usual control across 34 classrooms (Montague et al., 2014). Other work by Desoete et al. (2003) isolated the effects of metacognitive “prediction” questions for elementary school students, which taught students to ask themselves, “Do I think I can solve this exercise?”. Third-graders were assigned to work in small groups in one of five training conditions, only one of which contained the prediction questions. Children with the prediction training exhibited higher metacognitive skills and higher problem-solving performance compared to the other four groups.

These studies and others have demonstrated the malleability of metacognitive skills, the benefits of reflective questioning, and the importance of metacognition in mathematics. Yet, there remain gaps in the literature on metacognitive training. The majority of intervention studies focus on older students in middle school or beyond. Though some work has been done with students in third grade (as young as 8 years old), the benefits of metacognitive instruction for younger students remains unknown. Further, existing studies tend to focus on representing and solving word problems, but the effects of metacognitive instruction for other mathematics topics is less clear. Also, because these studies tend to focus on outcome measures within a single topic, it is difficult to know whether the benefits of metacognitive training are topic-specific or whether they generalize to un-instructed topics. The goal of the current study was to help fill these gaps by evaluating the effects of a metacognitive lesson on first- and second-grade students’ understanding of mathematical equivalence, as well as on their understanding of two uninstructed topics (arithmetic and place value).

The Importance of Mathematical Equivalence

Mathematical equivalence is the concept that two quantities are equal and interchangeable (e.g., Kieran, 1981; Carpenter et al., 2003). It is often represented symbolically by the equal sign and by open-ended equations with operations on both sides of the equal sign (e.g., 3 + 4 = 5 + __). Many researchers consider mathematical equivalence a foundational component of early algebraic thought (e.g., Jacobs et al., 2007; Kieran, 1981; Knuth et al., 2006). Further, evidence suggests that knowledge of mathematical equivalence is related to formal academic success (e.g., Matthews & Fuchs, 2020; McNeil et al., 2019).

We selected mathematical equivalence as the target topic for several reasons. First, many elementary school children in the U.S. experience difficulties with mathematical equivalence (e.g., McNeil & Alibali, 2005; Powell & Fuchs, 2010). For example, they often solve mathematical equivalence problems incorrectly by adding all the numbers (e.g., 3 + 4 = 5 + 12) or by adding only the numbers before the equal sign (e.g., 3 + 4 = 5 + 7; McNeil et al., 2011; Perry et al., 1988). Second, prior research suggests that brief, targeted instruction on mathematical equivalence problems can facilitate children’s understanding in this area (e.g., Fyfe & Rittle-Johnson, 2016; Perry, 1991; Rittle-Johnson, 2006).

The third reason is that existing data suggest that children’s metacognition may play a central role in their understanding of mathematical equivalence. Children’s difficulties with mathematical equivalence are thought to stem from their overgeneralization of arithmetic knowledge (see McNeil 2014). For example, children are frequently exposed to traditional arithmetic problems in an “operations = answer” format (e.g., 3 + 4 = __, Powell, 2012) that can be solved by adding all the numbers. Because these strategies are familiar and work well for arithmetic, children may be confident that they are solving mathematical equivalence problems correctly. This phenomenon in which familiarity produces overconfidence has been shown in other areas of math as well (e.g., fraction understanding; Fitzsimmons et al. 2020). In a recent study, elementary school students were correct on 47% of equivalence problems, but they thought they were correct on 84% of problems (Nelson & Fyfe, 2019). Despite this overconfidence, individual differences in students’ monitoring skills predicted their performance on a comprehensive assessment of mathematical equivalence. The current study expanded this correlational work by experimentally evaluating the causal effect of a metacognitive lesson on children’s understanding of mathematical equivalence – including their ability to solve equivalence problems as well as their metacognitive monitoring and control skills.

The Topic-Specificity of Metacognitive Training

The current study also expanded prior work by exploring whether the benefits of the metacognitive lesson were specific to the instructed topic or whether they generalized to other topics. We selected arithmetic and place value as these are important concepts for elementary school mathematics (e.g., NGAC & CCSSO, 2010), but they differ from mathematical equivalence in terms of problem types and the strategy knowledge needed to succeed on them.

Researchers have identified the topic-specificity of metacognition as an open question in the field (e.g., Desoete & De Craene, 2019). For example, Schneider and Artelt (2010) discuss the need for research on the “transferability of metacognition across situations, tasks, or domains” (p. 159). If children’s metacognitive skills generalize across topic, then training them to have good monitoring and control on mathematical equivalence problems may also facilitate their monitoring and control on other types of mathematics problems, including those tapping arithmetic and place value knowledge. If children’s metacognitive skills are topic-specific, then it is likely that metacognitive training needs to be tailored to each topic (Schunk, 2004).

Existing studies on metacognitive training in mathematics tend to rely on outcome measures that focus on the trained mathematics topic or on standardized assessments that do not tease apart the topics (e.g., Cornoldi et al., 2015; Montague et al., 2014). While some have examined transfer to untrained metacognitive skills or untrained tasks (e.g., Desoete et al., 2003), the transfer to entirely novel topics remains unclear, especially for younger students. For example, the investigation of the IMPROVE intervention in third-grade classes found benefits on both learned tasks (i.e., same format as problems taught in class) and transfer tasks (i.e., format not taught in class; Kramarski et al., 2010). However, both tasks focused on mathematical word problems with addition, subtraction, multiplication, and division.

Current Study

In the current study, first- and second-grade children completed a pretest assessment on their problem solving and metacognitive skills within each of three topics (i.e., mathematical equivalence, arithmetic, and place value). This initial pretest allowed us to quantify children’s monitoring and control skills and examine how they are related within and across mathematics topics. As in prior work, metacognitive monitoring was assessed by having children rate their certainty on each item they solved (e.g., van Loon et al., 2013) and metacognitive control of their behavior was assessed by having children select the items they thought they needed to study (e.g., Metcalfe & Finn, 2013). Then, children were assigned to receive a classroom lesson on mathematical equivalence with or without metacognitive questions; afterward, they completed an immediate posttest and two-week delayed retention test. These assessments allowed us to examine the effect of condition on children’s problem solving and metacognitive skills.

We expected children to have modest monitoring and control skills at pretest overall, but that these skills would be lower on the equivalence problems. We also hypothesized that children who received the Metacognitive Lesson would exhibit better accuracy, monitoring, and control on the mathematical equivalence items relative to children who received the Control Lesson. Further if the benefits were topic-specific, then we expected condition to interact with topic and only affect equivalence outcomes. If the benefits were generalizable, then we expected no such interaction. This study contributes to the literature by experimentally examining the effects of a metacognitive lesson (a) with a younger population, (b) on a novel topic, and (c) with uninstructed topics included in the outcome measures.

Method

Participants

Participants were recruited from 8 classrooms within 3 elementary schools in the Midwest of the U.S. during Spring 2019. While all the children in these classrooms were invited to participate, parents of these children could decline participation by signing an IRB-approved opt-out consent form. Of the 149 children in these classrooms, two did not participate as their parents chose the opt-out option. Twelve additional children were excluded from the final sample due to incomplete pretest or retention test assessments (n = 3) or missing the lesson (n = 9). The final sample reported here includes 135 children (59 first-graders and 76 second-graders). These children were from six classrooms in School 1 (n = 102), one classroom in School 2 (n = 18) and one classroom in School 3 (n = 15). Due to the opt-out consent protocol, we did not collect demographic data from individual participants. Publicly available data for the three participating schools indicate that the student populations ranged from 60–76% White, 7–8% Multiracial, 3–7% Black, 4–9% Asian, and 4–6% Hispanic. Further, the percentage of students within each school designated as economically disadvantaged was 32% for School 1, 9% for School 2, and 40% for School 3. Classroom data from the participating teachers indicated that the classroom samples ranged from 32-64% female. Finally, in the U.S., children in first-grade (the first school year after kindergarten) are typically 6-7 years old and children in second grade are typically 7-8 years old.

Materials and Coding

Assessments.

Children completed the mathematics assessment at three different points: at pretest (alpha = .84), posttest (alpha = .87), and retention test (alpha = .88). The assessment included 18 items covering three topics: mathematical equivalence, arithmetic, and place value (see the Appendix for a list of all 18 items on the pretest). Each topic included six items that varied in difficulty. The pretest and retention test included identical items; the posttest included items that were isomorphic but had unique numbers (e.g., 8 − 3 in place of 7 − 4). For every item in the assessment, children provided an answer to the problem and rated their certainty.

Figure 1 contains example assessment items. Each topic included a different item format to help ensure the three different item types were visually distinct in the assessment packet. The mathematical equivalence items were fill-in-the-blank style and presented in a horizontal equation format. Some items had the operation on the right side of the equal sign (e.g., 7 = 4 + __) and some items had operations on both sides of the equal sign (e.g., 3 + 4 = __ + 5). The arithmetic items were addition and subtraction facts presented in a vertical format. Some items included single-digit integers (e.g., 7 − 4) and some items included double-digit integers (e.g., 34 + 16). The place-value items presented a “which is closer” task (e.g., Russell & Ginsburg, 1984) in a triangle format, wherein children selected which of two numbers was closer to a target item in magnitude. Some items included double-digit integers (e.g., which is closer to 89: 87 or 90?), and other items included three- or four-digit integers.

Figure 1.

Example items from the pretest assessment

For each item, children rated their certainty via a 4-point scale presented as four traffic lights (see Figure 1). Selecting the leftmost light indicated highest certainty (“I know I got this problem right”), while selecting the rightmost light indicated lowest certainty (“I know I got this problem wrong”). The scale was adapted from prior studies with children in this age range (e.g., De Clercq, et al., 2000; Nelson & Fyfe, 2019). At pretest and retention test, children were also provided with purple pens to engage in the study selection task (adapted from van Loon et al. 2013). Children were asked to review their answers and mark any item they would need to re-study for a hypothetical test. Study selections were not completed at posttest due to time constraints in the classrooms (e.g., the combined lesson and posttest took the full class period).

Coding.

For each item at pretest, posttest, and retention test, we coded children’s accuracy and metacognitive monitoring. At pretest and retention test, we also coded children’s metacognitive control. Because we did not include the study selection task at posttest due to time constraints, we could not code metacognitive control at posttest.

Accuracy was based on children’s written solutions, and each item was worth one point (for a total of 18 points, 6 points per topic). For the arithmetic and equivalence items children had to write the exact numerical answer. For the place value items children had to circle the number closer in magnitude to the target.

For monitoring, we used an established calibration measure that assesses how well children’s certainty ratings matched their accuracy (Baars et al., 2018; Fyfe & Nelson, 2019). As shown in Table 1, each item received a monitoring score between 0 and 1 (i.e., 0, .33, .67, 1) based on the combination of certainty rating (1 to 4 with 4 being higher certainty of correctness) and accuracy (correct or incorrect). For example, a certainty rating of 3 on a correct response earned a monitoring score of .67, but a certainty rating of 3 on an incorrect response earned a monitoring score of .33. Then, within each topic, we calculated children’s average monitoring score across the six items. (The Supplemental Material contains descriptive information on a second measure of children’s monitoring, the Goodman-Kruskal gamma correlation.)

Table 1.

System for calculating metacognitive monitoring and control scores

Monitoring Score
	Accuracy on the problem
Certainty Rating	Correct	Incorrect
1 (I know I got this problem wrong)	0.00	1.00
2 (I think I got this problem wrong)	0.33	0.67
3 (I think I got this problem right)	0.67	0.33
4 (I know I got this problem right)	1.00	0.00
Control Score
	Select the problem for study
Certainty Rating	Yes	No
1 (I know I got this problem wrong)	1.00	0.00
2 (I think I got this problem wrong)	0.67	0.33
3 (I think I got this problem right)	0.33	0.67
4 (I know I got this problem right)	0.00	1.00

A similar system was used for scoring children’s metacognitive control, which assessed how well children’s study selections matched their certainty ratings¹. As shown in Table 1, each item received a control score between 0 and 1 based on the combination of study selection (opt to study or not study) and certainty rating (1 to 4). For example, a high certainty rating of 4 with the choice to re-study earned a control score of 0, but a high certainty rating of 4 with the choice to not re-study earned a control score of 1. Then, within each topic, we calculated children’s average control score across the six items.

Design and Procedure

The study had a pretest-lesson-posttest design followed by a two-week retention test. It occurred over three separate sessions, which all took place in children’s classrooms during their regularly scheduled mathematics period. The first session included the pretest, which children completed using paper and pencil. In the front of the class, a research assistant provided instructions including simplified examples of each item type and a warm-up activity to ensure children could use the certainty rating scale. Children worked through the assessment, writing a solution and circling a certainty rating on each item. After all children were finished, the research assistant asked the children to go back through their packets and use a purple pen to mark the problems they thought they would need to study to do well on an important hypothetical test.

The second session took place the next day and included the lesson and immediate posttest. Within each classroom, children were randomly assigned to either the Metacognitive Lesson condition (n = 70) or the Control Lesson condition (n = 66). Children in one condition remained in the classroom to receive their group lesson and children in the other condition went to a nearby room that was a familiar learning space (e.g., computer lab) to receive their group lesson. It was random (e.g., based on teacher choice) whether children in the Metacognition Lesson stayed in the classroom or whether children in the Control Lesson stayed in the classroom. In one classroom, inclement weather made it so everyone was required to stay in their classrooms; in that class both groups remained in the classroom and sat at opposite ends of the room to receive their respective group lessons. This design allowed us to maintain the rigor of a randomized experiment within a setting that was representative of children learning in their classrooms with their peers. There were three research assistants involved in data collection. Each one led at least one Metacognitive Lesson and one Control Lesson and completed a fidelity checklist after each session (see Appendix). Fidelity to critical lesson features was 99%.

In both the Metacognitive Lesson and the Control Lesson, children were taught how to solve mathematical equivalence problems using scripts and materials from prior work (e.g., Fyfe & Rittle-Johnson, 2017). See the Appendix for excerpts from the scripts. The research assistant provided strategy instruction on four target equivalence problems (e.g., 6 + 4 + 5 = 6 + __) focusing on the equalize strategy (i.e., adding up the numbers on the left side of the equal sign, then counting up from the number on the right side to get the same amount). For each problem, the researcher wrote the problem on a large sheet of paper displayed on an easel and then talked through the strategy. In both conditions, children were asked to answer questions throughout to help implement the strategy (e.g., what number will make this side of the equal sign also have 15?).

The Metacognitive Lesson also included a set of three reflective questions that the researcher taught the children. These questions were adapted from prior work (see Mevarech & Kramarski, 1997). The researcher introduced the following reflective questions at the start of the lesson as a helpful checklist for problem solving: (1) What information is given? (2) What steps do I need to take to get the right answer? and (3) How can I check that my answer is right? On the first three problems, the researcher named these questions while explaining the strategy for solving mathematical equivalence problems (see Appendix). On the last problem, the researcher asked the children in the Metacognitive Lesson to name the metacognitive questions as they worked through the problem (e.g., what is the first question we should ask?). Alternatively, children in the Control Lesson were only asked questions about implementing the strategy (e.g., what number plus four will equal seven on this side of the equal sign?).

The second session concluded with the posttest, on which children provided written solutions and circled certainty ratings for each of 18 items. Finally, the third session took place two weeks after the second session and included the retention test. The retention test was administered in the same way as the pretest as a paper and pencil classroom assessment.

Results

Quantifying Children’s Skills at Pretest

The first research aim was to quantify children’s monitoring and control skills and examine how they are related within and across three mathematics topics. To do so, we first examined children’s accuracy, monitoring, and control at pretest using a series of repeated-measures ANOVAs with mathematics topic (equivalence, arithmetic, place value) as a within-subject factor and condition (Metacognitive and Control) as a between-subject factor.² Including condition in the models allowed us to verify that conditions were well-matched at the outset of the study (see Table 2 for descriptive information by condition). Then, we computed correlations between children’s monitoring and control skills at pretest both within and across mathematics topics, controlling for their accuracy (see Table 3).

Table 2.

Descriptive statistics at pretest by condition

	Control Lesson M (SD)	Metacognitive Lesson M (SD)	Total M (SD)
	N = 65	N = 70	N = 135
Pretest Accuracy (% correct)
Arithmetic	75% (23)	73% (23)	74% (23)
Equivalence	57% (35)	55% (34)	56% (35)
Place Value	69% (28)	60% (28)	64% (28)
Pretest Certainty Ratings (out of 4.0)
Arithmetic	3.62 (0.46)	3.57 (0.43)	3.59 (0.45)
Equivalence	3.29 (0.69)	3.23 (0.64)	3.26 (0.66)
Place Value	3.45 (0.54)	3.42 (0.52)	3.43 (0.53)
Pretest Study Selections (out of 1.0)
Arithmetic	18% (23%)	23% (29%)	20% (26%)
Equivalence	43% (34%)	38% (33%)	40% (33%)
Place Value	40% (36%)	35% (34%)	37% (35%)
Pretest Monitoring Scores (out of 1.0)
Arithmetic	.79 (.18)	.76 (.18)	.77 (.18)
Equivalence	.72 (.23)	.69 (.23)	.70 (.23)
Place Value	.67 (.22)	.59 (.23)	.62 (.23)
Pretest Control Scores (out of 1.0)
Arithmetic	.84 (.17)	.79 (.21)	.81 (.19)
Equivalence	.73 (.23)	.72 (.21)	.72 (.22)
Place Value	.68 (.24)	.71 (.22)	.70 (.23)

Note. Pretest Accuracy is average percent correct (out of 100%). Pretest Certainty Ratings reflect average certainty on a scale from 1 to 4, with 4 being the highest certainty. Pretest Study Selections reflect the average percentage of items selected for re-study (out of 100%). Pretest Monitoring is average monitoring scores (out of 1.0). Pretest Control is average control scores (out of 1.0). Values in parentheses represent standard deviations.

Table 3.

Correlations across topics at pretest

Raw Correlations
	Arithmetic Accuracy	Equivalence Accuracy	Place Value Accuracy	Arithmetic Monitoring	Equivalence Monitoring	Place Value Monitoring	Arithmetic Control	Equivalence Control
Arithmetic Accuracy	--
Equivalence Accuracy	.59	--
Place Value Accuracy	.46	.46	--
Arithmetic Monitoring	.75	.36	.35	--
Equivalence Monitoring	.39	.69	.29	.37	--
Place Value Monitoring	.46	.45	.87	.38	.29	--
Arithmetic Control	.26	.22	.28	.28	.14	.27	--
Equivalence Control	.33	.37	.25	.37	.43	.25	.56	--
Place Value Control	.18	.07	.17	.21	.06	.23	.40	.40
Partial Correlations Controlling for Accuracy
	Arithmetic Accuracy	Equivalence Accuracy	Place Value Accuracy	Arithmetic Monitoring	Equivalence Monitoring	Place Value Monitoring	Arithmetic Control	Equivalence Control
Arithmetic Accuracy	--
Equivalence Accuracy	--	--
Place Value Accuracy	--	--	--
Arithmetic Monitoring	--	--	--	--
Equivalence Monitoring	--	--	--	.27	--
Place Value Monitoring	--	--	--	.08	.02	--
Arithmetic Control	--	--	--	.14	.01	.03	--
Equivalence Control	--	--	--	.24	.26	.04	.51	--
Place Value Control	--	--	--	.12	.02	.16	.36	.39

Note. Partial correlations are controlling for accuracy in the included domains. For example, the correlation between arithmetic monitoring and equivalence monitoring controls for arithmetic accuracy and equivalence accuracy. Bolded correlations: p < .05.

Accuracy.

Across all items, the average score was 64% (SE = 2.0%). There was a significant main effect of topic, F(2, 266) = 25.41, p < .001, η_p² = .16. Children scored highest on arithmetic items (M = 74%, SE = 2%), followed by place value items (M = 64%, SE = 2%), and lowest on equivalence items (M = 56%, SE = 3%). All three pairwise comparisons with a Bonferroni correction were statistically significant (ps < .016). This result is consistent with prior work documenting children’s difficulties with equivalence (McNeil, 2014). There was not a significant effect of condition, F(1, 133) = 1.01, p = .316, η_p² = .01, or a condition-by-topic interaction, F(2, 266) = 1.13, p = .324, η_p² = .16, on pretest accuracy scores.

Monitoring.

Across all items, the average monitoring score was 0.70 out of 1.00 (SE = 0.01). Children could receive high calibrated monitoring scores for two reasons: (A) solving the problem correctly and rating high certainty or (B) solving the problem incorrectly and rating low certainty. Children were more likely to have high monitoring scores for reason A. Across all items, children had high average certainty ratings (M = 3.43 out of 4.00, SE = 0.04). Further, across all items on which children earned the maximum monitoring score of 1, it was due to a high certainty rating of 4 on a correct answer 91% of the time. The ANOVA revealed a significant main effect of topic, F(2, 266) = 24.26, p < .001, η_p² = .15. Monitoring scores were highest on arithmetic items (M = 0.77, SE = 0.02), followed by equivalence items (M = 0.70, SE = 0.02), and lowest on place value items (M = 0.62, SE = 0.02). All three pairwise comparisons with a Bonferroni correction were statistically significant (ps < .016). Note, accuracy was lowest for the topic of equivalence, yet monitoring was lowest for the topic of place value, suggesting that differences in monitoring skills cannot simply be attributed to differences in children’s accuracy. There was not a significant effect of condition, F(1, 133) = 2.77, p = .098, η_p² = .02, or a condition-by-topic interaction, F(2, 266) = 0.93, p = .395, η_p² = .01, on pretest monitoring.

Control.

Across all items, the average control score was 0.75 out of 1.00 (SE = 0.02). Children could receive high control scores for two reasons: (A) having high certainty and opting not to study the item, and (B) having low certainty and opting to study the item. Children were more likely to have high control scores for reason A. Across all items, the percentage of time children opted to study the item was low (M = 32%, SE = 2%). Further, across all items on which children earned the maximum control score of 1, it was due to a high certainty rating of 4 and opting not to study the item 92% of the time. The ANOVA revealed a significant main effect of topic, F(2, 266) = 20.85, p < .001, η_p² = .14. Pairwise comparisons with a Bonferroni correction revealed that control scores were significantly higher on arithmetic items (M = 0.81, SE = 0.02) relative to equivalence items (M = 0.72, SE = 0.02) and place value items (M = 0.70, SE = 0.02), ps < .001. But control scores on equivalence and place value items were statistically similar, p = .498. There was not a significant effect of condition, F(1, 133) = 0.10, p = .754, η_p² = .00, or a condition-by-topic interaction, F(2, 266) = 2.08, p = .126, η_p² = .01, on pretest control scores.

Correlations.

Table 3 presents the correlations between children’s monitoring and control scores at pretest, accounting for their accuracy. There were three notable observations. First, monitoring in one topic was not always reliably related to monitoring in another topic after controlling for accuracy, rs = .02-.27. The exception was that arithmetic monitoring was significantly correlated with equivalence monitoring, r(132) = .27, p = .001. Second, control in one topic was reliably correlated with control in the other topics after controlling for accuracy, rs = .36-.51. This suggests control skills may be more topic-general. Third, monitoring and control within a topic were not always reliably related after controlling for accuracy, rs = .14-.26. The exception was that equivalence monitoring was correlated with equivalence control, r(132) = .26, p = .002. This suggests some dissociation between monitoring and control skills at this age.

Summary.

Children’s monitoring and control skills were modest and often based on high levels of certainty. Further, these skills tended to vary by topic, but not always in the same way. Monitoring and control were sometimes positively correlated with each other, but these correlations were weak and often became non-significant after accounting for accuracy.

Condition Differences Analysis Plan

The second and third research aims were to evaluate the effect of the metacognitive lesson on children’s understanding of equivalence and to determine whether the benefits generalized to the other topics. To analyze condition differences at posttest and retention test, we conducted a series of repeated measures ANCOVAs with condition (Metacognitive and Control) included as a between-subject effect and topic (equivalence, arithmetic, place value) included as a within-subject effect. Each model also included nine covariates: pretest measures of accuracy, monitoring, and control within each topic. Even though there were no statistically significant differences between the conditions on pretest performance, there were descriptive differences such that the Metacognitive Lesson condition had somewhat lower scores and therefore more room to grow (see Table 2). We included pretest measures as covariates to account for these descriptive differences and to minimize any effects that might be attributable to prior knowledge.

We were primarily interested in (a) the main effect of condition – to determine whether the Metacognitive Lesson had benefits relative to the Control Lesson, and (b) the condition-by-topic interaction – to determine whether any benefits depended on item type and were specific to equivalence. Exploratory analyses determined that the effects in the models remain unchanged when we control for the effects of school or classroom, so these variables were not included.

Condition Differences on the Immediate Posttest

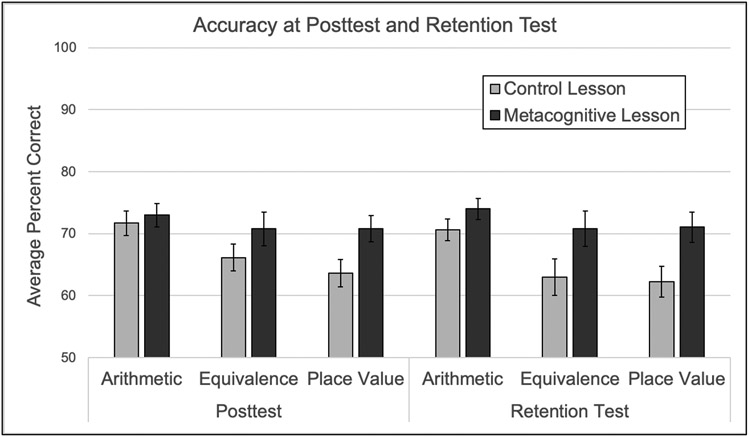
With accuracy at posttest as the dependent variable (see Figure 2), there was a significant main effect of condition, F(1, 124) = 4.58, p = .034, η_p² = .04, as children in the Metacognitive Lesson had higher overall accuracy at posttest (M = 72%, SE = 1%) relative to children in the Control Lesson (M = 67%, SE = 1%). There was also a significant main effect of topic, F(2, 248) = 4.15, p = .017, η_p² = .03, but the condition-by-topic interaction was not statistically significant, F(2, 248) = 0.84, p = .433, η_p² = .01.

Figure 2. Accuracy on the posttest and retention test by condition and topic.

Note. The chart shows estimated marginal means from our ANCOVA models with condition included as a between-subject factor and topic included as a within-subject factor. The models also include pretest accuracy, monitoring, and control within each topic as covariates. Error bars represent standard errors.

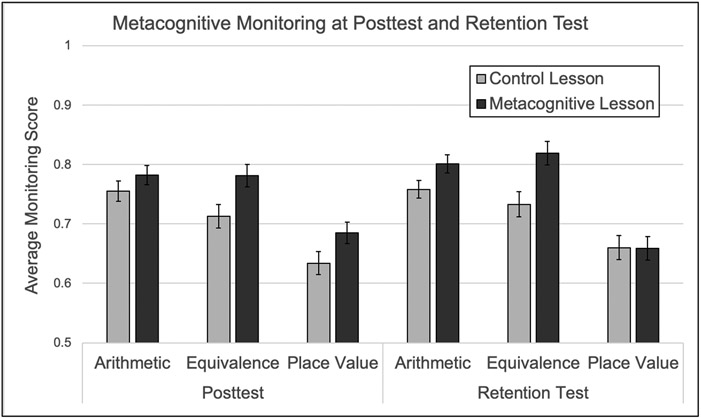
With monitoring scores at posttest as the dependent variable (see Figure 3), there was also a significant main effect of condition, F(1, 124) = 10.13, p = .002, η_p² = .08, as children in the Metacognitive Lesson had better overall monitoring at posttest (M = 0.75, SE = 0.01) relative to children in the Control Lesson (M = 0.70, SE = 0.01). There was a significant main effect of topic, F(2, 248) = 7.01, p = .001, η_p² = .05, but the condition-by-topic interaction was not statistically significant, F(2, 248) = 0.64, p = .530, η_p² = .00. To ensure that these differences in monitoring scores were not simply a function of children’s higher accuracy, we re-ran the ANCOVA controlling for children’s accuracy at posttest. There was still a significant main effect of condition after accounting for their posttest accuracy, F(1, 121) = 5.50, p = .021, η_p² = .04, and no condition-by-topic interaction, F(2, 242) = 2.74, p = .100, η_p² = .02.

Figure 3. Metacognitive monitoring on the posttest and retention test by condition and topic.

Note. The chart shows estimated marginal means from our ANCOVA models with condition included as a between-subject factor and topic included as a within-subject factor. The models also include pretest accuracy, monitoring, and control within each topic as covariates. Error bars represent standard errors.

Condition Differences on the Retention Test

For all ANCOVA models at retention, Mauchly’s tests indicated that sphericity could not be assumed, so degrees of freedom used the Greenhouse-Geisser correction. For accuracy at retention (see Figure 2), there was a significant main effect of condition, F(1, 124) = 7.86, p = .006, η_p² = .06, as children in the Metacognitive Lesson had higher overall accuracy at retention (M = 72%, SE = 2%) relative to children in the Control Lesson (M = 65%, SE = 2%). There was not a main effect of topic, F(1.87, 231.86) = 1.57, p = .210, η_p² = .01, and the condition-by-topic interaction was not significant, F(1.87, 231.86) = 0.87, p = .422, η_p² = .01.

For monitoring scores at retention (see Figure 3), there was a significant main effect of condition, F(1, 124) = 6.16, p = .014, η_p² = .05, as children in the Metacognitive Lesson had better overall monitoring at retention (M = 0.76, SE = 0.01) relative to children in the Control Lesson (M = 0.72, SE = 0.01). There was also a significant main effect of topic, F(1.84, 227.86) = 3.71, p = .029, η_p² = .03. The condition-by-topic interaction was not statistically significant, F(1.84, 227.86) = 2.98, p = .057, η_p² = .02. To ensure that these differences in monitoring scores were not simply a function of children’s higher accuracy, we re-ran the ANCOVA controlling for children’s accuracy at retention test. In this model, the main effect of condition was no longer significant, F(1, 121) = 1.24, p = .267, η_p² = .01, but there was a significant condition-by-topic interaction after accounting for retention test accuracy, F(1.77, 214.31) = 7,38, p = .001, η_p² = .06. Follow-up analyses indicated that the benefits of the Metacognitive condition were significant for arithmetic, p = .036, and equivalence, p = .026, but not for place value, p = .067.

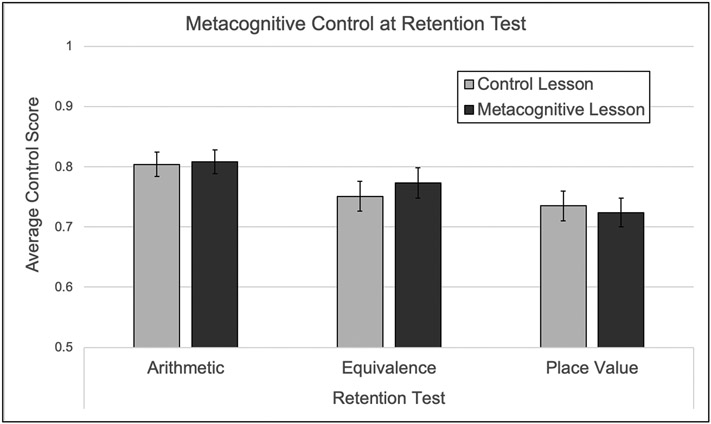
For control scores at retention (see Figure 4), there were no significant effects. Specifically, there was not a main effect of condition, F(1, 124) = 0.03, p = .868, η_p² = .00, topic, F(1.88, 231.86) = 0.24, p = .774, η_p² = .00, or a condition-by-topic interaction, F(1.88, 231.86) = 0.43, p = .637, η_p² = .01.

Figure 4. Metacognitive control on the retention test by condition and topic.

Note. The chart shows estimated marginal means from our ANCOVA model with condition included as a between-subject factor and topic included as a within-subject factor. The model also included pretest accuracy, monitoring, and control within each topic as covariates. Error bars represent standard errors.

Summary.

Condition differences favored the Metacognitive Lesson and were evident on accuracy scores and monitoring scores. Further, the effects were present on the immediate posttest and the delayed retention test. No effects were detected for control skills.

Discussion

Metacognition is theorized to play a central role in children’s mathematics learning. In the current study, we provided experimental evidence in support of this role. First- and second-grade students completed a pretest in one session, a lesson and posttest during a second session, and a two-week delayed retention test in a third session. The lesson was conducted in classrooms and children were randomly assigned to receive the lesson on mathematical equivalence with or without integrated metacognitive questions. Children exhibited modest monitoring and control scores at pretest that varied by mathematics topic. In line with our hypothesis, the lesson with metacognitive questions led to higher accuracy and monitoring scores on the equivalence items at posttest relative to the lesson without metacognitive questions, and these effects were maintained at the two-week retention test. Further, the benefits of the lesson sometimes generalized to the arithmetic and place value items as well. No condition effects were observed for children’s metacognitive control skills. The present results have important implications for research on children’s metacognition broadly and also for research on mathematical equivalence.

Implications for Research on Metacognition

Our results support the idea that metacognition is malleable, even within the confines of a brief classroom lesson. Children who received the metacognitive lesson had higher monitoring scores relative to children in the control lesson, which provides causal evidence that targeted metacognitive questions can help children align their certainty ratings with their performance (e.g., Montague et al., 2014; Desoete et al., 2003). We established this evidence using rigorous experimental methods (e.g., children randomly assigned to condition) within the context of a natural learning environment (e.g., children learning in their classrooms). Our results also suggest the benefits of metacognitive training can extend beyond the ages studied in prior work. The first- and second-grade children we recruited are younger than most metacognitive training participants, who primarily span from later elementary school (Kramarski et al., 2010; Desoete et al., 2003) to middle school (Mevarech & Kramarski, 1997; 2003).

In addition to benefiting children’s monitoring skills, the metacognitive lesson also led to better problem-solving accuracy at posttest and retention relative to the control lesson. This finding is noteworthy given that both conditions focused on how to solve mathematical equivalence problems correctly. That is, children in both conditions were exposed to the same amount of mathematical content; the difference was that children in the metacognitive lesson were also exposed to metacognitive questions. Generally, these benefits in accuracy are cohesive with existing literature demonstrating that metacognitive skills are related to and support mathematics achievement (e.g., Rinne & Mazzocco, 2014; Vo et al., 2014). Perhaps children in the metacognitive lesson were able to implement the self-questioning at posttest (e.g., can I check that my answer is right?) in ways that facilitated their accuracy on the math items.

In contrast to the benefits for metacognitive monitoring, we observed no condition differences for children’s metacognitive control at the retention test. That is, children’s calibrated study selections (e.g., selecting an item to study because they were uncertain on it), did not depend on the lesson they received. One potential explanation is that control skills are less malleable than monitoring skills in young children and less likely to be influenced by a brief lesson. Another possibility is that the metacognitive questions we implemented in the lesson reinforced monitoring more than control. Indeed, the reflective questions focused on ongoing problem solving (e.g., what steps do I need to take to get the right answer on this problem) and in-the-moment evaluations, which are closely aligned with monitoring skills (e.g., Nelson & Narens, 1994). Although one of our reflective questions targeted in-the-moment control behaviors (i.e., how can I check that my solution is correct?), the control skills we measured were related to post-hoc study decisions about subsequent behavior. Future research should examine the malleability of different types of control behaviors that occur during the problem-solving process (e.g., checking work, crossing out answers, asking for help).

It is an open question as to whether it is valuable to improve children’s metacognitive monitoring if they cannot use this information to successfully control future study behavior. Several theoretical models suggest that good monitoring is necessary, but not sufficient, for supporting the control of study strategies (e.g., Metcalfe & Finne, 2013). That is, students need to differentiate what they know and what they do not know to study efficiently, but they may not always put that knowledge to use. Indeed, children’s monitoring and control skills at pretest were not always correlated after accounting for children’s accuracy. This suggests improving monitoring is a good incremental first step, but additional support may be needed to help children integrate or make connections between their monitoring and control skills.

In addition to focusing on the malleability of metacognition, the present study also contributes to the on-going question of topic-specificity within metacognition. There is a need to know whether training metacognitive skills in one topic is related to metacognitive skills in another topic (Schneider & Artelt, 2010). Recent research suggests that metacognitive skills may start domain-specific in young children and transition to be more domain-general (e.g., Bellon et al., 2020). For example, Geurten et al. (2018) had children (ages 8-13) complete arithmetic and memory tasks. For younger children (ages 8–9), monitoring in one domain was unrelated to monitoring in the other. However, for older children (ages 10–13), measures of monitoring were correlated across domains. The current findings tentatively suggest that, within a domain, there may be some generalizability of training across topics; but our evidence is mixed. Even though children were only exposed to the metacognitive training in the context of equivalence items, the metacognitive lesson sometimes benefitted children’s arithmetic or place value outcomes.

Previous research has found mixed effects in terms of whether metacognitive lessons benefit untrained content or tasks (e.g., Desoete et al., 2003; Kramarski et al., 2010). Though our results were also a bit mixed, certain features of the lesson and materials in the current study may have supported some generalization to untrained topics. First, the metacognitive questions were introduced at the beginning of the lesson as a stand-alone set of questions that can help during problem-solving. This may have helped students understand the general applicability of the questions across different tasks, settings, topics, etc. Second, the researcher attempted to help children adopt these questions for self-reflection by having them re-iterate the questions. This form of prompting may have encouraged children to engage in self-explanation more generally, which has been shown to relate to mathematics learning (e.g., Rittle-Johnson, 2006). Third, the untrained topics maintained some similarity to the trained equivalence items (e.g., contained symbolic numbers, presented in the same assessment packet, etc.), which may have helped children recognize the applicability of the reflection questions across items.

Implications for Research on Mathematical Equivalence

Our results also contribute to the work focused on children’s understanding of mathematical equivalence, a standards-based topic that is critical for both arithmetic and algebra (e.g., Carpenter et al., 2003; Kieran, 1981). Our findings are consistent with prior research that suggests children’s performance on mathematical equivalence performance can be improved with brief targeted lessons (e.g., Fyfe & Rittle-Johnson, 2016; Matthews & Rittle-Johnson, 2009). For example, Watchorn et al. (2011) implemented a short intervention on mathematical equivalence with second- and fourth-graders, with students working in small groups over two lessons in their classrooms. Students who received the lessons outperformed students in a control group on a variety of metrics assessing their knowledge of mathematical equivalence. In the current study, children’s performance on equivalence problems benefitted from a brief classroom lesson.

A variety of techniques have been shown to support children’s understanding of equivalence, including direct instruction on the equal sign (e.g., Matthews & Rittle-Johnson, 2009), modeling with concrete manipulatives (e.g., Sherman & Bisanz, 2009), and comparison (e.g., Hattikudur & Alibali, 2010). The current study provides another beneficial technique – reflective metacognitive questions embedded in direct instruction on a correct procedure. Previous research suggests that other types of questions can be helpful for performance too. For example, Rittle-Johnson (2006) asked students in a one-on-one setting to self-explain why different answers to mathematical equivalence problems were correct or incorrect, and these self-explanations were related to better problem-solving accuracy. Self-explanation prompts and metacognitive questions may operate via different mechanisms. For example, self-explanation prompts are intended to help learners make sense of new information (e.g., Chi et al., 1994), whereas the current metacognitive questions are intended to help children internalize a checklist of steps for monitoring their problem-solving process (e.g., what information is given, what steps do I take, how do I check my answer). Future research should examine how different types of reflective questions influence children’s metacognition and performance.

Considering the benefits of our metacognitive lesson, this study has potential practical implications for mathematics education. The brief nature of our metacognitive lesson suggests that educators may be able to implement changes with relatively minor disruption to their lessons to improve children’s metacognition and mathematics performance. Specifically, introducing a small check-list of reflective questions and embedding them in instruction on a set of example problems may help students regulate their problem solving and performance.

Limitations and Future Directions

Despite the promising nature of the present results, further research is needed in key areas as limitations exist. For example, the manipulation occurred within a single researcher-led lesson. Researchers often suggest that enduring effects on metacognition require direct and prolonged exposure on various metacognitive skills as well as training for the classroom teachers (e.g., Desoete & DeCraene, 2019). An additional limitation is the homogenous nature of our sample, as we worked with children from a small set of schools that primarily served White families. Also, given our opt-out consent protocol, we were unable to collect individual demographic information at the student level, which prevented us from examining whether the condition effects depended on student characteristics. A recent review paper found gender differences in performance and confidence on a core math task; boys were more confident than girls even after controlling for accuracy (Rivers et al., 2020), suggesting that future research should consider gender as a potential moderating factor for metacognitive training.

Additional issues relate to the manipulation and measures in the current study. First, the manipulation focused primarily on one feature of larger metacognitive interventions – the use of reflective metacognitive questions embedded in instruction. More comprehensive interventions include additional components, such as targeted review exercises or individualized feedback (see Baten et al., 2017). This narrow focus may have been one reason we did not find any condition differences for children’s metacognitive control skills. Second, the metacognitive questions we selected targeted three in-the-moment processes (i.e., identifying the information given, selecting problem-solving steps, and checking work). It is impossible to know whether one question was more useful than another, or if different types of questions would be successful or not. Third, we selected three different item types that tap important knowledge for elementary school students, but they all fall within the domain of mathematics. And even though the different topics were only moderately correlated at pretest, the arithmetic and place value items resembled the equivalence items in content (e.g., containing symbolic numbers) and in administration (e.g., presented in the same assessment packet). Thus, it remains unclear whether any benefits of metacognitive training would extend to more dissimilar topics or domains. Also, we selected a relatively unfamiliar place value task (e.g., which number is closer to target using a triangle format), which may have disrupted children’s metacognitive skills in unanticipated ways. Monitoring scores were lower on place value items relative to the arithmetic and equivalence items, and monitoring scores on the place value items did not differ by condition at retention test. Future research should continue to broaden the scope of these investigations to other item types, topics, aspects of metacognition, and lesson durations.

In sum, the present study evaluated the causal link between a metacognitive lesson and elementary school children’s metacognitive skill and mathematical equivalence understanding. It also explored whether any benefits of the lesson extended beyond the topic of mathematical equivalence. In line with our hypothesis, children who received the metacognitive lesson in their classrooms had higher metacognitive monitoring scores and higher accuracy on the mathematics items relative to children who received the control lesson. Further, the benefits of the lesson sometimes (but not always) generalized to the arithmetic and place value items as well. Thus, improving children’s abilities to reflect on their own knowledge may have far-reaching effects for their educational attainment.

Educational Impact and Implications Statement.

The current study provides novel insights into children’s learning of mathematical equivalence (e.g., 3 + 4 = 5 + __) and their metacognitive skills, including their ability to evaluate their own knowledge (e.g., did I get that right?). Our results suggest that these skills can be improved after a brief classroom lesson for first and second grade children. Key components of the lesson included (a) a correct strategy for making both sides of the problem the same amount, and (b) a set of reflective questions (e.g., how can I check that my solution is correct?). Importantly, the lesson often resulted in better performance and metacognitive skills on arithmetic and place value items, which were not included in the lesson. These findings have implications for the development of classroom lessons focused on mathematics and metacognition.

Appendix

Items on the pretest assessment:

1. 7 − 4 = __

2. 1 + 4 = __

3. 12 + 6 = __

4. 14 − 2 = __

5. 26 − 17 = __

6. 34 + 16 = __

7. 8 = □ + 3

8. 7 = 4 + □

9. 2 + 7 = 6 + □

10. 3 + 4 = □ + 5

11. 3 + 7 + 6 = □ + 6

12. 7 + 6 + 4 = 7 + □

13. Which is closer to 89: 87 or 90

14. Which is closer to 41: 44 or 39

15. Which is closer to 322: 319 or 332

16. Which is closer to 395: 402 or 410

17. Which is closer to 3998: 4010 or 4030

18. Which is closer to 3001: 2985 or 2695

Excerpts from the lesson script:

Control Lesson	Metacognitive Lesson
There are two sides to this problem, one on this side of the equal sign [gesture to left side] and one on the other side of the equal sign [gesture to right side]. One side is 4 + 2 [gesture to left side] and the other side is 3 + box [gesture to right side].	Question 1 is what information is given [hold up one finger]. There are two sides to this problem, one on this side of the equal sign [gesture to left side] and one on the other side of the equal sign [gesture to right side]. One side is 4 + 2 [gesture to left side] and the other side is 3 + box [gesture to right side].
First, you add up the numbers on one side of the equal sign. Then, find the number that goes in the box that will make the other side of the equal sign have that same number.	Question 2 is what steps do I need to take to get the right answer [hold up two fingers]. First, you add up the numbers on one side of the equal sign. Then, find the number that goes in the box that will make the other side of the equal sign have that same number.
So for this problem, what is 4 + 2 [gesture to left side, wait for response]. Right, this side has 6 [draw vee below 4 + 2 and write 6], And what number goes in the box to make this side of the equal sign have 6 also? [gesture to right side, wait for response]. Right, 3, because 3 + 3 is also 6. [Write 3 in the box.]	So for this problem, what is 4 + 2 [gesture to left side, wait for response]. Right, this side has 6 [draw vee below 4 + 2 and write 6], And what number goes in the box to make this side of the equal sign have 6 also? [gesture to right side, wait for response]. Right, 3, because 3 + 3 is also 6. [Write 3 in the box.]
We have 6 on this side of the equal sign [point to 6 on left] and 6 on this side of the equal sign [point to 6 on right]. 4 + 2 = 6 AND 3 + 3 = 6. So we know we solved it correctly.	Okay, Question 3 is how can I check that my solution is correct [hold up three fingers]. We have 6 on this side of the equal sign [point to 6 on left] and 6 on this side of the equal sign [point to 6 on right]. 4 + 2 = 6 AND 3 + 3 = 6. So we know we solved it correctly.

Example checklist for recording fidelity of implementation in the Metacognitive Lesson:

General Introduction
1.	Gave a brief introduction to the lesson including the following information: these problems are like some of the problems you solved yesterday, might not be easy but try your best, and you solve the problems in steps.
2.	Stated each of the three metacognitive questions
3.	Used correct gestures when stating metacognitive questions
Problem #1: 4 + 2 = 3 + [ ]
1.	Broad introduction: these problems have a box, need to figure out what goes in the box, going to show you one way to solve these kinds of problems, remind kids that you will use metacognitive question checklist throughout
2.	State Metacognitive Question 1
3.	Introduce the 2 sides of the equal sign and label the elements
4.	State Metacognitive Question 2
5.	Explain the equalize strategy
6.	Repeat strategy
7.	Ask question about side 1 (4+2) and wait for response
8.	Ask question about box and wait for response
9.	State Metacognitive Question 3
10.	Last check that both sides are same amount
Problem #2: 6 + 4 + 5 = 6 + [ ]
1.	State Metacognitive Question 1
2.	Label the elements on each side of the equal sign and talk about finding what should go in the box
3.	State Metacognitive Question 2
4.	Explain the equalize strategy
5.	Ask question about side 1 (6 + 4 + 5) and wait for response
6.	Ask question about box and wait for response
7.	State Metacognitive Question 3
8.	Last check that both sides are the same amount
Problem #3: 5 + 4 = [ ] + 3
1.	State Metacognitive Question 1
2.	Label the elements on each side of the equal sign and talk about finding what should go in the box
3.	State Metacognitive Question 2
4.	Ask question about which side to start on and wait for response
5.	Echo child response or provide correct strategy instruction
6.	Ask question about side 1 (5 + 4) and wait for response
7.	Ask question about next step and wait for response
8.	Echo child response or provide strategy instruction about the box
9.	Ask question about box and wait for response
10.	State Metacognitive Question 3
11.	Last check that both sides are the same amount
Problem #4: 2 + 1 + 4 = [ ] + 4
1.	Ask children to provide Metacognitive Question 1 and wait for response
2.	Label the elements on each side of the equal sign and talk about finding what should go in the box
3.	Ask children to provide Metacognitive Question 2 and wait for response
4.	Ask question about what to do first and wait for response
5.	Echo child response or provide correct response
6.	Ask question about side 1 (2 + 1 + 4) and wait for response
7.	Ask question about what is on second side already and wait for response
8.	Ask question about box and wait for response
9.	Ask children to provide Metacognitive Question 3 and wait for response
10.	Last check that both sides are the same amount