Designing reverse logistics network for healthcare waste management considering epidemic disruptions under uncertainty

Abstract

Population growth and recent disruptions caused by COVID-19 and many other man-made or natural disasters all around the world have considerably increased the demand for medical services, which has led to a rise in medical waste generation. The improper management of these wastes can result in a serious threat to living organisms and the environment. Designing a reverse logistics network using mathematical programming tools is an efficient and effective way to manage healthcare waste. In this regard, this paper formulates a bi-objective mixed-integer linear programming model for designing a reverse logistics network to manage healthcare waste under uncertainty and epidemic disruptions. The concept of epidemic disruptions is employed to determine the amount of waste generated in network facilities; and a Monte Carlo-based simulation approach is used for this end. The proposed model minimizes total costs and population risk, simultaneously. A fuzzy goal programming method is developed to deal with the uncertainty of the model. A simulation algorithm is developed using probabilistic distribution functions for generating data with different sizes; and then used for the evaluation of the proposed model. Finally, the efficiency of the proposed model and solution approach is confirmed using the sensitivity analysis process on the objective functions’ coefficients.

1. Introduction

Among the numerous challenges ahead of humans, medical waste management is crucial as the increasing rate of the worldwide population, wars and infectious diseases has brought about a growing call for the receipt of medical services. World Health Organization (WHO) refers to medical waste as “the waste which is produced during the treatment, diagnosis, or immunization of humans or animals” [1]. As stated by Aung et al. [2], different problematic issues like environmental protection against contagious diseases, reduction of undesirable emissions, and the effective management of medical waste have arisen in this area throughout the world. The vast majority of such medical waste is generated by hospitals, while the rest of this waste is attributed to research centers, autopsy and mortuary centers, laboratories, and blood banks [3]. About 75 to 90 percent of the entire medical waste is claimed to be non-hazardous, and the remainder (i.e., 10 to 25 percent) is categorized as hazardous [4]. That part of medical waste that is not managed effectively brings a high probability of infection and injury for the working staff in this domain and even for common people. In addition, the spread of micro-organisms in this area has exposed the public to some risks, as well [5]. This phenomenon requires special attention to the network of hazardous materials in their lifecycle. So, infectious medical waste management is a vital part of controlling the epidemic disruptions that improper collection and treatment can boost the spread of disruption, leading to extra pressure on the community [6].

To this extent, the infectious waste management problems are categorized in reverse logistics networks that should be adequately designed to optimally reduce the potential harms to the people and extra cost to the managers [7]. Considering these challenges in real-world problems (regulations imposed by WHO for the collection and treatment) can lead to stochastic multi-objective mathematical models. Although several studies have been conducted on healthcare waste management in the context of supply chains, a few of them have considered its network design in case of disruptions and especially epidemic disruptions. In recent years, due to unpredictable disruptive events, designing supply chain networks has become a complex decision-making issue [8]. This process is vital for managing the waste flows and at the strategic level, it is important to build an integrated model that considers a wide range of decisions to find optimum solutions. To the best of the authors’ knowledge, designing a reverse network of healthcare waste in the presence of epidemic disruptions has not been addressed in the literature. Therefore, the contributions of this research are as follows.

• •Conceptualizing effect of an epidemic disruption on the waste management;
• •Developing a bi-objective mixed-integer linear programming (MILP) model for healthcare waste management under uncertainty and epidemic disruptions;
• •Applying a Monte Carlo-based simulation approach to determine the amount of waste generated;
• •Employing a fuzzy goal programming method to solve the proposed bi-objective model;

The rest of this paper is structured as follows. Section 2 reviews the related literature. The proposed model is formulated in Section 3. Modeling the epidemic disruption process is presented in Section 4. Sections 5, 6 are allocated to the multi-objective solution approach and experimental results, respectively. Sections 7, 8 present the managerial implications and conclusion, respectively.

2. Literature review

Designing a reverse logistics network seems to be the desired solution for proper healthcare waste management and as such, recent related papers, with an explicit focus on modeling features are investigated in this section to position the contribution of the research.

A MILP model was proposed in this area by Shi et al. [9] for the healthcare waste reverse logistics network. Its focus was on the minimization of the network costs using an improved genetic algorithm (GA) to solve the problem. In this regard, Budak and Ustundag [10] presented a MILP model while focusing on two elements including the optimization of the number and location of facilities by minimizing costs. Nolz et al. [11] worked on the development of an inventory routing problem for the better management of healthcare wastes. Two solution approaches were proposed for the best possible management of both visiting schedules and vehicle routing. In the same way, Windfeld and Brooks [1] analyzed how to manage medical waste in another area by assigning high importance to how to optimally manage medical waste as this type of waste was highly increasing in terms of quantity. Indeed, they addressed the issues pertaining to the transportation, collection, production, and disposal of such waste. They enumerated the status of medical waste in some developing countries. Makajic-Nikolic et al. [12] embarked on developing Fault Tree Analysis (FTA). It was an application program that aimed to evaluate the inherent risks in the management of infectious medical waste at the Serbian Clinical Center. All the existing risks in the management process of medical waste have been revealed. They reported that the wrong separation of trash and waste collection by hand was a highly risky issue in tackling this challenge.

Gergin et al. [13] developed an artificial bee colony algorithm to solve the facility location problem for disposing of healthcare waste. A novel pharmaceutical distribution and healthcare waste collection system was suggested by Osaba et al. [14]. They formulated a mixed-integer programming model to structure a heterogeneous vehicle routing problem with simultaneous pickup and delivery, taking into account the non-crossing routes. A metaheuristic algorithm was developed based on the bat algorithm to solve the problem. Kargar et al. [15] applied a multi-objective MILP model to design a reverse logistic network to manage medical waste under uncertainty. They controlled the uncertain parameters of the proposed model by a stochastic robust optimization approach. The goal of their model is to minimize total costs and uncollected infectious waste; and to select the best treatment technology. They employed a fuzzy goal programming method to solve the multi-objective model. In another research by Kargar et al. [16], a multi-objective MILP model was proposed for healthcare waste management during the outbreak of COVID-19. Their model minimizes population risk, total costs, and the maximum amount of uncollected infectious waste, simultaneously. They employed a goal programming-based approach to solve the multi-objective model.

To collect and dispose of hazardous healthcare waste, Homayouni and Pishvaee [17] formulated a bi-objective MILP model under uncertainty to minimize total network costs, and transportation and operational risks. They used a robust optimization approach to deal with uncertainty, and the augmented epsilon-constraint method was applied to solve their bi-objective model. Yu et al. [18] designed a reverse logistic network to manage healthcare waste during the COVID-19 epidemic by a multi-objective MILP model. They employed a fuzzy compromise programming method to solve their multi-objective model. In another paper by Yu et al. [19], a bi-objective stochastic MILP model was suggested to minimize “total costs” and “population risk” for healthcare waste management. A bi-level MILP model aimed at minimizing total costs and population risk for hazardous healthcare waste management by Saeidi-Mobarakeh et al. [20] was developed. They used a robust optimization approach to cope with uncertainty. Furthermore, by combining the particle swarm optimization (PSO) and GA, Saeidi-Mobarakeh et al. [21] proposed an efficient metaheuristic algorithm to solve the healthcare waste management problem to minimize environmental risk and total costs. A bi-objective MILP model to manage healthcare waste considering the location-routing problem was developed by Nikzamir and Baradaran [22]. Their model minimizes total costs of network and emissions, simultaneously. They engaged a new meta-heuristic algorithm to solve the large-scale problem.

Shadkam [23] designed a reverse logistic network using a MILP model considering both forward and reverse flows to manage COVID-19 wastes, especially vaccine wastes. In this vein, Govindan et al. [24] developed a bi-objective MILP model for collecting healthcare wastes during the outbreak of COVID-19. The multi-item, multi-period model has two-echelon including waste generation nodes and collection centers focused on minimizing total cost and population risk. They used a fuzzy goal programming method to deal with the multi-objective model. A multi-objective MILP model for designing a sustainable healthcare waste management network was proposed by Torkayesh et al. [25] with three objectives including minimizing total cost (economic aspect), maximizing job creation (social aspect), and minimizing environmental risks (environmental aspect). They used an “improved multi-choice goal programming approach” to solve the multi-objective model. Similarly, Tirkolaee and Aydin [26] proposed a bi-objective MILP model for transportation planning and outsourcing services during the COVID-19 pandemic outbreak with a sustainable perspective. A bi-objective MILP model to design a green reverse logistics for healthcare waste management was formulated by Govindan et al. [27]. The purposes of their model were to minimize total costs and population risk at the same time. They used a scenario-based approach to overcome the uncertainty of the amount of waste generated, and applied an improved augmented epsilon-constraint method to solve the bi-objective model.

In the last decade, many researchers have used mathematical programming models for healthcare waste management. The review of the literature reveals that facility location, population risk, and uncertainty are among the issues that have been widely addressed in the literature. On the other hand, issues such as capacity level and treatment technology selection have not received enough attention. In addition, previous studies failed to address the set covering problem and epidemic disruptions. Motivated by reviewed papers and the importance of the context, a bi-objective MILP model for healthcare waste management is presented considering facilities location, set covering, epidemic disruptions, treatment technology selection, population risk and capacity level under uncertainty. A Monte Carlo simulation approach is developed to consider epidemic disruptions. In addition, a multi-objective approach based on the fuzzy goal programming method is applied to solve the proposed bi-objective model. In Table 1, a comprehensive and accurate review of the literature is presented to show the research gaps and consequently, to position the contributions of this study.

Table 1.

Papers reviewed in the healthcare waste management area.

Author(s)	Model type	Multi-objective	Multi-item	Multi-period	Facilities location	Capacity level	Treatment technology	Set covering	Heterogeneous truck/ vehicle	Epidemic disruption	Population risk	Echelon					Uncertainty
												Waste generation node	Collection center	Treatment center	Recycling center	Disposal center	Stochastic	Fuzzy	Robust
Shi et al. [9]	MILP	–	✓	–	✓	–	–	–	–	–	–	✓	✓	✓	✓	–	–	–	–
Medaglia et al. [28]	MILP	✓	–	–	✓	–	–	–	–	–	✓	✓	✓	–	–	–	–	–	–
Nolz et al. [11]	MILP	✓	–	✓	–	–	–	–	–	–	✓	✓	–	–	–	✓	✓	–	–
Budak and Ustundag [10]	MILP	–	✓	✓	✓	–	–	–	–	–	–	✓	✓	✓	✓	✓	–	–	–
Mantzaras and Voudrias [29]	MINLP	–	✓	✓	✓	–	✓	–	–	–	–	✓	✓	✓	✓	✓	–	–	–
Alshraideh and Qdais [30]	MILP	–	–	✓	–	–	–	–	✓	–	–	✓	✓	–	–	–	✓	–	–
Osaba et al. [14]	MILP	–	–	✓	–	–	–	–	✓	–	–	✓	–	–	–	✓	–	–	–
Wang et al. [31]	MINLP	✓	–	✓	✓	–	–	–	–	–	–	✓	✓	✓	✓	✓	–	–	–
Kargar et al. [15]	MILP	✓	✓	✓	✓	–	✓	–	–	–	–	✓	✓	✓	✓	✓	–	✓	✓
Kargar et al. [16]	MILP	✓	–	✓	✓	–	–	–	–	–	✓	✓	–	✓	–	✓	–	✓	–
Homayouni and Pishvaee [17]	MILP	✓	✓	–	✓	–	✓	–	–	–	✓	✓	–	✓	✓	✓	–	–	✓
Taslimi et al [32]	MILP	✓	–	✓	–	–	–	–	–	–	✓	✓	✓	–	–	–	–	–	–
Yu et al. [18]	MILP	✓	–	✓	✓	–	–	–	–	–	✓	✓	–	✓	–	✓	–	✓	–
Yu et al. [19]	MILP	✓	✓	–	✓	–	✓	–	–	–	✓	✓	–	✓	✓	✓	–	–	✓
Saeidi-Mobarakeh et al. [20]	MILP	✓	✓	-	✓	✓	–	–	✓	–	✓	✓	–	✓	–	✓	✓	–	✓
Saeidi-Mobarakeh et al. [21]	MINLP	✓	✓	–	✓	✓	–	–	✓	–	✓	✓	✓	–	–	–	–	–	–
Nikzamir and Baradaran [22]	MILP	✓	✓	–	✓	–	✓	–	✓	–	–	✓	✓	✓	✓	✓	–	–	–
Nikzamir et al [33]	MILP	✓	✓	✓	✓	–	✓	–	✓	–	✓	✓	–	✓	✓	✓	–	–	–
Shadkam [23]	MILP	–	–	–	✓	–	–	–	–	–	–	✓	✓	✓	✓	✓	–	–	–
Torkayesh et al. [25]	MILP	✓	✓	✓	✓	–	–	–	✓	–	✓	✓	–	✓	✓	✓	–	–	–
Tirkolaee and Aydin [26]	MILP	✓	–	–	–	–	–	–	✓	–	✓	✓	✓	–	–	✓	–	–	–
Govindan et al. [24]	MILP	✓	✓	✓	✓	✓	–	–	✓	–	✓	✓	✓	–	–	–	–	✓	–
Mei et al. [34]	MINLP	✓	–	✓	✓	–	–	–	–	–	✓	✓	–	✓	–	✓	–	–	–
Tirkolaee et al. [35]	MILP	✓	–	✓	✓	–	–	–	✓	–	✓	✓	–	–	–	✓	✓	✓	–
Eren and Tuzkaya [36]	IP	✓	–	–	–	–	–	–	–	–	–	✓	✓	–	–	–	–	✓	–
Aydemir-Karadag [4]	MINLP	✓	✓	✓	✓	–	✓	–	✓	–	✓	✓	✓	✓	✓	✓	–	–	–
Faizal et al. [37]	IP	✓	✓	–	–	–	–	–	–	–	–	✓	✓	–	–	–	–	–	–
Valizadeh et al. [38]	MILP	✓	✓	–	✓	✓	–	–	–	–	–	✓	–	✓	✓	✓	–	–	✓
Polat [39]	MILP	✓	–	–	✓	–	–	–	✓	–	✓	✓	–	–	–	✓	–	✓	–
Lotfi et al. [40]	MILP	–	–	✓	✓	–	–	–	–	–	✓	✓	–	✓	✓	✓	✓	–	✓
Govindan et al. [27]	MILP	✓	✓	✓	✓	–	✓	–	✓	–	✓	✓	✓	✓	✓	✓	✓	–	–
This research	MILP	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	–

IP: Integer Programming; MILP: Mixed-Integer Linear Programming; MINLP: Mixed-Integer Non-Linear Programming

3. Proposed model

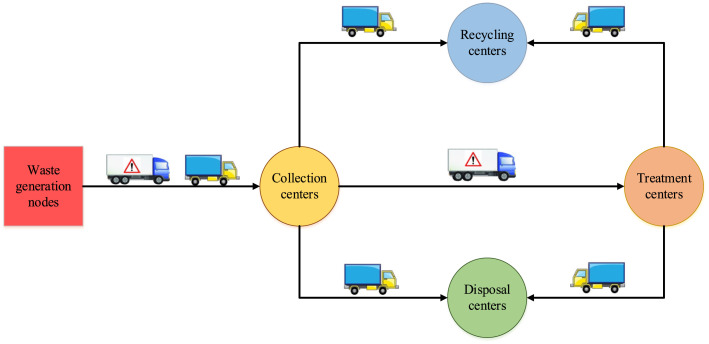
This section presents a bi-objective MILP model to manage medical waste under uncertainty. The network under study includes waste generation nodes, collection, treatment, recycling, and disposal centers. There are two types of waste generation nodes; the first type is hazardous nodes that all the waste produced by them is infectious, and the second type includes both “infectious” and “non-infectious” waste. All waste is transferred from the waste generation node to the collection centers, and then the infectious waste is transferred to the treatment centers. In the collection centers, non-infectious waste that is recyclable is shipped to the recycling centers, and the rest is delivered to the disposal centers. At the treatment center, after the treatment process, non-recyclable waste is moved to the disposal centers, and the rest of the waste is delivered to the recycling centers (See Fig. 1).

Fig. 1.

The structure of the investigated network in this study.

In the following, the assumptions of the proposed model are presented. The network includes a reverse flow; and is multi-item, multi-period, and multi-echelon. Both “infectious” and “non-infectious” wastes are considered. Infectious waste is either infectious in nature or generated by hazardous nodes. The geographical location of waste generation nodes is known, but the model determines the location of other centers. There are different technologies with various capacity levels for waste treatment. Infectious and non-infectious wastes should not be transferred by the same vehicle. Vehicles are heterogeneous. The amount of waste generated by each node is uncertain. Vehicles and centers are considered capacitated.

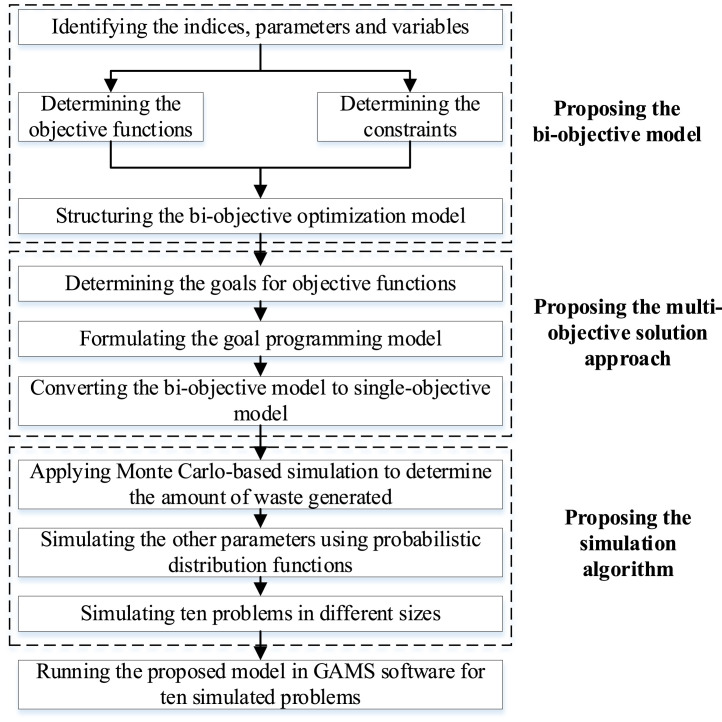
In this paper, first, the proposed model is formulated, and a multi-objective solution approach based on fuzzy goal programming is presented to convert the bi-objective MILP model to a single-objective one. Then, a simulation algorithm is developed to generate data, and finally, the proposed model is run in GAMS software. Fig. 2 shows the general structure of the research.

Fig. 2.

The general structure of the research.

The proposed mathematical model is as follows:

Mathematical model

Indices
$w\in \{1,2,\dots ,W\}$	Waste types
$v\in \{1,2,\dots ,V\}$	Vehicles
$n\in \{1,2,\dots ,N\}$	Waste generation nodes
$c\in \{1,2,\dots ,C\}$	Collection centers
$k\in \{1,2,\dots ,K\}$	Treatment centers
$r\in \{1,2,\dots ,R\}$	Recycling centers
$d\in \{1,2,\dots ,D\}$	Disposal centers
$l\in \{1,2,\dots ,L\}$	Capacity levels
$g\in \{1,2,\dots ,G\}$	Treatment technologies
$s\in \{1,2,\dots ,S\}$	Scenarios
$t\in \{1,2,\dots ,T\}$	Time periods
Parameters
$C{P}_v^{TR}$	The capacity of vehicle v
$C{P}_c^{CL-H}$	The capacity of collection center c for hazardous waste
$C{P}_c^{CL-N}$	The capacity of collection center c for non-hazardous waste
$C{P}_{wr}^{RC}$	The capacity of recycling center r for waste type w
$C{P}_{wd}^{DS}$	The capacity of disposal center d for waste type w
$W{G}_{wnts}$	The amount of type w waste generated at waste generation node n in period t, and under scenario s
$C{P}_{lg}^{UP}$	Maximum capacity level l for treatment technology g
$C{P}_{lg}^{LOW}$	Minimum capacity level l for treatment technology g
$C{E}_c^{CL}$	The cost of establishing collection center c
$C{E}_r^{RC}$	The cost of establishing recycling center r
$C{E}_k^{TRT}$	The cost of establishing treatment center k
$C{E}_d^{DS}$	The cost of establishing disposal center u
$C{I}_{lg}$	The cost of installing treatment technology g with capacity level l
$CT{R}_v$	The transportation cost for each unit of distance by vehicle v
$CP{R}_{wct}^{CL}$	The cost of processing type w waste at collection center c in period t
$CP{R}_{wkt}^{TRT}$	The cost of processing type w waste at treatment center k in period t
$CP{R}_{wrt}^{RC}$	The cost of recycling type w waste at recycling center r in period t
$CP{R}_{wdt}^{DS}$	The cost of disposing type w waste at disposal center d in period t
$DI{S}_{nc}^{HC}$	The distance between waste generation node n and collection center c
$DI{S}_{ck}^{CT}$	The distance between collection center c and treatment center k
$DI{S}_{cr}^{CR}$	The distance between collection center c and recycling center r
$DI{S}_{cd}^{CD}$	The distance between collection center c and disposal center d
$DI{S}_{kr}^{TR}$	The distance between treatment center k and recycling center r
$DI{S}_{kd}^{TD}$	The distance between treatment center k and disposal center d
$P{O}_{nc}$	Population living between waste generation node n and collection center c
$V{L}_w$	The volume of waste type w
$P{W}_{wlg}$	The amount of energy consumed for treating one unit of type w waste by treatment technology g with capacity level l
$Eng$	Energy unit price
${\xi }_{wn}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If waste generation node n is hazardous or type w waste is infectious,
	Otherwise
${\phi }_{nc}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If waste generation node n covered by collection center c,
	Otherwise
${\Omega }_{wct}$	Non-hazardous recyclable type w waste proportion shipped from collection center c to recycling centers in period t
${\Phi }_{wkt}$	Treated recyclable type w waste proportion shipped from treatment center k to recycling centers in period t
${\omega }_s$	Probability of scenario s
$\Psi$	A very large number
Variables
${\delta }_c^{CL}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If collection center c is established,
	Otherwise
${\delta }_k^{TRT}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If treatment center k is established,
	Otherwise
${\delta }_r^{RC}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If recycling center r is established,
	Otherwise
${\delta }_d^{DS}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If disposal center d is established,
	Otherwise
${\delta }_{lgk}\left\{\begin{array}{c}1\hfill \\ 0\hfill \end{array}\right)$	If treatment technology g with capacity level l is installed in treatment center k
	Otherwise
${\psi }_{\mathit{wncvts}}^{HC}$	The amount of type w waste shipped from waste generation node n to collection center c by vehicle v in period t, and under scenario s
${\psi }_{\mathit{wckvts}}^{CT}$	The amount of type w waste shipped from collection center c to treatment center k by vehicle v in period t, and under scenario s
${\psi }_{\mathit{wcrvts}}^{CR}$	The amount of type w waste shipped from collection center c to recycling center r by vehicle v in period t, and under scenario s
${\psi }_{\mathit{wcdvts}}^{CD}$	The amount of type w waste shipped from collection center c to disposal center d by vehicle v in period t, and under scenario s
${\psi }_{\mathit{wkrvts}}^{TR}$	The amount of type w waste shipped from treatment center k to recycling center r by vehicle v in period t, and under scenario s
${\psi }_{\mathit{wkdvts}}^{TD}$	The amount of type w waste shipped from treatment center k to disposal center d by vehicle v in period t, and under scenario s
$X_{\mathit{ncvts}}^{HC-H}$	The number of type v vehicles needed for shipping hazardous waste from waste generation node n to collection center c in period t, and under scenario s
$X_{\mathit{ncvts}}^{HC-N}$	The number of type v vehicles needed for shipping non-hazardous waste from waste generation node n to collection center c in period t, and under scenario s
$X_{\mathit{ckvts}}^{CT}$	The number of type v vehicles needed for shipping the waste from collection center c to treatment center k in period t, and under scenario s
$X_{\mathit{crvts}}^{CR}$	The number of type v vehicles needed for shipping the waste from collection center c to recycling center r in period t, and under scenario s
$X_{\mathit{cdvts}}^{CD}$	The number of type v vehicles needed for shipping the waste from collection center c to disposal center d in period t, and under scenario s
$X_{\mathit{krvts}}^{TR}$	The number of type v vehicles needed for shipping the waste from treatment center k to recycling center r in period t, and under scenario s
$X_{\mathit{kdvts}}^{TD}$	The number of type v vehicles needed for shipping the waste from treatment center k to disposal center d in period t, and under scenario s

Objective functions

$$\begin{array}{c}Min{Z}_1=\sum _{c}C{E}_c^{CL}\times {\delta }_c^{CL}\hfill \\ +\sum _{k}C{E}_k^{TRT}\times {\delta }_k^{TRT}+\sum _{r}C{E}_r^{RC}\times {\delta }_r^{RC}+\sum _{d}C{E}_d^{DS}\times {\delta }_d^{DS}+\hfill \\ \sum _{l,g,k}C{I}_{lg}\times {\delta }_{lgk}+\sum _{w,n,c,v,t,s}{\omega }_s\times CP{R}_{wct}^{CL}\times {\psi }_{\mathit{wncvts}}^{HC}\hfill \\ +\sum _{w,c,k,v,t,s}{\omega }_s\times CP{R}_{wkt}^{TRT}\times {\psi }_{\mathit{wckvts}}^{CT}+\hfill \\ \sum _{w,c,k,r,v,t,s}{\omega }_s\times CP{R}_{wrt}^{RC}\times ({\psi }_{\mathit{wcrvts}}^{CR}+{\psi }_{\mathit{wkrvts}}^{TR})\hfill \\ +\sum _{w,c,k,d,v,t,s}{\omega }_s\times CP{R}_{wdt}^{DS}\times ({\psi }_{\mathit{wcdvts}}^{CD}+{\psi }_{\mathit{wkdvts}}^{TD})+\hfill \\ \sum _{a,e,g,j,k,b,t,s}{\omega }_s\times Eng\times P{W}_{aeg}\times {\psi }_{\mathit{ajkbts}}^{CT}\hfill \\ +\sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-H}+\hfill \\ \sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-N}\hfill \\ +\sum _{c,k,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{ck}^{CT}\times X_{\mathit{ckvts}}^{CT}+\hfill \\ \sum _{c,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cr}^{CR}\times X_{\mathit{crvts}}^{CR}\hfill \\ +\sum _{c,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cd}^{CD}\times X_{\mathit{cdvts}}^{CD}+\hfill \\ \sum _{k,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kr}^{TR}\times X_{\mathit{krvts}}^{TR}\hfill \\ +\sum _{k,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kd}^{TD}\times X_{\mathit{kdvts}}^{TD}\hfill \end{array}$$ (1)

$$Min{Z}_2=\sum _{w,n,c,v,t,s}{\omega }_s\times P{O}_{nc}\times DI{S}_{nc}^{HC}\times {\psi }_{\mathit{wncvts}}^{HC}\times {\xi }_{wn}$$ (2)

$$s.t.\sum _{w,n,v}{\psi }_{\mathit{wncvts}}^{HC}\times {\xi }_{wn}\times V{L}_w\le C{P}_c^{CL-H}\forall c,t,s$$ (3)

$$\sum _{w,n,v}{\psi }_{\mathit{wncvts}}^{HC}\times (1-{\xi }_{wn})\times V{L}_w\le C{P}_c^{CL-N}\forall c,t,s$$ (4)

$$\sum _{c,v}{\psi }_{\mathit{wcrvts}}^{CR}+\sum _{k,v}{\psi }_{\mathit{wkrvts}}^{TR}\le C{P}_{wr}^{RC}\forall w,r,t,s$$ (5)

$$\sum _{c,v}{\psi }_{\mathit{wcdvts}}^{CD}+\sum _{k,v}{\psi }_{\mathit{wkdvts}}^{TD}\le C{P}_{wd}^{DS}\forall w,d,t,s$$ (6)

$$\sum _{w,c,v}{\psi }_{\mathit{wckvts}}^{CT}\times V{L}_w+\Psi \times (1-{\delta }_{lgk})>C{P}_{lg}^{LOW}\forall l,g,k,t,s$$ (7)

$$\sum _{w,c,v}{\psi }_{\mathit{wckvts}}^{CT}\times V{L}_w\le \Psi \times (1-{\delta }_{lgk})+C{P}_{lg}^{UP}\forall l,g,k,t,s$$ (8)

$$\sum _{l,g}{\delta }_{lgk}\le 1\forall k$$ (9)

$$\frac{\sum _w{\psi }_{\mathit{wncvts}}^{HC}\times V{L}_w\times {\xi }_{wn}}{C{P}_v^{TR}}\le X_{\mathit{ncvts}}^{HC-H}<\frac{\sum _w{\psi }_{\mathit{wncvts}}^{HC}\times V{L}_w\times {\xi }_{wn}}{C{P}_v^{TR}}+1\forall n,c,v,t,s$$ (10)

$$\frac{\sum _w{\psi }_{\mathit{wncvts}}^{HC}\times V{L}_w\times (1-{\xi }_{wn})}{C{P}_v^{TR}}\le X_{\mathit{ncvts}}^{HC-N}<\frac{\sum _w{\psi }_{\mathit{wncvts}}^{HC}\times V{L}_w\times (1-{\xi }_{wn})}{C{P}_v^{TR}}+1\forall n,c,v,t,s$$ (11)

$$\frac{\sum _w{\psi }_{\mathit{wckvts}}^{CT}\times V{L}_w}{C{P}_v^{TR}}\le X_{\mathit{ckvts}}^{CT}<\frac{\sum _w{\psi }_{\mathit{wckvts}}^{CT}\times V{L}_w}{C{P}_v^{TR}}+1\forall c,k,v,t,s$$ (12)

$$\frac{\sum _w{\psi }_{\mathit{wcrvts}}^{CR}\times V{L}_w}{C{P}_v^{TR}}\le X_{\mathit{crvts}}^{CR}<\frac{\sum _w{\psi }_{\mathit{wcrvts}}^{CR}\times V{L}_w}{C{P}_v^{TR}}+1\forall c,r,v,t,s$$ (13)

$$\frac{\sum _w{\psi }_{\mathit{wcdvts}}^{CD}\times V{L}_w}{C{P}_v^{TR}}\le X_{\mathit{cdvts}}^{CD}<\frac{\sum _w{\psi }_{\mathit{wcdvts}}^{CD}\times V{L}_w}{C{P}_v^{TR}}+1\forall c,d,v,t,s$$ (14)

$$\frac{\sum _w{\psi }_{\mathit{wkrvts}}^{TR}\times V{L}_w}{C{P}_v^{TR}}\le X_{\mathit{krvts}}^{TR}<\frac{\sum _w{\psi }_{\mathit{wkrvts}}^{TR}\times V{L}_w}{C{P}_v^{TR}}+1\forall k,r,v,t,s$$ (15)

$$\frac{\sum _w{\psi }_{\mathit{wkdvts}}^{TD}\times V{L}_w}{C{P}_v^{TR}}\le X_{\mathit{kdvts}}^{TD}<\frac{\sum _w{\psi }_{\mathit{wkdvts}}^{TD}\times V{L}_w}{C{P}_v^{TR}}+1\forall k,d,v,t,s$$ (16)

$$\sum _{c,v}{\psi }_{\mathit{wncvts}}^{HC}\times {\phi }_{nc}\ge W{G}_{wnts}\forall w,n,t,s$$ (17)

$$\sum _{n,v}{\psi }_{\mathit{wncvts}}^{HC}=\sum _{k,v}{\psi }_{\mathit{wckvts}}^{CT}+\sum _{r,v}{\psi }_{\mathit{wcrvts}}^{CR}+\sum _{d,v}{\psi }_{\mathit{wcdvts}}^{CD}\forall w,c,t,s$$ (18)

$$\sum _{k,v}{\psi }_{\mathit{wckvts}}^{CT}=\sum _{n,v}{\psi }_{\mathit{wncvts}}^{HC}\times {\xi }_{wn}\forall w,c,t,s$$ (19)

$$\sum _{r,v}{\psi }_{\mathit{wcrvts}}^{CR}={\Omega }_{wct}\times \sum _{n,v}{\psi }_{\mathit{wncvts}}^{HC}\times (1-{\xi }_{wn})\forall w,c,t,s$$ (20)

$$\sum _{c,v}{\psi }_{\mathit{wckvts}}^{CT}=\sum _{r,v}{\psi }_{\mathit{wkrvts}}^{TR}+\sum _{d,v}{\psi }_{\mathit{wkdvts}}^{TD}\forall w,k,t,s$$ (21)

$$\sum _{r,v}{\psi }_{\mathit{wkrvts}}^{TR}={\Phi }_{wkt}\times \sum _{c,v}{\psi }_{\mathit{wckvts}}^{CT}\forall w,k,t,s$$ (22)

$$\sum _{w,n,v}{\psi }_{\mathit{wncvts}}^{HC}\le \Psi \times {\delta }_c^{CL}\forall c,t,s$$ (23)

$$\sum _{w,k,v}{\psi }_{\mathit{wckvts}}^{CT}\le \Psi \times {\delta }_c^{CL}\forall c,t,s$$ (24)

$$\sum _{w,r,v}{\psi }_{\mathit{wcrvts}}^{CR}\le \Psi \times {\delta }_c^{CL}\forall c,t,s$$ (25)

$$\sum _{w,d,v}{\psi }_{\mathit{wcdvts}}^{CD}\le \Psi \times {\delta }_c^{CL}\forall c,t,s$$ (26)

$$\sum _{l,g}{\delta }_{lgk}\le {\delta }_k^{TRT}\forall k$$ (27)

$$\sum _{w,c,v}{\psi }_{\mathit{wckvts}}^{CT}\le \Psi \times \sum _{l,g}{\delta }_{lgk}\forall k,t,s$$ (28)

$$\sum _{w,r,v}{\psi }_{\mathit{wkrvts}}^{TR}\le \Psi \times \sum _{l,g}{\delta }_{lgk}\forall k,t,s$$ (29)

$$\sum _{w,d,v}{\psi }_{\mathit{wkdvts}}^{TD}\le \Psi \times \sum _{l,g}{\delta }_{lgk}\forall k,t,s$$ (30)

$$\sum _{w,c,v}{\psi }_{\mathit{wcrvts}}^{CR}\le \Psi \times {\delta }_r^{RC}\forall r,t,s$$ (31)

$$\sum _{w,k,v}{\psi }_{\mathit{wkrvts}}^{TR}\le \Psi \times {\delta }_r^{RC}\forall r,t,s$$ (32)

$$\sum _{w,c,v}{\psi }_{\mathit{wcdvts}}^{CD}\le \Psi \times {\delta }_d^{DS}\forall d,t,s$$ (33)

$$\sum _{w,k,v}{\psi }_{\mathit{wkdvts}}^{TD}\le \Psi \times {\delta }_d^{DS}\forall d,t,s$$ (34)

The first objective function minimizes the total cost including the cost of establishing collection, treatment, recycling, and disposal centers, the cost of installing treatment technology, costs of processing waste at collection, treatment, recycling, and disposal centers, the cost of energy consumed by technologies installed at treatment centers, and the cost of applying vehicles to transport waste between centers. The second objective function minimizes the population that is exposed to the spread of infection from the infectious waste.

The collection center consists of two parts, including infectious waste and non-infectious waste parts. These parts are capacitated. Constraints (3) and (4) are for controlling the capacity of infectious and non-infectious waste parts, respectively. The capacity limitation of recycling and disposal centers is also controlled by Constraints (5) and (6), respectively. The capacity levels for technologies installed in the treatment centers are determined by Constraints (7) and (8). Each treatment center is allowed to install a maximum of one technology with one capacity level. This condition is considered in Constraints (9). Constraints (10) to (16) are applied to calculate the number of vehicles used in the network to transport the waste. For example, the number of vehicles used to move the infectious waste from waste generation nodes to collection centers is considered by Constraint (10). Constraint (17) states that all waste should be collected from the waste generation nodes. Inventory balances at the collection centers are guaranteed by Constraints (18) to (20). Similarly, inventory balances at the treatment centers are controlled by Constraints (21), (22). The location condition for the collection centers is considered in Constraints (23) to (26). The prerequisite for installing the technology in the treatment centers is that the desired center has already been set up. This is satisfied by Constraint (27). The condition for entering/ leaving the waste to/ from the treatment center is that the treatment technology is installed in the center. Constraints (28) to (30) guarantee this condition. The location condition for the recycling centers is applied by Constraints (31) and (32). Finally, the location condition for the disposal centers is considered by Constraints (33) and (34).

4. Modeling the epidemic disruption process

Recently, epidemic disruptions have been a boundless threat to humankind that is affecting all aspects of our life. Epidemics could happen as natural disasters, such as the coronavirus outbreak (COVID-19) where the virus infected millions of people causing about 6 million deaths.1 These disruptions may occur as cautious bioterrorism mass destructions. Among others, anthrax and smallpox are the two most harmful biological agents that could be used in a probable man-made action [41]. From a sustainability point of view, when an epidemic disruption occurs, it directly affects the waste generation rate, results in a high demand rate in infected areas of the waste collection network.

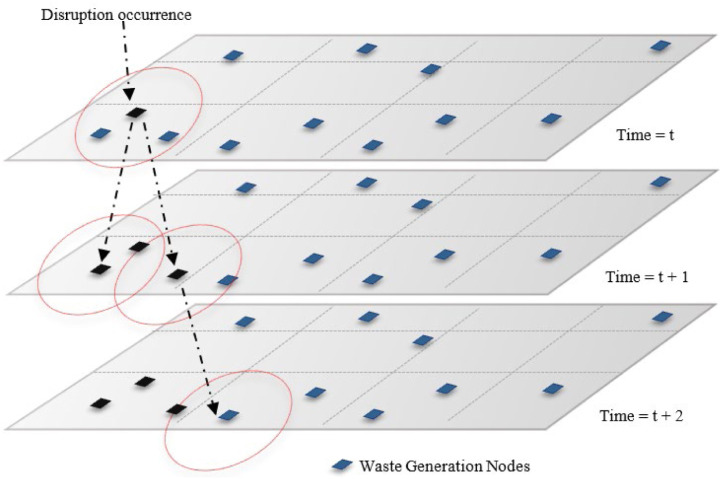
Therefore, a stochastic approach could be suitable for modeling the occurrence of epidemic disruptions and their direct effect on waste generation rate and the outbreak risk on the network. To the best of our knowledge, the epidemic disruption process has not been covered in the literature of waste management through quantitative methods. The graphical representation of the occurrence of an outbreak and its propagation through the network is presented in Fig. 3. As it is depicted, when an outbreak occurs at time t, the starting waste generation node is attained, and then it is probable that all the facilities of the network in the neighboring zones could be affected due to the propagations. The propagation risk level is mainly a function of the flow level between the facilities and their distance. It is clear that when the secondary facilities are contaminated, they could spread the disruption as well.

Fig. 3.

Propagation of epidemic disruption in a network through the time.

Modeling the described disruption occurrence and propagation process starts with the segmentation of the whole network into a set of zones and an exposure level is defined for each zone regarding its characteristics. The next section defines disruption and the required characteristics including arrival time and strength. Using the notation summarized in Table 2, the process will be modeled.

Table 2.

Disruption process notations.

$Z$	Set of partitioned zones ($z\in Z$);
${\pi }_z$	The risk exposure level of zone z;
${\beta }_e$	The proportion of demand affected at node $e$,binary parameter (0,1);
${\theta }_e$	Time for recovery of facilities, in time periods;
${\lambda }_z$	The time between two successive disruptions at each zone;
${\alpha }_{e|z\left(e\right)}$	The risk exposure level of the facility $e$ in case a disruption occurs in the zone;
$c_{e|e^{\prime }}$	Propagation probability of facility $e$ when the facility $e^{\prime }$ is affected by a disruption $\left(c_{e|e}=1\right)$;
$pr{o}_{e|e^{\prime }}$	Equals 1 if disruption is propagated from facility $e^{\prime }$ to facility $e$, otherwise 0 $\left(pr{o}_{e|e}=1\right)$.

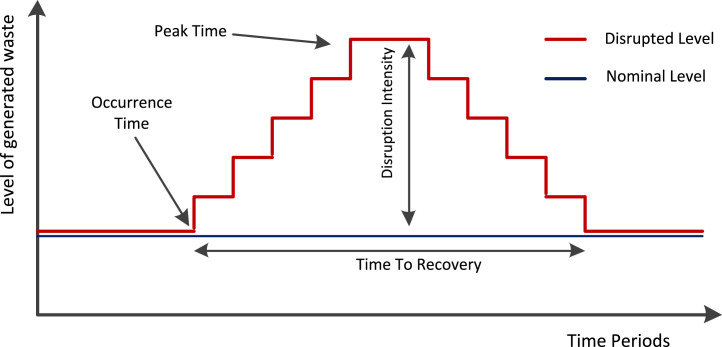
In general, when a node is disrupted, the strictness of the disruption could be defined through two elements, namely, intensity and time for recovery. Propagation is another aspect describing the disruption strictness and will be added here. These three dimensions are defined by the following parameters respectively: ${\beta }_e$, ${\theta }_e$, and $pr{o}_{e|e^{\prime }}$ for a given node e and the connected one e’. Disruptions do not homogeneously disturb the network. The corresponding impacts could be well defined via a phase-dependent recovery function, as illustrated in Fig. 4.

Fig. 4.

Generic loss-recovery functions.

4.1. Scenario generation framework

Scenario generation methodology is employed using the Monte-Carlo sampling method as a common approach that uses statistical data of uncertain parameters to generate comprehensive scenarios over a given planning horizon. This method mainly employs the inverse distribution function of the parameters using pseudo-random numbers. The main steps of generating scenarios according to the abovementioned descriptions are as follows.

• (1) Set pre-disruption capacity levels for all nodes in the network;
• (2) Generate disruption arrival time for each zone;
• (3) Generate disruption intensity;
• (4) Apply disruption propagation test;
• (5) Update capacity of disrupted facilities for disruption duration;
• (6)Aggregate these values over the time periods.

5. Multi-objective solution approach

Numerous methods are at play to deal with the multi-objective programming models. The “Goal programming” method is one of the most prevalent approaches that have been employed in various fields such as pharmaceutical supply chain [42], reverse logistics [43], waste management [24] and so on. In addition, the application of methods based on fuzzy theory in multi-objective problems seems to be a good option to deal with uncertainty [44]. Accordingly, this paper proposes a fuzzy goal programming method to cope with the multi-objective model as follows.

Step 1: Determining goals

First, decision-makers define the goals of the problem. To this end, it is desired to solve the proposed model taking into account each objective function separately. Then, the optimal values of the objective functions will be determined. Next, based on the optimal values, decision-makers will determine the goals of the problems. For instance, it is supposed that the optimal values of $Z_1^{\ast }$ and $Z_2^{\ast }$ are assigned to the first and second objective functions, respectively. Based on this, problem goals can be defined as follows where $G_1$ and $G_2$ represent the goals of the first and second objective functions, respectively.

$$\begin{array}{c}{G}_1=Z_1^{\ast }\hfill \\ G_2=Z_2^{\ast }\hfill \end{array}$$ (35)

Step 2: Goal programming model

In this step, the goal-programming model is defined as follows:

$$\begin{array}{c}MinD{V}_1^{+}\hfill \\ MinD{V}_2^{+}\hfill \\ s.t.\hfill \\ Z_1-D{V}_1^{+}+D{V}_1^{-}=G_1\hfill \\ Z_2-D{V}_2^{+}+D{V}_2^{-}=G_2\hfill \\ \hfill \\ \mathit{System}\mathit{Constraints}\hfill \end{array}$$ (36)

Where $D{V}_1^{+}$ and $D{V}_2^{+}$ denote the positive deviations, and $D{V}_1^{-}$ and $D{V}_2^{-}$ indicate the negative deviations from the first and second goals, respectively.

Step 3: Equivalent single objective model

This step is focused on converting the multi-objective goal-programming model extracted from the previous steps into a single-objective model for every nonconformity from the objective functions. Afterward, it comes to the development of a membership function via the proposed method by Zandkarimkhani et al. [42]. The main function of the present goal-programming model is to minimize the deviations from the goals already determined by the decision-makers; therefore, the following membership function is applied:

$${\mu }_{D{V}_i^{+}\left(x\right)}^{Min}=\left\{\begin{array}{cc}1\hfill & D{V}_i^{+}\left(x\right)>UD{V}_i^{+}\hfill \\ 0\hfill & D{V}_i^{+}\left(x\right)<LD{V}_i^{+}\hfill \\ \frac{UD{V}_i^{+}-D{V}_i^{+}\left(x\right)}{UD{V}_i^{+}-LD{V}_i^{+}}\hfill & LD{V}_i^{+}\le D{V}_i^{+}\left(x\right)\le UD{V}_i^{+}\hfill \end{array}\right)$$ (37)

In which, $UD{V}_i^{+}$ and $LD{V}_i^{+}$ represent the upper and lower bounds of unwanted deviations from goal i, respectively. Here, the membership function of these deviations from the goal is indicated by ${\mu }_{D{V}_i^{+}\left(x\right)}^{Min}$.

The values of $LD{V}_1^{+}$ and $LD{V}_2^{+}$ are always zero. To calculate $UD{V}_1^{+}$ and $UD{V}_2^{+}$, the upper bound of the objective functions 1 ($U{Z}_1$) and 2 ($U{Z}_2$) should first be calculated. These values are calculated by the lexicographic approach. Then, the values of $UD{V}_1^{+}$ and $UD{V}_2^{+}$ are determined by Eq. (38).

$$\begin{array}{c}D{V}_1^{+}=U{Z}_1-G_1\hfill \\ D{V}_2^{+}=U{Z}_2-G_2\hfill \end{array}$$ (38)

Finally, the equation below presents the fuzzy single-objective model:

$$\begin{array}{c}MaxFGP=\sum _i{w}_i\times M{F}_i\hfill \\ s.t.\hfill \\ M{F}_i\le {\mu }_{D{V}_i^{+}\left(x\right)}^{Min}\forall i\hfill \\ Z_i-D{V}_i^{+}+D{V}_i^{-}=G_i\forall i\hfill \\ \mathit{System}\mathit{Constraints}\hfill \end{array}$$ (39)

Where $w_i$ represents the weight of the objective function i.

6. Experimental results

This section is dedicated to examine the efficiency of the proposed model and solution approach using simulated data. For this purpose, first, the simulation process for data generation is explained, and the results obtained from the implementation of 10 simulated problems in GAMS software are presented. Then the efficiency of our proposed solution approach is evaluated in the comparative analysis sub-section. Finally, a discussions sub-section is provided based on the obtained results.

6.1. Data generation

In this sub-section, the parameters of the proposed model are simulated with the help of probabilistic distribution functions. The simulation process is designed to provide a feasible solution space for any desired amount of indices. In fact, to solve this problem, the capacities of the centers and vehicles we defined as a function of the amount of the generated waste. It should be noted that the Monte Carlo simulation approach presented in Section 4 will be used to simulate the parameter of the amount of waste generated at each node. Table 3 shows the proposed model of the simulation parameter algorithm.

Table 3.

The simulation algorithm for data generation.

Indices/ Parameters	Functions
$w,v,n,c,k,r,d,l,g,s,t$	The user determines the value of indices
$W{G}_{wnts}$	$\mathit{Monte}\mathit{Carlo}$
$V{L}_w$	$\mathit{Uniform}(0.5,0.6)$
$C{P}_v^{TR}$	$\mathit{Round}\left(\frac{{\sum }_{w,n,t,s}W{G}_{wnts}\times V{L}_w}{\mathit{Uniform}(6,10)\times T\times S}\right)$
$C{P}_c^{CL-H}$	$\mathit{Round}(\mathit{Uniform}(1.2,1.5)\times \frac{{\sum }_{w,n,t,s}W{G}_{wnts}\times V{L}_w}{C\times T\times S})$
$C{P}_c^{CL-N}$
$C{P}_{wr}^{RC}$	$\mathit{Round}\left(\frac{{\sum }_{n,t,s}W{G}_{wnts}}{R\times T\times S}\right)$
$C{P}_{wd}^{DS}$	$\mathit{Round}(\mathit{Uniform}(0.4,0.5)\times \frac{{\sum }_{n,t,s}W{G}_{wnts}}{D\times T\times S})$
$C{P}_{lg}^{UP}$	$\mathit{Round}(\mathit{Uniform}(1.5,2)\times \frac{{\sum }_{a,i,t,s}W{G}_{wnts}\times V{L}_w}{T\times S})$
$C{P}_{lg}^{LOW}$	0
$C{E}_c^{CL}$	$\mathit{Round}\left(\mathit{Uniform}(2\times 10^6,4\times 10^6)\right)$
$C{E}_r^{RC}$	$\mathit{Round}\left(\mathit{Uniform}(1\times 10^6,2\times 10^6)\right)$
$C{E}_k^{TRT}$	$\mathit{Round}\left(\mathit{Uniform}(1.5\times 10^6,3\times 10^6)\right)$
$C{E}_d^{DS}$	$\mathit{Round}\left(\mathit{Uniform}(1.2\times 10^6,2.2\times 10^6)\right)$
$C{I}_{lg}$	$\mathit{Round}\left(\mathit{Uniform}(8\times 10^5,9\times 10^5)\right)$
$CT{R}_v$	$\mathit{Round}\left(\mathit{Uniform}(1.8\times 10^2,2.3\times 10^2)\right)$
$CP{R}_{wct}^{CL},CP{R}_{wkt}^{TRT},CP{R}_{wrt}^{RC},CP{R}_{wdt}^{DS}$	$\mathit{Round}\left(\mathit{Uniform}(3.3\times 10^2,4\times 10^2)\right)$
$\begin{array}{c}DI{S}_{nc}^{HC},DI{S}_{ck}^{CT},DI{S}_{cr}^{CR}\hfill \\ DI{S}_{cd}^{CD},DI{S}_{kr}^{TR},DI{S}_{kd}^{TD}\hfill \end{array}$	$\mathit{Round}\left(\mathit{Uniform}(3\times 10^1,8\times 10^1)\right)$
$P{O}_{nc}$	$\mathit{Round}\left(\mathit{Uniform}(6\times 10^3,9\times 10^3)\right)$
$P{W}_{wlg}$	$\mathit{Round}\left(\mathit{Uniform}(2\times 10^1,3\times 10^1)\right)$
${\xi }_{wn}$	$\mathit{Round}\left(\mathit{Uniform}(0,1.5)\right)$
${\phi }_{nc}$	$\mathit{Round}\left(\mathit{Uniform}(0,1.5)\right)and{\sum }_j{\phi }_{ij}\ge 1\forall i$
${\Omega }_{wct},{\Phi }_{wkt}$	$\mathit{Uniform}(0.7,0.8)$
$Eng$	10

To validate the proposed model, 10 test problems are generated in different sizes by the proposed simulation algorithm and the proposed model is run on GAMS software using CPLEX solver. These problems are designed so that by increasing the number of the problem, the solution space and its complexity will be increased as well. Table 4 indicates the values of the simulated problems.

Table 4.

The size of the simulated problems.

Instance	$w$	$v$	$n$	$c$	$k$	$r$	$d$	$l$	$g$	$s$	$t$
INC1	2	1	3	3	2	2	2	1	1	6	6
INC2	2	1	4	3	2	2	2	2	2	7	6
INC3	2	2	4	3	2	2	2	2	2	8	6
INC4	3	2	4	3	3	2	2	2	2	9	6
INC5	3	2	5	3	3	3	3	2	2	9	6
INC6	3	2	5	4	3	3	3	2	3	10	6
INC7	3	2	5	4	3	3	3	3	3	10	8
INC8	4	3	6	4	4	4	4	3	3	11	8
INC9	4	3	7	4	4	4	4	3	3	12	12
INC10	4	3	7	5	4	4	4	4	3	13	12

In what follows, an example is provided to show how to generate data in GAMS software. For example, Table 5 represents the amount of the waste generated using Monte Carlo simulation for the first instance (INC1).

Table 5.

The amount of waste generated by nodes in INC1.

$W{G}_{wnts}$			$s=1$	$s=2$	$s=3$	$s=4$	$s=5$	$s=6$
w=1	n=1	$t=1$	32.9	34.2	30.5	31.2	34.7	29.4
		$t=2$	30.2	27	32.3	33.9	27.8	30.9
		$t=3$	28	29.1	29.6	28.9	26.6	28.9
		$t=4$	44.5	47.4	42.2	41.5	43.9	36.1
		$t=5$	46.2	37.8	48.8	49.4	42.1	43.4
		$t=6$	53	53.7	48	47.9	43.7	52
	n=2	$t=1$	25.7	33.2	30.3	28.7	25.1	33.9
		$t=2$	29.3	25.5	31.1	31.5	25.5	34
		$t=3$	33.2	26.7	33.7	33.3	28.1	31.2
		$t=4$	34.8	46	41.9	38.2	31.8	41.6
		$t=5$	44.9	35.8	47.1	45.9	38.6	47.7
		$t=6$	62.9	49.2	54.6	55.3	46.2	56.1
	n=3	$t=1$	34.9	31.5	32.5	25.4	29.6	32.3
		$t=2$	32.1	32.9	33	31.2	27	27.2
		$t=3$	32.3	27.5	31.7	32.2	30.5	34.8
		$t=4$	47.2	43.7	44.9	33.8	37.4	39.7
		$t=5$	49.1	46.2	49.9	45.5	40.8	38.2
		$t=6$	61.3	50.7	51.4	53.3	50.1	62.5
w=2	n=1	$t=1$	26.2	32.1	33.4	25.1	29.8	30.3
		$t=2$	27.1	31	33.3	30.2	26.5	26.2
		$t=3$	26.3	29.1	34.8	29.4	32.5	31.6
		$t=4$	35.4	44.4	46.1	33.5	37.7	37.3
		$t=5$	41.5	43.5	50.3	44.1	40.1	36.7
		$t=6$	49.8	53.7	56.5	48.8	53.5	56.9
	n=2	$t=1$	31.2	32.7	26.1	33.8	26.9	33.2
		$t=2$	30.1	31.3	28.5	28.3	28.4	25.3
		$t=3$	30.5	29.9	34.3	33.9	28.8	32.4
		$t=4$	42.1	45.3	36	45	34	40.8
		$t=5$	46	44	43.1	41.2	43	35.4
		$t=6$	57.7	55.2	55.7	56.2	47.4	58.2
	n=3	$t=1$	25.9	33.8	31.3	35	32.5	27.3
		$t=2$	26.6	25.4	29.6	26.5	29.1	31.3
		$t=3$	28.8	27.3	25.4	26.9	30.6	33.1
		$t=4$	35	46.8	43.2	46.5	41.1	33.5
		$t=5$	40.7	35.7	44.7	38.7	44.1	43.9
		$t=6$	54.5	50.3	41.1	44.5	50.3	59.6

The capacity of recycling centers can be calculated using the following formula. Table 6 shows the simulated data for the capacity of recycling centers.

$$C{P}_{wr}^{RC}=\mathit{Round}\left(\frac{\sum _{n,t,s}W{G}_{wnts}}{W\times T\times S}\right)$$ (40)

Table 6.

The capacity of recycling centers in INC1.

$C{P}_{wr}^{RC}$	$r=1$	$r=2$
$w=1$	57	57
$w=2$	56	56

6.2. Numerical examples

In this sub-section, the proposed multi-objective model is transformed into a single-objective model using proposed approach. The implementation process of the proposed solution approach for the simulated problems is as follows:

• Step 1: In this step, the model is executed using simulated data for each objective function, separately. The optimal values obtained for the objective functions are considered as their goals. In Table 7, the goal values for each problem are given.

Table 7.

The goals, upper bounds of objective functions and unwanted deviations from goals.

Instance	$G_1\left(Z_1^{\ast }\right)$	$G_2\left(Z_2^{\ast }\right)$	$U{Z}_1$	$U{Z}_2$	$UD{V}_1^{+}$	$UD{V}_2^{+}$
INC1	19,310,342	188,835,994	19,312,139	188,835,994	1,797	0
INC2	17,941,975	242,194,878	20,637,627	265,431,444	2,695,652	23,236,566
INC3	19,453,233	295,702,929	21,985,489	320,557,713	2,532,256	24,854,784
INC4	21,536,731	370,637,153	23,899,652	405,448,327	2,362,921	34,811,174
INC5	22,806,270	588,163,542	25,684,842	618,140,325	2,878,572	29,976,783
INC6	27,995,638	654,582,051	30,185,028	713,637,116	2,189,390	59,055,065
INC7	32,937,767	730,720,732	35,764,166	791,810,769	2,826,399	61,090,037
INC8	46,986,441	1,040,760,388	53,929,321	1,101,254,071	6,942,880	60,493,683
INC9	59,701,734	1,297,003,456	65,821,657	1,349,738,614	6,119,923	52,735,158
INC10	64,839,312	1,387,256,624	72,637,222	1,461,153,818	7,797,910	73,897,194

• Step 2: In this step, the goal-programming model is formulated by Eq. (36) based on the goals obtained. For example, the goal programming model for INC7 is as follows:

$$\begin{array}{c}MinD{V}_1^{+}\hfill \\ MinD{V}_2^{+}\hfill \\ s.t.\hfill \\ Z_1-D{V}_1^{+}+D{V}_1^{-}=32,937,767\hfill \\ Z_2-D{V}_2^{+}+D{V}_2^{-}=730,720,732\hfill \\ Z_1=\sum _{c}C{E}_c^{CL}\times {\delta }_c^{CL}+\sum _{k}C{E}_k^{TRT}\times {\delta }_k^{TRT}\hfill \\ +\sum _{r}C{E}_r^{RC}\times {\delta }_r^{RC}+\sum _{d}C{E}_d^{DS}\times {\delta }_d^{DS}+\hfill \end{array}$$

$$\begin{array}{c}\sum _{l,g,k}C{I}_{lg}\times {\delta }_{lgk}+\sum _{w,n,c,v,t,s}{\omega }_s\times CP{R}_{wct}^{CL}\times {\psi }_{\mathit{wncvts}}^{HC}\hfill \\ +\sum _{w,c,k,v,t,s}{\omega }_s\times CP{R}_{wkt}^{TRT}\times {\psi }_{\mathit{wckvts}}^{CT}+\hfill \\ \sum _{w,c,k,r,v,t,s}{\omega }_s\times CP{R}_{wrt}^{RC}\times ({\psi }_{\mathit{wcrvts}}^{CR}+{\psi }_{\mathit{wkrvts}}^{TR})\hfill \\ +\sum _{w,c,k,d,v,t,s}{\omega }_s\times CP{R}_{wdt}^{DS}\times ({\psi }_{\mathit{wcdvts}}^{CD}+{\psi }_{\mathit{wkdvts}}^{TD})+\hfill \\ \sum _{a,e,g,j,k,b,t,s}{\omega }_s\times Eng\times P{W}_{aeg}\times {\psi }_{\mathit{ajkbts}}^{CT}\hfill \\ +\sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-H}+\hfill \\ \sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-N}\hfill \\ +\sum _{c,k,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{ck}^{CT}\times X_{\mathit{ckvts}}^{CT}+\hfill \\ \sum _{c,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cr}^{CR}\times X_{\mathit{crvts}}^{CR}\hfill \\ +\sum _{c,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cd}^{CD}\times X_{\mathit{cdvts}}^{CD}+\hfill \\ \hfill \end{array}$$

$$\begin{array}{c}\sum _{k,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kr}^{TR}\times X_{\mathit{krvts}}^{TR}\hfill \\ +\sum _{k,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kd}^{TD}\times X_{\mathit{kdvts}}^{TD}\hfill \\ Z_2=\sum _{w,n,c,v,t,s}{\omega }_s\times P{O}_{nc}\times DI{S}_{nc}^{HC}\times {\psi }_{\mathit{wncvts}}^{HC}\times {\xi }_{wn}\hfill \\ \mathit{System}\mathit{Constraints}\hfill \end{array}$$ (41)

• Step 3: In this step, first, the upper and lower bounds of each objective function are calculated using the lexicographic approach. Then, the upper bound of undesirable deviation from the goals is determined by Eq. (38). In Table 7, these values are given for the simulated problems. In addition, membership functions for the upper bound of undesirable deviation from the goals are calculated by Eq. (37), which are also reported in Table 7. Finally, the fuzzy single-objective model is formulated. For example, the fuzzy single-objective model for INC7 is as follows (Put 0.6 and 0.4 for ${\mathit{w}}_1$ and ${\mathit{w}}_2$, respectively):

$$\begin{array}{c}MaxFGP=0.6\times M{F}_1+0.4\times M{F}_2\hfill \\ s.t.\hfill \\ M{F}_1\le \frac{2,826,399-D{V}_1^{+}}{2,826,399}\hfill \\ M{F}_2\le \frac{61,090,037-D{V}_2^{+}}{61,090,037}\hfill \\ Z_1-D{V}_1^{+}+D{V}_1^{-}=32,937,767\hfill \end{array}$$

$$\begin{array}{c}{Z}_2-D{V}_2^{+}+D{V}_2^{-}=730,720,73\hfill \\ Z_1=\sum _{c}C{E}_c^{CL}\times {\delta }_c^{CL}+\sum _{k}C{E}_k^{TRT}\times {\delta }_k^{TRT}\hfill \\ +\sum _{r}C{E}_r^{RC}\times {\delta }_r^{RC}+\sum _{d}C{E}_d^{DS}\times {\delta }_d^{DS}+\hfill \\ \sum _{l,g,k}C{I}_{lg}\times {\delta }_{lgk}+\sum _{w,n,c,v,t,s}{\omega }_s\times CP{R}_{wct}^{CL}\times {\psi }_{\mathit{wncvts}}^{HC}\hfill \\ +\sum _{w,c,k,v,t,s}{\omega }_s\times CP{R}_{wkt}^{TRT}\times {\psi }_{\mathit{wckvts}}^{CT}+\hfill \\ \sum _{w,c,k,r,v,t,s}{\omega }_s\times CP{R}_{wrt}^{RC}\times ({\psi }_{\mathit{wcrvts}}^{CR}+{\psi }_{\mathit{wkrvts}}^{TR})\hfill \\ +\sum _{w,c,k,d,v,t,s}{\omega }_s\times CP{R}_{wdt}^{DS}\times ({\psi }_{\mathit{wcdvts}}^{CD}+{\psi }_{\mathit{wkdvts}}^{TD})+\hfill \\ \sum _{a,e,g,j,k,b,t,s}{\omega }_s\times Eng\times P{W}_{aeg}\times {\psi }_{\mathit{ajkbts}}^{CT}\hfill \\ +\sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-H}+\hfill \\ \sum _{n,c,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{nc}^{HC}\times X_{\mathit{ncvts}}^{HC-N}\hfill \\ +\sum _{c,k,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{ck}^{CT}\times X_{\mathit{ckvts}}^{CT}+\hfill \\ \sum _{c,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cr}^{CR}\times X_{\mathit{crvts}}^{CR}\hfill \\ +\sum _{c,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{cd}^{CD}\times X_{\mathit{cdvts}}^{CD}+\hfill \\ \sum _{k,r,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kr}^{TR}\times X_{\mathit{krvts}}^{TR}\hfill \\ +\sum _{k,d,v,t,s}{\omega }_s\times CT{R}_v\times DI{S}_{kd}^{TD}\times X_{\mathit{kdvts}}^{TD}\hfill \\ Z_2=\sum _{w,n,c,v,t,s}{\omega }_s\times P{O}_{nc}\times DI{S}_{nc}^{HC}\times {\psi }_{\mathit{wncvts}}^{HC}\times {\xi }_{wn}\hfill \\ \mathit{System}\mathit{Constraints}\hfill \end{array}$$ (42)

By running the model on GAMS software, the optimal values of the objective functions and decision variables are obtained. The implementation steps of the proposed model in GAMS software for INC3 are shown in Appendix. The optimal values of the objective functions for each problem are shown in Table 8.

Table 8.

The optimal objective function values.

Instance	$Z_1^{FGP}$	$Z_2^{FGP}$
INC1	19,310,342	188,835,994
INC2	18,250,783	254,017,526
INC3	19,466,260	320,557,713
INC4	22,155,643	393,228,065
INC5	23,630,752	612,386,341
INC6	28,816,257	674,119,865
INC7	33,004,052	765,965,908
INC8	48,724,013	1,097,118,936
INC9	60,536,165	1,321,666,472
INC10	66,174,832	1,413,665,716

As it was stated, the optimal values of the objective functions presented in Table 8 are obtained by considering the values of 0.6 and 0.4 for ${\mathit{w}}_1$ and ${\mathit{w}}_2$, respectively. A sensitivity analysis is conducted to validate the proposed model and solution approach, and to find a set of efficient optimal solutions for various weight sets. Accordingly, the Pareto front can be drawn. In this vein, the strategies based on changing the values of these parameters are defined in Table 9, and the efficiency of the proposed model is examined for each strategy. In the defined strategies, as the coefficient of an objective function decreases (increases), the coefficient of another objective function increases (decreases), as well. It is expected that a decrease in the coefficient of an objective function will lead to no improvement of the optimal value of that objective function. On the other hand, an increase in the coefficient of the objective function will not lead to a deterioration of the optimal value of that objective function. In Table 9, the optimal values of the objective functions for INC7, INC8, and INC9 strategies have been presented.

Table 9.

The strategies for the sensitivity analysis process.

Strategy	$w_1$	$w_2$	INC7		INC8		INC9
			$Z_1^{FGP}$	$Z_2^{FGP}$	$Z_1^{FGP}$	$Z_2^{FGP}$	$Z_1^{FGP}$	$Z_2^{FGP}$
Str1	0.3	0.7	35,162,081	742,051,931	51,932,943	1,055,928,373	63,726,035	1,303,751,568
Str2	0.35	0.65	34,556,638	748,181,265	51,253,817	1,063,849,656	63,267,118	1,306,267,411
Str3	0.4	0.6	34,160,712	755,300,652	50,736,469	1,072,839,008	62,544,728	1,308,338,470
Str4	0.45	0.55	33,743,002	758,231,267	49,688,140	1,076,734,367	62,061,269	1,311,145,146
Str5	0.5	0.5	33,562,135	761,547,782	49,485,061	1,081,333,129	61,378,144	1,314,016,384
Str6	0.55	0.45	33,284,961	763,273,063	48,998,734	1,086,372,016	61,004,432	1,316,827,721
Str7 (Main problem)	0.6	0.4	33,004,052	765,965,908	48,724,013	1,097,118,936	60,536,165	1,321,666,472
Str8	0.65	0.35	32,998,945	768,413,519	48,156,728	1,098,332,934	60,471,458	1,329,839,657
Str9	0.7	0.3	32,996,308	773,997,332	47,621,245	1,098,944,515	60,288,813	1,337,746,264
Str10	0.75	0.25	32,976,447	780,341,277	47,308,827	1,100,763,931	59,943,467	1,342,165,048

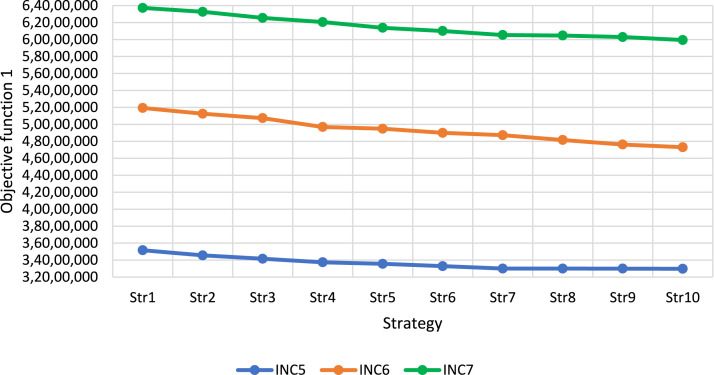
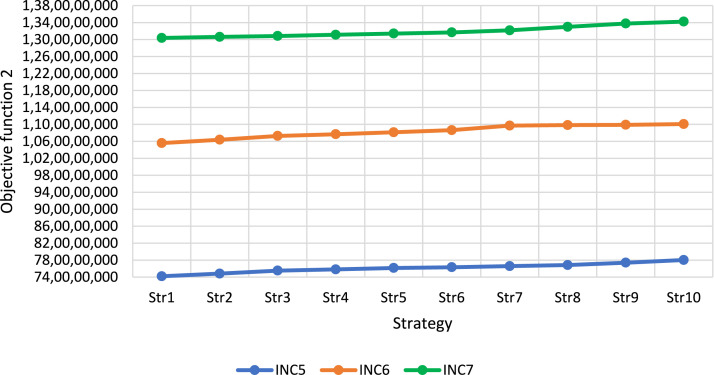
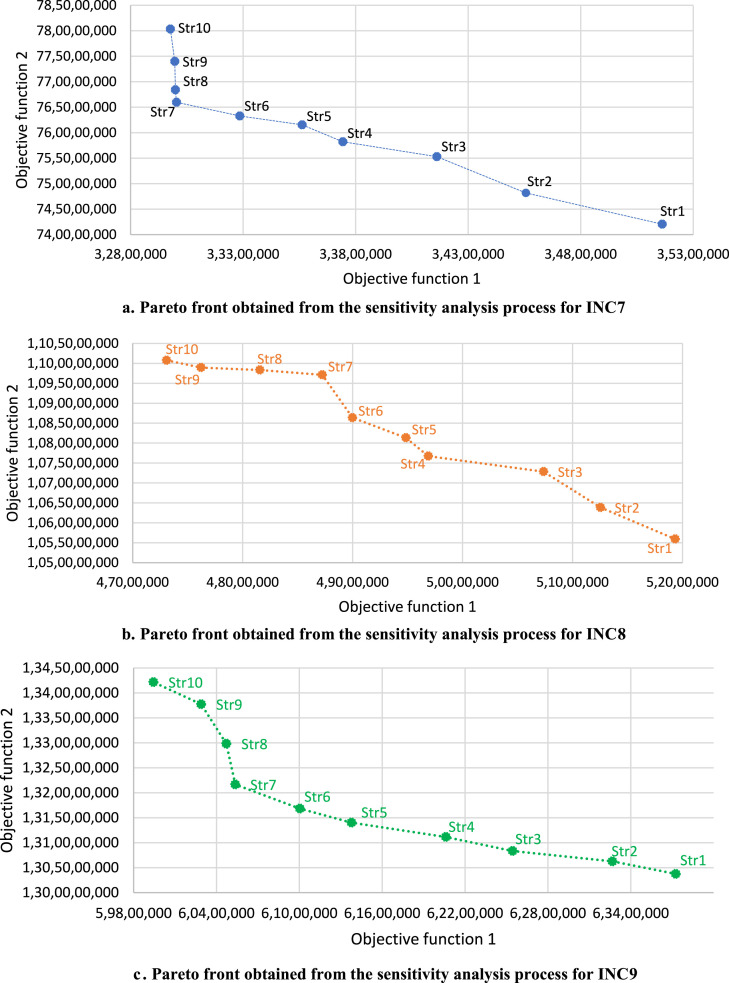
According to the results provided in Table 9, as the coefficient of each objective function increases (decreases), the optimal value of that objective function decreases (increases). These results exactly match the expectations. Therefore, the results obtained from the proposed model and solution approach indicate its efficiency and effectiveness. In addition, the behavior of the first and second objective functions in different strategies are depicted in Fig. 5, Fig. 6, and the Pareto front resulting from the defined strategies is shown in Fig. 7.

Fig. 5.

The behavior of the first objective function in the sensitivity analysis process.

Fig. 6.

The behavior of the second objective function in the sensitivity analysis process.

Fig. 7.

Pareto front obtained from the sensitivity analysis process.

Fig. 5, Fig. 6 show the behavior of the first and second objective functions, respectively, for INC7, INC8, and INC9 in different strategies. As seen in Table 9, the strategies are designed so that by going from strategy 1 to strategy 10, the weight of the first objective function increases and the weight of the second objective function decreases. Since both objective functions are in minimization form, the trend of the first and second objective functions from strategy 1 to strategy 10 are expected to be descending and ascending, respectively. The behavior of the objective functions depicted in Fig. 5, Fig. 6 confirms the effective performance of the proposed model.

The Pareto fronts obtained from the sensitivity analysis of the objective functions’ coefficients for INC7, INC8, and INC9 are illustrated in Fig. 7a, b, and c, respectively. The noteworthy point is that in each examined problem, 10 grid points are obtained, none of which dominate the other. Therefore, by applying the sensitivity analysis process to each problem, 10 sets of optimal solutions are provided. As seen in Fig. 7, as we move towards strategy 10, total costs decrease, but the population risk increases. Decision makers who care about human lives choose strategies that have the lowest population risk; in contrast, profit-seeking decision makers choose strategies that result in the lowest cost. In general, the results of the sensitivity analysis of the objective functions’ coefficients allow decision-makers to choose the preferred strategy in accordance with their organizational limitations such as budget constraints, maximum exposed people, etc.

6.3. Comparative analysis

In this section, we solve the proposed multi-objective model using simulated data by another multi-objective solution approach. Then, to indicate the efficiency of the proposed solution approach, the results obtained from both multi-objective solution approaches are compared. It is important to note that we are not allowed to use any multi-objective solution approach for comparison. In other words, we should use a multi-objective solution approach that has similar features to our solution approach. The three main features of our multi-objective solution approach are the consideration of weights for the objective functions, the use of fuzzy theory to consider uncertainty, and the consideration of goals for objective functions. Therefore, the comparative solution approach should have these three features. Nasr et al. [43] have presented a multi-objective solution approach based on the fuzzy goal programming method to solve the multi-objective model, which has all the three features. In this regard, 10 simulated problems are solved using the approach provided by Nasr et al. [43]. The optimal values of the objective functions for each simulated problem obtained from the Nasr et al. [43] approach are presented in Table 10.

Table 10.

The optimal objective functions value obtained from the approach presented by Nasr et al. [43].

Instance	$Z_1^{FGP}$	$Z_2^{FGP}$
INC1	19,310,342	188,835,994
INC2	18,348,051	253,873,121
INC3	19,466,260	320,557,713
INC4	22,099,167	398,581,637
INC5	23,462,721	613,233,009
INC6	28,956,335	671,426,497
INC7	33,367,816	759,064,478
INC8	47,911,263	1,099,011,554
INC9	60,859,357	1,302,628,123
INC10	65,735,422	1,432,390,624

One of the ways to examine the efficiency of multi-objective solution approaches is to compare the results of the proposed approach with the results of a solution approach whose efficiency has already been confirmed in the literature. If the solutions obtained from the proposed approach are not dominated by the solutions obtained from the comparative approach, the efficiency of the proposed approach is confirmed (Govindan et al. [45]). Comparing the results presented in Table 8, Table 10 reveals that the value of the objective functions for both approaches in INC1 and INC3 are similar. In other simulated problems (i.e., INC2, INC4, INC5, INC6, INC7, INC8, INC9, and INC10), none of the solutions set obtained from our proposed solution approach are dominated by the approach presented by Nasr et al. [43]. Therefore, it can be concluded that the proposed solution approach has a good performance and is sufficiently efficient.

6.4. Discussions

In general, this paper consists of three basic parts including modeling, data generation and solving the multi-objective model using a multi-objective solution approach. In the following, each part is discussed with emphasis on the relevant advantages.

The literature review reveals that many researchers have used mathematical programming tools for healthcare waste management. The noteworthy point is that a significant number of these papers have been presented in recent years with the emergence of COVID-19. This shows that healthcare waste management is important in epidemic conditions. Although healthcare waste management in epidemic conditions in articles such as Govindan et al. [24], Tirkolaee et al. [26], and Govindan et al. [27] have been addressed, none of them has considered epidemic disruptions in healthcare waste management, which is one of the unique features of this paper. Another special feature of this paper is the consideration of the set covering problem in the structuring the investigated network. Based on this problem, each potential collection center is allowed to cover a predetermined area, which is determined based on the maximum acceptable distance traveled by vehicles. In other words, the set covering problem is applied to reduce population risk. By removing this problem from the proposed model, the network costs may decrease, but the population risk will be increased.

In this regard, a bi-objective MILP model was formulated to design an efficient network for healthcare waste management under uncertainty using a mathematical programming tool. The objectives of the proposed model are to minimize total network costs and population risk, simultaneously. Network costs include strategic and operational costs. This means that the model incorporates both strategic and operational decisions into network design. Uncertainty is an integral part of problems that include epidemic disruptions; because these problems are faced with different conditions under various scenarios. Therefore, this paper employs a stochastic scenario-based approach to deal with the uncertainty of the proposed model.

In this paper, due to the lack of access to real-world data, an intelligent algorithm is designed to simulate data using probabilistic distribution functions. Intelligent simulation means that the algorithm is designed in such a way that for each optional value for indices, a feasible solution space is provided. For this purpose, different parameters such as the capacity of centers and vehicles that may create infeasible solution space are defined as a function of the amount of the waste generated. Other parameters such as the cost of establishing the centers, the distance between the centers, etc., which do not affect the infeasibility of the solution space, should be defined logically so that the simulated data is close to the real world. For example, the strategic cost should be defined as large enough compared to the operational costs. All these points are included in the proposed simulation algorithm.

Another feature of this paper is the development of a multi-objective solution approach based on fuzzy goal programming. One of the advantages of the goal programming method is that it determines a goal for each objective function, and it aims to minimize the difference between the objective functions and their goals. Considering the weight for objective functions enables the decision makers to assign a weight to each objective function according to its importance results in a Pareto front by changing the weights. In this paper, to examine the performance of the proposed model and to evaluate the efficiency of the proposed solution approach, 10 test problems are simulated in different sizes. Then, the proposed bi-objective model is converted into a single-objective model for these problems using the presented multi-objective solution approach. Finally, by running the single-objective model in the GAMS software, the optimal values of the objective functions and decision variables are calculated for each simulated problem. As mentioned, one of the features of the proposed solution approach is to consider weights for the objective functions. By changing these weights, a set of optimal solutions can be obtained. In this vein, 10 strategies based on changing the coefficients of the objective functions were defined and the proposed model was implemented for these strategies. For this purpose, the defined strategies were implemented on three simulated problems (i.e., INC7, INC8, and INC9). The results showed that the behavior of the proposed model in the process of sensitivity analysis of the objective functions’ coefficients is in accordance with the logical expectations. On the other hand, to investigate the accuracy of the proposed multi-objective solution approach performance, the results of the proposed approach were compared with the results of an approach applied in the literature and it was shown that the proposed solution approach is effective.

7. Managerial implications

The literature review shows that many papers have been presented in the field of reverse logistics network optimization for healthcare waste management. With the emergence of the COVID-19 pandemic, researchers’ attention around the world has been directed toward this disaster, and a significant number of papers associated with COVID-19 have been presented. Healthcare waste’s scholars are at the forefront of these researchers since improper waste management caused by COVID-19 can have irreparable effects. Location of facilities, population risk, and uncertainty about the amount of waste generated are among the main concerns of the researchers in healthcare waste management, which are abundantly observed in the literature of this field. The capacity level of facilities is also another important issue that is effective in healthcare waste management, especially during the outbreak of a pandemic. Indeed, this feature of facilities can be used to make the network more flexible. In addition to these issues, epidemic disruptions are very important during the outbreak of a pandemic because any disturbed node can cause disturbance in its neighboring nodes. In this research, epidemic disruptions are investigated during the outbreak of a pandemic for the first time. For this purpose, a Monte Carlo-based simulation approach is applied to simulate the amount of waste generated at each node. After simulating the amount of generated waste, a bi-objective MILP model is formulated for healthcare waste management under uncertainty. Since the amount of generated waste is inherently uncertain, a scenario-based approach is used to deal with its uncertainty, and a fuzzy goal programming approach is employed to solve the proposed bi-objective model.

From a systematic point of view, this model can help decision-makers by acting as a decision support system (DSS) for adopting strategic and operational decisions in the field of healthcare waste management. One of the advantages of the model is that it is not designed only for pandemic conditions, but it can also be implemented in normal conditions as well. Furthermore, the proposed model is flexible and not limited to a specific geographical location. Thus, with a few changes in its structure, it can be used in other areas such as hazardous and urban waste management. This methodological approach could help supply chain managers to deal with other sources of uncertainties when designing and planning a network.

8. Conclusion

This paper formulates a bi-objective MILP model to minimize total costs and risk population for the healthcare waste management system under uncertainty. In this paper, for the first time, concepts such as epidemic disruption, capacity level, set covering, treatment technology, and population risk are used simultaneously for designing a reverse logistics network to manage both infectious and non-infectious healthcare waste. In addition, a new concept of waste infection has been considered, in which if there is a hazardous node (for example, a COVID-19 patient care center), the whole waste produced in that node will be considered as infectious. Furthermore, a new concept of population risk has been formulated in the second objective function. In this objective function, population risk is defined as a function of the amount of infectious waste, the exposed population, and the distance between the waste production node and the collection center. To consider epidemic disruption, the Monte Carlo simulation approach has been applied, through which the amount of generated waste has been simulated for different scenarios. To solve the proposed bi-objective model, a solution approach based on fuzzy goal programming has been developed. Finally, the performance of the proposed model has been evaluated using ten simulated problems in different sizes.

8.1. Limitations and future research directions

The proposed model is categorized as an NP-hard problem and cannot be solved with commercial software such as GAMS in large sizes. Therefore, it is suggested that an efficient heuristic or meta-heuristic algorithm be developed to solve the proposed model on large-scale data sets. In this paper, it is assumed that disruptions affect the amount of waste generated. But these disruptions may also disrupt the capacity of the centers. In this case, a resilient network should be designed using strategies such as cooperation with third-party logistics or by considering overtime in centers, etc. The proposed model is validated using the simulated data. It is suggested that real-world data be applied to validate and evaluate the behavior of the proposed model and solution approach in future research.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

See Fig. A.1, Fig. A.2, Fig. A.3.

Fig. A.1.

Overview of INC3 in GAMS software.

Fig. A.2.

The process of converting the multi-objective model to a single-objective one in GAMS software.

Fig. A.3.

The results obtained from running the model in GAMS software for INC3.