In silico modelling of the function of disease-related CAZymes

Abstract

In silico modelling of proteins comprises a diversity of computational tools aimed to obtain structural, electronic, and/or dynamic information about these biomolecules, capturing mechanistic details that are challenging to experimental approaches, such as elusive enzyme-substrate complexes, short-lived intermediates, and reaction transition states (TS). The present article gives the reader insight on the use of in silico modelling techniques to understand complex catalytic reaction mechanisms of carbohydrate-active enzymes (CAZymes), along with the underlying theory and concepts that are important in this field. We start by introducing the significance of carbohydrates in nature and the enzymes that process them, CAZymes, highlighting the conformational flexibility of their carbohydrate substrates. Three commonly used in silico methods (classical molecular dynamics (MD), hybrid quantum mechanics/molecular mechanics (QM/MM), and enhanced sampling techniques) are described for nonexpert readers. Finally, we provide three examples of the application of these methods to unravel the catalytic mechanisms of three disease-related CAZymes: β-galactocerebrosidase (GALC), responsible for Krabbe disease; α-mannoside β-1,6-N-acetylglucosaminyltransferase V (MGAT5), involved in cancer; and O-fucosyltransferase 1 (POFUT1), involved in several human diseases such as leukemia and the Dowling–Degos disease.

Introduction

Until the end of the 20^th century, carbohydrates were mainly related to energy storage and structural support in living organisms. It was not until a few decades ago that scientists discovered that carbohydrates are also involved in much more complex biological processes, such as modulation of protein structures, signalling in multicellular systems, and cell–cell recognition. These processes are relevant for diseases including bacterial and virus infections, cancer [1–3], Alzheimer’s [4,5], lysosomal storage diseases (LSD) [6], or disruption in the gut microbiota [7]. Nowadays, carbohydrates (commonly named ‘sugars’) are used in drug delivery strategies, vaccine development, and disease therapeutics [8–12].

Carbohydrates can exhibit many stereochemistries, configurations, and conformations (Figure 1), which makes them very complex molecules to study. The vast amount of carbohydrate-based structures in nature needs a larger number of enzymes responsible for their degradation, synthesis, and modification. This is the role of carbohydrate-active enzymes (CAZymes), which include glycoside hydrolases (GHs), glycosyltransferases (GTs), polysaccharide lyases (PLs), and carbohydrate esterases (CEs) [1]. CAZymes are involved in many and various biological processes and thus they are keystones in human health. They are not only essential to life but also have important applications in food, detergent, oil, gas, and biotechnology industries [2,13]. Understanding the function of CAZymes at atomic detail can provide information on enzyme–substrate interactions that are critical for substrate recognition and catalysis, as well as the ‘shape’ (conformation) of the substrate along the catalytic reaction. These data can inform the design of substrate analogues or inhibitors that can efficiently bind to the active site of the enzyme, being potential drug candidates.

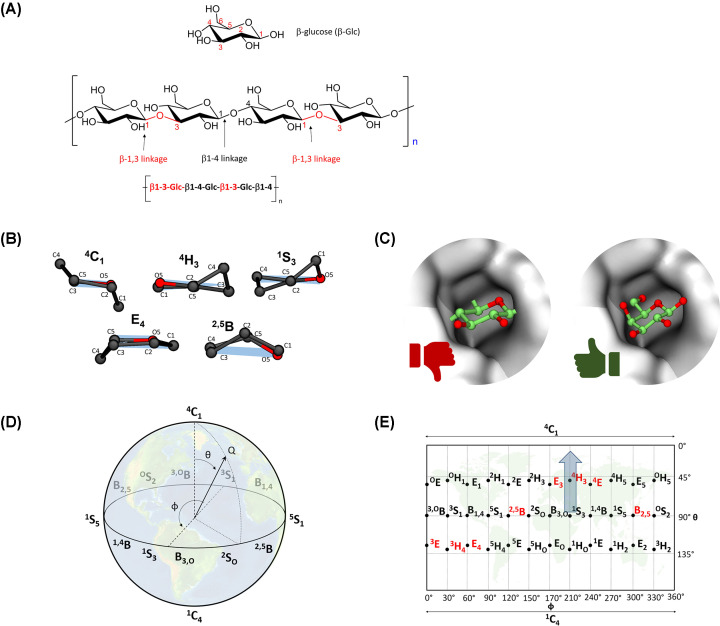
Figure 1. Diversity of sugar linkages and conformations.

(A) One of the most common β-glucans, a linear carbohydrate formed by glucose units with two types of glycosidic bond linkages, found in the cell wall of cereals, bacteria, and fungi. β-glucans can also display glycosidic linkage branching, such as β-1,6 branching in yeast and fungus. (B) The five possible types of conformations (C, H, S, E, and B) of a six-membered sugar ring. One example of each type is shown. The sugar reference plane is represented in light blue. The exocyclic groups of the sugars are not shown for clarity ( C). The active sites of CAZymes have evolved to only fit a particular type of sugar conformation. In the example, β-glucose (left) is not able to fit in the active site of a β-galactosidase, while β-galactose (right) adapts to it. ( D) The Cremer–Pople puckering sphere of pyranoses. The Earth is depicted as background to emphasise the similarity with an Earth map. (E) Mercator representation of the Cremer–Pople sphere. Conformations in which an oxocarbenium ion is stable are shown in red. The blue arrow shows one of the favoured conformational catalytic itineraries of β-glucosidases [ 14].

In the present review, we focus on the in silico modelling of CAZyme reaction mechanisms, highlighting the importance of sugar conformational changes during catalysis. We will start by describing how sugar conformations are determined and classified, and then introduce the two most abundant classes of CAZymes, GHs and GTs, along with their most common reaction mechanisms. Afterwards, we will briefly describe the basis of efficient computational methods used to uncover CAZyme reaction mechanisms, alongside a few examples of the application of these methods to unveil mechanisms of disease-related CAZymes. To make this text more understandable for the nonexperts, we provide standalone boxes to give more inside details of the concepts used in the present review.

Diversity of carbohydrate conformations

Carbohydrates can exhibit various types of linkages between their sugar units, as well as several stereochemistries (Figure 1A), leading to an enormous number of possible structures [1]. Ring conformation adds another level of complexity (Figure 1B). A six-membered sugar ring, or pyranose, can adopt 38 different ring conformations, which can be classified as chair (C), half-chair (H), skew-boat (S), envelope (E), or boat (B). These conformations are defined according to the position of their atoms with respect to a reference ring plane. When one or two atoms are placed below or above this plane, these atoms are denoted as subscripts or superscripts, respectively (e.g. ⁴C₁, ⁴H₃, etc.). From a mathematical point of view, all these conformations can be associated to points in the surface of a sphere of radius Q, the puckering sphere, defined by the sum of the perpendicular distance of all atoms to a reference ring plane. The 38 canonical conformations can be distinguished by their polar θ and φ coordinates, as introduced by Cremer and Pople in 1975 [15]. Usually, the puckering sphere (Figure 1D) is projected in two-dimensions, leading to the so-called Mercator representation, in a similar way as Earth is represented in maps (Figure 1D,E), although other representations (e.g. Stoddart reresentation) have also been used. The position and orientations of the sugar exocyclic groups in each of the 38 Cremer–Pople conformations are essential to understand the binding of sugars in the active site of CAZymes, as will be discussed below.

CAZymes

CAZymes are classified in families according to sequence similarities, and they are exquisitely curated in the CAZy database [16], which is steadily growing as genome sequencing projects increase. Complementary information about structure and catalytic mechanisms of CAZymes can also be found in CAZypedia [17]. The two most abundant types of CAZymes are GHs and GTs, which are responsible for the hydrolysis (GHs) and synthesis (GTs) of the glycosidic bond linkages between sugar units in carbohydrates.

GHs

GHs catalyse the cleavage of glycosidic bonds in carbohydrates and glycoconjugates (carbohydrates bound to other biomolecules such as lipids or protein residues). They can be classified as retaining or inverting, depending on whether or not the stereochemistry of the anomeric carbon changes during the reaction, by the similarity in their amino acid sequences (with more than 173 families to date) [16] or by the location of the scissile glycosidic bond within the carbohydrate chain. Endo-GHs cleave glycosidic bonds at the middle of the chain, whereas exo-GHs cleave the terminal ends of carbohydrates.

GTs

GTs catalyse the formation of glycosidic bonds in carbohydrates and glycoconjugates. These enzymes use activated sugars (i.e. sugars with good leaving groups such as phosphate) as glycosyl donors and transfer their glycosyl unit to an acceptor molecule (carbohydrate, lipid, or protein). Similar to GHs, they can either invert or retain the configuration of the donor anomeric carbon and are classified in families according to their amino acid sequence similarity, with 116 families to date [16]. GTs can also be classified in two groups depending on whether the donor sugar is activated by a nucleotide phosphate (Leloir GTs) or by another phosphate-substituted molecule (non-Leloir GTs) [18].

The chemistry behind CAZymes: GHs

Most GHs share a common mechanism in which two residues with a carboxylic acid side chain (Asp or Glu) assist the reaction. One of these residues acts initially as an acid (the so-called acid/base residue in retaining GHs, or catalytic acid in inverting GHs) and another one acts as a general base (inverting GHs) or as a nucleophile (retaining GHs) [19,20] (see Figure 2).

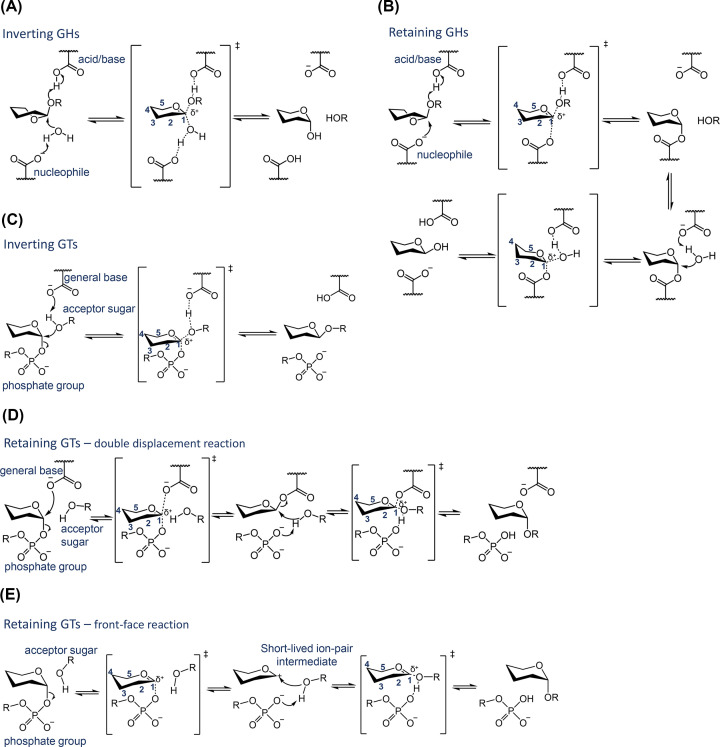
Figure 2. Main catalytic mechanisms of the two most abundant CAZymes, GHs and GTs.

Catalytic mechanisms of inverting GHs (A), retaining GHs (B), inverting GTs (C), retaining GTs operating by a double displacement reaction (D), and retaining GTs operating via a front-face type of reaction (E).

Most retaining GHs operate via two chemical steps (double displacement mechanism), each one being a S_N2-type of reaction (Figure 2B). In the first step, the general base attacks the anomeric carbon to form a covalent glycosyl-enzyme intermediate (GEI), while the acid/base residue assists the reaction by protonation of the glycosidic oxygen. The order of events and the degree of nucleophilic attack and glycosidic oxygen protonation at the TS varies from one GH to another. In the second step, a water molecule activated by the acid/base residue, which now acts as a base, attacks the anomeric carbon, leading to the products of the reaction. Inverting GHs (Figure 2A) operate by a single-displacement mechanism (one chemical step) with the participation of a nucleophilic water molecule that is deprotonated by the general base (see e.g. [21] and [22]).

Changes on sugar ring conformation along the chemical reaction

A number of structural analyses of GHs in complex with their carbohydrate substrates (Michaelis complexes, MCs) have shown that the substrate distorts upon binding to the enzyme. In particular, the reactive sugar (i.e. the one bearing the C–O bond to be hydrolysed by the enzyme) is distorted away from the ground-state ⁴C₁ conformation [21,23–25]. This change from a ‘ground state’ to a distorted – and typically higher energy – conformation promotes catalysis. In particular, the distortion orients the glycosidic bond axially and elongates it, making the sugar’s overall shape resemble that of the transition state (TS) of the reaction, thus preactivating the substrate for catalysis (Figure 2B). The specific distorted conformation that a sugar adopts depends on the particular GH family. However, computer simulations have shown that the ring conformations adopted by the substrate in the enzyme active site are the ones that exhibit certain ‘suitable’ structural, energetic, and electronic properties (long and axial C1–O bond, large anomeric charge, low energy, etc.) of the free sugars (i.e. in absence of the enzyme) [25]. In other words, GHs have evolved to use intrinsic properties of their sugar substrates for a most efficient catalysis [26].

The TS of the GHs reaction is characterised by a partial positive charge at the anomeric carbon and a partial double bond between the anomeric carbon and the ring oxygen [27–30]. These two properties are maximised when the C1, C2, O, and C5 atoms are on the same plane, i.e. the ring becomes planar around the anomeric carbon (e.g. conformation ⁴H₃ in Figure 1B). Only eight sugar conformations fulfil this condition in pyranoses, namely, ³E, ³H₄, E₄, ^2,5B, E₃, ⁴H₃, ⁴E, B_2,5 (Figure 1E). Thus, the sugar ring at the TS of glycosylation reactions needs to adopt a conformation that is close to one of these eight conformations.

The specific conformations that the reactive sugar adopts along the chemical reaction, especially those of the MC, TS, and product (P) complexes delineate the so-called catalytic conformational itinerary. This itinerary is specific for each GH family. For instance, members of family GH16, which are mostly β-glucosidases, display a ¹S₃ → [⁴H₃]^‡ → ⁴C₁ itinerary [14], whereas GH38 enzymes, which are α-mannosidases, display a ^OS₂ → [B_2,5]^‡ → ¹S₅ itinerary [31]. Identifying conformational catalytic itineraries of GHs is of great importance when designing selective inhibitors. Molecules that mimic the properties of the MC or the TS of GHs are often powerful inhibitors [32].

The chemistry behind CAZymes: GTs

GTs catalyse the synthesis of glycosidic bonds with retention or inversion of the anomeric configuration. Inverting GTs operate through a single-nucleophilic substitution reaction in which a general base assists the reaction by deprotonating the nucleophile acceptor (see Figure 2C) [17]. This mechanism is similar to that of inverting GHs (Figure 2A). In Leloir GTs, the nucleophile is a polar group of an acceptor (e.g. a hydroxyl group in the case of a sugar acceptor) and the leaving group is a phosphate group (Figure 2C). Many GTs have a divalent cation (typically Mg²⁺ or Mn²⁺) that coordinates to the nucleotide phosphates, although metal-independent enzymes have also been described [33].

The detailed mechanism of retaining GTs remains challenging, as two possible mechanisms have been proposed. A double displacement, Koshland-type mechanism was initially proposed by analogy with retaining GHs (Figure 2D). In this mechanism, an active site aspartate or glutamate plays the role of a nucleophile, reacting with the anomeric carbon of the donor sugar and forming a glycosyl−enzyme covalent intermediate. In a second step, an acceptor molecule attacks the anomeric carbon, breaking the glycosyl-enzyme covalent bond and forming a new glycosidic bond, with overall retention of stereochemistry. A similar mechanism has been recently proved by structural and mass spectrometry experiments on a GT99 [34]. There is theoretical evidence of a double-displacement mechanism for GT6 enzymes [35,36], although experimental detection of the covalent intermediate remains challenging [37,38].

The second proposed mechanism for retaining GTs involves a S_Ni-type of reaction, also termed front-face reaction [39]. In this mechanism, the nucleophile attacks from the same face of the donor sugar in which the phosphate group departs, without the direct intervention of an enzyme residue [16]. Whether the reaction is concerted or a stepwise remains controversial [40].

Sugar ring distortion is less relevant for GTs reactivity than for GHs since the phosphate leaving group is typically axially oriented, facilitating the nucleophilic displacement. However, ring distortions of the donor sugar to satisfy tight hydrogen-bond interactions have been reported [41]. For more information on GT structures and mechanisms, we recommend references [42,43].

Dissecting catalytic reaction mechanisms in CAZymes

The modelling of reaction mechanisms on CAZymes relies on the initial determination of the structure of the enzyme in complex with its substrate/s (MC complex), obtained by e.g. X-ray crystallography. The MC structure can inform in silico modelling, allowing to ‘visualise’ changes on the structure as the system evolves towards the products of the reaction at atomic and electronic detail.

Obtaining the structure of the enzyme in complex with its substrate/s

There are several methods to obtain the three-dimensional structure of a protein: NMR [44], cryo-electron microscopy [45], modelling via artificial intelligence (AlphaFold2 or RoseTTAFold) [46–48], and X-ray crystallography [49–51]. The latter has been traditionally used for the study of CAZyme mechanisms, as one can obtain a structure of the enzyme in complex with its substrate that is reliable enough to inform in silico modelling of the mechanism of action. For more information on obtaining protein structures, we refer to reference [52]. Nearly 200 000 protein structures determined using the above-mentioned methods (and more) are stored in the Protein Data Bank [53–55], but only 2363 CAZymes had at least one 3D structure in the PDB (1688 GHs and 332 GTs) when this manuscript is being written (January 2023) [16].

Ideally, an in silico study of a catalytic mechanism requires the structure of the complex between the wild-type enzyme and its natural substrate as input. Such structure is rarely available, as the reaction timescale (≈ms) is smaller than the time resolution of the experiment. However, structural biologists can use various strategies to slow down or knock-out the enzymatic reaction, being able to solve the structure of the MC. Among these strategies, the use of nonreactive analogue substrates, mutation of essential residues, and/or working at nonoptimal pH conditions have been used. These modifications perturb the system and may result in enzyme configurations that depart from the true MC (i.e. the complex of the wild-type enzyme with the natural substrate). However, the structure obtained can give essential clues to uncover the enzyme mechanism [17]. In addition, complementary techniques such as site-directed mutagenesis, spectroscopic, and in silico modelling can enormously contribute to decipher complex catalytic mechanisms [56].

In silico modelling of CAZymes reaction mechanisms

In silico approaches such as molecular dynamics (MD), based on molecular mechanics (MM) force fields, are often used to ensure that the enzyme and/or substrate modifications used in the laboratory to trap the MC have led to a catalytically competent enzyme–substrate configuration, or to transform the noncompetent crystal structures into competent ones. Once these modifications (e.g. residue mutations or substrate alterations) are reverted to the wild-type form, the MC complex is subjected to energy minimisation and thermal equilibration by MD. Afterwards, the reaction mechanism is modelled using quantum mechanics-molecular mechanics (QM/MM) approaches, which combine a QM treatment of a certain region (e.g. the enzyme-active site) with a MM treatment of the rest of the system (rest of the enzyme and solvent molecules). The basis of these approaches and the specific procedure is provided below.

Experimental and computational approaches can work in synergy to reach the final objective of deciphering how CAZymes work and, consequently, understanding how they influence health and disease in living organisms.

Specific procedure

To model CAZyme reaction mechanisms, we first focus on the MC, i.e. the enzyme in complex with the substrate, which is our ‘reactants complex.’ After building the initial model (see Box 1), we use methods based on MM (so-called ‘classical’ methods) to bring the system to a configuration that corresponds to the ensemble of structures accessible at the temperature of interest (e.g. 300 K). This procedure, called thermal equilibration, is part of the MD protocol (see Box 2). By using MD, we can also simulate how the system moves in the ns–µs timescale, capturing important protein structural rearrangements. Popular programs for performing MD of proteins are Amber [57,58], NAMD [59], Gromacs [60–62], and OpenMM [63] (Figure 3).

Box 1. Model building.

• To build a catalytically competent protein–substrate structure, we do the following:

  1. Starting from the available experimental structure, add the missing residues and/or loops. Several programs can be used, we name here just a few ones such as Modeller [64], standalone or as implemented in Chimera [65], or the web service MolProbity [66].
  2. Revert possible mutations of the structure that were needed to determine the MC structure, using e.g. VMD [67].
  3. Add the missing hydrogen atoms of the structure. MolProbity [66], PyMol [68], Chimera [65], VMD [67], pdb4amber, or tleap [57,58] are a few software examples.
  4. Inspect the protonation state of the titratable residues [69]. This can be done by visual inspection of the amino acid environment and/or using pKa predictor programs such as PropKa [70,71] and H++ [72].
  5. Solvate the protein, placing it into a water box periodically repeated in space. This can also be done with several tools included in MD packages, such as tleap [57].

Box 2. MD.

• The time propagation of the atoms in MD is obtained from the solution Newton’s equations of motion.

  $$\overrightarrow{F_l}\left(t\right)=m_i\overrightarrow{a_l}\left(t\right)\Rightarrow -\frac{\delta V\left(\overrightarrow{r}\right)}{\delta r_i}={\text{m}}_{\text{i}}\frac{{\delta }^2\overrightarrow{{\text{r}}_1}\left(\text{t}\right)}{\delta {\text{t}}^2}$$

• These equations can be solved by numerical methods, obtaining the coordinates of the system at small and consecutive time intervals, typically femtoseconds, but the simulation can be extended up to microseconds, even milliseconds. The procedure relies on a mathematical expression for the potential energy, V(r). In the so-called classical MD, the potential energy is approximated with a set of functions that describe the interactions among atoms and include predefined parameters. The resulting potential energy expression is called a force field. For an extensive review, see [73]. In the so-called ab initio MD (AIMD) [74], the potential energy is computed by QM, typically using density functional theory (DFT).

Figure 3. Types of force field parameters used to model a sugar molecule in classical MD (see [73] for the mathematical expression).

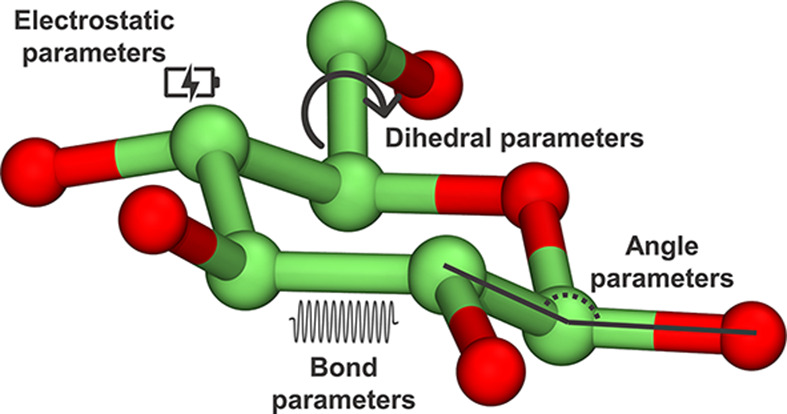
Each parameter describes interactions among pairs of atoms that are separated by one, two, or three covalent bonds (bond, angle, and dihedral parameters), or atoms that are further away in space (electrostatic and van der Waals interactions).

One limitation of classical MD is that it is unable to account for electronic rearrangements in atoms, thus preventing its use for modelling reaction mechanisms. To do that, it is necessary to include explicitly the electrons in the MD formalism, specifically in the calculation of the potential energy. This approach is named as AIMD. There are various MD methods that can do it, including Ehrenfest MD (EMD), Born-Oppenheimer MD (BOMD), or Car-Parrinello MD (CPMD) [75], based on the seminal work by Car and Parrinello [74] that enormously influenced the AIMD field. The potential energy, which is needed to propagate the equation of motion (Box 2), can be computed by wave function-based methods, such as coupled cluster of Moller–Plesset methods. However, it is still virtually impossible to do it for large systems, due to the exponentially increasing computational cost [76]. Usually, DFT [77,78], based on the calculation of the electronic density, is used (see [75] for detailed information). Two very popular computer programs to run AIMD simulations are CPMD [79] and CP2K [80]. The main drawback of AIMD is that it is restricted to around a few hundred atoms (see Figure 6), which precludes simulating most proteins. On the contrary, classical MD allows simulating large systems, but it describes them less accurately and cannot account for bond breaking/formation processes. Combining both methods, capitalising on the fact that the atoms involved in bond breaking/bond forming are in a small region of the whole biomolecule, overcomes the size limitation of AIMD. This is the basis of the QM/MM methodology, for which Karplus, Levitt, and Warshel were awarded the Nobel Prize in 2013, Box 3 (Figure 4).

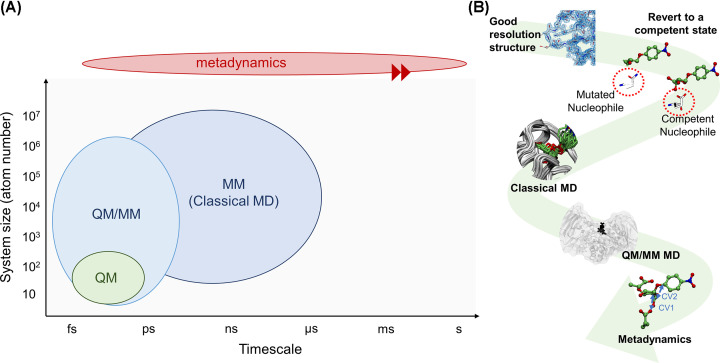
Figure 6. Schematic representations of the methodologies described in this review.

(A) Timescale vs system size representation of the methods described in this review. The accuracy and computational cost of the simulation decreases from bottom-left to top-right. Using enhanced sampling techniques such as metadynamics allows describing processes that would only be observed in long time scales, such as chemical reactions (ms-s time scale). (B) Computational protocol described in this review, from the static X-ray structure to the results of QM/MM MD and metadynamics simulations.

Box 3. QM/MM.

• The QM/MM approach is based on dividing the system in two regions. The so-called QM region comprises the group of atoms for which large electronic rearrangements are expected to take place (e.g. active site atoms). Atoms in this region are described by a QM method, e.g. DFT. The so-called MM region comprises the rest of the system, in which bonds are not expected to break or form. Atoms in the MM region are described by MM. Within a MD formalism, the method is named QM/MM MD (i.e. AIMD in the QM region and classical MD in the MM region). As a result, the whole system evolves under the Newton’s equations of motion and bonds are able to break and form in the QM region. In state-of-art QM/MM codes, the interaction between both systems is computed using the additive scheme:

  $$E=E^{QM}+E^{MM}+E^{QM/MM}$$

• in which E^QM is the energy of the QM region, E^MM is the energy of the MM region, and E^QM/MM is the interaction energy between the atoms in the QM region and the atoms of the MM region. The former are represented by an electron density, whereas the later are represented as particles with point charges and van der Waals radii. Particular care needs to be taken when there are covalent bonds at the frontier between both regions. In this case, the QM atom does not have the right number of neighbors (e.g. four for an sp3 carbon atom) to saturate the electron density, as the neighbouring MM atom is modelled by a point charge, thus it does not have electron density. Several methodologies, such that the use of dummy link atoms to saturate the border QM atoms, have been developed to describe the QM-MM boundary. For more information, we refer to the following reviews [81,82].

Figure 4. The two regions (QM and MM) involved in QM/MM calculations.

The MM region is shown in grey, the QM region is shown in black, and the interface between the two regions is shown in green.

Even though QM/MM methods can be used to describe larger enzymes with QM accuracy at the active site, chemical reactions cannot be observed in the time scale of QM/MM MD (tenths of picoseconds). This is because a sizable energy barrier, much higher than the energy available at room temperature, needs to be overcome when moving from reactants to products. In this scenario, the computational time needed to observe a transition from R to P is prohibitive [83]. Advanced methods have been developed to enhance the sampling of system configurations until the desired transition is observed. Some of these methods are based on the definition of a few degrees of freedom of the system (e.g. crucial distances or angles), named as collective variables (CVs), that describe the motion of interest with enough flexibility that reaction free energies and mechanisms can be obtained. Among these methods, steered MD, umbrella sampling, or metadynamics are commonly used [83–85]. Most of them are included in the Plumed software [86,87], which can be patched with standard MD packages. For more information, we recommend the following review [88] (Box 4).

Box 4. Enhanced sampling: metadynamics.

• Metadynamics is a MD-based method based on decreasing the probability that the system visits configurations/conformations (or compatible microstructures) that have already been visited during the MD simulation. In this way, it is easy for the system to escape from one energy minimum, such as the reactant state, to another one, such as the product state. This is achieved by adding a bias potential to the standard potential coming from the atomic/electronic system [89,90]. It can be demonstrated that in the time limit the total added biasing potential converges to the free energy change corresponding to the process of interest [91] (Figure 5).

  $$V_{bias}[t\to inf](s,t)\approx -\mathrm{\Delta }G\left(s\right)$$

• A proper choice of CVs ensures a satisfactory physical description of the process of interest, avoiding a prohibitively large computational cost to achieve full convergence [92]. In the particular case of chemical reactions, several studies have shown that appropriate CVs can be taken as combinations of distances corresponding to the bonds being broken and formed during the reaction.

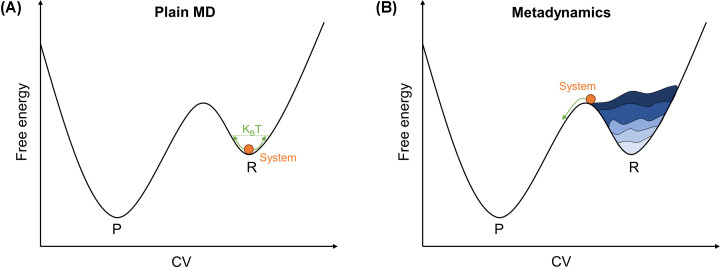
Figure 5. Comparison of the system evolution between plain (i.e. standard) MD and metadynamics.

Schematic representation of a fictitious particle in standard MD (A) and metadynamics (B). The system (orange circle) cannot escape from state R when using standard MD. In metadynamics, it can move through the ‘hills’ (in blue) that build up the bias potential, V_bias, crossing the energy barrier and sampling state P.

In summary, following equilibration of the system (enzyme MC complex) using classical MD, QM/MM MD along with an enhanced sampling technique is used to compute the reaction mechanisms, including the conformational catalytic itineraries of the substrate in GHs and GTs. We should note that these simulations require a significant computational cost; they cannot be performed in a personal desktop computer and often require access to high-performance computing (HPC) infrastructures. These centres are equipped with supercomputers (computers with more than one-hundred thousand processors, memories in the order of terabytes and disk storages in the order of petabytes) that can be accessed by academic and nonacademic groups according to specific policies from research centres, universities, governments, and other public bodies.

Examples

In silico modelling has been used to investigate a number of catalytic mechanisms of CAZymes in the last few years. We refer to past and recent reviews for a list of interesting examples [22,93–96]. Here, we focus on three disease-related CAZymes that have been recently studied.

β-galactocerebrosidase (GALC) is a retaining GH that is responsible for the cleavage of certain glycosphingolipids, i.e. sugars attached to lipid molecules. Deficiencies of GALC lead to Krabbe disease, an incurable neurodegenerative disorder caused by the accumulation of the unhydrolysed substrates (mainly β-galactocerebroside, GalCer, and psychosine) in the nervous system [97].

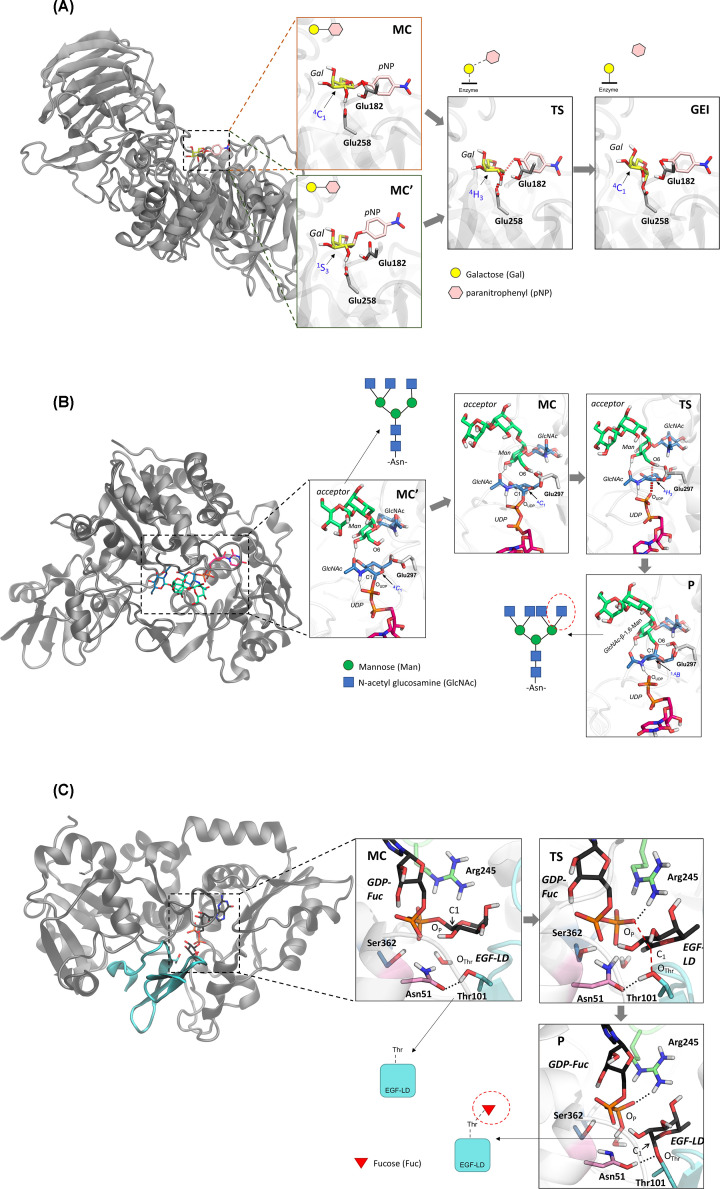
The structure of GALC in complex with a hydrolysable substrate, reported in [98], enabled the modelling of the enzyme mechanism of action for the first time. Strikingly, the reactive Gal was found in a relaxed ⁴C₁ conformation in the crystal structure. This is not a catalytically preactivated sugar conformation, as it displays the leaving group in an equatorial orientation, thus it was not clear whether the complex with the substrate in ⁴C₁ was representative of a true ‘snap-shot’ of the enzyme along the catalytic reaction. However, QM/MM metadynamics simulations by Nin-Hill and Rovira [99] showed that it is the case. Due to the solvent-exposed nature of the leaving group in exo-acting GHs, such as GALC, the glycosidic bond can be efficiently cleaved when the galactoside substrate adopts either a ⁴C₁ conformation (Figure 7A) or a distorted ¹S₃ conformation. Therefore, GALC can operate via two alternative conformational itineraries, either starting from a relaxed conformation (⁴C₁ → [⁴H₃]^‡ → ⁴C₁) or a distorted onen (¹S₃ → [⁴H₃]^‡ → ⁴C₁) [99], with the latter being slightly favoured. These specific conformations, discovered by in silico modelling, can be useful for the rational design of substrate analogues that can be used as conformational chaperones for Krabbe disease therapy.

Figure 7. Three disease-related CAZymes whose catalytic mechanisms have been recently investigated.

(A) Representative structures of the GALC catalytic mechanism, starting with the substrate in either ⁴C₁ or ¹S₃ conformation. (B) Representative structures along the MGAT5 catalytic mechanism. The image has been adapted with permission from [107], Copyright (2011), The American Chemical Society. (C) Representative structures of the POFUT1 catalytic mechanism. The epidermal growth factor-like domain (EGF-LD) containing the Thr where fucose will be attached to is depicted in cyan. The image has been adapted with permission from [41]. Copyright (2011), The American Chemical Society. The results shown were obtained by QM/MM metadynamics simulations in all cases. Hydrogen atoms attached to carbon atoms have been omitted for clarity.

Our second example focuses on α-mannoside β-1,6-N-acetylglucosaminyltransferase V (MGAT5, also GnT-V), a mammalian inverting GT involved in the formation of complex-type tetra-antennary N-glycans (carbohydrates linked to the nitrogen atom of asparagine residues in proteins). MGAT5 transfers N-acetylglucosamine (GlcNAc) from a UDP-GlcNAc glycosyl donor on to the core α-1,6 mannose (Man) of an N-glycan acceptor. The resulting branched GlcNAc-β-1,6-Man linkage is a precursor for the formation of complex tri- and tetra-antennary N-glycans, which are elaborated in the trans-Golgi by the addition of Gal-β-1,4-GlcNAc (LacNAc) disaccharides and sialic acids. Overexpression of MGAT5 strongly drives cancer [100–103], thus reducing the enzyme activity can inhibit tumour growth. To date, very few effective small-molecule inhibitors of MGAT5 have been developed [104–106] and understanding of its enzyme−substrate interactions and catalytic mechanisms is limited. The reaction mechanism of MGAT5 was recently uncovered by a combination of X-ray crystallography and QM/MM metadynamics simulations [107]. The results highlighted the key assisting role of Glu297 (the putative catalytic base) and revealed a distinct conformational itinerary for the GlcNAc ring during its transfer from donor to the acceptor (Figure 7B). This work provided a comprehensive molecular overview of MGAT5 catalysis that will guide inhibitor development efforts. In particular, it was suggested that pharmacological targeting of the MGAT5 donor subsite, using inhibitors inspired by conformational analysis, may also be effective for the development of compounds to control the activity of this GT.

Our last example concerns an inverting GT with a mechanism that departs from the classical S_N2-type of reaction. O-fucosyltransferase 1 (POFUT1) is an inverting GT involved in O-glycosylation, a protein modification essential to life. In particular, POFUT1 attaches L-fucose sugars to threonine or serine residues in certain protein sequences. POFUT1 is involved in the Notch signalling pathway (NSP), an essential cell–cell communication pathway conserved in all multicellular animals [108,109]. Malfunction of the NSP can cause several diseases in humans, from Dowling–Degos disease, to leukemia or colorectal cancer [110–112], thus POFUT1 is a relevant therapeutic target. Unlike most inverting GTs (e.g. the previous example, MGAT5), the active site of POFUT1 lacks a basic residue that can act as the catalytic base deprotonating the incoming nucleophile acceptor, thus the mechanism of action of POFUT1 remained puzzling. Using QM/MM metadynamics simulations, Piniello et al. [41] revealed that the reaction involves proton shuttling through an active site asparagine, conserved among species, which undergoes tautomerisation, i.e. it changes the side chain from amide to imidic acid form during the reaction. The enzyme retains the S_N2 mechanism of inverting GTs (Figure 1C), but an asparagine residue rather than a basic residue (Glu or Asp) deprotonates the hydroxyl group of the acceptor nucleophile. This novel mechanism, recently invoked in a related GT [113], could be found in other GTs yet to be discovered.

This short review shows that the use of state-of-art in silico approaches, such as QM/MM metadynamics, is providing unprecedented insight into enzyme catalytic mechanisms of CAZymes. We think that, in the future, this will facilitate the development of inhibitors and activity-based probes for CAZymes involved in diseases.

Summary

• CAZymes are the enzymes responsible for the processing of carbohydrates in nature. They are involved in many biological processes and thus they are keystones in human health.

• In silico modelling enables uncovering conformational catalytic itineraries and reaction mechanisms of CAZymes at atomic detail.

• We described three different examples in which in silico modelling was essential for the unravelling of complex enzymatic mechanisms.

Abbreviations

B

boat

BOMD

Born-Oppenheimer molecular dynamics

C

chair

CAZymes

carbohydrate-active enzymes

CE

carbohydrate esterase

CPMD

Car-Parrinello molecular dynamics

CV

collective variable

DFT

density functional theory

E

envelope

EMD

Ehrenfest molecular dynamics

GALC

β-galactocerebrosidase

GEI

glycosyl-enzyme intermediate

GH

glycoside hydrolase

GT

glycosyltransferase

H

half-chair

HPC

high-performance computing

LSD

lysosomal storage disease

MC

Michaelis complex

MD

molecular dynamics

MGAT5 or GnT-V

α-mannoside β-1,6-N-acetylglucosaminyltransferase V

NSP

Notch signalling pathway

PL

polysaccharide lyase

POFUT1

O-fucosyltransferase 1

QM/MM

quantum mechanics/molecular mechanics

S

skew-boat

TS

transition state

Competing Interests

The authors declare that there are no competing interests associated with the manuscript.

Funding

The authors acknowledged the Spanish Ministry of Science, Innovation and Universities [grant number MICINN/AEI/FEDER, UE, PID2020-118893GB-100]; the Spanish Structures of Excellence María de Maeztu [grant number CEX2021-001202-M]; the Agency for Management of University and Research Grants of Catalonia [grant number AGAUR, 2021-SGR-00680]; and the European Research Council [grant number ERC-2020-SyG-95123 ‘CARBOCENTRE’].

Author Contribution

C.R., A.N-H., and B.P. contributed to writing the manuscript. A.N-H. also produced the figures.