Structural credit risk model driven by Lévy process under knight uncertainty

Abstract

As per the projections of conventional credit risk structured model, the risky asset values tend to adhere to the geometric Brownian motion. On the contrary, the risky asset values remain a non-continuous and dynamic ones and jump based on the conditions. Is not possible to measure the real Knight Uncertainty risks in financial markets with the help of a single probability measure. In this background, the current research work analyzes a structural credit risk model that belongs to Levy market under Knight Uncertainty. With the help of Lévy-Laplace exponent, the authors developed a dynamic pricing model in this study and acquired the price intervals for default probability, stock value and the bond value of enterprise. To be specific, the study intended to establish explicit solutions for three value processes, discussed earlier, with an assumption that the jump process follows a log-normal distribution. At the end, the study also conducted numerical analysis to understand the crucial role played by Knight Uncertainty upon the pricing of default probability and the stock value of the enterprise.

Introduction

In the aftermath of sub-prime mortgage crisis that occurred in the year 2008, there has been increased attention paid upon the credit risk factors across the globe. Credit risk can be loosely defined as the possibilities in which either the lender or the borrower may end up in breaching the contract. Three investment banks such as the Bear Stearns, Lehman Brothers and Merrill Lynch went bankrupt due to the impact of global credit storm. It further degraded the credit ratings of a few countries such as Portugal, Italy, Ireland, Greece and Spain below Baa. Due to this unprecedented financial crisis that brought huge economic burden, the credit risk management tools have become essential from the initial stages itself. This phenomenon created the need for the development of a dynamic, reasonable and vibrant credit risk management model that includes precise and efficient numerical algorithms for financial forecasting.

A structured credit risk model was proposed in the study conducted by Merton (1974) upon asset pricing in line with the popular Black and Scholes (1973) (B–S) option pricing formula. This model triggered a series of concerns in both academic research and market finance. Currently, this model has been widely applied in credit risk management domain and has evolved into a huge model system. In practice, this structured model acts as the basis for KMV model, followed by Moody’s, while the latter is the most sought-after credit risk management model in this financial domain. In this structured credit risk model, a company’s asset values are continuously subjected to geometric Brownian motion while the model quotes only the continuous changes that occur in the asset values of a company. Interestingly, the model does not take abnormal events that may change the asset’s values into consideration, for instance, Brexit vote, COVID-19 pandemic etc., The Merton model has been explored and expanded in detail by various researchers, into jump process. The first research study to make use of pure jump to detail the values of corporate assets was conducted by Mason and Bhattacharya (1981). In the Hilberink and Rogers’s model proposed by the researchers (Hilberink & Rogers, 2002), Lévy process was introduced in the structured model since the direction of the jump occurs only from top to bottom. This phenomenon was revolutionized in the study conducted by Scherer (2005) who optimized the model so that the corporate asset values jump not only from top to bottom, but also in the opposite direction i.e., bottom to top. Xiong (2005) proposed the option pricing model in which the Lévy jump-diffusion process is followed to drive the underlying stocks. Based on this model, Xue and Wang (2008) detailed about a structural credit risk model based on Lévy process. The researchers further derived the formulae for bond price, credit spread and default probability. A reduced credit risk model was developed by Lin (2018) through the deployment of martingale method and Laplace transform techniques. The author determined both conditional as well as unconditional survival probabilities.

Liu (2020) developed a hybrid jump-diffusion KMV-logit model in which the author integrated the jump-diffusion KMV model and logit model. This conventional logit model was further supplemented with default distance in the form of an explanatory variable so as to develop the proposed model. This study established the model’s remarkable performance in terms of identifying the actual defaulters. On the basis of a hybrid exponential jump-diffusion model, Shi (2021) introduced a stochastic interest rate risk and the model was found to fit majority of the features that are usually encountered in the market.

Knight, a famous economist from the US, mentioned in 1921 that it is not possible to measure the financial markets using a single probability measure since the former is filled with unprecedented risks. This statement is otherwise called as Knight uncertainty risk (Knight, 1921). Ellsberg (1961) proposed a paradox named Ellsberg paradox in which he added that a single probability measure does not possess the potential to explain the existence of numerous choice behaviors in financial markets. Knight Uncertainty phenomenon has been explored by various scholars in different perspectives. The Backward Stochastic Differential Equations (BSDE) theory was first proposed by Chen and Larry Epstein (2002) to incorporate a mathematical model that mimics the knight uncertainty risks. The authors further investigated about the continuous time optimal consumption and portfolio models. Considering this work as a basis, Huang et al. (2016) investigated the deposit insurance pricing phenomenon under Knight uncertainty. The authors concluded that the role played by Knight uncertain risk in determining the premium of the bank of China was phenomenal. This occurred specifically, when the uncertainty parameter got increased during when there was an increase observed in the length of the insurance rate interval of every bank. In another study (Huang & Wang, 2017), the authors focused on the option pricing model under Knight Uncertainty that is gauged by Levy process. The study further deployed the upper and lower bounds’ model for the European option. In the study conducted by Liu et al. (2020), the authors expanded the hedge fund compensation price up to Knightian uncertainty market. The study arrived at the conclusion that when the Knight uncertainty value increases, then it erodes the values of both, the fees as well as the claim.

Based on the review of literature conducted above, it can be understood that the discussions made the scholars regarding credit risk problem, gauged by Levy process, often excluded the influence exerted by Knight Uncertainty. On the other hand, whenever the credit risk issue is investigated under the influence of Knight uncertain environment, no discussion takes place regarding the role played by actual jump of the underlying asset. In this background, the current research paper is motivated at detailing the structural corporate credit risk model, gauged by Levy process, under Knight uncertainty financial market. With the introduction of a viable control set for the purpose of characterizing the Knight Uncertainty in the financial market, the current study authors leverage Lévy-Laplace transform. This is performed to incorporate the dynamic pricing models for bond value, stock value and corporate default probability and obtain their pricing intervals accordingly. Simultaneously, the study also deals with the credit risk issue that occurs as a result of pure jump Lévy process. In this study, the dynamic pricing models’ explicit outcomes were attained, assuming that the jump variable is log-normally distributed. At the end, the authors used the numerical analysis technique to portray the crucial influence exerted by the Knight uncertain factor and the jump intensity upon the pricing intervals of bond value, stock value and the default probability.

The rest of the research article is constructed as briefed herewith. Section 2 provides an overview of the levy financial market under knight uncertainty along with a few features of the Levy process. In Sect. 3, the authors attained the pricing intervals for bond value, stock value and corporate default probability with the incorporation of dynamic pricing model. Section 4 analyzes the crucial influence exerted by both jump intensity as well as knight uncertain parameter upon the pricing intervals of these values. Section 5 concludes the research paper.

Lévy financial market under knight uncertainty

Let $\left(\mathrm{\Omega },F_t,P\right)$ be completely a continuous time trading economy with infinite horizon which satisfies the usual conditions. The information evolves according to the augmented filtration ${\left\{F_t\right\}}_{0\le t\le T}$ generated by a standard Brownian motion ${\left\{B_t\right\}}_{0\le t\le T}$ and an independent Lévy process ${\left\{X_t\right\}}_{0\le t\le T}$. And the Lévy process ${\left\{X_t\right\}}_{0\le t\le T}$ satisfies the following properties:

• (i)$X_0=0$ almost surely;
• (ii)${\left\{X_t\right\}}_{0\le t\le T}$ has independent stationary increments and is centered in its origin;
• (iii)The Laplace transform of ${\left\{X_t\right\}}_{0\le t\le T}$ is bounded. There exit $\tau >0$ and ${\omega }_2>0$ so that for every ${\omega }_1\in \left(\left(-\infty ,{\omega }_2\right]\right)$ $t\in \left[0,\tau \right]$, the Laplace transform $\omega \to E\left(e^{\omega X_t}\right)$ is bounded by two strictly positive constant over $\omega \in \left[{\omega }_1,{\omega }_2\right]$. There exist $M_1>0$ and

$M_2>0$ for every $\omega \in \left[{\omega }_1,{\omega }_2\right]$ and $t\in \left[0,\tau \right]$, it holds that $M_1\le E\left(e^{\omega X_t}\right)\le M_2.$

We also need the follow Lévy-Laplace exponent of $X_t$,

Lemma 1

(Applebaum 2009). There exists a function $\varphi :\left(-\infty ,\right)\left({\omega }_2\right]$ defined as for every $t\in R^{+}$ and $\omega \in \left(-\infty ,\left({\omega }_2\right]\right)$ satisfies

$$E\left[e^{\omega X_t}\right]=e^{\varphi (\omega )t},$$ 1

this function $\varphi :\left(-\infty ,\right)\left({\omega }_2\right]$ is called Lévy-Laplace exponent of $X_t$.

We assume that the enterprise value process is described by a geometric Brownian motion times the exponential of a Lévy process with no Brownian motion part. This leads to the following $V_t$:

$$V_t=V_{0}exp\left\{{\int }_0^t\left[{\mu }_s-\frac{{\sigma }_s^2}{2}\right]ds+{\int }_0^t{\sigma }_{s}d{B}_s+X_t\right\},t\in [0,T].$$ 2

where ${\mu }_s,{\sigma }_s$ are the expected return and volatility of the value of $V_t$ respectively, and assume they are integrable functions in $\left[0,T\right]\to R,$ and ${\sigma }_t>0$ for all $t\in [0,T].$

In theory, no arbitrage in the financial market means that the discounted asset is a martingale under the natural probability measure $P$, that is

$$E\left[exp\left\{-{\int }_0^t{r}_{s}ds\right\}{V}_t\right]=V_{0}a.s.,$$ 3

here $r_s$ is the zero-coupon interest rate. Bring $V_t$ into (3) we can get the following equations

$$\begin{array}{c}E\left[exp\left\{-{\int }_0^t{r}_{s}ds\right\}{V}_t\right]\\ =E\left[exp\left\{-{\int }_0^t{r}_{s}ds\right\}{V}_{0}exp\left\{{\int }_0^t\left[{\mu }_s-\frac{{\sigma }_s^2}{2}\right]ds+{\int }_0^t{\sigma }_{s}d{B}_t+X_t\right\}\right]\\ =V_{0}exp\left\{{\int }_0^t\left({\mu }_s-r_s\right)ds-{\int }_0^t\frac{1}{2}{\sigma }_s^{2}ds\right\}E\left[exp\left\{{\int }_0^t{\sigma }_{s}d{B}_s\right\}\right]E\left[exp\left\{X_t\right\}\right],\\ \end{array}$$

since ${\left\{B_s\right\}}_{0<t<T}$ is a standard Brownian motion under probability measure $P$_, and Lévy-Laplace exponent of $X_t$, the following two equations hold

$$E\left[exp\left\{{\int }_0^t{\sigma }_{s}d{B}_s\right\}\right]={\int }_0^t\frac{1}{2}{\sigma }_s^{2}ds,E\left[exp\left\{X_t\right\}\right]\text{= exp}\left\{\varphi (1)t\right\}.$$

Then

$$E\left[exp\left\{-{\int }_0^t{r}_{s}ds\right\}{V}_t\right]=V_{0}exp\left\{{\int }_0^t\left({\mu }_s-r_s\right)ds+\varphi (1)t\right\},$$

therefore we can get the no-arbitrage constraint in this financial market is

$${\int }_0^t{\mu }_{s}ds={\int }_0^t{r}_{s}ds-\varphi (1)t,t\in [0,T]$$ 4

In order to describe the risk of Knight uncertainty in financial markets, Knight (1921) introduced the following set $\mathrm{\Theta }$ called K-ignorance,

$$\mathrm{\Theta }=\left\{{({\theta }_t)}_{0\le t\le T},|{\theta }_t|\le ka.s.t\in [0,T]\right\},$$ 5

where $k>0$ is a constant. And ${\theta }_t$ reflects the amount of market information that financial investors can capture at time $t$. Namely there is a family of equivalent probability measurement spaces $\left(\mathrm{\Omega },F_t,P^{\theta }\right)$ with $\theta \in \mathrm{\Theta }$ in the financial market. ${\theta }_t=0$ indicates an rational investor, and the probability measurement spaces is $\left(\mathrm{\Omega },F_t,P\right)$ mentioned above.${\theta }_t>0$ indicates an pessimistic investors, the bigger the ${\theta }_t$, the stronger the pessimism;${\theta }_t<0$ indicates an optimistic investor, the smaller the ${\theta }_t$, the stronger the optimism.

Assume that the enterprise value process under Knight uncertainty

$$V_t=V_{0}exp\left\{{\int }_0^t\left[{\mu }_s-\frac{{\sigma }_s^2}{2}-{\sigma }_s{\theta }_s\right]ds+{\int }_0^t{\sigma }_{s}d{B}_s^{\theta }+X_t\right\},t\in [0,T].$$ 6

Structural credit risk model

Default probability

Let us denoted ${\left\{N_t\right\}}_{0\le t\le T}$ is a Poisson process of intensity $\lambda$ and a sequence of independent variable independent identically distributed ${\left\{U_i\right\}}_{i\in N^{+}}$ satisfied

$$\begin{array}{c}(i)U_0=1,U_i\in \left(-1,+\infty \right);\\ (ii)\forall u\in (-\infty ,1),E\left[{(1+U)}^u\right]<\infty .\\ \end{array}$$

Assume the standard Brownian motion ${\left\{B_t\right\}}_{0\le t\le T}$, Poisson process ${\left\{N_t\right\}}_{0\le t\le T}$ and ${\left\{U_i\right\}}_{i\in N^{+}}$ are independent and the filtration ${\left\{F_t\right\}}_{0\le t\le T}$ in this market is spanned by the three stochastic processes. In this framework, the enterprise asset value process (3) can be modeled as a risky asset with some stochastic jumps of stochastic intensity ${\left\{U_i\right\}}_{i\in N^{+}}$ which occur according to the Poisson process ${\left\{N_t\right\}}_{0\le t\le T}$. Between two jumps, the enterprise asset value process can be modeled by the standard Brownian motion ${\left\{B_t\right\}}_{0\le t\le T}$ as follows

$$V_t^{\theta }=V_{0}exp\left\{{\int }_0^t\left[{\mu }_s-{\sigma }_s{\theta }_s-\frac{{\sigma }_s^2}{2}\right]ds+{\int }_0^t{\sigma }_{s}d{B}_s^{\theta }\right\}\prod _{i=1}^{N_t}(1+U_i),t\in [0,T],\theta \in \mathrm{\Theta }.$$ 7

here $X_t=ln\left(\prod _{i=1}^{N_t}(1+U_i)\right)$ is a pure jump Lévy process, and define $\prod _{i=1}^0(1+U_i)=1$ means there is no jump in this market.

In order to get the Lévy-Laplace exponent of pure jump Lévy process $X_t$, we need the following proposition of Poisson process.

$$\begin{array}{cc}\hfill E\left[e^{X_t}\right]=& E\left[\underset{i=1}{\overset{N_t}{\mathrm{\Pi }}}(1+U_i)\right]\hfill \\ \hfill =& \sum _{n=0}^{\infty }E\left(\underset{i=1}{\overset{N_t=n}{\mathrm{\Pi }}}(1+U_i)\left|N_t=n\right)\right)P(N_t=n)\hfill \\ \hfill =& \sum _{n=0}^{\infty }{\left(E(1+U_1)\right)}^n\frac{e^{-\lambda t}{(\lambda t)}^n}{n!}\hfill \\ \hfill =& exp\left\{\lambda tE\left(U_1\right)\right\}\hfill \\ \hfill \end{array}$$

that is $\varphi (1)=\lambda E\left(U_1\right)$, then we get the concrete expression of the no-arbitrage constraint in this section:

${\int }_0^t{\mu }_{s}ds={\int }_0^t{r}_{s}ds-\lambda E\left(U_1\right)t,t\in [0,T]$.

Under the risk-neutral measure, enterprise value process

$$V_t^{\theta }=V_0\prod _{i=1}^{N_t}(1+U_i)exp\left\{{\int }_0^t\left[r_s-{\sigma }_s{\theta }_s-\frac{{\sigma }_s^2}{2}\right]ds-\lambda E\left(U_1\right)t+{\int }_0^t{\sigma }_{s}d{B}_s^{\theta }\right\},$$ 8

Let $E(t,V_t,T)$ and $D(t,V_t,T)$ be the value of the stock and bonds issued by the enterprise at time $t$, $T$ is the maturity date of the enterprise bonds. Assume that the enterprise's default time can only be the bond maturity date $T.$ Concretely, at the maturity date $T$, if $V_T<L$, the enterprise will default, and enterprise bond holders can only receive amount of wealth as $V_T$; if $V_T>L$, the enterprise will not default, enterprise bond holders will receive amount of wealth as $L.$ Here $L$ is the par value of enterprise bonds.

Theorem 1

Assume enterprise asset value process is described by (6), the enterprise's default probability under Knight uncertainty is.

$$p^{\theta }=P^{\theta }\left\{V_T^{\theta }<L\right\}=\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}N(-d_n^{\theta }),\theta \in \mathrm{\Theta }.$$ 9

where $N(·)$ is a standard normal distribution and

$$d_n^{\theta }=\frac{ln\frac{V_0}{L}+ln\left[\prod _{i=1}^n(1+U_i)\right]-\lambda TE(U_1)+{\int }_0^T\left[r_s-{\sigma }_s{\theta }_s-\frac{{\sigma }_s^2}{2}\right]ds}{\sqrt{{\int }_0^T{\sigma }_s^{2}ds}}.$$ 10

and the default probability interval is $[p^{-k},p^k],(k>0).$

Proof

According to the definition of enterprise default probability and enterprise value process (7), we can get.

$$\begin{array}{c}{P}^{\theta }\left\{V^{\theta }(T)<L\right\}\\ =P^{\theta }\left\{V_0\prod _{i=1}^{N_T}(1+U_i)exp\left\{{\int }_0^T\left[r_s-{\sigma }_s{\theta }_s-\frac{{\sigma }_s^2}{2}\right]ds-\lambda E\left(U_1\right)T+{\int }_0^T{\sigma }_{s}d{B}_s^{\theta }\right\}<L\right\}\\ =P^{\theta }\left\{\frac{{\int }_0^T{\sigma }_{s}d{B}_s^{\theta }}{\sqrt{{\int }_0^T{\sigma }_s^{2}ds}}<-d_n^{\theta }\right\},\\ \end{array}$$

For writing convenience, set

$$A=\left\{\frac{{\int }_0^T\sigma (s)d{B}^{\theta }(s)}{\sqrt{{\int }_0^T{\sigma }^2(s)ds}}<-d_n^{\theta }\right\},$$

then

$$\begin{array}{c}P=P^{\theta }\left\{V^{\theta }(T)<L\right\}=E^{\theta }\left[I_A\right]\\ =E^{\theta }\left[E^{\theta }\left(\left(I_A\right|N_T\right)\right]\\ =\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}{E}^{\theta }\left[I_A\left|N_T=n\right)\right]\\ =\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}{P}^{\theta }\left[A\left|N_T=n\right)\right]\\ =\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}{P}^{\theta }\left\{\frac{{\int }_0^T\sigma (s)d{B}^{\theta }(s)}{\sqrt{{\int }_0^T{\sigma }^2(s)ds}}<-d_n^{\theta }\right\}.\\ \end{array}$$

Since ${\int }_0^T\sigma (s)d{B}^{\theta }(s)$ is an standard normal distribution with mean $0$ and variance ${\int }_0^T{\sigma }^2(s)ds$ under probability measure $P^{\theta }$, then

$$p^{\theta }=\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}N(-d_n^{\theta }).$$

Easy to verify by the definition of set Knight uncertainty $\mathrm{\Theta }$, the default probability interval is $[p^{-k},p^k],(k>0).$

The conclusion in Ref Lin (2018), is the special case when $\theta =0$ here.

Enterprise bond value and stock value

In Sect. 3, we have analyzed that at time $i\in N^{+}$ if $V_T<L$, the enterprise will default, and enterprise bond value $D(V_T)$ will be $V_T,$ and stock value $E(V_T)$ will be $0$, due to the priority claim of bond. Contrarily, if $V_T>L$, the enterprise will not default, then enterprise bond value $D(V_T)$ will be $L$ and stock value $E(V_T)$ will be $V_T-L.$ That is,

$$E(V_T)=max\left\{V_T-L,0\right\};$$ 11

$$D(V_T)=L-max\left\{L-V_T,0\right\}.$$ 12

It means that stock value is a call option of the enterprise asset value. Enterprise bond value is equivalent to such a portfolio: buy a risk-free bond with a par value of $L$ and a maturity date of $T$, and sell a put option with an execution price of $L$ and a maturity date of $T$ for the assets of the enterprise at the same time. According to Black–Scholes formula (Black & Scholes, 1973) and martingale measure transformation, we get the following theorem 2 about the value of enterprise stock and enterprise bond.

Theorem 2

Assume enterprise asset value process is described by (6), the value of enterprise stock and enterprise bond under Knight uncertainty are

$$\begin{array}{cc}& E^{\theta }\left(0,V_0,T\right)=\sum _{n=1}^{\infty }{\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}E}^{\theta }\hfill \\ \hfill & \left[V_{0}exp\left\{-\lambda E\left(U_1\right)T-{\int }_0^T{\sigma }_s{\theta }_{s}ds\right\}\prod _{i=1}^{N_t}(1+U_i)N(d_{{}_{2,n}}^{\theta })-Lexp\left\{-{\int }_0^T{r}_{s}ds\right\}N(d_{1,n}^{\theta })\right],\hfill \end{array}$$ 13

$$D^{\theta }\left(0,V_0,T\right)={\text{V}}_0-E^{\theta }\left(0,V_0,T\right),$$ 14

where $N(·)$ is a standard normal distribution and

$$d_{1,n}^{\theta }=d_n^{\theta }=\frac{ln\frac{V_0}{L}+ln\left[\prod _{i=1}^n(1+U_i)\right]-\lambda TE(U_1)+{\int }_0^T\left[r_s-{\sigma }_s{\theta }_s-\frac{{\sigma }_s^2}{2}\right]ds}{\sqrt{{\int }_0^T{\sigma }_s^{2}ds}},$$ 15

$$d_{{}_{2,n}}^{\theta }=d_{1,n}^{\theta }+\sqrt{{\int }_0^T{\sigma }_s^{2}ds},$$ 16

and the enterprise stock value interval is $\left[E^k\left(0,V_0,T\right),E^{-k}\left(0,V_0,T\right)\right],(k>0),$ the enterprise bond value interval is $\left[D^{-k}\left(0,V_0,T\right),D^k\left(0,V_0,T\right)\right],(k>0).$

Proof

According to Black–Scholes formula (Black & Scholes, 1973) of call option

$$\begin{array}{cc}\hfill E^{\theta }\left(0,V_0,T\right)=& E^{\theta }\left[exp\left\{-{\int }_0^T{r}_{s}ds\right\}{\left(V_T^{\theta }-L\right)}^{+}\right]\hfill \\ \hfill =& E^{\theta }\left[exp,\left\{-,{\int }_0^T,r_{s}ds\right\},\left(V_0,\prod _{i=1}^{N_t},(1+U_i),exp,\left\{{\int }_0^T,\left[r_s,-,{\sigma }_s,{\theta }_s,-,\frac{{\sigma }_s^2}{2}\right],d,s\right)\right)\right)\hfill \\ \hfill & -\left({\left(\left(\lambda ,E,\left(U_1\right),T,+,{\int }_0^T,{\sigma }_s,d,B_s^{\theta }\right\},-,K\right)}^{+}\right]\hfill \\ \hfill =& \sum _{n=1}^{\infty }{\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}E}^{\theta }\left[V_0,exp,\left\{-,\lambda ,E,\left(U_1\right),T,-,{\int }_0^T,{\sigma }_s{\theta }_s,d,s\right\}\right)\hfill \\ \hfill & \left(\times ,\prod _{i=1}^{N_t},(1+U_i),N,(d_{{}_{2,n}}^{\theta }),-,L,exp,\left\{-{\int }_0^T{r}_{s}ds\right\},N,(d_{1,n}^{\theta })\right],\hfill \\ \hfill \end{array}$$

where

$$d_{1,n}^{\theta }=d_n^{\theta },d_{{}_{2,n}}^{\theta }=d_{1,n}^{\theta }+\sqrt{{\int }_0^T{\sigma }_s^{2}ds},$$

and the value interval of enterprise stock is $\left[E^k\left(0,V_0,T\right),E^{-k}\left(0,V_0,T\right)\right],(k>0).$

According to Black–Scholes formula (Black & Scholes, 1973) of put option

$$\begin{array}{cc}\hfill D^{\theta }\left(0,V_0,T\right)=& E^{\theta }\left[exp\left\{-{\int }_0^T{r}_{s}ds\right\}D(V_T^{\theta })\right]\hfill \\ \hfill =& exp\left\{-{\int }_0^T{r}_{s}ds\right\}{E}^{\theta }\left[L-max\left\{L-V_T,0\right\}\right]\hfill \\ \hfill =& Lexp\left\{-{\int }_0^T{r}_{s}ds\right\}-E^{\theta }\left[exp\left\{-{\int }_0^T{r}_{s}ds\right\}{\left(L-V_{{}_T}^{\theta }\right)}^{+}\right]\hfill \\ \hfill =& V_0-\sum _{n=1}^{\infty }{\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}E}^{\theta }\left[V_0,exp,\left\{-\lambda E\left(U_1\right)T-{\int }_0^T{\sigma }_s{\theta }_{s}ds\right\}\right)\hfill \\ \hfill & \times \left(\prod _{i=1}^{N_t},(1+U_i),N,(d_{{}_{2,n}}^{\theta }),-,L,exp,\left\{-{\int }_0^T{r}_{s}ds\right\},N,(d_{1,n}^{\theta })\right]\hfill \\ \hfill \end{array}$$

and the value interval is $\left[D^{-k}\left(0,V_0,T\right),D^k\left(0,V_0,T\right)\right],(k>0).$

For detailed certification of option pricing, please refer to Xue and Wang (2008).

Particular case

Furthermore, for any $i\in N^{+}$, we assume the jump process $(1+U_i)$ follows a log-normal distribution with mean and $\overline{\mu }$ volatility ${\overline{\sigma }}^2$, then the expectation of $U_1$ is

$$E(U_1)=exp\{\overline{\mu }+\frac{{\overline{\sigma }}^2}{2}\}-1.$$ 17

Their product $\prod _{i=1}^n(1+U_i)$ follows a log-normal distribution with mean and $n\overline{\mu }$ volatility $n{\overline{\sigma }}^2$ as $(1+U_i)$ are independently distributed. $Y=\left(\prod _{i=1}^n(1+U_i)-n\overline{\mu }\right)/\sqrt{n}\overline{\sigma }$ follows a standard normal distribution $(Y\sim N(0,1))$, then

$$\prod _{i=1}^n(1+U_i)=exp\left\{n\overline{\mu }+\sqrt{n}\overline{\sigma }Y\right\}.$$ 18

We also need the following important property of a centered normalized normal distribution $Y\sim N(0,1)$, for every $a_1,a_2,a_3\in R,$

$$E\left(exp\{a_{1}Y\}N(a_{2}Y+a_3)\right)=exp\left\{\frac{a_1^2}{2}\right\}N\left(\frac{a_1{a}_2+a_3}{\sqrt{1+a_2^2}}\right).$$ 19

Under this framework, assume the expected return $\mu$ and volatility ${\sigma }^2$ of enterprise value are constants.

Theorem 3

Under the assumption of the jump process $(1+U_i)$ follows a lognormal distribution with mean and $\overline{\mu }$ volatility ${\overline{\sigma }}^2$, the value of enterprise stock (13), enterprise bond (14) and default probability (9) under Knight uncertainty have the following expressions.

$$\begin{array}{cc}& E^{\theta }\left(0,V_0,T\right)=\sum _{n=1}^{\infty }\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}\hfill \\ \hfill & \left[V_{0}exp\left\{n\overline{\mu }+\frac{n{\overline{\sigma }}^2}{2}-\lambda TE\left(U_1\right)-{\int }_0^T\sigma {\theta }_{s}ds\right\}N\left({\overline{d}}_{{}_{2,n}}^{\theta }\right)-L{\text{e}}^{-rT}N\left({\overline{d}}_{{}_{1,n}}^{\theta }\right)\right],\hfill \end{array}$$ 20

$$D^{\theta }\left(0,V_0,T\right)={\text{V}}_0-E^{\theta }\left(0,V_0,T\right),$$ 21

$$p^{\theta }=P^{\theta }\left\{V_T^{\theta }<L\right\}=\sum _{n=1}^{+\infty }\frac{{(\lambda T)}^n{e}^{-\lambda T}}{n!}N(-{\overline{d}}_n^{\theta }),\theta \in \mathrm{\Theta }.$$ 22

where $N(·)$ is a standard normal distribution, and

$$E(U_1)=exp\left\{\overline{\mu }+\frac{{\overline{\sigma }}^2}{2}\right\}-1,$$

$${\overline{d}}_{1,n}^{\theta }={\overline{d}}_n^{\theta }=\frac{ln\frac{V_0}{L}+n\overline{\mu }+\left(r-\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}},{\overline{d}}_{2,n}^{\theta }={\overline{d}}_{1,n}^{\theta }+\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}.$$

Proof

Since $ln(1+U_i)\sim N(\overline{\mu },{\overline{\sigma }}^2)$ and formula (18) holds, the value of enterprise stock (13) can be rewritten as follows.

$E^{\theta }\left(0,V_0,T\right)=\sum _{n=1}^{\infty }\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}{E}^{\theta }\left[V_0,exp,\left\{-\lambda TE\left(U_1\right)-{\int }_0^T\sigma {\theta }_{s}ds\right\}\right)$ $\left(exp,\left\{n\overline{\mu }+\sqrt{n}\overline{\sigma }Y\right\},N,(d_{{}_{2,n}}^{\theta }),-,L,{\text{e}}^{-rT},N,(d_{1,n}^{\theta })\right]$ Set

$$A=E^{\theta }\left[exp\left\{n\overline{\mu }+\sqrt{n}\overline{\sigma }Y\right\}N(d_{{}_{2,n}}^{\theta })\right],B=E^{\theta }\left[L{\text{e}}^{-rT}N(d_{1,n}^{\theta })\right],$$

then

$$\begin{array}{cc}\hfill A=& e^{n\overline{\mu }}·E^{\theta }\left[exp\left\{\sqrt{n}\overline{\sigma }Y\right\}N\left(\frac{\sqrt{n}\overline{\sigma }}{\sigma \sqrt{T}}Y+\frac{ln\frac{V_0}{L}+n\overline{\mu }+\left(r+\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sigma \sqrt{T}}\right)\right]\hfill \\ \hfill =& e^{n\overline{\mu }}·exp\left\{\frac{n{\overline{\sigma }}^2}{2}\right\}N\left(\frac{n{\overline{\sigma }}^2+ln\frac{V_0}{L}+n\overline{\mu }+\left(r+\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sigma \sqrt{T}·\sqrt{1+\frac{n{\overline{\sigma }}^2}{{\sigma }^{2}T}}}\right)\hfill \\ \hfill =& exp\left\{n\overline{\mu }+\frac{n{\overline{\sigma }}^2}{2}\right\}N\left(\frac{ln\frac{V_0}{L}+n\overline{\mu }+n{\overline{\sigma }}^2+\left(r+\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}}\right)\hfill \\ \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill B=& L{\text{e}}^{-rT}{E}^{\theta }\left[N\left(\frac{\sqrt{n}\overline{\sigma }}{\sigma \sqrt{T}}Y+\frac{ln\frac{V_0}{L}+n\overline{\mu }+\left(r-\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sigma \sqrt{T}}\right)\right]\hfill \\ \hfill =& L{\text{e}}^{-rT}N\left(\frac{ln\frac{V_0}{L}+n\overline{\mu }+\left(r-\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}}\right)\hfill \\ \hfill \end{array}$$

Set

$${\overline{d}}_{1,n}^{\theta }=\frac{ln\frac{V_0}{L}+n\overline{\mu }+\left(r-\frac{{\sigma }^2}{2}-\lambda E(U_1)\right)T-{\int }_0^T\sigma {\theta }_{s}ds}{\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}},{\overline{d}}_{2,n}^{\theta }={\overline{d}}_{1,n}^{\theta }+\sqrt{{\sigma }^{2}T+n{\overline{\sigma }}^2}.$$

From the above analysis, we can get

$$\begin{array}{cc}\hfill E^{\theta }\left(0,V_0,T\right)=& \sum _{n=1}^{\infty }{\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}E}^{\theta }\left[V_0,exp\{-\lambda TE,\left(U_1\right)\right)\hfill \\ \hfill & -\left({\int }_0^T,\sigma {\theta }_{s}ds,\}exp,\left\{n\overline{\mu }+\sqrt{n}\overline{\sigma }Y\right\},N,(d_{{}_{2,n}}^{\theta }),-,L,{\text{e}}^{-rT},N,(d_{1,n}^{\theta })\right]\hfill \\ \hfill =& \sum _{n=1}^{\infty }\frac{e^{-\lambda T}{(\lambda T)}^n}{n!}\left[V_0,exp\{-\lambda TE,\left(U_1\right)\right)\hfill \\ \hfill & -\left({\int }_0^T,\sigma {\theta }_{s}ds,\}exp,\left\{n\overline{\mu }+\frac{n{\overline{\sigma }}^2}{2}\right\},N,\left({\overline{d}}_{{}_{2,n}}^{\theta }\right),-,L,{\text{e}}^{-rT},N,\left({\overline{d}}_{{}_{1,n}}^{\theta }\right)\right].\hfill \\ \hfill \end{array}$$

The same method can be used to prove (21) and (22).

Example analysis

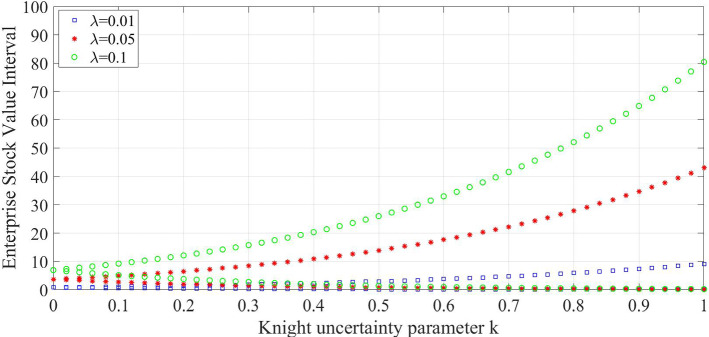
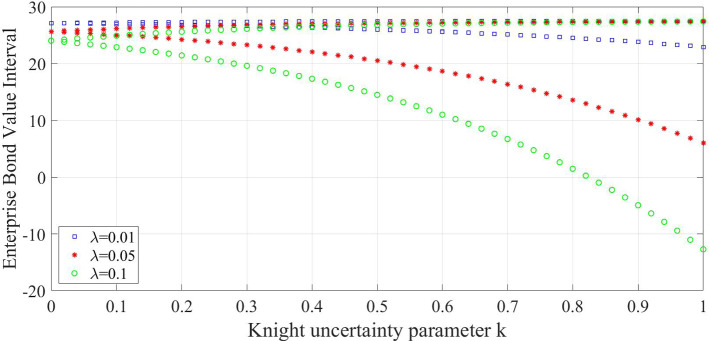
The current section analyzes the impact exerted by Knight parameter and Poisson intensity upon three varying price values discussed earlier. In order to perform the calculations easer, it has been assumed that the enterprise’ asset value at time $0$ was $V_0=55$ and its volatility was ${\sigma }^2=0.04$. Further, the risk free rate of interest was $r=0.05$ while the enterprise bond’s face value was $L=50$. The maturity of the enterprise bond was $T=3$. The mean value of the jump process is $\overline{\mu }=-0.15$ while its volatility $(1+U_i)$ is denoted by ${\overline{\sigma }}^2=0.01$. Knight uncertain parameter $k\in \left[0,1\right]$. As per the conclusion arrived in the section earlier, the default probability interval is $[p^{-k},p^k]$ whereas $\left[E^k\left(0,V_0,T\right),E^{-k}\left(0,V_0,T\right)\right]$ denots the enterprise’ stock value interval while the bond value interval is denoted by $\left[D^{-k}\left(0,V_0,T\right),D^k\left(0,V_0,T\right)\right]$. In this study, varying values of the Poisson intensity $\lambda =0.01$, $0.05$, and $0.1$ were considered to attain the three figures given below.

Figures 1, 2, and 3 infer the presence of a significant influence exerted by Poisson intensity $\lambda$ and Knight uncertain parameter upon the default probability, enterprise stock value and bond value interval respectively. Whenever the Poisson intensity $\lambda$ increased, there was an increase observed in the value of enterprise stocks as well as the default probability. However, the bond value got significantly reduced. This infers that it is not possible to ignore the impact created by jump intensity of the corporate assets, in financial markets, upon corporate default probability. However, when the Knight uncertain increased, there was a gradual increase observed in market uncertainty as well. On the other hand, the company’s default probability too increased in a gradual manner and started exhibiting rapid default probability interval too. This infers that the default probability increases in a phased manner along with the degree of uncertainty. The current study findings clearly established the impact created by Knight uncertainty on a company’s default probability, its stock and bond values. So, it becomes inevitable to consider the impact created by Knight uncertainty on a company’s default in actual operation.

Fig. 1.

The variation trend of the default probability interval on Knight uncertain parameter and Poisson intensity

Fig. 2.

The variation trend of the enterprise stock value interval on Knight uncertain parameters and Poisson intensity

Fig. 3.

The variation trend of the enterprise bond value interval on Knight uncertain parameters and Poisson intensity

Conclusions

The current research paper analyzed the credit risk measure of the listed firms in Levy market in the presence of Knight uncertainty environment. This study was conducted based on two unavoidable crucial elements of the Knight uncertainty risk in the financial markets along with jumps in the pricing process of risky assets. Based on the assumption that Levy process is followed to determine the values of the assets of the listed companies, the current study proposed a credit risk measure model under Knight uncertainty environment. On the contrary to the existing conventional credit risk structure model, there is no specific number exists for default probability of the public companies. However, there exists an interval, as a result of Knight uncertainty. In case of the uncertainty parameter being zero, then this uncertain credit risk model becomes the conventional structured credit risk model. By developing a credit risk measurement theory, the current research work empowers the investors with a new model for evaluating the credit risks of a firm.

Funding

Fund Name: Research on cost reduction and efficiency increase strategy of automobile maintenance enterprises based on the background of Internet Era (GJJ218520). Fund Project: Science and technology research project of Jiangxi Provincial Department of Education.