BAYESIAN ANALYSIS FOR IMBALANCED POSITIVE-UNLABELLED DIAGNOSIS CODES IN ELECTRONIC HEALTH RECORDS

Abstract

With the increasing availability of electronic health records (EHR), significant progress has been made on developing predictive inference and algorithms by health data analysts and researchers. However, the EHR data are notoriously noisy due to missing and inaccurate inputs despite the information is abundant. One serious problem is that only a small portion of patients in the database has confirmatory diagnoses while many other patients remain undiagnosed because they did not comply with the recommended examinations. The phenomenon leads to a so-called positive-unlabelled situation and the labels are extremely imbalanced. In this paper, we propose a model-based approach to classify the unlabelled patients by using a Bayesian finite mixture model. We also discuss the label switching issue for the imbalanced data and propose a consensus Monte Carlo approach to address the imbalance issue and improve computational efficiency simultaneously. Simulation studies show that our proposed model-based approach outperforms existing positive-unlabelled learning algorithms. The proposed method is applied on the Cerner EHR for detecting diabetic retinopathy (DR) patients using laboratory measurements. With only 3% confirmatory diagnoses in the EHR database, we estimate the actual DR prevalence to be 25% which coincides with reported findings in the medical literature.

1. Introduction.

The health care industry has become more computerized and digital in the past decade. The electronic health records (EHR), which are digitally archived data from hospitals and clinics, contain a tremendous amount of information on patients’ medical history. The rich information in EHR is vital for research in personalized medicine and clinic decision support systems, which are potentially revolutionary to many traditional medical fields.

While offering potential benefits to the clinical decision making process, EHR are highly subject to missing and inaccurate inputs (Hripcsak and Albers, 2012), which often leads to poor decisions. For instance, in many EHR-based predictive modelling, the diagnosis codes (e.g., the ICD-9 codes) are often used to determine the patient cohorts. Patients with certain codes of interest are identified as cases, and patients without such codes are typically assumed of no disease and thus identified as controls (Ng et al., 2016; Piri et al., 2017). However, such practices can be problematic with the assumption that missing diagnosis code equals to no disease. In fact, an underlying patient without the ICD-9 codes of interest may still have the disease but no examination was performed or the medical care was from a different health system. Ignorance of the uncertainty in the binary case-control labelling could severely dampen the performance of a predictive model (Zawistowski et al., 2017).

It is necessary to re-consider the data quality for any secondary analysis of EHR (Dziadkowiec et al., 2016; Botsis et al., 2010). In fact, the EHR data that we encounter are known as presence-only data in which a patient is either positively labelled or unlabelled. The problem of (re)labelling undiagnosed patients is referred to as the positive-unlabelled (PU) learning (Mordelet and Vert, 2014). The problem of PU learning arises from various situations, including disease-related gene identification (Yang et al., 2012; Mordelet and Vert, 2011), medical diagnosis (Zuluaga et al., 2011) and text classification (Li and Liu, 2003; Liu et al., 2003). Algorithm-based approaches are popular in the literature, for example, the two-step approach (Li and Liu, 2003; Liu et al., 2002; Li et al., 2009), biased support vector machine (SVM) (Liu et al., 2003) and ensemble algorithms based on bootstrap aggregating (Mordelet and Vert, 2014; Claesen et al., 2015).

The existing algorithm-based PU learning methods often perform poorly on heavy-tailed distributions (Xu, Crammer and Schuurmans, 2006) that are common for medical lab measurements. We also find that the existing algorithms can be sensitive to the positive proportion in the unlabelled group in simulation studies. Furthermore, parameter estimation and uncertainty quantification are in general unavailable for algorithm-based methods. There is a lack of model-based approaches for PU learning in the literature and a sophisticated statistical model can potentially address the aforementioned issues.

In this paper, we propose a Bayesian finite mixture model and use Markov Chain Monte Carlo (MCMC) for the Bayesian computation. It is noteworthy that although the finite mixture modelling has been extensively used in clustering and classification problems (Huang et al., 2005; Dean, Murphy and Downey, 2006; Martella et al., 2011; McNicholas, 2016), we are not aware of any direct application on the PU learning problem. There are two unique challenges when applying the Bayesian finite mixture model to our EHR data whose details are described in Section 6. First, the proposed finite mixture model should not suffer from the so-called label-switching issue with the presence of positively labelled observations. However, our real EHR data are extremely imbalanced with only 3% positively labelled cases, and we show that the label-switching occur and consequently estimates can be incorrect. Second, the Bayesian computation is intensive for the large EHR data so that an efficient computation is desired. In this paper, we propose to address the two challenges simultaneously by using the consensus Monte Carlo approach which splits data and then combines posterior subsamples.

Our contribution in this paper is twofold. First, on the methodological side, we develop a model-based approach for extremely imbalanced positive-unlabelled data, and show superior performance comparing with existing algorithm-based methods. Moreover, comparing with deterministic algorithms, the Bayesian finite fixture model offers better interpretability of the unlabelled records from a probabilistic perspective. The distributional assumptions and parameter specifications enable statistical inference for researchers and clinical physicians, allowing them to better understand the data generating process and population characteristics. Second, it is of practical significance to tackle the emerging problem of secondary analysis of EHR data. In the application of detecting patients with diabetic retinopathy (DR), with only 3% confirmatory diagnoses in the EHR database, we estimate the actual prevalence to be 25% which is consistent with reported findings from the medical community. In an external validation, we show that machine learning using classified results gain improvements. Finally, the proposed solution for PU-learning is generalizable for other types of applications that are beyond the scope of EHR data analysis.

The reminder of this paper is organized as follows. In section 2, we propose a Bayesian finite mixture model with multivariate t distributions conditional on categories. Section 3 is on the Bayesian computation, specifically the details of Gibbs sampling. In section 4, we illustrate the issue of label-switching for imbalanced data and propose a consensus Monte Carlo approach. We perform simulation studies in section 5 and show that our proposed approach outperforms existing approaches under various settings. The real Cerner EHR dataset for DR diagnosis and detection is extensively analyzed in section 6. Finally, section 7 contains concluding remarks for this paper.

2. Bayesian Finite Mixture Modelling.

2.1. Notations.

First we define useful notations. Let 𝒫 denote the set of positively labelled observations and 𝒰 denote the set of unlabelled observations, which is a mixture of positively and negatively labelled observations but the underlying label is unobserved. Let n_p and n_u denote the sample size of 𝒫 and 𝒰, respectively. Each observation in the data is a vector of measurements, which contains values of both categorical and numerical variables. Let $x_i=\left(x_i^d,x_i^c\right)$ be the feature vector, where $x_i^d$ is a one-dimensional categorical variable and $x_i^c$ is a vector of continuous variables. Note that multiple categorical variables can be collapsed into one categorical variable and thus it is sufficient that $x_i^d$ is one-dimensional.

2.2. The finite mixture of multivariate t distributions.

Let our samples be 𝒫 = {x_p,i}, i = 1, …, n_p and 𝒰 = {x_u,i}, i = 1, …, n_u. Assume that x_p,i ~ f₊(x) independently and x_u,i ~ f_u(x) independently, where

$$f_u(x)=\pi f_{+}(x)+(1-\pi )f_{-}(x),$$

where f₋(x) is the underlying distribution of the negatively labelled samples, and the mixing probability π is called the contamination rate, which is the proportion of positive instances in the unlabelled set. To model f₊(x) and f₋(x), recall that x has two components, of which x^d is categorical and x^c is continuous. It is natural that f₊(x) is modelled conditionally, f₊(x) = f₊(x^c | x^d = j)f₊(x^d = j), where f₊(x^d = j), j = 1, …, J is a categorical distribution with category probabilities p₁. Consider a multivariate t distribution for the conditional density f₊(x^c | x^d = j) = t(x^c | μ_1,j, Σ_1,j, ν_1,j), where μ_1,j is the location parameter, Σ_1,j is the scale matrix and ν_1,j is the degrees of freedom, and the density function for an h-dimensional t is

$$t\left(x^c\mid {\mu }_{1,j},{\Sigma }_{1,j},{\nu }_{1,j}\right)=\frac{\Gamma \left(\frac{h+{\nu }_{1,j}}{2}\right){\left|{\Sigma }_{1,j}\right|}^{-1/2}}{{\left(\pi {\nu }_{1,j}\right)}^{h/2}\Gamma \left(\frac{{\nu }_{1,j}}{2}\right){\left[1+{\left(x^c-{\mu }_{1,j}\right)}^{\prime }{\Sigma }_{1,j}^{-1}\left(x^c-{\mu }_{1,j}\right)/{\nu }_{1,j}\right]}^{\frac{h+{\nu }_{1,j}}{2}}}.$$

The degrees of freedom ν_1,j controls the thickness of distribution tails, and the multivariate t distribution approaches the multivariate normal distribution N(x^c | μ_1,j, Σ_1,j) as ν_1,j → ∞. Similarly, let f₋(x) = f₋(x^c | x^d = j)f₋(x^d = j), where f₋(x^d = j) is a categorical distribution with parameters p₂ and f₋(x^c | x^d = j) = t(x^c | μ_2,j, Σ_2,j, ν_2,j).

In a mixture model, it is convenient to introduce a latent indicator z_i ∈ {1, 2} for observations in 𝒰, for which z_i = 1 denotes a positively labelled observation and z_i = 2 denotes a negatively labelled observation. Hence, p(z_i = 1) = π and p(z_i = 2) = 1 − π. Given indicators z = {z_i, i = 1, …, n_u}, the likelihood function for the complete dataset {𝒫, 𝒰} can be written as

$$L\left(\left\{{\mu }_{k,j},{\Sigma }_{k,j},{\nu }_{k,j},p_k\right\},\pi ;𝒫,𝒰,z\right)=\prod _{x_{p,i}\in 𝒫}f\left(x_{p,i}^d=j\mid p_1\right)t\left(x_{p,i}^c\mid {\mu }_{1,j},{\Sigma }_{1,j},{\nu }_{1,j}\right)\prod _{x_{u,i}\in 𝒰}p\left(z_i=k\mid \pi \right)f\left(x_{u,i}^d=j\mid p_k\right)t\left(x_{u,i}^c\mid {\mu }_{k,j},{\Sigma }_{k,j},{\nu }_{k,j}\right)$$

for k = 1, 2 and j = 1, …, J. Note that a multivariate t distribution X ~ t(μ, Σ, ν) can be constructed hierarchically by a multivariate normal distribution and a gamma distribution

$$X\mid \tau ~\text{N}(\mu ,\Sigma /\tau ),\tau ~\text{Gamma}(\nu /2,\nu /2),$$

which is more convenient for statistical inference and computations. This model specification using multivariate t distributions has been considered in Andrews, McNicholas and Subedi (2011) for model-based classification problems, where the authors proposed an expectation-maximization algorithm for the inference. In this paper, we consider a Bayesian inference for the proposed model.

2.3. The prior distributions.

We now need to fully specify the Bayesian model by specifying the prior distributions for π and {μ_k,j, Σ_k,j, ν_k,j, p_k}, k = 1, 2, j = 1, …, J. With the normal-gamma mixture representation for the multivariate t distribution, we can choose semi-conjugate priors for most parameters in the model. Let π have a beta prior Beta(α₀, β₀) with α₀ = β₀ = 1 if no extra information is known for the mixing probability. Let p₁ and p₂ both be Dirichlet(λ₁, …, λ_J). Let μ_k,j ~ N(μ₀, Σ₀), Σ_k,j ~ Inv-Wishart(Φ₀, ξ₀) and ν_k,j ~ Gamma(a₀, b₀) for any k and j. We assign λ₁ = ⋯ = λ_J = 1, μ₀ = 0, Σ₀ = 10⁵I, Φ₀ = I and ξ₀ = 3 to make these priors only weakly informative. In our experience, the degrees of freedom parameter ν_k,j sometimes can be difficult to identify, depending on the data in practice. Therefore we suggest to use an informative prior to avoid a potential non-identifiability situation. In our applications, we choose a₀ = 5 and b₀ = 1 whose mean is 5 and variance is 5. In the literature, a fixed value of ν_k,j = 4 has been suggested to provide good protection against outliers (Lange, Little and Taylor, 1989; Stephens, 2000).

3. Bayesian Computations.

With priors specified in Section 2.3, we can use the Gibbs sampler to sample from the joint posterior distribution. Recall that n_p denotes the sample size of 𝒫 and n_u denotes the sample size for 𝒰. Define the following counts for convenience. Let n_p,1, …, n_p,J denote the counts for categories 1 to J in 𝒫, i.e. $n_{p,j}={\sum }_{x_{p,i}\in 𝒫}1\left(x_{p,i}^d=j\right)$, where 1(·) is an indicator function. Let n_u,p and n_u,n denote the counts of observations in 𝒰 that are classified into the positive group and the negative group, respectively, i.e. $n_{u,p}={\sum }_{x_{u,i}\in 𝒰}1\left(z_i=1\right)$ and $n_{u,n}={\sum }_{x_{u,i}\in 𝒰}1\left(z_i=2\right)$. Dividing n_u,p into J categories leads to the counts n_u,p,j, j = 1, …, J, i.e. $n_{u,p,j}={\sum }_{x_{u,i}\in 𝒰}1\left(z_i=1\cap x_{u,i}^d=j\right)$. We define n_u,n,j, j = 1, …, J similarly. The full conditional distributions for Gibbs sampling are given as follows.

1. Sample the mixing probability π from

   $$p(\pi \mid \text{others})~\text{Beta}\left({\alpha }_0+n_{u,p},{\beta }_0+n_{u,n}\right)$$
2. Sample the latent indicators z_i for x_u,i ∈ 𝒰 from Bernoulli with probability p(z_i = 1 | others) being

   $$\frac{\pi f\left(x_{u,i}^d=j\mid p_1\right)t\left(x_{u,i}^c\mid {\mu }_{1,j},{\Sigma }_{1,j},{\nu }_{1,j}\right)}{\pi f\left(x_{u,i}^d=j\mid p_1\right)t\left(x_{u,i}^c\mid {\mu }_{1,j},{\Sigma }_{1,j},{\nu }_{1,j}\right)+(1-\pi )f\left(x_{u,i}^d=j\mid p_2\right)t\left(x_{u,i}^c\mid {\mu }_{2,j},{\Sigma }_{2,j},{\nu }_{2,j}\right)}$$

   and p(z_i = 2 | others) = 1−p(z_i = 1 | others)

3. Sample p₁ from Dirichlet(λ₁ + n_p,1 + n_u,p,1, …, λ_J + n_p,J + n_u,p,J).

4. Sample p₂ from Dirichlet(λ₁ + n_u,n,1, …, λ_J + n_u,n,J).

5. Sample μ_1,j from $p\left({\mu }_{1,j}\mid \text{others}\right)\propto N\left({\tilde{\mu }}_{1,j},{\tilde{\Sigma }}_{1,j}\right)$, where ${\tilde{\Sigma }}_{1,j}^{-1}={\Sigma }_0^{-1}+{\Sigma }_{1,j}^{-1}\sum _{x_i\in {𝒟}_1}{\tau }_i$, ${\tilde{\mu }}_{1,j}={\tilde{\Sigma }}_{1,j}\left({\Sigma }_0^{-1}{\mu }_0+{\Sigma }_{1,j}^{-1}\sum _{x_i\in {𝒟}_1}{\tau }_i{x}_i^c\right)$, and define ${𝒟}_1=\left\{x_{p,i}:x_{p,i}^d=j\right\}\cup \left\{x_{u,i}:z_i=1\cap x_{u,i}^d=j\right\}$.

6. Sample μ_2,j from $p\left({\mu }_{2,j}\mid \text{others}\right)\propto N\left({\tilde{\mu }}_{2,j},{\tilde{\Sigma }}_{2,j}\right)$, where ${\tilde{\Sigma }}_{2,j}^{-1}={\Sigma }_0^{-1}+{\Sigma }_{2,j}^{-1}\sum _{x_i\in {𝒟}_2}{\tau }_i$, ${\tilde{\mu }}_{2,j}={\tilde{\Sigma }}_{2,j}\left({\Sigma }_0^{-1}{\mu }_0+{\Sigma }_{2,j}^{-1}\sum _{x_i\in {𝒟}_2}{\tau }_i{x}_i^c\right)$ and define ${𝒟}_2=\left\{x_{u,i}:z_i=2\cap x_{u,i}^d=j\right\}$.

7. Sample Σ_1,j from p(Σ_1,j | others) ∝ Inv-Wishart(A₁ + Φ₀, n_p,j + n_u,p,j + ξ₀), where $A_1=\sum _{x_i\in {𝒟}_1}{\tau }_i\left(x_i^c-{\mu }_{1,j}\right){\left(x_i^c-{\mu }_{1,j}\right)}^{\prime }$.

8. Sample Σ_2,j from p(Σ_2,j | others) ∝ Inv-Wishart(A₂ + Φ₀, n_u,n,j + ξ₀), where $A_2=\sum _{x_i\in {𝒟}_2}{\tau }_i\left(x_i^c-{\mu }_{2,j}\right){\left(x_i^c-{\mu }_{2,j}\right)}^{\prime }$.

9. Sample τ_p,i for x_p,i ∈ 𝒫 from

   $$p\left({\tau }_{p,i}\mid \text{others}\right)\propto \text{Gamma}\left(\frac{{\nu }_{1,j}+\text{dim}\left(x^c\right)}{2},\frac{{\nu }_{1,j}+{\left(x_{p,i}^c-{\mu }_{1,j}\right)}^{\prime }{\Sigma }_{1,j}^{-1}\left(x_{p,i}^c-{\mu }_{1,j}\right)}{2}\right),$$

   where dim(x^c) is the dimension of the continuous random vector x^c.

10. Sample τ_u,i for x_u,i ∈ 𝒰 from

    $$p\left({\tau }_{u,i}\mid \text{others}\right)\propto \text{Gamma}\left(\frac{{\nu }_{z_i,j}+\text{dim}\left(x^c\right)}{2},\frac{{\nu }_{z_i,j}+{\left(x_{u,i}^c-{\mu }_{z_i,j}\right)}^{\prime }{\Sigma }_{z_i,j}^{-1}\left(x_{u,i}^c-{\mu }_{z_i,j}\right)}{2}\right).$$
11. Sample ν_k,j from

    $$p\left({\nu }_{k,j}\mid \text{others}\right)\propto {\nu }_{k,j}^{a_0-1}{e}^{-b_0{\nu }_{k,j}}\prod _{{\mathit{x}}_i\in {𝒟}_k}\left\{\frac{{\left({\nu }_{k,j}/2\right)}^{{\nu }_{k,j}/2}}{\Gamma \left({\nu }_{k,j}/2\right)}{\tau }_i^{{\nu }_{k,j}/2}{e}^{-{\tau }_i{\nu }_{k,j}/2}\right\}.$$

We use the Metropolis-Hastings algorithm to sample from a transformed version of this density u_k,j = log(ν_k,j) so that the support is (−∞, ∞). The proposal distribution is then chosen to be a normal distribution.

4. Label Switching for Imbalanced Data.

4.1. Illustration of label switching.

The label switching is a well-known issue for finite mixture models due to that components are unidentifiable in the likelihood. However, it need not be an issue when the likelihood contains a component for the positively labelled data, theoretically. Despite components are identifiable in the finite mixture model for positive-unlabelled data, the identifiability can be weak if the data are extremely imbalanced, i.e. data only contain a small portion of positively labelled cases. It can be illustrated that label switching occurs in the computation due to the weak identifiability and consequently leads to incorrect estimation and inference.

For the purpose of illustration, consider a finite mixture model as follows,

$$x_{p,i}~f\left(x_{p,i}^d=j\mid p_{+}\right)t\left(x_{p,i}^c\mid {\mu }_{+,j},{\Sigma }_{+,j},{\nu }_{+,j}\right),$$

$$x_{u,i}~{\pi }_{+}f\left(x_{u,i}^d=j\mid p_{+}\right)t\left(x_{u,i}^c\mid {\mu }_{+,j},{\Sigma }_{+,j},{\nu }_{+,j}\right)+{\pi }_{-}f\left(x_{u,i}^d=j\mid p_{-}\right)t\left(x_{u,i}^c\mid {\mu }_{-,j},{\Sigma }_{-,j},{\nu }_{-,j}\right),$$

for x_p,i ∈ 𝒫 and x_u,i ∈ 𝒰, where π₋ = 1 − π₊. The log-likelihood function for this model can be written as follows,

$$l\left(\left\{{\pi }_{\pm },{\mu }_{\pm ,j},{\Sigma }_{\pm ,j},{\nu }_{\pm ,j},p_{\pm }\right\};𝒫,𝒰\right)=\sum _{j=1}^J\sum _{\underset{x_{p,i}^d=j}{x_{p,i}\in 𝒫}}\text{log}\left[p_{+,j}t\left(x_{p,i}^c\mid {\mu }_{+,j},{\Sigma }_{+,j},{\nu }_{+,j}\right)\right]+\sum _{j=1}^J\sum _{\underset{x_{u,i}^d=j}{x_{u,i}\in 𝒰}}\text{log}\left[{\pi }_{+}{p}_{+,j}t\left(x_{u,i}^c\mid {\mu }_{+,j},{\Sigma }_{+,j},{\nu }_{+,j}\right)+{\pi }_{-}{p}_{-,j}t\left(x_{u,i}^c\mid {\mu }_{-,j},{\Sigma }_{-,j},{\nu }_{-,j}\right)\right],$$

If we switch the positive label and the negative label, the log-likelihood will differ as the first term changes. This log-likelihood function is then unimodal and hence components are identifiable as long as there is at least one positively labelled case. However, when the data are extremely imbalanced, that is, the sample size of 𝒰 is much greater than that of 𝒫, the first term in the log-likelihood will be negligible. In that case, the log-likelihood will be practically multimodal, although the global maximum is unique. In this mixture model, each labelled group is further a mixture of J categories, and each category j is prone to labeling switching as well. Therefore there are practically 2^J modes with close likelihood values in the scenario of imbalanced labels.

To show the non-convergence of Markov chains under the multimodal scenario, we simulate two synthetic data sets. For both data sets, we assume n_p = 100, π₊ = 0.3, π₋ = 0.7, p_+,1 = p_+,2 = p_−,1 = p_−,2 = 0.5, μ_+,1 = (1, 1, 1)′, μ_+,2 = (2, 2, 2)′, μ_−,1 = (3, 3, 3)′, μ_−,2 = (4, 4, 4)′, Σ_+,1 = Σ_+,2 = Σ_−,1 = Σ_−,2 = I, ν_+,1 = ν_+,2 = 2 and ν_−,1 = ν_−,2 = 5. Then we assign n_u = 200 for data set 1 and n_u = 4, 000 for data set 2 to mimic the balanced scenario and the imbalanced scenario. Let {π₊, μ_+,1, μ_+,2, μ_−,1, μ_−,2, ν_+,1, ν_+,2, ν_−,1, ν_−,2, p_±, Σ_±,j} be the parameters of interest. It is obvious that the log-likelihood has the following 2² = 4 local maximums.

$$\left\{0.3,{(1,1,1)}^{\prime },{(2,2,2)}^{\prime },{(3,3,3)}^{\prime },{(4,4,4)}^{\prime },2,2,5,5,0.5,I\right\},$$

$$\left\{0.7,{(3,3,3)}^{\prime },{(4,4,4)}^{\prime },{(1,1,1)}^{\prime },{(2,2,2)}^{\prime },5,5,2,2,0.5,I\right\},$$

$$\left\{0.5,{(3,3,3)}^{\prime },{(2,2,2)}^{\prime },{(1,1,1)}^{\prime },{(4,4,4)}^{\prime },5,2,2,5,0.5,I\right\},$$

$$\left\{0.5,{(1,1,1)}^{\prime },{(4,4,4)}^{\prime },{(3,3,3)}^{\prime },{(2,2,2)}^{\prime },2,5,5,2,0.5,I\right\},$$

for which only the first one is the global maximum. For the sake of convenience, refer them as Modes 1 to 4, respectively. For the relatively balanced data set 1, we expect that Mode 1 be easily identified as the global maximum and label switching does not occur. On the other hand, for the extremely imbalanced data set 2, we expect that all four modes have close log-likelihood values and label switching occurs. Figure 1 subplots (a) and (b) overlap the log-likelihood as a function of π₊ with other parameters fixed at the four modes, respectively. Subplot (a) is for data set 1. It is clear that π₊ takes values 0.3, 0.5, 0.5, 0.7 at the four modes and Mode 1 with π₊ = 0.3 is the global maximum. Subplot (b) is for data set 2. Mode 1 with π₊ = 0.3 is still the global maximum but it is hardly distinguishable from other modes, indicating a weak identifiability. Figure 1 subplots (c) and (d) show MCMC trace plots for π₊ for data set 1 and 2, respectively. We purposely choose dispersed initial values for four Markov chains. In subplot (c), all chains converge to the correct mode of π₊. In subplot (d), the chains do not converge to the correct mode but stuck with local modes depending on the initial values. Thus, analysts should be careful about the label switching problem when their data appear to be imbalanced.

Fig 1.

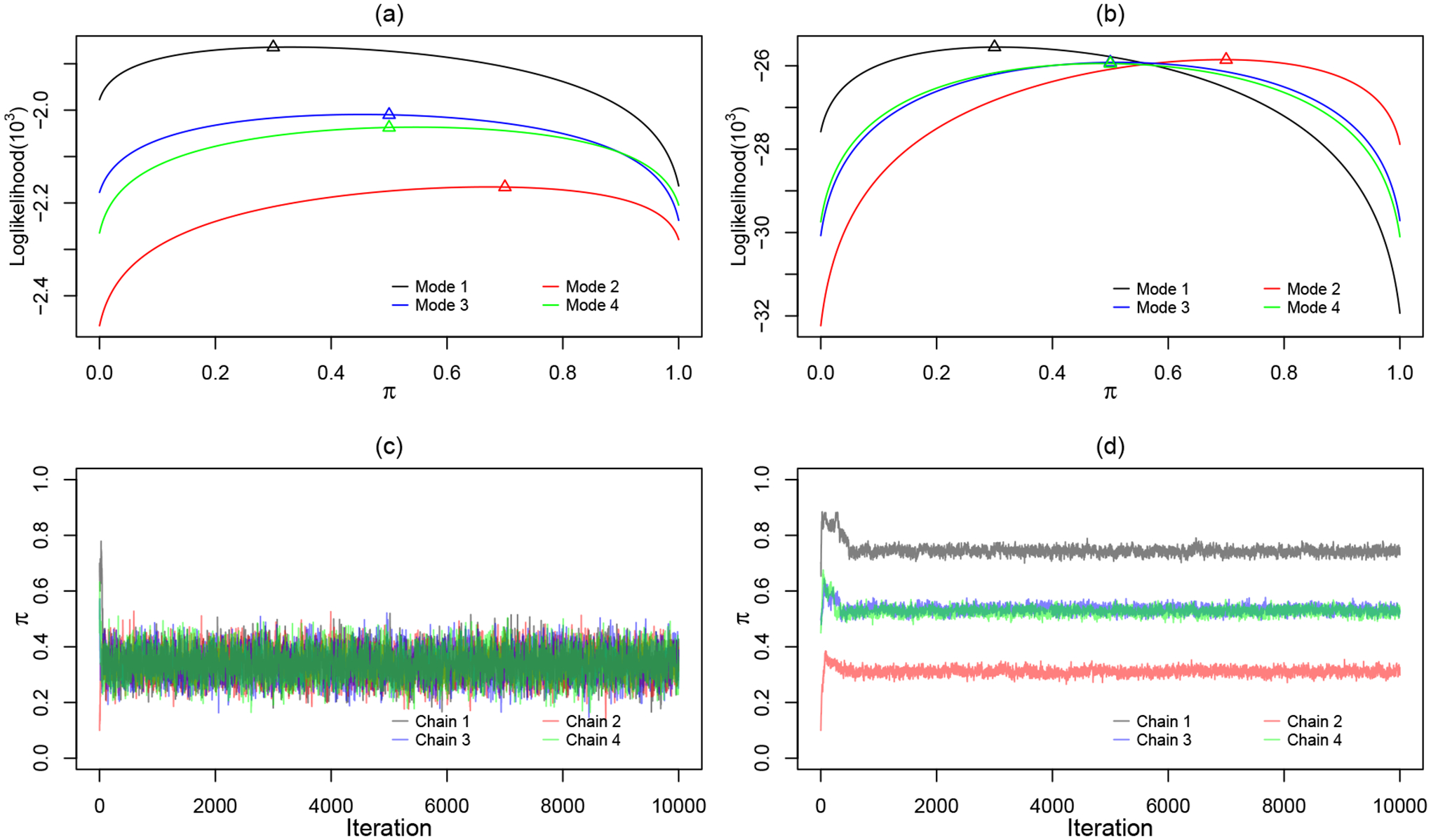
Plots of log-likelihood function with respect to π and MCMC trace plots with distinct initial values for π: (a)(c). Synthetic data set 1: n_p = 100, n_u = 200. (b)(d). Synthetic data set 2: n_p = 100, n_u = 4, 000

4.2. Consensus Monte Carlo.

It is obvious that the weak identifiability is not because of the model but is due to the imbalanced dataset. An immediate solution is to make the data relatively balanced. Let us equally split the unlabelled group 𝒰 into 𝒮 subgroups {𝒰⁽¹⁾,·⋯ , 𝒰^(S)} such that the sample size of a subgroup 𝒰^(s) is comparable to that of 𝒫. Consider S parallel sub-datasets: {𝒫,𝒰⁽¹⁾},·⋯ , {𝒫,𝒰^(S)}, and each of them is relatively balanced. We apply the finite mixture model and Bayesian computations on each sub-dataset, and write the sub-likelihood function as

$$L^{(s)}\left({\theta }_1^{(s)},{\theta }_2^{(s)},{\pi }^{(s)};𝒫,{𝒰}^{(s)}\right)=\prod _{x_i\in 𝒫}{f}_{+}\left(x_i;{\theta }_1^{(s)}\right)\prod _{x_i\in {𝒰}^{(s)}}\left[{\pi }^{(s)}{f}_{+}\left(x_i;{\theta }_1^{(s)}\right)+\left(1-{\pi }^{(s)}\right)f_{-}\left(x_i;{\theta }_2^{(s)}\right)\right].$$

To combine posterior samples obtained from the sub-likelihood functions, we utilize the consensus Monte Carlo (Scott et al., 2016), which was introduced for parallelizing MCMC. A more efficient computation is a by-product but also desired since EHR data are typically large. Note that our implementation is slightly different from the original consensus Monte Carlo in that 𝒫 is repeatedly used instead of being split. The proposed split-and-combine procedure is outlined as follows.

1. Split 𝒰 into S subgroups {𝒰⁽¹⁾,·⋯ , 𝒰^(S)} with equal size $n_u^{(s)}$.

2. For s = 1,·⋯ , S, in parallel, apply the Bayesian finite mixture model. The MCMC gives posterior samples from

   $$p\left(\Theta \mid 𝒫,{𝒰}^{(s)}\right)\propto p(\Theta )p\left(𝒫,{𝒰}^{(s)}\mid \Theta \right),$$

   where Θ = {{μ_k,j, Σ_k,j, ν_k,j, p_k}, π, z, τ}, k = 1, 2, j = 1, …, J.

3. Suppose for a parameter θ, we obtain sub-posterior draws from the S subgroups, ${\theta }_t^{(1)},\dots ,{\theta }_t^{(S)}$ at iteration t. To combine them to an aggregated posterior draw θ_t, according to Scott et al. (2016), compute a weighted average

   $${\theta }_t={\left(\sum _{s=1}^S{\omega }^{(s)}\right)}^{-1}\sum _{s=1}^S{\omega }^{(s)}{\theta }_t^{(s)},$$
   where ω^(s) is the weight for subgroup s.

   1. For parameters {μ_k,j, Σ_k,j, ν_k,j}, choose ω^(s) = Var(θ|𝒫,𝒰^(s))⁻¹, where Var(θ|𝒫,𝒰^(s)) is estimated by the sample variance of $\left\{{\theta }_1^{(s)},\cdots ,{\theta }_T^{(s)}\right\}$.
   2. For parameters {π, p_k}, which are [0, 1]-bounded, the arithmetic average tends to perform better in practice, that is to choose ω^(s) = 1.
4. After combining posterior samples, compute the posterior classification probabilities p(z_i = 1|𝒫,𝒰), for x_u,i ∈ 𝒰 with $x_{u,i}^d=j$, using the following expression

   $$\frac{1}{T-B}\sum _{t=B+1}^T\frac{{\pi }^{(t)}{f}_{+}\left(x_{u,i}\mid p_1^{(t)},{\mu }_{1,j}^{(t)},{\Sigma }_{1,j}^{(t)},{\nu }_{1,j}^{(t)}\right)}{{\pi }^{(t)}{f}_{+}\left(x_{u,i}\mid p_1^{(t)},{\mu }_{1,j}^{(t)},{\Sigma }_{1,j}^{(t)},{\nu }_{1,j}^{(t)}\right)+\left(1-{\pi }^{(t)}\right)f_{-}\left(x_{u,i}\mid p_2^{(t)},{\mu }_{2,j}^{(t)},{\Sigma }_{2,j}^{(t)},{\nu }_{2,j}^{(t)}\right)},$$

   where B is the burn-in sample size.

5. Classify an unlabelled individual i as a positive case if p(z_i = 1|𝒫,𝒰) ≥ 0.5, otherwise as a negative case.

A related alternative to address the imbalance issue is oversampling the minority group. Note that our proposed procedure is equivalent to using the following full likelihood function as we repeatedly use 𝒫 for S times,

$$L\left({\theta }_1,{\theta }_2,\pi ;𝒫,𝒰\right)=\prod _{x_i\in 𝒫}{\left[f_{+}\left(x_i;{\theta }_1\right)\right]}^S\prod _{x_i\in 𝒰}\left[\pi f_{+}\left(x_i;{\theta }_1\right)+(1-\pi )f_{-}\left(x_i;{\theta }_2\right)\right],$$

which is indeed similar as oversampling 𝒫 with S multiples. However, directly using an oversampled large dataset is computationally challenging, and thus a parallel computation has its advantages. It is theoretically difficult to justify an optimal choice of the splitting size S. The bottom line is that the sample sizes of 𝒰^(s) and 𝒫 are comparable so that label-switching is avoided.

5. Simulation Studies.

5.1. Comparing performance with algorithm-based methods.

In this section, we conduct a simulation study to compare our proposed mixture modelling approach with the state-of-the-art PU learning techniques. To mimic the real EHR data described in Section 6, we now let 𝒫 be the group of DR patients and 𝒩 be the group of non-DR patients. We let $x_i^d$ be a categorical variable gender ($x_i^d=1$ denotes male and $x_i^d=2$ denotes female) and let $x_i^c$ be a vector of three continuous laboratory variables. We consider three distribution settings for the data generation as follows.

1. We let $x_i^c$ for the male DR patients be generated from a multivariate t distribution with μ_1,1 = (1, 1, 1)′, Σ_1,1 = I and ν_1,1 = 2, and let $x_i^c$ for the female DR patients be from a multivariate t distribution with μ_1,2 = (2, 2, 2)′, Σ_1,2 = I and ν_1,2 = 2. For the non-DR group, we let $x_i^c$ for the male non-DR patients be from a multivariate t distribution with μ_2,1 = (3, 3, 3)′, Σ_2,1 = I and ν_2,1 = 5, and let $x_i^c$ for the female non-DR patients be from a multivariate t distribution with μ_2,2 = (4, 4, 4)′, Σ_2,2 = I and ν_2,2 = 5. Let the category probabilities be p₁₁ = p₁₂ = p₂₁ = p₂₂ = 0.5.

2. We consider a skewed distribution model. We let each variable of $x_i^c$ for the male DR patients be from Gamma(2, 1) and for the female DR patients be from Gamma(5, 2). We then shift both gamma distributions to the right by 2 units for the non-DR patients. Let the category probabilities be p₁₁ = p₁₂ = p₂₁ = p₂₂ = 0.5.

3. We consider Cauchy distributions for which outliers can be extreme. We let the male and female DR groups be Cauchy(1, 0.5) and Cauchy(2, 0.5) for $x_i^c$, respectively, where the first parameter is the location and the second parameter is the scale. We choose Cauchy(3, 0.5) and Cauchy(4, 0.5) for the male and female non-DR groups, respectively. Let the category probabilities be p₁₁ = p₁₂ = p₂₁ = p₂₂ = 0.5.

Note that in the above three cases, Cases 2 and 3 present a situation where the multivariate t mixture model is misspecified, and hence the robustness of each method is examined under skewed and heavy-tailed scenarios. For all three cases, we fix the sample size for the labelled DR group as n_p = 100 and that for the unlabelled group as n_u = 4,000 to represent imbalanced data in real applications. For each of the three cases, we randomly mix a portion of DR patients with non-DR patients with a mixing probability π ranging from 0.3 to 0.7. We randomly generate 30 datesets under each setting and implement the following four methods for each dataset: the two-step method, the biased-SVM, the bagging-SVM and our proposed Bayesian finite mixture model. For the two-step method, we adopt the version in Liu et al. (2003) for which a Naïve Bayesian classifier is built in Step 1 and the SVM is used in Step 2. For the biased-SVM described in Liu et al. (2003), we let C₊n_p = C₋n_u, where C₊ and C₋ are the penalties of misclassifying a positive and a negative, respectively. For the bagging-SVM described in Mordelet and Vert (2014), we set the bootstrap sample size K = n_p and the number of bootstrap samples T = 10. For both the biased-SVM and the bagging-SVM, we use the grid search and cross-validation to select the optimal cost parameter in a defined set {10⁻¹², 10⁻¹¹, …, 10¹, 10²}. For our proposed mixture modelling approach, we set the splitting size S = 20. We adopt the Box-Cox power transformations for skewed samples. Lo and Gottardo (2012) argue that the t-mixture model with Box-Cox transformation performs favorably in terms of accuracy and robustness compared with the skewed-t approach (Azzalini and Capitanio, 2003).

To evaluate the performance of each method, we adopt the conventionally used metrics in the PU learning literature. Let TP denote the number of true positives, TN denote the number of true negatives, FP denote the number of false positives and FN denote the number of false negatives. Define

$$\text{Accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}},\text{\hspace{1em}Precision}=\frac{\text{TP}}{\text{TP}+\text{FP}},$$

$$\text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}},\text{\hspace{1em}Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}}\text{,}$$

and also define the F-score as follows,

$$F=\frac{2\times \text{Precision}\times \text{Sensitivity}}{\text{Precision}+\text{Sensitivity}}.$$

The accuracy and the F-score are the most popular metrics for comparing PU learning methods in the literature.

The results are shown in Tables 1, 2 and 3 for the three distribution settings. A plot of accuracy versus π is shown in Figure 2 and a plot of F-score versus π is shown in Figure 3. As we can see from the tables and plots, in terms of both accuracy and F-score, the three algorithm-based methods appear to be sensitive to heavy-tailed distributions. We also notice that the performance of the three algorithm-based methods can be compromised by an increased mixing probability π. It should be pointed out that F-score does not exist for the two-step method because the two-step algorithm classifies all positive cases in the unlabelled group as negative. In all settings with various π values, our proposed mixture modelling approach seems to be quite stable and outperforms the other methods in general.

Table 1.

Performance metrics under Case 1: t-distribution. Table shows mean metrics (standard deviation).

π	Method	Accuracy	F-score	Sensitivity	Specificity
0.3	Two-step	0.6991 (0.0067)	-	0 (0)	1 (0)
	Biased-SVM	0.8968 (0.0237)	0.8137 (0.0571)	0.7675 (0.1034)	0.9526 (0.0137)
	Bagging-SVM	0.9182 (0.0055)	0.8587 (0.0103)	0.8269 (0.0179)	0.9574 (0.0061)
	Mixture model	0.9223 (0.0051)	0.8696 (0.0104)	0.8586 (0.0258)	0.9498 (0.0091)
0.4	Two-step	0.5992 (0.0074)	-	0 (0)	1 (0)
	Biased-SVM	0.8111 (0.1159)	0.6462 (0.1440)	0.5785 (0.3160)	0.9679 (0.0230)
	Bagging-SVM	0.8996 (0.0087)	0.8649 (0.0132)	0.8031 (0.0222)	0.9641 (0.0058)
	Mixture model	0.9144 (0.0041)	0.8921 (0.0068)	0.8890 (0.0174)	0.9311 (0.0090)
0.5	Two-step	0.4991 (0.0073)	-	0 (0)	1(0)
	Biased-SVM	0.7511 (0.1882)	0.5760 (0.0792)	0.5348 (0.3939)	0.9703 (0.0233)
	Bagging-SVM	0.8709 (0.0121)	0.8567 (0.0156)	0.7721 (0.0249)	0.9700 (0.0046)
	Mixture model	0.9112 (0.0061)	0.9115 (0.0068)	0.9134 (0.0196)	0.9087 (0.0192)
0.6	Two-step	0.4009 (0.0074)	-	0 (0)	1 (0)
	Biased-SVM	0.5581 (0.2157)	0.3130 (0.0454)	0.2945 (0.3963)	0.9522 (0.1811)
	Bagging-SVM	0.8328 (0.0256)	0.8410 (0.0270)	0.7403 (0.0379)	0.9713 (0.0110)
	Mixture model	0.9111 (0.0078)	0.9264 (0.0065)	0.9381 (0.0167)	0.8713 (0.0259)
0.7	Two-step	0.3009 (0.0067)	-	0 (0)	1 (0)
	Biased-SVM	0.5082 (0.2436)	0.3527 (0.0467)	0.3028 (0.3553)	0.9858 (0.0193)
	Bagging-SVM	0.7796 (0.0469)	0.8142 (0.0472)	0.6983 (0.0659)	0.9690 (0.0179)
	Mixture model	0.9136 (0.0123)	0.9393 (0.0082)	0.9560 (0.0147)	0.8154 (0.0523)

Table 2.

Performance metrics under Case 2: gamma distribution. Table shows mean metrics (standard deviation).

π	Method	Accuracy	F-score	Sensitivity	Specificity
0.3	Two-step	0.6988 (0.0062)	-	0 (0)	1 (0)
	Biased-SVM	0.9178 (0.1160)	0.8781 (0.0782)	0.8443 (0.0377)	0.9496 (0.1795)
	Bagging-SVM	0.9380(0.0042)	0.8888 (0.0090)	0.8233 (0.0238)	0.9875 (0.0059)
	Mixture model	0.9481 (0.0067)	0.9058 (0.0131)	0.8303 (0.0233)	0.9989 (0.0010)
0.4	Two-step	0.5986 (0.0064)	-	0 (0)	1 (0)
	Biased-SVM	0.9010 (0.0836)	0.8360 (0.0109)	0.7720 (0.2110)	0.9879 (0.0069)
	Bagging-SVM	0.9131 (0.0091)	0.8796 (0.0144)	0.7923 (0.0255)	0.9940 (0.0035)
	Mixture model	0.9402 (0.0073)	0.9197 (0.0106)	0.8542 (0.0198)	0.9979 (0.0017)
0.5	Two-step	0.4982 (0.0062)	-	0 (0)	1 (0)
	Biased-SVM	0.8320 (0.1507)	0.7402 (0.0133)	0.6734 (0.3071)	0.9909 (0.0069)
	Bagging-SVM	0.8780 (0.0136)	0.8620 (0.0174)	0.7608 (0.0276)	0.9961 (0.0034)
	Mixture model	0.9333 (0.0100)	0.9290 (0.0115)	0.8713 (0.0223)	0.9958 (0.0034)
0.6	Two-step	0.4014 (0.0064)	-	0 (0)	1 (0)
	Biased-SVM	0.6536 (0.2411)	0.4715 (0.0150)	0.4255 (0.4052)	0.9948 (0.0064)
	Bagging-SVM	0.8367 (0.0200)	0.8421 (0.0221)	0.7292 (0.0337)	0.9972 (0.0031)
	Mixture model	0.9310 (0.0116)	0.9390 (0.0112)	0.8895 (0.0224)	0.9928 (0.0061)
0.7	Two-step	0.3012 (0.0063)	-	0 (0)	1 (0)
	Biased-SVM	0.3755 (0.1901)	0.1184 (0.0347)	0.1152 (0.3015)	0.9759 (0.0906)
	Bagging-SVM	0.7858 (0.0220)	0.8188 (0.0224)	0.6946 (0.0321)	0.9975 (0.0034)
	Mixture model	0.9292 (0.0136)	0.9472 (0.0103)	0.9109 (0.0249)	0.9720 (0.0563)

Table 3.

Performance metrics under Case 3: Cauchy distribution. Table shows mean metrics (standard deviation).

π	Method	Accuracy	F-score	Sensitivity	Specificity
0.3	Two-step	0.6994 (0.0062)	-	0 (0)	1 (0)
	Biased-SVM	0.6746 (0.1430)	0.4143 (0.2151)	0.4759 (0.3115)	0.7604 (0.2360)
	Bagging-SVM	0.8146 (0.1036)	0.7422 (0.0705)	0.8372 (0.0468)	0.8047 (0.1614)
	Mixture model	0.8570 (0.0141)	0.7819 (0.0133)	0.8509 (0.0352)	0.8596 (0.0326)
0.4	Two-step	0.5991 (0.0066)	-	0 (0)	1 (0)
	Biased-SVM	0.6101 (0.1161)	0.3326 (0.2237)	0.3550 (0.3290)	0.7819 (0.2557)
	Bagging-SVM	0.7906 (0.0953)	0.7581 (0.0887)	0.7957 (0.0790)	0.7871 (0.1385)
	Mixture model	0.8418 (0.0093)	0.8219 (0.0079)	0.9104 (0.0278)	0.7959 (0.0303)
0.5	Two-step	0.4911 (0.0068)	-	0 (0)	1 (0)
	Biased-SVM	0.5193 (0.0561)	0.2312 (0.2179)	0.2286 (0.2854)	0.8127 (0.2630)
	Bagging-SVM	0.7275 (0.1225)	0.7303 (0.1148)	0.7277 (0.1170)	0.7275 (0.1743)
	Mixture model	0.8468 (0.0077)	0.8612 (0.0056)	0.9484 (0.0191)	0.7448 (0.0291)
0.6	Two-step	0.4009 (0.0066)	-	0 (0)	1 (0)
	Biased-SVM	0.4549 (0.0768)	0.2302 (0.2137)	0.2146 (0.2818)	0.8130 (0.2729)
	Bagging-SVM	0.6719 (0.1523)	0.6992 (0.1646)	0.6588 (0.1735)	0.6908 (0.2009)
	Mixture model	0.8614 (0.0073)	0.8935 (0.0052)	0.9703 (0.0105)	0.6987 (0.0272)
0.7	Two-step	0.3006 (0.0061)	-	0 (0)	1 (0)
	Biased-SVM	0.3800 (0.0997)	0.2329 (0.2107)	0.1995 (0.2483)	0.8010 (0.2483)
	Bagging-SVM	0.6058 (0.1291)	0.6736 (0.1193)	0.5984 (0.1445)	0.6230 (0.2268)
	Mixture model	0.8837 (0.0062)	0.9221 (0.0041)	0.9845 (0.0053)	0.6500 (0.0238)

Fig 2.

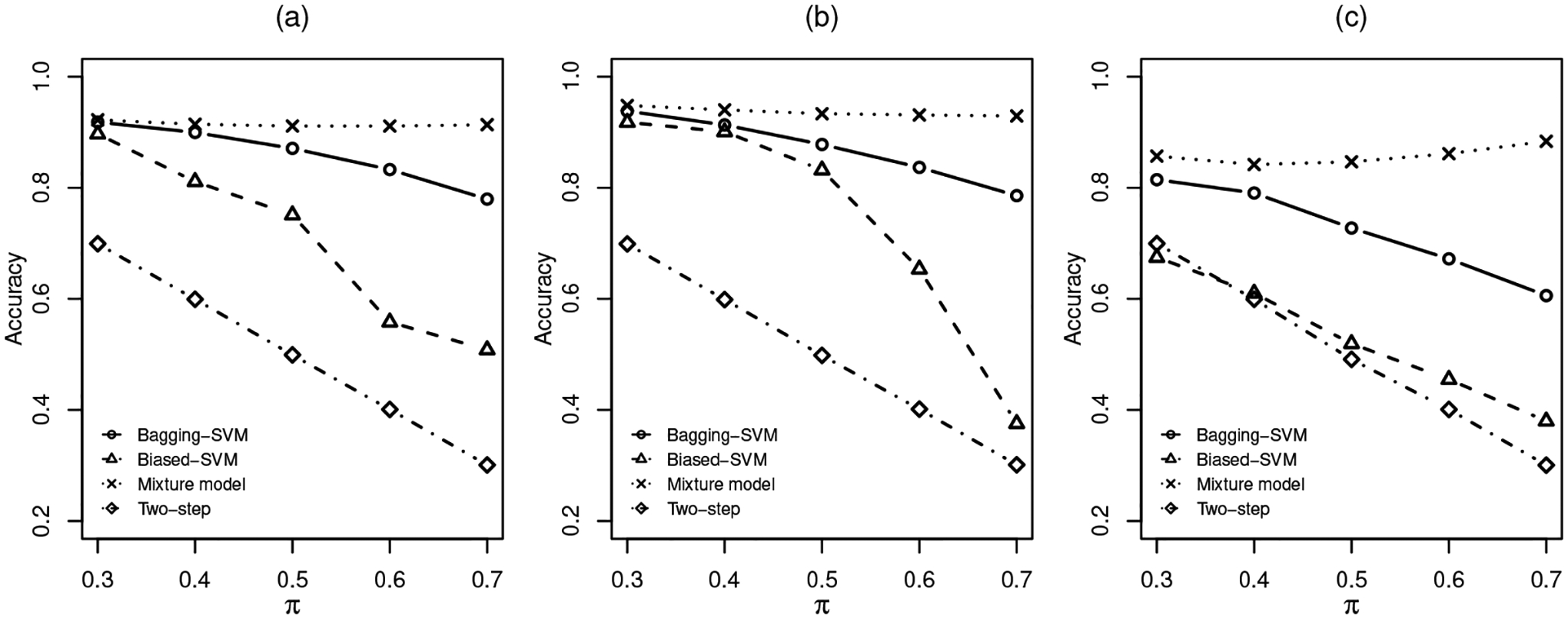
Accuracy under different settings: (a). Multivariate t. (b). Gamma. (c). Cauchy

Fig 3.

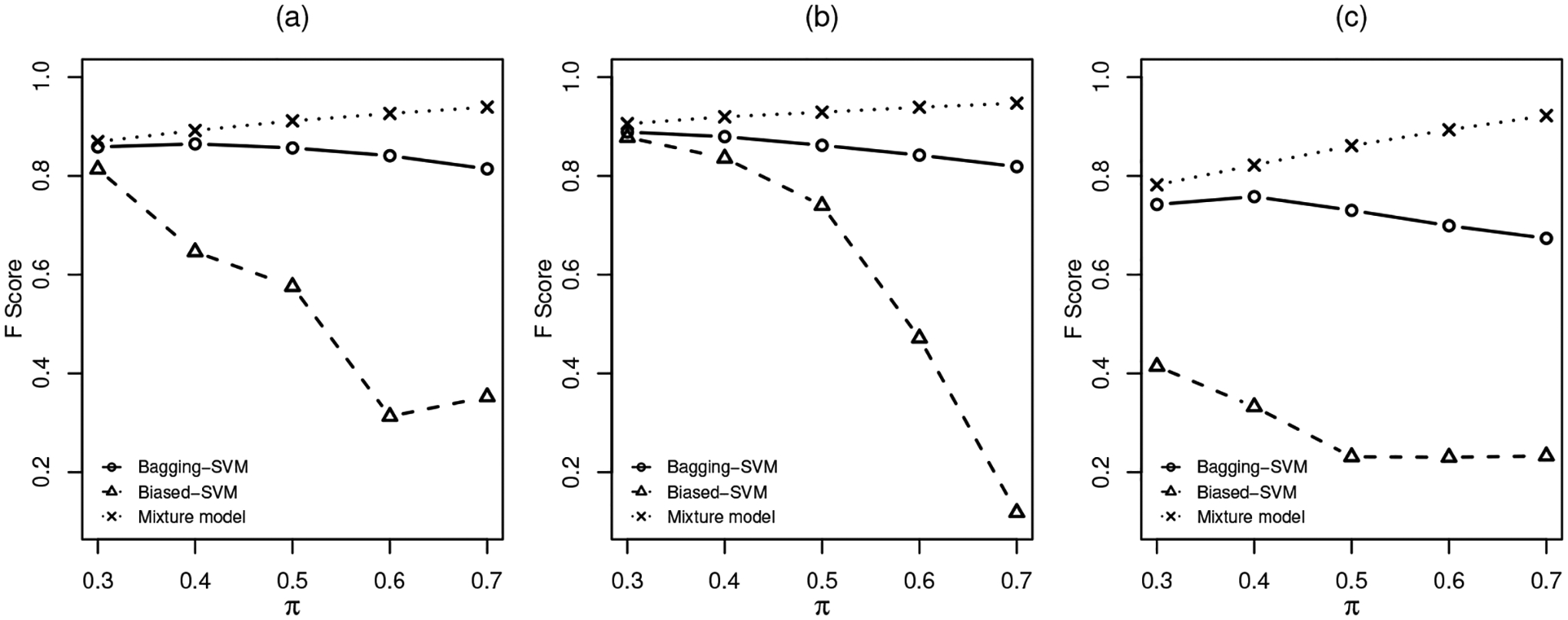
F-score under different settings: (a). Multivariate t. (b). Gamma. (c). Cauchy

5.2. Parameter estimation in the mixture model.

One advantage of using a model-based method is that parameter estimation and statistical inference are possible, which are of interest for medical practitioners as the interpretability is an important issue despite the goal of classification. Suppose that in our simulation scenarios, besides the mixing probability π, a medical practitioner would also like to know the proportion of male patients in the DR group p₁₁ and that in the non-DR group p₂₁. The practitioner also wants to estimate the difference between the DR and non-DR groups in the lab variables for both the male and female populations, that is, to estimate μ_21l − μ_11l and μ_22l − μ_12l, for l = 1, 2, 3. Table 4 assesses the posterior mean estimates for those parameters of interest under the correct t-distribution model. Both the bias and the mean squared error (MSE) seem to be reasonably small for all parameters. Note that we cannot offer comparisons with the algorithm-based methods since they simply do not produce such parameter estimates.

Table 4.

Parameter estimation under the t-distribution for π = 0.3

		True Value	Bias	MSE
	π	0.3	0.0019	0.0192
	p 11	0.5	−0.0164	0.0294
	p 21	0.5	0.0063	0.0109
Male	μ211 – μ111	2	0.0043	0.1147
	μ212 – μ112	2	−0.0682	0.1113
	μ213 – μ113	2	−0.0027	0.1027
Female	μ221 – μ121	2	−0.0079	0.0842
	μ222 – μ122	2	−0.0127	0.0867
	μ223 – μ123	2	−0.0257	0.0963

6. Classifying Unspecified Diagnosis Codes in EHR.

6.1. Data description and preliminary analyses.

Diabetic retinopathy is a vision-threatening microvascular complication of diabetes and a leading cause of blindness among working-aged adults globally (Kobrin and Barbara, 2007; Yau et al., 2012). While diabetes is a common chronic disease worldwide, almost all patients with type 1 diabetes and more than 60% of patients with type 2 diabetes develop retinopathy during their first twenty years of diabetes (Fong et al., 2004). Retinopathy is often asymptomatic in early stages and the vision loss can only be prevented but not restored. Therefore it is imperative to detect and treat patients in their early stages. However, early detection and screening of DR face challenges from poor adherence to annual examination guideline and lack of resources to deploy comprehensive screening programs (Ting, Cheung and Wong, 2016; Ciulla, Amador and Zinman, 2003). It is crucial to develop cost-effective early detection techniques for medical communities, especially for those rural communities. It is conjectured that routine laboratory measurements can be useful in detecting DR without needing comprehensive eye exams. With abundant laboratory information in EHR data, analysts and researchers have been developing predictive models or algorithms for the DR research in recent years, for instance, Piri et al. (2017), Saleh et al. (2016), Sun and Zhang (2019) and Skevofilakas et al. (2010).

The Cerner Health Facts EHR database (Cerner Corporation, Kansas City, MO) is one of the largest de-identified and HIPAA complied databases in the United States. The database contains time-stamped encounter, diagnosis, procedure, medication, and laboratory test data contributed voluntarily from hospitals running a Cerner EHR system across the U.S. from 2000 to 2018. In the step of data pre-processing, the ICD-9 diagnosis codes were used to specify the study cohort. Patients with one or more 250.xx ICD-9 codes were defined as diabetic patients. Within the set of diabetic patients, those who have 362.0x ICD-9 codes were identified as DR patients (case group), and those without any 362.0x code were considered non-DR patients (control group). Note that labelling patients without any 362.0x code as non-DR is questionable since these codes are in fact unspecified. It is, however, a common practice when pre-processing EHR data for secondary analyses.

Based on the existing literature on clinical predictions of DR, we initially included 26 laboratory variables and 3 demographic variables. For the labelled DR patients, we extracted feature values at their first DR diagnosis encounter, and for the labelled non-DR patients, we extracted feature values from their most recent hospital visit. In total 1, 207 labelled DR patients and 39, 767 labelled non-DR patients were finally included in the study cohort. Figure 4 shows the data extraction process. The whole dataset was then divided into a training set (70%) and a testing set (30%). To handle the imbalanced dataset at this initial stage, we implemented the synthetic minority over-sampling technique (SMOTE) which comprises over-sampling the synthetic minority class and under-sampling the majority class (Chawla et al., 2002). We then applied the random forest (Breiman, 2001) on the training dataset and used a ten-fold cross-validation to select the optimal model in terms of the area under the receiver operating characteristic curve (ROC AUC). The model was evaluated on the testing set and the AUC was 0.8709. The model performance was satisfactory on the testing set but in a later section we will see that the prediction can be disappointing in a completely external validating.

Fig 4.

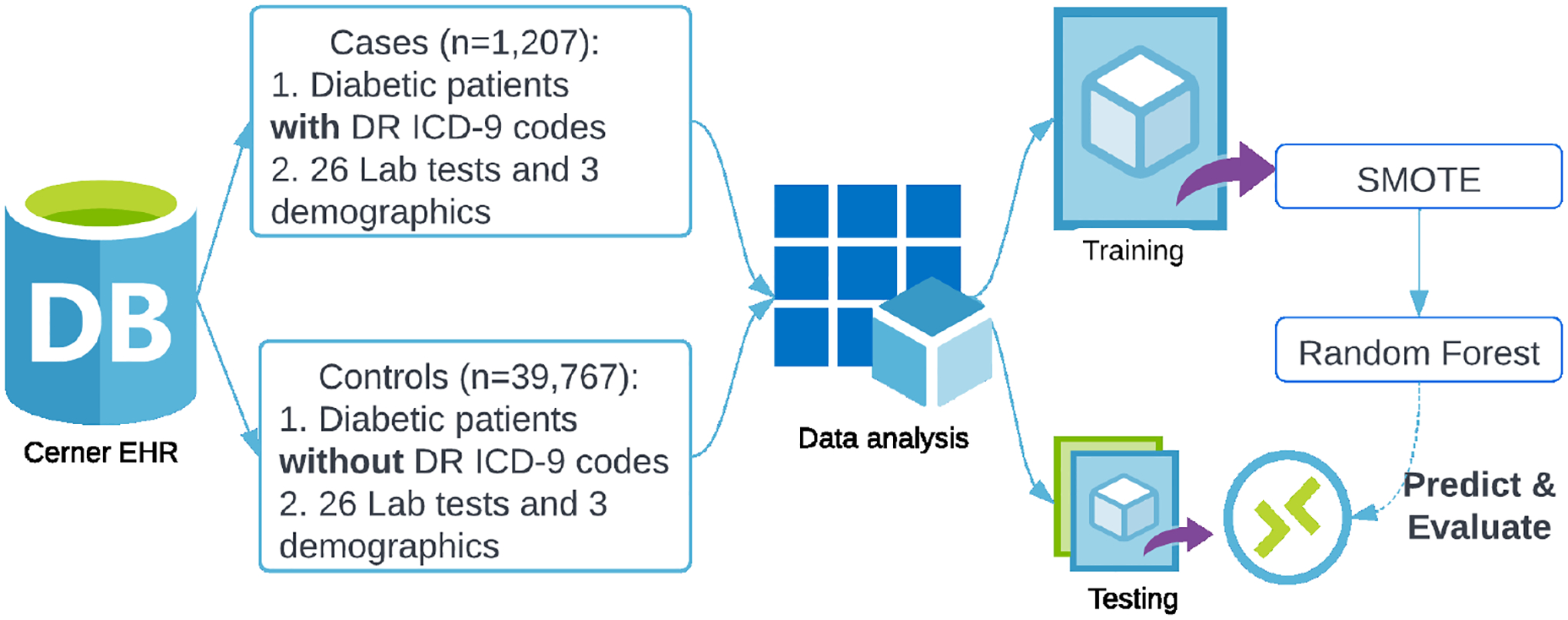
Data extraction and initial analysis

6.2. Applying the proposed PU learning method.

It is a questionable practice to treat patients without any 362.0x code as non-DR patients. As discussed in Section 1, it often happens when a medical examination is not performed on the underlying patient or the record of examination is missing. The apparent consequence is that any secondary analysis based on these data may be misleading as the key label is unreliable. In this section, we consider such a problem as a PU learning task and by applying the proposed Bayesian mixture model, we are able to re-label patients with unspecified codes. Under the PU learning framework, the case group is denoted by 𝒫 and the control group is denoted by 𝒰.

The preliminary analysis using machine learning algorithms helped us to identify a few important predictors. We also carefully surveyed the relevant medical literature and determined three laboratory variables that would be used in the PU learning: HbA1c, hemoglobin and BUN. There is also a general interest to compare male patients with female patients so that the categorical variable gender is also included. It is noteworthy that distributions of laboratory measurements are often skewed and heavy-tailed (MIT-Critical-Data, 2016). Therefore, the proposed multivariate t-mixture after appropriate Box-Cox transformations is suitable for such data. The prior distributions are chosen based on Section 2.3. We divided 𝒰 into S = 20 subgroups. For each subgroup, we ran three Markov chains with distinct initial values and each chain had 10, 000 iterations with burn-in size 4, 000. The convergence for the key parameter π is shown in Figure 5 for an illustration. The Gelman-Rubin diagnostic (Gelman and Rubin, 1992) is performed on all continuous parameters {π, μ_k,j, Σ_k,j, ν_k,j, p_k} and the worst-case potential scale reduction factor is 1.02 (97.5% upper bound 1.06), well below the commonly used threshold of 1.1.

Fig 5.

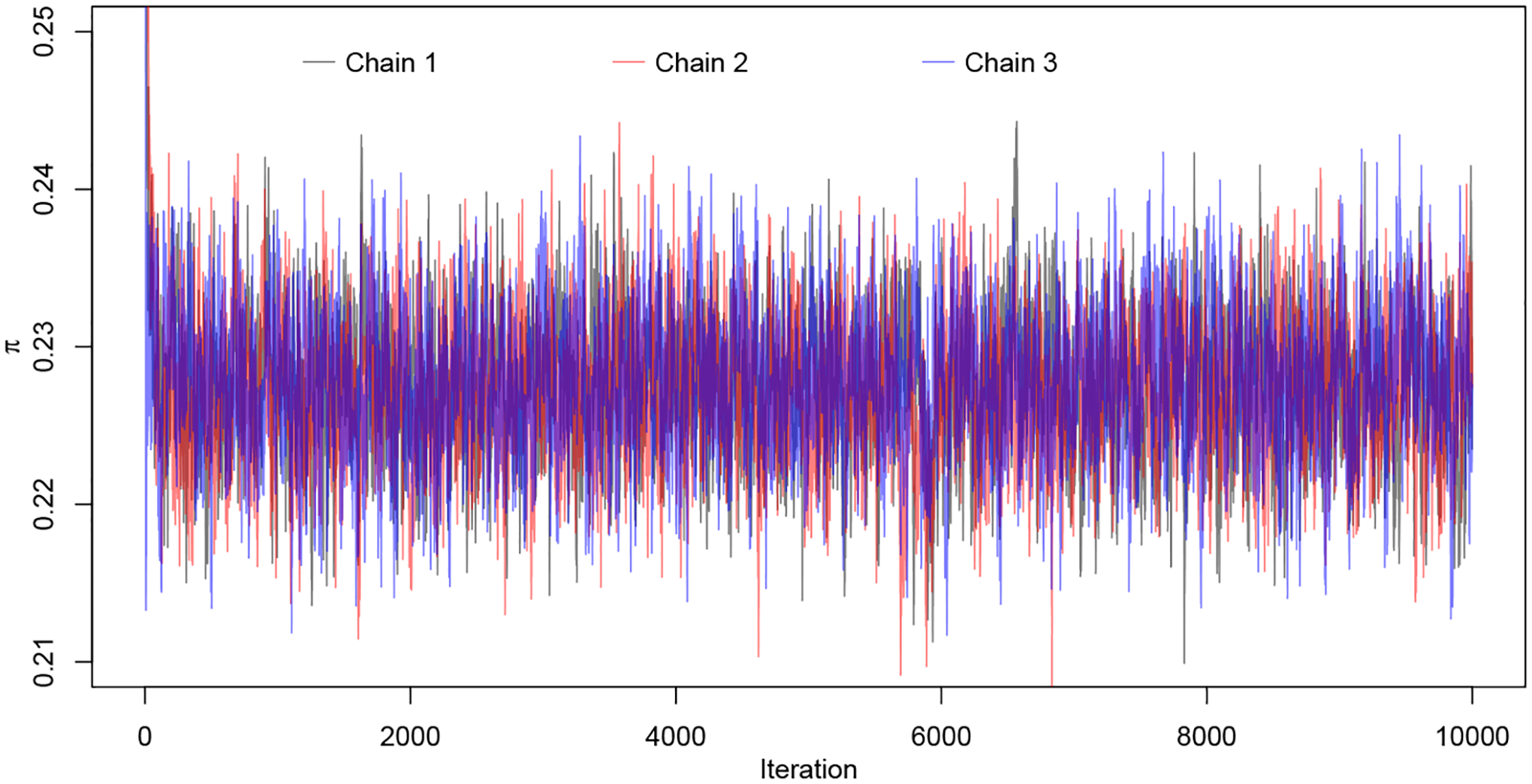
MCMC convergence for π: three chains with distinct initial values.

From the posterior samples, we obtained the posterior mean and standard deviation for the mixing probability π as 0.23 and 0.0043, respectively, indicating roughly one fourth of unspecified cases may be classified into the DR patients group based on the extracted laboratory measurements. From the posterior mean of π, we can estimate the DR prevalence rate for the Cerner Health Facts EHR database, which is $\frac{n_p+\pi n_u}{n_p+n_u}=0.25$. This estimate is in line with the reported incidence of DR among US adults with diabetes, which is 28.5% (95% CI : 24.9% – 32.5%) (Zhang et al., 2010).

For inferential interest in parameters, the posterior estimates for p₁, p₂ and μ_k,j are given in Table 5. Notice that while some categories are not distinguishable (HbA1c DR female vs. non-DR female), some others are clearly distinct (Hemoglobin DR male vs. non-DR male). A patient was classified into the DR group if the posterior probability p(z_i = 1 | Data) ≥ 0.5. Eventually, among 39, 767 unspecified diabetic patients, 7, 010 were classified into the DR patients group. Figure 6 shows, for all three continuous laboratory variables, the distributions of the positive group 𝒫, the unlabelled group 𝒰, re-labelled positives from the unlabelled group 𝒰_p and re-labelled negatives from the unlabelled group 𝒰_n.

Table 5.

Posterior means (standard deviations) for parameters of inferential interest in the mixture model for Cerner EHR data.

	DR		Non-DR
	Male	Female	Male	Female
Proportion	0.5344 (0.0030)	0.4656 (0.0030)	0.4735 (0.0032)	0.5265 (0.0032)
HbA1c	0.9503 (0.0004)	0.8901 (0.0004)	0.9303 (0.0005)	0.8678 (0.0004)
Hemoglobin	4.0014 (0.0037)	2.1320 (0.0012)	4.6537 (0.0034)	2.2783 (0.0010)
BUN	3.7724 (0.0067)	3.2758 (0.0057)	3.1203 (0.0042)	2.7608 (0.0039)

Fig 6.

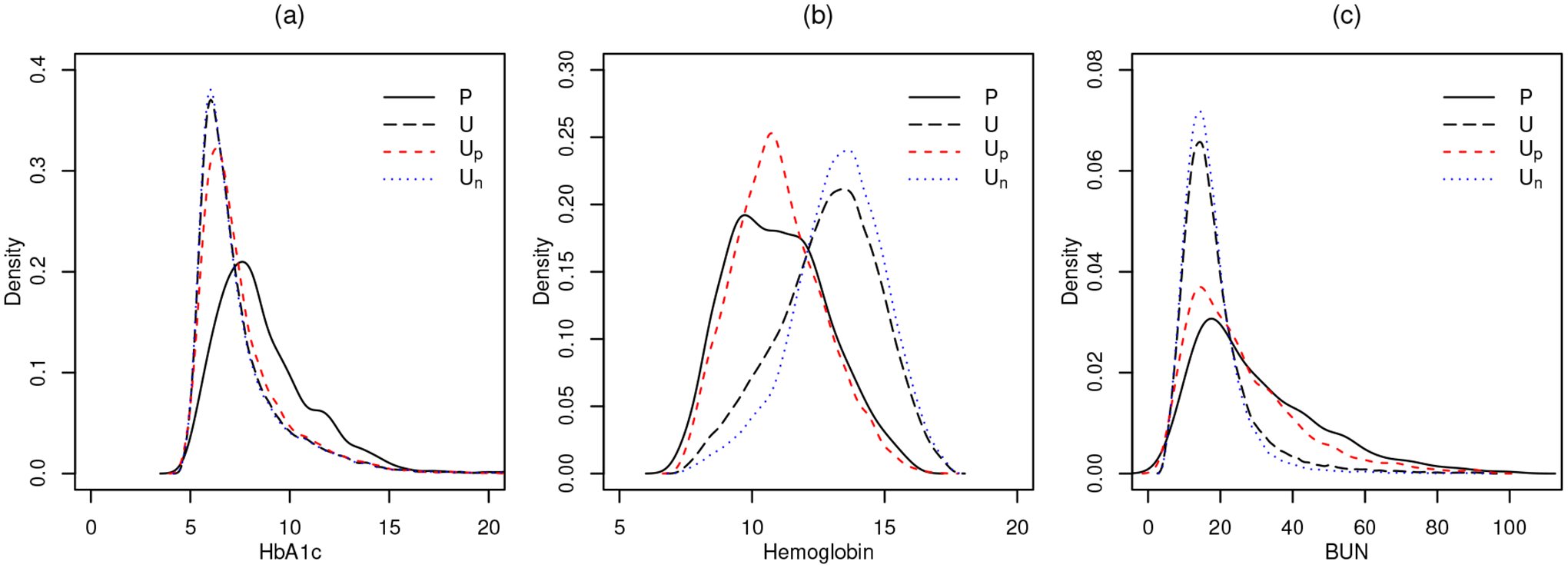
Distributions of the positive group 𝒫 (black solid line), the unlabelled group 𝒰 (black dashed line), the re-labelled positives 𝒰_p (red dashed line) and the re-labelled negatives 𝒰_n (blue dotted line). Plot (a): HbA1c; plot (b): Hemoglobin; plot (c): BUN.

To assess the classification accuracy in the environment of real data analysis, we conduct a further simulation study. We acknowledge that the misclassification rate cannot be properly evaluated due to that true labels are unknown in the unlabelled group. Instead, a simulation that mimics the real data situation is used. Consider now all 1207 positive cases are known positives, and we resample 1207 negative cases from patients who are labelled “negative” after mixture model analysis. These samples are treated as known positives and negatives in the simulation setting. Then 30% randomly selected positive cases are masked and mixed with all negative cases, called unlabelled patients. We fit the Bayesian finite mixture model using the synthetic dataset and record classification accuracy and the area under the receiver operating characteristics curve (AUC). The simulation is repeated for 30 times. The mean accuracy is 0.8982 with standard deviation 0.0115, and the mean AUC is 0.8996 with standard deviation 0.0092.

6.3. Sensitivity Analysis.

We conduct a sensitivity analysis for the mixing probability π with both a formal approach and an informal approach. We adopt a formal sensitivity analysis in Roos et al. (2015) for the Bayesian ϵ-local sensitivity. Given a scalar parameter θ, we denote the base prior and the corresponding marginal posterior by p_γ0(θ) and p_γ0(θ | y), where γ₀ denotes fixed hyperparameters in the base prior. The ϵ-local circular sensitivity $S_{{\gamma }_0}^c(ϵ)$ is defined as

$$S_{{\gamma }_0}^c(ϵ)=\left\{\frac{d\left(p_{\gamma }(\theta \mid y),p_{{\gamma }_0}(\theta \mid y)\right)}{ϵ},\text{ for }\gamma \in G_{{\gamma }_0}(ϵ)\right\},$$

where the grid G_γ0(ϵ) is a contour line around γ₀ and G_γ0(ϵ) = {γ : d(p_γ(θ), p_γ0(θ)) = ϵ}. In Roos et al. (2015), the distance d(·, ·) is recommended to be the Hellinger distance, and ϵ = 0.00354 as it is calibrated to measure the distance between N(0, 1) and N(0.01, 1), a local perturbation. In our case, the base prior chosen for the mixing probability is a beta distribution with γ₀ = (α₀, β₀) = (1, 1). Such a contour line G_γ0(ϵ) is depicted in Figure 7 (a). It is recommended to check the worst-case sensitivity $\text{max}\left\{S_{{\gamma }_0}^c(ϵ)\right\}$ in the ϵ-local grid. A sensitivity value larger than 1 leads to the scenario of super-sensitivity as the marginal posterior changes more than the prior change. Figure 7 (a) shows that our worst-case sensitivity is 0.021, indicating that the marginal posterior is robust against a prior change.

Fig 7.

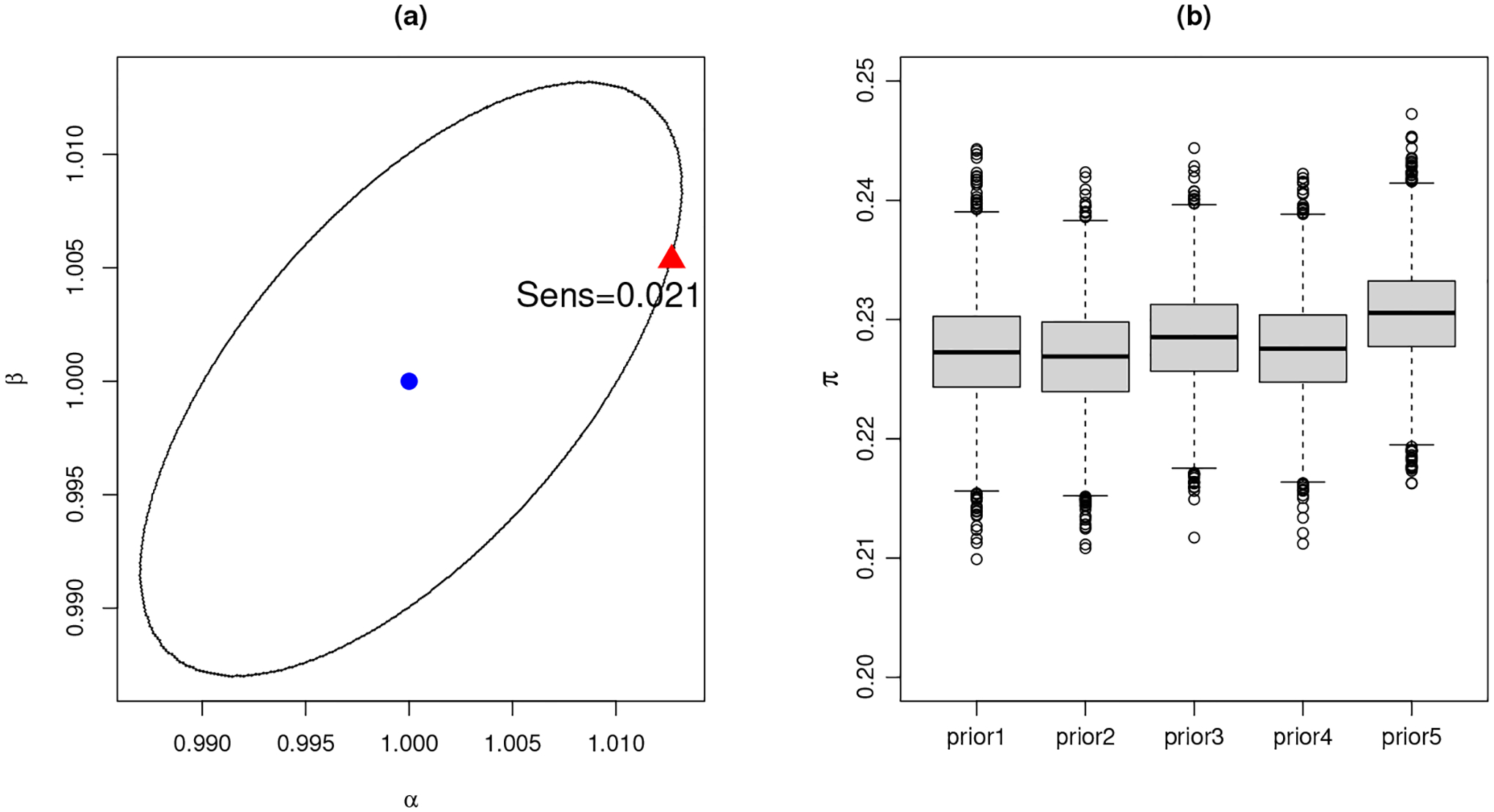
Sensitivity analysis for π: (a). The ϵ-local circular sensitivity. The ellipse is the contour line around the centroid (blue dot) at (α, β) = (1, 1) with Hellinger distance ϵ = 0.00354. The worst-case sensitivity is obtained at the red triangle with sensitivity value 0.021. (b). An ad hoc sensitivity analysis with modified prior hyperparameters. The box plots show posterior samples of π with respect to each prior modification.

An informal sensitivity analysis is then performed by modifying prior hyperparameters in an ad hoc way. The following five scenarios are considered: (1) base-case with no modification; (2) Beta(0.5, 0.5) for π; (3) Beta(5, 12) for π, which centers at about 0.3 with 95% interval (0.1, 0.5); (4) Beta(5, 12) for π and Gamma(3, 1) for the degrees of freedom ν_k,j; (5) Beta(5, 12) for π and Gamma(10, 1) for ν_k,j. For all scenarios, models are re-fitted and resulting marginal posterior distributions for π against each prior choice are shown in Figure 7 (b). The marginal posterior distribution is in general robust against prior modifications.

6.4. Secondary analyses and external validation.

After we re-labelled the EHR dataset based on the PU learning, an analyst now can use the “new” dataset for a secondary analysis. In this section, we show that a machine learning algorithm using the “new” re-labelled data will enjoy a great improvement in terms of predicting a completely external dataset, comparing with using the original dataset.

Suppose now an analyst wants to build a DR predictive model using our Cerner EHR data. We provide him/her two datasets: the original dataset where unspecified patients are labelled non-DR and the re-labelled dataset where unspecified patients are classified based on our PU learning results. The analyst has an external EHR dataset from the University of Kansas Medical Center, which contains 1, 060 confirmed DR patients and can be used as a validation dataset. The validation dataset includes 19 laboratory variables so the analyst builds a random forest model using 19 laboratory variables and 3 demographic variables from the Cerner EHR data. The SMOTE technique has been used for both the original EHR dataset and the re-labelled EHR dataset before building the random forest model. The analyst then uses the fitted model to predict DR cases from the 1, 060 confirmed cases in the validation dataset. Using the original EHR dataset, the analyst is able to detect only 338 or 32% DR patients from the validation dataset, while using the re-labelled EHR dataset, he/she is able to detect 587 or 55% DR patients, which is a remarkable improvement. It is noteworthy that in this validation, the specificity cannot be computed because the number of true negatives is unknown.

7. Concluding Remarks.

In this paper, we proposed to use a Bayesian finite mixture model with multivariate t distributions to solve a PU learning problem that arises from labelling diagnosis codes in EHR data. A split-and-combine strategy known as consensus Monte Carlo is used to address the issue of imbalanced data and improve computational efficiency. We demonstrated its performance in the simulation study compared with existing algorithm-based PU learning methods. We applied the proposed approach to a real application where diabetic patients’ DR codes need to be re-labelled and showed an improved predictive performance in an external validation. It has been warned in the literature that the quality of EHR data is often compromised due to missing or erroneous inputs. In this paper, we showed that a large EHR database only contains about 3% diagnosed DR cases, which is inconsistent with the medical consensus. We estimate about one fourth of diabetic patients potentially labelled as DR patients, in line with the literature. The proposed method can be used as a pre-processing tool for secondary analyses on positive unlabelled EHR data.