Comparison between all-on-four and all-on-six treatment concepts on stress distribution for full-mouth rehabilitation using three-dimensional finite element analysis: A biomechanical study

Abstract

Purpose:

The current study intended to provide a comparison of biomechanical behaviors of two different treatment concepts for full-mouth rehabilitation with dental implants placed according to the “All-on-four” concept and “All-on-six” concept with analysis of the stress patterns of the implant support system using three-dimensional finite element analysis (FEA).

Materials and Methods:

The edentulous mandible was treated with two different implant designs. “All-on-Four” implant placement concept was used in Model 1 with two central axial implants and two distally tilted implants at 17° and in Model 2, “All-on-Six” concept was applied with six vertically placed implants. Individual vertical and horizontal load of 100 N and oblique load of 141 N at 45° was applied to all implants. To evaluate and compare the results in terms of maximum principal stress, we used FEA.

Results:

All-on-six showed smaller maximum principal stress values on the cortical bone and implants. However, maximum principal stress values obtained on trabecular bone was smaller in the All-on-four design for vertical and horizontal loading conditions.

Conclusions:

The All-on-six approach showed more favorable biomechanical behavior.

INTRODUCTION

Dental implants in resorbed mandible often are inadequate to place with their length (>10 mm) because of the vicinity to inferior alveolar nerve in the posterior areas of atrophic mandible. Originally, Branemark had proposed fixed dental implant prosthesis on four and/or six implants for an edentulous mandible.[1] Studies with integrated tilted implants in between interforaminal region for compromised mandible optimize the anterior posterior spread of implants in a way avoidance of neurovascular bundle. This led to acceptance of popular concept of “All on Four “where there is angular placement of distal implants to avoid vital structures.[2] However, there are conflicting evidence with bone resorption and high stress concentration with cortical bone around tilted implants.[3-7] Marginal bone stability circling the dental implants is critical for its longevity and its loss will impact the treatment prognosis. The three-dimensional (3D) finite element method (FEM) is a numeric stimulation used for engineering analysis. Structural stresses, strains, and displacements can be verified when subjected to external and internal loads. Our study compared biomechanical behaviors around distally placed implants of two treatment concepts (all on four and all on six) with implant rehabilitation for moderately atrophic edentulous mandible.

MATERIALS AND METHODS

The study was designed in vitro to provide a comparison of biomechanical behaviors of two different treatment designs for full-mouth rehabilitation with dental implants. Before starting the study, approval was taken from the ethical committee of the university. The concept all on four and all on six for edentulous mandible and their stress patterns generated within the cortical and cancellous bone were analyzed with 3D finite element analysis (FEA).[8–10]

Model fabrication

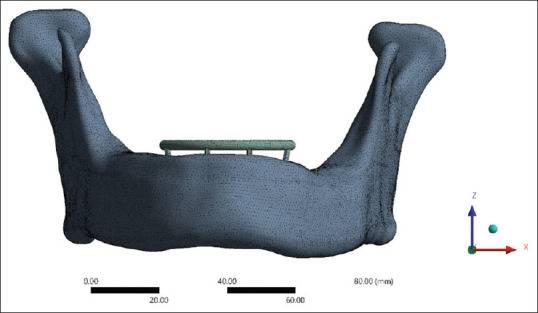
From the patient’s computed tomography, an edentulous mandible was simulated that would be rehabilitated with full arch fixed dental implant prosthesis[11] [Figures 1 and 2]. MIMICS19.0 (Materialise, Leuven, Belgium), a medical imaging and editing program, was used to rebuild the 3D geometry of an edentulous mandible.[12] Semi-autonomic algorithm was applied along with region-growing algorithm to interpolate two-dimensional DICOM image data so as to regenerate the 3D model.[13] The anterior region of the mandible was remeshed with 0.5 mm triangle edge length[14] [Figure 3]. Local smoothing, removal of overlapping triangles, and fixing of bad edges were performed to effectively work the model in FEA. Nonuniform rational B-splines were used to patch surfaces and convert surface model into solid model of mandible[15] [Figure 4]. A 1.006-mm cortical bone layer was defined around the cancellous core[16] [Figure 5]. Implants were designed using the software creo parametric 5.0 student version. Dimensions were retrieved from the scientific literature and catalogs of the used implant in the patient (RAPID DENTIN-Dental Implants Technologies Ltd, Israel) [Figure 6]. Two cylindrical titanium abutments (3 mm high) with a straight profile were modeled and placed on the vertical implants, and 2 abutments angled at 17° were joined to the tilted implants for Model A. Model B had six vertical cylindrical titanium abutments for all the six implants. A rigid cobalt chromium 3 mm thick and 10 mm long, in the shape of an arc, was designed to serve as a framework joined to the implant abutments.[9] The final model represented a completely fixed prosthetic replacement for an edentulous mandible supported by 4 implants (Model A) according to the All-on-4 technique and 6 implants (Model B) [Figures 7-10 and Table 1].

Figure 1.

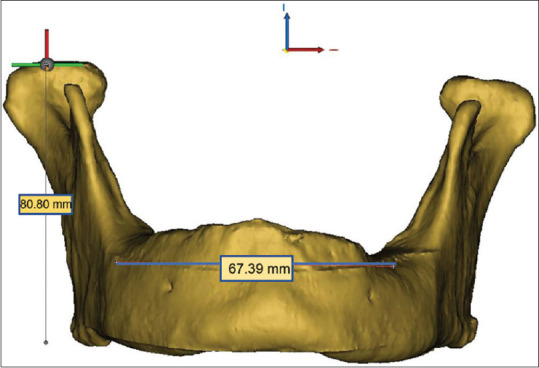
3D model with measurements (frontal view). 3D – Three-dimensional

Figure 2.

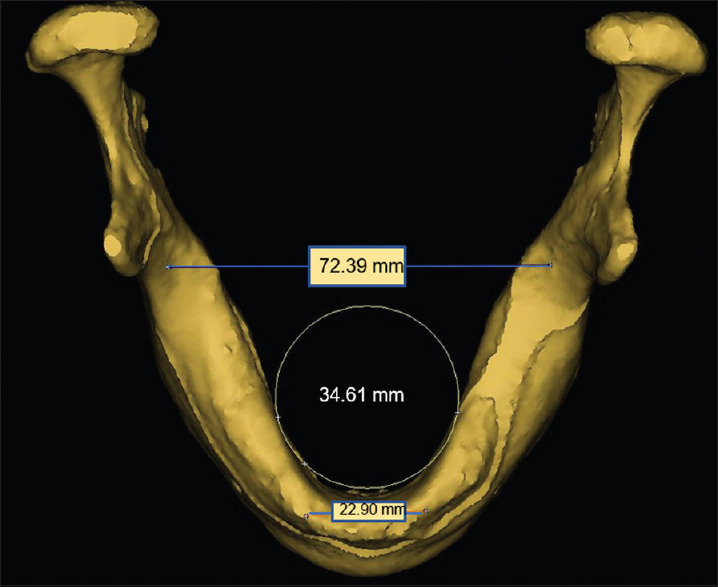
3D model with measurements (occlusal view). 3D – Three-dimensional

Figure 3.

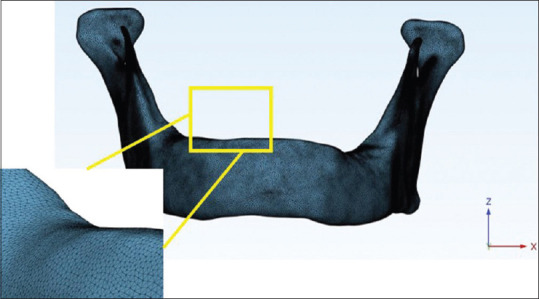
Adaptive remeshing

Figure 4.

Local smoothing, removal of overlapping triangles and fixing of bad edges

Figure 5.

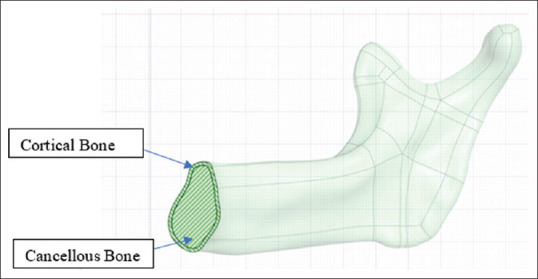
Model depicting cortical and cancellous bone

Figure 6.

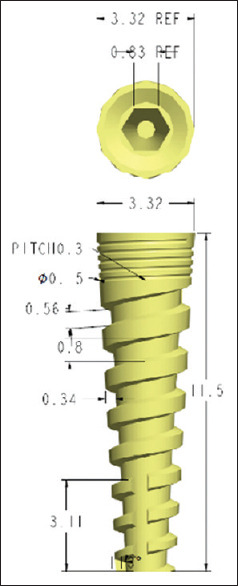
Implant model (3.3 mm × 11.5 mm)

Figure 7.

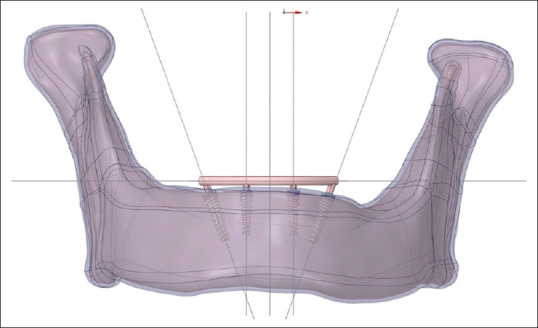
3D model with all-on-four concept. 3D – Three-dimensional

Figure 10.

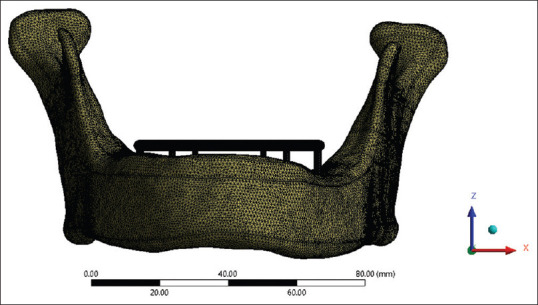
Meshing for model B (All on six)

Table 1.

Description of models

Clinical situation	Implant number	Implant location	Implants positioning	Implant dimensions (mm)	References
All on 4	4	2-lateral incisor	Vertical	3.3×11.5	[2,17]
		2-second premolar	Inclined 17°to distal	3.8×11.5	[18]
All on 6	6	2-lateral incisor	Vertical	3.3×11.5	[9,19]
		2-second premolar	Vertical	3.8×11.5
		2-second molar	Vertical	4.2×11.5

Figure 8.

Meshing for model A (all on four)

Figure 9.

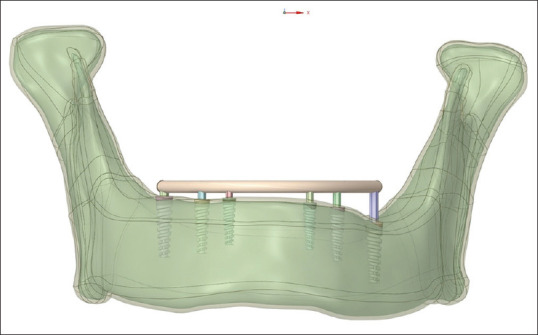
3D model with all-on-six concept. 3D – Three-dimensional

Finite element analysis

The 3D geometry was exported to FEA software ANSYS (ANSYS Inc, Canonsburg, Pa, USA) and was graphically simulated in the computer in the form of a mesh that defined its geometry. In a procedure known as discretization, the mesh was split into a number of linear tetrahedral components called elements that were connected at points called nodes. The precision of the computations depended on the size of the elements. The Models A and B were meshed with the following parameters: element size for cortical and trabecular bone: 0.5 mm element size for abutment, bar framework, and implant: 0.2 mm [Table 2].

Table 2.

Element and node numbers for Model A and B

Model	Nodes	Elements
A (all on 4)	1,039,145	605,946
B (all on 6)	2,182,276	1,384,964

All materials were considered to be isotropic, linearly elastic, and homogeneous. The mechanical properties of the materials used in this study are presented in Table 3. The configurations in this study were deliberately constrained in the mandible so as to simulate the boundary conditions most closely to the anatomical constraints. To simulate a fully osseointegrated state, bone–implant interface was deemed to be completely fixed, with no crestal bone loss around implants, and without any gap at the implant–abutment junction. A perfect fit was assumed between the implants, the bone, and the prosthetic structures. For evaluating and subsequent comparison of stress distribution on the bone–implant interface in each model, the following three loading conditions were evaluated[24] [Figure 11].

Table 3.

Mechanical properties of the materials used

Material	Young’s modulus (MPa)	Poisson’s ratio	Reference
Ti Grade 23 (Ti6Al4V-ELI)	113,800	0.3	[20]
Cortical bone	13,700	0.3	[21]
Trabecular bone	1370	0.3	[22]
Cobalt chromium	218,000	0.3	[23]

Figure 11.

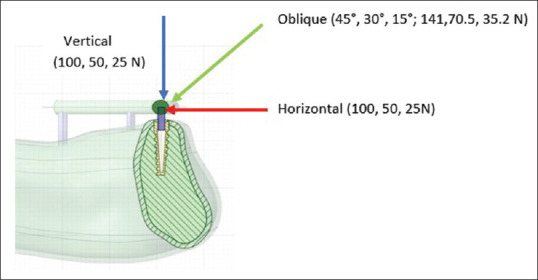
Loading conditions

• Loading 1: Individual vertical load of 100 N was applied to all the implants

• Loading 2: Individual horizontal load of 100 N was applied to all the implants

• Loading 3: Individual oblique load at 45° buccolingually of 141 N was applied to all the implants.

The mathematical solutions were translated into visual outputs with varying degrees of color, ranging from red to blue, with red signifying the highest stress levels. The simulations’ findings were evaluated in terms of the maximum principal stress levels. Stress in a particular zone was analyses by UMAT Subroutine. The maximum stress values were obtained primarily for the purpose of comparing the two models and not for the purpose of reporting absolute values.

RESULTS

Tables 4 and 5 depict maximum principal stress (smax) experienced in cortical bone, trabecular bone, all implants, and left and right distal most implants. The maximum principal stress values (MPa) were more in Model A with respect to Model B for cortical bone, all implants, and the two distal most implants. However, the stress values for trabecular bone were in opposite trend under vertical and horizontal loading conditions.

Table 4.

Maximum principal stress on different components (MPa)

Components	Model	Vertical load (100 N)	Horizontal load (100 N)	Oblique 45° load (141 N)
Cortical bone	Model A (4)	77.56	16.11	139.85
	Model B (6)	8.76	6.87	5.47
Trabecular bone	Model A (4)	1.28	0.88	1.52
	Model B (6)	2	1.94	0.96
All implants	Model A (4)	438.85	52.21	244.43
	Model B (6)	21.8	37.75	35.51
Left distal most implant	Model A (4)	13.87	47.64	49.96
	Model B (6)	21.08	23.66	22.25
Right distal most implant	Model A (4)	18	49.39	244.33
	Model B (6)	14.32	37.75	31.51
Left central (anterior) implant	Model A (4)	438.85	41.13	25.08
	Model B (6)	15.64	14.47	10.06
Right central (anterior) implant	Model A (4)	15.79	52.21	29.29
	Model B (6)	13.37	16.74	9.49

Table 5.

Maximum principal stress on different components (Mpa) (Representation on 3 D models)

Component	Model	Vertical load (100 N)	Horizontal load (100 N)	Oblique 45° load (141 N)
Cortical bone	Model A (4)
	Model B (6)
Trabecular bone	Model A (4)
	Model B (6)
All implants	Model A (4)
	Model B (6)
Left distal most implant	Model A (4)
	Model B (6)
Right distal most implant	Model A (4)
	Model B (6)
Left central (anterior) implant	Model A (4)
	Model B (6)
Right central (anterior) implant	Model A (4)
	Model B (6)

When compared to the same implant in the “All-on-Four” model, the six-implant model showed less stress, with a notable drop in the most mesial implant. Also, it was observed that stress was concentrated in the same way in both models at the implant neck in all of the loading situations.

DISCUSSION

The manner in which stresses are distributed to the surrounding bone is a major element in deciding whether a dental implant prosthesis succeeds or fails.[25] Vertical and transverse loads from mastication result in stress gradients in the implant as well as on the bone.[26] These forces create deformations within the surrounding bone and induce strain in the implant and supporting tissue contact zone.[27] Hence, stress analysis become important to examine the biomechanical behavior of implant-based restorations and the surrounding tissues under functional forces. The present study compared biomechanical behaviors of two different treatment concepts of edentulism with full-mouth rehabilitation with dental implants (all-on-four-Model A and all-on-six-Model B). The clinical and radiographic versions of both these concepts are shown in Figures 12 and 13.

Figure 12.

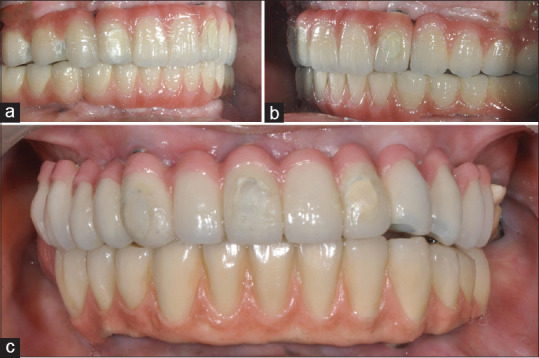
(a) Right lateral view, (b) Left lateral view, (c) Frontal view

Figure 13.

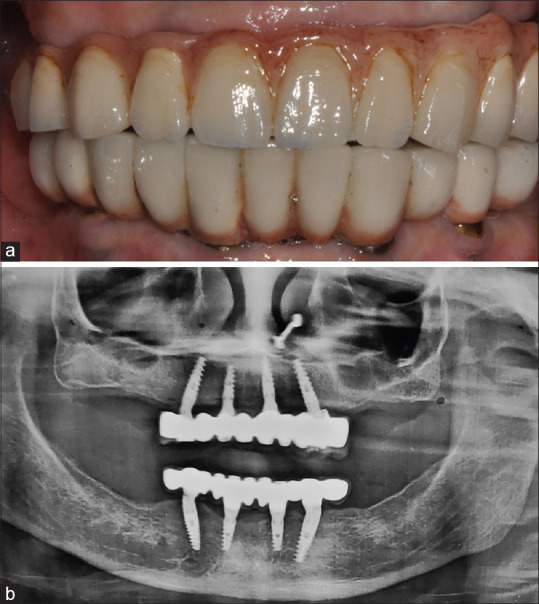
All-on-four (a) Frontal intra-oral view (b) Orthopantomogram

The ultimate oblique masticatory forces for several cylindrical implants were determined by Demenko et al.[28] They calculated the 118.2 N masticatory force by simulating it at a 75° angle to the occlusal plane. According to several researches, oblique forces better reflect occlusal stresses.[29,30] In our study, simulation of mastication was evaluated with the application of the vertical and horizontal loads (100 N) as well as a combined oblique load (141 N) at 45° inclination to the occlusal plane individually to each implant.[24] In all loading situations, irrespective of the model, the maximum principal stress was concentrated on the implant neck, as observed in other studies.[30,31,32,33] Model B (six implants) resulted in better overall stress distribution patterns. For this model, the stress was dispersed over a greater area, extending from implant #6 to implant #1 (cortical bone, trabecular bone, and implants). Presence of a distal support in this group (implant #6) led to a better stress distribution spanning a greater area. Further, all-on-six configuration showed lower maximum principal stress (smax) values on the cortical bone and implants when compared with Model A which consistently showed higher stress values in all the loading conditions.

However, considering the smax in the trabecular bone, Model B showed a higher value than the Model A in horizontal and vertical loading conditions. Previous research evaluating treatment techniques for the edentulous mandible have found similar results.[26] According to an in vivo study, the inclusion of additional implants leads to reduction in stress demonstrating a lower value in the axial loads in a six implant-supported prosthesis when compared to a prosthesis supported by four or three implants.[34] With a larger number of implants, Model B in our study was better able to transmit force to the implants and supporting tissues. Ozdemir Dogan et al. found that the six-implant model performed better than the four-implant type in the mandible.[10] However, they examined only the minimal principal stress on bone tissue while using a titanium framework. Almeida et al. observed lower maximum and minimum principal stress values with the six-implant model than with the four-implant model with a titanium framework.[19] In addition, their models have been simplified (i.e., there was no anatomical framework or implant threads). Silva et al. compared the biomechanical behavior of the “All-on-Four” system to that of a six-implant-supported maxillary prosthesis with slanted distal implants.[9] The scientists discovered that the two models’ stress locations and distribution patterns were similar. However, the addition of implants reduced the maximum von Mises stress values, but the presence of a cantilever increased the stress significantly. Overloading in cortical and trabecular bone occurs when the max exceeds 100–130 MPa and 5 MPa, respectively, according to physiological limits (ultimate bone strength).[35,36] The values found in both the treatment ideas were lower than those considered pathologic to bone tissue based on these parameters. The encouraging results of the six-implant concept suggested that in the cases of biomechanical risk (e.g., bruxism, low-quality bone), a larger number of implants may be required.[9] A further benefit is the elimination of a cantilever in this concept by using distal most implants. Rubo et al. and Bevilacqua et al. demonstrated that implants experience an increase in stress proportional to cantilever length.[37,38] This is a primary contributor to implant dentistry clinical failures.[36,39] Zampelis et al. in their two-dimensional study observed that when cantilever segments were removed, stress concentrations at the most coronal bone–implant contact site were subsequently lowered.[31] In our study, distal most implants experienced greater stress in the four-implant model than in the six-implant model. It was in agreement with a similar study done by Naini et al.[40] The authors fabricated 3-D finite element models of mandibular bone and four dental implants which were subsequently placed in two different configurations – with the distal most implants tilted (model A) or placed parallel (model S). They found that the posterior tilted implants experienced higher stresses in every loading scenario. Several investigations, however, have revealed that tilting the distal implants produces no significant difference in patterns of stress distribution, rather provides a biomechanical advantage by reducing cantilever segments.[31,41] Five to six implants were employed in the majority of clinical investigations evaluating tilted implants and demonstrated favorable outcomes.[42-44]

In FEA, the authenticity of the findings is largely dependent on the precise representation of the geometry of interest in the analyzed model. There are, however, some limitations to FEM, mainly in biologic simulations, that compel studies to assume simplifications.[44] Bone is an incredibly complicated living structure and its characteristics vary from individual to individual. In addition, the use of FEM when studying the extremely accurate anatomy of a bone structure may limit the analysis to that particular structure. As a result, a few simplifications were made to generalize the findings and make the study easier to conduct without jeopardizing the validity of the findings. The models in this study were assumed to be homogeneous and isotropic, ideal conditions were established, including 100% bone-to-implant contact and perfect fit of implants, abutments, and prosthetic bars. Since this study was comparative in nature, such assumptions would not interfere with the aims as they were present in both models. Furthermore, the screws at the implant–abutment and prosthesis–abutment interfaces were not modeled, and the connections were designed to be rigid. As finite element 3D models are simplified representations of the investigated structures, it is appropriate to interpret the numeric values reported in this study as biomechanical indications.

CONCLUSIONS

It could be inferred from the findings obtained in our study that the all-on-six treatment concept (Model B) which showed better biomechanical behavior could be considered a viable alternative for long-standing edentulous mandible rehabilitation. The additional number of implants in the six-implant model increased the prosthesis support and experienced reduced maximum principal stress with better distribution of stress over a larger region. The results of our study suggest that particularly in the cases of biomechanical risk (e.g., bruxism, low-quality bone), larger number of implants may be required for better stress distribution and in atrophic ridges, “All-on-Four” design could be a good alternative.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.