Predicting cumulative lead (Pb) exposure using the Super Learner algorithm

Abstract

Chronic lead (Pb) exposure causes long term health effects. While recent exposure can be assessed by measuring blood lead (half-life 30 days), chronic exposures can be assessed by measuring lead in bone (half-life of many years to decades). Bone lead measurements, in turn, have been measured non-invasively in large population-based studies using x-ray fluorescence techniques, but the method remains limited due to technical availability, expense, and the need for licensing radioactive materials used by the instruments. Thus, we developed prediction models for bone lead concentrations using a flexible machine learning approach–Super Learner, which combines the predictions from a set of machine learning algorithms for better prediction performance. The study population included 695 men in the Normative Aging Study, aged 48 years and older, whose bone (patella and tibia) lead concentrations were directly measured using K-shell-X-ray fluorescence. Ten predictors (blood lead, age, education, job type, weight, height, body mass index, waist circumference, cumulative cigarette smoking (pack-year), and smoking status) were selected for patella lead and 11 (the same 10 predictors plus serum phosphorus) for tibia lead using the Boruta algorithm. We implemented Super Learner to predict bone lead concentrations by calculating a weighted combination of predictions from 8 algorithms. In the nested cross-validation, the correlation coefficients between measured and predicted bone lead concentrations were 0.58 for patella lead and 0.52 for tibia lead, which has improved the correlations obtained in previously-published linear regression-based prediction models. We evaluated the applicability of these prediction models to the National Health and Nutrition Examination Survey for the associations between predicted bone lead concentrations and blood pressure, and positive associations were observed. These bone lead prediction models provide reasonable accuracy and can be used to evaluate health effects of cumulative lead exposure in studies where bone lead is not measured.

GRAPHICAL ABSTRACT

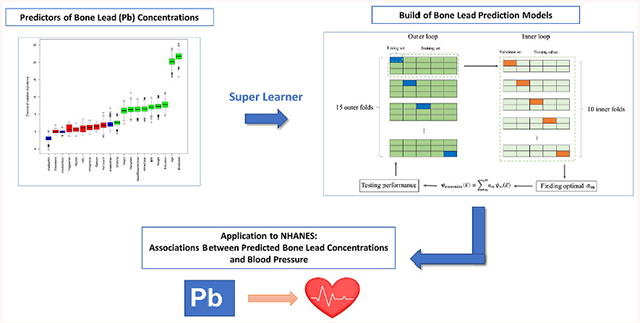
1. Introduction

Lead exposure and related health and societal effects remain a significant public health concern in the United States and globally. Since the 1970s, primary preventative initiatives such as the removal of lead from gasoline and lead solder from food cans have considerably reduced environmental sources of lead (Pirkle et al., 1994). Nonetheless, the general population has been exposed to lead through various sources, including ambient air, smoking, drinking water, and food (Frank et al., 2019). Furthermore, lead from environmental exposures can accumulate in the body, notably in bones, for decades. Bone lead levels have been shown to be associated with cross-sectionally and prospectively with adverse health consequences including cardiovascular disease, neurodegenerative disease, and mortality in aging populations (Bakulski et al., 2020; Lanphear et al., 2018; Navas-Acien et al., 2007).

Blood lead concentration has been the primary biomarker used to quantify lead exposure in biomonitoring programs, screening and diagnostic processes, and epidemiologic studies. However, blood lead reflects, for the most part, recent lead exposure due to its short half-life of approximately 30 days. Cumulative lead exposure, on the other hand, is more relevant than recent exposure for assessing the lead effects on chronic health outcomes (Hu et al., 2007). Once lead enters the body from external environmental exposure, circulating lead in the blood is deposited into multiple bone sites, where it has a half-life on the order of years to decades (Wilker et al., 2011). In adults, bone lead accounts for more than 95% of the total lead body burden (Barry and Mossman, 1970), rendering bone lead a better indicator of cumulative lead exposure. Bone lead can be assessed with the noninvasive K-shell X-ray fluorescence (KXRF) technique (Hu et al., 1995). Several studies have reported associations of bone lead concentrations as measured by KXRF with a series of chronic health outcomes (Ding et al., 2018,2016; Park et al., 2010; Payton et al., 1998; Weisskopf et al., 2009). However, logistical challenges including the cost and technical expertise required to operate KXRF, licensing issues for the use of radioactive materials, and participant burden (travel, measurement time, radiation exposure) have often precluded the bone lead measurement as an exposure indicator in large population-based studies.

Advances in prediction modeling using modern machine learning algorithms have paved the way for essential applications in environmental exposure assessment (Di et al., 2019; Verner et al., 2015). Park et al. developed a prediction model for bone lead concentration using linear regression where a set of bone lead determinants including blood lead and other demographic, socioeconomic, and clinical variables were incorporated (Park et al., 2009). This model imposed stringent assumptions on the association between bone lead concentrations and its predictors, such as linear and additive relationships. Given the complexities of predicting bone lead concentrations, such assumptions may be violated, limiting prediction performance if the model is incorrectly specified—hence, a more flexible modeling option would be favored.

The goal of this study is to develop and validate an updated prediction model for bone lead concentrations (patella and tibia) using a more flexible machine learning approach, namely Super Learner (Van der Laan et al., 2007), which combines the predictions from a set of individual machine learning algorithms to yield a final ensemble of prediction function that has been proven to be asymptotically as accurate as of its best possible component algorithm across different settings. We used data from the Normative Aging Study (NAS) where KXRF-assessed bone lead and potential predictors of bone lead are available. In addition, we evaluated the applicability of this prediction model by examining the associations between predicted bone lead concentrations and blood pressure in the National Health and Nutrition Examination Survey (NHANES).

2. Materials and methods

2.1. Study population

The NAS is a prospective cohort study of community-dwelling men with no known occupational lead exposure (Hu et al., 1995). In 1961 and 1962, 2280 men aged 21–80 years were enrolled from the Greater Boston area. All participants were free of any chronic medical conditions at the time of enrollment, including heart disease, cancer, diabetes, peptic ulcer, gout, bronchitis, sinusitis, recurrent asthma, or hypertension. Participants returned for regular examinations approximately every three to five years. At each clinical visit, a thorough physical examination was conducted, and blood specimens for routine clinical analysis and for blood lead assay, and information on medical history and other aspects that might impact health were collected. Between 1991 and 2002, a subset of 871 participants underwent patella and tibia bone lead measurements using KXRF. Bone lead concentrations were measured at a one-time point within approximately six weeks of a clinical visit. For the current study, we excluded 9 participants with high bone lead concentration uncertainties (> 15 μg/g for patella lead, and >10 μg/g for tibia lead), and 167 participants with missing information on bone lead predictors, yielding a final analytic sample of 695 men for building the bone lead prediction models.

2.2. Bone and blood lead measurements

Bone lead concentrations were directly measured at two bone sites, the patella and mid-tibial shaft, using a KXRF instrument (ABIOMED, Danvers, MA, USA), as described in detail previously (Hu et al., 1995). The patella is nearly entirely made up of trabecular bone, whereas the mid-tibia is made up of cortical bone. Lead accumulates faster in trabecular bone, with a half-life of a few years, compared to cortical bone, which has a half-life of decades (Wilker et al., 2011). As a result, tibia bone lead has often been seen as a biomarker of lifetime cumulative lead exposure, while patella bone lead has been recognized as more current, mobilizable lead reserves. The KXRF provides unbiased estimates of bone lead concentrations, expressed as μg of lead per g of bone mineral (μg/g). Negative values can be returned by the KXRF when the bone lead concentrations are close to zero. All the values, including the negative ones, were retained in the construction of bone lead prediction models (Park et al., 2009). KXRF also derives an estimate of the measurement uncertainty that reflects the variance both in the X-ray signal and in the background underlying the signal, and it is equivalent to the standard deviation one would expect from multiple measurements. Participants with high bone lead concentration uncertainties (>15 μg/g for patella lead, and >10 μg/g for tibia lead) were excluded because these measurements usually reflect excessive participant movement during the measurement or a degraded signal of X-ray (Aro et al., 1994). Whole blood samples were obtained from venous blood draw into trace metal-free tubes containing ethylenediaminetetraacetic acid. Blood lead concentration was determined using graphite furnace atomic absorption spectroscopy (ESA Laboratories, Chelmsford, MA, USA). The limit of detection (LOD) for blood lead was 1 μg/dL. Less than 1% of participants had blood lead concentrations below the LOD, and these values were imputed with the LOD divided by the square root of two.

2.3. Predictor selection

A total of 17 candidate predictors was initially included as shown in Table 1 based on their determinant roles and data availability (Park et al., 2009). Health conditions, such as blood pressure and disease diagnosis, were not included in this list because the previous study found that using predicted bone lead concentrations from these variables would lead to inflated significant results when examining the associations with the related health outcomes (Park et al., 2009). We next employed the Boruta algorithm (Kursa and Rudnicki, 2010), a novel variable selection approach, to select the most important predictors for patella and tibia lead concentrations, respectively. An initial step screening often improves prediction if signal to noise ratio is not high. The Boruta algorithm is an extension of the random forest algorithm and selects important variables by comparing the importance of variables with the shadows (permutations) of those variables, which performs well across various variable distributions and provides a subset of all the independent variables for a given regression task rather than minimal subsets specified to different algorithms. Briefly, this process consists of the following four steps:

Table 1.

Distributions of lead concentrations and their potential determinants in the Normative Aging Study (NAS) (N = 695). All participants were White men.

Characteristics	Mean (SD) or n (%)	Range
Bone lead concentrations
Patella lead (μg/g)	31.1 (19.5)	−9 – 165
Tibia lead (μg/g)	21.6 (13.3)	−5 – 126
Candidate predictors
Blood lead (μg/dL)	5.0 (1.9)	0.7–27.9
Age (year)	67.1 (7.2)	48–94
Height (m)	1.7 (0.1)	1.5–2.0
Weight (kg)	83.6 (13.0)	52.7–128.5
Body mass index (kg/m2)	27.8 (3.7)	16.7–42.4
Waist circumference (cm)	98.2 (9.6)	70.1–129.7
Serum calcium (mg/dL)	9.6 (0.4)	8.3–11.3
Serum phosphorus (mg/dL)	3.1 (0.5)	1.9–4.6
Total cholesterol (mg/dL)	228 (37)	145–438
High-density lipoprotein (mg/dL)	48 (13)	15–131
Triglyceride (mg/dL)	150 (79)	24–470
Hematocrit (%)	434 (3)	29–52
Alcohol consumption (gram/day)	13 (18)	0–104
Cumulative cigarette (pack-year)	22 (26)	0–136
Smoking status
Never	214 (30.8)
Former	418 (60.1)
Current	63 (9.1)
Education
High school dropout	71 (10.2)
High school of some college	425 (61.2)
College and above	199 (28.6)
Job type
White collar	367 (52.8)
Non-white collar	328 (47.2)

1. Create random permutated copies of real variables, which are called shadow variables.

2. Fit the random forest on the entire data, including both real and shadow variables, and compute the z-scores of importance of each variable (the difference in the average absolute error of the random forest models with and without this variable).

3. Compare the mean z-scores of the variable importance between real and shadow variables and remove the real variables with significantly lower z-scores than the highest shadow variables.

4. Repeat the iterations until all variables are retained or removed or reach a specified limit of random forest iterations (2000 in our study).

All variables retained in the Boruta algorithm were included as predictors in patella and tibia lead prediction models. Hereafter, we refer to these models as “full models.” We also built prediction models for patella and tibia lead based on a subset of seven predictors that are selected in the Boruta algorithm and widely available in population-based studies, including blood lead concentration, age, education, job type, body mass index (BMI), smoking status, and cumulative cigarette pack-years. We refer to these models as “reduced models.”

2.4. Construction and validation of prediction models

We implemented Super Learner, an ensemble machine learning algorithm seeking optimal prediction by calculating a weighted combination of predicted values from a collection of candidate algorithms (Van der Laan et al., 2007), to build bone lead prediction models. In our study, we utilized the following eight algorithms, including linear regression, generalized additive model (Wood, 2017), ridge regression (Hoerl and Kennard, 1970), least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996), elastic-net (ENET) (Zou and Hastie, 2005), classification and regression tree (CART) (Loh, 2011), random forest (Breiman, 2001), and XGBoost (Chen and Guestrin, 2016). R packages for implementation of each algorithm and corresponding hyperparameters that we tuned are summarized in Table S1. A Super Learner ensemble was then calculated as a weighted sum of predictions from these eight algorithms by

$${\psi }_{\mathit{ensemble}}(E)={\sum }_m^M{a}_m{\psi }_m(E)$$

where ψ_m(E) is the prediction from the m-th algorithm (m = 1, 2, 3, …, M) and a_m is the corresponding weight. In our study, we log-transformed blood lead concentration, and standardized each continuous variable due to scaling requirements for some algorithms and coded categorical variables as dummy variables. Bone lead concentrations were not log-transformed because the distributions were not skewed, and worse prediction performances were observed if log-transformed bone lead concentrations were used to train the models.

We used nested cross-validation to find the optimal weighted Super Learner predictions and evaluate their performance (Fig. 1). Nested cross-validation is a method for optimizing model hyperparameters and selecting models that seek to address the problem of overfitting the training dataset (Cawley and Talbot, 2010). This procedure consists of two cross-validation loops– outer and inner loops. Fifteen-fold cross--validation was used for the outer loop, and ten-fold was for the inner loop. The optimal weight a_m for each algorithm in the Super Learner was estimated in the inner loop. Briefly, cross-validated predictions for each algorithm were calculated in each validation set. A constrained regression was then fitted in which the observed bone lead was dependent and predictions for different algorithms were independent variables, and an optimal convex combination of regression coefficients was determined, corresponding to a_m for each algorithm such that each a_m ≥ 0 and ${\sum }_M^m{a}_m=1.$ This procedure of obtaining optimal weighted Super Learner prediction by subdividing the data into distinct training and validation sets was repeated 15 times (outer loop), and the performance of each Super Learner prediction was assessed with an additional layer of cross-validation (testing sets) that has not been used in the training process. Cross-validated mean-squared errors (CV-MSE) for the Super Learner and component algorithms predictions were calculated in each testing set and then averaged over all 15 testing sets. We also calculated the Pearson’s correlation coefficients and the Lin’s concordance correlation coefficients (CCC) (Lin, 1989) to evaluate the agreement between observed and predicted bone lead concentrations in the testing sets. The R package “SuperLearner” (Van der Laan et al., 2007) was used to predict the bone lead concentrations in our study.

Fig. 1.

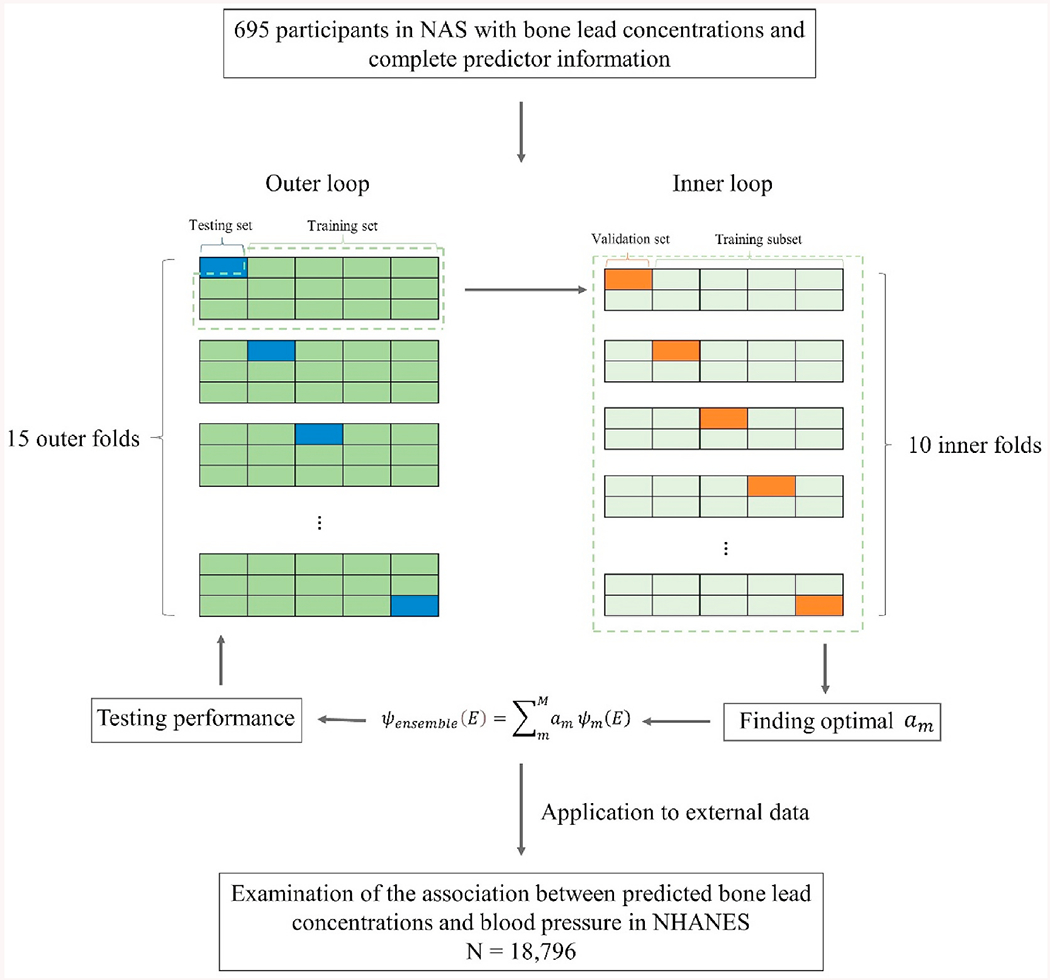
Flow chart of predicted bone lead concentration model development, validation, and application. Normative Aging Study (NAS); National Health and Nutrition Examination Survey (NHANES).

2.5. Predicted bone lead concentrations and blood pressure in NHANES

To test the prediction models’ applicability in other studies where bone lead concentrations were not measured, we evaluated the associations between predicted bone lead concentrations and blood pressure, using data from NHANES, a representative sample of the civilian, non-institutionalized U.S. population. The study sample consists of 18,796 adults aged 20 years and older from 8 continuous cycles (1999–2000 to 2013–2014) who had no missing information on predictors used in bone lead prediction models and blood pressure. Linear regression models were used to examine the associations between blood pressure (systolic blood pressure, SBP, and diastolic blood pressure, DBP) and predicted patella/tibia lead concentrations (from full model and reduced model) while adjusting for age, gender, race/ethnicity, education, NHANES survey cycles, smoking status, cumulative cigarette smoking (pack-year), body mass index, and alcohol consumption. If participants reported current use of anti-hypertensive medicines, a constant of 10 mmHg and 5 mmHg were added to their SBP and DBP, respectively, according to an established method to correct for medication use (Tobin et al., 2005). We also examined blood lead for comparison. Blood lead was log-transformed because the association was close to log-linear. Adjusted differences in SBP and DBP were computed for an interquartile range (IQR) increase in each lead variable. We further stratified associations between blood pressure and predicted bone lead by gender and age (≥50 vs. < 50 years) to assess the potential effect modifications and generalizability of our prediction models, considering that they were built in men majorly aged 50 years and older.

2.6. Sensitivity analyses

Several sensitivity analyses were conducted to test the robustness of our findings. First, we log2-transformed predicted bone lead and blood lead concentrations to better compare the effect size in relation to blood pressure in NHANES. The effect size was interpreted as changes in blood pressure of per doubling increase in each lead metal concentration. Second, we additionally adjusted for the bone lead predictors, including job type, weight, height, and waist circumference, in the associations of blood pressure with blood lead and predicted bone lead concentrations. Finally, to explore the impact of missing values on the associations between lead exposures and blood pressure, we conducted multiple imputations by chained equations (Azur et al., 2011) to impute missing values. All analyses were conducted using R, version 4.0.5 (www.R-project.org) and the prediction models are available (https://github.com/XinWangUmich/Bone-Lead-Prediction-Models).

3. Results

3.1. Prediction models

Distributions of bone lead concentrations and their candidate predictors in the NAS are shown in Table 1. The mean (range) age of 695 study participants was 67.1 (48–94) years. Most participants had a high school degree or higher (89.8%) and had either former or current smoked (69.2%). The mean (standard deviation, SD) of lead concentration was 31.1 (19.5) μg/g for patella lead, 21.6 (13.3) μg/g for tibia lead, and 5.0 (1.9) μg/dL for blood lead.

Fig. 2 summarizes the results of predictor selection by the Boruta algorithm that predictors showing higher mean importance z-score (green boxes) than the highest shadow variable (blue box) are retained as “important” predictors of bone lead concentrations. A total of 10 predictors were selected for patella lead, with the most important predictor of blood lead concentration, followed by age, education, weight, BMI, job type, waist circumference, cumulative cigarette smoking (pack-year), height, and smoking status. For the tibia lead, the same 10 predictors were selected. At the same time, two additional variables—serum phosphorus and serum hematocrit, were identified as tentative predictors, which have a higher but not statistically significant mean importance Z-score than the maximum value of the shadow variables. We only kept serum phosphorus because it had a higher median importance Z-score than that of the highest shadow variable. Thus, 11 predictors were selected for tibia lead, with the most important predictors being age, followed by blood lead concentration.

Fig. 2.

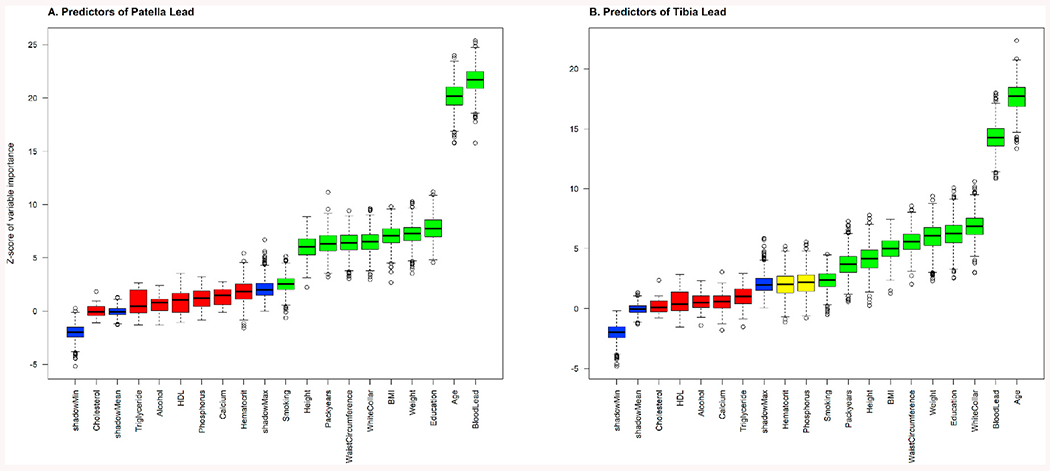
Predictor importance for A) patella lead, and B) tibia lead in the Boruta algorithm. Ten variables (green) were identified as important predictors for patella lead, including blood lead concentration, age, education, weight, body mass index, job type, waist circumference, cumulative cigarette smoking (pack-year), height, and smoking status. Serum phosphorus was additionally identified as an important predictor for tibia lead. A predictor was considered important if it had a significantly higher mean importance Z-score than the maximum value of the shadow variables (blue). Otherwise, a predictor (red) was excluded if it had a significantly lower mean importance Z-score than the maximum value of the shadow variables. Two tentative variables (yellow), which has higher but not statistically significant mean importance Z-score than the maximum value of the shadow variables, were identified as tentative predictors for tibia lead. We only kept serum phosphorus because it had a higher median importance Z-score than the shadow variable.

Fig. S1 shows the performance of Super Learner prediction, together with its 8 component algorithms, for the patella lead prediction, assessed by the CV-MSEs averaged across 15 testing sets. The Super Learner predictions outperformed all individual component algorithms in both full and reduced models, with CV-MSE (standard error, SE) of 253.1 (27.0) for the full model and 253.0 (26.6) for the reduced model, slightly better than the best performed individual algorithms-random forest, with CV-MSE (standard error, SE) of 255.8 (27.1) for the full model and 253.6 (26.7) for the reduced model. Similarly, the Super Learner showed the best performance in tibia lead concentration prediction compared to any component algorithms (Fig. S2). For the individual algorithms predicting tibia lead, the generalized additive model had the highest individual performance in the full model, while the random forest was the best in the reduced model.

The full model and reduced model for patella lead predictions show similar agreement measures (Fig. 3). The Pearson’s correlation coefficients between observed and predicted patella lead was 0.580 for both the full and reduced model. The CCC was 0.482 for the full model and 0.476 for the reduced model. Similar performance in terms of agreement measures between the full and reduced models was also observed for tibia lead predictions (Fig. S3). The Pearson’s correlation coefficient was 0.519, and CCC was 0.416 for the full model. For the reduced model, Pearson’s correlation coefficient was 0.518, and CCC was 0.416.

Fig. 3.

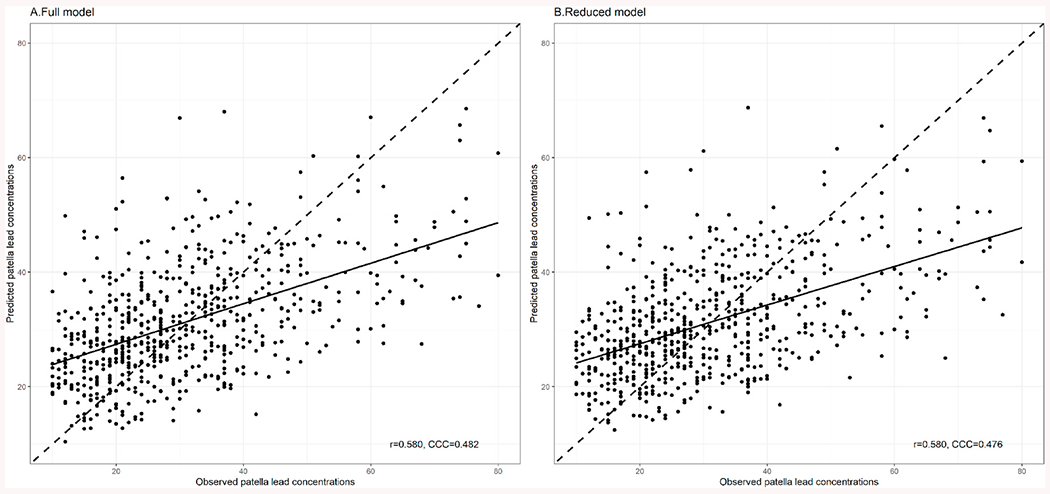
Validation of the patella lead prediction A. full model and B. reduced model in outer cross-validated testing sets. The solid lines drawn on the plots showed indicate the regression line from the simple linear regression. The dashed lines indicate the equiangular observed–predicted line. R: the Pearson correlation coefficient; CCC: the Concordance Correlation Coefficient. Full model included blood lead concentration (log-transformed), age, education, job type, weight, height, body mass index, waist circumference, smoking status, and cumulative cigarette smoking (pack-year). Reduced model included blood lead concentration (log-transformed), age, education, job type, body mass index, smoking status, and cumulative cigarette smoking (pack-year).

3.2. Application to NHANES

The distributions of bone lead predictors in the NHANES were summarized in Table S2. The study sample consists of 18,796 participants (10,060 mens and 8736 womens) with a mean (range) age of 42.5 (20–85 and above) years. The mean (SD) of blood lead concentration was 1.7 (1.8) μg/dL. Predicted bone lead concentrations were shown in Table S3. Mean (SD) of predicted patella lead concentration was 32.0 (12.6) μg/g for the full model and 31.9 (11.9) μg/g for the reduced model. Mean (SD) of predicted tibia lead concentration was 21.9 (8.3) μg/g for the full model and 21.9 (8.4) μg/g for the reduced model. Participants aged 50 years and older had higher predicted patella and tibia lead concentrations than those younger than 50 years.

Positive associations of SBP with blood and predicted bone lead concentrations were observed (Table 2). After adjusting for age, gender, race/ethnicity, education, NHANES survey cycles, smoking status, cumulative cigarette smoking, BMI, and alcohol consumption, an IQR increase in bone lead concentrations was associated with 1.45 (95% CI: 0.96, 1.93) mmHg higher SBP for predicted patella lead from the full model, 1.98 (95% CI: 1.16, 2.80) mmHg for predicted patella lead from the reduced model, 2.09 (95% CI: 1.55, 2.63) mmHg for predicted tibia lead from the full model, and 2.21 (95% CI: 1.69, 2.74) mmHg for predicted tibia lead from the reduced model. By comparison, an IQR increase in log-transformed blood lead concentration was associated with 0.91 (95% CI: 0.57, 1.25) mmHg higher SBP. Stronger positive associations between predicted bone lead concentrations and SBP were observed in women except for predicted patella lead from the full model. Participants aged 50 years and older showed stronger associations between predicted bone lead and SBP than those aged 50 years and younger.

Table 2.

Adjusted differences (95% confidence intervals) in systolic blood pressure (mmHg) associated with an interquartile range increase (IQR) in lead concentrations in the National Health and Nutrition Examination Survey (NHANES).

	Log blood lead	Predicted patella lead		Predicted tibia lead
		Full model	Reduced model	Full model	Reduced model
All participantsa	0.91 (0.57, 1.25)	1.45 (0.96, 1.93)	1.98 (1.16, 2.80)	2.09 (1.55, 2.63)	2.21 (1.69, 2.74)
By genderb
Men	0.74 (0.31, 1.19)	1.74 (1.15, 2.34)	1.86 (1.21, 2.51)	2.27 (1.63, 2.91)	2.35 (1.70, 2.99)
Women	0.46 (−0.07, 0.99)	1.44 (0.60, 2.29)	2.21 (1.31, 3.11)	2.51 (1.52, 3.51)	2.54 (1.63, 3.45)
By age
≥50 years	1.52 (0.72, 2.37)	2.15 (1.28, 3.03)	2.32 (1.36, 3.27)	2.53 (1.57, 3.50)	2.37 (1.45, 3.28)
<50 years	0.44 (0.09, 0.78)	0.60 (−0.01, 1.21)	1.18 (0.51, 1.85)	1.38 (0.71, 2.05)	1.62 (0.93, 2.31)

Note: Interquartile range (IQR) for bone lead is 16.2 μg/g for predicted patella lead from the full model, 16.0 μg/g for predicted patella lead from the reduced model, 10.9 μg/g for predicted tibia lead from the full model, and 10.8 μg/g for predicted tibia lead from the reduced model. Interquartile range for log-transformed blood lead is 0.89.

^aModels for all participants were adjusted for age, gender, race/ethnicity, education, NHANES survey cycles, smoking status, cumulative cigarette smoking (pack-year), body mass index, and alcohol consumption.

^bStratified models by gender have the same covariates included in the model for all participants except gender.

Similar to SBP, positive associations were found between lead concentrations and DBP, where effects of predicted bone lead were stronger than blood lead (Table S4). In stratified analysis by gender, stronger positive associations between predicted bone lead and DBP were found in women. In stratified analysis by age, positive associations between predicted bone lead and DBP were observed in participants aged 50 years and older. By contrast, significant associations were only observed with predicted patella and tibia lead from reduced models in those younger than 50 years.

3.3. Sensitivity analyses

In sensitivity analyses, stronger positive associations between predicted bone lead concentrations and blood pressure were observed than blood lead in models where all lead concentrations were log2-transformed (Table S5 and Table S6). Additional adjustments for job type, weight, height, and waist circumference (Table S7 and Table S8) and pooled analysis of imputed datasets (Table S9 and Table S10) did not alter the associations.

4. Discussion

To allow for the testing of cumulative lead exposure with health effects in studies where direct bone lead measurements are not possible, this study derived prediction models for the bone lead concentration—the biomarker for cumulative lead exposure, using the Super Learner’s ensemble machine learning algorithm. The reduced model, which included blood lead concentration, age, education, job type, BMI, smoking status, and cumulative cigarette pack-years as predictors, showed reasonable performance in the validation datasets as demonstrated by the goodness of fit of models and agreement between predicted and measured bone lead concentrations. When we compared this reduced model to the full model incorporating more predictors, we found no differences in prediction performance. We further applied the prediction models to the NHANES and found that predicted bone lead concentrations were associated with higher blood pressure, whereas blood lead concentrations were not, which agrees with previous findings in the NAS that bone lead but not blood lead was associated with elevated blood pressure (Cheng et al., 2001).

To our knowledge, this study was the first to derive the bone lead prediction models based on blood lead and a few predictors that are available in most population-based studies using the flexible machine learning approach—Super Learner. More than 12 years ago, Park et al. (2009) constructed the prediction models for a similar purpose using the NAS data. However, the bone lead prediction models derived previously were based on linear regression, and assumptions underlying this parametric approach may be violated, as the relationship between bone lead concentrations and their determinants may be highly complex and hence unlikely to be accurately captured by a linear equation. The Super Learner algorithm we used here embraced the possible complex relationships and has been shown to achieve the prediction performance as good as optimum (but unknown) algorithm in the different scenarios by stacking predictions from a wide range of modeling algorithms (Van der Laan et al., 2007). In addition, the previous prediction model with the highest performance included health outcomes as predictors (for example, blood pressure), precluding the testing of predicted lead exposure with those health outcomes. Our Super Learner based bone lead prediction model did not use these variables as predictors, which allows for more expanded possible future research directions. The overall prediction performances of our models are not very high, indicating a moderate signal to noise ratio in the dataset. However, improvement in the performance of both patella and tibia lead predictions with our Super Learner based bone lead prediction model (r = 0.58 for patella lead and r = 0.52 for tibia lead) was achieved compared the performance of the previously constructed linear regression (r = 0.50 for patella lead and r = 0.43 for tibia lead) in the same NAS dataset (Park et al., 2009). We used Super Learner to build the prediction models as other studies will have a different setting and strength of the signal, but Super Learner will pick out the best predictions data adaptively. Future studies may be able to achieve further advances in the prediction performances.

Blood lead and age were the two most important predictors of bone lead concentration in the Boruta predictor selection (Fig. 2). When exposed to lead in the environment, blood and other soft tissues comprise the first receptacle of absorbed lead. Over weeks, lead in these compartments continues to circulate, with some being excreted via urine (and, to some extent bile), but about 10% accumulating into various skeletal locations for decades throughout mineral deposition. From there, lead can then be mobilized over ensuing years through bone resorption and remodeling (Tsaih et al., 2001). In the aging population with elevated bone resorption, blood lead can capture recent external exposure as well as endogenous exposure of the released lead from bone into the circulation (Wang et al., 2019). The high predictor importance of blood lead and age was supported by the strong positive associations of blood lead and age with bone lead concentrations in other cohorts where both blood and bone lead data were available (Korrick et al., 2002; Kosnett et al., 1994). To note, blood lead showed the highest importance for patella lead, while age was identified as the most important predictor for tibia lead in our analysis. This could be explained by different bone compositions, i.e., patella lead is mainly made up of trabecular bone which resorbs more rapidly than the cortical bone in the tibia (Hu et al., 2007). Thus, a closer relationship between blood lead and patella lead is expected, given patella lead’s role as a marker of the internal mobilizable lead reserves. By contrast, the strong association between age and tibia lead suggests tibia lead’s role as an indicator of lifetime cumulative lead exposure as well as a potential marker of the birth cohort effect associated with an age cohort that had much higher exposure as young adults than the young adults of today.

Our analysis detected positive associations between predicted bone lead concentrations and blood pressure in the NHANES datasets, adding to the literature that cumulative lead exposure contributes to elevated blood pressure in the U.S. general population (Navas-Acien et al., 2008). The larger magnitudes of the association for the predicted bone lead than that of blood lead highlight the practical value of our prediction models, in particular, in the examination of associations between cumulative lead exposure and health outcomes. Notably, predicted patella lead concentrations from the reduced model were more strongly associated with blood pressure than the patella lead predicted from the full model. It should be pointed out that more highly correlated predictors (weight, height, BMI, and waist circumference) were included in the full patella prediction model because the Boruta tended to select all-relevant predictors rather than a minimal subset (Kursa and Rudnicki, 2010), and this could lead to greater prediction error due to the potential overfitting. When predicted bone lead is treated as exposure in the associations with health outcomes, the prediction error in the bone lead can be recast as measurement error in the exposure, resulting in downward bias (i.e., towards null) in the estimates of the effect coefficient of the bone lead. Another possible explanation could be that weight, height, BMI, and waist circumference are risk factors for high blood pressure, and they could also be affected by lead exposure (Wang et al., 2018). Thus, the downward bias in the bone lead effect estimates could happen.

In the stratified analysis, much larger effect estimates of predicted bone lead were observed in participants aged 50 years and older. This could be explained by the fact that older people are more susceptible to risk factors of elevated blood pressure (Setters and Holmes, 2017) and also that age was one of the most important predictors in our bone lead prediction models and participants aged 50 years and older showed higher concentrations of predicted bone lead than those younger than 50. Stronger associations between predicted bone lead and blood pressure were also observed in women compared to men. Gender is another potentially important predictor of bone lead concentrations given the accelerated bone resorption rate in postmenopausal women, leading to increased lead mobilization from bone into the circulation (Korrick et al., 2002). However, gender was not included in our prediction models due to the design of NAS of a cohort of men. Thus, the associations between bone lead and blood pressure in women could still be underestimated. Possible biological mechanisms underlying the associations between lead exposure and blood pressure include oxidative stress, inflammation, renin-angiotensin system dysfunction, and impaired autonomic nervous system function (Navas-Acien et al., 2007).

Our prediction models did not account for all potential determinants of bone lead concentrations (Table 1). Blood lead, sociodemographic factors, lifestyle factors, and BMI showed the highest predictor importance in the Boruta algorithm, suggesting that sociodemographic and lifestyle factors and BMI provides more information about cumulative lead exposure than other blood biomarkers when blood lead concentration is available. Furthermore, the reduced model with only seven predictors showed similar goodness-of-fit as the full model and minimized the risk of potential overfitting, as discussed previously. This way, we developed the most parsimonious, rather than complete, model for bone lead concentration prediction, leveraging the most critical factors required to estimate the cumulative lead exposure, which boosts the applicability of our model in epidemiologic studies where extensive blood biomarkers and clinical phenotypes are not available.

The main strength of our study is the application of the Super Learner, for the first time, to model the bone lead concentration in a flexible way. Hyperparameters for the machine learning algorithms embedded in the Super Learner were also tuned for better prediction performance (Wong et al., 2019). Nevertheless, this study has several limitations. First, our prediction models were derived from a cohort of middle-aged-to-elderly White men. The bone lead concentrations in other populations, such as women, non-White race groups, or different age groups, may not be accurately predicted. Our models should also be used cautiously to predict bone lead concentrations in populations with higher bone turnover rates, for example, pregnant women or postmenopausal women. Separate models trained in women and younger populations with different sets of predictors will give a more accurate estimate of bone lead concentrations and less biased associations with health outcomes in the corresponding subpopulations in the future. Additionally, due to data unavailability, other determinants of lead exposures, such as family income (Mahaffey et al., 1982), degree of urbanization of the place of residence (Mahaffey et al., 1982), and environmental and dietary sources (Gump et al., 2020; Hanna-Attisha et al., 2016), were not included in the building of prediction models. Inclusion of such predictors could potentially improve the model prediction performance. Finally, when training the models for predicting bone lead concentrations in other settings or other chemical exposures, it should be noted that hyperparameters and performances of machine learning algorithms may vary due to differences in sample size, number and types of variables, and the relationships between predictors and outcomes.

5. Conclusions

In summary, this study provides the prediction models for bone lead concentration, a marker of cumulative lead exposure, based on blood lead concentration and other standard predictors including age, education, job type, BMI, smoking status, and cumulative cigarette pack-years using the Super Learner algorithm in the NAS. The positive associations between predicted bone lead concentration and blood pressure in the NHANES suggest the practical value of the prediction models in evaluating the health effects of cumulative lead exposure in studies where bone lead measurements are not available. Future studies are needed to train the model in different populations, for example, women, non-white racial groups, and younger populations, to further increase the prediction accuracy.

HIGHLIGHTS.

• Bone lead is an indicator of cumulative lead exposure.

• Bone lead measurement is limited in large population-based studies due to technical availability and expense.

• We developed prediction models for bone lead concentrations using Super Learner.

• The model provides reasonable accuracy and can be used to evaluate health effects of cumulative lead exposure.

Abbreviations:

BMI

body mass index

CART

classification and regression tree

CCC

concordance correlation coefficients

CV-MSE

cross-validated mean-squared errors

DBP

diastolic blood pressure

ENET

elastic-net

IQR

interquartile range

KXRF

K-shell X-ray fluorescence

LASSO

least absolute shrinkage and selection operator

LOD

limit of detection

NAS

Normative Aging Study

NHANES

National Health and Nutrition Examination Survey

SBP

systolic blood pressure

Data availability

Data will be made available on request.