Conceptualizing teachers’ interactions with resources in crossing languages and cultures

Abstract

This paper introduces this special issue aiming to deepen and extend research on mathematics teachers’ work, from a resource perspective, by taking language and culture into account, and exploring two questions: How are teachers’ interactions with resources interpreted and modeled across contexts? And, What challenges and insights emerge through recent efforts to engage these models in cross-cultural (and linguistic) research? The fields of resources, language and culture in mathematics education are each extensive, and we do not attempt to survey comprehensively across them. We have chosen instead to propose three approaches on resources in mathematics teachers’ work that developed somewhat contemporaneously from three different countries with differing linguistic, curricular, and social contexts, corresponding to the work of the three guest editors. The models developed through these approaches are driven by the educational, and so cultural and material conditions of the time and the location of each author, and allow us to propose preliminary answers to our two guiding questions. We then move to pull the threads from these models together, and discuss the contributions to this Special Issue. This results in more robust and nuanced responses to our questions, and in identifying two themes that emerge from research that sit at the convergence of studies of teachers’ interactions with resources, languages, and cultures: an invisibility-visibility dialectic and a local-global tension. Finally, this study leads us to consider a new region of mathematics education research.

Introduction

This special issue (SI) aims to deepen and extend research on mathematics teachers’ work, from a resource perspective, by crossing studies that make evident in diverse ways how language and culture intersect with this perspective. The impetus for bringing together these lenses arises out of increasing efforts to extend understanding of teachers’ resourcing work across linguistic and cultural boundaries. The terms resource, language and culture, can be interpreted differently, thus we use these terms generally at this point. They are discussed further in the following sections.

The papers in this SI highlight conceptual challenges and insights that emerge when mathematics teachers and/or researchers seek to communicate meanings in mathematics teaching, as they engage with varying resources, across languages and so cultures. These papers do not represent a single, established domain of research in the typical sense. Even though the fields of research on mathematics teachers’ use of resources, including language as a resource, are understood as established fields, they are just the starting points for the domain that this SI aims to investigate. The papers in this issue explore the way these fields function, interact, and are challenged when they travel across cultures and languages, uncovering inherent but often unmarked/unremarked ties between research frameworks and the contexts from which they emerge and the need for deeper understanding of the cultural contexts that take them up. In many ways, the focus of this SI is not what is currently known about a domain of research, but what is not known, but is newly revealed when similar research frameworks and questions are taken up by researchers from different cultural and linguistic contexts. Given this focus, we do not offer a survey of a well defined domain. Instead we identify and illustrate the culturally encoded nature of our research lenses and begin the conversation about how such lenses intersect with language and culture in their use.

In this paper, we lay the groundwork for considering the contributions to this special issue by offering different perspectives on resources in relation to research on mathematics teachers’ work across linguistic and cultural boundaries, approaching this task through two guiding questions: (Q1) How are teachers’ interactions with resources interpreted and modeled across contexts? (Q2) What challenges and insights emerge through recent efforts to engage these models in cross-cultural (and linguistic) research? These different perspectives are structured around three models, drawn from the work of the three guest editors of the SI, with the intention of both introducing readers to the fields of mathematics teachers’ use of resources and illustrating the ways in which research frameworks are cultural artifacts. These models emerged somewhat contemporaneously from three different countries with differing linguistic, mathematics, and educational contexts. As such, they reflect, and are driven by, the educational, and so cultural and material conditions of the time and the location of each author.

These models are presented in three successive sections:

• In Sect. 2, Luc Trouche, from France, describes the emergence of a ‘resource’ approach to teachers’ work, marking the convergence of old issues, such as the uses of textbooks, and more recent ones, such as the design of digital resources. This emergence went hand in hand with conceptual developments grounded in didactics (Vergnaud, 2009) and ergonomics (Vérillon & Rabardel, 1995), leading to a holistic point of view on teachers’ resource systems, embedded in cultures and languages;

• In Sect. 3, Jill Adler, from South Africa, offers a perspective first on the notion of language as resource, and then on a conceptualisation of resources-in-use. These emerged in a rapidly changing, multilingual and resource-constrained context, and were driven by an equity agenda. Whether as language, material or, more recently, ideational resources, a key concept that re-emerges in resourcing teachers’ practices is their relational ‘transparency’ (Lave & Wenger, 1991; Wenger, 1998);

• In Sect. 4, Janine Remillard, from the United States, describes the emergence of the ‘participatory’ approach for conceptualizing and studying teachers’ interactions with mathematics curriculum materials. Informed by sociocultural theories (Vygotsky, 1978; Wertsch, 1998), this perspective emerged in the context of a growing body of research seeking to understand the dialectical relationship between teachers and curriculum materials.

In each of these sections, we also describe insights from studies that use, adapt and/or extend these particular frameworks, among others, to new cultural contexts.

In Sect. 5, pulling together the threads from the previous three sections and introducing the contributions to this SI, we identify and elaborate two themes that emerge from research that sits at the convergence of studies of teachers’ interactions with resources, languages, and cultures: an invisibility-visibility dialectic and a local-global tension. Building on these themes, we argue that the ‘domain’ emerging from this work might be understood as akin to Bernstein’s (2000) notion of region.

From an isolated view on a teacher’s use of tools to a holistic view of teachers’ interactions with resources

In this section, I (Luc Trouche) propose a view from France, marked by a didactic culture (Artigue & Trouche, 2021), sharing common features with the European one (Blum et al., 2019). These features include: a strong connection with mathematicians; the key role of theory, and of the design of activities for learning and teaching. In the case of France, this importance of design is reinforced by the pedagogical freedom, which is institutionally recognized for each teacher (for choosing/designing resources in the frame of a given curriculum).

It is a view from a certain time (1980-today), marked by: the development of the network of IREM (Institute of Research for Mathematics Teaching), gathering pioneering teachers working hand in hand with researchers around the ‘questions of the profession’ (Trouche, 2016); and by the irruption of calculators in classrooms and of the Internet in society.

Finally, it is a view from my personal experience: as a mathematics teacher in secondary school, then a teacher educator in an IREM, and finally a researcher in an institute of research in education.

Given these qualifications, my intent in this section is to embrace, as far as possible, the evolution of the field of research related to teachers interacting with resources, distinguishing three major periods: the first one marked by the digitalization of tools (Sect. 2.1); the second one by the emergence of a holistic notion of ‘resource’ (Sect. 2.2); and the third one by the emergence of the issues of languages and cultures (Sect. 2.3).

Mathematics education and the digitalization of tools (1980–2000)

This period was marked by the integration of digital tools in mathematics education, and the increasing awareness of the teacher’s role for mastering this integration.

Digital tools seen, beyond the controversies, as a chance for learning mathematics

From the 1960s, computers brought a new vision of what technologies could be for education in general, and mathematics education in particular. An emblematic illustration of this new vision was given by Seymour Papert, contributing to the creation of a computer language1, Logo, leading to the development of learning environments as ‘incubators for powerful ideas’ (Papert, 1980). For the mathematics education community, these advancements gave rise to the first ICMI Study2 (Churchhouse et al., 1986). Computers and software, by their capacity of representing mathematical entities and manipulating these representations, constituted what Noss and Hoyles (1996), largely inspired by Papert, called ‘Windows on mathematical meanings’. This period was also marked by the importation into classrooms, by the students themselves, of more and more powerful handheld calculators, leading pioneering teachers to design new tasks that took advantage of this power. This need to rethink the tasks undoubtedly explains the hesitation of most teachers, and of the curriculum, to integrate these tools

The duality between the tools considered for their potential, and the tools considered as raising new difficulties, produced heated discussions which Monaghan (in Monaghan et al., 2016) coined the ‘calculator debate’. These discussions led to the development of new theoretical frameworks, coming from the field of sociocultural anthropology (Wertsch, 1998) or from the field of ergonomics (Vérillon & Rabardel, 1995), both frameworks inspired by Vygotsky (1978). The notion of appropriation appears as a critical point: for Wertsch (ibid., p. 53), appropriation means ‘taking something that belongs to others and making it one’s own’. For Vérillon & Rabardel (ibid.), appropriation means developing an artifact into an instrument: an artifact is a product of human activity, socially and historically situated (e.g. a calculator); an instrument is a hybrid entity made of this artifact and of a scheme (Sect. 2.2.2) developed for using it within the subject’s activity. This development combines two processes: instrumentation (expressing the influence of the artifact on the subject’s activity) and instrumentalisation (expressing the adaptation of the artifact when appropriated by the subject). Guin and Trouche (1998) combined this latter approach with the theoretical frameworks of French didactics, under the label of the instrumental approach to mathematics education (Artigue & Trouche, 2021).

Modeling the teacher’s role for supporting students’ interaction with tools

The work in this period illuminates the need to take into account the tools in their interactions with learners, in the course of their situated activity. In these interactions, the focus was mostly on one digital tool (e.g. a calculator, or some software), the teacher being understood as a facilitator of these interactions. At the turn of the century, a large meta study (Lagrange et al., 2003) evidenced the trends of the research (between 1992 and 1998) as shifting from a focus on how learners used tools to a more global concern: the role assigned to tools by the curriculum, the tasks at stake, the responsibility of the teachers’ monitoring learners’ interaction with tools, and the interactions of teachers themselves with a diversity of tools, which opens the door to a focus on resources for teachers.

The emergence of a holistic notion of resources for teaching mathematics (2000–2010)

The word resource, already used in many scientific fields (economics, biology and psychology, among others) appeared in the field of education during the 1960s, “referring specifically to curriculum-related materials intended to support learning or teaching activities” (Ruthven, 2019, p. 44). Its uses experienced a new boom with the emergence of the Internet, giving birth to the notion of digital resources (Heine et al., 2022, online). This section considers first the emergence of this notion, then the modeling of a teacher’s interactions with resources, and lastly the collective aspect of teachers’ interactions with resources.

Naming what is available for re-sourcing mathematics teacher work

The word resource comes from the Latin ‘resurgere’, meaning ‘rise again’, meeting Adler’s (2000) understanding of resource as ‘re-source’, evoking both - at least in English - noun and verb. Adler’s paper, published just at the beginning of this century, inaugurated a questioning of this notion in mathematics education (Sect. 3). Beyond a word, what appeared clearly was the potential of this notion for leading different fields of research to interact, mainly the fields or research on: tools and technologies (Hoyles & Lagrange, 2010); task design (Watson & Ohtani, 2015); curriculum materials (Pepin et al., 2017b; Remillard, 2012) and textbooks (Fan et al., 2018), offering a more conceptual perspective on the work of teaching mathematics in relation to a diversity of tools.

This holistic point of view on resources considers all things that are available for resourcing mathematics teachers’ work: provided by the curriculum (see Sect. 4 the notion of curriculum resources) or/and developed by teachers; dedicated to, or used for, or designed for, doing, learning, teaching mathematics, an increasing number of them entering under the umbrella of digital resources.

Modeling the teacher’s interactions with resources, focusing on the notion of resource system

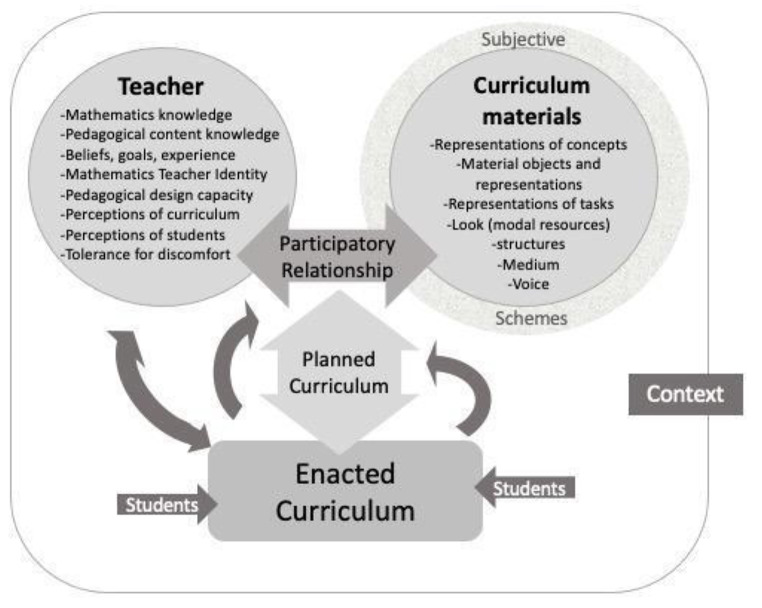
The modeling I present here, the Documentational approach to didactics (DAD), emerged in France (Gueudet & Trouche, 2009), in the thread of the instrumental approach (Sect. 2.2.1) and grounded in a view of teacher autonomy and decision making that are part of French culture (see the introduction of Sect. 2). It then developed at an international level (Trouche et al., 2020). DAD analyzes the interactions between a teacher (her knowledge and beliefs) and a set of resources (their potential, affordances and constraints (Fig. 1), for facing a given class of situations, in terms of a documentational genesis, giving birth to a document. A document (for teaching something) is a hybrid entity, made of recombined resources and a scheme (Vergnaud, 2009) of usage of these resources.

Fig. 1.

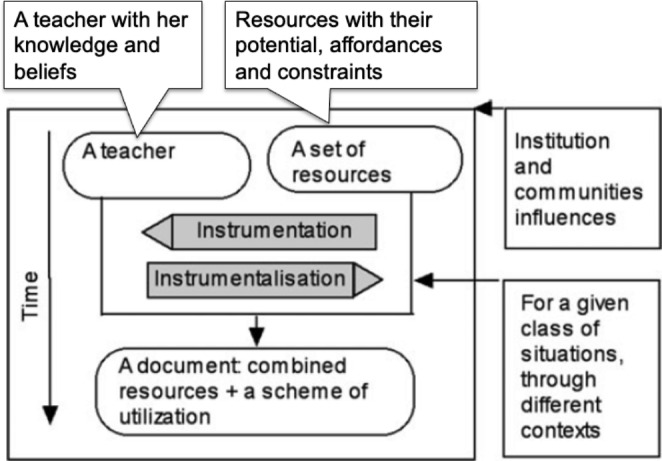
 A representation of a teacher documentational genesis.

(adapted from Gueudet & Trouche 2012, p. 26)

The resources can be: material (a textbook, a lesson plan, or a software) or symbolic (an algorithm, or a mathematical property); local (such as an idea of a mathematics activity) or global (such as a computer vs. a natural language). They do not include the teacher’s knowledge, dispositions or identity. This knowledge component is taken into account via the notion of scheme, which is the invariant organization of activity for facing a class of situations, i.e. a set of teaching situations sharing the same global aim. Each scheme is indeed structured by the teacher’s knowledge, often implicit, guiding, and developed by, the design and use of resources. A documentational genesis is a long developmental process, from lesson preparation to lesson implementation, followed by reflection and revision. It is a process during which the resources involved evolve (effect of the instrumentalisation process, Sect. 2.1.1), and the teacher’s knowledge evolves too (effect of the instrumentation process). A documentational genesis encapsulates the joint evolution of the teacher’s knowledge and resources.

These lively interactions could be related to Remillard’s participatory perspective (Sect. 4) and, more generally, to the frame of ‘curriculum ergonomics’ (Choppin et al., 2018), which conceptualizes the relationship between curriculum design and use, evidencing: a) the active role of the teacher as designer, b) how teachers’ transformation of curriculum resources may or may not align with designers’ intentions; c) the role of the curriculum materials in the teacher-curriculum relationship; d) the dissolution of the designer-use boundaries in the context of digital resources.

DAD proposes the concept of a resource system for designing the structured set of resources that a teacher has appropriated and reorganized alongside her interactions with a diversity of resources for facing a variety of classes of situations. The teacher’s resource system, combining local and global resources, is structured according to different features (mathematics topics, school level, or place given to students’ activity). It is considered as a living entity, developing hand in hand with this teacher’s activity system (Trgalová et al., 2019, p. 211). It could be related to the notion of resource system introduced by Ruthven (2009) as one of the structuring features of classroom practice. For Ruthven (ibid.), the resource system focuses ”on the combined operation of the mathematical tools and curriculum materials in classroom use” (p. 136).

Taking into account the whole resource system each teacher is dealing with leads to the consideration of the multiple factors influencing this system (Fig. 1), coming from the institutions, communities, or contexts that compel and nurture teachers’ activity. The book produced by the International Resource conference held in Lyon in 2018 (Trouche et al., 2019) provides examples of the application of DAD in various contexts, evidencing the evolution of the approach, particularly for taking into account the collective aspects of teacher work.

Taking into account the collective aspects of teachers’ interactions with resources

The emergence of the Internet came with new ways of communicating, designing and sharing resources, giving rise to new phenomena, for example, the emergence of mathematics teacher online associations. In France, it was the case of Sesamath (https://www.sesamath.net/), which gathered thousands of mathematics teachers and had “the essential vocation of making available to all, via the Internet, free educational resources and free professional tools used for the teaching of mathematics”. It can be considered as emblematic of the evolutions of teachers’ work with new resources in the Internet era, revealing and amplifying phenomena that existed of course before this era.

This awareness of the influence of teachers’ collective work led to an evolution of the research on teachers’ interactions with resources, becoming more sensitive to situated learning (Lave & Wenger, 1991) and cultural-historical approaches (Engeström, 2001). The Documentational approach to didactics thus proposed an evolution of its initial model (Fig. 1). Instead of the interaction between one teacher and a set of resources, attention was on the interactions between a community of practice (Wenger, 1998) and a set of resources (Gueudet et al., 2012), supporting the development of new knowledge, that Sabra (2016) coined mathematics teachers’ collective documentation work. According to this approach, a community in itself is not a resource, but a context favoring the co-development and the enrichment of teachers’ resources and knowledge.

The collective work of teachers appears even more necessary when it comes to responding to new conditions of teachers’ work needing new resources, and so what happens in times of curriculum change (Leufer et al., 2019), and recently during the Covid 19 pandemic (Huang et al., 2023). Considering resources as artifacts led naturally to consider the social and cultural contexts that shaped their design. But taking into account teachers’ collective work reinforced the need for this consideration, opening a large window into these contexts.

Teachers’ interactions with resources embedded in history and culture (2010 - ongoing)

To understand the documentary work of teachers, I first emphasize the need to take into account the curricular context in which interactions between teachers and their resources develop, then the language or languages in which these interactions are expressed. Finally, I propose a reflexive point of view on this view from France, questioning its extension to a more general perspective.

Taking into account the curricular background of teachers’ interactions with resources

I consider here a curriculum as “a determined arrangement or state of a teaching system” (Chevallard, 1992), keeping in mind that it also represents “a selection from the culture of a society” (Chevallard, ibid.). As teachers’ resource systems are indeed the substrate of their professional activity, these systems constitute a window into their expertise, understood as a system of curricular norms (Pepin et al., 2017a in the case of Chinese teachers. Often at the center of teachers’ resource systems are textbooks that constitute crucial interfaces between culture, policy and teacher curricular practice (Pepin et al., 2013).

The knowledge of a given curriculum, more generally the knowledge of teachers’ working conditions, allows one to understand the direction in which their documentation work could develop. For example, Wang (2019) showed how the working conditions of Chinese teachers (e.g. rooms and time dedicated to teachers’ collective work for preparing lessons) could explain the existence, over a long time, of very active Teaching Research Groups in each school. Analyzing the cultural similarities between Japan and China (social orientation of people; school-based professional development via teachers’ collaboration) allows us to understand some common features of teachers’ interaction with resources (Wang et al., this issue). Knowing what is considered by teachers as an effective way of teaching mathematics, within a given curriculum, is also a condition for understanding their interactions with teaching resources. In the case of Chinese teachers, Zhang (2022) evidenced how the roots of teachers’ documentation work need to be found in the curricular Chinese tradition of ‘teaching mathematics through variations’.

Finally, taking the curriculum into account is necessary for sharing resources across borders, as is the case in a number of European projects. For example, the project I2G (Interoperable Interactive Geometry for Europe, see Kortenkamp et al., 2010), aimed to share resources for teaching Geometry all over Europe, where the resources are written in different languages for different curricula. Reaching this objective led the project to conceive each curriculum as a complex structure characterized by a set of concepts and of links structuring them: passing a resource from one curriculum to another supposes a complex process of delocation / relocation. This last project, among others, brought into view the issue of languages and cultures in which the resources are developed and the issue of language as a resource per se.

Language as a window into teachers’ interactions with resources

The language in which the resources are expressed, and through which teachers are thinking and communicating, emerges as a blind spot in most studies developed in the frame of DAD. During the International Resource Conference held in 2018, this issue was underlined as a critical one to be addressed (Trouche et al., 2019, p. 447). This reflection led to the DAD-Multilingual project (Trouche, 2020), which is studying the translation of the concepts of DAD into fourteen different languages. The aim of this project is to deepen DAD through challenging the instantiation of its main concepts in various linguistic contexts. It evidenced the need for a technical and conceptual apparatus instrumenting this translation work (Ruthven, this issue). An outcome of this project was that language as translation hit up against cultural practices in which names are also a function. Basturk-Sahin & Tapan-Broutin, Gosztonyi & Varga, Shao et al., Wang et al. (this issue) go further in addressing these translation issues in research or teaching, by taking into account the curricular and cultural contexts targeted by the translation.

Of course the research on teachers’ interactions with resources through a language lens can’t be reduced to the work on translation. It should also consider, for example, the work of teachers facing different languages/cultures in their classrooms. For example, Sayah (2018, p. 67) evokes teachers’ difficulties when combining resources written resp. in French or Arabic. But the consequences of such difficulties were not sufficiently studied. Moreover, studies considering the multilingual contexts and practices in school teaching (see the network Plurimath https://plurimaths2022.sciencesconf.org/) have developed in France, but the connection between this field and the resource approach to mathematics education is yet to be conceptualized.

Reflecting on the view from France – extending selectively outside

In this section, I have tried to analyze how teachers’ interactions with resources are interpreted and modeled across contexts, focusing on our first guiding question (Q1). Even if it was rooted in a French didactic tradition (Trouche, 2016), this approach has developed at an international level, crossing different contexts. The book presenting the instrumental approach (Guin et al., 2005) was at the heart of the preparatory document for the 17th ICMI study (Hoyles & Lagrange, 2010). The documentational approach to didactics has given rise to different books (among them: Gueudet et al., 2012; Trouche et al., 2019) which have made it possible to cross it with other approaches, in particular those brought by the two other editors of this special issue (Sects. 3 and 4). But my experiences, and the experiences of a community developing in the frame of DAD, are marked by the research on the integration of resources, mainly digital, into the teaching of mathematics, which took place mainly in countries where the availability of resources was not an issue. The related conceptualization moved from an isolated view on “a teacher using tools” to a holistic view on teachers interacting with resources embedded in curricula and languages.

New challenges and insights emerge through these efforts to engage this model in cross-cultural (and linguistic) research (Q2). The DAD-Multilingual project (Trouche, 2020) evidenced the need for rethinking the notion of resource itself (“re-sourcing” as a definition works only in some languages, e.g. French or English). The notion of resource system (teacher centered, or school centered) or the dialectic structure of a framework (e.g. the duality instrumentation/instrumentation) does not work as well in cultures based on a more dialogic structure.

At the end of this section, curricula and languages appear as critical issues to be taken into account. The consideration of language and culture as resources (see following section) is certainly a condition for such consideration, together with the appropriation of sociolinguistic frameworks that would allow the conceptualization of these issues.

Resourcing mathematics teaching and levering educational change

This section offers a perspective from the ‘South’ on the meaning of resource(s) and what this entails for understanding and supporting teachers’ work where across many contexts the availability of resources cannot be taken-for-granted. The perspective is shaped by research in South Africa and driven by an equity agenda. South Africa is a multilingual, middle-income country, and notwithstanding massive political and social change since its first democratic elections in 1994, deep social and economic inequality persists. Alongside an affluent minority, the majority live and learn in low-income or poverty-stricken communities. It is well known that socio-economic status is the strongest predictor of educational success in school (e.g. Hoadley, 2010). Studies of educational quality show what is less appreciated: in countries with very low per capita incomes, attainment is “more sensitive to the availability of school resources” (e.g. Gamoran & Long, 2006, p. 1). It is thus not surprising in such contexts, that resources and resourcing (the verb) teaching matter deeply for any intervention aimed at levering educational change.

Two inter-related interpretations and models of resources and resourcing emerged in the later 1990s and early 2000s that have since extended out, within and beyond South Africa. First is the notion of ‘language as resource’ (Sect. 3.1). Second is a reconceptualization of resources as both noun and verb, together with an extension of resources beyond the material and physical, and the importance of their transparency for enabling access and learning (Sect. 3.2). These merge in current approaches to ‘translanguaging’ and ‘language responsive teaching’ (Sect. 3.3) in useful ways for exploring teachers’ interactions with resources, languages and culture in levering change, issues taken up in papers in this special issue.

Language as resource, the multilingual classroom and a resources approach

​​The notion of ‘language as resource’ (Ruiz, 1984) in mathematics education has its roots in research in the 1990s on teaching and learning mathematics in multilingual classroom contexts (Adler,1999) i.e. where many students’ and often the teacher’s main languages are different from the official language of instruction. The notion introduced a shift from a discourse of ‘language as problem’, a deficit discourse circulating in research on language and the bilingual learner that not only disregarded the linguistic repertoires that bi/multilingual students brought to their learning, but also viewed these as an obstacle to learning (Moschkovich, 2000). This led to greater appreciation of the complexities of teachers’ work if they were to include their own and students’ languages as resources for meaning-making in classroom processes.

This shift coincided with intense attention to the relationship between language and the learning and teaching of mathematics. Pimm’s (1987) investigation into mathematics education with a ‘language lens’ explored what it means to read, write and speak (i.e. communicate) mathematically. This seminal work drew the field’s attention to Halliday’s notion of a mathematics register or “… a set of meanings that is appropriate to a particular function of language, together with the words and structures which express these meanings … and that a language must express if it is being used for mathematical purposes” (Halliday, 1978, p. 175). For Pimm, learning mathematics entails “… acquiring the forms and the meanings and the ways of seeing enshrined in the mathematics register” (Pimm, op cit, p. 207) with inevitable opportunities and tensions in teachers’ work as learners’ everyday ways of speaking and sense-making enter the classroom. These need to be brought closer to specialized ways of communicating mathematics. There were accompanying calls for, and research into, pedagogical shifts towards more communicative classrooms (NCTM, 1989; Cockcroft, 1982), entailing greater language-in-use (especially learner talk) and changing social and mathematical norms (e.g. Cobb & Yackel, 1996). Here too opportunities and tensions in teachers’ work emerged highlighting the significance of attention to the quality, and not only the presence, of more mathematical talk and writing (e.g. Sfard et al., 1998; Morgan, 1998). Yet, the implications of this work for the multilingual classroom – a condition of learning and teaching for millions particularly in the global south - was out of view.

At that time I (Jill Adler) was working with postgraduate students, mostly practicing teachers who were teaching in multilingual classrooms in South and Southern Africa, and in working conditions described above. We confronted a disjuncture between mainstream mathematics education research and the students’ lived realities, leading to a study of teachers’ knowledge of their practices in multilingual settings in South Africa (Adler, 2001). Situated in the ‘social turn’ (Lerman, 2000), and sociocultural theories (Vygotsky, 1978, 1986; Lave & Wenger, 1991), I worked with teachers in classrooms constituted by different forms of linguistic diversity. Tensions and opportunities in teachers’ work emerged. Most obvious was the dilemma of code-switching, or moving between languages - what today I would refer to as translanguaging (Wei & Lin, 2019). Teachers knew that the learners’ spoken language(s) were a critical resource for meaning-making. Yet they were responsible for learners’ learning the official language of instruction, and thus the mathematics register in English. It was not trivial to draw on learners’ main language resources. South Africa has 11 official languages, but these do not function equitably. English remains (even today) the language of power through access to higher education, and to commerce and government (Setati & Adler, 2001). I return to the significance of translanguaging and semiotic resources-in-use particularly in postcolonial contexts in Sect. 3.3.

More pertinent to the work of this SI is the dilemma of transparency (Adler, 2001, p. 115–116) - acute in classrooms with a wide mix of spoken languages, including English. This dilemma illuminated the importance of explicit teaching of the English mathematics register. While made visible (so it could be used), it simultaneously needed to be invisible so that it could be seen through to encoded mathematical ideas. Lave and Wenger (1991, p. 102–103) captured this dialectic, demonstrating that access to a social practice was a function of the transparency of its resources, of the extent to which their use in practice was both visible and invisible.

The dilemmas of code-switching and transparency persist as inevitable, interacting in teachers’ work in linguistically diverse classrooms across contexts (e.g. Barwell 2009; Barwell et al., 2016; Turner et al., 2019). Power relations and sociocultural conditions complicate this work. As intimated above, languages have different social power, particularly in postcolonial contexts where the colonial language remains dominant. Studies in South Africa (e.g. Setati 2005) and elsewhere (e.g. Khisty & Chval 2003), drawing on notions of discourse and power (Gee, 1996), illuminate challenges and opportunities in teachers’ work as they navigate this complexity.

Crossing languages and cultures is thus embedded in the work emerging from studies in multilingual classrooms with an orientation to language as resource. There has been rapid and extensive growth of this field, evidenced in numerous collections each with a specific survey. For example, Moschkovich (2010) explores “Resources, challenges, in issues for research: Language(s) and learning mathematics”, drawing in contributions with diverse perspectives. A maturing field is further evident in the open source volume of the 21st ICMI Study: “Mathematics education and language diversity” (see Barwell et al., 2016). Locally, studies have expanded out in South Africa and into the multilingual and postcolonial contexts of Malawi, Kenya and Tanzania with a recent review by McLachlan and Essien (2022).

The notion of language as resource is not without contention. Planas (2018), using Halliday (1978), provided a theoretical and conceptualisation of language as resource as the dialectical interaction between competing forces. The ‘language of mathematics’ (the school mathematics register in use) and the ‘language of instruction’ (e.g. Spanish) are institutionalized systems, and are in tension with the (non-institutionalised) systems of language(s) that learners bring (their everyday language) to school. At the same time, crossing these systems is the meaning potential in all languages, and so possibilities for wide-ranging language use (translanging) in meaning-making. There are inevitable tensions as teachers manage multiple mathematical meanings produced in classroom interaction and how these support or not canonical curriculum meanings.

There is debate as to whether ‘language as resource’ captures the multiple sources of meaning learners draw on, and the fluidity with which language enters classroom communication meaning-making (see Barwell 2016; Barwell and Radford et al. this issue). Barwell (this issue) agrees that there are inherent tensions between inclusive processes and curriculum goals for mathematics learning and particularly so in contexts of linguistic diversity, arguing that tensions are acted on in situ rather than ‘resolved’. For Planas et al. (this issue) related tensions are emerging in research and in teacher education. The teacher’s role with respect to specialized mathematics language, particularly her oral communication (talk) in classroom processes, while tension-filled, is an important resource for opening opportunities for learning mathematics in multilingual settings; it can promote dialogue, and so the production of situated meanings.

This view into the multilingual classroom through the notion of language as resource backgrounds teachers’ interactions with material/digital resources, illustrating the complexity of all being simultaneously in focus. The papers by Sabra & Alshwaikh and Kazima et al. (this issue), situated in Palestine and postcolonial, multilingual Malawi respectively, take steps towards integration. Each illuminates teachers’ work as they interact with the language(s) of learning and the language(s) in material resources, like textbooks and, while more implicit, the cultural practices in which these reside. Both studies are located in resource-constrained contexts, conditions that led to a re-conceptualisation of ‘resources’.

(Re)conceptualizing resources in mathematics teacher education

While work on teachers’ documentation practices was underway (Sect. 2), and reform curriculum materials were in focus in the USA (Sect. 4), curriculum policy changes were afoot in South Africa with new national curriculum statements and related textbooks. Mathematics professional development (PD) programs geared to these changes rolled out, all in an inequitable and resource-constrained system. Questions emerged in research and PD practices as to what counts as resource(s) in and for mathematics teaching (Sect. 3.2.1), and their use as levers for educational change (Sect. 3.2.2), with further insight into ideational resources and resource transparency (Sect. 3.2.3).

Expanding what counts as resource(s)

In a study of teachers’ take-up of resources offered in a PD program, a common, understandable lament of teachers was their ‘lack of resources’. Yet I found that many worked productively with what they had. Classroom research led to a three-dimensional conceptualization of resources-in-use (Adler, 2000): (a) an extension of what counted as a resource beyond ‘basic’ physical and human resources (e.g. sufficient classrooms; teacher-pupil ratios) to artifacts, materials and symbolic resources, as well as language and other cultural and social resources e.g. time and community, (b) attention to resource as both noun and verb, and so beyond availability to use-in-practice and (c) as with language, a theorisation of resources-in-use as a function of their transparency (Lave & Wenger, 1991). If a resource (e.g. a calculator, textbook or number line), was to be productively used, it needed to be both visible (available, seen) and invisible, seen through to the mathematics embedded in it.

Critical to this conceptualisation, contrasting with Sect. 2, is the notion that the teacher and her knowledge are a key resource in the teaching process. Teachers are key to levering educational change, particularly in contexts of limited material resources. Teachers’ knowledge(s) fundamentally shape their interaction with other resources (including language) (Adler, 2012). Working in mathematics PD and research at this time, it was obvious that teachers’ mathematical knowledge for teaching (MKT) (Ball et al., 2008) could not be taken-for-granted. Resourcing teachers’ mathematics and professional knowledge(s) became a cornerstone of many programs and crucial to levering substantive change in the quality of teaching for learning, though not without contradictions and ethical dilemmas (e.g. Adler & Sfard 2017). For how do you attend to teachers’ knowledges and not construct them as in deficit? While this phenomenon with its challenges could be considered specific to South Africa, where many teachers were undereducated under apartheid, there are other contexts where teachers’ MKT cannot be assumed e.g. out of field teachers (Goos et al., 2020), as well as in more resourced contexts like the US if MKT is not a focus in teacher education.

Resources and levering educational change

Venkat & Graven (2017) built on Adler (2000) to engage with a resources approach to levering change in primary mathematics education in resource-constrained environments. Their model of potential resource levers (Venkat & Graven, ibid., p. 168) distinguishes human (teachers’ MKT, morale and identity) from material (curriculum coverage, artifacts) and cultural resources (language, structured use of time). By framing human and cultural resources as mediators of material resources, Venkat & Graven (ibid.) implicitly illustrate ‘resource’ as a verb. They argue why and how material resources can be scaled i.e. provided across a system relatively easily. Productive use, however, is a function of cultural and human resources, where scaling is not trivial. PD is labor intensive, costly and takes time. And further to (c) above, it would be the role of PD to explicitly mediate the cultural values related to mathematics and pedagogy encoded in artifacts and material resources. The salience of their model is that it enables insight into what different resources mean for levering systemic change. Interventions aimed at levering change require resource-based design choices, with consequences particular to resource-constrained contexts.

The inclusion of teacher morale and identities as resourcing teaching reflects growing research on identity in mathematics education (Graven & Heyd-Metzuyanim, 2019). In Ntow & Adler (2019), with a resource lens, we explored mathematics teacher learning through PD using an adaptation of Nasir & Cooks’ (2009) notion of identity resources and the distinctions they make between material, ideational and relational resources. In their study of athletes, material (eg. shoes, starting blocks), ideational (eg. representations - verbal or visual - of a ‘good’ athlete) and relational (eg. with coach, other athletes) resources all mattered for learning. By adapting work on resources from outside of mathematics education, we found a blurred boundary between material and ideational resources: curriculum materials are ultimately ideational, shot through with cultural values and implicit messages of good teaching. The complex relationship between teachers and curriculum resources is discussed in detail in Sect. 4.

Ideational resources and the notion of relational transparency

Conceptual frameworks can be ideational resources for mathematics teaching - representing ideas of ‘good’ teaching. Recent research suggests these too can be levers for educational change. A secondary level research and PD project in South Africa included such a resource in its model of the teacher-resources relationship. The project aimed to lever educational change through enabling “access to a practice” (mathematics teaching), and theorized the relationship through the notion of relational transparency (Adler, 2021). The model (Fig. 2) posits a mathematics teaching framework (MTF), an ideational resource that makes explicit valued mathematics and mathematics teaching practices and their related mediational means (Adler et al., 2022). The MTF can function as a bridging tool in the inevitable gap between curriculum resources and their potentialities, and teachers’ interpretation and use of these in practice, or as discussed in Sect. 4, between objective conditions and subjective schemes (see Remillard & Kim, 2020). The assumptions underlying this model are firstly that the gap is a function of sociocultural practices, impacting the transparency (visibility/invisibility) of the curriculum materials. Secondly, and consequently, supporting teachers’ in their resourcing work includes assisting them in making visible the invisible to guide their use of resources. Transparent use is, crucially, both procedural (the ‘how’ - steps that can be followed) and cultural (the ‘what’ and ‘why’ - embedded values, meanings and rationales) (Wenger, 1998). The bridging tool itself thus requires explicit mediation, through PD, with transparency ultimately a function of the teacher-resources relationship.

Fig. 2.

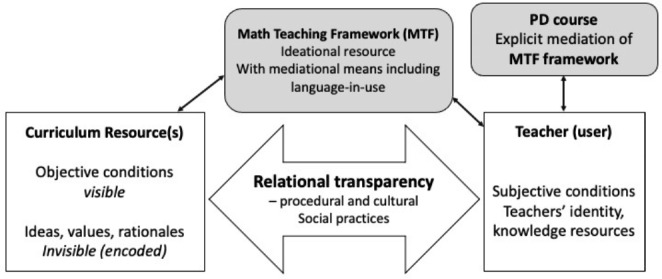
Access to a practice through its resources is a function of relational transparency (adapted from Adler 2021, p. 1210)

The MTF includes mediational means like examples and representational forms that can illuminate mathematical ideas, as well as word use and justifying in mathematics teaching and learning, promoting related valued teaching practices e.g. selection and sequencing of examples. Attention to word-use and justifying links directly back to language-as-resource, connecting it with other resources functioning in the teacher(s)-resource(s) interaction, and to a consideration of two important strands in current work on mathematics education and linguistic diversity: translanguaging and language responsive teaching.

Translanguaging and language responsive teaching

Fluid use of more than one language in learning is currently referred to as “translanguaging”. There is extensive literature on how the addition of ‘trans’ and ‘ing’ is significant in distinguishing fluid mixing of languages and modes (oral, written) for meaning-making, from language ‘separation’ implied in ‘code-switching’ and ‘multilingual’ (see e.g. Wei & Lin, 2019). Relevant research includes a study of teaching number in two South African Grade 3 classrooms where Sepedi was the main language of learners and the teacher. Using Duval’s (2006) distinctions between diverse ‘registers’ of semiotic representations, Poo & Venkat (2021) described translanguaging as including spoken and written registers and a range of other cognitive and semiotic resources to make meaning (p. 45). They illustrated the complexity of the teacher’s translanguaging practices, whose moves between Sepedi and English included explicit links between oral and written forms in either language, and simultaneously, moves between representational forms. They argued that it is precisely in resource-constrained classrooms that the teacher’s oral language (teaching talk) was a critical resource for learning, illustrated by frequent links with symbolic representations. Poo’s (2017) wider study also showed the affordances of different languages. Sepedi number names reflect their decimal and place value structure (eg. eleven is spoken as “one ten, one”). When these structures are made explicit, they function as a transparent resource to support learning.

Poo & Venkat (op. cit.) argue that attention to the epistemic (the specific mathematical knowledge at stake) is necessary in research on language and learning, a view mirrored in research on language responsive teaching (e.g. Prediger 2019; Erath et al., 2021) in linguistically diverse mathematics classrooms particularly in Germany (e.g. Uribe & Prediger 2021). For Prediger and her team, language responsive teaching is an intersection of crossing language registers (including the mathematics register) and mathematical representations, all of which have content specific implications for epistemic access. Understanding the complexity of crossing language registers and representations is a perspective to bring to bear on teachers’ interactions with resources - be these digital/material/curriculum.

The papers by Sabra & Alshwaikh and Kazima et al. (this issue), are illustrative of the merging of content and language as they engage respectively, in their linguistic contexts, with the teaching of function and the introduction of the concept of zero. Both studies, and those in the translanguaging and language responsive teaching research discussed above, include textbooks and/or artifacts in use. Yet, these curriculum materials and the language and culture encoded into them are largely out of focus.

Reflecting on the view from the ‘South’

The model in Fig. 2 (answering Q1) emerged to work on and interpret teachers’ interactions with curriculum resources in a context where their transparency is relational, a function of sociocultural practices. Here, an ideational resource is pivotal in the teacher-resources relationship, requiring its explicit mediation in PD. With respect to Q2, the view from the South brought language as resource with its roots in research in multilingual classrooms into interaction with a resources approach. New insights and challenges are reflected across the papers in this SI pointing again to its pertinence and timeliness.

Research on mathematics curriculum materials and teachers across contexts

In this section, I (Janine Remillard) discuss research on teachers’ interactions with mathematics curriculum materials that emerged from conditions and perspectives in the United States. The focus of this section builds on the previous two sections. The holistic view of teachers interacting with a system of resources within specific cultural and linguistic contexts, developed in Sect. 2, offers a broad framework for locating teachers’ interactions with curriculum materials. Sect. 3, then, offers a reconceptualized notion of resources in teaching to also include the human, ideational, linguistic, and discursive practices that mediate these interactions, particularly in contexts where access to material resources is constrained. This expanded understanding of resources and resource-use also intersects with the participatory lens offered in this section.

I view ‘curriculum materials’ as part of the broader class of resources discussed in Sect. 2. They are focal to this section because of their influential role in the U.S. educational system. I expand on the technical and theoretical meaning of the term in Sect. 4.1. In 4.2, I present the participatory perspective (Remillard, 2005), along with a model for conceptualizing and studying teachers’ interaction with curriculum materials. I then describe how the model has been extended in subsequent research (Sect. 4.3) and offer examples of research that examines these interactions across different languages and cultures (Sect. 4.5).

Mathematics curriculum materials characterized and theorized

I use the term curriculum materials to refer to a set of materials designed to guide a program of instruction and student learning over time (Pepin et al., 2017b). The term curriculum, stemming from the Latin word currere or “to run a course”, refers to a planned course or pathway for learning and teaching. The term official curriculum refers to expectations for what should be taught, specified and distributed by national, provincial, or local governing entities (Valverde et al., 2002). Thus, in many school systems, when the descriptor ‘curriculum’ is used with materials or resources, it signals their role in guiding teaching and learning along the path of the official curriculum. In this way, as indicated in both Sects. 2 and 3, these resources operate at the intersection of policy, culture, and teaching practice.

Characterizing curriculum materials

Curriculum materials generally have a number of components, including a teacher’s guide and student textbook, which together comprise a curriculum program. Increasingly, these resources include digital components. I view curriculum materials and curriculum resources, as used in Sect. 3, as overlapping terms, however, I use ‘materials’ to adopt the term most commonly used in the U.S.

Curriculum materials play a multiplicity of roles in school systems. They are a central and unquestioned component of many systems and are seen as mechanisms of state regulation and potential levers of reform (Shimizu & Vithal, 2023; Valverde et al., 2002). Redesigned curriculum materials have been at the center of the major curriculum reforms in the U.S. over the last 60 years. For the majority of teachers, curriculum materials are part of the presumed context of their work and, as described in Sect. 2, hold a primary place in their resource systems. Curriculum materials can also spark learning and change for teachers (Collopy, 2003; Remillard, 2000); some argue they might be intentionally designed to accomplish this aim (Ball & Cohen, 1996).

Although curriculum materials feature in the majority of mathematics classrooms around the world, their particular contents, language, and physical arrangements reflect the cultural practices of their context. As noted in Sect. 3, they are ‘shot through with cultural values’. This point is illustrated by comparative analyses of how lesson guides communicate to teachers through written language and multimodal characteristics, discussed in Sect. 4.3. Curriculum materials (specifically teacher’s guides and textbooks) are a presence in many of the articles in this special issue, even when they are not the focus of the research.

Theorizing curriculum materials as a distinct form of communication

The research approach discussed in this section takes up a particular theorisation of curriculum materials, which I develop in greater detail elsewhere (Remillard, 2012; Remillard & Kim, 2020). Curriculum materials are designed to communicate to teachers about their teaching of mathematics. In this sense, they are a particular genre of communication. They seek to guide action, yet encoded in their guidance are culturally specific messages about what it means to learn mathematics, what mathematics is valued, and the roles of teachers and students in the process. Moreover, how curriculum materials communicate to teachers (the forms of communication) and what they communicate about (the focus), transmit different underlying ideas and values.

These types of communication illustrate Otte’s (1986) distinction between the observable features of curriculum materials, called “objectively given structures” (what can be observed) and “subjective schemes” (how they are perceived within a particular culture). This distinction also links back to the discussion of curriculum resources as both ideational and material, in Sect. 3 (Fig. 2). This perspective on curriculum materials suggests that reading and using them is not a straightforward proposition, but involves interpretive work and, to build on Sect. 3, resourcing. As proposed in the following section, this work is mediated by features of the materials and how they are perceived by teachers.

The participatory perspective: a model for guiding research

In this section, I introduce the participatory perspective and related model. Introduced in the early 2000s, this model reflects a particular point in time in the U.S., following the curriculum reform efforts proposed by the National Council of Teachers of Mathematics (NCTM, 1989) and a subsequent flurry of curriculum development activity and related research. This model emerged from a review of research on teachers’ use of curriculum materials (Remillard, 2005), which found that this aspect of mathematics teachers’ work was undertheorized. To guide future research, I proposed a model of the teacher-curriculum relationship, which incorporated many findings from empirical research and their theoretical underpinnings, but also centered the participatory perspective.

The participatory perspective assumes that teachers’ use of curriculum materials involves co-participation with materials, similar to the instrumentation-instrumentalisation duality described in Sect. 2. Drawing on Vygotskian-inspired theories of human tool use, this perspective understands all human activity as mediated by tools or artifacts, which themselves are products of human activity (Vygotsky, 1978; Wertsch, 1998). Further, teachers’ curriculum activity operates on multiple levels. As depicted in Fig. 3, teachers participate with curriculum materials when they read and interpret them in order to design lessons. The product of this activity, the planned curriculum, is shaped by the relationships between agent and tool. From this perspective, examining teachers’ work with curriculum materials requires taking into account these interactions, as well as how they are mediated by the teacher, the materials, and the context. The enacted curriculum, which is co-constructed by teacher and students in a particular context, may resemble the teacher’s plans, but comes alive in unique and emergent ways in the classroom. Further, the enacted curriculum influences the teacher and subsequent curriculum activity, also described in Sect. 2.

Fig. 3.

The participatory relationship between the teacher and curriculum materials, adapted from Remillard (2005, p. 235)

Many studies have illustrated how various teacher characteristics, including knowledge and capacity, beliefs, commitments, and identity, influence how teachers interact with curriculum materials. Some of these are listed in the ‘Teacher’ circle in Fig. 3. Similarly, studies have also identified characteristics of ‘curriculum materials’ that tend to vary and have been shown to influence how teachers use them.

Further conceptualizations of the participatory relationship

Over the last 15 years, researchers around the world have taken up the participatory perspective, expanding understanding of teacher and curriculum characteristics at play and of the participatory relationship itself. The following sections describe key developments in this domain pertinent to the SI.

Evolving understanding of the teacher in the participatory relationship

A major theme of research that further conceptualizes aspects of the teacher’s work is the complex process of reading and interpreting the layered contents of curriculum materials to design mathematics lessons. This type of work might be best captured by the Japanese term kyozaikenkyu, or “studying teaching materials for establishing deeper understanding for better teaching” (Watanabe et al., 2008). Teachers in Japan are introduced to this approach to materials in their preparation programs and it is a consistent component of Japanese lesson study, yet the idea that teaching materials might be a focus of study and relevant learning is less developed in the U.S. Dietiker et al. (2018) build on the research on teachers’ professional noticing, or profession-specific ways of seeing and interpreting events to propose the concept of curricular noticing. Through the iterative processes of attending, interpreting, and responding, teachers make sense of and use the variety of opportunities in print or digital curriculum materials. Remillard (2012) proposed the concept of modes of engagement to characterize the variations in what teachers read for, which parts of the materials they read, and how they position themselves in relation to the materials. These variations are substantiated by empirical studies, which finds selective and varied reading and differing interpretations of guidance in materials.

Work in this area has also expanded concepts related to teacher knowledge and capacity associated with interpreting curriculum materials. Brown (2009) used the term pedagogical design capacity (PDC) to identify the teacher’s “capacity to perceive and mobilize existing resources in order to craft instructional episodes” (p. 29). This ability, he argues, is not solely contingent on what the teacher brings to the interaction, but is also shaped by the affordances of the resources. Others have added to this construct by further articulating components of PDC. Remillard and Kim (2017), for example, proposed that the work of “reading, interpreting, and drawing on the mathematics resources in curriculum materials to skillfully design instruction” (p. 70) involves a type of specialized knowledge, or knowledge of curriculum embedded mathematics. This concept builds on the the view that mathematics teaching requires specialized content knowledge situated in the work of teaching (e.g., Ball et al., 2008; Rowland, 2013) and reflects the finding that goals for mathematics tasks in curriculum materials are rarely made explicit to teachers.

In Sect. 3, papers in this SI from Palestine and the postcolonial, multilingual context of Malawi are used to illustrate how the notion of language as a resource in teaching can be brought into conversation with teachers’ interactions with material resources, including textbooks. These papers also illustrate how Brown’s (2009) notion of pedagogical design capacity can be extended to include the work teachers do to navigate across languages and cultures to perceive and mobilize the mathematics resources in their curriculum materials. Sabra and Alshwaikh (this issue) introduce the concept of Mathematical Arabic For Teaching (MAFT), a mathematics register (Halliday, 1978) necessary to read and make use of the mathematics content in the textbook. They also find that teachers’ MAFT is shaped by the Arabic terms used in their textbooks to refer to mathematics concepts. Kazima and colleagues (this issue) illustrate the work that primary school teachers do when navigating between a teacher’s guide, written in English, and student textbooks, written in Chichewa.

Expanding understanding of curriculum material in the participatory relationship

Research on the characteristics of curriculum materials as designed objects that teachers interact with has expanded significantly in the last 15 years. At the same time, the forms of communication and sources of curriculum materials have also expanded as a result of digitization and distribution through the Internet Pepin et al., 2017b and described in Sect. 2). Research that examines curriculum materials can make visible consequential characteristics beyond the objectively given structures (Remillard & Kim, 2020). Differing analytical approaches further illustrate the complexity of curriculum materials as designed artifacts, having both visible and ideational components. They also bring attention to the variety of forms and languages of communication embedded in curriculum materials and the way these resources encode cultural messages.

Some efforts to examine how curriculum materials communicate with teachers have attended to the voice of the text. Herbel-Eisenman (2007) used discourse analysis techniques to examine how characteristics of the language used in textbooks position students, the teacher, the textbook and mathematics in relation to one another. She found that despite the reform-based intentions of the curriculum program, specific word choices emphasize the mathematical authority of the text and position the student as a passive recipient of knowledge. I have collaborated with colleagues from the U.S. and Europe to explore the voice curriculum authors use when communicating with teachers. Undertaking this analysis with curriculum materials from three different cultures, Flanders, Sweden, and the U.S., revealed important differences in modes of communication that aligned with cultural assumptions about mathematics teaching and learning (Remillard et al., 2016). We have extended this work by examining multimodal means of communication in the same curriculum programs. Our findings reveal ways that decisions made about arrangement of images and other components on the page can reinforce messages about positioning and authority in relation to teaching and learning mathematics (Van Steenbrugge & Remillard, this issue).

Some researchers and designers have sought to bring greater intentionality to the ways curriculum materials communicate, and thus support teachers in their use of these resources to design and enact lessons (Ball & Cohen, 1996; Davis & Krajcik, 2005). This proposition is a response to a common practice among curriculum material authors of communicating through teachers, by directing their actions, with little transparency about intent or rationale (Adler, 2021; Remillard, 2000). Educative curriculum materials have been conceptualized as those that communicate to teachers. This idea has had great appeal as a strategy to help teachers engage with the ideas behind the design. Some curriculum developers have experimented with features intended to make design rationale explicit, help teachers anticipate student responses, and elaborate key mathematics concepts (Remillard & Kim, 2020; Stein & Kaufman, 2010).

Analyses of curriculum materials like those described above are less common in research on teachers’ interactions with curriculum materials. More often, as with a number of pieces in this special issue, textbooks and teacher’s guides are understood as critical components in teachers’ work, but their contents, form, or voice are rarely scrutinized.

Research on the participatory relationship

Building on the idea that teachers’ curriculum material use is a dynamic and co-participatory process, some research has sought to uncover characteristics of the participatory relationship, taking into account mediational influences of both the teacher and the materials. These studies consider the different ways teachers mobilize various supports in their materials, including when they modify or follow closely, factors that influence these decisions, and resulting curriculum enactments and sometimes teacher learning. For example, Leshota (2020) studied 10th grade teachers in the project in South Africa, referred to in Sect. 3. She analyzed the textbook to identify affordances and constraints in its representation of content and investigated how teachers mobilized these resources in their teaching, finding that variation in how teachers used the textbook mapped onto their understanding of its affordances. In Sect. 3, Adler describes the use of a framework as an ideational resource to support teachers’ reading and resourcing of the textbook by making implicit values more visible. Hill and Charalambos (2012) illustrate how mathematics knowledge for teaching (MKT) mediated how middle school teachers in the U.S. mobilized guidance in their materials and made either productive or unproductive modifications. These examples illustrate how research that explores the participatory relationship attends to the dynamic process of curriculum use, while situated within a single cultural or linguistic context. In Sect. 4.4, I discuss research that explores these questions across cultural contexts, in consideration of our second guiding question.

Research on the participatory relationship across languages and cultures

Research that explores the teacher-curriculum relationship across cultures is relatively rare, however, some examples illustrate the way both curriculum materials and the ways teachers interact with them are deeply cultural. Hemmi and colleagues’ (2019) study of Swedish primary teachers using translated Finnish mathematics curriculum materials over a four year period illustrates this phenomenon. Finnish and Swedish approaches to mathematics teaching are notably different, and these differences are reflected in typical materials: Swedish materials privilege students working individually and position the teacher as reactive to their needs, while Finnish materials position the teacher to work proactively with the whole class of students. Hemmi et al. (2019) found that Swedish teachers who used the Finnish materials closely began to adopt aspects of the Finnish approach. At the same time, when not using the Finnish materials, the teachers’ practices reflected those typical in Sweden. In addition to highlighting the pull of cultural traditions, the researchers posit that the lack of design transparency in the materials may have constrained teachers’ ability to navigate between the two approaches when not following the materials closely.

The central role that culture plays in understanding teachers’ curriculum use is also evident in the Mathematics 3C Study, which examines primary teachers’ use of print and digital materials in Finland, Flanders (Belgium), Sweden, and the U.S. Studying teachers’ curriculum use simultaneously in four contexts surfaced differences in cultural practices and values related to how classroom lessons are structured, the role of the materials in lessons, and teacher autonomy (Remillard et al., 2021). These differing practices and values also influenced the research process. Condon et al. (this issue) report on the team’s analysis of instances where conceptual or linguistic misunderstandings emerged among the researchers and the process of negotiating common understanding. Reflective of findings from the DAD-Multilingual project, described in Sect. 2, as well as Shao et al. and Wang et al. (this issue), we found that challenges arriving at common meanings for the purpose of data collection and analysis were most intense when they related to phenomena or practices with no comparable equivalent in other contexts (culturally or structurally) or they involved emerging digital resources, where neither language nor common usage had been established.

Cross-cultural challenges and insights

Considering Q1, the participatory model, while overlapping with the models offered in Sects. 2 and 3, hones in on teachers’ interactions with a particular type of resource commonly used around the world that carries cultural and institutional values. Scholars taking up this model, including those outside of the U.S., have added depth and complexity to each dimension, as reported in Sect. 4.3. Looking to Q2, studies that apply the model in cross-cultural research make evident the influence of culture in every dimension, as well as in how researchers name and examine them, a theme also illustrated by Artigue et al. (this issue). A challenge that surfaces is the question of what is made visible and invisible. Because mathematics curriculum materials are treated as part of the landscape and context in most educational systems, their language, including forms and modes of communication, the ways that teachers interact with them, and the way they encode cultural values can be overlooked in research on mathematics teaching, including research that explores the use of resources. It is often through cross-cultural examination of these artifacts and teachers’ use of them that the invisible begins to become visible.

Pulling out threads/themes for cross-discussion, and introducing the SI

Our aim in the previous three sections was to offer three different models of resources and resourcing in relation to mathematics teachers’ work and to do so in ways that make evident the cultural and historically situatedness of each. In this section, our aim is to look across the models, along with the additional contributions to the SI, to surface more robust and nuanced responses to our two guiding questions:

Q1. How are teachers’ interactions with resources interpreted and modeled across contexts? What becomes visible when these are juxtaposed?

Q2. What challenges and insights emerge through recent efforts to engage these models in cross-cultural (and linguistic) research? What possibilities arise for reflection on how the SI can deepen and extend the resources approach, and uncover what is and isn’t in focus, sharpening our lenses on what is often missed in cross-cultural and cross-languaging research in mathematics education.

In this process, we introduce two themes that emerge when studies of teachers’ interactions with resources, languages, and cultures are brought together: an invisibility-visibility dialectic and a local-global tension. We conclude by proposing that the domain of research introduced in the SI might be understood using Bernstein’s (2000) concept of region.

It is important to note that, in restating these questions, we have extended them to emphasize a theme that has emerged in our efforts to develop an understanding across our research-produced models, as socio historical and cultural artifacts: that they make visible particular aspects of a phenomenon, while rendering others invisible. This invisible-visible dialectic was at play throughout the considerable work involved in coming to a deep understanding of each other, including the way we used the same English words (e.g., resources; language, knowledge; curriculum materials; registers; to name just a few) to tell different stories. Through this work, we have become acutely aware how: (a) the lenses we use and produce are cultural artifacts and not always visible even to the researchers themselves, let alone users of it; and (b) developing models involves an inevitable foregrounding and backgrounding of research objects and processes, thus influencing what can be ‘observed’ and interpreted. These insights did not simply ‘happen’. The context embeddedness of our work became more apparent through our deliberate crossing of research focuses, languages and cultures, enabling us to critically reflect on how we name and narrate our work, and then what it means as it is interpreted and used across contexts.

We see these deliberate efforts and reflections as an initial step taken on in this SI and as a precursor to the potential insights brought to the fore when looking across the papers as a set. When soliciting contributions, we sought work by cross-cultural teams, working in varying ways to illuminate mathematics teachers’ resourcing work, crossing languages and cultural practices. Looking across our work and the contents of the papers in the SI, a second theme emerges: there is an inevitable and ongoing tension between the local and the general/global in educational research processes and practices. This tension points to a profoundly ethical issue, where cultural specificity and meaning ‘meet’ the desire for generalizable models and frameworks, raising the question of whose local becomes the global and with what consequences. It is not that this issue is unknown or new – rather that it needs critical engagement and particularly at this juncture in a post pandemic and increasingly fractured and inequitable world.

We explore these issues in the following two sections. In Sect. 5.1, with respect to Q1, we consider what looking across the three models makes visible or obscures. In Sect. 5.2, with respect to Q2, we broaden our lens in considering all papers in the SI and exploring challenges and insights that emerge. And in Sect. 5.3, we consider a new region of research emerging from this SI.

Looking across interpretations and models: what becomes visible/obscured?

In Fig. 4, we re-present the three figures representing the central frameworks discussed in each Sects. 2, 3 and 4. Juxtaposing our models surfaced tacit assumptions and critical differences that led each of us to adapt our own original models. Still, each model is a locally derived and culturally situated representation of relationships at stake in our conceptualization of mathematics teachers’ resource work.

Fig. 4.

Contrasting Figs.1, 2, and 3

Modeling the teacher-resources relationship – the visible and invisible

It is difficult to overlook that all three models share a socio-cultural orientation, evidenced in the common reference to Vygotsky, and thus an underlying understanding of the teacher-resources interaction as deeply rooted in social and cultural practices. While these relationships figure centrally in each figure, they do so differently. Each is a model of the teacher–resources relationship, described as both a process and product, which includes evolution over time. In Fig. 1, the core construct of genesis, developed through the dialectic process of ‘instrumentation’ and ‘instrumentalization,’ results in a document, encapsulating both resources and knowledge in/for use, taken up in subsequent stages of the genesis process. In Fig. 3, the core construct of ‘participation’ captures the dialectic interplay between a teacher and curriculum materials, which shape teachers’ curricular plans. This model includes a further product of this process, the enacted curriculum, which subsumes the contributions of students in the classroom and goes on to influence all stages of subsequent interactions. In Fig. 2, the core construct of ‘relational transparency’ is both a product of a framework-guided professional development for teachers and a mediational process by which these teachers enact new ideational resources to decode, make use of, and navigate curriculum resources. In this model, the product of the interplay between resources and teacher is the relationship itself, increased relational transparency and deeper understanding, and so a re-sourcing process that can enrich teachers’ subsequent interactions with resources. All three models account for, although differently, how the interactive process contributes to development of the teacher and the evolution of the resources at stake and the relationship with resources, over time.

The differences across the models are less obvious, but crucial in usage across contexts. The centrality of the teacher in each model is instructive. We know that across cultural contexts, constructions of the teacher in general and mathematics teacher in particular differ widely. In France, teachers tend to be viewed as agents and decision makers in their interactions with new resources; in South Africa and the U.S. policy landscapes, teachers are viewed as objects of change, responsive to externally imposed regulations; and, at the same time, they are positioned as key agents of change through their use of new resources.

In each context, research sought to simultaneously understand teachers’ work in relation to pressures and opportunities specific to the environment and in relation to their day-to-day work and subsequent potential for learning and development. An aspect of this work that often remains obscured in researchers’ models, but begins to become visible through deliberations across contexts, is the researchers’ role in naming and representing teachers’ practice. Through this process, the researcher melds themselves, their language and cultural meanings, into a mode–a particular representation of teaching. At the same time, through conceptualizing in a model, the researcher begins to bring the local and particular into the general sphere. The model offers a way of talking about practice. And when these models are considered across boundaries, the general, as constructed by the researchers, becomes reinterpreted locally. What is not always visible in this process is the ways that tendrils of the researchers’ perspective persist and are inscribed in any subsequent interpretations.

The important general point is that adaptations of any model require engaging with the sociocultural location of the teacher and the language used to describe their work – and so a deep understanding of the local-global tension.

How language and culture become visible

A key aim of the special issue is to make evident diverse ways that language and culture intersect with the understanding of teachers’ work with resources, like those described above. In Sect. 2, issues of language and culture emerged later in the development of the ‘resource’ approach, through cross-cultural work, and are thus backgrounded in Fig. 1. Language and culture are more visible in Fig. 3 through the notion of ‘voice’ and multimodal communication in curriculum resources, and the way that cultural practices and assumptions form a veil of subjective schemes surrounding curriculum materials. Both language and culture are threaded throughout in Fig. 2, given its emergence from an inequitable, multilingual, and resource constrained educational context in which language can serve as a key resource for meaning making. Language-in-use, invoked in this section refers to both spoken languages and a social practice, and the transparency of curriculum materials as both procedural and cultural.

It is not surprising that ‘language’ is used in different ways across the three sections of this paper and those in the entire special issue, as such variation was also identified in studies focused on language and mathematics education (Morgan et al., 2014). While we described a broad understanding of ‘language’ in the call for papers for this SI, the term ‘crossing languages’ in the title suggests a conception of a language – like French, English or Sepedi – and may not invite detailed consideration of the forms and functions of language-in-use, or communication more broadly. In both Sects. 3 and 4, though in different ways, it is the latter that is the concern. In Sect. 2, the first conception of language is taken into account: multilingualism and translanguaging practices are invoked to support communication about teaching and extend a conceptual model across languages and cultures.

The different placements of language in the three perspectives also reflects the cross-cutting focus of the SI. Work on language as resource (e.g., Adler 1999; Planas, 2018) has not been directly engaged in developments in the ‘resource’ approach and studies of curriculum materials. Bringing them into the conversation is a guiding aim of this special issue, prompted by increasing efforts to extend understanding of teachers’ resourcing work across linguistic and cultural boundaries. At the same time, holding both language as resource and the language of resources in classroom teaching is complex as a problem of research, with one or the other often out of view.

The different ways in which culture emerges in and across the models is less easily described - the models themselves are cultural artifacts - with culture as ‘everywhere,’ yet often invisible. While the cultural thread remains less developed across the pieces in the SI, together, they provide evidence that cross-cultural research can make cultural practices in mathematics teaching more visible. Each of the papers in this SI makes visible different aspects of the relationships at stake and grapples with the local-global tension in some form. We now bring the 13 additional contributions to the SI into the conversation, and our insights into Q2.

Introducing the contributions to this SI

All of the 13 contributions, in some way, explore how language and culture intersect with mathematics teaching and teachers’ resources. The majority of the papers are also the result of cross-cultural and cross-language collaborations, where researchers come together to examine and theorize these issues. Looking across them, and in light of what was discussed in the previous section, we identify three foci that emerge, raising challenges and offering new insights.

Focus 1: ‘Navigating between languages and models about resourcing’

Rooted primarily in Sect. 2, the first focus is associated with studies that use and translate frameworks across contexts, translate teachers’ talk, and talk, as researchers, about teaching, surfacing potential insights and challenges (mostly Baştürk-Şahi̇n & Tapan-Broutin, Radford et al., Ruthven, Shao et al., Wang et al.). Through these papers we understand, from the ‘inside’, that developing research frameworks as we have repeated, is, in the first instance, a cultural practice of naming and conceptualizing aspects of teaching, which itself is a cultural practice (Artigue et al.). And, as stated above, it also veers into the global. When researchers take up and adapt these models in their own local context, they must navigate the names in use and seek meanings for their underlying conceptions. Moreover, adopting researchers’ models and naming systems across contexts involves uncovering the implicit relationship between teacher and researcher encoded in the model, as these relationships are certainly not global. In other words, there are multiple layers through which the products of this work are deeply cultural.

Focus 2: ‘Language(s) and culture(s) as resources’

Rooted primarily in Sect 3, it is associated with language as resource for communicating and negotiating meaning within and across cultural contexts. Papers adopting this focus highlight language and other resources in use in classroom activity (a teaching and learning discourse -, Barwell, Kazima et al., Planas et al., Radford et al., Sabra & Alshwaikh), the language about classroom activity and teaching and its use across contexts (Artigue et al., Condon et al., Kazima et al., Planas et al.). The former take forward our appreciation of teachers’ work in multilingual contexts and moreso postcolonial contexts where the power of different languages in use matter for teaching/learning; and how cultural meanings in textual resources (words and visual representations) can remain invisible to teachers, with implications then for teacher education. The latter opens a new window in the language as resource field, placing talk about teaching as a critical resource in this professional practice, and how as a profession there is at its heart here the local-global tension (illustrated by Artigue et al.). A common professional lexicon can build the profession, but it is clear, given the sociocultural nature of educational practice, that accompanying narratives, and so contextual location awareness, are needed to support communication across languages and cultures.

Focus 3: ‘Language(s) and culture(s) of resources’

Rooted primarily in Sect. 4, this also surfaces in the two previous sections. This focus acknowledges resources as artifacts of culture and components of the social practices surrounding their use. Textbooks and curriculum materials, in particular, are constituted by language and other semiotic modes of communication, and are thus carriers of cultural meanings, including mathematics meanings (Gosztonyi & Varga, Kazima et al., Radford et al., Sabra & Alshwaikh, Shao et al., Van Steenbrugge & Remillard). We also associate the practice of naming mathematical and pedagogical activity with this focus, where these culturally produced names signal underlying assumptions and values (Artigue et al., Condon et al., Shao et al., Wang et al., & Planas et al.). The papers here take forward our appreciation of resources as complex and layered cultural artifacts that encode cultural meanings and messages through multimodal means, including language. Because they are part of the educational landscape, the “language” of resources is / can be overlooked in research on teachers’ use of resources. Importantly, contemporary resources (especially curriculum resources) are already being translated and used across contexts. More attention needs to be paid to the cultural values encoded in these resources and implications for their translation.

Mapping the contributions to this SI

In Fig. 5, we represent these three foci, each with sub-foci, and have mapped the set of papers into a space representing their inter-relationships3. As is evident, most of the papers explore the ideas of at least two foci, with one of the three downplayed or remaining out of view. For example, the contributions of Shao et al. and Wang et al. address the same issue of translating and using frameworks across contexts, with a special interest in Wang et al. in the teachers’ and researchers’ talk. Both papers, though Shao more directly, also touch on questions of language and culture in curriculum resources.

Fig. 5.

The contributions to the special issue, sketching a network between three foci

Naturally, the picture reflects the invitations to contribute to the SI, and we can now ask “what is missing?“. There are fewer papers in the intersection of languages and culture as resources and languages about resources. For example, out of view are studies that explicitly navigate the languages and culture of material and ideational resources together with translanguaging teaching/learning practices. Also, teachers’ collective work, or students’ languaging, or new forms of communicating via digital means, or studies of mathematics itself in various languages have not emerged across the SI as a whole.

With regard to the latter, current commognitive research (Sfard, 2008) has introduced a discursive lens to cross-cultural studies with studies of mathematics directly in focus. Morris (2021), for example, shows how in “Tongan language and the Tongan way of life” the concept of probability is “almost redundant in Tongan day-to-day discourse”. That mathematical discourse itself raises critical questions in cross-linguistic contexts is pointed to in Kazima et al. (this issue). Commognitive research has not entered the contributions in the SI. We are thus aware that this SI as a whole does not cover the entirety of the domain we envisaged at the outset.

Considering a ‘region’ of research

Finally, we consider the extent to which the frameworks discussed in the previous sections, along with the collection in this SI as mapped in Fig. 5, might converge to form a new ‘domain’ of research related to resources, languages and cultures. In the introduction, we identified our aim as deepening and extending approaches to teachers’ interactions with resources and uncovering what is and isn’t in focus, sharpening our lenses on what is often missed in cross-cultural and cross-languaging research in mathematics education. What has emerged as inherent in this work is captured in the invisibility-visibility dialectic and a local-global tension, both of which thread through the foci discussed and represented above. We thus do not conclude with an emerging set of coherent and structured propositions. Our work instead brings into clear view inherent tensions and their in-betweenness. How then to describe this expanse of research? To this end, we find Bernstein’s (2000) characterization of ‘regions’ helpful. In contrast to disciplines which are singular, composed of specialized, discrete knowledge and discourses, regions comprise multiple perspectives. They are the result of the recontextualization of disciplines into broader intellectual fields that are both responsive to and depend on a field of external practice, its agents and their interests. Across the body of work in a region, one would anticipate tensions and dialectics.

We find this notion provocative, as it suggests a way of naming the work begun in this SI. It further offers an approach to take it forward, by looking across domains and locating research findings within their cultural and linguistic contexts, and in so doing, opening up some awareness of the socio-political tendrils that infiltrate research. In describing this work as a ‘region’ and illustrating it in the map in Fig. 5, we seek to emphasize the overall map as a cross-cutting domain, and the placement of each rectangle as one among other possible representations. We all draw on theoretical and conceptual frameworks as well as analytic tools that have developed over time, and often in ‘other’ contexts and languages. At a more practical level, we hope that through this SI both new and established researchers are able to take forward the yet to be studied questions of what is lost and gained in the translanguaging activity that permeates our work.