Biogenic carbon pool production maintains the Southern Ocean carbon sink

Significance

The Southern Ocean (SO) plays a central role in mitigating global warming, accounting for ~40% of ocean’s anthropogenic CO₂ absorption and 60 to 90% of ocean warming caused by human activities. The biological pump (BP), where biologically produced carbon is transferred from the surface to depth, is a critical process in ocean carbon cycling with a poorly constrained influence on ocean CO₂ uptake. Using a unique method and observations from autonomous robots, we quantify key aspects of the SO BP and find a latitudinal gradient in carbon production and its impact on air–sea CO₂ exchange. Due to its outsized role in global climate, understanding the influence of biology on the SO carbon sink, and its variability, is essential.

Abstract

Through biological activity, marine dissolved inorganic carbon (DIC) is transformed into different types of biogenic carbon available for export to the ocean interior, including particulate organic carbon (POC), dissolved organic carbon (DOC), and particulate inorganic carbon (PIC). Each biogenic carbon pool has a different export efficiency that impacts the vertical ocean carbon gradient and drives natural air–sea carbon dioxide gas (CO₂) exchange. In the Southern Ocean (SO), which presently accounts for ~40% of the anthropogenic ocean carbon sink, it is unclear how the production of each biogenic carbon pool contributes to the contemporary air–sea CO₂ exchange. Based on 107 independent observations of the seasonal cycle from 63 biogeochemical profiling floats, we provide the basin-scale estimate of distinct biogenic carbon pool production. We find significant meridional variability with enhanced POC production in the subantarctic and polar Antarctic sectors and enhanced DOC production in the subtropical and sea-ice-dominated sectors. PIC production peaks between 47°S and 57°S near the “great calcite belt.” Relative to an abiotic SO, organic carbon production enhances CO₂ uptake by 2.80 ± 0.28 Pg C y⁻¹, while PIC production diminishes CO₂ uptake by 0.27 ± 0.21 Pg C y⁻¹. Without organic carbon production, the SO would be a CO₂ source to the atmosphere. Our findings emphasize the importance of DOC and PIC production, in addition to the well-recognized role of POC production, in shaping the influence of carbon export on air–sea CO₂ exchange.

The Southern Ocean (SO; south of 35 ^∘S) exercises significant influence on global climate, accounting for ~40% of the ocean’s annual anthropogenic carbon absorption (1, 2) and 60 to 90% of the ocean’s annual anthropogenic heat absorption (3). Through the unique SO circulation, physical and biological processes interact to shape regional biogeochemistry that influences the global ocean interior (4). Prevailing upwelling south of the Antarctic Circumpolar Current brings deep waters rich in dissolved inorganic carbon (DIC) into contact with the atmosphere (5). Simultaneously, upwelled nutrients fuel biological activity that facilitates the consumption of DIC and subsequent export of biogenic carbon to depth, lowering the near-surface partial pressure of CO₂ (pCO₂) and maintaining the vertical carbon gradient (6). However, micronutrient limitation in the SO (7, 8) prevents phytoplankton from fully utilizing the available nutrients and consuming the associated respired DIC brought to the surface during upwelling. The excess annual supply of respired DIC due to biological pump (BP) inefficiencies causes carbon dioxide gas (CO₂) outgassing to the atmosphere locally. The unused nutrients are subsequently transported to the low-latitude ocean via large-scale circulation, affecting subtropical and tropical ocean biogeochemistry (4). The seasonal pattern of carbon cycling in the SO is shaped by the temporal decoupling of physical and biological processes, with biological production at a maximum during spring and summer and deep-water mixing being most vigorous during fall and winter. Understanding the strength (the amount of carbon biologically fixed and exported back to the ocean interior) and efficiency (the ratio of biological carbon uptake to the supply of carbon to the surface ocean from the deep) is crucial for a comprehensive understanding of the SO carbon cycle.

Biological processes can transform DIC into multiple types of carbon, including particulate organic carbon (POC), dissolved organic carbon (DOC), and particulate inorganic carbon (PIC or calcium carbonate). The production of each biogenic carbon pool has a distinct impact on surface ocean pCO₂ and the efficiency of carbon transfer to the ocean interior. For example, POC and DOC production reduces surface ocean pCO₂; however, POC is more efficiently exported to depth via gravitational sinking while DOC relies on downward mixing for export (9, 10). The formation of PIC increases surface ocean pCO₂, but PIC can also act as a ballast material for POC, increasing the overall particle transfer efficiency (11). Despite the well-established importance of biology in affecting natural regional carbon cycling, little is known about the specific roles of each biogenic carbon pool in mediating air–sea CO₂ exchange and carbon export, in the SO and globally. This knowledge gap is relevant for understanding not only the natural carbon cycle but also for the anthropogenic carbon cycle, as a change in the efficiency of the biological carbon pump could alter the strength of the anthropogenic carbon sink on timescales relevant to humans (12, 13).

Characterizing fundamental aspects of the biological carbon pump remains a challenge, largely due to the expense and difficulty in simultaneously measuring biological rates, biogenic carbon pools, and air–sea CO₂ fluxes persistently across large ocean realms. In the past decade, advances in autonomous platforms and sensors have opened the door for expansive data collection that is now leading to advances in data analysis and interpretation. For example, recent work has demonstrated the potential for using autonomous platforms to partition marine biogenic carbon pools and quantify the role of biology in air–sea CO₂ exchange at local and regional scales (14–17). Largely thanks to the Southern Ocean Carbon and Climate Observations and Modeling Project (18), a large array of profiling floats equipped with numerous biogeochemical (BGC) sensors has been deployed in the SO and is providing unprecedented spatiotemporal resolution of ocean biogeochemistry. Using 107 seasonal cycle observations from 63 BGC SO floats, we evaluate the production of distinct biogenic carbon pools and quantify the role of biology in regulating the SO air–sea CO₂ flux.

Results and Discussion

Productive Season Export Potential.

We apply a tracer budget approach to a combination of datasets from floats, ships, satellites, and reanalysis products (Materials and Methods) to isolate the influence of net biological production from physically induced tracer changes during the SO productive season [defined as the late winter maximum to the spring–summer minimum in the euphotic zone DIC inventory following Johnson et al. (19), Arteaga et al. (20)]. We use three chemical [DIC, total alkalinity (TA), and nitrate] and one bio-optical (POC estimated from the particle backscattering coefficient: ${\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}$ ) tracers (Fig. 1) within the euphotic zone (defined here as the 1% light level, SI Appendix, Fig. S1A). The productive period typically starts in September and persists through March of the subsequent year with a duration ranging from 72 to 156 d, depending on latitude (SI Appendix, Fig. S1 B and C). We limit our analysis to the productive season given that most biological production occurs during this period (21, 22) and the difficulty of parameterizing vertical transport and mixing during fall and winter. We average our results into 5° latitude bands (based on the mean float location during each productive season) for interpretation, achieving similar results when averaging to the four main SO frontal regions (SI Appendix, Figs. S2–S4).

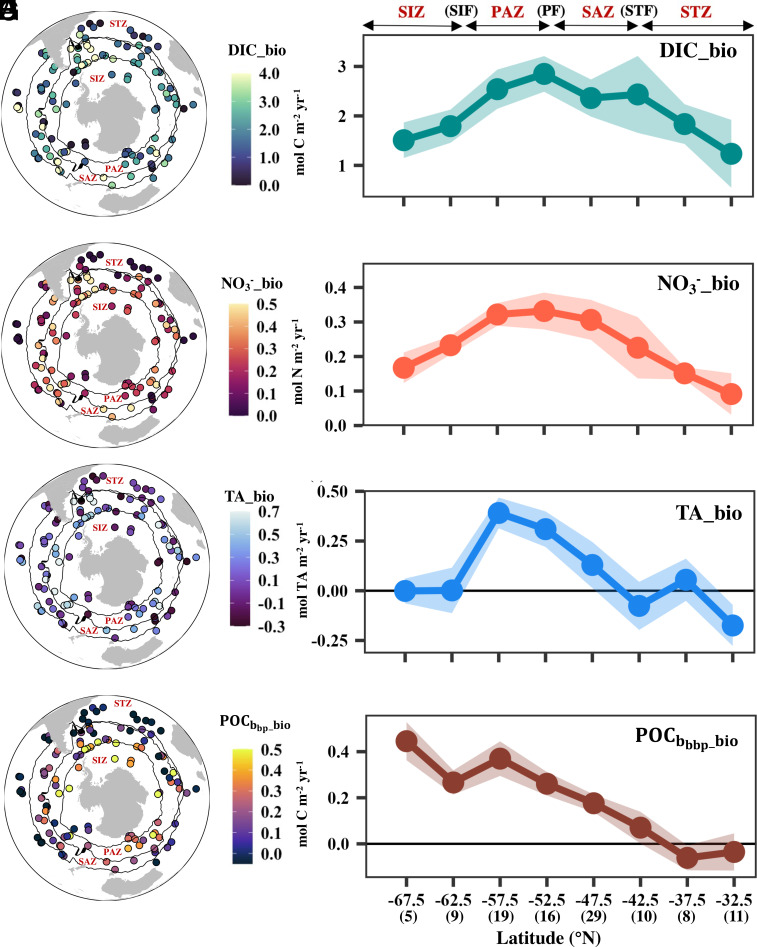
Fig. 1.

Euphotic zone net biological production during the SO productive season. Left panels (A, C, E, G) show the net biological production estimated for each seasonal cycle from various floats (individual circles indicate the mean float location during each productive season). Black lines denote the climatological locations (mean of 2004 to 2014) of SO fronts determined using an argo-based climatology of temperature and salinity (23). Right panels (B, D, F, H) show the meridional pattern of net biological production from each tracer. Numbers in parentheses at the bottom of the right column indicate the number of float seasonal cycles used to compute the average in each zonal band (5° bin). Labels above the right column indicate the approximate locations of frontal regions, with more precise locations found in the left column maps. Shading in the Right panels reflects the propagated error. STF: subtropical front; STZ: subtropical zone; SAZ: subantarctic zone; PF: polar front; PAZ: polar Antarctic zone; SIF: seasonal ice front; SIZ: sea ice zone; bio: biological production term; DIC: dissolved inorganic carbon; NO₃: nitrate; TA: total alkalinity; ${\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}$ : particulate organic carbon based on the backscattering coefficient.

The net biological production terms represent the excess of total tracer removal relative to supply, which reflects the carbon available for export (i.e., export potential) from the upper ocean (24). Among the four tracers, the DIC and nitrate (NO₃) biological terms are most similar, with maxima between 47 and 60°S in the subantarctic and polar Antarctic zones (SAZ and PAZ), followed by intermediate values south of 65°S in the seasonal ice coverage zone (SIZ, Fig. 1 A–D). This meridional pattern aligns with that of prior work based on seasonal surface NO₃ drawdown (19, 25) and mesopelagic oxygen consumption (21) (SI Appendix, Fig. S5). The NO₃-based biological term exhibits a more pronounced decline in the low-latitude subtropical zone (STZ; 30 to 40°S) and SIZ relative to the DIC-based biological term, as reflected by the elevated C:N ratio in these two regions (Fig. 2A). The TA-based biological term is insignificant in most regions excluding 47 to 57°S (Fig. 1 E and F). The ${\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}$-based biological term increases poleward and its magnitude is approximately one-tenth of the DIC-based biological term (Fig. 1 G and H).

Fig. 2.

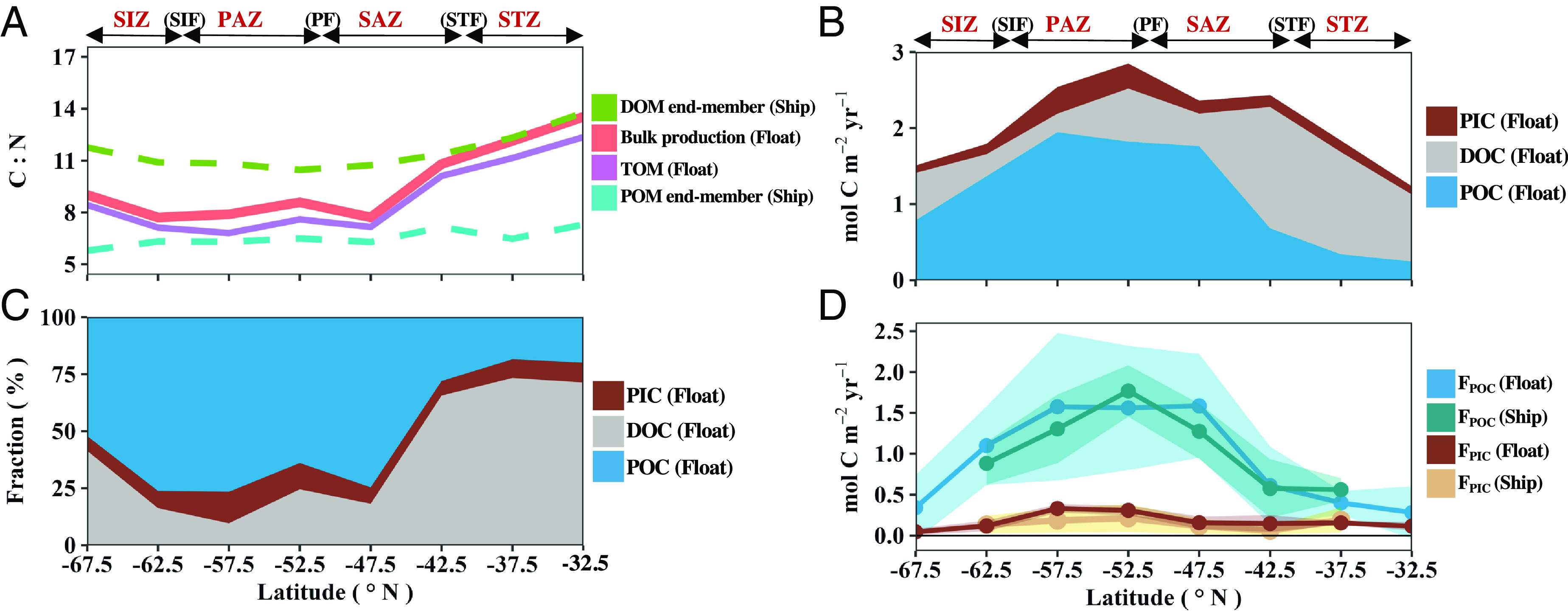
Meridional patterns of euphotic zone biogenic carbon pool production during the SO productive season. (A) Carbon-to-nitrogen ratios (C:N) of biological production from the float observations and compilations of existing ship-based datasets (SI Appendix, Text S1.1). (B) Magnitude and (C) fraction of biogenic carbon pool export potential. (D) Sinking flux of particulate organic carbon (F_POC) and particulate inorganic carbon (F_PIC) from float and ship-based analyses (SI Appendix, Text S1.2). Shading represents the propagated error. Frontal zones as described in Fig. 1. DOM: dissolved organic matter; POM: particulate organic matter; TOM: total organic matter; PIC: particulate inorganic carbon; DOC: dissolved organic carbon; POC: particulate organic carbon.

Discrepancies between the tracer biological terms reflect their differing abilities to capture various carbon pool dynamics (14). For example, NO₃ tracks the total organic matter (TOM) production, DIC and TA track the TOM and PIC production, and ${\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}$ tracks the in situ particles. We leverage these tracer differences, along with well-constrained carbon-to-nitrogen end-member ratios for organic matter production from compilations of ship-board datasets (Fig. 2A), to solve a system of equations and differentiate the carbon pools, including the sinking particle fraction (Materials and Methods).

Productive Season Biogenic Carbon Pool Contributions.

During the productive season, POC comprises ~85% of the total carbon (TC) production in the PAZ and SAZ regions, while DOC comprises ~75% of the TC production in the STZ and ~35% in the SIZ (Fig. 2 B and C). This latitudinal pattern is consistent with the results of Roshan and DeVries (26) who used a neural network estimate of the global DOC distribution and a data-constrained ocean circulation model to quantify the fractional DOC contribution to TOM export over the annual cycle. The DOC:TC production ratio is positively correlated with sea surface temperature (SST) and light availability and negatively correlated with NO₃ concentration (SI Appendix, Fig. S6). Nutrient limitation can impede heterotrophic bacteria from degrading newly produced DOM, resulting in seasonal DOM accumulation in the upper oligotrophic ocean (27). Additionally, high-light and low-nutrient conditions can cause photosynthesis to outpace cell growth and trigger phytoplankton excretion of excess fixed carbon in the form of DOC as an adaptive strategy to reduce photochemical damage (10). Since DOM is produced with nearly double the C:N (C:N_DOM = ~10 to 14) of POM (C:N_POM = ~5 to 7, Fig. 2A), the dominance of N-poor DOM production in the STZ drives the C:N of TOM production to 10-12 (Fig. 2A), deviating significantly from the classical Redfield Ratio [~6.6; Redfield (28) and Johnson et al. (29)]. This helps to explain the conundrum of pronounced seasonal DIC consumption and oxygen production observed in the nutrient-devoid subtropical, sunlit oceans (30, 31).

In the SIZ, nutrients are abundant and the DOC:TC production ratio is slightly elevated (Fig. 2C). Prior work has identified elevated subsurface oxygen-to-phosphorus remineralization ratios in the high-latitude SO, which indicates that elevated carbon-to-nutrient organic matter is being consumed, and likely produced, in this region (32). Elevated light levels in the SIZ, due to shallow mixed layers and long polar days during summer (SI Appendix, Fig. S1E), may also be driving the regionally elevated DOC contribution to TC production (32). Overall, we find that the DOC:TC production ratio is significantly correlated with SST. This aligns with results from previous mesocosm experiments that reported elevated DOC:TC production at warmer temperatures (33, 34). However, the global synthesis by Roshan and DeVries (26) suggests that this relationship breaks down in tropical ocean where SST values exceed 20 °C, higher than the temperatures in our study (SI Appendix, Fig. S1D). Thus, further evaluation is required to determine whether the positive relationship between DOC:TC production and SST observed in our study is caused by a metabolic temperature dependence (35) or is simply an empirical correlation across the polar to the subtropical ocean.

PIC export potential and its associated sinking flux peak around 47 to 57°S in the PAZ (Fig. 2 B–D) where elevated PIC concentrations, which may account for ~30% of the global suspended PIC pool, have been observed via satellite imagery and field observations (36). Importantly, the TA values used in our study are derived from empirical relationships (37), which integrate the smeared imprint of calcium carbonate processes. Therefore, we cannot resolve high-frequency calcium carbonate events (15). Additionally, such empirical relationships may not accurately capture TA dynamics in the SIZ due to sparse ship-based observations during ice coverage that limit the available training data (37). Nevertheless, encouraging agreement between the PIC sinking fluxes estimated from floats and measured from ships (Fig. 2D) provides confidence that our methodology is capturing the broad pattern of calcium carbonate cycling. Additionally, elevated float backscatter-to-chlorophyll-a ratios may indicate the presence of calcifying phytoplankton (38) and excess nitrate relative to silicate concentrations, in conjunction with moderate dissolved iron concentrations, in the PAZ (SI Appendix, Fig. S7 and Text S1.3) are thought to reflect favorable conditions for nitrate-dependent algae (i.e., coccolithophores) to outcompete silicate-dependent algae (39).

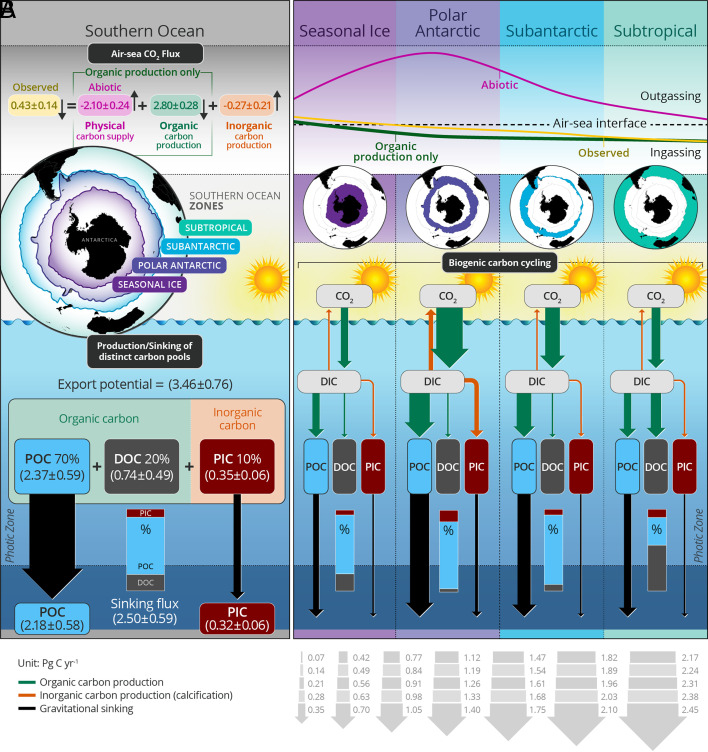
The area-weighted cumulative carbon export potential for the SO productive season is 3.07 ± 0.68 Pg C y⁻¹. This is comprised of 2.15 ± 0.54 Pg C y⁻¹ POC, 0.61 ± 0.41 Pg C y⁻¹ DOC, and 0.31 ± 0.05 Pg C y⁻¹ PIC production (SI Appendix, Fig. S4). During this period, 90% of the POC and 95% of the PIC production is exported out of the euphotic zone as sinking flux, yielding a seasonal SO rain ratio (PIC:POC export) of 0.16 (SI Appendix, Fig. S8), nearly triple the annual global average of 0.06 (40). Our finding that DOC accounts for ~22% of the area-weighted cumulative SO TOM production aligns with the global average of ~20% from previous studies (10, 26).

Influence of Biology on Air–Sea CO₂ Exchange.

To evaluate how biogenic carbon pool production regulates the SO carbon sink, we calculate seawater pCO₂ values, sea–air pCO₂ gradients (ΔpCO₂ = pCO_{2 sea} − pCO_{2 air}), and CO₂ gas fluxes before and after removing biological production terms from DIC and TA budgets to reconstruct an ocean that is instantaneously abiotic or experiences only TOM production (Materials and Methods). Our method for estimating biological production has elevated uncertainty during the unproductive season due to challenges associated with parameterizing key physical processes (e.g., mixing and turbulence). Therefore, to estimate the annual influence of biology on the SO carbon sink, we rely on a data-constrained model (B-SOSE, an ocean circulation model with biogeochemical components embedded (41)) to estimate the fraction of total annual biological production that occurs during the unproductive season (Materials and Methods, and SI Appendix, Fig. S9). Combining this information with our productive season results (Figs. 1 and 2), we can estimate biological production during the unproductive period and reconstruct seawater pCO₂, ΔpCO₂, and CO₂ gas fluxes over the full annual cycle for the abiotic, and only TOM production ocean. Rerunning the reconstructions while assuming zero production during the unproductive season yielded similar results (SI Appendix, Fig. S10). We attribute this to low levels of biological activity during the unproductive season as well as slow erosion of the pCO₂ anomaly created by vigorous biological activity during the productive period.

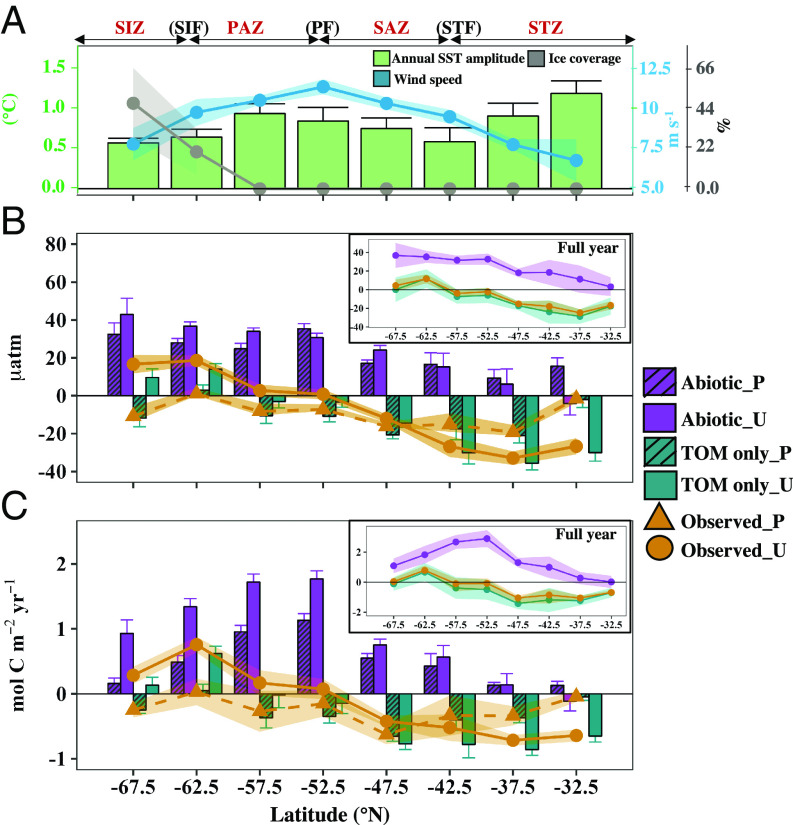
Our reconstructed abiotic ocean indicates that the SO would act as a strong CO₂ source, releasing 2.10 ± 0.24 Pg C y⁻¹ to the atmosphere over the annual cycle, in the case of no biological activity (Figs. 3C and 4). The most extensive outgassing occurs in the SIZ and PAZ where upwelling (5) and high wind speeds prevail (Fig. 3A). In these regions, ΔpCO_{2 abiotic} increases from the productive season to the unproductive season due to deep winter mixing (SI Appendix, Fig. S1A), which outcompetes the partially compensating effect of seasonal cooling. In contrast, in the subtropical ocean, ΔpCO_{2 abiotic} decreases from the productive season to the unproductive season due to seasonal cooling (Fig. 3A) because temperature is the dominant seasonal pCO₂ driver at these latitudes (42, 43).

Fig. 3.

Influence of biology on air–sea CO₂ exchange in the SO. Meridional pattern of (A) seasonal SST range, annual average wind speed, and percentage sea ice cover; (B) average sea–air pCO₂ difference (ΔpCO₂ = pCO_{2 sea} − pCO_{2 air}); and (C) cumulative CO₂ flux over the productive (P) and unproductive seasons (U) for the different productivity scenarios, with annual results shown in subpanels. The shading and error bars reflect the propagated uncertainty. Frontal zones as described in Fig. 1. Positive values in B and C indicate a source of CO₂ to the atmosphere. Abiotic: reconstructed, abiotic ocean; TOM only: reconstructed ocean with only total organic carbon production; Observed: observed, biotic ocean including both TOM and PIC production.

Fig. 4.

(A) Schematic of SO annual carbon cycling with results for the four frontal regions shown in panel B. Contributions of distinct biogenic carbon pools to the total biological carbon production and the associated impacts on air–sea CO₂ flux. Arrow sizes are proportional to the area-weighted, cumulative carbon flux magnitude within each frontal zone presented in SI Appendix, Fig. S4. Inset bar plots show the percentage contributions of each biogenic carbon pool to the export potential. Note that the annual biological production estimate is scaled from the float-based productive season estimate (shown in Figs. 1 and 2) based on information extracted from a data-assimilative SO model at each float location (Methods and Materials and SI Appendix, Fig. S9). A similar diagram illustrating results for the productive season only is provided in SI Appendix, Fig. S11.

Including TOM production (but no PIC production) transforms the SO from a strong CO₂ source to a net CO₂ sink over the annual scale, absorbing 0.70 ± 0.15 Pg C y⁻¹ from the atmosphere (Fig. 3C). The most substantial change in ΔpCO₂, relative to the abiotic ocean, is observed in the SAZ and PAZ, where biological production is highest (Figs. 1 and 2). During the productive season, vigorous biological activity works to bring ΔpCO_{2 TOM} below zero, driving CO₂ invasion throughout the SO. The SIZ is also transformed into a carbon sink during this season; however, the presence of sea ice (Fig. 3A) reduces the efficacy of air–sea gas exchange [air–sea CO₂ flux is scaled by the ice fraction, following McNeil et al. (44), Materials and Methods]. During the unproductive season, ΔpCO_{2 TOM} in high-latitude regions becomes positive, driving CO₂ evasion to the atmosphere. This increase in ΔpCO_{2 TOM} is primarily due to physical processes, as evidenced by similar seasonal differences in ΔpCO₂ for the abiotic ocean. Conversely, during the unproductive season in the subtropical ocean, the combined influence of biological production (~20% of annual biological production occurs during the unproductive season, SI Appendix, Fig. S9) and cooling work to reduce ΔpCO_{2 TOM}, further enhancing carbon uptake. Despite weak biological production during the unproductive season, differences in ΔpCO₂ between the biotic, TOM-only, and abiotic scenarios persist beyond the productive season (Fig. 3B). Seasonal cooling and enhanced mixing/upwelling cause similar changes in scenario pCO₂ values, while the relative difference between scenario pCO₂ values is determined by erosion of the existing pCO₂ (and DIC and TA) anomaly in response to unproductive period biological production, which works to maintain the discrepancy, and DIC accumulation/loss through air–sea gas exchange, which works to reduce the discrepancy. Even with minimal biological production, the rectifying effect of gas exchange is not enough to eliminate the pCO₂ difference between scenarios by the end of the 1-y reconstruction period. The sustained difference in pCO₂ between scenarios, coupled with elevated wind speed during the unproductive season (SI Appendix, Fig. S1G), enhances the ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ uptake disparity between scenarios (Fig. 3C).

Finally, including PIC production (i.e., the observed conditions) elevates ΔpCO₂ and reduces the ocean CO₂ sink over the annual scale (relative to the ocean with only TOM production) to absorbing 0.43 ± 0.14 Pg C y⁻¹ from the atmosphere. The most notable CO₂ flux changes associated with adding PIC production are in the PAZ (Fig. 3C) where prior ship-based observations have found elevated seawater pCO₂ in regions of active coccolithophore blooms (39). In summary, TOM production alone increases SO annual CO₂ uptake by 2.80 ± 0.28 Pg C y⁻¹ compared to an instantaneously abiotic ocean while including the influence of PIC production reduces the annual sink strength by 0.27 ± 0.21 Pg C y⁻¹ (Fig. 4). Overall, our study confirms the crucial role of biology in maintaining the modern annual SO carbon sink of 0.43 ± 0.14 Pg C y⁻¹.

Our results suggest that the SO BP plays an important role in counteracting what would otherwise be a large, physically driven CO₂ source to the atmosphere. On an annual average, biological activity lowers the SO sea–air pCO₂ gradient by ~28 μatm relative to an abiotic ocean, maintaining a negative sea–air pCO₂ gradient (~−8.1 μatm) at present atmospheric CO₂ levels (Fig. 3B). This allows the SO to be a significant CO₂ sink. Assuming the upward physical supply of carbon in the SO is dominated by old, remotely regenerated material rather than the respiration of locally produced carbon, a ~28% reduction in seasonal TOM potential export would reverse the sign of the sea–air pCO₂ gradient and CO₂ flux.

Over the past few decades, the SO air–sea CO₂ flux has undergone substantial decadal variability, shifting from a weakening carbon sink in the 1990s to a strengthening carbon sink after the year 2000 (5). Prior studies have tried to link such interannual variability to a change in ocean circulation strength (45) or external forcing [i.e., atmospheric pCO₂, McKinley et al. (46)], while assuming a constant BP efficiency. Given the large role of biology in sustaining the SO carbon sink, consideration of natural or anthropogenic perturbations to the efficiency of the biological carbon pump (e.g., altered micronutrient supply due to changing stratification induced by shifting winds, or altered DOC:POC production ratios due to rising SST) is needed for a comprehensive understanding of interannual variability in the SO CO₂ sink.

Our study presents insights into the meridional pattern of biogenic carbon pool production and the role of each carbon pool in affecting the SO carbon sink (Fig. 4); however, there are important limitations to consider. We rely on a data-constrained model to infer the fraction of biological production occurring during the unproductive season and assume the same ratio of biogenic carbon pool production in all seasons. While we have demonstrated that our annual CO₂ flux reconstruction is not significantly affected by our productivity estimates during the unproductive season (SI Appendix, Fig. S10), the real ocean may be more complex. For example, observations from the subarctic North Pacific reveal simultaneous net POC production and net DOC consumption during the winter (14). Such decoupling between POC and DOC pools leads to a significant difference in the POC:DOC ratio of carbon production during this period compared to the ratio observed during the productive season. In addition, POC produced during spring and summer that escapes the euphotic zone may not escape the maximum winter mixing depth, and carbon could be reentrained and ventilated (47). Improved ability to parameterize vertical mixing and horizontal transport would help extend our tracer budget approach to the full annual cycle and provide a more accurate estimate of annual biological production.

Additionally, our study focuses on the immediate influence of PIC formation on the air–sea CO₂ flux through elevating pCO₂ values; however, PIC can also impact the POC transfer efficiency on longer timescales (11). Modeling studies suggest that the PIC:POC export ratio (aka rain ratio) exerts a significant impact on atmospheric CO₂ (48). We find the highest rain ratio in the low-latitude subtropical ocean and not in the PAZ where the PIC sinking flux is greatest (SI Appendix, Fig. S8), which aligns with prior studies showing a poleward decrease in the rain ratio (39, 40). A more nuanced analysis is required to fully explore the overall impact of PIC production on the efficiency of the biological carbon pump.

Each biogenic carbon pool has a different ecological origin and may respond differently to climate change. PIC production and mineral stability may be sensitive to ocean acidification (49). A warmer and more stratified ocean will increase light exposure while reducing nutrient supply; conditions associated with elevated DOC:POC production. Modification of biogenic carbon pool production ratios in response to climate change could impact the regional efficiency of the biological carbon pump, altering the SO carbon sink magnitude. Moreover, a change in the SO BP strength or efficiency would in turn affect the amount of residual nutrients delivered to the lower latitude ocean (4), having far-reaching long-term impacts on global biogeochemical cycling. Our study not only provides a baseline estimate for the production and export of distinct biogenic carbon pools and their quantitative role in regulating air–sea CO₂ flux, but also demonstrates a basin-scale example of how autonomous platforms and shipboard observations could be leveraged as a cost-effective means to monitor the functionality of global marine ecosystems and their response to future climate change.

Materials and Methods

Float Data.

Float data used in this study are downloaded from the Argo Global Data Assembly Center at https://www.seanoe.org/data/00311/42182/. Floats simultaneously equipped with conductivity–temperature–depth, oxygen, pH, nitrate, and bio-optical sensors operating in the SO before September 2021 are used in the analysis (SI Appendix, Fig. S12 and Table S1). The bio-optical sensor measures backscattering (b_bp) at 700 nm (scattering angle of 150°) and fluorescence at 695 nm, which is induced by the blue light at 470 nm. Quality-control procedures for the biogeochemical sensor data are outlined in the studies by Johnson et al. (18) and Maurer et al. (50), and only data with quality flags of 1 (good data) are used herein. Some prior SO BGC float studies have applied an adjustment to quality-controlled float pH values (51) prior to computing seawater pCO₂ (1, 52) to address a perceived internal consistency issue with the carbonate system (53). Following the recent recommendation made by the U.S. Ocean Carbon and Biogeochemistry Program working group entitled the Ocean Carbonate System Intercomparison Forum (SI Appendix, Text S1.8), our study does not apply this adjustment. We evaluate the accuracy of surface seawater pCO₂ estimates from floats through comparison with pCO₂ measurements made on underway ships (SI Appendix, Fig. S13). The float-based pCO₂ values in this study are ~5 μatm higher than prior SO float-based pCO₂ analyses, which applied the additional pH-dependent pH adjustment [e.g., Bushinsky et al. (1), Gray et al. (52), and Williams et al. (54)]. However, our annual air–sea CO₂ flux estimates ( ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ ) suggest greater ocean CO₂ uptake compared to previous float estimates, which may be due to differences in float coverage and interannual variability (SI Appendix, Text S1.4). Despite the various approaches used, the exact annual ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ in the SO remains uncertain and varies greatly (1, 5, 55–57). Our study focuses on the biologically mediated component of ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ , which is calculated by differencing ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ values derived from the observed and reconstructed (abiotic and TOM production only) conditions. Therefore, our conclusions are less sensitive to the absolute value of seawater pCO₂.

Additional procedures are required before use of the bio-optical sensor data. Float b_bp data are processed using a seven-point running median filter followed by a seven-point running mean to remove spikes caused by zooplankton, aggregates, and/or instrument noise (58). The despiked values are then converted to POC based on a global empirical relationship. This empirical conversion may cause POC estimates to be biased high in regions with coccolithophore blooms [i.e., 47 to 57°S, Balch et al. (39)]. However, further analysis (SI Appendix, Text S1.5) indicates that such a bias would have a limited impact on biogenic carbon pool partitioning. Raw fluorescence data are first adjusted by subtracting the minimum fluorescence between 100 m and 300 m (dark value) and then by applying a correction for nonphotochemical quenching (59). The processed fluorescence data are converted to chlorophyll-a concentration using an empirical conversion factor of six derived from paired comparisons between float and collocated, contemporaneous ship-boarded samples (18). TA is estimated from float observations of temperature, salinity, and oxygen using the CANYON-B neural network algorithm, which achieves a prediction accuracy of 6.3 μmol kg⁻¹ (37). DIC and pCO₂ are calculated from estimated TA and float measured pH using the “seacarb” package in R (60) with the equilibrium constants as recommended by Wanninkhof et al. (61). Johnson et al. (29) recently compared SO float-based estimates of DIC with discrete bottle samples collected during float deployments and found excellent agreement (r² = 0.91, RMSE = 5 μmol kg⁻¹).

All of the quality-controlled float profile data are interpolated to 1-m vertical resolution and smoothed in time using a five-point moving average to reduce high-frequency fluctuations (16).

Computing the Residual, Net Biological Term.

The euphotic-zone (z_eu) net biological term ( ${\frac{\partial \mathrm{T}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}})$ is determined from the observed tracer change ( ${\frac{\partial \mathrm{T}}{\partial \mathrm{t}}|}_{\mathrm{O}\mathrm{b}\mathrm{s}}$ ) minus the estimated abiotic processes acting on the tracer in a one-dimensional mass balance model (Eq. 1):

$$\begin{array}{l}\frac{\partial {\text{T}}_{\left(\text{DIC},\text{TA},{\text{NO}}_3^{-},{\text{POC}}_{{\text{b}}_{\text{bp}}}\right)}}{\partial \text{t}}{|}_{\text{Bio}}=\frac{{\text{dT}}_{\left(\text{DIC},\text{TA},{\text{NO}}_3^{-},{\text{POC}}_{{\text{b}}_{\text{bp}}}\right)}}{\text{dt}}{|}_{\text{Obs}}-\frac{\partial {\text{T}}_{\left(\text{DIC}\right)}}{\partial \text{t}}{|}_{\text{Gas}}\\ -\frac{\partial {\text{T}}_{\left(\text{DIC},\text{TA},{\text{NO}}_3^{-},{\text{POC}}_{{\text{b}}_{\text{bp}}}\right)}}{\partial \text{t}}{|}_{\text{Phys}}-\frac{\partial {\text{T}}_{\left(\text{DIC},\text{TA},{\text{NO}}_3^{-},{\text{POC}}_{{\text{b}}_{\text{bp}}}\right)}}{\partial \text{t}}{|}_{\text{EP}}\end{array}$$ [1]

where subscripts Gas, Phys, and EP represent the air–sea gas exchange, physical transport and mixing at the base of euphotic zone, and evaporation and precipitation, respectively. Calculation of each abiotic term follows the study by Huang et al. (14), with a slight modification to the Ekman pumping estimate (SI Appendix, Text S1.6). The along float trajectory z_eu value is retrieved from contemporaneous satellite observations (8-d average provided by the Ocean Color website), where z_eu is defined as 1% of the surface light field (62). The average z_eu throughout the productive season is then used as the integration depth to close the tracer budget for each float year.

In this study, we rely on DIC, NO₃, TA, and ${\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}$ as tracers, excluding oxygen because its mass balance model is very sensitive to the parametrization of air–sea gas exchange and is highly dependent on sensor performance and calibration (63). Additionally, because the end-member ratio of oxygen to nitrate or carbon for POM and DOM production remains poorly constrained, the inclusion of an oxygen-based biological term contributes minimally to biogenic carbon pool partitioning.

We focus our tracer budget analysis on the stratified austral spring and summer seasons given that most biological production occurs during this period (SI Appendix, Fig. S9) and due to the difficulty in parameterizing physical transport, particularly diapycnal diffusion, during the fall and winter. For each float and year, the productive season is defined as the late winter maximum to the spring–summer minimum in the euphotic zone DIC inventory. The productive period start-and-end points range from August to November and from January to March, respectively (19, 20). We rule out seasonal cycles where the absolute change in NO₃ concentration is less than 0.5 μmol kg⁻¹ (most notably in the subtropical ocean), following the threshold adopted in the study by Johnson et al. (29). Such minimal NO₃ changes are near the instrument signal-to-noise ratio (50) and have large uncertainty, causing unrealistically high C:N ratios (>20) for the associated net biological terms. In addition, we only use floats with >6 profiles during the productive period to ensure sufficient seasonal coverage. After applying these constraints, 107 season cycles from 63 floats (SI Appendix, Table S1) are used to evaluate net biological production.

Even though biological production dominates the observed time-rate-of-change for each tracer during our study period (SI Appendix, Figs. S14 and S15), the omission of horizontal advection in our budget model could lead to nontrivial biases in the biological term estimates for individual season cycles. To minimize such error, we average seasonal net biological terms into 5° latitude bands based on the mean location of the float during each productive season to capture the mean meridional pattern. Johnson et al. (19) and Arteaga et al. (20) also used 5° latitude bins to average SO float observations of seasonal surface nitrate drawdown and mesopelagic oxygen consumption, respectively, for comparison with organic carbon export simulated by Earth system models. Agreement between the observed and simulated meridional patterns in these prior studies suggests that a 1-D tracer model can capture, to first order, the magnitude and spatial pattern of marine carbon export in the SO. We also assess the representativeness of the spatial variability of carbon export derived from the float locations by subsampling B-SOSE model output [a data-constrained biogeochemical ocean model (41)]. Our analysis reveals that the large-scale pattern of carbon export derived from float observations closely resembles the pattern obtained by averaging all model grids (1° × 1°) within each subregion (SI Appendix, Fig. S16).

Another caveat to our tracer budget approach is the inability to directly account for external nitrogen sources from N₂ fixation, which could cause the nitrate-based biological term to be biased low. To address this, we use a climatology of N₂ fixation from a data-driven inverse model [SI Appendix, Fig. S17A; Wang, et al. (64)] to correct the ${\frac{\partial {\mathrm{N}\mathrm{O}}_3^{-}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ term. This correction is negligible outside of the STZ (SI Appendix, Figs. S2E and S17B) and, once applied, constrains the observed C:N of TOM to within the expected end-member range for POM and DOM based on discrete observations (SI Appendix, Fig. S17C).

Partitioning Biogenic Carbon Pools.

We partition biogenic carbon pools using a system of equations following the procedures outlined in the studies by Huang et al. (14), Fassbender et al. (15), and Haskell et al. (16) using our 5°-binned net biological terms and well-constrained end-member C:N ratios for DOM and POM production derived from the compilation of existing shipboard observations (SI Appendix, Fig. S18). A diagram illustrating the workflow for carbon pool partitioning is presented in SI Appendix, Fig. S19. Briefly, the seasonal export potential of PIC ( ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}$ ) and TOM ( ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}$ ) can be separated using the DIC and TA net biological production terms (Eqs. 2 and 3):

$${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}=\frac{{\frac{\partial \mathrm{T}\mathrm{A}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}-\left({\frac{1}{{\mathrm{D}\mathrm{I}\mathrm{C}:\mathrm{T}\mathrm{A}}_{\mathrm{P}\mathrm{I}\mathrm{C}}}\times \frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}\right)}{\left(\frac{1}{{\mathrm{D}\mathrm{I}\mathrm{C}:\mathrm{T}\mathrm{A}}_{\mathrm{T}\mathrm{O}\mathrm{M}}}-\frac{1}{{\mathrm{D}\mathrm{I}\mathrm{C}:\mathrm{T}\mathrm{A}}_{\mathrm{P}\mathrm{I}\mathrm{C}}}\right)}$$ [2]

$${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}={\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}-{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}$$ [3]

where ${\mathrm{D}\mathrm{I}\mathrm{C}:\mathrm{T}\mathrm{A}}_{\mathrm{T}\mathrm{O}\mathrm{M}}$ (−116/17) and ${\mathrm{D}\mathrm{I}\mathrm{C}:\mathrm{T}\mathrm{A}}_{\mathrm{P}\mathrm{I}\mathrm{C}}$ (2) are the stoichiometric ratios of TOM and PIC production, respectively (65). After solving for ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}$ , we can combine it with ${\frac{\partial {\mathrm{N}\mathrm{O}}_3^{-}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ (after the nitrogen fixation correction, SI Appendix, Fig. S17) to differentiate the export potential of particulate organic matter ( ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{O}\mathrm{M}}$ ) and dissolved organic matter ( ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{D}\mathrm{O}\mathrm{M}}$ , Eqs. 4 and 5):

$${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{D}\mathrm{O}\mathrm{M}}=\frac{{\frac{\partial {\mathrm{N}\mathrm{O}}_3^{-}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}-\left({\frac{1}{{\mathrm{C}:\mathrm{N}}_{\mathrm{P}\mathrm{O}\mathrm{M}}}\times \frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}\right)}{\frac{1}{{\mathrm{C}:\mathrm{N}}_{\mathrm{D}\mathrm{O}\mathrm{M}}}-\frac{1}{{\mathrm{C}:\mathrm{N}}_{\mathrm{P}\mathrm{O}\mathrm{M}}}}$$ [4]

$${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{O}\mathrm{M}}={\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}-{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{D}\mathrm{O}\mathrm{M}}$$ [5]

where ${\mathrm{C}:\mathrm{N}}_{\mathrm{D}\mathrm{O}\mathrm{M}}$ and ${\mathrm{C}:\mathrm{N}}_{\mathrm{P}\mathrm{O}\mathrm{M}}$ are the nutrient ratios of DOM and POM production, respectively. The ${\mathrm{C}:\mathrm{N}}_{\mathrm{P}\mathrm{O}\mathrm{M}}$ is determined from the mean C:N ratio of suspended particles in z_eu based on the compilation of existing shipboard samples (Fig. 2A and SI Appendix, Fig. S18). The ${\mathrm{C}:\mathrm{N}}_{\mathrm{D}\mathrm{O}\mathrm{M}}$ is derived from the seasonal DOC and dissolved organic nitrogen inventory changes reconstructed from a recent global compilation of DOM data (Fig. 2A and SI Appendix, Fig. S18 and Text S1.1).

${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{O}\mathrm{M}}$ represents the amount of POM produced during the productive season, which can accumulate within z_eu or be exported as a sinking flux. By contrast, ${\frac{\partial {\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ tracks the in situ suspended POM inventory, which reflects the imbalance between POM production and removal via gravitational sinking ( ${\mathrm{F}}_{\mathrm{P}\mathrm{O}\mathrm{M}}$ ). Their difference equates to the sinking flux (Eq. 6):

$${\mathrm{F}}_{\mathrm{P}\mathrm{O}\mathrm{M}}={\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{O}\mathrm{M}}-{\frac{\partial {\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$$ [6]

Similarly, we can estimate the sinking flux of PIC ( ${\mathrm{F}}_{\mathrm{P}\mathrm{I}\mathrm{C}}$ ) by linking ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{P}\mathrm{I}\mathrm{C}}$ with the in situ suspended PIC inventory change ( ${\frac{\partial {\mathrm{P}\mathrm{I}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ ), which we estimate by multiplying the ${\frac{\partial {\mathrm{P}\mathrm{O}\mathrm{C}}_{{\mathrm{b}}_{\mathrm{b}\mathrm{p}}}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ term by the sea surface PIC:POC ratio determined from collocated and contemporaneous satellite observations of PIC and POC (PIC:POC_sat):

$${\text{F}}_{\text{PIC}}=\frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_\text{PIC}}-\frac{\partial {\text{POC}}_{{\text{b}}_{\text{bp}}}}{\partial \text{t}}{|}_{\text{Bio}}\times \text{PIC}:{\text{POC}}_{sat}\underset{}{\underbrace{\frac{\partial {\text{PIC}}_{{\text{b}}_{\text{bp}}}}{\partial \text{t}}{|}_{\text{Bio}}}}$$ [7]

Note, this approach assumes a homogeneous PIC:POC ratio within z_eu, which may introduce a limited degree of error in the F_PIC estimate (SI Appendix, Text S1.5). To validate our float sinking flux estimates, we compile published datasets of shipboard POC and PIC sinking flux observations determined by ²³⁴Th–²³⁸U disequilibrium (SI Appendix, Fig. S20 and Text S1.2).

Air–Sea CO₂ Gas Flux F_CO2.

Daily ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ is computed according to Eq. 8:

$${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}={(1-\mathrm{f}}_{\mathrm{i}\mathrm{c}\mathrm{e}})\times \mathrm{k}\times {\mathrm{K}}_{\mathrm{H}}\times {(p\mathrm{C}\mathrm{O}}_{2 \mathrm{s}\mathrm{e}\mathrm{a}}-{p\mathrm{C}\mathrm{O}}_{2 \mathrm{a}\mathrm{i}\mathrm{r}})$$ [8]

where k is the gas piston velocity parameterized from 10-m wind speeds (National Centers for Environmental Prediction, Reanalysis II) along the float track (66), K_H is the temperature and salinity dependent CO₂ solubility (67), pCO_{2 sea} and pCO_{2 air} are pCO₂ values at the sea surface (from float observations) and atmospheric boundary layer (from the National Oceanic and Atmospheric Administration, Greenhouse Gas Marine Boundary Layer Reference), respectively. We account for the impact of sea-ice fraction ( ${\mathrm{f}}_{\mathrm{i}\mathrm{c}\mathrm{e}}$ , derived from remote sensing) on ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ by assuming that it proportionally reduces the efficacy of air–sea gas exchange (44).

To quantify the role of biology in SO CO₂ uptake, we reconstruct time series of DIC and TA as well as the associated pCO₂ and ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ for different productivity scenarios. The reconstructed scenarios include an abiotic ocean, and an ocean with only TOM production. Each scenario reconstruction is performed on individual float annual cycles from the start of each productive season to the start of the next productive season, with the time step adjusted according to the float sampling frequency.

Reconstructions over the full annual cycle require time series of biological production both in the productive and unproductive seasons. The time series of biological production during the productive season ( ${{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}}_{\mathrm{P}}$ , ${{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}}_{\mathrm{P}}$ , ${{\frac{\partial \mathrm{T}\mathrm{A}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}}_{\mathrm{P}} ,and {{\frac{\partial \mathrm{T}\mathrm{A}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}}_{\mathrm{P}}$ ) are solved using tracer budget approach, whereas unproductive season biological terms ( ${{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}}_{\mathrm{U}}$ , ${{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}}_{\mathrm{U}}$ , ${{\frac{\partial \mathrm{T}\mathrm{A}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}}}_{\mathrm{U}},and{ {\frac{\partial \mathrm{TA}}{\partial \mathrm{t}}|}_{\mathrm{Bio}\_\mathrm{PIC}}}_{\mathrm{U}}$ ) remain unconstrained. To gap-fill the biological production during the unproductive season, we scale the time-integrated productive season biological production by the fraction of annual production that occurs during the productive period (R_P:A), as determined from B-SOSE model output (41) at the corresponding mean float location during the production season, as follows, using DIC as an example:

$$\sum \frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_{\text{TOM}}_{\text{U}}}=\sum \frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_{\text{TOM}}_{\text{P}}}\times \left(\left(1/{\text{R}}_{\text{P}:\text{A}}\right) -1\right)$$ [9]

$$\sum \frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_{\text{PIC}}_{\text{U}}}=\sum \frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_{\text{PIC}}_{\text{P}}}\times \left(\left(1/{\text{R}}_{\text{P}:\text{A}}\right) -1\right)$$ [10]

This approximation assumes that the fractional breakdown of distinct biogenic carbon pool production is identical during the unproductive and productive seasons. We then solve for the initial biological production rate at the beginning of the unproductive period and its temporal trend by assuming a linear decline to a value of zero at the end of the unproductive period, with the constraint that time-cumulative biological production during this period must equal $\sum \frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}\_{\text{TOM}}_{\text{U}}}$ (or $\sum {{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}}}_{\mathrm{U}}$ ). With this information, we can reconstruct time series of ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{T}\mathrm{O}\mathrm{M}\_\mathrm{U}}$ and ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}\_\mathrm{P}\mathrm{I}\mathrm{C}\_\mathrm{U}}$ . A visual example of the method is provided in SI Appendix, Fig. S23.

Here, we present an example of the DIC and TA time series reconstruction calculations for the abiotic scenario. TA for the abiotic scenario (TA_{Abiotic_n}) is reconstructed by subtracting the time integral of TA-based biological production ( ${\sum }_{\mathrm{d}\mathrm{a}{\mathrm{y}}_1}^{\mathrm{d}\mathrm{a}{\mathrm{y}}_{\mathrm{n}-1}}{\frac{\partial \mathrm{T}\mathrm{A}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ ) from the float-observed TA concentration ( ${\mathrm{T}\mathrm{A}}_{\mathrm{O}\mathrm{b}\mathrm{s}\_\mathrm{n}}$, Eq. 11):

$${\mathrm{TA}}_{\mathrm{Abiotic\_n}} = {\mathrm{TA}}_{\mathrm{Obs\_n}} – {\sum }_{{\mathrm{day}}_1}^{{\mathrm{day}}_{\mathrm{n}-1}}{\frac{\mathrm{\partial }\mathrm{TA}}{\mathrm{\partial }\mathrm{t}}|}_{\mathrm{Bio}}$$ [11]

DIC for the abiotic scenario ( ${\mathrm{DIC}}_{\mathrm{Abiotic\_n}}$ ) is reconstructed by subtracting the time integral of DIC-based biological production ( ${\sum }_{\mathrm{d}\mathrm{a}{\mathrm{y}}_1}^{\mathrm{d}\mathrm{a}{\mathrm{y}}_{\mathrm{n}-1}}{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{B}\mathrm{i}\mathrm{o}}$ ) from the float-observed DIC (DIC_{Obs_n}) and accounting for the difference in air–sea gas exchange between the observed, biotic conditions ( ${\sum }_{\mathrm{d}\mathrm{a}{\mathrm{y}}_1}^{\mathrm{d}\mathrm{a}{\mathrm{y}}_{\mathrm{n}-1}}{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{G}\mathrm{a}\mathrm{s}}$ ) and the reconstructed, abiotic conditions ( ${\sum }_{\mathrm{d}\mathrm{a}{\mathrm{y}}_1}^{\mathrm{d}\mathrm{a}{\mathrm{y}}_{\mathrm{n}-1}}{\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{G}\mathrm{a}\mathrm{s}\_\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{o}\mathrm{t}\mathrm{i}\mathrm{c}}$) (Eq. 12):

$$\begin{array}{l}{\text{DIC}}_{\text{Abiotic}\_n }= {\text{DIC}}_{\text{Obs}\_n} –{\sum }_{{\text{day}}_1}^{{\text{day}}_{n-1}}\frac{\partial \text{DIC}}{\partial \text{t}}{|}_{\text{Bio}}\\ - \left({\sum }_{{\text{day}}_1}^{{\text{day}}_{n-1}}\frac{\partial \text{DIC}}{\partial t}{|}_{\text{Gas}}- {\sum }_{{\text{day}}_1}^{{\text{day}}_{n-1}}\frac{\partial \text{DIC}}{\partial t}{|}_{\text{Gas}\_\text{abiotic}}\right)\end{array}$$ [12]

We use the reconstructed $\mathrm{T}{\mathrm{A}}_{\mathrm{Abiotic}}$ and $\mathrm{D}\mathrm{I}{\mathrm{C}}_{\mathrm{Abiotic}}$ to compute the abiotic seawater pCO₂ (pCO_{2_sea_abiotic}) and associated ${\mathrm{CO}}_2 \mathrm{gas} \mathrm{flux}$ ( ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_{2\_\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{o}\mathrm{t}\mathrm{i}\mathrm{c}}}$ or ${\frac{\partial \mathrm{D}\mathrm{I}\mathrm{C}}{\partial \mathrm{t}}|}_{\mathrm{G}\mathrm{a}\mathrm{s}\_\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{o}\mathrm{t}\mathrm{i}\mathrm{c}}$ ) for the preceding time step (following Eq. 12), and iteratively step forward in time through the calculations (see details in SI Appendix, Text S1.7).

In total, we produce 107 sets of time series of observed and reconstructed productivity scenarios over the full annual cycle. For each annual cycle, we compute the seasonal (productive and unproductive periods) and annual mean pCO₂ value and the time-integrated ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ for each productivity scenario. For simplicity, we use the same criteria applied earlier (the mean float location during each productive season; Fig. 1) to group seasonal and annual results into 5° latitude bands (Fig. 3), given small differences between mean float location for the productive, unproductive, and full seasonal cycle (SI Appendix, Fig. S24).

Overall, B-SOSE suggests that a relatively low of amount of productivity occurs during the unproductive season, with values ranging from <5% in high-latitude regions to ~20% in the subtropical ocean (SI Appendix, Fig. S9). This aligns with the results of Arteaga et al. (23), who used remotely sensed net primary production and carbon export ratio estimates to quantify carbon export in the SO across different seasons. A comparison of the unproductive period ${\mathrm{F}}_{{\mathrm{C}\mathrm{O}}_2}$ from our reconstruction of a biotic versus an abiotic ocean over just the unproductive period reveals very similar results (SI Appendix, Fig. S10). This suggests that our findings are not highly sensitive to estimates of biological productivity during the unproductive season.

Uncertainty Estimates.

The propagation of errors in our study includes contributions from interannual and spatial variability (σ_v) among the multiple float estimates averaged within each latitudinal bin (calculated as a SE) and the aggregated error (σ_a) inherited from a range of sources including the float sensors, satellite and reanalysis data products, parametrizations of physical processes, and end-member C:N ratios for the DOM and POM carbon pools. To quantify σ_a, we use a Monte Carlo approach with the error magnitudes for each parameter presented in SI Appendix, Table S2. The propagated error is calculated as $\sqrt{{{\sigma }_{\mathrm{v}}}^2+{{\sigma }_{\mathrm{a}}}^2}$.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All data used in this study are publicly available at the following links: Argo float data: ftp://ftp.ifremer.fr/ifremer/argo. NASA OceanColor data (PAR, PIC, POC and euphotic zone): https://oceandata.sci.gsfc.nasa.gov/directdataaccess/Level-3%20Mapped/Aqua-MODIS. NCEP-DOE) reanalysis II data (wind speed, air pressure, and relative humidity): https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.html. Global Sea Ice Concentration Climate Data (sea ice coverage): https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-ice-concentration?tab=overview. Advanced Scatterometer product (wind stress): https://manati.star.nesdis.noaa.gov/datasets/ASCATData.php. B-SOSE model output (export potential of total organic carbon above the euphotic zone): http://sose.ucsd.edu/index.html. NOAA Greenhouse Gas Marine Boundary Layer Reference data (atmospheric xCO₂): https://gml.noaa.gov/ccgg/mbl/mbl.html. Hansell et al. (2021) shipboard DOM compilation: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.nodc:0227166 (68). Martiny et al. (2015) shipboard POM compilation: https://www.bco-dmo.org/dataset/526747 (69). POC/PIC sinking flux: Henson et al. (2019) (archived from the supporting information in the citation), Moigne et al. (2014) (archived in Table 1 of the citation), and Rosengard et al. (2015) (archived from Table 2 in the citation) (70–72). Huang et al. (14) dissolved iron model output: https://zenodo.org/record/6994318#.Y0TNWezMJhE. nitrogen fixation model output: Wang et al. (64).