Machine learning estimation of human body time using metabolomic profiling

Significance

For individual timing of medical treatment or diagnosis of circadian disorders, it is essential that practical methods are being developed which allow estimation of individual circadian phase in the clinic. Our machine learning algorithm outperforms previously published approaches by using targeted metabolomics data from one or two optimally timed blood samples to reliably estimate circadian phase of melatonin specifically for men or women. It thereby provides a relatively cheap method for potential circadian applications in the clinic after appropriate validation.

Abstract

Circadian rhythms influence physiology, metabolism, and molecular processes in the human body. Estimation of individual body time (circadian phase) is therefore highly relevant for individual optimization of behavior (sleep, meals, sports), diagnostic sampling, medical treatment, and for treatment of circadian rhythm disorders. Here, we provide a partial least squares regression (PLSR) machine learning approach that uses plasma-derived metabolomics data in one or more samples to estimate dim light melatonin onset (DLMO) as a proxy for circadian phase of the human body. For this purpose, our protocol was aimed to stay close to real-life conditions. We found that a metabolomics approach optimized for either women or men under entrained conditions performed equally well or better than existing approaches using more labor-intensive RNA sequencing-based methods. Although estimation of circadian body time using blood-targeted metabolomics requires further validation in shift work and other real-world conditions, it currently may offer a robust, feasible technique with relatively high accuracy to aid personalized optimization of behavior and clinical treatment after appropriate validation in patient populations.

The circadian system in humans influences many behavioral, physiological, and molecular processes in the body, causing considerable variation in body function and cellular constitution over the course of the 24-h day (1). Chronomedicine seeks to exploit this 24-h variation to optimize timing for pharmaceutical application (“clocking the drug”) or diagnostic sampling for treatment of circadian clock abnormalities [“drugging the clock;” (2–4)]. Taking such “body time” approaches into clinical practice is thought to reduce medication load, improve treatment outcome, and increase accuracy and specificity of diagnosis. Here, we exploit diurnal variation in the amount of circulating metabolites in humans to estimate body time by using optimized timing in a minimal number of samples (5).

In modern society, humans show considerable variation in sleep timing (6), due to differences in the phase of circadian entrainment caused by variation in genetics, lifestyle, and especially light–dark environment. For this reason, chronomedical approaches, where a clinical diagnostic or treatment method is applied at a specific time of day, is still suboptimal. Personalized chronotherapeutic approaches, in which the entrained phase of the individual body is estimated and used to determine treatment/diagnostic timing, are expected to maximize the outcomes of chronomedicine. The current gold standard for human body time estimation is the local time of the onset of pineal melatonin synthesis under controlled lighting conditions (dim light melatonin onset, DLMO). DLMO is considered to be a reliable measure of the phase of the circadian pacemaker located in the hypothalamic suprachiasmatic nuclei. This is based on partial or full melatonin profiles measured in the evening or overnight using long sampling periods (8 to 20 h), and specific dim lighting and controlled posture conditions. Such a body time estimation method is not practical in real-world settings and therefore there is a strong need for validated alternative estimates of human body time.

One approach is to estimate human body time from ambulatory physiological and environmental signals. Such an approach has been shown to find high correlations with DLMO, using activity, body position, and subjective sleep measures [r² between 0.5 and 0.7 (7)]. Heart rate, rest/activity, and light measurements were used as inputs into an autoregressive model to estimate DLMO in individuals with relatively high accuracy (8). Woelders et al. found good accuracy using ambulatory core body temperature measurements and improved DLMO prediction using Kronauer’s human circadian light entrainment model (9).

An alternative approach is to exploit -omics technologies to estimate circadian phase from one or two blood samples. The underlying concept here is that many transcripts exhibit daily patterns that vary widely in phase; as such, it should be possible to estimate phase from a single sample by comparing the relative values of these transcripts when they are treated as “features” in machine learning and other analytical approaches. A first approach was the “TimeTable” method (5, 10) using the mouse liver transcriptome to estimate sample time. Sample time estimation methods were also applied on transcriptomics data from various mouse tissues using a supervised machine learning technique coined “ZeitZeiger” (11). For practical application in forensic science, sample time estimation methods were applied using human blood mRNA data to classify blood deposition time in three 8-h time frames across the day (12) and a similar approach was taken by including blood metabolite data (13). Machine learning techniques using an Elastic Net approach on entrained human blood transcriptomics data were applied in a method coined “TimeSignature,” which was initially also used to estimate sample time from two samples 12-h apart (14).

Machine learning techniques were also applied to estimate DLMO using molecular markers in blood (15–17). Using transcriptomics from blood monocytes, Wittenbrink and coworkers showed high accuracy for estimating DLMO using the ZeitZeiger method (17). Laing et al. (15) demonstrated that the partial least squares regression (PLSR) approach outperformed TimeTable and ZeitZeiger for predicting DLMO. In comparison, it was eventually shown that the TimeSignature approach also performed equally well in predicting DLMO from human transcriptomics data (18).

It is conceivable that individual DLMO-based body time estimation approaches will yield more accurate results, when input data are based on molecular measures that have a closer relationship to rhythmic metabolic processes in the body. This possibility was recently exploited using untargeted metabolomics analyses to predict melatonin onset and offset in plasma samples (4 h sampling interval over 20 h), from young men and women combined in a PLSR-based approach (19). Here, we want to expand on this approach by using targeted human metabolomics data (2 h sampling interval over 34 h), as input to a PLSR machine learning approach, to estimate DLMO phase in entrained humans using a separate analysis of men and women. We evaluate sampling design by comparing the phase estimation error under single, double, and triple blood sampling while analyzing optimal sampling timing.

Results

Overview of All Metabolites.

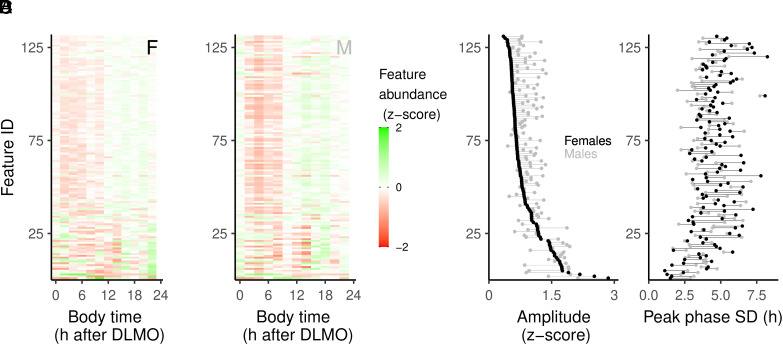
The data analyzed in this study originate from previous publications (20, 21). Overview of the rhythmic behavior of all 131 compounds is provided for females (Fig. 1A) and males (Fig. 1B). Amplitude (Fig. 1C) and peak phase (Fig. 1D) were assessed for each metabolite time series by evaluating the peak concentration and peak phase of a local polynomial regression (Loess) fit. Sex differences in the amplitude of metabolite rhythms showed that most features had a higher amplitude in males (Fig. 1C). Phase analysis shows that there are features that robustly peak at a given body time for males, but less so for females, and vice versa (Fig. 1D).

Fig. 1.

Overview of metabolite rhythms. (A) Normalized abundance over time for female data, ordered by amplitude. (B) Normalized abundance over time for male data, using the same ordering as for the female data. Rhythmic amplitude (C) and peak phase SD (D) are plotted for female (black) and male (gray) data and connected with a line for each metabolite. For each metabolite, a line to the right of a black dot indicates a higher amplitude (C) or phase SD (D) in males, lines to the left indicate a higher amplitude (C) or phase SD for females (D).

Model Fitting and Predictions.

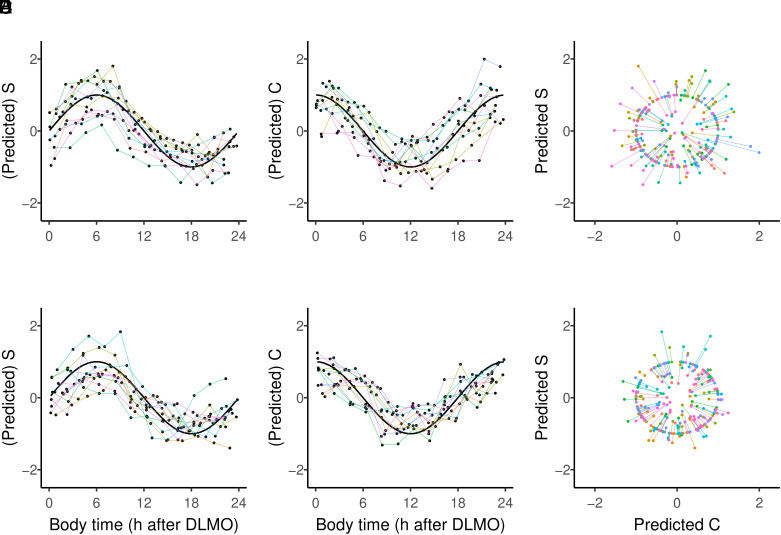
A graphical overview of the fitting procedure and the results is presented for female (Fig. 2 A–C) and male (Fig. 2 D–F) data. Each individual sample provides two predictions (one S and one C coordinate; Fig. 2 A, B, D, and E). Note that these are the predictions of n different models on n different independent datasets. The predicted S and C coordinates were then used to calculate an angle [(1,0) = 0°] by projection onto a unit circle (discarding amplitude variation; Fig. 2 C and F). Finally, the angles were converted to body time on a 24-h scale.

Fig. 2.

Model fitting and predictions. Overview of (predicted) S and C coordinates for female data (A and B) and male data (D and E), together with the actual S and C coordinates of measured body time projected on a unit circle for females (C) and males (F). Predictions of n models are color-coded and connected for each left-out participant/model prediction. Black curves (A, B, D, and E) show the sine or cosine function for sample time in hours after DLMO, and each participant is represented by a single color line.

Included Rhythmic Metabolites.

The majority of compounds contributing to the DLMO prediction are shared between females and males (58, 51.8%), while 17 (15.2%) are female specific and 37 (33%) are male specific. Sex differences in metabolomics data have previously been reported (for review, see study by Costanzo et al. (22)). Although sex differences in the timing of metabolite rhythms are less well studied, our data suggest that there is sexual dimorphism. OverRepresentation Analysis (ORA) and pathway analysis of the metabolites that were statistically significant in the C and S models in both sexes were performed. A total of 9 different pathway identifiers were found to be significantly overrepresented (False Discovery Rate (FDR) for multiple testing, P < 0.05; SI Appendix, Table S2). The only pathway that was consistently significant in both C and S models and in both sexes was aminoacyl-t-RNA biosynthesis. Phenylalanine, tyrosine and tryptophan biosynthesis was enriched in males (both C and S models) and in the female S model. Arginine biosynthesis; nitrogen metabolism; and D-glutamine and D-glutamate metabolism was enriched in the females (both C and S models) and in the male C model. Additional significant pathways (n = 4, FDR < 0.05) were only found in the female S model, namely valine, leucine and isoleucine biosynthesis; glutathione metabolism; glyoxylate and dicarboxylate metabolism, and phenylalanine metabolism.

Model Performance.

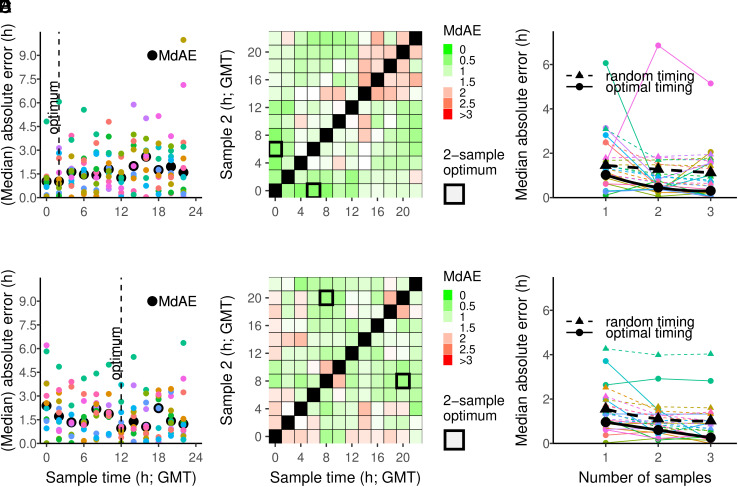
For a single sample analysis, the average prediction error (median absolute error, MdAE) was 1.54 h for the female data (Fig. 3A) and 1.48 h for the male data (Fig. 3D and Table 1). In order to accurately predict individual DLMO timing by a single blood sample, the optimal sampling time appeared to be at 2:00 h for females (Fig. 3A) and at 12:00 h for males (Fig. 3D). When two samples were taken, the optimal sampling times were 00:00 h and 6:00 h for females (Fig. 3B) and 8:00 h and 20:00 h for males (Fig. 3E). We also determined the prediction errors for a 3-sample procedure for females (SI Appendix, Fig. S2) and males (SI Appendix, Fig. S3), to deduce optimal timing for the three samples. To compare the performance of the PLSR procedure when based on one, two, or three optimally timed samples, we combined the errors in one plot and compared the values with randomly chosen sample times (Fig. 3 C and F). For the female data, the model performance significantly improved from one-sample MdAE = 1.54, to 1.16 and 1.02 when two or three random samples were taken [Χ²(2) = 17.42, P < 0.0001], respectively. When optimally timed samples were used, the model performance increased from one-sample MdAE = 1.02, to 0.45 and 0.30 when two or three samples were used, respectively, although this improvement was not significant [Χ²(2) = 1.95, P < 0.37]. Optimally timed prediction errors for females were on average 0.65 h lower than when samples were timed randomly (Fig. 3C and Table 1). For the male data, the model performance significantly improved from one-sample MdAE = 1.48, to 1.15 and 1.01 when instead of one, two, or three random samples were taken [Χ²(2) = 26.79, P < 0.0001]. When optimally timed samples were used, the model performance increased from one-sample MdAE = 0.96, to 0.60 and 0.26 when two or three samples were used [Χ²(2) = 7.16, P < 0.03], respectively. Optimally timed prediction errors were on average 0.60 h lower than when samples were timed randomly (Fig. 3F and Table 1). Optimal sample timing landscapes for the three samples are also provided for females (S2) and males (S3). Interestingly, increasing the number of samples mostly improved the prediction performance when using random samples, but less so when using optimally timed sampling.

Fig. 3.

Prediction accuracy of DLMO estimation using 1-, 2-, and 3-sample procedures. (A and D) Prediction accuracy (absolute error) and median absolute error per sample time for the 1-sample procedure. Predictions of n models are color-coded per left-out participant/model. (B and E) Median absolute errors in the 2-sample procedure. (C and F) Median absolute errors for the optimal and random 1-, 2-, and 3-sample procedures. Analyses presented separately for females (A–C) and males (D–F).

Table 1.

Comparison with DLMO estimation studies in humans using blood molecular markers

Refence		Condition	Sex	N	Age (y)	Method	#F	Measures	T	R2	MdAE (h)
Laing et al. (15)*		CR†, FD‡	f;m	24;25	27.1 (3.7)	TimeTable	73	Blood mRNA	1	0.49	3.13
									2	0.69	2.45
									3	0.82	1.87
						ZeitZeiger	107		1	0.47	3.18
									2	0.69	2.43
									3	0.78	2.07
						PLSR	100		1	0.74	2.22
									2	0.83	1.80
									3	0.88	1.52
						dTimeTable	73		2	0.78	1.67
						dPLSR	100		2	0.90	1.13
Wittenbrink et al. (17)§	(1)	CR	m	12	25.3 (2.6)	ZeitZeiger	32	RNAseq	1	-	1.6
							30		2	-	1.4
	(2)						30	NanoString	1	-	0.8
							29		2	-	0.7
	(3)	NL	f, m	17, 11	26.9 (5.7)		2		1	-	0.54
							2		2	-	0.75
Kervezee et al. (23)		CR	f, m	1, 10	24.1 (18–30)	PLSR	200	Blood mRNA	1	0.83	2.1
Braun et al. (18)*	(1)	CR†	f, m	12, 14¶	27.5 (4.3)	TimeSignature	41	Blood mRNA	2	-	1.2
	(2)	FD‡	f, m	11, 11¶	26.3 (3.4)					-	1.85
	(3)	CR	-	11	-					-	1.20
	mean										1.42
	(1)	CR†	f, m	12, 14¶	27.5 (4.3)	dPLSR	100	Blood mRNA	2	-	0.98
	(2)	FD‡	f, m	11, 11¶	26.3 (3.4)					-	2.17
	(3)	CR	-	11					-	-	1.10
	mean										1.42
Cogswell et al. (19)	(1)	LD baseline	f, m	8, 8	22.4 (4.8)	PLSR (DLMO)	100	Untargeted blood metabolites	1	0.61	2.2
	(2)	LD 5h sleep								0.6	2.1
	(3)	LD 9h sleep								0.56	2.6
	mean									0.6	2.2
	(1)	LD baseline				PLSR (DLMOff)	300		1	0.91	1.1
	(2)	LD 5h sleep								0.44	3.7
	(3)	LD 9h sleep								0.5	3.3
	mean									0.62	1.8
Woelders et al., 2023 (this study)		LD	f	12	24.8 (4.4)	PLSR	131	Targeted blood metabolites	1	-	1.02 (1.54)
									2	-	0.45 (1.16)
									3	-	0.30 (1.02)
			m	12	22.7 (4.5)	PLSR	131	Targeted blood metabolites	1	-	0.96 (1.48)
									2	-	0.60 (1.15)
									3	-	0.26 (1.01)

Variables: condition (FD, forced desynchrony; CR, constant routine; LD, light-dark cycle), sex (f= female, m= male), N=sample size for constructing the model (females, males), age [average and (SD)], method (statistical modeling approach), #F (number of features: 24-h gene expression or metabolite profiles required to train the model), measures (type of measurements used), T (number of sample timepoints used to construct a daily profile for each feature), R² (model fit), MdAE (median absolute error) indicating the median central measure of the individual differences in hours between the estimated and true DLMO. Where necessary, MdAE was estimated from SD given in the original reference by 100,000 Monte Carlo simulation runs. For the current study (bottom rows), our random sample selection (in brackets) compares favorably with the error estimates of the other studies. Improving DLMO estimation by optimized timing of samples according to sex improved the performance of the algorithm considerably (bold MdAE values).

^*The combined datasets of Archer et al. (24) and Möller-Levet et al. (25) were used in Laing et al. (15), which respectively correspond to datasets (1) and (2) that were re-analysed by Braun et al. (18).

^†Collection under dim light CR with or without prior sleep restriction.

^‡Collection under dim light and darkness during FD with sleep in or out of phase with melatonin.

^§Measured in isolated monocytes.

^¶Participants were exposed to either both FD conditions, or both CR conditions.

Discussion

We have shown that human plasma metabolomics data can be used as an input for a PLSR machine learning approach to predict DLMO phase as an indicator of body time in entrained young men and women when using two or three blood samples. Using two optimally timed blood samples, we obtained high accuracy in body time prediction, resulting in an MdAE of 0.45 h in women and 0.60 h in men (Fig. 3 C and F and Table 1). Adding a third optimally timed sample showed more improvement in males than in females on model performance (MdAE females 9 min; males 21 min). This finding suggests that circadian phase estimation in humans can be improved by distinguishing different approaches for women and men, an issue that is systematically addressed in our study.

Comparison to Other Blood Sample-Based Body Time Estimation Techniques.

We compared the performance of our approach using different input sets; melatonin only, cortisol only, metabolome only, and all possible combinations of these three (SI Appendix, Table S1). In the random timed samples, metabolomics-based estimation outperforms melatonin and cortisol only, and combining melatonin or cortisol with metabolome improves the model performance. Relatively high accuracy can also be found in optimally timed samples using only melatonin and/or cortisol, but these can be sex specific when more than one sample is used (SI Appendix, Table S1). In line with mRNA-based methods (14, 15, 17), we show that the temporal separation of two optimally timed samples is 6 h apart for both females and 12 h apart for males. Using such optimal timing of two blood samples, the MdAE in estimating DLMO is on average 0.53 h for women and men (Table 1). This is considerably more accurate than that of previously published molecular blood-based approaches (14, 15, 17); however, these studies reported average estimates of pairs of randomly chosen samples at a specific distance when evaluating a two sample-based method. When we applied a similar methodology, our metabolomics-based method produced an MdAE of 1.16 h for women and 1.15 h for men. The DLMO phase estimation accuracy of our PLSR metabolomics approach therefore is very similar to that of previously reported methods using TimeSignature or dPLSR methods [Table 1, (14, 15) and outperforms PLSR, TimeTable, and ZeitZeiger methods using blood-based RNA sequencing data (Table 1, (15, 17)]. However, almost a doubling in accuracy for random sampling was found when the NanoString RNA analysis platform based on isolated monocytes was used for two random samples [Table 1, (17)]. The recent metabolomics-based approach used by Cogswell et al. (19) holds promise. Their untargeted metabolomics analyses provide a wide coverage of the metabolome; however, infrequent sampling (4 h across 20 h) may have limited the number of rhythmic features detected (100 compounds for predicting DLMO) and the estimated phase accuracy of each rhythmic compound, potentially hindering the accuracy of the DLMO estimation. In addition, targeted metabolomics analyses have the advantage of quantifying known metabolites against standard calibration curves and internal standards. Since these are not available in untargeted metabolomics analyses, only putative features can be reported. The targeted metabolomics platform we have used is fully validated and reproducible, which provides confidence that the metabolites identified and measured by this method are real and that the data generated can be replicated in other facilities (26).

It is important to note that the various studies compared in Table 1 have not used the same protocols for their participants during sample collection. Laing et al. (15) used forced desynchrony protocols with sleep in and out of phase with melatonin, and no sleep during a constant routine protocol with and without prior sleep debt. Braun et al. (14) used three datasets: constant routine with and without sleep debt (1), forced desynchrony in phase and out of phase sleep (2), and a constant routine baseline—sleep deprivation—recovery (3). Wittenbrink et al. (17) used a constant routine protocol, which reduces behavioral influences on internal physiology and perhaps on gene transcription. Kervezee et al. (23) analyzed mRNA in a constant routine-like procedure but combined dim light and bright light treatment in their PLSR melatonin midpoint estimation. Cogswell and coworkers used untargeted metabolomics data under a baseline light–dark cycle, followed by adequate (9 h) or insufficient (5 h) sleep (19). Under baseline conditions, they found a high DLMO offset prediction accuracy that approaches our optimal timed prediction. Most of the protocols reviewed above were designed to isolate circadian information independent of sleep or sleep timing, or isolate the effect of sleep duration per se. Such conditions may be quite different from what people experience during normal day life (20, 21, 27). Our approach was aimed to generate prediction values closer to real-life conditions and could be considered more realistic because entrained participants were studied in a light/dark cycle with an 8 h sleep opportunity, with meals at normal habitual times (breakfast, lunch, dinner, and evening snack, SI Appendix, Fig. S1).

Evaluation of Included Metabolites.

ORA and pathway analysis revealed that the only statistically significant pathway common to both sexes and both C and S models was aminoacyl-t-RNA biosynthesis. Aminoacyl-t-RNA synthases play a central role in protein biosynthesis and are involved in a number of regulatory processes via their product, the charged t-RNA. Circadian control of translation of mRNAs for ribosomal proteins has been demonstrated in plants (28) and in eukaryotes where the levels of charged versus uncharged t-RNAs underpin circadian changes in mRNA translation, cellular energy and nutrient metabolism (29). Pathway analysis of a human metabolomics dataset also showed aminoacyl-t-RNA biosynthesis as the most predominant pathway in both simulated day and night shift conditions (30).

Many amino acids have shown time of day and/or circadian variation in human metabolomics studies (31) including in the current datasets (20, 21). Many of these amino acids were significant in the C and S models and form part of the aminoacyl-t-RNA biosynthesis pathway and the other significant pathways (arginine biosynthesis; phenylalanine, tyrosine and tryptophan biosynthesis). In the female C and S models, and in the male C model, glutamine and glutamate were also significant explaining enrichment of D-glutamine and D-glutamate metabolism and nitrogen metabolism in these datasets. The four additional significant pathways only observed in the female S model (glutathione metabolism; valine, leucine and isoleucine biosynthesis; glyoxylate and dicarboxylate metabolism; and phenylalanine metabolism) match with amino acids, glycine, ornithine, glutamate, isoleucine, valine, glutamine, phenylalanine, and tyrosine. Sex differences in some of these amino acids have been previously reported in serum metabolomics studies (32). In addition, we have reported sex differences in the timing of some of these metabolite rhythms (21).

Possible Advantages of Metabolomics for Body Time Estimation.

There are some advantages and disadvantages considering metabolomics-based methods over RNA-based methods in circadian body time estimation using human blood samples. First, metabolomics analysis is relatively cheap compared to RNA sequencing approaches. Second, metabolomics requires minimal data treatment. RNA sequencing data, on the contrary, require considerable bioinformatics treatment including error correction, data filtering, interpretation of alternative splice variants, and optical duplicate filtering. Moreover, these approaches are continuously developing and require specialist bioinformatics expertise. In contrast, if a quantitative targeted metabolomics approach is used, as in the current study, the original data are accurate and reproducible, making use of standards and quality controls (QCs) for reliability and batch correction (26) before entering the machine learning algorithm of choice. Third, DLMO estimation accuracy may be improved by using a single cell type from the blood sample [for instance, monocytes, (17)], but this also entails an additional cell-sorting step that requires specialist expertise, which is not required for blood-based metabolomics approaches. Fourth, metabolomics approaches may better reflect the functional phenotype than changes in RNA and proteins. The end products of actual metabolic and physiological processes may be closer to our interest when seeking a measure of body time (30, 33). Fifth, while many of the metabolites in a blood sample may have different tissue sources, certain lipids (e.g., cholesterol and its metabolites) and bile acids originate primarily in the liver. Specifically tracking the phase of these metabolite rhythms may permit estimation of the timing of the liver clock.

Limitations of Metabolite-Based Body Time Estimation.

An important limitation of using metabolomics data for diurnal and circadian analyses is the influence of ingested food on some specific metabolites, especially amino acids. Differences in diet may in part explain different model performance between our study and the study of Cogswell et al. (19). In our study, food was controlled and timed normally at the four events spread over the day. However, the effect of different diets on metabolite-based body time estimation remains to be resolved, as is the potential solution to minimize these effects of diet by including a period of fasting before a blood sample is taken. Validating the applied method after several hours of fasting may form an important practical improvement, since it would exclude the immediate effect of diet on the metabolome, and may also better match clinical practice because many patients may arrive at the hospital after an overnight fast. Furthermore, it should be noted that our metabolomics-based approach has only been validated in healthy young women and men under entrained conditions, thus possibly limiting its application in night work and shiftwork or in different age groups and clinical conditions. In order to realize the potential of our approach, validation in people that may suffer from altered circadian organization is needed. The same limitation, however, applies for most of the previous studies. In addition, all previous studies, including our own, have not addressed the possible additional variation emerging from estimating DLMO and molecular measures at different times of the year or at different latitudes.

One Sample-, Two Sample-, and Three Sample-Based Methods.

All studies evaluating multiple sampling report an improvement of DLMO estimation by using two or even three samples over a one sample-based method. We also confirm that three sample DLMO estimations outperform one- or two sample-based estimations, for random sampling as well as for optimally timed sampling. However, we also found diminishing returns when increasing the number of samples and the optimal number of samples may well be two for females and one for males, depending on sampling effort and costs involved. Furthermore, choosing an optimal time for these samples is important for minimizing estimation error, but a precise understanding of these optimal time points is subject for further research. Whether the improvement of optimal timing reflects a biologically relevant process or merely reflects the lower bound of a statistical distribution in prediction errors remains to be shown in future studies designed to address this particular question.

Conclusions and Future Perspectives.

For estimation of human DLMO using one or two blood samples, the metabolomics approach using PLSR on two optimally timed samples performs equally well or outperforms general blood RNA sequencing approaches. RNA-based analysis on isolated monocytes using the NanoString approach (17) seems to outperform other methods, but requires additional analytical laboratory steps and considerable bioinformatics. Metabolomics-based methods may therefore be a cheaper, faster, and more relevant approach for practical applications in the laboratory and the clinic for whole-body phase estimation using DLMO as a proxy for body time, although a combined metabolomics/RNA seq methodology may very well offer considerable improvement for body time estimation. Together, these body time estimation approaches should provide a measure that helps circadian-based clinical therapies. As such, metabolomics may offer a more feasible approach in that it is closer to the functional phenotype and specific clinical disorders. In addition, it potentially offers the possibility that the overarching term body time is replaced with tissue-specific estimation of circadian phase by using a specific set of metabolites.

Materials and Methods

The study was approved by the University of Surrey Ethics Committee. All participants provided written informed consent prior to any procedures being performed and the participants were allowed to withdraw at any time. All participant information was coded and held in strictest confidence according to the Data Protection Act (UK, 1998). The study was conducted in accordance with the Declaration of Helsinki and the principles of Good Clinical Practice.

Laboratory sessions were conducted at the Surrey Clinical Research Centre at the University of Surrey, with 12 females [25 ± 4 y (mean ± SD)] and 12 males [23 ± 5 y (mean ± SD)] participating. The analyzed data originate from two previously published studies that used identical study protocols [male study (20); female study (21)]. All were healthy, were medication free (except females took combined oral contraceptives and were on active phase during the laboratory session), were non-smokers, and had a regular sleep/wake schedule (23:00 to 07:00 h) in the 7 d prior to the in-laboratory session. Full details of the study eligibility criteria, screening procedures, baseline-at-home conditions, and laboratory protocols are presented (SI Appendix). In brief, the participants were kept in controlled entrained conditions (23:00 to 07:00 h: recumbent (sleep opportunity), 0 lux; 18:00 to 23:00 h and 07:00 to 09:00 h: semi-recumbent, <5 lux; 09:00 to 18:00 h: freely moving, ~100 lux) (SI Appendix, Fig. S1). Standardized meals were given at 07:10, 13:00, and 19:00 h with a snack at 22:00 h; water was available ad libitum.

Sampling and Analysis.

From the full dataset, only samples under entrained conditions were used, taken from 12:00 on day 2 until 22:00 h on day 3 (SI Appendix, Fig. S1). Following an adaptation night, hourly blood samples were collected from 12:00 h for 34 h. Two-hourly samples were analyzed for targeted metabolomics analysis and hourly samples were analyzed for hormone levels (melatonin, cortisol). Plasma fractions for metabolomics analysis were stored at −80 °C until derivatization and liquid chromatography/mass spectrometry (LC/MS) analysis; plasma for hormone assays was stored at −20 °C until analysis. Plasma melatonin and cortisol concentrations were measured by radioimmunoassay (Stockgrand Ltd, University of Surrey) as described previously (34). Targeted LC/MS was performed on two-hourly plasma samples to quantify metabolite concentrations, using the AbsoluteIDQ® p180 targeted metabolomics kit (Biocrates Life Sciences AG, Innsbruck, Austria), and a Waters Xevo TQ-S tandem quadrupole mass spectrometer coupled to an Acquity UPLC system (Waters Corporation, Milford, MA) as previously described (20, 21, 35). The kit provides absolute concentrations of 184 metabolites from six different compound classes (acylcarnitines, amino acids, biogenic amines, lysophosphatidylcholines, glycerophospholipids, and sphingolipids).

Plasma samples were prepared according to the manufacturer’s instructions. The sample order was randomized and three levels of QC were run on each 96-well plate. Data were normalized between batches using the QC level 2 (QC2) repeats across each plate (n = 4) and between plates using Biocrates METIDQ software (QC2 correction). We excluded metabolites where either >25% concentrations were below the limit of detection (<LOD), or below the lower limit of quantification, or above the limit of quantification, or the blank was out of range, or the QC2 coefficient of variance was >30% (21).

Entrained Female and Male Datasets.

For females, the total set of targeted metabolites above the detection threshold (see Sampling and Analysis section below) was 130, for males 141 (21). To enable comparison between females and males in this analysis, we used those 129 metabolites that both datasets had in common. To increase the accuracy and precision of the approach, we added the hormones melatonin and cortisol, leading to a total of 131 compounds to enter the model (SI Appendix, Tables S1 and S2).

PLSR Modeling.

In our datasets, there are many more predictors (features) than samples. Additionally, not all features are necessarily uncorrelated (i.e., multicollinearity). Multiple linear regression provides unstable solutions in this scenario. PLSR is a linear regression technique that can handle situations where requirements for multiple linear regression are violated. It is a dimensionality reduction technique, as it constructs latent variables (LV) that are linear combinations of the features that are correlated with the dependent variable, but also to one another. The dependent variable is then regressed onto this latent variable, reducing the dimensionality from f features to 1. Roughly speaking, each latent variable is a vector of weights (one for each feature belonging to the latent variable), where the weight coefficient depends on the covariance between the feature and the dependent variable. Two highly correlated features therefore both receive very similar weights (which is not given in ordinary least-squares regression). The measured values for the features in a sample can be multiplied element wise, then summed to this latent variable, and then summed in order to obtain a latent variable score. PLSR ensures that the weights of the latent variable are chosen in such a way that the covariance between the dependent variable and all latent variable scores (one per sample) is maximal. Additional LV can be constructed to explain orthogonal variance in the residual (i.e., deflated) datasets until no further variance can be statistically explained. When all LV are calculated, a standard regression model in the form $\widehat{Y}=X\widehat{B}$ can be constructed from the LV, where $\widehat{Y}$ is the model prediction, X contains the measured feature values, and $\widehat{B}$ contains the regression coefficients (one for each feature in the PLSR model). Models were constructed in R (v4.2.1; RStudio shell v2022.07.2), using the spls method from the “mixOmics” package (version 6.20.0).

Fitting Models Using Leave-One-Out Crossvalidation (LOOCV).

The main goal of this work was to construct a predictive model, that can be used to predict body time for future observations. This means that data that are used to construct the model cannot be used to evaluate the predictive performance of the model, as it is not independent of the fitting process. One way to handle this problem is to split the dataset into two parts: one to fit the model, and one to validate the model. To optimize the use of our data, however, we decided to employ the method of LOOC) instead. In this approach, n (participants) models are constructed, each time keeping the data of one participant aside to test the predictive value of each model.

Fitting Models Using Nested LOOCV.

The LOOCV procedure outlined above is a simplified version of the LOOCV procedure we eventually employed. The reason being that it is unknown a-priori how many LV should be constructed in the n models to prevent overfitting and underfitting. Determining this optimal value for each of the n models was done by implementing a second LOOCV procedure on the (n – 1) data used to construct the n models, also known as nested crossvalidation. The nested LOOCV procedure works by nesting an inner LOOCV loop inside an outer LOOCV loop: At the first iteration of the outer loop, the data for one participant are set aside. The remaining data are used for the inner loop. In one iteration of the inner loop, again, the data for one participant are set aside, and LV models are constructed on the remaining (n – 2) data. For each of these LV models, the performance (mean squared prediction error) is determined by predicting the data of the participant that was left out in the inner loop. The inner loop then iterates to the next participant, until LV models are constructed for each left-out participant (n – 1) in the inner loop. The value for LV that, on average, resulted in the lowest prediction error was then used to fit a final model on the inner loop data. This model was finally used to predict body time for the participant left out in the outer loop (data independent of the entire fitting procedure, including hyperparameter optimization). This process was repeated n times until the outer loop was completed, resulting in one final model for each outer loop iteration. A final overall model can be constructed by calculating the average regression coefficients of the n models (SI Appendix, Tables S3–S6). We do not know the predictive value of this model, although it can be inferred from the average prediction error of the n constructed models, under the assumption that our sample is representative of the population.

Body Time.

For each participant, the body time of each sample was expressed in hours after DLMO (DLMO_25%) for that participant. DLMO_25% was determined using a threshold of 25% of the range between the highest and lowest melatonin concentrations as the threshold [min + (max-min)*0.25], and then find the clock time where that threshold is crossed using linear interpolation.

Transformation of Body Time to Cartesian Coordinates.

Body time is circular, not linear (for example, a body time of 22 h is as close to DLMO (body time 0 h) as a body time of 2 h). Therefore, statistical problems will occur during any linear regression where time is expressed on a 24-h scale, as a predicted value of 22 at body time 0 will yield a residual value of 22, whereas it should be –2. Therefore, body time was expressed by converting hours since DLMO to angles, and then to Cartesian coordinates by projecting the body time onto a unit circle (i.e., a circle with radius of 1). The horizontal (C) and vertical (S) coordinates were calculated for each sample as follows: $\mathrm{S}=\sin [2\pi \times \left(\frac{\mathit{BT}}{24}\right)]$ and $\mathrm{C}=\cos [2\pi \times \left(\frac{\mathit{BT}}{24}\right)]$ , where BT is the body time of the sample. The calculated S and C coordinate values thus refer, respectively, to the Sine and Cosine components of body time projected on a circle and should therefore not be confused with processes S and C of the two-process sleep model. The rationale for this transformation is therefore that samples with similar body times have similar S and C coordinates, even when the difference in time expressed on a 24-h scale is large. In this system, DLMO corresponds to S = 0 and C = 1.

Transformation of Predicted Cartesian Coordinates to Predicted Angles.

Two PLSR models were constructed for each dataset: one to predict the S coordinates and one to predict the C coordinates of the samples. By constructing two linear models (one for the S and one for the C coordinate), it is possible to reconstruct the body time angle from the fitted S and C coordinates. A predicted angle was calculated for each sample ( $\widehat{\theta }=\mathrm{atan}2(\widehat{s}, \widehat{c})$ ). With the native R atan2 function, $\widehat{\theta }$ is signed (−π < $\widehat{\theta }$ ≤ π) with counterclockwise angles being positive and clockwise angles being negative.

Construction of Predictive Models.

The predicted body times ( $\widehat{\mathit{BT}}$ ) were then calculated from the predicted angles by transforming to the original 24-h scale, using $\widehat{\mathit{BT}}=\widehat{\theta }\times \frac{24}{2\pi }$ . Because $\widehat{\theta }$ is calculated from the predicted S and C coordinates ( $\widehat{s}$ and $\widehat{c}$ ), a final model that incorporates the two PLSR models is then described as: $\widehat{\mathit{BT}}=\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}2\left({\stackrel{-}{y}}_s+\sigma y_{s}X{\widehat{\beta }}_s,{\stackrel{-}{y}}_c+\sigma y_{c}X{\widehat{\beta }}_c\right)\times \frac{24}{2\pi }$ . Here, the two arguments passed to the atan2 function are the predicted Cartesian coordinates $\widehat{s} \mathrm{a}\mathrm{n}\mathrm{d} \widehat{c}$ , using the regression coefficients of the two PLSR models ( ${\widehat{\beta }}_s \mathrm{a}\mathrm{n}\mathrm{d} {\widehat{\beta }}_c$ ). For construction of the LV, PLSR requires the features and dependent data to be scaled and centered (each feature and each dependent variable is centered then scaled). Therefore, the X matrix is the scaled feature matrix (containing z-transformed metabolites using the SDs and means of our dataset) and $\sigma y_s$ and $\sigma y_c$ and ${\stackrel{-}{y}}_s \mathrm{a}\mathrm{n}\mathrm{d} {\stackrel{-}{y}}_c$ are the SDs and means, respectively, used for scaling and centering of the dependent variable.

The Relationship between Predicted and Observed Body Time.

One final step was required to assess the linear relationship (and prediction error) between predicted and observed body times (in hours after DLMO). Negative $\widehat{\mathit{BT}}$ values were corrected to positive values by adding 24 (e.g., a predicted body time of −1 becomes 23). For a subset of samples, this step yielded $\widehat{\mathit{BT}}$ values where ( $\widehat{\mathit{BT}}$ − BT > 12) or ( $\widehat{\mathit{BT}}$ − BT < −12). These values were corrected by subtracting 24 from $\widehat{\mathit{BT}}$ (when $\widehat{\mathit{BT}}$ −BT > 12) or by adding 24 to $\widehat{\mathit{BT}}$ (when $\widehat{\mathit{BT}}$ − BT< −12), as we know the maximal prediction error to be 12 h in either positive or negative direction.

Comparison of One-, Two-, and Three-Fold Sampling.

We additionally set out to determine whether one-, two-, or three-fold sampling frequency would be optimal to obtain more accurate circadian-phase predictions. In addition, we were also interested in the optimal sampling times themselves, for which we performed a grid search to obtain a measure of prediction accuracy for all combinations of first, second, and third sampling times. We first calculated the predicted DLMO from the predicted body time for each sample separately. For one-fold sampling, we then calculated the prediction error in DLMO separately for each sampling time. For the two-fold and three-fold samplings, we calculated the average predicted DLMO, for which additional steps were required. We first converted the measured and predicted DLMOs to angles (in radians), where an angle of 0° corresponds to DLMO. Then, we calculated the average for the predicted and measured angles separately. Angles were averaged using $\overline{\theta }=\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}2(\frac{1}{n}{\sum }_{j=1}^n{\mathrm{s}\mathrm{i}\mathrm{n}\theta }_j,\frac{1}{n}{\sum }_{j=1}^n{\mathrm{c}\mathrm{o}\mathrm{s}\theta }_j)$ , where n denotes the number of angles to be averaged. These average angles were then converted to body time (hours since DLMO) on a 24-h scale, followed by calculation of the prediction error.

For these procedures, only the samples taken within 24 h of the first sample were included. We preferred this approach over, for example, an initial averaging of predictions per sampling time point (as some time points were measured multiple times in the protocol), as the latter might yield an overly optimistic estimate of prediction accuracy by increasing the number of samples per time point. The rationale here is that in practical situations, such as a clinical setting, it is unrealistic that for these time points two or more samples are taken, which would mean these have to be taken at least 24 h apart and would substantially increase the number of visits a patient or client has to make to the clinical practice. What we thus tried to assess here, is the prediction accuracy for one-, two-, or three-sampling procedures while restricting the sampling window to 23 h or less in the case of multiple sampling. To test the significance of model improvement by increasing sample number, we ran a linear mixed-effects model to account for between-subjects variation, using the lme4 package (v1.1-30) in R, with the number of samples as a fixed effect (categorical factor) and subject ID as a random effect.

Metabolites that were statistically significant in the C and S models were converted to Human Metabolome Database IDs and submitted to Metabolite Set Enrichment Analysis and Pathway Analysis (MetaboAnalyst 5.0 https://www.metaboanalyst.ca/). ORA was performed using the hypergeometric test to evaluate whether a particular metabolite set was represented more than expected by chance within the given compound list. One-tailed p values were provided after adjusting for multiple testing. Pathway analysis was performed using a Homo sapiens Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway library.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Rscripts, other associated code data have been deposited in FigShare (https://figshare.com/articles/journal_contribution/Woelders_et_al_2023_Supplementary_data_and_analysis/22567783/1) (36). All study data are included in the article and/or SI Appendix. Previously published data were used for this work (20, 21).