Abstract
Quick response codes (QRCs) are found on many consumer products and often encode security information. However, information retrieval at receiving end may become challenging due to the degraded clarity of QRC images. This degradation may occur because of the transmission of digital images over noise channels or limited printing technology. Although the ability to reduce noises is critical, it is just as important to define the type and quantity of noises present in QRC images. Therefore, this study proposed a simple deep learning-based architecture to segregate the image as either an original (normal) QRC or a noisy QRC and identifies the noise type present in the image. For this, the study is divided into two stages. Firstly, it generated a QRC image dataset of 80,000 images by introducing seven different noises (speckle, salt & pepper, Poisson, pepper, localvar, salt, and Gaussian) to the original QRC images. Secondly, the generated dataset is fed to train the proposed convolutional neural network (CNN)-based model, seventeen pre-trained deep learning models, and two classical machine learning algorithms (Naïve Bayes (NB) and Decision Tree (DT)). XceptionNet attained the highest accuracy (87.48%) and kappa (85.7%). However, it is worth noting that the proposed CNN network with few layers competes with the state-of-the-art models and attained near to best accuracy (86.75%). Furthermore, detailed analysis shows that all models failed to classify images having Gaussian and Localvar noises correctly.
Keywords: Noisy images, Quick-response code, Noise identification, Noise classification, Machine learning, Deep learning, CNN
1. Introduction
A QRC, also known as a matrix barcode, is devised in 1994 by the Japanese automaker Denso Wave [1]. The two-dimensional barcode in question was developed in Japan expressly for use in the automotive industry [2]. A QRC offers the benefits of a large information volume, high dependability, a wide range of information including graphics and text, and high security [3]. The emergence of QRCs progressively catches the attention of vendors [4]. However, the QRC's initial look was not intended for hominid eyes to perceive. Individuals cannot comprehend such codes with the naked eye since a normal QRC has white and black modules only. Thus, such coding architecture makes it difficult to modify its look. QRCs have risen in demand in parallel with smartphones' growing usage and popularity. Because of the apparent advantages of enormous data capacity and simplicity of data retrieval, QRCs have largely replaced linear barcodes throughout many areas. And it has a leading position among the numerous 2D bar codes due to its large capacity, error correction, and quick response [5]. We may retrieve selected information instantaneously by scanning the code. However, due to interference of the transmission channel, overheating of the device, lack of light at the moment of taking an image, broken image sensor, or printers' methods and limited printing technology, noise is inevitable in images.
Noises are frequently introduced during digital image acquisition, collection, and transmission [6]. Various sorts of noises, including Salt and Pepper, Poisson, Gaussian, and many more noises, can degrade the clarity of a QRC image. Such noises are generated by post-filtering, a small focal length, poor compression, faulty memory allocation, and other adverse circumstances in the environment or from image-capturing devices. Consequently, there is a need for some effective ways to precisely categorize different noise types so that they can be simply eliminated [7].
Artificial intelligence is a hot topic in the information technology industry right now [8], and with cause; it represents a significant advancement and substantial leap in how computers learn. The emergence of huge volumes of data, known as big data, and evolving technology have made the use of machine learning extremely popular. Many contemporary image processing methods use deep neural networks (DNN) and other machine learning models to make changes to pictures for a range of objectives, including enhancement of particular image aspects, adjustment of its quality, and addition of artistic filters for computer vision-based applications [9]. An area of machine learning known as “deep learning” has seen some of the most significant recent advancements and research hotspots [10]. CNN, a type of neural network (NN) based on deep learning, represents a significant advancement in image recognition. It extracts characteristics from images to do its operation. This eliminates the requirement for manual feature extraction. The characteristics have not been trained! They are acquired as the model trains on a series of images. Deep learning models are therefore exceptionally accurate for computer vision applications. CNN learns feature detection by alternating between tens or hundreds of hidden layers [11]. The complexity of the learned characteristics grows with each layer.
A CNN is a powerful image classification approach that employs dense, convolutional, and pooling layers in the training phrase. It consists of many neurons with trainable biases and weights in a multi-layer NN fashion [12]. Emerging CNNs have recently surpassed prior techniques in several computer vision challenges, including image categorization and object recognition. This deep NN model is contrived and feasible by powerful and robust GPUs, which allow the bundling of deep layers and administering numerous image data characteristics [13]. In addition, traditional machine learning techniques like DT and NB have been prominent in the field of information technology [8]. These algorithms are used in the process of resolving a variety of classification issues.
Noisy images are detrimental elements in the training of CNN, lowering the networks’ classification performance [13]. Noise in an image can progressive or cumulative [9]. The noise model based on cumulative, boosts the noisy content in the original signal to obtain a highly corrupt noisier signal that follows the rule given in (1), where m (y, z) represents the image brightness level and a (y, z) represents the noise used to produce the corrupted signal q (y, z) at (y, z) spatial location. The progressive noise model, on the other hand, multiplicates the original content with the noisy content as given in (1).
| (1) |
To our knowledge, numerous studies have made efforts to classify image noise. For example, Milan Tripathi [14] developed, put into practice, and evaluated a CNN-based model using performance metrics (accuracy) to recognize noisy images, later suggested a UNET-based network to mitigate noise from images using optimal structural similarity index measure (SSIM) and peak-signal-to-noise ratio (PSNR) values. For different application contexts, Lue et al. [15] suggested an image-noise-level classification strategy using two NNs by comparing various image quality assessment approaches. They investigated why classification accuracy was poor and devised a gentle solution of establishing a tolerance rate to attain greater acceptable accuracy. Working on nine different noise distributions (Poisson, Rayleigh, Erlang, uniform, lognormal, exponential, speckle, Gaussian, and salt and pepper), researchers in Ref. [16] compared two different CNNs, VGG-16 and Inception-v3, to automatically identify noise distributions and concluded that Inception-v3 network adequately distinguishes these noise. For each of the noisy image sets, later correlated the FFDNet performance with noise clinic. Furthermore, they discovered that, with an average PSNR improvement of 16%, CNN-based denoising outperforms blind denoising in general.
Authors in Ref. [17] studied a noisy image categorization method based on five different supervised DNN architectures, denoising autoencoder CNN (DAE-CNN), convolutional denoising autoencoder CNN (CDAE-CNN), denoising variational autoencoder CNN (DVAE-CNN), denoising autoencoder-convolutional denoising autoencoder-CNN (DAE-CDAE-CNN), and denoising variational autoencoder-convolutional denoising autoencoder-CNN (DVAE-CDAE-CNN), were used to categorize the reconstructed image. It was discovered that the first three algorithms work well on images with a small level of noise, while the final two methods are good for categorizing large amounts of noisy data. Scientists in Ref. [18] exploited stochastic gradient descent optimization and backpropagation approaches to recognize image noise of various sorts and intensities using a CNN-based model. Moreover, to boost the model's computational efficiency and acquire data-adaptive filter banks, they incorporated a filter generation approach known as principal component analysis (PCA). In Ref. [19], a Noise-Robust CNN (NR-CNN) model made it possible to effectively classify noisy images without any prior processing. When compared to ResNet, VGG-Net- (slow and medium), and GoogleNet, experimental findings show that the suggested CNN performs better in noisy image categorization. Additionally, their suggested CNN requires no pre-processing for noise reduction, which expedites the categorization of noisy images.
We can retrieve precise information synchronously by scanning the QRC. The standard QRC, which is made up of white and black modules, is unappealing to the eye and difficult to recognize. The use of graphic QRCs in product packaging and marketing campaigns has risen in recent years. On the other hand, when a user scans a printed visual QRC, it encounters a noise phenomenon that hinders recognition and results in failure. Automatic noise detection and identification in QRC images is infancy state. Authors in Ref. [20] generated a QRC image dataset of 20,000 samples and investigated CNN, logistic regression (LR), and support vector machine (SVM) to detect the noise presence. For the two-class classification problem (with-noise or without-noise), SVM and LR performed better than CNN by achieving an overall accuracy of 97.50% and 97.25%. Their CNN model (having four convolutional layers) secured 95.95% accuracy to identify whether the given QRC image has noise or not. Later, they expanded their work [21] by exploiting several other machine learning classifiers (DT, NB, and random forest) and pre-trained networks (Xception and ResNet101) to detect the noise presence in QR code images that have four different types of noises. It is noted from the work that Xception and ResNet101 attained 100% accuracies, and thus outperformed other models. Once the system identifies the noise type then applying appropriate reversal of degradation operation can help restoring the actual QRC, such as authors in Ref. [22] proposed a doubly CNN framework for deblurring QRC. However, due to the lack of such noise identification system in the literature, we looked forward to developing an intelligent noise classification approach. The justification for this is that once the specific form of noise that constitutes an image has been identified, a suitable noise reduction filter may be practiced.
Since, QRCs are commonly utilized presently and can be found practically anywhere, including cosmetics, general stores, and advertisements. It has now become a significant component of daily life. It has been so user and mobile-friendly as an information-sharing medium that anyone can acquire the information contained in it with a single scan using a smartphone. Therefore, the influence of any kind of noise in the QRC image reduces its quality and causes it to lose part of its crucial information. As stated, the ability to reduce noises is critical, it is just as important to define the type and quantity of noises present in QRC images. For addressing this issue, besides the proposed CNN architectural network, we also exploited several pre-trained deep and classical machine learning-based models to adequately segregate types of noises (salt & pepper, salt, speckle, pepper, Poisson, localvar, and Gaussian) in QRC images. The paper contributes the following to the research community.
-
•
The application of the proposed system can contribute noise eradication system for QRC images by identifying its type.
-
•
Extensive literature review to conclude that no such prior studies and noisy QRC dataset exist.
-
•
Creation of a QRC image data set of 16 gigabytes.
-
•
Expanding the dataset by introducing 7 different noises to QRC images.
-
•
Performs noise classification by exploiting eighteen different deep and two machine learning architectures.
-
•
Provides analysis of noise classification with different architectural structures.
-
•
Evaluates the effectiveness of several models using a number of criteria, including recall, precision, F1-score, and accuracy for each of the eight classes in all exploited models.
The rest of the script is structured as follows: Section 2 covers the suggested methodology. The experiment findings and comparison/discussion are given in Section 3. Section 4 describes the result, and the paper ends with a conclusion, limitations, and future work in Section 5.
2. Materials and methods
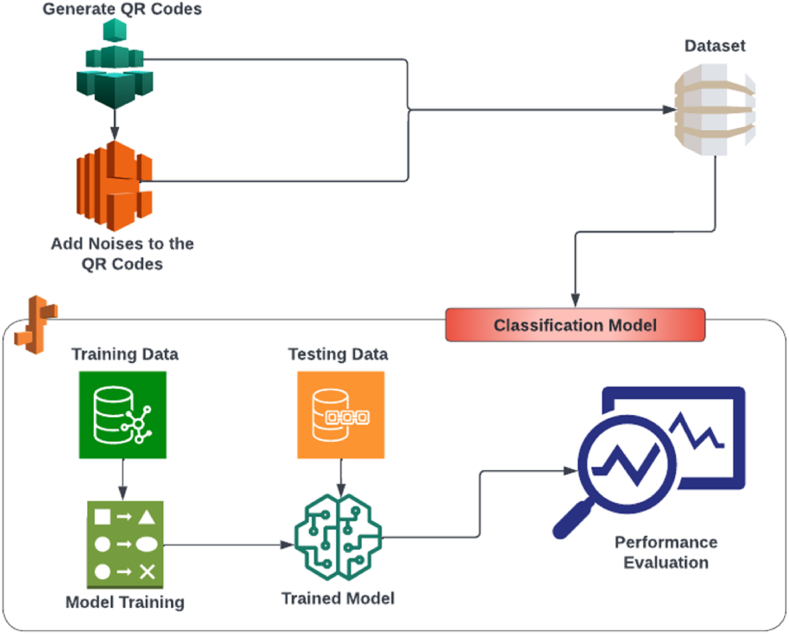
In order to identify a QRC image as either an authentic QRC (that is clean) or a noisy image by predicting the type of noise, this work aims to develop classification models that take QRC images as input. As per our knowledge, no such dataset exists in the literature, therefore, according to the suggested study's workflow (see Fig. 1), for this work we first created a normal dataset by generating QRC images without noise, later we incorporated several distinct noises to these initially generated images. The noises include salt & pepper, salt, speckle, pepper, Poisson, localvar, and Gaussian, thus the dataset consists of eight labels (original QRC and seven noises). Later it performs some scaling and pre-processing methods and after properly splitting data into the train and test sets the data is fed to the proposed CNN classification models to segregate QRC images into eight different labels. Besides this, seventeen other deep learning-based models (such as InceptionV3, Xception, ResNet50, etc.) and two machine learning-based NB and DT architectures are also exploited to evaluate and compare their performance with proposed CNN architecture to determine noisy images by correctly predicting their type.
Fig. 1.
The suggested study's workflow.
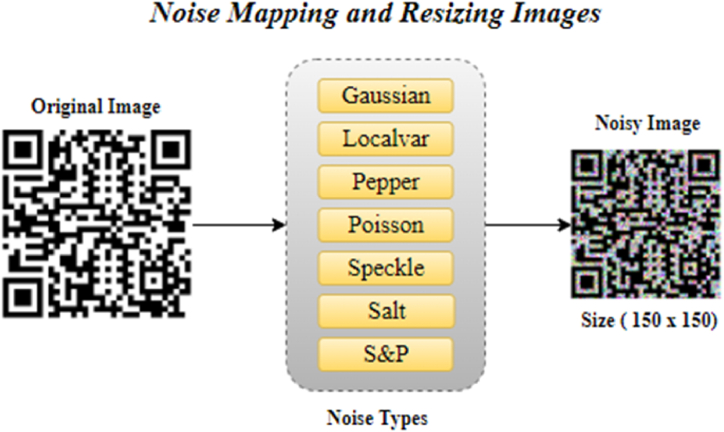
The study's objectives include analyzing generated QRC images, resizing them, mapping noise to these generated clean/original images (see Fig. 2), encoding the labels, training the proposed models, identifying the type of noise, and producing the classified class/label. To handle the noise type classification challenge, we used the deep learning framework TensorFlow [23].
Fig. 2.
The quick response code (QRC) image dataset creation by mapping noise. Each original QRC image (of varying sizes) is resized to a (150 × 150) ratio and then mapped seven distinct types of noise. Each noise is mapped separately as a class.
2.1. Dataset analogy
For this study, we produced a unique dataset consisting of 80,000 images including clean (original) and noisy QRCs. The dataset highly varies; certain classes contain images of various image quantities and sizes; thus, we pre-processed the images to resize them into a constant size of (150 × 150) ratio because our neural network requires a fixed-size input. Each generated QRC image has a bitmap format (BMP) and the total size of the dataset is about 16.1 Gigabytes. Fig. 2 depicts the procedure for resizing the images and assigning various types of noise to the clean (normal) QRC images.
First, we generated 10,000 images of original (normal/clean) QRC images without mapping any noise. Later, we separately mapped seven different noises to each original QRC image. As a result, the study expanded the dataset by forming seven different noisy images against each original QRC image. Thus, the dataset contains eight classes; the original class and seven additional classes produced by combining the original class with noises of seven different types including salt & pepper, salt, speckle, pepper, Poisson, localvar (white noise with a zero-mean Gaussian distribution and an intensity-dependent variance), and Gaussian. The following sub-sections provide a short description of the noises introduced for the formation of the dataset.
2.1.1. Salt-and-pepper noise
The term “salt-and-pepper noise”, referred to as impulse noise, is used to describe a variety of techniques that all lead to the same basic image degradation [24]. This noise may be caused by abrupt and quick changes in the visual signal. It appears to be an uneven distribution of white and black pixels. In salt pepper noise, a and b do not have the same values. Each one has an average likelihood of less than 0.1. The image has a “salt and pepper” appearance when the damaged pixels alternate between the lowest and greatest value.
2.1.2. Speckle noise
Contrary to Salt-&-Pepper or Gaussian noise, a less common noise known as speckle noise is a multiplicative type of noise [25]. The original image's pixels are multiplied by the noise components. It closely resembles the Rayleigh and Gamma distributions and deviates from the normal distribution, thus frequently present in coherent imaging systems and makes it difficult to deal with as it alters the image's intensity levels and lowers its resolution and contrast. As a result, the observer's ability to recognize fine details in the images diminishes.
2.1.3. Poisson noise
The Poisson process can be used to quantitatively represent Poisson noise, also referred to as Shot noise [26]. Poisson noise is produced by the nonlinear responses of image detectors and recorders. This type of noise is determined by the image data. Electronics experience shot noise due to the discrete nature of the electric charge. Due to the particle nature of light, shot noise may also be seen in photon enumeration in optical systems. Quantum (photon) noise is another name for this type of noise.
2.1.4. Gaussian noise
The Gaussian distribution sometimes referred to as Gaussian noise [27], is a type of statistical noise with a probability density function which indicates that the noise values are dispersed normally along a Gaussian curve. The probability density function of a Gaussian distribution features a bell-shaped curve. The most popular application of Gaussian noise is additive white Gaussian noise.
2.2. CNN as classification model
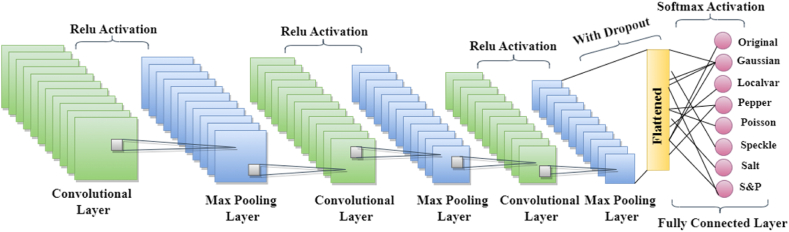
For classifying the sounds in QRC images, this study suggested a CNN model. In Table 1 and Fig. 3, the developed network architecture is shown. The proposed architecture includes a dense layer, a flatten layer, a dropout layer, a softmax, three polling layers, and three convolutional layers. Layers like MaxPooling2D and Conv2D produce a 3D tensor (h, w, c), where h refers to height, w refers to the width, and c refers to the channel. As we progress deeper into the network, the width and height measurements begin to reduce. For each Conv2D layer, the first argument controls the number of output channels. Furthermore, an output volume's spatial dimensions are then reduced using the max-pooling layer. In general, we can afford to increase the number of output channels in each Conv2D layer as the width and height decrease. The random selection of input units at each training phase by dropout layer avoids overfitting. Later, the softmax layer normalizes the results generated by the prior layer so that it takes into account the chance that the actual input image will correspond to the identified classes.
Table 1.
Network topology of proposed CNN model and hyperparameters.
| Layers | Output Shape | Parameters |
|---|---|---|
| Conv2D | (None, 148, 148, 32) | 896 |
| MaxPooling2D | (None, 74, 74, 32) | 0 |
| Conv2D | (None, 72, 72, 64) | 18,496 |
| MaxPooling2D | (None, 36, 36, 64) | 0 |
| Conv2D | (None, 34, 34, 128) | 73,856 |
| MaxPooling2D | (None, 17, 17, 128) | 0 |
| Flatten | (None, 36,992) | 0 |
| Dropout | (None, 36,992) | 0 |
| Dense | (None, 8) | 295,944 |
| Total Parameters | : 389,192 | |
| Optimizer | : Adam | |
| Epoch | : 100 | |
| Batch Size | : 120 | |
| Loss | : categorical cross-entropy | |
| Metrics | : accuracy |
Fig. 3.
The architecture of the proposed CNN model.
For classification, the convolutional base's final output tensor (of shape (17, 17, 128)) is then fed into a single Dense layer for classification. To prevent overfitting, we first flatten the 3D output to 1D, then add one Dropout layer for regularization. As we can see, before passing through the Dense layer, our (17, 17, 128) outputs were flattened into vectors of the form (36,992). Finally, we employ another dense layer with 8 neurons and softmax activation as our dataset has 8 output classes.
2.2.1. Convolutional (Conv2D) layer
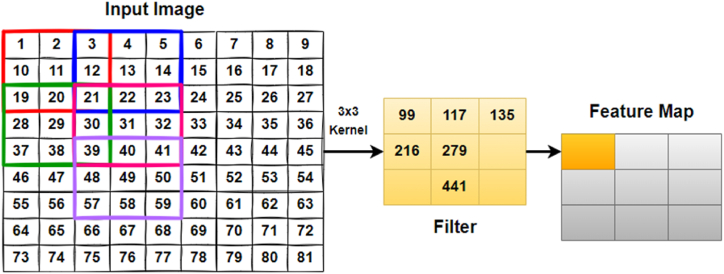
The convolutional layer is the core element of a ConvNet and is responsible for the majority of the computation [28]. The 2D convolution layer is the most often used kind of convolution and is frequently abbreviated as conv2D. The parameters of the layer are a set of learnable filters. These filters are used with feature maps to generate a 2-dimensional activation map. In a conv2D layer, a filter or kernel “slides” across the 2D input data, executing elementwise multiplication. As a consequence, the findings will be summed into a single output pixel. Fig. 4 depicts the operation of a convolutional layer.
Fig. 4.
The convolutional layer process utilizes a 3 × 3 filter with a stride length of 2, in which the input data matrix is element-by-element combined with the feature descriptor to generate a feature map with 2 pixels shifts over the input matrix.
2.2.2. Max-pooling layer
The pooling layer's major responsibility is to sub-sample the feature maps [8], which is accountable for lowering the spatial size of the convolved feature. Max pooling is a pooling technique that chooses the largest important element from the filter's feature map range. As a result, its output will be a feature map comprising only the most important features from the prior feature map (see Fig. 5). The dimensions of the output after a pooling layer for a feature map with dimensions (h x w x c) are shown in (2).
| (2) |
Where refers width of the feature map, indicates its height, denotes the number of channels in the feature map, denotes the filter size, and denotes the stride length.
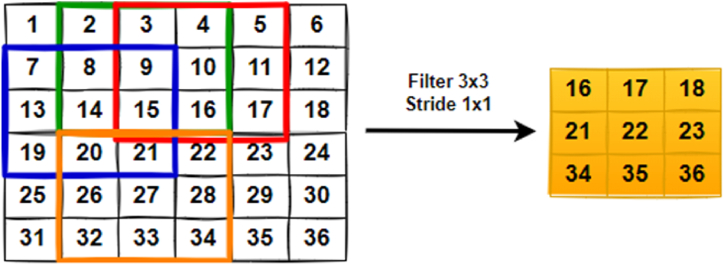
Fig. 5.
Max-pooling layer operation with 3 × 3 filter and 1 × 1 stride over 6 × 6 convolved feature is demonstrated to down-sampling of each 3 × 3 block to map in 1 block (pixel).
2.2.3. Fully connected (dense) layer
The last layers of machine learning models are often fully-connected layers, this implies that each node included within a fully connected layer is directly connected to each node contained within the previous and subsequent levels [29]. The final Convolutional Layer's output is flattened and sent into the fully connected layer as an input.
2.2.4. ReLU layer
Rectified linear unit (ReLU) is the most often utilized function in the CNN context. This function is used in the hidden layer to prevent the vanishing gradient problem and improve computation performance. It transforms the input's entire values into positive integers. It is mathematically represented in (3) [10].
| (3) |
2.2.5. Softmax function
In neural network models that forecast multinomial probability distributions, the softmax function is utilized as the activation function in the output layer. When more than two class labels are required for membership, this activation function is used in multi-class classification scenarios. The mathematical version is shown in (4) [14].
| (4) |
2.3. Deep learning pre-trained models
2.3.1. InceptionV3 as classification model
The Inception V3 [30] model contains a total of 42 layers, which is a higher number than the number of layers that can be found in the Inception V1 and V2 models. On the other hand, the effectiveness of using such a method is quite astounding to consider. The Inception V3 model has a lower error rate than its early pioneers did when compared to other models. It has been shown that the image recognition model known as Inception V3 can achieve an accuracy of more than 78.1% when applied to the ImageNet dataset. This model is utilized widely nowadays. To achieve a high level of model adaptability, the Inception V3 model used a variety of approaches, each of which was intended to improve the performance of the network. It is far more effective and has a wider network than that of the Inception V1 and V2 networks.
2.3.2. Xception as classification × odel
The theory that underpins Xception [31], which brings the concepts of Inception to its logical conclusion, is referred described as “Extreme Inception.” The Xception architecture is a useful one that implements depth-wise separable convolution. This architecture is more effective, except the initial and final modules, the convolutional layers are formulated into modules and grouped. Except for the very earliest and very final modules, all of these modules have linear residual connections surrounding them. Convolutional layers are piled on top of one another to generate Xception. These layers are isolated from one another along the depth dimension and contain residual connections.
2.3.3. ResNet50 as classification model
The Resnet50 [32] architecture has been designed from the ResNet34 model. However, there is a big difference in the form of the building block's transition into a bottleneck design in response to the concerns about the amount of time necessary to train the layers. The stack utilized by Resnet50 consisted of three levels as opposed to the ResNet34 which was two levels. As a result of this, the design of Resnet50 was developed by replacing each of the two-layer blocks that were included in ResNet34 with a bottleneck block that had three layers. This was done to build Resnet 50. The accuracy of this model significantly outperforms the performance of the 34-layer ResNet model. P performance of 3.8 billion floating-point transactions per second may be attained by the 50-layer ResNet (FLOPS).
2.4. Traditional machine learning strategies
2.4.1. NB as classification model
The NB Classifier is both a supervised learning approach and a statistical classification method [33]. It underpins a Bayesian predictive model and lets us logically describe model uncertainty by describing the possibilities' probabilities and it's based on Bayes' Theorem. The Bayes' Theorem calculates the likelihood of an event occurring based on the possibility of another event occurring. equation (5) expresses Bayes' theorem mathematically.
| (5) |
Where and are events and . denotes the prior probability of before evidence is seen and denotes the posterior probability of after evidence is seen.
2.4.2. DT as classification model
A DT is among the most well-known categorization techniques due to its ease and relatively quick and straightforward formulation procedure [34]. It is a tree-structured classification method in which internal nodes contain dataset attributes, branches indicate decision rules, and every leaf node depicts the result.
3. Results and discussion
For this study, we generated 10,000 different QRC images storing random information, and then introduced seven different noises separately, to generate seven new noisy images against each original image. As a result, we formed a dataset of 80,000 images and 8 labels: Fig. 6 shows a few of those samples.
Fig. 6.
Samples of the generated dataset containing images of noisy quick response code (QRC). For reader understandability, a class-label is written above each QRC image to show the diversity of QRC in each class.
To do QRC noise classification, we fine-tuned the mentioned pre-trained deep neural networks by adding a dense layer with 8 neurons as a number of outputs. This allowed us to execute the task successfully. In addition, to contrast the results of these deep learning models with those of traditional machine learning strategies, the two algorithms, namely, NB and DT have also been explored. We first resized, shuffled and then randomly selected the images from dataset before giving it to any classification model. After that, we expanded the value distribution using the standard scaler. We used the properties of criteria to entropy, as well as the maximum depth of three, with the DT classifier.
We used a dataset with more than 80,000 QRC images including several noises to assess the performance of each exploited model. The train and test sets of the dataset are formed with ratios of 70:30, respectively. More details about the dataset split can be found in Table 2.
Table 2.
The detailed information of generated QRC image dataset; training and testing split.
| Class/Label | Training Set | Testing Set | Total |
|---|---|---|---|
| Normal/Original QR | 7000 | 3000 | 10,000 |
| Gaussian | 7000 | 3000 | 10,000 |
| Lacalvar | 7000 | 3000 | 10,000 |
| Pepper | 7000 | 3000 | 10,000 |
| Poisson | 7000 | 3000 | 10,000 |
| Speckle | 7000 | 3000 | 10,000 |
| Salt | 7000 | 3000 | 10,000 |
| Salt & Pepper | 7000 | 3000 | 10,000 |
| Total | 56,000 | 24,000 | 80,000 |
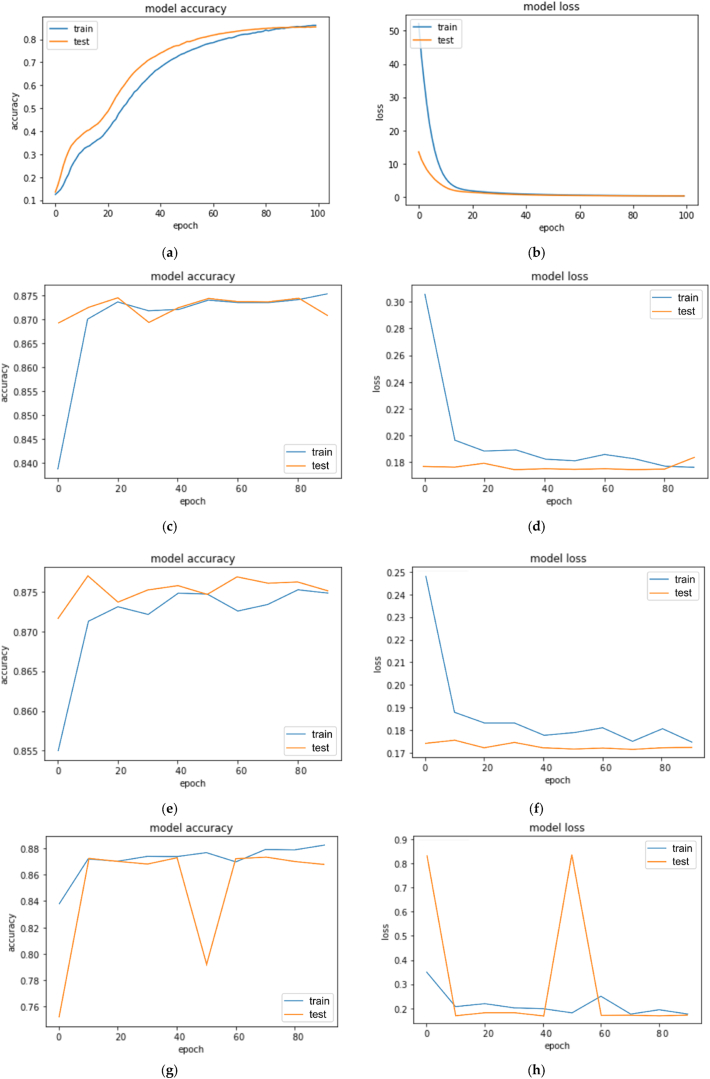
In each cycle following successful training, the accuracy was calculated using all images from the test dataset. To check the robustness and generalization of the exploited networks and proposed models, the experiments are repeated 5 times and average performance is considered to evaluate the performance. Fig. 7 (a)-(h) depicts the performance curves of the top four models (XceptionNet, InceptionNetV3, ResNet50 and CNN) that performed well as compared with the rest of the pre-trained models and machine learning classifiers for noise classification. For this study, we repeated experiments several times to find the best combination of layers in the CNN model. After evaluating the CNN model, we applied techniques such as adding a dropout layer with an experimental value of 0.4, which had a big impact on increasing the accuracy of the model and adding more than one convolutional layer with ReLU activation function, the proposed CNN model achieved an accuracy of 86.75% and kappa of 84.9%.
Fig. 7.
Performance curves of top models for quick response code noisy images classification. (a) Accuracy curves of convolutional neural network (CNN); (b) loss curves of CNN; (c) accuracy curves of InceptionV3 network; (d) loss curves of InceptionV3 network; (e) accuracy curves of Xception network; (f) loss curves of Xception network; (g) accuracy curves for ResNet50 network and (h) loss curves of ResNet50 network.
From the accuracy and loss graphs obtained against the ResNet50 model, depicted in Fig. 7 (g)–(h), it is noted that the model was not certain when it predicts at least at the stage of training around 50th epoch. After analyzing the step-wise epoch performance (logged in Anaconda Notebook), it is inferred that this sudden drop in accuracy was due to a change in the learning rate when the optimizations reaches a plateau, which was later adjusted with the use of FactorScheduler. Accuracy, precision, recall, and f1-score are the four metrics that we used to assess the performance and usefulness of each model. Precision and recall are typically utilized to have a better understanding of the performance of the classifier. The important elements in Fig. 7 are accuracy curves of CNN, InceptionV3 network, Xception network, and ResNet50 network. The following are their formulas given in (6), (7), (8), (9) [35]:
| (6) |
| (7) |
| (8) |
| (9) |
TP (True Positive) is the number of occurrences that are relevant and were properly detected by the model. The number of occurrences when the model mistakenly classifies them as relevant is referred to as FP (False Positive). The number of occurrences where the model properly classifies them as not relevant is denoted by TN (True Negative). The number of occurrences when the model mistakenly labels them as not relevant is represented by FN (False Negative). Table 3 lists the performance accuracies of seventeen pre-trained networks, a proposed CNN model, and three machine learning classifiers. Among all explored and proposed models, XceptionNet succeeded in topping the list by attaining an overall accuracy of 87.48% with 85.7% kappa. Whereas InceptionV3, ResNet50, and CNN compete by achieving an accuracy of 86.99%, 86.83%, and 86.75%, respectively. Contrarily, the DT hardly secured an accuracy of 44.67% and the kappa of 36.8%. The detailed performance analysis of all models against each class can be found in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23.
Table 3.
Comparative performance analysis of proposed and explored models.
| Model | Accuracy (%) | Kappa (%) |
|---|---|---|
| XceptionNet | 87.48 | 85.7 |
| InceptionV3 | 86.99 | 85.1 |
| ResNet50 | 86.83 | 84.9 |
| CNN | 86.75 | 84.9 |
| ResNet101 | 85.96 | 84.0 |
| DenseNet121 | 85.75 | 83.7 |
| DenseNet169 | 85.72 | 83.7 |
| ResNet18 | 85.24 | 83.1 |
| ResNet152 | 84.96 | 82.8 |
| VGG16 | 84.66 | 82.5 |
| MobileNetV2 | 84.52 | 82.3 |
| DenseNet201 | 84.09 | 81.8 |
| DenseNet263 | 84.01 | 81.7 |
| EfficientNetB0 | 83.69 | 81.4 |
| GoogleNet | 83.39 | 81.0 |
| AlexNet | 82.04 | 79.5 |
| VGG19 | 81.77 | 79.2 |
| SqueezeNet | 81.26 | 78.6 |
| Naïve Bayes | 63.13 | 57.9 |
| Decision Tree | 44.67 | 36.8 |
Table 4.
Class-wise performance analysis of AlexNet.
| Class | NAC a | NCC b | Accuracy | SDc | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3112 | 98.68% | 1.02 | 0.93 | 0.97 | 0.95 |
| Gaussian | 3000 | 4062 | 84.59% | 4.77 | 0.41 | 0.56 | 0.48 |
| Localvar | 3000 | 1781 | 84.59% | 5.01 | 0.30 | 0.18 | 0.23 |
| Pepper | 3000 | 3039 | 99.2% | 0.42 | 0.96 | 0.97 | 0.97 |
| Poisson | 3000 | 2941 | 99.25% | 0.38 | 0.98 | 0.96 | 0.97 |
| Salt&Pepper | 3000 | 3007 | 99.6% | 0.10 | 0.98 | 0.99 | 0.98 |
| Salt | 3000 | 3075 | 99.47% | 0.29 | 0.97 | 0.99 | 0.98 |
| Speckle | 3000 | 2983 | 98.7% | 1.01 | 0.95 | 0.94 | 0.95 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 5.
Class-wise performance analysis of the convolutional neural network.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3042 | 99.75% | 0.14 | 0.98 | 1.0 | 0.99 |
| Gaussian | 3000 | 4035 | 87.25% | 6.03 | 0.49 | 0.66 | 0.57 |
| Localvar | 3000 | 1961 | 87.3% | 5.94 | 0.49 | 0.32 | 0.39 |
| Pepper | 3000 | 3004 | 99.98% | 0.01 | 1.0 | 1.0 | 1.0 |
| Poisson | 3000 | 2943 | 99.75% | 0.11 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3008 | 99.95% | 0.02 | 1.0 | 1.0 | 1.0 |
| Salt | 3000 | 3050 | 99.79% | 0.14 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2957 | 99.75% | 0.19 | 1.0 | 0.98 | 0.99 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 6.
Class-wise performance analysis of DenseNet121.
| Class | NAC a | NCCb | Accuracy | SDc | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3059 | 99.59% | 0.09 | 0.97 | 0.99 | 0.98 |
| Gaussian | 3000 | 3980 | 86.64% | 6.05 | 0.47 | 0.63 | 0.54 |
| Localvar | 3000 | 2000 | 86.55% | 5.71 | 0.44 | 0.30 | 0.35 |
| Pepper | 3000 | 3011 | 99.82% | 0.11 | 0.99 | 0.99 | 0.99 |
| Poisson | 3000 | 2948 | 99.68% | 0.22 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3013 | 99.87% | 0.02 | 0.99 | 1.0 | 0.99 |
| Salt | 3000 | 3054 | 99.74% | 0.18 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2935 | 99.6% | 0.26 | 0.99 | 0.97 | 0.98 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 7.
Class-wise performance analysis of DenseNet169.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3050 | 99.64% | 0.13 | 0.98 | 0.99 | 0.99 |
| Gaussian | 3000 | 3981 | 86.53% | 5.80 | 0.47 | 0.62 | 0.54 |
| Localvar | 3000 | 2002 | 86.46% | 5.92 | 0.44 | 0.29 | 0.35 |
| Pepper | 3000 | 3007 | 99.84% | 0.08 | 0.99 | 0.99 | 0.99 |
| Poisson | 3000 | 2943 | 99.7% | 0.13 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3014 | 99.88% | 0.01 | 0.99 | 1.0 | 1.0 |
| Salt | 3000 | 3058 | 99.76% | 0.05 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2945 | 99.62% | 0.17 | 0.99 | 0.98 | 0.98 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 8.
Class-wise performance analysis of DenseNet201.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3097 | 99.28% | 0.18 | 0.96 | 0.99 | 0.97 |
| Gaussian | 3000 | 3967 | 85.7% | 4.81 | 0.45 | 0.59 | 0.51 |
| Localvar | 3000 | 1946 | 85.74% | 5.33 | 0.39 | 0.25 | 0.31 |
| Pepper | 3000 | 3032 | 99.41% | 0.22 | 0.97 | 0.98 | 0.98 |
| Poisson | 3000 | 2942 | 99.45% | 0.10 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3015 | 99.78% | 0.05 | 0.99 | 0.99 | 0.99 |
| Salt | 3000 | 3063 | 99.65% | 0.04 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2938 | 99.17% | 0.31 | 0.98 | 0.96 | 0.97 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 9.
Class-wise performance analysis of DenseNet263.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3086 | 99.24% | 0.10 | 0.96 | 0.98 | 0.97 |
| Gaussian | 3000 | 3978 | 85.61% | 5.01 | 0.44 | 0.59 | 0.51 |
| Localvar | 3000 | 1941 | 85.65% | 4.97 | 0.39 | 0.25 | 0.30 |
| Pepper | 3000 | 3030 | 99.43% | 0.17 | 0.97 | 0.98 | 0.98 |
| Poisson | 3000 | 2938 | 99.47% | 0.11 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3017 | 99.8% | 0.03 | 0.99 | 0.99 | 0.99 |
| Salt | 3000 | 3065 | 99.66% | 0.14 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2945 | 99.15% | 0.24 | 0.97 | 0.96 | 0.97 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 10.
Class-wise performance analysis of proposed decision tree network.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3940 | 87.87% | 2.01 | 0.51 | 0.67 | 0.58 |
| Gaussian | 3000 | 3673 | 72.39% | 2.89 | 0.0063 | 0.0077 | 0.0069 |
| Localvar | 3000 | 3175 | 74.27% | 3.99 | 0.0 | 0.0 | 0.0 |
| Pepper | 3000 | 2588 | 88.97% | 2.35 | 0.57 | 0.49 | 0.53 |
| Poisson | 3000 | 2261 | 91.58% | 1.44 | 0.72 | 0.54 | 0.62 |
| Salt&Pepper | 3000 | 3112 | 99.4% | 0.01 | 0.69 | 0.71 | 0.70 |
| Salt | 3000 | 3225 | 94.96% | 0.77 | 0.78 | 0.84 | 0.81 |
| Speckle | 3000 | 2026 | 86.91% | 4.32 | 0.46 | 0.31 | 0.37 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 11.
Class-wise performance analysis of EfficientNetB0.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3094 | 99.15% | 0.23 | 0.95 | 0.98 | 0.97 |
| Gaussian | 3000 | 3974 | 85.43% | 3.88 | 0.44 | 0.58 | 0.50 |
| Localvar | 3000 | 1922 | 85.48% | 4.31 | 0.37 | 0.24 | 0.29 |
| Pepper | 3000 | 3023 | 99.44% | 0.21 | 0.97 | 0.98 | 0.98 |
| Poisson | 3000 | 2938 | 99.43% | 0.33 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3018 | 99.76% | 0.02 | 0.99 | 0.99 | 0.99 |
| Salt | 3000 | 3071 | 99.61% | 0.19 | 0.97 | 1.0 | 0.98 |
| Speckle | 3000 | 2960 | 99.08% | 0.38 | 0.97 | 0.96 | 0.96 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 12.
Class-wise performance analysis of GoogleNet.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3105 | 99.05% | 0.20 | 0.95 | 0.98 | 0.96 |
| Gaussian | 3000 | 3988 | 85.26% | 4.02 | 0.43 | 0.57 | 0.49 |
| Localvar | 3000 | 1905 | 85.32% | 4.00 | 0.36 | 0.23 | 028 |
| Pepper | 3000 | 3014 | 99.43% | 0.18 | 0.98 | 0.98 | 0.98 |
| Poisson | 3000 | 2931 | 99.4% | 0.13 | 0.99 | 0.96 | 0.98 |
| Salt&Pepper | 3000 | 3019 | 99.76% | 0.09 | 0.99 | 0.99 | 0.99 |
| Salt | 3000 | 3080 | 99.6% | 0.10 | 0.97 | 1.0 | 0.98 |
| Speckle | 3000 | 2958 | 98.98% | 0.51 | 0.97 | 0.95 | 0.96 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 13.
Class-wise performance analysis of InceptionV3.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3028 | 99.8% | 0.19 | 0.98 | 1.0 | 0.99 |
| Gaussian | 3000 | 4067 | 87.37% | 3.99 | 0.50 | 0.67 | 0.57 |
| Localvar | 3000 | 1920 | 87.38% | 5.05 | 0.49 | 0.32 | 0.38 |
| Pepper | 3000 | 2997 | 99.99% | 0.00 | 1.0 | 1.0 | 1.0 |
| Poisson | 3000 | 2952 | 99.8% | 0.16 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3003 | 99.99% | 0.01 | 1.0 | 1.0 | 1.0 |
| Salt | 3000 | 3048 | 99.8% | 0.14 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2965 | 99.85% | 0.03 | 1.0 | 0.99 | 0.99 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 14.
Class-wise performance analysis of MobileNetV2.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3084 | 99.32% | 0.04 | 0.96 | 0.99 | 0.97 |
| Gaussian | 3000 | 3962 | 85.92% | 2.99 | 0.45 | 0.60 | 0.51 |
| Localvar | 3000 | 1968 | 85.96% | 3.62 | 0.41 | 0.27 | 0.32 |
| Pepper | 3000 | 3020 | 99.57% | 0.22 | 0.98 | 0.99 | 0.98 |
| Poisson | 3000 | 2936 | 99.49% | 0.31 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3027 | 99.84% | 0.05 | 0.99 | 1.0 | 0.99 |
| Salt | 3000 | 3060 | 99.69% | 0.11 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2943 | 99.26% | 0.23 | 0.98 | 0.96 | 0.97 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 15.
Class-wise performance analysis of Naïve Bayes network.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3572 | 93.98% | 2.18 | 0.72 | 0.85 | 0.78 |
| Gaussian | 3000 | 3472 | 75.51% | 8.49 | 0.086 | 0.099 | 0.092 |
| Localvar | 3000 | 2686 | 76.31% | 6.80 | 0.0 | 0.0 | 0.0 |
| Pepper | 3000 | 3097 | 94.75% | 2.03 | 0.78 | 0.81 | 0.79 |
| Poisson | 3000 | 2912 | 97.2% | 1.11 | 0.90 | 0.87 | 0.89 |
| Salt&Pepper | 3000 | 2976 | 97.29% | 1.73 | 0.89 | 0.89 | 0.89 |
| Salt | 3000 | 2973 | 98.51% | 0.10 | 0.94 | 0.94 | 0.94 |
| Speckle | 3000 | 2312 | 92.72% | 2.63 | 0.77 | 0.59 | 0.67 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 16.
Class-wise performance analysis of ResNet18.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3070 | 99.47% | 0.20 | 0.97 | 0.99 | 0.98 |
| Gaussian | 3000 | 3959 | 86.35% | 2.71 | 0.47 | 0.61 | 0.53 |
| Localvar | 3000 | 2006 | 86.35% | 4.33 | 0.43 | 0.29 | 0.35 |
| Pepper | 3000 | 3000 | 99.7% | 0.10 | 0.99 | 0.99 | 0.99 |
| Poisson | 3000 | 2937 | 99.57% | 0.24 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3034 | 99.85% | 0.02 | 0.99 | 1.0 | 0.99 |
| Salt | 3000 | 3059 | 99.73% | 0.06 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2935 | 99.47% | 0.19 | 0.99 | 0.97 | 0.98 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 17.
Class-wise performance analysis of ResNet50.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3046 | 99.81% | 0.04 | 0.98 | 1.0 | 0.99 |
| Gaussian | 3000 | 4021 | 87.26% | 3.19 | 0.49 | 0.66 | 0.56 |
| Localvar | 3000 | 1974 | 87.28% | 2.45 | 0.49 | 0.32 | 0.39 |
| Pepper | 3000 | 3002 | 99.99% | 0.00 | 1.0 | 1.0 | 1.0 |
| Poisson | 3000 | 2941 | 99.75% | 0.09 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3006 | 99.97% | 0.01 | 1.0 | 1.0 | 1.0 |
| Salt | 3000 | 3053 | 99.78% | 0.07 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2957 | 99.82% | 0.03 | 1.0 | 0.99 | 0.99 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 18.
Class-wise performance analysis of ResNet101.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3062 | 99.65% | 0.11 | 0.98 | 1.0 | 0.99 |
| Gaussian | 3000 | 3912 | 86.63% | 4.02 | 0.47 | 0.62 | 0.54 |
| Localvar | 3000 | 2084 | 86.7% | 3.19 | 0.45 | 0.32 | 0.37 |
| Pepper | 3000 | 3002 | 99.91% | 0.01 | 1.0 | 1.0 | 1.0 |
| Poisson | 3000 | 2947 | 99.71% | 0.09 | 1.0 | 0.98 | 0.99 |
| Salt&Pepper | 3000 | 3017 | 99.91% | 0.01 | 0.99 | 1.0 | 1.0 |
| Salt | 3000 | 3046 | 99.77% | 0.14 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2930 | 99.64% | 0.24 | 1.0 | 0.97 | 0.99 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 19.
Class-wise mean performance analysis of ResNet152.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3077 | 99.45% | 0.08 | 0.97 | 0.99 | 0.98 |
| Gaussian | 3000 | 3944 | 86.17% | 5.16 | 0.46 | 0.60 | 0.52 |
| Localvar | 3000 | 2012 | 86.19% | 4.88 | 0.42 | 0.28 | 0.34 |
| Pepper | 3000 | 3003 | 99.65% | 0.23 | 0.99 | 0.99 | 0.99 |
| Poisson | 3000 | 2935 | 99.51% | 0.03 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3033 | 99.86% | 0.01 | 0.99 | 1.0 | 0.99 |
| Salt | 3000 | 3061 | 99.71% | 0.14 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2935 | 99.38% | 0.02 | 0.99 | 0.96 | 0.97 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 20.
Class-wise performance analysis of SqueezeNet.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3134 | 98.78% | 0.41 | 0.93 | 0.97 | 0.95 |
| Gaussian | 3000 | 4220 | 83.71% | 2.28 | 0.39 | 0.55 | 0.46 |
| Localvar | 3000 | 1627 | 83.94% | 3.53 | 0.24 | 0.13 | 0.17 |
| Pepper | 3000 | 3046 | 99.16% | 0.06 | 0.96 | 0.97 | 0.97 |
| Poisson | 3000 | 2936 | 99.23% | 0.31 | 0.98 | 0.96 | 0.97 |
| Salt&Pepper | 3000 | 3012 | 99.54% | 0.18 | 0.98 | 0.98 | 0.98 |
| Salt | 3000 | 3084 | 99.5% | 0.24 | 0.97 | 0.99 | 0.98 |
| Speckle | 3000 | 2941 | 98.65% | 0.99 | 0.96 | 0.94 | 0.95 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 21.
Class-wise performance analysis of VGG16.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3065 | 99.34% | 0.31 | 0.96 | 0.98 | 0.97 |
| Gaussian | 3000 | 3943 | 86% | 5.22 | 0.45 | 0.60 | 0.52 |
| Localvar | 3000 | 2011 | 86.11% | 3.10 | 0.42 | 0.28 | 0.33 |
| Pepper | 3000 | 3022 | 99.57% | 0.02 | 0.98 | 0.99 | 0.98 |
| Poisson | 3000 | 2940 | 99.49% | 0.31 | 0.99 | 0.97 | 0.98 |
| Salt&Pepper | 3000 | 3027 | 99.83% | 0.05 | 0.99 | 1.0 | 0.99 |
| Salt | 3000 | 3056 | 99.69% | 0.09 | 0.98 | 1.0 | 0.99 |
| Speckle | 3000 | 2936 | 99.3% | 0.29 | 0.98 | 0.96 | 0.97 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 22.
Class-wise performance analysis of VGG19.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3135 | 98.79% | 1.01 | 0.93 | 0.97 | 0.95 |
| Gaussian | 3000 | 4105 | 84.29% | 3.75 | 0.41 | 0.56 | 0.47 |
| Localvar | 3000 | 1707 | 84.38% | 3.99 | 0.28 | 0.16 | 0.20 |
| Pepper | 3000 | 3052 | 99.13% | 0.28 | 0.96 | 0.97 | 0.97 |
| Poisson | 3000 | 2938 | 99.28% | 0.32 | 0.98 | 0.96 | 0.97 |
| Salt&Pepper | 3000 | 3020 | 99.6% | 0.19 | 0.98 | 0.99 | 0.98 |
| Salt | 3000 | 3064 | 99.48% | 0.18 | 0.97 | 0.99 | 0.98 |
| Speckle | 3000 | 2979 | 98.6% | 0.89 | 0.95 | 0.94 | 0.94 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
Table 23.
Class-wise performance analysis of XceptionNet.
| Class | NAC a | NCC b | Accuracy | SD c | Precision | Recall | F1-score |
|---|---|---|---|---|---|---|---|
| Original | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
| Gaussian | 3000 | 5693 | 87.48% | 3.99 | 0.50 | 0.95 | 0.65 |
| Localvar | 3000 | 307 | 87.48% | 5.87 | 0.49 | 0.050 | 0.091 |
| Pepper | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
| Poisson | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
| Salt&Pepper | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
| Salt | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
| Speckle | 3000 | 3000 | 100% | 0.0 | 1.0 | 1.0 | 1.0 |
Number of actual cases in a class.
Number of cases classified as belonging to a class.
Standard Deviation.
From Table 4, it is noted that AlexNet misclassified even original QRC images as Gaussian, Laocalvar, and Speckle. Moreover, it misjudged Gaussian noisy images. Out of 3000 Gaussian noisy images, 42, 1191, 48, and 37 are classified as original, localvar, pepper, and speckle noisy images. Similarly, 65, 2312, 36, and 46 localvar noisy images are labeled as original, Gaussian, pepper, and speckle noisy images. However, it performed well to classify Salt&Pepper noisy images. According to the performance metrics given in Table 5, CNN also misclassified Gaussian as localvar noisy images and vice-versa, nonetheless, the number is less as compared to AlexNet and others. Other than this, unlike other models, only a few ones of Gaussian as localvar noisy images are classified as original images. Besides most noisy classes, CNN performed well on original images, and it only misclassified 9 original QRC images as speckle noisy images. Evidently from Table 6, Table 7, Table 8, Table 9, DenseNet121 performed well among all other variants of DenseNet models. However, all of these DenseNet variants misjudged original QRC images as Gaussian, localvar, and speckle. In addition, numerous false positives for Gaussian and localvar noisy images, they also didn't perform well for speckle noisy images. Among these, the DenseNet169 model correctly identified salt noisy images. From Table 10, it is noted that DT performs worst among models as it labeled a large number of images from each noisy class (even from salty noisy images) as the original. The DT was unable to correctly identify a single sample from the localvar class, also its performance degraded for speckle noisy images. As depicted in Table 11, Table 12, EfficientNetB0, and GoogleNet perform identically the same as SqueezeNet (see Table 20), however, their performance for speckle noisy images is better than the SqueezeNet model. Even though the performance of InceptionV3 is nearly the same as obtained by the CNN model, however, InceptionV3 correctly identified all original and Salt&Pepper noisy images and performed well for speckle noisy images as compared to the CNN model (see Table 13). The performance of MobileNetV2 degrades for original images as compared to other models (see Table 14). To be understood, machine learning algorithms did not match the performance of deep learning-based models, thus Naïve Bayes classifier stands second worst among all exploited models. According to Table 15, it could not detect any sample of localvar noisy class. As depicted in Table 16, Table 17, Table 18, Table 19, ResNet50 performs well among other ResNet variants. Moreover, ResNet152 and ResNet101 performances to identify speckle noisy images do not meet the standards attained by the other two variants. From Table 23, it is concluded that XceptionNet outperformed all models by correctly identifying instances of all classes (except localvar and Gaussian noisy classes). Nonetheless, unlike other models, it misclassified Gaussian as localvar, and localvar as Gaussian only.
From Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, all the models misclassified QRC images having Localvar noise and Gaussian noise. Even the best performing model (XceptionNet) classified QRC Lovalvar noisy image as Gaussian noise. Thus, it can be derived from the experimental results that explored models that considered Localvar noisy images and Gaussian noisy images to share similar characteristics, thus unable to identify them correctly. Furthermore, it is also evident that all models performed well in the classification of QRC salt noisy images. Moreover, it is also noted that the proposed traditional machine learning classifiers (DT and Naïve Bayes) are not good choices for noise classification in QRC images, however, it is worth noting that a CNN model even with a limited number of layers performed well and accomplished near to best model's accuracy for the same test set.
There are several limitations of the work. However, the first and most important limitation is that this study is based on a deep learning-based CNN model that must be pre-trained models. Nevertheless, if the model is not pre-trained, the results' accuracy might not be achieved. Furthermore, the dataset generated does not include all types of noises, as it has only seven different types of noises. Secondly, the suggested and exploited classification models require a fixed input-size image. Thus, image dimensions are essential. Third, the study caters to only a single type of noise per image, whereas in reality, a printed QR code image may have multiple noises. Finally, the comparative performance analysis of the proposed and explored models is based on all types of noises. The percentage of accuracy and kappa may vary in the case of different noises.
4. Conclusions and future work
The study aims to segregate noisy QRCs from original QRC images by predicting the type of noise present inside the given image. For this, a new dataset of 80,000 images, each having a QRC of various sizes, is formed. The composed dataset contains 10,000 images of each of eight different classes, including original, pepper, salt & pepper, salt, speckle, localvar, Poisson, and Gaussian. The study proposed effective deep learning-based CNN and explored seventeen various pre-trained models including InceptionV3, Xception, ResNet50 model, and two machine learning-based classifiers namely, Decision Tree and Naïve Bayes that are trained with 70% of the total dataset, while the rest of 30% is reserved for testing purposes. Extensive experiments were conducted with various combinational layers of models, and the Xception network outperformed all others by achieving 87.48% accuracy. Moreover, the proposed limited layers-based CNN model also stands in the top 5 best-performing models for noise classification in QRC images by attaining an accuracy of 86.75%. Even though the results are promising, there is still a gap for improvement. As a future work, we aim to enhance the system performance by exploiting and analyzing various machine learning and deep learning algorithms, along with some computer vision and image processing-based amalgam approaches as images in the dataset vary in size and to cater multiple noises in an image. Moreover, we are also planning to build and enhance the image dataset by adding images captured of printed QR codes to train and test on real scenarios.
Author contribution statement
Sadaf Waziry: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
Ahmad Bilal Wardak: Performed the experiments; Contributed reagents, materials, analysis tools or data.
Jawad Rasheed, Ph.D.: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Raed M. Shubair, Ph.D.; Khairan Rajab, Ph.D.: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Asadullah Shaikh, Ph.D.: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Groups Funding Program grant code (NU/RG/SERC/12/33).
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.I. 18004 . 2000. International Organization for Standardization: Information Technology - Automatic Identification and Data Capture Techniques - Bar Code Symbology - QR Code. [Google Scholar]
- 2.Zhang X., Duan J., Zhou J. 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC) IEEE; 2018. A robust secret sharing QR code via texture pattern design; pp. 903–907. [DOI] [Google Scholar]
- 3.Chen J., Huang B., Mao J., Li B. 2019 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE) IEEE; 2019. A novel correction algorithm for distorted QR-code image; pp. 380–384. [DOI] [Google Scholar]
- 4.Lee J.-K., Wang Y.-M., Lu C.-S., Wang H.-C., Chou T.-R. 2019 8th International Conference on Innovation, Communication and Engineering (ICICE) IEEE; 2019. The enhancement of graphic QR code recognition using convolutional neural networks; pp. 94–97. [DOI] [Google Scholar]
- 5.Cai H.-L., Yan B., Chen N., Pan J.-S., Yang H.-M. Beautified QR code with high storage capacity using sequential module modulation. Multimed. Tool. Appl. 2019;78:22575–22599. doi: 10.1007/s11042-019-7504-9. [DOI] [Google Scholar]
- 6.Hosseini H., Hessar F., Marvasti F. Real-time impulse noise suppression from images using an efficient weighted-average filtering. IEEE Signal Process. Lett. 2015;22:1050–1054. doi: 10.1109/LSP.2014.2381649. [DOI] [Google Scholar]
- 7.Rasheed J., Wardak A.B., Abu-Mahfouz A.M., Umer T., Yesiltepe M., Waziry S. An efficient machine learning-based model to effectively classify the type of noises in QR code: a hybrid approach. Symmetry. 2022;14:2098. doi: 10.3390/sym14102098. [DOI] [Google Scholar]
- 8.Alzubaidi L., Zhang J., Humaidi A.J., Al-Dujaili A., Duan Y., Al-Shamma O., Santamaria J., Fadhel M.A., Al-Amidie M., Farhan L. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. Journal of Big Data. 2021;8:53. doi: 10.1186/s40537-021-00444-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lendave Vijaysinh. Developers Corner; 2021. A Guide to Different Types of Noises and Image Denoising Methods.https://analyticsindiamag.com/a-guide-to-different-types-of-noises-and-image-denoising-methods/ (accessed August 1, 2022) [Google Scholar]
- 10.Al-Saffar A.A.M., Tao H., Talab M.A. 2017 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET) IEEE; 2017. Review of deep convolution neural network in image classification; pp. 26–31. [DOI] [Google Scholar]
- 11.Zhang Q., Zhang M., Chen T., Sun Z., Ma Y., Yu B. Recent advances in convolutional neural network acceleration. Neurocomputing. 2019;323:37–51. doi: 10.1016/j.neucom.2018.09.038. [DOI] [Google Scholar]
- 12.Yu S., Jia S., Xu C. Convolutional neural networks for hyperspectral image classification. Neurocomputing. 2017;219:88–98. doi: 10.1016/j.neucom.2016.09.010. [DOI] [Google Scholar]
- 13.Yim J., Sohn K.-A. 2017 International Conference on Digital Image Computing: Techniques and Applications (DICTA) IEEE; 2017. Enhancing the performance of convolutional neural networks on quality degraded datasets; pp. 1–8. [DOI] [Google Scholar]
- 14.Tripathi M. Facial image noise classification and denoising using neural network. Sustainable Engineering and Innovation. 2021;3:102–111. doi: 10.37868/sei.v3i2.id142. [DOI] [Google Scholar]
- 15.Geng L., Zicheng Z., Qian L., Chun L., Jie B. 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS) IEEE; 2020. Image noise level classification technique based on image quality assessment; pp. 651–656. [DOI] [Google Scholar]
- 16.Sil D., Dutta A., Chandra A. TENCON 2019 - 2019 IEEE Region 10 Conference (TENCON) IEEE; 2019. Convolutional neural networks for noise classification and denoising of images; pp. 447–451. [DOI] [Google Scholar]
- 17.Roy S.S., Ahmed M.U., Akhand M.A.H. Noisy image classification using hybrid deep learning methods. Journal of Information and Communication Technology. 2018;17:233–269. doi: 10.32890/jict2018.17.2.8253. [DOI] [Google Scholar]
- 18.Khaw H.Y., Soon F.C., Chuah J.H., Chow C. Image noise types recognition using convolutional neural network with principal components analysis. IET Image Process. 2017;11:1238–1245. doi: 10.1049/iet-ipr.2017.0374. [DOI] [Google Scholar]
- 19.Momeny M., Latif A.M., Agha Sarram M., Sheikhpour R., Zhang Y.D. A noise robust convolutional neural network for image classification. Results in Engineering. 2021;10 doi: 10.1016/j.rineng.2021.100225. [DOI] [Google Scholar]
- 20.Wardak A.B., Rasheed J., Yahyaoui A., Yesiltepe M. In: Advances in Intelligent Systems and Computing. Shakya S., Du K.-L., Ntalianis K., editors. Springer Singapore; 2023. Noisy QR code smart identification system; pp. 471–481. [DOI] [Google Scholar]
- 21.Wardak A.B., Rasheed J., Yahyaoui A., Waziry S., Alimovski E., Yesiltepe M. 2022 12th International Conference on Advanced Computer Information Technologies (ACIT) IEEE; 2022. Noise presence detection in QR code images; pp. 489–492. [DOI] [Google Scholar]
- 22.Pu H., Fan M., Yang J., Lian J. Quick response barcode deblurring via doubly convolutional neural network. Multimed. Tool. Appl. 2019;78:897–912. doi: 10.1007/s11042-018-5802-2. [DOI] [Google Scholar]
- 23.Prakash K.B., Ruwali A., Kanagachidambaresan G.R. In: EAI/Springer Innovations in Communication and Computing. Prakash K.B., Kanagachidambaresan G.R., editors. Springer; 2021. Introduction to tensorflow package; pp. 1–4. [DOI] [Google Scholar]
- 24.Boncelet C. In: The Essential Guide to Image Processing. second ed. Bovik A., editor. Elsevier; 2009. Image noise models; pp. 143–167. [DOI] [Google Scholar]
- 25.Nath A. 2013 International Conference on Communication Systems and Network Technologies. IEEE; 2013. Image denoising algorithms: a comparative study of different filtration approaches used in image restoration; pp. 157–163. [DOI] [Google Scholar]
- 26.Talbot H., Phelippeau H., Akil M., Bara S. 2009 16th IEEE International Conference on Image Processing (ICIP) IEEE; 2009. Efficient Poisson denoising for photography; pp. 3881–3884. [DOI] [Google Scholar]
- 27.Barbu T. 2013. Variational Image Denoising Approach with Diffusion Porous Media Flow, Abstract and Applied Analysis; pp. 1–8. [DOI] [Google Scholar]
- 28.Aloysius N., Geetha M. 2017 International Conference on Communication and Signal Processing (ICCSP) IEEE; 2017. A review on deep convolutional neural networks; pp. 588–592. [DOI] [Google Scholar]
- 29.Albawi S., Mohammed T.A., Al-Zawi S. 2017 International Conference on Engineering and Technology (ICET) IEEE; 2017. Understanding of a convolutional neural network; pp. 1–6. [DOI] [Google Scholar]
- 30.Szegedy C., Vanhoucke V., Ioffe S., Shlens J., Wojna Z. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) IEEE; 2016. Rethinking the inception architecture for computer vision; pp. 2818–2826. [DOI] [Google Scholar]
- 31.Chollet F. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) IEEE; 2017. Xception: deep learning with depthwise separable convolutions; pp. 1800–1807. [DOI] [Google Scholar]
- 32.He K., Zhang X., Ren S., Sun J. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) IEEE; 2016. Deep residual learning for image recognition; pp. 770–778. [DOI] [Google Scholar]
- 33.Karthick G., Harikumar R. 2017 4th International Conference on Electronics and Communication Systems (ICECS) IEEE; 2017. Comparative performance analysis of Naive Bayes and SVM classifier for oral X-ray images; pp. 88–92. [DOI] [Google Scholar]
- 34.Supianto A.A., Julisar Dwitama A., Hafis M. Decision tree usage for student graduation classification: a comparative case study in faculty of computer science brawijaya university, 3rd international conference on sustainable information engineering and technology. SIET 2018 - Proceedings. 2018:308–311. doi: 10.1109/SIET.2018.8693158. [DOI] [Google Scholar]
- 35.Hand D.J. Assessing the performance of classification methods. Int. Stat. Rev. 2012;80:400–414. doi: 10.1111/j.1751-5823.2012.00183.x. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.