Abstract
Microneedle arrays are patches of needles at micro- and nano-scale, which are competent and versatile technologies that have been merged with microfluidic systems to construct more capable devices for biomedical applications, such as drug delivery, wound healing, biosensing, and sampling body fluids. In this paper, several designs and applications are reviewed. In addition, modeling approaches used in microneedle designs for fluid flow and mass transfer are discussed, and the challenges are highlighted.
I. INTRODUCTION
Microneedle arrays (MNAs) have been gaining much attention over the past decade due to their advantages over conventional systems. For example, the minimally invasive nature of MNAs makes them suitable setups for biological fluid extraction and in situ analysis.1–3 In addition, with decreased administration pain, MNAs offer a solution to needle phobia; for instance, 144 patients subjected to both venipuncture and MNA blood sampling stated that they had significantly less pain associated with MNAs than standard venipuncture.4 In addition to being less painful, MNAs utilized for wound healing demonstrated shorter times for healing and wound closure.5,6 Furthermore, MNAs have been used in drug delivery procedures for several purposes, such as birth control,7 vaccine administration,8 and cancer therapy.9 Also, MNAs have been reported to improve vaccination immunogenicity and thermostability while decreasing vaccination costs.10,11 With an estimated annual growth rate of 7.8%, the market size for MNA drug delivery systems is expected to reach $9.1 × 109 billion by 2027, approximately one-fifth of the entire drug delivery market.12,13 Microneedles can be solid,14 hollow,15 dissolving,16 or coated,17 and they can be made utilizing various materials, such as metals,18 polymers,19 and inorganic materials,20 depending on their application purposes.
Drug and cell delivery with detachable MNAs are reported as simple, painless, minimally invasive, user-friendly, and effectively targeted procedures.19–23 Unique mechanical characteristics of flexible substrates, such as polymeric MNAs,26,27 enable their conformability for attachment to different surfaces of the human body.28 The participants in a study to determine the sentiments and thoughts of both the public and healthcare professionals regarding the use of MNAs in clinical practice thought self-administration of microneedle therapies could be advantageous in lessening visits to hospitals or clinics.29 Patients can administer microneedles at point-of-care (POC) without the assistance of healthcare professionals and with minimal pain.30 The capacity to release chemicals gradually for controlled drug delivery provided by MNAs encourages the prospective use of MNAs for long-term therapies. In addition to enabling a minimally invasive injection experience, MNAs can help with the advancement of wearable sensors31 (with adherent MNA patches) for continuous health monitoring, leading to early disease detection, improving the rate of success of medicines, lowering healthcare expenses, and finally advancing society’s well-being, which results in an acceleration of the adoption and commercialization of MNAs.30
After the invention of the soft lithography method using polydimethylsiloxane (PDMS) by George Whitesides,32 microfluidic systems have been extensively utilized for biological and chemical experimentation,31–33 such as Polymerase Chain Reaction (PCR) enrichment,36 DNA assay dilution,37 and transcriptome sequencing.38 Not only can microfluidic devices be biocompatible,31–37 optically transparent, and high-throughput systems but they also require low volumes (microliters or nanoliters) of the sample to operate.32,38–41 Microfluidic systems combined with electrical and optical detection systems facilitated the emergence of POC diagnostic devices; for example, Abbott i-STATT is a commercialized POC device to analyze blood gases using biosensors.44 Since both MNAs and microfluidic systems reap the benefits of laminar flow, such as moving particles in specific streamlines, combining them is emerging to enable the fabrication of advanced setups for biosensing of interstitial fluid (ISF) and blood biomarkers, drug delivery, and wound healing.43–46 MNAs integrated with microfluidic systems provide an easy-to-use experience and pave the way for a decentralized healthcare system, eliminating the need for healthcare professionals for diagnostics and therapeutics.28–48
Mathematical models combined with high-fidelity computational methods have been employed to simulate experimental conditions in the design stage of the proposed systems. The fluid flow involved in microneedle applications is usually laminar, so it is well described by the Navier–Stokes equations. Furthermore, the inertial effects are often negligible, so even the Stokes equations can be reliably used in the analysis. The modeling becomes complicated mainly due to the multi-physics effects, such as non-homogeneous and subject-dependent tissue structure with porosity and non-Newtonian behavior of biological fluids. Despite these challenges, the computational methods have been successfully used to analyze flow in microchannels integrated with MNAs using various models ranging from the simplified one-dimensional flow resistance model (i.e., the modified Bernoulli equation) to the solution of the full Navier–Stokes equations for testing the scenarios in the design stage as well as examining the performance of the final design. Machine Learning (ML), one of the subcategories of Artificial Intelligence (AI), has also emerged to predict and optimize certain parameters in MNA systems to control flow characteristics.51 ML uses statistics theory for mathematical model building, and a computer program executes the learning procedure.48–52 For instance, by integrating ML with microdroplet-based microfluidic systems, the flow rate was controlled to generate droplets.55 For the devices integrating MNAs with microfluidic chips, modeling fluid flow characteristics both in the stratum corneum where the MNA is inserted and in the microfluidic channels where fluid transport occurs is important in order to accomplish optimum designs.33–54 In addition, accurate modeling before fabrication leads to decreased time and financial costs for extra experiments.30
In recent literature, the structural mechanics of MNAs and their drug diffusion properties have been reviewed. For example, case studies of microneedle solid mechanics simulations and drug diffusion equations were reviewed,57 while another study discussed mathematical modeling of dermal diffusion and the stratum corneum.58 Other reviews also have presented the deformation modeling of solid microneedles and the simulation of drug concentration of coated microneedles through the skin,59 summary of key considerations for designing microneedle systems, including needle mechanics and fluid flow,60 and the geometry of MNAs and solid mechanics modeling of skin tissue.61 Additionally, penetration enhancement techniques through various drug diffusion mathematical models were reviewed in a work,62 and last, mathematical formulations for fabricating microneedles using drawing lithography techniques were reviewed as well.63 Although previous literature has reviewed various modeling approaches for the structural design and drug diffusion properties of microneedles, the fundamental mathematical principles of fluid transportation in MNAs integrated with microfluidic systems, as well as the simplifying assumptions, validity, and limitations of these models for microchannels and microneedles, have yet to be fully explored. A comprehensive understanding of the underlying physical principles of fluid flow and mass transfer through microchannels, different types of microneedles, and the interaction with skin tissue is crucial for researchers to accurately simulate and design integrated systems efficiently and cost-effectively. In this study, microneedle applications are reviewed with a focus on fluid administration applications, such as interstitial fluid sampling, biosensing, drug delivery, and wound healing. Next, the modeling and analysis of drug delivery and fluid sampling are reviewed. In particular, we review the simplified one-dimensional flow resistance models (the modified Bernoulli's equation), the viscous-dominated flow (the Stokes flow), the modeling of porous walls (Darcy's law), and diffusive mass transfer (Fick's law) applied to flow and mass transfer in MNAs integrated with microfluidic channels, and present some analytical solutions that are relevant for the microneedle design. Microfluidic chips integrated with MNAs have the potential to enable advanced healthcare setups.
II. EMERGING APPLICATIONS
A. Interstitial fluid (ISF) sampling
Owing to their minimally invasive nature, microneedles were employed for extracting biomarkers from ISF and for continuous biosampling for long-term healthcare monitoring, such as glucose tracking.64 In a combined form of the MNA and microfluidic chip, a porous and flexible PDMS MNA with a “sponge-like” structure was designed to increase the durability in long-term use. The skin of a mouse was punctured, and ISF was extracted continuously with porous PDMS MNA. For the purpose of improving the sharpness along with increasing the mechanical strength of the MNAs, the porous PDMS MNAs were coated with hyaluronic acid (HA). However, upon filling the microneedles with ISF, the changes in the glucose measurements were not being tracked accurately. As a result, a microfluidic chip was integrated with an open capillary pump, which was continuously sampled with MNAs. In order to have a compensated capillary connection between the pores of the MNA and the microchannels, interconnecting channels were designed inside the chip. These microchannels were merged into one channel where the glucose sensor was placed. The fabricated porous MNAs were then utilized to extract phosphate-buffered saline (PBS) from an agarose gel model, followed by the direct collection of the fluid through the microfluidic chip utilizing capillary action. It was demonstrated that reducing the hydraulic resistance of the fluidic system, including the porous MNAs and the microfluidic chip, was necessary to obtain adequate flow rates for continuous monitoring of glucose.
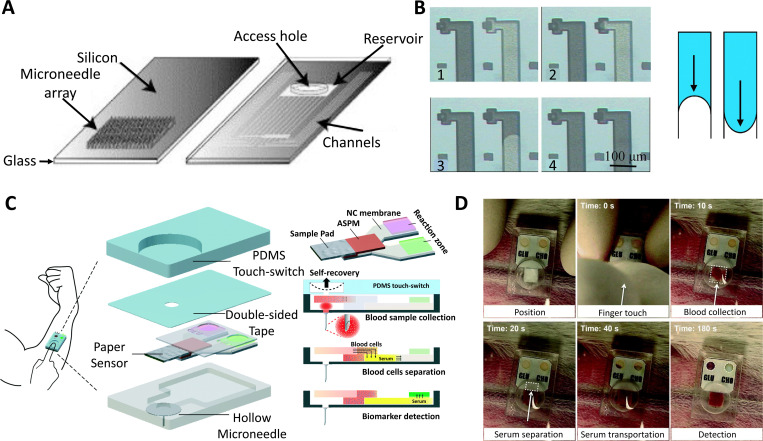
Another ISF sampling study for glucose monitoring purposes was designed as a microfluidic chip that integrates microchannels with MNA [Figs. 1(a) and 1(b)].1,2 The fluid flow from the MNA into the channels was enabled by capillary action using an imbalance of the intermolecular forces at the interface. The integrated MNA and channels consisted of a silicon/glass bilayer chip, and a reservoir that was connected to the hollow MNA located on the silicon wafer's backside. The contact angle between the liquid and solid was reduced to a minimum to keep the capillary force at the maximum amount, which, however, led to discontinuity and force imbalance. To overcome this problem, a continuous surface was provided beyond the opening of the microchannel, and the vent from the needle part was designed in such a way that a section of the circular exit hole wall was enlarged to touch the glass lid. It was demonstrated that the silicon MNAs were appropriately sharp to pierce into the epidermal multilayer and were suitably robust to endure repeated penetrations. Test results showed that although capillary forces could be used for ISF sampling, an initial latent time of 20–30 min was required in order for the backside channels and the microneedle’s borehole to be filled with adequate ISF.
FIG. 1.
Microneedle arrays (MNAs) are used in conjunction with microfluidic devices for sampling and diagnostic applications. (a) Capillary action was used to fill the integrated microneedle–microchannel device with non-biological [glycerol, surrogate interstitial fluid (ISF), ethanol, and water] along with biological (ISF and whole blood) fluids. A silicon/glass bilayer chip and a reservoir for samples of the fluids were connected to the hollow MNA on the backside of the silicon wafer by one or more micro-channels in the integrated MNA. The channels were transparently sealed to allow visual inspection during and after filling, and certain holes were drilled into the glass cover to access the reservoir. (b) A collection of photographs taken through the glass lid showed the channel filling from MNA, and the schematic depicts the difference between pressure-driven flow and surface tension-driven flow. When the needle tips touched the fluid’s surface, all fluids flew into the microchannels. There is a 20–30 min latent time required to generate adequate ISF to fill the microneedle’s borehole. (c) Schematics of a one-touch-activated blood multi-diagnostic system (OBMS). The structure of the OBMS, diagram of the paper-based multiplex sensor consisting of the sample pad, asymmetric polysulfide membrane, nitrocellulose membrane, and reaction zones. (d) In vivo glucose and cholesterol blood testing is initiated by a single touch. Administration of the one-touch-activated blood multidiagnostic system (OBMS) in the ear artery of a rabbit. The last image illustrating the color change was obtained after 5 min. Subfigures (a) and (b) were adapted with permission from Mukerjee et al.,1 Sens. Actuator A 114(2–3), 267–275 (2004). Copyright 2004 Elsevier B.V. Subfigures (c) and (d) were adapted with permission from Li et al.,2 Lab Chip 15(16), 3286–329292 (2015). Copyright 2015 Royal Society of Chemistry.
In another study, an epidermal wearable device that integrated an MNA with an iontophoresis (IP) process for a pristine class of nasopharyngeal carcinoma (NPC) monitoring and prognosis was proposed.45 The device was combined with hydrogel microneedles and reverse IP for sensitive label-free detection of NPC biomarkers, i.e., Epstein-Barr virus cell-free DNA (EBV CfDNA). The platform consisted of a spray-gun deposited functional Au@carbon nanotube, an EBV CfDNA isolation control, hydrogel MNAs, a detection control unit, and a recombinase polymerase amplification (RPA) electrochemical microfluidic biosensor. The device was capable of isolating targeted cell-free DNA from the ISF by facilitating human body heat in ∼10 min. The maximum capturing efficiency of the system was more than 95%, and the threshold of isolation was sensitive to 5 copies per μL. As a compact, wearable, and adaptable platform, it also collected and detected EBV CfDNA on immunodeficient tumor-bearing mice.
Another study demonstrated the use of EBV CfDNA as a model to explore the possible uses of a wearable MNA paired with an electrochemically flexible microfluidic technology for recombinase polymerase amplification (RPA) testing for circulating cancer DNA identification.46 The functionalized MNA for EBV CfDNA sampling from ISF and the flexible electrochemical microfluidic setup for analysis of EBV CfDNA quantification made up the device, which incorporated detection and sampling of EBV DNA. The functionalized hydrogel MNA grew when ISF was absorbed into the epidermal layer of the skin. Then, using a double spatially oriented recognition effect based upon an initial triple helix and a secondary methylene blue (MB) ligand intercalation, the EBV CfDNA biomarkers of ISF freed from nasopharyngeal carcinoma tumor cells beneath the epidermal layer of skin were collected onto the facet of the MNA matrix. The MNA and the collected EBV CfDNA were then stripped from the skin and carried to the flexible electrochemical microfluidic setup in order to execute quantitative detection. Quantitative detection for EBV CfDNA testing was enabled by utilizing adaptable wearable technologies and an RPA electrochemical platform.
Another finger-actuated hollow MNA platform was proposed for body fluid sampling in which fluid flow, transport of fluid through the device, and collection of fluid were simulated using a finite element model.30 This device included an MNA that was connected to a microfluidic chip consisting of a dome-shaped button for actuation by a finger. This actuation provided the required force for the flow of fluid from MNA to the reservoir. The MNA consisted of 100 hollow microneedles in a square array with a 700 μm height, an 80 μm tip diameter, and a 300 μm base diameter for each microneedle. The proposed MNA was connected to a duct that ushered the extracted fluid to the reservoir via two channels. The extracted fluid amount was studied along with mass flow rate curve generation at the reservoir, and six different scenarios were simulated at varying boundary conditions for two fluids of the human body: blood and ISF. The simulation results demonstrated that the device was able to extract around 15.5 g of human blood and 77.4 × 103 μl of ISF in 1 min, respectively.
B. Biosensing
MNAs integrated with microfluidic systems can be used in biosensing applications, as reported in a study in which a horizontal biosensor MNA was used for measuring molecular interactions between a small number of molecules and detecting proteins and nucleic acids.65 Two horizontally placed microneedles faced each other with a microchannel between them, and electronic sensing was used to detect biological interactions. The horizontally placed microneedle structure consisted of three layers of the thin film: an insulator layer, which was placed between two conductive layers, and an oxide layer to protect above and below sensors, which prevented the exposure of electrodes to the solution. Phosphate-buffered saline (PBS) was inserted into the microchannel, and the measured impedance was considered a baseline for all subsequent measurements. Afterward, biotinylated Bovine Serum Albumin (BSA), acting as a protein receptor, was injected into the microchannel, which led to managing the exact value of measurements for three iterations. A concentration of 100 μg/ml was reported for the biotinylated BSA solution that was suspended in PBS. According to the reported equation, there were about 2400 molecules attached to the sensor’s surface.
Another research reported a MNA biosensor for detecting pH, glucose, and lactate in tissue environments simultaneously.66 The MNA, which consisted of hollow microneedles, was fabricated with a dynamic light micro-stereolithography system in which several openings were created using a CO2 laser ablation in the top insulation layer of the flexible flat cable that exposed the underlying conductors. A laser-ablated single-sided polyester tape with well-defined patterns was also used, which corresponded to the flexible flat cable openings and was aligned and adhered to the flexible flat cable. A second layer of tape, which was adhesive-coated, double-sided, and laser-ablated, was used to link the MNA to the flexible flat cable, which enabled a microfluidic microchannel for the sample. Rhodium-modified carbon pastes have been considered for detecting glucose and lactate, and microneedle paste electrodes were created by chemically depositing Fast Blue RR diazonium salt for detecting pH. With this technique, each electrode could be connected to a single conductor of the flexible flat cable, which was interfaced with a circuit board using a connection with a low insertion force. A material that restricted macrophage adherence over 48 h was placed on the acrylate-based polymer used to make microneedles. It was demonstrated that the designed MNA detected pH, lactate, and glucose changes selectively, indicating that they could be used to characterize complicated biological environments.
For Human Immunodeficiency Virus (HIV) detection, a microelectromechanical system (MEMS) microfluidic system was designed with a combination of a MNA consisting of sharp-edged microneedles in order to minimize penetration pain and skin resistance, and a microfluidic channel to direct the flow of blood samples through the MNA.67 The microfluidic channel was designed with thousands of constrictions coated with anti-human CD4 monoclonal antibodies for capturing CD4 T+, which is used to detect HIV in the human body. The proteins' adsorption occurred when more energy was released than was gained via the MNA to trap CD4 T+ cells with the constrictions in the microfluidic channel. Then, an alternating current (AC) impedimetric analysis method was used to detect CD4 T+ cells in the channel based on the frequency shift of the input signal. A linear approach was demonstrated to model the AC impedimetric system, which was represented by resistor and capacitor elements. The number of resistor–capacitor elements presented in the equivalent electrical circuit of the microchannel was related to the number of CD4 T+ cells adsorbed in the entire microchannel; hence, the possibility of determining the CD4 T+ cells by electrical determination was demonstrated. The output voltage from the voltage converter to frequency was processed in the model, as well as conditioning circuits to identify the CD4 T+ count, resulting in detecting HIV in the body.
In another study, a POC diagnostic system that facilitated hollow MNA combined with a microfluidic system that contained lithium heparin as an anticoagulant was designed for painless automated capillary blood sample collection and storage for on-site testing of hemoglobin A1C.4 The MNA that consisted of 30 microneedles with 350 μm width, 50 μm thickness, and 1000 μm length was considered for the device. The MNA puncture sites were exposed to vacuum, which promoted localized blood flow, expanded the puncture sites, and significantly raised blood flow rates. As blood emerged from the MNA puncture sites, the sample was collected by the microneedles and mixed with anticoagulant in three steps: (i) in the immediate vicinity of the puncture sites, a capillary ring came into contact with the blood and wicked it from the skin into the device; (ii) the capillary ring's dried anticoagulant was slowly dissolved by the blood as it entered the device; and (iii) the anticoagulant was uniformly distributed into the sample during sample collection due to mixing elements in a flow channel that connected the capillary ring to the sample collecting reservoir. The results that were gathered from 144 participants in a clinical setting show that hemoglobin A1C measurements were equivalent for both venous blood and device-collected samples. Moreover, premarket clearance was given to the developed device by the United States Food and Drug Administration.
Another work integrated a single hollow MNA with a low-cost paper-based sensor, which led to a One-touch-activated Blood Multi-diagnostic System (OBMS).1,2 Blood collection, serum separation, and in vivo cholesterol and glucose diagnosis were all demonstrated in this device [Figs. 1(c) and 1(d)]. A biocompatible film made of parylene was coated on the hollow microneedle's inner and outer surfaces to improve biomedical compatibility. The soft lithography method was used to fabricate a touch switch with PDMS as the mother material, which contained a cylindrical chamber. The working mechanism of the paper-based sensor for multi-diagnosis blood sampling was represented in three stages: blood sample collection, blood cell separation, and biomarker detection. A one-touch finger press initiated the sample collection into the sensor's chamber and then went to the sample pad. The serum was then separated from the sample and transported into the reaction zones using an asymmetrical polysulfone membrane. The chamber volume was optimized to collect blood samples of approximately 30 μl as the blood sample was collected via negative pressure induced by the self-recovery of the deformable PDMS cylindrical chamber. OBMS was applied to a rabbit ear artery, and color change was observed in 5 min. The results demonstrated that the volume of the deformable PDMS touch-switch could be used to control the operational blood sample volume. Furthermore, by selecting the appropriate raw materials and creating the correct paper sensor pattern, the flow rate could be controlled.
The reproducible insulation, sensor modification, and sealing operations provide significant technological challenges for microneedle sensors.31 While accurate liquid dispensers and carefully regulated spray coating techniques could be used to reliably modify microscale sensors with polymers and bioreagents, well-defined masking procedures are required to specify the electrode region. Foreign body response and biofouling are among the challenges that hinder the MNA biosensors' ability to operate on the body for a long period of time.31 Potential solutions exist for this problem by using fine-tunable polymeric protective coatings to prevent surface-active macromolecules at the tissue–device interface.68 Another approach for improving the long-term stability of MNA biosensors is to sequentially expose and activate each sensor using a variety of subarrays with different transient coating thicknesses.69
C. Drug delivery and wound healing
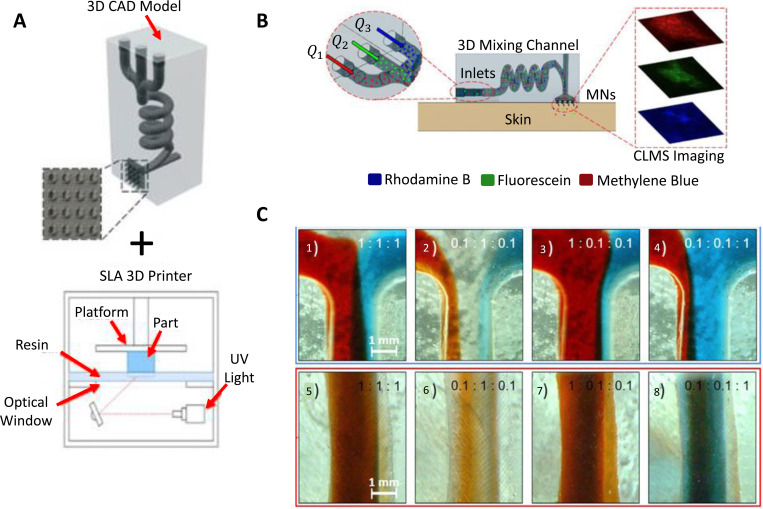
Both tiny chemicals like lidocaine and macromolecules like proteins can penetrate into the tissue under the skin with the use of microneedles, which can make microholes on the skin surface by penetrating the outermost skin layer.47 The transdermal delivery method based on microneedles is a self-manageable, patient-friendly, and effective administration route for drug delivery and wound healing applications because the length of these microneedles is a few hundred micrometers and the penetration depth is small enough to avoid the lower reticular dermis's nerve receptors.47 An elaborate hollow microneedle design was proposed with the purpose of mixing multiple molecules for drug delivery (Fig. 2).70 In order to enable programmable drug administration in combinational therapy-based applications, a 3D-printed structure with a hollow MNA and a hydrodynamic mixing module linked to it [Fig. 2(a)] allowed for the modification of the input fluid flow rates of the solutions. The device was used to inject model drug molecules, rhodamine B, fluorescein isothiocyanate, and methylene blue, into porcine skin [Fig. 2(b)]. The characterization results revealed that the composition of the delivered fluid as well as the homogenized mixing of several reagents at the outlet can be achieved by controlling the injected flow rates at the inlet [Fig. 2(c)]. The device proved useful in preclinical studies on combinational medication therapy, where the in situ mixing of several pharmaceuticals and the adjusting of their physicochemical properties proved effective in ways that were superior to those of premixed or single agents alone.
FIG. 2.
3D printing of microfluidic-integrated hollow MNAs for transdermal drug delivery. (a) Design of the setup, which was fabricated with an SLA 3D printer. (b) Characterization of ex vivo transdermal delivery of the model drugs (Rhodamine B, methylene blue, and fluorescein isothiocyanate,) to porcine skin in the experimental setup with confocal scanning laser microscope (CLSM) imaging. (c) Mixing characterization using microscopic images of the 3D spiral chamber's inlet junction and outlet under different ratios of flow rate for solutions of red-dyed, clear, and blue-dyed (Q1:Q2:Q3). The results of the characterization demonstrated that by regulating the injected inlet flow rate, the composition of the delivered fluid along with the homogenized mixing of various reagents at the outlet can be achieved. Adapted from Yeung et al.,70 Biomicrofluidics 13, 064125 (2019), licensed under a Creative Commons Attribution (CC BY) license.
For drug loading and delivery purpose, a disposable and flexible microneedle fluidic system was developed consisting of five layers.47 The first layer was a micropump that could also act as a storage chamber. The second and third layers had cavities and two holes to form check valves. The fourth layer had a microfluidic channel that contained four crescent openings for the purpose of drug delivery. Finally, the fifth layer had a MNA that could penetrate the stratum corneum layer of the skin and create microchannels in the tissue. The drug was loaded into the microfluidic system by micropumps, flowed to the top-side of the microfluidic system through the connection microchannel, and then flowed through crescent openings. The tissues under the skin were then given these drugs after they were delivered through the microchannels made by the microneedles. The MNA was applied to a skin sample of a rat, and for staining the skin surface, methylene blue solution was used to test the penetration capability of MNAs. The stained dots revealed that the inserted microneedles successfully created microchannels since the methylene blue solution diffused into the penetrated holes.
Another combination of easy-to-fabricate, intelligent, origami silk fibroin microneedle-structured dressing (i-SMD) with a drug delivery system and a biosensor was developed in which a controlled drug release was accomplished by employing N-isopropylacrylamide (NIPAM) hydrogel and inverse opal (IO) photonic crystals (PCs) for enhancing fluorescence intensity to increase system sensitivity.5 The patterned microfluidic channels on the flexible substrate utilized multiple inflammatory factors for sensing, i.e., interleukin 6 and C reactive protein. Moreover, motion sensing was accomplished at varying bending angles by capturing and monitoring the motion frequency of the finger, wrist, and elbow using microelectronic circuits integrated on the i-SMD. The system was tested on full-thickness cutaneous wounds in diabetic mice, and wound healing occurred in 12 days. The results showed that the flow velocity could be controlled by selecting MNAs with various intervals and diameters. Also, it was shown that compared to no therapy and blank i-SMD methods, drug-loaded i-SMD treated wounds had a higher rate of recovery and a lower wound area.
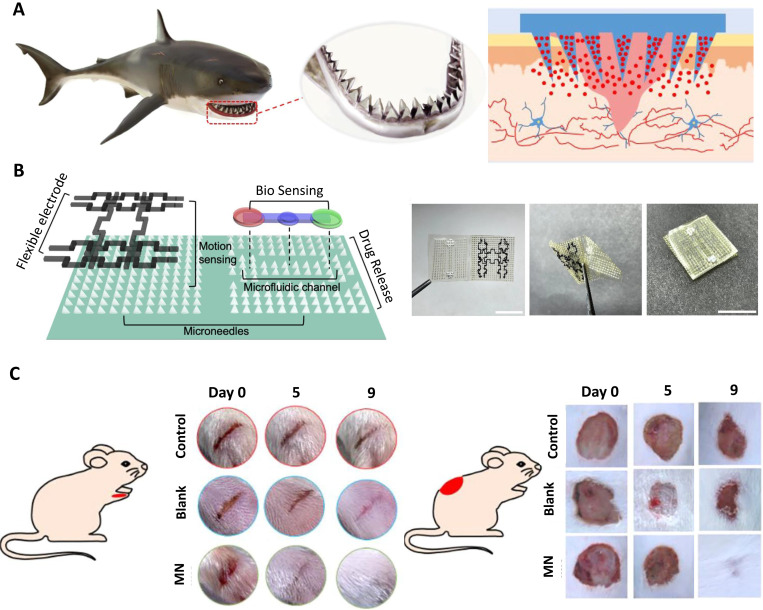
In another work, microneedle dressing inspired by shark-tooth [Fig. 3(a)] for intelligent wound management was demonstrated.71 The biomimetic MNA was a multifunctional, foldable origami chip that provided chronic wound recovery in the long term, showing stable adhesion [Fig. 3(b)]. The system combined biochemical sensing of several inflammatory factors (lactate and calprotectin) in a microfluidic channel, controllable drug release from microneedles by utilizing temperature-responsive NIPAM hydrogel, motion sensing with flexible titanium (IV) carbide (MXene) electrodes, and wound healing. With laser-engraved and negative-replicated molds, rapid fabrication of the patch was achieved. In vivo diabetic rat experiments [Fig. 3(c)] showed that the drug-loaded biomimetic patch healed full-thickness, stripe-shaped, and circular cutaneous wounds in 9 days.
FIG. 3.
A flexible, multifunctional, and biocompatible biomimetic microneedle dressing for intelligent wound management. (a) Shark-teeth-inspired microneedles, (b) Multifunctional microneedle dressing combined with microfluidic channels for bio-sensing, drug release, and motion sensing. (left) Schematic of the proposed device. The device consisted of MNAs, microchannels, and flexible electrodes. (right) Images of the origami chip before, during, and after fold-in. (c) Microneedle dressing applied wound healing on diabetic mice, (left) Strip-shaped and (right) circular wounds were cut on the diabetic mice's foot and back, respectively. MNA-based dressing showed a better result with respect to no dressing in 9 days. Reproduced with permission from Guo et al.,71 ACS Nano 15, 9 (2021). Copyright 2021 American Chemical Society.
In addition to replica molding, 3D printing technology has been used to demonstrate a wirelessly controlled, flexible, smart bandage that is comprised of 3D-printed hollow MNAs for active drug delivery in chronic diabetic wounds.6 The platform benefited from multiple miniaturized pumps that could be wirelessly operated using a customized mobile application and a smartphone-sized module that could be reused and included all of the electronic components. Islands of MNAs were distributed throughout the bandage to deliver active compounds into deeper layers of the tissue and improve the bioavailability of drugs. In vitro testing proved the MNAs' efficiency at delivering the active compounds through necrotic tissues and wound crust. The platform had two modules: (i) a wearable bandage integrated with MNAs that was connected to the control module, and (ii) a wirelessly communicated smartphone for controlling drug delivery. This programmable platform administered different pharmacological agents at independent temporal profiles to critical layers of the wound bed during different stages of tissue regeneration in a minimally invasive way. It was shown that the drug delivery method and the spatial distribution were key factors in dermal wound healing, in addition to administering suitable therapeutics. Vascular endothelial growth factor (VEGF) was chosen as a key parameter to assess wound healing in mice, and the proposed platform was used to administer VEGF to chronic wounds. Compared to topical delivery, a significant increase in hair growth, angiogenesis, wound closure, and re-epithelialization was observed.
III. THEORY
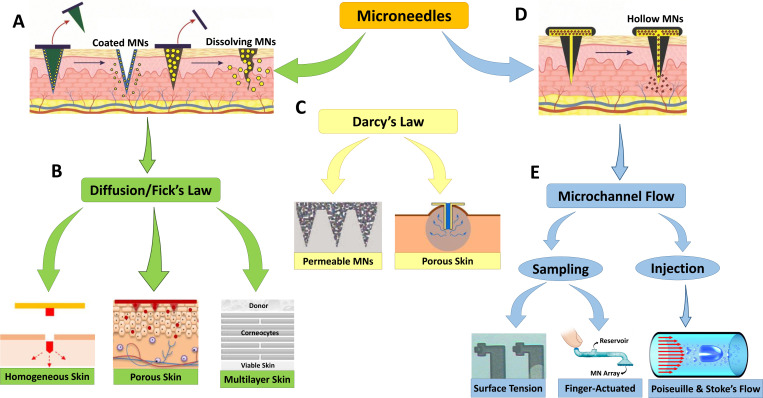
Various ranges of devices integrating MNAs with microfluidics have been reviewed in Sec. II, all dealing with different types of non-biological fluids, such as glucose and water in biosensing, as well as biological fluids, such as blood and ISF in sampling and drug delivery. Although different flow parameters may be relevant for specific applications, low Reynolds number flow and mass transfer at the microscale are common in all of them. There are two main mechanisms at work in these devices: injection of a drug through the skin by microneedles and its diffusive transport to the bloodstream through skin layers. Fluid flow in a microchannel is driven by an applied pressure gradient and can be approximated as a fully developed laminar channel flow (Poiseuille's law). On the other hand, the diffusion phenomenon is governed by Fick's law. Figure 4 demonstrates an overview of the models and principles that apply to drug delivery and sampling with the various types of microneedles reviewed here. Considering microfluidic devices integrated with microneedles, it is critical to model the fluid flow and mass transfer to understand how to implement MNA systems more efficiently. Accurate modeling of fluid flow and mass transfer can provide indispensable information about the drug concentration distribution in the tissue as well as the timing of drug delivery or sampling, which is extremely difficult to measure experimentally, if not impossible. In addition, modeling significantly shortens the design process by cutting down on costs and time-consuming lab experiments.72
FIG. 4.
Brief explanation of the models and principles that apply to drug delivery and sampling in different types of microneedles used in the reviewed studies. (a) Drug transport through the skin in dissolving and coated microneedle applications occurs via a (b) diffusion mechanism that follows Fick’s law, in which the skin can be modeled as a homogeneous, porous, or multilayer medium. (c) Considering skin as a porous material as well as existing wicking conditions, Darcy's law can model fluid delivery through the skin. Darcy’s law conditions can also be used to model fluid transport in permeable microneedles as used in the literature. (d) Drug transport through the microchannel to the skin in hollow microneedle applications occurs via (e) fluid transport mechanisms that follow Poiseuille's law and Stokes' flow equation. To extract body fluids, surface tension between solid and liquid interfaces can be used, but faster techniques, such as finger-actuated microneedle devices, can also be applied. Subfigure (a) was reproduced from Dsouza et al.,101 Biomed. Microdevices 22, 1–11 (2020); licensed under a Creative Commons Attribution (CC BY) license. Subfigure (b) elements were reproduced from Wu et al.,90 J. Drug Deliv. Sci. Technol. 61, 102192 (2021); licensed under a Creative Commons Attribution (CC BY) license; with permission from Zoudani et al.,87 Eur. J. Pharm. Sci. 150 (2020). Copyright 2020 Elsevier B.V.; and with permission from Hansen et al.,93 Eur. J. Pharm. Biopharm. 68, 2 (2008). Copyright 2008 Elsevier B. V. Subfigure (c) elements were reproduced with permission from Cahill et al.,98 J. Acta Biomater. 80 (2018). Copyright 2018 Acta Materialia Inc. Published by Elsevier Ltd.; and with permission from Shrestha and Stoeber,99 with the permission of AIP Publishsing. Subfigure (d) was reproduced from Dsouza et al., Biomed. Microdevices 22, 1–11 (2020); licensed under a Creative Commons Attribution (CC BY) license. Subfigure (e) elements were reproduced with permission from Mukerjee et al.,1 J. Sens. Actuator A 114, 2–3 (2004). Copyright 2004 Elsevier B.V.; with permission from Sarabi et al.,30 Appl. Sci. 11, 5329 (2021), licensed under a Creative Commons Attribution (CC BY) license; and with permission from Pommella et al.,102 J. Soft Matter. 13, 37 (2017). Copyright 2017 Royal Society of Chemistry.
A. Fluid flow inside MNAs
Fluid flow in MNAs is generally viscous-dominated and highly laminar, mainly due to small length scales. In addition, the Reynolds number is small (often on the order of unity or smaller) so that the convective terms of the flow equations are negligible.73 Thus, flow can be well described by the incompressible Stokes equations with no-slip boundary conditions at the wall, and classical solutions are often relevant and useful.74 As a result, the typical velocity profile in MNAs is parabolic in simple geometries when the flow is driven by an applied pressure difference, as is the case in all MNA applications. The geometrical parameters of the microneedle, the number of microneedles on the array, and fluid characteristics such as fluid viscosity affect the required pressure difference for fluid flow through the microneedle. In a research on 3D printing of microneedles,75 three primary geometric parameters for a microneedle were studied: needle base diameter, needle height, and angle of the draft. While 3D-printed cylindrical microneedles were fabricated more efficiently, manufacturing conical microneedles with a design draft angle of or showed considerable resolution limits. For MNA biosensors that intend to continuously monitor analytes, achieving effective and reliable skin penetration and microneedle-tissue interlocking is crucial, especially regarding the variation in skin thickness originated from differences in age, gender, and body mass index, and the elasticity of the skin, which results in a counteracting force to the penetration.31 To overcome this challenge, a precise optimization of the microneedle geometrical parameters, such as the tip radius, height, needle density, base diameter, and spacing, which determine the insertion and fracture forces, leads to reliable skin penetration.76 The ability to penetrate via hollow silicon MNAs for glucose monitoring with tapered and straight profiles was studied both theoretically and experimentally.77 Two important parameters for penetration calculation and pain estimation were reported for the mentioned microneedle profiles: (i) the kinetic energy of the prototype, which has a direct effect on both penetration and pain sensation for the human subject; (ii) the stopping distance of MNAs inside skin tissue that is related to the mechanical properties of the skin. The experimental results revealed that the existence of a cutting edge in the straight profile MNAs dramatically reduced the minimum required penetration pressure, despite the fact that the tapered profile MNAs were more likely to penetrate into most skin types given the same amount of kinetic energy.77 Microneedles can be made of a variety of materials, including polymers and metals, depending on the patch’s design and component parts.78 Although silicon has sufficient mechanical strength for skin insertion and can be precisely manufactured with short, sharp tips using deep reactive ion etching and photolithography methods, silicon microneedles can cause a risk to patient safety if they break away from the skin and pieces remain in the tissue.79 The most popular metal used to make hollow, coated, and solid microneedles that can readily pass through the skin is stainless steel, but it corrodes more quickly than Ti alloys.80 The polymers used to manufacture microneedles should be soluble in water, biocompatible, and strong enough to penetrate the skin.78 Various types of polymers, such as hydroxypropyl methylcellulose (hypromellose), hyaluronic acid (HA), carboxymethyl cellulose (CMC), polyvinyl pyrrolidone (PVP), and poly-lactic-co-glycolic acid (PLGA), can be used in the solvent casting procedure to fabricate dissolving or hydrogel microneedles. On the other hand, due to the micro-scale diameters of microneedles, flow resistance is high. Measurements and predictions of fluid dynamics are critical when developing microneedles for transdermal drug delivery so that the microneedle is small enough to avoid pain while being sharp enough to penetrate into the skin easily and large enough to achieve the appropriate flow rate.81
1. Modeling flow in microneedle
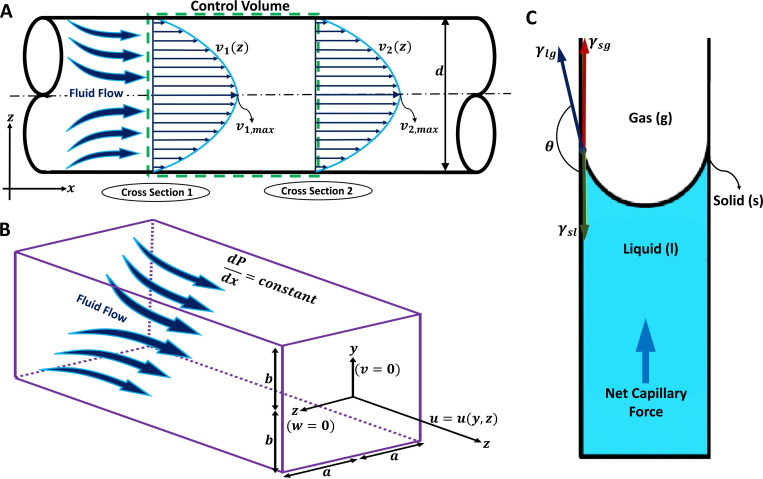
The drug is usually delivered through a straight circular or rectangular channel in the microneedle and the flow can be well approximated by a fully developed uni-directional laminar flow except for the inlet and exit sections. Figure 5(a) illustrates a schematic representation of such a microchannel with a circular cross section. Several analytical solutions in the fully developed region for a wide range of cross sections exist.82 For an incompressible steady flow in a circular channel, applying the energy conservation equation between two locations in Fig. 5(a) yields79–81
| (1) |
where subscripts 1 and 2 describe the up- and downstreams of the control volume, respectively. The terms on the left-hand side denote the work done by pressure difference, changes in the kinetic energy and the potential energy, respectively, with , and z being pressure, fluid density, average velocity in the channel, the gravitational acceleration, and elevation, respectively. The terms on the right-hand side represent the major and minor losses, respectively, where L and d are length and diameter of the microchannel, respectively, while f is the Darcy–Weisbach friction factor and K is the minor loss coefficient. For a fully developed laminar flow in a circular pipe, the Darcy–Weisbach friction factor is given by , where the Reynolds number is defined as with being the fluid viscosity.48 The minor loss coefficient, K, is defined to account for the additional losses due to entrance/exit flows, expansion/contraction, bends, tees, and the like. In a typical microneedle, the change in the potential energy is negligible compared to the other terms. In addition, for a fully developed flow in a constant cross-sectional channel, the mass conservation requires . Thus, Eq. (1) can be further simplified by neglecting the gravity effects in comparison with the rest of the equation, and that the channel has a constant circular cross-sectional area,
| (2) |
where is the applied pressure difference, is the volume flow rate, and and are the minor loss coefficients associated with the entrance and exit flows, respectively.51 Assuming that losses at the needle’s entrance and exit are negligible, Eq. (2) reduces to Poiseuille's law given by
| (3) |
FIG. 5.
Fluid flow transportation modeling in hollow microchannels and microchannels for drug delivery and sampling applications. (a) A two-dimensional microchannel demonstration with a circular cross section and diameter d is illustrated. The fully developed fluid flow equations inside the microchannel can be determined by applying the energy equation to the control volume. Considering fully developed flow, velocity profile, v, will be only a function of z in each cross section. The maximum velocity profile in each cross section should be considered for calculating the average fluid velocity for each cross section. (b) A three-dimensional microchannel demonstration with a rectangular cross section in which corresponds to the width and considered as the height. The fully developed fluid flow equations inside the microchannel can be determined using the Poiseuille flow equation. Considering a constant pressure distribution in x direction, the fluid velocity vector only has its x component which is a function of y and z in each cross section. (c) Schematic diagram of the capillary action for fluid extraction from the skin. Three surface tensions act on the solid–liquid–gas boundaries, which are demonstrated as solid–liquid surface tension, , liquid–gas surface tension, , and solid–gas surface tension, in which represents the angle between and . Subfigure (c) reproduced with permission from Mukerjee et al.,1 Sens. Actuator A 114(2–3), 267–275 (2004). Copyright 2004 Elsevier B.V.
Similar results can be obtained for channels with different cross sections. Here, the rectangular channel will be discussed as it is more relevant for the microneedle applications, and we refer to Ref. 82 for other cross sections.
2. Fluid flow in rectangular ducts
When the microneedle's cross section is rectangular rather than circular,84,85 analytical solutions for the velocity profile and associated flow rate can be obtained for a fully developed laminar flow. Adopting a Cartesian coordinates of , and z and considering a rectangular cross section with and as shown in Fig. 5(b), the axial velocity profile and flow rate can be given by82
| (4) |
| (5) |
where is the width of the microchannel, is the height of the microchannel, is an applied pressure gradient in the x direction, and is the viscosity of the fluid.82 For a rectangular channel with height and width , the volume flow rate is correlated to the pressure drop over a length of L approximately as86
| (6) |
where denotes the error term of order of . This term can be approximated as yields less than 10% error when . For , Eq. (6) becomes .
B. Biological fluid extraction
A minimally invasive method for sampling biological fluids is necessary to enable either periodic or continuous monitoring of physiological systems, and important markers of many health and disease states are biomarkers, which are components found in blood and interstitial fluid.1 Many diabetic individuals use transdermal sampling of tiny amounts of blood for glucose concentration assessment as part of their daily routine to monitor their disease’s symptoms. The design, construction, and testing of a hollow MNA with integrated microfluidic microchannels have been presented, in which capillary action is used to fill integrated microchannels with non-biological (ethanol, glycerol, water, and surrogate ISF) and biological (whole blood and ISF) fluids.1 An intermolecular force imbalance at an interface, known as surface tension, controls how fluid fills a hydrophilic micro-capillary. The sum of the surface tensions between two phases, such as solid and liquid, minus the force of molecular attraction between them, can be utilized to estimate the total surface tension between those phases [Fig. 5(c)]. The triple interfaces (gas, liquid, and solid) establish force equilibrium when the surface tension of the solid–liquid, , interface plus the projection of the liquid–gas, , surface tension equals the solid–gas, , surface tension. The total interface surface energy is given by
| (7) |
where is the area of each interface. As the volume of fluid entering the barehole grows, the wetted area changes in proportion to the change in volume. As a result, the fluid pressure can be determined as
| (8) |
where V is the volume and is the contact angle that relates and .1 Based on Ref. 1, the microneedle’s borehole required to be filled with ISF after an initial 20–30 min of latent time, and the backside channels at the distal opening above the reservoir maintained the pressure gradient in place so that the fluid could be drawn in continuously by capillary action.
C. Drug delivery through skin
A drug injected into the skin must pass through skin layers to reach the bloodstream. The skin layers have a porous structure with different material properties. Various models have been used to model drug transport to the blood stream and determine the drug concentration profiles, ranging from simple diffusion models based on Fick's law to porous skin models in which the skin is treated as a layered porous material.
1. Diffusion models
Diffusion models, based on Fick's law, assume that drug molecules are transported in the skin and its stratum corneum layer by molecular diffusion. Fick's first law relates the diffusive flux to the concentration gradient via a diffusion coefficient as , where is the diffusive mass flux, C is the drug concentration, and D is the molecular diffusivity. In the simplest case, the diffusion coefficient is assumed to be constant and is usually determined by a homogenization procedure. This model is commonly used to predict the drug concentration profile in the microneedle treated skin.57,58 When a drug is applied to the skin, it passes through the stratum corneum and viable epidermis to reach the inner layers of the skin.58 According to Fick’s laws of diffusion, passive diffusion happens in the direction of the concentration gradient or from higher to lower concentration. Assuming a homogenous passive diffusion, the drug concentration evolves by a convection–diffusion equation as
| (9) |
where t is the time, is the velocity field, and D is the constant molecular diffusivity. The convection term can be neglected due to the insignificant velocity of fluid flow around the microneedles in the skin;72–85 thus, Eq. (9) reduces to be Fick's second law that has the same form as the heat equation. The effective diffusion coefficient, which is related to the characteristics of the skin as well as the size of the drug molecules, is a crucial factor. Many studies established various methods for determining diffusion coefficient, where the skin is modeled as a homogeneous material, a porous material, and a multilayer structure.
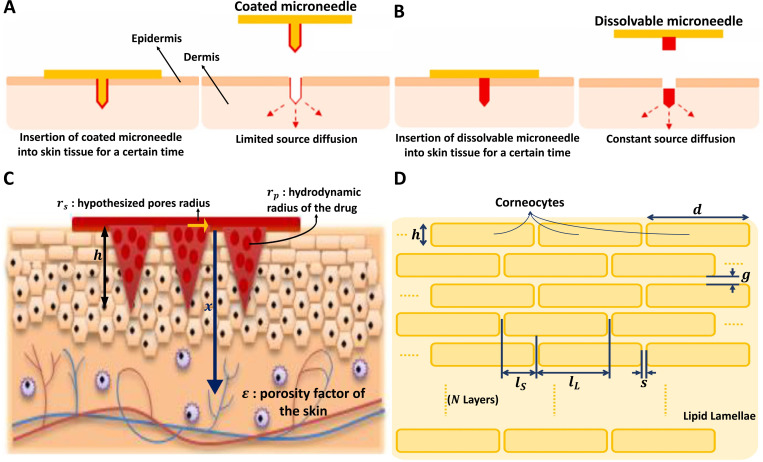
In the absence of the convective term, Eq. (9) becomes linear and can be solved analytically for various initial and boundary conditions. In microneedle applications, two cases are particularly relevant.88 In the first case [Fig. 6(a)], through the use of a microneedle, a drug is injected into skin tissue, resembling a point-source diffusion problem where diffusion happens symmetrically in all directions.89 Using a spherical coordinate system and assuming that diffusion occurs only in the radial direction, the solution to Fick's law can be determined as a Gaussian distribution for a limited point-source deposited as
| (10) |
where is the initial deposited mass, r is the distance from the surface of the diffusion source, and t represents the elapsed time. The diffusion coefficient, D, can be estimated experimentally using the assumed linear diffusion model.89 In the second case [Fig. 6(b)], the concentration at the side of a drug injection is assumed to be constant, which mimics a slow and continuous injection, the solution is given by
| (11) |
FIG. 6.
Drug diffusion from the microneedle through the homogenous skin is based on two different models: (a) Limited source diffusion model for coated microneedles, and (b) Constant source diffusion model for dissolving microneedles. (c) Drug diffusion demonstration through a porous skin model with porosity of . Significant parameters for this model are the hydrodynamic radius of the drug and the hypothesized pore radius created on the skin that can be used to evaluate parameter . Geometric parameter considerations are the length of the microneedles, h, number of microneedles in a MNA, n, and the diffusion path length x. (d) Schematic diagram for a multilayer skin model. The structure consists of corneocytes blocks that are organized in a lipid lamellae medium. Significant geometric parameters in the multilayer skin model for drug diffusion are length, d, and height, h, of the corneocytes, horizontal gap, s, and vertical gap, g, between corneocytes layers, longest overlapping lipid path, , shortest overlapping lipid path, , and the number of layers, N. Subfigures (a) and (b) were reproduced from Wu et al.,90 J. Drug Deliv. Sci. Technol. 61, 102192 (2021); licensed under a Creative Commons Attribution (CC BY) license. Subfigure (c) was reproduced with permission from Zoudani et al.,87 Eur. J. Pharm. Sci. 150 (2020). Copyright 2020 Elsevier B.V.
where is the constant concentration and in the complementary error function defined as90
| (12) |
a. Skin as a porous material
Skin is not a homogenous material, and different layers have different material properties. To account for its porous and inhomogeneous structure, the skin is treated as a porous medium in which small pores are assumed to serve as pathways for the transport of drug molecules, as sketched in Fig. 6(c). In this model, the diffusion coefficient is given by87
| (13) |
where is the diffusion coefficient of the drug at infinite dilution, is the porosity of the skin, and is the hindrance factor defined to account for the interaction of drag molecules with the tortuous wall of pores. In this model, tortuous channels are assumed to exist as conduits for the transfer of drug molecules. The hindrance factor depends on the ratio of the hydrodynamic radius of drug molecules, , to the skin pore radius, ,
| (14) |
In drug delivery through MNAs, the skin pore radius can be estimated as
| (15) |
| (16) |
where is the volume of skin pores prior to microneedle insertion, is the volume of each microneedle, x is the diffusion path length, and n is the number of microneedles in the array.91 In Eq. (16), is the tortuosity factor and h is the height of the microneedle.87
For , can be calculated as60
| (17) |
For , several correlations are suggested by Deen.92
b. Skin as a multilayer structure
This model describes skin penetration as a series of partition and diffusion steps that may be quantified in terms of partition coefficients, K, and diffusion coefficients, D. With a variety of diffusion models with different degrees of complexity in use, estimating model parameters becomes exceedingly challenging.93 One of these models has been expanded by adding a homogenous epidermal/dermal compartment and increasing the number of corneocyte layers to 16.94 As a result, the model membrane is made up of three distinct phases: corneocytes, surrounding lipids, and the viable deeper skin layers.93 The stratum corneum is a biphasic arrangement of corneocytes sandwiched between intercellular lipid lamellae rather than a uniform membrane.95 In its most basic form, stratum corneum geometry can be illustrated as a two-dimensional “brick and mortar” structure [Fig. 6(d)]. The membrane is made up of N layers of corneocytes, which have a width of d and a thickness of h. The thickness of the lipid lamella is g in the horizontal direction and s in the vertical direction. As a result, the effective diffusion path length for the ordered structure can be defined as . The membrane thickness can be determined as when many layers are considered, and the lipid path length is calculated by . Several dimensionless parameters can then be determined,95 such as corneocyte offset ratio , where is the length of the longest overlapping lipid path and is the length of the shortest overlapping section. Other dimensionless parameters are corneocyte aspect ratio , slit shape , and the fractional volume loading of corneocytes, which can be approximated by when . The total steady state flux, , through a homogenous membrane with a thickness of , an area of , and concentration difference between two surfaces is given in
| (18) |
where is the diffusion coefficient of homogenous isotropic lipids.95 The lag time can also be defined for the assumed membrane as . Considering all parameters mentioned for a heterogeneous skin model, the effective flux, , and the effective lag time, , are determined in the literature as58
| (19) |
| (20) |
2. Porous medium model and Darcy's law
The wicking phenomenon is the spontaneous movement of a liquid through a porous medium due to capillary suction at liquid–gas contacts on the surface or within the porous medium.96 Darcy's law relates the flow rate to the pressure drop in wicking, which is based on fluid permeability and is only valid for slow viscous flows.97 Darcy’s law, which is based on the fluid being wicked up microneedle's pore diameters and percentage porosity, can be used to determine the flow rate through the porous metal-based microneedles.98 Darcy's law in the radial direction is given by
| (21) |
where the permeability of the skin, K, the cross-sectional area perpendicular to the flow, A, the pressure gradient along the radial direction, , and the dynamic viscosity of the fluid, , are related to volume flow rate, Q.99 Although the permeability can be measured experimentally,97 it can be computed for a biological porous medium, such as skin a function of the volumetric strain, , in the solid matrix and the macroscopic material constants and m as
| (22) |
where the initial effective permeability of the skin at the start of the analysis is denoted by . The nonlinearity in permeability is represented by parameter m. For an increase in volumetric strain , a larger value of m implies a more significant increase in permeability K.99
IV. CONCLUDING REMARKS
Using the formulation methods discussed in Sec. III, fluid transport and concentration profiles within the microneedles integrated with microfluidic systems can be modeled appropriately in microscale. For hollow microneedles, the most encountered methods were reviewed: first, deriving Poiseuille’s law from the modified Bernoulli equation for a microneedle with a circular duct; and second, solving Stokes' equation by simplifying the Navier–Stokes equation for a microneedle with a rectangular duct. It was also reviewed that drug diffusion in coated or dissolving microneedles can be studied using various skin models. The porous skin model, which represented the skin via several properties for driving the drug delivery process, was the most typically found in the reviewed literature; however, the multilayer model offered more similarity to the human skin. Darcy's law was also reported to be used for modeling the skin as a porous material when wicking conditions exist. On the other hand, a homogenous model could be used for applications that involve a simpler skin model. Also, microneedles are routinely used to collect biological fluids, such as blood and ISF from the skin, which can be modeled using capillary action driven by surface tensions between solid and fluid surfaces as the principal technique.
Microfluidic systems integrated with MNAs are emerging in various areas, such as drug delivery, wound healing, sampling body fluids, and biosensing, which were reviewed in this paper. The importance of modeling in the fabrication and optimization of MNA systems is receiving much attention, as indicated by the growing number of publications.57 Accordingly, this review concludes that developing mathematical models of MNA systems can enable the efficient design of these systems as they are developed for a wider range of applications. The integration of AI and ML algorithms with the design parameters of the MNA systems in computational simulation leads to a lower cost of the experimental fabrication and predicts possible problems with the MNA systems.73–98 The interactions between MNAs and the skin, as well as drug diffusion profiles in the skin, can be resolved with additional information obtained from MNA experiments in vivo and in vitro. This will address a number of issues that arise throughout the preclinical and clinical testing of novel formulations and delivery methods, finally leading to more advanced healthcare setups.
ACKNOWLEDGMENTS
S.T. acknowledges the Tubitak 2232 International Fellowship for Outstanding Researchers Award (No. 118C391), the Alexander von Humboldt Research Fellowship for Experienced Researchers, the Marie Skłodowska-Curie Individual Fellowship (No. 101003361), and the Royal Academy Newton-Katip Çelebi Transforming Systems Through Partnership Award (No. 120N019) for financial support of this research. Opinions, interpretations, conclusions, and recommendations are those of the author and are not necessarily endorsed by the TÜBİTAK. This work was partially supported by Science Academy's Young Scientist Awards Program (BAGEP), Outstanding Young Scientists Awards (GEBİP), and Bilim Kahramanlari Dernegi—The Young Scientist Award. This study was conducted using the service and infrastructure of Koç University Translational Medicine Research Center (KUTTAM). The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Abdollah Ahmadpour: Writing – original draft (equal). Pelin Kubra Isgor: Writing – review & editing (equal). Berk Ural: Writing – review & editing (equal). Busra Nimet Eren: Writing – review & editing (equal). Misagh Rezapour Sarabi: Writing – review & editing (equal). Metin Muradoglu: Writing – review & editing (equal). Savas Tasoglu: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Supervision (equal); Writing – review & editing (equal).
DATA AVAILABILITY
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
REFERENCES
- 1.Mukerjee E. V. et al. , “Microneedle array for transdermal biological fluid extraction and in situ analysis,” Sens. Actuators, A 114(2–3), 267–275 (2004). 10.1016/j.sna.2003.11.008 [DOI] [Google Scholar]
- 2.Li C. G. et al. , “One-touch-activated blood multidiagnostic system using a minimally invasive hollow microneedle integrated with a paper-based sensor,” Lab Chip 15(16), 3286–3292 (2015). 10.1039/C5LC00669D [DOI] [PubMed] [Google Scholar]
- 3.Dabbagh S. R. et al. , “3D-printed microneedles in biomedical applications,” iScience 24(1), 102012 (2021). 10.1016/j.isci.2020.102012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blicharz T. M. et al. , “Microneedle-based device for the one-step painless collection of capillary blood samples,” Nat. Biomed. Eng. 2(3), 151–157 (2018). 10.1038/s41551-018-0194-1 [DOI] [PubMed] [Google Scholar]
- 5.Gao B. et al. , “Intelligent silk fibroin based microneedle dressing (i-SMD),” Adv. Funct. Mater. 31(3), 2006839 (2021). 10.1002/adfm.202006839 [DOI] [Google Scholar]
- 6.Derakhshandeh H. et al. , “A wirelessly controlled smart bandage with 3D-printed miniaturized needle arrays,” Adv. Funct. Mater. 30(13), 1905544 (2020). 10.1002/adfm.201905544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li W. et al. , “Rapidly separable microneedle patch for the sustained release of a contraceptive,” Nat. Biomed. Eng. 3(3), 220–229 (2019). 10.1038/s41551-018-0337-4 [DOI] [PubMed] [Google Scholar]
- 8.Mistilis M. J., Bommarius A. S., and Prausnitz M. R., “Development of a thermostable microneedle patch for influenza vaccination,” J. Pharm. Sci. 104(2), 740–749 (2015). 10.1002/jps.24283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bhatnagar S. et al. , “Zein microneedles for localized delivery of chemotherapeutic agents to treat breast cancer: Drug loading, release behavior, and skin permeation studies,” AAPS PharmSciTech 19(4), 1818–1826 (2018). 10.1208/s12249-018-1004-5 [DOI] [PubMed] [Google Scholar]
- 10.Arya J. and Prausnitz M. R., “Microneedle patches for vaccination in developing countries,” J. Controlled Release 240, 135–141 (2016). 10.1016/j.jconrel.2015.11.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Larrañeta E. et al. , “Microneedle arrays as transdermal and intradermal drug delivery systems: Materials science, manufacture and commercial development,” Mater. Sci. Eng., R: Rep. 104, 1–32 (2016). 10.1016/j.mser.2016.03.001 [DOI] [Google Scholar]
- 12.Global Microneedle Drug Delivery Systems Market by Type, by Material, by Application, by Regional Outlook, Industry Analysis Report and Forecast, 2021–2027, October 2021.
- 13.Drug Delivery Systems Market Size, Share & COVID-19 Impact Analysis, by Type (Inhalation, Transdermal, Injectable, and Others), by Device Type (Conventional and Advanced), by Distribution Channel (Hospital Pharmacies, Retail Pharmacies, and Others), and Regional Forecast, 2022–2029. 2022, Fortune Business Insights.
- 14.Prausnitz M. R., “Engineering microneedle patches for vaccination and drug delivery to skin,” Annu. Rev. Chem. Biomol. Eng. 8(1), 177–200 (2017). 10.1146/annurev-chembioeng-060816-101514 [DOI] [PubMed] [Google Scholar]
- 15.van der Maaden K. et al. , “Hollow microneedle-mediated micro-injections of a liposomal HPV E743–63 synthetic long peptide vaccine for efficient induction of cytotoxic and t-helper responses,” J. Controlled Release 269, 347–354 (2018). 10.1016/j.jconrel.2017.11.035 [DOI] [PubMed] [Google Scholar]
- 16.Chu L. Y. and Prausnitz M. R., “Separable arrowhead microneedles,” J. Controlled Release 149(3), 242–249 (2011). 10.1016/j.jconrel.2010.10.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen Y. et al. , “Fabrication of coated polymer microneedles for transdermal drug delivery,” J. Controlled Release 265, 14–21 (2017). 10.1016/j.jconrel.2017.03.383 [DOI] [PubMed] [Google Scholar]
- 18.Verbaan F. J. et al. , “Assembled microneedle arrays enhance the transport of compounds varying over a large range of molecular weight across human dermatomed skin,” J. Controlled Release 117(2), 238–245 (2007). 10.1016/j.jconrel.2006.11.009 [DOI] [PubMed] [Google Scholar]
- 19.Aoyagi S. et al. , “Laser fabrication of high aspect ratio thin holes on biodegradable polymer and its application to a microneedle,” Sens. Actuators A 139(1), 293–302 (2007). 10.1016/j.sna.2006.11.022 [DOI] [Google Scholar]
- 20.Lee K., Lee C. Y., and Jung H., “Dissolving microneedles for transdermal drug administration prepared by stepwise controlled drawing of maltose,” Biomaterials 32(11), 3134–3140 (2011). 10.1016/j.biomaterials.2011.01.014 [DOI] [PubMed] [Google Scholar]
- 21.Gualeni B. et al. , “Minimally invasive and targeted therapeutic cell delivery to the skin using microneedle devices,” Br. J. Dermatol. 178(3), 731–739 (2018). 10.1111/bjd.15923 [DOI] [PubMed] [Google Scholar]
- 22.Kim J. D. et al. , “Droplet-born air blowing: Novel dissolving microneedle fabrication,” J. Controlled Release 170(3), 430–436 (2013). 10.1016/j.jconrel.2013.05.026 [DOI] [PubMed] [Google Scholar]
- 23.Xue P. et al. , “Flexible PEGDA-based microneedle patches with detachable PVP–CD arrowheads for transdermal drug delivery,” RSC Adv. 5(92), 75204–75209 (2015). 10.1039/C5RA09329E [DOI] [Google Scholar]
- 24.Gill H. S. et al. , “Effect of microneedle design on pain in human subjects,” Clin. J. Pain 24(7), 585 (2008). 10.1097/AJP.0b013e31816778f9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim M., Jung B., and Park J.-H., “Hydrogel swelling as a trigger to release biodegradable polymer microneedles in skin,” Biomaterials 33(2), 668–678 (2012). 10.1016/j.biomaterials.2011.09.074 [DOI] [PubMed] [Google Scholar]
- 26.Lee W. et al. , “Conformable microneedle pH sensors via the integration of two different siloxane polymers for mapping peripheral artery disease,” Sci. Adv. 7(48), eabi6290 (2021). 10.1126/sciadv.abi6290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Srivastava A. K. et al. , “Long term biopotential recording by body conformable photolithography fabricated low cost polymeric microneedle arrays,” Sens. Actuators A 236, 164–172 (2015). 10.1016/j.sna.2015.10.041 [DOI] [Google Scholar]
- 28.Woodhouse I. et al. , “Flexible microneedle array patch for chronic wound oxygenation and biofilm eradication,” ACS Appl. Bio Mater. 4(7), 5405–5415 (2021). 10.1021/acsabm.1c00087 [DOI] [PubMed] [Google Scholar]
- 29.Birchall J. C. et al. , “Microneedles in clinical practice–an exploratory study into the opinions of healthcare professionals and the public,” Pharm. Res. 28(1), 95–106 (2011). 10.1007/s11095-010-0101-2 [DOI] [PubMed] [Google Scholar]
- 30.Sarabi M. R. et al. , “Finger-actuated microneedle array for sampling body fluids,” Appl. Sci. 11(12), 5329 (2021). 10.3390/app11125329 [DOI] [Google Scholar]
- 31.Teymourian H. et al. , “Lab under the skin: Microneedle based wearable devices,” Adv. Healthcare Mater. 10(17), 2002255 (2021). 10.1002/adhm.202002255 [DOI] [PubMed] [Google Scholar]
- 32.Xia Y. and Whitesides G. M., “Soft lithography,” Annu. Rev. Mater. Sci. 28(1), 153–184 (1998). 10.1146/annurev.matsci.28.1.153 [DOI] [Google Scholar]
- 33.Yigci D. et al. , “3D bioprinted glioma models,” Prog. Biomed. Eng. 4(4), 042001 (2022). 10.1088/2516-1091/ac7833 [DOI] [Google Scholar]
- 34.Sokullu E. et al. , “3D engineered neural co-culture model and neurovascular effects of marine fungi-derived citreohybridonol,” AIP Adv. 12(9), 095102 (2022). 10.1063/5.0100452 [DOI] [Google Scholar]
- 35.Sokullu E. et al. , “Microfluidic invasion chemotaxis platform for 3D neurovascular Co-culture,” Fluids 7(7), 238 (2022). 10.3390/fluids7070238 [DOI] [Google Scholar]
- 36.Tewhey R. et al. , “Microdroplet-based PCR enrichment for large-scale targeted sequencing,” Nat. Biotechnol. 27(11), 1025–1031 (2009). 10.1038/nbt.1583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Niu X. et al. , “A microdroplet dilutor for high-throughput screening,” Nat. Chem. 3(6), 437–442 (2011). 10.1038/nchem.1046 [DOI] [PubMed] [Google Scholar]
- 38.Streets A. M. et al. , “Microfluidic single-cell whole-transcriptome sequencing,” Proc. Natl. Acad. Sci. U.S.A. 111(19), 7048–7053 (2014). 10.1073/pnas.1402030111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sarabi M. R. et al. , “Disposable paper-based microfluidics for fertility testing,” iScience 25(9), 104986 (2022). 10.1016/j.isci.2022.104986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Baret J.-C. et al. , “Fluorescence-activated droplet sorting (FADS): Efficient microfluidic cell sorting based on enzymatic activity,” Lab Chip 9(13), 1850–1858 (2009). 10.1039/b902504a [DOI] [PubMed] [Google Scholar]
- 41.Tasoglu S., “Toilet-based continuous health monitoring using urine,” Nat. Rev. Urol. 19(4), 219–230 (2022). 10.1038/s41585-021-00558-x [DOI] [PubMed] [Google Scholar]
- 42.Temirel M., Yenilmez B., and Tasoglu S., “Long-term cyclic use of a sample collector for toilet-based urine analysis,” Sci. Rep. 11(1), 1–11 (2021). 10.1038/s41598-021-81842-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ghaderinezhad F. et al. , “Sensing of electrolytes in urine using a miniaturized paper-based device,” Sci. Rep. 10(1), 1–9 (2020). 10.1038/s41598-020-70456-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.i-STAT ALINITY, see poctinnovators.com/vendor/abbott-point-of-care/ (last accessed March 17, 2022).
- 45.Yang B., Fang X., and Kong J., “Engineered microneedles for interstitial fluid cell-free DNA capture and sensing using iontophoretic dual-extraction wearable patch,” Adv. Funct. Mater. 30(24), 2000591 (2020). 10.1002/adfm.202000591 [DOI] [Google Scholar]
- 46.Yang B., Fang X., and Kong J., “In situ sampling and monitoring cell-free DNA of the Epstein–Barr virus from dermal interstitial fluid using wearable microneedle patches,” ACS Appl. Mater. Interfaces 11(42), 38448–38458 (2019). 10.1021/acsami.9b12244 [DOI] [PubMed] [Google Scholar]
- 47.Xiang Z. et al. , “Development of a flexible and disposable microneedle-fluidic-system with finger-driven drug loading and delivery functions for inflammation treatment,” J. Microelectromech. Syst. 24(3), 565–574 (2015). 10.1109/JMEMS.2015.2429675 [DOI] [Google Scholar]
- 48.Dabbagh, S. R., Sarabi M. R., Birtek M. T., Mustafaoglu N., Zhang Y. S., and Tasoglu S., “3D bioprinted organ-on-chips,” Aggregate 4(1), e197 (2022). 10.1002/agt2.197 [DOI] [Google Scholar]
- 49.Sarabi M. R. et al. , “3D printing of microneedle arrays: Challenges towards clinical translation,” J. 3D Print. Med. 5, 65–70 (2021). 10.2217/3dp-2021-0010 [DOI] [Google Scholar]
- 50.Sarabi M. R., Yetisen A. K., and Tasoglu S., “Magnetic levitation for space exploration,” Trends Biotechnol. 40(8), 915–917 (2022). 10.1016/j.tibtech.2022.03.010 [DOI] [PubMed] [Google Scholar]
- 51.Waljee A. K. and Higgins P. D., “Machine learning in medicine: A primer for physicians,” Am. J. Gastroenterol. 105(6), 1224–1226 (2010). 10.1038/ajg.2010.173 [DOI] [PubMed] [Google Scholar]
- 52.Williamson D. J. et al. , “Machine learning for cluster analysis of localization microscopy data,” Nat. Commun. 11(1), 1493 (2020). 10.1038/s41467-020-15293-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Samuel A. L., “Some studies in machine learning using the game of checkers: II: Recent progress,” IBM J. Res. Dev. 11, 601–617 (1967). 10.1147/rd.116.0601 [DOI] [Google Scholar]
- 54.Rezapour Sarabi M. et al. , “Biomedical optical fibers,” Lab Chip 21(4), 627–640 (2021). 10.1039/D0LC01155J [DOI] [PubMed] [Google Scholar]
- 55.Hadikhani P. et al. , “Learning from droplet flows in microfluidic channels using deep neural networks,” Sci. Rep. 9(1), 8114 (2019). 10.1038/s41598-019-44556-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Dabbagh S. R. et al. , “3D-printed microrobots from design to translation,” Nat. Commun. 13(1), 5875 (2022). 10.1038/s41467-022-33409-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yadav P. R. et al. , “Mathematical modelling, simulation and optimisation of microneedles for transdermal drug delivery: Trends and progress,” Pharmaceutics 12(8), 693 (2020). 10.3390/pharmaceutics12080693 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Couto A. et al. , “Dermic diffusion and stratum corneum: A state of the art review of mathematical models,” J. Controlled Release 177, 74–83 (2014). 10.1016/j.jconrel.2013.12.005 [DOI] [PubMed] [Google Scholar]
- 59.Yan Q. et al. , “The finite element analysis research on microneedle design strategy and transdermal drug delivery system,” Pharmaceutics 14(8), 1625 (2022). 10.3390/pharmaceutics14081625 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lhernould M. S., “Optimizing hollow microneedles arrays aimed at transdermal drug delivery,” Microsyst. Technol. 19(1), 1–8 (2013). 10.1007/s00542-012-1663-1 [DOI] [Google Scholar]
- 61.Ebrahiminejad V. et al. , “Microneedle arrays for drug delivery and diagnostics: Toward an optimized design, reliable insertion, and penetration,” Adv. Mater. Interfaces 9(6), 2101856 (2022). 10.1002/admi.202101856 [DOI] [Google Scholar]
- 62.Khare N. and Shende P., “Microneedle system: A modulated approach for penetration enhancement,” Drug Dev. Ind. Pharm. 47(8), 1183–1192 (2021). 10.1080/03639045.2021.1992421 [DOI] [PubMed] [Google Scholar]
- 63.Lee K. and Jung H., “Drawing lithography for microneedles: A review of fundamentals and biomedical applications,” Biomaterials 33(30), 7309–7326 (2012). 10.1016/j.biomaterials.2012.06.065 [DOI] [PubMed] [Google Scholar]
- 64.Takeuchi K. et al. , “Microfluidic chip connected to porous microneedle array for continuous ISF sampling,” Drug Deliv. Transl. Res. 12(2), 435–443 (2022). 10.1007/s13346-021-01050-0 [DOI] [PubMed] [Google Scholar]
- 65.Esfandyarpour R. et al. , “Microneedle biosensor a method for direct label-free real time protein detection,” Sens. Actuators, B 177, 848–855 (2013). 10.1016/j.snb.2012.11.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Miller P. R. et al. , “Multiplexed microneedle-based biosensor array for characterization of metabolic acidosis,” Talanta 88, 739–742 (2012). 10.1016/j.talanta.2011.11.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ganesan A. V. et al. , “MEMS based microfluidic system for HIV detection,” in 2013 13th IEEE International Conference on Nanotechnology (IEEE-NANO 2013) (IEEE, 2013). [Google Scholar]
- 68.Windmiller J. R. et al. , “Microneedle array-based carbon paste amperometric sensors and biosensors,” Analyst 136(9), 1846–1851 (2011). 10.1039/c1an00012h [DOI] [PubMed] [Google Scholar]
- 69.Ruiz-Valdepeñas Montiel V. et al. , “Delayed sensor activation based on transient coatings: Biofouling protection in complex biofluids,” J. Am. Chem. Soc. 140(43), 14050–14053 (2018). 10.1021/jacs.8b08894 [DOI] [PubMed] [Google Scholar]
- 70.Yeung C. et al. , “A 3D-printed microfluidic-enabled hollow microneedle architecture for transdermal drug delivery,” Biomicrofluidics 13(6), 064125 (2019). 10.1063/1.5127778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Guo M. et al. , “Shark tooth-inspired microneedle dressing for intelligent wound management,” ACS Nano 15(9), 15316–15327 (2021). 10.1021/acsnano.1c06279 [DOI] [PubMed] [Google Scholar]
- 72.Jahanbin A. and Goodarzi M., Mathematical Modeling for Nanofluids Simulation: A Review of the Latest Works (IntechOpen, 2016). [Google Scholar]
- 73.White F. M., Fluid Mechanics, 8th ed. (McGraw Hill, 2016), p. 773. [Google Scholar]
- 74.Zahn J. D., Trebotich D., and Liepmann D., “Microdialysis microneedles for continuous medical monitoring,” Biomed. Microdevices 7(1), 59–69 (2005). 10.1007/s10544-005-6173-9 [DOI] [PubMed] [Google Scholar]
- 75.Rezapour Sarabi M. et al. , “Machine learning-enabled prediction of 3D-printed microneedle features,” Biosensors 12(7), 491 (2022). 10.3390/bios12070491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Donnelly R. F. et al., Microneedle-mediated Transdermal and Intradermal Drug Delivery (Wiley, 2012). [Google Scholar]
- 77.Chua B. et al. , “Effect of microneedles shape on skin penetration and minimally invasive continuous glucose monitoring in vivo,” Sens. Actuators, A 203, 373–381 (2013). 10.1016/j.sna.2013.09.026 [DOI] [Google Scholar]
- 78.Jung J. H. and Jin S. G., “Microneedle for transdermal drug delivery: Current trends and fabrication,” J. Pharm. Investig. 51(5), 503–517 (2021). 10.1007/s40005-021-00512-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.McGrath M. G. et al. , “Determination of parameters for successful spray coating of silicon microneedle arrays,” Int. J. Pharm. 415(1-2), 140–149 (2011). 10.1016/j.ijpharm.2011.05.064 [DOI] [PubMed] [Google Scholar]
- 80.Amalraju D. and Dawood A., “Mechanical strength evaluation analysis of stainless steel and titanium locking plate for femur bone fracture,” Eng. Sci. Technol., An Int. J. 2(3), 381–388 (2012). [Google Scholar]
- 81.Bodhale D. W., Nisar A., and Afzulpurkar N., “Structural and microfluidic analysis of hollow side-open polymeric microneedles for transdermal drug delivery applications,” Microfluid. Nanofluid. 8(3), 373–392 (2010). 10.1007/s10404-009-0467-9 [DOI] [Google Scholar]
- 82.White F. M., Viscous Fluid Flow, 3rd ed. (McGraw Hill, 2006), p.. 629. [Google Scholar]
- 83.Stoeber B. and Liepmann D., “Fluid injection through out-of-plane microneedles,” in 1st Annual International IEEE-EMBS Special Topic Conference on Microtechnologies in Medicine and Biology. Proceedings (Cat. No. 00EX451) (IEEE, 2000). [Google Scholar]
- 84.Trebotich D., Zahn J., and Liepmann D., “Complex fluid dynamics in BioMEMS devices: Modeling of microfabricated microneedles,” in Proceedings of the 2002 International Conference Modeling Simulation Microsystems, San Juan, Puerto Rico (Citeseer, 2002). [Google Scholar]
- 85.Zahn J. D. et al. , “Microfabricated polysilicon microneedles for minimally invasive biomedical devices,” Biomed. Microdevices 2(4), 295–303 (2000). 10.1023/A:1009907306184 [DOI] [Google Scholar]
- 86.Stone H. A., Stroock A. D., and Ajdari A., “Engineering flows in small devices: Microfluidics toward a lab-on-a-chip,” Annu. Rev. Fluid Mech. 36(1), 381–411 (2004). 10.1146/annurev.fluid.36.050802.122124 [DOI] [Google Scholar]
- 87.Zoudani E. L. and Soltani M., “A new computational method of modeling and evaluation of dissolving microneedle for drug delivery applications: Extension to theoretical modeling of a novel design of microneedle (array in array) for efficient drug delivery,” Eur. J. Pharm. Sci. 150, 105339 (2020). 10.1016/j.ejps.2020.105339 [DOI] [PubMed] [Google Scholar]
- 88.Kim K. S., Ita K., and Simon L., “Modelling of dissolving microneedles for transdermal drug delivery: Theoretical and experimental aspects,” Eur. J. Pharm. Sci. 68, 137–143 (2015). 10.1016/j.ejps.2014.12.008 [DOI] [PubMed] [Google Scholar]
- 89.Mansoor I. et al. , “A microneedle-based method for the characterization of diffusion in skin tissue using doxorubicin as a model drug,” Biomed. Microdevices 17(3), 1–10 (2015). 10.1007/s10544-015-9967-4 [DOI] [PubMed] [Google Scholar]
- 90.Wu L. et al. , “Characterization method for calculating diffusion coefficient of drug from polylactic acid (PLA) microneedles into the skin,” J. Drug Deliv. Sci. Technol. 61, 102192 (2021). 10.1016/j.jddst.2020.102192 [DOI] [Google Scholar]
- 91.Olatunji O., Das D. B., and Nassehi V., “Modelling transdermal drug delivery using microneedles: Effect of geometry on drug transport behaviour,” J. Pharm. Sci. 101(1), 164–175 (2012). 10.1002/jps.22736 [DOI] [PubMed] [Google Scholar]
- 92.Deen W. M., “Hindered transport of large molecules in liquid-filled pores,” AIChE J. 33(9), 1409–1425 (1987). 10.1002/aic.690330902 [DOI] [Google Scholar]
- 93.Hansen S. et al. , “In-silico model of skin penetration based on experimentally determined input parameters.: Part I: Experimental determination of partition and diffusion coefficients,” Eur. J. Pharm. Biopharm. 68(2), 352–367 (2008). 10.1016/j.ejpb.2007.05.012 [DOI] [PubMed] [Google Scholar]
- 94.Heisig M. et al. , “Non steady-state descriptions of drug permeation through stratum corneum. I.: The biphasic brick-and-mortar model,” Pharm. Res. 13(3), 421–426 (1996). 10.1023/A:1016048710880 [DOI] [PubMed] [Google Scholar]
- 95.Frederick Frasch H. and Barbero A. M., “Steady-state flux and Lag time in the stratum corneum lipid pathway: Results from finite element models,” J. Pharm. Sci. 92(11), 2196–2207 (2003). 10.1002/jps.10466 [DOI] [PubMed] [Google Scholar]
- 96.Beyhaghi S. et al. , “Wicking and evaporation of liquids in porous wicks: A simple analytical approach to optimization of wick design,” AIChE J. 60(5), 1930–1940 (2014). 10.1002/aic.14353 [DOI] [Google Scholar]
- 97.Nannan L. and Jing C., “Characterization of fluid resistance in nanostructured TiO2 (NST) film,” in The 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems (IEEE, 2013). [Google Scholar]
- 98.Cahill E. M. et al. , “Metallic microneedles with interconnected porosity: A scalable platform for biosensing and drug delivery,” Acta Biomater. 80, 401–411 (2018). 10.1016/j.actbio.2018.09.007 [DOI] [PubMed] [Google Scholar]
- 99.Shrestha P. and Stoeber B., “Imaging fluid injections into soft biological tissue to extract permeability model parameters,” Phys. Fluids 32(1), 011905 (2020). 10.1063/1.5131488 [DOI] [Google Scholar]
- 100.Rezapour Sarabi M., Nakhjavani S. A., and Tasoglu S., “3D-Printed microneedles for point-of-care biosensing applications,” Micromachines 13(7), 1099 (2022). 10.3390/mi13071099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Dsouza L., Ghate V. M., and Lewis S. A.. “Derma rollers in therapy: The transition from cosmetics to transdermal drug delivery,” Biomed. Microdev. 22(4), 77 (2020). 10.1007/s10544-020-00530-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Pommella A. et al. , “Dynamic behaviour of multilamellar vesicles under Poiseuille flow,” Soft Matter 13(37), 6304–6313 (2017). 10.1039/C7SM00867H [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.