Abstract
Adapting flexibly to changing circumstances is guided by memory of past choices, their outcomes in similar circumstances, and a method for choosing among potential actions. The hippocampus (HPC) is needed to remember episodes, and the prefrontal cortex (PFC) helps guide memory retrieval. Single-unit activity in the HPC and PFC correlates with such cognitive functions. Previous work recorded CA1 and mPFC activity as male rats performed a spatial reversal task in a plus maze that requires both structures, found that PFC activity helps reactivate HPC representations of pending goal choices but did not describe frontotemporal interactions after choices. We describe these interactions after choices here. CA1 activity tracked both current goal location and the past starting location of single trials; PFC activity tracked current goal location better than past start location. CA1 and PFC reciprocally modulated representations of each other both before and after goal choices. After choices, CA1 activity predicted changes in PFC activity in subsequent trials, and the magnitude of this prediction correlated with faster learning. In contrast, PFC start arm activity more strongly modulated CA1 activity after choices correlated with slower learning. Together, the results suggest post-choice HPC activity conveys retrospective signals to the PFC, which combines different paths to common goals into rules. In subsequent trials, prechoice mPFC activity modulates prospective CA1 signals informing goal selection.
SIGNIFICANCE STATEMENT HPC and PFC activity supports cognitive flexibility in changing circumstances. HPC signals represent behavioral episodes that link the start, choice, and goal of paths. PFC signals represent rules that guide goal-directed actions. Although prior studies described HPC–PFC interactions preceding decisions in the plus maze, post-decision interactions were not investigated. Here, we show post-choice HPC and PFC activity distinguished the start and goal of paths, and CA1 signaled the past start of each trial more accurately than mPFC. Postchoice CA1 activity modulated subsequent PFC activity, so rewarded actions were more likely to occur. Together, the results show that in changing circumstances, HPC retrospective codes modulate subsequent PFC coding, which in turn modulates HPC prospective codes that predict choices.
Keywords: CA1, learning, mPFC
Introduction
Adapting to changing circumstances requires cognitive flexibility, the ability to compare and switch among different concepts (Magnusson and Brim, 2014). Cognitive flexibility entails recalling past choices and outcomes in similar circumstances and selecting among available options and potential outcomes in the present. In nonhuman animals, cognitive flexibility is demonstrated by differential responses to identical cues according to internal or external context (Scott, 1962). This behavioral flexibility often depends on abilities supported by the hippocampus (HPC) and prefrontal cortex (PFC; Rich and Shapiro, 2009; Eagle et al., 2016; Place et al., 2016).
Episodic memory for behavioral episodes helps guide cognitive flexibility. In people, episodic memories represent past experiences in spatial and personal context (Tulving, 1983) and is impaired by damage to the HPC (Scoville and Milner, 1957). In nonhuman animals, including rats, HPC damage impairs episodic-like memory (Clayton and Dickinson, 1998), for example, remembering where food was found recently (Ferbinteanu and Shapiro, 2003; Avigan et al., 2020). Neuronal activity in the rat HPC supports episodic-like memory. HPC single units fire in place fields, local patches within specific environments (O'Keefe and Dostrovsky, 1971), and ∼30 HPC units predict a the environmental location of a rat to within 2 cm2 (Wilson and McNaughton, 1993). Beyond location, HPC unit activity distinguishes episodic-like memory demands (Frank et al., 2000; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Ferbinteanu et al., 2006). HPC units with place fields in a plus maze start arm demonstrate prospective coding, firing at different rates that predict the goal choice of a rat (Ferbinteanu and Shapiro, 2003; Ferbinteanu et al., 2006). Units with fields in the goal arms show retrospective coding by firing at different rates depending on the starting location of the rodent. HPC cells thereby signal paths, spatiotemporal trajectories that link the start and end of behavioral episodes (Ferbinteanu and Shapiro, 2003).
Rules that differentiate responses to identical stimuli contribute to cognitive flexibility by distinguishing task features that predict choice outcomes. Damage to the PFC in humans impairs rule switching, for example, in the Wisconsin Card sorting task (Janowsky et al., 1989). In rodents, medial PFC (mPFC) dysfunction impairs tasks with analogous demands (Rich and Shapiro, 2007; Guise and Shapiro, 2017). mPFC activity reflects such rule computation in single-unit firing patterns that vary, for example, with egocentric and spatial response strategies (Rich and Shapiro, 2009).
Frontotemporal interactions may support cognitive flexibility by integrating rules with episodic memories. In the start arms of a spatial memory task that requires both structures, PFC rules helped select HPC prospective codes before choices, as though guiding memory retrieval (Guise and Shapiro, 2017). We hypothesized that after choices, frontotemporal interactions could guide reversal learning, for instance, by signaling the current goal. Both CA1 and mPFC ensembles recorded after choices discriminated the current goal accurately. CA1 signaled path starts more accurately than PFC, and predicted both PFC prospective coding in subsequent trials and reversal learning speed. After choices, HPC signals may convey the starts of different paths to the same goal to the mPFC, which combines these into rules. In subsequent trials, PFC rules help activity HPC path codes that inform decision-making.
Materials and Methods
Behavioral physiology
The behavioral and physiological results reported here describe new analyses of data collected previously (Guise and Shapiro, 2017). The next sections summarize key details of the behavioral and electrophysiological approach.
Maze apparatus
Behavior testing and recording was performed on a matte black-painted elevated plus maze (64 × 6.5 cm) and waiting platform centered in a room decorated with high-contrast posters. The maze was fitted with purpose-built infrared emitter/sensor pairs interfaced with a PC via a NI-DAQ 6008 (National Instruments) to log animal responses (Guise and Shapiro, 2017).
Behavior training
Animals were introduced to the behavioral testing room after handling. Male rats were first exposed to a waiting platform covered with chocolate sprinkles. Once the rat consumed all the food, the rat was then placed in the north start arm facing away from the choice point and allowed to explore the maze until all the food in both goal arms was consumed. The rat was returned to the waiting platform, and the goal arms were rebaited. After ∼1 min, the rat was then placed in the south start arm of the maze and allowed to explore the maze until all the food in both goal arms was consumed. The rat was then returned to the waiting platform for ∼1 min and then returned to its home cage. Training on the behavioral tasks started the next day (Guise and Shapiro, 2017).
Spatial memory task
Rats were trained to perform a spatial memory task that requires CA1 function. In each trial, a goal arm was baited with food. Afterward, a rat was taken from the waiting platform and placed in a pseudorandomly chosen start arm. The rat was allowed to enter a goal arm and was then returned to the waiting platform. The same goal arm was rewarded throughout a block of trials while the rat learned to apply one of two mutually exclusive rules to find food (either go East or go West). After a correct choice, a rat was allowed to consume the food reward before it was returned to the waiting platform. Errors were counted when a rat placed all four paws into the nonrewarded goal arm. During the first three trials of a block, a rat was allowed to self-correct; otherwise, the trial ended when the rat reached the end of the incorrect goal arm or attempted to turn around. After the rat got 10 of the last 12 consecutive trials correct, the reward contingencies were reversed, and the animal learned to use the opposite rule to find food. The procedure was repeated until animals completed ∼50 trials. Rats were trained in the task until they performed at or above 80% accuracy for three of four consecutive training days (Guise and Shapiro, 2017).
Electrophysiology
Hyperdrive implants and tetrode lowering
Custom hyperdrives with 24 independently movable tetrodes were used for recording. Tetrodes were spun from 12.5 μm nichrome wire (Kanthal Precision Technologies), loaded into the hyperdrive, and cut and goldplated until the impedance on each wire was ∼200 kΩ measured at 1000 Hz. During implantation, an electrode interface board (EID 2624TT, Neuralynx) was connected via 0.003 inch stainless steel wire to four ground screws distributed across the skull and two reference screws above the cerebellum (CA1, AP −3.6, ML 2.0; mPFC, AP 3.0, ML 0.5). Tetrodes were lowered 1.4 mm into the cortex after surgery and, following a 1 week waiting period, advanced slowly (μm/day) toward the recording target. Tetrodes reached CA1 and mPFC after ∼2.5–3 weeks. Proximity of CA1 tetrodes to the pyramidal cell layer was estimated by sharp wave-ripple (SWR) profiles (Csicsvari et al., 1999; Guise and Shapiro, 2017); tetrodes were lowered into the mPFC by turning the Microdrive screw 10.6–14.2 times. To ensure recording stability, tetrodes were not adjusted for at least 24 h before behavioral testing and recording (Guise and Shapiro, 2017).
Recording apparatus
Multiunit neuronal activity and local field potentials (LFPs) were acquired using a Digital Lynx SX system (Neuralynx) with an electrode interface board. Tetrodes were connected to a head stage with unit gain amplifiers to minimize cable motion artifact.
Unit activity was filtered between 600 and 9000 Hz and digitized at 32 kHz before online spike detection. Amplitude thresholds were manually set per tetrode to maximize the signal-to-noise ratio for spike detection. When the amplitude on a single wire exceeded the threshold, the waveform around the crossing and timestamp were saved. Waveforms were later sorted off-line into individual units. LFP signals were sampled continuously at 2 kHz with a bandpass filter (1–512 Hz) and were recorded with the active electrode referenced directly to a skull screw (Guise and Shapiro, 2017).
Animal position was recorded using an overhead video camera (digitized at ∼30 Hz), which tracked LED lights mounted on the head stage. LED positions were converted to timestamped X Y coordinates and stored for off-line analysis (Guise and Shapiro, 2017).
Behavioral and recording analyses
General behavior analyses
Maze behavior was categorized into four possible journey types—northwest (NW), northeast (NE), southwest (SW), and southeast (SE). Running speed was assessed on a trial-by-trial basis to generate a distribution of velocities at each point on the maze. Positions on the maze within a trial in which the speed of an animal fell outside 2 SDs of the mean for that position were removed from subsequent analyses (Guise and Shapiro, 2017).
Spike sorting
Spikes recorded on individual tetrodes were clustered into functional units assuming single neurons as the putative sources. Waveform shape and relative amplitude parameters were used to define the basis for a space in which clustering was performed. Semiautomatic clustering was performed as follows: (1) KlustaKwik (Kadir et al., 2014) was first used to cluster the detected parameters, (2) noise clusters were manually rejected, (3) the remaining data were automatically clustered again, and then (4) edited to identify well-segregated clusters of spikes. The well-segregated clusters were assigned to functional units (Guise and Shapiro, 2017).
Local field potentials
LFPs were segmented into single-trial epochs and marked as usable on a per-trial basis. For each ensemble, one tetrode from mPFC and CA1 was used for analysis by the proportion of usable trials and number of recorded units. For CA1, LFPs showing sharp waves with positive deflections were selected to ensure fair comparisons of theta phase across recording. After rereferencing, the LFPs were again bandpass filtered (2–250 Hz) for further analysis (Guise and Shapiro, 2017).
Neuronal ensemble and unit counts
The results below are based on eight simultaneously recorded CA1 and mPFC ensembles (CA1, mean = 61 units/ensemble, 488 units total; mPFC, mean = 28 units/ensembles, 224 units total) from three different rats (Table 1).
Table 1.
Rat from which each ensemble was recorded, and number of CA1 and mPFC units per ensemble
| Ensemble | Rat | CA1 units | mPFC units |
|---|---|---|---|
| 1 | 1 | 53 | 37 |
| 2 | 1 | 69 | 28 |
| 3 | 1 | 60 | 23 |
| 4 | 2 | 63 | 24 |
| 5 | 2 | 61 | 31 |
| 6 | 2 | 62 | 25 |
| 7 | 3 | 55 | 26 |
| 8 | 3 | 65 | 30 |
Eight ensembles from 3 different male rats consisting of an average of 61 CA1 and 28 mPFC units were used in the analyses.
Operational definition of learning and calculating learning rate
To determine how well animals learned which goal was being rewarded, we derived learning curves using the Smith expectation-maximization algorithm (Smith et al., 2004). The Smith algorithm uses all trial outcomes during a learning epoch to calculate the probability (with confidence intervals) that a rodent will select the rewarded goal during a specific trial. We found the first trial at which the Smith algorithm predicted with 95% confidence that the animal would select the correct goal with a probability >50%. This trial and subsequent trials during a single learning epoch were classified as stable performance. Preceding trials were classified as early learning. These operational definitions categorized single trials for physiological analyses to compare interactions between the mPFC and CA1 during standardized levels of learning and stable performance.
The learning speed/rate during a single contingency block was defined as the inverse of the percentage of the contingency block elapsed before the animal achieved stable performance, that is, total number of trials/number of early learning trials in the contingency block. To determine animal learning speed across a session, the contingency block learning speed was averaged across all contingency blocks during the day of testing.
Goal arm population vectors
For each testing session, ensembles of CA1 and mPFC single units were represented as arrays of population vectors (PVs). Each PV described ensemble activity in a single trial, and each element of a PV was based on the mean firing rate of one unit. PVs recorded as the rat moved through the 2D maze were converted into 128 cm linearized paths, and spiking in a 57 cm segment of the linearized path (71–128 cm of the linearized path) described neural activity in the goal arm. PV arrays were z-score normalized across trials and smoothed with a Gaussian of one trial SD. Smoothing was conducted on a per-neuron basis across trials by padding the trialwise rate vector with a time-reversed copy of itself, interpolating data from missing trials because of poor video tracking, and the resulting padded vector was convolved with the Gaussian by multiplication in the frequency domain and then transformed back to the time domain. The padded portion and interpolated elements were then discarded. Per-trial rate vectors were then normalized to unit length (Guise and Shapiro, 2017).
Ensemble coding and the kernel trick
To assess the similarity of neural representations over the course of learning, we measured the correlation of PVs in all pairs of trials recorded in a session. Correlation was defined by the pairwise dot product of nonlinear rate vectors, and expanded using a third-order inhomogeneous polynomial kernel (Schölkopf, 2001; Schölkopf and Smola, 2003), which included the similarity among rate vectors comprising unit firing rates and unit pair and triplet interactions. CA1 and mPFC ensembles were analyzed separately. Past work analyzed only start arms PVs, and the current work replicated and extended the analyses to goal arm PVs.
Support vector machines
We used support vector machines (SVMs) to quantify the extent to which CA1 and mPFC ensembles recorded in the goal arms (71–128 cm of the linearized path) decoded current and past locations. Goal arm activity consisted of firing rate PVs of the raw firing rate of each unit normalized by unit across trials and then normalized to unit length per trial. Separate SVMs were trained using either CA1 or mPFC activity to categorize trials by the goal arm, either East or West, that is, the current location of the rat; other SVMs categorized the same trials as having started in either the North or South, or the past starting location of the rat. Each SVM was trained using a leave-one-out approach (Cheng et al., 2017; Guise and Shapiro, 2017), and model accuracy was defined as the percentage of accurate classifications of the held-out trial.
To determine whether SVMs were predicting locations by discovering task structure or unrelated noise, we repeated the above procedure using the same input feature data with shuffled trial labels. The prediction accuracy of each model was determined on the testing sets following 1000 separate shuffles of the data to determine whether observed decoding exceeded chance via permutation testing. CA1 and mPFC model decoding accuracy was compared using ANOVA.
Start and goal spatial information per population vector
To determine whether differences in CA1 and mPFC SVM decoding accuracy were because of differences in the information content of CA1 and mPFC PVs or merely a function of ensemble size, we calculated total spatial information, start arm information, and goal arm information of each CA1 and mPFC unit. We used the information theoretic approach previously described by Skaggs et al. (1992, 1996) and calculated information as follows:
where the spatial information is measured as bits/spike, a = 1, 2, … N is the number of nonoverlapping spatial bins in the environment, π refers to the occupancy probability of bin a, λa is the mean firing rate of the unit in bin a, and λ is the overall mean firing rate of the unit across all the bins. To calculate the start arm information, we only considered bins from either the North or South start arm of the plus maze, and similarly, to calculate goal arm information, we only included bins from either the East or West goal arm in the above formulation.
We then calculated the start arm information and goal arm information in the CA1 and mPFC goal arm population vector in each trial by multiplying the number of spikes from each unit by its information per spike. We summed these totals and normalized by ensemble unit count. More precisely, the normalized start and goal information was calculated as follows:
where Z is the number of units in the population, IStart,u is the start arm information for unit u, IGoal,u is the goal arm information for unit u, and Nu is the number of spikes unit u fires.
We compared the normalized start arm information and goal arm information between CA1 and mPFC population vectors using Mann–Whitney U testing.
Bayesian decoding of position
To investigate PV representations of task-relevant information, we used Bayesian linear regression. Bayesian regression uses PVs as input to a look-up table based on mean firing rate maps of the maze and calculates the probability that the rat occupies each location in the maze. We used Bayesian regression to generate spatiotemporal representations of the path of a rodent through the plus maze using 33 ms PVs. Each 33 ms PV consisted of unit firing rates (normalized to unit length). Each PV was augmented by including correlated activity between pairs of units. Correlated activity was calculated by dividing each 33 ms time slice into 16 bins of 2 ms. For each unit, a bin had a value of one if a spike occurred or zero if not. Pearson's r was calculated between each pair of units using these 16 bins, and the r values were appended to the end of the rate PV. For a 10 unit ensemble, a single 33 ms input vector would have a length of 55–10 firing rates normalized to unit length followed by 45 r values corresponding to pairwise coactivity between each pair of units. From these PVs, we predicted position using Bayesian linear regression model of the following form:
where Y is the position vector (x position in cm, y position in cm), X is the 33 ms PV, and B is a coefficient matrix of size unit count × 2, and E is an intercept vector of length 2. Priors were estimated using the mean firing rate of all units and the average position of the rodent during task performance, from start to goal arm and reward consumption, for all trials in each testing session. Fitted models were validated via a leave-one-out probability integral transform that performs marginal checks on all model parameters (coefficient and intercept terms) to ensure they fit a normal distribution, as expected with an appropriately dispersed Gaussian regression model. For each session, we used the fitted model to estimate the position of the rat for each 33 ms augmented PV in each 2 × 2 cm bin throughout the maze. We defined the decoded current location of the animal as the integrated probability of the rat being within 10 cm of the video tracking coordinates.
Prospective and retrospective decoding
Prospective decoding was defined by the probability that a rat occupied a correct goal arm based on neuronal activity recorded in a start arm, for example, the predicted likelihood that the rat was in the East goal arm while it was actually in the North start arm. This delocalized decoding was quantified as the integrated probability that the animal was in the set of 2 × 2 cm bins of the goal arm. Retrospective decoding was defined as the probability that the rat was in the start arm based on PVs recorded while the animal occupied the goal arm, for example, the probability that the predicted location of a rat was in the North start arm while the rat was actually in the East goal arm.
Determining CA1 place fields and mPFC firing fields
CA1 place fields were identified from putative pyramidal cells, defined operationally by firing rate and spike shape and excluded units with firing rates that changed systematically across the recording session (α = 0.05, Spearman's rank correlation coefficient). A firing rate map was constructed for each unit in a session by dividing the plus maze into 1 × 1 cm position bins and calculating the mean firing in each bin. The firing rate bins were smoothed with a Gaussian kernel (s = 3 bins). The smoothed bins were fitted with Gaussian curves centered at the location of each local maximum, and curves that bound a volume <80% of the largest Gaussian curve were discarded. The remaining Gaussian curves defined unit firing fields (Kaufman et al., 2020); the arm with the largest volume defined the North, South, East, West, or Choice Point firing field of the cell. The same approach was used to identify firing fields from single mPFC units.
Identifying sharp wave ripples
For each recording session, one tetrode from mPFC and CA1 was selected for LFP analysis by the proportion of usable trials and the number of recorded units. For CA1, LFPs showing positive-going sharp waves were selected to ensure fair comparison of theta phase across recordings. These LFPs were filtered (2–250 Hz) for further analysis (Buzsáki, 2002; Guise and Shapiro, 2017). Candidate SWR events were extracted from these selected recordings of LFP activity.
Candidate SWR events were detected using a previously developed filter (Karlsson and Frank, 2009). Briefly, peaks in LFP activity were identified from CA1 units. The raw LFP data were bandpass filtered between 150 and 250 Hz (gamma) and 8–14 Hz (theta). The Hilbert transform was then applied on these filtered signals to construct the SWR envelope, smoothed by a Gaussian (s = 4 ms). SWRs were defined as the time periods during which the gamma power of the envelope exceeded 3 SDs of the mean for at least 15 ms on one electrode. Candidate SWRs were further filtered by ensuring animal movement speed was < 2 cm/s during the event, and at least five place cells (described above) fired at least one spike each.
Nonlocal spiking analyses
Prospective and retrospective decoding imply units fire reliably outside their statistically defined place fields. To quantify in and out of field activity, each spike recorded in a trial was classified as either local, when a unit fired within the same arm as its field, or nonlocal when it fired in another arm, for every 33 ms video sample. The percentage of nonlocal spikes was determined by averaging the proportion of nonlocal spikes across all 33 ms periods per trial. Local and nonlocal spiking was analyzed separately for prospective and retrospective epochs, and percentages from CA1 and mPFC ensembles were compared using Mann–Whitney U testing.
To test whether different brain states influenced nonlocal spiking, we found the time periods during which sharp wave-ripples occurred (described above). We then correlated the percentage of nonlocal spiking in CA1 and mPFC during periods of prospective and retrospective decoding with the percentage of the decoding period that consisted of sharp wave-ripples. We then subdivided the periods of prospective and retrospective decoding into ripple and nonripple periods and found the percentage of nonlocal spikes that occurred during ripple and nonripple periods. We compared ripple and nonripple nonlocal spiking percentages between CA1 and mPFC using two-way ANOVA.
Granger prediction analysis
We used Granger prediction analyses to determine whether decoding by one brain area predicted decoding by the other during learning or stable memory performance. Granger prediction analyzes temporally directed statistical relationships between two time series by measuring how well the recent history of one time series predicts current events in a second time series beyond that predicted by the history of the second series alone. The Granger value quantifies this prediction as the log ratio of the residual variances for the model incorporating only the target series and the model incorporating both. Larger Granger values indicate increased gains in prediction by including the second time series (Granger, 1969).
We constructed individual time series of prospective and retrospective decoding from CA1 and mPFC activity recorded in each trial of a session and how well decoding in the previous three trials predicted decoding in the current trial. For example, CA1 prospective decoding in trials 1, 2, and 3 was used to predict mPFC prospective decoding in trial 4. Three trials minimized the Bayesian information criterion, described below, to optimize model fit and parameter number.
To determine whether Granger values exceeded chance, we shuffled the trial order of the nontarget series 1000 times and calculated the Granger value for each shuffle, generating a null distribution. Shuffling eliminates the temporal correspondence between the two series and helps delineate the extent to which any increase in explained variance of the target was produced merely by the number of predictors in the nontarget series.
We assessed the predictive relationships between CA1 prospective decoding on mPFC prospective and retrospective decoding, CA1 retrospective decoding on mPFC prospective and retrospective decoding, and vice versa. We also assessed the relationship between Granger values and learning speed using linear regression.
Selecting optimal granger prediction models
The dependent variable for each observation used in Granger prediction analysis was the similarity of prospective or retrospective decoding of a given trial to that observed at the end of the previous three trials. The number of independent variables (three) was determined by minimizing the Bayes's information criterion (BIC) with respect to trial number. This aided in model selection by balancing model fit with parsimony of model parameters. BIC was calculated as follows:
where n is the number of observations in the model, RSS is the residual sum of squares, and k is the number of parameters in the model, which includes both time series (Guise and Shapiro, 2017).
Statistical analyses
Statistical analyses were conducted using parametric approaches, for example, standard ANOVAs. Nonparametric equivalents to parametric statistical tests were used when appropriate, for instance, comparing model accuracy values with Mann–Whitney U testing or comparing Granger values to chance with permutation testing. All correlations were assessed with Pearson correlations unless otherwise noted.
Data availability
All code was developed in Python 3.7, Anaconda 2019.07, with several open-source libraries (van der Walt et al., 2011; Salvatier et al., 2016; Virtanen et al., 2020). Code is available on request and online at https://github.com/learningandmemorylab/Goal_Arm.
Results
Eight CA1 and mPFC ensembles were recorded simultaneously as rats (N = 3) performed spatial reversals in a plus maze (CA1, mean = 61.0 units/ensemble, total = 488 units; mPFC, mean = 28.0 units/ensemble, total = 224 units; Table 1). Each session included ensemble activity recorded as rats learned an initial spatial discrimination and three reversals. The results describe new analyses of data recorded previously (Guise and Shapiro, 2017).
Goal arm PVs discriminate the goal and predict the start of single trials
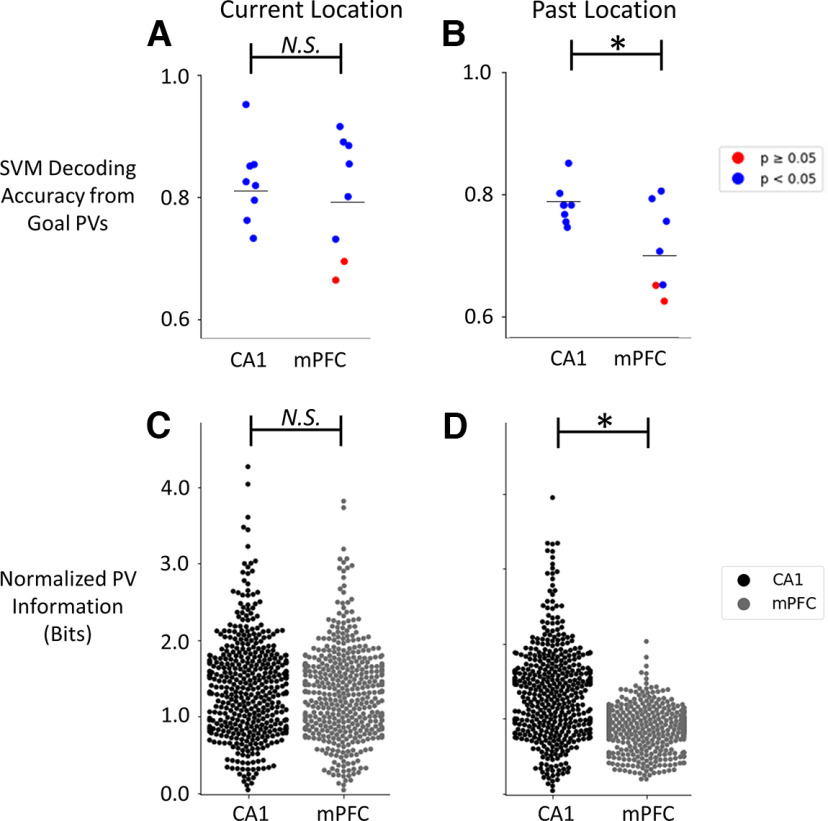
To quantify the extent to which goal arm ensembles reliably predicted task features, we trained SVMs to discriminate the start or goal of each trial. The SVMs trained using the CA1 and mPFC ensembles were sufficient to accurately discriminate the goal and predict the start of each trial. All eight CA1 and six of eight mPFC goal arm PVs discriminated current goal arm locations better than chance (goal arm discrimination, mean percentage correct ± SEM, CA1 = 81.5 ± 2.20%, mPFC = 79.6 ± 3.20%). The proportion of CA1 and mPFC ensembles that accurately discriminated goal arms was similar (Fisher's exact test, CA1 vs mPFC, p = 0.47; Fig. 1A). The same PVs were used to train SVMs to categorize the start arms of each trial to assess retrospective decoding. The same proportion of ensembles predicted the start arm better than chance (start arm prediction, mean percentage correct ± SEM, CA1 = 79.2 ± 1.07%, mPFC = 70.3 ± 2.8%; Fig. 1B), and the proportion of CA1 and mPFC ensembles that accurately predicted start arms was similar (Fisher's exact test, CA1 vs mPFC, p = 0.47; Fig. 1B). CA1 SVMs discriminated current and past locations with similar accuracy, whereas mPFC SVMs discriminated current more accurately than past locations (two-way ANOVA, Brain Region × Maze Location, F(1,28) = 3.61, p = 0.034; Main Effect Region, F(1,28) = 4.23, p = 0.024; Main Effect Location, F(1,28) = 4.84, p = 0.019; Tukey HSD post hoc testing, PFC decoding past location different from all other groups, p < 0.05).
Figure 1.
CA1 and mPFC ensembles signal current and previous locations; CA1 signals previous locations with greater accuracy than mPFC ensembles. A, B, CA1 support vector machines assessed the extent to which CA1 and mPFC population activity recorded in the goal arm signaled current (A) and past (B) locations. All eight CA1 and six of eight mPFC ensembles signaled current location with greater than chance accuracy (A, blue, p < 0.05; red, p ≥ 0.05, permutation testing). mPFC and CA1 current location decoding accuracy was statistically indistinguishable (Mann–Whitney U test; SVM, U = 31.0, p > 0.05). All eight CA1 and six of eight mPFC ensembles signaled past starting locations with greater than chance accuracy (B). CA1 decoded starting locations more accurately than mPFC (Mann–Whitney U test; SVM, U = 15.0, p < 0.05). C, CA1 and mPFC population vectors contained similar amounts of normalized information about the current location in the goal arm (NCA1 = 446 trials, NmPFC = 446 trials; Mann–Whitney U test; normalized goal arm information, U = 94 001.0, p > 0.05). D, mPFC population vectors contained less normalized information about previous start arms than CA1 population vectors (NCA1 = 446 trials, NmPFC = 446 trials; Mann–Whitney U test; normalized start arm information, U = 50 617.0, p < 0.05). Each dot represents one ensemble; gray horizontal lines correspond to the mean decoding accuracy (A, B). Each dot represents the normalized spatial information from a single population vector from one trial (C, D); *p < 0.05, N.S., Not significant (A–D).
The SVMs showed goal arm PVs in each region could, in principle, inform downstream brain areas about the start and goal of paths. CA1 and mPFC categorized goal arms with similar accuracy, but CA1 predicted the start arms more accurately than mPFC (two-way ANOVA; Region × Maze Location; F(1,28) = 3.61, p = 0.034, main effect of Region: F(1,28) = 4.23, p = 0.024, main effect of Maze Location, F(1,28) = 4.84, p = 0.019; Tukey HSD post hoc testing, PFC Decoding of Starts different from all other groups, p < 0.05; Fig. 1A,B). Although goal arm ensembles from each region distinguished the start and goal, CA1 signaled the past start in single trials more accurately than mPFC.
CA1 populations contain more information about starts than mPFC
The SVMs suggest CA1 and mPFC population vectors contain similar amounts of information about goals, but CA1 population vectors contain more information about starts. However, the differences in SVM decoding accuracy could reflect different ensemble sizes; on average, CA1 ensembles had twice the number of units as mPFC ensembles (CA1 vs mPFC units, 61 vs 28). To determine whether differences in SVM decoding accuracy were better attributed to ensemble size or information content signaled by CA1 and mPFC units, we calculated the start arm and goal arm information provided by PVs normalized to ensemble unit count. CA1 signaled spatial information more strongly than mPFC (Spatial Information, mean ± SEM; CA1 PVs = 1.38 ± 0.021, CA1 Single Units = 1.45 ± 0.060, mPFC PVs = 1.10 ± 0.017, mPFC Single Units = 1.15 ± 0.083; two-way ANOVA; Region × Maze Location; F(3,1780) = 83.4, p ≪ 0.01; main effect of Region, F(1,1782) = 106, p ≪ 0.01; main effect of Location, F(1,1782) = 83.6, p ≪ 0.01; Tukey HSD post hoc testing, PFC Normalized Start Information different from all other groups, p < 0.05; Fig. 1C,D).
To compare the extent to which ensemble size and spatial information content contributed to SVM decoding, we determined how well each measure correlated with SVM decoding accuracy. SVM decoding accuracy was not correlated with ensemble size (R2 = 0.157, p = 0.45). However, SVM decoding accuracy correlated with both ensemble-averaged PV and single-unit information (Decoding Accuracy × PV Spatial Information, CA1 Start, R2 = 0.664, p = 0.032; CA1 Goal, R2 = 0.713, p = 0.026; PFC Start, R2 = 0.760, p = 0.021; PFC Goal, R2 = 0.684, p = 0.029; Decoding Accuracy × Unit Spatial Information, CA1 Start, R2 = 0.753, p = 0.022; CA1 Goal, R2 = 0.778, p = 0.019; PFC Start, R2 = 0.806, p = 0.011; PFC Goal, R2 = 0.781, p = 0.014). Spatial information content of single units and ensembles predicted SVM decoding accuracy, whereas ensemble size did not, suggesting that although both CA1 and mPFC distinguish starts and goals, CA1 signals the past start of single trials more strongly than mPFC.
CA1 and mPFC ensembles decode current, past, and future locations
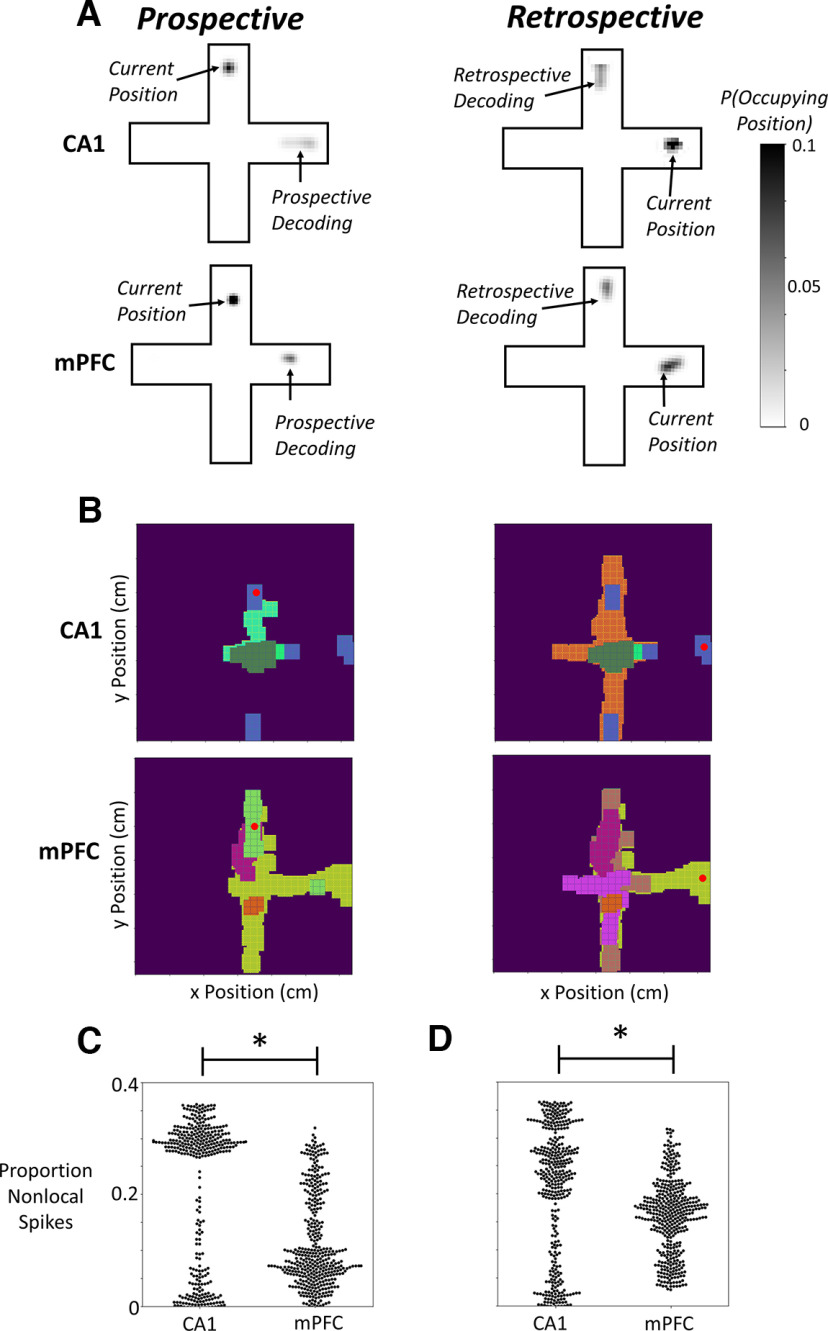
SVM results show that goal arm PVs tracked learning and contained sufficient information to identify the start and discriminate the goal of single trials but do not describe the nature of the coded information. Bayesian regression revealed that CA1 and mPFC ensembles decoded past, present, and future locations (Fig. 2). Each ensemble was described by a separate Bayesian model that computed the probabilities that the rat occupied every maze location every 33 ms of each trial from PVs consisting of single-unit firing rates augmented with pairwise correlations. CA1 (Wilson and McNaughton, 1993) and mPFC (Zielinski et al., 2019) ensembles decoded the current location of the animal (Integrated Probability within 10 cm of Rat Position, current location, PFC = 93.2 ± 0.002%, CA1 = 81.8 ± 0.003%; other maze locations, mPFC = 6.7 ± 0.2%, CA1 = 18.2 ± 0.3%). Because place decoding is modulated by salient task demands (Kelemen and Fenton, 2013), we expected that current maze locations would be decoded simultaneously with other relevant locations and conjectured that task-relevant decoding would differ among brain circuits. For example, mPFC might represent start and goal arms categorically as parts of a task schema, whereas CA1 might associate the start and goal of single trials as episodic boundaries (Bahar et al., 2011; Bahar and Shapiro, 2012).
Figure 2.
Delocalized spiking in CA1 and mPFC contributes to prospective and retrospective decoding in each structure. A, To determine how CA1 and mPFC activity represented the location of the animal in the plus maze, we performed Bayesian decoding of position from CA1 and mPFC activity. The color bar indicates the likelihood of an animal occupying a maze location, with black showing the highest likelihood an animal occupies a specific position. CA1 and mPFC activity recorded in the start arm decoded future goal locations, prospective decoding. Similarly, CA1 and mPFC activity recorded in the goal arm decoded the past locations of the animal, retrospective decoding. B, During periods of both prospective and retrospective decoding, spikes from CA1 and mPFC units with firing fields outside the current location of the animal (red dot) indicated its future goal location during periods of prospective decoding and past starting location during periods of retrospective decoding. Each color in B illustrates the principal firing field of one unit and is not shared across the figure. C, D, CA1 units demonstrated more prospective and retrospective decoding than mPFC units (Mann–Whitney U test, prospective, U = 52 488, p < 0.05; retrospective, U = 56381, p < 0.05). Individual dots in C, D represent single trials; *p < 0.05, N = 446 trials.
To determine whether ensembles categorized arm types, we compared decoding of pairs of corresponding arms (e.g., the start arms) to other maze locations. If PVs categorized start and goal arms, then, for example, PVs recorded in the North arm should decode the South arm, and vice versa, more strongly than other maze locations. We found no evidence that either brain region categorized arm pairs by their task role. Rather, while the animal was in the start arm, PVs from each region decoded the currently occupied start arm more strongly than other start arm and simultaneously decoded nonlocal positions in the goal arms (start arm PVs, p(arm decoding ± SEM) current, same category, all others; CA1, 61.7 ± 0.40%, 0.14 ± 0.14%, 38.2 ± 1.58%; mPFC, 65.3 ± 0.41%, 3.17 ± 0.17%, 31.8 ± 1.9%). Similarly, while the animal was in the goal arm, goal arm PVs decoded the currently occupied goal arm more strongly than the other goal arm and nonlocally decoded the start arms (goal arm PVs, p(arm decoding ± SEM) goal arm PVs, current, same category, all others; CA1, 62.7 ± 1.19%, 2.37 ± 0.35%, 34.9 ± 1.56%; mPFC, 66.5 ± 1.26%, 6.46 ± 0.40%, 27.1 ± 1.86%). CA1 decoded precise locations within occupied arms less accurately than mPFC (CA1 vs mPFC, start = 61.7% vs 65.3%, goal = 62.7% vs 66.5%; two-sample t test, start, t(786) = 6.28, p ≪ 0.01; goal, t(786) = 2.19, p = 0.029). However, CA1 decoded the occupied maze arms throughout a trial more accurately than mPFC when decoding included both current location and either the pending goal or previous starting location [p(occupied locations within a trial ± SEM), start arm PVs, CA1 = 96.1 ± 0.38%, mPFC = 93.2 ± 0.42%; goal arm PVs, CA1 = 93.5 ± 0.29%, mPFC = 91.3 ± 0.32%; ANOVA interaction of brain region × occupied arm, F(3,3140) = 6782.0, p ≪ 0.01; occupied vs unoccupied arms, F(1,3142) = 6640.1, p ≪ 0.01; CA1 vs mPFC, F(1,3142) = 1109.2, p ≪ 0.01]. The more accurate decoding of maze arms suggested CA1 represented locations framed by task structures, places identified as specific starts and goals of paths.
Nonlocal spiking reflects associations between the start and goal arms
If ensembles represent associations between start and goal arms, then the pending goal should be decoded from start arm PVs, and the prior start of each trial should be decoded from goal arm PVs. These patterns are illustrated by decoding maps for CA1 and mPFC PVs (Fig. 2A,B), suggesting that each brain region represented past and future locations within single trials. In the start arm, prospective decoding was quantified as the differential probability that decoded positions were within the chosen versus other goal arm. Start arm PVs in CA1 and mPFC decoded the pending goal, and prospective decoding was stronger in CA1 than mPFC [p(goal decoding ± SEM) pending goal, other goal, CA1 = 34.4 ± 1.64%, 3.8 ± 1.07%; mPFC = 27.9 ± 2.12%, 3.9 ± 1.17%; ANOVA interaction of brain region by decoded goal arm, F(3,1568) = 755.5, p ≪ 0.01; main effect of decoded goal arm, F(1,1570) = 1456.9, p ≪ 0.01; main effect of brain region, F(1,1570) = 140.9, p ≪ 0.01; Mann–Whitney U test, CA1 vs mPFC = 19 078.0, p ≪ 0.01]. In the goal arm, retrospective decoding was quantified as the differential probability that decoded positions were within the actual versus opposite start arm of the trial. Goal arm PVs in CA1 and mPFC decoded the start arms in single trials, and retrospective decoding was stronger in CA1 than mPFC [p(start decoding ± SEM) previous start, other start, CA1 = 30.8 ± 1.01%, 4.1 ± 1.19%; mPFC = 24.8 ± 1.42%, 2.3 ± 0.61%; ANOVA interaction of brain region by decoded start arm, F(3,1568) = 422.3, p ≪ 0.01; main effect of decoded start arm, F(1,1570) = 34.4, p ≪ 0.01; main effect of brain region, F(1,1570) = 650.1, p ≪ 0.01; Mann–Whitney U test, CA1 vs mPFC = 70 397.0, p ≪ 0.01].
Prospective and retrospective decoding imply that nonlocalized spiking—when a unit fires outside of its principal place field (Hok et al., 2007)—associates current locations with either the pending goal or past start of a trial. We therefore quantified the spatial firing field of each unit, counted the number of spikes a unit fired in an arm outside its principal field, and compared the proportion of spikes by units with place fields in corresponding start or goal arms. For example, during a prospective decoding epoch in a start arm, we compared the number of spikes by units with firing fields in the East and West arms. Delocalized spikes were more common in CA1 than mPFC during both prospective and retrospective decoding epochs (mean ± SEM percentage of spikes during decoding epochs, prospective, CA1 = 19.5 ± 0.71%, mPFC = 11.1 ± 0.7%, Mann–Whitney U = 52488, p ≪ 0.01; retrospective, CA1 = 19.4 ± 0.6%; mPFC = 15.9 ± 0.3%, Mann–Whitney U = 56381, p ≪ 0.01; Fig. 2C,D). Nonlocalized spikes in each brain region occurred most often in the pending choice of goal arm or the previously occupied start arm (mean ± SEM percentage of spikes, prospective, chosen vs other goal arm, CA1 = 75.7 ± 7.74%, 24.3 ± 7.74%; mPFC = 76.7 ± 7.75%, 23.3 ± 7.75%; retrospective, previously occupied vs other start arm, CA1 = 74.7 ± 7.32%, 25.3 ± 7.32%; mPFC = 75.5 ± 7.64%, 24.5 ± 7.64%).
Because we defined out-of-field spiking as occurring when a unit fired in an arm different from the arm in which its principal field was located, the results could be influenced by field size. Hence, if CA1 fields extended across fewer maze arms than mPFC, then CA1 units could be more likely to fire out of field. Alternately, if CA1 and mPFC fields extended across a similar number of maze arms, then field size should not influence the observed nonlocal spiking measures. We therefore calculated the proportion of the maze and the number of arms subtended by each CA1 and mPFC principal field. Although CA1 fields were smaller than mPFC fields (percentage of Maze Bound ± SEM, CA1 = 19.0 ± 1.02%, mPFC = 24.3 ± 1.03%; Mann–Whitney U, CA1 vs mPFC, U = 26 782.0, p ≪ 0.01), they subtended similar arm numbers (Number Maze Arms Bound ± SEM, CA1 = 1.33 ± 0.96, mPFC = 1.42 ± 0.107; Mann Whitney U test, CA1 vs mPFC, U = 30 575.0, p = 0.52). Hence, field size was unlikely to influence the results of the nonlocal spiking analysis used here.
Nonlocal spiking in CA1 and mPFC could arise from different functional network states, for example, theta versus ripple states. Because nonlocal spiking is more frequent during ripples than theta network states (Foster and Wilson, 2006; Gupta et al., 2010; Jadhav et al., 2016; Tang et al., 2017; Yu and Frank, 2021), we expected that prospective and retrospective decoding would correlate with nonlocal spiking during ripples. Indeed, prospective and retrospective decoding events were correlated with ripple frequency (Nonlocal Spiking × Ripple Frequency; Prospective Decoding, CA1, R2 = 0.298, p = 0.037; mPFC, R2 = 0.274, p = 0.041; Retrospective Decoding, CA1, R2 = 0.290, p = 0.039; mPFC, R2 = 0.258, p = 0.046).
We then compared the proportion of nonlocal spikes that occurred during ripples and other network states during prospective and retrospective decoding events. As expected, the percentage of nonlocal spiking was higher during ripples in both CA1 and mPFC. Moreover, nonlocal spiking was higher in CA1 than mPFC during both network states (Prospective Decoding Periods, percentage of Nonlocal Spiking ± SEM; CA1 Ripple = 25.9 ± 0.5%, CA1 Nonripple = 7.73 ± 0.14%; mPFC Ripple = 17.1 ± 0.3%, mPFC NonRipple = 4.47 ± 0.15%; two-way ANOVA Region × Ripple Network State, F(3,1780) = 940, p ≪ 0.01; main effect of Region, F(1,1782) = 342, p ≪ 0.01; main effect of Ripple Network State, F(1,1782) = 2458, p ≪ 0.01). Similar results were observed during periods of retrospective decoding; more nonlocal spiking occurred during ripple events in both CA1 and mPFC, and more nonlocal spiking was observed in CA1 than mPFC (Retrospective Decoding Periods, percentage of Nonlocal Spiking ± SEM, CA1 Ripple = 22.5 ± 0.5%, CA1 NonRipple = 7.23 ± 0.18%; mPFC Ripple = 16.7 ± 0.4%, mPFC Nonripple = 5.49 ± 0.06%; two-way ANOVA Region × Ripple Network State, F(3,1780) = 573, p ≪ 0.01; main effect of Region, F(1,1782) = 72.8, p ≪ 0.01; main effect of Ripple Network State, F(1,1782) = 1647, p ≪ 0.01). Nonlocal spiking was more frequent during ripples in both mPFC and CA1.
The magnitude of delocalized spiking associated with prospective and retrospective decoding epochs likely contribute to different spatial decoding accuracy by mPFC and CA1 ensembles. For each single unit, place decoding accuracy varies inversely with the proportion of visited locations that trigger spikes, and out-of-field spiking increases that proportion. CA1 spiking was more delocalized than mPFC overall, but CA1 spatial signals were more accurate than mPFC during epochs without prospective or retrospective decoding (decoding of position in epochs without nonlocal decoding [p(occupied locations within a trial ± SEM); CA1 = 95.0 ± 0.16%, mPFC = 94.3 ± 0.13%; Mann–Whitney U = 66 823.0, p ≪ 0.01]. mPFC nonlocal spiking decoded arbitrary locations more accurately than CA1, but CA1 spiking decoded task-relevant locations more accurately than mPFC.
Prospective and retrospective representations modulate one another within and between brain structures
mPFC and CA1 ensembles decode past, present, and future locations in single trials. To investigate potential interactions between brain regions, we used Granger analyses to quantify the extent to which decoding in one area predicted changes in the other. We first assessed frontotemporal decoding predictions separately in start and goal PVs and found bidirectional interactions in both task phases. Sequences of CA1 prospective decoding changes predicted changes in mPFC prospective decoding and vice versa (permutation testing, additional variance explained, CA1→mPFC = 3.38%, p ≪ 0.01; mPFC→CA1 = 6.55%, p ≪ 0.01; Fig. 3E,F). Similarly, retrospective decoding dynamics in each brain region predicted changes in the other (permutation testing, additional variance explained, CA1→mPFC = 7.07%; p ≪ 0.01; mPFC→CA1 = 5.83%, p ≪ 0.01; Fig. 3E,F). As rats performed spatial reversals, CA1 and mPFC ensembles interacted bidirectionally so that prospective and retrospective decoding dynamics in one structure predicted changes in the other.
Figure 3.
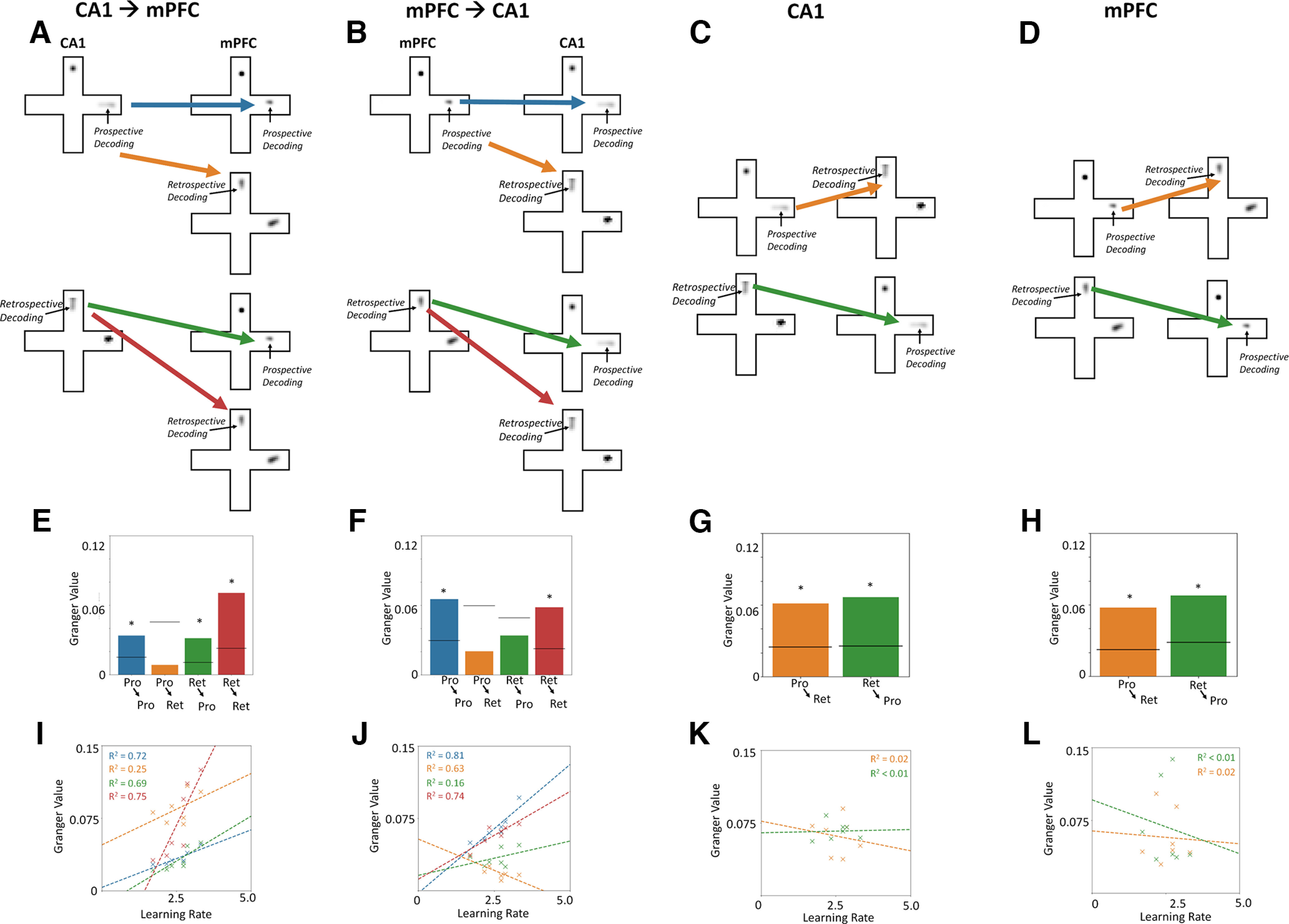
Bidirectional CA1-mPFC prospective and retrospective decoding interactions are correlated with learning, intrastructure interactions are not correlated with learning. A, Frontotemporal interaction schematics, CA1→mPFC. B, mPFC→CA1. Each type of frontotemporal decoding interaction is shown by a colored line; arrows (→) indicate the direction of information flow; blue, Prospective→Prospective; orange, Prospective→Retrospective; green, Retrospective→Retrospective; red, Retrospective→Prospective. C, D, Within-region interaction schematics, C, within CA1. D, Within mPFC. Each type of decoding interaction within a structure is shown by a colored line; orange, Prospective→Retrospective; green, Retrospective→Prospective. E, CA1 prospective decoding modulated mPFC prospective, but not retrospective, decoding (CA1Pro→mPFCPro, Granger value = 3.38%, p < 0.05; CA1Pro→mPFCRet, Granger value = 0.85%, p > 0.05). CA1 retrospective decoding modulated both retrospective and prospective decoding by mPFC (Granger values, CA1Ret→mPFCPro = 3.16%, p < 0.05; CA1Ret→mPFCRet = 7.07%, p < 0.05). F, mPFC prospective decoding modulated prospective, but not retrospective decoding by CA1 (Granger values, mPFCPro→CA1Pro = 6.55%, p < 0.05; mPFCPro→CA1Ret = 2.04%, p > 0.05). mPFC retrospective decoding did not influence current CA1 prospective decoding (mPFCRet→CA1Pro = 3.40%, p > 0.05) but did modulate CA1 retrospective decoding (mPFCRet→CA1Ret = 5.83%, p < 0.01). G, CA1 prospective and retrospective decoding modulated one another (CA1Pro→CA1Ret, Granger value = 6.13%; CA1Ret→CA1Pro, Granger value = 6.66%, p < 0.05). H, mPFC prospective and retrospective decoding modulated one another (mPFCPro→mPFCRet, Granger value = 5.74%; mPFCRet→mPFCPro, Granger value = 6.79%, p < 0.05). I, CA1 modulation of mPFC decoding predicted learning speed in three of four frontotemporal decoding interactions. The magnitude of modulation of CA1 retrospective decoding of mPFC prospective and retrospective decoding predicted learning speed (linear regression of decoding modulation times proportion contingency block complete before criterion, CA1Ret→mPFCPro, R2 = 0.69, p < 0.05; CA1Ret→mPFCRet, R2 = 0.75, p < 0.05). Modulation of CA1 prospective decoding of mPFC retrospective decoding did not vary with learning speed (CA1Pro→mPFCRet, R2 = 0.25, p > 0.05), but modulation of CA1 prospective decoding of mPFC prospective decoding did (CA1Pro→mPFCPro, R2 = 0.72, p < 0.05). J, mPFC prospective and retrospective decoding modulated CA1 prospective decoding and predicted learning speed (mPFCPro→CA1Pro, R2 = 0.81, p < 0.05; mPFCPro→CA1Ret, R2 = 0.63, p < 0.05). mPFC modulation of retrospective decoding of CA1 predicted learning (mPFCRet→CA1Ret, R2 = 0.74, p < 0.05), but mPFC's modulation of CA1 prospective decoding did not (mPFCRet→CA1Pro, R2 = 0.16, p > 0.05). K, L, Learning speed was unrelated to prospective or retrospective decoding interactions within CA1 (K, CA1Pro→CA1Ret, R2 = 0.03, p > 0.05; CA1Ret→CA1Pro, R2 < 0.01, p > 0.05) or mPFC (L, mPFCPro→mPFCRet, R2 < 0.01, p > 0.05; mPFCRet→mPFCPro, R2 = 0.02, p > 0.05). Bar colors in E–H represent the direction of frontotemporal (E, F) or intrastructure (G, H) decoding interactions, blue, Prospective (Pro)→Prospective; orange, Prospective→Retrospective (Ret); green, Retrospective→Prospective; red, Retrospective→Retrospective. Bar heights show the obtained Granger value, black lines represent the upper bound of the 95% confidence interval of the null distribution of Granger values obtained permutations; *p < 0.05. I–L, Individual crosses show the Granger values of single sessions, dashed lines show linear regression lines, and line colors indicate the four interactions as in E–H.
Representations of the past start and future goal modulated one another across trials in both CA1 and mPFC. To assess circuit dynamics that might link the start and goal of behavioral episodes, we analyzed the extent to which changes in prospective and retrospective decoding predicted one another within and between brain structures. Within structures, changes in prospective decoding predicted changes in retrospective decoding and vice versa (permutation testing, additional variance explained, prospective→retrospective, CA1 = 6.13%, p ≪ 0.01; mPFC = 5.74%, p ≪ 0.01; retrospective→prospective, CA1 = 6.66%, p ≪ 0.01; mPFC = 6.79%, p ≪ 0.01; Fig. 3G,H). Of the four potential interactions between both the two brain areas and decoding types, only retrospective decoding changes in CA1 reliably predicted prospective decoding changes in mPFC (additional variance explained = 3.16%; p ≪ 0.01; Fig. 3E,F, orange and green bars). CA1 representation of the recently occupied start arm in one trial predicted changes in mPFC representation of the pending choice at the start of the next trial.
Reversal learning speed covaries with frontotemporal interactions
To determine the extent to which CA1–mPFC interactions varied with learning, we assessed the correlation between Granger values and the proportion of trials required for rats to perform better than chance within each contingency block. The magnitude of bidirectional frontotemporal interactions within the start and goal arms considered separately predicted learning speed (correlation of mean Granger value and learning rate, prospective decoding, CA1→mPFC, R2 = 0.72, p = 0.020; mPFC→CA1: R2 = 0.81, p ≪ 0.01; retrospective decoding, CA1→mPFC: R2 = 0.75, p = 0.029, mPFC→CA1: R2 = 0.74, p = 0.020; Fig. 3I,J, blue and red lines). Interactions between start and goal representations within brain structures were unrelated to learning (Fig. 3K,L). Coordinated, bidirectional frontotemporal activity could support communication between brain areas that represent past episodes and future choices.
Learning in the plus maze requires using current outcomes to make future choices, for example, by associated reward location in one trial with goal prediction in the next trial. If reward location signals conveyed from CA1 to mPFC support these associations, then CA1 activity in the goal arm of one trial should modulate mPFC activity in the start arm of subsequent trials. If CA1 modulation of mPFC is important for learning, then its magnitude should predict learning rate. Changes in CA1 retrospective decoding predicted changes in mPFC prospective decoding, and the Granger value predicted learning speed (correlation of mean Granger value and learning rate, CA1 retrospective→mPFC prospective decoding, R2 = 0.69, p = 0.028; Fig. 3I, green line). Faster learning occurred when CA1 representations of places past predicted subsequent mPFC representations of future goals. In contrast, CA1 prospective decoding changes did not reliably predict changes in mPFC retrospective decoding (Fig. 3E, orange bar), and Granger values did not predict learning (correlation of mean Granger value and learning rate, CA1 prospective→mPFC retrospective, R2 = 0.25, p = 0.19; Fig. 3I, orange line). In other words, CA1 representations of recent start locations predicted subsequent mPFC representations of future goals, but CA1 representations of future goals did not predict subsequent mPFC representations of recent starts (Fig. 3E, green vs orange bars). mPFC retrospective decoding did not predict CA1 prospective decoding (Fig. 3F, green bar), nor did its magnitude predict learning rate (mPFC retrospective→CA1 prospective decoding, R2 = 0.16, p = 0.12; Fig. 3J). Although mPFC prospective decoding did not reliably predict changes in CA1 retrospective decoding (Fig. 3F, orange bar), the Granger magnitude inversely predicted learning rate (mPFC prospective→CA1 retrospective decoding, R2 = 0.63, p < 0.05; Fig. 3J, orange line). Learning was impaired to the extent that mPFC representations of future goals modulated subsequent CA1 representations of recent starts.
Discussion
CA1 and mPFC neuronal ensembles were recorded as rats performed a spatial memory task in a plus maze that requires both structures. Ensemble activity in each structure predicted pending choices and signaled recent start locations. In both structures, bidirectional associations between start and goal arm representations were decoded and accompanied by out-of-field spiking, when units with place fields in a goal arm fired wile the rat was in the start arm and vice versa. Activity in each structure modulated the other, and the interactions affected learning rate. Across successive trials, faster learning was predicted by mPFC modulation of CA1 in the start arm, and by CA1 activity in the goal arm that modulated mPFC at the start of subsequent trials. Learning was impaired, however, by mPFC start arm activity that modulated CA1 goal arm activity.
The results replicate and extend previous findings on bidirectional frontotemporal interactions that guide flexible cognition. Before the choice point, both structures tracked reversal learning, and mPFC signals improved subsequent goal prediction by CA1 (Guise and Shapiro, 2017). The results described here show both structures also track learning after the choice point, when CA1 signals improve subsequent goal prediction by mPFC. Together, the results suggest how bidirectional and temporally ordered frontotemporal interactions could guide decision-making. After a rat chooses a goal, HPC representations of the behavioral episode are conveyed to the mPFC, which integrates paths to the same goal into representations of abstract rules or goals. At the start of the next trial, mPFC signals activate HPC representations of the appropriate goal-directed episode.
Different forms of augmented population vectors contain similar information
The different analyses used slightly different methods to quantify unit interactions within PVs. The SVM models relied on kernel-expanded population vectors, whereas the Bayesian modeling used population vectors augmented with pairwise cross-correlations between unit spike trains. As described in the results, the same general pattern was obtained with both methods, suggesting that interactions between units contribute to robust CA1 and mPFC population-level coding.
Goal arm ensembles track reversal learning
CA1 and mPFC ensemble dynamics signaled overlapping but distinct task features. Although activity in each structure discriminated past, present, and future task epochs, both SVM and information analyses found CA1 PVs recorded in the goal arm discriminated starting locations more accurately than mPFC (Fig. 1). Whereas CA1 distinguished the full temporal extent of behavioral episodes, mPFC grouped spatially and temporally separate paths to the same goal.
Nonlocal representations did not emphasize differential single-unit firing
Individual CA1 and mPFC ensembles represented the future goal and past start of single trials decoded from 33 ms PVs. The present analyses averaged activity across the entire start arm (prospective) or goal arm (retrospective) PVs and therefore excluded path selective firing within arms. Hence, a unit firing at the beginning of a start arm for East-going trials and at the end of the start arm on West-going trials would not contribute to our measure of prospective decoding. The new results show CA1 PVs represent past and future locations framed by task structure, discriminating the starts and goals of specific paths.
Past and future locations are represented by delocalized spiking at gamma time scales
Prospective and retrospective decoding was supported by out-of-field spiking (Fig. 2). As rats began paths in the start arm, prospective decoding occurred as units with primary fields in the goal arm fired. At the end of paths, retrospective decoding occurred as units with primary fields in the start arm fired. Prospective and retrospective decoding accuracy corresponded with the primary fields of nonlocal spikes, and in both brain structures, ∼75% of nonlocal spikes occurred in the maze arms occupied during the trial.
Prospective and retrospective decoding interact within circuits
Plasticity coordinated by delocalized spiking could associate the start and goal of paths by linking prospective and retrospective decoding in each circuit. Prospective and retrospective decoding dynamics predicted one another across trials within CA1 and mPFC ensembles (Fig. 3G,H). If these within-circuit associations were sufficient for learning, then prediction magnitude should vary with learning speed, but it did not (Fig. 3K,L). Rather, learning speed varied with the magnitude of cross-circuit CA1–mPFC decoding interactions. Inactivating or disrupting synaptic plasticity within local circuits impairs learning (Avigan et al., 2020), suggesting within-circuit decoding dynamics are likely necessary for learning. The present results cannot determine the contribution of within-structure dynamics to learning, for example, as prerequisites for frontotemporal interactions, discussed next.
Bidirectional frontotemporal interactions predict learning rate
Specific interactions between mPFC and CA1 within and between task epochs either improved or impaired learning. In the start arm, the magnitude of mPFC modulation of CA1 prospective coding predicted faster subsequent learning (Guise and Shapiro, 2017). mPFC modulation of CA1 prospective decoding also predicted faster learning here (Fig. 3F,J). In contrast, mPFC activity in the start arm slowed learning to the extent that it modulated CA1 retrospective decoding (Fig. 3J). mPFC signals may therefore reduce or increase proactive interference, depending on their effects on CA1. mPFC signals that generalize the two start arms and reduce CA1 retrospective decoding in the goal arm could interfere with path discrimination. In contrast, the magnitude of activity of CA1 goal arm modulation of mPFC predicted faster learning (Fig. 3E,I) perhaps by allowing the mPFC to integrate the different paths to a common goal.
CA1-mPFC decoding interactions quantified here by Granger analyses measured activity changes in trial sequences with single trials based on ∼500 ms PVs separated by ∼10 s, a time scale too coarse to assess subsecond mechanisms of neuronal transmission and plasticity. The statistical prediction could therefore arise from many causal mechanisms, including polysynaptic recurrent signals among extended circuits. However, we observed decoding in gamma-scale intervals that could coordinate spike timing, engage synaptic transmission and plasticity mechanisms, and support activity patterns that link the start and goal of paths within and between mPFC and CA1 circuits.
Such mechanisms could be engaged after goal choice and before the rat consumes reward, the epoch analyzed here, during reward consumption, or both. Reward consumption triggers reverse replay, sequential reactivation of representations of a path from its end in the current goal back to its start (Foster and Wilson, 2006) during HPC sharp wave-ripples (Ramadan et al., 2009; Buzsáki, 2015; Joo and Frank, 2018). Retrospective decoding before consummatory behavior, nonlocalized representations of the starting location while a rodent is in the goal as described here, could initiate synaptic events (Buzsáki, 1989) for replay triggered by subsequent reward. Such a replay could allow reward history to strengthen CA1 retrospective decoding thereby strengthening mPFC prospective codes in subsequent trials. Forward replay, the sequential activity of units with place fields in trajectories from current locations to potential goals (Pfeiffer and Foster, 2013), may play an analogous role in prospective decoding, nonlocalized representation of the goal while the rat is in the start arm. Forward replay that could strengthen sequential associations between start and goal representations in CA1 and mPFC and support prospective decoding (Pfeiffer and Foster, 2013), consistent with mPFC modulation of CA1 prospective decoding that predicts faster learning (Guise and Shapiro, 2017).
The spatial memory task requires several cognitive processes to perform accurately. Although the start arms can be discriminated from environmental cues (Lennartz, 2008; Knierim and Hamilton, 2011), choosing the correct goal requires memory of recent outcomes (Ferbinteanu and Shapiro, 2003). Remembering these outcomes requires communication from CA1 to mPFC after choices. Selectively inactivating CA1 axons terminating on mPFC neurons blocks spatial working memory only when the inactivation occurs in the goal arm (Spellman et al., 2015). Retrieving correct goals requires communication from mPFC to CA1. Inactivating the nucleus reuniens (RE) of the thalamus blocks CA1 prospective decoding (Ito et al., 2015). The RE has reciprocal monosynaptic connections with both the HPC and mPFC, and RE dysfunction impairs performance in tasks that require mPFC-CA1 interactions (Hembrook and Mair, 2011). Inactivating the mPFC with muscimol impairs spatial reversal learning and reduces CA1 prospective coding (Guise and Shapiro, 2017).
Together with previous results, the present study suggests a model for bidirectional mPFC–CA1 interactions that link past and future choices as follows: (1) after a correct choice, CA1 activity in the goal arm includes nonlocalized activity of cells with fields in the recently exited start arm, (2) the decoding epochs trigger reverse replay that consolidates memory for the path (Joo and Frank, 2018) as CA1 firing sequences of CA1 units convey spatiotemporal sequences of past and present locations to the mPFC, and (3) paths sharing common goals are combined into rules (Ito et al., 2015; Guise and Shapiro, 2017). On subsequent trials, mPFC activity triggers CA1 prospective codes that predict the rewarded goal before the rat exits the maze choice point (Ferbinteanu and Shapiro, 2003; Guise and Shapiro, 2017). Further investigation of replay during gamma oscillations and sharp wave-ripples (Jadhav et al., 2012; Tang and Jadhav, 2019) will help evaluate this model.
Footnotes
This work was supported by National Institutes of Health–National Institute of Mental Health Grants 2R01MH073689, MH118297, and MH119523 (M.L.S.) and NVIDIA.
The authors declare no competing financial interests.
References
- Avigan PD, Cammack K, Shapiro ML (2020) Flexible spatial learning requires both the dorsal and ventral hippocampus and their functional interactions with the prefrontal cortex. Hippocampus 30:733–744. 10.1002/hipo.23198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahar AS, Shapiro ML (2012) Remembering to learn: independent place and journey coding mechanisms contribute to memory transfer. J Neurosci 32:2191–2203. 10.1523/JNEUROSCI.3998-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahar AS, Shirvalkar PR, Shapiro ML (2011) Memory-guided learning: CA1 and CA3 neuronal ensembles differentially encode the commonalities and differences between situations. J Neurosci 31:12270–12281. 10.1523/JNEUROSCI.1671-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G (1989) Two-stage model of memory trace formation: a role for “noisy” brain states. Neuroscience 31:551–570. 10.1016/0306-4522(89)90423-5 [DOI] [PubMed] [Google Scholar]
- Buzsáki G (2002) Theta oscillations in the hippocampus. Neuron 33:325–340. 10.1016/s0896-6273(02)00586-x [DOI] [PubMed] [Google Scholar]
- Buzsáki G (2015) Hippocampal sharp wave-ripple: a cognitive biomarker for episodic memory and planning. Hippocampus 25:1073–1188. 10.1002/hipo.22488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng H, Garrick DJ, Fernando RL (2017) Efficient strategies for leave-one-out cross validation for genomic best linear unbiased prediction. J Anim Sci Biotechnol 8:38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton NS, Dickinson A (1998) Episodic-like memory during cache recovery by scrub jays. Nature 395:272–274. 10.1038/26216 [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurkó A, Mamiya A, Buzsáki G (1999) Fast network oscillations in the hippocampal CA1 region of the behaving rat. J Neurosci 19:RC20. 10.1523/JNEUROSCI.19-16-j0001.1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eagle AL, Gajewski PA, Robison AJ (2016) Role of hippocampal activity-induced transcription in memory consolidation. Rev Neurosci 27:559–573. 10.1515/revneuro-2016-0010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferbinteanu J, Kennedy PJ, Shapiro ML (2006) Episodic memory–from brain to mind. Hippocampus 16:691–703. 10.1002/hipo.20204 [DOI] [PubMed] [Google Scholar]
- Ferbinteanu J, Shapiro ML (2003) Prospective and retrospective memory coding in the hippocampus. Neuron 40:1227–1239. 10.1016/s0896-6273(03)00752-9 [DOI] [PubMed] [Google Scholar]
- Foster DJ, Wilson MA (2006) Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440:680–683. 10.1038/nature04587 [DOI] [PubMed] [Google Scholar]
- Frank LM, Brown EN, Wilson M (2000) Trajectory encoding in the hippocampus and entorhinal cortex. Neuron 27:169–178. 10.1016/s0896-6273(00)00018-0 [DOI] [PubMed] [Google Scholar]
- Granger CWJ (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37:424–438. 10.2307/1912791 [DOI] [Google Scholar]
- Guise KG, Shapiro ML (2017) Medial prefrontal cortex reduces memory interference by modifying hippocampal encoding. Neuron 94:183–192.e8. 10.1016/j.neuron.2017.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MAA, Touretzky DS, Redish AD (2010) Hippocampal replay is not a simple function of experience. Neuron 65:695–705. 10.1016/j.neuron.2010.01.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hembrook JR, Mair RG (2011) Lesions of reuniens and rhomboid thalamic nuclei impair radial maze win-shift performance. Hippocampus 21:815–826. 10.1002/hipo.20797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hok V, Lenck-Santini P-P, Roux S, Save E, Muller RU, Poucet B (2007) Goal-related activity in hippocampal place cells. J Neurosci 27:472–482. 10.1523/JNEUROSCI.2864-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito HT, Zhang S-J, Witter MP, Moser EI, Moser M-B (2015) A prefrontal-thalamo-hippocampal circuit for goal-directed spatial navigation. Nature 522:50–55. 10.1038/nature14396 [DOI] [PubMed] [Google Scholar]
- Jadhav SP, Kemere C, German PW, Frank LM (2012) Awake hippocampal sharp-wave ripples support spatial memory. Science 336:1454–1458. 10.1126/science.1217230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav SP, Rothschild G, Roumis DK, Frank LM (2016) Coordinated excitation and inhibition of prefrontal ensembles during awake hippocampal sharp-wave ripple events. Neuron 90:113–127. 10.1016/j.neuron.2016.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janowsky JS, Shimamura AP, Kritchevsky M, Squire LR (1989) Cognitive impairment following frontal lobe damage and its relevance to human amnesia. Behav Neurosci 103:548–560. 10.1037//0735-7044.103.3.548 [DOI] [PubMed] [Google Scholar]
- Joo HR, Frank LM (2018) The hippocampal sharp wave-ripple in memory retrieval for immediate use and consolidation. Nat Rev Neurosci 19:744–757. 10.1038/s41583-018-0077-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadir SN, Goodman DFM, Harris KD (2014) High-dimensional cluster analysis with the masked EM algorithm. Neural Comput 26:2379–2394. 10.1162/NECO_a_00661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MP, Frank LM (2009) Awake replay of remote experiences in the hippocampus. Nat Neurosci 12:913–918. 10.1038/nn.2344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman AM, Geiller T, Losonczy A (2020) A role for the locus coeruleus in hippocampal CA1 place cell reorganization during spatial reward learning. Neuron 105:1018–1026.e4. 10.1016/j.neuron.2019.12.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E, Fenton AA (2013) The organization of neuronal discharge on timescales of milliseconds and seconds is related to the spatial response properties of hippocampal neurons. In: Advances in cognitive neurodynamics (III) (Yamaguchi Y, ed), pp 421–427. Dordrecht, The Netherlands: Springer. [Google Scholar]
- Knierim J, Hamilton D (2011) Framing spatial cognition: neural representations of proximal and distal frames of reference and their roles in navigation. Physiol Rev 91:1245–1279. 10.1152/physrev.00021.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lennartz R (2008) The role of extramaze cues in spontaneous alternation in a plus-maze. Learn Behav 36:138–144. 10.3758/lb.36.2.138 [DOI] [PubMed] [Google Scholar]
- Magnusson KR, Brim BL (2014) The aging brain. In: Reference module in biomedical sciences. Elsevier. https://www.sciencedirect.com/science/article/pii/B9780128012383001586. [Google Scholar]
- O'Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175. 10.1016/0006-8993(71)90358-1 [DOI] [PubMed] [Google Scholar]
- Pfeiffer BE, Foster DJ (2013) Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497:74–79. 10.1038/nature12112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Place R, Farovik A, Brockmann M, Eichenbaum H (2016) Bidirectional prefrontal-hippocampal interactions support context-guided memory. Nat Neurosci 19:992–994. 10.1038/nn.4327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramadan W, Eschenko O, Sara SJ (2009) Hippocampal sharp wave/ripples during sleep for consolidation of associative memory. PLoS One 4:e6697. 10.1371/journal.pone.0006697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich EL, Shapiro M (2009) Rat prefrontal cortical neurons selectively code strategy switches. J Neurosci 29:7208–7219. 10.1523/JNEUROSCI.6068-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich EL, Shapiro ML (2007) Prelimbic/infralimbic inactivation impairs memory for multiple task switches, but not flexible selection of familiar tasks. J Neurosci 27:4747–4755. 10.1523/JNEUROSCI.0369-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvatier J, Wiecki TV, Fonnesbeck C (2016) Probabilistic programming in Python using PyMC3. PeerJ Comput Sci 2:e55. 10.7717/peerj-cs.55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schölkopf B (2001) The kernel trick for distances. In Proceedings of the 13th International Conference on Neural Information Processing Systems (NIPS'00), pp 283–289. Cambridge, MA: MIT. [Google Scholar]
- Schölkopf B, Smola AJ (2003) A short introduction to learning with kernels. In: Advanced lectures on machine learning: machine learning summer school 2002 Canberra, Australia, February 11–22 (Mendelson S, Smola AJ, eds), pp 41–64. Berlin: Springer. [Google Scholar]
- Scott WA (1962) Cognitive complexity and cognitive flexibility. Sociometry 25:405–414. 10.2307/2785779 [DOI] [Google Scholar]
- Scoville WB, Milner B (1957) Loss of recent memory after bilateral hippocampal lesions. J Neurol Neurosurg Psychiatry 20:11–21. 10.1136/jnnp.20.1.11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaggs W, McNaughton B, Gothard K (1992) An information-theoretic approach to deciphering the hippocampal code. In: Advances in neural information processing systems 5, pp 1030–1037. San Francisco: Morgan Kaufmann. [Google Scholar]
- Skaggs WE, McNaughton BL, Wilson MA, Barnes CA (1996) Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6:149–172. [DOI] [PubMed] [Google Scholar]
- Smith AC, Frank LM, Wirth S, Yanike M, Hu D, Kubota Y, Graybiel AM, Suzuki WA, Brown EN (2004) Dynamic analysis of learning in behavioral experiments. J Neurosci 24:447–461. 10.1523/JNEUROSCI.2908-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spellman T, Rigotti M, Ahmari SE, Fusi S, Gogos JA, Gordon JA (2015) Hippocampal-prefrontal input supports spatial encoding in working memory. Nature 522:309–314. 10.1038/nature14445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang W, Jadhav SP (2019) Sharp-wave ripples as a signature of hippocampal-prefrontal reactivation for memory during sleep and waking states. Neurobiol Learn Mem 160:11–20. 10.1016/j.nlm.2018.01.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang W, Shin JD, Frank LM, Jadhav SP (2017) Hippocampal-prefrontal reactivation during learning is stronger in awake compared with sleep states. J Neurosci 37:11789–11805. 10.1523/JNEUROSCI.2291-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulving E (1983) Elements of episodic memory. Oxford UP. [Google Scholar]
- van der Walt S, Colbert SC, Varoquaux G (2011) The NumPy array: a structure for efficient numerical computation. Comput Sci Eng 13:22–30. 10.1109/MCSE.2011.37 [DOI] [Google Scholar]
- Virtanen P, et al. (2020) SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17:261–272. 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL (1993) Dynamics of the hippocampal ensemble code for space. Science 261:1055–1058. 10.1126/science.8351520 [DOI] [PubMed] [Google Scholar]
- Wood ER, Dudchenko PA, Robitsek RJ, Eichenbaum H (2000) Hippocampal neurons encode information about different types of memory episodes occurring in the same location. Neuron 27:623–633. 10.1016/s0896-6273(00)00071-4 [DOI] [PubMed] [Google Scholar]
- Yu JY, Frank LM (2021) Prefrontal cortical activity predicts the occurrence of nonlocal hippocampal representations during spatial navigation. PLoS Biol 19:e3001393. 10.1371/journal.pbio.3001393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zielinski MC, Shin JD, Jadhav SP (2019) Coherent coding of spatial position mediated by theta oscillations in the hippocampus and prefrontal cortex. J Neurosci 39:4550–4565. 10.1523/JNEUROSCI.0106-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All code was developed in Python 3.7, Anaconda 2019.07, with several open-source libraries (van der Walt et al., 2011; Salvatier et al., 2016; Virtanen et al., 2020). Code is available on request and online at https://github.com/learningandmemorylab/Goal_Arm.