Abstract
Aerial photography is a long-range, non-contact method of target detection technology that enables qualitative or quantitative analysis of the target. However, aerial photography images generally have certain chromatic aberration and color distortion. Therefore, effective segmentation of aerial images can further enhance the feature information and reduce the computational difficulty for subsequent image processing. In this paper, we propose an improved version of Golden Jackal Optimization, which is dubbed Helper Mechanism Based Golden Jackal Optimization (HGJO), to apply multilevel threshold segmentation to aerial images. The proposed method uses opposition-based learning to boost population diversity. And a new approach to calculate the prey escape energy is proposed to improve the convergence speed of the algorithm. In addition, the Cauchy distribution is introduced to adjust the original update scheme to enhance the exploration capability of the algorithm. Finally, a novel “helper mechanism” is designed to improve the performance for escape the local optima. To demonstrate the effectiveness of the proposed algorithm, we use the CEC2022 benchmark function test suite to perform comparison experiments. the HGJO is compared with the original GJO and five classical meta-heuristics. The experimental results show that HGJO is able to achieve competitive results in the benchmark test set. Finally, all of the algorithms are applied to the experiments of variable threshold segmentation of aerial images, and the results show that the aerial photography images segmented by HGJO beat the others. Noteworthy, the source code of HGJO is publicly available at https://github.com/Vang-z/HGJO.
1. Introduction
Aerial imagery is an important component of modern photography and scientific research. Through aerial photography technology, we can obtain high-resolution images of natural landscapes and urban architecture with previously unparalleled accuracy and detail. These images can be used in various fields such as map drawing [1], urban planning [2], land use planning [3], environmental monitoring [4], and agricultural and forestry resource management [5]. However, these high-resolution images may suffer from distortion due to external environmental factors, which can make subsequent work difficult. Therefore, preprocessing aerial images is particularly important.
By segmenting, denoising, enhancing, and other operations on aerial images, we can effectively improve the quality and accuracy of the images, providing more reliable data support for subsequent applications. On the other hand, segmentation technology can also reduce the complexity of high-resolution images, making subsequent processing more efficient and accurate. Image segmentation is one of the most critical processes in computer vision. Preprocessing through segmentation technology can effectively reduce the complexity of subsequent processes.
Segmentation technology is the process of dividing images into several categories based on pixels, with threshold segmentation being the most effective and commonly used method [6]. Due to its simplicity and stable performance, threshold segmentation has always been the preferred segmentation technology [7]. In addition, there are clustering-based [8], edge-based [9], and region-based [10] segmentation methods that have also attracted the attention of researchers. However, these methods are currently only effective for binary segmentation problems. As the number of segmentation targets increases beyond two, their processing capabilities decrease exponentially. This phenomenon is due to the exponential growth in complexity of multi-threshold image segmentation problems compared to binary segmentation, making traditional segmentation methods unable to calculate feasible solutions within a limited time frame. Therefore, researchers have focused their attention on metaheuristics for these types of problems. In recent years, some of the most popular meta-heuristics used to solve engineering problems include Genetic Algorithms (GA) [11], Particle Swarm Optimization (PSO) [12], Differential Evolution (DE) [13], Ant Colony Optimization (ACO) [14], Whale Optimization Algorithm (WOA) [15], and Grey Wolf Optimization (GWO) [16]. In addition, some recently proposed metaheuristics have also been widely recognized by researchers, such as Arithmetic Optimization Algorithm [17], Aquila Optimizer (AO) [18], Ebola Optimization Search Algorithm (EOSA) [19], Dwarf Mongoose Optimization Algorithm (DMO) [20], Reptile Search Algorithm (RSA) [21], Prairie Dog Optimization Algorithm (PDO) [22], and Gazelle Optimization Algorithm (GOA) [23]. These algorithms have achieved good results in dealing with real word engineering problems, providing new ideas for the development of multi-threshold image segmentation. The following is a summary of the meta-heuristics used by scholars in various fields to solve multilevel segmentation problems in recent years.
Yin [24] proposed a recursive method to optimize the minimum cross entropy thresholding (MCET), which is combined with particle swarm optimization to search for the near-optimal MCET. The experimental results demonstrate that the MCET obtained by the proposed algorithm is very close to the optimal MCET. Osuna-Enciso, Cuevas and Sossa [25] presented a mixture of Gaussian functions to approximate the 1D histogram of a gray level image, which is combined with Particle Swarm Optimization, Artificial Bee Colony Optimization, and Differential Evolution. The experimental outcomes indicate that each algorithm has its own advantages and disadvantages, and all of them could achieve more satisfactory results. Gao, Kwong, Yang and Cao [26] suggested a novel Particle Swarm Optimization with an intermediate perturbation search strategy, which is called IDPSO. The proposed algorithm is compared with 10 different improved PSO algorithms which achieved outstanding performance on multilevel threshold segmentation problems. Jiang, Yeh, Hao and Yang [27] introduced a new hybrid algorithm which is based on honey bee mating algorithms and cooperative learning, furthermore a new initialization population strategy is employed. Upon extensive experimental analysis, the algorithm is demonstrated to be able to be applied to complex image processing problems. Han, Yang, Zhou and Gui [28] used the State Transfer Algorithm (STA) to fit the optimal parameters of a linear combined normal distribution functions. The competitive capability of the STA in thresholding segmentation is illustrated by comparison with the classical meta-heuristics. He and Huang [29] proposed an effective improved multilevel color image thresholding firefly algorithm using Kapur’s entropy, minimum cross-entropy and inter-class variance method as the objective function. The experimental outcomes indicate that the proposed algorithm is superior to other classical metaheuristic algorithms in all aspects. Ishak [30] developed a two-dimensional multilevel thresholding technique based on Rényi and Tsallis entropies, which combines Quantum Genetic Algorithm and Differential Evolutionary to solve the segmentation problem of multimodal noisy images.
A multi-level threshold image segmentation method using the Fruit Fly Optimization Algorithm was developed by Ding, Dong and Zou [31]. Extensive experimental indicate that the proposed algorithm could significantly reduce the time cost and also achieve satisfactory computational accuracy. To effectively segment coastal video images, a multilevel thresholding method based on Cuckoo Search Algorithm was designed by Widyantara et al [32]. This method was successful in overcoming a series of problems caused by nonlinear variations in image quality and opaque areas. Bohat and Arya [33] propose a novel threshold heuristic algorithm for the multilevel thresholding problem, which embeds the proposed algorithm into the Whale Optimization Algorithm, Gray Wolf Optimizer and Particle Swarm Optimization. Experiments illustrate that this work reduced the computation time of all the embedded algorithms. Singh, Mittal and Singh [34] presented an efficient multilevel thresholding image segmentation method based on Learning enthusiasm-based Teaching-Learning-Based Optimization. This method conquered the problem with increasing the level of redundant thresholds makes the computational complexity grow exponentially. Qualitative experimental outcomes demonstrate that the proposed algorithm is efficient in the field of image segmentation. Xing [35] proposed a novel color image segmentation method based on Emperor Penguin Optimization for Berkeley images, Satellite images, and Plant canopy images. The experimental shows that the method has superior segmentation accuracy. In addition, the computational complexity does not increase exponentially due to the increase of thresholds. Upadhyay and Chhabra [36] suggested a Kapur’s entropy based Crow Search Algorithm to solve the optimal solution for multilevel thresholding image segmentation. By comparing with the classical meta-heuristics, the proposed algorithm achieves satisfactory performance with respect to both quality and consistency. Mousavirad and Ebrahimpour-Komleh [37] proposed a multilevel thresholding for image segmentation using Human Mental Search. This method combines Kapur’s entropy and Otsu method to achieve significant advantages in multi-threshold segmentation problems.
Zhao et al. [38] proposed an improved Slime Mould Algorithm, which introduced a diffusion mechanism to increase the diversity of population. In addition, this methodology was successfully applied to the CT image segmentation of chronic obstructive pulmonary disease, which could help physicians to analyze the lesion tissues qualitatively and quantitatively, moreover improving the accuracy of diagnosis. Swain et al. [39] developed a multilevel thresholding image segmentation method based on differential exponential entropy. The method was combined with Equilibrium-Cuckoo Search Optimizer to achieve satisfactory performance in satellite image segmentation. Furthermore, the method is suggested in the paper for segmentation of the brain MR images. Houssein et al. [40] proposed a fresh approach based on the black widow optimizer to overcome the problem of high computational cost of multilevel thresholding image segmentation. This method has been compared with six well-known meta-heuristics. The comparison reveals that this method is the most potential alternative. Ma and Yue [41] proposed an improved multilevel thresholding image segmentation method based on the Whale Optimization Algorithm. The proposed method obtains satisfactory results for image segmentation in both grayscale and color images, respectively. Emam et al. [42] proposed an enhanced RSA algorithm for global optimization and image segmentation, which overcomes the tendency of RSA to get stuck in local optima by combining it with the RUNge Kutta Optimizer (RUN) [43] and applies it to brain MRI image segmentation. The results showed that it outperformed other advanced meta-heuristics in terms of segmentation accuracy and computational efficiency. To further advance research on COVID-19, Houssein et al. [44] used the opposition-based learning mechanism to improve the Manta Ray Foraging Optimization. Experimental results showed that the proposed method has higher robustness compared to existing meta-heuristics. Additionally, in [45], the Equilibrium Optimizer was further improved to advance research on COVID-19, and experimental results showed that the proposed method can be an effective tool for image segmentation. These two works further advance the research on image segmentation for COVID-19, making effective contributions to prevent the spread of COVID-19. In addition, Houssein et al. [46] introduced the opposition-based learning strategy into the Marine Predator Algorithm (MPA) [47] to accelerate the convergence speed of MPA. Finally, Otsu and Kapur entropy were used as objective functions to perform segmentation experiments on benchmark images. The experimental results showed that the proposed algorithm outperformed other methods.
In [48], the authors used an improved Golden Jackal Optimization (GJO) [49] to segment skin cancer images, enhancing the original GJO algorithm using the opposition-based learning and comparing it with seven different meta-heuristics. The experimental results showed that the proposed method outperformed other alternative algorithms and effectively solved the segmentation problem. However, the improvement of this work is limited for the GJO algorithm, as the time complexity of thresholding increases exponentially with increasing image resolution, and the single opposition-based learning mechanism cannot achieve satisfactory results on high-resolution images. Although meta-heuristics have been widely used in image segmentation, there are still shortcomings in multi-level threshold image segmentation for complex images. In other words, researchers are currently working on developing a method that can maintain consistent results when dealing with complex problems. The GJO algorithm is a novel and highly scalable swarm intelligence optimization algorithm proposed in 2022, which has been widely used by scholars [50–52]. Therefore, in this paper, we propose an efficient image segmentation method based on the GJO algorithm to further advance multi-level threshold segmentation work at high resolution and apply it to aerial image segmentation.
In this study, we make further improvements to the original GJO to enhance its potential in multi-level thresholding image segmentation. In order to evaluate the effectiveness of the improvements, the proposed algorithm is compared with numerous classical and novel algorithms on CEC2022 benchmark functions. Moreover, we used Peak Signal to Noise Ratio (PSNR) [53], Structural Similarity Index (SSIM) [54], and Feature Similarity Index (FSIM) [55] to determine the performance of image segmentation. The main contributions of this study are as follows:
The Opposition-Based Learning (OBL) strategy is integrated into the initialization of the GJO. The OBL strategy could dramatically improve the quality of the candidate solution to escape from the local optimal solution.
The Cauchy distribution is introduced to enhance the raw single Lévy flight, strengthening the distributivity of the population to improve the capability of the algorithm to search the global optimum. Furthermore, a new approach to calculate the prey escape energy is proposed. It is a more reasonable nonlinear method of calculation, which leads to a better balance of exploration and exploitation.
“Helpers” are introduced to improve the performance of GJO for the first time. They are some special individuals of the golden jackal population. The overall disturbance of the population by the “Helpers” before the end of each iteration can effectively prevent the algorithm trapped into local optimum.
The proposed HGJO was compared with numerous classical and novel algorithms on CEC2022 benchmark functions, and a lot of the segmentation of aerial images. The outcomes demonstrate that the proposed HGJO has remarkably superior performance and enables to challenge the current existing algorithms.
The rest of this paper is structured as follows: Section 2 encompasses a review of the multilevel threshold segmentation and the original GJO algorithm. The Improved Golden Jackal optimization is proposed in Section 3. Section 4 introduces, discusses, and analyzes the results of CEC2022 benchmark functions. Section 5 investigates the performance of the segmentation of aerial images. Finally, Section 6 concludes by summarizing the research and making recommendations for future work.
2. Literature review
2.1.Multilevel thresholding image segmentation
Threshold segmentation, as the name implies, is the division of an image into two parts based on the pixel values, with a given threshold. However, for the current needs of computer vision tasks, it is often not enough to simply segment the image into two parts. Therefore, depending upon the current requirements, most scholars are investigating multilevel thresholding. In general, multilevel thresholding is the addition of more thresholds to binary thresholding to segment the image into more units. At the current stage, the most commonly used thresholding method for segmentation is the Otsu method. The Otsu method involves histogram of the image as the input, where the generated class information is employed to calculate the optimal threshold for segmenting the image. The Otsu method was firstly proposed by Otsu in 1979 [56] to segment the grey scale image by maximizing the variance between classes. The approach considers L to represent the different gray levels in an image which has the size of M*N.
| (1) |
| (2) |
where n means the total number of pixels in the image, ni denotes the number of pixels for gray level i, and pi indicates the probability distribution of gray levels.
Suppose there is a threshold k, in which 0<k<L−1, then the current input image will be segmented into two classes, namely C1 and C2, where C1 and C2 contain all pixels with the grayscale in [0, k] and [k+1, L−1], respectively.
| (3) |
where P1(k) and P2(k) represent the probability of a pixel has been classified into C1 or C2, respectively.
| (4) |
| (5) |
| (6) |
where m1(k) and m2(k) indicate the average gray value of the pixels in C1 and C2, respectively. mk denotes the average grayscale from 0 to k. mG represents the average grayscale of the whole image. Hence, we can derive Eq (7) without ambiguity. Then the between class variance can be expressed as Eq (8).
| (7) |
| (8) |
| (9) |
As shown by Eq (8), we are able to determine a k* to make the maximum of , which is denoted as Eq (9). Therefore, the Otsu method can be used as an objective function of an optimization problem to solve the optimal threshold value for segmented images.
2.2.Golden jackal optimization
GJO is a novel metaheuristic algorithm proposed by Chopra and Ansari in 2022 [49]. GJO simulates the behavior of the golden jackal in natural environments for hunting. The search agents of this algorithm follow male and female jackals to seek, encircle and attack the prey, while the male jackal is considered as the global optimal solution of the problem. The entire description of the GJO is given below:
1. Initialization
As mentioned above, GJO is a population-based meta-heuristic. Therefore, the initialization of GJO is consistent with most meta-heuristics. The process of the initialization is described in detail in Eq (10).
| (10) |
where X denotes the prey matrix, indicates the position of the prey, n represents the size of population, and stand for the lower and upper boundary, respectively. is a random vector between 0 and 1.
Algorithm 1 Pseudo-code of the GJO
Inputs: The Population Size N and the Max iterations T.
Outputs: The best solution.
1. Initialization the population X.
2. while (t<T)
3. Calculating the fitness of the population.
4.
5.
6. foreach (X(t))
7. Update the Evasion Energy (E) according Eq (13).
8. if (|E|≥1)
9. Update the population according Eqs (11) and (12).
10. else
11. Update the population according Eqs (14) and (12).
12. end if
13. end foreach
14. t = t+1
15. end while
16. return the best solution ()
1. Exploration
In the exploration phase, the algorithm will search for as many potential solutions as possible over the search space. The position update is performed by a male jackal leading a female jackal, which is shown in the following mathematical model:
| (11) |
| (12) |
where t is the current iteration, stand for the position after it has been updated, means the current position. and denote the current positions of the male and female jackals, respectively, which are best and second-best fitness of the population. is a random vector which is based on Lévy motion. is the Evasion Energy of prey which is calculated as follows:
| (13) |
where E1 is the decreasing energy of the prey, is the initial energy of the prey. T stands for the maximum iterations.
1. Exploitation
As most of the meta-heuristics, the exploitation phase is based on the exploration phase. Through the exploitation of the candidate solutions which have been searched, the global optimal solution is approximated as closely as possible. The mathematical is shown as follows:
| (14) |
It is worth noting that all of the variables are given in 2.2.2. Therefore, we do not repeat them. In addition, the pseudo-code of the GJO is shown in Algorithm 1.
3. Improved golden jackal optimization
3.1.Opposition-based learning strategy
Since the generation for initial solution of GJO is consistent with most meta-heuristics, this approach may cause the initial population to be unevenly distributed and converge sluggishly. However, the performance of the algorithm is strongly influenced by the initial population. A high-quality initial population not only improves the convergence speed of the algorithm but even has the potential to determine the final outcomes. Enhancing population diversity can effectively avoid the algorithm from maturing prematurely and falling into a local optimum. Therefore, the Opposition-Based Learning(OBL) [57] strategy is used to assist with the generation of the initial population in this study. Each individual in the population was given an Opposition solution to select the better individual as the initial solution, which could improve the convergence performance of GJO. The mathematical model of the OBL is shown as follows:
| (15) |
where is the opposing individual of in the search space. If the fitness of is better than , then will be retained as the initial individual.
3.2.Cauchy distribution and dynamic balance strategy
3.2.1.Cauchy distribution
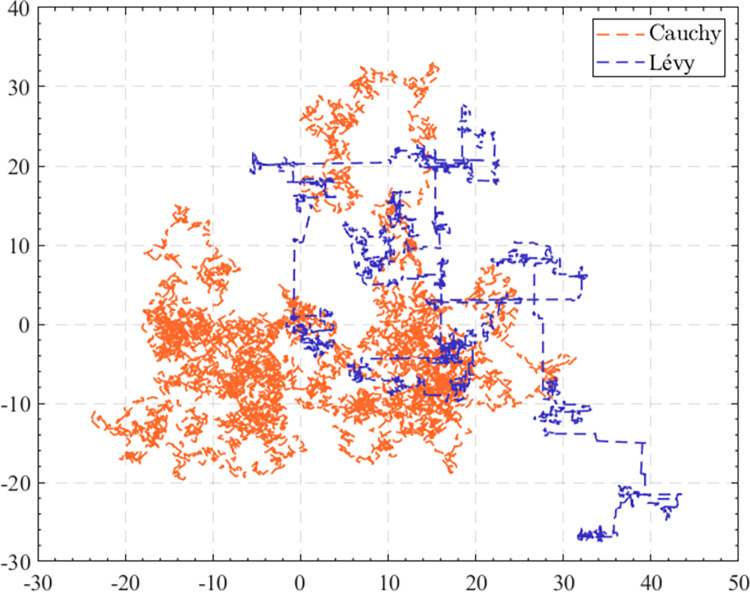
The Cauchy distribution is a continuous probability distribution without mathematical expectation. Better outcomes tended to be achieved when the motion state of the population was portrayed by the Cauchy distribution [58]. Fig 1 is a comparison of the motion trajectory employing the Cauchy distribution and the Lévy flight, which can be visualized that the Cauchy distribution is able to perform a comprehensive search in a given search space. Therefore, it is a more sensible choice to adopt the Cauchy distribution in the exploration stages. The probability density function of the Cauchy distribution is shown below:
| (16) |
Fig 1. The movement of Cauchy distribution and Lévy flight.
where x0 represents the position parameter, specifying the position of the peak of the distribution. γ denotes the scale parameter, which specifies the half-width at half-maximum. The Cauchy distribution which obeys X~C(0, 0.5) is utilized in this work. Where γ is fixed at 0.5 was determined by experimental analysis. Table 1 shows the effect of the algorithm using different γ on the test results of IEEE CEC 2022. In this experiment, the population size was set to 60, the number of iterations was 10000, and 31 independent experiments were conducted. Finally, the results of 31 times were validated to Friedman mean rank test. Through observation of the data in Table 1, we can realize that although when the value of γ is set to 0.5 does not achieve the optimal results on all test functions, it is still a best choice in general. In addition, the results given by the Friedman calibration, γ set to 0.5 is also the best choice. Therefore, in this paper, the Cauchy distribution which obeys X~C(0, 0.5) is used.
Table 1. The experimental of HGJO with different γ.
| Problem | γ = 0.25 | γ = 0.5 | γ = 0.75 | γ = 1 | γ = 1.5 | |
|---|---|---|---|---|---|---|
| F1 | Mean | 300 | 300 | 300 | 300 | 300 |
| Std | 3.91E-13 | 7.190E-14 | 1.651E-13 | 3.226E-13 | 2.044E-13 | |
| F2 | Mean | 403.94923 | 400 | 403.47218 | 404.04741 | 403.60078 |
| Std | 2.13E+00 | 4.896E-10 | 1.359E+00 | 1.636E+00 | 1.198E+00 | |
| F3 | Mean | 600.00001 | 600.00001 | 600.00001 | 600.00001 | 600.00001 |
| Std | 9.11E-06 | 1.446E-05 | 5.991E-06 | 1.747E-05 | 2.060E-05 | |
| F4 | Mean | 809.56445 | 804.65384 | 809.53234 | 808.28063 | 808.89044 |
| Std | 3.52E+00 | 5.963E-01 | 3.102E+00 | 2.509E+00 | 2.436E+00 | |
| F5 | Mean | 900 | 900 | 900 | 900 | 900 |
| Std | 4.00E-13 | 1.164E-12 | 5.142E-12 | 1.415E-12 | 1.925E-13 | |
| F6 | Mean | 1800.1992 | 1800.2297 | 1800.2195 | 1800.2166 | 1800.2062 |
| Std | 1.12E-01 | 8.529E-02 | 1.190E-01 | 1.087E-01 | 9.270E-02 | |
| F7 | Mean | 2010.8465 | 2002.9588 | 2010.7526 | 2008.7908 | 2005.678 |
| Std | 9.43E+00 | 4.874E+00 | 9.548E+00 | 9.465E+00 | 7.783E+00 | |
| F8 | Mean | 2201.6878 | 2201.8592 | 2202.8334 | 2201.4274 | 2201.1876 |
| Std | 1.50E+00 | 1.340E+00 | 4.659E+00 | 1.191E+00 | 9.500E-01 | |
| F9 | Mean | 2529.2844 | 2529.2844 | 2529.2844 | 2529.2844 | 2529.2844 |
| Std | 0.00E+00 | 0.000E+00 | 0.000E+00 | 0.000E+00 | 0.000E+00 | |
| F10 | Mean | 2500.2164 | 2500.2173 | 2500.2308 | 2503.8003 | 2500.2212 |
| Std | 4.38E-02 | 5.886E-02 | 3.934E-02 | 1.990E+01 | 4.141E-02 | |
| F11 | Mean | 2600 | 2600 | 2600 | 2600 | 2600 |
| Std | 5.87E-11 | 1.422E-10 | 2.445E-10 | 4.723E-10 | 1.364E-10 | |
| F12 | Mean | 2860.0375 | 2859.0842 | 2860.0648 | 2859.8318 | 2860.2065 |
| Std | 1.21E+00 | 4.359E-01 | 1.138E+00 | 1.199E+00 | 1.103E+00 | |
| Friedman mean rank | 2.7500 | 2.3333 | 3.5417 | 3.4583 | 2.9167 | |
| Rank | 2 | 1 | 5 | 4 | 3 | |
3.2.2.Dynamic balance strategy
The balance of exploration and exploitation essentially determines the performance of an algorithm [59]. It is not hard to see the escape energy () in the GJO determines the exploration and exploitation. However, the calculation of is defined by E1, which is a value that varies linearly according to the iteration. Thus, GJO might cause exploration and exploitation to be insufficiently balanced during the iteration. In order to overcome this drawback, we propose a novel formula to calculate , which is shown in Eq (17). Fig 2 compares the variation curves of the two escape energies.
Fig 2. The variation curves of the two escape energies.
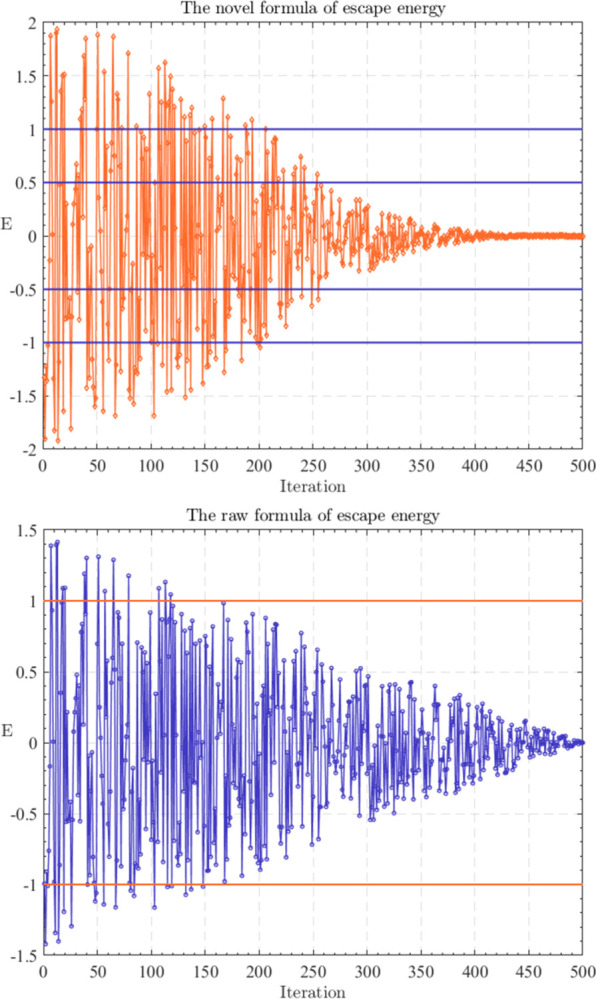
| (17) |
All variables have the same implications as those mentioned in the previous section. Therefore, they are not explained here. Note that how the proposed new escape energy will affect the exploration and exploitation of the algorithm is described in detail in Section 3.3.
3.3.The new update strategy
Combined with the improvements proposed in the previous two sections, the position update strategy is also modified in this section. In the raw algorithm, exploration and exploitation are divided into two opposite parts, the algorithm will proceed to exploration when the escape energy is greater than 1, and vice versa. However, in this study, we split the iteration into three parts. First, there is the stage where the escape energy is greater than 1. In this stage, all individuals will explore. Then, there is a phase with escape energy greater than 0.5, in which a part of the individuals in the population explores and the rest exploits. Finally, the stage with escape energy less than 0.5, in which all individuals were exploiting. The detailed mathematical model is shown below:
1. In the first stage, when , the population will explore. However, their exploration is divided into two parts, part with reference to the current position of the individual, and the other part with reference to the center position of the whole population.
| (18) |
where means a random vector generated by the Cauchy distribution, which obeys X~C(0, 0.5). rand denotes a random number between 0 and 1. mean(X) represents the central position of the current population. The rest of the variables have the same meaning as before.
2. In the second stage, when , the population will transition from exploration to exploitation. In this process, a portion of the individuals will maintain the exploration, while the rest will transform to exploitation.
| (19) |
All the variables have the same meaning as before.
3. In the last stage, when , the population will enter the exploitation stage. In this stage, a part of the individuals will be exploitation depending on themselves, while the rest of the individuals will be exploitation depending on the center position of the population.
| (20) |
As well, all variables have the same meaning as mentioned before. Therefore, there is no need to go into too much detail.
3.4.The helper mechanism
In general, there are individuals in the golden jackal group which are called “helpers” [49]. These helpers are the previous offspring of the golden jackal. Golden jackal populations are strengthened by helpers. This study focuses on “helpers” to enhance the global searchability of the algorithm with the introduction of “helpers”, which can effectively prevent the algorithm trapped into local optimal.
1. The first part of the “helpers” is to support the growth of the golden jackal pups. The mathematical model of this part is shown below:
| (21) |
where and represent three random individuals, respectively. If the obtained offspring has a better fitness than the current updated individual, the individual position is updated to the position of the offspring.
2. The second part of the “helpers” is to take care of the pups while the golden jackal parents are out hunting. When other foragers are present, or something happens which could be harmful to the safety of the pups, the “helpers” will assist the pups in avoiding the danger. This part of the mechanism can be shown by how the algorithm escapes from the local optimal solution, which the mathematical model is as follows.
| (22) |
where represent two random individuals, respectively. rand denotes a random number between 0 and 1. At this point, the improvement of IGJO is almost complete. The pseudo-code of HGJO is given in Algorithm 2.
Algorithm 2 Pseudo-code of the HGJO
Inputs: The Population Size N and the Max iterations T.
Outputs: The best solution.
1. Initialization the population X according Eq (15).
2. while (t<T)
3. Calculating the fitness of the population.
4.
5.
6. foreach (X(t))
7. Update the Evasion Energy () according Eq (17).
8. if ()
9. Update the population according Eqs (12) and (18).
10. elseif ()
11. Update the population according Eqs (12) and (19).
12. else
13. Update the population according Eqs (12) and (20).
14. end if
15. Calculating, comparing and updating the fitness of offspring and current individual according Eq (21).
16. end foreach
17. Global perturbation with helpers according Eq (22).
18. t = t+1
19. end while
20. return the best solution ()
3.5.Computational complexity
3.5.1. Time complexity
Based on the pseudo-code in Algorithm 2, we could derive the time complexity of HGJO without difficulty. In which, the initial population spends O(N*M) time to generated, where N denotes the size of the population, M represents the dimensions of the decision space. Then, the fitness of the population needs O(T*N*Of) time to calculate, where T indicates the maximum iterations, Of is the cost of object function. In addition, the population needs O(T*N*M) time to be updated. Therefore, the total time complexity is O(N*(T*(Of+M)+M)).
3.5.2. Space complexity
Since no additional memory space is used in the computation, the space complexity of HGJO is limited only by the population size. Hence, the space complexity of HGJO is O(M*N).
4. Experimental results and analysis
In this section, we will evaluate the performance of the proposed algorithm. We will compare HGJO with six existing meta-heuristics on the CEC2022 test suite. These six meta-heuristics include the original GJO algorithm, the first variant of GJO algorithm called IGJO which uses OBL for improvement, two recently proposed widely used meta-heuristics, the RUN algorithm and the Archimedes Optimization Algorithm (AOA) [60], and the two most classical and stable algorithms, DE and PSO. Additionally, to further ensure that combining the OBL operator with the GJO algorithm is the most feasible option, we also included the OBL operator in the DE and PSO algorithms for comparison in the experiments. There are 12 different test functions in the CEC2022 test suite, which can cover a majority of the real-world problems. Therefore, the contents of this section enable us to make a preliminary understanding of the performance for HGJO. The details of the CEC2022 test suite are given in Table 2 and the runtime environment is also shown in Table 3. All algorithms are iterated with a population size of 60 and a maximum iteration of 1000. Furthermore, in consideration of the suggestion by Arcuri et al. [61], all algorithm parameters are kept at their default values which are derived from their raw papers to ensure they are in a relatively optimal state, and these parameters are provided in Table 4. Moreover, the source code of the CEC2022 test set is available at: https://github.com/P-N-Suganthan/2022-SO-BO.
Table 2. The benchmark functions of CEC2022.
| Problem No. | Problem name | Dim | Range | F_min |
|---|---|---|---|---|
| F1 | Zakharov Function | 10 | [–100, 100] | 300 |
| F2 | Rosenbrock’s Function | 10 | [–100, 100] | 400 |
| F3 | Schaffer’s F7 | 10 | [–100, 100] | 600 |
| F4 | Rastrigin’s Function | 10 | [–100, 100] | 800 |
| F5 | Levy Function | 10 | [–100, 100] | 900 |
| F6 | Hybrid Function 1 | 10 | [–100, 100] | 1800 |
| F7 | Hybrid Function 2 | 10 | [–100, 100] | 2000 |
| F8 | Hybrid Function 3 | 10 | [–100, 100] | 2200 |
| F9 | Composition Function 1 | 10 | [–100, 100] | 2300 |
| F10 | Composition Function 2 | 10 | [–100, 100] | 2400 |
| F11 | Composition Function 3 | 10 | [–100, 100] | 2600 |
| F12 | Composition Function 4 | 10 | [–100, 100] | 2700 |
Table 3. Runtime environment.
| Configurations | |
|---|---|
| Hardware | |
| CPU | Intel(R) Core(TM) i9-10980HK CPU @ 2.40GHz |
| GPU | NVIDIA GeForce RTX 3080 Laptop GPU |
| RAM | 64.0 GB |
| Software | |
| OS | Microsoft Windows [Version 10.0.19043.1826] |
| Interpreter | IntelliJ IDEA 2021.3.2 (Ultimate Edition) |
| Language | MATLAB R2021a (9.10.0.1602886) |
Table 4. The parameters setting of all algorithms.
| Algorithm | Parameters |
|---|---|
| HGJO | C1 = 2 |
| GJO | C1 = 1.5 |
| IGJO | C1 = 1.5 |
| RUN | a = 20, b = 12 |
| AOA | C1 = 2, C2 = 6, C3 = 2, C4 = 0.5 |
| DE(OBL) | PCr = 0.8, F = 0.85 |
| PSO(OBL) | C1 = 1.49445, C2 = 1.49445 |
4.1.Statistical results on CEC2022
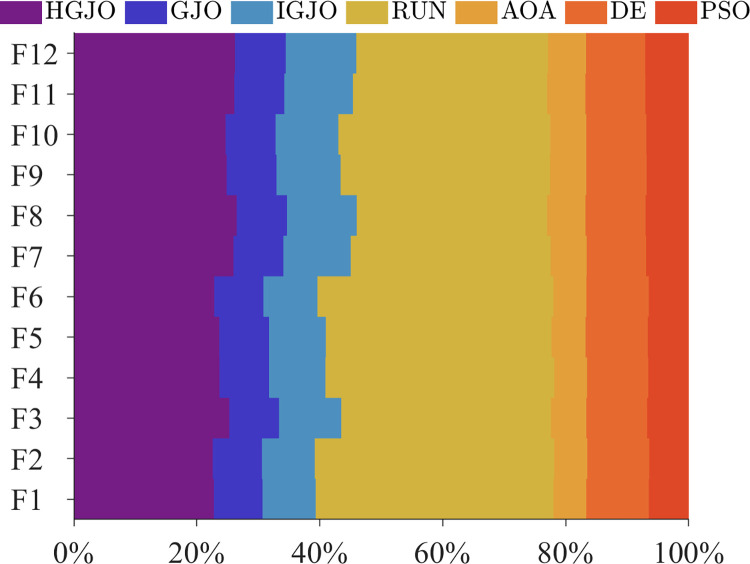
As mentioned above, the CEC2022 test suite is used to measure the performance of each algorithm, which includes both quantitative and qualitative metrics. The quantitative metrics include the mean, median, and standard deviation obtained by all algorithms. Qualitative metrics are illustrated by convergence curves, which reflect the evolution of the optimal solution throughout the iterations of the algorithm. To ensure the fairness of the experiments, all algorithms were run 31 times independently on the CEC2022 benchmark test function. Table 5 provides the average time spent by all algorithms over the 31 runs, and lists the median, mean, and standard deviation of the best values obtained by all algorithms, the best results (minimum value) was highlighted in bold. The Friedman mean rank [62] was used to determine the overall rank of each algorithm. According to the data in Table 5, we can see that the proposed method is optimal for most problems in terms of mean and median, except for F9 where AOA obtains the most accurate value. Similarly, the proposed algorithm also achieves satisfactory results for standard deviation in most problems. Therefore, we can consider that the proposed algorithm has excellent solving performance in CEC2022. However, in terms of running time, the AOA algorithm is the shortest in all problems, while the HGJO algorithm has some shortcomings compared to it. Considering that the introduction of OBL and Cauchy operator will affect the efficiency of the algorithm to some extent, Fig 3 further analyzes the running time of all algorithms in CEC2022. Fig 3 is the average time slot of all algorithms running in CEC2022, which can reflect the percentage of time each algorithm consumes when processing the same problem. The horizontal coordinate is the percentage of time consumed, and the vertical coordinate is the test function. Through Fig 3, we can clearly observe that compared with the original GJO, the time complexity of HGJO has increased significantly, but it still has some advantages compared with RUN. In addition, through the observation of 12 test functions, we can see that the running time of HGJO has not fluctuated significantly. Although OBL and Cauchy operator will increase certain time costs, the proposed algorithm shows the most satisfactory results in terms of overall performance. In addition, the Friedman mean rank is also used to comprehensively rank the algorithms, and the top three algorithms are HGJO, DE(OBL), and AOA, respectively.
Table 5. The results of CEC2022 for all algorithm.
| Problem | HGJO | GJO | IGJO | RUN | AOA | DE | PSO | |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 300.000 | 682.748 | 699.541 | 300.000 | 300.001 | 1215.047 | 1220.769 |
| Median | 300.000 | 439.932 | 456.433 | 300.000 | 300.000 | 1153.934 | 1217.032 | |
| Std | 1.228E-13 | 7.593E+02 | 7.395E+02 | 6.385E-05 | 1.627E-03 | 3.405E+02 | 6.384E+01 | |
| Time | 1.072 | 0.362 | 0.395 | 1.973 | 0.268 | 0.524 | 0.329 | |
| F2 | Mean | 403.472 | 425.274 | 422.150 | 403.587 | 405.245 | 405.504 | 434.336 |
| Median | 403.987 | 411.882 | 409.887 | 400.013 | 400.257 | 404.124 | 427.549 | |
| Std | 1.359E+00 | 2.210E+01 | 1.993E+01 | 4.363E+00 | 1.139E+01 | 2.219E+00 | 1.857E+01 | |
| Time | 1.149 | 0.362 | 0.389 | 1.976 | 0.271 | 0.533 | 0.327 | |
| F3 | Mean | 600.000 | 605.511 | 605.925 | 611.779 | 600.245 | 600.064 | 615.090 |
| Median | 600.000 | 604.463 | 605.740 | 608.887 | 600.097 | 600.061 | 612.536 | |
| Std | 1.419E-05 | 4.645E+00 | 4.768E+00 | 6.793E+00 | 2.906E-01 | 2.314E-02 | 5.356E+00 | |
| Time | 1.460 | 0.457 | 0.572 | 2.241 | 0.371 | 0.639 | 0.437 | |
| F4 | Mean | 808.762 | 819.404 | 822.509 | 823.847 | 817.139 | 861.592 | 845.546 |
| Median | 808.955 | 818.711 | 821.114 | 823.879 | 817.909 | 861.478 | 845.007 | |
| Std | 2.819E+00 | 5.913E+00 | 7.876E+00 | 6.765E+00 | 5.615E+00 | 1.967E+00 | 2.538E+00 | |
| Time | 1.246 | 0.394 | 0.448 | 2.041 | 0.303 | 0.568 | 0.363 | |
| F5 | Mean | 900.000 | 959.189 | 967.710 | 977.192 | 908.414 | 900.041 | 977.753 |
| Median | 900.000 | 951.961 | 942.420 | 968.285 | 900.454 | 900.014 | 977.414 | |
| Std | 3.771E-13 | 6.716E+01 | 8.875E+01 | 4.827E+01 | 3.302E+01 | 6.664E-02 | 6.523E+00 | |
| Time | 1.275 | 0.399 | 0.457 | 2.066 | 0.307 | 0.542 | 0.369 | |
| F6 | Mean | 1800.226 | 7151.939 | 7110.417 | 2921.693 | 2532.632 | 1814.253 | 4354616.518 |
| Median | 1800.211 | 8154.988 | 8182.686 | 2533.530 | 2171.087 | 1814.067 | 4264276.228 | |
| Std | 9.605E-02 | 2.193E+03 | 1.907E+03 | 1.012E+03 | 9.174E+02 | 1.567E+00 | 7.624E+05 | |
| Time | 1.202 | 0.371 | 0.408 | 1.988 | 0.280 | 0.540 | 0.343 | |
| F7 | Mean | 2006.963 | 2032.196 | 2037.376 | 2037.731 | 2021.994 | 2019.993 | 2064.246 |
| Median | 2001.372 | 2031.836 | 2034.197 | 2037.757 | 2021.643 | 2021.894 | 2062.244 | |
| Std | 8.907E+00 | 1.136E+01 | 1.121E+01 | 9.988E+00 | 9.576E+00 | 6.431E+00 | 5.565E+00 | |
| Time | 1.674 | 0.510 | 0.689 | 2.138 | 0.398 | 0.654 | 0.457 | |
| F8 | Mean | 2201.458 | 2224.956 | 2225.259 | 2223.042 | 2219.205 | 2210.591 | 2247.440 |
| Median | 2201.065 | 2225.255 | 2225.280 | 2223.540 | 2221.317 | 2207.073 | 2235.872 | |
| Std | 1.409E+00 | 4.580E+00 | 2.978E+00 | 1.564E+00 | 6.726E+00 | 8.650E+00 | 3.649E+01 | |
| Time | 1.667 | 0.548 | 0.761 | 2.302 | 0.482 | 0.747 | 0.528 | |
| F9 | Mean | 2529.284 | 2549.393 | 2551.107 | 2529.285 | 2493.923 | 2529.284 | 2545.972 |
| Median | 2529.284 | 2531.291 | 2541.380 | 2529.284 | 2493.923 | 2529.284 | 2536.194 | |
| Std | 0.000E+00 | 3.477E+01 | 2.645E+01 | 2.205E-04 | 8.775E-05 | 0.000E+00 | 3.849E+01 | |
| Time | 1.436 | 0.470 | 0.604 | 2.127 | 0.375 | 0.608 | 0.426 | |
| F10 | Mean | 2500.230 | 2570.959 | 2543.721 | 2530.174 | 2551.838 | 2500.876 | 2579.107 |
| Median | 2500.225 | 2614.641 | 2500.606 | 2500.631 | 2500.519 | 2500.874 | 2648.197 | |
| Std | 4.586E-02 | 6.120E+01 | 5.936E+01 | 5.094E+01 | 5.767E+01 | 6.567E-02 | 7.631E+01 | |
| Time | 1.350 | 0.460 | 0.579 | 2.026 | 0.352 | 0.580 | 0.413 | |
| F11 | Mean | 2600.000 | 2800.106 | 2725.587 | 2622.627 | 2644.051 | 2600.001 | 2808.208 |
| Median | 2600.000 | 2735.136 | 2731.824 | 2600.018 | 2600.001 | 2600.001 | 2761.214 | |
| Std | 1.947E-10 | 1.735E+02 | 9.684E+01 | 7.946E+01 | 1.051E+02 | 4.481E-04 | 1.260E+02 | |
| Time | 1.711 | 0.531 | 0.729 | 2.175 | 0.431 | 0.695 | 0.513 | |
| F12 | Mean | 2859.847 | 2865.104 | 2865.137 | 2863.978 | 2878.827 | 2861.082 | 2866.534 |
| Median | 2859.369 | 2864.532 | 2864.505 | 2863.883 | 2867.589 | 2861.405 | 2866.482 | |
| Std | 1.183E+00 | 3.054E+00 | 4.156E+00 | 1.668E+00 | 1.965E+01 | 9.283E-01 | 7.997E-01 | |
| Time | 1.699 | 0.554 | 0.768 | 2.202 | 0.443 | 0.699 | 0.513 | |
| Friedman mean rank | 1.1667 | 4.8333 | 5.0833 | 3.9583 | 3.3333 | 2.9583 | 6.6667 | |
| Rank | 1 | 5 | 6 | 4 | 3 | 2 | 7 | |
Fig 3. The average time slots for all algorithms.
Table 6 uses the Wilcoxon rank-sum test [63] to further evaluate the running results of each algorithm. The Wilcoxon rank-sum test is used to verify whether there is a significant difference between algorithms. When the p-value is less than 0.05, it can be considered that there is a significant difference between algorithms. On the contrary, it means that the performance of the proposed algorithm is similar to that of the compared algorithm. To better represent the analysis of values, we use the symbols "++" and "—" to indicate the cases where the p-value is less than 0.05 and greater than 0.05, respectively. From Table 6, we can clearly see that the proposed algorithm has significant differences compared with the original GJO, IGJO, RUN, and PSO(OBL). Combined with the data in Table 5, we can consider that it has significant improvements compared with the above algorithms. For AOA and DE(OBL), only similar performance was shown in F2 and F9, respectively. It is worth noting that we can see from the data in Table 5 that AOA achieved the best result in F9, which is also reflected in the Wilcoxon rank-sum test (significant difference between HGJO and AOA). Overall, according to the results of the Wilcoxon rank-sum test, we can consider that the proposed HGJO algorithm has higher performance on the CEC2022 test set.
Table 6. The Wilcoxon signed-rank test for CEC2022.
| Problem | HGJO vs. GJO | HGJO vs. IGJO | HGJO vs. RUN | HGJO vs. AOA | HGJO vs. DE | HGJO vs. PSO |
|---|---|---|---|---|---|---|
| F1 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F2 | 6.018E-07 ++ | 1.588E-06 ++ | 4.457E-02 ++ | 3.001E-01 — | 6.352E-06 ++ | 6.018E-07 ++ |
| F3 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F4 | 7.329E-07 ++ | 6.642E-07 ++ | 6.018E-07 ++ | 1.588E-06 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F5 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F6 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F7 | 1.192E-06 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.252E-05 ++ | 2.308E-02 ++ | 6.018E-07 ++ |
| F8 | 6.018E-07 ++ | 6.018E-07 ++ | 6.642E-07 ++ | 1.312E-06 ++ | 2.906E-03 ++ | 6.018E-07 ++ |
| F9 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | NaN — | 6.018E-07 ++ |
| F10 | 6.018E-07 ++ | 6.018E-07 ++ | 6.642E-07 ++ | 6.018E-07 ++ | 6.642E-07 ++ | 6.018E-07 ++ |
| F11 | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ | 6.018E-07 ++ |
| F12 | 6.642E-07 ++ | 6.018E-07 ++ | 1.192E-06 ++ | 5.057E-04 ++ | 1.451E-02 ++ | 6.018E-07 ++ |
Fig 3 further shows the average time slots achieved by each algorithm on the IEEE CEC2022 benchmark test function. The figure displays the percentage of time consumed by each algorithm in processing the same test function. The horizontal coordinate is the percentage of time consumed, and the vertical coordinate is the test function. Through this figure, we can observe that the time consumption of the HGJO algorithm increases to some extent, but there is no significant fluctuation for the overall. Therefore, this phenomenon verifies that the performance of the proposed algorithm is not limited to a particular problem. This makes the algorithm more extensible and can be more widely ap-plied to other optimization problems.
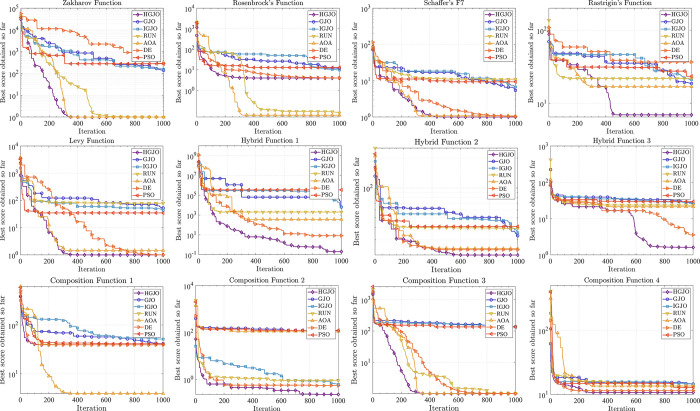
4.2.Convergence behavior analysis
This subsection further presents the results of the convergence analysis of HGJO compared to other meta-heuristics. Fig 4 shows the convergence curves of all the algorithms for the CEC2022 benchmark test function. It is worth noting that all the curves in Fig 4 are calculated as the difference between the optimal values of their benchmark functions. It does not alter the exact meaning of the convergence curves but additionally enhances the observability of the images on the logarithmic axis. In short, the value closer to 0 indicates that the optimal solution obtained by the algorithm is closer to the true optimal solution. With these convergence plots, we can see that the proposed algorithm reaches a stable point in all benchmark test functions, which can further indicate that the proposed algorithm is convergent. In addition, for most test functions, HGJO achieved the optimal solution with the least number of iterations, except for F2 and F9 where it was surpassed by RUN and AOA. Therefore, by analyzing the convergence of the proposed algorithm and other competing algorithms, the superiority of HGJO is further validated, making it possible for HGJO to replace existing algorithms to solve complex problems.
Fig 4. The convergence curves for all algorithms on CEC2022 benchmark functions.
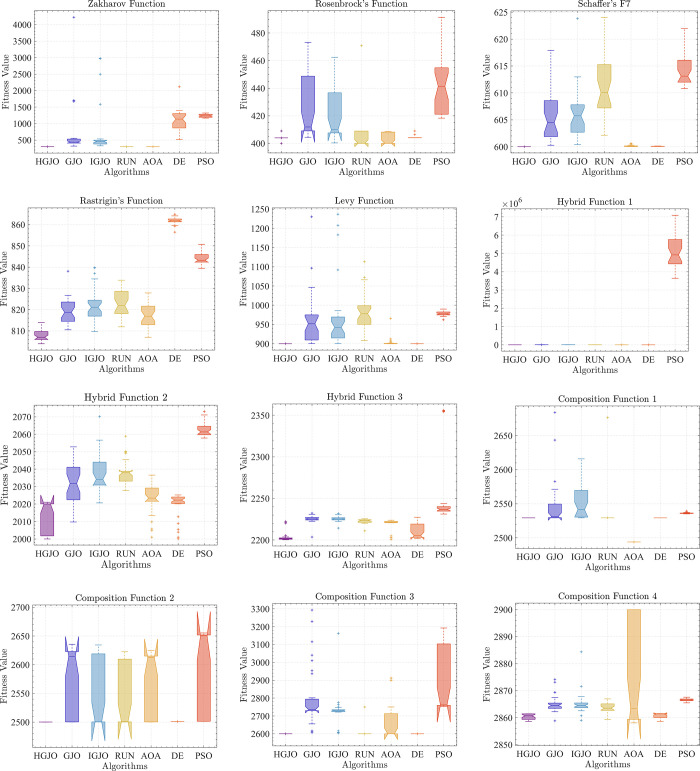
4.3.Boxplot behavior analysis
Due to the many local optima of the CEC2022 benchmark test functions, solving these problems can easily fall into local optima. In order to analyze the algorithmic results more intuitively, in this section we use boxplots to analyze HGJO and other metaheuristics. Fig 5 shows boxplots for all algorithms on the CEC2022 benchmark test function. The boxplots provide a visual representation of the distribution characteristics of the data, with the maximum and minimum values of the data corresponding to the highest and lowest points of the image, respectively. Therefore, the narrower the image reflects, the more stable the data. For most benchmark test functions, the proposed method has the narrowest and lowest boxplots. In fact, HGJO outperforms other metaheuristic algorithms in most test functions, except for F9. Combining the performance analysis of HGJO mentioned above, we can reasonably speculate that the proposed algorithm has the ability to solve complex engineering problems in the real world, providing a new candidate solution for scientific researchers to choose from. In the next section, we will use HGJO to handle the optical aerial image segmentation problem.
Fig 5. The box plots for all algorithms on CEC2022 benchmark functions.
5. The optical aerial image segmentation
In this section, HGJO is applied to a real-world scenario of multi-level thresholding segmentation. The HGJO and all the comparison algorithms in the previous section are used to perform threshold segmentation on the optical aerial image. The objective function used is the Otsu method introduced in Section 2.1. Finally, all algorithms are evaluated by PSNR, SSIM, and FSIM obtained after processing.
5.1.Dataset and runtime environment
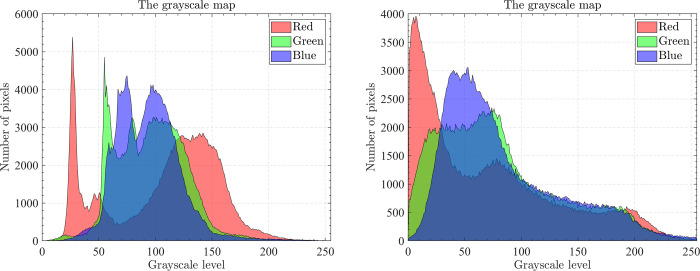
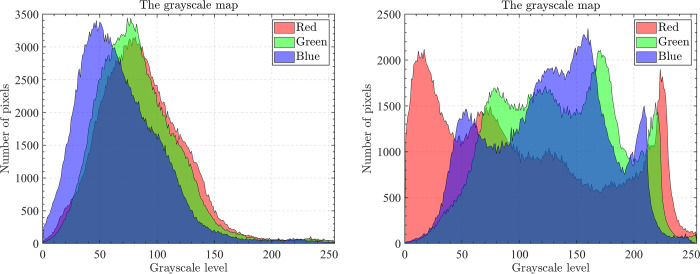
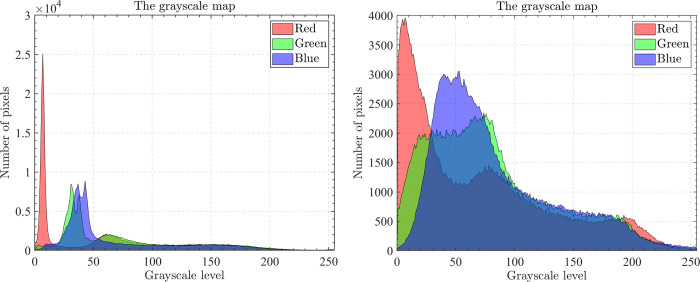
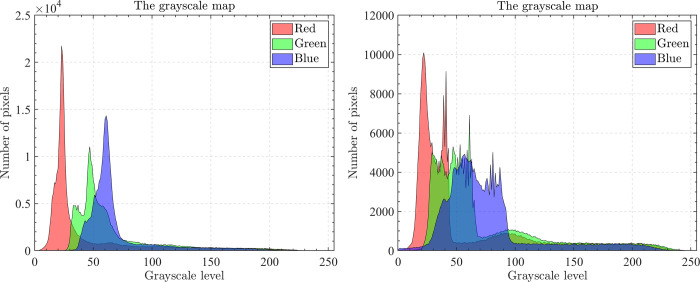
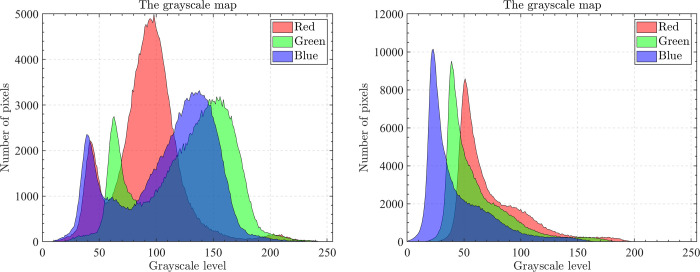
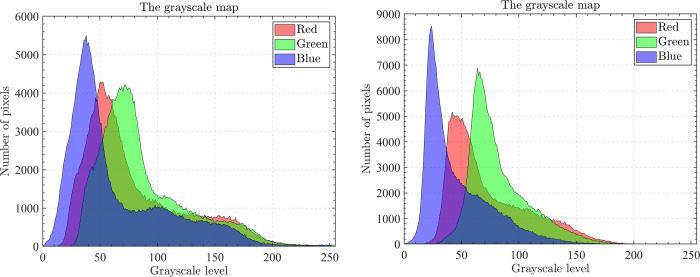
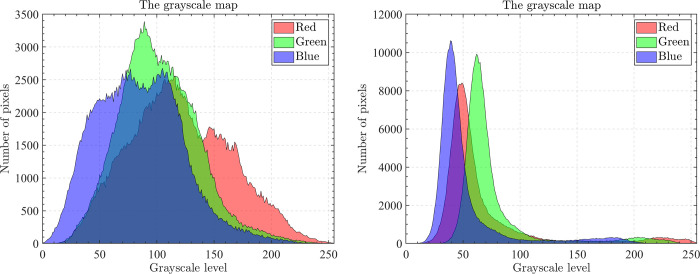
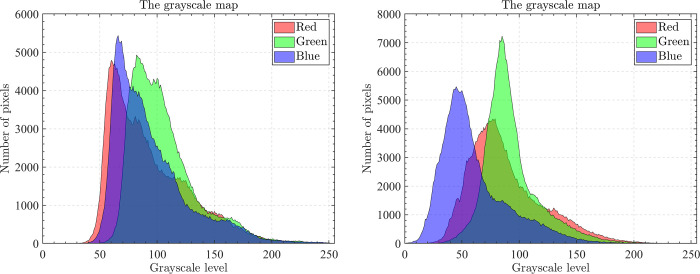
The optical aerial image used for image segmentation experiments are from the MASATI dataset [64], where each image has a size of 512×512. In this study, 16 images are selected for segmentation, which were named C0080, C0088, C0132, C0135, C0180, C0536, C1088, L0032, L0064, L0135, L0158, L0226, L0699, L0879, L1074, and X0017, as shown in Fig 6. All of these images are characterized by their own features which cover the vast majority of optical aerial image types. Furthermore, Figs 7–14 show the RGB histogram of all the selected images. The threshold values of each image are set to 8, 16, 24, 32, respectively. To ensure the fairness of the experiments, the population size was fixed to 60, the maximum number of iterations was set to 1000 and all the algorithms were run independently 31 times with the same configured environment.
Fig 6. The selected images for segmentation.
Fig 7. The RGB histogram of C0080 and C0088.
Fig 14. The RGB histogram of L1074 and X0017.
Fig 8. The RGB histogram of C0132 and C0135.
Fig 9. The RGB histogram of C0180 and C0536.
Fig 10. The RGB histogram of C1088 and L0032.
Fig 11. The RGB histogram of L0064 and L0135.
Fig 12. The RGB histogram of L0158 and L0226.
Fig 13. The RGB histogram of L0699 and L0879.
5.2.The evaluation metrics
As mentioned above, in this study PSNR, SSIM, and FSIM will be used as the performance metrics for image segmentation. This subsection will describe the effects of these three metrics in detail.
First is PSNR, peak signal-to-noise ratio, which is used to measure the difference between two images, which has a minimum value of 0 to represent the maximum difference. The mathematical formula of PSNR can be described as follows:
| (23) |
where RMES is the root mean square error, Iin and Iout are the original image and the segmented image, which have the size of M×N, respectively.
Next is SSIM, Structural Similarity, which is used to evaluate the similarity between two images. The value of SSIM is between 0 and 1, and if two images are completely identical, then the SSIM is equal to 1. Its mathematical model can be described as follows:
| (24) |
where μIin and μIout are the mean intensities of the original image and segmented image, respectively, σIin and σIout are the standard deviations of the original image and segmented image, respectively, σIin,Iout is the covariance of the original and segmented images, and C1 and C2 are two constants.
Finally, is FSIM, Feature Similarity, which is calculated by Phase Consistency (PC) and Gradient Magnitude (GM). It reflects the difference in features between the two images. The FSIM has the same value as the SSIM, which is also between 0 and 1, and the closer to 1 indicates that the feature information of the two images is more similar. It can be described as follows:
| (25) |
| (26) |
| (27) |
| (28) |
where PCIin and PCIout are the PC of the original image and segmented image, respectively, and T1 is a positive constant used to increase the stability of SPC. GIin and GIout represent the gradients of the original and segmented images, respectively, while T2 is also a positive constant that controls the range of GM. α and β are two constants, respectively. In short, for all three metrics, PSNR, SSIM, and FSIM, the bigger the better.
5.3.Experimental results and analysis
In this section, the experimental outcomes of multilevel thresholding segmentation are analyzed by combining images and tables. To verify the adaptivity of HGJO in handling the segmentation task, the selected optical aerial images were segmented at threshold levels of 8, 16, 24, and 32, respectively. The algorithms involved in the segmentation comparison are consistent with the previous section, and the experimental results are evaluated by three metrics: PSNR, SSIM, and FSIM. In addition, the comprehensive performance of all algorithms is ranked using the Friedman mean rank test, and the Wilcoxon rank-sum test is used to analyze the fitness of all algorithms on the Otsu method.
Tables 7–9 show the mean and std value of the PSNR, SSIM, and FSIM, respectively. It is noteworthy that the maximum mean and minimum std are highlighted in the tables. In addition, it should be mentioned that the segmentation results of the same algorithm on different images may behave differently. This is because each image corresponds to a different problem being processed. When compared to other algorithms, HGJO performs exceptionally well at the specified threshold level. Additionally, as the threshold level increases, this performance does not degrade.
Table 7. The PSNR results for all algorithms.
| Image Name | Level | HGJO | GJO | IGJO | RUN | AOA | DE | PSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| C0080 | 8 | 24.49 | 4.05E-02 | 22.23 | 7.44E-01 | 23.29 | 4.29E-01 | 22.48 | 6.72E-01 | 23.35 | 2.77E-01 | 24.38 | 1.37E-02 | 18.67 | 1.23E+00 |
| 16 | 29.64 | 1.23E-01 | 27.32 | 9.44E-01 | 27.37 | 9.60E-01 | 28.06 | 6.36E-01 | 28.32 | 5.83E-01 | 27.62 | 3.88E-01 | 23.61 | 9.81E-01 | |
| 24 | 34.82 | 5.66E-01 | 30.57 | 8.25E-01 | 29.67 | 1.13E+00 | 31.79 | 5.29E-01 | 31.60 | 6.71E-01 | 29.30 | 1.08E+00 | 26.08 | 1.35E+00 | |
| 32 | 37.86 | 2.54E-01 | 31.39 | 1.12E+00 | 31.66 | 9.20E-01 | 33.13 | 7.09E-01 | 34.18 | 6.69E-01 | 31.09 | 1.16E+00 | 29.66 | 1.01E+00 | |
| C0088 | 8 | 24.43 | 3.82E-03 | 23.80 | 1.87E-01 | 24.14 | 9.64E-02 | 24.19 | 5.86E-02 | 24.32 | 3.60E-02 | 24.42 | 6.67E-03 | 19.90 | 9.88E-01 |
| 16 | 30.31 | 3.29E-02 | 27.69 | 5.86E-01 | 28.11 | 5.34E-01 | 28.63 | 3.54E-01 | 29.67 | 1.49E-01 | 28.87 | 1.31E-01 | 25.37 | 7.67E-01 | |
| 24 | 33.88 | 7.34E-02 | 30.29 | 7.56E-01 | 30.99 | 4.90E-01 | 31.65 | 3.20E-01 | 32.76 | 1.47E-01 | 31.43 | 2.36E-01 | 26.86 | 8.28E-01 | |
| 32 | 36.45 | 1.20E-01 | 32.80 | 6.64E-01 | 32.77 | 5.70E-01 | 33.59 | 5.92E-01 | 35.21 | 1.44E-01 | 33.11 | 3.22E-01 | 29.08 | 8.26E-01 | |
| C0132 | 8 | 25.06 | 9.41E-03 | 24.04 | 3.70E-01 | 24.00 | 3.24E-01 | 24.50 | 1.32E-01 | 24.47 | 1.84E-01 | 25.06 | 2.55E-03 | 21.80 | 7.87E-01 |
| 16 | 30.21 | 1.12E-01 | 28.45 | 4.60E-01 | 28.44 | 5.82E-01 | 28.83 | 3.68E-01 | 28.56 | 3.12E-01 | 27.15 | 7.10E-01 | 24.53 | 1.03E+00 | |
| 24 | 33.67 | 1.32E-01 | 30.53 | 8.49E-01 | 30.76 | 5.64E-01 | 31.96 | 4.37E-01 | 32.31 | 2.78E-01 | 30.18 | 6.07E-01 | 27.45 | 8.25E-01 | |
| 32 | 36.54 | 2.06E-01 | 31.11 | 1.11E+00 | 33.01 | 7.12E-01 | 34.66 | 4.48E-01 | 34.42 | 3.38E-01 | 31.44 | 7.07E-01 | 29.51 | 9.41E-01 | |
| C0135 | 8 | 24.88 | 1.49E-02 | 22.72 | 6.23E-01 | 23.80 | 2.50E-01 | 24.62 | 7.07E-02 | 24.66 | 4.91E-02 | 24.85 | 1.29E-02 | 20.93 | 6.83E-01 |
| 16 | 30.86 | 2.71E-02 | 27.30 | 7.52E-01 | 28.88 | 4.79E-01 | 29.04 | 3.22E-01 | 29.84 | 1.88E-01 | 28.69 | 3.60E-01 | 22.41 | 1.42E+00 | |
| 24 | 34.36 | 5.83E-02 | 31.40 | 4.87E-01 | 30.84 | 7.32E-01 | 31.60 | 4.42E-01 | 32.33 | 3.44E-01 | 31.46 | 2.91E-01 | 28.01 | 8.52E-01 | |
| 32 | 36.99 | 1.55E-01 | 33.25 | 7.34E-01 | 32.73 | 8.07E-01 | 33.97 | 5.09E-01 | 34.77 | 2.39E-01 | 33.18 | 3.62E-01 | 28.91 | 1.12E+00 | |
| C0180 | 8 | 25.93 | 7.28E-15 | 24.13 | 7.54E-01 | 24.14 | 4.32E-01 | 25.79 | 4.54E-02 | 24.48 | 6.67E-01 | 25.92 | 1.60E-02 | 19.93 | 1.34E+00 |
| 16 | 31.50 | 1.29E-01 | 28.27 | 8.29E-01 | 29.09 | 7.22E-01 | 29.28 | 4.50E-01 | 29.58 | 6.41E-01 | 28.28 | 5.83E-01 | 26.59 | 1.08E+00 | |
| 24 | 35.56 | 1.79E-01 | 30.85 | 9.47E-01 | 31.25 | 9.23E-01 | 31.90 | 6.97E-01 | 31.40 | 8.09E-01 | 31.20 | 7.19E-01 | 26.83 | 1.45E+00 | |
| 32 | 38.02 | 3.85E-01 | 33.10 | 7.69E-01 | 34.51 | 5.80E-01 | 34.81 | 7.18E-01 | 34.78 | 6.03E-01 | 32.67 | 8.31E-01 | 29.27 | 1.46E+00 | |
| C0536 | 8 | 23.96 | 1.20E-02 | 23.10 | 5.06E-01 | 23.15 | 3.92E-01 | 23.96 | 1.72E-01 | 23.92 | 1.30E-01 | 23.93 | 7.28E-15 | 19.21 | 9.90E-01 |
| 16 | 30.47 | 2.06E-01 | 27.36 | 8.19E-01 | 28.59 | 5.59E-01 | 29.66 | 3.74E-01 | 28.43 | 4.67E-01 | 28.44 | 5.46E-01 | 25.25 | 1.10E+00 | |
| 24 | 34.82 | 2.39E-01 | 30.63 | 8.74E-01 | 31.74 | 6.40E-01 | 32.40 | 3.95E-01 | 32.08 | 3.16E-01 | 30.74 | 6.31E-01 | 26.26 | 1.42E+00 | |
| 32 | 37.09 | 2.12E-01 | 32.63 | 1.08E+00 | 33.44 | 6.58E-01 | 34.26 | 5.18E-01 | 34.63 | 3.94E-01 | 33.00 | 5.55E-01 | 30.15 | 1.10E+00 | |
| C1088 | 8 | 22.72 | 3.61E-02 | 21.41 | 6.58E-01 | 20.96 | 6.48E-01 | 21.90 | 5.84E-01 | 22.55 | 1.57E-01 | 22.64 | 1.70E-02 | 14.25 | 2.08E+00 |
| 16 | 30.20 | 1.52E-01 | 25.01 | 1.14E+00 | 26.89 | 8.42E-01 | 27.74 | 5.48E-01 | 28.49 | 6.76E-01 | 26.10 | 9.36E-01 | 20.20 | 1.72E+00 | |
| 24 | 34.42 | 2.71E-01 | 28.28 | 1.25E+00 | 28.86 | 8.17E-01 | 29.57 | 8.20E-01 | 31.94 | 7.32E-01 | 30.19 | 8.93E-01 | 25.24 | 1.76E+00 | |
| 32 | 37.08 | 2.96E-01 | 29.26 | 1.13E+00 | 30.97 | 1.08E+00 | 30.14 | 1.23E+00 | 33.39 | 8.25E-01 | 32.09 | 7.79E-01 | 25.89 | 1.83E+00 | |
| L0032 | 8 | 19.41 | 8.40E-02 | 18.27 | 3.89E-01 | 18.27 | 3.90E-01 | 18.27 | 1.36E+00 | 18.77 | 3.27E-01 | 19.13 | 5.91E-04 | 17.15 | 1.24E+00 |
| 16 | 23.11 | 2.20E-01 | 18.27 | 3.27E+00 | 19.61 | 3.33E+00 | 20.23 | 3.08E+00 | 20.01 | 2.88E+00 | 21.07 | 9.06E-01 | 19.21 | 1.87E+00 | |
| 24 | 26.59 | 5.89E-01 | 22.93 | 2.89E+00 | 21.06 | 3.70E+00 | 28.12 | 1.30E+00 | 22.29 | 2.55E+00 | 20.99 | 1.83E+00 | 19.33 | 3.11E+00 | |
| 32 | 33.67 | 1.51E+00 | 24.71 | 2.36E+00 | 26.27 | 2.36E+00 | 23.23 | 3.22E+00 | 24.63 | 2.52E+00 | 21.87 | 2.73E+00 | 21.09 | 3.25E+00 | |
| L0064 | 8 | 22.97 | 9.47E-02 | 21.97 | 4.48E-01 | 22.70 | 2.81E-01 | 21.11 | 7.57E-01 | 22.70 | 2.40E-01 | 22.70 | 8.62E-02 | 20.32 | 7.46E-01 |
| 16 | 29.35 | 2.97E-01 | 26.34 | 1.38E+00 | 28.05 | 9.55E-01 | 29.90 | 3.12E-01 | 27.30 | 1.18E+00 | 25.09 | 9.36E-01 | 22.62 | 1.72E+00 | |
| 24 | 33.15 | 3.16E-01 | 27.95 | 1.45E+00 | 30.39 | 8.34E-01 | 32.42 | 5.99E-01 | 31.42 | 8.71E-01 | 28.40 | 9.43E-01 | 23.92 | 1.75E+00 | |
| 32 | 37.55 | 6.83E-01 | 32.91 | 8.16E-01 | 32.90 | 1.06E+00 | 34.96 | 6.14E-01 | 33.69 | 6.63E-01 | 29.35 | 1.70E+00 | 24.30 | 2.22E+00 | |
| L0135 | 8 | 22.65 | 2.40E-03 | 21.18 | 5.20E-01 | 22.15 | 8.36E-01 | 21.20 | 9.25E-01 | 22.64 | 2.73E-01 | 22.64 | 2.51E-03 | 18.91 | 1.23E+00 |
| 16 | 26.98 | 2.31E-01 | 24.73 | 1.78E+00 | 23.84 | 2.53E+00 | 27.72 | 1.25E+00 | 25.12 | 2.11E+00 | 24.58 | 1.10E+00 | 22.73 | 1.42E+00 | |
| 24 | 34.26 | 1.30E+00 | 27.25 | 2.22E+00 | 27.33 | 2.12E+00 | 32.20 | 1.07E+00 | 27.91 | 2.58E+00 | 25.72 | 1.54E+00 | 24.53 | 2.32E+00 | |
| 32 | 37.40 | 2.29E+00 | 31.09 | 1.32E+00 | 28.63 | 2.04E+00 | 31.15 | 1.81E+00 | 28.48 | 2.80E+00 | 26.62 | 1.69E+00 | 26.11 | 2.46E+00 | |
| L0158 | 8 | 22.18 | 3.73E-02 | 20.09 | 8.82E-01 | 20.95 | 4.25E-01 | 22.15 | 7.18E-01 | 21.80 | 3.12E-01 | 22.01 | 7.28E-15 | 16.66 | 1.40E+00 |
| 16 | 28.77 | 3.08E-01 | 25.99 | 1.28E+00 | 25.58 | 1.38E+00 | 28.95 | 5.23E-01 | 28.96 | 5.72E-01 | 25.42 | 9.80E-01 | 21.43 | 2.13E+00 | |
| 24 | 33.98 | 5.43E-01 | 29.91 | 9.75E-01 | 28.55 | 1.47E+00 | 32.27 | 4.67E-01 | 32.12 | 6.11E-01 | 25.62 | 1.27E+00 | 23.21 | 2.32E+00 | |
| 32 | 36.91 | 6.09E-01 | 32.29 | 8.77E-01 | 30.86 | 1.50E+00 | 31.23 | 1.23E+00 | 33.77 | 8.02E-01 | 29.66 | 1.42E+00 | 25.87 | 1.86E+00 | |
| L0226 | 8 | 21.42 | 7.28E-15 | 19.79 | 9.06E-01 | 21.40 | 2.31E-01 | 21.29 | 5.09E-01 | 21.02 | 2.70E-01 | 21.42 | 1.58E-03 | 19.04 | 1.48E+00 |
| 16 | 29.47 | 4.40E-01 | 26.65 | 1.48E+00 | 26.62 | 1.75E+00 | 28.15 | 1.14E+00 | 25.90 | 1.91E+00 | 24.03 | 1.62E+00 | 21.29 | 2.26E+00 | |
| 24 | 36.22 | 6.15E-01 | 32.38 | 8.56E-01 | 32.12 | 9.04E-01 | 34.04 | 4.84E-01 | 32.57 | 9.25E-01 | 25.81 | 2.38E+00 | 25.16 | 2.00E+00 | |
| 32 | 39.28 | 2.34E-01 | 33.20 | 9.84E-01 | 34.61 | 8.55E-01 | 36.43 | 4.99E-01 | 35.06 | 6.74E-01 | 28.01 | 2.30E+00 | 25.39 | 2.28E+00 | |
| L0699 | 8 | 21.47 | 3.64E-15 | 18.85 | 1.04E+00 | 20.49 | 5.91E-01 | 20.50 | 1.39E+00 | 20.50 | 8.32E-01 | 21.47 | 3.64E-15 | 17.97 | 1.52E+00 |
| 16 | 30.10 | 5.00E-01 | 24.33 | 2.06E+00 | 27.08 | 1.34E+00 | 25.85 | 1.87E+00 | 27.55 | 1.56E+00 | 24.52 | 1.57E+00 | 20.41 | 2.70E+00 | |
| 24 | 36.47 | 6.57E-01 | 28.99 | 1.53E+00 | 29.70 | 1.47E+00 | 27.37 | 1.95E+00 | 32.20 | 9.90E-01 | 28.58 | 1.94E+00 | 23.38 | 3.08E+00 | |
| 32 | 39.63 | 3.95E-01 | 31.96 | 1.50E+00 | 31.48 | 1.66E+00 | 31.51 | 1.21E+00 | 35.91 | 6.84E-01 | 29.68 | 2.19E+00 | 24.74 | 2.34E+00 | |
| L0879 | 8 | 21.24 | 2.73E-04 | 20.50 | 5.17E-01 | 19.65 | 9.02E-01 | 20.50 | 1.29E+00 | 21.24 | 1.96E-01 | 21.24 | 3.64E-15 | 19.04 | 1.04E+00 |
| 16 | 27.92 | 4.45E-01 | 25.16 | 2.11E+00 | 24.97 | 2.05E+00 | 29.20 | 9.69E-01 | 24.41 | 2.17E+00 | 23.62 | 1.07E+00 | 21.55 | 1.50E+00 | |
| 24 | 33.62 | 8.29E-01 | 29.70 | 1.29E+00 | 24.72 | 2.66E+00 | 31.98 | 1.05E+00 | 26.94 | 2.52E+00 | 25.51 | 1.89E+00 | 20.90 | 2.84E+00 | |
| 32 | 38.05 | 1.48E+00 | 29.03 | 1.84E+00 | 30.59 | 1.70E+00 | 30.69 | 1.98E+00 | 33.78 | 1.39E+00 | 26.49 | 2.54E+00 | 24.02 | 2.54E+00 | |
| L1074 | 8 | 24.33 | 8.48E-03 | 23.13 | 6.21E-01 | 23.10 | 3.77E-01 | 24.49 | 2.97E-01 | 24.30 | 2.08E-01 | 24.30 | 7.28E-15 | 20.66 | 1.03E+00 |
| 16 | 31.32 | 1.25E-01 | 28.94 | 5.60E-01 | 29.48 | 4.96E-01 | 30.08 | 3.87E-01 | 29.82 | 4.15E-01 | 28.31 | 5.99E-01 | 25.21 | 9.50E-01 | |
| 24 | 35.34 | 1.26E-01 | 31.97 | 5.45E-01 | 32.37 | 6.48E-01 | 32.90 | 4.09E-01 | 33.08 | 2.61E-01 | 31.26 | 4.99E-01 | 25.63 | 1.33E+00 | |
| 32 | 38.08 | 1.89E-01 | 33.39 | 6.92E-01 | 34.05 | 8.71E-01 | 35.33 | 4.20E-01 | 35.10 | 3.77E-01 | 32.96 | 5.24E-01 | 29.60 | 8.36E-01 | |
| X0017 | 8 | 23.45 | 8.22E-03 | 22.19 | 4.50E-01 | 22.10 | 4.04E-01 | 22.72 | 1.84E-01 | 23.25 | 5.07E-02 | 23.39 | 1.47E-02 | 20.65 | 6.03E-01 |
| 16 | 29.26 | 7.51E-02 | 26.58 | 7.20E-01 | 27.56 | 4.75E-01 | 27.48 | 3.74E-01 | 28.68 | 1.21E-01 | 27.58 | 2.35E-01 | 24.42 | 9.23E-01 | |
| 24 | 32.99 | 6.53E-02 | 30.39 | 4.81E-01 | 29.71 | 7.04E-01 | 30.36 | 4.55E-01 | 32.18 | 1.29E-01 | 30.40 | 2.57E-01 | 27.84 | 5.01E-01 | |
| 32 | 35.60 | 9.65E-02 | 32.26 | 6.18E-01 | 32.25 | 7.39E-01 | 32.36 | 5.06E-01 | 34.54 | 1.36E-01 | 32.14 | 3.50E-01 | 28.82 | 7.64E-01 | |
| Friedman mean rank | 1.1328 | 4.9844 | 4.5781 | 3.0156 | 2.8828 | 4.4219 | 6.98441 | ||||||||
| Rank | 1 | 6 | 5 | 3 | 2 | 4 | 7 | ||||||||
Table 9. The FSIM results for all algorithms.
| Image Name | Level | HGJO | GJO | IGJO | RUN | AOA | DE | PSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| C0080 | 8 | 0.975 | 1.33E-04 | 0.962 | 4.17E-03 | 0.970 | 2.03E-03 | 0.964 | 3.40E-03 | 0.971 | 1.18E-03 | 0.975 | 3.94E-05 | 0.885 | 2.12E-02 |
| 16 | 0.992 | 2.11E-04 | 0.984 | 2.12E-03 | 0.987 | 2.02E-03 | 0.988 | 1.49E-03 | 0.990 | 9.56E-04 | 0.986 | 1.52E-03 | 0.939 | 1.04E-02 | |
| 24 | 0.997 | 5.07E-04 | 0.993 | 1.23E-03 | 0.993 | 1.33E-03 | 0.996 | 4.77E-04 | 0.996 | 6.36E-04 | 0.990 | 1.48E-03 | 0.977 | 3.62E-03 | |
| 32 | 0.998 | 2.77E-04 | 0.995 | 9.76E-04 | 0.993 | 1.17E-03 | 0.997 | 3.93E-04 | 0.998 | 4.65E-04 | 0.992 | 1.43E-03 | 0.992 | 1.91E-03 | |
| C0088 | 8 | 0.988 | 1.61E-05 | 0.986 | 6.69E-04 | 0.987 | 3.89E-04 | 0.987 | 3.53E-04 | 0.987 | 3.03E-04 | 0.988 | 3.22E-05 | 0.957 | 7.57E-03 |
| 16 | 0.997 | 1.62E-04 | 0.995 | 6.08E-04 | 0.995 | 5.93E-04 | 0.995 | 3.75E-04 | 0.997 | 9.38E-05 | 0.995 | 6.02E-04 | 0.989 | 2.20E-03 | |
| 24 | 0.999 | 5.39E-05 | 0.997 | 5.21E-04 | 0.998 | 3.82E-04 | 0.998 | 2.77E-04 | 0.999 | 5.21E-05 | 0.998 | 3.63E-04 | 0.991 | 1.30E-03 | |
| 32 | 0.999 | 3.48E-05 | 0.998 | 3.44E-04 | 0.997 | 3.99E-04 | 0.998 | 1.92E-04 | 0.999 | 3.25E-05 | 0.998 | 1.97E-04 | 0.996 | 8.69E-04 | |
| C0132 | 8 | 0.972 | 3.60E-04 | 0.963 | 5.11E-03 | 0.974 | 1.56E-03 | 0.976 | 5.06E-04 | 0.976 | 2.05E-03 | 0.972 | 3.03E-04 | 0.951 | 9.26E-03 |
| 16 | 0.993 | 2.17E-04 | 0.988 | 1.28E-03 | 0.989 | 1.69E-03 | 0.990 | 9.38E-04 | 0.991 | 9.38E-04 | 0.989 | 2.02E-03 | 0.977 | 6.35E-03 | |
| 24 | 0.996 | 2.06E-04 | 0.993 | 1.42E-03 | 0.995 | 1.09E-03 | 0.995 | 6.34E-04 | 0.996 | 4.78E-04 | 0.993 | 1.20E-03 | 0.983 | 3.29E-03 | |
| 32 | 0.998 | 2.79E-04 | 0.992 | 1.47E-03 | 0.996 | 9.72E-04 | 0.998 | 3.16E-04 | 0.998 | 2.39E-04 | 0.997 | 5.51E-04 | 0.990 | 2.11E-03 | |
| C0135 | 8 | 0.977 | 8.04E-06 | 0.968 | 2.00E-03 | 0.976 | 4.70E-04 | 0.976 | 4.25E-04 | 0.978 | 2.87E-04 | 0.977 | 7.67E-06 | 0.944 | 8.20E-03 |
| 16 | 0.995 | 1.73E-04 | 0.987 | 1.87E-03 | 0.992 | 1.10E-03 | 0.990 | 9.83E-04 | 0.994 | 4.07E-04 | 0.989 | 1.27E-03 | 0.951 | 8.64E-03 | |
| 24 | 0.998 | 1.60E-04 | 0.994 | 9.36E-04 | 0.994 | 1.19E-03 | 0.996 | 4.94E-04 | 0.997 | 1.81E-04 | 0.995 | 6.62E-04 | 0.984 | 2.68E-03 | |
| 32 | 0.999 | 9.61E-05 | 0.997 | 7.34E-04 | 0.997 | 5.38E-04 | 0.997 | 3.68E-04 | 0.999 | 1.57E-04 | 0.996 | 6.31E-04 | 0.995 | 1.33E-03 | |
| C0180 | 8 | 0.956 | 0.00E+00 | 0.947 | 4.18E-03 | 0.948 | 2.06E-03 | 0.951 | 1.22E-03 | 0.955 | 3.55E-03 | 0.955 | 3.45E-04 | 0.917 | 2.50E-02 |
| 16 | 0.986 | 6.60E-04 | 0.974 | 3.50E-03 | 0.978 | 3.18E-03 | 0.979 | 2.06E-03 | 0.980 | 1.59E-03 | 0.979 | 2.74E-03 | 0.961 | 8.50E-03 | |
| 24 | 0.995 | 2.80E-04 | 0.982 | 3.12E-03 | 0.985 | 2.72E-03 | 0.988 | 1.51E-03 | 0.987 | 1.59E-03 | 0.987 | 2.30E-03 | 0.954 | 1.14E-02 | |
| 32 | 0.998 | 4.18E-04 | 0.991 | 2.08E-03 | 0.992 | 1.16E-03 | 0.995 | 9.35E-04 | 0.992 | 1.19E-03 | 0.991 | 2.81E-03 | 0.967 | 6.64E-03 | |
| C0536 | 8 | 0.947 | 1.43E-04 | 0.941 | 7.41E-03 | 0.942 | 5.99E-03 | 0.947 | 6.61E-03 | 0.947 | 2.75E-03 | 0.947 | 4.55E-16 | 0.934 | 1.08E-02 |
| 16 | 0.988 | 1.77E-03 | 0.981 | 2.34E-03 | 0.983 | 2.10E-03 | 0.985 | 1.29E-03 | 0.983 | 1.02E-03 | 0.981 | 4.16E-03 | 0.967 | 8.89E-03 | |
| 24 | 0.996 | 7.85E-04 | 0.990 | 2.24E-03 | 0.990 | 1.86E-03 | 0.992 | 1.19E-03 | 0.989 | 8.61E-04 | 0.986 | 2.58E-03 | 0.972 | 9.37E-03 | |
| 32 | 0.997 | 2.70E-04 | 0.990 | 2.03E-03 | 0.995 | 1.17E-03 | 0.995 | 6.55E-04 | 0.995 | 7.87E-04 | 0.991 | 1.78E-03 | 0.979 | 3.89E-03 | |
| C1088 | 8 | 0.951 | 8.77E-04 | 0.928 | 8.46E-03 | 0.921 | 8.23E-03 | 0.937 | 5.06E-03 | 0.947 | 1.83E-03 | 0.949 | 4.13E-04 | 0.799 | 4.52E-02 |
| 16 | 0.990 | 6.26E-04 | 0.963 | 6.40E-03 | 0.975 | 4.30E-03 | 0.985 | 1.73E-03 | 0.983 | 2.61E-03 | 0.975 | 4.34E-03 | 0.878 | 2.48E-02 | |
| 24 | 0.996 | 4.42E-04 | 0.982 | 3.54E-03 | 0.989 | 1.61E-03 | 0.992 | 1.46E-03 | 0.994 | 1.00E-03 | 0.994 | 2.96E-03 | 0.979 | 1.06E-02 | |
| 32 | 0.998 | 2.02E-04 | 0.990 | 1.57E-03 | 0.993 | 1.68E-03 | 0.993 | 1.31E-03 | 0.996 | 7.79E-04 | 0.994 | 1.83E-03 | 0.971 | 7.71E-03 | |
| L0032 | 8 | 0.921 | 6.75E-04 | 0.917 | 1.76E-03 | 0.917 | 1.57E-03 | 0.917 | 1.25E-02 | 0.919 | 1.96E-03 | 0.919 | 1.44E-04 | 0.884 | 3.37E-02 |
| 16 | 0.943 | 1.93E-03 | 0.917 | 2.62E-02 | 0.923 | 2.59E-02 | 0.927 | 1.88E-02 | 0.924 | 2.33E-02 | 0.924 | 9.88E-03 | 0.926 | 2.44E-02 | |
| 24 | 0.980 | 8.13E-03 | 0.944 | 1.74E-02 | 0.932 | 2.61E-02 | 0.994 | 2.82E-03 | 0.900 | 2.24E-02 | 0.972 | 2.24E-02 | 0.918 | 3.44E-02 | |
| 32 | 0.997 | 5.54E-03 | 0.955 | 9.36E-03 | 0.974 | 7.09E-03 | 0.947 | 1.52E-02 | 0.958 | 1.34E-02 | 0.829 | 3.63E-02 | 0.939 | 2.12E-02 | |
| L0064 | 8 | 0.969 | 5.92E-04 | 0.965 | 1.73E-03 | 0.968 | 1.98E-03 | 0.958 | 4.17E-03 | 0.967 | 1.31E-03 | 0.967 | 5.74E-04 | 0.944 | 1.07E-02 |
| 16 | 0.993 | 6.84E-04 | 0.985 | 3.19E-03 | 0.991 | 1.23E-03 | 0.995 | 4.15E-04 | 0.990 | 2.22E-03 | 0.983 | 4.46E-03 | 0.980 | 7.06E-03 | |
| 24 | 0.997 | 3.60E-04 | 0.991 | 1.65E-03 | 0.994 | 1.10E-03 | 0.997 | 4.47E-04 | 0.997 | 9.12E-04 | 0.996 | 1.80E-03 | 0.975 | 7.58E-03 | |
| 32 | 0.999 | 2.20E-04 | 0.998 | 6.91E-04 | 0.997 | 6.62E-04 | 0.999 | 3.46E-04 | 0.998 | 2.71E-04 | 0.996 | 2.42E-03 | 0.990 | 5.83E-03 | |
| L0135 | 8 | 0.967 | 4.77E-04 | 0.950 | 4.98E-03 | 0.963 | 3.52E-03 | 0.950 | 5.04E-03 | 0.967 | 5.39E-04 | 0.967 | 4.28E-04 | 0.865 | 3.01E-02 |
| 16 | 0.992 | 1.15E-03 | 0.978 | 3.88E-03 | 0.972 | 5.53E-03 | 0.993 | 1.86E-03 | 0.982 | 4.50E-03 | 0.979 | 4.13E-03 | 0.952 | 9.37E-03 | |
| 24 | 0.998 | 6.89E-04 | 0.992 | 1.43E-03 | 0.991 | 1.36E-03 | 0.995 | 9.63E-04 | 0.995 | 8.49E-04 | 0.990 | 2.44E-03 | 0.981 | 7.88E-03 | |
| 32 | 0.999 | 3.56E-04 | 0.996 | 7.33E-04 | 0.996 | 7.45E-04 | 0.994 | 1.70E-03 | 0.995 | 8.54E-04 | 0.987 | 2.41E-03 | 0.984 | 6.54E-03 | |
| L0158 | 8 | 0.964 | 5.09E-04 | 0.948 | 7.99E-03 | 0.954 | 3.67E-03 | 0.967 | 5.80E-03 | 0.960 | 3.09E-03 | 0.962 | 0.00E+00 | 0.921 | 1.65E-02 |
| 16 | 0.992 | 1.14E-03 | 0.983 | 3.95E-03 | 0.981 | 5.72E-03 | 0.996 | 7.57E-04 | 0.994 | 1.24E-03 | 0.988 | 6.61E-03 | 0.959 | 1.48E-02 | |
| 24 | 0.998 | 7.64E-04 | 0.994 | 1.22E-03 | 0.991 | 2.42E-03 | 0.998 | 2.76E-04 | 0.998 | 3.94E-04 | 0.990 | 2.85E-03 | 0.977 | 1.17E-02 | |
| 32 | 0.999 | 3.70E-04 | 0.998 | 3.13E-04 | 0.994 | 1.37E-03 | 0.997 | 4.39E-04 | 0.998 | 3.72E-04 | 0.992 | 1.80E-03 | 0.984 | 3.77E-03 | |
| L0226 | 8 | 0.960 | 0.00E+00 | 0.941 | 5.84E-03 | 0.963 | 1.44E-03 | 0.953 | 2.15E-03 | 0.961 | 1.00E-03 | 0.961 | 2.56E-04 | 0.876 | 2.49E-02 |
| 16 | 0.990 | 8.55E-04 | 0.986 | 2.51E-03 | 0.986 | 2.03E-03 | 0.987 | 1.25E-03 | 0.984 | 3.05E-03 | 0.989 | 3.25E-03 | 0.972 | 8.56E-03 | |
| 24 | 0.998 | 4.03E-04 | 0.994 | 1.01E-03 | 0.991 | 1.49E-03 | 0.995 | 7.68E-04 | 0.996 | 6.68E-04 | 0.988 | 2.81E-03 | 0.981 | 7.68E-03 | |
| 32 | 0.999 | 1.09E-04 | 0.995 | 1.05E-03 | 0.996 | 6.03E-04 | 0.997 | 4.02E-04 | 0.997 | 3.57E-04 | 0.995 | 1.75E-03 | 0.991 | 3.28E-03 | |
| L0699 | 8 | 0.943 | 0.00E+00 | 0.918 | 9.03E-03 | 0.937 | 3.67E-03 | 0.936 | 9.32E-03 | 0.937 | 6.95E-03 | 0.943 | 0.00E+00 | 0.948 | 2.85E-02 |
| 16 | 0.986 | 2.34E-03 | 0.960 | 8.36E-03 | 0.973 | 5.58E-03 | 0.968 | 6.71E-03 | 0.974 | 5.98E-03 | 0.958 | 8.86E-03 | 0.923 | 2.14E-02 | |
| 24 | 0.997 | 9.79E-04 | 0.987 | 3.22E-03 | 0.985 | 3.11E-03 | 0.981 | 4.08E-03 | 0.990 | 2.14E-03 | 0.979 | 6.18E-03 | 0.935 | 1.77E-02 | |
| 32 | 0.999 | 2.49E-04 | 0.994 | 1.88E-03 | 0.993 | 2.09E-03 | 0.995 | 8.85E-04 | 0.999 | 7.23E-04 | 0.982 | 5.05E-03 | 0.953 | 1.18E-02 | |
| L0879 | 8 | 0.962 | 7.77E-05 | 0.955 | 4.93E-03 | 0.944 | 8.41E-03 | 0.955 | 8.43E-03 | 0.962 | 1.80E-03 | 0.962 | 2.28E-16 | 0.958 | 2.30E-02 |
| 16 | 0.993 | 1.05E-03 | 0.987 | 2.93E-03 | 0.985 | 3.04E-03 | 0.994 | 8.56E-04 | 0.984 | 3.28E-03 | 0.987 | 3.62E-03 | 0.975 | 1.08E-02 | |
| 24 | 0.998 | 5.37E-04 | 0.995 | 9.02E-04 | 0.983 | 3.30E-03 | 0.997 | 4.97E-04 | 0.992 | 1.82E-03 | 0.985 | 2.70E-03 | 0.958 | 9.37E-03 | |
| 32 | 0.999 | 3.64E-04 | 0.994 | 1.08E-03 | 0.997 | 5.13E-04 | 0.998 | 1.49E-03 | 0.998 | 2.75E-04 | 0.995 | 1.86E-03 | 0.990 | 6.74E-03 | |
| L1074 | 8 | 0.983 | 1.08E-04 | 0.978 | 2.66E-03 | 0.978 | 1.74E-03 | 0.983 | 7.57E-04 | 0.983 | 8.91E-04 | 0.983 | 0.00E+00 | 0.982 | 8.03E-03 |
| 16 | 0.996 | 2.65E-04 | 0.994 | 8.05E-04 | 0.993 | 1.17E-03 | 0.996 | 5.68E-04 | 0.996 | 6.06E-04 | 0.994 | 1.36E-03 | 0.989 | 3.70E-03 | |
| 24 | 0.999 | 1.15E-04 | 0.998 | 6.61E-04 | 0.998 | 6.14E-04 | 0.997 | 3.67E-04 | 0.999 | 9.92E-05 | 0.996 | 9.59E-04 | 0.995 | 1.89E-03 | |
| 32 | 0.999 | 7.77E-05 | 0.999 | 3.86E-04 | 0.998 | 5.77E-04 | 0.999 | 1.52E-04 | 0.999 | 4.11E-05 | 0.998 | 3.90E-04 | 0.994 | 1.60E-03 | |
| X0017 | 8 | 0.984 | 4.13E-05 | 0.979 | 1.94E-03 | 0.979 | 1.70E-03 | 0.980 | 1.13E-03 | 0.984 | 2.07E-04 | 0.984 | 9.19E-05 | 0.968 | 4.20E-03 |
| 16 | 0.996 | 1.18E-04 | 0.990 | 1.52E-03 | 0.993 | 8.46E-04 | 0.993 | 8.67E-04 | 0.995 | 1.69E-04 | 0.991 | 9.11E-04 | 0.981 | 3.24E-03 | |
| 24 | 0.998 | 1.31E-04 | 0.996 | 3.31E-04 | 0.996 | 5.48E-04 | 0.996 | 3.13E-04 | 0.998 | 1.13E-04 | 0.995 | 6.34E-04 | 0.990 | 1.91E-03 | |
| 32 | 0.999 | 7.92E-05 | 0.997 | 3.82E-04 | 0.997 | 4.43E-04 | 0.998 | 2.82E-04 | 0.999 | 5.66E-05 | 0.997 | 3.27E-04 | 0.990 | 1.43E-03 | |
| Friedman mean rank | 1.5547 | 5.0938 | 4.4531 | 3.2031 | 2.6484 | 4.3125 | 6.7344 | ||||||||
| Rank | 1 | 6 | 5 | 3 | 2 | 4 | 7 | ||||||||
According to the analysis of the results of PSNR recorded in Table 7, the proposed HGJO algorithm obtained the best experimental data in terms of accuracy and stability in the segmentation experiments of C0080, C0088, C0132, C0135, C0180, C1088, L0226, L0699 and X0017 for a total of 9 images. The other compared algorithms did not obtain the best results in the segmentation experiments for any of the images. The top three algorithms ranked by the Friedman mean rank test are as follows: the first ranked is the proposed HGJO algorithm, the AOA algorithm ranks second, and the RUN ranks third.
In Table 8, which records the results about SSIM, the proposed algorithm achieves optimal results in the segmentation experiments of C0080, C0536, and X0017 for a total of 3 images. The rest of the algorithms also did not achieve optimal results on any of the images. According to the Friedman mean rank test, the top three algorithms were, HGJO, RUN, and AOA.
Table 8. The SSIM results for all algorithms.
| Image Name | Level | HGJO | GJO | IGJO | RUN | AOA | DE | PSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| C0080 | 8 | 0.892 | 8.99E-04 | 0.833 | 1.74E-02 | 0.868 | 7.74E-03 | 0.844 | 1.39E-02 | 0.869 | 5.55E-03 | 0.890 | 3.69E-04 | 0.660 | 4.64E-02 |
| 16 | 0.957 | 1.16E-03 | 0.937 | 9.46E-03 | 0.940 | 9.50E-03 | 0.945 | 6.07E-03 | 0.945 | 5.63E-03 | 0.932 | 5.13E-03 | 0.840 | 2.12E-02 | |
| 24 | 0.987 | 3.13E-03 | 0.966 | 4.53E-03 | 0.963 | 6.18E-03 | 0.977 | 2.34E-03 | 0.974 | 3.20E-03 | 0.951 | 8.67E-03 | 0.900 | 1.83E-02 | |
| 32 | 0.993 | 5.42E-04 | 0.973 | 4.29E-03 | 0.970 | 4.15E-03 | 0.983 | 1.95E-03 | 0.985 | 1.84E-03 | 0.963 | 6.76E-03 | 0.948 | 8.88E-03 | |
| C0088 | 8 | 0.938 | 4.63E-04 | 0.933 | 1.56E-03 | 0.937 | 7.18E-04 | 0.940 | 6.52E-04 | 0.940 | 8.79E-04 | 0.937 | 2.69E-04 | 0.841 | 2.42E-02 |
| 16 | 0.983 | 1.40E-04 | 0.970 | 2.84E-03 | 0.974 | 2.33E-03 | 0.978 | 1.41E-03 | 0.980 | 8.15E-04 | 0.976 | 1.17E-03 | 0.951 | 6.26E-03 | |
| 24 | 0.993 | 1.33E-04 | 0.984 | 1.82E-03 | 0.986 | 1.25E-03 | 0.989 | 6.29E-04 | 0.990 | 4.02E-04 | 0.985 | 1.03E-03 | 0.961 | 5.25E-03 | |
| 32 | 0.996 | 1.14E-04 | 0.991 | 1.11E-03 | 0.991 | 7.98E-04 | 0.993 | 6.94E-04 | 0.994 | 2.35E-04 | 0.989 | 8.64E-04 | 0.974 | 3.34E-03 | |
| C0132 | 8 | 0.859 | 2.48E-04 | 0.835 | 1.06E-02 | 0.809 | 1.59E-02 | 0.838 | 5.96E-03 | 0.837 | 6.73E-03 | 0.859 | 6.78E-04 | 0.615 | 6.47E-02 |
| 16 | 0.940 | 1.50E-03 | 0.917 | 1.31E-02 | 0.937 | 1.45E-02 | 0.944 | 3.81E-03 | 0.911 | 8.40E-03 | 0.872 | 1.77E-02 | 0.795 | 3.49E-02 | |
| 24 | 0.977 | 1.68E-03 | 0.951 | 8.95E-03 | 0.945 | 8.01E-03 | 0.974 | 2.32E-03 | 0.965 | 3.12E-03 | 0.938 | 9.27E-03 | 0.859 | 2.28E-02 | |
| 32 | 0.989 | 1.13E-03 | 0.939 | 1.05E-02 | 0.980 | 5.62E-03 | 0.986 | 1.57E-03 | 0.978 | 2.33E-03 | 0.941 | 8.56E-03 | 0.927 | 1.57E-02 | |
| C0135 | 8 | 0.907 | 7.95E-04 | 0.858 | 1.58E-02 | 0.882 | 5.95E-03 | 0.914 | 2.17E-03 | 0.910 | 1.88E-03 | 0.905 | 7.59E-04 | 0.759 | 3.13E-02 |
| 16 | 0.974 | 3.54E-04 | 0.946 | 6.34E-03 | 0.960 | 4.39E-03 | 0.968 | 1.96E-03 | 0.964 | 2.18E-03 | 0.951 | 4.17E-03 | 0.775 | 3.83E-02 | |
| 24 | 0.989 | 2.38E-04 | 0.979 | 2.56E-03 | 0.977 | 3.05E-03 | 0.981 | 1.45E-03 | 0.980 | 1.58E-03 | 0.976 | 2.09E-03 | 0.939 | 9.22E-03 | |
| 32 | 0.993 | 3.01E-04 | 0.985 | 1.74E-03 | 0.984 | 2.36E-03 | 0.989 | 8.99E-04 | 0.988 | 7.17E-04 | 0.981 | 1.69E-03 | 0.948 | 9.13E-03 | |
| C0180 | 8 | 0.888 | 1.14E-16 | 0.845 | 2.11E-02 | 0.843 | 1.32E-02 | 0.890 | 1.75E-03 | 0.849 | 2.03E-02 | 0.888 | 1.32E-04 | 0.689 | 5.44E-02 |
| 16 | 0.962 | 1.93E-03 | 0.928 | 1.05E-02 | 0.939 | 8.61E-03 | 0.945 | 5.41E-03 | 0.939 | 8.48E-03 | 0.908 | 1.18E-02 | 0.885 | 2.21E-02 | |
| 24 | 0.986 | 8.68E-04 | 0.957 | 6.91E-03 | 0.958 | 6.82E-03 | 0.970 | 3.44E-03 | 0.956 | 6.58E-03 | 0.949 | 7.61E-03 | 0.900 | 2.12E-02 | |
| 32 | 0.992 | 1.11E-03 | 0.977 | 4.08E-03 | 0.980 | 2.45E-03 | 0.984 | 2.33E-03 | 0.980 | 2.55E-03 | 0.960 | 6.16E-03 | 0.926 | 1.60E-02 | |
| C0536 | 8 | 0.832 | 5.78E-04 | 0.812 | 1.58E-02 | 0.814 | 1.36E-02 | 0.832 | 8.51E-03 | 0.830 | 6.65E-03 | 0.831 | 3.41E-16 | 0.626 | 5.13E-02 |
| 16 | 0.959 | 4.78E-03 | 0.932 | 1.09E-02 | 0.925 | 9.92E-03 | 0.951 | 5.21E-03 | 0.925 | 9.26E-03 | 0.923 | 1.14E-02 | 0.862 | 2.94E-02 | |
| 24 | 0.987 | 1.46E-03 | 0.963 | 6.30E-03 | 0.970 | 4.19E-03 | 0.979 | 2.26E-03 | 0.969 | 3.01E-03 | 0.951 | 7.51E-03 | 0.868 | 2.90E-02 | |
| 32 | 0.992 | 6.71E-04 | 0.974 | 5.01E-03 | 0.984 | 2.64E-03 | 0.986 | 1.56E-03 | 0.984 | 1.69E-03 | 0.968 | 5.25E-03 | 0.961 | 1.08E-02 | |
| C1088 | 8 | 0.847 | 1.02E-03 | 0.812 | 1.97E-02 | 0.795 | 2.03E-02 | 0.824 | 1.71E-02 | 0.842 | 4.92E-03 | 0.845 | 4.82E-04 | 0.240 | 1.59E-01 |
| 16 | 0.965 | 2.46E-03 | 0.898 | 1.87E-02 | 0.926 | 1.08E-02 | 0.954 | 4.77E-03 | 0.941 | 1.15E-02 | 0.907 | 1.40E-02 | 0.655 | 5.95E-02 | |
| 24 | 0.988 | 1.26E-03 | 0.938 | 9.89E-03 | 0.960 | 5.27E-03 | 0.968 | 4.17E-03 | 0.983 | 2.66E-03 | 0.952 | 8.91E-03 | 0.886 | 2.28E-02 | |
| 32 | 0.993 | 4.01E-04 | 0.966 | 5.92E-03 | 0.977 | 4.26E-03 | 0.974 | 3.72E-03 | 0.986 | 1.80E-03 | 0.969 | 4.01E-03 | 0.884 | 2.23E-02 | |
| L0032 | 8 | 0.582 | 6.35E-03 | 0.496 | 2.95E-02 | 0.496 | 2.92E-02 | 0.496 | 7.65E-02 | 0.534 | 2.39E-02 | 0.561 | 1.41E-05 | 0.533 | 9.14E-02 |
| 16 | 0.778 | 8.88E-03 | 0.496 | 1.24E-01 | 0.595 | 1.08E-01 | 0.639 | 7.73E-02 | 0.620 | 8.59E-02 | 0.684 | 3.84E-02 | 0.576 | 9.30E-02 | |
| 24 | 0.869 | 1.39E-02 | 0.773 | 5.81E-02 | 0.686 | 9.87E-02 | 0.916 | 1.50E-02 | 0.742 | 5.78E-02 | 0.521 | 8.35E-02 | 0.579 | 1.19E-01 | |
| 32 | 0.963 | 2.15E-02 | 0.829 | 3.49E-02 | 0.865 | 3.35E-02 | 0.797 | 5.47E-02 | 0.880 | 3.06E-02 | 0.799 | 4.73E-02 | 0.702 | 8.43E-02 | |
| L0064 | 8 | 0.812 | 3.68E-03 | 0.781 | 1.39E-02 | 0.802 | 1.10E-02 | 0.751 | 2.72E-02 | 0.802 | 9.50E-03 | 0.802 | 3.33E-03 | 0.702 | 3.21E-02 |
| 16 | 0.941 | 5.31E-03 | 0.894 | 2.56E-02 | 0.919 | 1.84E-02 | 0.964 | 4.50E-03 | 0.907 | 2.09E-02 | 0.853 | 2.07E-02 | 0.813 | 4.32E-02 | |
| 24 | 0.972 | 3.10E-03 | 0.921 | 1.53E-02 | 0.947 | 8.76E-03 | 0.984 | 1.84E-03 | 0.959 | 8.91E-03 | 0.916 | 1.35E-02 | 0.819 | 3.57E-02 | |
| 32 | 0.992 | 3.66E-03 | 0.980 | 2.92E-03 | 0.972 | 6.22E-03 | 0.988 | 1.33E-03 | 0.978 | 3.10E-03 | 0.927 | 1.84E-02 | 0.827 | 3.80E-02 | |
| L0135 | 8 | 0.793 | 1.37E-04 | 0.740 | 1.85E-02 | 0.778 | 3.00E-02 | 0.740 | 3.41E-02 | 0.793 | 1.05E-02 | 0.793 | 1.48E-04 | 0.582 | 5.97E-02 |
| 16 | 0.904 | 4.98E-03 | 0.857 | 3.03E-02 | 0.834 | 4.23E-02 | 0.923 | 1.39E-02 | 0.863 | 3.45E-02 | 0.847 | 2.41E-02 | 0.790 | 3.71E-02 | |
| 24 | 0.982 | 1.37E-02 | 0.910 | 2.34E-02 | 0.909 | 2.27E-02 | 0.979 | 3.20E-03 | 0.918 | 2.40E-02 | 0.875 | 2.30E-02 | 0.846 | 3.80E-02 | |
| 32 | 0.990 | 1.30E-02 | 0.961 | 6.98E-03 | 0.929 | 1.42E-02 | 0.971 | 5.55E-03 | 0.924 | 2.05E-02 | 0.890 | 2.18E-02 | 0.884 | 3.26E-02 | |
| L0158 | 8 | 0.865 | 1.03E-03 | 0.809 | 2.35E-02 | 0.834 | 1.07E-02 | 0.868 | 1.58E-02 | 0.855 | 7.76E-03 | 0.861 | 4.55E-16 | 0.670 | 4.68E-02 |
| 16 | 0.960 | 3.19E-03 | 0.931 | 1.34E-02 | 0.924 | 1.58E-02 | 0.970 | 3.64E-03 | 0.963 | 5.19E-03 | 0.918 | 1.31E-02 | 0.825 | 3.69E-02 | |
| 24 | 0.988 | 2.69E-03 | 0.968 | 5.32E-03 | 0.957 | 8.87E-03 | 0.987 | 1.13E-03 | 0.983 | 2.22E-03 | 0.915 | 1.35E-02 | 0.880 | 2.94E-02 | |
| 32 | 0.994 | 1.82E-03 | 0.983 | 2.24E-03 | 0.972 | 5.72E-03 | 0.979 | 3.31E-03 | 0.987 | 2.18E-03 | 0.962 | 8.50E-03 | 0.921 | 1.78E-02 | |
| L0226 | 8 | 0.680 | 2.28E-16 | 0.614 | 4.48E-02 | 0.679 | 1.04E-02 | 0.684 | 2.44E-02 | 0.661 | 1.23E-02 | 0.680 | 7.45E-05 | 0.561 | 6.85E-02 |
| 16 | 0.910 | 1.07E-02 | 0.866 | 3.50E-02 | 0.840 | 4.26E-02 | 0.912 | 2.30E-02 | 0.822 | 4.62E-02 | 0.760 | 4.64E-02 | 0.664 | 8.24E-02 | |
| 24 | 0.987 | 5.91E-03 | 0.951 | 1.01E-02 | 0.973 | 9.77E-03 | 0.984 | 1.89E-03 | 0.953 | 1.11E-02 | 0.809 | 4.83E-02 | 0.798 | 4.95E-02 | |
| 32 | 0.994 | 1.03E-03 | 0.953 | 8.19E-03 | 0.984 | 3.13E-03 | 0.990 | 1.09E-03 | 0.971 | 4.35E-03 | 0.859 | 3.39E-02 | 0.791 | 4.62E-02 | |
| L0699 | 8 | 0.760 | 2.28E-16 | 0.670 | 3.33E-02 | 0.727 | 1.83E-02 | 0.728 | 3.77E-02 | 0.728 | 2.37E-02 | 0.760 | 2.28E-16 | 0.601 | 5.31E-02 |
| 16 | 0.934 | 7.78E-03 | 0.832 | 3.56E-02 | 0.889 | 2.27E-02 | 0.865 | 2.85E-02 | 0.896 | 2.45E-02 | 0.833 | 2.84E-02 | 0.662 | 7.43E-02 | |
| 24 | 0.988 | 4.64E-03 | 0.922 | 1.65E-02 | 0.925 | 1.43E-02 | 0.897 | 2.04E-02 | 0.953 | 8.70E-03 | 0.905 | 2.32E-02 | 0.808 | 7.42E-02 | |
| 32 | 0.994 | 1.22E-03 | 0.960 | 6.83E-03 | 0.960 | 1.03E-02 | 0.963 | 6.47E-03 | 0.984 | 2.45E-03 | 0.920 | 1.91E-02 | 0.788 | 4.26E-02 | |
| L0879 | 8 | 0.789 | 9.89E-06 | 0.765 | 1.71E-02 | 0.733 | 3.13E-02 | 0.765 | 4.03E-02 | 0.789 | 6.74E-03 | 0.789 | 2.28E-16 | 0.705 | 4.08E-02 |
| 16 | 0.936 | 7.58E-03 | 0.891 | 2.92E-02 | 0.884 | 2.79E-02 | 0.963 | 6.92E-03 | 0.873 | 2.91E-02 | 0.853 | 2.23E-02 | 0.792 | 4.52E-02 | |
| 24 | 0.981 | 5.95E-03 | 0.959 | 8.38E-03 | 0.877 | 2.76E-02 | 0.983 | 2.66E-03 | 0.919 | 1.91E-02 | 0.893 | 2.59E-02 | 0.760 | 5.82E-02 | |
| 32 | 0.994 | 5.51E-03 | 0.945 | 1.09E-02 | 0.961 | 7.91E-03 | 0.969 | 6.45E-03 | 0.981 | 4.26E-03 | 0.908 | 2.60E-02 | 0.857 | 3.41E-02 | |
| L1074 | 8 | 0.929 | 6.34E-05 | 0.909 | 1.08E-02 | 0.909 | 7.15E-03 | 0.932 | 6.41E-03 | 0.929 | 4.24E-03 | 0.929 | 0.00E+00 | 0.833 | 2.63E-02 |
| 16 | 0.986 | 8.00E-04 | 0.976 | 2.79E-03 | 0.976 | 2.51E-03 | 0.983 | 1.33E-03 | 0.978 | 2.20E-03 | 0.965 | 5.00E-03 | 0.944 | 1.01E-02 | |
| 24 | 0.995 | 2.31E-04 | 0.989 | 9.63E-04 | 0.989 | 1.60E-03 | 0.991 | 6.29E-04 | 0.990 | 5.82E-04 | 0.981 | 2.24E-03 | 0.923 | 1.32E-02 | |
| 32 | 0.997 | 1.56E-04 | 0.992 | 9.63E-04 | 0.993 | 1.08E-03 | 0.995 | 3.91E-04 | 0.994 | 4.66E-04 | 0.986 | 1.69E-03 | 0.969 | 4.78E-03 | |
| X0017 | 8 | 0.921 | 2.38E-04 | 0.898 | 8.22E-03 | 0.896 | 7.49E-03 | 0.908 | 3.50E-03 | 0.918 | 1.06E-03 | 0.921 | 3.04E-04 | 0.869 | 1.15E-02 |
| 16 | 0.978 | 3.25E-04 | 0.959 | 4.91E-03 | 0.966 | 2.80E-03 | 0.966 | 2.54E-03 | 0.975 | 6.07E-04 | 0.966 | 1.63E-03 | 0.924 | 1.02E-02 | |
| 24 | 0.989 | 3.28E-04 | 0.981 | 1.50E-03 | 0.979 | 2.33E-03 | 0.981 | 1.50E-03 | 0.988 | 3.13E-04 | 0.980 | 1.48E-03 | 0.964 | 3.61E-03 | |
| 32 | 0.994 | 1.62E-04 | 0.988 | 1.50E-03 | 0.987 | 1.67E-03 | 0.988 | 1.12E-03 | 0.993 | 2.16E-04 | 0.986 | 1.16E-03 | 0.969 | 3.93E-03 | |
| Friedman mean rank | 1.3203 | 4.7969 | 4.4219 | 2.5469 | 3.1172 | 4.8750 | 6.9219 | ||||||||
| Rank | 1 | 5 | 4 | 2 | 3 | 6 | 7 | ||||||||
Table 9 shows the experimental results of FSIM, which are similar to Tables 7 and 8. By evaluating the FSIM metrics, the proposed HGJO algorithm achieves optimal results in a total of 7 images, C0080, C0088, C0180, C0536, C1088, L1074, and X0017. The performance far exceeds that of other comparable algorithms. According to the Friedman average ranking test, the top three algorithms are HGJO, AOA, and RUN.
In addition, Table 10 shows the results of the Wilcoxon rank-sum test. Consistent with the evaluation criteria in the previous section, if P>0.05, the null hypothesis is true; otherwise, the alternative hypothesis is true. By analyzing the results of the Wilcoxon rank-sum test, we can see that the proposed method has significant differences with other compared algorithms in all experiments, except for some experiments where it performs similarly to DE(OBL). Therefore, we can conclude that the performance of HGJO is significantly different from other algorithms.
Table 10. Comparison of the Wilcoxon signed-rank test for Otsu method.
| Image Name | Level | HGJO vs. GJO | HGJO vs. IGJO | HGJO vs. RUN | HGJO vs. AOA | HGJO vs. DE | HGJO vs. PSO |
|---|---|---|---|---|---|---|---|
| C0080 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.906E-03 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C0088 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 1.734E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C0132 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.578E-05 ++ | 6.104E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C0135 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 1.090E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C0180 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 9.766E-02 — | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C0536 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 8.411E-05 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| C1088 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 8.731E-03 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0032 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 1.289E-01 — | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 2.875E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 2.643E-05 ++ | 3.051E-05 ++ | 2.489E-05 ++ | |
| L0064 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 6.168E-02 — | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0135 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 8.356E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0158 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 1.367E-02 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0226 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | NaN — | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0699 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 4.648E-01 -- | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L0879 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 9.766E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| L1074 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 6.250E-02 — | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| X0017 | 8 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 5.662E-04 ++ | 3.090E-05 ++ |
| 16 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 24 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | |
| 32 | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ | 3.090E-05 ++ |
Despite the fact that the algorithms used for comparison have some competitiveness on some images. In all, however, the proposed algorithm is still outstanding in optical aerial image segmentation. These results demonstrate that the HGJO algorithm can achieve better results in processing optical aerial images. Combined with the analysis of the results for CEC2022 test suite in the previous section, it is reasonable to presume that the current results can be maintained when HGJO is applied to a wider range of optical aerial image segmentation in the future. In addition, an interesting phenomenon worth our attention is that the improved algorithm has a certain loss in the performance of land images which is named at the beginning of “L”. By comparing with the original image, we can observe that these images all have a common feature, including many small objects, which greatly increases the difficulty of segmentation. Therefore, in the future work, we can further optimize the segmentation problem of such images.
Fig 15 displays the segmentation results of each algorithm on the test image C0180 with a threshold level of 8. They are the original image, HGJO segmentation result, GJO segmentation result, IGJO segmentation result, RUN segmentation result, AOA segmentation result, DE(OBL) segmentation result and PSO(OBL) segmentation result in order. It is worth noting that only the image results with a threshold level of 8 are shown here, because it is impossible to intuitively feel the quality of the segmentation results in the high threshold segmentation results through human eye observation. Therefore, image results with a threshold level above 8 are not listed separately. With this figure, we can intuitively feel that the island in the optical aerial image segmented by HGJO have more distinct contours. In addition, by comparing the seabed distribution features in the segmentation results, we can observe that the competition algorithms ignore these details. However, HGJO preserves almost all the features of ocean distribution. Therefore, it can be concluded that HGJO can effectively segment complex ocean distribution optical aerial images with high quality. In summary, the proposed HGJO can effectively handle optical aerial image segmentation and provide effective help for the subsequent data processing and data acquisition.
Fig 15. The segmentation results for C0180.
Furthermore, the segmentation histogram for each channel is also shown in Appendix A–G in S1 Appendix. By comparing these images, we can see that, the results of HGJO segmentation on the red, green, and blue channels can retain more details. This shows that for optical aerial images, the proposed algorithm has more advantages and can retain more details after segmentation than other algorithms, which is helpful for subsequent image processing.
6. Conclusions
Aerial photography images can provide a wealth of information for scientific researchers. Multi-level threshold segmentation of aerial images can effectively reduce the complexity of subsequent image processing while preserving the original features. This paper introduces a new optimization algorithm, the Golden Jackal Optimization (GJO) algorithm, which suffers from convergence issues and the tendency to get stuck in local optima. Therefore, an improved version of GJO, which is named HGJO, is proposed in this paper to enhance the search capabilities and avoid getting stuck in local optima, to optimize the process of multilevel thresholding segmentation. The performance of the proposed method is compared with six different meta-heuristics, including GJO, IGJO, RUN, AOA, DE(OBL), and PSO(OBL), on the IEEE CEC2022 benchmark test function. Based on the experimental results, the proposed algorithm outperforms all other algorithms in terms of convergence accuracy and stability. In addition, the Otsu method is used as an objective function to perform multi-level threshold segmentation on a set of aerial images. PSNR, SSIM, and FSIM are used as evaluation metrics to assess the quality of the segmented images produced by each algorithm. Moreover, the Friedman mean rank test and the Wilcoxon rank-sum test are used to verify the segmentation results. The experimental results show that HGJO outperforms other algorithms in terms of overall performance. The proposed algorithm can effectively reduce the image complexity while preserving the original features, thereby improving the efficiency of the subsequent image processing. In general, the results of this study are satisfactory, but there are certain shortcomings. Firstly, the introduction of OBL and Cauchy operators increases the computation time of the original algorithm, making the proposed method less efficient than most algorithms (only better than RUN). Secondly, there is a performance loss in complex image segmentation, such as test images L0032, L0064, and L0135, thus further work is needed to improve the algorithm’s performance in these types of image segmentation.
In future work, we will further validate and improve the proposed algorithm through more extensive problems, such as medical image segmentation. In addition, we will try to apply HGJO to other more complex problems, such as neural networks, remote sensing data processing, and UAV path analysis. Furthermore, improving the computational efficiency of HGJO would be a significant contribution.
Supporting information
(DOCX)
(ZIP)
Acknowledgments
The authors would like to thank two anonymous reviewers for providing their valuable insights that could improve the quality of this study.
Data Availability
All of the source code of this paper is publicly available at https://github.com/Vang-z/HGJO.
Funding Statement
This study was supported in the form of funding by the National Natural Science Foundation of China (Grant No. 21466008) awarded to Dr. Yuanbin Mo, the Natural Science Foundation of Guangxi Province (Grant No. 2019GXNSFAA185017) awarded to Dr. Yuanbin Mo, the Guangxi Minzu University Scientific Foundation (Grant No. 2021MDKJ004) awarded to Dr. Yuanbin Mo, and the Innovation Project of Guangxi Graduate Education (Grant No. YCSW2022255) awarded to Mr. Yucheng Lyu.
References
- 1.Fu Y, Liang S, Chen D, Chen Z. Translation of Aerial Image Into Digital Map via Discriminative Segmentation and Creative Generation. IEEE Transactions on Geoscience and Remote Sensing. 2022;60: 1–15. doi: 10.1109/TGRS.2021.3110894 [DOI] [Google Scholar]
- 2.Vanegas CA, Aliaga DG, Benes B, Waddell P. Visualization of Simulated Urban Spaces: Inferring Parameterized Generation of Streets, Parcels, and Aerial Imagery. IEEE Transactions on Visualization and Computer Graphics. 2009;15: 424–435. doi: 10.1109/TVCG.2008.193 [DOI] [PubMed] [Google Scholar]
- 3.Saing Z, Djainal H, Deni S. Land use balance determination using satellite imagery and geographic information system: case study in South Sulawesi Province, Indonesia. Geodesy and Geodynamics. 2021;12: 133–147. doi: 10.1016/j.geog.2020.11.006 [DOI] [Google Scholar]
- 4.Manfreda S, McCabe MF, Miller PE, Lucas R, Pajuelo Madrigal V, Mallinis G, et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sensing. 2018;10: 641. doi: 10.3390/rs10040641 [DOI] [Google Scholar]
- 5.Shahbazi M, Théau J, Ménard P. Recent applications of unmanned aerial imagery in natural resource management. GIScience & Remote Sensing. 2014;51: 339–365. doi: 10.1080/15481603.2014.926650 [DOI] [Google Scholar]
- 6.Elaziz MA, Ewees AA, Yousri D, Alwerfali HSN, Awad QA, Lu S, et al. An Improved Marine Predators Algorithm With Fuzzy Entropy for Multi-Level Thresholding: Real World Example of COVID-19 CT Image Segmentation. IEEE Access. 2020;8: 125306–125330. doi: 10.1109/ACCESS.2020.3007928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Al-amri SS, Kalyankar NV, D KS. Image Segmentation by Using Threshold Techniques. arXiv; 2010. doi: 10.48550/arXiv.1005.4020 [DOI] [Google Scholar]
- 8.Siva Raja PM, rani AV. Brain tumor classification using a hybrid deep autoencoder with Bayesian fuzzy clustering-based segmentation approach. Biocybernetics and Biomedical Engineering. 2020;40: 440–453. doi: 10.1016/j.bbe.2020.01.006 [DOI] [Google Scholar]
- 9.Esnet: Edge-Based Segmentation Network for Real-Time Semantic Segmentation in Traffic Scenes. [cited 11 Jul 2022]. Available: https://ieeexplore.ieee.org/abstract/document/8803132/.
- 10.Lewis JJ O ’Callaghan RJ, Nikolov SG, Bull DR, Canagarajah N. Pixel- and region-based image fusion with complex wavelets. Information Fusion. 2007;8: 119–130. doi: 10.1016/j.inffus.2005.09.006 [DOI] [Google Scholar]
- 11.Mirjalili S. Genetic Algorithm. In: Mirjalili S, editor. Evolutionary Algorithms and Neural Networks: Theory and Applications. Cham: Springer International Publishing; 2019. pp. 43–55. doi: 10.1007/978-3-319-93025-1_4 [DOI] [Google Scholar]
- 12.Bansal JC. Particle Swarm Optimization. Evolutionary and Swarm Intelligence Algorithms. 2019; 11–23. doi: 10.1007/978-3-319-91341-4_2 [DOI] [Google Scholar]
- 13.Das S, Suganthan PN. Differential Evolution: A Survey of the State-of-the-Art. IEEE Transactions on Evolutionary Computation. 2011;15: 4–31. doi: 10.1109/TEVC.2010.2059031 [DOI] [Google Scholar]
- 14.Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Computational Intelligence Magazine. 2006;1: 28–39. doi: 10.1109/MCI.2006.329691 [DOI] [Google Scholar]
- 15.Mirjalili S, Lewis A. The Whale Optimization Algorithm. Advances in Engineering Software. 2016;95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008 [DOI] [Google Scholar]
- 16.Mirjalili S, Mirjalili SM, Lewis A. Grey Wolf Optimizer. Advances in Engineering Software. 2014;69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007 [DOI] [Google Scholar]
- 17.Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The Arithmetic Optimization Algorithm. Computer Methods in Applied Mechanics and Engineering. 2021;376: 113609. doi: 10.1016/j.cma.2020.113609 [DOI] [Google Scholar]
- 18.Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-qaness MAA, Gandomi AH. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Computers & Industrial Engineering. 2021;157: 107250. doi: 10.1016/j.cie.2021.107250 [DOI] [Google Scholar]
- 19.Oyelade ON, Ezugwu AE-S, Mohamed TIA, Abualigah L. Ebola Optimization Search Algorithm: A New Nature-Inspired Metaheuristic Optimization Algorithm. IEEE Access. 2022;10: 16150–16177. doi: 10.1109/ACCESS.2022.3147821 [DOI] [Google Scholar]
- 20.Agushaka JO, Ezugwu AE, Abualigah L. Dwarf Mongoose Optimization Algorithm. Computer Methods in Applied Mechanics and Engineering. 2022;391: 114570. doi: 10.1016/j.cma.2022.114570 [DOI] [Google Scholar]
- 21.Abualigah L, Elaziz MA, Sumari P, Geem ZW, Gandomi AH. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Systems with Applications. 2022;191: 116158. doi: 10.1016/j.eswa.2021.116158 [DOI] [Google Scholar]
- 22.Ezugwu AE, Agushaka JO, Abualigah L, Mirjalili S, Gandomi AH. Prairie Dog Optimization Algorithm. Neural Comput & Applic. 2022;34: 20017–20065. doi: 10.1007/s00521-022-07530-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Agushaka JO, Ezugwu AE, Abualigah L. Gazelle optimization algorithm: a novel nature-inspired metaheuristic optimizer. Neural Comput & Applic. 2023;35: 4099–4131. doi: 10.1007/s00521-022-07854-6 [DOI] [Google Scholar]
- 24.Yin P-Y. Multilevel minimum cross entropy threshold selection based on particle swarm optimization. Applied Mathematics and Computation. 2007;184: 503–513. doi: 10.1016/j.amc.2006.06.057 [DOI] [Google Scholar]
- 25.Osuna-Enciso V, Cuevas E, Sossa H. A comparison of nature inspired algorithms for multi-threshold image segmentation. Expert Systems with Applications. 2013;40: 1213–1219. doi: 10.1016/j.eswa.2012.08.017 [DOI] [Google Scholar]
- 26.Gao H, Kwong S, Yang J, Cao J. Particle swarm optimization based on intermediate disturbance strategy algorithm and its application in multi-threshold image segmentation. Information Sciences. 2013;250: 82–112. doi: 10.1016/j.ins.2013.07.005 [DOI] [Google Scholar]
- 27.Jiang Y, Yeh W-C, Hao Z, Yang Z. A cooperative honey bee mating algorithm and its application in multi-threshold image segmentation. Information Sciences. 2016;369: 171–183. doi: 10.1016/j.ins.2016.06.020 [DOI] [Google Scholar]
- 28.Han J, Yang C, Zhou X, Gui W. A new multi-threshold image segmentation approach using state transition algorithm. Applied Mathematical Modelling. 2017;44: 588–601. doi: 10.1016/j.apm.2017.02.015 [DOI] [Google Scholar]
- 29.He L, Huang S. Modified firefly algorithm based multilevel thresholding for color image segmentation. Neurocomputing. 2017;240: 152–174. doi: 10.1016/j.neucom.2017.02.040 [DOI] [Google Scholar]
- 30.Ben Ishak A. A two-dimensional multilevel thresholding method for image segmentation. Applied Soft Computing. 2017;52: 306–322. doi: 10.1016/j.asoc.2016.10.034 [DOI] [Google Scholar]
- 31.Ding G, Dong F, Zou H. Fruit fly optimization algorithm based on a hybrid adaptive-cooperative learning and its application in multilevel image thresholding. Applied Soft Computing. 2019;84: 105704. doi: 10.1016/j.asoc.2019.105704 [DOI] [Google Scholar]
- 32.Widyantara IMO, Pramaita N, Asana IMDP, Adnyana IBP, Pawana IGNA. Multilevel Thresholding for Coastal Video Image Segmentation Based on Cuckoo Search Algorithm. Proceedings of the 2019 5th International Conference on Computing and Artificial Intelligence. New York, NY, USA: Association for Computing Machinery; 2019. pp. 143–149. doi: 10.1145/3330482.3330515 [DOI]
- 33.Bohat VK, Arya KV. A new heuristic for multilevel thresholding of images. Expert Systems with Applications. 2019;117: 176–203. doi: 10.1016/j.eswa.2018.08.045 [DOI] [Google Scholar]
- 34.Singh S, Mittal N, Singh H. A multilevel thresholding algorithm using LebTLBO for image segmentation. Neural Comput & Applic. 2020;32: 16681–16706. doi: 10.1007/s00521-020-04989-2 [DOI] [Google Scholar]
- 35.Xing Z. An improved emperor penguin optimization based multilevel thresholding for color image segmentation. Knowledge-Based Systems. 2020;194: 105570. doi: 10.1016/j.knosys.2020.105570 [DOI] [Google Scholar]
- 36.Upadhyay P, Chhabra JK. Kapur’s entropy based optimal multilevel image segmentation using Crow Search Algorithm. Applied Soft Computing. 2020;97: 105522. doi: 10.1016/j.asoc.2019.105522 [DOI] [Google Scholar]
- 37.Mousavirad SJ, Ebrahimpour-Komleh H. Human mental search-based multilevel thresholding for image segmentation. Applied Soft Computing. 2020;97: 105427. doi: 10.1016/j.asoc.2019.04.002 [DOI] [Google Scholar]
- 38.Zhao S, Wang P, Heidari AA, Chen H, Turabieh H, Mafarja M, et al. Multilevel threshold image segmentation with diffusion association slime mould algorithm and Renyi’s entropy for chronic obstructive pulmonary disease. Computers in Biology and Medicine. 2021;134: 104427. doi: 10.1016/j.compbiomed.2021.104427 [DOI] [PubMed] [Google Scholar]
- 39.Swain M, Tripathy TT, Panda R, Agrawal S, Abraham A. Differential exponential entropy-based multilevel threshold selection methodology for colour satellite images using equilibrium-cuckoo search optimizer. Engineering Applications of Artificial Intelligence. 2022;109: 104599. doi: 10.1016/j.engappai.2021.104599 [DOI] [Google Scholar]
- 40.Houssein EH, Helmy BE, Oliva D, Elngar AA, Shaban H. A novel Black Widow Optimization algorithm for multilevel thresholding image segmentation. Expert Systems with Applications. 2021;167: 114159. doi: 10.1016/j.eswa.2020.114159 [DOI] [Google Scholar]
- 41.Ma G, Yue X. An improved whale optimization algorithm based on multilevel threshold image segmentation using the Otsu method. Engineering Applications of Artificial Intelligence. 2022;113: 104960. doi: 10.1016/j.engappai.2022.104960 [DOI] [Google Scholar]
- 42.Emam MM, Houssein EH, Ghoniem RM. A modified reptile search algorithm for global optimization and image segmentation: Case study brain MRI images. Computers in Biology and Medicine. 2023;152: 106404. doi: 10.1016/j.compbiomed.2022.106404 [DOI] [PubMed] [Google Scholar]
- 43.Ahmadianfar I, Heidari AA, Gandomi AH, Chu X, Chen H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Systems with Applications. 2021;181: 115079. doi: 10.1016/j.eswa.2021.115079 [DOI] [Google Scholar]
- 44.Houssein EH, Emam MM, Ali AA. Improved manta ray foraging optimization for multi-level thresholding using COVID-19 CT images. Neural Comput & Applic. 2021;33: 16899–16919. doi: 10.1007/s00521-021-06273-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Houssein EH, Helmy BE, Oliva D, Jangir P, Premkumar M, Elngar AA, et al. An efficient multi-thresholding based COVID-19 CT images segmentation approach using an improved equilibrium optimizer. Biomedical Signal Processing and Control. 2022;73: 103401. doi: 10.1016/j.bspc.2021.103401 [DOI] [Google Scholar]
- 46.Houssein EH, Hussain K, Abualigah L, Elaziz MA, Alomoush W, Dhiman G, et al. An improved opposition-based marine predators algorithm for global optimization and multilevel thresholding image segmentation. Knowledge-Based Systems. 2021;229: 107348. doi: 10.1016/j.knosys.2021.107348 [DOI] [Google Scholar]
- 47.Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Systems with Applications. 2020;152: 113377. doi: 10.1016/j.eswa.2020.113377 [DOI] [Google Scholar]
- 48.Houssein EH, Abdelkareem DA, Emam MM, Hameed MA, Younan M. An efficient image segmentation method for skin cancer imaging using improved golden jackal optimization algorithm. Computers in Biology and Medicine. 2022;149: 106075. doi: 10.1016/j.compbiomed.2022.106075 [DOI] [PubMed] [Google Scholar]
- 49.Chopra N, Mohsin Ansari M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Systems with Applications. 2022;198: 116924. doi: 10.1016/j.eswa.2022.116924 [DOI] [Google Scholar]
- 50.Rezaie M, karamnejadi azar K, kardan sani A, Akbari E, Ghadimi N, Razmjooy N, et al. Model parameters estimation of the proton exchange membrane fuel cell by a Modified Golden Jackal Optimization. Sustainable Energy Technologies and Assessments. 2022;53: 102657. doi: 10.1016/j.seta.2022.102657 [DOI] [Google Scholar]
- 51.Zhang J, Zhang G, Kong M, Zhang T. Adaptive infinite impulse response system identification using an enhanced golden jackal optimization. J Supercomput. 2023. [cited 12 Mar 2023]. doi: 10.1007/s11227-023-05086-6 [DOI] [Google Scholar]
- 52.Mahdy A, Hasanien HM, Turky RA, Abdel Aleem SHE. Modeling and optimal operation of hybrid wave energy and PV system feeding supercharging stations based on golden jackal optimal control strategy. Energy. 2023;263: 125932. doi: 10.1016/j.energy.2022.125932 [DOI] [Google Scholar]
- 53.Huynh-Thu Q, Ghanbari M. Scope of validity of PSNR in image/video quality assessment. Electronics Letters. 2008;44: 800–801. [Google Scholar]
- 54.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing. 2004;13: 600–612. doi: 10.1109/tip.2003.819861 [DOI] [PubMed] [Google Scholar]
- 55.Zhang L, Zhang L, Mou X, Zhang D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Transactions on Image Processing. 2011;20: 2378–2386. doi: 10.1109/TIP.2011.2109730 [DOI] [PubMed] [Google Scholar]
- 56.Otsu N. A threshold selection method from gray-level histograms. IEEE transactions on systems. 1979;9: 62–66. [Google Scholar]
- 57.Tizhoosh HR. Opposition-Based Learning: A New Scheme for Machine Intelligence. International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06). 2005. pp. 695–701. doi: 10.1109/CIMCA.2005.1631345 [DOI] [Google Scholar]
- 58.Ali M, Pant M. Improving the performance of differential evolution algorithm using Cauchy mutation. Soft Comput. 2011;15: 991–1007. doi: 10.1007/s00500-010-0655-2 [DOI] [Google Scholar]
- 59.Hashim FA, Hussien AG. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowledge-Based Systems. 2022;242: 108320. doi: 10.1016/j.knosys.2022.108320 [DOI] [Google Scholar]
- 60.Hashim FA, Hussain K, Houssein EH, Mabrouk MS, Al-Atabany W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl Intell. 2021;51: 1531–1551. doi: 10.1007/s10489-020-01893-z [DOI] [Google Scholar]
- 61.Arcuri A, Fraser G. Parameter tuning or default values? An empirical investigation in search-based software engineering. Empir Software Eng. 2013;18: 594–623. doi: 10.1007/s10664-013-9249-9 [DOI] [Google Scholar]
- 62.Friedman M. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. Journal of the American Statistical Association. 1937;32: 675–701. doi: 10.1080/01621459.1937.10503522 [DOI] [Google Scholar]
- 63.Liao C, Li S, Luo Z. Gene Selection Using Wilcoxon Rank Sum Test and Support Vector Machine for Cancer Classification. In: Wang Y, Cheung Y, Liu H, editors. Computational Intelligence and Security. Berlin, Heidelberg: Springer; 2007. pp. 57–66. doi: 10.1007/978-3-540-74377-4_7 [DOI] [Google Scholar]
- 64.Gallego A-J, Pertusa A, Gil P. Automatic Ship Classification from Optical Aerial Images with Convolutional Neural Networks. Remote Sensing. 2018;10: 511. doi: 10.3390/rs10040511 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(ZIP)
Data Availability Statement
All of the source code of this paper is publicly available at https://github.com/Vang-z/HGJO.