Image reconstruction algorithm for laser-induced ultrasonic imaging: The single sensor scanning synthetic aperture focusing technique

Abstract

This paper aims to implement a laser-induced ultrasound imaging reconstruction method based on the delay-and-sum beamforming through the synthetic aperture focusing technique (SAFT) for a circular scanning, performed with a tomograph that had one acoustic sensor and a system that rotates the sample around a fixed axis. The proposed method, called the Single-sensor Scanning Synthetic Aperture Focusing Technique, considers the size of the sensor and the detection procedure inside the SAFT's algebra. This image reconstruction method was evaluated numerically, using the Green function for the laser-induced ultrasound wave equation to generate a forward problem, and experimentally, using a solid object of polylactic acid, and a Sprague–Dawley rat heart located in a tissue-mimicking phantom. The resulting images were compared to those obtained from the time reversal and the conventional delay-and-sum reconstruction algorithms. The presented method removes the sidelobe artifacts and the comet tail sign, which produces a more distinguishable target on the image. In addition, the proposed method has a faster performance and lower computational load. The implementation of this method in photoacoustic microscopy techniques for image reconstruction is discussed.

I. INTRODUCTION

Laser-induced ultrasound (LIU), or pulsed photoacoustic (PA) effect, is the generation of ultrasound stress waves in the surrounding medium of an optically absorbent material when it is irradiated by a short-time laser pulse. Image reconstruction is one of the main focuses of LIU because of its biomedical imaging applications (Li and Wang, 2022), which combines electromagnetic excitation with ultrasonic detection. Even though the x-ray is one of the main tools for biomedical imaging (Sampaio et al., 2021), because the LIU technique can be generated with visible light, avoiding all the stochastic effects, such as cancer induction, laser-induced ultrasonic imaging is considered to be a promising technique for biomedical imaging.

This technique consists of the reconstruction of images from the set of ultrasonic waves generated by an optically absorbent sample and its corresponding electrical signal acquired along an observation surface that surrounds it. Even though the geometry of the observation surface could be any that contains the region of interest of the imaged sample, the most common geometry of detection are linear and circular. The mathematical formulation to state the problem of recovering an intensity image from the set of electrical signals acquired, and physical parameters of the propagation medium, is called photoacoustic inverse problem. The main inversion methods, or solutions to the inverse problem, are: the back-projection formulae (Xu and Wang, 2005), the eigenfunction expansion (Kunyansky, 2007), and the time reversal method (Hristova et al., 2008).

The delay-and-sum (DAS) beamforming, a subclass of the back-projection formula (Petschke and La Riviére, 2013), is a common algorithm in ultrasound imaging, when a linear sensor array (LSA) is used to acquire the electrical signals, due to the simplicity in its implementation and real time reconstruction capability. The beamformer, $y_{\text{DAS}}$, obtained in the DAS algorithm is (Mozaffarzadeh et al., 2018)

$$y_{\text{DAS}}({\tau }_k)=\sum _{i=1}^N{P}_i({\tau }_k-{\tau }_i),$$

where τ_k is the time index, P_i is the detected electrical signal by the ith sensor in the array, formed by N elements, and τ_i is its corresponding time delay. The outputs $y_{\text{DAS}}$, for a set of time indexes, are used to form the digital image.

The DAS method presents limitations from the appearance of sidelobe artifacts and low image resolution (Mozaffarzadeh et al., 2018), motivated by this, other proposals have emerged in terms of modifications and optimization of the DAS algorithm, such as the delay-multiply-and-sum (DMAS) (Lim et al., 2008), the DMAS with coherence factor (Seungwan et al., 2019), and the double stage DMAS (Mozaffarzadeh et al., 2018). These proposals resulted in a set of reconstruction algorithms based on the DAS algebra.

In this paper, a new reconstruction method for LIU imaging, based on the DAS formulation and implemented following the synthetic aperture focusing technique (SAFT) (Schmerr and Lester, 2015) ideas, is presented. This method, called the single-sensor scanning synthetic aperture focusing technique (SSC-SAFT), considers the size of the acoustic sensor and a particular acoustic wave detection procedure inside the SAFT algebra. The signal acquisition procedure consists of the use of just one acoustic sensor and a sample rotation system that emulates a circular sensing surface. The proposed method results in a more distinguishable target in the image, removing the sidelobe and comet tail artifacts.

The acoustic detection using an array of sensors, and the image reconstruction methods ad hoc to this measurement technique, are currently predominant in the PA imaging investigations (Kalva et al., 2018a,b). Nevertheless, the single-element measurement has been used in laser-induced ultrasonic imaging, especially in PA microscopy systems, as an alternative to obtain photoacoustic images and to study its potential applications in specific fields of interest (Guo et al., 2020; Lee et al., 2022; Siphanto et al., 2005; Valluru and Willmann, 2016). In addition, the single-element detection has been widely used in the LIU field because the non-contact detection is performed using point-to-point laser sensing (Choi and Jhang, 2018; Gao et al., 2021; Malmström et al., 2022; Morales et al., 2022). The method presented in this paper is proposed as an image reconstruction method ad hoc to the single-element measurement technique, that solves the issues or disadvantages in the images obtained when reconstruction methods designed for multiple-detector measurement are used.

II. PROPOSED METHOD: THE SINGLE SENSOR SCANNING SYNTHETIC APERTURE FOCUSING TECHNIQUE

To overcome the artifact formation and the low definition issues in the DAS-SAFT image reconstruction method, we propose a new reconstruction method based on the SAFT and suitable for a particular experimental configuration that involves a circular scan using a single acoustic sensor and a mechatronic system that rotates the sample (presented in Sec. II E). The SAFT was proposed in ultrasound imaging for a single transducer scanning and adapted to LIU when a linear sensor array is used, then, considering the modifications implemented in the proposed method, it is called the single-sensor scanning synthetic aperture focusing technique. This method considers the effective area of detection in the acoustic sensor, avoiding the assumption of a point-like and omnidirectional detector, while the measurement technique favors the detection to be in the direction of the maximum directivity of the sensor. In the SSC-SAFT, we propose to perform the image reconstruction following the SAFT ideas but considering exclusively the sensor detection region, performing, in some fashion, a segmented reconstruction, where every segment (or region) is delimited by the size, position, and area of detection of the acoustic sensor in the image grid.

A. Theoretical background

The synthetic aperture focusing technique is an image reconstruction method of the DAS imaging class. It was proposed for ultrasonic imaging as a single transducer scanning along a detection line (Fairchild et al., 1997), emulating a LSA. Although the SAFT was proposed for a linear detection, the concept can be implemented for a circular sensor array (CSA) in a simple way. The main idea in the SAFT is: for each pixel in the desired image, the intensity value $I_{\text{SAFT}}$ of a pixel is calculated as the sum of the electrical signal of each sensor following the equation (Schmerr and Lester, 2015)

$$I_{\text{SAFT}}(\mathbf{k})=\sum _{i=1}^{N}V{\left[{\mathbf{s}}_i,t-\tau ({\mathbf{s}}_i,\mathbf{k})\right]}_{t=0},$$ (1)

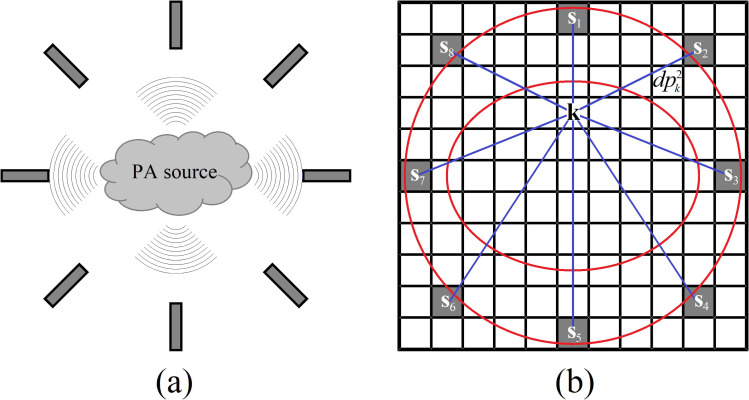
where k is an index to describe the Cartesian coordinates of the pixel k in the image, ${\mathbf{s}}_i$ is the location of the centroid of the ith sensor in the detection array, formed by N elements and, V its acquired electrical signal during a time t. τ is the time delay calculated from the distance between the pixel k and the pixel coordinates of ${\mathbf{s}}_i$. τ is calculated following the relation $\tau =(d{p}_k^i/c)\Delta x$, where $d{p}_k^i$ is the number of pixels between the pixel k and the location of the ith sensor, c is the medium sound speed, and $\Delta x$ is the length of the pixel, which will be discussed in Sec. II C. Figure 1 is a schematic representation of the image formation in the SAFT for a circular scanning.

FIG. 1.

(Color online) (a) Experimental configuration for a circular array of detection. The source is placed inside the CSA, formed by eight elements. Typically, the detection is performed in the backward mode of propagation. (b) Schematic representation of the SAFT procedure in the image formation for a circular scanning. The red lines represent the distance between a pixel k in the image and the location of a sensor. The gray-scale value of this pixel depends on the time delays calculated for the distance between this pixel and every sensor location, following Eq. (1).

The SAFT was proposed originally for ultrasonic imaging. The adaptation to laser-induced ultrasonic imaging is based on the fact that in ultrasonic imaging, the time delay τ is calculated considering that the acoustic wave travels from the actuator to the sample and returning to the sensor, while, in the LIU technique, the acoustic waves are generated by the sample. Then, the considered time delay is $\tau /2$. To simplify the notation, this consideration will be obviated in the rest of the analysis.

There are critical approximations in the conventional SAFT reconstruction: (i) the sensors in the detection array are supposed to be point-like, and then, omnidirectional, (ii) the medium where the acoustic waves are propagated is homogeneous and acoustically non-absorbent. Then, the resulting image provides qualitative information of the sample as the geometry (characteristic lengths and position in the region of observation) at the expense of low resolution, sidelobe artifacts, and comet tail signs. These artifacts in conventional SAFT images are due to the high sensitivity of the algorithm to the off-axis signals (Mozaffarzadeh et al., 2018), meaning that, in the SAFT approximations, every element in the sensor array is acquired immediately following the laser illumination. All of the sensors contribute to all of the pixels in the image, as can be seen in Eq. (1), despite that not every sensor detects the PA signal for every region of the reconstructed image.

B. The computational grid

The first step to implement the proposed algorithm is to define a space where the calculations will be performed. The desired image is a matrix where each element represents the position of a pixel, and its numerical entry represents the intensity value. The aim of the SSC-SAFT is to calculate this numerical entry for each element of the matrix based on the electrical signals acquired during the scanning. As a result, an intensity image that represents the initial pressure distribution that generates these electrical signals is obtained. This matrix, in conjunction with its physical attributes, is called the computational grid.

The computational grid represents the region of space where the PA scanning occurs; in the case of a circular scanning, a square matrix is the optimal shape. The elements to build the computational grid are: the number of nodes (entries), $N_x\times N_x$ in the case of a square grid, and the horizontal (and then vertical) spatial length x that the grid spans. Considering the single sensor scanning discussed in this methodology, let r be the distance between the axis of rotation of the sample and the detection area of the sensor, then, the minimum length that the grid must cover is $x_{\text{min}}=2r$. Note that, in the case of a circular array of sensors, r is just the radius of this array.

Considering a computational grid of N_x nodes per side, and x, the length it covers, the spatial resolution of the grid, meaning the size of a single pixel in the image, is $\Delta x=x/N_x$. Therefore, given a fixed x, the greater N_x is, the higher the resolution. To set a proper number of nodes in the grid, it is necessary to consider the sampling interval given by the acquisition system, as the computational grid is the discretization of the region of space where the measurements are performed, then the minimum size of a pixel can be expressed as

$$\Delta x_{\text{min}}=c\Delta t\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{or}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Delta x\ge c\Delta t,$$

where $\Delta t$ is, by Nyquist sampling theorem, the double of the temporal sampling interval. Since $\Delta x=x/N_x$ and $x_{\text{min}}=2r$, a condition for the number of nodes in the computational grid can be established as

$$N_x\le \frac{r}{c\Delta t}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{or}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{N}_x\le f\frac{r}{c},$$ (2)

where f is the Nyquist frequency, half of the sampling rate. Therefore, the image resolution is delimited by the data acquisition frequency and the proximity between sample and detector. Besides, the image resolution is delimited by physical parameters of the experiment, such as the acoustic attenuation, which implies that the medium sound speed depends on the frequency, and it varies in a range $[c_{\text{min}},c_{\text{max}}]$, then the image resolution is optimized when $c=c_{\text{min}}$ is considered. However, given that an algorithm that does not depend on any physical model for the LIU, these parameters are not considered in the SSC-SAFT method.

C. Image formation

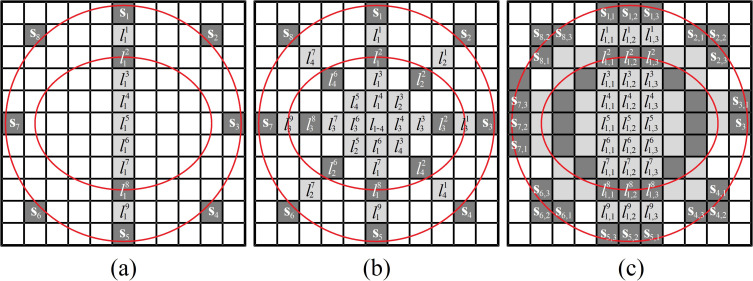
Figure 2 is a representation of the SSC-SAFT process for the case of a circular scanning achieved with eight positions of the sensor. In this example, the dotted circle represents the path covered by the sensor when moving during the scanning, and the dotted ellipse represents the position of the hypothetical source to be reconstructed. The square computational grid has 121 entries (N_x = 11).

FIG. 2.

(Color online) Schematic representation of the SSC-SAFT process. (a) Perform the SAFT reconstruction on the line l₁ of pixels (entries of the computational grid) that connects the position of the sensor centroid ${\mathbf{s}}_{\mathbf{1}}$ with its diametrically opposite pixel on the detection surface. (b) Repeat step (a) for the rest of the sensor positions. (c) For each sensor position ${\mathbf{s}}_{i,k}$, repeat the SAFT reconstruction over the neighboring line $l_{i,k}^j$ so the effective area of detection of the sensor is covered in the grid. To avoid confusion due to the stack of letters in (c), the labels $l_{i,k}^j$ are shown only for the case of the sensor ${\mathbf{s}}_{1,k}$.

Once the computational grid is constructed, the positions of the sensor centroid during the scanning are located on it. Let ${\mathbf{s}}_i$ be the ith position of the sensor centroid, then, the SAFT reconstruction is performed over the line of pixels that connects ${\mathbf{s}}_1$ and the position of the diametrically opposite pixel [see Fig. 2(a) for the case of the mentioned example]. This process is repeated for every position ${\mathbf{s}}_i$, obtaining an image of N lines, N being the number of positions of the sensor. As the line of reconstruction described in this step of the process connects two diametrically opposite points (pixels) of the detection surface formed by the sensor positions, then, the number of pixels of each line is $M=\mathrm{round}(2r/\Delta x)$, where $\mathrm{round}(a)$ means the rounded value of a. Then, the intensity value of the pixel j in the line l_i corresponding to the position ${\mathbf{s}}_i$ is

$$I_{\text{SSC}-\text{SAFT}}\left(l_i^j\right)=V{\left[{\mathbf{s}}_i,t-\tau \left({\mathbf{s}}_i,l_i^j\right)\right]}_{t=0}$$ (3)

for $j=1,2,\dots ,M$, where V is the voltage vector acquired during a time t by the sensor whose centroid is in the position ${\mathbf{s}}_i$. $l_i^j$ represents the position of the pixel j in the line i, with τ being the corresponding time delay calculated as in the SAFT procedure discussed in Sec. II A [see Fig. 2(b) or a representation of this step of the reconstruction for the sensor centroid positions 1–4].

In addition to having considered the position of the sensor centroid, the next step is to look up its effective area of detection in the image reconstruction plane. Then, it is necessary to calculate the number of pixels that covers this portion of the computational grid. Since the reconstruction is performed in a plane, the image obtained can be understood as an image of a slice of the sample, the portion of the sensor involved in this plane of reconstruction is the length considered in this method. Let A be the length of this mentioned segment, the number of pixels that it covers is $A/\Delta x$. The reconstruction procedure described in the Eq. (3) is repeated for as many contiguous lines as the rounded value of $A/\Delta x$, considering now, instead of ${\mathbf{s}}_i$, the positions ${\mathbf{s}}_{i,k}$, where i is a label to describe the ith position of the sensor, and k is an index to describe the coordinates of the pixel that conforms the effective region of detection discussed, generating a segmented region of reconstruction that encompasses the portion of the sample that was illuminated and its corresponding detection surface. Following these ideas, the gray-scale value $(I_{\text{SSC}-\text{SAFT}})$ of a pixel in a PA image obtained by the SSC-SAFT reconstruction method can be summarized in the following relation:

$$I_{\text{SSC}-\text{SAFT}}\left(l_{i,k}^j\right)=V{\left[{\mathbf{s}}_i,t-\tau \left({\mathbf{s}}_{i,k},l_{i,k}^j\right)\right]}_{t=0}$$ (4)

for $j=1,2,\dots ,M$ and $k=1,2,\dots ,\mathtt{round}(A/\Delta x)$, where V is the voltage vector acquired during a time t by the sensor in its ith position ${\mathbf{s}}_i$, k is the position of a pixel that conforms the effective region of detection, with length A, of the referred sensor position in the computational grid. $l_{i,k}^j$ is the pixel j on the line of pixels $l_{i,k}$, formed by M pixels, that connects k with its diametrically opposite pixel, τ is the corresponding time delay for a given medium speed of sound. The process is performed for every pixel k in the line $l_{i,k}$, and repeated for every value of k, the sensor size is covered by considering all the values of k that fills the space occupied by the sensor, and then, the calculation is repeated for every sensor position ${\mathbf{s}}_i$.

Figure 2(c) represents this last part of the reconstruction process. In this example, the considered sensor has a region of detection equivalent to 3 pixels of length (k = 1, 2, 3) and ${\mathbf{s}}_{i,2}$ corresponds to the barycenter of the ith position of the pixel. In general, ${\mathbf{s}}_{i,b}={\mathbf{s}}_i$ with $b=\mathtt{round}(A/2\Delta x)$.

Because of the discretization process, the low resolution in this example (N_x = 11) provokes the sensor to have a different effective region of detection at different positions in the grid; however, for computational grids of greater resolution, this approximation effect is avoided. Generally, for reconstructions on a grid where circular scanning is involved, the number of pixels touched by the circular path will vary, affecting the shape of the considered circular path in the grid. A Fourier collocation method (Wise et al., 2019) could be implemented to correct this issue.

Because of the implementation of the SAFT reconstruction over a line of pixels, note that now, the intensity value of a pixel is not a sum of voltage values, instead, this is directly related to the voltage amplitude of the signal acquired by the sensor in the position involved. Then, the variation of the intensity value of the pixels in the line is proportional to the waveform of the signal acquired. In addition, the high sensitivity of the SAFT reconstruction to off-axis signals is avoided, removing the sidelobe artifacts as shown in the Secs. III and IV.

As with any image reconstruction method, there are some disadvantages of the SSC-SAFT that should be considered: (i) given that an image reconstruction method considers a single-element detector scanning, moreover to ex-vivo biomedical studies, the SSC-SAFT could not be a practical technique for medical PA imaging. Nevertheless, it can be adequate when PA microscopy is performed. (ii) The SSC-SAFT considers a finite sensor as formed by a set of punctual detectors; however, it does not consider any compensation or weighted function between their received signals, which would bring a better accuracy when the sensor is modeled. (iii) Because of the rounding process during the image formation in the SSC-SAFT, the sampling could be subject to staircasing (Wise et al., 2019). Overcoming these disadvantages conforms a potential future work.

Being a DAS-based reconstruction algorithm, the SSC-SAFT is independent of any mathematical model of the LIU, such as the PA wave equation, and then, suitable to recover the image of any sample that generates a proper acoustical signal through the photoacoustic effect.

D. Processing complexity

Following the described notation, the number of operations to perform the reconstruction over a line is $2r/\Delta x$; in the second step of the reconstruction, the number of operations required are N times the operations for a line of reconstruction, that is $(2r/\Delta x)N$, and then, the number of operations to perform the SSC-SAFT is $(A/\Delta x)(2r/\Delta x)N$. Recalling that $\Delta x=N·x$ and $x_{\text{min}}=2r$, the number of operations to recover a PA image through the SSC-SAFT is $(NA/\Delta x)N_x$. For the SAFT, the operations required are $(N)N_x^2$; therefore, the order of computational complexity of the SAFT is $O(N_x^2)$, and for the SSC-SAFT is $O(N_x)$, which is an exponentially lower computational cost that will lead to a faster performance.

E. The measurement technique

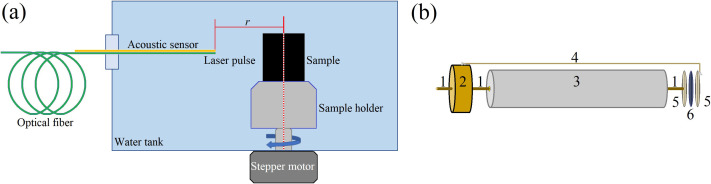
The experimental configuration involved in the physical foundations of the SSC-SAFT method is presented in the Fig. 3. A lab-made polyvinylidene difluoride (PVDF)–based sensor with a circular sensing surface with 1 mm of diameter (A = 1 mm) was used to perform the scanning. An optical fiber was used to guide the emitted pulse of a Q-switched neodymium-doped yttrium aluminum garnet (Nd-YAG) laser (Quantel Brilliant b, Lumibird, Lannion, France) with a pulse duration of 10 ns and pulse energy of 1.2 mJ, emitting at 532 nm of wavelength. The sample was placed in a sample-holder that is connected to a stepper motor, so the sample can be rotated about an axis that matches with the center of the sample-holder. The system is submerged in a water tank so the acoustic impedance-matching is achieved. It is not the aim of this work to present the manufacturing or characterization of the PVDF sensor as the same set of electrical signals is used to evaluate and compare the algorithm with other image reconstruction methods, and the parameters and characteristics of the sensor does not affect the performance of the algorithms.

FIG. 3.

(Color online) Schematic representation of (a) the measurement system, (b) the structure of the acoustic sensor implemented. The sensor elements are 1, conductive wire; 2, connector (sub-miniature version a); 3, support conduit tube; 4, conductive base; 5, gold coating; 6, PVDF/lead zirconate titanate membrane. The scanning is achieved with one acoustic sensor and a rotation of the sample. The signals are acquired with a single laser pulse.

The acquisition system is a USB scope Analog Arts SA985 (Analog Arts Inc., Lynnfield, MA), with a sampling rate of 100 MHz, programmed to save the electrical signal each time the laser is fired. An Arduino (Arduino, New York) board is used to control the system, generating a transistor-transistor logic signal to enable the laser and controlling the activation of the stepper motor. Once the sample is collocated in the holder, and the sensor and the optical fiber are placed in the water tank, the distance between the detection face of the sensor and the axis of rotation is measured, obtaining the value of r in Eq. (2). The first step to perform the tomography is to fire the laser beam. Once the sample is illuminated with a single pulse, the electrical signal is acquired and stored, then, the sample is rotated 1.8 sexagesimal degrees ( $\pi /100$ rad). The process is repeated 200 times, so a circular surface of observation is emulated. Previous works, such as Wang et al. (2003), have been proposed for the laser-induced ultrasonic imaging using a rotation system and one acoustic sensor, but with an expanded laser beam that illuminates the sample in a direction parallel to the normal of the imaged plane, so the image formation and physical considerations differ from those presented in this work.

Once the electrical signals are acquired and stored, the image reconstruction was performed in a computer with a 64 bit central processing unit [Intel(R) Core i7-10700K] at 3.8 GHz, 32 GB random access memory, and without a graphics processing unit board. To compare the resulting images obtained using the DAS-SAFT, time reversal, and the proposed SSC-SAFT method, the DAS-SAFT and SSC-SAFT algorithms were programmed in matlab (The MathWorks, Natick, MA). To perform the time reversal method, the k-Wave matlab toolbox (Treeby and Cox, 2010) was used.

III. NUMERICAL EVALUATION OF THE ALGORITHM PERFORMANCE

The Green function for the LIU wave equation in space, for a thermal point-like particle (Alba-Rosales et al., 2018; Pérez-Solano et al., 2012), was used to calculate the forward problem. Here, it is proposed that the pressure p measured in x at the time t, generated by a single PA source of acoustic diameter d₀ whose center is in $\mathbf{x}\prime$ is described by (Sigrist and Kneubühl, 1978)

$$p(\mathbf{x}-\mathbf{x}\prime ,t)=p_0\frac{ct-\left|\mathbf{x}-\mathbf{x}\prime \right|}{\left|\mathbf{x}-\mathbf{x}\prime \right|}{\mathrm{e}}^{-{\left[(ct-\left|\mathbf{x}-{\mathbf{x}}^{\prime }\right|)/(d_0/2)\right]}^2},$$ (5)

where c is the medium sound speed, $p_0=\alpha /d_0^3$ is the initial pressure generated by the particle, with α being a parameter that depends on the energy per laser pulse, the sound speed and the heat capacity at constant pressure of the propagation medium, and the thermal expansion coefficient of the particle.

Equation (5) is an approximation of the thermoacoustic pressure for a thermal particle, and here it was used to calculate the LIU response generated by an acoustic target of 500 μm diameter measured in different positions over a circular path. The aim of this numerical example is to compare the resulting image of the simplest case of an ideal circular target located in the center of the observation surface obtained with the proposed SSC-SAFT, in comparison with the DAS-SAFT and the time reversal method. The numerical calculation was performed considering a sampling rate of 100 MHz, moving the observation position (x) over a circular path of 5 mm radius covered with 200 equidistant positions, resulting in a rotation step of 1.8°, and a medium sound speed of 1500 m/s. This procedure is not focused on the quantitative capabilities of the laser-induced ultrasonic imaging, then the value of α in the Eq. (5) is not relevant, as this just modulates the amplitude of the solution. The finite sensor signal was constructed following the approximations discussed in the Sec. II C, and calculated so that the sensor positions covered the perimeter of the circular sensing surface, the resulting sensor length is 158 μm. The conditions have been idealized to be a proof of concept of the proposed image reconstruction method and to show how the simplest case of a singular and isolated target in the image generates sidelobe artifacts for the DAS-SAFT and time reversal reconstructions, artifacts that will be inherited for more complex structures, and how the SSC-SAFT avoids these issues.

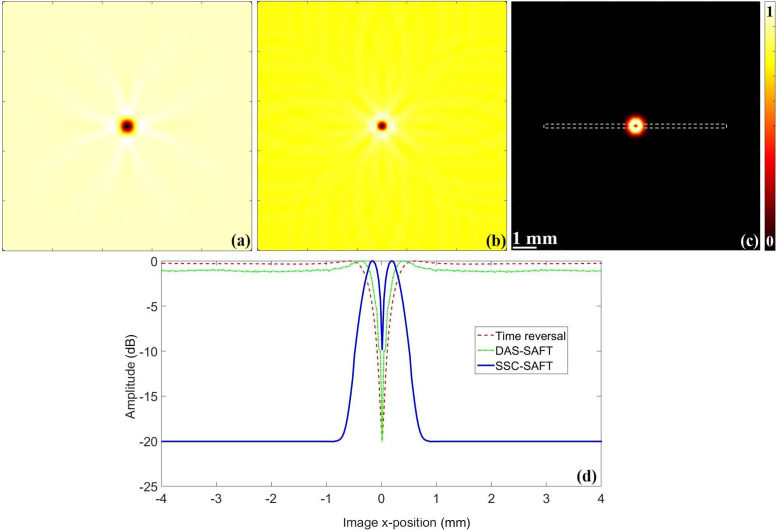
Once the forward problem was calculated, the solutions were used to perform the image reconstruction with the DAS-SAFT, time reversal, and the SSC-SAFT methods. Following the notation and relation given in Eq. (2), the parameters defined to carry out the reconstruction are c = 1500 m/s, f = 100 MHz, r = 5 mm, x = 2r + r/10, N_x = 333, and a resulting pixel length of $\Delta x=31.5\hspace{0.17em}\mu$m. The images were normalized with the aim of comparing them quantitatively; the results are shown in the Figs. 4(a)–4(c). The processing time to obtain the gray-scale images are: 4.96 s for time reversal, 54.08 s for DAS-SAFT, and 4.76 s for SSC-SAFT.

FIG. 4.

(Color online) Resulting images using the (a) time reversal, (b) DAS-SAFT, (c) SSC-SAFT reconstruction method. The signals to recover the images were calculated as a solution of Eq. (5), moving the observation position over a 5 mm radius circular path, covered with a rotation step of 1.8° and considering a sampling rate of 100 MHz. (d) Lateral variation profiles of the region highlighted with the dotted rectangle in (c).

The images obtained reveal that DAS-SAFT and time reversal result in a distinguishable object in the image at the expense of the appearance of the sidelobe artifacts, while the SSC-SAFT completely removes this kind of artifact, resulting in a clearer and high contrast target. To quantitatively compare the quality of the images, the lateral variation profiles are presented in Fig. 4(d). The lateral variation of an image profile was calculated following the relation

$$I_{\text{dB}}(j)=-10\hspace{0.17em}{\text{log}}_{10}\left(\frac{I_{\text{max}}}{I(j)}\right),$$ (6)

where I(j) is the intensity of the pixel j in the studied image section with its maximum intensity $I_{\text{max}}$, and $I_{\text{dB}}(j)$ is the resulting lateral variation amplitude in decibels. Then, this vector is a description of the variation of the pixel intensities in a determined region of the image. The studied row to construct the lateral variation profiles contains the center of the image target, and is enclosed with a dotted rectangle in Fig. 4(c) corresponding to the SSC-SAFT image. The same region was studied for the case of the time reversal and DAS-SAFT.

Because of the waveform bipolarity of the solutions calculated from Eq. (5), the positive part produces the high-intensity region of the recovered images, which corresponds to the acoustical target boundary, and the negative part provokes a dark spot in its center. This effect is observed in the lateral profiles, with a decrease of the lateral variation profile amplitude in the 0 mm of the x-position, indicating the position of the dark spot. Then, the curve to the left (or right, which is totally symmetric) of this point represents the intensity variation of the recovered boundary of the acoustic target. This curve was analyzed to estimate the full width at half maximum (FWHM) for the three images, obtaining a FWHM of about 389 μm for time reversal, 376 μm for DAS-SAFT, and 346 μm for SSC-SAFT. Following the lateral profiles, the sidelobe level of the DAS-SAFT image is about −0.189 dB, while the time reversal and SSC-SAFT profiles are free of sidelobe artifacts.

The SSC-SAFT results in a clear and high contrast image, removing the sidelobe artifacts and maintaining a proper value of the FWHM.

IV. EXPERIMENTAL EVALUATION OF THE ALGORITHM PERFORMANCE

The lab-made tomograph was used to perform the scanning of three different samples: a solid object made of polylactic acid (PLA), a Sprague–Dawley rat heart, and a Sprague–Dawley rat heart embedded in gelatine with 20% of milk concentration as a tissue-mimicking phantom.

The distance r between the axis of rotation and the detection surface was measured through a photography of the experimental setup using the software ImageJ. A known scale (1 mm) was placed to appear in the photograph, which was taken from the frontal perspective, where the sample and the sensor face were clearly defined. The spatial size of the computational grid x was calculated as x = 2r + r/10. As mentioned, the system was submerged in water and backward signals were acquired, so the medium sound speed was set to 1500 m/s. N_x was calculated using Eq. (2).

For the three different samples, the laser-induced ultrasonic images were obtained through the time reversal, DAS-SAFT, and the proposed SSC-SAFT methods. With the aim to remove the electrical noise as much as possible, an electrical signal processing procedure was performed:

• (1)The set of raw signals were normalized in the range [0,1], to increase the signals with a low amplitude and to enhance contrast.
• (2)An exponential moving average filter was implemented to remove the high-frequency noise.
• (3)A region of interest was selected.
• (4)A non-negative threshold was applied.

Following the signal processing procedure, it can be assured that the artifacts that appeared on the images were due to the reconstruction method implemented, and not from the electrical noise. In addition, from the samples studied, the electrical signals should be bipolar (Wang and Wu, 2009). Then, a bipolar lateral profile of the images is expected, but because of the non-negative thresholding, the lateral variation profiles are expected to be unipolar and irregularities on its shape will be due to the artifact superposition, and not to the electrical noise.

To quantitatively compare the quality of the obtained images, the lateral variation profile of each image was calculated using Eq. (6) for the region highlighted with a dotted rectangle in each case. The lateral variation allows us to estimate the sidelobe levels and the FWHM for the region studied. Another relevant parameter to evaluate the quality of an image is its signal-to-noise ratio (SNR); it was calculated following the relation

$$\text{SNR}(I)=10\hspace{0.17em}{\text{log}}_{10}\left(\frac{I_{\text{max}}-I_{\text{min}}}{\sigma (I)}\right),$$ (7)

where I is the digital image, $I_{\text{max}}$ and $I_{\text{min}}$ are its maximum and minimum intensity, respectively, and $\sigma (I)$ is its standard deviation. To present the numerical results of the quality image study in a compact way, the image quality parameters of the PLA prism (Sec. IV A), the rat heart (Sec. IV B), and the tissue-mimicking phantom (Sec. IV C) are presented in the Table I.

TABLE I.

Quantitative parameters of the images obtained. The sidelobe levels and FWHM were estimated from the lateral variation profiles. The SNR was calculated from the whole image.

Sample	Quality parameters	Time reversal	DAS-SAFT	SSC-SAFT
	Side-lobe level (dB)	−6.14, −3.88	−11.12, −5.12	–
Decagrammic prism	FWHM (μm)	307	347	198
	SNR (dB)	28.09	24.07	26.49
	Processing time (s)	19.4	100.7	1.8
	Side-lobe level (dB)	−12.95, −6.42	−15.32, −4.74	–
Rat heart	FWHM (μm)	441	471	246
	SNR (dB)	24.88	23.01	25.23
	Processing time (s)	17.2	75.5	1.5
	Side-lobe level (dB)	−6.52, −2.73	−7.16, −1.22	–
Tissue phantom	FWHM (μm)	819	440	440
	SNR (dB)	26.82	21.50	24.98
	Processing time (s)	33.3	151.9	2.2

A. Solid object of polylactic acid

The sample was fabricated with a three-dimensional printer and consists of a decagrammic prism, shown in Figs. 5(a) and 5(b). The distance between the sensing surface, and the axis of rotation was r = 11.93 mm. The prism was illuminated in the perimeter of its transverse section, so the expected PA image is a 10-point star. The resulting images are shown in Figs. 5(c)–5(e). Noise reduction and contrast enhancement can be noted. The SSC-SAFT method reduces the sidelobe artifacts as well, favoring the correct interpretation of the structures in the image.

FIG. 5.

(Color online) (a) Front view, (b) aerial view of the experimental setup. A PLA three-dimensional printing was scanned using the tomograph. The sample consists of a decagrammic prism. Resulting images of the PLA decagrammic prism using the (c) time reversal, (d) DAS-SAFT, (e) SSC-SAFT reconstruction method. (f) Lateral variation profiles of the region highlighted with the dotted rectangle in (e). The FWHM was estimated from the curves enclosed in the black-dotted oval.

Because of the geometry of the decagrammic prism and the directionality of the acoustic sensors, the peaks of the prism will generate an electrical signal of greater intensity than the flat region that connects a pair of peaks. Then, the resulting image could be affected and distorted because of the sidelobe artifacts and high sensitivity to noise and off-axis signals, as can be seen in the time reversal and DAS-SAFT images [see Figs. 5(c) and 5(d)]. Even with the understanding of the sidelobe effects, the time reversal and DAS-SAFT images apparently retrieve a decagon-like pattern and 10 isolated objects with a comet-tail sign, which does not correspond to the scanned object. At the same time, since in the DAS-SAFT algebra every sensor contributes equally to all of the pixels, the objects in the resulting image are blurry, and targets that generates a low SNR could not appear in the final image. The SSC-SAFT, whose image is presented in Fig. 5(e), shows the correction of these issues; because of the segmented reconstruction, the main and high intensity sidelobe artifacts and comet-tail signs are completely removed. Considering the length of the effective sensor surface causes targets that generate a weak signal, like the flat region that connects a pair of peaks, to appear in the image. While time reversal and DAS-SAFT lose these targets, the SSC-SAFT reconstruct them with a differentiable intensity from the background.

The lateral variation profile was calculated for the region highlighted with a dotted rectangle in Fig. 5(e), which corresponds to a pair of peaks of the 10-point star that is well defined in the three images [the resulting profiles are presented in the Fig. 5(f)]. The estimated values of the sidelobe levels, the FWHM of the first peak of the region studied (enclosed in a black-dotted oval), the SNR, along with the total processing time for the images obtained, are shown in the Table I. The lateral variation profiles reveal that the SSC-SAFT removes the sidelobe artifacts in the image, maintaining a suitable value of the SNR and FWHM parameters. Another important parameter, that does not affect the image quality, but is highly relevant if real-time imaging wants to be achieved, is the processing time. The SSC-SAFT algorithm is performed in 10% and 2% of the time required to compute the time reversal and DAS-SAFT algorithms, respectively.

B. Ex vivo tissue: Sprague–Dawley rat heart

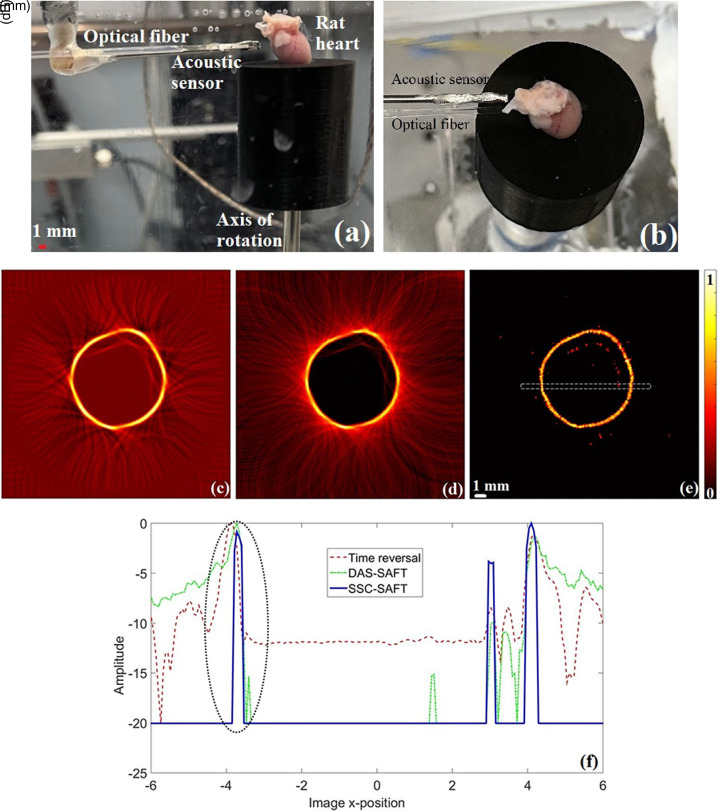
To achieve the results presented in this section, and Sec. IV C, a rat heart was scanned using the tomograph. The experiments were performed on a male, 3-week-old Sprague–Dawley rat. The animal was housed in a 12:12 h light–dark cycle with food and water available ad libitum. The animal was deeply anesthetized, decapitated, and the heart was removed. Experiments were performed following the National Institutes of Health Guide for the Care and Use of Laboratory Animals guidelines. Animal protocols were approved by the University of Missouri and Pennington Biomedical Research Center Animal Care and Use Committees.

The rat heart was scanned using the lab-made tomograph [see Figs. 6(a) and 6(b)]. For this scanning, the distance between the sensor and the axis of rotation was r = 9.49 mm. The resulting images are shown in Figs. 6(c)–6(e). The lateral variation profile, for each of the images obtained, was calculated in a region that contains two well-defined diametrically opposed portions of the transverse section of the heart studied, so at least two peaks are expected in the lateral variation profile. The resulting profiles are presented in the Fig. 6(f), the region studied is highlighted in the SSC-SAFT image [Fig. 6(e)] with a dotted rectangle. The FWHM of the first prominent peak was calculated. The image quality parameters, along with the total processing time for each method, are presented in the Table I.

FIG. 6.

(Color online) Sprague–Dawley rat heart during the scanning. (a) Front view, (b) aerial view. Resulting images of the rat heart using the (c) time reversal, (d) DAS-SAFT, (e) SSC-SAFT reconstruction method, (f) lateral variation profiles of the region enclosed with the dotted rectangle in (e). The FWHM was estimated from the curves enclosed in the black-dotted oval.

Qualitatively, the three images obtained recover the structure of the section of the heart scanned; however, the sidelobe artifacts are present with a high intensity in the time reversal and DAS-SAFT images, giving a blurry target, while the SSC-SAFT removes these artifacts, giving a cleaner image. Because of the structure of the SSC-SAFT, the appreciable intensity variations in the target of the SSC-SAFT image are due to the voltage variation in the electrical signals. It can be observed that there is no information from the internal structure of the heart; this is not an issue concerning the algorithms' performance, it is because the electrical signals were acquired in the backward mode, and the electromagnetic radiation was absorbed in the external heart surface. Because of the electrical signal processing procedure, there is no information arising from the internal structure of the heart. The quantitative parameters of the image reveals that the SSC-SAFT has an adequate FWHM, along with a proper SNR. For this study, the SSC-SAFT shows to be 91% and 98% faster than the time reversal and DAS-SAFT methods, respectively. Recalling that, in the SSC-SAFT, the number of operations depends directly on the number of nodes (N_x), or pixels, in the image, and, following Eq. (2), this number is related to the proximity between the sensor and the sample during the scanning.

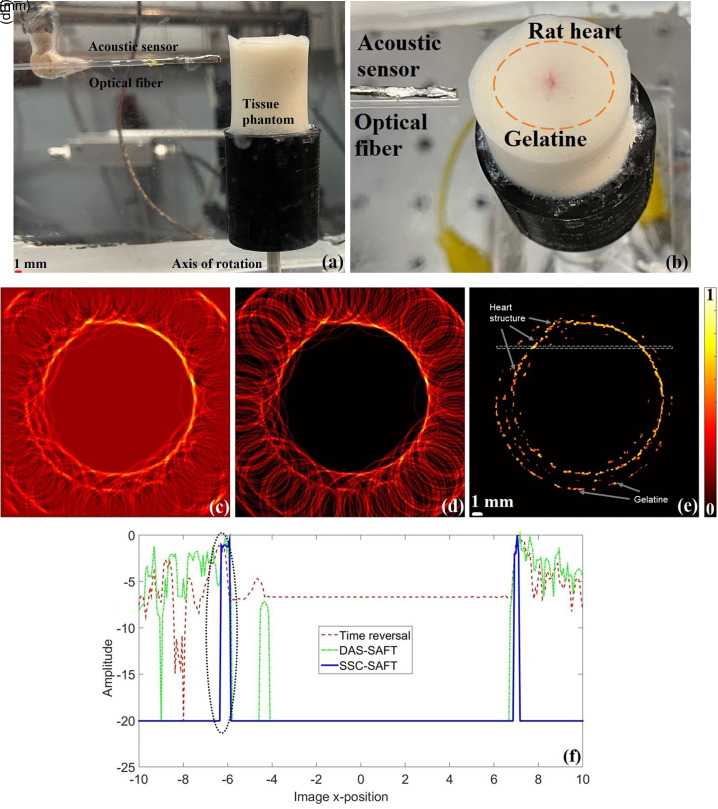
C. Tissue-mimicking phantom

The Sprague–Dawley rat heart was used to create a tissue-mimicking phantom, generating a situation whereby the heart is not exposed directly to the laser radiation, but it is covered by a material that scatters the radiation, emulating a more realistic condition. To achieve this, the rat heart was embedded in a gelatin with 20% milk concentration, and the phantom was scanned using the tomograph [see Figs. 7(a) and 7(b)], with a separation of 13.70 mm between the axis of rotation and the sensing surface. The image reconstruction was performed using the three different methods discussed; the results are presented in the Figs. 7(c)–7(e). The lateral variation profile was calculated in the region indicated by a dotted rectangle in Fig. 7(e) for each of the obtained images. The resulting profiles are presented in the Fig. 7(f). The FWHM was estimated for the first prominent peak in the lateral variation profile (highlighted with a black-dotted oval in the graphs). These parameters, along with the sidelobe levels, the SNR, and the processing time, are presented in the Table I.

FIG. 7.

(Color online) Tissue-mimicking phantom scanned using the lab-made tomograph. (a) Front view, (b) aerial view. Resulting images of the phantom using the (c) time reversal, (d) DAS-SAFT, (e) SSC-SAFT reconstruction method, (f) lateral variation profiles of the region highlighted with the dotted rectangle in (e). The FWHM was estimated from the curves enclosed in the black-dotted oval.

Although the FWHM of the time reversal image is affected in this case, compared to the value obtained with the DAS-SAFT, the FWHM value of the SSC-SAFT image along with its SNR is adequate. The SSC-SAFT image shows the cross section of the heart and the perimeter of the gelatin where it is embedded. The recovered structure is disconnected because, given that a more complex material that emulates a biological tissue, the optical scattering is the reason that not every position of the sensor received an electrical signal from the heart. Due to the SSC-SAFT reconstruction procedure, these regions with no signal from the heart generate a low pixel intensity (in this case, the intensity of the background) that results in the discontinuity appearance. This aspect of the SSC-SAFT image is desirable because it represents the regions of the sample that generates a proper electrical signal. As the same set of electrical signals were used to recover the three images, the regions with no electrical signal from the heart are also observed in the DAS-SAFT and time reversal images with a lower pixel intensity than the image targets. However, the superposition of the sidelobe artifacts smooths the recovered sample, giving a continuous appearance, which does not accurately represent the information acquired during the experiment. Moreover, that being a cleaner image, by removing these artifacts, the image obtained through the proposed SSC-SAFT reconstruction method, allows us to give a proper interpretation of the targets obtained in the image.

V. CONCLUSIONS

The SSC-SAFT is proposed as an LIU image reconstruction method for an experimental setup that involves a scanning achieved with one acoustic sensor moved in different positions along the illuminated sample, avoiding the need for multiple characterized sensors and the multiplexing in the data acquisition, resulting in a simple and low-cost experimental system to obtain PA images and to study its capabilities. The proposed image reconstruction method was compared, through experimental and numerical models, with the DAS-SAFT and the time reversal method. The SSC-SAFT qualitatively and quantitatively improves the image quality obtained preserving the resolution in the target region of the image, calculated through an estimation of the FWHM, and maintaining a proper value of the image SNR, given that the removal of the sidelobe artifacts and comet-tail signs are its main attribute. Additionally, the processing time required to perform the SSC-SAFT is 10% and 2% the time required to perform the time reversal and DAS-SAFT algorithms, respectively.

It was numerically demonstrated that, a singular and isolated target in the image causes the appearance of sidelobe artifacts in the time reversal and DAS-SAFT reconstructions, while the SSC-SAFT avoid them. Experimentally, it was shown that sources that generate LIU signals with a low SNR are distorted in the images obtained with time reversal and DAS-SAFT, and due to the high sensitivity to off-axis signals, these objects are represented with an intensity value close to the value of the image noise, the SSC-SAFT corrects this issues and generates a better representation of the imaged region.

The proposed SSC-SAFT reconstruction method considers the size of the sensor involved in the plane of reconstruction, considering this region of detection as formed by a set of points, given that the pixel is the minimum size that can be defined in the image space. As stated in the method algorithm, the process considers that each element resulting from the decomposition of the sensor acquires the same signal. Although considering that a finite sensor as formed by infinitesimal elements could be a good estimation, it is not the purpose of this work to establish a proper approximation to the signal formation in such a model. Nevertheless, further work in this area could be implemented in the SSC-SAFT. The method is presented for a circular detection because of its potential biomedical applications through the tomographic reconstruction. Nevertheless, because of its geometrical construction, the SSC-SAFT can be implemented for an arbitrary geometry of detection. The measurement technique and the physical considerations implemented, makes the SSC-SAFT an image reconstruction method with potential capabilities to photoacoustic microscopy imaging.