Challenges for biophysical modeling of microstructure

Abstract

The biophysical modeling efforts in diffusion MRI have grown considerably over the past 25 years. In this review, we dwell on the various challenges along the journey of bringing a biophysical model from initial design to clinical implementation, identifying both hurdles that have been already overcome and outstanding issues. First, we describe the critical initial task of selecting which features of tissue microstructure can be estimated using a model and which acquisition protocol needs to be implemented to make the estimation possible. The model performance should necessarily be tested in realistic numerical simulations and in experimental data – adapting the fitting strategy accordingly, and parameter estimates should be validated against complementary techniques, when/if available. Secondly, the model performance and validity should be explored in pathological conditions, and, if appropriate, dedicated models for pathology should be developed. We build on examples from tumors, ischemia and demyelinating diseases. We then discuss the challenges associated with clinical translation and added value. Finally, we single out four major unresolved challenges that are related to: the availability of a microstructural ground truth, the validation of model parameters which cannot be accessed with complementary techniques, the development of a generalized standard model for any brain region and pathology, and the seamless communication between different parties involved in the development and application of biophysical models of diffusion.

1. Introduction

The development of various microscopy tools has undoubtedly revolutionized our understanding of brain tissue in terms of its microstructure (i.e. the structure at the micron scale), composition and alterations with physiological and pathological processes. However, most of microscopy methods, such as light, x-ray or electron microscopy, can only be deployed on a small volume of ex vivo, chemically prepared tissue. Two-photon microscopy has the advantage of being usable in vivo, but remains very invasive and with shallow penetration, often limited to the inspection of rodent cortex. None of the existing microscopy tools are therefore eligible as in vivo non-invasive methods, usable on human living subjects. Yet there would be tremendous value and potential in the ability to characterize the microstructure of human brain tissue over the course of development, aging and disease.

Magnetic resonance imaging (MRI) is an exquisite radiological tool to examine the human brain, but its spatial resolution is on the order of the millimeter, too coarse for any microscopy ambition. However, diffusion MRI (dMRI) has emerged in the recent years as a highly promising “super-resolution” technique which can provide sub-pixel information about tissue microstructure. In an MRI experiment, water molecules in the brain have time to diffuse over a few microns and their path is mainly influenced by cellular membranes and other features of tissue architecture encountered over that distance. Therefore, the diffusion-weighted signal encodes information about microstructure features on the order of the micron, much smaller than the actual MR image resolution, and that we otherwise cannot spatially resolve in vivo and non-invasively.

The main challenge in the field of Microstructural dMRI (Alexander et al., 2019; Novikov et al., 2018a, 2019) is to decode the information contained in the diffusion-weighted signal to retrieve these specific features of tissue microstructure, by developing quantitative techniques that combine astute dMRI protocols with biophysical modeling. The ultimate goal is to bring MRI to the level of a non-invasive in vivo microscope, which would open entire new avenues for studying processes of development, aging, disease, injury and response to treatment.

The MRI signal as a function of diffusion weighting (b-value) can be described using mathematical formulae that are independent of the underlying medium in which diffusion is taking place, i.e. the tissue. The most iconic examples of such “signal representations” are Diffusion Tensor Imaging (DTI) (Basser et al., 1994) and Diffusion Kurtosis Imaging (DKI) (Jensen et al., 2005).

Biophysical models on the contrary assume a given simplified geometry – a “sketch” – of the underlying tissue, and rely on the analytical expression or numerical estimation of the diffusion signal in such an environment (Fig. 1).

Fig. 1.

Biophysical models are sketches of reality which aim at selecting the most meaningful features and disregarding the rest, according to our current knowledge of tissue microstructure (mostly deriving from microscopy). For example, when modelling a white matter bundle, we could identify only a few relevant features, such as the axonal radius R, intra- and extra-axonal diffusivities ${\mathrm{D}}_{\mathrm{a},\parallel },{\mathrm{D}}_{\mathrm{e},\parallel }$ and ${\mathrm{D}}_{\mathrm{e},\perp }$, as well as the relative volume fraction of intra- and extra-axonal space. In microstructure imaging, these features are estimated for each voxel of the acquired diffusion-sensitized images by voxel-wise model fitting. As a result, maps of model parameters estimates can be obtained and linked to the relevant feature of the tissue microstructure.

The first implication of this is that there is no single biophysical model of microstructure, but multiple biophysical models, each developed to describe the microstructure of a specific type of tissue. It is also important to bear in mind that we are aiming to develop biophysical models of diffusion in a given tissue. Indeed, everything is not about the geometry of the tissue, but also about the diffusion process given this geometry – diffusivity values and diffusion regimes are very important.

The bedrock of biophysical models of diffusion is water compartmentalization, which implies that “tissue compartments” can be characterized individually in terms of geometry, relative size and diffusion properties (Beaulieu and Allen, 1994) (Fig. 2). We note however that compartment-free frameworks also exist, such as effective medium theory which relies on statistical approaches to characterize tissue heterogeneity and characteristic lengths instead (Novikov and Kiselev, 2010). Using biophysical models, we can thus access more meaningful and specific parameters of the tissue microstructure than signal representations, provided the chosen model accurately captures all of the relevant features of the tissue. Taking the example of a white matter (WM) bundle, demyelination, axonal loss or edema would all result in an increase in radial diffusivity (i.e. the diffusivity perpendicular to the axons) estimated from DTI but the latter cannot disentangle further between these different tissue alterations. Using biophysical modeling, estimates of axonal and free water compartment sizes and of the tortuosity of the extra-axonal compartment have better potential to inform specifically about axonal loss, edema or demyelination, respectively (Chiang et al., 2014; Hoy et al., 2014; Jelescu et al., 2016a).

Fig. 2.

Biophysical models of diffusion in biological tissue rely on the water compartmentalization assumption: the overall measured dMRI signal can be described as weighted sum of signals generated by water diffusing in different compartments. Each compartment corresponds to a specific portion of tissue (e.g., intra-cellular space) and is characterized by a given geometry (e.g., cylinder), diffusion properties (e.g., isotropic “ball” diffusivity), a characteristic size (or distribution of sizes) and orientation distribution. For the simple geometries shown in figure (adapted from (Fick et al., 2019), with permission), analytical expressions exist to link the compartment features to the corresponding dMRI signal, providing great control and flexibility to build any compartmental model, with arbitrary degree of complexity. Such compartment models are at the core of popular microstructure imaging techniques such as CHARMED (Assaf and Basser, 2005), AxCaliber (Assaf et al., 2008), WMTI (Fieremans et al., 2011) and NODDI (Zhang et al., 2012). Multi-compartment model figures adapted from (Fick et al., 2019) and white matter electron microscopy reconstruction adapted from (Lee et al., 2019b), with permission.

Increased specificity through biophysical modeling comes however at an additional cost: a) a given biophysical model cannot be applied to reliably analyze any dMRI dataset, both from the perspective of the tissue of interest and the acquisition protocol, b) the acquisition protocol is essential and must support model assumptions, c) because of points a) and b), some features of tissue microstructure are at the moment inaccessible using clinical scanners – we will come back to this.

Mathematical models are used everywhere in science and are extremely powerful tools for transforming an infinitely complex problem into one that we better know how to solve. The reason they are associated with several important challenges is that resorting to models is inherently tricky. We can never be certain that our model is similar enough to the tissue we want to characterize in the ways that really matter. Capturing all the relevant features of the tissue, i.e., those that impact the measured diffusion signal significantly, is perhaps the first major challenge of developing a valuable model. Once the sketch is optimally drawn – neither too simple nor too complex – remain outstanding challenges of: accuracy and precision of estimated model parameters, robustness, maintained validity in the face of pathological tissue changes and clinical translation. The main objective of this review is to propose a roadmap towards identifying these challenges, addressing them when/if possible, and ultimately developing a reliable and valuable biophysical model of diffusion for a given tissue. Our alternative title could have been “The assault course for valuable microstructure models of diffusion”.

Thus, this review takes a scenic drive across the “challenges in biophysical modeling” landscape (Fig. 3), highlighting potential roadblocks along the way. All the while emphasizing that the process is constantly iterating and improving upon itself in a possibly roundabout way. We first discuss the challenges associated with parameter estimation and validation (Section 2) related to identifying tissue features we intend to model, investigating performance in simulations, various fitting strategies, and ending with a review of lessons learned when validating these modeling strategies. Second, the manuscript then calls attention to the applications, and most importantly the limitations, of these models

Fig. 3.

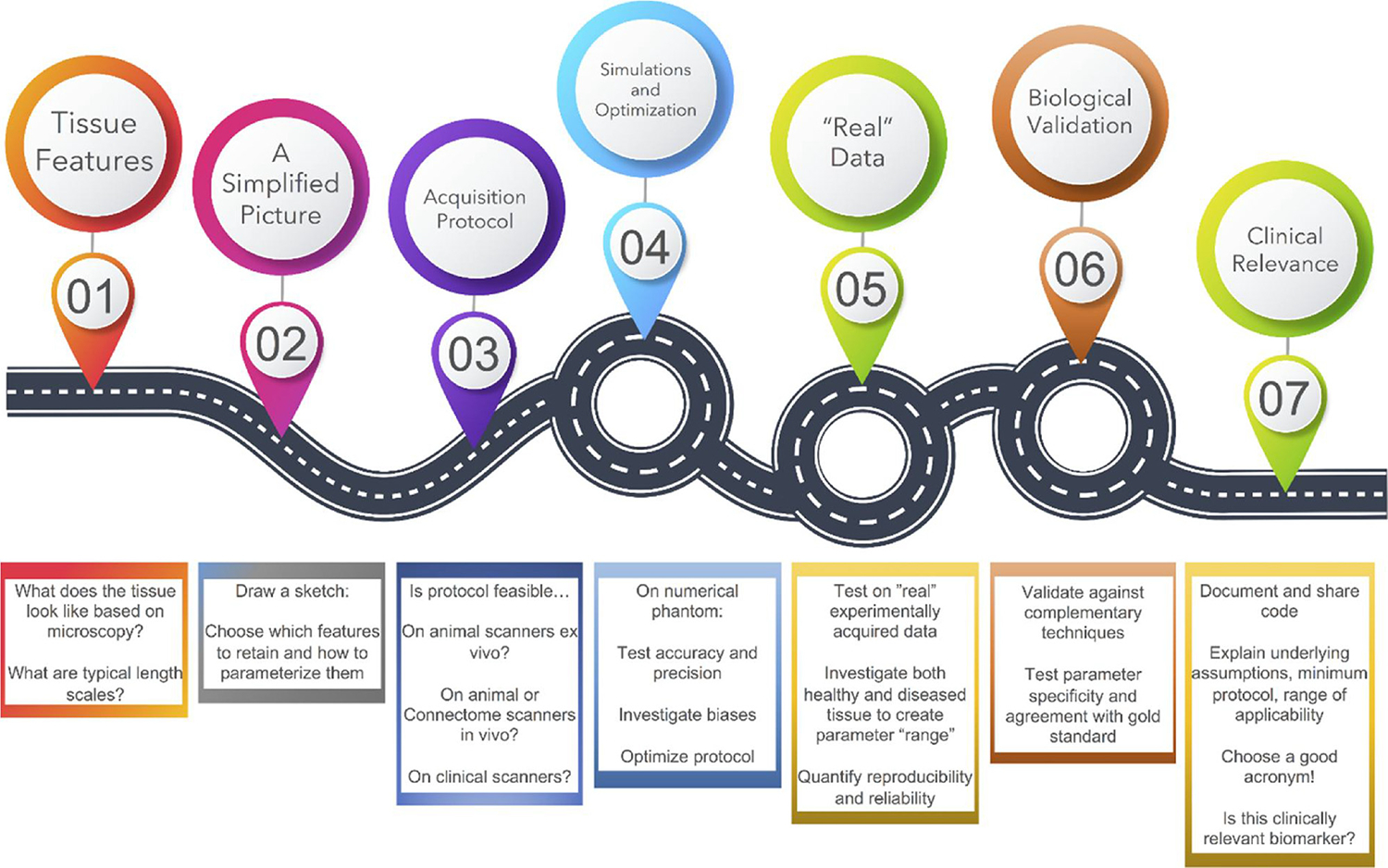
Roadmap of the challenges of microstructure biophysical modeling. The main objective of this review is to propose a roadmap for development of a reliable biophysical model of diffusion in a given tissue. Discrete steps along this course are shown above, although the entire process is very much a continuous and iterative process of validation, adaptation, and application.

in pathology (Section 3). We end with a set of proposed keys to success for the translation of these models into the clinic (Section 4) with the ultimate objective to enable useful biomarkers to ultimately inform the prevention, detection, diagnosis, and treatment of disease and disability.

2. Parameter estimation & validation

2.1. A simplified picture

Because it is a simplified sketch of reality, every biophysical model can account for only a few, relevant, features of the tissue it is designed to model. What is relevant in this context is defined by the microstructure features that affect the signal beyond the noise and the appropriateness of the experimental design to access them. Hence, experimental design is crucial in biophysical modelling to define a sensible model and to guide model assumptions. It is essential to design each experiment (i.e. pulse sequence, protocol parameters, etc.) according to what is sought to be estimated using the model.

For example, a simple model of parallel cylinders of given radius R could be used to characterize highly coherent WM bundles and applied to dMRI data to estimate axonal radius R (i.e. the relevant features captured by the model). However, in order to reliably access this feature without being biased by other tissue properties that are not included in the model, such as non-parallel axons, extra-axonal water, water exchange across the cell membrane, etc., the experiment has to be designed as follows: short diffusion time (to make exchange negligible), ultra-strong diffusion weighting (to gain sensitivity to small axons ~1 μm and minimize the contribution from extra-axonal water signal) and a large number of diffusion gradient directions (to factor out imperfect axon orientation coherence, i.e. dispersion, after direction-averaging, or to factor in dispersion, after redefining the model accordingly). Only under these experimental conditions, such a simple model can estimate the relevant microstructural features of the tissue in a reliable way. It is of course possible to apply such a simple model of WM to any dMRI dataset, but the estimates of axonal radius would be increasingly biased and unreliable as each of the model assumptions is inconsistent with the experimental design. A good model fit to the data does not guarantee that the estimated model parameters have a sensible physiological meaning. Similarly, a “nice looking map” of quantitative indices also does not guarantee physiologically meaningful parameter estimates. As we will see in the next section, this is just one example of many possible models that have been proposed for WM microstructure quantification over the last decade, each with their own assumptions and experimental regime of validity.

2.1.1. White matter

Biophysical models of diffusion in WM have gained a lot of traction because the myelin sheath around axons is thought to ensure compartment “impermeability” over a broad range of timescales, i.e. inter-compartment exchange can be safely neglected. The current “standard model” for diffusion in WM considers two or three non-exchanging compartments (typically intra-axonal, extra-axonal and cerebrospinal fluid (CSF)) defined by their intra-compartment diffusivities and relative sizes (Fig. 1). For acquisition parameters achievable on clinical scanners – diffusion time $t_{\mathrm{d}}>20\mathrm{m}\mathrm{s}$ and diffusion weighting $b<10\mathrm{m}\mathrm{s}/\mathrm{\mu }{\mathrm{m}}^2$, the axons can effectively be modeled as sticks, i.e. cylinders with zero radius (Veraart et al., 2019). Using advanced hardware with very strong field gradients – such as animal scanners or Connectom scanners (Jones et al., 2018) – some sensitivity to axon diameter can be retrieved (De Santis et al., 2016; Duval et al., 2015; Veraart et al., 2020). The orientations of the collection of axons within a voxel is characterized by their Orientation Distribution Function (ODF). The ODF can be parametrized to whatever level of complexity, from perfectly aligned cylinders (Alexander et al., 2010; Fieremans et al., 2010) to complex distributions requiring coefficients representing basis functions over a sphere (i.e., spherical harmonic coefficients) (Jespersen et al., 2010), bearing in mind that a large number of parameters may make the fit less stable and degrade the precision of parameter estimation (Fig. 2).

Building on this standard model, a constellation of implementations has been proposed, each with its own acronym and its own – valid or invalid – simplifying assumptions (Assaf et al., 2008; Fieremans et al., 2011; Zhang et al., 2012; Alexander et al., 2010; Jespersen et al., 2010; Assaf et al., 2004; Jespersen et al., 2018; Kaden et al., 2016; McKinnon et al., 2018; Novikov et al., 2018b; Reisert et al., 2017; Scherrer et al., 2016; Wang et al., 2011). It is however critical to validate model assumptions because they have a direct impact on the accuracy and specificity of derived microstructure features.

The validation of assumptions in WM models has been a long winding road for the dMRI community – these efforts will be covered in the following sections – but we are now at a time when a solid foundation has been laid and this standard model can be used more confidently.

2.1.2. Gray matter

In order to provide a fully comprehensive “in vivo brain microscope”, research efforts should also tackle biophysical modeling of cortical and deep gray matter (GM) structures, e.g. thalamus and basal ganglia, which are a complex mixture of WM and GM. As for WM, DTI and other MR contrasts such as $T_2^{\ast }$ mapping or magnetization transfer have so far been used to describe cortical and subcortical microstructure (Duyn, 2018; Edwards et al., 2018; Lehéricy et al., 2012; Sled, 2018), but they are all again unspecific, with various types of microstructural changes potentially leading to the same effect in terms of these MRI metrics.

The main challenge that has stalled biophysical modeling of diffusion in GM so far is arguably accounting for an overall more complex tissue composition and for water exchange across the cell membrane (Fig. 2). Cortical GM is roughly constituted of 15–30% extra-cellular space, 10–40% cell bodies (soma), 40–75% neurites (thin cylindrical extensions of the cell that form numerous connections to other neurons) and 1–5% vasculature (Bondareff and Pysh, 1968; Motta et al., 2019; Spocter et al., 2012). Furthermore, the functional form of the powder-averaged diffusion signal at high b-values is different in GM than in WM, with a clear deviation from the impermeable stick behavior of $S(b)\propto \frac{1}{\sqrt{b}}$, which suggests non-negligible water exchange between neurites and extra-cellular space and/or soma (Veraart et al., 2020, 2018a; Jelescu and Novikov, 2020). The exchange between neurites and other compartments is plausible over typical diffusion times of MRI experiments (20–100 ms), especially since most neurites are unmyelinated. Modeling and estimating water exchange across the cell membrane will be covered in a dedicated section. On the up-side, neurites in GM can be assumed to be randomly oriented and described by a uniform ODF, which simplifies the model.

One approach to circumvent exchange is to be in a short diffusion time regime, where it can still be neglected even for unmyelinated cell membranes. The former route has been recently taken by Palombo and colleagues who proposed a GM model of three non-exchanging compartments (neurites, soma and extracellular space), dubbed SANDI for Soma And Neurite Density Imaging (Palombo et al., 2020). However, the SANDI model is currently only applicable to data acquired on human Connectom scanners and animal scanners: very high b-values need to be reached $\left(b=10\mathrm{m}\mathrm{s}/\mu {\mathrm{m}}^2\right)$ within very short diffusion times $(t_{\mathrm{d}}<20\mathrm{m}\mathrm{s})$ to keep the assumption of impermeable compartments – presumably – valid.

Another approach consists in explicitly modeling the inter-compartment exchange, which increases the fit complexity substantially. GM models that account for exchange are work in progress (Veraart et al., 2020; Jelescu and Novikov, 2020; Lee et al., 2020).

While deep brain structures such as the thalamus or striatum are already a complex mixture of white and GM, for which neither of the white or gray matter models above applies straightforwardly, pathological processes can also affect the tissue to an extent that may require adapting the underlying picture. Challenges specific to modeling pathology will be discussed in a dedicated Section 3.

Once a simplified picture is drawn and desired protocol developed, the next stop along the modeling roadmap is to evaluate the performance of estimating model parameters in numerical simulations and optimize the acquisition protocol. This is followed by testing on “real” experimentally acquired data to assess parameter range, reproducibility, and reliability, and next by biological validation in order to ensure biological specificity and agreement with gold measures.

2.2. Model performance in simulations

2.2.1. Numerical simulators for diffusion MRI

Both physical and numerical phantoms are essential tools for the validation of biophysical models of diffusion in brain tissue. Here we provide a brief review of the most recent strategies for validating biophysical models using numerical simulations. For a more exhaustive review of numerical simulations for modelling of dMRI, we recommend (Fieremans and Lee, 2018).

Numerical phantoms (Fig. 4) are complementary to physical phantoms, as they offer a controlled and flexible tool to simulate the effect of different mechanisms such as diffusion, exchange, relaxation and magnetic susceptibility variations on the MR signal in a given microstructural geometry, known by design.

Fig. 4.

Numerical phantoms of brain microstructure have been an active area of research for decades. Considerable effort has been invested in improving the realism of numerical phantoms (from left to right), by either developing generative models of realistic microstructure (first row) or refining the three-dimensional reconstructions from microscopy data of real tissue (second row). While challenges concerning white matter has been tackled first, recent developments carry great promise for gray matter too (third row). Note that realism and complexity of phantoms generally increase from left to right. In addition to more intricate geometries, features of exchange and detailed morphology are new developments. Illustrations adapted from (Hall and Alexander, 2009; Budde and Frank, 2010; Nilsson et al., 2012; Ginsburger et al., 2018, 2019; Callaghan et al., 2020; Chin et al., 2004; Panagiotaki et al., 2009; Kleinnijenhuis et al., 2020; Lee et al., 2019a; Hansen et al., 2013; Palombo et al., 2016; Van Nguyen et al., 2015; Palombo et al., 2019a), with permission.

Concerning the simulation of the diffusion process, the most widely used approaches can be divided into three major classes: matrix formalism; Monte Carlo (MC) methods and Finite Element/Difference methods. There are several open-source tools freely available that implement each of these methods for dMRI simulations. For instance, MISST (http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.MISST) (Ianus et al., 2016) based on matrix formalism; CAMINO (http://camino.cs.ucl.ac.uk) (Cook et al., 2006), DW-MRI Random Walk Simulator (www.NITRC.org: project name: “DW-MRI Random Walk Simulator”) (Landman et al., 2010), DIFSIM (http://csci.ucsd.edu/software/difsim.html) (Balls and Frank, 2009), and Diffusion Microscopist Simulator (Yeh et al., 2013) based on MC; SPINDOCTOR (https://github.com/jingrebeccali/SpinDoctor) (Li et al., 2019) based on Finite Element/Difference methods.

We focus here on MC simulations, because of their simplicity, flexibility and power in terms of simulating different MR contrasts in disparate realistic microgeometries. In MC simulations, many particles (corresponding, for instance, to water protons) are initiated in a microscopic geometry (namely digital substrate) and the diffusion process is simulated as random walk of these particles in space. The walkers can randomly hop on a pre-defined lattice (the simplest possible implementation) or in a continuous space with a fixed or dynamic step size. The dMRI signal is then calculated by accumulating the resulting phase changes from the random walkers’ trajectories and the chosen diffusion gradient sequence.

2.2.2. Monte-Carlo simulations for model validation

It is important to underline that MC simulations rely on the approximation of the diffusion process as a random walk (Einstein and Fürth, 1956), i.e. a sum of many fully independent steps. As a consequence, it is worthwhile to note that processes such as chemical-physical interactions are considered negligible at the time scales of the simulation (typically from μs to s). Moreover, MC simulations use the ensemble average of numerous particles’ trajectories to estimate statistically meaningful parameters. Therefore, to achieve an accurate parameter estimation of the ensemble average, a large number of steps and a large number of particles are required. Hence, it is necessary to properly setup the simulations to avoid undesired biases. For example, the number of particles and the step size have to be carefully chosen to avoid spurious biases or artifacts in the dMRI simulation. For a complete list of criteria and recommendations on how to setup and proof check MC simulations we refer the reader to (Hall and Alexander, 2009; Fieremans and Lee, 2018; Rafael-Patino et al., 2020). Once properly setup and proof checked, an MC simulator can be used to assess the performance of a specific biophysical model and investigate the regime of validity of its assumptions.

MC simulations have been widely used to validate microstructural modeling of neural tissues particular for diffusion. For WM micro-structure, MC simulations of diffusion have been used to investigate the performance of biophysical models to reliably estimate relevant axonal features such as inner axon diameter and intra-axonal volume fraction (Alexander et al., 2010; Lee et al., 2019c), as well as to evaluate bias due to unaccounted orientation dispersion (Ginsburger et al., 2019; Callaghan et al., 2020, 2019) and crossing-fiber resolution (Ramirez-Manzanares et al., 2011). Furthermore, MC simulations have been used to explore how physiological and pathological changes of neurite morphology can be potentially detected by dMRI, e.g., neurite beading (Budde and Frank, 2010), nodes of Ranvier (Ginsburger et al., 2018), undulation (Nilsson et al., 2012; Brabec et al., 2020), dendritic spines (Palombo et al., 2017a) and branching (Palombo et al., 2016; Vincent et al., 2020). Furthermore, diffusion simulations have been shown particularly useful to assess the effect of varying axonal water fraction on diffusion metrics such as fractional anisotropy (Stikov et al., 2011) and to disentangle demyelination from axonal loss (Fieremans et al., 2008). Several works also used simulations of water exchange to investigate its impact on biophysical modeling (Fieremans et al., 2010; Nilsson et al., 2010; Brusini et al., 2019), e.g., the regime of applicability of the Kärger model (Fieremans et al., 2010; Nilsson et al., 2010).

2.2.3. Limitations and challenges

Despite so many successful and useful applications, numerical phantoms have been strongly limited by a poor level of realism (Fig. 4). In order to be indeed useful validation tools, numerical phantoms have to mirror the complexity of real tissue microarchitecture as close as possible. In practice, this is still an unmet need and an active area of research. So far, the majority of the validation works based on numerical simulations have been focusing on WM because WM microstructure is – to some extent – simpler than GM one. However, the most used numerical phantoms for WM are still over-simplifications of the reality: axons are often modelled as densely packed cylinders of different radii, straight or undulating, and with or without planar dispersion. However, microscopy techniques such as 3D EM have clearly shown that axonal morphology in WM is significantly more complex than simple packed cylinders (Kleinnijenhuis et al., 2020; Lee et al., 2019c) (Fig. 4).

To address this limitation, a lot of effort has been recently invested by the dMRI community to design more realistic numerical phantoms. Two main strategies have been developed: one uses directly the real structure of brain tissue from 3D EM reconstructions as digital substrate MC simulations (Lee et al., 2019b; Panagiotaki et al., 2010; Berry et al., 2018) (Fig. 4, second row); the other uses generative models of digital tissues based on our current knowledge derived from microscopy (Ginsburger et al., 2019; Callaghan et al., 2020; Palombo et al., 2016, 2019; Callaghan et al., 2019) (Fig. 4, first row).While the first approach can provide ultra-realistic digital substrates, it lacks flexibility and is unable to reproduce large volumes of tissue. On the contrary, generative models are very flexible and can be scaled to reproduce large volumes of digital tissues, but they can inevitably represent only simpler architecture. Both these approaches still mainly focus on increasing the realism of WM digital phantoms, although some encouraging developments for GM digital phantoms have also been recently proposed (Palombo et al., 2016; Palombo et al., 2019) (Fig. 4, third row). Perhaps the most immediate challenge to be addressed is running numerical simulations of diffusion (e.g. using Monte Carlo approaches) on a more realistic substrate, for instance based on electron microscopy (EM) segmentation. “Simple” analytical models can then be tested for their ability to render the main microstructure features of that tissue. This approach is however very challenging, mainly due to the difficulty of obtaining a reliable segmentation of a significant volume of EM imaged tissue, transposing the segmentation into a numerical substrate, the time-consuming nature of MC simulations in such a substrate and the final amount of data to store and process.

Overall, there are several “big challenges” in numerical simulations for validation of diffusion modelling for dMRI that are still open. We could summarize them in: how to build a) ultra-realistic computational models of brain architecture at the micron scale, that are b) highly flexible, c) very well characterized (to provide full control on a solid ground-truth) and at the same time d) can scale up to reproduce large volumes (on the order the cubed millimeter, the typical MRI voxel size).

The recent developments in microscopy technologies and machine learning are opening encouraging and exciting perspectives towards possible solutions to these challenges. New innovative techniques for ultra-resolved microscopy (Motta et al., 2019) are driving our ever-expanding knowledge on the finest details of brain microarchitecture, providing precious databases from which to learn how exactly an ultra-realistic numerical phantom of brain tissue should look like. This may offer a well characterized ground-truth that can be used to inform the design of ultra-realistic digital substrates. Memory burden and computational cost, the current major bottleneck for the flexibility and scalability of more realistic numerical phantoms, may be mitigated by the recent developments in deep learning and computational hardware. We are living exciting times, that carry great potential to open the way towards the next-generation numerical phantoms for virtual experiments that can really represent the ultimate tool for the validation of microstructure models. Fitting strategies are also greatly evolving to overcome issues related to parameter estimation.

2.3. Fitting strategies

On the front of parameter estimation, most models rely on nonlinear fitting, which is strongly affected by noise and local minima (Harms et al., 2017; Jelescu et al., 2016b). In general, non-linear fitting is computationally expensive and the quality, accuracy and precision of the fit is often uncertain. To tackle these challenges, each of the popular models comes with its own constraints, optimization algorithm, noise model and initialization strategy to estimate its parameter maps. This creates challenges to comparability and generalization of results from diffusion microstructure models.

A novel strategy, that bypass non-linear fitting, relies on the explicit derivation of model parameters from the signal moments or cumulants (e.g. starting from a DKI fit) (Fieremans et al., 2011; Jespersen et al., 2018; Novikov et al., 2018b; Jensen et al., 2017) which has two substantial advantages: a) the problem is largely linearized, b) the acquisition protocol is more easily compatible with clinical scanners $\left(b_{\mathrm{m}\mathrm{a}\mathrm{x}}\le 2.5\mathrm{m}\mathrm{s}/\mu {\mathrm{m}}^2\right)$ and with a reasonable acquisition time. The downside of this approach is however the fundamental difficulty in obtaining accurate and precise estimates of cumulants (Chuhutin et al., 2017). Within this family of model implementations, Jespersen and colleagues have recently derived the analytical correspondence between signal cumulants and model parameters for the standard model with a Watson distribution of axons: “WMTI-Watson” (Jespersen et al., 2018). This ODF, characterized by a single concentration parameter $\kappa$, assumes axial symmetry of the WM bundle but otherwise allows any configuration from perfectly aligned $(⟨(\mathrm{c}\mathrm{o}\mathrm{s}\psi {)}^2⟩\equiv c_2=1\iff \kappa =\mathrm{\infty })$ to fully isotropic $(⟨(\mathrm{c}\mathrm{o}\mathrm{s}\psi {)}^2⟩\equiv c_2=1/3\iff \kappa =0)$ axons (Zhang et al., 2012; Jespersen et al., 2018).

Since non-linear fitting is still the most used approach for model’s parameters estimation, here we briefly discuss challenges and perspectives involving non-linear fitting approaches.

2.3.1. Model degeneracy

Several works have investigated strategies to make non-linear fitting robust, reproducible and fast, e.g. (Novikov et al., 2019; Harms et al., 2017; Alexander, 2009; Veraart et al., 2013; Panagiotaki et al., 2012; Harms and Roebroeck, 2018). The main challenge for robustness and reproducibility (in terms of precision) is how to resolve, mitigate or characterize any existing degeneracies. By degeneracy we mean the existence of multiple sets of model parameters values that all explain the measured dMRI signal equally well (Novikov et al., 2018b; Jelescu et al., 2016b). This behavior is due to the existence of multiple local minima in the fitting landscape, and/or to the flatness/shallowness of the landscape around each minimum (Fig. 5). The global minimum is barely identifiable based on goodness-of-fit criteria and the fit output becomes very sensitive to noise and initialization. Noise in particular can make numerous sets of solutions equally probable, if the global minimum is not “deep” or marked enough. Therefore, in the presence of degeneracy, it is impossible to choose a unique set of model parameters values, without relying on some priors or constraints. This unresolved ambiguity leads to poor generalizability and reproducibility of model based dMRI technique for microstructure imaging. As a consequence, our confidence in biophysical models’ predictions, especially in pathological conditions, is low, hampering the use of this class of techniques in clinical practice.

Fig. 5.

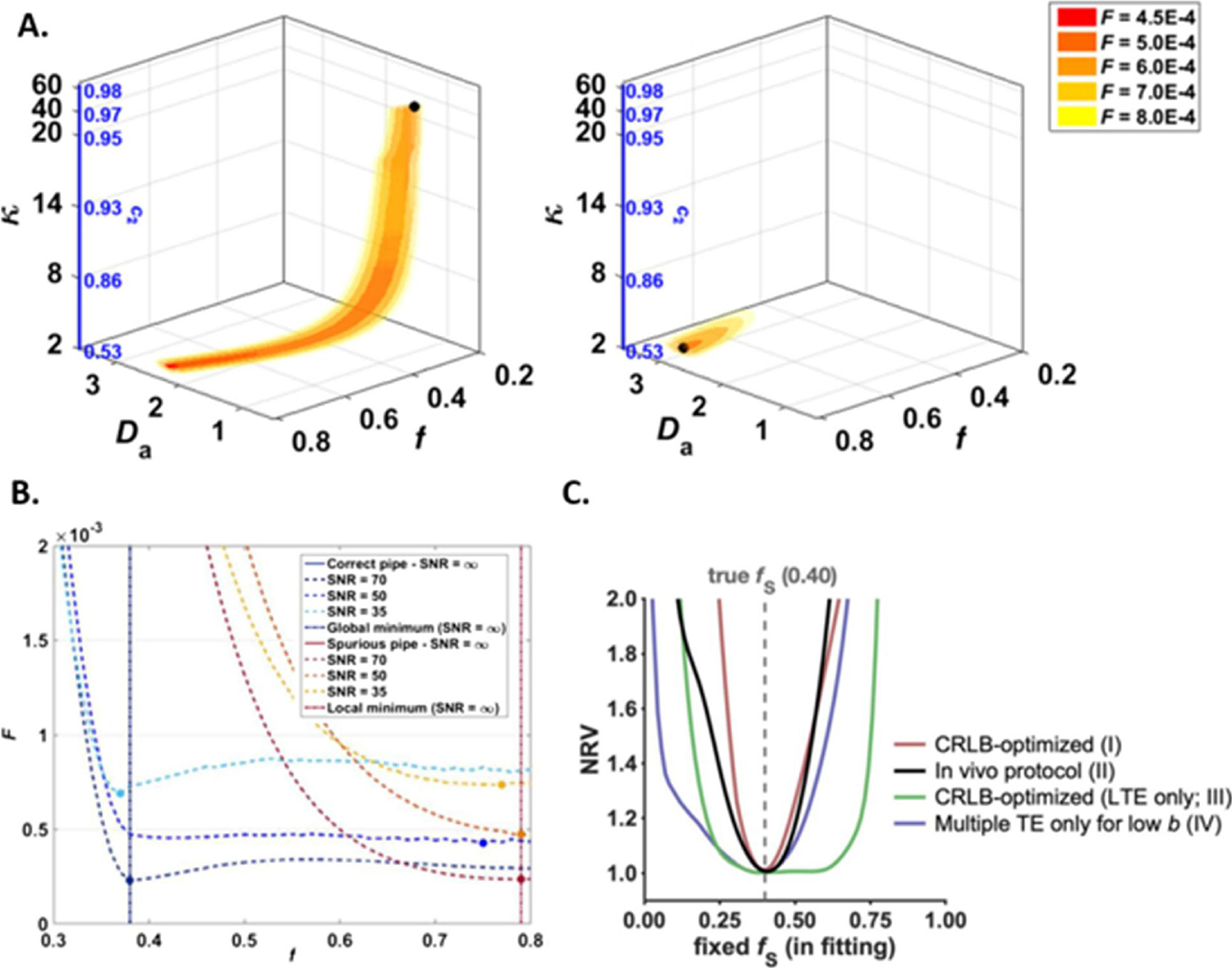
Parameter estimation in multi-compartment models of diffusion is challenging due to the existence of multiple local minima and an overall “flat” fitting landscape which makes a large ensemble of solution equally probable in the presence of noise. A: A two-compartment model (e.g. intra- and extra-axonal water) described by 5 free parameters ($\mathrm{f},D_a,D_{e,\parallel },D_{e,\perp }$ and $\kappa$ the concentration parameter of the Watson distribution) displays two disconnected minima (left: true minimum, right: spurious minimum). In the presence of noise, a “pipe” ensemble of solutions around each minimum displays a low objective function value, and the fit may end anywhere along this pipe. B: Projections of the objective function values along a single parameter, here f, showcasing the flat landscape around the minima and the wide range of plausible values. C: Using more advanced acquisition schemes including linear and spherical tensor encoding as well as multiple TE’s, the degeneracy can be lifted and the minimization landscape becomes much steeper around the true minimum, improving the fit accuracy and precision considerably. Illustrations adapted from (Jelescu et al., 2016b) (A and B) and (Lampinen et al., 2020) (C), with permission.

The degeneracy is mostly due to the incapacity of the acquired dMRI data to support the model complexity, that is the number of free parameters to be estimated from the data. In fact, dMRI data normally carry only a limited amount of information and support the estimation of just a few model parameters (Novikov et al., 2019). In some cases, multi-modal approaches such as combined diffusion-relaxation acquisitions (Lampinen et al., 2020) or generalized gradient waveform techniques (Reymbaut et al., 2020; Lampinen et al., 2019, 2017) can increase the amount of information in the measured data and remove the degeneracy for some models. However, this often comes at the cost of unconventional sequence implementation (meaning sequences that are not provided by the scanner manufacturer) and lengthy acquisitions.

2.3.2. Model constraints

To mitigate the degeneracy using more conventional and clinically feasible dMRI acquisitions, some of the current model based dMRI techniques use hard constraints (i.e. fixing some of the model parameters to arbitrarily chosen values) during the non-linear fitting procedure. This approach may sound sensible – or at least “appealing” for practical purposes, but it has to be used with caution. Indeed, priors on model parameters that can be reasonable and also validated for some cases (e.g. healthy brain or a particular brain disease) do not necessarily generalize (e.g. to a different brain disease). For example, in NODDI (Zhang et al., 2012), a widely used dMRI technique for Neurite Orientation Dispersion and Density Imaging, the intra-neurite axial diffusivity (i.e. the apparent diffusion coefficient along the neurite axis of water restricted within neurites) is fixed to a pre-defined value of 1.7 μm²/ms and the extra-neurite axial and radial diffusivities are linked to the neurite signal fraction and the intra-neurite axial diffusivity by a tortuosity model proposed by Szafer et al. (1995). This approach based on constraining the model fitting provides more precise estimation of the model parameters also with minimum dataset and produces reasonable parametric maps of good quality, but it may provide biased and inaccurate estimates of the model parameters, especially in pathological scenarios, where the model assumptions and the fitting constraints may not be sensible choices anymore. For instance, Wen et al. (2015) cautioned against interpreting their finding of a neurite density contrast within gliomas as actually due to neurites. More recently, Lampinen et al. (2019), 2017 have shown that different sets of constraints in the NODDI fit result in different estimated values for the neurite signal fraction in the human brain, proving a non-negligible bias due to the arbitrary priors on the model parameters constraints. As bottom line, hard constraints in non-linear fitting can be a viable solution to mitigate degeneracy and stabilize the fitting only if coupled with rigorous validation, clear understanding and acknowledgement of the limits of validity of the model constraints and caution with results interpretation.

A simple way to assess how important the degeneracy is and how the chosen constraints bias the model parameters estimation is by computing the normalized residual variance (NRV), given a specific model, the dMRI data and the standard deviation of the experimental noise (Lampinen et al., 2020):

$$NRV=\frac{1}{I}\sum _{i=1}^I\sum _{n=1}^N\frac{{\left(S_n-{\bar{S}}_n\right)}^2}{(N-M){\sigma }_{noise}^2}$$

Where the average is across $I$ realizations of Gaussian noise with standard deviation ${\sigma }_{noise},S_n$ is the noised signal, ${\bar{S}}_n$ is the fitted signal, $N$ is the protocol’s number of measurements and $M$ is the number of free model parameters.

Plotting the NRV against one of the model parameters p, fixed in the fitting to a different value p* each time, illustrates how precisely this parameter p can be determined given the specific acquisition protocol (Fig. 5). In the presence of degeneracy, the curve NRV(p*) is very wide, with a global minimum spanning different values of p* all providing similar goodness-of-fit. Imposing a specific hard constraint to the fit results in narrowing and sharpening the minimum in the NRV(p*) landscape. This minimum corresponds to the estimated value for the parameter p that necessarily depends on the chosen constraint itself. If there is such dependence, then the hard constraint is biasing the estimation of the parameter p. In cases where the “true value” of the parameter p is known, the constraint can be chosen in a reasonable way. For example, if p is the neurite density, in an ex-vivo experiment with healthy mouse brain, its “ground truth” value can be estimated by histological analysis and the fitting constraint can be accordingly chosen to improve model fitting performance. However, such constraint would be valid only for that specific situation (experimental setup, acquisition protocol, etc) and any further generalization should be taken with extreme care.

2.3.3. Optimization algorithms

Fitting an analytical model to some experimental data is an optimization problem. In the case of dMRI data, models are optimized by finding the set of free parameter values p that minimize the objective function of the modeling errors $\left[{\mathrm{S}}_{\text{measured}}-{\mathrm{S}}_{\text{model}}\left(\mathrm{p}\right)\right]$, with ${\mathrm{S}}_{\text{measured}}$ the observed data and ${\mathrm{S}}_{\text{model}}\left(\mathrm{p}\right)$ the model signal prediction. In general, the objective function is formulated as the negative log likelihood function which embeds a noise model for the data (Alexander, 2009; Panagiotaki et al., 2012; Alexander, 2008). How to model the noise in dMRI images and how to incorporate it in the fitting procedure is still an open problem. Some of the most popular approaches and their performances are described and compared for instance in (Veraart et al., 2013).

Commonly used optimization algorithms can be divided into two classes: gradient free algorithms, such as Nelder-Mead Simplex (Nelder and Mead, 1965) and Powell’s conjugate-direction (Powell, 1964), and gradient-based algorithms, such as Levenberg-Marquardt (1963), trust region (Steihaug, 1983) and active-set (Nocedal and Wright, 2006), for which the gradients can either be given analytically or approximated numerically. The accuracy of the solution and the quality of the fit depend on the algorithm chosen. Therefore, it is always a good practice to try different optimization algorithms on simulated data to determine which one performs the best for the specific model fitting task. For example, a comprehensive analysis of three of the above-mentioned algorithms (Nelder-Mead Simplex, Powell’s conjugate-direction and Levenberg-Marquardt) by Harms et al. (2017) showed that the gradient-free Powell conjugate-direction algorithm was found to outperform other common algorithms in terms of run time, fit, accuracy and precision for the common biophysical models like NODDI (Zhang et al., 2012) and CHARMED (Assaf and Basser, 2005). Moreover, different parameter initialization approaches were found to be relevant especially for more complex models, such as those involving several fiber orientations per voxel.

The parameter initialization is another very important aspect of all these optimization procedures. It defines the initial point (i.e. initial guess) from which the chosen optimization algorithm starts looking for the global minimum of the objective function. When the objective function is particularly complex, and/or the impact of the noise particularly strong, spurious local minima may occur. In this case, different parameter initializations may lead to different final estimates, corresponding to the closest local minima, rather than the global minimum. To mitigate this problem, a typical approach is the automatic definition of the parameter initial values by using exhaustive grid-search algorithms or initializing subsets of parameters of complex models with results from earlier simpler model optimizations. However, these solutions increase considerably the computational time of the overall fitting procedure and they do not guarantee general immunity to local minima. Nevertheless, they have been successfully used to fit complex models in a wide range of applications (Alexander et al., 2010; Harms et al., 2017; Panagiotaki et al., 2012; Huang et al., 2015, 2019).

Finally, a different optimization approach worth mentioning here is the Bayesian optimization (Shahriari et al., 2015) which does not require a simple closed form of the objective function (and does not need it to be the negative log likelihood function either). In Bayesian optimization, any objective function $f$ is treated as a black-box that can be evaluated at any arbitrary query point $x$ in its domain of existence. Basically, we assume that we can only observe the function $f$ through unbiased noisy point-wise observations $y$. To find the best estimates for a given model’s parameters set, we consider a sequential search algorithm which, at every iteration $\mathrm{n}$, selects a set of values $x_{\mathrm{n}+1}$ at which to query $f$ and observe $y_{\mathrm{n}+1}$. After $\mathrm{N}$ queries, the algorithm makes a final recommendation $x_{\mathrm{N}}$, which represents the algorithm’s best estimate of the model’s parameters set that optimize $f$. Although not required for Bayesian optimization, when gradients of $f$ are available, they can be incorporated in the algorithm as well. Bayesian optimization has been impacting a wide range of areas, including robotics (Wolfram et al., 2008) information extraction (Wang et al., 2014a), automatic machine learning (Swersky et al., 2013), adaptive Monte Carlo (Mahendran et al., 2012) and more. We will see in the next section how machine learning methods based on Bayesian optimization have been used for brain microstructure imaging, and we will discuss the pros and cons.

2.3.4. Strategies for accelerated fitting

There are several possible solutions to accelerate data fitting of complex non-linear models: parallel computing, dictionary matching/learning and machine learning.

2.3.4.1. Parallel computing.

One possibility is to use the parallel power of Graphical Processing Units (GPUs) to speed up the optimization. Nowadays, there are some GPU-based model fitting toolboxes for dMRI modeling freely available, such as the Maastricht Diffusion Toolbox (MDT) (Harms et al., 2017) at https://github.com/cbclab/MDT and the CUDA Diffusion Modelling Toolbox (cuDIMOT) (Hernandez-Fernandez et al., 2019) at https://users.fmrib.ox.ac.uk/~moisesf/cudimot/DesignModel.html. Another useful toolbox for accelerated biophysical model fitting is the Diffusion Microstructure Imaging in Python (Dmipy) (Fick et al., 2019) https://github.com/AthenaEPI/dmipy/, but it uses multi-core CPUs rather than GPUs, so it is (at the moment) slower than MDT or cuDIMOT for non-linear fitting.

2.3.4.2. Dictionary matching/learning.

Another approach to accelerate non-linear fitting consists of using methods based on dictionary matching/learning. The main idea behind these methods is to exploit the sparse property of a well-designed dictionary based on the desired biophysical model, in order to recover the diffusion signal and estimate the model parameters. A popular example of such approach is AMICO (Accelerated Microstructure Imaging via Convex Optimization) (Daducci et al., 2015) available at https://github.com/daducci/AMICO/. In AMICO, the strategy is to re-formulate non-linear biophysical models as convenient linear systems and use dictionary matching/learning for the fast and efficient solution. An advantage of these dictionary-based approaches is that the biophysical model chosen to represent the dMRI signal can be described by mathematical expressions (e.g. as in Daducci et al., 2015) or by computational models (e.g. as in (Rensonnet et al., 2019)). The latter uses numerical simulations (often MC based) to create a dictionary of dMRI signals, corresponding to specific tissue features used to generate the synthetic substrate (see Section 2.2). A dictionary matching/learning method is then used to estimate the tissue features from real dMRI signal in a regularized fashion (110). The advantages of these methods are several: they are first of all very fast, enabling on-the-flight processing of large volumes of data (once the dictionaries have been previously built and stored); they can more easily account for noise and incorporate spatial regularization, resulting in higher precision of the estimated parameters values and in parametric maps of better quality. However, this comes with some downsides: they provide less accurate estimate of the model parameters (109); they do not generalize, meaning that for a new application (different acquisition protocol, different biophysical model, different tissue etc.) a new dictionary has to be built; therefore the dictionary generation require careful design and tuning that is often different from one application to another; because of all the above-mentioned reasons, the reproducibility of the results is not always guaranteed.

2.3.4.3. Machine learning.

More recent approaches, based on modern machine learning, have been proposed to overcome some of the limitations of dictionary-based approaches and to speed up biophysical model fitting. Following (Ravi et al., 2019), we can divide them into three main categories, according to the method used: Random Forest (RF) regression; Bayesian Modeling or inference (BM) and Deep Learning (DL). RF are an ensemble learning method and a type of supervised learning algorithm which can be also used for regression tasks. It works by constructing a number of decision trees (forest) during training, one to each bootstrap sample drawn from the full set of training data. Once trained, the model typically outputs the mean value of the predictions over the full set of trees in the forest. RF has been successfully employed for microstructural parameter mapping task. For example, Nedjati-Gilani et al. (2014), 2017 proposed a RF approach to map axonal permeability in the healthy and Multiple Sclerosis diseased human brain, Hill et al. (2019) validated this approach in mouse model of demyelination induced by cuprizone intoxication and a similar approach is presented in (Fick et al., 2017) to map axon diameter from dMRI with a RF trained on matching histological data. Although powerful for fast biophysical model fitting, RF regressor has a main limitation in its poor generalizability outside the training set. Differently, BM relies on Bayes’ theorem for updating the probability of a hypothesis as more evidence is obtained. Bayesian modeling is especially useful when data is limited, avoids overfitting and can model uncertainty on parameters estimates (Park et al., 2010). For example, Reisert et al. (2017) have proposed a supervised machine learning approach based on a Bayesian estimator to disentangle the microscopic cell properties of the human brain from the effects of the mesoscopic structure. The model is both simple to implement and has the ability to handle noise. The main limitation of BM approaches is the requirement of priors, which can sometimes be very difficult to formulate, and they can be very computationally expensive, especially for more complex models with a large number of parameters. Finally, in dMRI, DL has been successfully used for ultrafast biophysical model parameter prediction. The basic unit of every DL model is an artificial neural network: an ensemble of perceptrons, where a perceptron is defined by a non-linear transfer function f and by two set of parameters: W (the weights) and b (the bias). The output of each neuron is the linear combination of the input x with the W added to the bias b, followed by the application of the transfer function (e.g. sigmoid or hyperbolic tangent function). One of the most popular artificial neural networks are the Multi-Layered Perceptrons that organize the neurons in many different layers. When many hidden layers can be added to an artificial neural network, we refer to it as a deep neural network or DL model. DL networks are usually trained through different steps, where at each step a new input sample or batch of samples are presented to the network. In this process, the weights are adjusted using a delta rule and a back-propagation function. Initially, random values are usually assigned to the network parameters and through this iterative training process, the parameters are updated to minimize the difference between the network predictions and the desired outputs. However, training a DL model is not always trivial, mainly due to possible numerical instabilities that could make the updated weights negligible (vanishing gradient problem), and adequate training countermeasures must be considered to avoid these issues. As successful applications in dMRI, we can for example mention a Multi-Layered Perceptron model used for a voxel-wise parameter estimation of the combined intravoxel incoherent motion and kurtosis model in (Bertleff et al., 2017); Golkov et al. (2016) proposed a method called q-space deep learning which allows mapping scalar parameters, such as diffusion kurtosis or orientation dispersion from significantly reduced acquisitions and detecting abnormalities without the intermediate steps of diffusion models; Ye et al. (2020) compare different DL models for the estimation of complex biophysical model parameters (e.g., NODDI) and propose an improved model which additionally provides an estimate of the error and the uncertainty associated with the model prediction. For a more exhaustive review of DL in MRI applications we refer the reader to dedicated reviews, such as (Litjens et al., 2017).

While the fitting performance can be improved in terms of speed and precision, the accuracy of parameter estimates with respect to the biological ground truth should also be estimated. Indeed, since biophysical models promised specificity, then it is critical to ensure that what the model labels as a “neurite fraction” for example is indeed a reliable estimate of the neurite fraction. This validation part is best achieved by comparing dMRI model estimates to those from other modalities or complementary techniques.

2.4. Validation against other modalities and complementary techniques

After choosing model features and their parameterization based on simplified sketches of the tissue, designing a suitable acquisition protocol for a given application, and optimizing the acquisition and fitting strategies, the next step is to validate results against complementary techniques (Fig. 3). Because classical histological analysis of tissue specimens provides exquisite anatomical detail, it is often considered the gold standard against which models are compared (Fig. 6). However, validation is not limited to comparisons against histology and can involve any information from orthogonal (independent) techniques, including additional simulations to investigate potential biases, acquisition across populations or conditions to assess parameter ranges and reproducibility, additional diffusion or non-diffusion sequences with contrasts sensitive to similar features, or simple experimentally acquired data in order to test well-defined hypothesis or in order to validate theory.

Fig. 6.

Comparison of histology and biophysical diffusion modeling organized by tissue features of interest. Biophysical modeling ultimately aims to enable a “virtual biopsy” by allowing non-invasive, non-destructive, repeatable measure of tissue microstructure, over a large field of view with fast data acquisition and processing. Shown are imaging indices of neurite density (A-D) (Zhang et al., 2012; Jespersen et al., 2010; Lampinen et al., 2017), orientation and dispersion (E-G) (Kaden et al., 2016; Leergaard et al., 2010; Tournier et al., 2004), axon diameter (H-L) (Duval et al., 2015; Alexander et al., 2010; Barazany et al., 2009; Ong and Wehrli, 2010), cell shape and heterogeneity (M-P) (Szczepankiewicz et al., 2015; Shemesh et al., 2012; Lawrenz and Finsterbusch, 2013), and myelination (Q-T) (Laule et al., 2008; Deoni et al., 2011; Whittall et al., 1997). Please refer to original illustration by Alexander et al. (2019), for detailed descriptions of models used. Figure adapted from Alexander et al. (2019), with permission.

In the sections that follow, we describe several techniques and strategies that have been utilized to validate various features of biophysical models of diffusion, and describe both limitations and successes, as well as lessons learned throughout.

2.4.1. Compartment fractions

The relative sizes of the different water pools can readily provide information about the physical sizes of the underlying compartments. However, this information is intrinsically an indirect one as several aspects preclude the direct estimation of physical compartment sizes from dMRI.

First of all, each compartment weight $f_{est}$ should in fact be understood as a relative signal fraction $f_{comp}{e}^{-\frac{TE}{T2,comp}}$, where the physical compartment fractions are most heavily weighted by the compartment $T_2$’s (although the compartment fractions are also weighted by $T_1$ and proton density, the T₁-weighting is minimal because the TR is typically quite long for diffusion MRI, and we do not expect different proton densities between the compartments, although this has not been thoroughly investigated in the literature). As it is still unclear whether intraand extra-cellular $T_2$ are similar or substantially different, this can potentially affect the estimate significantly. The most extreme case is that of myelin water, whose $T_2$ is so short (~10 ms) it is typically “MRinvisible” in diffusion-weighted scans where the echo time is relatively long due to the spin-echo design. One increasingly popular approach to deal with this limitation is to estimate compartment diffusion and relaxation properties jointly (Lampinen et al., 2019; Benjamini and Basser, 2017; Veraart et al., 2018b). In an effort to make up for the missing myelin compartment and estimate the axon g-ratio (i.e. the ratio of axon inner to outer diameter), combined dMRI and quantitative magnetization transfer have also been explored (Campbell et al., 2018). While the idea is interesting, its implementation requires reliable and thoroughly validated models on both ends (i.e. both diffusion and magnetization transfer).

In principle, compartment sizes estimated from dMRI models can be cross-validated against histology and EM. However, there are intrinsic differences between these techniques and MRI that preclude a one-to-one correspondence and the use of ex vivo microscopy as a “gold standard”. Most often, the dMRI measurement is done in vivo, and the microscopy slides are on ex vivo fixed tissue. Chemical fixation is known to alter tissue properties, in particular by preferentially shrinking the extra-cellular space versus the intra-cellular. There are alternative tissue preparation techniques for EM based on cryofixation that preserve in vivo proportions more faithfully (Mobius et al., 2016; Ohno et al., 2007), and these should definitely be favored in any validation study. However, even so, the volume of tissue that can be characterized and quantified with EM is usually much smaller than the MRI voxel size. Then remains the question whether the small EM sample is representative of the entire structure encompassed by the MRI voxel.

Lastly, the compartment fractions can be dramatically affected by inter-compartment exchange, if the latter is de facto substantial but not accounted for in the model. For instance, studies of microscopic anisotropy using diffusion tensor encoding techniques have shown that the “neurite fraction” typically mirrors myelinated neurites and axons, and not unmyelinated ones (Lampinen et al., 2017). But to conclude on an optimistic note, intra-axonal fraction estimated from dMRI models in WM usually agrees reasonably well and correlates strongly with the matching metric derived from light and electron microscopy (Jelescu et al., 2016a; Jespersen et al., 2010; Duval et al., 2017; Grussu et al., 2015; Jespersen et al., 2007; Stikov et al., 2015).

2.4.2. Orientations

A fundamental aspect of nearly all biophysical models is the description of the tissue orientation distribution. In the WM, this function would capture the direction(s) and dispersion of the different fascicles within a voxel and is often referred to in the literature as the fiber orientation distribution (FOD), or fiber orientation distribution function (fODF). This structure is often represented in the spherical harmonic basis, which are a set of basis functions defined over a sphere. Alternatively, many models are based on functional descriptions of orientation, for example Watson or Bingham distributions representing discrete fiber populations and their dispersion.

By far, the most common application of the FOD is in providing voxel-wise estimates of WM directionality for diffusion fiber tractography, a process which seeks to map the structural connections of the brain (Mori et al., 1999; Basser et al., 2000; Behrens et al., 2003). Tractography has been widely used to investigate brain development, cognition, and (dys)function, and shows promise in revealing clinically relevant structural information during neurosurgical procedures. Because the FOD forms the basis of nearly all tractography algorithms, validating the ability to accurately characterize structural geometry and orientation is a necessity for anatomically accurate tractography. For this reason, validation efforts have focused on applications to tractography, although the accurate estimation of orientation and directional heterogeneity is relevant not only as a potential biomarker, but also to fully disentangle macroscopic orientation information from the scalar tissue microstructural features (compartment sizes, diffusivities, etc.).

2.4.2.1. Validating fiber orientation distribution.

The validation framework of choice for a majority of orientation reconstruction algorithms has been through simulations (Fig. 7). Major limitations of many algorithms are first identified using these methods. For example, several studies utilized synthetic data to highlight the failure of DTI to characterize intra-voxel orientation when more than a single fiber population is present (Alexander, 2005), a challenge which came to be known as the crossing fiber problem and is known to affect a majority of voxels in the brain (Schilling et al., 2017; Jeurissen et al., 2013). A large number of models have since been developed to solve this problem, many of which are first validated through simulations (Descoteaux et al., 2007; Aganj et al., 2010; Ozarslan et al., 2006; Tournier et al., 2007; Tuch et al., 2002; Yeh et al., 2010), typically by optimizing selection of algorithmic and acquisition parameters.

Fig. 7.

Validating fiber orientation distributions through simulations, physical phantoms, and biological phantoms. Fields of simulated fiber orientations (left) (Daducci et al., 2014) can be used to asses model performance in estimating the correct number and orientation of fiber populations in each voxel. Simulations offer the ability to assess a great number of physical and experimental conditions but are often overly simplistic and rely on a given model in order to generate the diffusion signal. Physical phantoms can also be used to investigate the effects of reconstruction and acquisition strategies (middle) (Tournier et al., 2007, Tournier et al., 20082008). These phantoms are well characterized and offer the realism of both acquisition (and associated artifacts) and a signal based on real diffusion processes, however, these are often overly simplistic and may not truly represent the geometric complexity and sizes scales of real tissue. Finally, fiber reconstruction techniques can be compared against histological analysis (right) (Leergaard et al., 2010). This method inherently contains the microstructural and geometric complexity associated with the tissue, but may face challenges associated with limited fields of view, characterizing relevant tissue features on histological sections, and inability to modify acquisition or analysis after sectioning.

Simulations further offer the ability to compare the performance of different algorithms under varying physical conditions. For example, using multi-Gaussian test functions across a range of crossing fiber angles, fiber volume fractions, and noise levels has given insight into the successes and limitations of competing approaches (Alexander and Barker, 2005), or the effects of algorithmic choices and modeling assumptions (Canales-Rodriguez et al., 2018), in identifying the minimum resolvable crossing angle, angular error in identifying fiber orientation, and ability to identify volume fractions of multiple fiber compartments. Notably, a recent community challenge, the “HARDI Reconstruction Challenge” (Daducci et al., 2014) used fields of simulated Gaussian functions to compare the behavior of a large number of models for recovering orientations, evaluating the correct assessment of the number of fiber populations in each voxel and the angular accuracy in their orientation. The main conclusions are that the relationship between the signal and fiber orientation is fairly well understood, and despite the large number of modeling strategies in literature, they generally well reflect the underlying fiber orientation distributions in each voxel. There still exist differences in resolvable crossing angles, angular accuracy, and successes in identifying fiber populations, but there was no “optimal” method for a given acquisition, none outperformed others in every evaluation criteria (Daducci et al., 2014).

While computer simulations are useful for comparative studies over a range of fiber geometries and in ensuring a new method behaves as intended, they are likely an over-simplification of both the geometric complexity of brain tissue and the diffusion process within this tissue. Towards this end, analysis of post-mortem histology has become a valuable validation resource which inherently contains the complex structural characteristics of the central nervous system. Using light microscopy of stained tissue sections, techniques such as manual tracing of fibers (Leergaard et al., 2010), filter matching (Choe et al., 2012), or structure tensor analysis (Budde and Frank, 2012) have been used to quantify the histological, or ground-truth FOD. Studies in both human and primate tissue have investigated the accuracy of the DTI primary eigenvector, and the relationship between fiber density, spread, and anisotropy with the error in orientation estimates (Choe et al., 2012; Seehaus et al., 2015). Models able to resolve crossing fibers have been investigated by comparisons against myelin-stained sections in the mouse brain (Leergaard et al., 2010), concluding that the FOD obtained from high-angular resolution diffusion data provides accurate representations of the myeloarchitecture in regions of crossing fibers.

Typically, histological specimens have been limited to 2D analysis, restricting the analysis to fibers oriented in the plane of tissue slice. Recently, validation techniques have since been extended to 3D histological acquisitions. For example, two-photon microscopy (Kamagata et al., 2016), optical coherence tomography (Wang et al., 2015), confocal microscopy (Schilling et al., 2016; Khan et al., 2015), and polarized light imaging (Axer et al., 2016) have allowed visualization of continuous 3D images of tissue sections, and quantification of 3D orientations, with results in agreement with the primary fiber orientations estimated with DTI (Khan et al., 2015), and even used to perform histological fiber tractography (Wang et al., 2015). Comparing histological FODs to those estimated from a number of modelling approaches, confirms simulation results that there is no model that consistently outperforms others in every quality criteria and that all methods describe the overall structure of the FOD quite well (Schilling et al., 2018). However, while the overall shape of the fiber distribution is well-described by existing modelling approaches, histological evaluation highlights limitations in extracting discrete measures from the FOD (number of peaks and primary orientation) as well as the inability to resolve fiber populations that cross at sharp angles. Importantly, these histological analyses highlight that real brains have rich geometries, with orientation dispersions, undulations, fanning, and bending geometries, and emphasize the importance of considering multiple fiber populations with varying partial volumes and varying anisotropies within a voxel.

In addition to limitations associated with the 2D nature of most light microscopy, and the difficulty in characterizing and analyzing large, high resolution datasets, another complication of histological validation is accurate alignment of histology with MRI data, which is a requirement for comparison of directionality on a voxel-by-voxel basis. This alignment is often facilitated through an intermediate imaging modality, typically a digital photograph of the tissue blockface during serial sectioning, that allows registration of slices to a volumetric stack of blockface images, followed by a registration of from this space to that of MRI. These techniques have been applied successfully in rodent and primate models (Choe et al., 2011) and recently in whole human hemispheres (Mancini et al., 2020). Several optical techniques are now able to image the blockface directly, for example two-photon microscopy (Kamagata et al., 2016) and optical coherence tomography (Wang et al., 2015; Jones et al., 2020), which directly reduces distortions and should facilitate direction comparisons with dMRI.

While tailored towards tractography, these FOD validation studies provide valuable insights into modeling. There are currently very few models that consider multiple fiber populations AND can reliably estimate them (Assaf and Basser, 2005; Scherrer et al., 2016; Wang et al., 2011; Farooq et al., 2016) – almost all utilizing very strong constraints to stabilize the fit, for example imposing too strict of assumptions on FOD shape, or factoring out an assumed shape to estimate microstructure parameters, or vice versa. This means that most current models are not representative of the majority of voxels in the brain, and those that are may be too restrictive in either the features of orientation or features of diffusivities and volume fractions. It appears as if there are a crossroads between capturing a complex orientation at the same time as a complex number of microstructural properties and the intrinsic degeneracy in parameter estimation. Alternative strategies, for example model-fitting strategies (Henriques et al., 2019) or utilizing tractography to inform microstructure (in contrast to the reverse: microstructure-informed tractography (Girard et al., 2017) which has greatly regularized connectome construction) may be necessary to both capture orientation complexity and the range of biophysical measures expected in tissue.

2.4.2.2. Validating orientation dispersion.

Rather than assessing the number and directionality of fiber populations, it is also important to evaluate the directional coherence, or alternatively the dispersion, of the fiber geometries within a voxel. It has been well demonstrated with histology that WM tracts are not composed of perfectly parallel sets of myelinated fibers, but rather a dispersion or undulation of between 15–25 degrees is present in WM of rodents (Leergaard et al., 2010), primates (Schilling et al., 2016, 2018), and human samples (Ronen et al., 2014; Jonas et al., 1990; Lontis et al., 2009), which if not appropriately modelled can affect subsequent microstructural measures (Brabec et al., 2020). In the GM, there was strong agreement between a standard two compartment model of cylindrical elements with a Watson distribution and histological staining (Jespersen et al., 2012). As a form of validation against prior knowledge, it has been shown that the NODDI model with a Bingham orientation distribution is able to capture the cortical fibers adjacent to and within the cortex that are known to exhibit fanning and bending distributions throughout the neocortex (Tariq et al., 2014). In the spinal cord WM, the NODDI-derived dispersion index agreed well with histological dispersion in both healthy and lesioned post-mortem spinal cords (Grussu et al., 2017), suggesting a potentially specific biomarker of spinal cord pathology. In agreement, recent work in the brain WM also revealed strong correlation between the dispersion index derived from NODDI and that from 3D confocal z-stacks (Schilling et al., 2018). However, the same study also showed a systematic bias of the true histology-based dispersion, as well as evidence that the tissue dispersion influenced and biased estimation of other model parameters.

Overall, evidence suggests that both representations of the FOD in the spherical harmonic basis, as well as functional forms of orientation adequately capture fiber orientation and orientation dispersion, and are able to resolve multiple fiber populations in a voxel – with results dependent on acquisition parameters, data quality, and chosen modelling approach and reconstruction method.

2.4.3. Sizes and shapes

As opposed to estimating tissue directionality, which emphasizes sampling the signal along many orientations, models for estimating cell sizes and shapes usually require orthogonal diffusion information – typically multiple diffusion times, or diffusion encoding shapes.

2.4.3.1. Axon diameters.

Axon diameters have been estimated by varying diffusion times or diffusion weightings and modeling the time dependence or diffusion-weighted dependence of diffusion within axons. The first challenge in estimating diameters, or sizes of structures in general, is determining the relationship between that characteristic scale and its effects on the diffusion-weighted signal in $q-t$ space, where $q$ is the phase warp imparted to the particles and $t$ is the diffusion time $\left(b=q^{2}t\right)$. Early studies showed optimistic results, with axons diameters of the optic and sciatic nerves (which have larger diameters than axons of the cerebrum) agreeing well in animal models both ex vivo and in vivo (Assaf et al., 2008; Barazany et al., 2009). Unfortunately, this agreement was lost when translating to clinical scanners on the human brain, with diameters overestimated by as much as an order of magnitude (Alexander et al., 2010). The first obstacle here lies in the resolution limit of estimating diameters imposed by the hardware – typically clinical gradient strengths $(60\mathrm{m}\mathrm{T}/\mathrm{m}-80\mathrm{m}\mathrm{T}/\mathrm{m})$ do not support estimation of diameters below 4–8 μm, while axons in the human brain WM are typically 1–2 μm (Nilsson et al., 2017). The silver lining is that recent progress in technology with dedicated gradient coils allows more accurate estimation of diameters in the living human brain (Veraart et al., 2020). Two important regimes have also been identified more clearly: a “weak” diffusion weighting regime where the diffusion time-dependence is dominated by extra-axonal water and which gives access to axon outer diameters (De Santis et al., 2016; Burcaw et al., 2015; Fieremans et al., 2016; Lee et al., 2018) and a “strong” diffusion weighting regime – not accessible on clinical scanners – where the diffusion time-dependence is dominated by intra-axonal water and which gives access to axon inner diameters (Duval et al., 2015; Veraart et al., 2020). The earlier models that yielded axon diameter estimates off by an order of magnitude were in the former case yet incorrectly modeled the extra-axonal compartment as Gaussian anisotropic, attributing all the experimental time-dependence to the intra-axonal compartment, where this time-dependence was in fact very weak given the diffusion weightings achieved.

The second challenge in diameter estimation is related to tissue complexity. An underlying assumption of most models is that axons are straight impermeable cylinders, however, an increasing body of evidence points to the need to take into account variation of diameters along the length of axons (Lee et al., 2019a) or an axonal “beading” (Budde and Frank, 2010), and an undulation or sinusoidal trajectory of axons (Nilsson et al., 2012). Specifically, by simulating a substrate from a 3D EM volume of tissue in the mouse corpus callosum, Lee et al. (2019a) first highlight that different methods of calculating axon diameter may bias comparisons across studies (i.e., short axis length, long axis length, equivalent circle diameter, etc.) and that the assumption of a Gamma distribution of diameters may be overly simplistic in tissue (Lee et al., 2019a). They further show that significant along-axon variation of diameters exists, and contribute to non-trivial time dependence of MRI-derived axon diameters suggesting that perfectly cylindrical axons are overly simplistic models. These local enlargement and constrictions of axons along their length (i.e., axonal “beading”) and sinusoidal undulations of axons - have been observed in histological slides in both humans and non-human samples (Brabec et al., 2020; Schilling et al., 2018; Lontis et al., 2009; Lee et al., 2019a). By simulating these environments, studies have shown that beading effects can affect the measured diffusivity in both intracellular and extracellular compartments. In a beading geometry, a reduced intracellular diffusivity in the direction parallel to the fibers was observed by Budde & Frank (Budde and Frank, 2010), offering a potential mechanism for reduced apparent diffusion coefficient (ADC) after stroke. Additionally, beading resulted in a linear change of the extra-axonal perpendicular diffusivity with diffusion time (Ginsburger et al., 2018). Finally, undulating geometries have been shown to increase perpendicular diffusivity measures (Nilsson et al., 2012) and also give rise to time dependence substantially different from that expected from straight cylinders. In combination with insights from diffusion time dependence and diffusion regimes, these geometric effects may lead to an overestimation by an amount proportional to the undulation amplitude, an effect most prominent at longer diffusion times (Brabec et al., 2020). Together, these highlight that non-straight and non-uniform geometries of axons should not be overlooked when decoding the diffusion signal, and emphasize the importance of considering these geometries when validating the successes and limitations of new models. On a highly positive note, the typical distance between axon irregularities along their axis can also be estimated using time-dependent diffusion and appropriate models, and can be highly informative of microstructure feature such as boutons, nodes of Ranvier, beading, or distance between mitochondria (Fieremans et al., 2016). A summary of the challenges facing axon diameter estimation is shown in Fig. 8.

Fig. 8.

Challenges in biophysical modeling of axon diameter. First, histology may not be a perfect “gold standard” for model comparisons due to tissue processing effects and limitations associated with 2D quantification (see Section 2.4.1) (Lee et al., 2018b; Dyrby et al., 2018). Second, axons are not perfect cylinders and exhibit both variation of diameters along their lengths (B) (Lee et al., 2018b) as well as an undulation pattern (C) (Nilsson et al., 2012). Third, the diffusion signal may show a decreased sensitivity (smaller signal change) to smaller displacements associated with small diameters and there are theoretical prediction limits set by gradient amplitude and gradient waveforms (D) (Nilsson et al., 2017). However, improved understanding of the diffusion signal (for example it’s time dependence (E)) (De Santis et al., 2016) may lead to improved estimates of axon diameter, as well as improved creation and availability of complex simulated substrates (Ginsburger et al., 2019) that will complement future validation studies. Figure modified and adapted from (Nilsson et al., 2012; Ginsburger et al., 2019; Lee et al., 2019b; Nilsson et al., 2017; Burcaw et al., 2015) with permission.

2.4.3.2. Cell sizes.

Cell size estimation can also be done through varying diffusion times and acquisition strategies. Many models of cell size have been thoroughly investigated, particularly with application to tumor models. Most commonly, the tumor environment has been modelled as impermeable spheres of a given radius within an extracellular space, with acquisitions requiring multiple PGSE (Pulsed Gradient Spin Echo) diffusion times or a combination of PGSE + OGSE (Oscillating Gradient Spin Echo) measurements to probe several time domains. OGSE acquisitions give access to much shorter diffusion times, but strong diffusion weighting is not achievable. One method, Imaging Microstructural Parameters Using Limited Spectrally Edited Diffusion (IMPULSED) (Jiang et al., 2017) utilizes a single PGSE acquisition at long diffusion times and OGSE with multiple frequencies for shorter times to probe cell size and density. Both mean axon diameter (Xu et al., 2014) and cell size estimates correlated strongly with histological measurements in vitro and in vivo (Jiang et al., 2017) in a colorectal cancer xenograft model $(\mathrm{r}=0.81)$ analyzed using light microscopy. Further investigations into the effects of water exchange (which isn’t explicitly modelled) and the effects of fixing diffusivity parameters have been performed using simulations, with results suggesting that with sufficient signal-to-noise ratio (SNR), estimates of cell size are robust against both simplifying assumptions (Li et al., 2017). Another model, the Pulsed and Oscillating gradient MRI for Assessment of Cell size and Extracellular space (POMACE) (Reynaud et al., 2016) uses high frequency OGSE to estimate measures of restriction (surface-to-volume ratios) and free diffusivity, and uses these as fixed values when fitting low-frequency OGSE and multiple long-time PGSE to model impermeable spherical geometries. When introducing the model, the authors validated uncertainty in parameters estimates due to noise, and also potential biases introduced in estimating diffusivity parameters (specifically, assuming a constant extracellular space diffusivity over a given range of times and frequencies). Results show that the model, the assumptions, and fit procedure are robust to parameter degeneracy, and in vivo and ex vivo estimates of cell radii in mice glioma models were in good agreement with those from EM images, suggesting the use of this method for noninvasive cell size estimation (Reynaud et al., 2016). Finally, the Vascular, Extracellular, and Restricted Diffusion for Cytometry in Tumors (VERDICT) (Panagiotaki et al., 2014) model estimates cell size and intra/extra cellular components, in addition to an anisotropic vascular compartment, and can be utilized with PGSE (or combination of PGSE and OGSE) at multiple diffusion times. In its original implementation in the prostate, this model was validated in two ways (Panagiotaki et al., 2014). First, by evaluating two human colorectal carcinoma cell lines with known tissue pathology, VERDICT was able to accurately characterize densely packed, less perfused, and smaller cell sizes of the LS174 T cell line (presented as low extra-cellular volume fraction, low perfusion fraction, and lower cell size) against the higher perfusion of the SW1222 line. Second, cell apoptosis due to the effect of chemotoxic agents was observed as changes in volume fractions and confirmed by flow cytometry. Direct comparisons of cell size against light microscopy indicated a slight overestimation (12%) of size, which was attributed to shrinkage during tissue preparation. Improvements in fitting and linearization (see Section 2.3) have led to an AMICO-VERDICT framework (Bonet-Carne et al., 2019) which has since been applied in human glioma patients (Zaccagna et al., 2019). Optimistic results suggest that the linearized VERDICT is able to distinguish highgrade from low-grade glioma (smaller larger intracellular component and smaller vascular component) in agreement with histology, with a good agreement with histological cell size, and again a slight overestimation compared to histological sections (Zaccagna et al., 2019). Overall, these modeling strategies emphasize the benefit of incorporating alternative information in the form of acquisition and/or diffusion times in the modeling approach.

2.4.3.3. Multiple diffusion encodings.

One important and trending approach is that of diffusion-encoding schemes complementary to single pulsed field gradient pairs (PFG, often combined with a spin-echo acquisition), that have unique potential to disentangle microstructural shapes and sizes from their orientation distribution within the voxel in an unambiguous way that does not rely on modeling. We refer the reader to (Topgaard, 2017) for a dedicated review. The first large family of non-PFG methods is that of double, or more generally, multiple PFG that originated from solid-state NMR spectroscopy and the estimation of pore sizes in porous media (Cheng and Cory, 1999; Mitra, 1995) but quickly found applications to biological tissue and even demonstrated feasibility on human clinical systems (Lawrenz and Finsterbusch, 2013; Avram et al., 2013; Koch and Finsterbusch, 2011; Lawrenz and Finsterbusch, 2019). The most widespread implementation is the double PFG, or double diffusion encoding (DDE) – see (Shemesh et al., 2016) for a review and nomenclature disambiguation – which exploits the dependence of the signal on the angle between the first and second pair of PFG’s. Briefly, at long diffusion times, short mixing times between the two gradient pairs provide information on elementary feature (“pore”) sizes, while long mixing times provide information on the so-called microscopic anisotropy (μFA), i.e. microstructural anisotropy of the elementary features, independently of their orientation distribution within the voxel. For example, it is possible to distinguish a voxel of spherical cell bodies from a voxel of randomly oriented neurites, although both scenarios would yield similar diffusion signatures in single diffusion-encoding methods. Rotationally-invariant acquisition schemes for DDE have also been proposed to alleviate any prior knowledge of the underlying tissue symmetries with respect to the applied gradients (Jespersen et al., 2013; Lawrenz et al., 2010). DDE experiments have demonstrated clear added value with respect to single diffusion-encoding in terms of lifting degeneracy in model parameter estimation (Coelho et al., 2019; Reisert et al., 2019) and in removing crossing-fiber confounds by exhibiting sustained high μFA in WM regions of low FA (Lawrenz and Finsterbusch, 2013). Applications already include improved delineation of multiple sclerosis lesions (Yang et al., 2018a) and characterization of tumor microstructure (Duchêne et al., 2020). Remarkably, DDE characterization of μFA revealed lower values for GM than WM (Lawrenz and Finsterbusch, 2019), which suggests a prominent role of spherical cell bodies and of water exchange between compartments in GM modeling. On the down side, DDE is associated with long acquisition times, in spite of recent efforts to propose minimal designs compatible with clinical settings (Yang et al., 2018a; Kerkelä et al., 2020).

The second main approach is the so-called q-space trajectory imaging, or diffusion tensor (b-tensor) encoding (DTE), which consists in using time-varying diffusion gradients instead of pulsed blips to probe a variety of orientations at once, rather than just one diffusion direction (Topgaard, 2017; Westin et al., 2016). This technique is conceptually close to that of multiple PFG in the sense that free gradient waveforms can be generated to produce planar tensor encoding similarly to DDE, or spherical tensor encoding similarly to TDE (triple diffusion encoding). However, these particular b-tensor geometries (planar and spherical encoding) are only special cases of DTE, which can in principle be used to design any q-space trajectory. Furthermore, free gradient waveforms are less demanding in terms of gradient amplitude and slew rate than multiple PFG design, for the same resulting b-tensor. However, unlike multiple PFG, the diffusion time is ill-defined in DTE which may be problematic or a source of confounds given the well-known diffusion time-dependence in biological tissue (de Swiet and Mitra, 1996; Jespersen et al., 2019). Notwithstanding, DTE has demonstrated outstanding potential in support of biophysical modeling and microstructure characterization. Applications range from the discrimination between various types of tumors characterized by different cell geometries (Szczepankiewicz et al., 2015; Nilsson et al., 2020; Szczepankiewicz et al., 2016), probing the relevance of a “dot” compartment (i.e. immobile water) in biophysical models of brain tissue (Tax et al., 2020) to assessing kidney microstructure (Nery et al., 2019). Furthermore, DTE techniques have also shown to be instrumental in lifting degeneracies of models estimated from single tensor encoding alone, as detailed in Section 2.3 on Fitting Strategies, and Sections 2.4.1 and 2.4.4 on validating compartment fractions and diffusivities.

2.4.4. Diffusivities

Diffusivities are arguably the model parameters most difficult to cross-validate, because there are no alternative methods to NMR for measuring the self-diffusion coefficient of water. Yet diffusivities carry highly relevant information about the microstructure medium (e.g. cytosol viscosity, molecular crowding, etc.), and a biophysical model of diffusion should not be reduced to its sheer geometry while diffusivities are fixed to ad hoc values.

The initial drive for measuring compartment-specific diffusivities was to better understand the origin of the dramatic drop in apparent diffusion coefficient following ischemic stroke. Using compartment-specific exogenous tracers based on X-nuclei, such as cesium, sodium and fluorine, it has been suggested that the apparent diffusivities in the intra- and extracellular environments for molecules of these sizes are approximately similar to one another (Duong et al., 2001, 1998; Goodman et al., 2008, 2005). The limitation of these probes is that they have different sizes and affinity to charged surfaces than water, as well as possibly different exchange dynamics across the cell membrane, and their diffusion behavior cannot be immediately translated to that of water molecules. However, a similar experiment using extra-cellular gadolinium as a way of selectively suppressing the extra-cellular water signal reported the same trend of comparable diffusivities between intra- and extra-cellular compartments (Silva et al., 2002). These measurements were all performed in rat GM where neurite orientations are random and averaged out, and their result should therefore be interpreted as diffusion tensors in each compartment having similar traces (or mean diffusivity).

Endogenous compartment-specific probes such as brain metabolites have also been used to determine compartment diffusivities, again with the same limitation associated to the consideration of a molecule different from water. Note that the interpretation of brain metabolites’ diffusion-weighted signal is challenging because brain metabolites are molecules heavily involved in brain metabolism, active transport and other physico-chemical processes. However, numerous studies, performed with different techniques in different species (rodents, monkeys and human), have shown strong evidences that the diffusion of some brain metabolites (such as N-acetyl aspartate (NAA), Glutamate, Choline and Myoinositol) can be interpreted and modeled in terms of cell microstructure/geometry, as also usually done for water diffusion (Cao and Wu, 2017; Ronen and Valette, 2015; Palombo et al., 2018). Furthermore, a few studies have investigated the correlation between relaxation and diffusion of these metabolites, showing small or negligible effects (Ligneul et al., 2016), supporting the interpretation and modeling of metabolite diffusion primarily based on geometry, irrespective of relaxation properties. Studies of diffusion-weighted MR spectroscopy overall reported an intra-axonal diffusivity for NAA – which is overwhelmingly present in neurons – of 50–70% of aqueous NAA (Ronen et al., 2014; Ellegood et al., 2007; Kroenke et al., 2004; Palombo et al., 2017b). To measure metabolite intra-cellular diffusivity at very short time-scales and access information about cytoplasm viscosity (by also ruling out contribution from active transport) (Valette et al., 2018), experiments were performed in the rat (Marchadour et al., 2012) and mouse brain (Ligneul and Valette, 2017) using oscillating gradients with frequencies up to ~250 Hz, corresponding to diffusion times down to ~0.5–1 ms. They showed that metabolites apparent diffusivity increased by ~50% when the frequency increased from ~20 to 250 Hz for NAA, Choline, and Creatine (also for Myoinositol and Taurine in the mouse brain), approaching diffusivity values of ~0.2–0.30 μm²/ms (corresponding ~25–40% of the free NAA diffusion in aqueous solution at body temperature (Kan et al., 2012)) at the highest frequency. More quantitatively, modeling metabolites diffusivities acquired in the rodent brain with oscillating gradients (Marchadour et al., 2012; Ligneul and Valette, 2017) using frequencydomain formalism for diffusion in cylinders or spherical pores (Stepisnik, 1981; Callaghan and Stepisnik, 1995) yielded typical asymptotic intracellular diffusivities to be ~0.5–0.6 μm²/ms, i.e., corresponding to a low-viscosity cytosol, less than twice the viscosity of pure water. This is in good agreement with fluorescence-based estimates of fluid-phase cytoplasm viscosity being quite similar to bulk water (Fushimi and Verkman, 1991; Luby-Phelps et al., 1993). These results were also recently confirmed by studies in human brain (even though at lower frequencies) (Doring and Kreis, 2019) and using very high b values (Lundell et al., 2020). Finally, studies of acetate diffusion suggested extra-cellular diffusivity of this metabolite to be faster than the intra-cellular one (Dehghani et al., 2017; Palombo et al., 2017c). In contrast to NAA, Acetate is present in both intra- and extra-cellular compartments. Bi-exponential analysis of the Acetate diffusion signal suggested that ~45% of Acetate diffuses in the extra-cellular space (Dehghani et al., 2017; Palombo et al., 2017c). Using biophysical modeling of Acetate diffusion, Palombo et al. (2017c) reported preliminary results of Acetate diffusivity being ~20–35% faster in the extra- than the intra-cellular space, suggesting that the viscosity/tortuosity may be lower in the extra-cellular space. These results are again consistent with viscosity estimations based on the diffusivity of fluorescent particles captured with two-photon microscopy techniques, which suggest that the extra-cellular viscosity is lower than the intracellular, but also point to variable viscosity in soma cytosol, nucleus, dendritic branches, actin cytoskeleton, etc. (Xiang et al., 2020; Zheng et al., 2017) (Fig. 9). We stress however that fluorescence measurements typically yield diffusivity averaged over all directions and probe short diffusion distances – yielding actual viscosity – compared to clinical dMRI – where the apparent diffusivity is a combination of viscosity and μm-scale restrictions.

Fig. 9.

Approaches for estimating compartment-specific diffusivities in neurons. A: Using a planar filter of increasing strength to suppress extra-cellular water contribution in highly aligned white matter bundles exhibits an asymptotic behavior of axial diffusivity which towards intra-axonal diffusivity $D_a\approx 2.4\mu m^2/ms$. B: Measurement of diffusion coefficient of fluorescent particles using two-photon microscopy techniques (here: TR-FAIM: Time-Resolved Fluorescence Anisotropy Imaging) shows however that on ex vivo brain slices the viscosity of the intra-cellular space is higher than that of the extra-cellular space, and that there is substantial heterogeneity in diffusion in the intra-cellular space between soma, dendritic branches and thorny excrescences (TE). Remarkably, mean diffusivity in dendritic branches estimated to be 30% of free tracer diffusivity is compatible with axial diffusivity inside axons at 80% of free water diffusivity (i.e. $D_a\approx 2.4\mu m^2/ms$, assuming $D_{a,\perp }\approx 0$). Illustrations adapted from (Dhital et al., 2019) (A) and (Zheng et al., 2017) (B), with permission.

The renewed drive across the community to characterize compartment-specific diffusivities was recently fueled by the finding that the simple two-compartment model of diffusion in WM (intra- and extra-axonal water) had two mathematical solutions, neither of which could be easily discarded based on goodness-of-fit criteria or biological plausibility (Novikov et al., 2018b; Jelescu et al., 2016b). These works further showed that the two solutions consisted in opposing inequalities between the intra- and extra-axonal parallel diffusivities $D_{a,\parallel }$ and $D_{e,\parallel }$: either $D_{a,\parallel }<D_{e,\parallel }$ or the other way around. As a by-product, this result questioned the WM models published thus far – including the very popular NODDI – that set intra- and extra-axonal diffusivities equal to each other, and even fixed to a given value (Zhang et al., 2012; Alexander et al., 2010; Kaden et al., 2016).

Pointing to serious issues of models is valuable, but proposing solutions to address the issues is better. The puzzle of which parallel diffusivity was faster, the intra- or the extra-axonal, triggered a wave of research efforts across the community and fostered great creativity in solving the problem. Remarkably, nearly all approaches came to the same conclusion: that $D_{a,\parallel }>D_{e,\parallel }$ was the biologically-valid solution. These approaches included: comparing compartment tensor traces using isotropic diffusion weighting (Szczepankiewicz et al., 2015; Dhital et al., 2018), performing selective suppression of the extra-axonal signal using either gadolinium (Kunz et al., 2018) or double-diffusion encoding planar filter (Dhital et al., 2019; Skinner et al., 2017), assessing functional forms of compartment time-dependent diffusivities (Jespersen et al., 2018) and fitting diffusivities jointly with $T_2$ (Veraart et al., 2018b) (Fig. 9). Additional works have also shown that the degeneracy of solutions can be lifted by considering the 6th order moments of the signal (Novikov et al., 2018b), or combining linear and planar diffusion encodings (Reisert et al., 2019). It is noteworthy that the $D_{a,\parallel }>D_{e,\parallel }$ solution in WM also yields similar tensor traces for both compartments: $\mathrm{T}\mathrm{r}({\widehat{D}}_a)\approx \mathrm{T}\mathrm{r}(\widehat{D_e})$ (since $D_{a,\perp }=0$ and $D_{e,\perp }>0$ in the long-time limit), which is consistent with reports of negligible isotropic kurtosis in WM (Szczepankiewicz et al., 2015). Very recently however, a study that combined linear and spherical tensor encoding schemes showed that the degeneracy could also be lifted by such an acquisition protocol with a very well-defined minimum across the fitting landscape, and that the retained “solution” verified the $D_{a,\parallel }<D_{e,\parallel }$ inequality rather than the other way around, though the mean squared residuals for that fit were highest in WM (Lampinen et al., 2020). These regular twists in findings show that biophysical modeling of diffusion in tissue is an active “re-search” field, constantly questioning itself.

Another conflict between geometry and diffusivity was the widespread use of the “tortuosity model” as a simplifying assumption (Zhang et al., 2012; Alexander et al., 2010; Kaden et al., 2016). In WM, the latter links the extra-cellular perpendicular diffusivity $D_{e,\perp }$ to the neurite water fraction $f$ completely: $D_{e,\perp }=(1-f)D_{e,\parallel }$. However, this relationship has been shown to break for tight packings – which is the regime of WM bundles (Novikov and Fieremans, 2012). Its enforcement has been shown to produce significant discrepancies between estimate neurite water fraction and measurements of microscopic anisotropy using diffusion tensor encoding (Lampinen et al., 2017) and to simply not be verified when the assumption is released (Lampinen et al., 2020). Furthermore, it has been shown on the contrary that $f$ and $D_{e,\perp }$ can bring genuinely complementary information about the microstructure, with $f$ being most sensitive to patchy demyelination or myelinated axon loss and correlate best with axonal water fraction derived from EM, while $D_{e,\perp }$ was most sensitive to widespread demyelination and correlate best with the g-ratio derived from EM (Jelescu et al., 2016a).

Validating these various aspects of the biophysical model of diffusion in WM has required widespread efforts across the community but we have certainly gained confidence in its value and in the specificity of microstructure estimates during this process. Hopefully, this knowledge can now be transferred to the benefit of GM models – e.g. expected fast diffusivity along neurites – such that we can focus on validating aspects specific to GM, such as compartment exchange or the presence of a soma compartment.

2.4.5. Compartment exchange

As mentioned, water transport across the cell membrane is potentially an important feature for GM models. Water molecules can travel from one compartment to another across the cell membrane as a result of diffusion, permeation through aquaporins and transport via ion channels and active carriers. Permeation through the lipid bilayer and aquaporins are thought to dominate this process (Reuss, 2012). Here, we refer to the combined contribution of all four mechanisms indistinctively as “membrane permeability”. The exchange time is then the characteristic time of water exchange between two different compartments and the residence time is the characteristic time a water molecule spends in a given compartment before moving into a different compartment.

Most neurites are unmyelinated and, it is often speculated that in the absence of a myelin sheath, water inter-compartment exchange is non-negligible over typical diffusion times of MRI experiments (20–100 ms). Neurites refer to either axons or dendrites, thin cylindrical extensions of the cell that form numerous connections to other neurons, but glial cell processes that have a similar thin cylindrical geometry likely also contribute to the same “compartment” in diffusion MRI models. A “simple” illustration of the relevance of exchange in GM is that non-exchanging compartment models applied to the whole brain typically yield much higher neurite compartment fractions in WM than in GM (Zhang et al., 2012; Jespersen et al., 2010; Lampinen et al., 2020, 2017) while histology analyses point to a large 40–75% neurite fraction in cortical GM (Bondareff and Pysh, 1968; Spocter et al., 2012; Motta et al., 2019). When exchange is not accounted for, part of the “neurite water” is assimilated to extracellular space – or large soma – because its diffusion behavior is indeed no longer restricted to a closed cylinder.

Dedicated sequence designs such as FEXI (Filter-Exchange Imaging) have however estimated exchange times ranging 0.63–1.25 s in human WM, where the longer times were associated with higher myelination (Nilsson et al., 2013), as also hypothesized in WM modeling. The same study reported shorter exchange times of 350 ms in meningiomas, also showing that pathology can significantly affect microstructure parameters.

For GM, several methods have also been devised to estimate water exchange time across the cell membrane, which have so far yielded diverse results. In vivo studies of human and rat GM (Jelescu and Novikov, 2020; Veraart et al., 2018a) using the Kärger model of two exchanging compartments (Kärger, 1985) yielded consistent estimates of 10–30 ms. Using the DEXSY (Diffusion Exchange Spectroscopy) method (Benjamini and Basser, 2017), exchange time in perfused mouse spinal cords was also estimated at 10–30 ms between water pools “far from and close to membranes”, without a specific compartment attribution (Williamson et al., 2019). It is noteworthy that the neonatal mouse spinal cord is far from fully myelinated, whereby these estimates are much shorter than estimates for exchange time in human WM. Experiments exploiting compartment-specific ${\mathrm{R}}_1$ relaxation rates and extracellular signal suppression using contrast agents in living rat brain (Quirk et al., 2003) and rat cortical cultures (Bai et al., 2018) or using rapid flow in astrocyte and neuron cultures (Yang et al., 2018b) yielded longer estimates spanning 100–150 ms. The common ground between all these studies however is that exchange time in GM, though it broadly spans 10–150 ms with considerably uncertainty, is much shorter than in WM and the non-exchanging compartment hypothesis would hold only for very short diffusion times $\left(t_{\mathrm{d}}<20\mathrm{m}\mathrm{s}\right)$. In case of longer diffusion times, exchange should be explicitly accounted for.

3. Pathology: how do models hold in disease?

Multi-compartment diffusion modeling in the diseased central nervous system shows potential as a key biomedical tool in both research and clinical domains, unlocking insight into the biological basis of a disease, or facilitating and increasing specificity of diagnosis or treatment monitoring. However, the key hurdle in this domain is variability. This includes biological variability introduced by the disease, variability across differing anatomies and pathologies, and variability introduced in modeling.

As described above (Section 2.3.1), the degeneracy in parameter estimation is observed when measured data is equally well fit by multiple combinations of model parameters (Jelescu et al., 2016b), and is typically tackled by constraining or fixing parameters or introducing functional dependencies between them. An obvious risk with this approach is that bias in parameters estimates will results whenever these constraints are invalid. While we are beginning to understand the subtle effects of these choices in healthy tissue (Jelescu et al., 2016b; Lampinen et al., 2017; Novikov and Fieremans, 2012; Jelescu et al., 2015; Hutchinson et al., 2017) (in particular, WM), the consequences in pathological tissue are still poorly understood. A given disease or injury is expected to greatly increase the biological variability within tissue, potentially altering the number and diffusivities of modeled compartments, violating the modeling assumptions and consequently introducing bias.

This becomes an even greater obstacle due to the second source of variability – the differences in pathologies across different diseases or across time. While one disease may be expected to alter compartment fractions and/or numbers, another may affect shape, size, and scale (or compartment exchange, diffusivities, heterogeneity, etc.). Even the same disease may produce different alterations at different stages. The range of possible pathologies is possibly too large to be adequately described by a single model, and any constraints imposed are almost certainly violated in different disease mechanisms.

Finally, it is critical to not only disentangle, but to understand, the relative variability in the underlying biology versus the inherent variability of the model (Novikov et al., 2018a). The biological variability, in both health and disease, is the quantity that we ultimately want to quantify and understand, but it can be confounded and obscured by variability in the acquisition (scanner, protocol, and artifact effects) (Tax et al., 2019), in the reconstruction (fitting effects) (Harms et al., 2017), and in the model itself (range of validity, SNR, and constraints effects) (Hutchinson et al., 2017). To fully understand these effects, and ideally to minimize modeling effects, validating the behavior of the model in a number of settings becomes critical, particularly in disease. This is particularly true for multi-center studies or comparisons between studies/sites (Cetin Karayumak et al., 2019; Mirzaalian et al., 2016, 2018).

When it comes to model validation applied to pathology, one of the main concerns with biophysical models is their claim of greater sensitivity when comparing their metrics to DTI. However, the main promise of biophysical models is specificity and not sensitivity. Greater sensitivity than DTI likely comes from going beyond the Gaussian approximation, as most of these models rely on multi-shell data. A fairer comparison would be to DKI, which relies on two shells and is expected to be sensitive but not specific.

To date, application of biophysical diffusion models to disease has been predominantly in tumors, in demyelinating diseases, and cerebral ischemia. In all cases, DTI and DKI form the majority of studies applied to disease, but below we focus only on the applications of biophysical models in each, and their successes and limitations.

3.1. Tumors

The characterization of tumors definitely needs to rely on dedicated models (Fig. 10), as the tissue becomes extremely different from healthy brain (Jiang et al., 2017; Reynaud et al., 2016; Panagiotaki et al., 2014). The tumor microenvironment might consist of a heterogeneous population of cancer cells, host cells, secreted factors and extracellular matrix proteins. The main features of most tumor models are impermeable spheres with a given radius, or radius distribution, surrounded by an extracellular space, although standard multi-compartment models of healthy WM have also been applied in these regions. The assumptions and validity of these models are reviewed in detail in (Reynaud, 2017). Using combined linear and spherical tensor encoding has also demonstrated great potential for characterizing tumor microstructure based on cell shape (Nilsson et al., 2018) and for example discriminating between glioma and meningioma (Szczepankiewicz et al., 2016). While realistic geometry is a first important modeling step, membrane permeability could also play an important role in tumors. The FEXI method showed for instance that it was possible to differentiate between viable and necrotic parts (Nilsson et al., 2013), and between astrocytoma and meningioma (Lampinen et al., 2017) based on permeability. Time-dependent diffusion in the extracellular space should also be carefully considered and not neglected a priori. In addition to the models estimating cell size and shape (Section 2.4.3), other multi-compartment models have been applied in tumor models, for example NODDI provided unique contrast not seen in FA/ADC maps (or anatomical images) within human glioma lesions (Wen et al., 2015). However, contrast should not be interpreted as reflecting biological reality, for example neurite density has been shown to be artificially high even in the known absence of neurites (Lampinen et al., 2017), another example of the challenge of achieving high specificity. In this case, there are limitations of separating anisotropy from cell density variations using standard diffusion encoding sequences alone, with potential solutions including alternative encodings or diffusion times.

Fig. 10.

Dedicated modeling for tumor microstructure. A: Electron microscopy (EM) images of glioma guide the modeling as uncrowded spheres and the derivation of time-dependent diffusivity in this geometry. B: Estimates of extra-cellular space (ECS) in glioma using the POMACE model and correspondence to light microscopy slides. C: Discriminating between meningioma and glioma based on tumor cell shape (sticks for the former, spheres for the latter) using combined linear and spherical tensor encoding. Illustrations adapted from Reynaud, Front. Physics (A) (Reynaud, 2017), Reynaud et al., NMR in Biomed 2016 (Reynaud et al., 2016) (B) and Szczepankiewicz et al., NeuroImage 2016 (Szczepankiewicz et al., 2016) (C), with permission.

3.2. Ischemia

The most common clinical application of dMRI to date is in the detection of acute cerebral ischemia (Moseley et al., 1990a). Within minutes of symptom onset, diffusion within the extent of the stroke is reduced by nearly one half – due to mechanisms hypothesized to be related to ionic imbalance and consequent cell swelling and cytotoxic edema. Subsequently, inflammatory factors are released, affecting the integrity of the blood-brain barrier and consequent vasogenic edema and extracellular fluid accumulation. Clearly, multiple overlapping pathological changes to compartments fractions, sizes, permeability, and diffusivities are occurring, and biophysical modeling may shed light on these processes. In fact, as a biomarker, dMRI (in combination with a T₂-weighted or FLAIR sequence) has become the standard of care in stroke imaging as it is the most sensitive sequence for diagnosis to detect abnormality, and in dating the stroke for prognosis and treatment planning. However, these clinical applications have not been in the form of biophysical models, and involve only a single (or sometimes three) DWI with a computed trace map.

Despite this, biophysical modeling may represent a critical tool to probe the mechanisms of decreased diffusivity (Fig. 11). Decreases in intracellular diffusivity are consistent with hypotheses related to neuronal beading (Budde and Frank, 2010; Baron et al., 2015), while decreases in extracellular diffusivity would be consistent with a reduction in extracellular space due to axonal swelling (Hall and Alexander, 2009; Latour et al., 1994). Validation with compartment specific tracers indicate that both mechanisms contribute to the decreased diffusivity (Duong et al., 2001, 1998; Goodman et al., 2008, 2005; Silva et al., 2002; Le Bihan et al., 2012; Moseley et al., 1990b), with some studies suggesting a much greater intracellular diffusivity decrease with a somewhat lesser extracellular decrease (Benveniste et al., 1992). Probing multiple time scales with combinations of OGSE and PGSE in animal models has shown a smaller reduction of diffusivity as shorter time scales (Schachter et al., 2000; Does et al., 2003; Wu et al., 2014), providing evidence that diffusivity decreases during ischemia are due to structural rather than permeability or viscosity changes (Does et al., 2003; Novikov et al., 2014), specifically, structural changes on the length scales typical of cell sizes (~2–4 μm) (Does et al., 2003). OGSE has also been applied to human stroke patients (Baron et al., 2015), with a shorter diffusion time resulting in dramatically reduced diffusion contrast between normal and ischemic tissue (Baron et al., 2015), again implicating structural changes of beading and/or swelling in ischemic tissue. Multi-compartment models have also been applied to acute human stroke, with quite distinct results. WMTI demonstrates a large reduction in intracellular (axonal) parallel diffusivity, and smaller reduction in extracellular parallel diffusivity (Hui et al., 2012) (although assuming $D_{a,\parallel }<D_{e,\parallel }$, which may lead to mis-interpretation of compartments, see Section 2.4.4) consistent with tracer studies. Alternatively, NODDI demonstrates significant increases in orientation dispersion and increase in neurite density (Adluru et al., 2014). Multiphoton imaging of animal models of ischemia may be consistent with the loss of structural organization, depending on time after onset and location of damage (Murphy et al., 2008), although not consistent with the increase in neurite/dendritic density. These are likely caused by models fixed diffusivities leading to misleading interpretations when these assumptions are violated.

Fig. 11.

Modeling microstructure changes in ischemia. A: Beading of axons/neurites is sufficient to cause a dramatic drop in ADC. B: Going beyond the Gaussian approximation with DKI provides even more sensitive markers of tissue change than ADC and using a white matter biophysical model helps untangle the contribution from each compartment. C: Time-dependent diffusion in the cortex is dominated by one-dimensional structural disorder (along neurites), which increases with global ischemia. Illustrations adapted from (Budde and Frank, 2010) (A), (Hui et al., 2012) (B) and (Novikov et al., 2014) (C), with permission.

3.3. Demyelination

At this point, the challenges of modeling in disease are clear: multiple concurrent pathologies that may affect the environment (and diffusion properties of the environment) in diverse ways. Demyelinating diseases represent perhaps the most complex of the models. These disorders are often associated with inflammation, gliosis, and axonal loss/injury, in addition to being inherently defined by demyelination – thus exhibiting multiple confounding factors that present challenges to biophysical models that aim to achieve high specificity.

To date, a mouse model of demyelination induced through cuprizone toxicity has been the model of choice to validate diffusion-based measures against histological variables. In a study of the temporal evolution of diffusion metrics, Guglielmetti et al. (2016), show that while DTI and DKI metrics are able to differentiate between control and cuprizone-treated groups, the biophysical WMTI model was best able to distinguish the different stages of the disease (Fig. 12A). Specifically, intra-axonal diffusivity decreased during the acute inflammatory demyelinating phase (again hypothesized to be related to both axon swelling and/or beading) whereas the axonal water fraction was decreased and able to discern long-lasting changes associated with the remyelination period. Further, two independent histological validation studies showed strong correlations between WMTI axonal water fraction and the EM-derived axonal fraction, with no significant correlation to other histology measures (Jelescu et al., 2016a; Kelm et al., 2016) – indicating both high sensitivity and specificity (Fig. 12B). Additionally, a measure of extracellular perpendicular diffusivity strongly correlated to the g-ratio (Jelescu et al., 2016a), a measure of myelination, and no correlation with other histology measure, together suggesting these as promising candidates to distinguish myelin changes from axonal loss. Another series of histological validation studies used DBSI modeling and demonstrated strong correlations between radial diffusivity and number of myelinated axons, and between a cellularity ratio measure and histological cell counts in cuprizone treated mice (Wang et al., 2011), in experimental autoimmune encephalomyelitis (Wang et al., 2014b), and optic neuritis (Chiang et al., 2014) mice models.

Fig. 12.

Biophysical models in demyelination. (A) In a study of cuprizone induced demyelination, Guglielmetti et al. (2016) show that while both DTI measures (MD) and DKI measures (MK) are sensitive and able to detect white matter alterations, they are confounded by multiple co-occurring processes. Measures from the WMTI model provide increase specificity – with intrinsic diffusivity decreased during acute inflammatory demyelination and AWF indicating a long-lasting decrease even after recovery. (B) (Jelescu et al. (2016a)) further emphasize the improved specificity of biophysical modeling over signal representations (DTI RD), with AWF and extra-axonal diffusivity parameters indicating different degrees and patterns of demyelination, with further validation against electron microscopy. (C) In human multiple sclerosis, T2 lesions and chronic black holes are modeled using SMT and show significant differences in axonal volume fractions and axial diffusivities (Bagnato et al., 2019), suggesting sensitivity to pathological changes in in vivo tissue. Figures adapted from Jelescu et al. (2016a); Guglielmetti et al. (2016); Bagnato et al. (2019) with permission.

In the human, multiple sclerosis (MS) has received the most attention to date, with biophysical modeling in both the brain and spinal cord. Grussu et al. (2015), showed the feasibility of multi-compartment modeling in the healthy spinal cord, showing that quality of fit is increased in the NODDI model over DTI (as assessed by Bayesian information criteria which maximizes likelihood and penalizes free parameters) Grussu et al. (2015). Again, while quality of fit is an indicator that a model is capturing expected trends in the signal, sensitivity and specificity remain critical. In light of this, subsequent studies of both NODDI (Schneider et al., 2017) and Spherical Mean Technique (SMT) (By et al., 2018) in the MS cord showed the high sensitivity of these models to provide both lesion contrast (as and decreased neurite density/volume fraction, decreased dispersion, increased isotropic volume fraction) in normal appearing WM in the MS cord. Of particular importance, the neurite dispersion parameter has been shown to be particularly sensitive to histological measures of neurofilament, astrocytic, myelin, and microglia dispersion as measured in the ex vivo spinal cord, at the same time providing the greatest contrast between lesion and non-lesioned WM (Grussu et al., 2017). Despite tremendous sensitivity, specificity is still not assured, even in the healthy spinal cord. In a comparison of multi-compartment models to a histological spinal cord atlas, a number of parameters were revealed to be sensitive to measures of axon diameter, density, and volume fraction, myelination, and number of axons, however very few parameters are highly specific to the one metric they intend to uncover – for example dispersion indices are sensitive to a number of histology measures (Schilling et al., 2019), however it should be pointed out that due to its location, size, and movement, the in vivo cord may represent a worse-case scenario of partial volume effects, motion, susceptibility distortions, and signal-to-noise and acquisition limitations. In the brain, biophysical models (SMT) have again shown great ability to distinguish not only tissue from lesion, but also types of lesions (Bagnato et al., 2019). MS lesions typically show as hyper-intense signal in T₂w images, however those that also present as hypo-intense on T₁w sequences have been termed chronic black holes, and are known through histopathologic studies to represent advanced disease pathology and significant axonal loss, and are semi-quantitative biomarkers of axonal integrity. Despite this, relaxometry remains poorly specific to pathology. SMT showed the ability to distinguish T₂-lesions from normal appearing WM (lower axonal volume fraction) and more importantly the ability to identify chronic black holes from T₂ lesions (significantly lower axonal volume fraction and higher axonal diffusivity) (Bagnato et al., 2019) (Fig. 12C). These results were optimistically interpreted as a first step towards specific characterization of in vivo pathology.

4. Clinical translation and added value

The final major challenge of a biophysical model of diffusion is certainly its successful translation to clinical studies and its added value in terms of characterizing physiological and pathological processes in the human brain on a routine basis, informing on progression and response to treatment, and perhaps even inspiring new therapeutic strategies. While the measurement of the ADC has revolutionized the fast diagnosis of stroke (Moseley et al., 1990a, b), microstructure models proposed since 1997 (Stanisz et al., 1997) have so far failed to reach that “game-changer” level, with DTI still being the default protocol and analysis in most studies, and neuroradiologists still mainly looking at the “trace” image, i.e. the mean diffusivity calculated from DTI.

4.1. Clinically-acceptable scan time & acquisition protocol

The first hurdle to clinical translation is the advanced acquisition protocol typically required for biophysical model fitting: multi-shell data, high b-values and large number of directions sampled. First, these protocols are synonymous with long acquisition times, which can be incompatible with clinical studies. Clinicians can afford to add at most a 10-minute scan, with 20 minutes already being the exception and only suitable for very dedicated studies. Second, implementing these protocols on clinical scanners can result in poor data quality, given the more limited hardware performance compared to animal scanners or human research scanners such as Connectom. Indeed, with limited gradient performance, high b-values can only be achieved by increasing the diffusion time significantly and thereby also the echo time, which results in a $e^{-\mathrm{T}\mathrm{E}/{\mathrm{T}}_2}$ attenuation from the start, on top of which substantial diffusion attenuation is added (high b-values). These two mechanisms combined will lead to low SNR in the images. Moreover, clinical dMRI data is almost exclusively acquired using an echo-planar imaging read-out, for which long echo times introduce significant geometric distortions in regions of strong field inhomogeneity (such as orbitofrontal lobe, ear and eye cavities etc.) and further degrade image quality. Long scan times also increase the chances of subject motion. Finally, protocol requirements for some models (e.g. short diffusion time and ultra-high b-values) are simply not feasible on clinical systems yet.

However, there has been tremendous progress made on all these fronts in recent years, which are slowly but surely bridging the gap between research and clinical settings. Acquisition acceleration techniques such as GRAPPA (Bhagat et al., 2007; Griswold et al., 2002) can help reduce the echo time and thereby improve image quality, while the simultaneous multi-slice (Setsompop et al., 2012) and 3D multislab (Chang et al., 2015a) techniques reduce the scan time without compromising on brain coverage. Compressed sensing can be used to undersample both k-space and q-space (Lustig et al., 2007; Mani et al., 2015; Paquette et al., 2015; Welsh et al., 2013; Menzel et al., 2011; Michailovich and Rathi, 2010), also resulting in a dramatic gain in scan time.

So far, dMRI acquisitions had compromised on spatial resolution to mitigate long scan time and low SNR issues. The clinical standard is 2 mm isotropic or above. However, coarse spatial resolution has an important impact on microstructure mapping by introducing unwanted mixture of tissues in a voxel, which over-complicates or confounds the modeling problem. In particular, brain structures that are thin and with an intricate geometry, such as the cortex, typically suffer from partial volume effects with neighboring CSF and WM. Here also, super-resolution techniques have been proposed to boost the spatial resolution (Ning et al., 2016; Poot et al., 2013; Scherrer et al., 2012; Setsompop et al., 2018; Van Steenkiste et al., 2016). Most recently, an extension of the generalized slice-dithered enhanced resolution (gSlider) (Setsompop et al., 2018) to undersample in both radiofrequency encoding space and q-space (gSlider-SR) has demonstrated feasibility of a HARDI-like acquisition (64 directions at $\mathrm{b}=2\mathrm{m}\mathrm{s}/\mathrm{\mu }{\mathrm{m}}^2$) at 860 μm isotropic resolution in ten minutes on a clinical scanner equipped with 80 mT/m gradients (Ramos-Llordén et al., 2020).

On the topic of field gradient capabilities, several vendors now offer systems with 80 mT/m gradients, which is double the clinical standards of a few years ago and contribute to increasing the achievable diffusion weighting (b-value) as well as shortening the echo time. Although human Connectom scanners with 300 mT/m gradient capabilities are only a handful across the world, it is probably only a matter of time until this technology becomes more widespread.

Finally, valuable pre-processing tools have been developed to improve data quality, ranging from thermal noise reduction based on Marchenko-Pastur random matrix theory (Veraart et al., 2016), Gibbs ringing correction to avoid mixture of WM and CSF signals in particular (Kellner et al., 2016), and eddy current, motion and distortion corrections (Andersson et al., 2003). The high performance of this processing pipeline has been recently demonstrated and is freely available online (Ades-Aron et al., 2018).

4.2. Added clinical value

The potential for added clinical value of biophysical models of diffusion over typical analyses such as DTI is enormous, although in practice the clinical translation has so far not been very successful in most cases. There are several reasons for this overall unpopularity.

One of the main reasons could be the perpetual questioning and reconsideration of biophysical models for a given tissue, which is a natural process for research, but understandably not very reassuring for clinicians. For example, there is recent overwhelming evidence that in WM intra-axonal diffusivity is faster than extra-axonal diffusivity (Jespersen et al., 2018; McKinnon et al., 2018; Kunz et al., 2018; Dhital et al., 2019), which invalidates the assumptions of models such as NODDI (which assumes $D_a=D_{e,\parallel }=1.7\mathrm{m}\mathrm{s}/\mathrm{\mu }{\mathrm{m}}^2$) (Zhang et al., 2012) and WMTI (which assumes $D_a\le D_{e,\parallel }$) (Fieremans et al., 2011). Unfortunately, NODDI is probably the model that has so far been the most successful in drawing the interest of clinicians, while the specificity and reliability of its estimates has been questioned on multiple levels (Jelescu et al., 2016a, b; Lampinen et al., 2020, 2017).

Encouragingly, numerous reports nevertheless highlighted the added value of biophysical models over DTI, both in terms of sensitivity and specificity, in a variety of applications including human brain development (Jelescu et al., 2015; Huber et al., 2019; Nemanich et al., 2019), aging (Benitez et al., 2018; Chang et al., 2015b; Toschi et al., 2020; Fan et al., 2019), dementia (Dong et al., 2020; Fieremans et al., 2013; Vogt et al., 2019), multiple sclerosis (Bagnato et al., 2019; Cercignani and Gandini Wheeler-Kingshott, 2019; de Kouchkovsky et al., 2016), concussion (Churchill et al., 2017), inflammation (Chiang et al., 2014) and spinal cord characterization (Grussu et al., 2015). The key advantage of biophysical models is going beyond the Gaussian approximation regime, where really interesting and subtle features of microstructure become manifest. The devil’s advocate would argue that DKI is also going beyond the Gaussian approximation and is applicable to any tissue type (signal representation). For the future, we recommend the performance of biophysical models be compared to that of DKI rather than DTI – the added value of modeling vs model-free approaches such as DKI should lie in the specificity of the microstructure characterization – which remains to be demonstrated for most models.

With the proven sensitivity to a range of cellular level biophysical parameters, and the promise of increased specificity through biophysical modelling, dMRI at first seems capable of providing a great number of imaging biomarkers – defined as a quantifiable characteristic of a biological process that can be used to distinguish normal or abnormal processes, of conditions or diseases, or to measure response to treatment for a disease or condition (Kessler et al., 2015). In addition to the continual fluctuation (and hopefully, improvement) in modeling, and improper and invalid assumptions mentioned above, the process from biomarker invention to its use as a reliable tool for medical science requires a number of translational gaps (Nilsson et al., 2018) including [1] technical validation, [2] biological validation, [3] and clinical validation – in effect, critically evaluating whether the biomarker has both validity and relevance.

Technical and biological validation assess several levels of biomarker validity. Technical validation asks whether the proposed biomarker is capable of being measured objectively, and with high repeatability, reproducibility, and reliability. The aim is to identify the variability that exists under identical imaging conditions (repeatability), the variability that exists under different imaging conditions (reproducibility), and that across a population (reliability) – Importantly, understanding this will help to disentangle the variability across tissues and pathologies. These validations are commonly seen in biophysical models, and we would argue are a bare minimum requirement for introduction of a possible model to the community. Repeatability can be done with test-retest scans of the same subject and same scanner, assessing effects of noise, while reproducibility is most often accomplished with traveling subjects on different scanners (Bagnato et al., 2019; Szczepankiewicz et al., 2019), with many datasets acquired and tailored specifically for these studies (Tax et al., 2019; Froeling et al., 2017; Nath et al., 2020). These validation steps can additionally be done on simulated data or physical phantoms to investigate effects of noise, artifacts, or fitting procedures.

Second, biological validation takes the process a step past precision and reproducibility and assesses accuracy, typically ensuring that an imaging biomarker correlates strongly with a property of interest. This has been performed with a number of estimated features as described throughout this manuscript – the property of interest can for example be fiber orientations or volume fractions, relevant pathological features of cellularity or tissue heterogeneity, or dose-response relationships between treatment variables and biomarker changes.

This is what many would consider “validating” a biomarker, however a strong correlation is again not enough; if a biomarker “passes” biological validation it does not necessarily mean the biophysical model is validated, per se (notwithstanding open-ended questions regarding how strong a correlation is required). Rather, the validation is limited to a specific conclusion under well-defined circumstances, and the model may not generalize across acquisitions populations or varying acquisition domains. For example, if a model (or component of a model) is proposed as correlative with axon diameter as a function of development in healthy aging, and independent evidence supports this proposal, then the biomarker is validated in this case; however, that does not mean that this index is validated as a biomarker in an aging population with Alzheimer’s disease, for example. It is clear that multiple, orthogonal biological validations are necessary, in addition to technical validation, to ensure model validity.

Finally, clinical validation requires relevance. The key here is asking whether the model or index can provide medically useful information for an intended purpose, be it diagnosis, prognosis, prediction, screening, monitoring, or disease confirmation. An index may be a perfect estimator (biologically unbiased and technically precise) of axonal volume fraction for example but may not be a clinically meaning endpoint or differentiator of health and disease. Thus, the final hurdle facing modeling is a quote often repeated both in the diffusion field as well as in multitude of self-help books: we have to make what’s important measurable, rather than make what’s measurable important. While diffusion-weighted images, or trace-images, in stroke are the prime example clinical relevance – both diagnosis and prognosis with high sensitivity, specificity, and tremendous effect size – other models are beginning to realize relevance in tumor grading and differentiation, infection and inflammatory conditions, and neurodegenerative disorders.

4.3. Keys to success for clinical translation

Clinicians recognize that conventional, non-quantitative MRI techniques are sensitive but not specific to pathology, a factor that often precludes a timely diagnosis and outcome prognostication (Bagnato et al., 2020). Over the last decades, a number of quantitative MRI methods have been developed; however, with the exception of DWI for acute ischemic stroke, Creutzfeldt-Jakob disease and prolonged seizure (Koksel et al., 2018) or MR spectroscopy for a limited number of brain tumors and metabolic disorders, none of them has witnessed a successful clinical translation (Sitter et al., 2019).

To be considered viable biomarkers and make it to clinical translation, imaging metrics must be validated against histopathology, correlate with clinical status and be predictive of outcome. There are at least four different stages any given promising imaging tool must pass to become a biometric of disease. One must differentiate among these four stages during which goals and challenges may differ.

A first important step is the histopathologic validation. Diffusion models are particularly difficult to be validated on human samples, postmortem, as most of the diffusivity properties are lost in a fixed tissue. Thus, effort must be devoted toward studies based on biopsy samples and animal models of diseases. Several methods fail clinical translation due to lack of histopathologic validations, which discourage pursing its use further.

The second stage is the immediate clinical-research application. Here a small number of patients may be studied to test specific biological hypothesis on disease mechanisms and disability accretion. At this stage, it is fundamental that images allow a clear demarcation of anatomical structures and an as accurate as possible characterization of pathology. Resolution and precision are more important than pragmatism. Different open source codes of easy and immediate access to the scientific community are also key. This phase of translation is fundamental as it allows performing small but numerous studies across different centers. Investigations of this nature prove consistency of the methods across scanners and different post-processing methods, across clinical conditions subtended by similar pathobiological processes. Ultimately, this phase of translation provides opportunities to the inventors and to developers to refine and advance the model.

Consistency across studies and ability to reflect clinical impairments in small but numerus studies, may encourage the application of advanced diffusion methods in the setting of phase II and phase III clinical trials. In this third stage, quantitative MRI techniques may inform on mechanisms of action of novel biological compounds, reveal novel treatment targets and deliver innovative biomarkers. For example, there is an urgent need to develop a biomarker of neurodegeneration and repair of the central nervous system, for proof-of-concept clinical trials testing molecules with neuroprotective effects (Bagnato et al., 2020).

In this clinical-research setting, one can still likely afford a relatively long scan time and a relatively elaborated post-processing algorithm. However, it is important to note that not all clinical centers may be equipped with state-of-the art scanners. Thus, for this translational stage it is essential that the newly proposed methodologies can be easily adapted to less advanced platforms. An analytical algorithm must also be of easy access and execution.

Once these technical barriers have been addressed, it will be important to consider that any given metric must be dynamic and sensitive to small changes occurring in a short time window. Indeed, to be proven effective, medications need to act upon a short time window and on visible and measurable biotargets.

The final stage is the day-to-day clinical routine. Here, MRI scans are performed for diagnostic and prognostic purposes, as well as to assess intervention outcome. In this setting, scans are acquired in hospitals or outpatient facilities for which short acquisition and evaluation times are imperative. One reason is that the facility needs to deliver the highest number of scans achievable in the shortest time possible. With longer acquisition times one must also expect a high degree of motion artifacts due to inability of patients to remain still inside a magnet. Thus, the incorporation of a post-processing tool that correct motion artefacts automatically is key for a successful translation.

At the evaluation site, qualitative rather than quantitative metrics are more likely to be adopted by clinical radiologists because they are deemed to be more practical and more reproducible across different readers.

All in all, clinical translation of newly developed imaging metrics spans across different stages characterized by different barriers. It is unfortunate that: 1) many promising and innovative methods do not pass the first stage due to insufficient efforts to transition from one stage to the other, 2) the significance of several imaging biometrics is often in time overestimated by clinicians who may not be trained to appreciate the technical limitations of the method. Strengthening collaborations between inventors and clinicians is certainly a key factor. It is likely that once developed, advanced diffusion methods need to undergo several refinements to make it to the final stage.

Ultimately, advancing imaging metrics from bench to bedside will require several years of dedicated collaborative effort between inventors and clinicians.

5. Conclusion

Biophysical modeling of diffusion in brain tissue is certainly a challenging field that has slowly come to maturity over the past 25 years by overcoming already a large number of hurdles at the levels of parameter estimation, validation and developing solutions for both healthy and diseased tissue. To conclude, we would like to emphasize what we consider to be the next roadblocks in the field, i.e. the remaining challenges that should give impetus to our future endeavors as a research community.

• In order to inform the simplified pictures of tissue, a better understanding of the microscopic organization of brain tissue is needed, ideally in all regions of the rodent and human brain. As an example, histological measurements of axon diameters are typically available in the corpus callosum only. More importantly, while individual building blocks of compartment models have been fairly well characterized using complementary microscopy techniques, how these elementary structures are de facto assembled in brain in vivo remains poorly understood. Therefore, different fields of microscopy could work conjunctly with the MRI field to bridge the gap between whole brain in vivo estimates of microstructure and electron microscopy images of ex vivo thin tissue slices. Differences between the two techniques lie in tissue condition (in vivo vs ex vivo, non-linearly shrunk and distorted), spatial coverage (whole brain vs stacked thin slices of a small volume) and temporal fluctuations (in vivo microstructure undergoes dynamic changes on the order of the second or even shorter).

• The past years have witnessed the development of a variety of models suited for specific types of tissue, e.g. single white matter bundle, cortex, glioblastoma, etc. There is great interest in developing a unified model of microstructure that could be expected to be applicable to any brain region, including complex mixtures of white and gray matter such as thalamus and striatum. The successful implementation of such a model can be expected to rely on very rich datasets, characterized by multiple shells up to high b-values, multiple diffusion times and combinations of different diffusion tensor encoding schemes. From the perspective of clinical translation and utility, such a generalized standard model could be narrowed back down to different minimal models focused on given pathologies or applications.

• Compartment diffusivities and inter-compartment exchange times remain the most challenging features to validate as they do not benefit from a microscopy counterpart and are only accessible via NMR methods. While compartment viscosity can perhaps be successfully inferred from the diffusion of fluorescent particles, the transport of molecules across the cell membrane is largely molecule-specific such that water exchange times can currently only be validated by targeting specific channels such as aquaporins.

• Finally, improving communication and transparency between the different parties involved in biophysical modeling and its applications is critical for exploiting the full potential of this field, which ultimately benefits patients. Two simple examples of messages which, in our opinion, have not come across sufficiently yet are the following:

  • Models should only be applied to the tissue, acquisition protocol, and diffusion regime, for which they were designed, even if they fit the data “perfectly” in other cases too. In other words, quality of fit is not a determining criterion for the performance of a model. If a model is used outside of its realm of applicability, the estimated parameters are no longer specific of any microstructural features and it is best to rely on signal representations in this case;
  • The main argument for using biophysical models is specificity and not sensitivity. Greater sensitivity than DTI likely comes from going beyond the Gaussian approximation, as most of these models rely on multi-shell data, but this can also be achieved with DKI or other higher-order signal representations. On the developers’ side, this implies that the performance of models should be tested against a fair signal-representation counterpart (e.g. higher-order cumulants, and not DTI). On the clinicians’ side, if they are in search of a binary or qualitative tissue assessment, then other diffusion metrics are likely better suited for this purpose than microstructure estimates from biophysical models.