Abstract
The manifold scattering transform is a deep feature extractor for data defined on a Riemannian manifold. It is one of the first examples of extending convolutional neural network-like operators to general manifolds. The initial work on this model focused primarily on its theoretical stability and invariance properties but did not provide methods for its numerical implementation except in the case of two-dimensional surfaces with predefined meshes. In this work, we present practical schemes, based on the theory of diffusion maps, for implementing the manifold scattering transform to datasets arising in naturalistic systems, such as single cell genetics, where the data is a high-dimensional point cloud modeled as lying on a low-dimensional manifold. We show that our methods are effective for signal classification and manifold classification tasks.
1. Introduction
The field of geometric deep learning, (Bronstein et al., 2017) aims to extend the success of neural networks and related architectures to data sets with non-Euclidean structure such as graphs and manifolds. On graphs, convolution can be defined either through localized spatial aggregations or through the spectral decomposition of the graph Laplacian. In recent years, researchers have used these notions of convolutions to introduce a plethora of neural networks for graph-structured data (Wu et al., 2020). Similarly, on manifolds, convolution can be defined via local patches (Masci et al., 2015), or via the spectral decomposition of the Laplace Beltrami operator (Boscaini et al., 2015). However, neural networks for high-dimensional manifold-structured data are much less explored, and the vast majority of the existing research on manifold neural networks focuses on two-dimensional surfaces.
In this paper, we are motivated by the increasing presence of high-dimensional data sets arising in biomedical applications such as single-cell transcriptomics, single-cell proteomics, patient data, or neuronal activation data (Tong et al., 2021b; Moon et al., 2018; Wang et al., 2020). Emergent high-throughput technologies are able to measure proteins at single-cell resolution and present novel opportunities to model and characterize cellular manifolds where combinatorial protein expression defines an individual cell’s unique identity and function. In such settings, the data is often naturally modelled as a point cloud lying on a d-dimensional Riemannian manifold some . The purpose of this paper is to present two effective numerical methods, based on the theory of diffusion maps (Coifman & Lafon, 2006), for implementing the manifold scattering transform, a model of spectral manifold neural networks, for data living on such a point cloud. This is the first work on the scattering transform to focus on such point clouds.
The original, Euclidean scattering transform was introduced in Mallat (2010; 2012) as a means of improving our mathematical understanding of deep convolutional networks and their learned features. Similar to a convolutional neural network (CNN), the scattering transform is based on a cascade of convolutional filters and simple pointwise nonlinearities. The principle difference between the scattering transform and other deep learning architectures is that it does not learn its filters from data. Instead, it uses predesigned wavelet filters. As shown in (Mallat, 2012), the resulting network is provably invariant to the actions of certain Lie groups, such as the translation group, and is Lipschitz stable to diffeomorphisms which are close to translations.
While the initial motivation of Mallat (2012) was to understand CNNs, the scattering transform can also be viewed as a multiscale, nonlinear feature extractor. In particular, for a given signal of interest, the scattering transform produces a sequence of features called scattering moments (or scattering coefficients). Therefore, the methods we will present here can be viewed as a method for extracting geometrically informative features from high-dimensional point cloud data. In addition, similar to the way GNNs can offer embeddings of nodes as well as the entire graphs, the manifold scattering transform can offer an embedding of points in the cloud as well as the entire point cloud.
Recently, several works have proposed versions of the scattering transform for graphs (Gama et al., 2019b; Zou & Lerman, 2019a; Gao et al., 2019) and manifolds (Perlmutter et al., 2020) using different wavelet constructions. Gao et al. (2019) uses wavelets constructed from the lazy random walk matrix , where W is the weighted adjacency matrix of the graph and D is the corresponding degree matrix, and Gama et al. (2019b) uses wavelets constructed from . (The wavelets used in Zou & Lerman (2019a) are based off of Hammond et al. (2011) and are substantially different than other wavelets discussed here which are based off of Coifman & Maggioni (2006).)
Here, we present a manifold scattering transform which uses wavelets based on the heat semigroup on . The semigroup describes the transition probabilities of a Brownian motion on . Therefore our wavelets have a similar probabilistic interpretation to those used in Gao et al. (2019).
In this work, we do not assume that we have global access to the manifold and our data does not come pre-equipped with a graph structure. Instead, we construct a weighted graph with weighting schemes based on Coifman & Lafon (2006) that aim to ensure that the spectral geometry of the graph mimics the spectral geometry of the underlying manifold. We then implement discrete approximations of the heat semigroup which are not, in general, equivalent to a lazy random walk on a graph.
Our construction improves upon the manifold scattering transform presented in Perlmutter et al. (2020) by using a more computationally efficient family of wavelets as well as formulating methods for embedding and classifying entire manifolds. The focus of Perlmutter et al. (2020) was primarily proposing a theoretical framework for learning on manifolds and showing that the manifold scattering transform had similar stability and invariance properties to its Euclidean counterpart. Thus, the numerical experiments in Perlmutter et al. (2020) were somewhat limited and only focused on two-dimensional manifolds with predefined triangular meshes.
The purpose of this paper is to overcome this limitation by presenting effective numerical schemes for implementing the manifold scattering transform on arbitrarily high-dimensional point clouds. It uses methods inspired by the theory of diffusion maps (Coifman & Lafon, 2006) to approximate the Laplace Beltrami operator.
To the best of our knowledge, this work is the first to propose deep feature learning schemes for any spectral manifold network outside of two-dimensional surfaces. Therefore, our work can also be interpreted as a blueprint for how to adapt spectral networks to higher-dimensional manifolds. For example, the theory presented in Boscaini et al. (2015) uses the Laplace Beltrami operator on two-dimensional surfaces and could in principle be extended to general manifolds, but the numerical methods are restricted to two-dimensional surfaces in that work. One could use the techniques presented here to extend such methods to higher-dimensional settings.
Organization.
The rest of this paper is organized as follows. In Section 2, we will present the definition of the manifold scattering transform, and in Section 3, we will present our methods for implementing it from point cloud data. In Section 4, we will further discuss related work concerning geometric scattering and manifold neural networks. In Section 5, we present numerical results on both synthetic and real-world datasets before concluding in Section 6.
Notation.
We let denote a smooth, compact, connected d-dimensional Riemannian manifold without boundary isometrically embedded in for some . We let denote the set of functions that are square integrable with respect to the Riemannian volume dx, and let −Δ denote the (negative) Laplace-Beltrami operator on . We let and , denote the eigenfunctions and eigenvalues of −Δ with . We will let , denote a collection of wavelets constructed from a semigroup of operators . For and , we will let , , and denote zeroth-, first-, and second-order scattering moments.
2. The Manifold Scattering Transform
In this section, we present the manifold scattering transform. Our construction is based upon the one presented in (Perlmutter et al., 2020) but with several modifications to increase computational efficiency and improve the expressive power of the network. Namely, i) we use different wavelets, which can be implemented without the need to diagonalize a matrix (as discussed in Section 3.2) and ii) we include q-th order scattering moments to increase the discriminative power of our representation.
Let denote a smooth, compact, connected d-dimensional Riemannian manifold without boundary isometrically embedded in . Since is compact and connected, the (negative) Laplace Beltrami operator −Δ has countably many eigenvalues, and there exists a sequence of eigenfunctions such that and forms an orthonormal basis for . Following the lead of works such as Shuman et al. (2013), we will interpret the eigenfunctions as generalized Fourier modes and define the Fourier coefficients of by
Since form an orthonormal basis, we have
In Euclidean space, the convolution of a function f against a filter h is defined by integrating f against translations of h. While translations are not well-defined on a general manifold, convolution can also be characterized as multiplication in the Fourier domain, i.e., . Therefore, for , we define the convolution of f and h as
| (1) |
In order to use this notion of spectral convolution to construct a semigroup , we let be a nonnegative, decreasing function with and for all t > 0, and let Ht be the operator corresponding to convolution against , i.e.,
| (2) |
By construction, forms a semigroup since and is the identity operator. We note that since the function g is defined independently of , we may reasonably use our network, which is constructed from , to compare different manifolds. Moreover, it has been observed in Levie et al. (2021) that if g is continuous, then Ht is stable to small perturbations of the spectrum of −Δ. We also note that one may imitate the proof of Theorem A.1 of (Perlmutter et al., 2020) to verify that the definiton of does not depend on the choice of eigenbasis .
As our primary example, we will take , in which case, one may verify that, for sufficiently regular functions, satisfies the heat equation
since we may compute
Thus, in this case is known as the heat-semigroup.
Given this semigroup, we define the wavelet transform
| (3) |
where , , and for
| (4) |
These wavelets aim to track changes in the geometry of across different diffusion time scales. Our construction uses a minimal time scale of 1. However, if one wishes to obtain wavelets which are sensitive to smaller time scales, they may simply change the spectral function g. For example, if we set and , then the associated operators satisfy .
We note that this wavelets differ slightly from those considered in Perlmutter et al. (2020). For , the wavelets constructed there are given by
| (5) |
By contrast, the wavelets given by (4) satisfy
(Similar relations hold for AJ and W0.) The removal of the square root is to allow for efficient numerical implementation. In particular, in Section 3.2, we will show that H1 can be approximated without computing any eigenvalues or eigenvectors. Therefore, the entire wavelet transform can be computed without the need to diagonalize a (possibly large) matrix. We note that our wavelets, unlike those presented in Perlmutter et al. (2020), are not an isometry. However, one may imitate the proof of Proposition 4.1 of Gama et al. (2019b) or Proposition 2.2 of Perlmutter et al. (2019) to verify that our wavelets are a nonexpansive frame.
The scattering transform consists of an alternating sequence of wavelet transforms and nonlinear activations. As in most papers concerning the scattering transform, we will take our nonlinearity to be the pointwise absolute value operator | · |. However, our method can easily be adapted to include other activation functions such as sigmoid, ReLU, or leaky ReLU.
For and , we define first-order q-th scattering moments by
and define second-order moments, for , by
Zeroth-order moments are defined simply by
We let Sf denote the union of all zeroth-, first-, and second-order moments. If one is interested in classifying many signals, , on a fixed manifold, one may compute for each signal and then feed these representations into a classifier such as a support vector machine. Alternatively, if one is interested in classifying different manifolds , one can pick a family of generic functions such as randomly chosen Dirac delta functions or SHOT descriptors (Tombari et al., 2010). Concatenating the scattering moments of each fi gives a representation of each , which can be input to a classifier.
3. Implementing the Manifold Scattering Transform from Pointclouds
In this section, we will present methods for implementing the manifold scattering transform on point cloud data. We will let and assume that the xi are sampled from a d-dimensional manifold for some . As alluded to in the introduction, in the case, where d = 2, it is common (see e.g. Boscaini et al. (2015)) to approximate with a triangular mesh. However, this method is not appropriate for larger values of d. Our methods, on the other hand, are valid for arbitrary values of d.
Our first method relies on first computing an N × N matrix which approximates the Laplace Beltrami operator and then computing its eigendecomposition. It is motivated by results which provides guarantees for the convergence of the eigenvectors and eigenvalues (Cheng & Wu, 2021b). (See also Dunson et al. (2021).) For large values of N, computing eigendecompositions is computationally expensive. Therefore we also present a second method which does not require the computation of any eigenvectors or eigenvalues. In either case, we identify f with the vector , and so once Ht has been computed, it is then straightforward to implement the wavelet transform described in (3) and (4) and then compute the scattering moments.
We let be an affinity kernel and given K, we define an affinity matrix W and a diagonal degree matrix D by
| (6) |
3.1. Approximating Ht via the Spectrum of the Data-Driven Laplacian
In this section, for , we define by
| (7) |
We then construct a discrete approximation −Δ by
where D and W are as in (6). We denote the eigenvectors and eigenvalues of by and so that . Using the first κ eigenvectors and eigenvalues of , we define
To motivate this method, we note Theorem 5.4 of (Cheng & Wu, 2021b), which shows that if we set , assume that data points are sampled i.i.d. uniformly from and certain other mild conditions hold, then there exist scalars with such that
| (8) |
| (9) |
for with probability at least , where μk are the true eigenvalues of the Laplace Beltrami operator −Δ, the vk are vectors obtained by subsampling (and renormalizing) its eigenfuctions , and the implicit constants depend on both and .
3.2. Approximating H without Eigenvectors
The primary drawbacks of the method of the previous section are that it requires one to compute the eigendecomposition of , and it does not account for the possibility that the data is sampled non-uniformly. One method for handling this problem is to use an adaptive method which scales the bandwidth of the kernel at each data point (Zelnik-Manor & Perona, 2004; Cheng & Wu, 2021a) Here, we let denote the distance from x to its k-th nearest neighbor and define an adaptive kernel by
| (10) |
Then, letting W and D be as in (6), with , we define an approximation of H1 by
| (11) |
We may then approximate via matrix multiplication without computing any eigenvectors or values. We note that while in principle is a dense matrix, by construction, most of its entries will be small (if k is sufficiently small). Therefore, if one desires, they may use a thresholding operator to approximate by a sparse matrix for increase computational efficiency.
The approximation (11) can be obtained by approximating −Δ with the Markov normalized graph Laplacian and then setting in (2). We note that this is similar to the approximation proposed in Coifman & Lafon (2006), but we use Markov normalization rather than symmetric normalization.
4. Related work
In this section, we summarize related work on geometric scattering as well as neural networks defined on manifolds.
4.1. Graph and Manifold Scattering
Several different works (Zou & Lerman, 2019a; Gama et al., 2019b; Gao et al., 2019) have introduced different versions of the graph scattering transform using wavelets based on Hammond et al. (2011) or Coifman & Maggioni (2006). Zou & Lerman (2019a) and Gama et al. (2019b) provided extensive analysis of their networks stability and invariance properties. These analyses were later generalized in Gama et al. (2019a) and Perlmutter et al. (2019). Gao et al. (2019), on the other hand, focused on empirically demonstrating the effectiveness of their network for graph classification tasks.
Several subsequent works have proposed modifications to the graph scattering transform for improved performance. Tong et al. (2021a) and Ioannidis et al. (2020) have proposed data-driven methods for selecting the scales used in the network. Wenkel et al. (2022) incorporated the graph scattering transform incorporated into a hybrid network which also featured low-pass filters similar to those used in networks such as (Kipf & Welling, 2016). We also note works using the scattering transform for graph generation (Zou & Lerman, 2019b; Bhaskar et al., 2021), for solving combinatorial optimization problems (Min et al., 2022), and work which extends the scattering transform to spatio-temporal graphs (Pan et al., 2020).
The work most closely related to ours is Perlmutter et al. (2020) which introduced a different version of the manifold scattering transform. The focus of this work was primarily theoretical, showing that the manifold scattering transform is invariant to the action of the isometry group and stable to diffeomorphisms, and the numerical experiments presented there are limited to two-dimensional surfaces with triangular meshes. Our work here builds upon Perlmutter et al. (2020) by introducing effective numerical methods for implementing the manifold scattering transform when the intrinsic dimension of the data is greater than two or when one only has access to the function on a point cloud. We also note McEwen et al. (2021), which optimized the construction of Perlmutter et al. (2020) for the sphere.
4.2. Manifold Neural Networks
In contrast to graph neural networks, which are very widely studied (see, e.g., Bruna et al. (2014); Veličkovič et al. (2018); Hamilton et al. (2017)), there is comparatively little work developing neural networks for manifold-structured data. Moreover, unlike our method, much of the existing literature is either focused on a specific manifold of interest or is limited to two-dimensional surfaces.
Masci et al. (2015) defines convolution on two-dimensional surfaces via a method based on geodesics and local patches. They show that various spectral descriptors such as the heat kernel signature (Sun et al., 2009) and wave kernel signature (Aubry et al., 2011) can be obtained as special cases of their network. In a different approach, (Schonsheck et al., 2022) defined convolution in terms of parallel transport. (Boscaini et al., 2015), on the other hand, used spectral methods to define convolution on surfaces via a windowed Fourier transform. This work was generalized in (Boscaini et al., 2016) to a network using an anisotropic Laplace operator. We note the many of the ideas introduced in Boscaini et al. (2015) and Boscaini et al. (2016) could in principle be applied to manifolds of arbitrary dimensions. However, their numerical methods rely on triangular meshes. In more theoretical work, Wang et al. (2021b;a) also proposed networks constructed via functions of the Laplace Beltrami operator and analyzed the networks’ stability properties.
In a much different approach, Chakraborty et al. (2020) proposed extending convolution to manifolds via a weighted Fréchet mean. Unlike the work discussed above, this construction is not limited to two-dimensional surfaces. It does, however, require that the manifold is known in advance. We also note that there have been several papers which have constructed neural networks for specific manifolds such as the sphere (Cohen et al., 2018), Grassman manifolds (Huang et al., 2018), or the manifold of positive semi-definite n×n matrices (Huang & Van Gool, 2017) or for homogeneous spaces (Chakraborty et al., 2018; Kondor & Trivedi, 2018).
5. Results
We conduct experiments on synthetic and real-world data. These experiments aim to show that i) the manifold scattering transform is effective for learning on two-dimensional surfaces, even without a mesh and ii) our method is effective for high-dimensional biomedical data1.
5.1. Two-dimensional surfaces without a mesh
When implementing convolutional networks on a two-dimensional surfaces, it is standard, e.g., (Boscaini et al., 2015; 2016) to use triangular meshes. In this section, we show that mesh-free methods can also work well in this setting. Importantly, we note that we are not claiming that mesh-free methods are better for two-dimensional surfaces. Instead, we aim to show that these methods can work relatively well thereby justifying their use in higher-dimensional settings.
We conduct experiments using both mesh-based and mesh-free methods on a spherical version of MNIST and on the FAUST dataset which were previously considered in Perlmutter et al. (2020). In both methods, we use the wavelets defined in Section 2 with J = 8 and use an RBF kernel SVM with cross-validated hyperparameters as our classifier. For the mesh-based methods, we use the same discretization scheme as in Perlmutter et al. (2020) and set Q = 1 which was the setting implicitly assumed there. For our mesh-free experiments, we use the method discussed in Section 3.1 with Q = 4. We show that the information captured by the higher-order moments can help compensate for the structure lost by not using a mesh.
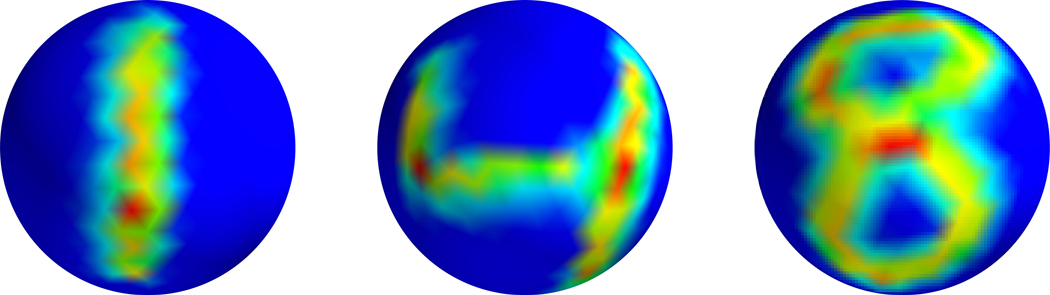
We first study the MNIST dataset projected onto the sphere as visualized in Figure 1. We uniformly sampled N points from the unit two-dimensional sphere, and then applied random rotations to the MNIST dataset and projected each digit onto the spherical point cloud to generate a collection of signals {fi} on the sphere. Table 1 shows that for properly chosen κ, the mesh-free method can achieve similar performance to the mesh-based method. As noted in Section 3.2, the implied constants in (8) and (9) depend on κ and inspecting the proof in Cheng & Wu (2021b) we see that for larger values of κ, more sample points are needed to ensure the convergence of the first κ eigenvectors. Thus, we want κ to be large enough to get a good approximation of H1, but also not too large.
Figure 1.
The MNIST dataset projected onto the sphere.
Table 1.
Classification accuracies for spherical MNIST.
| Data type | N | κ | Q | Accuracy |
|---|---|---|---|---|
| Point cloud | 1200 | 200 | 4 | 79% |
| Point cloud | 1200 | 400 | 4 | 88% |
| Point cloud | 1200 | 642 | 4 | 84% |
| Mesh | 642 | 642 | 1 | 91% |
Next, we consider the FAUST dataset, a collection of surfaces corresponding to scans of ten people in ten different poses (Bogo et al., 2014) as shown in Figure 2. As in Perlmutter et al. (2020), we use 352 SHOT descriptors (Tombari et al., 2010) as our signals. We used the first κ = 80 eigenvectors and eigenvalues of the approximate Laplace-Beltrami operator of each point cloud to generate scattering moments. We achieved 95% classification accuracy for the task of classifying different poses. This matches the accuracy obtained with meshes in Perlmutter et al. (2020).
Figure 2.
Wavelets on the FAUST dataset, j = 1, 3, 5 from left to right. Positive values are red, while negative values are blue.
5.2. Single-cell datasets
In this section, we present two experiments leveraging the inherent manifold structure in single-cell data to show the utility of manifold scattering in describing and classifying biological data. In these experiments, single-cell protein measurements on immune cells obtained from either melanoma or SARS-COV2 (COVID) patients are featurized using the log-transformed L1-normalized protein expression feature data of the cell. This leads to one point in high-dimensional space corresponding to each cell, and we model the set of points corresponding to a given patient as lying on a manifold representing the immunological state of that patient. In this context, it is not reasonable to assume that data are sampled uniformly from the underlying manifold so we use the method presented in Section 3.2 to approximate Ht.
For both experiments, we set k = 3, use third-order scattering moments with J = 8 and Q = 4, reduce dimensions of scattering features with PCA, and use the top 10 principle components for classification with a decision tree. As a baseline comparison, we perform K-means clustering on all cells and predict patient outcomes based on cluster proportions.
We first consider data from Ptacek et al. (2021). In this dataset, 11,862 T lymphocytes from core tissue sections were taken from 54 patients diagnosed with various stages of melanoma and 30 proteins were measured per cell. Thus, our dataset consists of 54 manifolds, embedded in 30-dimensional space with 11,862 points per manifold. All patients received checkpoint blockade immunotherapy, which licenses patient T cells to kill tumor cells. Our goal is to characterize the immune status of patients prior to treatment and to predict which patients will respond well. In our experiments, we first computed a representation of each patient via either K-means cluster proportions, with K = 3 based on expected T cell subsets (killer, helper, regulatory), then calculated scattering moments for protein expression feature signals projected onto the cell-cell graph. We achieved 46% accuracy with clustering and 82% accuracy with scattering.
We next analyze 148 blood samples from COVID patients and focus on innate immune (myeloid) cells, a population that we have previously shown to be predictive of patient mortality (Kuchroo et al., 2022). 14 proteins were measured on 1,502,334 total monocytes. To accommodate the size of these data, we first perform diffusion condensation (Kuchroo et al., 2022) for each patient dataset; we determine the lowest number of steps needed to condense data into less than 500 clusters and use those cluster centroids as single points in high-dimensional immune state space. Protein expression is averaged across cells in each cluster, and diffusion scattering is performed on these feature signals projected onto the centroid graph. For K-means we use K = 3 based on expected monocyte subtypes (classical, non-classical, intermediate). When used to predict patient mortality, we achieved 40% accuracy with cluster proportions and 48% accuracy with scattering features.
6. Conclusions
We have presented two efficient numerical methods for implementing the manifold scattering transform from point cloud data. Unlike most other methods proposing neural-network like architectures on manifolds, we do not need advanced knowledge of the manifold, do not need to assume that the manifold is two-dimensional, and do not require a predefined mesh. We have demonstrated the numerical effectiveness of our method for both signal classification and manifold classification tasks.
Table 2.
Classification accuracies for patient outcome prediction.
| Data set | N M | Clustering | Scattering |
|---|---|---|---|
| Melanoma | 54 | 46% | 82% |
| COVID | 148 | 40% | 48% |
Acknowledgements
Deanna Needell and Joyce Chew were partially supported by NSF DMS 2011140 and NSF DMS 2108479. Joyce Chew was additionally supported by the NSF DGE 2034835. Matthew Hirn and Smita Krishnaswamy were partially supported by NIH grant R01GM135929. Matthew Hirn was additionally supported by NSF grant DMS 1845856. Smita Krishnaswamy was additionally supported by NSF Career grant 2047856 and Grant No. FG-2021-15883 from the Alfred P. Sloan Foundation. Holly Steach was supported by NIAID grant T32 AI155387.
Footnotes
All of our code is available at our GitHub.
References
- Aubry M, Schlickewei U, and Cremers D. The wave kernel signature: A quantum mechanical approach to shape analysis. In 2011 IEEE international conference on computer vision workshops (ICCV workshops), pp. 1626–1633. IEEE, 2011. [Google Scholar]
- Bhaskar D, Grady JD, Perlmutter MA, and Krishnaswamy S. Molecular graph generation via geometric scattering. arXiv preprint arXiv:2110.06241, 2021.
- Bogo F, Romero J, Loper M, and Black MJ FAUST: Dataset and evaluation for 3D mesh registration. In Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2014. [Google Scholar]
- Boscaini D, Masci J, Melzi S, Bronstein MM, Castellani U, and Vandergheynst P. Learning class-specific descriptors for deformable shapes using localized spectral convolutional networks. In Computer Graphics Forum, volume 34, pp. 13–23. Wiley Online Library, 2015. [Google Scholar]
- Boscaini D, Masci J, Rodolà E, and Bronstein M. Learning shape correspondence with anisotropic convolutional neural networks. In Advances in Neural Information Processing Systems 29, pp. 3189–3197, 2016. [Google Scholar]
- Bronstein MM, Bruna J, LeCun Y, Szlam A, and Vandergheynst P. Geometric deep learning: Going beyond Euclidean data. IEEE Signal Processing Magazine, 34 (4):18–42, 2017. [Google Scholar]
- Bruna J, Zaremba W, Szlam A, and LeCun Y. Spectral networks and deep locally connected networks on graphs. In International Conference on Learning Representations (ICLR), 2014. [Google Scholar]
- Chakraborty R, Banerjee M, and Vemuri BC A cnn for homogneous riemannian manifolds with applications to neuroimaging. arXiv preprint arXiv:1805.05487, 2018.
- Chakraborty R, Bouza J, Manton J, and Vemuri BC Manifoldnet: A deep neural network for manifold-valued data with applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020. [DOI] [PubMed]
- Cheng X. and Wu H-T Convergence of graph Laplacian with kNN self-tuned kernels. Information and Inference: A Journal of the IMA, 09 2021a. ISSN 2049-8772. doi: 10.1093/imaiai/iaab019. URL . [DOI] [Google Scholar]
- Cheng X. and Wu N. Eigen-convergence of gaussian kernelized graph laplacian by manifold heat interpolation. arXiv preprint arXiv:2101.09875, 2021b.
- Cohen TS, Geiger M, Koehler J, and Welling M. Spherical cnns. In Proceedings of the 6th International Conference on Learning Representations, 2018. [Google Scholar]
- Coifman RR and Lafon S. Diffusion maps. Applied and Computational Harmonic Analysis, 21:5–30, 2006. [Google Scholar]
- Coifman RR and Maggioni M. Diffusion wavelets. Applied and Computational Harmonic Analysis, 21(1):53–94, 2006. [Google Scholar]
- Dunson DB, Wu H-T, and Wu N. Spectral convergence of graph laplacian and heat kernel reconstruction in l∞ from random samples. Applied and Computational Harmonic Analysis, 55:282–336, 2021. ISSN1063-5203. doi: 10.1016/j.acha.2021.06.002. URL https://www.sciencedirect.com/science/article/pii/S1063520321000464. [DOI] [Google Scholar]
- Gama F, Bruna J, and Ribeiro A. Stability of graph scattering transforms. In Advances in Neural Information Processing Systems 33, 2019a. [Google Scholar]
- Gama F, Ribeiro A, and Bruna J. Diffusion scattering transforms on graphs. In International Conference on Learning Representations, 2019b. [Google Scholar]
- Gao F, Wolf G, and Hirn M. Geometric scattering for graph data analysis. In Proceedings of the 36th International Conference on Machine Learning, PMLR, volume 97, pp. 2122–2131, 2019. [Google Scholar]
- Hamilton W, Ying Z, and Leskovec J. Inductive representation learning on large graphs. Advances in neural information processing systems, 30, 2017. [Google Scholar]
- Hammond DK, Vandergheynst P, and Gribonval R. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 30:129–150, 2011. [Google Scholar]
- Huang Z. and Van Gool L. A riemannian network for spd matrix learning. In Thirty-First AAAI Conference on Artificial Intelligence, 2017. [Google Scholar]
- Huang Z, Wu J, and Van Gool L. Building deep networks on grassmann manifolds. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 32, 2018. [Google Scholar]
- Ioannidis VN, Chen S, and Giannakis GB Pruned graph scattering transforms. In International Conference on Learning Representations, 2020. [Google Scholar]
- Kipf T. and Welling M. Semi-supervised classification with graph convolutional networks. Proc. of ICLR, 2016.
- Kondor R. and Trivedi S. On the generalization of equivariance and convolution in neural networks to the action of compact groups. arXiv:1802.03690, 2018.
- Kuchroo M. et al. Multiscale phate identifies multimodal signatures of covid-19. Nature Biotechnology, 2022. ISSN 1546-1696. doi: 10.1038/s41587-021-01186-x. [DOI] [PMC free article] [PubMed]
- Levie R, Huang W, Bucci L, Bronstein M, and Kutyniok G. Transferability of spectral graph convolutional neural networks. Journal of Machine Learning Research, 22(272):1–59, 2021. [Google Scholar]
- Mallat S. Recursive interferometric representations. In 18th European Signal Processing Conference (EUSIPCO-2010), Aalborg, Denmark, 2010. [Google Scholar]
- Mallat S. Group invariant scattering. Communications on Pure and Applied Mathematics, 65(10):1331–1398, October 2012. [Google Scholar]
- Masci J, Boscaini D, Bronstein MM, and Vandergheynst P. Geodesic convolutional neural networks on riemannian manifolds. In IEEE International Conference on Computer Vision Workshop (ICCVW), 2015. [Google Scholar]
- McEwen JD, Wallis CG, and Mavor-Parker AN Scattering networks on the sphere for scalable and rotationally equivariant spherical cnns. arXiv preprint arXiv:2102.02828, 2021.
- Min Y, Wenkel F, Perlmutter M, and Wolf G. Can hybrid geometric scattering networks help solve the maximal clique problem?, 2022. URL https://arxiv.org/abs/2206.01506.
- Moon KR, Stanley III JS, Burkhardt D, van Dijk D, Wolf G, and Krishnaswamy S. Manifold learning-based methods for analyzing single-cell rna-sequencing data. Current Opinion in Systems Biology, 7:36–46, 2018. [Google Scholar]
- Pan C, Chen S, and Ortega A. Spatio-temporal graph scattering transform. arXiv preprint arXiv:2012.03363, 2020.
- Perlmutter M, Gao F, Wolf G, and Hirn M. Understanding graph neural networks with asymmetric geometric scattering transforms. arXiv preprint arXiv:1911.06253, 2019.
- Perlmutter M, Gao F, Wolf G, and Hirn M. Geometric scattering networks on compact Riemannian manifolds. In Mathematical and Scientific Machine Learning Conference, 2020. [PMC free article] [PubMed] [Google Scholar]
- Ptacek J, Vesely M, Rimm D, Hav M, Aksoy M, Crow A, and Finn J. 52 characterization of the tumor microenvironment in melanoma using multiplexed ion beam imaging (mibi). Journal for ImmunoTherapy of Cancer, 9(Suppl 2):A59–A59, 2021. [Google Scholar]
- Schonsheck SC, Dong B, and Lai R. Parallel transport convolution: Deformable convolutional networks on manifold-structured data. SIAM Journal on Imaging Sciences, 15(1):367–386, 2022. [Google Scholar]
- Shuman DI, Narang SK, Frossard P, Ortega A, and Vandergheynst P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Processing Magazine, 30(3):83–98, 2013. [Google Scholar]
- Sun J, Ovsjanikov M, and Guibas L. A concise and provably informative multi-scale signature based on heat diffusion. In Computer graphics forum, volume 28, pp. 1383–1392. Wiley Online Library, 2009. [Google Scholar]
- Tombari F, Salti S, and Di Stefano L. Unique signatures of histograms for local surface description. In European conference on computer vision, pp. 356–369, 2010. [Google Scholar]
- Tong A, Wenkel F, Macdonald K, Krishnaswamy S, and Wolf G. Data-driven learning of geometric scattering modules for gnns. In 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), pp. 1–6, 2021a. doi: 10.1109/MLSP52302.2021.9596169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong AY, Huguet G, Natik A, MacDonald K, Kuchroo M, Coifman R, Wolf G, and Krishnaswamy S. Diffusion earth mover’s distance and distribution embeddings. In International Conference on Machine Learning, pp. 10336–10346. PMLR, 2021b. [Google Scholar]
- Veličković P, Cucurull G, Casanova A, Romero A, Liò P, and Bengio Y. Graph attention networks. In International Conference on Learning Representations, 2018. [Google Scholar]
- Wang S-C, Wu H-T, Huang P-H, Chang C-H, Ting C-K, and Lin Y-T Novel imaging revealing inner dynamics for cardiovascular waveform analysis via unsupervised manifold learning. Anesthesia & Analgesia, 130 (5):1244–1254, 2020. [DOI] [PubMed] [Google Scholar]
- Wang Z, Ruiz L, and Ribeiro A. Stability of manifold neural networks to deformations. arXiv preprint arXiv:2106.03725, 2021a.
- Wang Z, Ruiz L, and Ribeiro A. Stability of neural networks on manifolds to relative perturbations. arXiv preprint arXiv:2110.04702, 2021b.
- Wenkel F, Min Y, Hirn M, Perlmutter M, and Wolf G. Overcoming oversmoothness in graph convolutional networks via hybrid scattering networks. arXiv preprint arXiv:2201.08932, 2022.
- Wu Z, Pan S, Chen F, Long G, Zhang C, and Philip SY A comprehensive survey on graph neural networks. IEEE transactions on neural networks and learning systems, 32(1):4–24, 2020. [DOI] [PubMed] [Google Scholar]
- Zelnik-Manor L. and Perona P. Self-tuning spectral clustering. Advances in neural information processing systems, 17, 2004. [Google Scholar]
- Zou D. and Lerman G. Graph convolutional neural networks via scattering. Applied and Computational Harmonic Analysis, 49(3)(3):1046–1074, 2019a. [Google Scholar]
- Zou D. and Lerman G. Encoding robust representation for graph generation. In International Joint Conference on Neural Networks, 2019b. [Google Scholar]