Methodology for Online Reliability Studies: A Primer for Orthopedic Surgeons

Abstract

In orthopedic surgery, there is an increasing number of papers about online studies on the reliability of classification systems. Useful classification systems need to be reliable and valid. Measurement of validity can be variable and is prone to observer bias.

These online collaboratives derive adequate power to study reliability by having a large group of trained surgeons review a small number of cases instead of the “classic” reliability studies in which a small number of observers evaluate many cases. Large online interobserver studies have advantages (i.e., less than 15 minutes to complete the survey, the ability to randomize, and the ability to study factors associated with reliability, accuracy, or decision-making). This ‘handbook’ paper gives an overview of current methods for online reliability studies. We discuss the study design, sample size calculation, statistical analyses of results, pitfalls, and limitations of the study design.

Introduction

Classification systems can help surgeons characterize the nature of clinical problems, indicate a potential prognosis, provide guidance for optimal treatment decision-making, establish an expected outcome for a natural history of a condition or injury, and offer a standardized approach to reporting, documenting, and comparing results from clinical and epidemiological data. ^1,2

Useful classification systems need to be reliable and valid (accurate). ¹ Measurement of validity can be variable and prone to observer bias. Thus, studies often tend to focus on establishing reliability (precision) at the outset and as a minimum requirement – often focusing on intra-observer (agreement between repeated observations by one observer) and inter-observer (agreement between different observers) reliability. Classification systems should have substantial to a good interobserver agreement to be useful in clinical practice. Since the level of agreement can be highly variable, it is important to understand the approach and sources of bias and disagreement.

This ‘handbook’ paper gives an overview of current methods for online reliability studies. We discuss the study design, sample size calculation, statistical analyses of results, pitfalls, and limitations of the study design. This ‘handbook’ paper is a systematic overview of the methodological framework for online reliability studies [Figure 1]. These studies are performed mainly by (surgeon) researchers.

Figure 1.

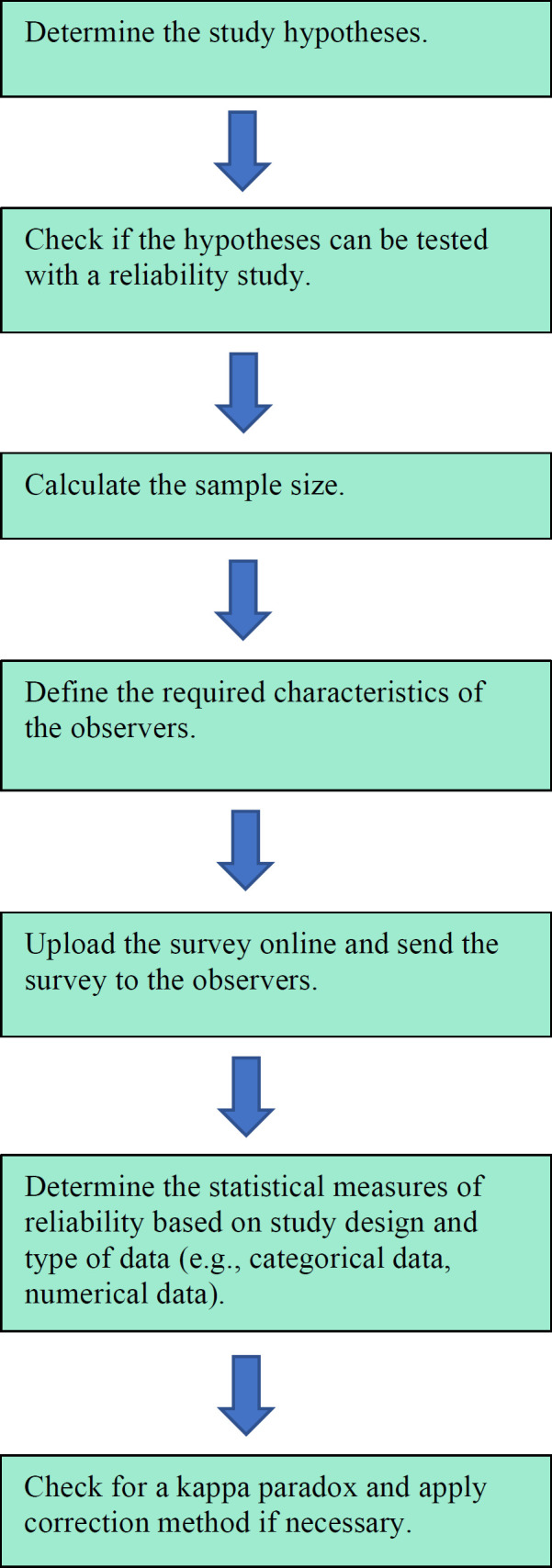
Flowchart of the methodological process for reliability studies

Study Design

In “classic” reliability studies, a small number of observers (around six or so) evaluate many cases (usually more than 50). In contrast, online collaboratives derive adequate power to study reliability (e.g., COAST collaborative and the Science of Variation Group (SOVG)) by having a large group of trained surgeons (more than 60) review a small number of images or patient scenarios. ³ The advantages of these large online interobserver studies are that the survey can be completed within 15 minutes and the ability to randomize and study factors associated with reliability, accuracy, or decision-making.

To have a large database of observers, the SOVG recruited trained surgeons from all over the world. Furthermore, new independent members through societies of different specialties –i.e., Orthopedic Trauma (www.traumaplatform.org), Shoulder and Elbow platform (www.shoulderelbowplatform.org) and Foot & Ankle surgeons (www.ankleplatform.com) were included.

With the introduction of online reliability studies with many observers, new designs for interobserver studies were developed. Depending on the number of observers and cases, an appropriate design has to be chosen. In most studies, all measurements or images will be rated by all observers, a factorial or fully crossed design. In studies with many cases or multiple measurements or images per patient and/or where the rating is time-consuming, selecting a subset of observers that rates only a subset of measurements/images can be more practical and efficient. When this latter option is chosen, it must be decided whether the measurements or images of a single patient will be rated by the same set of observers or whether the assessments are completely random. These split-plot designs are frequently used in clinical imaging studies. ⁴

Example

To identify the optimal projection angle to visualize the posterior aspect of the talus, radiographs of 13 different projection angles of 40 ankles were used. Because of the large number of images, a split-plot design was chosen. The images were distributed using a web-based rating application following an eight-block balanced split-plot design. Each block consisted of radiographs of 13 different projection angles of five different patients. Images were randomly assigned to the eight blocks, and each observer was randomly assigned to one of the blocks. Thus, each observer assessed 65 (13 x 5) images.

Online Presentation of Cases

Previously the SOVG used youtube.com and surveymonkey.com, which comprised movies of MRIs and 2-dimensional (2D)/ 3-dimensional (3D) CTs to present the cases. New features, such as a web-based viewer to facilitate online window leveling and contrast enhancement to improve the visualization of radiographs, were included via www.dicomlibrary.com. In addition, a digital imaging and communications in medicine (DICOM) viewer facilitates scrolling through MRI and CT images.

After logging in to the website, observers had to provide demographic and professional information: (1) sex, (2) location of practice, (3) years in independent practice, (4) supervising trainees in the operating room, (5) number of fractures/injuries treated per year, and (6) subspecialty. ⁵ Usually, observers are unaware of the hypothesis to reduce the chance of observer bias.

Primary and Secondary Hypotheses

Online interobserver studies can test hypotheses regarding classification systems, fracture/injury characteristics, radiographic methods, and surgical techniques. The null hypothesis should test no difference because it can be rejected if the P-value is smaller than 0.05. If the number of observers is high enough, it is possible to test a secondary hypothesis.

Example

We addressed the following study question: is the Minami, Berndt and Harty, Ferkel and Sgaglione, or Anderson Classification system more reliable for classification of osteochondritis dissecans of the humeral capitellum.^6-9 Our null hypothesis was that there is no difference in reliability of the Minami-, Berndt and Harty-, Ferkel and Sgaglione- and Anderson classification systems for the classification of osteochondritis dissecans of the humeral capitellum. ¹⁰

If the number of observers is high enough, it is possible to test a secondary hypothesis. Subgroup analysis can be performed. For example, suppose the primary null hypothesis assesses no agreement between surgeons on which implants will loosen or break after surgery for a distal humerus fracture in the subgroup analysis. In that case, no difference in interobserver agreement according to subgroups (e.g., experience surgeons, location of practice) can be tested. ¹¹

Recommended Sample size

Although reliability studies are common, the literature on sample size estimation for interobserver reliability studies is limited. ^12-17 In general, statistical power is based on the total number of observations. To sustain enough power, a higher number of observers is needed if there are fewer cases. ¹⁸ But, a larger number of cases better represents case distribution in day-to-day practice. Depending on the availability of observers and the purpose of the study, the most appropriate ratio of observers and patients should be selected.

Two ways of calculating the sample size are described based on the hypothesis testing approach and confidence interval approach. ^19,20 With the hypothesis testing approach, the hypothesis that the reliability coefficient is above a predefined level is tested. The confidence interval approach allows one to obtain a prespecified level of precision around an estimated reliability coefficient.

Usually, it is relevant to compare the reliability coefficients of different classifications or diagnostic methods. Different complex calculations are developed to compare these correlated reliability coefficients. ²¹ But, if the number of observations is large enough, the coefficient distribution is approaching a normal distribution. So, two-sample independent z-tests can be used to compare two different reliability coefficients. In addition, sample size calculation could be based on this test. ¹⁸

Number of Observers versus Number of Cases

Example

After defining the null hypothesis, the number of cases and the minimal number of observers that will result in a power of at least 80% should be calculated. The power is based on the number of observers and cases. For example, if a higher number of cases is used, a lower number of observers is needed for significant power.

“Classic” study: five observers – 23 cases

Doornberg et al. assessed whether three-dimensional reconstructed CT scans have greater intraobserver and interobserver reliability and improved accuracy compared with two-dimensional images on the characterization, classification, and treatment choice in the evaluation of fractures of the distal aspect of the humerus.¹⁴

Power analysis revealed that a minimum sample of 23 fractures would provide 80% power (a = 0.05, ß = 0.20) to detect significant intraobserver and interobserver agreement using the kappa coefficient.

“Contemporary” study: 107 observers – 15 cases

Bruinsma et al. tested the null hypothesis that interobserver reliability of the Arbeitsgemeinschaft für Osteosynthesefragen classification of proximal humeral fractures, the preferred treatment, and fracture characteristics is the same for 2-D and 3-D CT. ²²

It was calculated that the 107 observers would have yielded 80% power (a = 0.05, ß = 0.20) to detect a difference of 0.15 in the kappa value for the fracture classification.

Pre- and Post-hoc Power Analysis

In a pre-hoc analysis, the power and number of observers are calculated before the experiment, contrary to a posthoc analysis, where the power is calculated after the experiment. In practice, post-hoc analyses are usually concerned with finding associations between subgroups that would otherwise be undetected and if the pre-hoc analysis was not possible. ¹ It is also important to notice that more observers are needed to detect a smaller effect size to result in statistical power.

Example

Six observers – xx cases

Pre-hoc analysis

Doornberg et al. assessed whether 3D CT reconstructions can improve the reliability of complex tibial plateau fracture characterization and classification. ²³

A power analysis revealed that a sample size of 45 fractures would provide 95% power (a = 0.05; b = 0.95) to detect a significant difference in intraobserver and interobserver agreement with the use of the kappa coefficient.

xx observers – 15 cases

Post-hoc analysis

Claessen et al. tested the primary null hypothesis that the Minami-, Berndt and Harty-, Ferkel and Sgaglione- and Anderson classification systems are equally reliable for the classification of osteochondritis dissecans of the humeral capitellum. ¹⁰

It was calculated that a minimum sample of 22 cases evaluated by a minimum of 32 observers would provide 80% power to detect a clinically significant difference of one categorical rating of k = 0.20.

Hypothetical study

Diagnostic Performance Characteristics

For diagnostic scenarios with a reliable reference standard, diagnostic performance characteristics can be calculated. This is uncommon in interobserver studies.

Sensitivity and Specificity

The sensitivity of a test is the proportion of patients with the disease with a positive test. The specificity of a test is the proportion of patients without the disease with a negative test. These parameters are usually less relevant in the clinical setting because the clinician typically does not know whether the patient has the disease or not. ¹

Negative- and Positive Predictive Value

More relevant in clinics are the probability of the patient having the disease when the test result is positive (positive predictive value) and the probability of the patient not having the disease when the test result is negative (negative predictive value). ¹ The calculation of the diagnostic performance depends on the study design. In studies whereby all observers have rated all cases, the average performance of all observers can be used to calculate the diagnostic performance characteristics. In more complex designs, like split-plot studies, the calculation of diagnostic performance is more challenging and requires advanced statistics [Table 1].

Table 1.

Different designs and statistical analysis

		Diagnostic performance		Interobserver reliability
		Sensitivity/Specificity		Categorical data	Nummerical
Factorial Design (Fully-crossed)
	All cases assessed by all observers All observers asses all cases	Average sensitivity/specificity		Lights’ kappa Davies and Fleiss Krippendorf’s alpha	Two-Way mixed or fixed ICC Krippendorf’s alpha
Split-plot design
	Each subset of cases assessed by a subset of observers Each observers rates all images/measurements of a patient	More advanced statistics like general linear models		Lights’ kappa Davies and Fleiss Krippendorf’s alpha	Two-Way mixed or fixed ICC Krippendorf’s alpha
	Each subset of cases assessed by a subset of random observers Each observer assess a random group of cases	More advanced statistics like general linear models		Fleis generalized kappa Krippendorf’s alpha	One-way ICC Krippendorf’s alpha

Absence of Reference Standard

Without a “gold standard,” it is difficult to calculate diagnostic performance characteristics. In this case, latent class analysis is a statistical method that can be used. ^24,25 The latent class analysis evaluates groups of test results representing disease probability levels. The latent classes cannot be assessed directly (e.g., a fracture), but the resultant (e.g., no bone bridging) can be observed. ²⁴

Example

Buijze et al. ²⁴ compared diagnostic performance characteristics of CT, MRI, bone scintigraphy, and physical examination to identify true fractures among suspected scaphoid fractures.

Percentage of Agreement

Interobserver variability is usually reported with kappa values or intra-class correlation (ICC) instead of percentages of agreement. ¹ When reporting only percentages of the agreement, no adjustment for agreement due to chance alone is tested. ²⁶

Reliability

Many different statistical reliability measures have been described based on study design and type of data (e.g., categorical data, numerical data).

Categorical data

Observer reliability is commonly reported in kappa values. Kappa is a chance-corrected measure of agreement that compares the observed measure of agreement with the level of agreement expected by chance alone for categorical data. ^26-28 Zero represents no agreement. The value of -1.00 means total disagreement, and +1.00 indicates perfect agreement. ^27,29

The original kappa described by Cohen is only suitable when there are two observers. ³⁰ In online interobserver studies, there are usually more than two observers; in that case, standard kappa statistics are unsuitable. There are some variants for situations with more than two observers. Fleiss described a kappa-like formula in which, for each case, a constant number of observers is sampled randomly from a large population. ³¹ It is assumed that for each case, a different sample of observers is selected, and thus Fleiss kappa coefficient is not suitable for studies with fully crossed designs.

For studies in which all cases are rated by the same group of observers, Light proposed calculating a kappa statistic for each pair of observers and using the arithmetic mean of the kappa coefficients. ³² A similar approach was described by Davies and Fleiss. ³³

In addition to the kappa statistics, Krippendorf proposed an alternative reliability measure, Krippendorff’s alpha.³⁴ This alpha is less well-known but more flexible and can be used for all data types. Besides, it allows missing data, which makes it suitable for incomplete designs. It embraces a large number of reliability coefficients. It calculates disagreements instead of correcting the percentage of agreement, resulting in fewer limitations. Alpha is presented as a scale from 0.000, indicating the absence of reliability to 1.000 (perfect reliability). ³⁵

Numerical data

ICC is a commonly used measure to assess the reliability of numerical data and is obtained from the analysis of variance models for quantitative measurements (ANOVA). ²⁹ ICC is a measure of agreement between observers, adjusted for agreement due to chance alone, taking into account the measure of disagreement. Potential ICC values ranging from -1 to 1 (perfect agreement), with negative values indicating systematic disagreement and 0 only random agreement. It can be used for two or more observers and is suitable for different study designs.

There are several variants of the ICC. Depending on the type of data and study purpose, the correct type of ICC has to be chosen. The one-way ICC is required if a random observer is selected for every case. Two-way is chosen if there is a sample of observers for the different cases. Then, it has to be decided whether the study aims to generalize the results of the observers in the study to a larger population. In other words, are the observers a random sample of a larger population (random or mixed method), or are you only interested in these specific observers (fixed method). For online interobserver studies, generally, the two-way mixed method is appropriate. Furthermore, the ICC can be based on absolute values or based on consistency. When the average score of many ratings is used, an average measure ICC should be calculated. ^35,36

Interpretation of reliability coefficients

Although some arbitrary classifications exist, there is no standard for interpreting reliability coefficients. ³⁶ Landis and Koch proposed a commonly used classification for kappa values: 0.01 to 0.20 indicating slight agreement; 0.21 to 0.40, fair agreement; 0.41 to 0.60, moderate agreement; 0.61 to 0.80, substantial agreement; and 0.81 or more, almost perfect agreement. ²⁹ However, Krippendorff suggested a more conservative classification: no conclusions can be made for values less than 0.67, conclusions can tentatively be made for values between 0.67 and 0.80, and definite conclusions can be made for values above 0.80. ³⁴

Discussion

Treatment variation and differences in prognosis are unwanted in medical practice.

Classification systems help indicate a potential prognosis and guide optimal treatment decision-making. Classification systems need to be reliable and valid, but measurement of validity can be variable and is prone to observer bias. Thus, there is a growing number of papers about online studies on the reliability of classification systems. This ‘handbook’ paper is a systematic overview of the methodological framework for online reliability studies. It can be helpful for researchers who want to conduct a reliability study.

The strengths of interobserver studies include a large number of observers, which allows randomization and subgroup analysis to increase the generalizability of the results. ²² A large number of experienced and internationally distributed observers, and many cases improving both statistical power and external validity. ³⁷

Most studies are limited to the interobserver agreement only because it is less relevant to clinical practice, as surgeons mostly agree with themselves and not so much with each other. In addition, it is less time efficient if an observer has to complete the survey several times.

Another limitation is the possible observer bias that can arise with this study type. To reduce the chance of observer bias, the observers are usually unaware of the hypothesis.

Many investigators are not aware of an important disadvantage of kappa. Similar to positive and negative predictive values, the calculation of the kappa is affected by prevalence. If the prevalence of an outcome is low, it generates a lower kappa than one might expect. ^22,27,28,38

The first kappa paradox –a low value but high values of the observed proportion of agreement– will occur only if the marginal totals are highly symmetrically unbalanced. The second paradox –producing higher kappa values for asymmetrical than for symmetrical imbalance– can be associated with high values of the observed proportion of agreement if the imbalances have different degrees of high symmetry. ²⁷

Example

Bruinsma et al. ²² found poor to fair (k= 0.09-0.35) interobserver agreement after testing the null hypothesis that interobserver reliability of the Arbeitsgemeinschaft fur Osteosynthesefragen and Neer classifications, preferred treatment, and fracture characteristics are the same for two-dimensional CT and three-dimensional CT scans, while the percentage of agreement was higher (87-97%).

Data should be tested for the kappa paradoxes, and if this is the case, it is useful to describe the percentage of agreement as well. There are some formulas to correct for the kappa paradox.

Siegel and Castellan proposed an alternative formula that corrects the prevalence and imbalance problems. ³⁹

For ordinal data, Cohen described a weighted kappa variant in which disagreements are penalized based on the amount of disagreement. ³⁰ There is a linear and a quadratic variant. The quadratic variant of the weighted kappa is similar to the two-way mixed, consistency intra-class correlation coefficient (ICC).

In conclusion, a high agreement between observers is important to guide treatment and predict clinical outcomes. Thus, reliable and valid classification systems should be developed, and several existing classification systems should be simplified. In future studies, observer error and bias may be reduced by clear consensus definitions, measurement techniques, and diagnostic criteria.