Abstract
In recent years, several deep learning models recommend first to represent Magnetic Resonance Imaging (MRI) as latent features before performing a downstream task of interest (such as classification or regression). The performance of the downstream task generally improves when these latent representations are explicitly associated with factors of interest. For example, we derived such a representation for capturing brain aging by applying self-supervised learning to longitudinal MRIs and then used the resulting encoding to automatically identify diseases accelerating the aging of the brain. We now propose a refinement of this representation by replacing the linear modeling of brain aging with one that is consistent in local neighborhoods in the latent space. Called Longitudinal Neighborhood Embedding (LNE), we derive an encoding so that neighborhoods are age-consistent (i.e., brain MRIs of different subjects with similar brain ages are in close proximity of each other) and progression-consistent, i.e., the latent space is defined by a smooth trajectory field where each trajectory captures changes in brain ages between a pair of MRIs extracted from a longitudinal sequence. To make the problem computationally tractable, we further propose a strategy for mini-batch sampling so that the resulting local neighborhoods accurately approximate the ones that would be defined based on the whole cohort.
We evaluate LNE on three different downstream tasks: (1) to predict chronological age from T1-w MRI of 274 healthy subjects participating in a study at SRI International; (2) to distinguish Normal Control (NC) from Alzheimer’s Disease (AD) and stable Mild Cognitive Impairment (sMCI) from progressive Mild Cognitive Impairment (pMCI) based on T1-w MRI of 632 participants of the Alzheimer’s Disease Neuroimaging Initiative (ADNI); and (3) to distinguish no-to-low from moderate-to-heavy alcohol drinkers based on fractional anisotropy derived from diffusion tensor MRIs of 764 adolescents recruited by the National Consortium on Alcohol and NeuroDevelopment in Adolescence (NCANDA). Across the three data sets, the visualization of the smooth trajectory vector fields and superior accuracy on downstream tasks demonstrate the strength of the proposed method over existing self-supervised methods in extracting information related to brain aging, which could help study the impact of substance use and neurodegenerative disorders. The code is available at https://github.com/ouyangjiahong/longitudinal-neighbourhood-embedding.
Keywords: Self-supervised learning, Contrastive learning, Longitudinal brain MRI, Classification
1. Introduction
The application of deep learning to neuroimaging studies partly owes it success to the ability to learn powerful representations from raw magnetic resonance imaging (MRI) (Lipton et al., 2015; Santeramo et al., 2018; Gao et al., 2019; Cui and Liu, 2019; Ghazi et al., 2019; Ouyang et al., 2020). The interpretability and generalizability of the representations generally depend on the ability of the underlying latent space to explicitly encode factors aiding in performing a downstream task (Wang et al., 2021; Li et al., 2020; Kim and Mnih, 2018; Burgess et al., 2018; Xie et al., 2016; Guo et al., 2017; Zhao et al., 2019a). For example, encoding the continuum of brain age in the latent space can aid in the downstream task of differentiating subjects with cognitive impairment from healthy controls (Zhao et al., 2021a; Louis et al., 2019).
A useful approach for learning such a stratified space is to model the similarity of training samples within a neighborhood (Sabokrou et al., 2019; Wang et al., 2021; Li et al., 2020). A neighborhood refers to a region in the latent space such that samples in that region are considered to be similar. This concept is frequently used by self-supervised learning techniques, which encourage related samples to be mapped into the same neighborhood while unrelated samples are not (Sabokrou et al., 2019; Wang et al., 2021; Li et al., 2020). For example, the self-supervised approach by Dufumier et al. (2021) derived a latent space so that cross-sectional T1-weighted (T1-w) brain MRIs of subjects with similar age were mapped in close proximity to each other.
Another example is Longitudinal Neighborhood Embedding (LNE) (Ouyang et al., 2021), which was the first attempt at exploring the neighborhood concept within the context of applying self-supervised learning to longitudinal images. Specifically, we view the longitudinal T1-w brain MRIs of a subject as a trajectory in the latent space. To encode brains with similar brain age (which is unknown) to exhibit similar trajectories, the projection of the longitudinal MRIs onto that space is done so that trajectories within a neighborhood are maximally aligned (Fig. 1, lower right-hand box). The derived latent space explicitly captures brain aging, which resulted in better predictions of chronological age from T1-w brain MRIs compared with encodings derived from other self-supervised methods (i.e., Auto-Encoder (AE), Variational Auto-Encoder (VAE) (Kingma and Welling, 2013), Simple Framework for Contrastive Learning (SimCLR) (Chen et al., 2020), and Longitudinal Self-Supervised Learning (LSSL) (Zhao et al., 2021a)). When deriving these representations from the T1-w MRIs studies of the Alzheimer’s Disease Neuroimaging Initiative (ADNI), the LNE-based classifier was most accurate in distinguishing Normal Control (NC) from patients diagnosed with Alzheimer’s Disease (AD), and patients diagnosed with stable Mild Cognitive Impairment (sMCI) from those with progressive Mild Cognitive Impairment (pMCI).
Fig. 1.
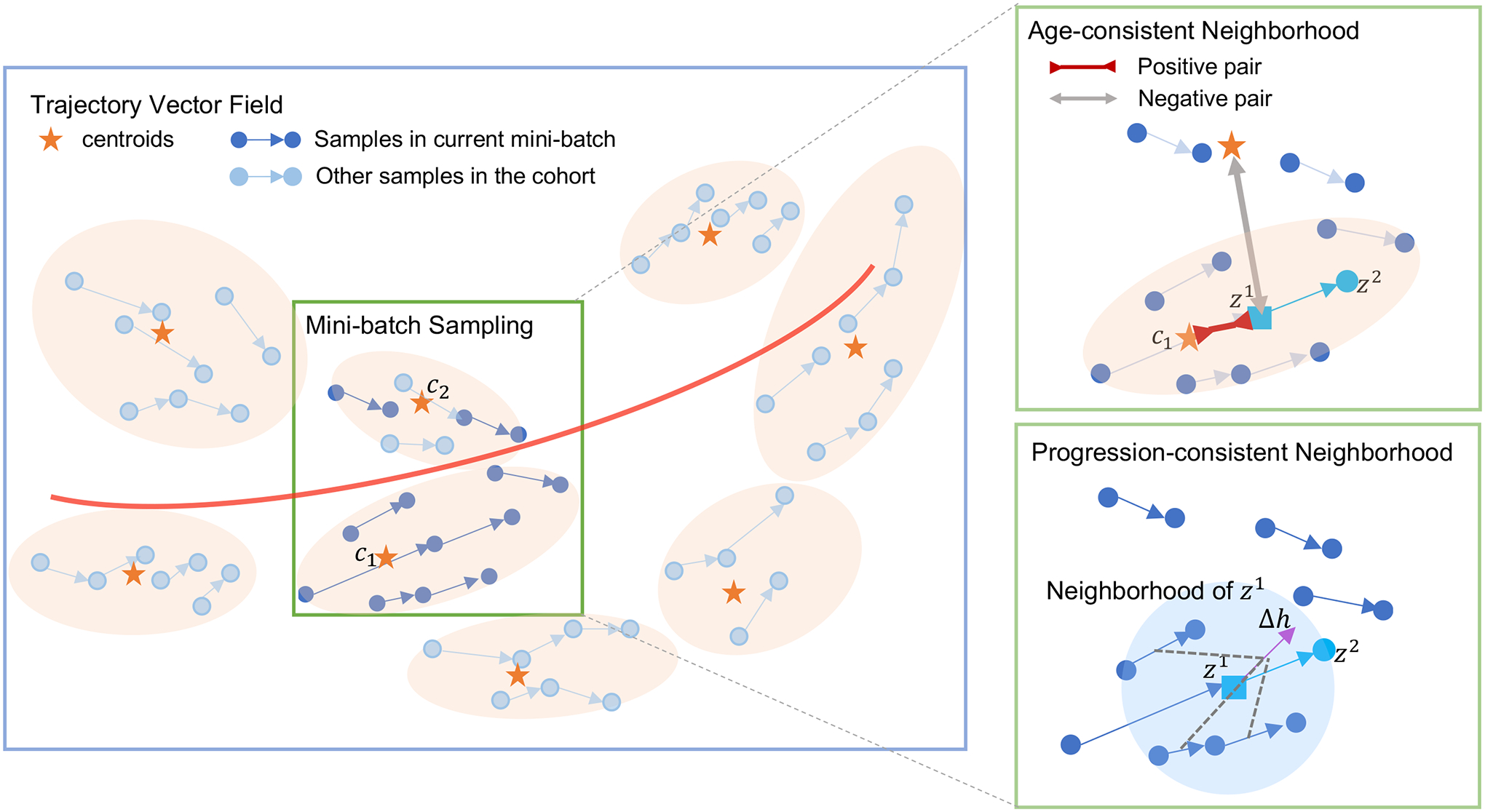
Overview of the latent space derived from the proposed method. All trajectories form a vector field (blue box) modeling brain aging (red curve). Each trajectory is assigned to a cluster centroid (orange star). During training, mini-batches are sampled from neighboring clusters (orange blob) until it reaches the desired size for the mini-batch. Mapping into a neighborhood is regularized according to brain age and progression consistency. For example, in the cyan trajectory in the upper-right box is first encouraged to be similar (inward red arrow) to its corresponding cluster centroid and dissimilar (outward gray arrow) to other centroids. Furthermore, as shown in the lower right green box, we encourage the direction of this vector to be consistent with (purple), a vector aggregated from the neighborhood of . (blue circle).
We now review the progression-consistent neighborhood in the LNE model (Ouyang et al., 2021) and further improve on its modeling of neighborhoods by learning to derive a latent space so that MRIs of similar brain age are in close proximity of each other. We do so by (1) automatically partitioning the latent space into clusters where each cluster defines an age-consistent neighborhood (orange blobs in Fig. 1). We then extend the loss function of LNE with a term that encourages samples to be close to their assigned cluster centroid and far from others (see upper right-hand box in Fig. 1). Moreover, (2) we observed that identifying neighbors of a sample requires computing distance from all other samples, which is usually computationally impracticable to repeat in each iteration. Consequently, we propose to confine each mini-batch to samples from the same or nearby clusters so that the neighborhood built within the mini-batch should approximate its construction based on all samples (see also green box in Fig. 1). Beyond the two innovations introduced in our conference publication (Ouyang et al., 2021), this work now
(3) creates synthetic brain MRIs at different brain ages to visualize the effects of aging and disease,
(4) quantitatively evaluates the quality of neighborhoods,
(5) expands the comparison to other self-supervised methods (i.e., Momentum Contrast (MoCo) (He et al., 2020) and Bootstrap Your Own Latent (BYOL) (Grill et al., 2020)), and
(6) evaluates the approach on a new image modality (i.e., fractional anisotropy (FA) derived from diffusion weighted imaging (DWI)) provided by a dataset previously not considered (i.e., data acquired by the National Consortium on Alcohol and NeuroDevelopment in Adolescence (NCANDA)).
Specifically, we evaluate our method on three longitudinal MRI datasets:
SRI: encode brain age as captured by T1-w MRIs (i.e., cortical thickness is reducing while ventricles are enlarging with age) of 274 healthy individuals (baseline age: 20 to 90 years) to predict their chronological age,
ADNI: encode brain age from T1-w MRIs of 632 subjects (consisting of NC, sMCI, pMCI, or AD) to distinguish in the downstream task differences in aging progression between NC and AD and between sMCI and pMCI,
NCANDA: encode the aging of micro-structural brain integrity based on the FA images of 764 adolescents (baseline age: 12–21 years) (Pohl et al., 2016b) to then distinguish no-to-low from moderate-to-heavy drinkers, whose micro-structural brain development can be delayed (Zhao et al., 2021b).
Across these datasets, the 2D visualization of the latent space confirms that neighborhoods are defined by smooth trajectory vector fields and the resulting representations led to more accurate predictions on the downstream tasks than alternative self-supervised, pre-trained models.
2. Related works
2.1. Longitudinal neuroimaging studies
Analysis of longitudinal MRIs traditionally relies on applying statistical approaches to a set of a priori selected brain measurements (e.g., volume and cortical thickness of the region of interest). Applied to each measurement is a general linear model (GLM) to compute the average developmental trajectory of a cohort (Fjell et al., 2009; Sabuncu et al., 2011; Frings et al., 2012) or a linear mixed effect model (LME) capturing subject-specific trajectories (Bernal-Rusiel et al., 2013a,b; Poulet and Durrleman, 2021). However, these univariate analyses ignore the multivariate correlations underlying the high-dimensional information captured by brain MRIs (Habeck and Stern, 2010).
One way to capture such correlations is via data-driven supervised learning (Lipton et al., 2015; Santeramo et al., 2018; Gao et al., 2019; Cui and Liu, 2019; Ghazi et al., 2019; Ouyang et al., 2020). These models reduce the longitudinal MRIs to a sequence of informative representations by, for example, a Convolutional Neural Network (CNN) to extract representations with a Recurrent Neural Network to predict a label (e.g., age or diagnosis group) (Lipton et al., 2015; Santeramo et al., 2018; Gao et al., 2019; Cui and Liu, 2019; Ghazi et al., 2019; Ouyang et al., 2020). However, these methods generally need to be trained on a large number of carefully labeled MRIs, which is often expensive or unrealistic to acquire (Carass et al., 2017). To reduce this need, a recent trend in deep learning is to train models by utilizing the repeated measures, and temporal order in the longitudinal setting via self-supervision (Louis et al., 2019; Zhao et al., 2021a; Ouyang et al., 2021; Couronné et al., 2021).
2.2. Self-supervised learning
Self-supervised models reduce the need for ground-truth labels by first learning representations based on a pretext task that is loosely related to the supervised downstream task of interest (Kolesnikov et al., 2019). Example of pretext tasks are colorization (Zhang et al., 2016), super-resolution (Dong et al., 2014), Jigsaw (Noroozi and Favaro, 2016), and contrastive learning (van den Oord et al., 2018; Sabokrou et al., 2019; Caron et al., 2020; Hassani and Khasahmadi, 2020; Tian et al., 2020), i.e., learning representations by distinguishing between similar and dissimilar images. These methods build similar (positive) pairs by, for example, augmenting samples (Chen et al., 2020), generating multiple views of the same scene (Tian et al., 2020), and performing dictionary look-up (He et al., 2020). In computer vision, positive pairs of images are also defined by their temporal proximity in a video sequence (Misra et al., 2016; Wang and Gupta, 2015).
Analogous to videos, a longitudinal MRI dataset capturing the slow progression of disease consists of individual MRIs that are similar to each other. Thus, this sequence of MRIs can be used to disentangle the time-varying effect (e.g., aging and disease progression) from the static factors (e.g. sex), which is critical for the success of longitudinal analyses (Ellwood-Lowe et al., 2018; Garcia and Marder, 2017; Tan et al., 2012). For example, Couronné et al. (2021) achieved disentanglement by identifying the order of longitudinal MRIs. Other works captured the time-varying effects by explicitly modeling the aging direction in the latent space (Zhao et al., 2021a; Louis et al., 2019; Ouyang et al., 2021). Louis et al. (2019) represented both brain aging and disease progression along linear directions while also explicitly modeling disease on-set and pace of progression. Inspired by the prior model, LSSL (Zhao et al., 2021a) also encoded the process of brain aging as a linear direction in the latent space but then encouraged the representation between two MRIs of the same subject to be maximally aligned with this direction. To capture more complex aging patterns, the proposed LNE approach derives a latent space in which age progression can be non-linear.
2.3. Modeling neighborhood in the latent space
Neighborhoods in the latent space capture similarities among samples and thus are critical for learning informative representations (Sabokrou et al., 2019; Fortuin et al., 2019; Manduchi et al., 2019, 2021). For example, neighborhoods are defined by the relative position of objects in the physical space (Gupta et al., 2018; Sadeghian et al., 2019; Zhao et al., 2019b) or the similarity of the semantic labels and appearance (Wei et al., 2020). Another example is using the output of clustering algorithms to define neighborhoods according to clusters (Sabokrou et al., 2019; Li et al., 2020) or by the topological characteristics of the resulting low dimensional embedding (Fortuin et al., 2019; Manduchi et al., 2019, 2021).
However, defining neighborhoods in the context of self-supervised learning is still a challenge as (1) defining neighborhoods in high dimensional latent spaces is computationally expensive or intractable, and (2) the representations defining the neighborhood are iteratively updated (since the encoder changes during each iteration of the training), and hence it is computationally-challenging to update the neighborhood on the whole data set in each iteration. One way of dealing with the computational complexity associated with (1) and (2) is to define neighborhoods specific to a mini-batch, but how to relate those neighborhoods to the entire data set is unclear. Our LNE model aims to address this challenge in the context of longitudinal MRIs.
3. Method
The longitudinal MRIs of a subject can be encoded by a set of MRI pairs , where the MRI was scanned before the MRI and the time interval between those two scans is . Let be the encoder that maps an MRI to the latent space, then and are the latent representations of and . Now we view the latent representations of the MRI pair as a trajectory capturing brain aging (see blue arrows in Fig. 1). One way to encode this trajectory is by the initial point and direction (or progression) , where the length of should relate to the speed of brain aging. For simplicity, we denote as . Meanwhile, the latent space should be stratified by brain age, i.e., representations of subjects with similar brain ages should be in close proximity of each other in the latent space. To derive a latent space with these properties, we first introduce in Section 3.1 the pairwise training strategy applied to the set of all longitudinal MRI pairs derived from all training subjects. We then expand the objective function so that the representation of the first MRI (initial points) with similar brain ages are in close proximity to each other in the latent space (Section 3.2). Finally, we ensure that the normalized vectors define a smooth vector field in the latent space (shown by blue box in Fig. 1) by having the embedding enforce the progression of nearby trajectories to have similar directions (Section 3.3). To make the learning process computationally tractable, training is confined to mini-batches. We introduce a sampling strategy such that neighborhoods constructed within the mini-batch approximate construction of neighborhoods taking into account the entire data set (Section 3.4).
3.1. Pairwise training strategy
We train the embedding on all MRI pairs to account for the variance in the number of MRIs associated with each subject. This also substantially increases the number of training samples compared to the common approach of Recurrent Neural Networks that view each longitudinal MRI as a single training sample (Ouyang et al., 2020). At each iteration of the training, our self-supervised learning approach derives an and a decoder , which reconstructs the MRIs and based on the latent representation. Then we ensure that the latent representation does not reduce to a trivial constant solution by deriving an and that minimize the following reconstruction loss (Zhao et al., 2021a; Grill et al., 2020):
| (1) |
denotes the expectation, represents the Euclidean norm, and is the sampling strategy on , which will be described in Section 3.4.
3.2. Age-consistent neighborhood
To ensure that the initial points with similar brain age are in close proximity to each other, we start an epoch by mapping each MRI pair in into the latent space, i.e., . Next, we perform k-means clustering on for times, where each run differs in the number of clusters (in Fig. 1 orange blobs are the clustering results from one run). We then record the set of centroids of the clusters , where is the centroid for the th cluster of the th run. By doing so, each is associated with centroids. We refer to the neighborhood around each centroid as age-consistent neighborhood . To ensure this consistency, we minimize the ProtoNCE loss (Li et al., 2020), which encourages to be more similar to its assigned centroids compared to other centroids:
| (2) |
where is a positive centroid assigned to in the th run of k-means clustering. To reduce computational complexity, the normalization term is based on negative centroids, which are a subset of centroids to which is not assigned. denotes the estimation of concentration of each centroid. Specifically, a cluster has a large concentration when the average distance between the centroid and the points within the cluster is small or when the cluster contains more samples. This normalization term should be small for a large concentration. Therefore, is defined as:
| (3) |
where is the number of samples in the age-consistent neighborhood and is a smoothing parameter to prevent small clusters from having overly-large . By doing so, the similarity between embedding and centroid in a cluster is normalized by its concentration , yielding clusters with similar concentrations.
3.3. Progression-consistent neighborhood
Deriving an encoding so that longitudinal MRIs with similar (unknown) brain age have similar age progression results in a latent space defined by a smooth vector field and thus encourages consistency across progressions within a neighborhood. In each iteration during training, a neighborhood is encoded as a directed graph . Specifically, each node represents a vector with defining the location of the node. For each node , we compute the Euclidean distances to other nodes. The 1-hop neighborhood of Node is then defined by the nearest nodes with respect to the Euclidean distance, which is encoded by the directed edges from node in the directed graph . Thus, the adjacency matrix of is:
| (4) |
where so that neighbors that are closer to node have higher edge weights.
Next, we aim to define a representation that captures the vector field within the neighborhood. Inspired by the process of graph diffusion (Klicpera et al., 2019), we define a neighborhood-specific trajectory (e.g., the purple arrow in the lower right green box in Fig. 1) as the weighted average of from its neighbors, which, for node is
| (5) |
where the diagonal matrix is the out-degree matrix of the graph encoding the sum of the weights for outgoing edges at each node.
To encourage the local smoothness of the vector field, we encourage the vector to be maximally aligned with the neighborhood-specific trajectory , i.e., a zero angle between and . This notion is captured by the progression loss:
| (6) |
By minimizing the loss, the resulting vector field maintains the local consistency in the neighborhood and captures the (global) non-linear direction of aging. As a result, subjects of similar ages will have similar learned representations (as demonstrated in prior works (Zhao et al., 2021a; Ouyang et al., 2021)).
3.4. Sampling strategy for mini-batches
To have the autoencoder derive a latent space with age- and progression-consistent neighborhoods, we add the ProtoNCE loss (Eq. (2)) and the progression loss (Eq. (5)) to the standard mean squared reconstruction loss, i.e.,
| (7) |
with and being the weighting parameters. The objective function encourages the low-dimensional latent space of the images to be informative while maintaining the consistency of embeddings within the age-consistent neighborhood and the smoothness of the vector fields representing age progression . In terms of convergence of the auto-encoder, the convergence of was proven in (Li et al., 2020) and the two loss functions and are differentiable. However, the minimization problem is computationally too complex to be performed on the entire data set so we instead perform it on mini-batches. To increase the likelihood of neighborhoods computed on mini-batches being accurate approximates of those derived on the entire data set, the rest of this section will focus on a sampling strategy for constructing mini-batches.
Inspired by Wu et al. (2017), Harwood et al. (2017), we aim to sample the mini-batch from a local region in the latent space. We do so by sampling from nearby clusters derived in Section 3.2. Specifically, when sampling a mini-batch from , we first randomly select a centroid , e.g., from run . From the same run, We then order the centroids with increasing Euclidean distance to , i.e., with being the closest centroid of . We then sample the image pairs without replacement from each neighborhood according to this order until the number of samples reach the desired size of the mini-batch. To keep the same number of iterations with random sampling without replacement, in each epoch, mini-batches are sampled. The entire sampling strategy is summarized by Algorithm 1, which is a way to select samples in a mini-batch and thus does not affect the mentioned convergence properties of the objective function (Eq. (7)).
Note, our method can be regarded as a dual contrastive learning method. For of an MRI pair, the sample pairs in the corresponding progression-consistent neighborhood serve as positive pairs, and the cosine loss is the corresponding contrastive loss. With respect to , its corresponding centroids serve as positive pairs and other centroids as negative pairs.
4. Experimental setting
4.1. Datasets
We first evaluated the proposed method for predicting chronological age from 582 T1-w MRIs of 274 healthy individuals (Male/Female: 138/136) with age ranging from 20 to 90 years (age: years) recruited at SRI International (SRI). T1-weighted Inversion-Recovery Prepared SPGR images were acquired on a GE scanner using an eight-channel phased-array head coil (, , , , , ). Each subject had up to 13 scans with an average of 2.3 MRIs spanning an average time interval of 3.8 years.

The second data set comprised 2389 T1-w MRIs from 632 subjects (at least two and up to six visits per subject) from ADNI1 (Mueller et al., 2005), which consisted of 185 NC (Male/Female: 95/90, age: years), 119 subjects with AD (Male/Female: 58/61, age: years), 193 subjects diagnosed with sMCI (Male/Female: 124/69, age: years), and 135 subjects diagnosed with pMCI (Male/Female: 84/51, age: years). There was no significant age difference between the NC and AD cohorts (, two-sample -test) or between the sMCI and pMCI cohorts . MRIs from ADNI were acquired via a 1.5T 3D MPRAGE sequence defined across GE, Siemens, and Phillips scanners ; ; section ; 256 reconstructed axial sections) (Jack et al., 2008). The third data set is provided by NCANDA (distribution release: NCANDA_PUBLIC_6Y_REDCAP_V04 (Pohl et al., 2022c), NCANDA_PUBLIC_6Y_STRUCTURAL_V01 (Pohl et al., 2022a), and NCANDA_PUBLIC_6Y_DIFFUSION_V02 (Pohl et al., 2022b); distributed to the public according to the NCANDA Data Distribution agreement https://www-niaaa-nih-gov.stanford.idm.oclc.org/research/majo r-initiatives/national-consortium-alcohol-and-neurodevelopment-adole scence/ncanda-data), consisting of 3830 DWI MRIs (processed to yield FA maps as described next) from 764 adolescents with ages between 12 and 24 years (Male/Female: 381/383, age: years). Scans were acquired on 3T GE or Siemens scanners with protocols described in (Pohl et al., 2016b). Each visit was labeled as no-to-low or moderate-to-heavy alcohol drinking based on the youth-adjusted Cahalan drinking score (Zhao et al., 2021b). The demographics of the three datasets are summarized in Table 1.
Table 1.
Demographics of the three datasets.
| Dataset | Cohorts | # of subjects | Gender (M/F) |
Age (Yrs) |
|---|---|---|---|---|
| SRI | Healthy | 274 | 138/136 | 49.8 ± 15.9 |
| ADNI | NC | 185 | 95/90 | 75.6 ± 5.1 |
| AD | 119 | 58/61 | 75.2 ± 7.6 | |
| sMCI | 193 | 124/69 | 75.6 ± 6.6 | |
| pMCI | 135 | 84/51 | 75.9 ± 5.4 | |
| NCANDA | All | 764 | 381/383 | 16.2 ± 2.5 |
Note, visits of an NCANDA participant are not always assigned to just one cohort, i.e., the participant can be a no-to-low drinker at some visits while a medium-to-heavy drinker at others.
4.2. Data preprocessing
In line with our prior studies (Zhao et al., 2021a; Ouyang et al., 2021, 2020), all longitudinal T1-w MRIs were preprocessed by a pipeline composed of denoising, bias field correction, skull stripping, affine registration to a template, re-scaling to a volume, and transforming image intensities to z-scores. NCANDA DTI scans were skull-stripped by aligning B0 images to the corresponding T1-W MRI. Bad single shots were removed, and corrections were applied for structural and eddy-current distortion. The UCL Camino Diffusion MRI toolkit (Zhao et al., 2021b) was used to create the FA maps.
Next, we split the data set into training, validation, and testing sets. After randomly selecting 10% subjects as the validation set, the remaining subjects were split into 5 folds for cross-validation (folds split based on subjects). For ADNI and NCANDA, stratified cross-validation was conducted to keep the same ratio between cohorts for downstream tasks in each fold. The same data splitting was used for pre-training and training of the regression model to ensure that the same individuals selected to create the representations were not part of the test sets used for measuring the accuracy of the regression model. To increase the size of the training set by a factor of 10, we performed data augmentation as in (Ouyang et al., 2021), i.e., by applying the same random shift (within 4 pixels), rotation (within 2 degrees), and random flipping of brain hemispheres to each pair of MRIs. By doing so, we preserve the intrasubject changes that our model aims to learn (i.e., aging and disease effects). This augmentation strategy also allowed for direct comparison with our previous works (Zhao et al., 2021a; Ouyang et al., 2021).
4.3. Implementation details
Regarding the architecture, our model was based on an Encoder–Decoder structure (Kingma and Welling, 2013) (see also Fig. 2). Specifically, let denote an Encoder Block, i.e., a stack of a Convolution layer (k channels, kernel size of ) followed by a BatchNorm, LeakyReLU (with the slope of 0.2), and a MaxPool layer (kernel size of 2), and as Decoder Block, i.e., a stack of a Convolution layer (k channels, kernel size of ) followed by a BatchNorm, LeakyReLU (with the slope of 0.2) and a MaxPool layer (kernel size of 2). Then the architecture of our model can be described as followed by a convolution layer for the final reconstruction. The networks were trained for 50 epochs by the Adam optimizer (Kingma and Ba, 2014) with a learning rate of and weight decay of . The regularization weights were set to and . To make the algorithm computationally efficient, we built the graph dynamically on the mini-batch of each iteration. Hyperparameters are set to mini-batch size , neighbor size , number of clusters , where is the number of subjects, and smooth parameter . We denote the original LNE (Ouyang et al., 2021) described in Sections 3.1 and 3.3 as LNE*, and the proposed method as LNE.
Fig. 2.
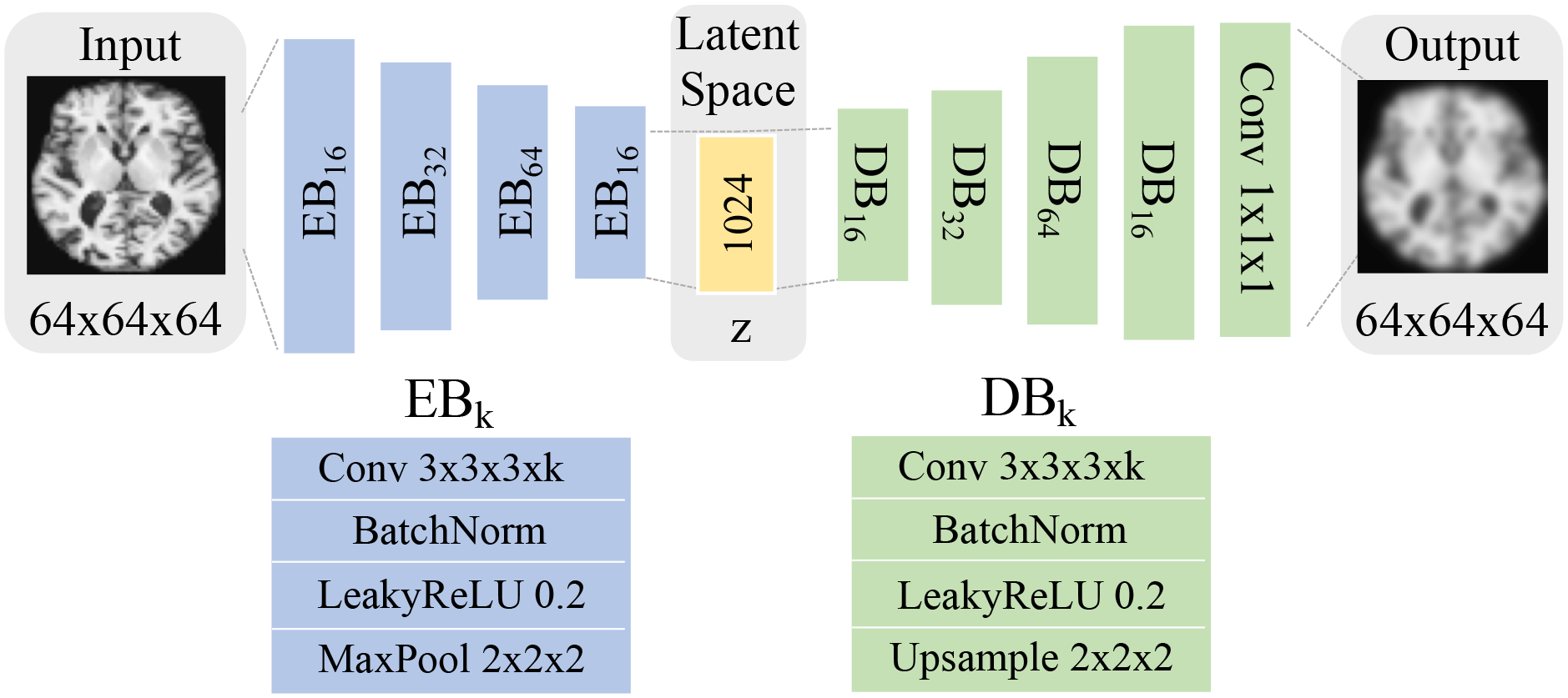
The network structure of the proposed method. Blue blocks correspond to the encoder that reduces an input MRI to a 1024-dimensional latent representation , from which the decoder (green) reconstructs the MRI.
4.4. Evaluation
We first visualized the vector field in 2D space by projecting the 1024-dimensional representations and to their first two principal components. Next, we quantitatively evaluated the quality of the representations by using them for downstream tasks. The classifier was designed as a multi-layer perceptron (Haykin, 2004) containing two fully connected layers of dimension 1024 (2048 if and were used) and 64 with LeakyReLU activation (Maas et al., 2013). In a separate experiment, we fine-tuned the LNE representation by incorporating the encoder into the classification models. On the SRI dataset, we used the representation to predict the chronological age of each MRI to show that age is disentangled in the latent space, despite not being used to train the model. Accuracy metrics were Coefficient of determination (R2) (Nagelkerke et al., 1991) and root-mean-square error (RMSE). For ADNI, the diagnosis label remained the same across all visits of a subject, so we predicted the label associated with each image pair based on both and trajectory to highlight the aging speed between visits (an important marker for AD). To enable fair comparison, the competing methods also used and in downstream tasks. In addition to classifying NC and AD, we also attempted the more challenging task of distinguishing pMCI from sMCI. To account for the different number of samples in each cohort, we measured the classification accuracy via the balanced accuracy (BACC) (Brodersen et al., 2010). We also computed the area under the ROC curve (AUC) (Fawcett, 2006) and F1 score (Sasaki et al., 2007) for reference. Note, all 4 cohorts (NC, sMCI, pMCI, AD) were included in pre-training as the method was impartial to diagnosis, i.e., labels were omitted for training. For NCANDA, we used the representation to distinguish no-to-low from moderate-to-heavy drinkers at each given visit and computed BACC, AUC, and F1 to evaluate the accuracy of the classification. As there is a significant age difference between the two cohorts of NCANDA, no-to-low and moderate-to-heavy cohorts were matched with respect to age on the test set.
We compared the recorded accuracy to those of models using the same overall architecture but the encoders were pre-trained by other representation learning methods, including self-supervised methods (AE, VAE (Kingma and Welling, 2013), SimCLR (Chen et al., 2020), MoCo (He et al., 2020), BYOL (Grill et al., 2020)), and a longitudinal self-supervised method (LSSL (Zhao et al., 2021a)). We modified the training strategy of SimCLR, MoCo, and BYOL to adapt to our longitudinal neuroimaging setting. As in Chen et al. (2020), the self-supervised training viewed two MRIs of the same subject as a positive pair while two MRIs from different subjects were a negative pair.
Moreover, we performed an ablation study to evaluate the contribution of each component of LNE. We noticed that methods could achieve similar regression or classification accuracy even when the quality of neighborhoods produced by those methods is very different. We evaluate the quality of the progression-consistent neighborhood according to the Silhouette Coefficient (SC) (Rousseeuw, 1987), which is defined by the ratio between the mean distance between a sample to other samples within its neighborhood versus samples that are outside the neighborhood, i.e., characterizes the density of the neighborhood:
| (8) |
Note, and larger values suggest higher quality, i.e., a better approximation of the neighborhood defined on the whole data set. In addition, we compute the Revised Variance Ratio Criterion (RVRC) (Caliński and Harabasz, 1974) to compare the variance of distance between a sample with other samples within its neighborhood to the variance in the distance to samples outside the neighborhood:
| (9) |
Note, larger values of RVRC suggest a higher quality of the neighborhood.
5. Results & discussion
5.1. Healthy aging
We first evaluated the proposed methods for encoding healthy brain aging with respect to the SRI dataset. Fig. 3 illustrates the vector field derived on one of the five folds by MoCo and the proposed method. We observe that the proposed method yielded a smooth field with a non-linear global aging direction from lower left to upper right, which indicates the disentanglement of the aging effect in the latent space (Fig. 3(b)). Note, such aging direction was solely learned by the self-supervised training on MRI pairs with an average interval between scans of 3.8 years (without using their age). On the contrary, without regularizing the longitudinal changes, MoCo did not lead to a clear disentanglement of brain age in the latent space (Fig. 3(a)).
Fig. 3.
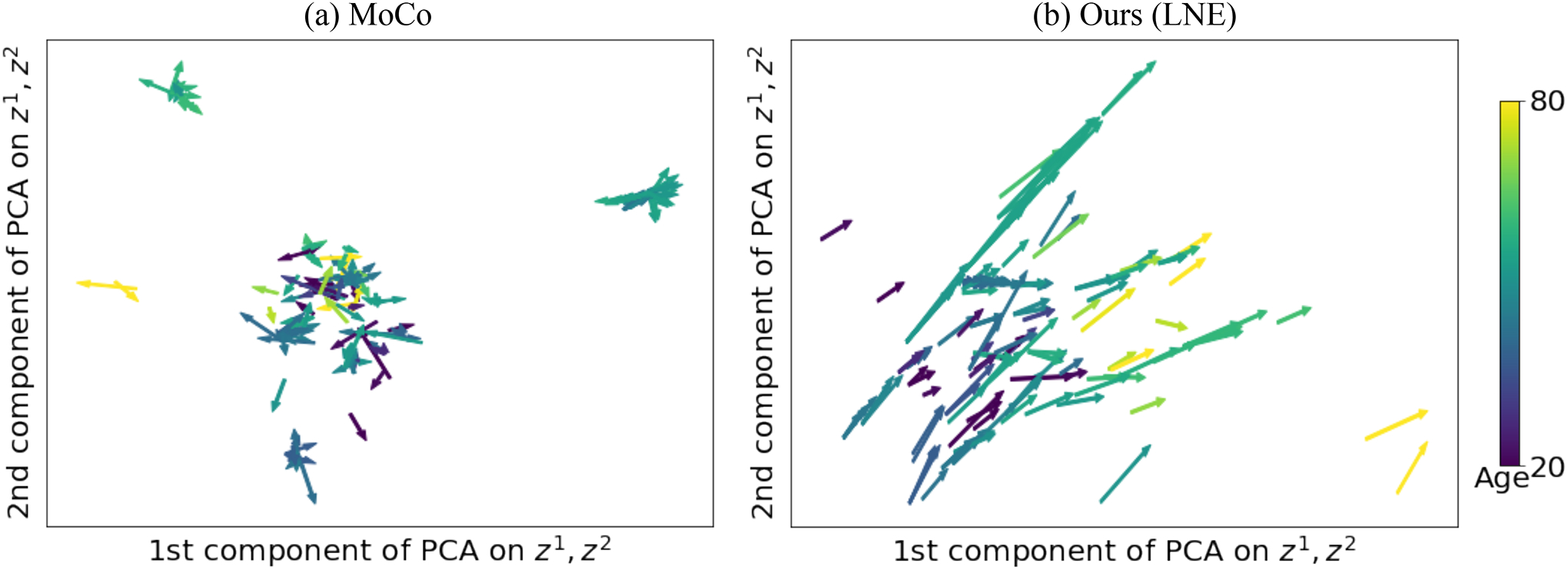
Experiments on healthy aging: Latent space of (a) MoCo (He et al., 2020) and (b) the proposed LNE projected into 2D PCA space of and . Arrows represent and are color-coded by the age of .
We then utilized the latent representation to predict the chronological age of the subjects (Table 2). With the frozen encoder, the proposed method achieved the best R2 score of 0.63 and RMSE of 10.0 years, which are significantly better (, paired two-sample t-test on RMSE) than the second-best method LSSL (R2 = 0.59; RMSE=10.8 years). These results confirmed our expectation that a pre-trained self-supervised model that explicitly modeled brain aging and progression leads to more accurate age prediction in the proceeding analysis. Using a fine-tuned encoder, both LNE and LSSL achieved an R2 score of 0.74 and RMSE of 8.4 years. Visualizing the fine-tuned latent space via t-SNE (Van der Maaten and Hinton, 2008), the Supplemental Figure S1 displays a latent space produced by LNE that is stratified by age, suggesting that the derived representation is a good starting point for age prediction.
Table 2.
Chronological age prediction on the SRI dataset.
| Methods | Chronological age prediction | |||
|---|---|---|---|---|
| Frozen | Fine-tuned | |||
| R2 ↑ | RMSE ↓ | R2 ↑ | RMSE ↓ | |
| No pretrain | – | – | 0.72 | 8.7† |
| AE | 0.53 | 11.4† | 0.69 | 9.3† |
| VAE (Kingma and Welling, 2013) | 0.51 | 11.6† | 0.69 | 9.4† |
| SimCLR (Chen et al., 2020) | 0.56 | 11.1† | 0.73 | 8.9† |
| MoCo (He et al., 2020) | 0.58 | 10.9† | 0.73 | 8.6 |
| BYOL (Grill et al., 2020) | 0.54 | 11.3† | 0.72 | 9.0† |
| LSSL (Zhao et al., 2021a) | 0.59 | 10.8† | 0.74 | 8.4 |
| LNE | 0.63 | 10.0 | 0.74 | 8.4 |
The best accuracy scores are in bold.
Significant (, paired two-tailed t-test) lower accuracy scores compared to LNE in term of RMSE.
5.2. Alzheimer’s disease classification and progression of cognitive impairment
Fig. 4(c) shows the trajectories by diagnosis groups according to the encoding produced by LNE. While the initial points of different diagnosis groups were uniformly spread across the latent space, vectors of AD (pink) and pMCI (brown) were significantly (, two-sided t-test, see also Figure S2) longer (i.e, progressed faster) than NC (cyan) and sMCI (orange) suggesting that the proposed method identified cohort difference in the progression speed of brain age. This finding aligned with previous AD studies (Toepper, 2017) suggesting that AD and pMCI are associated with accelerated brain aging. Similar to previous experiments, MoCo did not capture the aging direction and the differences between diagnosis groups (Fig. 4(a)). Though LSSL (Fig. 4(b)) captured the direction of brain aging in the latent space, it ignored that brain aging is a non-linear process. The non-linear curve by LNE seems to be a more accurate representation of brain aging, given that it resulted in a significantly more accurate classifier compared to LSSL (Tables 3 and 4)
Fig. 4.
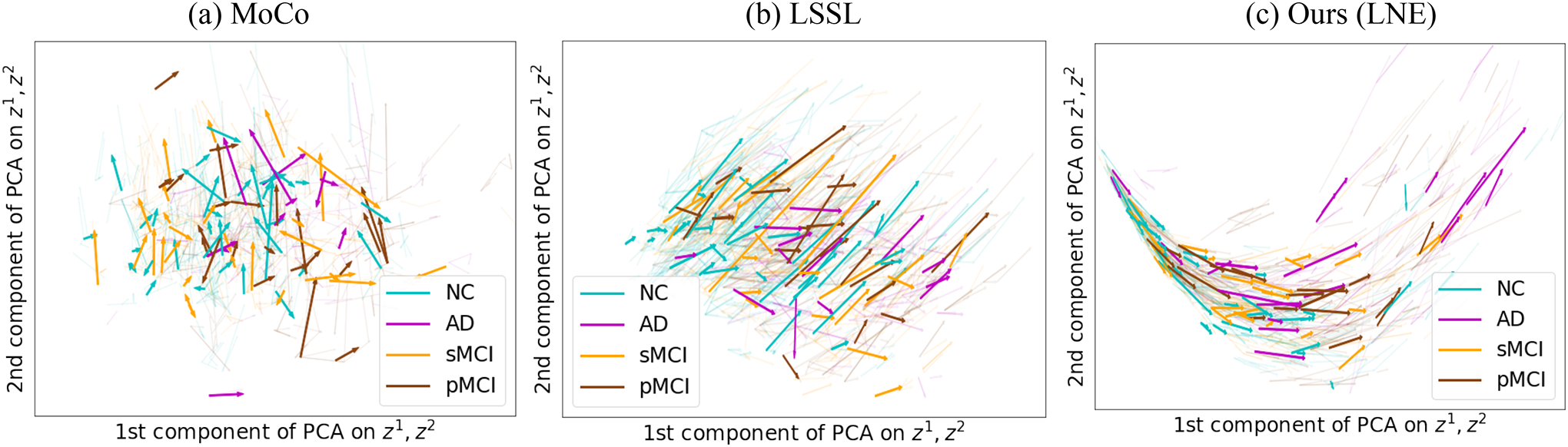
Experiments on ADNI: Latent space of (a) MoCo (He et al., 2020), (b) LSSL (Zhao et al., 2021a), and (c) the proposed LNE projected into 2D PCA space of and .Arrows represent and are color-coded by the diagnosis of the subject. Only LNE encodes brain aging as a non-linear process.
Table 3.
Classification accuracy for NC vs. AD (ADNI data).
| Methods | NC vs. AD | |||||
|---|---|---|---|---|---|---|
| Frozen | Fine-tuned | |||||
| BACC | AUC | F1 | BACC | AUC | F1 | |
| No pretrain | – | – | – | 79.4 | 83.1 | 80.3 |
| AE | 72.2 | 75.4 | 74.9 | 80.7 | 84.5 | 82.1 |
| VAE (Kingma and Welling, 2013) | 66.7 | 70.0 | 71.5 | 77.0 | 81.3 | 78.2 |
| SimCLR (Chen et al., 2020) | 72.9 | 75.9 | 75.4 | 82.4 | 86.2 | 83.4 |
| MoCo (He et al., 2020) | 73.2 | 76.4 | 76.4 | 82.8 | 85.4 | 83.8 |
| BYOL (Grill et al., 2020) | 73.0 | 76.4 | 75.9 | 82.3 | 85.3 | 82.7 |
| LSSL (Zhao et al., 2021a) | 74.2 | 77.8 | 77.0 | 82.1 | 85.3 | 83.4 |
| LNE | 82.1 | 85.4 | 83.0 | 83.5 | 85.8 | 83.5 |
The highest accuracy scores are in bold. The classifier based on the LNE encoding was significantly more accurate than the alternative methods for both frozen and fine-tuned encoder (, DeLong’s test).
Table 4.
Classification accuracy for sMCI vs. pMCI (ADNI data).
| Methods | sMCI vs. pMCI | |||||
|---|---|---|---|---|---|---|
| Frozen | Fine-tuned | |||||
| BACC | AUC | F1 | BACC | AUC | F1 | |
| No pretrain | – | – | – | 69.3 | 71.6 | 70.9 |
| AE | 62.6 | 65.4 | 62.8 | 69.5 | 71.8 | 71.1 |
| VAE (Kingma and Welling, 2013) | 61.3 | 64.8 | 62.9 | 63.8 | 65.9 | 64.3 |
| SimCLR (Chen et al., 2020) | 63.3 | 66.3 | 64.4 | 69.5 | 71.9 | 70.6 |
| MoCo (He et al., 2020) | 64.6 | 66.5 | 65.7 | 70.8 | 72.4 | 71.4 |
| BYOL (Grill et al., 2020) | 64.2 | 66.4 | 64.9 | 70.3 | 72.2 | 71.4 |
| LSSL (Zhao et al., 2021a) | 69.4 | 71.8 | 70.5 | 71.2 | 73.7 | 72.8 |
| LNE | 71.1 | 73.7 | 71.8 | 73.5 | 75.6 | 74.4 |
The highest accuracy scores are in bold. The classifier based on the LNE encoding was significantly more accurate than the alternative methods for both frozen and fine-tuned encoder (, DeLong’s test).
We visualized the effect of aging on the brain by creating synthetic MRIs. For AD and NC, we separately fitted a linear mixed effect model to the 2D space shown in Fig. 4(c) in order to encode the global trajectory of each cohort. As the 1st component of PCA roughly corresponds to (brain) aging, we then mapped the chronological age range to the value range of this coordinate. For a given age and diagnosis group, we then computed an average representation in 2D, i.e., the 1st coordinate was defined by the given age, and the 2nd coordinate was the average of all subjects in the given cohort. This average was converted to 1024-dimension by the inverse transform of PCA, and then the decoder reconstructed the corresponding MRI. Fig. 5(a) shows the normal morphological changes between the MRI at a specific age and at the age of 65 years, which, as expected, increase with older age and focus on the ventricles and frontal lobes. When we subtract the synthetic brain MRIs of NC from AD at the same age (Fig. 5(b)), the difference between the cohorts decreases with age, suggesting that subjects with NC and AD converge to the similar aging pattern at older ages. These results agree with recent findings that brain atrophy of early-onset AD patients is distinctly different from age-matched controls, but less so when comparing older AD patients to older controls (Rhodius-Meester et al., 2017).
Fig. 5.
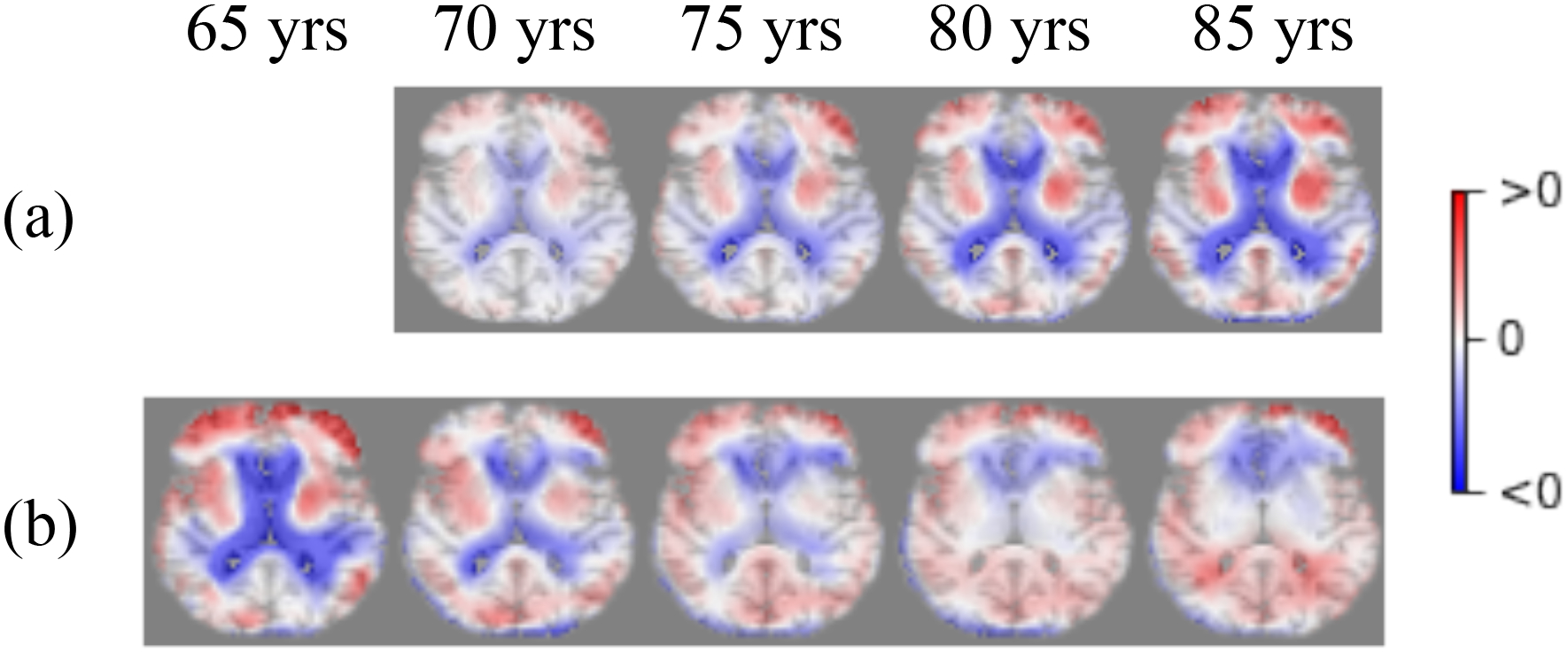
Visualization of the difference between synthetic generated brain MRIs. (a) Synthetic MRIs of normal controls at a given age minus the one at age 65 years; (b) Synthetic MRI of normal controls subtracted from those diagnosed with AD at the corresponding age. Red suggests having positive intensity difference and blue suggests negative.
As the prior findings suggest that the length of is informative, we used both and generated by each method as the features for classification. According to Tables 3 and 4, the representations learned by the proposed method yielded significantly more accurate predictions than all baselines (, DeLong’s test). Note that the accuracy of our model with the frozen encoder even closely matched up to other methods after fine-tuning. This was to be expected because only our method and LSSL explicitly modeled the longitudinal effects, which led to a more informative . Compared to modeling aging as a linear process by LSSL, the focus of our method was to capture potentially non-linear effects underlying the morphological change over time, which led to more informative trajectories according to the improved accuracy scores of the proceeding classifier. Moreover, as suggested in Table 5, LNE achieved higher or similar accuracy in sMCI vs. pMCI classification compared to other state-of-the-art methods that relied only on structural MRIs (Cui and Liu, 2019; Shen et al., 2021; Nguyen et al., 2021). Accurately distinguishing those two cohorts is of interest to clinicians as differences in brain structure might reveal why some MCI patients develop AD later in life (a.k.a. pMCI) while others do not (a.k.a., sMCI). Note, while the proposed self-supervised approach is explicitly designed to model brain aging in the latent space, the resulting representations can potentially be used to improve the accuracy of other state-of-the-art methods developed for different tasks, such as Graph Convolution Network modeling relationships between regions (Nguyen et al., 2021) and auxiliary information from other modalities (Shen et al., 2021). Finally, visualizing the fine-tuned latent space of this experiment (see Supplemental Figure S3) revealed a manifold stratified according to the Mini Mental State Exam (MMSE) (Balsis et al., 2015).
Table 5.
Comparison of the proposed method with other traditional methods and deep-learningbased methods in sMCI/pMCI classification on ADNI dataset.
| Method | Type | Modalities | sMCI/pMCI | BACC |
|---|---|---|---|---|
| Cross-sectional | ||||
| Liu et al. (2018) | D | MRI | 465/205 | 62.2 |
| Zu et al. (2016) | N | MRI, PET | 56/43 | 69.0 |
| Suk et al. (2014) | N+D | MRI | 128/76 | 63.8 |
| Lin et al. (2018) | D | MRI | 100/164 | 73.0* |
| Huang et al. (2019) | D | MRI, PET | 441/326 | 76.9 |
| Zhou et al. (2019a) | N | MRI, PET, SNP | 205/157 | 74.3* |
| Zhou et al. (2019b) | N | MRI, PET | 114/71 | 78.3 |
| Zeng et al. (2021) | D | MRI, clinical measures | 82/95 | 87.8* |
| Nguyen et al. (2021) | D | MRI | 129/171 | 74.0 |
| Yuan et al. (2021) | N | MRI, SNP | 115/113 | 82.4 |
| Shen et al. (2021) | N | MRI | 59/55 | 65.7 |
| Longitudinal | ||||
| Gray et al. (2012) | N | MRI, PET | 64/53 | 62.7 |
| Cui and Liu (2019) | D | MRI | 236/167 | 71.7 |
| Platero and Tobar (2020) | N | MRI, clinical measures | 215/206 | 77.1 |
| Ours | D | MRI | 193/135 | 73.5 |
‘D’ denotes deep-learning methods, and ‘N’ denotes non-deep-learning methods.
Refers to ACC scores, i.e., classification accuracy not accounting for imbalance between cohort sizes. The proposed method achieved the second-highest accuracy among all methods that were solely based on structural MRI.
5.3. Influence of alcohol on adolescent microstructural brain development
On the NCANDA data set, MoCo (Fig. 6(a)) again failed to capture brain aging (a.k.a. brain development), while LNE disentangled a brain development direction along the 1st PCA component (Fig. 6(b)). When age-matching the visits of no-to-low with moderate-to-heavy alcohol drinkers (which were generally older than the no-to-low drinkers), the moderate-to-heavy drinkers had a significant shorter progression trajectory (, t-test, see also Fig. 6(c)), which aligns with the finding that alcohol consumption during adolescence delays micro-structural brain development (Bava and Tapert, 2010; Zhao et al., 2021b). This qualitative assessment is also supported by the accuracy scores reported in Table 6, where the frozen encoder based on our method achieved a significantly (, DeLong’s test) higher balanced accuracy (i.e., 63.7%), higher AUC (i.e., 66.1), and higher F1 (i.e., 62.5) than LSSL (), the second-best method. The fine-tuned encoder based on LNE was also significantly more accurate , than any other method (, DeLong’s test).
Fig. 6.
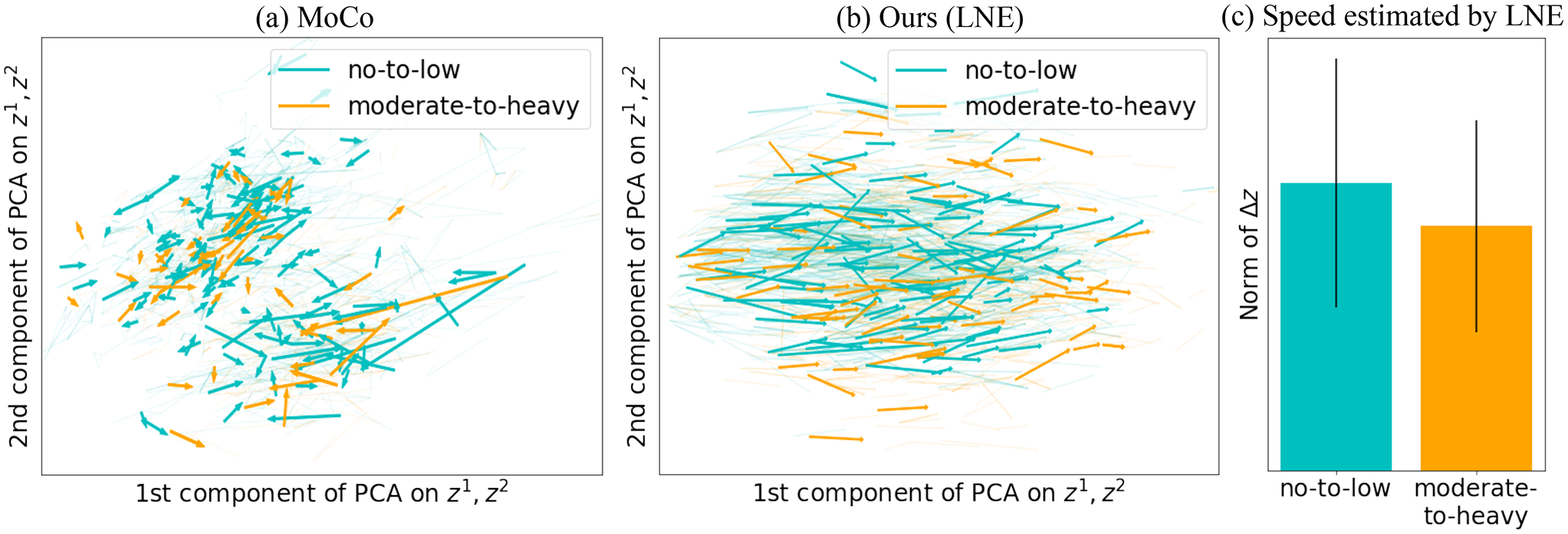
Experiments on NCANDA: Latent space of (a) MoCo (He et al., 2020) and (b) the proposed LNE projected into 2D PCA space of and . Arrows represent and are color-coded by the label of . (c) Boxplot of the norm the speed of aging (i.e., ) for the two groups as encoded by LNE.
Table 6.
Classification accuracy for no-to-low vs. moderate-to-heavy drinkers (NCANDA data).
| Methods | No-to-low vs. moderate-to-heavy | |||||
|---|---|---|---|---|---|---|
| Frozen | Fine-tuned | |||||
| BACC | AUC | F1 | BACC | AUC | F1 | |
| No pretrain | – | – | – | 69.3 | 71.8 | 69.2 |
| AE | 58.9 | 60.2 | 59.5 | 69.8 | 72.2 | 69.6 |
| VAE (Kingma and Welling, 2013) | 56.7 | 58.2 | 57.4 | 66.9 | 68.4 | 67.3 |
| SimCLR (Chen et al., 2020) | 60.2 | 62.8 | 60.1 | 70.2 | 73.1 | 69.7 |
| MoCo (He et al., 2020) | 61.4 | 63.9 | 61.3 | 70.6 | 73.2 | 69.8 |
| BYOL (Grill et al., 2020) | 60.4 | 62.7 | 60.2 | 70.3 | 73.1 | 70.0 |
| LSSL (Zhao et al., 2021a) | 62.1 | 64.3 | 62.2 | 70.4 | 73.2 | 70.6 |
| LNE | 63.7 | 66.1 | 62.5 | 71.2 | 74.0 | 70.5 |
The highest accuracy scores are in bold. The classifier based on the LNE encoding was significantly more accurate than the alternative methods for both frozen and fine-tuned encoder (, DeLong’s test).
5.4. Ablation study
We quantitatively assessed the contribution of the mini-batch sampling strategy (SS) and the age-consistent neighborhood mapping by recording the balanced accuracy and the quality of the neighborhoods on all four downstream tasks based on frozen encoders. For ADNI, we confined computing the neighborhood quality to the two cohorts specific to the downstream tasks. As shown in (Table 7), adding both SS and the age-consistent neighborhood mapping (ProtoNCE) obtained the best scores in three settings compared to omitting either component, while omitting both components (LNE*) resulted in the worst scores in all four settings. Regarding the neighborhood quality metrics, including either component on LNE* led to significant improvement (, t-test), and adding both achieved the best neighborhood quality. Moreover, we quantitatively evaluated the effect of the number of clusters used in the k-means algorithm (Table 8). Our default setting is , where is the number of subjects. Comparing with smaller number of clusters (more samples in each cluster), the default setting achieved higher or similar BACC, and the quality of the neighborhoods was higher on the two classification tasks performed on ADNI based on frozen encoders.
Table 7.
Ablation studies on models pre-trained representations and downstream tasks with frozen encoder.
| Methods | Age prediction | NC vs. AD | sMCI vs. pMCI | no-to-low vs. moderate-to-heavy drinkers | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | SC | RVRC | BACC | SC | RVRC | BACC | SC | RVRC | BACC | SC | RVRC | |
| LNE* (Ouyang et al., 2021) | 10.3 | 0.72† | 88.9† | 81.9† | 0.76† | 98.4† | 70.6† | 0.78† | 101.2† | 62.8† | 0.70† | 86.5† |
| LNE*+Proto | 10.1 | 0.74† | 91.2† | 82.0 | 0.79† | 102.3† | 70.8† | 0.80† | 103.7† | 63.2† | 0.72† | 89.3† |
| LNE*+SS | 10.0 | 0.79 | 99.6 | 82.2 | 0.83† | 104.1† | 70.9 | 0.85† | 106.8† | 63.4† | 0.78† | 100.5† |
| LNE | 10.0 | 0.81 | 103.2 | 82.1 | 0.87 | 106.5 | 71.1 | 0.88 | 108.2 | 63.7 | 0.81 | 102.3 |
Silhouette Coefficient (SC) and revised Variation Ratio Criterion (RVRC) were computed on the pre-trained representations to evaluate the quality of the neighborhood. +Proto means adding the age-consistent neighborhood regularization to LNE*, and +SS denotes the mini-batch sampling strategy.
Significant lower scores compared to LNE, which includes both Proto and SS.
Table 8.
Ablation studies on the number of clusters used in k-means clustering.
| Number of clusters | NC vs. AD | sMCI vs. pMCI | ||||
|---|---|---|---|---|---|---|
| N km | BACC | SC | RVRC | BACC | SC | RVRC |
| {N/20,N/40,N/80} | 81.8† | 0.77† | 102.1† | 70.7† | 0.78† | 103.1† |
| {N/10,N/20,N/40} | 82.2 | 0.82† | 104.2† | 70.8† | 0.84† | 105.8† |
| {N/5,N/10,N/20} | 82.1 | 0.87 | 106.5 | 71.1 | 0.88 | 108.2 |
The highest scores are in bold. refers to the number of subjects, i.e., for NC vs. AD and for sMCI vs. pMCI.
Significantly lower scores (, DeLong’s test for BACC, and paired two-tailed t-test for SC and RVRC) than the default setting, i.e., .
5.5. Computational costs
Compared to existing self-supervised methods (e.g. SimCLR (Chen et al., 2020), MoCo (He et al., 2020), LSSL (Zhao et al., 2021a)), the extra computational cost comes from k-means clustering taking around 2 min for each epoch on ADNI. The computational cost of the other components of our approach is similar to SimCLR and MoCo (i.e., the computational cost of their NCE loss is similar to the proposed ProtoNCE loss) or negligible, i.e., mini-batch sampling and performing operations on matrices of the dimension of the batch size to derive progression-consistent neighborhoods.
5.6. Limitations
LNE only explicitly models brain aging, while other time-dependent factors are simplified to accelerating aging (e.g., AD) or decelerating aging (e.g., effect of alcohol consumption in adolescents). Another simplification is the independence between brain aging and other static factors, such as sex. On the SRI dataset, this assumption was supported by a post-hoc analysis that revealed that the speed of brain aging (the length of ) was not significantly different (, t-test) between the sexes.
Moreover, the age-consistent neighborhood was built based on the clusters formed by the k-means algorithm, thus the number of clusters needs to be defined a priori, which increases the complexity of the hyperparameter tuning. In addition, k-means is initially applied to the representations resulting from randomly initialized model weights. This could potentially lead to instability at the beginning of the training. However, we found that the training of the model first focuses on minimizing the reconstruction and progression loss. The optimization minimizes the ProtoNCE loss (that is based on k-means clusters) in later iterations when the latent space is more informative as it is stratified by brain age.
Finally, our model generated progression-consistent neighborhoods via an encoding that ensured that longitudinal MRIs with similar brain ages also had similar progression trajectories. However, the brain of an old healthy subject might be of similar brain age to a younger subject diagnosed with AD while their progression trajectories might not be similar. One possible way to model the different progression patterns for brains with similar brain age is by jointly considering the progression speed and representation in defining progression-consistent neighborhoods.
6. Conclusion
In this work, we proposed a self-supervised representation learning framework that derives a latent space explicitly modeling brain aging. With the age-consistent neighborhood, brain MRIs of similar brain ages are mapped in close proximity to each other. By modeling progression-consistent neighborhoods, the resulting encoding yielded a smooth vector field in the latent space while maintaining a globally consistent progression trajectory that represented brain aging. The novel mini-batch sampling strategy encouraged the progression-consistent neighborhood on the mini-batch to approximate its construction with respect to the whole data set. On the macro-structural SRI data, the latent space was stratified by age (Fig. 3), which illustrated the ability of our approach to capture the progression of healthy aging (in that cohort). It also successfully modeled the accelerated aging effect caused by cognitive impairment as captured by the T1w MRI acquired by ADNI data, and the decelerated micro structural brain development in NCANDA adolescents induced by alcohol drinking. The informative representations lead to better chronological age prediction (SRI), and better capability of differentiating diagnosis groups (ADNI) and alcohol drinking levels (NCANDA) compared to other self-supervised methods. These results suggested that the proposed LNE method is superior to existing self-supervised methods for modeling brain aging. The learned latent space is stratified by brain age and the trajectory represents the speed of brain aging, which enables LNE to be used for detecting the effect of diseases and substances that cause brain aging to become abnormal.
Supplementary Material
Acknowledgments
This work was partly supported by funding from the National Institute of Health (NIH; MH113406, AA021697, AA017347, AA010723, AA005965, and AA028840) and by the Stanford HAI Google Cloud Credit. The collection and distribution of the NCANDA data were supported by National Institute of Health, United States of America funding AA021697, AA021695, AA021692, AA021696, AA021681, AA021690, and AA02169.
Footnotes
Declaration of competing interest
The authors had no financial interests/personal relationships which may be considered as potential competing interests.
Appendix A. Supplementary data
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.media.2022.102571.
Data availability
The authors do not have permission to share data.
References
- Balsis S, Benge JF, Lowe DA, Geraci L, Doody RS, 2015. How do scores on the ADAS-Cog, MMSE, and CDR-SOB correspond? Clin. Neuropsychol 29 (7), 1002–1009. [DOI] [PubMed] [Google Scholar]
- Bava S, Tapert SF, 2010. Adolescent brain development and the risk for alcohol and other drug problems. Neuropsychol. Rev 20 (4), 398–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal-Rusiel JL, Greve DN, Reuter M, Fischl B, Sabuncu MR, 2013a. Statistical analysis of longitudinal neuroimage data with linear mixed effects models. NeuroImage 66, 249–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal-Rusiel JL, Reuter M, Greve DN, Fischl B, Sabuncu MR, 2013b. Spatiotemporal linear mixed effects modeling for the mass-univariate analysis of longitudinal neuroimage data. NeuroImage 81, 358–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodersen KH, Ong CS, Stephan KE, Buhmann JM, 2010. The balanced accuracy and its posterior distribution. In: 20th International Conference on Pattern Recognition pp. 3121–3124. [Google Scholar]
- Burgess CP, et al. , 2018. Understanding disentangling in β-VAE. arXiv preprint arXiv:1804.03599 [Google Scholar]
- Caliński T, Harabasz J, 1974. A dendrite method for cluster analysis. Comm. Statist. Theory Methods 3 (1), 1–27. [Google Scholar]
- Carass A, et al. , 2017. Longitudinal multiple sclerosis lesion segmentation: resource and challenge. NeuroImage 148, 77–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caron M, Misra I, Mairal J, Goyal P, Bojanowski P, Joulin A, 2020. Unsupervised learning of visual features by contrasting cluster assignments. Adv. Neural Inf. Process. Syst 33, 9912–9924. [Google Scholar]
- Chen T, Kornblith S, Norouzi M, Hinton G, 2020. A simple framework for contrastive learning of visual representations. In: International Conference on Machine Learning pp. 1597–1607. [Google Scholar]
- Couronné R, Vernhet P, Durrleman S, 2021. Longitudinal self-supervision to disentangle inter-patient variability from disease progression. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science, vol. 12902. pp. 231–241. [Google Scholar]
- Cui R, Liu M, 2019. RNN-based longitudinal analysis for diagnosis of Alzheimer’s disease. Comput. Med. Imaging Graph 73, 1–10. [DOI] [PubMed] [Google Scholar]
- Dong C, Loy CC, He K, Tang X, 2014. Learning a deep convolutional network for image super-resolution. In: European Conference on Computer Vision pp. 184–199. [Google Scholar]
- Dufumier B, et al. , 2021. Contrastive learning with continuous proxy meta-data for 3D MRI classification. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science, vol. 12902. pp. 58–68. [Google Scholar]
- Ellwood-Lowe ME, Humphreys KL, Ordaz SJ, Camacho MC, Sacchet MD, Gotlib IH, 2018. Time-varying effects of income on hippocampal volume trajectories in adolescent girls. Dev. Cognit. Neurosci 30, 41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fawcett T, 2006. An introduction to ROC analysis. Pattern Recognit. Lett 27 (8), 861–874. [Google Scholar]
- Fjell AM, et al. , 2009. One-year brain atrophy evident in healthy aging. J. Neurosci 29 (48), 15223–15231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortuin V, Hüser M, Locatello F, Strathmann H, Rätsch G, 2019. SOM-VAE: Interpretable discrete representation learning on time series. In: International Conference on Learning Representations [Google Scholar]
- Frings L, Mader I, Landwehrmeyer BG, Weiller C, Hüll M, Huppertz H-J, 2012. Quantifying change in individual subjects affected by frontotemporal lobar degeneration using automated longitudinal MRI volumetry. Hum. Brain Mapping 33 (7), 1526–1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao R, et al. , 2019. Distanced LSTM: Time-distanced gates in long short-term memory models for lung cancer detection. In: International Workshop on Machine Learning in Medical Imaging, Lecture Notes in Computer Science, vol. 11861. pp. 310–318. [PMC free article] [PubMed] [Google Scholar]
- Garcia TP, Marder K, 2017. Statistical approaches to longitudinal data analysis in neurodegenerative diseases: Huntington’s disease as a model. Curr. Neurol. Neurosci. Rep 17 (2), 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghazi MM, et al. , 2019. Training recurrent neural networks robust to incomplete data: Application to Alzheimer’s disease progression modeling. Med. Image Anal 53, 39–46 [DOI] [PubMed] [Google Scholar]
- Gray KR, Wolz R, Heckemann RA, Aljabar P, Hammers A, Rueckert D, 2012. Multi-region analysis of longitudinal FDG-PET for the classification of Alzheimer’s disease. NeuroImage 60(1), 221–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill J-B, et al. , 2020. Bootstrap your own latent-a new approach to self-supervised learning. Adv. Neural Inf. Process. Syst 33, 21271–21284. [Google Scholar]
- Guo X, Liu X, Zhu E, Yin J, 2017. Deep clustering with convolutional autoencoders. In: International Conference on Neural Information Processing pp. 373–382. [Google Scholar]
- Gupta A, Johnson J, Fei-Fei L, Savarese S, Alahi A, 2018. Social GAN: Socially acceptable trajectories with generative adversarial networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition pp. 2255–2264. [Google Scholar]
- Habeck C, Stern Y, 2010. Multivariate data analysis for neuroimaging data: overview and application to Alzheimer’s disease. Cell Biochem. Biophys 58 (2), 53–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harwood B, Kumar BG V, Carneiro G, Reid I, Drummond T, 2017. Smart mining for deep metric learning. In: Proceedings of the IEEE International Conference on Computer Vision pp. 2821–2829. [Google Scholar]
- Hassani K, Khasahmadi AH, 2020. Contrastive multi-view representation learning on graphs. In: International Conference on Machine Learning pp. 4116–4126. [Google Scholar]
- Haykin S, 2004. A comprehensive foundation. Neural Netw 2 (2004), 41. [Google Scholar]
- He K, Fan H, Wu Y, Xie S, Girshick R, 2020. Momentum contrast for unsupervised visual representation learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition pp. 9729–9738. [Google Scholar]
- Huang Y, Xu J, Zhou Y, Tong T, Zhuang X, 2019. Diagnosis of Alzheimer’s disease via multi-modality 3D convolutional neural network. Front. Neurosci 13, 509–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR Jr., et al. , 2008. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI methods. J. Magn. Resonance Imaging 27 (4), 685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Mnih A, 2018. Disentangling by factorising. In: International Conference on Machine Learning pp. 2649–2658. [Google Scholar]
- Kingma DP, Ba J, 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 [Google Scholar]
- Kingma DP, Welling M, 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114 [Google Scholar]
- Klicpera J, Weißenberger S, Günnemann S, 2019. Diffusion improves graph learning. Adv. Neural Inf. Process. Syst 32, 13366–13378. [Google Scholar]
- Kolesnikov A, Zhai X, Beyer L, 2019. Revisiting self-supervised visual representation learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition pp. 1920–1929. [Google Scholar]
- Li J, Zhou P, Xiong C, Hoi S, 2020. Prototypical contrastive learning of unsupervised representations. In: International Conference on Learning Representations [Google Scholar]
- Lin W, et al. , 2018. Convolutional neural networks-based MRI image analysis for the Alzheimer’s disease prediction from mild cognitive impairment. Front. Neurosci 12,777–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton ZC, Kale DC, Elkan C, Wetzel R, 2015. Learning to diagnose with LSTM recurrent neural networks. arXiv preprint arXiv:1511.03677 [Google Scholar]
- Liu M, Zhang J, Adeli E, Shen D, 2018. Landmark-based deep multi-instance learning for brain disease diagnosis. Med. Image Anal 43, 157–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louis M, Couronné R, Koval I, Charlier B, Durrleman S, 2019. Riemannian geometry learning for disease progression modelling. In: International Conference on Information Processing in Medical Imaging, Lecture Notes in Computer Science, vol. 11492. pp. 542–553. [Google Scholar]
- Maas AL, et al. , 2013. Rectifier nonlinearities improve neural network acoustic models. Int. Conf. Mach. Learn 30 (1), 3–8. [Google Scholar]
- Van der Maaten L, Hinton G, 2008. Visualizing data using t-SNE. J. Mach. Learn. Res 9 (11). [Google Scholar]
- Manduchi L, Hüser M, Faltys M, Vogt J, Rätsch G, Fortuin V, 2021. T-DPSOM: An interpretable clustering method for unsupervised learning of patient health states. In: Proceedings of the Conference on Health, Inference, and Learning pp. 236–245. [Google Scholar]
- Manduchi L, Hüser M, Vogt J, Rätsch G, Fortuin V, 2019. DPSOM: Deep probabilistic clustering with self-organizing maps. arXiv preprint arXiv:1910.01590 [Google Scholar]
- Misra I, Zitnick CL, Hebert M, 2016. Shuffle and learn: unsupervised learning using temporal order verification. In: European Conference on Computer Vision pp. 527–544. [Google Scholar]
- Mueller SG, et al. , 2005. The Alzheimer’s Disease Neuroimaging Initiative. Neuroimaging Clin 15 (4), 869–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerke NJ, et al. , 1991. A note on a general definition of the coefficient of determination. Biometrika 78 (3), 691–692. [Google Scholar]
- Nguyen H-D, Clément M, Mansencal B, Coupé P, 2021. Deep grading based on collective artificial intelligence for AD diagnosis and prognosis. In: Interpretability of Machine Intelligence in Medical Image Computing, and Topological Data Analysis and Its Applications for Medical Data pp. 24–33. [Google Scholar]
- Noroozi M, Favaro P, 2016. Unsupervised learning of visual representations by solving jigsaw puzzles. In: European Conference on Computer Vision pp. 69–84. [Google Scholar]
- van den Oord A, Li Y, Vinyals O, 2018. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748 [Google Scholar]
- Ouyang J, et al. , 2020. Longitudinal pooling & consistency regularization to model disease progression from MRIs. IEEE J. Biomed. Health Inf 25 (6), 2082–2092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang J, et al. , 2021. Self-supervised longitudinal neighbourhood embedding. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science, vol. 12902. pp. 80–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platero C, Tobar MC, 2020. Predicting Alzheimer’s conversion in mild cognitive impairment patients using longitudinal neuroimaging and clinical markers. Brain Imaging Behav 1–11. [DOI] [PubMed] [Google Scholar]
- Pohl KM, et al. , 2016b. Harmonizing DTI measurements across scanners to examine the development of white matter microstructure in 803 adolescents of the NCANDA study. NeuroImage 130, 194–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl KM, et al. , 2022a. The ‘NCANDA_PUBLIC_6Y_STRUCTURAL_V01’ data release of the national consortium on alcohol and NeuroDevelopment in adolescence (NCANDA). Sage Bionetw. Synapse 10.7303/syn32773308. [DOI] [Google Scholar]
- Pohl KM, et al. , 2022b. The ‘NCANDA_PUBLIC_6Y_DIFFUSION_V02’ data release of the national consortium on alcohol and NeuroDevelopment in adolescence (NCANDA). Sage Bionetw. Synapse 10.7303/syn32640372. [DOI] [Google Scholar]
- Pohl KM, et al. , 2022c. The ‘NCANDA_PUBLIC_6Y_REDCAP_V04’ data release of the national consortium on alcohol and NeuroDevelopment in adolescence (NCANDA). Sage Bionetw. Synapse 10.7303/syn26951066. [DOI] [Google Scholar]
- Poulet P-E, Durrleman S, 2021. Mixture modeling for identifying subtypes in disease course mapping. In: International Conference on Information Processing in Medical Imaging, Lecture Notes in Computer Science, vol. 12729. pp. 571–582. [Google Scholar]
- Rhodius-Meester HF, et al. , 2017. MRI visual ratings of brain atrophy and white matter hyperintensities across the spectrum of cognitive decline are differently affected by age and diagnosis. Front. Aging Neurosci 9, 117–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseeuw PJ, 1987. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math 20, 53–65. [Google Scholar]
- Sabokrou M, Khalooei M, Adeli E, 2019. Self-supervised representation learning via neighborhood-relational encoding. In: Proceedings of the IEEE/CVF International Conference on Computer Vision pp. 8010–8019. [Google Scholar]
- Sabuncu MR, et al. , 2011. The dynamics of cortical and hippocampal atrophy in Alzheimer disease. Arch. Neurol 68 (8), 1040–1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadeghian A, Kosaraju V, Sadeghian A, Hirose N, Rezatofighi H, Savarese S, 2019. Sophie: An attentive GAN for predicting paths compliant to social and physical constraints. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition pp. 1349–1358. [Google Scholar]
- Santeramo R, Withey S, Montana G, 2018. Longitudinal detection of radiological abnormalities with time-modulated LSTM. In: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Lecture Notes in Computer Science, vol. 11045. pp. 326–333. [Google Scholar]
- Sasaki Y, et al. , 2007. The truth of the F-measure. Teach. Tutor. Mater 1 (5), 1–5. [Google Scholar]
- Shen HT, et al. , 2021. Heterogeneous data fusion for predicting mild cognitive impairment conversion. Inf. Fusion 66, 54–63 [Google Scholar]
- Suk H-I, Lee S-W, Shen D, 2014. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage 101, 569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan X, Shiyko MP, Li R, Li Y, Dierker L, 2012. A time-varying effect model for intensive longitudinal data. Psychol. Methods 17 (1), 61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian Y, Krishnan D, Isola P, 2020. Contrastive multiview coding. In: European Conference on Computer Vision pp. 776–794. [Google Scholar]
- Toepper M, 2017. Dissociating normal aging from Alzheimer’s disease: A view from cognitive neuroscience. J. Alzheimer’s Dis 57 (2), 331–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Gupta A, 2015. Unsupervised learning of visual representations using videos. In: Proceedings of the IEEE International Conference on Computer Vision pp. 2794–2802. [Google Scholar]
- Wang T, Yue Z, Huang J, Sun Q, Zhang H, 2021. Self-supervised learning disentangled group representation as feature. Adv. Neural Inf. Process. Syst 34, 18225–18240. [Google Scholar]
- Wei L, et al. , 2020. Can semantic labels assist self-supervised visual representation learning? arXiv preprint arXiv:2011.08621 [Google Scholar]
- Wu C-Y, Manmatha R, Smola AJ, Krahenbuhl P, 2017. Sampling matters in deep embedding learning. In: Proceedings of the IEEE International Conference on Computer Vision pp. 2840–2848. [Google Scholar]
- Xie J, Girshick R, Farhadi A, 2016. Unsupervised deep embedding for clustering analysis. In: International Conference on Machine Learning pp. 478–487. [Google Scholar]
- Yuan S, Li H, Wu J, Sun X, 2021. Classification of mild cognitive impairment with multimodal data using both labeled and unlabeled samples. IEEE/ACM Trans. Comput. Biol. Bioinform 18 (6), 2281–2290. [DOI] [PubMed] [Google Scholar]
- Zeng N, Li H, Peng Y, 2021. A new deep belief network-based multi-task learning for diagnosis of Alzheimer’s disease. Neural Comput. Appl 1–12. [Google Scholar]
- Zhang R, Isola P, Efros AA, 2016. Colorful image colorization. In: European Conference on Computer Vision pp. 649–666 [Google Scholar]
- Zhao Q, Adeli E, Honnorat N, Leng T, Pohl KM, 2019a. Variational autoencoder for regression: Application to brain aging analysis. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science, vol. 11765. pp. 823–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao H, Jiang L, Fu C-W, Jia J, 2019b. Pointweb: Enhancing local neighborhood features for point cloud processing. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition pp. 5565–5573. [Google Scholar]
- Zhao Q, Liu Z, Adeli E, Pohl KM, 2021a. Longitudinal self-supervised learning. Med. Image Anal 71, 102051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Q, et al. , 2021b. Association of heavy drinking with deviant fiber tract development in frontal brain systems in adolescents. JAMA Psychiatry 78 (4), 407–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Liu M, Thung K-H, Shen D, 2019a. Latent representation learning for Alzheimer’s disease diagnosis with incomplete multi-modality neuroimaging and genetic data. IEEE Trans. Med. Imaging 38 (10), 2411–2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, et al. , 2019b. Deep multi-modal latent representation learning for automated dementia diagnosis. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science, vol. 11767. pp. 629–638. [Google Scholar]
- Zu C, et al. , 2016. Label-aligned multi-task feature learning for multimodal classification of Alzheimer’s disease and mild cognitive impairment. Brain Imaging Behav 10 (4), 1148–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors do not have permission to share data.


