Abstract
Red blood cell (RBC)-hitchhiking, in which different nanocarriers (NCs) shuttled on the erythrocyte membrane and disassociated from RBCs to the first organ downstream of the intravenous injection spot, has recently been introduced as a solution to enhance target site uptake. Several experimental studies have already approved that cellular hitchhiking onto RBC membrane can improve the delivery of a wide range of NCs in mice, pigs, and ex-vivo human lungs. In these studies, the impact of NC size, NC surface chemistry, and shear rate on the delivery process and biodistribution have been widely explored. To shed light on the underlying physics in this type of drug delivery system, we present a computational platform in the context of lattice Boltzmann method, spring connected network, and frictional immersed boundary method. The proposed algorithm simulates nanoparticles (NPs) dislodgment from RBC surface in shear flow and biomimetic microfluidic channels. The numerical simulations are performed for various NP sizes and RBC-NP adhesion strengths. In shear flow, NP detachment increases with increasing the shear rate. RBC-RBC interaction can also significantly boost shear-induced particle detachment. Larger NPs have a higher propensity to be disconnected from the RBC surface. The results illustrate that changing the interaction between NP and RBCs can control the desorption process. All the findings agree with in-vivo and in-vitro experimental observations. We believe the proposed setup can be exploited as a predictive tool to estimate optimum parameters in NP-bounded RBCs for better targeting procedures in tissue microvasculature.
Keywords: Red Blood Cell, Nanoparticles, Cellular Hitchhiking, Drug Delivery, Numerical Modeling
1. Introduction
Nanoparticle (NP)-based drug delivery systems (DDSs) have been extensively explored to promote the existing therapeutic procedures for cancer and other diseases [1]-[3]. Drug loading into NPs owns significant merits over free drug injection including precise accumulation and prolonged delivery. However, NPs performance is commonly hindered by poor pharmacokinetics (PK) of the curative agent [4], [5]. NPs rapid clearance by the mononuclear phagocytic system (MPS), primarily available in the liver and spleen which are part of the reticuloendothelial system (RES) [6], diminishes NP concentration in different target organs such as heart, lung and brain [7]. Therefore, multiple approaches have been devised to improve drug bioavailability within the bloodstream and in target organs. The most common strategy is to graft polyethylene glycol (PEG) on the NP surface to extend circulation time and reduce MPS uptake [8]-[10]. However, it has been shown that pegylated NPs can stimulate the immune system and lose effectiveness following continual injections [11]. Furthermore, the surface modification is effective only for small particles (up to 200 nm), which confines the medicine delivery capacity [12], [13]. Recently, the idea of coupling of drugs onto the red blood cells (RBCs) surface has generated favorable routes for safe and widely sound improvement of nanomedicine to circumvent mentioned challenges [5], [7], [12]-[14].
Erythrocytes or RBCs, which are anucleate biconcave discs with a diameter of ~ 8 μm, thickness ~ 2 μm and membrane surface area ~ 160 μm2 render unique and stunning transporter for drug delivery [15]. There are 5 million RBCs in one microliter of human blood and the whole number of RBCs in the human body reaches up to 30 trillion [15]. Healthy human RBCs longevity is 100–120 days. They can travel nearly 250 km through the cardiovascular system and act as oxygen carriers. RBCs bioavailability, biocompatibility, access to most organs, and unique lifespan caused researchers to test the nanomedicine coupling possibility to the RBC membranes. The idea of exploiting RBCs as drug delivery vehicles was inspired by observing the way invented by specific bacteria, for example, hemobartonella, that attach to erythrocyte membrane and sustain in blood for several weeks [12]. Adsorption of NPs or other nanocarriers (NCs) to the erythrocyte membrane and injection intravenously (IV) and intra-arterially (IA) using catheters is called (RBC)-hitchhiking (RH) [7]. This strategy exhibits the employment of a synergistic combination of "nano-micro-macro": nanoscale drug carriers + micro-scale RBCs + macro-scale IV/IA catheters.
In 2004, Chambers and Mitragotri [12] anchored polymeric NPs with a diameter ranging from 100 nm to 1 μm to the RBCs surface. They observed that the circulation time of NPs larger than 450 nm would dramatically increase after adsorption to the RBC membrane. The in-vivo experimental results also revealed that larger NPs could be detached and cleared by RES more quickly than smaller NPs. It was also shown that NP numbers could influence detachment kinetics because NPs are removed from RBCs with a higher number more rapidly. They hypothesized that the adhesion strength between NP and RBCs is an important player in the NP detachment. It is worth mentioning modified RBCs remained in the blood flow after the detachment process. As the underlying physics in NP removal from RBCs was still unclear, in 2007, Chambers and Mitragotri [13] conducted another study to disclose the effects of RBC-RBC interaction, shear rate, and NPs surface chemistry on the NPs biodistribution and clearance mechanisms. Their in-vitro results illustrated that the NPs detachment occurs in a shear-dependent manner, and RBC-RBC collision can enhance the detachment process. NPs surface chemistry also changed the clearance time and detachment process. Anselmo et al. [4] used noncovalent bounding of NPs to RBCs to test NP effectivity in lung microvasculature. Their results showed that RBC-laden NPs increased lung/liver and lung/spleen NPs deposition by more than 15-fold and 10-fold, respectively. Brenner et al. [7] experimentally showed that RH injection increased NCs uptake in mice, pigs, and ex vivo human lungs without damaging RBC. Pan et al. [16] investigated the effect of NP and RBC on each other due to the attachment procedure. The research demonstrated that RBCs could change the NP PK such that NP clearance is deaccelerated while NP ttransfer to the vascular cells is facilitated. On the other hand, NP adsorption can lead to RBC damage and agglutination. A high-throughput microfluidic approach to capture loaded RBC indentation due to interactions with NPs was also invented by Dias et al. [17]. Their setup captured RBC morphology change due to attachment and detachment of different NPs. Very recently, chemokine-encapsulating was anchored to the RBCs to treat lung metastasis [18]. The results revealed that RH technique immunotherapy could provide a general and impressive strategy for cancer vaccination. More details about using RBCs as natural drug carriers can be found in [5], [7], [14], [15], [19], [20].
Despite several successful experiments, the NP detachment mechanism from the erythrocyte membrane is not well-understood. This phenomenon results from an interplay of transport, hydrodynamic force, and multivalent interactions with targeted organs. It is very challenging to understand and model these phenomena experimentally in vivo because of NPs small size, and the complexity of the detachment procedure in a highly vascular environment. In addition, an accurate quantitative measuring of the PK of NPs and carrier RBC in circulation in vivo is a challenge. Multi-isotope tracing of carrier RBC labeled with 51Chromium, and NP labeled with 125Iodine or 111In isotope represents a high-fidelity methodology, but its use is limited, whereas tracing of fluorescently labeled NPs and RBCs is of variable accuracy and prone artifacts.
Numerical simulations have been used to better understand transportation, margination, and adhesion of different NPs in blood circulation. For example, Tan et al. [21] developed a novel three-dimensional Immersed Finite Element Method (IFEM) to model NP transport with RBCs in microcirculation. In this study, the movement and adhesion of NPs were simulated via Brownian adhesion dynamics. The accumulation of NPs adjacent to the vessel walls was found non-uniform. The RBCs tumbling in the vessel center induced higher NP dispersion. Recently, they implemented their approach by coupling of Parallel Lattice Boltzmann Solver (Palabos) and Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [22]. Margination of micro- and nano-particles in blood flow was simulated using dissipative particle dynamics (DPD) and spring connected network (SN) by Muller et al. [23]. They concluded that micron-sized ellipsoidal particles were suitable for drug delivery compared to sub-micron spherical particles. Front-tracking and immersed boundary method (IBM) was also used to quantify the effect of the microparticle shape on the margination and adhesion dynamics [24]. Margination of deformable particles in blood flow was performed by Muller et al. [25] using DPD. They concluded that deformable particles have less margination tendency than rigid particles. In another study, LAMMPS package and DPD were used to simulate different particle localization towards the vessel wall [26]. The results confirmed that RBC presence enhances both margination and adhesion processes. Ye et al. [27]-[32] also developed a computational module in LAMMPS by resorting to the lattice Boltzmann method (LBM), IBM, and SN to model the dynamics of a wide range of particles in blood flow. Liu et al. [33], [34] devised a three-dimensional multiscale and multicomponent blood flow solver to capture the behavior of different particles with different shapes and sizes ranging from nano- to-microscale in tubular flows along with RBCs. Their results provided the dominance of RBC-enhanced shear-induced diffusivity (RESID) and Brownian diffusivity (BD) in different regions observed in confined blood flows.
In the current paper, we propose a computational platform in the context of LBM, SN, and IBM to model the NP dislodgment from RBCs in shear flow and biomimetic microfluidic channels. The remainder of the paper is organized as follows. In section 2, different elements of the numerical solver are described. In section 3, the numerical algorithm is validated by modeling an RBC deformation under tension, shear flow and inside a constricted microchannel. Section 4 presents the numerical results of NP detachment for different NP sizes, different NP-RBC adhesion strengths at different shear rates. In the last section, the parametric study is concluded.
2. Numerical Algorithm
In this paper, the numerical simulation is initiated by solving the flow field without RBCs and NPs as the warmup solution. The warmup solution is continued until the stable flow field inside the channel is achieved. The reason for using a warmup solution is to avoid getting suddenly unphysical changes on both RBC membrane and NPs surface due to un-converged flow field forces. In the main loop, the flow field is solved by an LBM solver. Flow field variables in terms of forces and velocities are coupled with SN on RBC and NP surfaces through a frictional-based IBM. Our model is implemented in the free, open-source package ESPResSo version 4.1.4 [35]. ESPResSo uses parallelization computations and can be used on desktop machines, clusters, and supercomputers with hundreds of CPUs. All the simulations in this study were performed on a workstation with a 3.2 GHz with 12 Intel Core-i7 CPUs and 16.0 GB RAM. ESPResSo has some modules to support GPU acceleration. In this package, C++ source codes are controlled by the scripting language Python. For modeling membranes, we used PyOIF [36]-[38] which provides validated computational models for cell flow modeling. The PyOIF module is integrated into the ESPResSo with some modifications and is available under the GNU General Public License terms. Like ESPResSo, PyOIF is combined C++ codes in the software core and Python scripting to control the core. The simulation works with a different set of units based on the Lattice–Boltzmann (LB) units. To convert physical units to LB ones, the following scales are taken into account for the time , length , and mass , respectively:
| (1) |
For example, in all the simulations, the time step is set to 0.1, equal to 10−7 sec. In the subsections below, different components of the numerical approach are explained in detail. The numerical results are visualized by ParaView version 5.8.0-RC1. We used GPU-accelerated version of our code and each simulation on our workstation took less than 30 minutes to complete. This indicates that the simulation of this problem in larger domains like complex vascular network with higher number of RBCs and NPs is possible using high performance computing.
2.1. Flow Solver
As it was mentioned earlier, LBM is here used as the flow solver. This method is extensively used in fluid mechanics and computational hemodynamics [36], [38], [39]. In this approach, the Boltzmann kinetic equation [40] is solved instead of the Navier-Stokes equations. The Boltzmann kinetic equation's unknown is the distribution function for fictitious particles. Macroscopic properties can also be computed after finding the distribution function. The lattice is made of cubic cells. The lattice is unalterable during the computational procedure. D3Q19 version of the LBM (three dimensions with 19 discrete velocities) is utilized in this paper. A structured grid with constant spacing is also constructed with a set of discretized velocity velocities, . The LBM dynamics in the presence of an external force involve streaming and collision steps can be written as follows [40]:
| (2) |
where is time step, relaxation time, is the equilibrium function related to macroscopic variables velocity and density. is the external force applied to the fluid. It should be mentioned that is also essential where the existence of the cell domain is replaced through a force density. Also, is:
| (3) |
is the lattice speed of sound. Macroscale density and velocity can be calculated as follows:
| (4) |
2.2. Spring Connected Network
SN model is widely used in the simulating of biological problems [36], [38], [41]. Both RBC and NP membranes are discretized to triangular meshes, as shown in Figure 1. There are different strategies to deliver the NC to the RBC membrane. However, NP attachment is probably due to van der Waals, electrostatic, hydrogen bonding, and hydrophobic forces between NPs and the RBCs [12]. However, NPs do not have a propensity to be bound to the particular site on the RBC membrane; images in [12] depict NPs adhere to the central dimple. Here, we hypothesize that all the NPs are located on the RBC center, and we do not consider the effect of NP location on the detachment process. In the SN approach, geometrical parameters such as mesh edge, mesh face, and the angle between adjacent faces are implemented in proper mathematical relations to model stretching, bending stiffness, and other cell characteristics. The nodal points on the membrane, which are called immersed boundary (IB) points, are moved by the Newton equation of motion as follows:
| (5) |
in which, is the coordinates vector of IB points. is the IB point's acting force comprises two terms: fluid forces and elastomechanical forces from membranes. The fluid-induced forces are described in the following sub-section, and the cell force field is explained here. It should be mentioned that we did not consider any random dynamics/motion for NPs or RBCs since the size of computational domain for all the problems is small. In other words, the RBCs and NPs doe does not have that much space and considering the random motions for NPs and RBCs will not change the results considerably. Hence, all the data were reported only based on one trajectory [21], [42].
Figure 1:
(a) RBCs carrying 450 nm and 1100 nm polystyrene NPs (b) NP model (c) a sample of NP-laden RBC model (NP diameter is equal to 1000 nm)
To capture the membrane properties, we use different moduli acting in the spring network. The first one is the stretching modulus. The stretching force is nonlinear and applied between two mesh points A, B symmetrically. This force for point A can be written as follows [36], [37]:
| (6) |
is the stretching coefficient, is the unit vector pointing from A towards B, stands for neo-Hookean nonlinearity. is the initial or relaxed length of mesh edge AB, whereas is the present edge AB length. is edge extension or compression. The second class of moduli is area constrains moduli. To implement these restrictions, we compute the surface variations of triangle ABC from resting condition . The area constrain is applied by assigning a shrinking/expanding force for every vertex [36], [37]:
| (7) |
where is the area coefficient, and is the unit vector emitting from the centroid of triangle ABC towards vertex A. The same calculations are employed for area forces on vertexes B and C. The area force should be very restrictive; therefore, a global area force is also applied to the cell [36], [37]:
| (8) |
As can be seen, the area force is divided into two parts: local and global parts . The third force is called the bending force. The source of this force is changing the angle between two neighboring triangles. Assuming as the resting angle between two adjacent triangles, the bending force can be related to angle deviation as below [36], [37]:
| (9) |
is the normal unit vector to the triangle ABC. The last force is the volume force to keep the whole volume constant. This force is also a global force. This force is related to triangle ABC and divided into three separate parts and applied at triangle vertices:
| (10) |
where is the volume coefficient. stands for volume change between the current state and initial state . is also the normal unit vector to the plane ABC pointing inside the cell. In the SN model, different moduli can be related to the macroscopic properties. Indeed, by comparing SN coefficients and physical properties, it can be shown that [36], [37]:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
where, , , , and are shear modulus, compression modulus, Young's modulus, Poisson's ratio, respectively. is the macroscopic bending modulus measured by micropipette aspiration. Since the RBC membrane is fluidic and exhibits resistance against shearing, in the SN model, the viscosity force should be considered as below [36], [37]:
| (16) |
where is the viscosity coefficient, L denotes the distance between points A and its neighboring points, and stands for time derivative. To model the RBC-RBC interaction, a weak depletion attractive and strong electrostatic repulsive forces at far and near distances is applied as follows [43]:
| (17) |
Here, is the distance between two RBC membrane points, is the equilibrium distance, and is the energy well depth. Also, determines the potential width. For , there is no interaction between RBCs and . An attractive Morse potential is also used to generate forces between NP-RBC and NP-wall. For these potentials, is set as 10 nm [21], [32], [42]. The distance between NPs and RBC is minimized such that the distance between all RBC points and all NP points is larger than and there is no overlap between them due to the surface curvature. The interaction force between different NPs and live cells was reported to be in the range of 20-1200 pN [44]. Since we have thousands of interactive pairs on RBC and NPs, the force magnitude should be estimated in the order of femtonewtons [45]. In our simulations, the maximum attractive force generated by Morse potential at the cutoff distance is set between 20-1200 fN for NP-RBC. For NP-wall, the cutoff distance is set as 10 nm [35]. value determines the maximum force at the cutoff distance [45]. for NP-RBC and NP-wall is changed to mimic the behavior of different NPs with RBC membrane and endothelial cells. A repulsive Lennard-Jones potential is used to describe the interaction NP-NP and avoid their overlap [21]:
| (18) |
is the equilibrium distance and is the potential energy strength. A constant force is applied to the LB points to drive the channel flow to create our desired average cell velocity. The details of this approach are available in [35]. To avoid the RBC collision with the channel walls, a repulsive potential called soft-sphere potential is applied between wall and RBC membrane points as follows [35]:
| (19) |
where is the inter-particle distance and is the potential energy. For , is equal to zero. In our simulation is sufficient to prevent the cell from colliding with the channel wall. The physical values and LB units for the parameters used in this paper along with corresponding references, in which these parameters within the same range have been used, are listed in Table 1.
Table 1:
The values for different parameters used in this study
| Parameter | Physical Value | LB Value | Ref |
|---|---|---|---|
| RBC diameter (D) | 8× 10−6m | 32.00 | [21], [41], [42], [46], [47] |
| RBC stretching coefficient | 6 × 10−6 Nm−1 | 0.0015 | [36], [37], [47], [48] |
| RBC local area constraint | 1 × 10−6 Nm−1 | 0.00025 | [36], [37], [47], [48] |
| RBC global area constraint | 5 × 10−4 Nm−1 | 0.125 | [36], [37], [47], [48] |
| RBC bending coefficient | 8 × 10−18 Nm | 0.002 | [36], [37], [47], [48] |
| RBC volume constraint | 9.0 × 10−5 Nm−2 | 0.056 | [36], [37], [47], [48] |
| RBC viscous constraint | 1.5 × 10−6 Nm−1s | 0.375 | [36], [37], [47], [48] |
| NP diameter (Dp) | 200-1000× 10−9m | 0.8-4 | [12], [13] |
| NP stretching coefficient | 1 × 10−3 Nm−1 | 0.25 | [47], [49] |
| NP local area constraint | 1 × 10−3 Nm−1 | 0.05 | [47], [49] |
| NP global area constraint | 4 × 10−3 Nm−1 | 1.00 | [47], [49] |
| NP bending coefficient | 1 × 10−14 Nm | 0.025 | [47], [49] |
| NP volume constraint | 1.6 × 10−4 Nm−2 | 0.625 | [47], [49] |
| NP viscous constraint | 0.00 Nm−1s | 0.00 | [47], [49] |
| Morse and LJ equilibrium distance | 0.01× 10−6m | 0.04 | [21], [32], [42] |
| Morse cutoff distance | 1.5× 10−6m | 6.00 | [21], [32], [42] |
| LJ cutoff distance | 0.01× 10−6m | 0.04 | [21], [32], [42] |
| Morse energy well width | 2×10−6 m−1 | 0.25 | [21], [32], [42] |
| LJ energy well depth | 10−15 Nm | 0.04 | [21], [42] |
| Fluid viscosity | 0.003 Pa. s | 0.033 | [46] |
| Fluid density | 1050 kgm−3 | 0.018 | [46] |
2.3. Fluid-Structure Interaction
In this paper, the interaction between fluid and IB points in the SN model is handled through dissipative or frictional coupling [40]. This approach works based on the drag flow applied on the RBC and NP mesh points. The drag force is comparable with the velocity difference between lattice points (u) and IB points as follows (v):
| (20) |
Here is a friction coefficient, and it is expressed in . It should be noticed that linear interpolation is utilized for calculating v in the cell points based on the neighboring lattice velocities. This technique naturally guarantees the no-slip conditions between fluid and membranes because it enforces minimal velocity difference between fluid and soft membranes. The prevalent friction coefficient role is to convey the drag force of the fluid onto the cell membrane and vice versa. does not depend on any physical quantity and is completely phenomenological. Hence, we should identify its proper value [48]. It was shown that the friction coefficient's fair value is a function of different parameters [48]. It has been shown that for a cell constructed of mesh points and with the surface area of S, the friction coefficient can be computed as follows:
| (21) |
Reference values can be found in [49]. These values also depend on fluid density and viscosity. For example, is equal to 1.82 for , , and . We assume that the inside and outside of the RBC is occupied with the same fluid (see Table 1 for the fluid properties). In the simulations, is the same for both NPs and RBC [47]. To have the equal for both membranes, they should have the same . For the coupling of fluid and cell, enters as a part of in Eq. (5). The coupling is mutual, so the opposite force is exerted on the fluid and enters Eq (2). It should be mentioned that, however determining proper values of the friction coefficient is challenging and depends on the fluid-cell model and other parameters, the described model has been successfully applied in several problems [36]-[38], [47]-[49]. Also, we intended to implement our algorithm in an open-source and parallelized package such that we can extend our simulations for modeling the real vasculature domain with larger number RBCs and NPs. ESPResSoMD provided us with such a platform in which the dissipative coupling is already implemented and used for modeling fluid-structure interaction rather than conventional IBM [37]. It should be mentioned, not considering the boundary mass, challenges in choosing proper coupling function and computational cost are some of the problems of conventional IBMs [49].
3. Validation
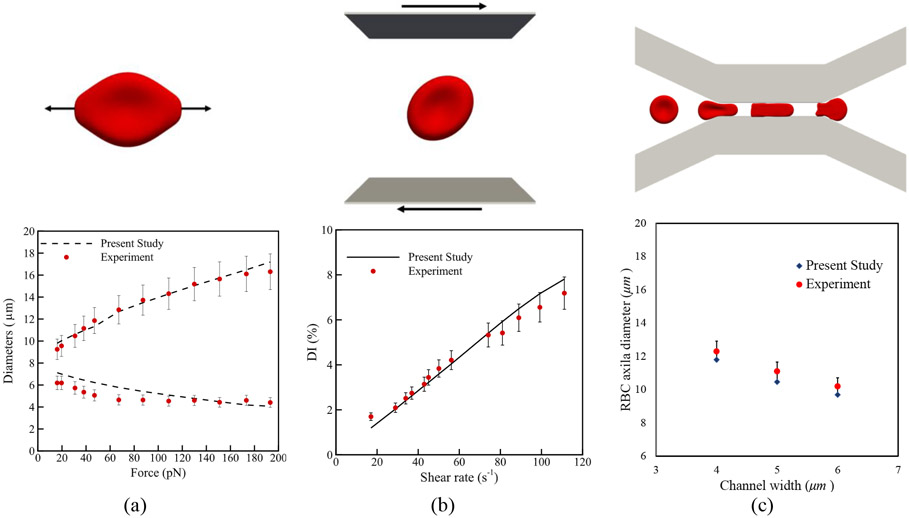
Three standard test cases are solved to validate the computational algorithm, and the results are compared with corresponding experiments. The computational models for these problems are shown in Figure 2. In the first test case (Figure 2 (a)), according to the optical-tweezers experiment [50], two opposite forces are applied on each side of the erythrocyte membrane. The stable values for axial and transversal diameters of the cell are calculated and compared with experimental data reported in [50]. As the second test problem (Figure 2 (b)), the RBC deformation index, i.e. , in which and are the initial diameter of the RBC (8 μm) maximum diameter due to different shear rates, is compared with a similar experiment performed in [51]. In the third problem, the RBC deformation during squeezing through a slit with 2.7 μm high, 30 μm long, and 4-6 μm wide is measured (Figure 2 (c)). The RBC axial diameter at the channel center for three different slit widths is compared with experimental observations in [52]. In all the test cases, a good agreement is observed between numerical and experimental results. More details about mentioned test cases can be found in our previous studies [41], [46], [53], [54].
Figure 2:
Validation test cases: (a) optical-tweezers experiment [50] (b) shear flow experiment [51] (c) RBC squeezing experiment [52]
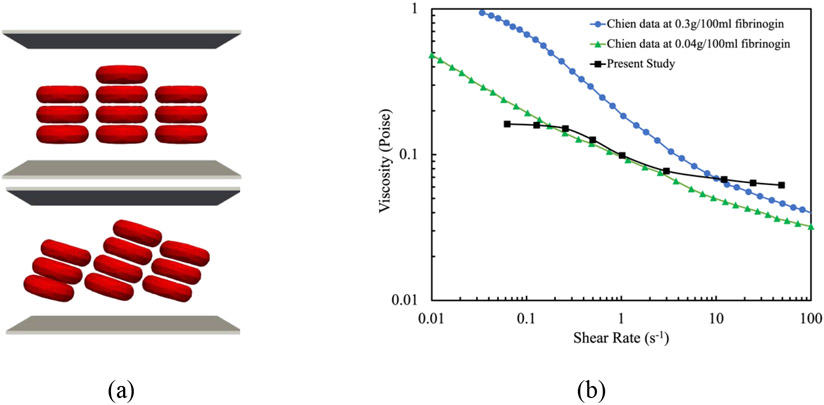
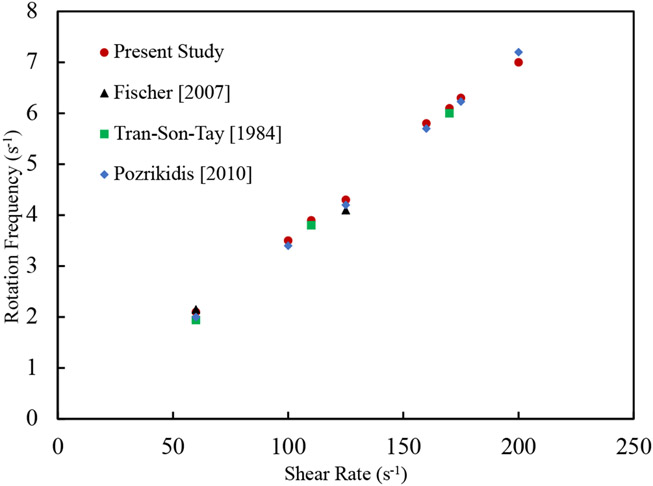
Since behavioral patterns of both single RBC and RBC suspensions in a shear flow dictates the NP detachment, the proposed numerical algorithm is validated for two other test cases. Generally, an RBC under a shear flow (Figure 2 (b)) elongates and adjust itself at a specific angle with respect to the flow direction. Depending on the shear rates, the RBC may exhibit tumbling motion, tank-treading motion or both [53], [55]. Experimental observations also reports the tumbling and tank-treading frequency [56], [57]. The rotation speed during the tumbling and tank-treading depends on the shear rate. Such a dependency has been measured in the context of RBC tank- treading frequency and corresponding data can be found in [56]-[58] just a few to name. In this test case, during the simulation shown in (Figure 2 (b)), the coordinates of RBC mesh points are stored for different shear rates ranging from 0 s−1 to 200 s−1 and the rotation frequency is calculated. As Figure 5 shows, good agreement is observed between numerical results and experimental data from [56]-[58]. Finally, in the last test case, to prove the capability of the model in capturing the physical interaction between RBCs and cell aggregation on hemorheology, we simulate 10 RBCs under different share rates (Figure 4 (a)). It should be mentioned that the number of RBCs and domain size are selected to achieve a RBC concentration close to the hematocrit of human blood i.e. 33%. In this test case the blood effective viscosity can be calculated by in which is the applied velocity on the lower and upper domain boundaries, L is the domain width, H is the half of domain height, and F is the shear force per unit width experienced by the walls. As Figure 4 (b) illustrates, computed effective viscosity agrees with the experimental results by Chien et al [59]. More details about this test case can be found in our previous study [43].
Figure 5:
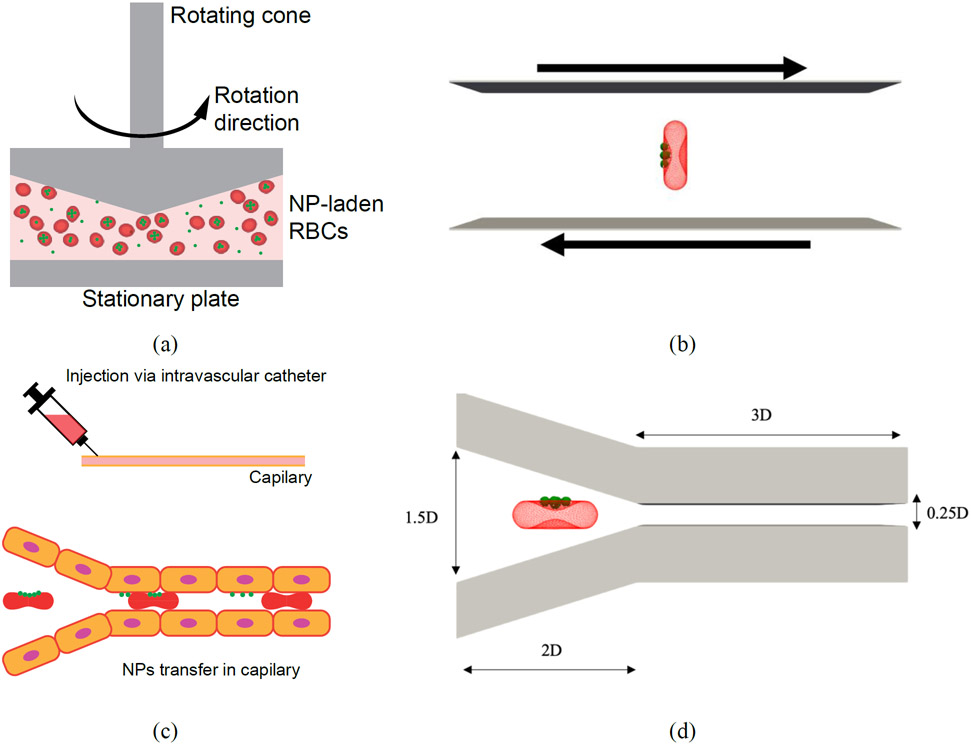
(a) schematic of NP-coated RBCs in a rheometer (b) computational model for an NP-coated RBC under shear flow(c) schematic of particle detachment from RBCs in small capillaries in lung microvasculature (d) computational model for an NP-coated RBC flowing through a biomimetic microchannel
Figure 4:
Comparison between effective viscosities of blood at different shear rates obtained from numerical and experimental studies: (a) computational model (b) viscosity versus shear rate
4. Results and Discussion
The NP detachment mechanism from engineered RBCs has been analyzed in in-vitro and in-vivo experiments. In in-vitro experiments, a plate and plate rheometer is utilized to apply various shear rates ranging from 1 Pa to 10 Pa on NP-laden RBCs [12], [13] (Figure 5 (a)). The number of NPs adhered to the RBCs before and after 30 mins of shear is specified by flow cytometry. In in-vivo experiments, intravascular injection of RBC-hitchhiking causes NPs to be transferred to the microvascular network downstream of the injection due to the close contact with endothelium (Figure 5 (c)) [4], [7]. The in-vitro setup can generate pure shear flow to study the contribution of shear force on the RBC deformation, RBC-RBC collision, and NP detachment process. However, the flow and stress condition under in-vivo setup is much more complex, which involves coupled factors from shear flow near wall, contact adhesion between NP and wall, and deformation of RBC. Here, we justify the experimental observations for both in-vitro and in-vivo studies using numerical modeling. For modeling the rheometer test, an RBC coated with 5 NPs on one side under shear is simulated as shown in Figure 5 (b). However recent studies demonstrate that the NPs number on the erythrocyte can reach up to 50, for the sake of simplicity and consistency with the experimental data in [12], [13], we consider only 5 NPs on the RBC surface (Figure 1 (c)). In the shear test, the computational box is a cuboid with height, width, and depth of , and , respectively. is the diameter of the RBC. In the microfluidic channel, the RBC transports 5 NPs on one side too (Figure 5 (d)). The dimensions of the microchannel are shown in Figure 5 (d). Channel depth is equal to 1.5D. We assume that the channel walls can mimic the behavior of endothelium. In references [12] and [13], RBC-hitchhiking has been used for large NPs between 200-1200 nm. For this range of NPs, surface modification is not effective, and the NPs are cleared from circulation very fast. In this case, NPs are anchored to the RBC membrane to increase circulation time. For the sake of consistency with experimental data in [12] and [13], we selected this range of diameters for the NPs. In both problems, to ensure our results are independent of computational mesh resolution, simulations were done for 500, 1000, 1500, 2000, and 3000 vertex points on the RBC membrane. For having the same friction coefficients for RBCs and NPs, the NPs nodal points were obtained considering the same for NPs and RBCs (Eq. (21)). The Lattice points resolution was also set such that the average edge length in NPs approximately equal to the spatial discretization step in the computational domain [60]. The results showed no significant change beyond 2000 vertex points on the RBC membrane. The results for these test cases are presented in the following sub-sections.
4.1. Shear Flow
In this problem, the effect of the shear rate, NP size, and RBC-RBC collision on the NP detachment process is analyzed. The shear rate varies between 1000 s−1 to 3000 s−1 consistent with the rheometer test in [12], [13]. To examine the effect of NP size, NPs with 1000 nm and 500 nm of diameter are modeled. RBC-RBC interaction role is modeled by simulating three RBCs located next together with 3 μm distance between their centers. All the simulations are performed for 0.05 sec which is smaller than the time scale in the experiment because the mesoscale time step is small and equal to 10−7 sec. However, even in this small-time interval, the simulation can duplicate the trend of the detachment process. In all the simulation, in Morse potential at the cutoff distance is set as 700 fN, which is consistent with the average value in experimental data [45].
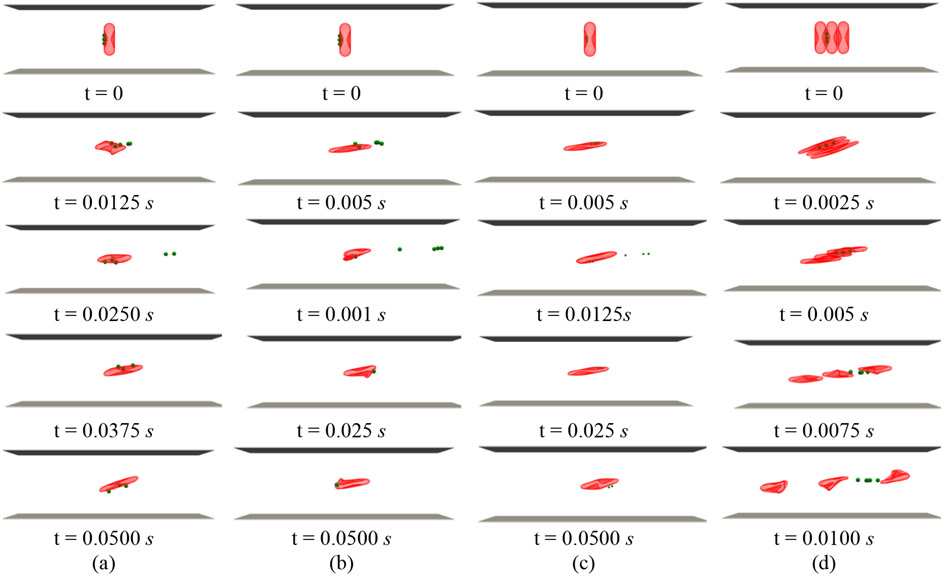
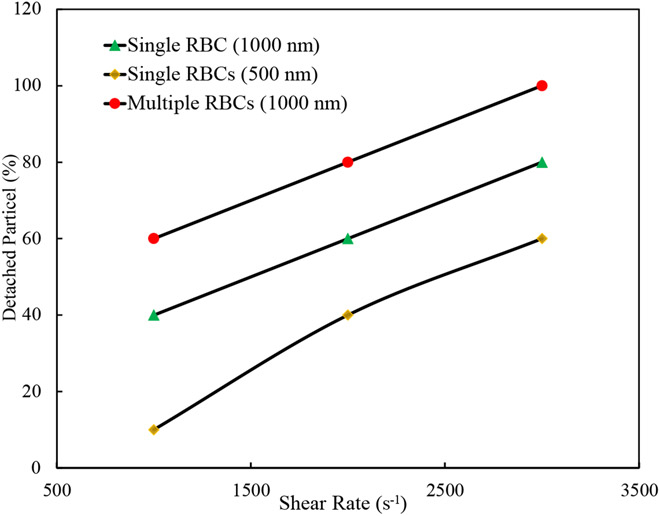
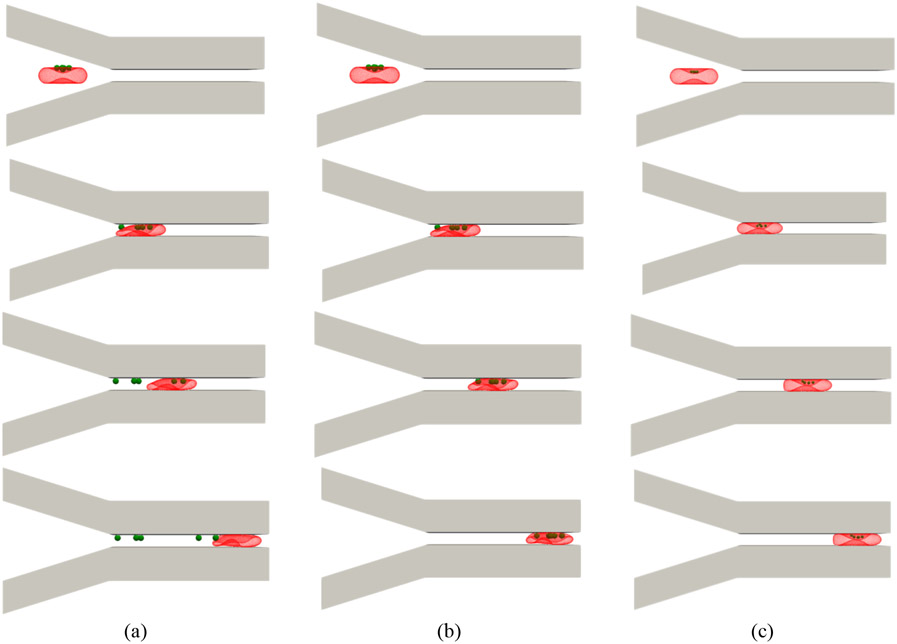
Figure 6 (a) and (b) show the snapshots of the simulation at five different time instances for 1000 nm NPs under 1000 s−1 and 3000 s−1 shear rates, respectively. As the figures show, the NP detachment percentage increases from 40% to 80% by three times increase in the shear rate due to larger fluid drag force on the NPs. It should be noticed that after detachment and when NPs are far enough from the RBC, they are removed from the computational box. Detachment of 500 nm NPs from RBC under 3000 s−1 is displayed in Figure 6 (c). As it can be observed, since the smaller NPs experience less drag force with respect to larger NPs, only three numbers of NPs equal to 60% are decoupled. It is worth mentioning that the same behavior is observed for NPs with other diameters, however, to better illustrate the diameter effect, only the results for 1000 nm and 500 nm are shown in this section. As Figure 6 (d) illustrates, RBC-RBC interaction significantly enhances the detachment process. In this case, all NPs are detached in a shorter time. The NP detachment percentage with respect to shear rate for different NPs with and without RBC-RBC interaction is plotted in Figure 7. As the plot shows and consistent with Figure 6, increased shear rate, bigger NP size, and RBC-RBC interaction will lead to more significant NP detachment. These findings are in agreement with the results repotted experimentally [12], [13].
Figure 6:
RBC-hitchhiking in shear flow (a) NP size = 1000 nm, shear rate = 1000 s−1 (b) NP size = 1000 nm, shear rate = 3000 s−1 (c) NP size = 500 nm, shear rate = 3000 s−1 (d) 3 RBCs, NP size = 1000 nm, shear rate = 3000 s−1
Figure 7:
Percentage of NP detached from RBCs under shear flow for different test cases.
In [12], it has been demonstrated the circulation time of NP-coated erythrocytes depend on NP diameter. Among NPs with different diameters ranging from 200-1000 nm, 450 nm particles had the longest circulation times. The time required for clearance of 450 nm NPs was more than 7 hours. However, NPs larger than 450 nm was cleared from circulation very fast [12]. It should be mentioned while all the NPs are eventually removed form circulation, the RBCs circulation time was not affected [12]. Therefore, NPs shorter circulation time can be considered as an indicator for faster and easier NPs dislodgment from RBCs membranes. In this sense, numerical and experimental results agree. For the effect of shear rate on the NPs disassociation, Chambers and Mitragotri [13] experimentally and via rheometer showed that NP detachment doubles by increasing the shear stress from 1 Pa-10 Pa. They also confirmed that increasing blood hematocrit from 10% to 50% enhances the NP detachment from nearly 30% to 70%. Increasing hematocrit can be related to increasing RBC-RBC collision. Numerical results also demonstrate that RBC-RBC interaction significantly increases NPs detachment. However numerical results qualitatively have the same trend as experimental observations, quantitative comparison is prohibited by the limited computational domain, number of RBCs and NPs used in the simulation, simulation time as well as other complex biochemical factors in real blood that is not included in our computational model. The mentioned issues will be investigated in our future works. To the best of our knowledge, the current research is the first paper which utilizes direct numerical modeling to link the effects of shear rate, NP size and RBC-RBC interaction to the NP detachment from NP-bounded RBCs. It should be noted that however experimental studies have shown the effects of the mentioned factors, they have not provided clear justification for their observations. Also, visualizing the effect of the pertinent parameter at cellular level is complex in the experiment.
4.2. NP Detachment in Capillary Vessel
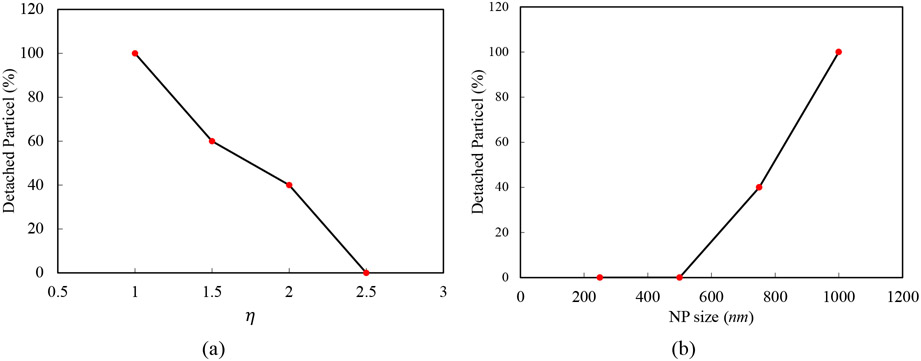
Upon injection of NP-coated RBCs in upstream of the target tissue microvasculature, NPs desorption occurs because of shear and direct contact of NP-endothelium [4]. In this test case, we assume that the channel walls can mimic the behavior of endothelium in a capillary. We do not investigate the effect of the channel geometry on the NP detachment. The RBC average velocity in the narrow part remains constant at 0.5 mm/s, which is in the range of RBC velocity in human capillaries [61]. NP size, NP-RBC adhesion and NP-wall adhesion are important parameters in this section. The adhesion force between NPs, erythrocyte and endothelium can be calibrated using lectins, peptides, antibodies, or covalent binding [12], [13]. As it was mentioned earlier, the interaction force between different NPs and live cells was reported to be in the range of 20-1200 pN [44]. Since we have thousands of interactive pairs on RBC and NPs, the force magnitude should be estimated in the order of femtonewtons [45]. Here, for modeling the effect of NP-RBC and NP-wall adhesion, we assume that NP-wall force at the cutoff distance is 450 fN [44], and change the NP-RBC adhesion strength such that in which is the Morse energy well depth. In this way, all possible scenarios can be covered. In Figure 8 (a), the attractive Morse potential between 1000 nm NPs and wall is set to be equal to that between RBC and NPs, i.e. . As it can be observed, as the RBC proceeds inside the channel, all the NPs are separated from the RBC membrane and attached to the capillary wall. In this case, the prolonged contact between NPs and wall finally removes all the NPs. Therefore, all the NPs are delivered to capillary wall. Simulation snapshots for 1000 nm NPs at are illustrated in Figure 8 (b). As the figures show, by strengthening the NP-RBC interaction force, none of NPs can be delivered to the capillary wall. To show the effect of NP size on the detachment process, the simulation of a RBC coupled with NPs with 500 nm as the diameter and are shown in Figure 8 (c). As it can be observed, since there is no contact between wall and NPs, detachment is not observed. It is worth mentioning that the same behavior is observed for NPs with other diameters, however, to better illustrate the diameter effect, only the results for 1000 nm and 500 nm are shown in this section.
Figure 8:
Simulations snapshots for an NP-laden RBC in a microchannel (a) NP size = 1000 nm and normal RBC-NP interaction (b) NP size = 1000 nm and strong RBC-NP interaction (c) NP size = 500 nm and normal RBC-NP interaction
Detached NP percentage for different and NP sizes are displayed in Figure 9 (a) and Figure 9 (b) respectively. As the graphs indicate, increasing the NP size facilitates the detachment process, while fortifying NP-RBC interaction leads to detachment reduction. As we expressed in previous sub-section, experimental studies also demonstrate that larger NPs can detach more easily [12], [13], but they do not provide physical and clear justifications for this observation. In accordance with the numerical simulation, larger NPs have larger contact area with the tissue microvasculature which leads to the easier detachment. The experimental data indicate that NPs surface chemistry can change the NP uptake in the target organ [7]. For example, among RBCs coated with nanogel, polystyrene NPs (PS-NPs), albumin-NPs (alb-NPs), poly (lactic-co-glycolic acid), nanogel-coated RBCs have higher uptake in lung microvasculature. Based on the numerical simulations, this type of observations can be linked to the adhesion force between RBC, endothelium and NPs.
Figure 9:
(a) detached NP percentage versus the , (b) detached NP percentage versus NP diameter
5. Conclusion
A numerical algorithm was suggested to simulate the NPs detachment from RBCs-hitchhiking under shear flow and flowing through microfluidic channels. LBM, SN, and IBM were the three main components of the proposed algorithm. The method performance was validated by simulating the deformation of an RBC under uniaxial stretch, RBCs under shear flow, and an RBC squeezing through a constricted microchannel. To interpret the results obtained from in-vitro and in-vivo experiments on RBC-hitchhiking, a parametric study was conducted. The effect of the shear rate, NP size, interaction strength between NP-RBC and RBC-RBC interaction on the detachment process were analyzed. The results showed that NPs decoupling was enhanced by increased shear rate and NPs sizes. Changing the adhesion strength could also control the detachment process. Finally, RBC-RBC contact led to detachment enhancement. The mentioned findings agree with experimental observations. This is the first attempt to utilize a numerical approach to study the drug delivery via cellular hitchhiking onto the erythrocyte membranes. Yet, the model is simple because we did not include the adhesion effect of RBCs and NPs on their mechanical properties. To have a predictive tool, the RBC-RBC, NP-NP, RBC-NP, NP-vessel, and RBC-vessel should be quantified experimentally, and the obtained data should be used to calibrate different potentials more accurately in the numerical approach. Some other parameters such as RBC orientation, NPs configuration, NPs shape, and vascular geometry will be analyzed in the future considering more compressive experimental data. The complete model can be used to predict the drug delivery via NP-carrying RBCs in complex vascular networks. The model can provide guideline for RH-based drug delivery systems. Also, the model can propose new approaches to attach NPs to the erythrocyte surface to have a specific strength between RBC and NPs to optimize and engineer this type of drug delivery.
Figure 3:
Comparison between RBC rotation frequency in a shear flow obtained from numerical and experimental studies
Acknowledgment
This work was supported by the National Institutes of Health grant R01HL131750, R01HL143806 and National Science Foundation grant CBET 2039310. We would also like to thank Dr. Iveta Jancigova from the cell-in-fluid biomedical modeling and computation group at the University of Zilina, Zilina, Slovakia, for her constructive comments on ESPResSo and PyOIF.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- [1].Awasthi R, Roseblade A, Hansbro PM, Rathbone MJ, Dua K, and Bebawy M, “Nanoparticles in Cancer Treatment: Opportunities and Obstacles,” Curr. Drug Targets, vol. 19, no. 14, pp. 1696–1709, 2018. [DOI] [PubMed] [Google Scholar]
- [2].Mitchell MJ, Billingsley MM, Haley RM, Wechsler ME, Peppas NA, and Langer R, “Engineering precision nanoparticles for drug delivery,” Nature Reviews Drug Discovery. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Luo YY, Xiong XY, Tian Y, Li ZL, Gong YC, and Li YP, “A review of biodegradable polymeric systems for oral insulin delivery,” Drug Delivery, vol. 23, no. 6. pp. 1882–1891, 2016. [DOI] [PubMed] [Google Scholar]
- [4].Anselmo AC et al. , “Delivering nanoparticles to lungs while avoiding liver and spleen through adsorption on red blood cells,” ACS Nano, vol. 7, no. 12, pp. 11129–11137, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Villa CH, Pan DC, Zaitsev S, Cines DB, Siegel DL, and Muzykantov VR, “Delivery of drugs bound to erythrocytes: New avenues for an old intravascular carrier,” Therapeutic Delivery, vol. 6, no. 7. pp. 795–826, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Gustafson HH, Holt-Casper D, Grainger DW, and Ghandehari H, “Nanoparticle uptake: The phagocyte problem,” Nano Today, vol. 10, no. 4. pp. 487–510, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Brenner JS et al. , “Red blood cell-hitchhiking boosts delivery of nanocarriers to chosen organs by orders of magnitude,” Nat. Commun, vol. 9, no. 1, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Farrell CL and Pardridge WM, “Blood-brain barrier glucose transporter is asymmetrically distributed on brain capillary endothelial lumenal and ablumenal membranes: An electron microscopic immunogold study,” Proc. Natl. Acad. Sci. U. S. A, vol. 88, no. 13, pp. 5779–5783, 1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Yang H et al. , “Glutl deficiency syndrome and erythrocyte glucose uptake assay,” Ann. Neurol, vol. 70, no. 6, pp. 996–1005, 2011. [DOI] [PubMed] [Google Scholar]
- [10].Perry JL et al. , “PEGylated PRINT nanoparticles: The impact of PEG density on protein binding, macrophage association, biodistribution, and pharmacokinetics,” Nano Lett., vol. 12, no. 10, pp. 5304–5310, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Ishida T et al. , “Injection of PEGylated liposomes in rats elicits PEG-specific IgM, which is responsible for rapid elimination of a second dose of PEGylated liposomes,” J. Control. Release, vol. 112, no. 1, pp. 15–25, 2006. [DOI] [PubMed] [Google Scholar]
- [12].Chambers E and Mitragotri S, “Prolonged circulation of large polymeric nanoparticles by non-covalent adsorption on erythrocytes,” J. Control. Release, vol. 100, no. 1, pp. 111–119, 2004. [DOI] [PubMed] [Google Scholar]
- [13].Chambers E and Mitragotri S, “Long circulating nanoparticles via adhesion on red blood cells: Mechanism and extended circulation,” Exp. Biol. Med, vol. 232, no. 7, pp. 958–966, 2007. [PubMed] [Google Scholar]
- [14].Han X, Wang C, and Liu Z, “Red Blood Cells as Smart Delivery Systems,” Bioconjug. Chem, vol. 29, no. 4, pp. 852–860, 2018. [DOI] [PubMed] [Google Scholar]
- [15].Muzykantov VR, “Drug delivery by red blood cells: Vascular carriers designed by mother nature,” Expert Opinion on Drug Delivery, vol. 7, no. 4. pp. 403–427, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Pan DC et al. , “Nanoparticle Properties Modulate Their Attachment and Effect on Carrier Red Blood Cells,” Sci. Rep, vol. 8, no. 1, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Dias A, Werner M, Ward KR, Fleury JB, and Baulin VA, “High-throughput 3D visualization of nanoparticles attached to the surface of red blood cells,” Nanoscale, vol. 11, no. 5, pp. 2282–2288, 2019. [DOI] [PubMed] [Google Scholar]
- [18].Zhao Z et al. , “Systemic tumour suppression via the preferential accumulation of erythrocyte-anchored chemokine-encapsulating nanoparticles in lung metastases,” Nat. Biomed. Eng, 2020. [DOI] [PubMed] [Google Scholar]
- [19].Villa CH, Anselmo AC, Mitragotri S, and Muzykantov V, “Red blood cells: Supercarriers for drugs, biologicals, and nanoparticles and inspiration for advanced delivery systems,” Advanced Drug Delivery Reviews, vol. 106. pp. 88–103, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Villa CH, Cines DB, Siegel DL, and Muzykantov V, “Erythrocytes as Carriers for Drug Delivery in Blood Transfusion and Beyond,” Transfusion Medicine Reviews, vol. 31, no. 1. pp. 26–35, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Tan J, Thomas A, and Liu Y, “Influence of red blood cells on nanoparticle targeted delivery in microcirculation,” Soft Matter, vol. 8, no. 6, pp. 1934–1946, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Tan J, Sinno TR, and Diamond SL, “A parallel fluid–solid coupling model using LAMMPS and Palabos based on the immersed boundary method,” J. Comput. Sci, vol. 25, pp. 89–100, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Müller K, Fedosov DA, and Gompper G, “Margination of micro- and nano-particles in blood flow and its effect on drug delivery,” Sci. Rep, vol. 4, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Vahidkhah K and Bagchi P, “Microparticle shape effects on margination, near-wall dynamics and adhesion in a three-dimensional simulation of red blood cell suspension,” Soft Matter, vol. 11, no. 11, pp. 2097–2109, 2015. [DOI] [PubMed] [Google Scholar]
- [25].Müller K, Fedosov DA, and Gompper G, “Understanding particle margination in blood flow - A step toward optimized drug delivery systems,” Med. Eng. Phys, vol. 38, no. 1, pp. 2–10, 2016. [DOI] [PubMed] [Google Scholar]
- [26].Cooley M, Sarode A, Hoore M, Fedosov DA, Mitragotri S, and Sen Gupta A, “Influence of particle size and shape on their margination and wall-adhesion: implications in drug delivery vehicle design across nano-to-micro scale,” Nanoscale, vol. 10, no. 32, pp. 15350–15364, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ye H, Shen Z, and Li Y, “Computational modeling of magnetic particle margination within blood flow through LAMMPS,” Comput. Mech, vol. 62, no. 3, pp. 457–476, 2018. [Google Scholar]
- [28].Ye H, Shen Z, Yu L, Wei M, and Li Y, “Manipulating nanoparticle transport within blood flow through external forces: An exemplar of mechanics in nanomedicine,” in Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2018, vol. 474, no. 2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Ye H, Shen Z, and Li Y, “Shear rate dependent margination of sphere-like, oblate-like and prolate-like micro-particles within blood flow,” Soft Matter, vol. 14, no. 36, pp. 7401–7419, 2018. [DOI] [PubMed] [Google Scholar]
- [30].Ye H, Shen Z, Yu L, Wei M, and Li Y, “Anomalous Vascular Dynamics of Nanoworms within Blood Flow,” ACS Biomater. Sci. Eng, vol. 4, no. 1, pp. 66–77, 2018. [DOI] [PubMed] [Google Scholar]
- [31].Ye H, Shen Z, and Li Y, “Interplay of deformability and adhesion on localization of elastic micro-particles in blood flow,” J. Fluid Mech, vol. 861, pp. 55–87, 2019. [Google Scholar]
- [32].Ye H, Shen Z, Wei M, and Li Y, “Red blood cell hitchhiking enhances the accumulation of nano- And micro-particles in the constriction of a stenosed microvessel,” Soft Matter, vol. 17, no. 1, pp. 40–56, 2021. [DOI] [PubMed] [Google Scholar]
- [33].Liu Z, Clausen JR, Rekha RR, and Aidun CK, “A unified analysis of nano-to-microscale particle dispersion in tubular blood flow,” Phys. Fluids, vol. 31, no. 8, 2019. [Google Scholar]
- [34].Liu ZL et al. , “Heterogeneous partition of cellular blood-borne nanoparticles through microvascular bifurcations,” Phys. Rev. E, vol. 102, no. 1, 2020. [DOI] [PubMed] [Google Scholar]
- [35].Weik F et al. , “ESPResSo 4.0 – an extensible software package for simulating soft matter systems,” Eur. Phys. J. Spec. Top, vol. 227, no. 14, pp. 1789–1816, 2019. [Google Scholar]
- [36].Cimrák I, Gusenbauer M, and Schrefl T, “Modelling and simulation of processes in microfluidic devices for biomedical applications,” Comput. Math. with Appl, vol. 64, no. 3, pp. 278–288, 2012. [Google Scholar]
- [37].Cimrák I, Gusenbauer M, and Jančigová I, “An ESPResSo implementation of elastic objects immersed in a fluid,” Comput. Phys. Commun, vol. 185, no. 3, pp. 900–907, 2014. [Google Scholar]
- [38].Jančigová I, Kovalčíková K, Weeber R, and Cimrák I, “PyOIF: Computational tool for modelling of multi-cell flows in complex geometries,” PLoS Comput. Biol, vol. 16, no. 10, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Kushchenko YK and Belyaev AV, “Effects of hydrophobicity, tethering and size on flow-induced activation of von Willebrand factor multimers,” J. Theor. Biol, vol. 485, 2020. [DOI] [PubMed] [Google Scholar]
- [40].Ahlrichs P and Dünweg B, “Simulation of a single polymer chain in solution by combining lattice Boltzmann and molecular dynamics,” J. Chem. Phys, vol. 111, no. 17, pp. 8225–8239, 1999. [Google Scholar]
- [41].Nikfar M, Razizadeh M, Paul R, and Liu Y, “Multiscale modeling of hemolysis during microfiltration,” Microfluid. Nanofluidics, vol. 24, no. 5, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Tan J, Keller W, Sohrabi S, Yang J, and Liu Y, “Characterization of nanoparticle dispersion in red blood cell suspension by the lattice boltzmann-immersed boundary method,” Nanomaterials, vol. 6, no. 2, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Liu Y and Liu WK, “Rheology of red blood cell aggregation by computer simulation,” J. Comput. Phys, vol. 220, no. 1, pp. 139–154, 2006. [Google Scholar]
- [44].Vasir JK and Labhasetwar V, “Quantification of the force of nanoparticle-cell membrane interactions and its influence on intracellular trafficking of nanoparticles,” Biomaterials, vol. 29, no. 31, pp. 4244–4252, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Tan J, Ding Z, Hood M, and Li W, “Simulation of circulating tumor cell transport and adhesion in cell suspensions in microfluidic devices,” Biomicrofluidics, vol. 13, no. 6, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Nikfar M, Razizadeh M, Zhang J, Paul R, Wu ZJ, and Liu Y, “Prediction of mechanical hemolysis in medical devices via a Lagrangian strain-based multiscale model,” Artif. Organs, vol. 44, no. 8, pp. E348–E368, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Cimrak I and Jancigova I, Computational Blood Cell Mechanics: Road Towards Models and Biomedical Applications. Taylor & Francis, 2018. [Google Scholar]
- [48].Cimrák I, “Effect of dissipative coupling parameter in a computational model on the inclination angle of red blood cells in a shear flow,” in ACM International Conference Proceeding Series, 2018. [Google Scholar]
- [49].Bušík M, Slavík M, and Cimrák I, “Dissipative Coupling of Fluid and Immersed Objects for Modelling of Cells in Flow,” Comput. Math. Methods Med, vol. 2018, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Mills JP, Qie L, Dao M, Lim CT, and Suresh S, “Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers.,” Mech. Chem. Biosyst, vol. 1, no. 3, pp. 169–180, 2004. [PubMed] [Google Scholar]
- [51].Yao W et al. , “Low viscosity Ektacytometry and its validation tested by flow chamber,” J. Biomech, vol. 34, no. 11, pp. 1501–1509, 2001. [DOI] [PubMed] [Google Scholar]
- [52].Quinn DJ et al. , “Combined simulation and experimental study of large deformation of red blood cells in microfluidic systems,” Ann. Biomed. Eng, vol. 39, no. 3, pp. 1041–1050, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Sohrabi S and Liu Y, “A Cellular Model of Shear-Induced Hemolysis,” Artif. Organs, vol. 41, no. 9, pp. 80–91, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Sohrabi S, Tan J, Yunus DE, He R, and Liu Y, “Label-free sorting of soft microparticles using a bioinspired synthetic cilia array,” Biomicrofluidics, vol. 12, no. 4, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Nakamura M, Bessho S, and Wada S, “Spring-network-based model of a red blood cell for simulating mesoscopic blood flow,” Int. j. numer. method. biomed. eng, vol. 29, no. 1, pp. 114–128, 2013. [DOI] [PubMed] [Google Scholar]
- [56].Fischer TM, “Tank-tread frequency of the red cell membrane: Dependence on the viscosity of the suspending medium,” Biophys. J, vol. 93, no. 7, pp. 2553–2561, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Tran-Son-Tay R, Sutera SP, and Rao PR, “Determination of red blood cell membrane viscosity from rheoscopic observations of tank-treading motion,” Biophys. J, vol. 46, no. 1, pp. 65–72, 1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Pozrikidis C, Computational Hydrodynamics of Capsules and Biological Cells. CRC Press, 2010. [Google Scholar]
- [59].Chien S, Usami S, Dellenback RJ, and Gregersen MI, “Shear-dependent interaction of plasma proteins with erythrocytes in blood rheology.,” Am. J. Physiol, vol. 219, no. 1, pp. 143–153, 1970. [DOI] [PubMed] [Google Scholar]
- [60].Krüger T, Computer simulation study of collective phenomena in dense suspensions of red blood cells under shear, vol. 9783834823. 2012. [Google Scholar]
- [61].Jeong JH, Sugii Y, Minamiyama M, and Okamoto K, “Measurement of RBC deformation and velocity in capillaries in vivo”, Microvasc. Res, vol. 71, no. 3, pp. 212–217, 2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.